Simulation of Water Level Fluctuations in a Hydraulic System Using a Coupled Liquid-Gas Model
Abstract
:1. Introduction
2. Governing Equations and Numerical Methods
2.1. 1D Water Hammer Equations
2.2. 1D Governing Equations for Gas Flow
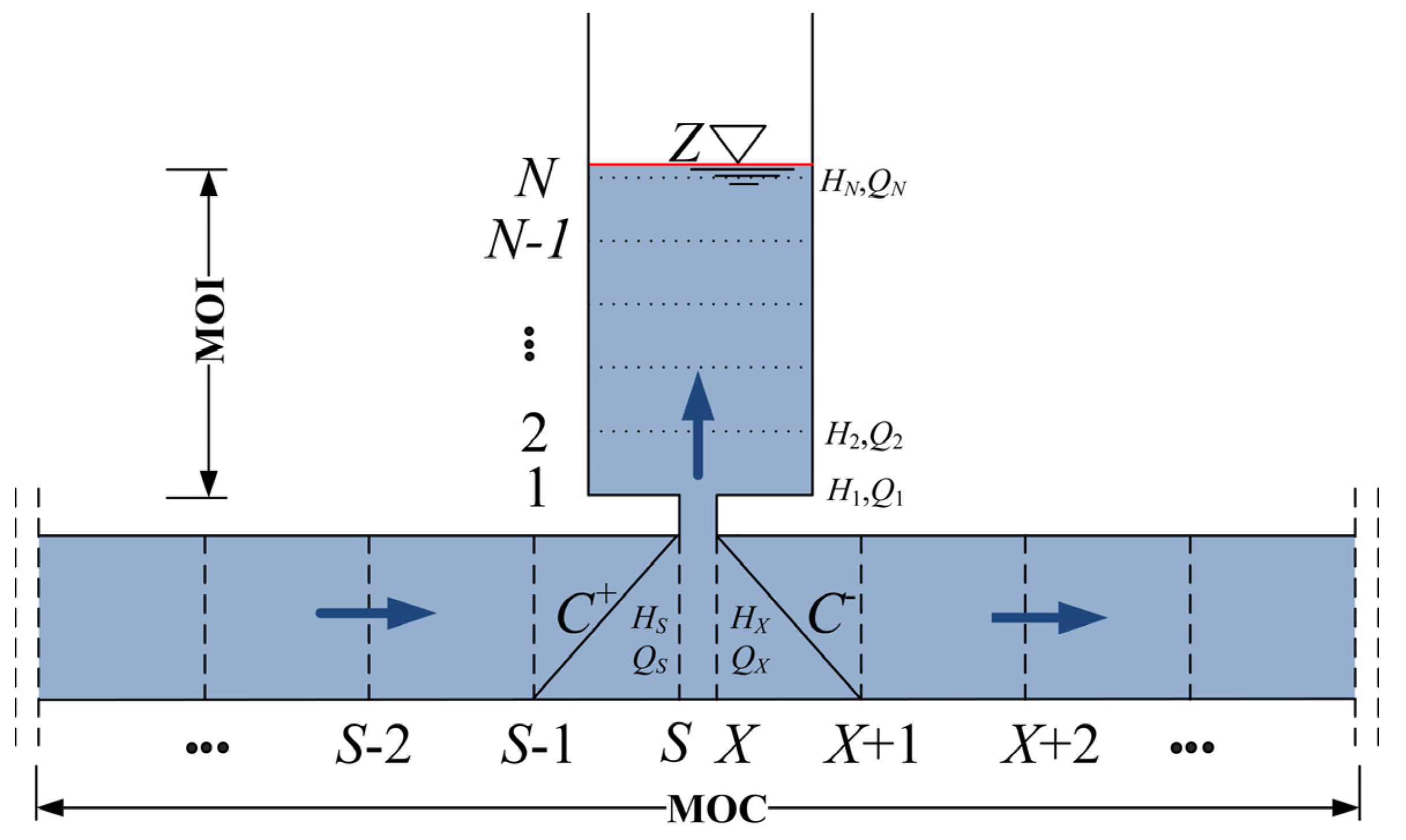
2.3. Solution of the Governing Equations
2.3.1. Finite Difference Scheme
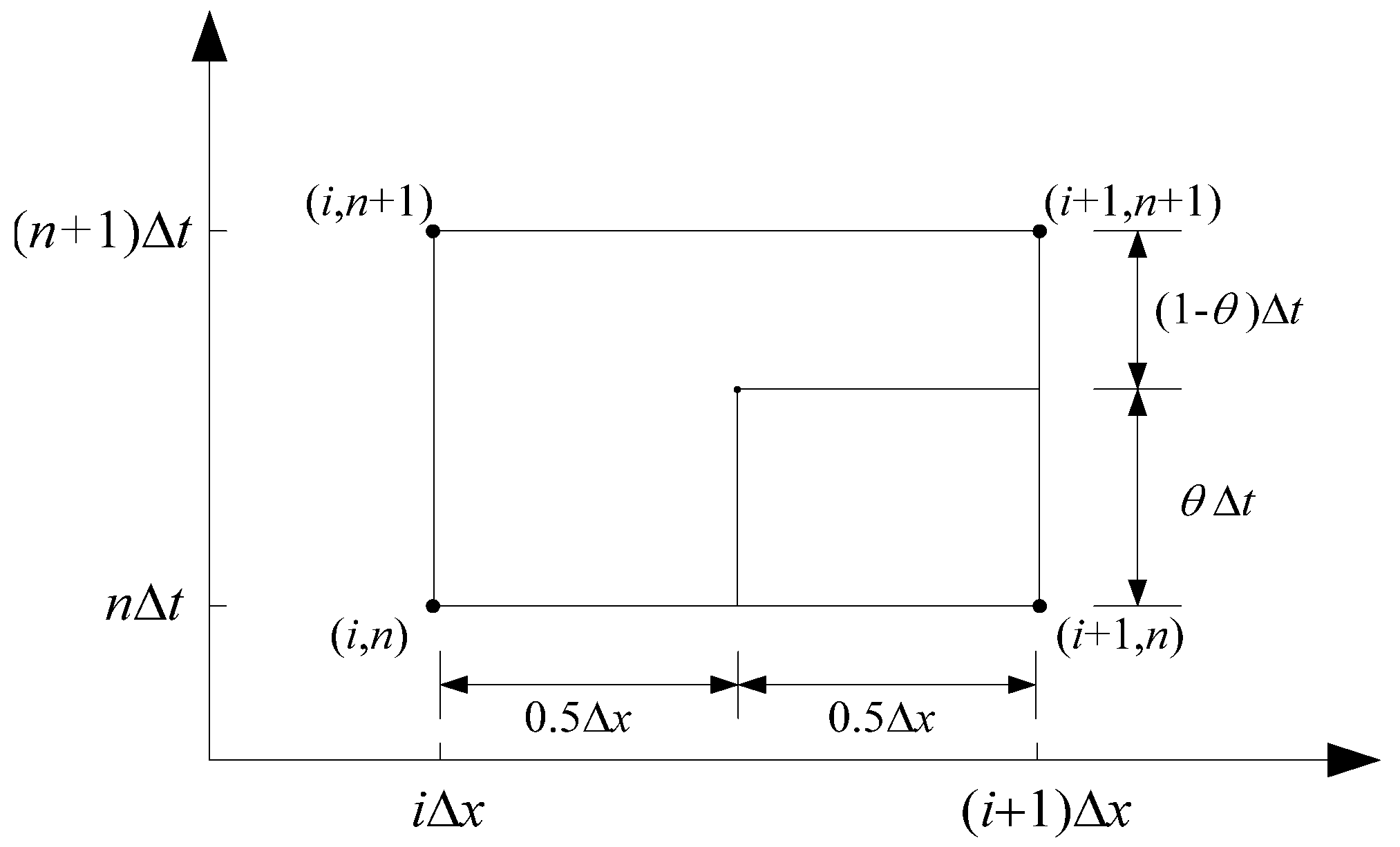
2.3.2. Solution Method
3. Verification of the Scheme
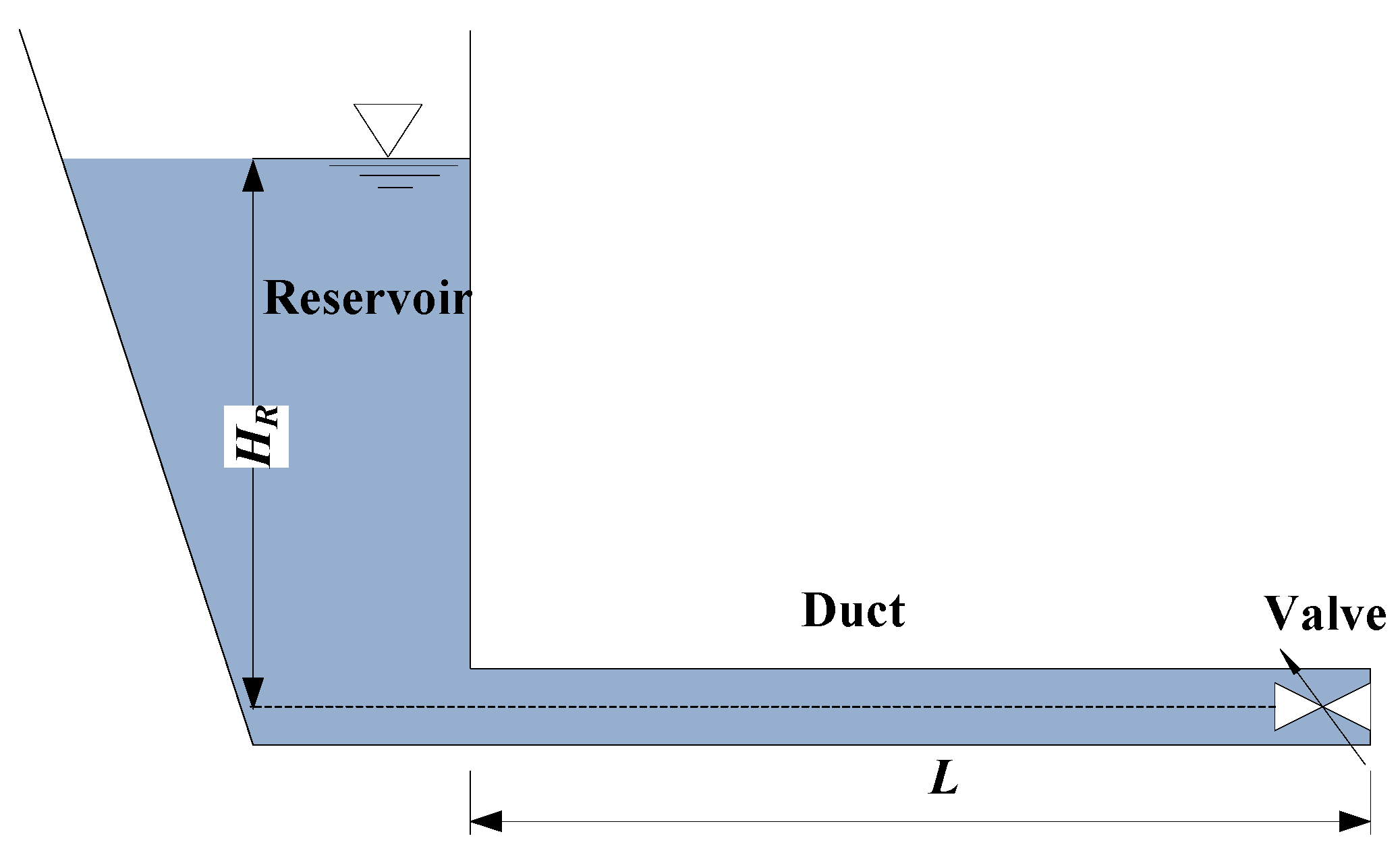
3.1. Verification of the Liquid Phase
- Case 1: Infinite reservoir with a steady head of 100 m, with the valve closed suddenly;
- Case 2: Infinite reservoir with a steady head of 100 m, with the valve closed linearly over 4 s;
- Case 3: Infinite reservoir with a steady head of 200 m, with the valve closed linearly over 4 s.

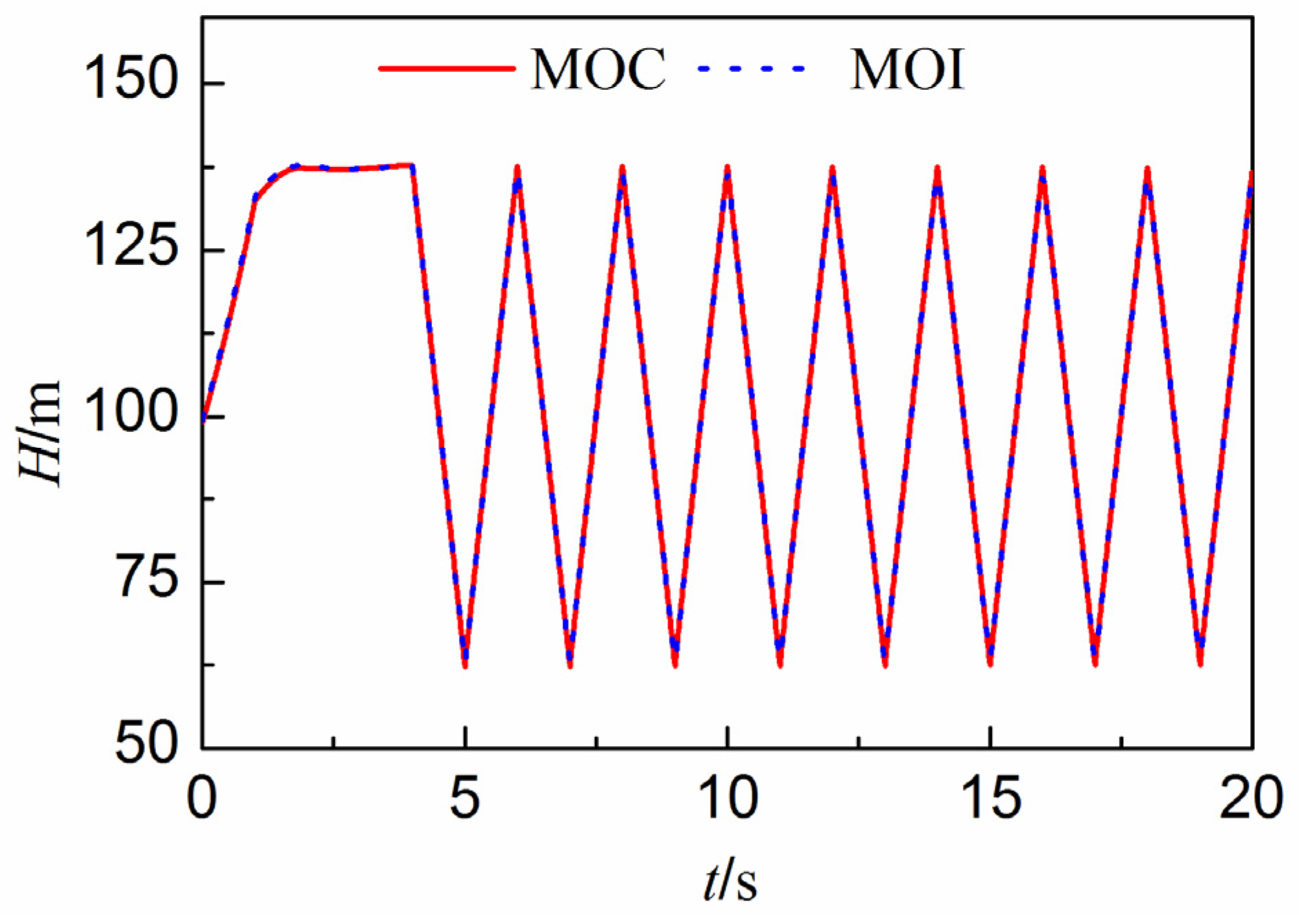
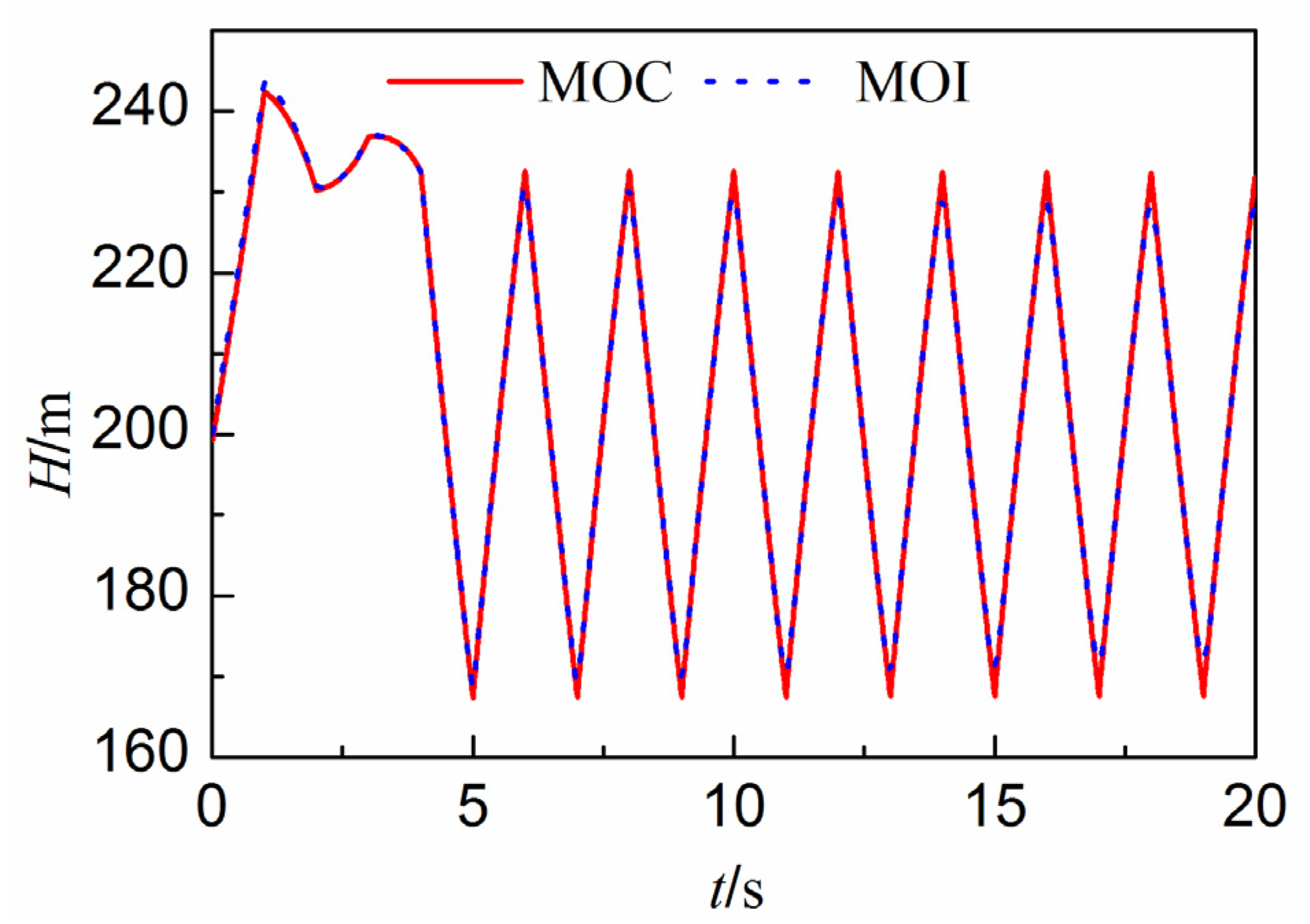
3.2. Verification of the Gas Phase
3.2.1. A Single Straight Gas Pipe
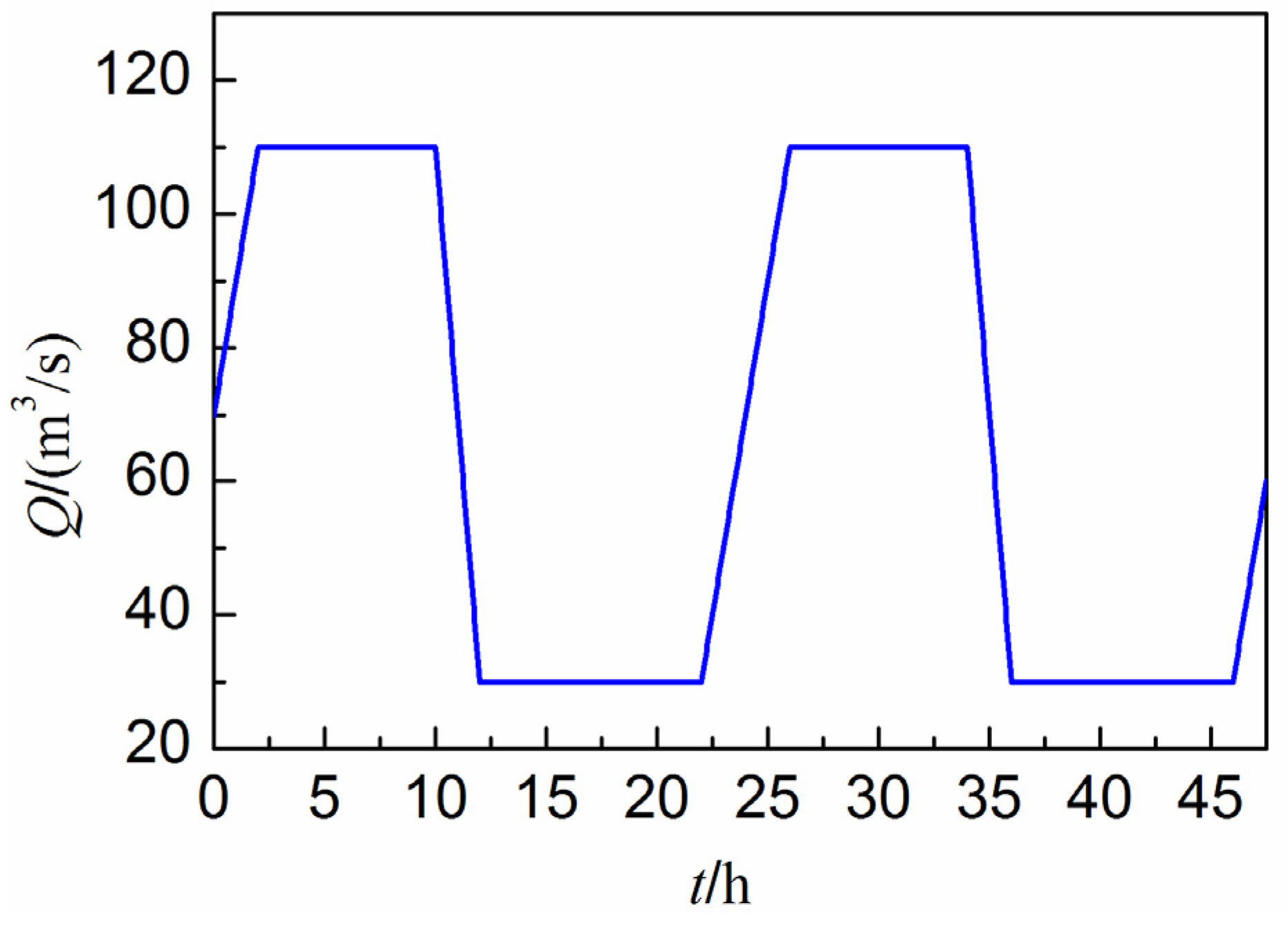
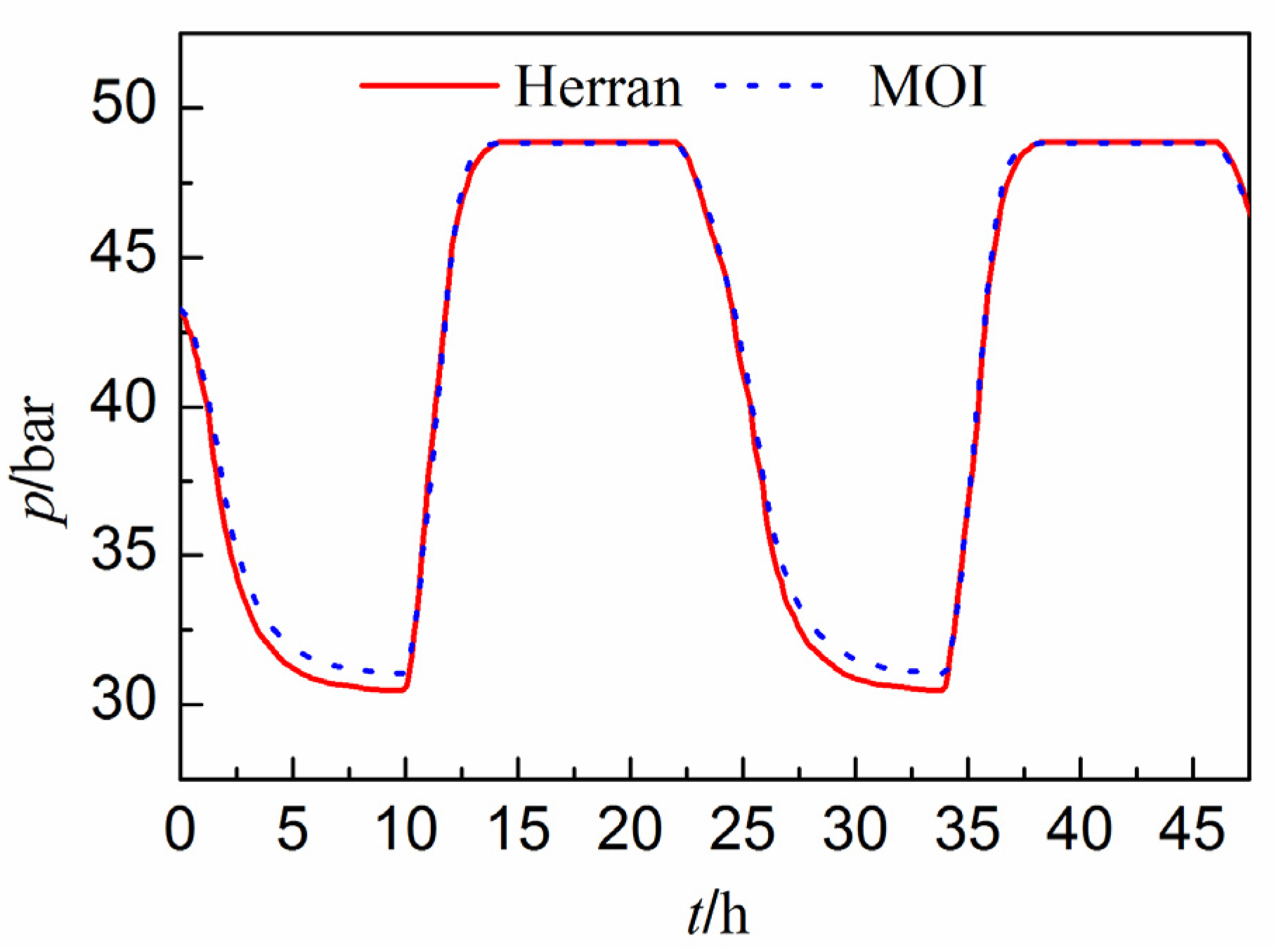
3.2.2. A Gas Pipeline Network
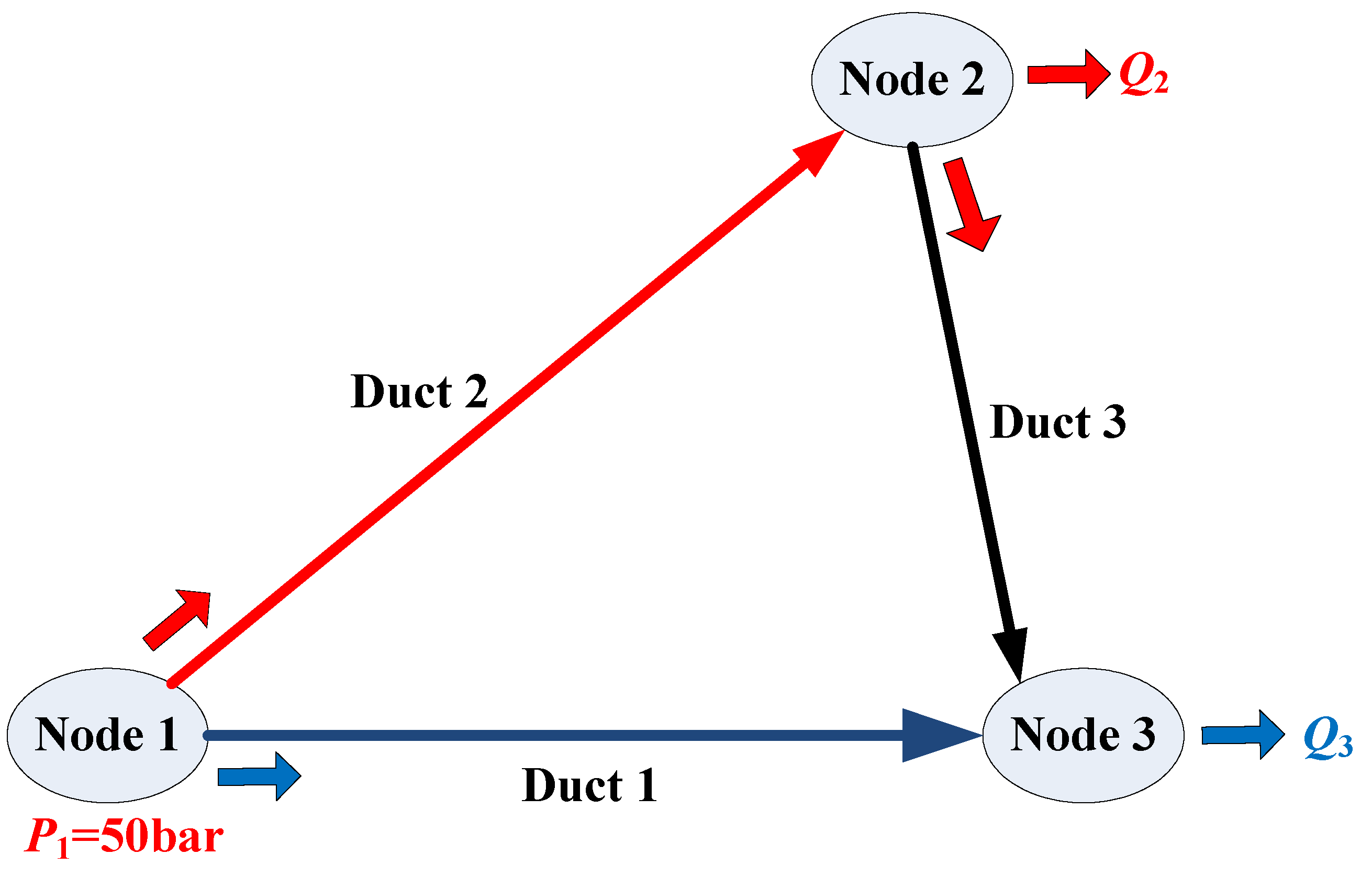
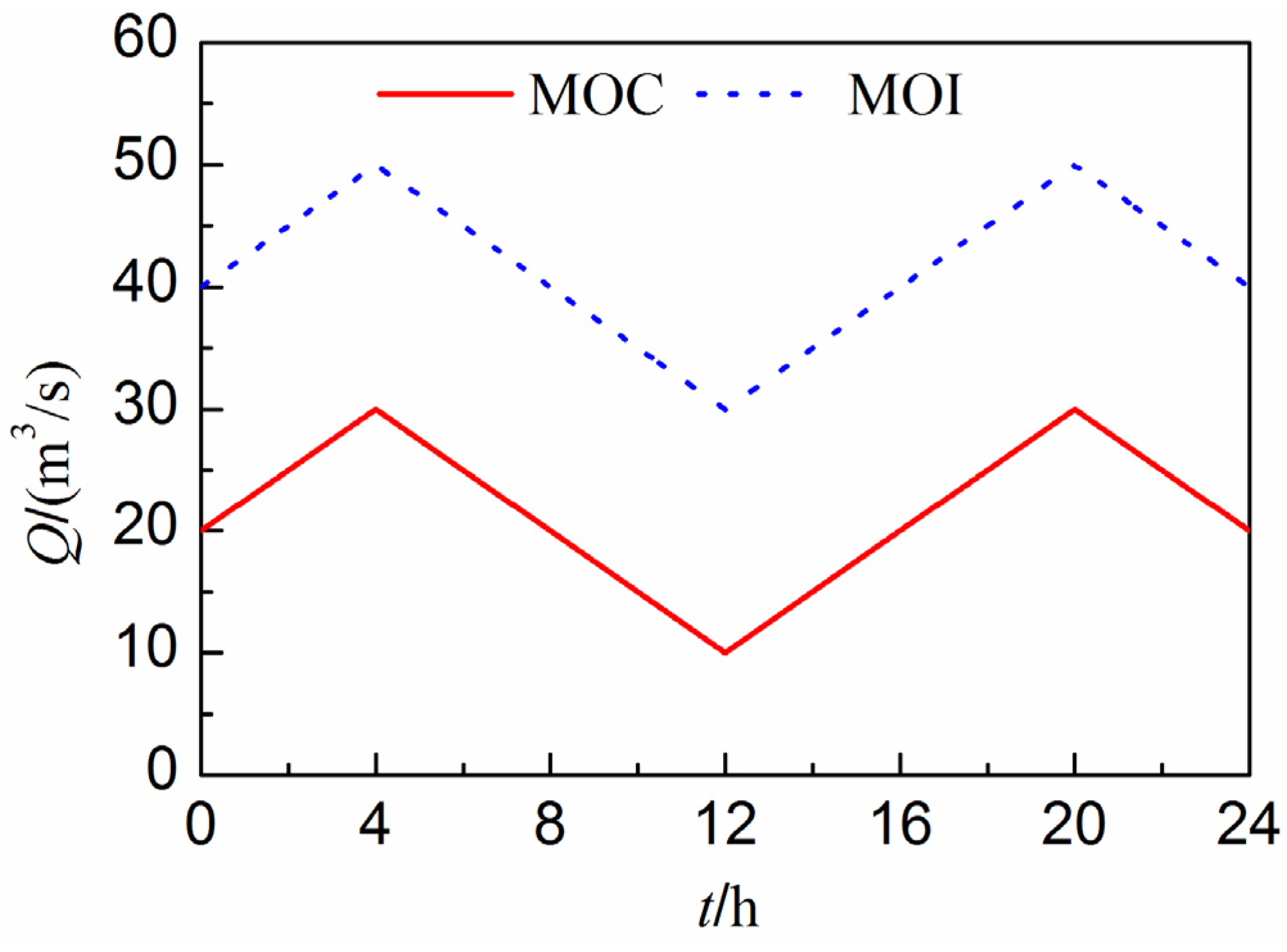
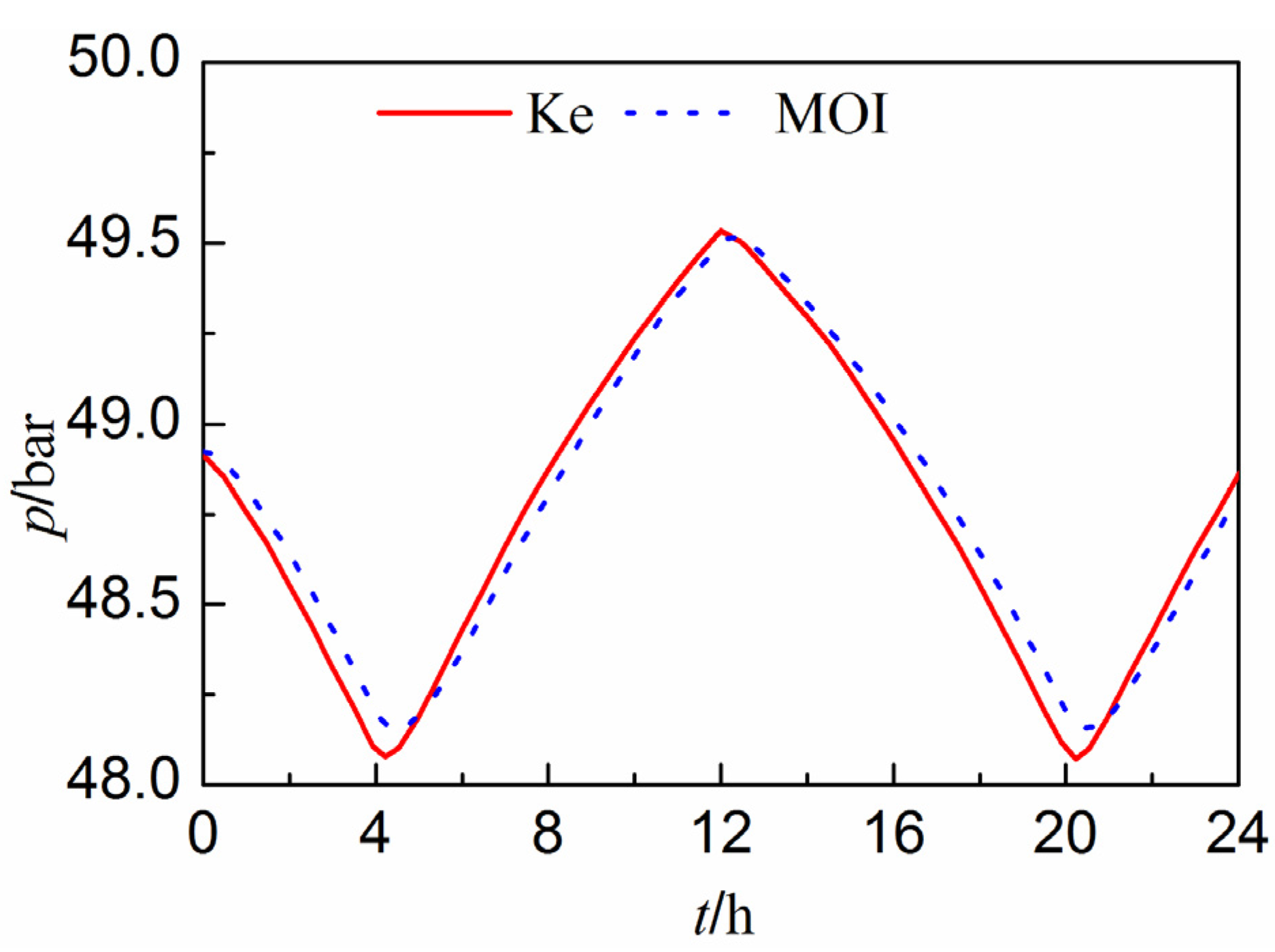
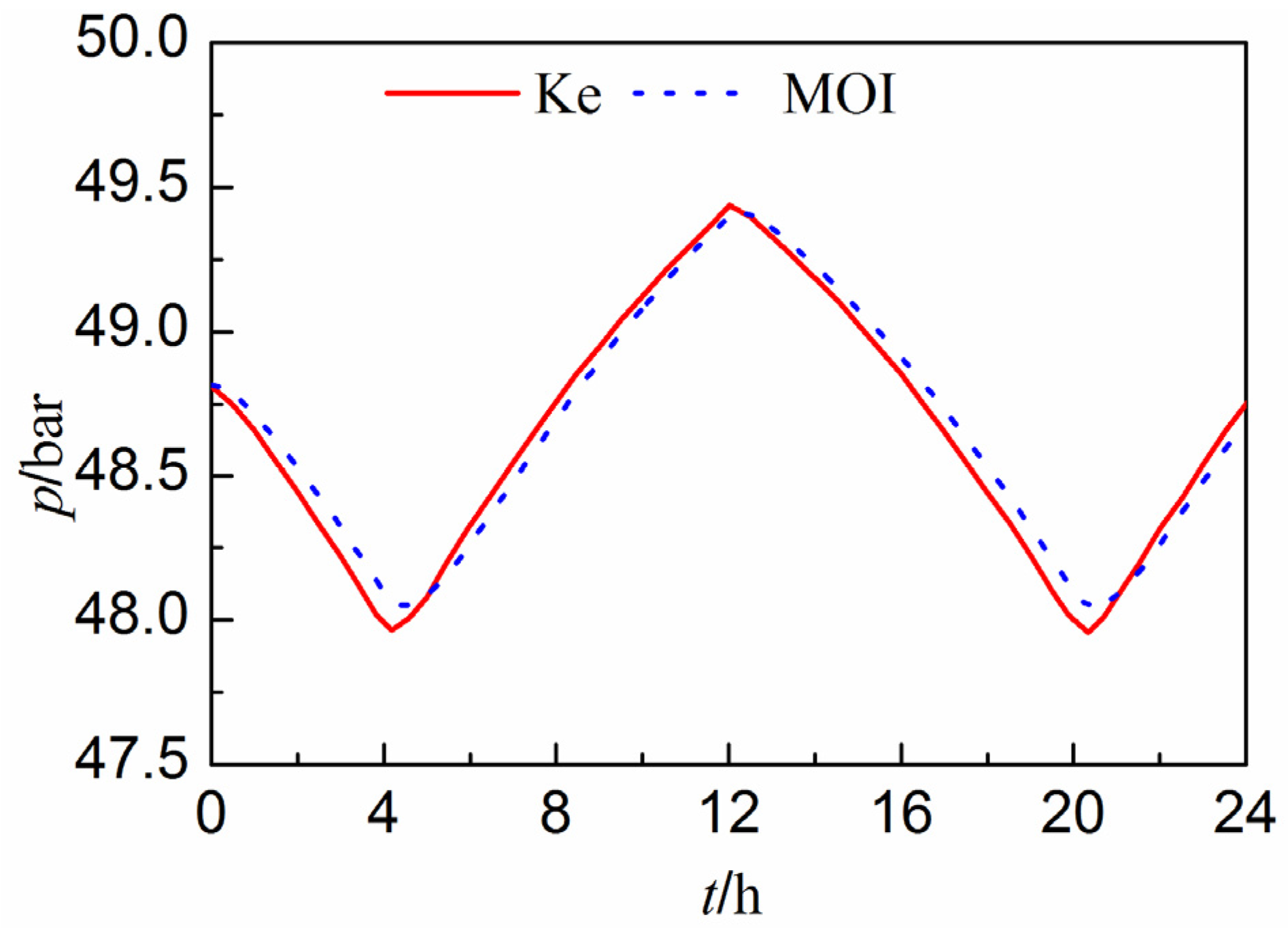
4. Simulation of Water Level Fluctuations
4.1. Neglecting the Influence of the Gas Phase
4.1.1. Water Level Fluctuations in an Open Surge Tank
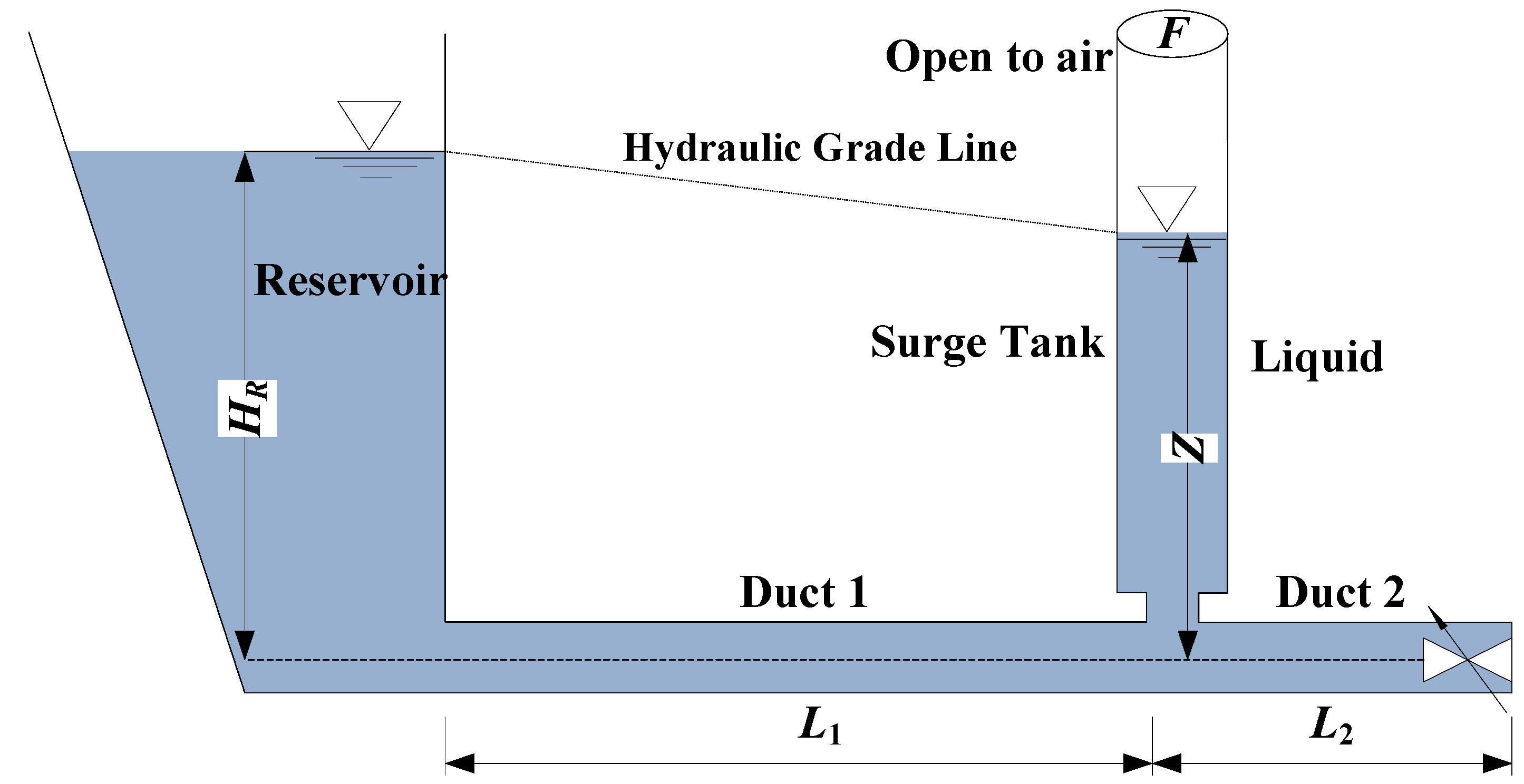
- Case 1: The water level of the reservoir is 10 m, and the valve discharge reduces to zero linearly;
- Case 2: The water level of the reservoir is 80 m, and the valve discharge reduces to zero linearly.
4.1.2. Water Level Fluctuations in a U-tube
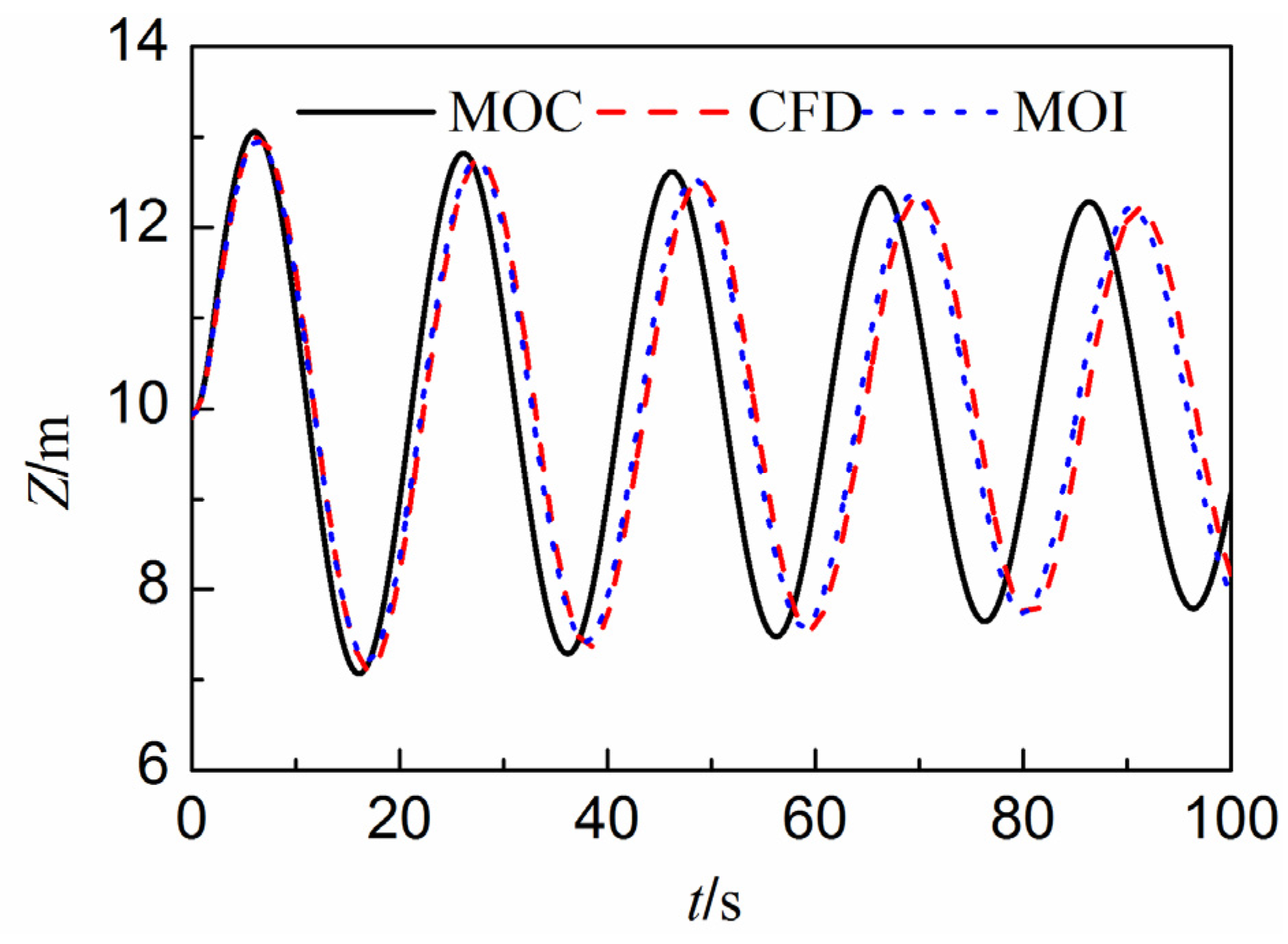
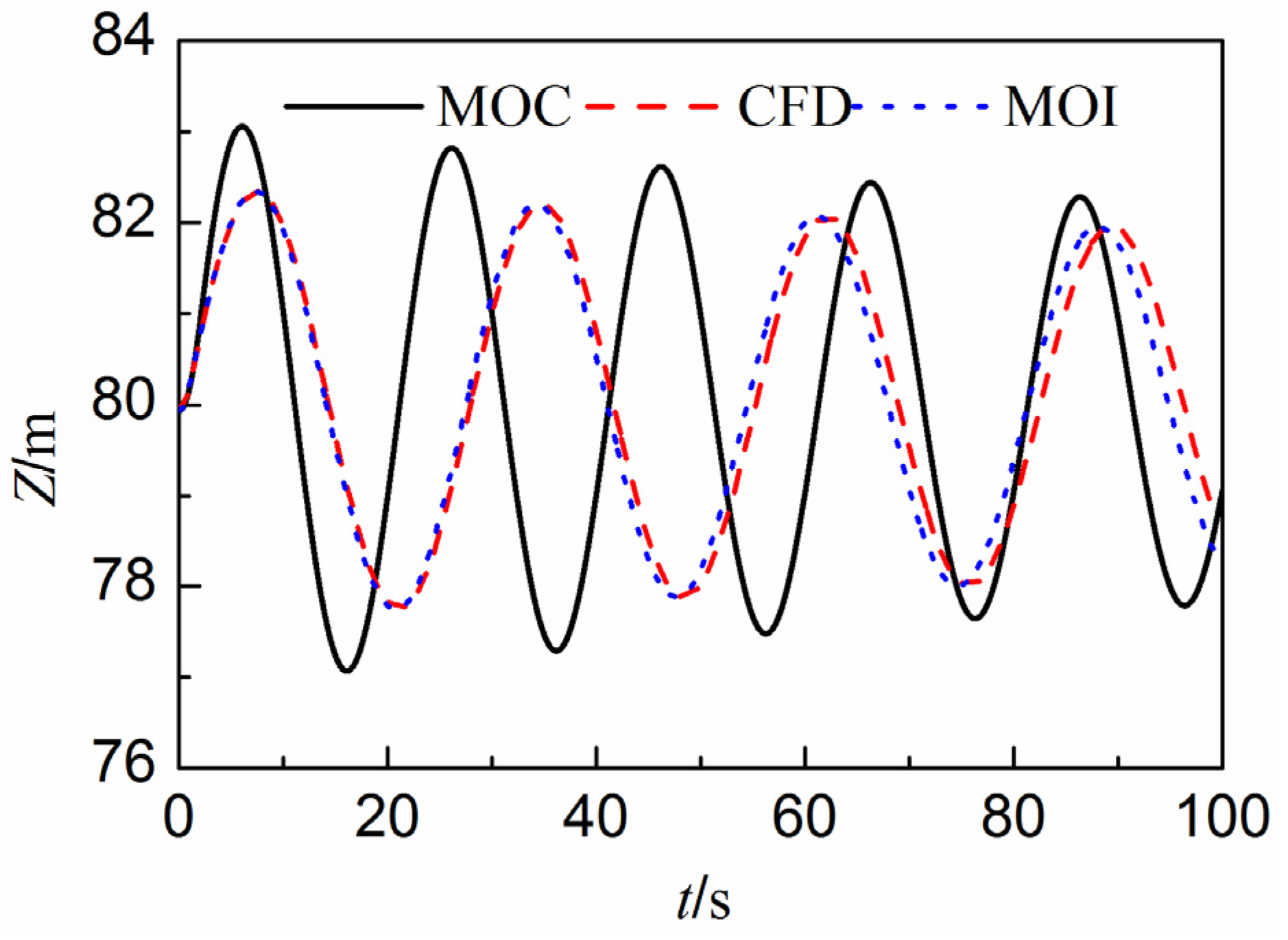
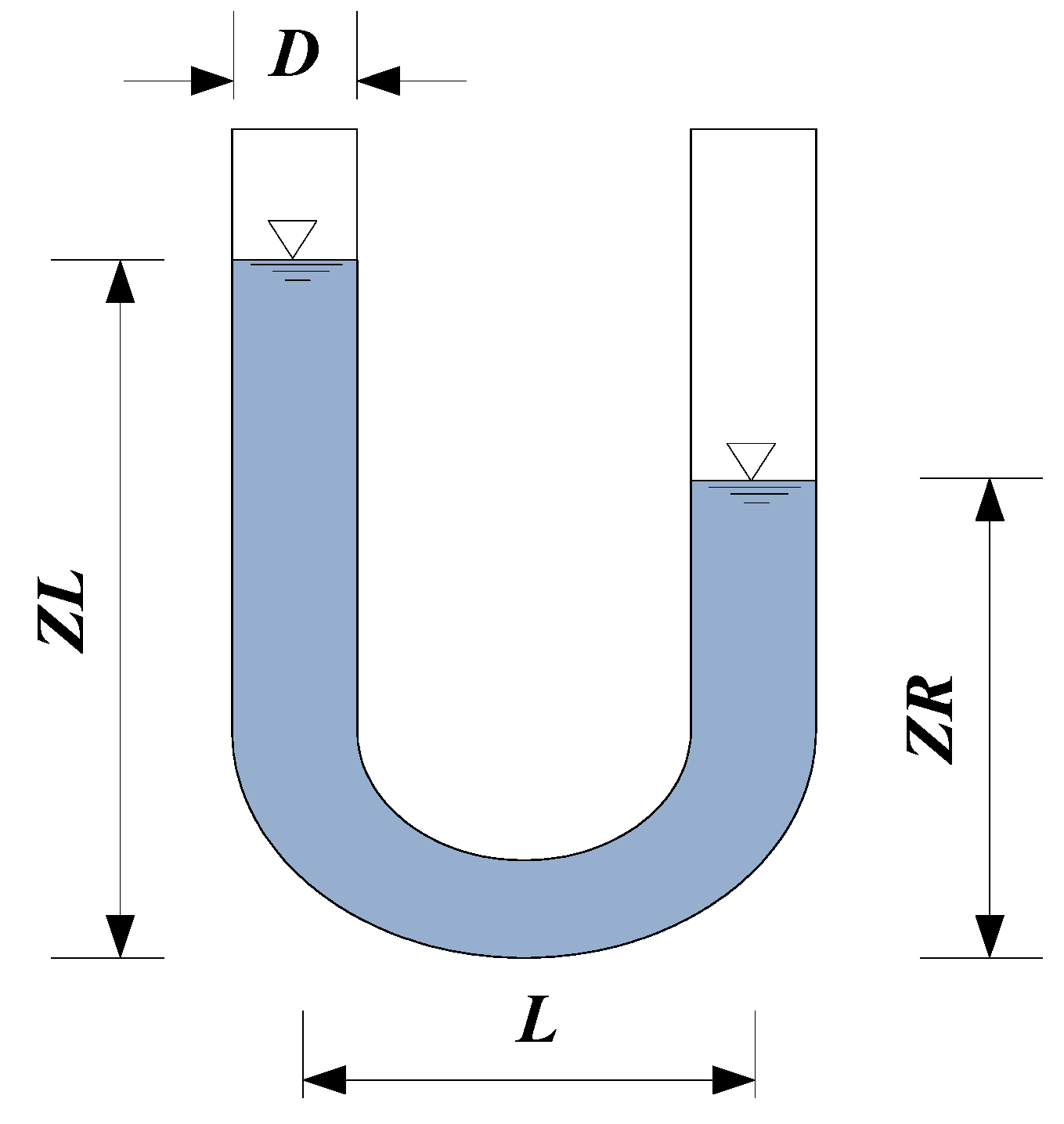
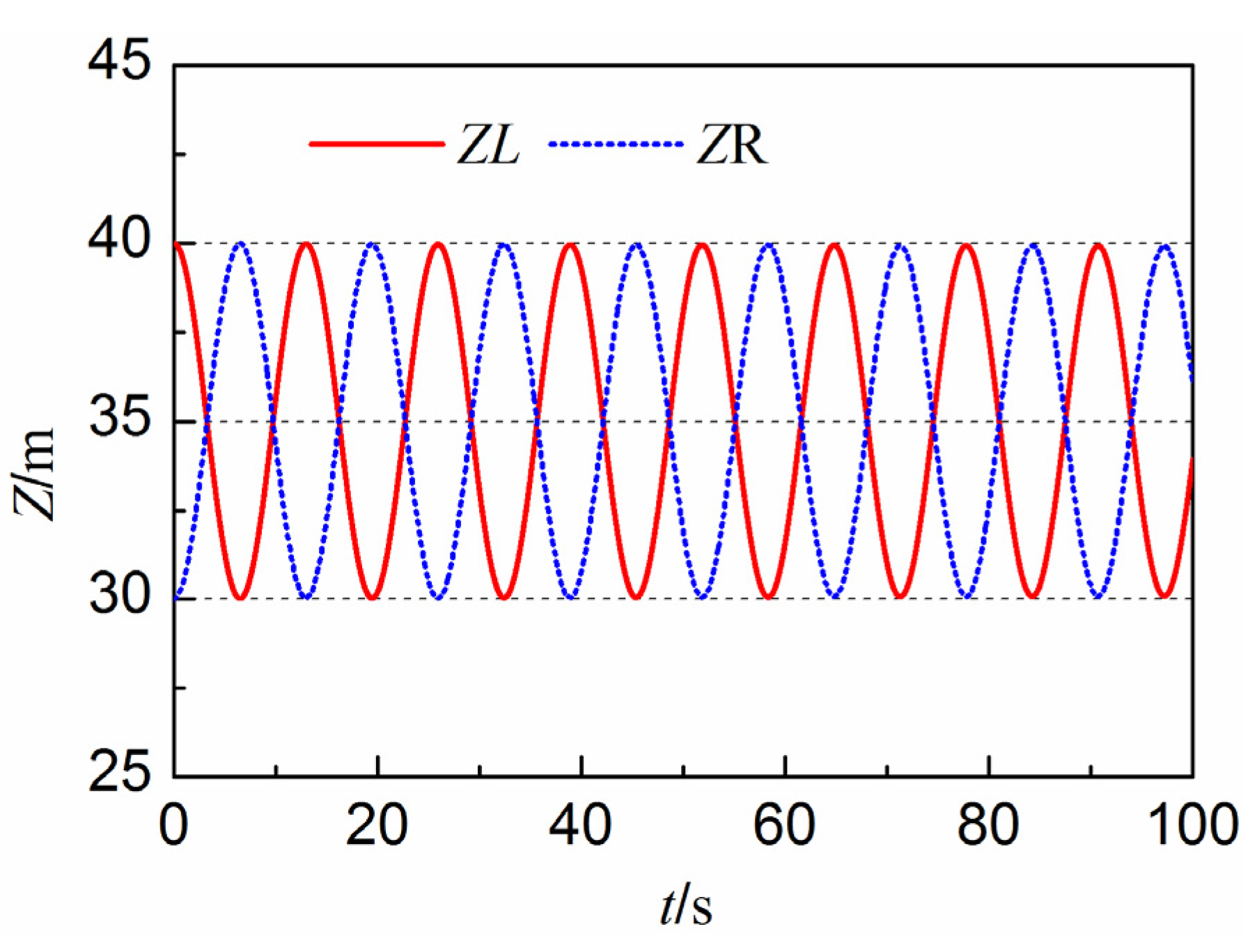
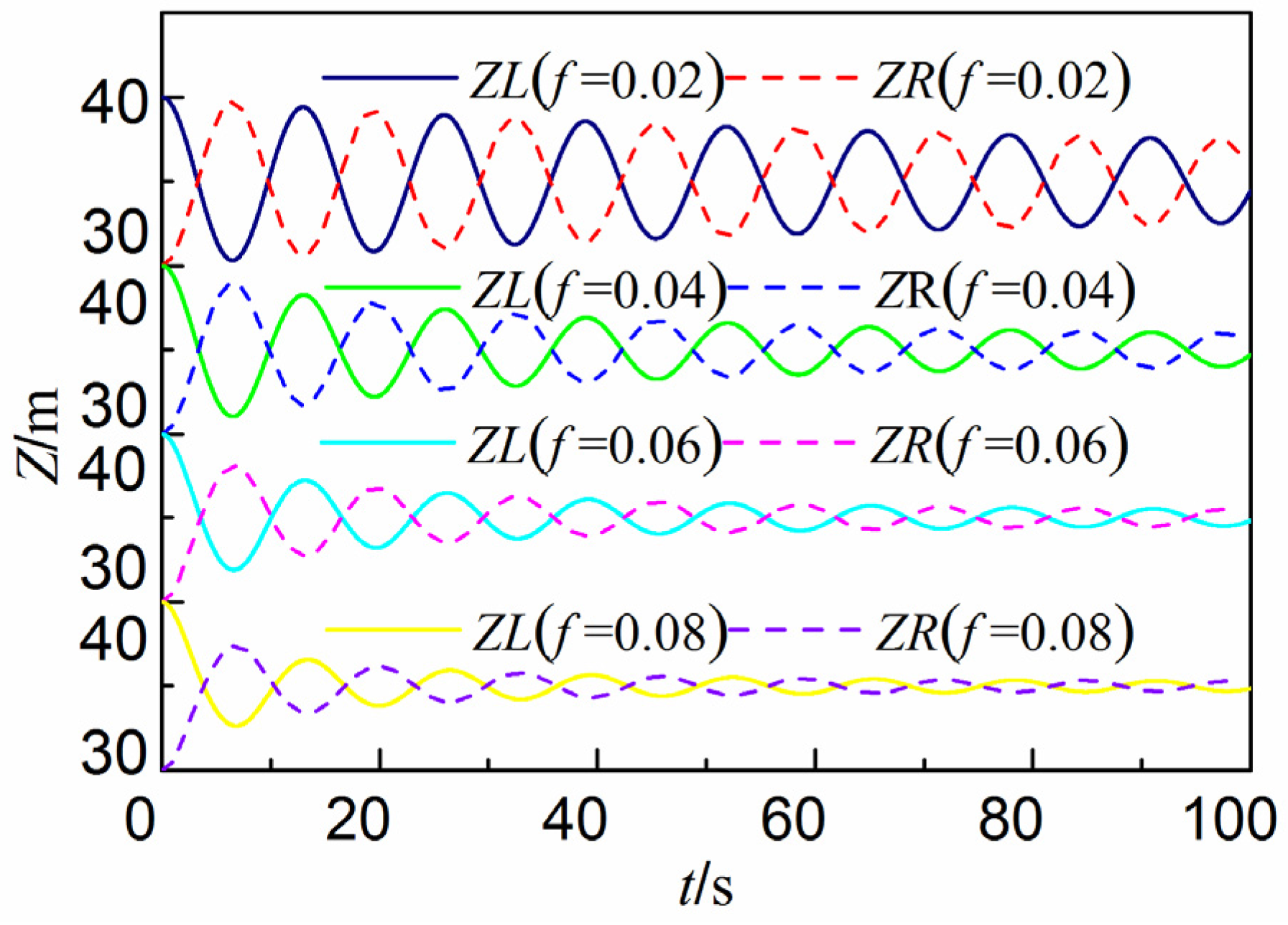
4.2. Gas Phase Limited in a Chamber
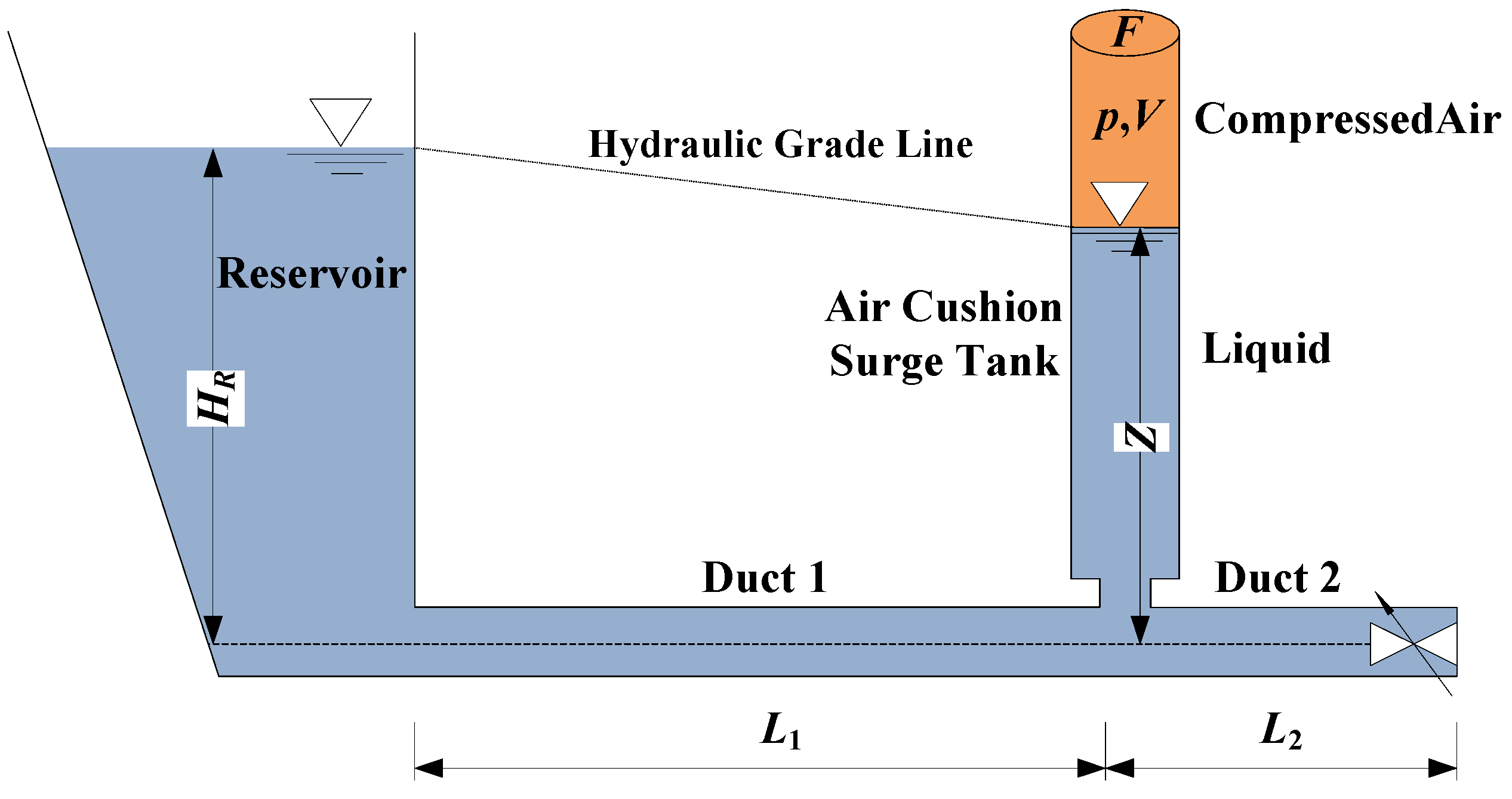
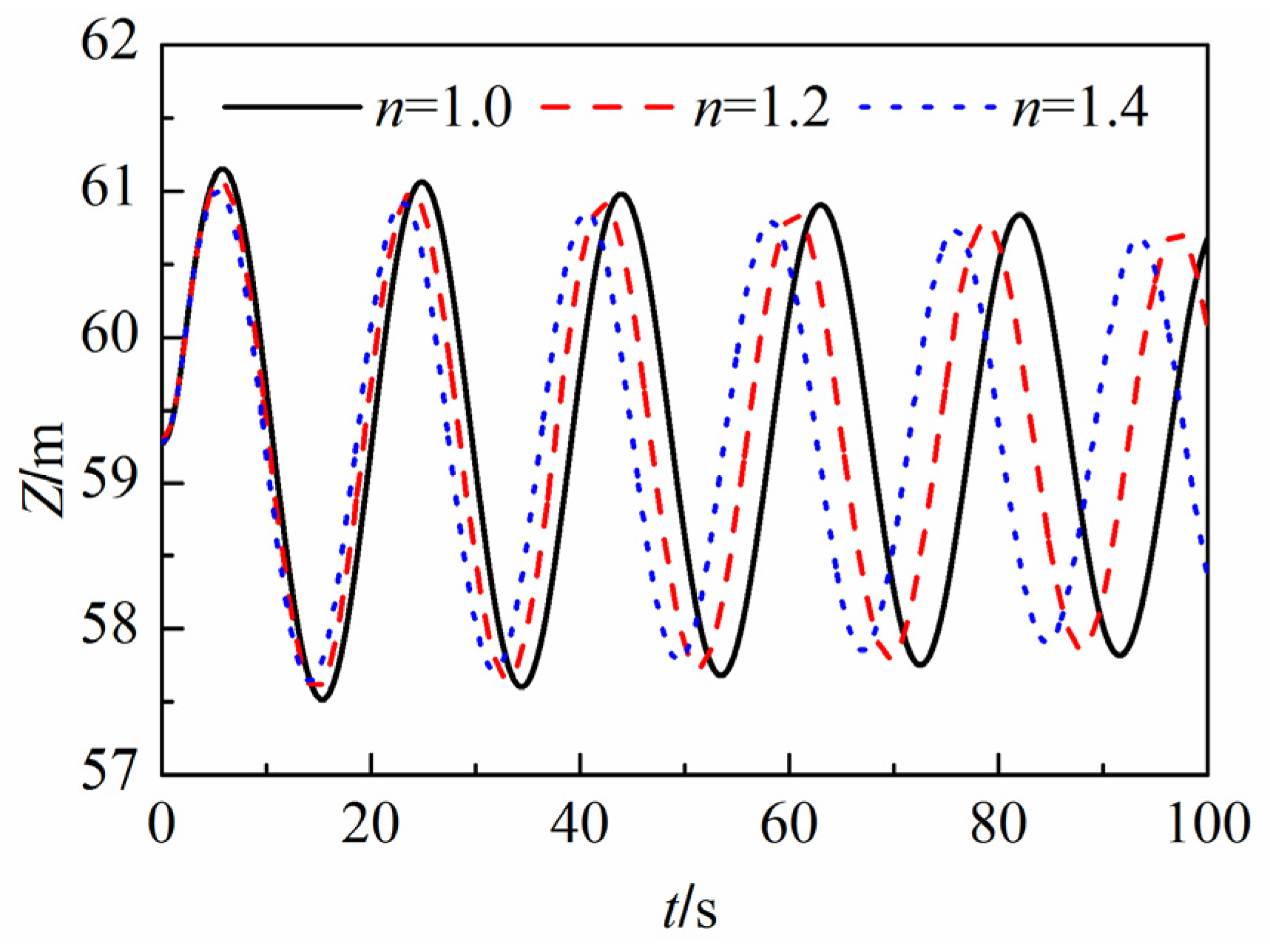
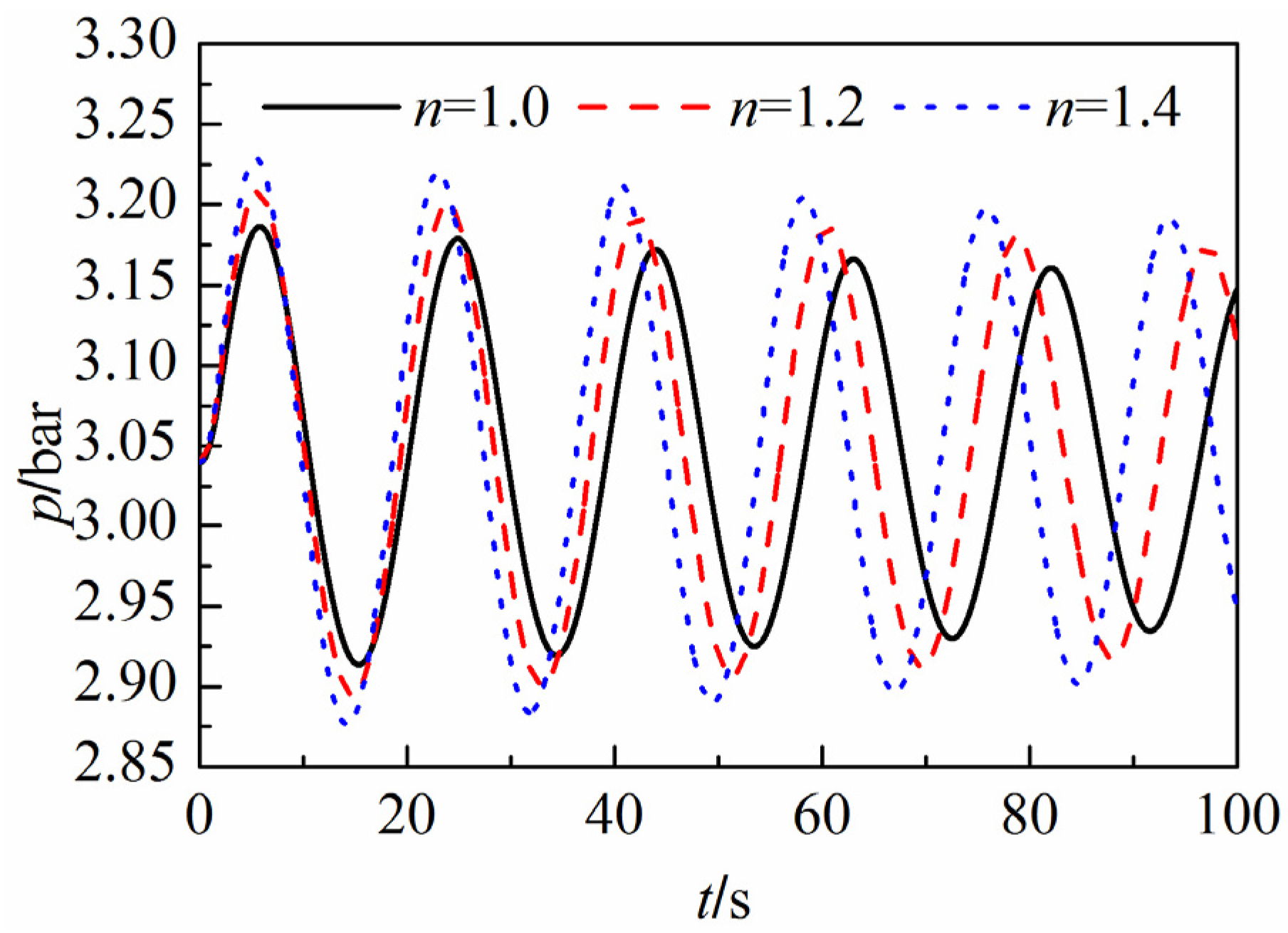
4.3. Gas Phase Flow in Ducts
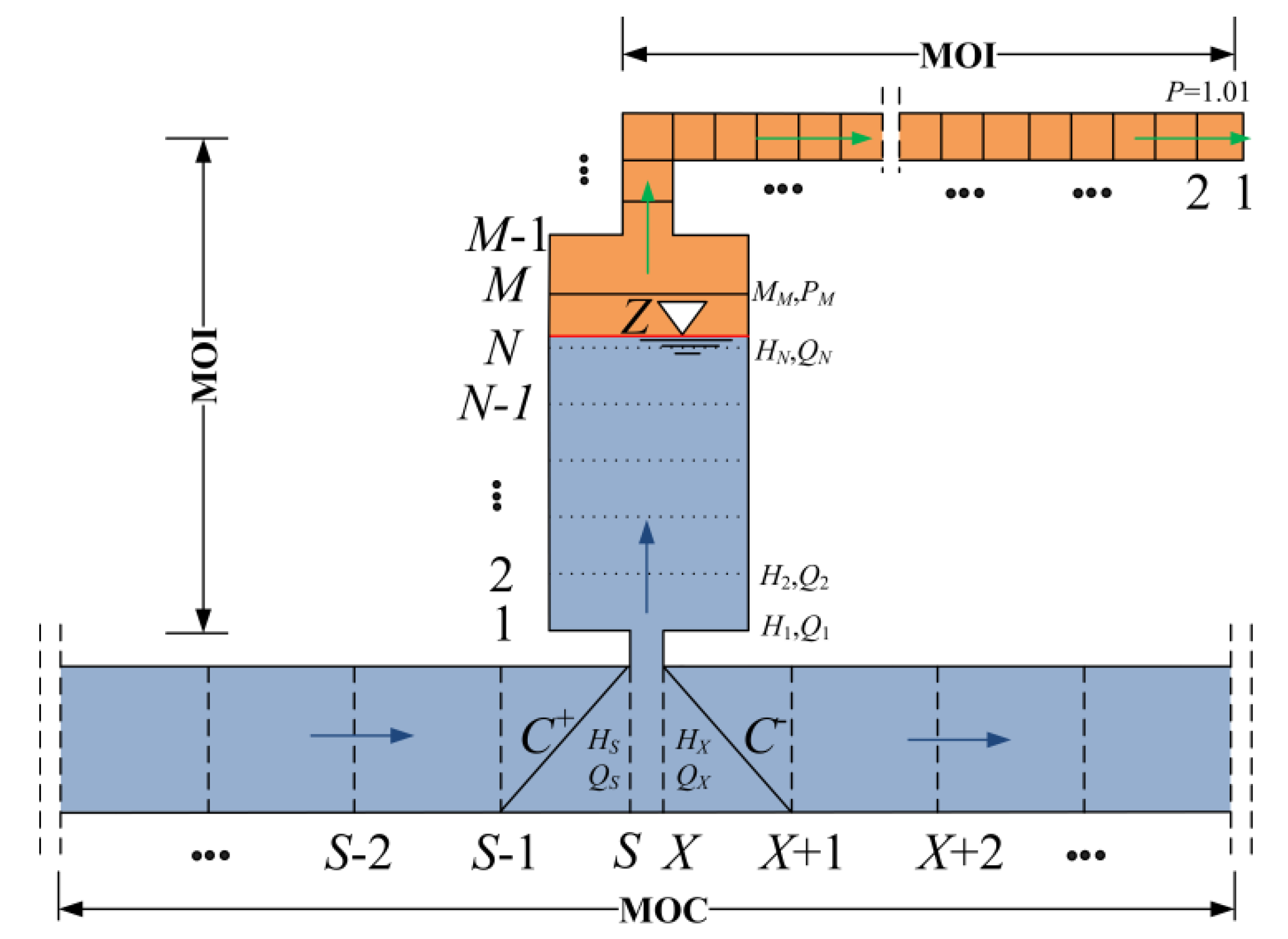
4.3.1. Synchronous Coupling of Liquid and Gas Phases (Model A)
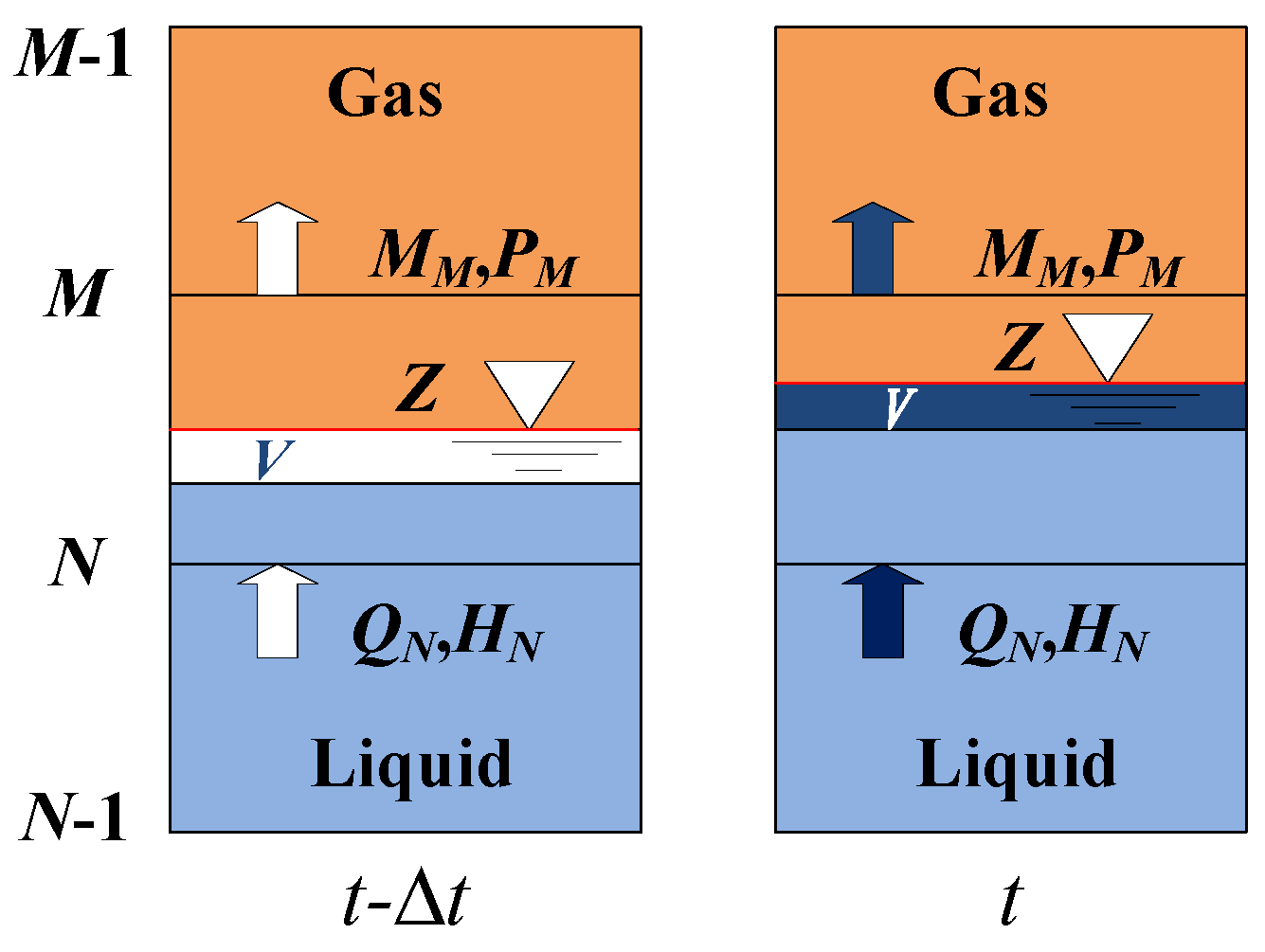
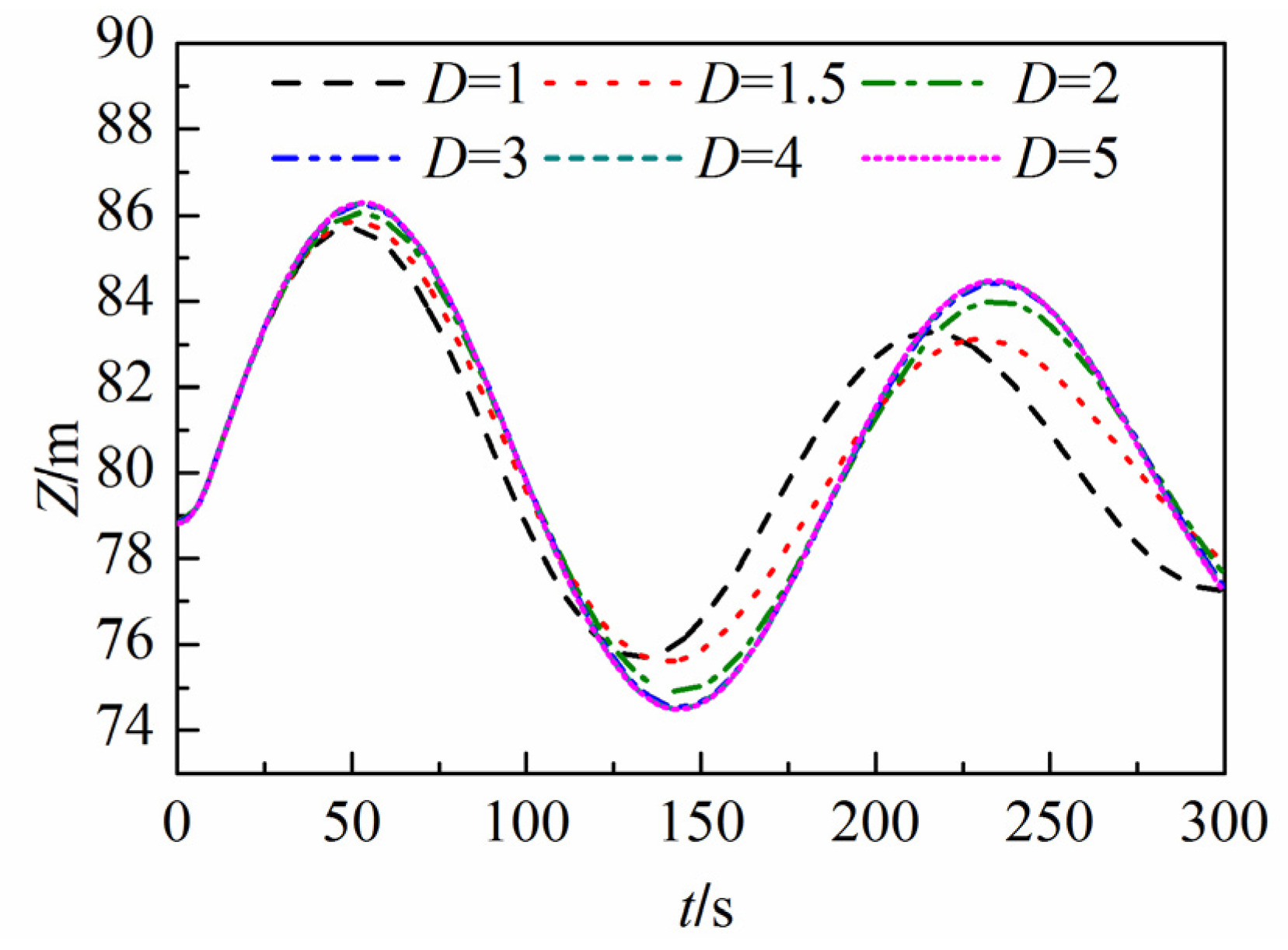
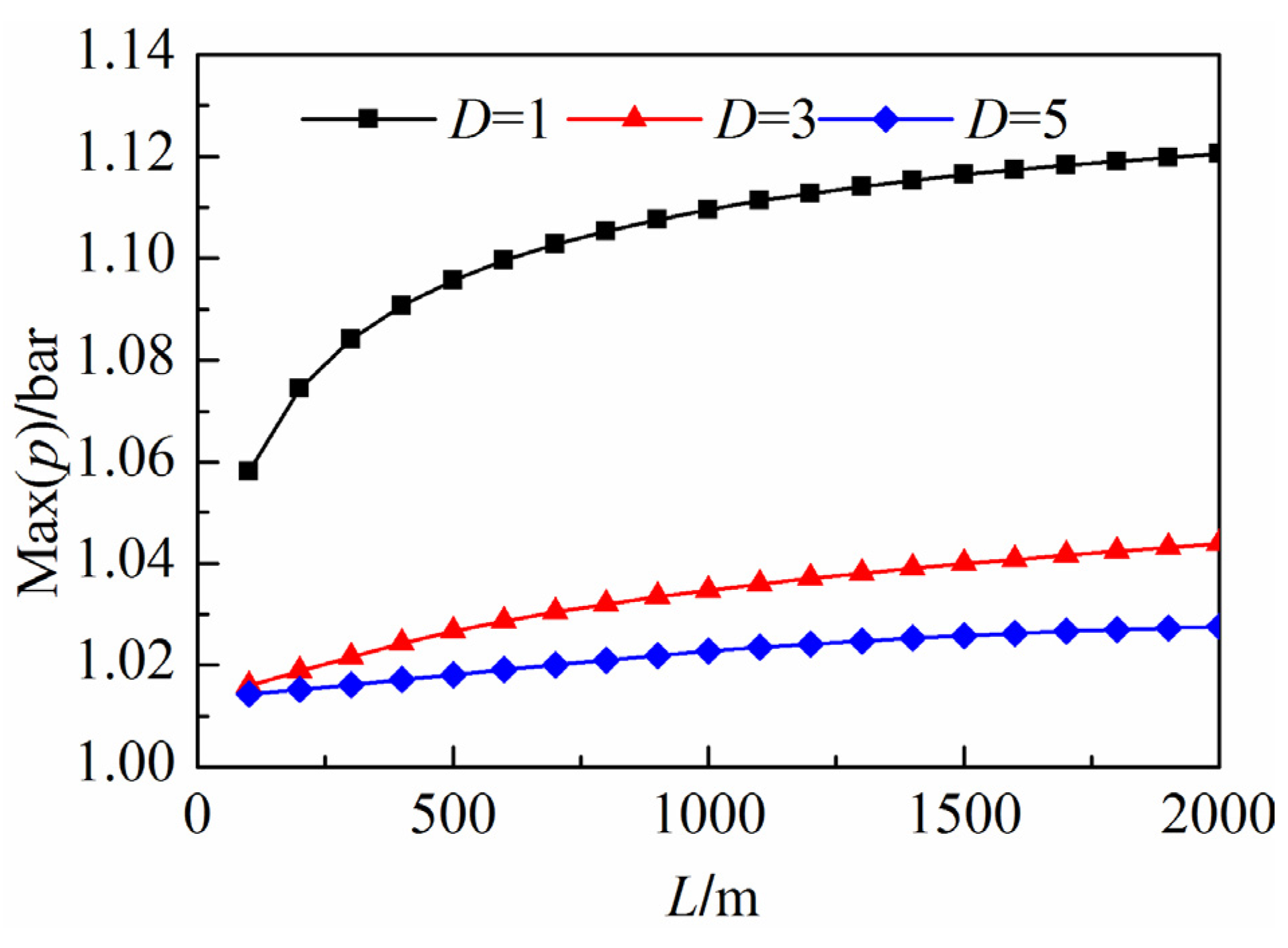
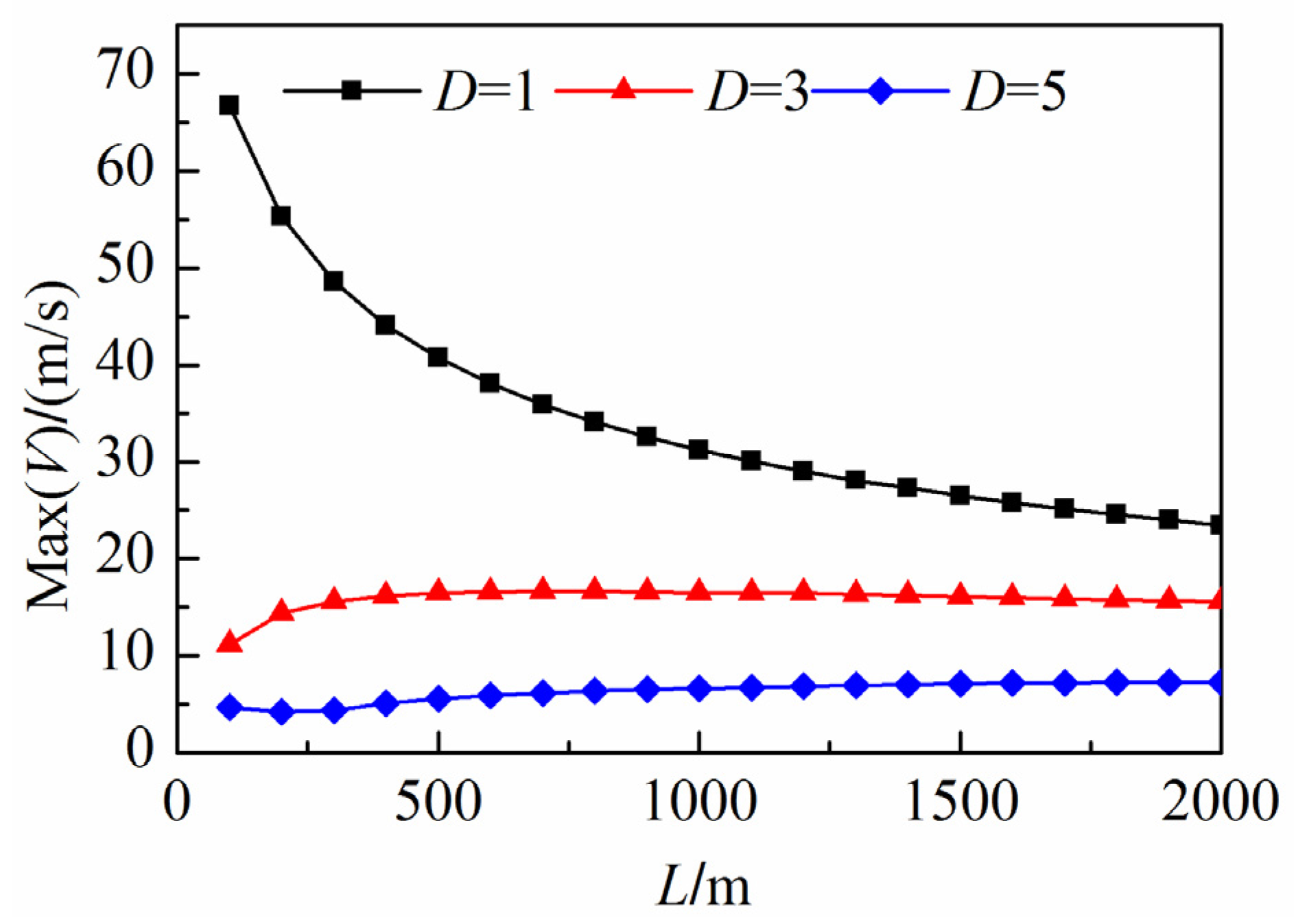
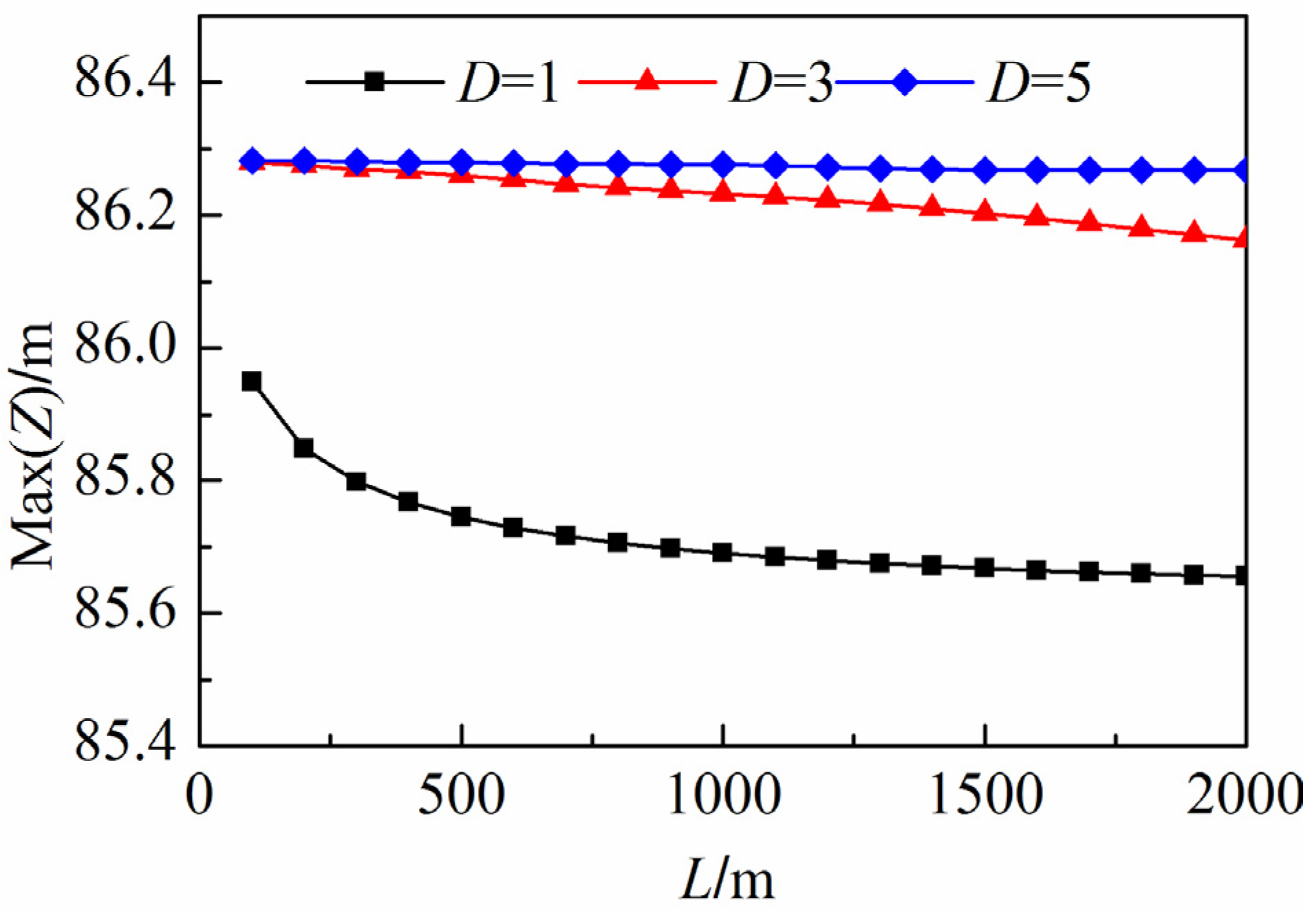
4.3.2. Neglecting the Effect of the Gas Phase on the Liquid Phase (Model B)
4.3.3. Asynchronous Coupling of Liquid and Gas Phases (Model C)
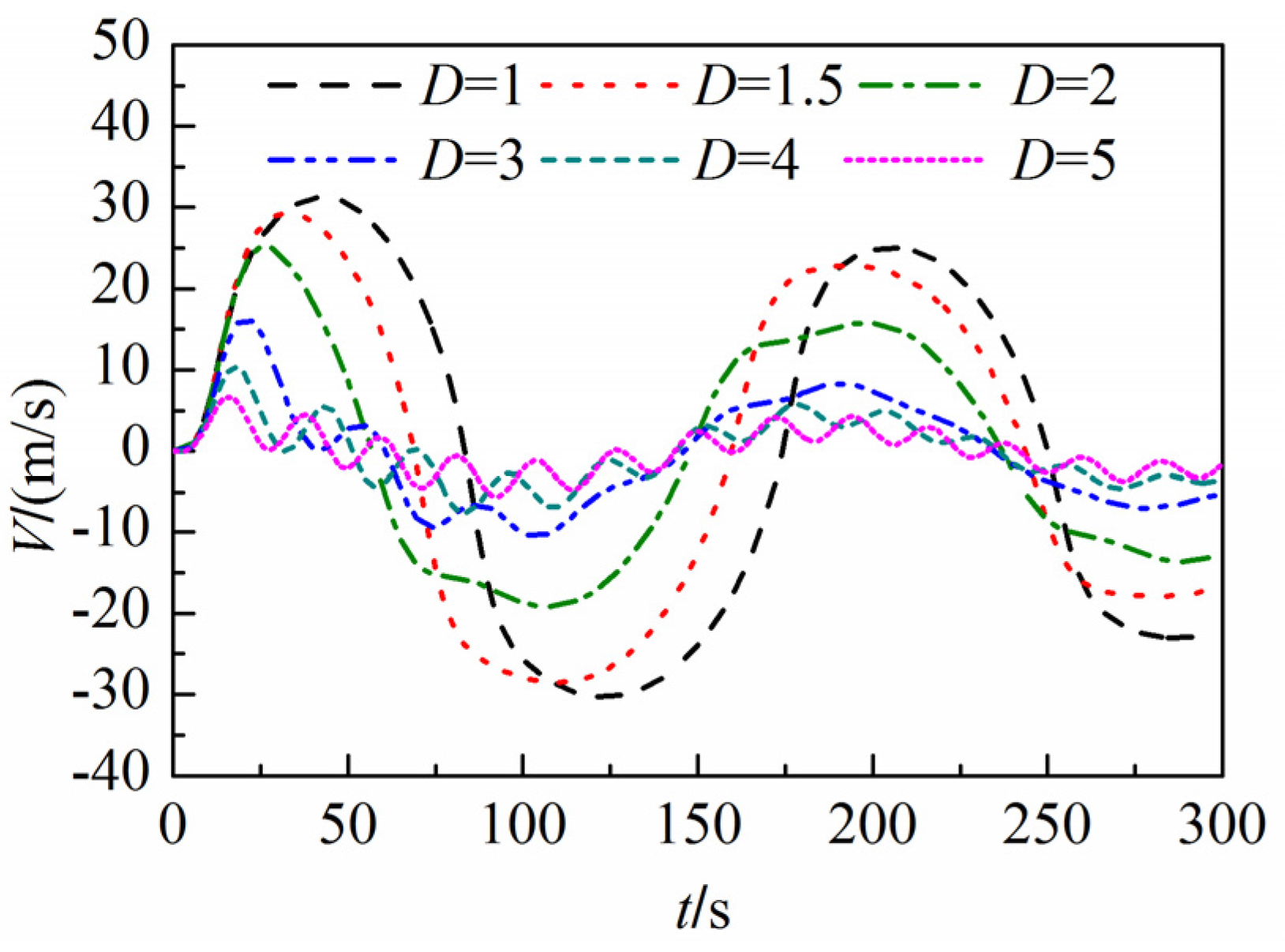
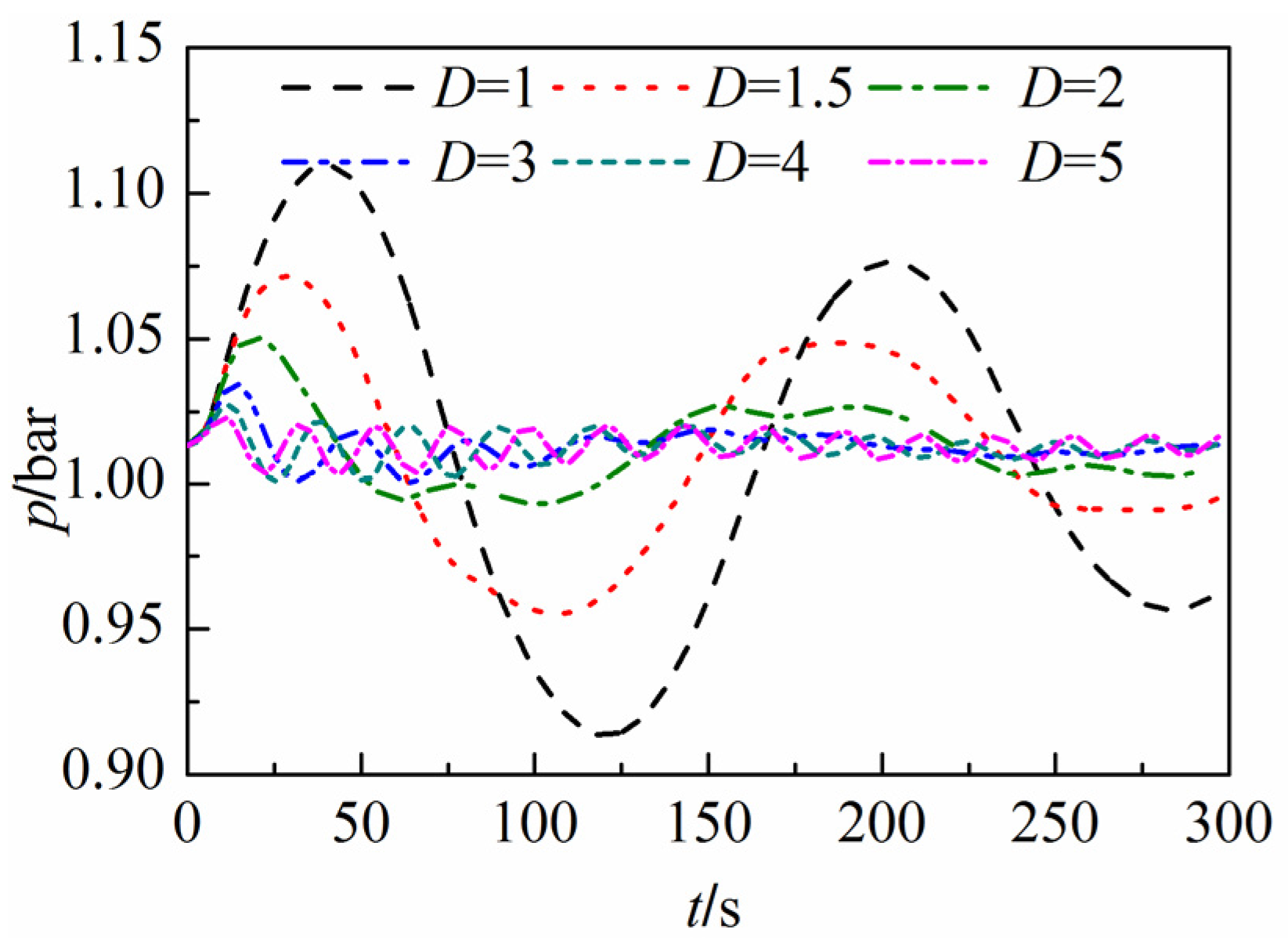
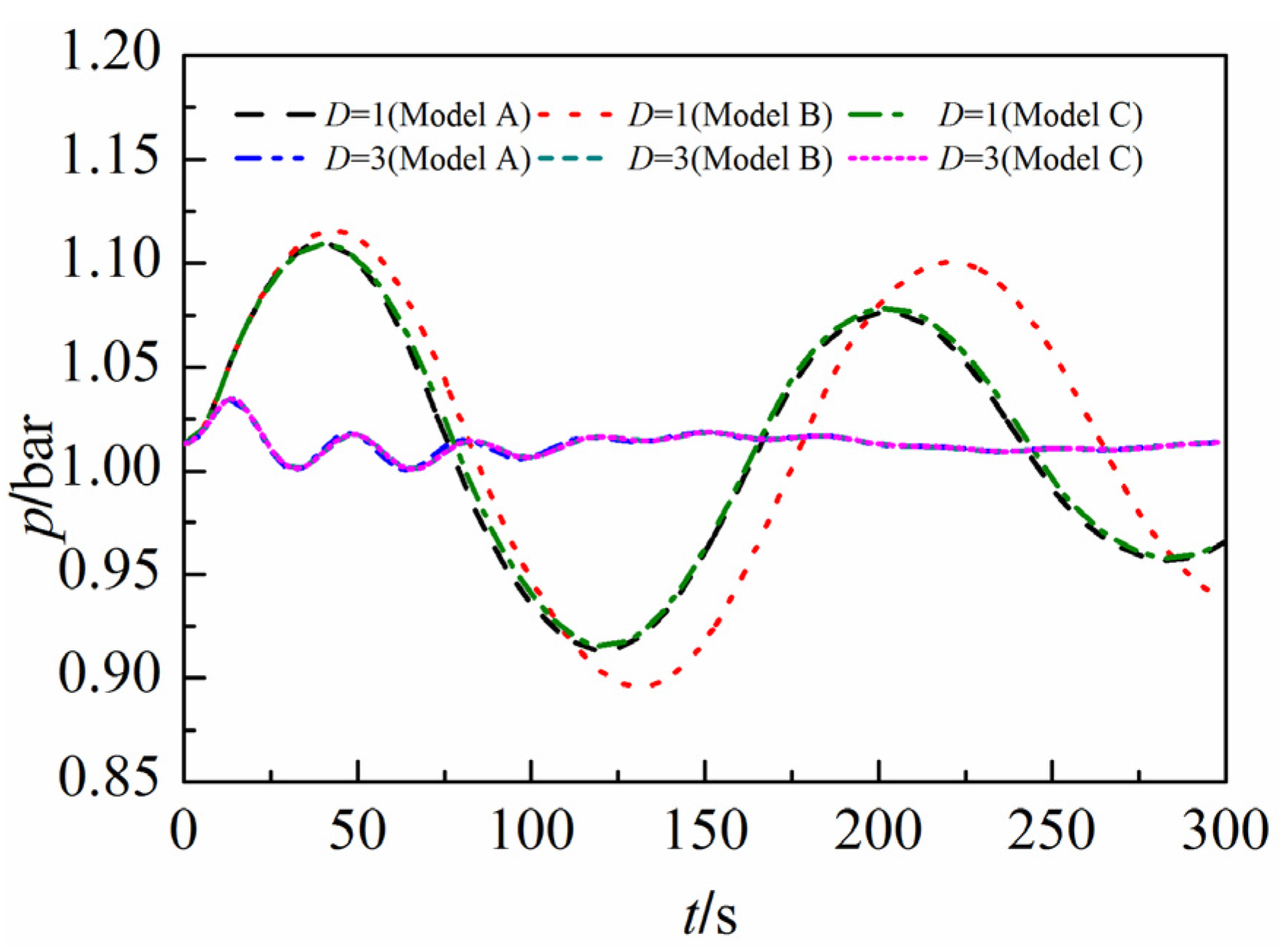
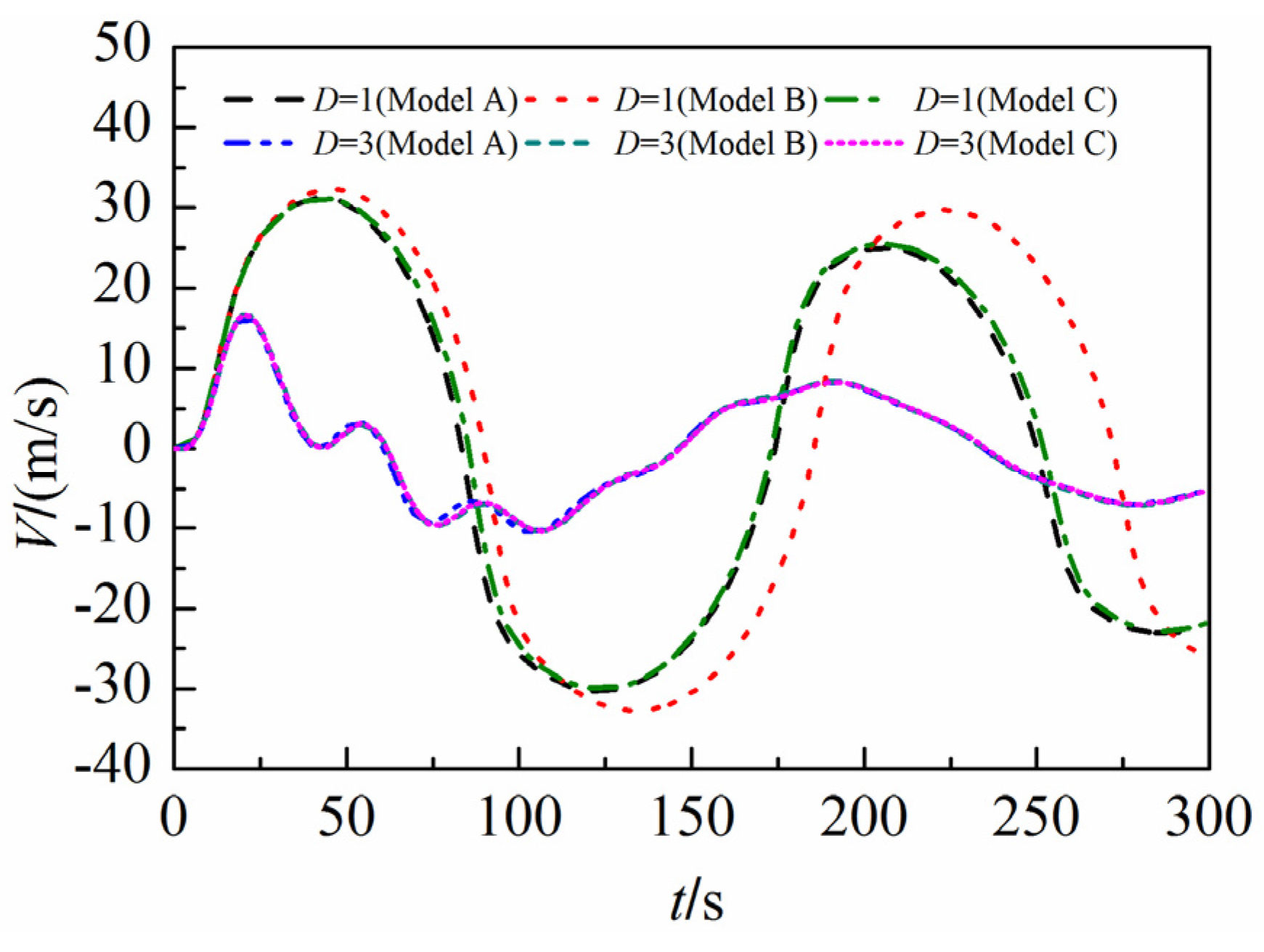
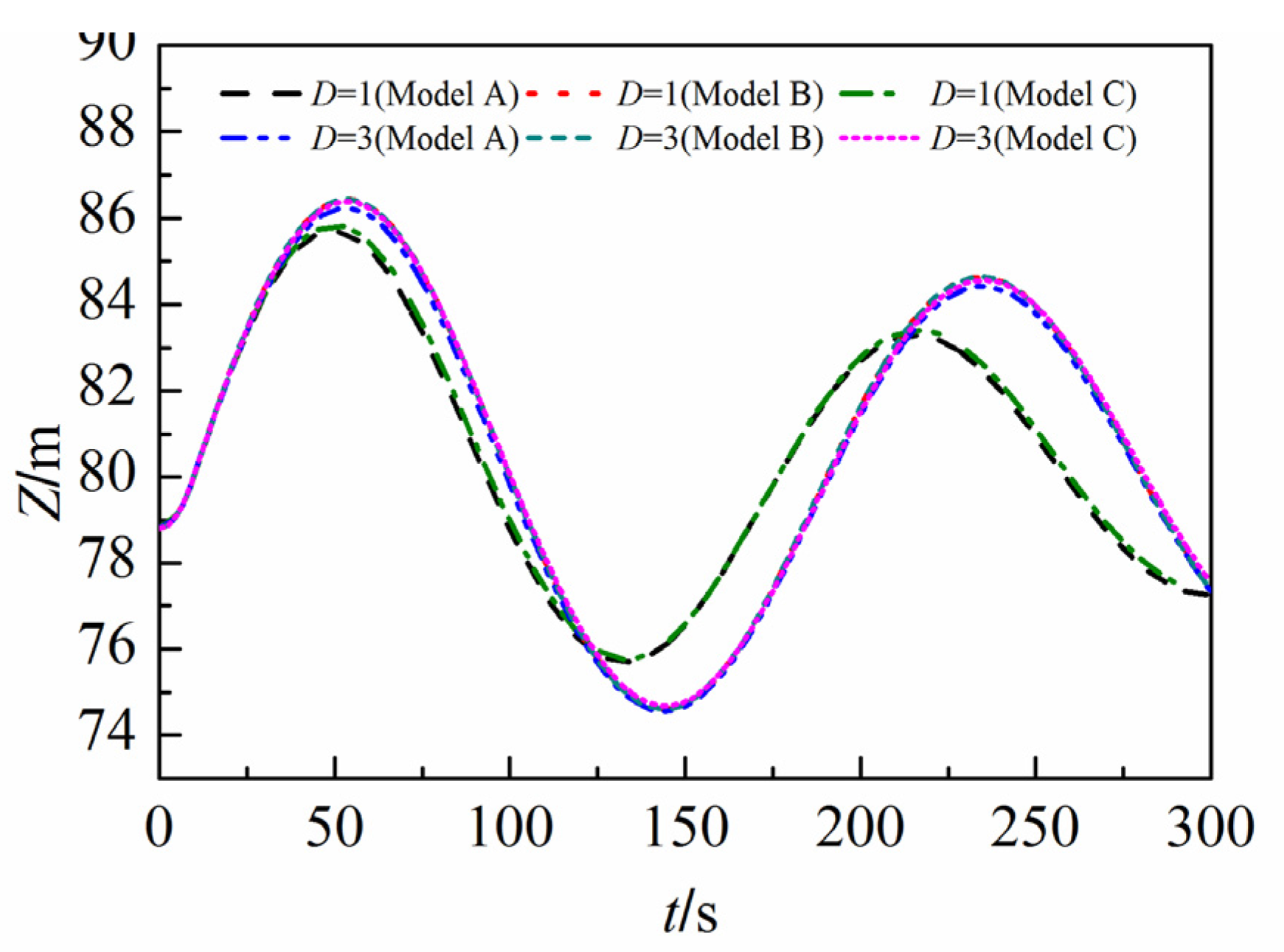
- When the duct diameter is large (e.g., D = 3.0 m), the gas pressure variation in the surge tank is not significant enough to affect the liquid phase. Therefore, traces of gas pressure, water level in the surge, and the gas flow velocity agree for all three models.
- When the duct diameter is small enough (e.g., D = 1.0 m) such that the gas pressure varies greatly compared to the initial state, the gas behavior during the transient process has a significant influence on the water level fluctuations. However, the water level results calculated by Model B, which neglect the effect of the gas phase on the liquid phase, are unaffected by the variation of the gas duct diameter, so the simulations are not accurate under this circumstance. The peak wind speed at the duct outlet and the maximum gas pressure in the surge obtained by Model B are larger than the results obtained by Models A and C.
- Independent of the change in the gas duct diameter, the water level, the pressure, and the wind speed are very similar for Models A and C. This illustrates that the asynchronous coupling model captures the interaction between the liquid and gas phases as accurate as the synchronous coupling model.
5. An Engineering Application
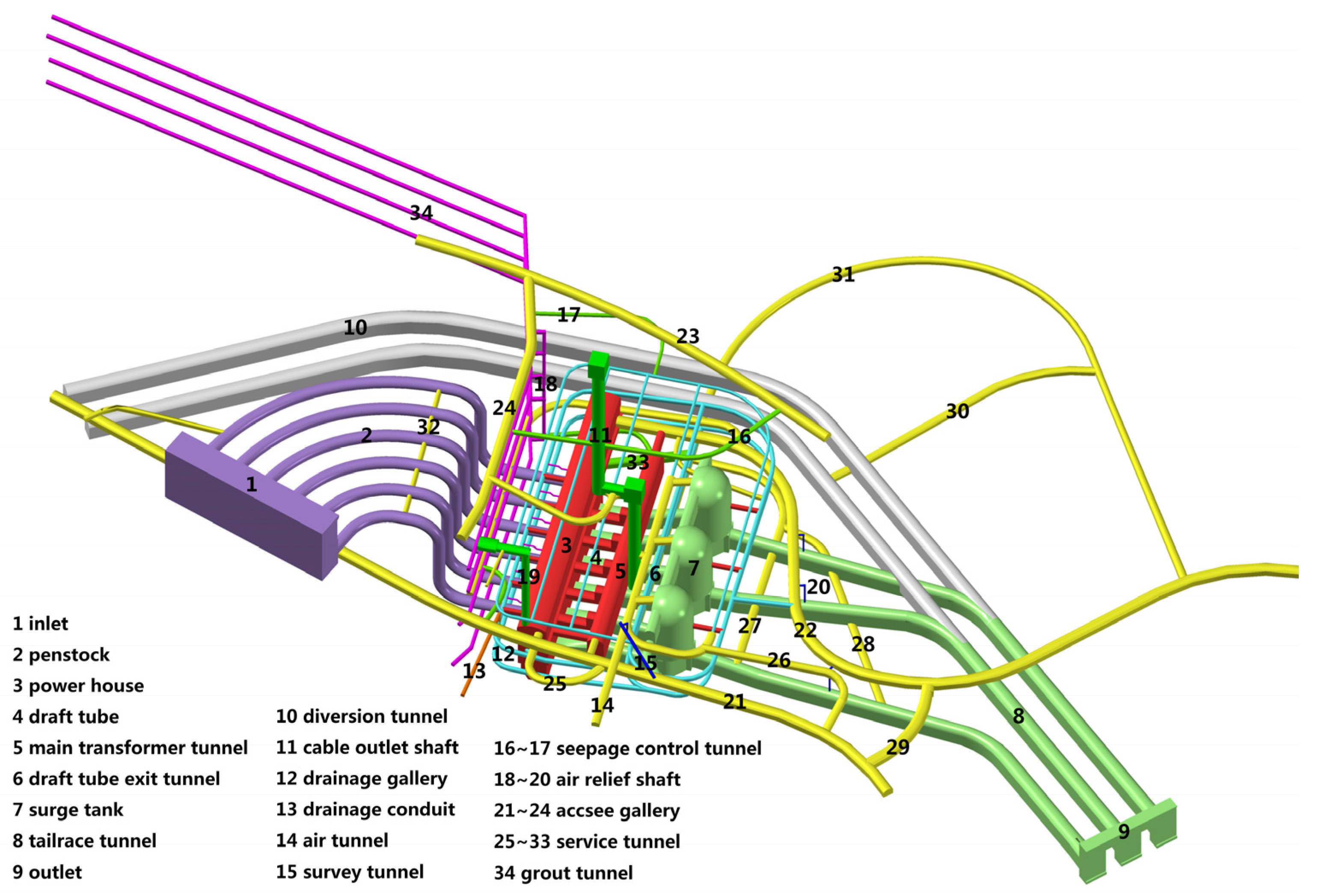
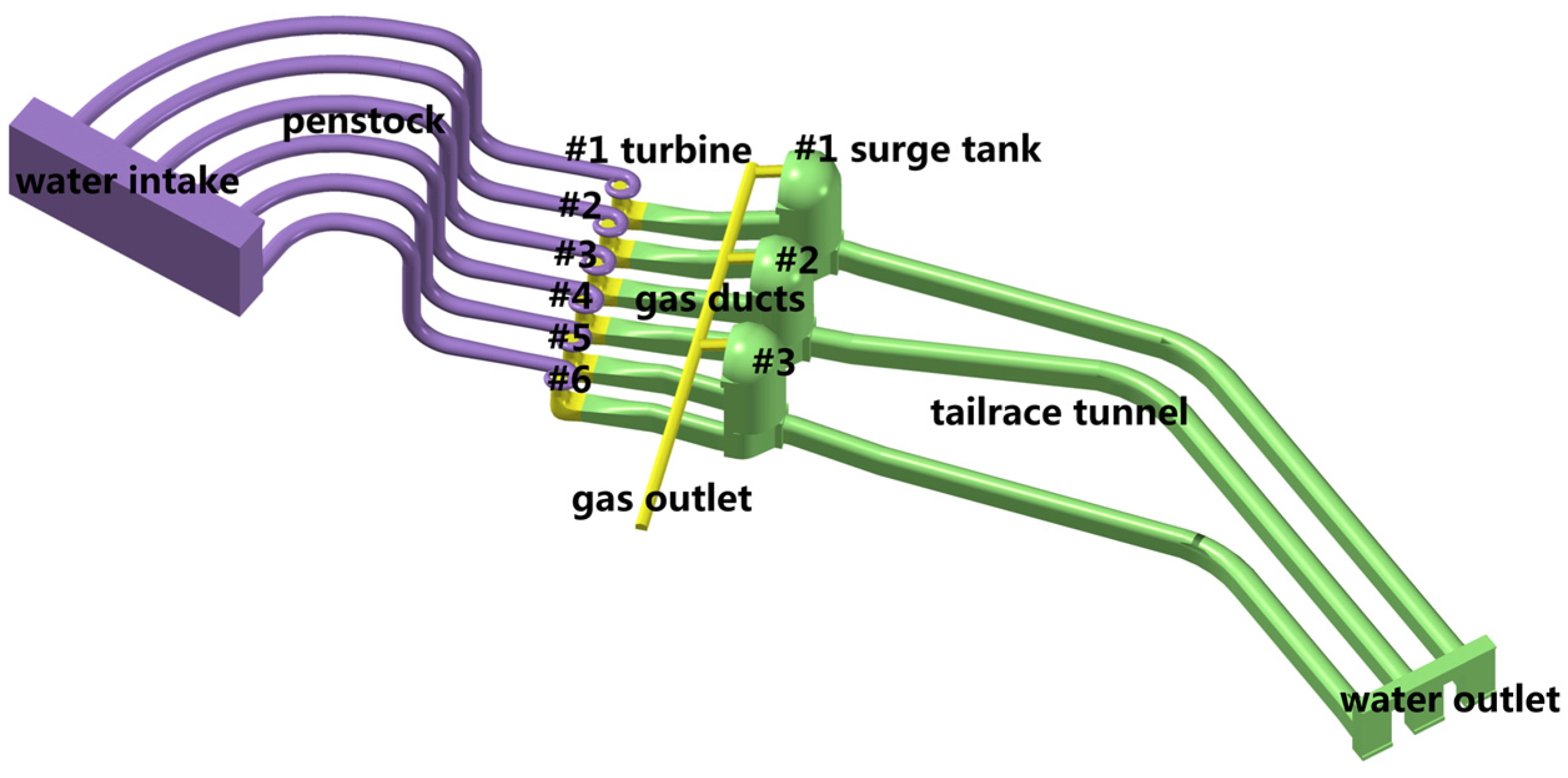
5.1. Case 1: Six Turbines Load Reject Simultaneously
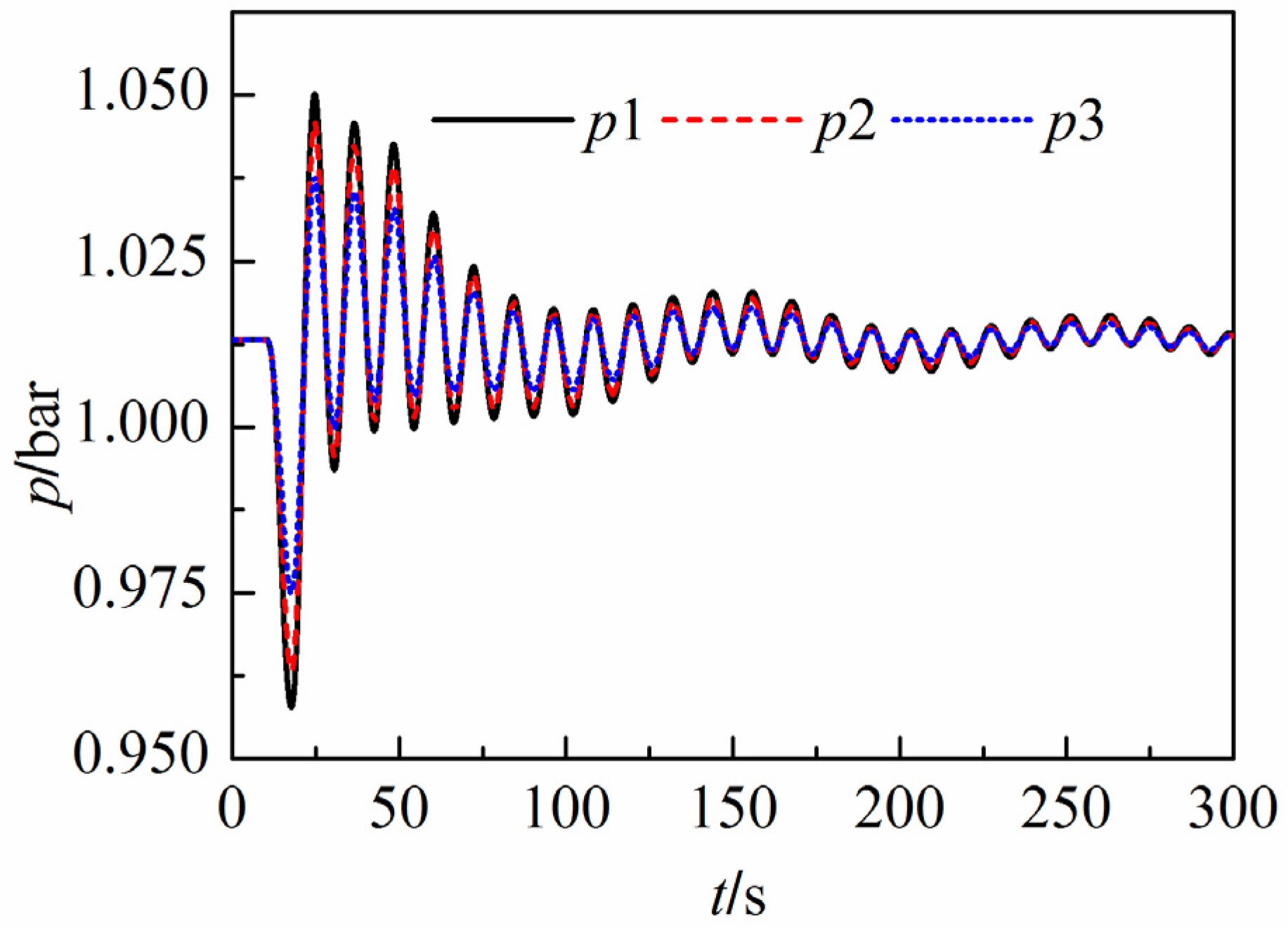
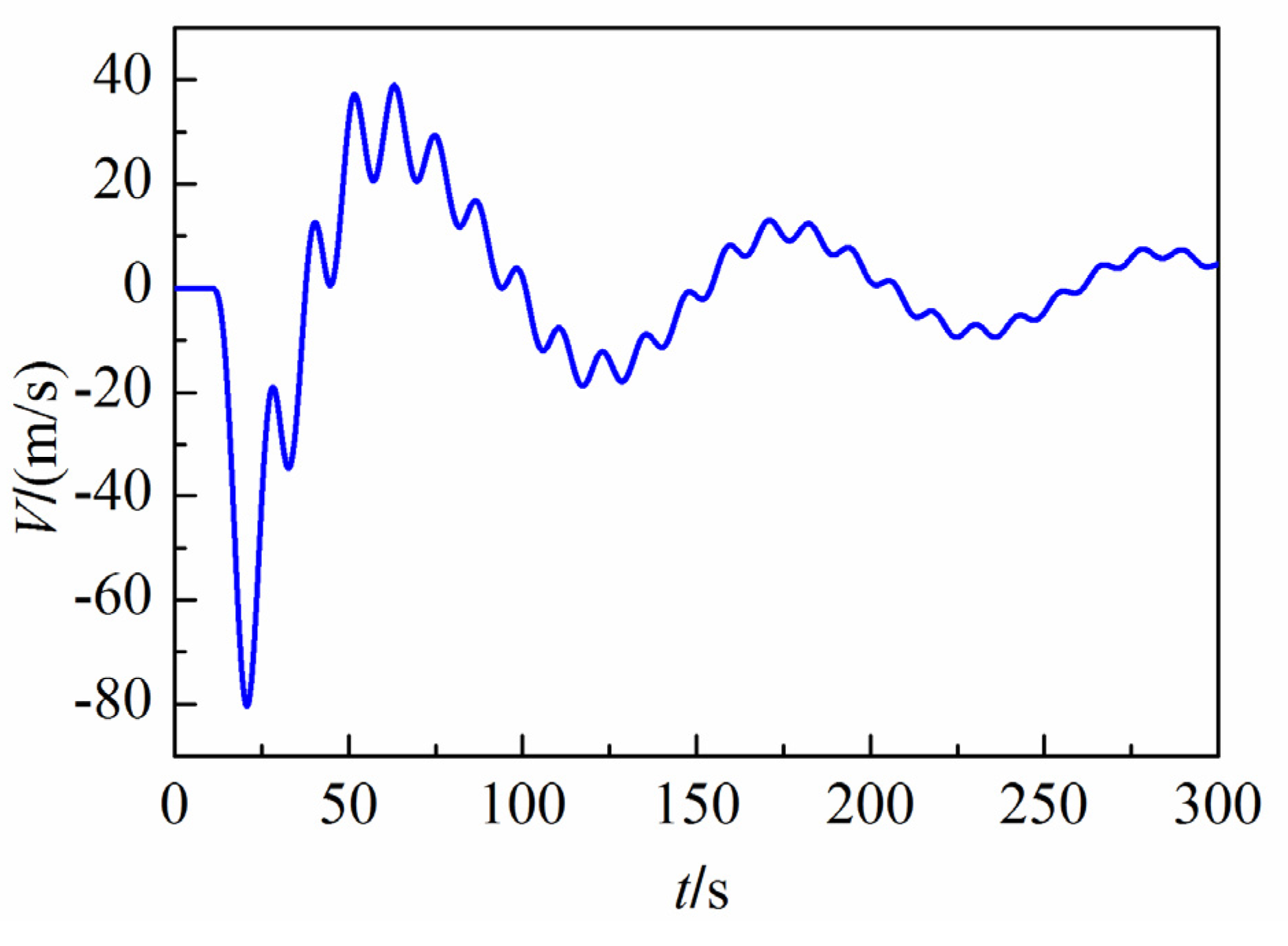
5.2. Case 2: Four Turbines Load Reject and Two Turbines Operate Properly
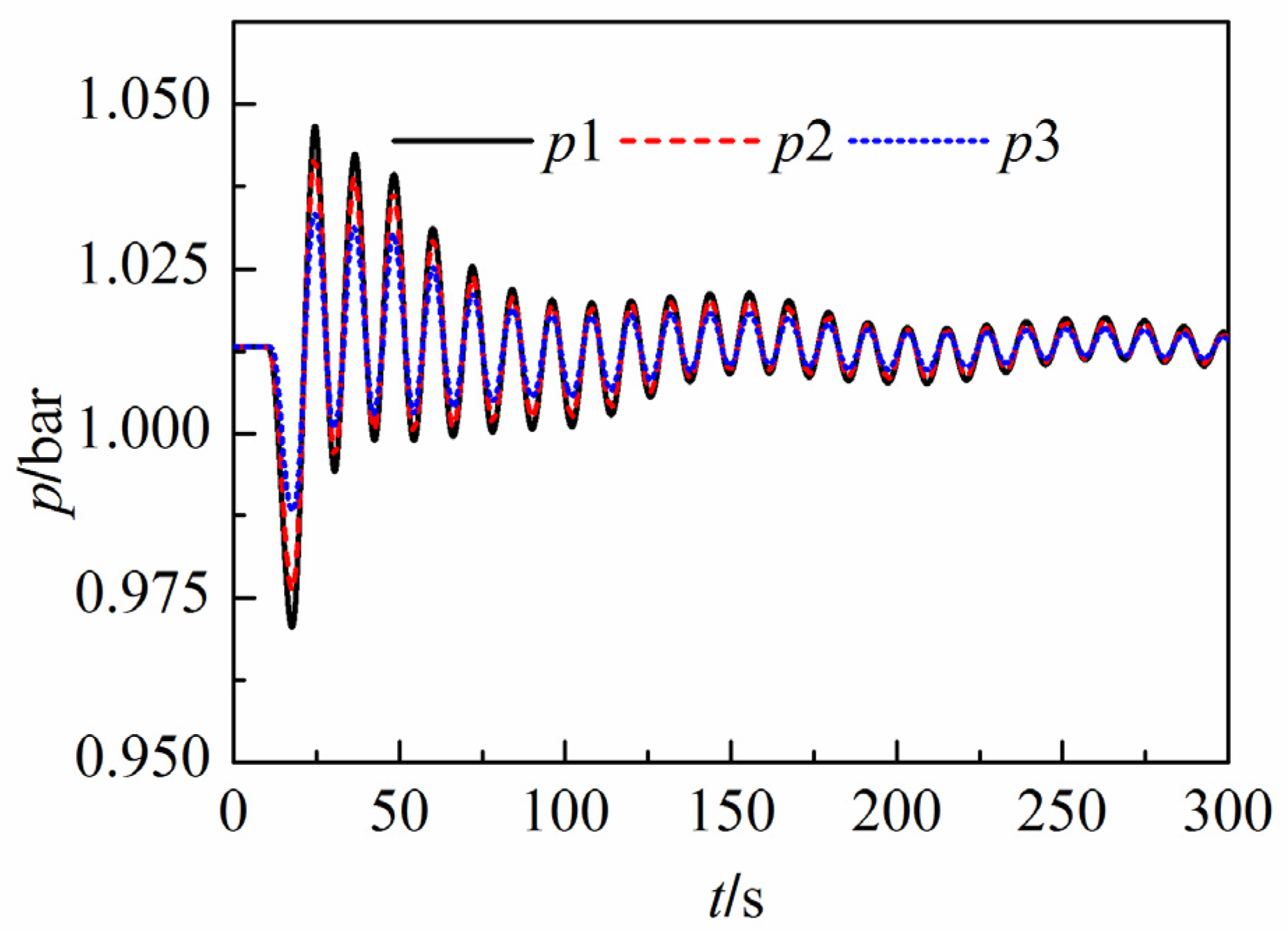
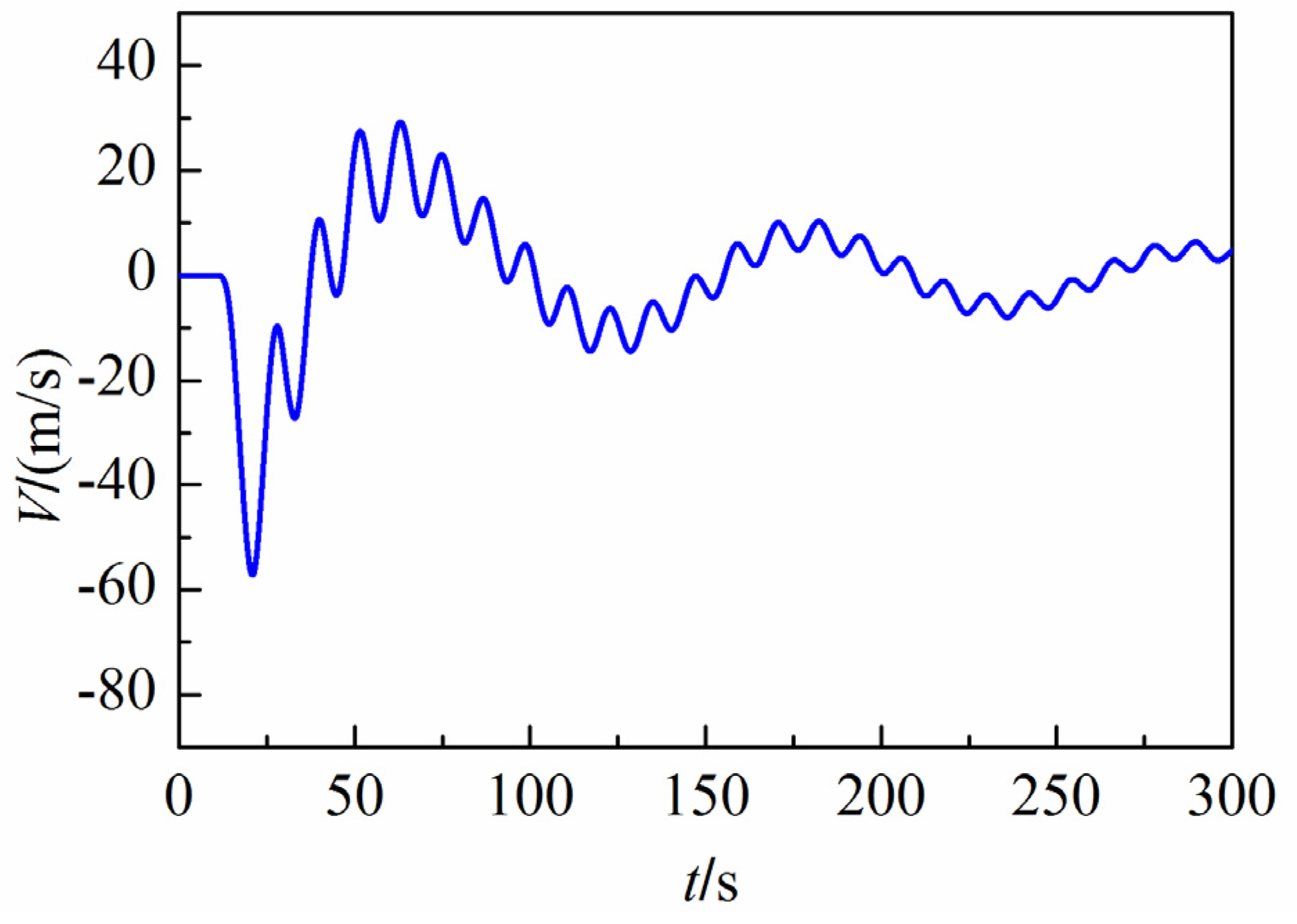

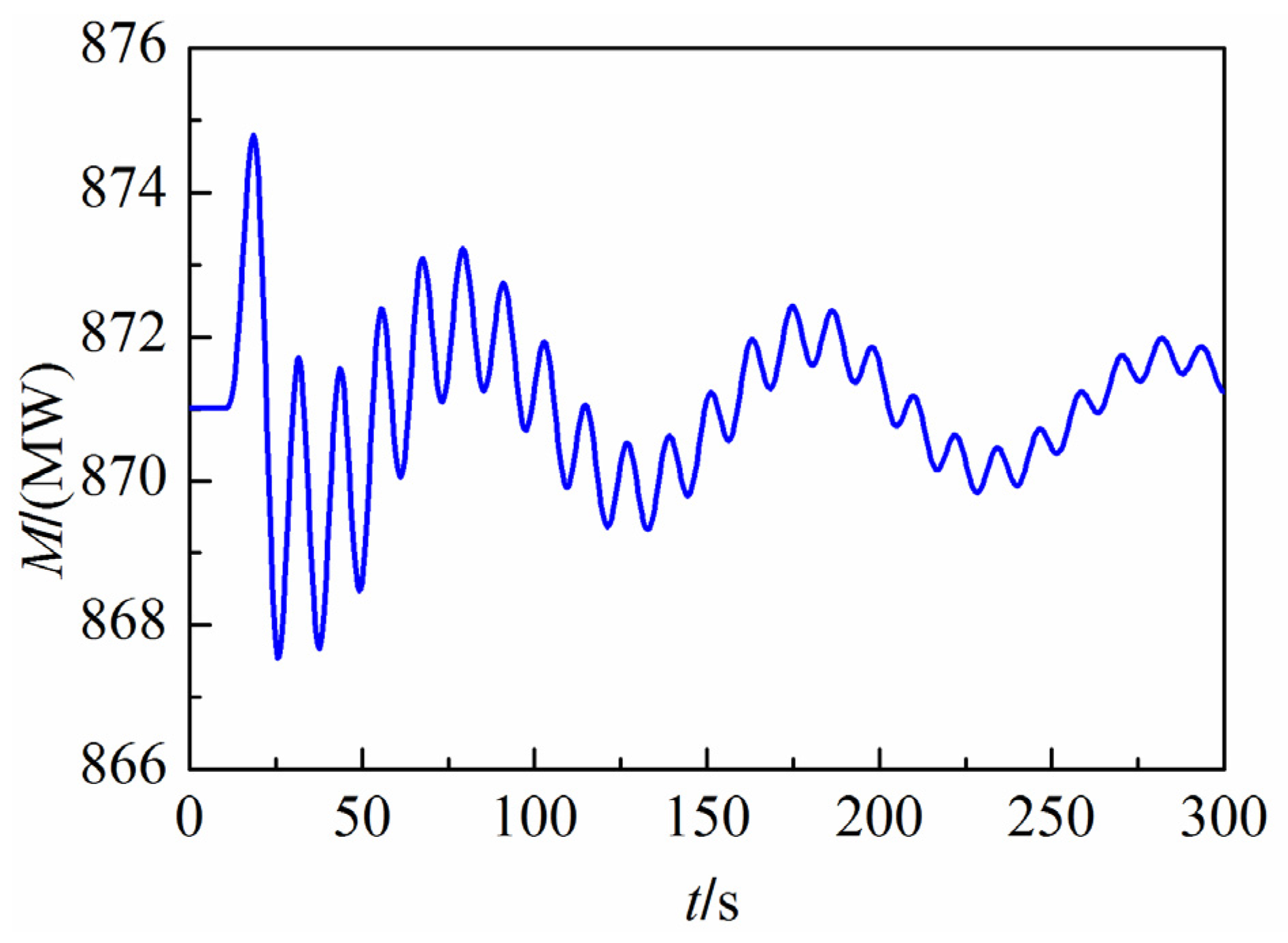
6. Discussion
7. Conclusions
- Some classic water hammer examples and transient gas flow behavior in pipes and the networks of pipes are solved using the Preissmann method. The reliability and accuracy of the method are verified by comparison with other approaches.
- A dynamic mesh method is applied to the water hammer equations and is used to solve the water level fluctuation in an open surge tank and a U-tube. The model considers the effect of inertial forces and friction in the tank, which is shown to be more precise and physically reasonable compared to other simplified models.
- A model for coupling the water hammer equations and the ideal gas state equations is presented to solve for the water level fluctuation in an air cushion surge tank. The effect of the polytropic exponent for the gas phase is studied.
- Transient flows of liquids and gases in pipelines are solved using the proposed method, and a model for coupling the liquid and gas phases is given to study the interaction between the water level fluctuations and the gas behavior in the duct. Two simplified models are presented and it is shown that an asynchronous coupled model operates as well as the synchronous coupled model.
- The proposed methods are used for the calculation of transient processes in a hydropower station. Peak wind speed in the air channel, and hydraulic disturbances caused by the gas phase, are studied in an engineering project.
Acknowledgments
Author Contributions
Conflicts of Interest
Notation
| A | pipe cross sectional area |
| B | wave speed in gas pipe |
| C | gas compressibility factor |
| a | wave speed in liquid pipe |
| D | pipe inner diameter |
| F | surge tank cross sectional area |
| f | Darcy-Weisbach friction factor |
| g | gravitational acceleration |
| H | pressure head |
| n | polytropic exponent |
| p | gas absolute pressure |
| Q | liquid volume flow rate |
| R | gas constant |
| t | time |
| V | mean velocity |
| x | distance along pipe centerline |
| Z | water level |
| α | impedance loss coefficient |
| β | pipe slope |
| ρw | water density |
| ρG | gas density |
| θ | weight coefficient |
| ΔH | increments of pressure head |
| ΔQ | increments of discharge |
| Δp | increments of pressure |
| ΔM | increments of mass flow rate |
Superscripts
| 0 | value of last time step |
Subscripts
| i | number of mesh line |
| M | last mesh line in gas pipe |
| N | last mesh line in liquid pipe |
Appendix A
Appendix B
- Rated output: 867.35 MW;
- Rated speed: 93.75 r/min;
- Rated flow: 716.77 m3/s;
- Rated head: 137 m;
- Runner inlet diameter: 8.9 m;
- Draft tube inlet diameter: 8.9 m;
- Rotary inertia: 340,000 t·m2;
- Rated guide vane opening: 81.7%;
- Upstream water elevation: 975 m;
- Downstream water elevation: 835 m;
- Closing regulation: Close in 10 s linearly;
- Penstock lengths: 628.29 m (#1), 83.57 m (#2), 538.85 m (#3), 494.14 m (#4), 449.42 m (#5), 404.70 m (#6);
- Penstock diameter: 13.5 m;
- Surge tank cross-sectional area (each): 1417 m2;
- Surge tank throttled area: 100 m2.
References
- Chaudhry, M.H. Applied Hydraulic Transients; Van Nostrand Reinhold: New York, NY, USA, 1987. [Google Scholar]
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transient in Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A review of water hammer theory and practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Hwang, Y. Development of a characteristic particle method for water hammer simulation. J. Hydraul. Eng. 2013, 139, 1175–1192. [Google Scholar] [CrossRef]
- Wiggert, D.C.; Sundquist, M.J. Fixed-grid characteristics for pipeline transients. J. Hydraul. Div. 1977, 103, 1403–1415. [Google Scholar]
- Goldberg, D.E.; Wylie, E.B. Characteristics method using time-line interpolations. J. Hydraul. Eng. 1983, 109, 670–683. [Google Scholar] [CrossRef]
- Lai, C. Comprehensive method of characteristics models for flow simulation. J. Hydraul. Eng. 1989, 114, 1074–1095. [Google Scholar] [CrossRef]
- Almeida, A.B.; Koelle, E. Fluid Transients in Pipe Networks; Elsevier: New York, NY, USA, 1992. [Google Scholar]
- Karney, B.W.; Ghidaoui, M.S. Flexible discretization algorithm for fixed grid MOC in pipeline systems. J. Hydraul. Eng. 1997, 123, 1004–1011. [Google Scholar] [CrossRef]
- Larock, B.E.; Jeppson, R.W.; Watters, G.Z. Hydraulics of Pipeline Systems; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Holly, F.M.; Preissmann, A. Accurate calculation of transport in two dimensions. J. Hydraul. Div. 1977, 103, 1259–1277. [Google Scholar]
- Rohani, M.; Afshar, M.H. Simulation of transient flow caused by pump failure: Point-implicit method of characteristics. Ann. Nucl. Energy 2010, 37, 1742–1750. [Google Scholar] [CrossRef]
- Afshar, M.H.; Rohani, M. Water hammer simulation by implicit method of characteristic. Int. J. Press. Vessels Pip. 2008, 85, 851–859. [Google Scholar] [CrossRef]
- Chaudhry, M.H.; Hussaini, M.Y. Second-order accurate explicitly finite-difference schemes for water hammer analysis. J. Fluids Eng. 1985, 107, 523–529. [Google Scholar] [CrossRef]
- Jin, M.; Coran, S.; Cook, J. New one-dimensional implicit numerical dynamic sewer and storm model. Glob. Solut. Urban Drain. 2002. [CrossRef]
- Pezzinga, G. Quasi-2D model for unsteady flow in pipe networks. J. Hydraul. Eng. 1999, 125, 676–685. [Google Scholar] [CrossRef]
- Guinot, V. Riemann solvers for water hammer simulations by Godunov method. Int. J. Numer. Methods Eng. 2000, 49, 851–870. [Google Scholar] [CrossRef]
- Hwang, Y.H.; Chung, N.M. A fast godunov method for the water-hammer problem. Int. J. Numer. Methods Fluids 2002, 40, 799–819. [Google Scholar] [CrossRef]
- Zhao, M.; Ghidaoui, M.S. Godunov-type solutions for water hammer flows. J. Hydraul. Eng. 2004, 130, 341–348. [Google Scholar] [CrossRef]
- León, A.; Ghidaoui, M.S.; Schmidt, A.; García, M. Godunov-type solutions for transient flows in sewers. J. Hydraul. Eng. 2006, 132, 800–813. [Google Scholar] [CrossRef]
- Sabbagh-Yazdi, S.R.; Mastorakis, N.E.; Abbasi, A. Water hammer modeling by Godunov type finite volume method. Int. J. Math. Comput. Simul. 2007, 4, 350–355. [Google Scholar]
- Greyvenstein, G.P. An implicit method for the analysis of transient flows in pipe networks. Int. J. Numer. Methods Eng. 2002, 53, 1127–1143. [Google Scholar] [CrossRef]
- Pretorius, J.J.; Malan, A.G.; Visser, J.A. A flow network formulation for compressible and incompressible flow. Int. J. Numer. Methods Heat Fluid Flow 2008, 18, 185–201. [Google Scholar]
- Wylie, E.B.; Streeter, V.L. Fluid Transients; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Osiadacz, A.J. Simulation and Analysis of Gas Pipeline Networks; E. & F.N. Spon: London, UK, 1987. [Google Scholar]
- Kessal, M. Simplified numerical simulation of transients in gas networks. Chem. Eng. Res. Des. 2000, 78, 925–931. [Google Scholar] [CrossRef]
- Thorley, A.R.D.; Tiley, C.H. Unsteady and transient flow of compressible fluids in pipelines—A review of theoretical and some experimental studies. Int. J. Heat Fluid Flow 1987, 8, 3–15. [Google Scholar] [CrossRef]
- Ibraheem, S.O.; Adewumi, M.A. On total variation diminishing schemes for pressure transients. J. Energy Resour. Technol. 1999, 121, 122–130. [Google Scholar] [CrossRef]
- Zhou, J.; Adewumi, M.A. Simulation of transients in natural gas pipelines using hybrid TVD schemes. Int. J. Numer Methods Fluid. 2000, 32, 407–437. [Google Scholar] [CrossRef]
- Einfeldt, B. On godunov-type methods for gas dynamics. SIAM J. Numer. Anal. 1988, 25, 294–318. [Google Scholar] [CrossRef]
- Herrán-González, A.; de La Cruz, J.M.; de Andrés-Toro, B.; Risco-Martín, J.L. Modeling and simulation of a gas distribution pipeline network. Appl. Math. Model. 2009, 33, 1584–1600. [Google Scholar] [CrossRef]
- Behbahani-Nejad, M.; Bagheri, A. The accuracy and efficiency of a MATLAB-Simulink library for transient flow simulation of gas pipelines and networks. J. Pet. Sci. Eng. 2010, 70, 256–265. [Google Scholar] [CrossRef]
- Alamian, R.; Behbahani-Nejad, M.; Ghanbarzadeh, A. A state space model for transient flow simulation in natural gas pipelines. J. Nat. Gas Sci. Eng. 2012, 9, 51–59. [Google Scholar] [CrossRef]
- Ke, S.L.; Ti, H.C. Transient analysis of isothermal gas flow in pipeline network. Chem. Eng. J. 2000, 76, 169–177. [Google Scholar] [CrossRef]
- Geem, Z.W. Multiobjective optimization of water distribution networks using fuzzy theory and harmony search. Water 2015, 7, 3613–3625. [Google Scholar] [CrossRef]
- Padulano, R.; del Giudice, G.; Carravetta, A. Experimental analysis of a vertical drop shaft. Water 2013, 5, 1380–1392. [Google Scholar] [CrossRef]
- Wang, C.; Yang, J.D. Water hammer simulation using explicit-implicit coupling methods. J. Hydraul. Eng. 2014, 141. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Yang, J.; Nilsson, H. Simulation of Water Level Fluctuations in a Hydraulic System Using a Coupled Liquid-Gas Model. Water 2015, 7, 4446-4476. https://doi.org/10.3390/w7084446
Wang C, Yang J, Nilsson H. Simulation of Water Level Fluctuations in a Hydraulic System Using a Coupled Liquid-Gas Model. Water. 2015; 7(8):4446-4476. https://doi.org/10.3390/w7084446
Chicago/Turabian StyleWang, Chao, Jiandong Yang, and Håkan Nilsson. 2015. "Simulation of Water Level Fluctuations in a Hydraulic System Using a Coupled Liquid-Gas Model" Water 7, no. 8: 4446-4476. https://doi.org/10.3390/w7084446
APA StyleWang, C., Yang, J., & Nilsson, H. (2015). Simulation of Water Level Fluctuations in a Hydraulic System Using a Coupled Liquid-Gas Model. Water, 7(8), 4446-4476. https://doi.org/10.3390/w7084446




