Uncertainty in Various Habitat Suitability Models and Its Impact on Habitat Suitability Estimates for Fish
Abstract
:1. Introduction
2. Materials and Methods
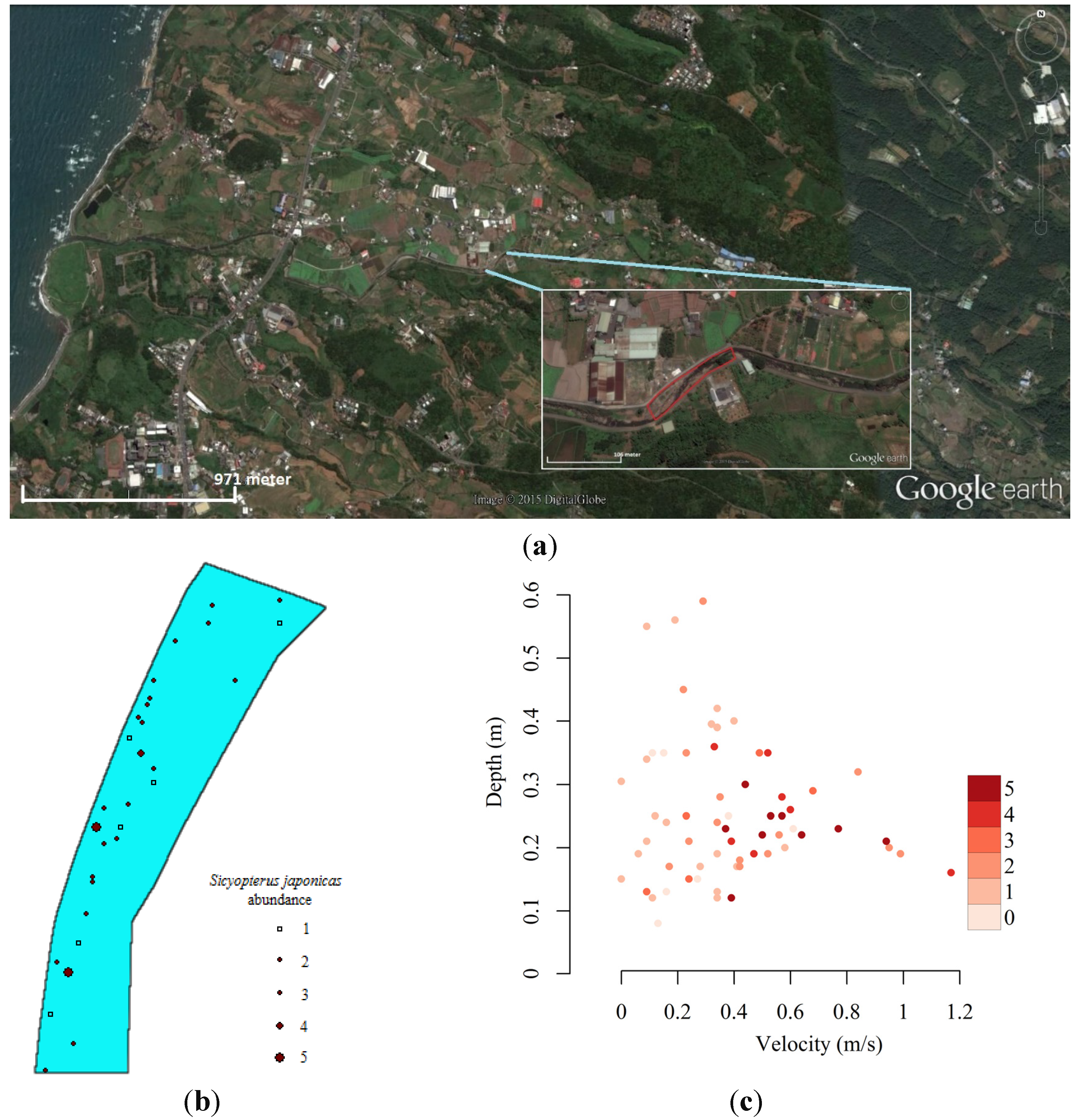
2.1. Hydraulic Model and Model Units
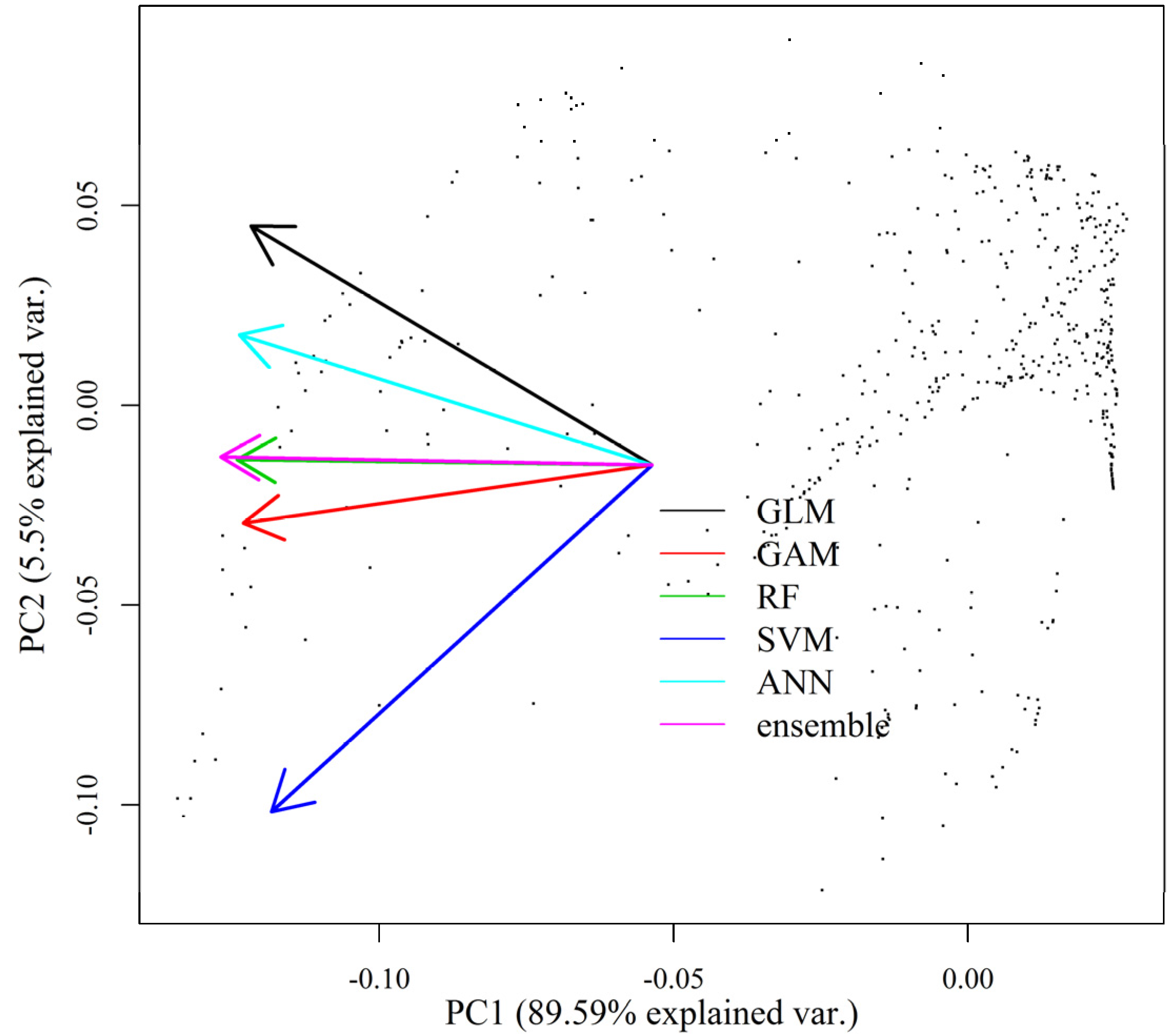
2.2. Ensemble Modeling of Species Distribution and Model Evaluations
2.3. Weighted Usable Area
2.4. Spatial Heterogeneity of Flow Conditions and Habitat Suitability
2.5. Quantifying Variability in Habitat Suitability Index for Each Model
3. Results
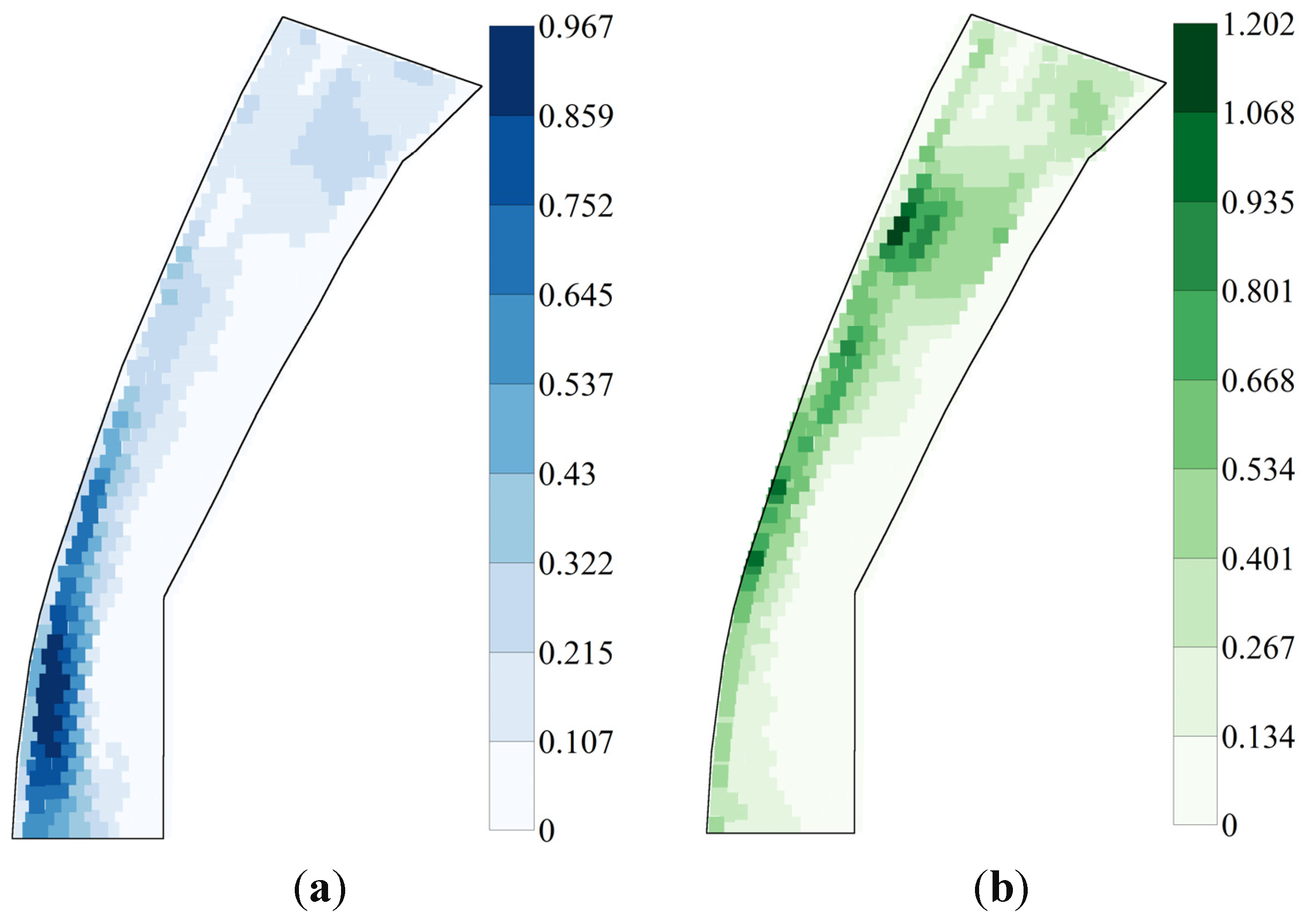
3.1. River 2D Simulations of Flow Conditions
3.2. HSI Obtained from SDMs and Ensemble Models
| Model Performance | GLM | GAM | RF | SVM | ANN | Ensemble |
|---|---|---|---|---|---|---|
| RMSE | 1.551 ± 0.212 | 1.518 ± 0.218 | 1.562± 0.221 | 1.531 ± 0.221 | 1.517 ± 0.208 | 1.505 ± 0.206 |
| AIC | 72.445 ± 3.814 | 74.313 ± 3.846 | – | 63.661 ± 7.407 | 34.805 ± 5.555 | – |
| KL | 0.250 ± 0.088 | 0.240 ± 0.086 | 0.247 ± 0.084 | 0.249 ± 0.093 | 0.234 ± 0.081 | 0.232 ± 0.081 |
| V+ D* | 30.90% | 39.00% | 74.10% | 33.80% | 32.60% | 37.20% |
| V* | 22.60% | 23.20% | 62.90% | 21.70% | 19.30% | 22.50% |
| D* | 8.30% | 15.80% | 11.60% | 12.10% | 13.70% | 14.60% |



3.3. Spatial Heterogeneity of Flow Conditions and of HSI

| Model | Mean | Standard Deviation | Median | Min | Max | Range | Skew | Kurtosis |
|---|---|---|---|---|---|---|---|---|
| GLM | 0.74 | 0.09 | 0.76 | 0.18 | 0.89 | 0.71 | –1.67 | 3.68 |
| GAM | 0.60 | 0.23 | 0.69 | 0.03 | 0.89 | 0.85 | –1.05 | –0.06 |
| RF | 0.63 | 0.05 | 0.63 | 0.45 | 0.80 | 0.35 | –0.08 | 0.03 |
| SVM | 0.67 | 0.06 | 0.67 | 0.46 | 0.84 | 0.38 | –0.22 | –0.36 |
| ANN | 0.59 | 0.12 | 0.60 | 0.29 | 0.86 | 0.57 | –0.21 | –0.46 |
| Ensemble | 0.64 | 0.10 | 0.66 | 0.04 | 0.83 | 0.79 | –1.03 | 1.93 |
3.4. Variability in Maps of HSI and WUA
| Model | GLM | GAM | RF | SVM | ANN | Ensemble |
|---|---|---|---|---|---|---|
| GLM | – | 0.85 | 0.88 | 0.70 | 0.91 | 0.93 |
| GAM | – | – | 0.87 | 0.83 | 0.87 | 0.96 |
| RF | – | – | – | 0.84 | 0.91 | 0.96 |
| SVM | – | – | – | – | 0.77 | 0.87 |
| ANN | – | – | – | – | – | 0.96 |
| Ensemble | – | – | – | – | – | – |
4. Discussion
4.1. Usefulness of River 2D in Simulating Flow Conditions
4.2. SDM-Determined Suitability of Habitat with Respect to Spatial Heterogeneity
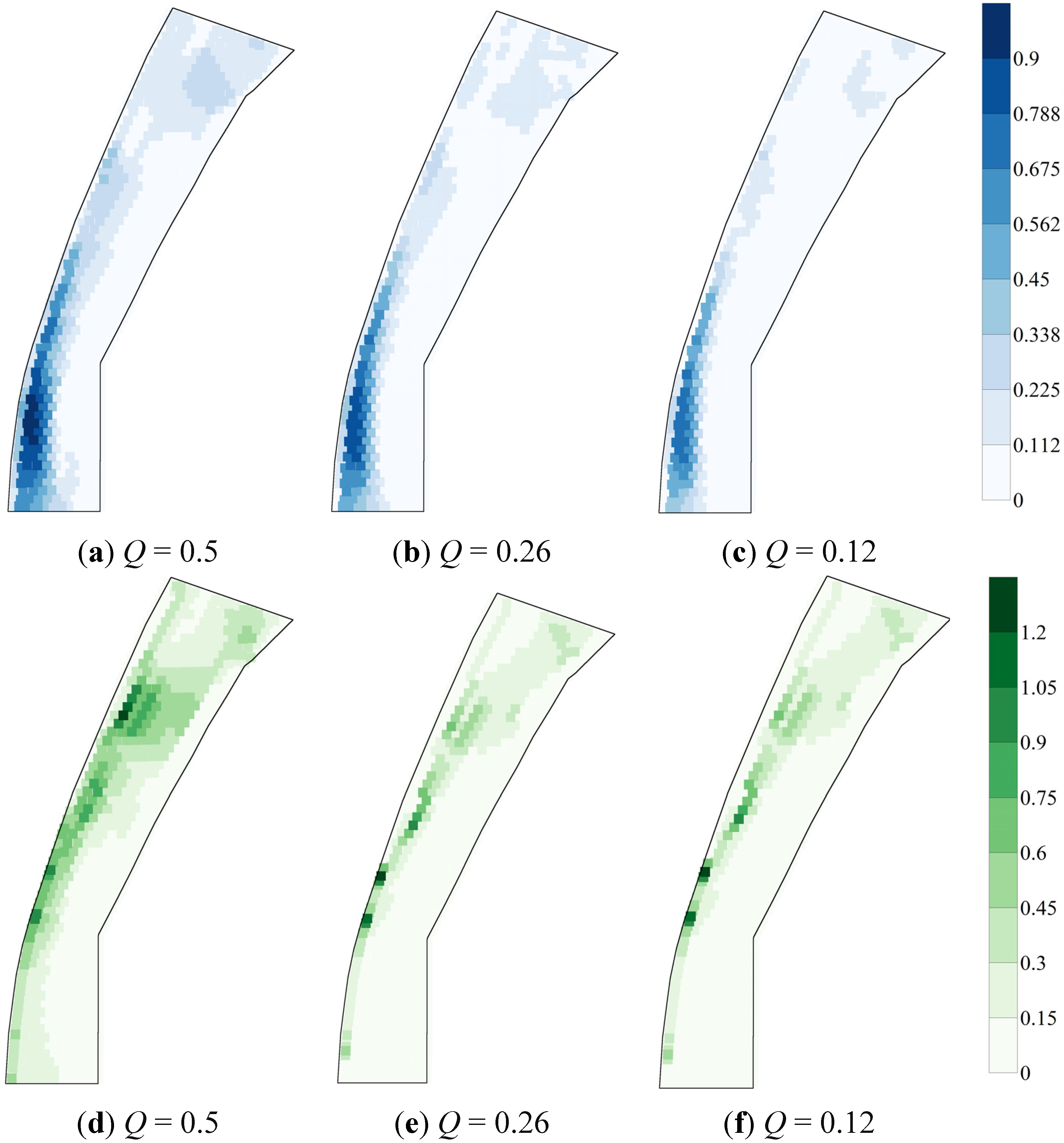
4.3. Variability in HSI That Originates from Various Sources of Uncertainty
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schwartz, J.S.; Herricks, E.E. Fish use of ecohydraulic-based mesohabitat units in a low-gradient illinois stream: Implications for stream restoration. Aquat. Conserv. Mar. Freshw. Ecosyst. 2008, 18, 852–866. [Google Scholar] [CrossRef]
- Steffler, P.; Blackburn, J. River2d: Two-Dimensional Averaged Model of River Hydrodynamics and Fish Habitat; University of Alberta: Edmonton, AB, Canada, 2002. [Google Scholar]
- Boavida, I.; Santos, J.; Cortes, R.; Pinheiro, A.; Ferreira, M. Benchmarking river habitat improvement. River Res. Appl. 2012, 28, 1768–1779. [Google Scholar] [CrossRef]
- Koljonen, S.; Huusko, A.; Mäki-Petäys, A.; Louhi, P.; Muotka, T. Assessing habitat suitability for juvenile atlantic salmon in relation to in-stream restoration and discharge variability. Restor. Ecol. 2013, 21, 344–352. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Wang, C.-L.; Yu, H.-H.; Huang, C.-W.; Wang, Y.-C.; Chen, Y.-W.; Wu, W.-Y. Monitoring and estimating the flow conditions and fish presence probability under various flow conditions at reach scale using genetic algorithms and kriging methods. Ecol. Model. 2011, 222, 762–775. [Google Scholar] [CrossRef]
- Fukuda, S.; Hiramatsu, K. Prediction ability and sensitivity of artificial intelligence-based habitat preference models for predicting spatial distribution of japanese medaka (oryzias latipes). Ecol. Model. 2008, 215, 301–313. [Google Scholar] [CrossRef]
- Schweizer, S.; Borsuk, M.E.; Jowett, I.; Reichert, P. Predicting joint frequency distributions of depth and velocity for instream habitat assessment. River Res. Appl. 2007, 23, 287–302. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Ayllón, D.; Almodóvar, A.; Nicola, G.; Elvira, B. Interactive effects of cover and hydraulics on brown trout habitat selection patterns. River Res. Appl. 2009, 25, 1051–1065. [Google Scholar] [CrossRef]
- Domisch, S.; Kuemmerlen, M.; Jähnig, S.C.; Haase, P. Choice of study area and predictors affect habitat suitability projections, but not the performance of species distribution models of stream biota. Ecol. Model. 2013, 257, 1–10. [Google Scholar] [CrossRef]
- Shearer, K.; Hayes, J.; Jowett, I.; Olsen, D. Habitat suitability curves for benthic macroinvertebrates from a small new zealand river. N. Z. J. Mar. Freshw. Res. 2015, 49, 1–14. [Google Scholar] [CrossRef]
- Fukuda, S.; Tanakura, T.; Hiramatsu, K.; Harada, M. Assessment of spatial habitat heterogeneity by coupling data-driven habitat suitability models with a 2D hydrodynamic model in small-scale streams. Ecol. Inf. 2014, in press. [Google Scholar] [CrossRef]
- Vezza, P.; Martinez Capel, F.; Muñoz Más, R.; Alcaraz-Hernandez, J.D.; Comoglio, C.; Mader, H.; Kraml, J. Habitat suitability modeling with random forest as a tool for fish conservation in mediterranean rivers. In Proceedings of the 9th International Symposium on Ecohydraulics, Vienna, Austria, 17–21 September 2012.
- Mocq, J.; St-Hilaire, A.; Cunjak, R. Assessment of atlantic salmon (salmo salar) habitat quality and its uncertainty using a multiple-expert fuzzy model applied to the Romaine River (Canada). Ecol. Model. 2013, 265, 14–25. [Google Scholar] [CrossRef]
- Mouton, A.; Alcaraz-Hernández, J.; de Baets, B.; Goethals, P.; Martínez-Capel, F. Data-driven fuzzy habitat suitability models for brown trout in Spanish Mediterranean Rivers. Environ. Model. Softw. 2011, 26, 615–622. [Google Scholar] [CrossRef]
- Muñoz-Mas, R.; Martinez-Capel, F.; Garófano-Gómez, V.; Mouton, A. Application of probabilistic neural networks to microhabitat suitability modelling for adult brown trout (Salmo trutta L.) in Iberian rivers. Environ. Model. Softw. 2014, 59, 30–43. [Google Scholar] [CrossRef]
- Segurado, P.; Araujo, M.B. An evaluation of methods for modelling species distributions. J. Biogeogr. 2004, 31, 1555–1568. [Google Scholar] [CrossRef]
- Beale, C.M.; Lennon, J.J. Incorporating uncertainty in predictive species distribution modelling. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 247–258. [Google Scholar] [CrossRef] [PubMed]
- Buisson, L.; Thuiller, W.; Casajus, N.; Lek, S.; Grenouillet, G. Uncertainty in ensemble forecasting of species distribution. Glob. Chang. Biol. 2010, 16, 1145–1157. [Google Scholar] [CrossRef]
- Gallo, J.; Goodchild, M. Mapping uncertainty in conservation assessment as a means toward improved conservation planning and implementation. Soc. Nat. Resour. 2012, 25, 22–36. [Google Scholar] [CrossRef]
- Meller, L.; Cabeza, M.; Pironon, S.; Barbet-Massin, M.; Maiorano, L.; Georges, D.; Thuiller, W. Ensemble distribution models in conservation prioritization: From consensus predictions to consensus reserve networks. Divers. Distrib. 2014, 20, 309–321. [Google Scholar] [CrossRef] [PubMed]
- Grenouillet, G.; Buisson, L.; Casajus, N.; Lek, S. Ensemble modelling of species distribution: The effects of geographical and environmental ranges. Ecography 2011, 34, 9–17. [Google Scholar] [CrossRef]
- Bartley, R.; Rutherfurd, I. Measuring the reach-scale geomorphic diversity of streams: Application to a stream disturbed by a sediment slug. River Res. Appl. 2005, 21, 39–59. [Google Scholar] [CrossRef]
- Yarnell, S. Quantifying Physical Habitat Heterogeneity in an Ecologically Meaningful Manner: A Case Study of the Habitat Preferences of the Foothill Yellow-Legged Frog (Rana Boylii); Nova Science Publishers: New York, NY, USA, 2008. [Google Scholar]
- Stewart, G.; Anderson, R.; Wohl, E. Two-dimensional modelling of habitat suitability as a function of discharge on two colorado rivers. River Res. Appl. 2005, 21, 1061–1074. [Google Scholar] [CrossRef]
- Maddock, I. The importance of physical habitat assessment for evaluating river health. Freshw. Biol. 1999, 41, 373–391. [Google Scholar] [CrossRef]
- Wallis, C.; Maddock, I.; Visser, F.; Acreman, M. A framework for evaluating the spatial configuration and temporal dynamics of hydraulic patches. River Res. Appl. 2012, 28, 585–593. [Google Scholar] [CrossRef]
- Brown, B.L. Spatial heterogeneity reduces temporal variability in stream insect communities. Ecol. Lett. 2003, 6, 316–325. [Google Scholar] [CrossRef]
- Torgersen, C.E.; Close, D.A. Influence of habitat heterogeneity on the distribution of larval pacific lamprey (Lampetra tridentata) at two spatial scales. Freshw. Biol. 2004, 49, 614–630. [Google Scholar] [CrossRef]
- Cadenasso, M.; Pickett, S.; Grove, J. Dimensions of ecosystem complexity: Heterogeneity, connectivity, and history. Ecol. Complex. 2006, 3, 1–12. [Google Scholar] [CrossRef]
- Wang, C.-L. Flow Condition Preference Study using Kriging and Sequential Indicator Simulation: The Case of Sicyopterus Japonicus in Datuan Stream. Master’s Thesis, National Taiwan University, Taipei, Taiwan, July 2010. [Google Scholar]
- Lin, Y.-P.; Wang, C.-L.; Chang, C.-R.; Yu, H.-H. Estimation of nested spatial patterns and seasonal variation in the longitudinal distribution of sicyopterus japonicus in the datuan stream, taiwan by using geostatistical methods. Environ. Monit. Assess. 2011, 178, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.-Y. Application of Genetic Programming and River2d to Assess the Habitat Preference of Riverine Fish: A case Study of Sicyopterus Japonicus in Datuan Stream. Master’s Thesis, National Taiwan University, Taipei, Taiwan, July 2011. [Google Scholar]
- McCullagh, P.; Nelder, J.A.; McCullagh, P. Generalized Linear Model; CRC Press: London, UK, 1989. [Google Scholar]
- Team, R.C. R: A language and environment for statistical computing. Available online: http://www.gbif.org/resource/81287 (accessed on 1 March 2015).
- Wood, S.N.; Augustin, N.H. Gams with integrated model selection using penalized regression splines and applications to environmental modelling. Ecol. Model. 2002, 157, 157–177. [Google Scholar] [CrossRef]
- Hastie, T. Gam: Generalized additive models. Available online: http://cran.fyxm.net/web/packages/gam/ (accessed on 1 March 2015).
- Breiman, L. Random forests. Machine Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. E1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly e1071), TU Wien. Available online: https://cran.r-project.org/web/packages/e1071/index.html (accessed on 1 March 2015).
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S-Plus; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Kullback-leibler information as a basis for strong inference in ecological studies. Wildl. Res. 2001, 28, 111–119. [Google Scholar] [CrossRef]
- Parasiewicz, P. Mesohabsim: A concept for application of instream flow models in river restoration planning. Fisheries 2001, 26, 6–13. [Google Scholar] [CrossRef]
- Shannon, C.E. The mathematical theory of communication. 1963. MD Comput. Comput. Med. Pract. 1996, 14, 306–317. [Google Scholar]
- Lin, W.-C.; Lin, Y.-P.; Lien, W.-Y.; Wang, Y.-C.; Lin, C.-T.; Chiou, C.-R.; Anthony, J.; Crossman, N.D. Expansion of protected areas under climate change: An example of mountainous tree species in taiwan. Forests 2014, 5, 2882–2904. [Google Scholar] [CrossRef]
- Araújo, M.B.; Whittaker, R.J.; Ladle, R.J.; Erhard, M. Reducing uncertainty in projections of extinction risk from climate change. Glob. Ecol. Biogeogr. 2005, 14, 529–538. [Google Scholar] [CrossRef]
- Thuiller, W. Patterns and uncertainties of species’ range shifts under climate change. Glob. Chang. Biol. 2004, 10, 2020–2027. [Google Scholar] [CrossRef]
- Waddle, T.J.; Holmquist, J.G. Macroinvertebrate response to flow changes in a subalpine stream: Predictions from two-dimensional hydrodynamic models. River Res. Appl. 2013, 29, 366–379. [Google Scholar] [CrossRef]
- Egrioglu, E.; Aladag, C.H.; Gunay, S. A new model selection strategy in artificial neural networks. Appl. Math. Comput. 2008, 195, 591–597. [Google Scholar] [CrossRef]
- Demyanov, S.; Bailey, J.; Ramamohanarao, K.; Leckie, C. Aic and bic based approaches for svm parameter value estimation with Rbf kernels. In Proceedings of 4th Asian Conference on Machine Learning, Singapore, 4–6 November 2012; pp. 97–112.
- Lee, S.; Park, I.; Koo, B.J.; Ryu, J.-H.; Choi, J.-K.; Woo, H.J. Macrobenthos habitat potential mapping using GIS-based artificial neural network models. Marine Pollut. Bull. 2013, 67, 177–186. [Google Scholar] [CrossRef] [PubMed]
- Marmion, M.; Parviainen, M.; Luoto, M.; Heikkinen, R.K.; Thuiller, W. Evaluation of consensus methods in predictive species distribution modelling. Divers. Distrib. 2009, 15, 59–69. [Google Scholar] [CrossRef]
- Shen, C.-C.; Tzeng, C.-T. Maintenance and management of ecological campuses—A case study in west cigu campus, national university of tainan. Avaliable online: http://www.irbnet.de/daten/iconda/CIB14386.pdf ( accessed on 2 November 2009).
- Hermoso, V.; Kennard, M.J. Uncertainty in coarse conservation assessments hinders the efficient achievement of conservation goals. Biolog. Conserv. 2012, 147, 52–59. [Google Scholar] [CrossRef]
- Regan, H.; Ensbey, M.; Burgman, M. Conservation Prioritization and Uncertainty in Planning Inputs; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Guisan, A.; Thuiller, W. Predicting species distribution: Offering more than simple habitat models. Ecol. Lett. 2005, 8, 993–1009. [Google Scholar] [CrossRef]
- Wilson, K.A.; Westphal, M.I.; Possingham, H.P.; Elith, J. Sensitivity of conservation planning to different approaches to using predicted species distribution data. Biol. Conser. 2005, 122, 99–112. [Google Scholar] [CrossRef]
- Stalnaker, C.; Lamb, B.L.; Henriksen, J.; Bovee, K.; Bartholow, J. The Instream Flow Incremental Methodology: A Primer for Ifim; United States Department of Interior National Biological Service: Washinton, DC, USA, 1995. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.-P.; Lin, W.-C.; Wu, W.-Y. Uncertainty in Various Habitat Suitability Models and Its Impact on Habitat Suitability Estimates for Fish. Water 2015, 7, 4088-4107. https://doi.org/10.3390/w7084088
Lin Y-P, Lin W-C, Wu W-Y. Uncertainty in Various Habitat Suitability Models and Its Impact on Habitat Suitability Estimates for Fish. Water. 2015; 7(8):4088-4107. https://doi.org/10.3390/w7084088
Chicago/Turabian StyleLin, Yu-Pin, Wei-Chih Lin, and Wei-Yao Wu. 2015. "Uncertainty in Various Habitat Suitability Models and Its Impact on Habitat Suitability Estimates for Fish" Water 7, no. 8: 4088-4107. https://doi.org/10.3390/w7084088
APA StyleLin, Y.-P., Lin, W.-C., & Wu, W.-Y. (2015). Uncertainty in Various Habitat Suitability Models and Its Impact on Habitat Suitability Estimates for Fish. Water, 7(8), 4088-4107. https://doi.org/10.3390/w7084088







