1. Introduction
In recent decades, since the damage caused by flood has been extremely severe, flood-diversion zones are often used for mitigating flooding disasters in many countries [
1]. However, various human activities still exist and even expand in such a floodplain (
i.e., flood-diversion zones) due to the pressures of increasing populations and developing economies. Particularly in some developing countries, annual human activities (e.g., resident, agriculture and industry) on the floodplain can decrease the retention capacity of water bodies, and varied runoff patterns under changing climatic conditions, which results in losses caused by flood exceeding the benefit of the floodplain [
2]. These lead to a variety of adverse impacts on development of economy and sustainability of human life [
3,
4]. Therefore, a sound strategy for water resources planning of floodplain is desired to address challenges of water shortage, flood events, unreliable water supply, and incremental water demand [
5]. However, uncertainties existing in planning processes are often impacted by social, economic, environmental, technical, and political factors, which are caused by not only limited data availabilities, but also imitations of artificial cognitions/statistics. Particularly in water resources management of floodplain (WMF), the non-flood and flood periods corresponding to deficit penalties and flooding losses exist in a WMF system synchronously; thus, the complexities of water resources plans would be intensified. Such uncertainties and their interrelationships can bring about enormous troubles and challenges for water managers to generate desired decision alternatives [
6]. Consequently, an effective plan of WMF for tackling uncertainties and their interactions is important for facilitating sustainable development in watershed systems [
7].
In WMF, multiple uncertainties can be expressed as various manners (e.g., probabilistic, fuzzy and nonlinear manners) caused by random unpredictable nature process, imitations of human understanding and error in accounting. Therefore, numbers of uncertain optimization methods can be introduced to tackle various manners of uncertainties, which can support water managers facing challenges of violated-risk due to uncertainties and their interactions [
8,
9,
10,
11,
12,
13,
14,
15]. For example, spatial and temporal variations (e.g., stream flows) and frequencies of peaks are associated with the net system benefit that would be the function of the stochastic factors, which can be expressed as probabilistic distributions due to data limited data availability. Meanwhile, water targets of human activities also comprise uncertainties that are associated with economic implications (e.g., deficient penalties) if the promised targets are violated [
16]. Therefore, one type of stochastic programming (SP) named two-stage stochastic programming (TSP) can be advocated to handle uncertainties expressed as probabilistic distributions. TSP is effective to provide an effective linkage between policies and the economic penalties, which has advantages in reflecting complexities of system uncertainties as well as analyzing policy scenarios when the pre-regulated targets are violated [
17]. However, it cannot handle fuzziness in water resources system due to the lack of data and limitations of human understanding/accounting. For example, water flow may be related to errors in acquired data, variations in spatial and temporal units, and incompleteness or impreciseness of observed information in water resources management [
18]. Fuzzy programming (FP) is effective to deal with decision problems under fuzzy goal or constraints caused by imprecision and vagueness, when the quality and quantity of uncertain information is often not satisfactory enough to be presented as probabilistic distribution [
19,
20]. However, since many other uncertain components (e.g., economic data, allocation target, and trading ratio) are often not straightforward enough to be expressed as probability/possibility distributions, interval-parameter programming (IPP) can be introduced to deal with uncertainties due to limited data availabilities existing in the model’s left- and/or right-hand sides, where interval numbers are acceptable as its uncertain inputs [
6,
7,
21]. Previously, a number of researchers have incorporated TSP, FP and IPP into a framework for water resources management. For example, Maqsood
et al. (2005) developed an interval-fuzzy two-stage stochastic programming method for planning water resources management systems associated with multiple uncertainties [
16]. Li
et al. (2007) proposed a mixed interval-fuzzy two-stage programming method for flooding diversion planning within a multi-reservoir system [
5]. Guo
et al. (2010) proposed an fuzzy-chance-constrained two-stage mixed-integer linear programming (IFCTIP) method for flood management under multiple uncertainties, which can facilitate dynamic programming for decisions of capacity-expansion planning under fuzzy-stochastic conditions. However, the developed methods had difficulties in dealing with vague information such as errors in acquired data and impreciseness of observed information [
1]. Zhang
et al. (2011) proposed an inexact credibility-constrained programming (ICP) method for planning water allocation, which could measure fuzzy uncertainties by credibility measure (
i.e., an average of the possibility measure and the necessity measure) to improve abilities on encode the vagueness of information [
21,
22]. However, for a real-world water resources management problem, nonlinear relationships can exist among many system components where revenue and cost parameters are expressed as functions of water demand and supply. The credibility-constrained programming has difficulties in tackling such problems. Quadratic programming (QP) can reflect nonlinearity in cost/benefit objectives, and has global optimum under a number of system conditions [
23,
24,
25,
26]. Unfortunately, few studies were focused on the IPP, FP and QP method for sustainable WMF planning within a two-stage context previously.
Therefore, the objective of this study is to develop a mix inexact-quadratic fuzzy water resources management model of floodplain (IQT-WMMF). The developed IQT-WMMF method is an integrated optimization technique for tackling multiple uncertainties expressed as discrete intervals, probability distributions, nonlinearity and fuzzy sets. The method is applied to a real case study of water resources management of Dahuangbaowa floodplain, China. The study region is threatened by water deficit and frequent flood contemporarily, where the vulnerable ecological system and human-induced soil erosion/vegetation degradation may intensify conflicts between ecological preservation and economic development in water resources utilization. The obtained results with various credibility levels will be used for identifying optimized water-allocation alternatives, lessening the losses of water deficits and floods, and achieving socioeconomic and ecological sustainability. The method can provide a scientific support for large-scale regional water-resources management under uncertainties at the watershed level.
2. Methodology
In a real-world problem of water resources management, uncertainties may be expressed as random variables, which result in the relevant decisions being made under varying probability levels. Such a problem can be formulated as a two-stage stochastic programming (TSP) model [
4,
5]. However, in a water resources management system, the impacts of marginal utility about uncertain benefit and penalty data (
i.e., interval values) may lead to the relevant objective function nonlinearity. Interval quadratic programming (IQP) can handle the nonlinearities in the objective function and reflect uncertainty expressed as interval values [
23,
24]. Therefore, introducing IQP into TSP model, an inexact two-stage quadratic programming (ITQP) model can be formulated as follows:
subject to
where
is vector of first-stage decision variables, which presents water demand in a water resources management problem usually [
16]. Since water demand (
i.e., first-stage decision variables) is often confirmed by decision makers according to empirical value previously, it would be rectified by random event in actual water resources situations in planning periods, which would obtain first-stage benefits
[
25].
ph is probability of random event, where
pth is probability of occurrence for scenario
h [
16].
is recourse at the second-stage under the occurrence of event (presents water shortages), which obtain expected value of the second-stage penalties
[
23]. Since economic data are nonlinear in such a water recourses problem,
,
,
and
are used for tackle relevant objective function nonlinearity.
and
have a function relation to first-stage variables (
i.e., (
)) to use for expressing unit system benefit of water being delivered;
and
have a function relation to recourse variables (
i.e., (
)) to serve the purpose of showing unit penalty (
i.e., unit loss) of water not being delivered. Therefore, a recourse action between first- and second-stage variables (
i.e.,
and
) would tend to higher unit system benefit and lower penalty of water resources, which results in optimal values of
f±,
and
are coefficients of
and
;
is random variable of constraint
i, which is associated with probability level
ph [
5]. In Equations (1a)–(1e), the decision variables are divided into two subsets: those that must be determined before the realizations of random variables are disclosed (
i.e.,
), and those (recourse variables) that can be determined after the realized random-variable values are available (
i.e.,
). Since some of these coefficients in Equation (2b) can be fuzzy numbers, credibility theory would be introduced to tackle fuzzy uncertainties [
27,
28].
Credibility theory was initialized by Liu and Liu [
29] in 2002, which is superior to traditional possibility measure and necessity measure to tackle fuzzy uncertainties due to its property of self-dual [
30]. Let
be a fuzzy set of imprecise right-hand sides with possibility distributions, Equation (2b) can be expressed as follows:
where credibility of satisfying of
should be greater than or equal to level λ.
is a fuzzy set of imprecise right-hand sides with possibility distributions [
27]. Let
Bj be a fuzzy variable with membership function μ, and let μ and
r be real numbers. The possibility of a fuzzy event, characterized by
, is defined by
, while the necessity of a fuzzy event, characterized by
, is defined by
[
31]. The credibility measure (Cr) is an average of the possibility measure and the necessity measure [
32]:
Let
be a triangle fuzzy number and it is adopted in this study due to its computational efficiency. Accordingly, the credibility of the constraint
could be defined as follows [
33,
34], and the corresponding credibility measures are as follows:
where λ is credibility level. In the optimization process for management and planning, it is usually assumed that the credibility level should be no less than 0.5 [
35]. Thus, Equation (2a) can be rewritten as:
where it can be transformed into a deterministic constraint as follows:
Then, an interactive two-step solution algorithm is proposed for solving the inexact-quadratic two-stage programming (IQT) model, which is different from normal interval analysis and best/worst-case analysis [
3,
15]. The IQT model can be transformed into two sets of deterministic submodels, which correspond to the lower and upper bounds of the desired objective function value. The resulting solutions can provide intervals for the objective function and decision variables with different levels of risk in violating the constraints. A two-step solution method is proposed for solving the IQT model as shown in
Appendix [
15,
35].
3. Case Study
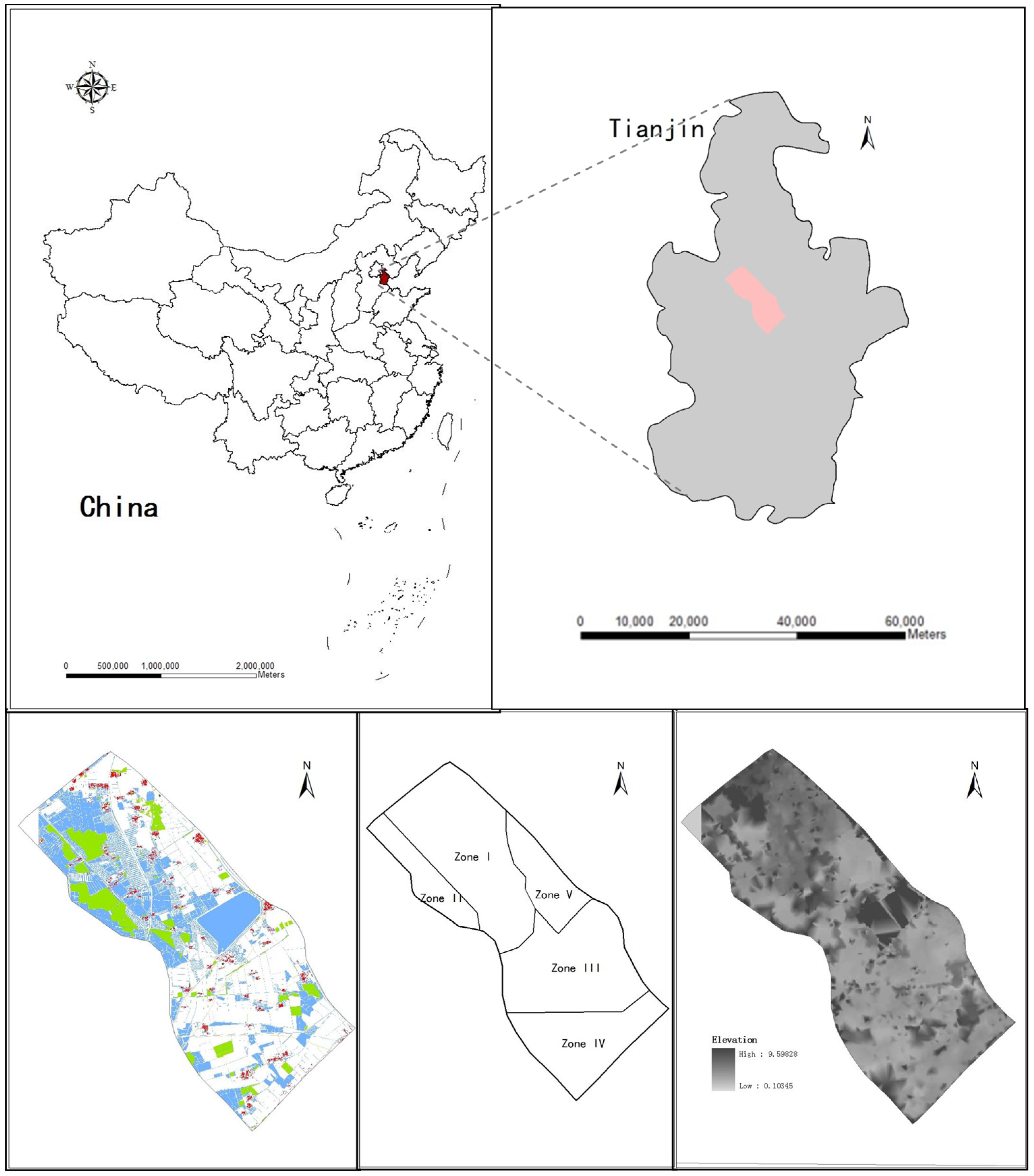
Dahuangbaowa floodplain is located at the junction of Baodi, Wuqing and Ninghe counties of Tianjin province, which is flanked by Hai River (as shown in
Figure 1). The Dahuangbaowa floodplain is located in the continental monsoon climate zone, with an average year temperature of 11.5 °C and average rainfall about 578 mm per year [
36,
37,
38,
39]. Precipitation varies largely among different seasons, of which more than 75% of the total annual precipitation falls from May to September, and less than 20% of the total falls from November to the following April [
40]. Since the floodplain locates at the downstream of Hai River, it is used for mitigating flooding disasters when flood occurs. However, with pressures of high-speed economic development and increased population growth, many human activities can exist even expand in this region. Particular in recent years, agriculture, fishery and livestock are developing at a high speed in this region; while agricultural products processing and manufacturing has been developed due to moderate natural conditions for the growing crops (e.g., wheat, corn, sugar beet, tomato, and fruit), fishing and breeding. Up until 2011, the gross national product (GDP) of floodplain reaches $ 0.61 billion and the population exceeds 46.8 thousand spreading 33 villages [
41,
42,
43,
44].
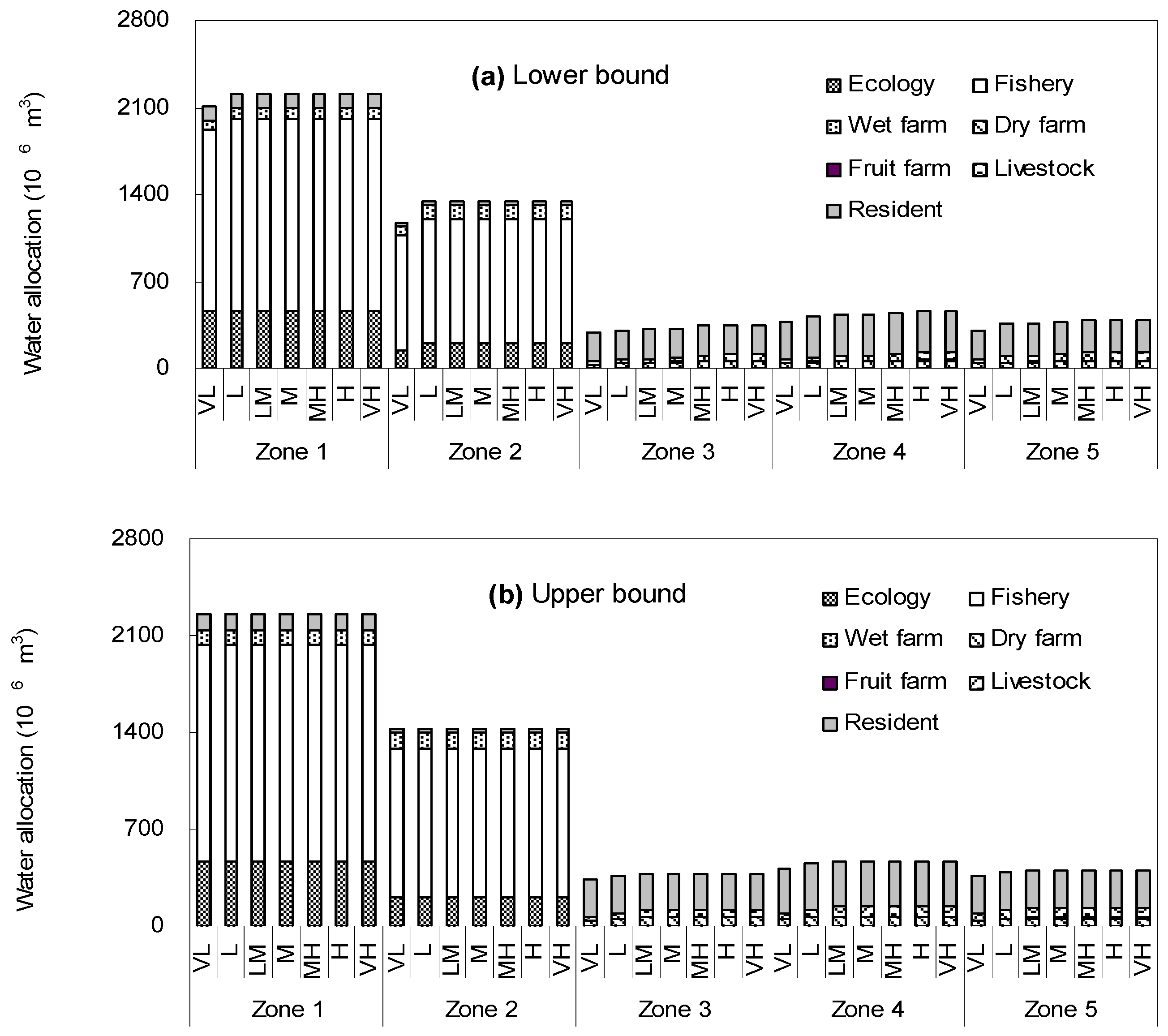
Figure 1 shows the division of study regions, which is based Geographic Information System (GIS). In this study, GIS is used to express land use information in study region, where the data of land-use is acquired based on the second national land survey data (2009) [
45]. Meanwhile, through the 2765 measured elevation point in the region, the DEM diagram is achieved based on inverse distance weighted interpolation. According to actual terrains and land-use of floodplain, five regions can be divided (
i.e., conclude floodplain places and flood buffer areas), where water demands of users (e.g., municipal, agricultural, and ecological users) rely on river’s stream-flow. Regions 1 and 2 (denoted as zones 1 and 2) are floodplain places, which are near to the flood discharge valve. They are deemed as diversions for flood discharges during flood time; while they are used for fishery, ecology and wet farm during other time. When the water inflows exceed water-conveyance capacity of river, it may overflow during flooding events. Then water managers would release floods water to diversion regions, which results in submerging zones 1 and 2. Regions 3 to 5 (denoted as zones 3, 4 and 5) (far away from flood discharge valve) are flood buffer areas with aim to buffer flood, which conclude livestock, resident and dry farm. When flood events occur, the released flood water would overwhelm zones 1 and 2 firstly, then it submerge zones 3 to 5. Since regions 1 and 2 have already relieved the main pressures of flooding, zones 3 to 5 would encounter minor spates (
i.e., lower damages) usually, which indicate that important infrastructure and intensive human activities may exist within these regions. Moreover, the depths of the flood diversion regions are different for various kinds of diversion regions. For example, for a lake, the depth of the diversion region can be as high as 50 m, but for a plain place of the diversion region, the depth of the diversion region can only be as low as 2 m. Therefore, the capacities of acceptant flood water can be acquired that zones 1 and 2 are relative low-lying to adopt more flood water, while zones 3 to 5 are high-lying to encounter less released water.
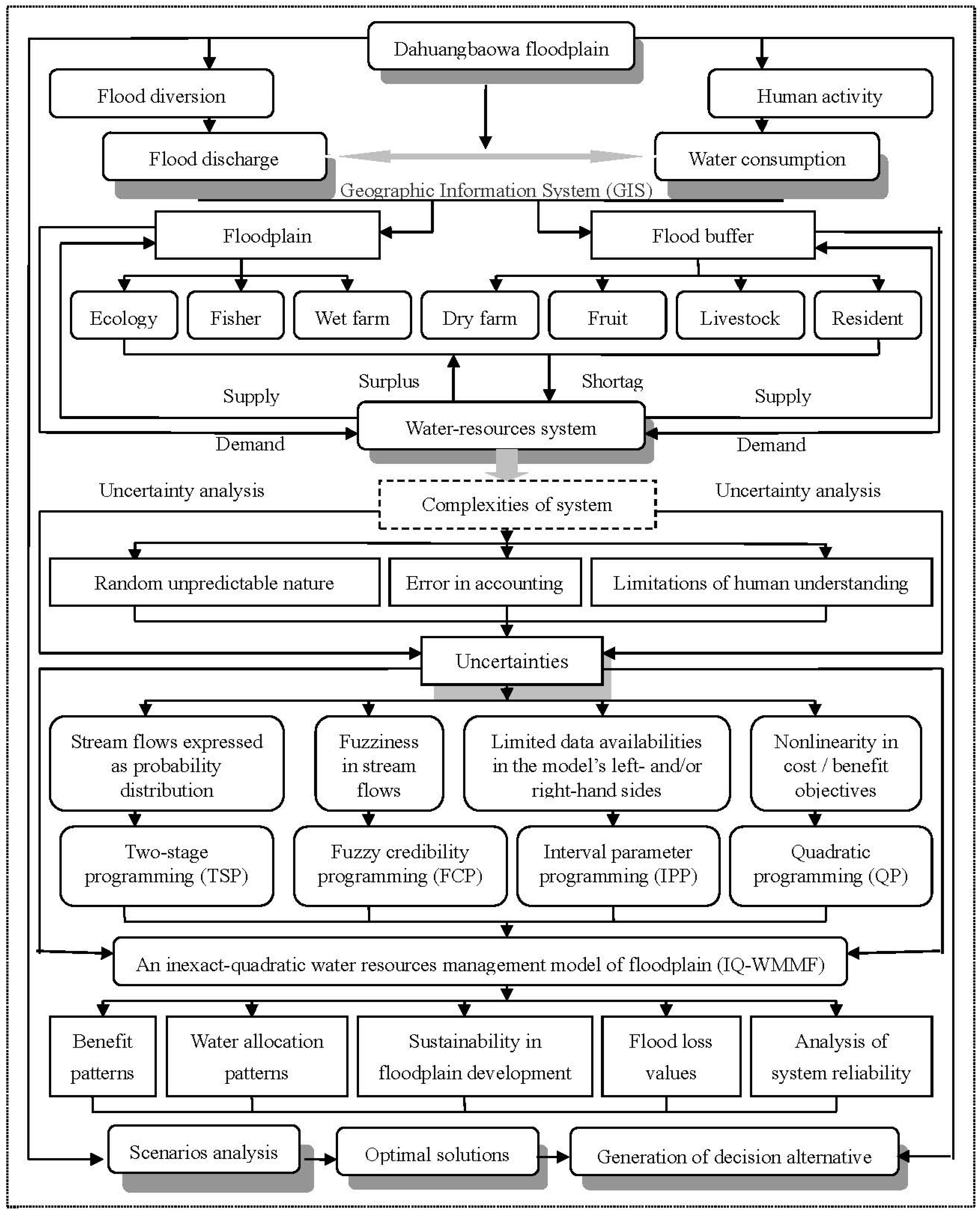
Figure 2 presents the framework of IQT-WMMF application of the Dahuangbaowa floodplain. Since the functions of the Dahuangbaowa floodplain conclude flood mitigations and water consumptions, an effective plan to support sustainability in this region can be proposed. In the divided five zones (concluding floodplain and flood buffer), various water users (e.g., ecology, fishery, wet farm, dry farm, fruit farm, livestock and resident) would encounter different risks of flood damages and water deficits. The local authority of floodplain is charge of delivering water to meet demands for the development of regional economy and human life in no-flooding period; meanwhile it is responsible for minimizing the damage of flood when flood occurs. Due to spatial and temporal variations of the relationships between water demand and supply, the desired water-allocation patterns would vary under different strategies of allocation target and outcomes of stream inflow. If water-allocation target pre-regulated by the authority is too high (
i.e., higher than the available water), the pre-regulated water could not be successfully delivered; shortage would thus be generated. Correspondingly, either the water must be obtained from higher priced alternatives or the demand must be curtailed with reduced production activities, resulting in a decreased net system benefit (
i.e., penalty from the shortfalls). On the other hand, if the target as pre-regulated by the authority is too low (
i.e., much lower than the available water), more surplus may be generated. When the surplus exceeds the storage capacities of the reservoirs, spill would occur, which might potentially lead to a flooding event. Losses can hardly be avoided when occurs [
16]. Meanwhile, since tremendous changes in stream flow in flooding and no-flooding seasons, water shortages and surplus (flood water) would be amplified. Consequently, an optimal strategy for water-allocation target, which is associated with the minimized shortage and surplus, is desired. However, uncertainties exist in many system examples; in a water resources management problem, it is more direct to specify the cost and benefit coefficients within an interval range. Moreover, it is often unreliable to obtain the probability density functions (PDFs) of a random event with probability fit when stream- inflow data are not enough; however, such uncertain data are relatively easy to be expressed as several interval values or fuzzy-interval numbers. These uncertainties and complexities lead to further challenges in identifying optimal water-allocation strategies.
Figure 2.
Framework of IQT-WMMF application of Dahuangbaowa floodplain.
Figure 2.
Framework of IQT-WMMF application of Dahuangbaowa floodplain.
The proposed IQT-WMMF method is considered to be applicable for tackling such a problem. Thus, we have:
where
presents system benefits when water demand targets are delivered (satisfied) ($);
is losses of water shortage (under probability
pj) in no-flooding season ($);
is losses of inundation in flooding season ($). The objective is to maximize the expected net system benefit in no-flooding/flooding season.
where
j denotes name of region (
j = 1, 2, …, 5). The regions 1 and 2 (
j = 1 and 2) are floodplain places for flood diversions during flood time; while the regions 3 to 5 (
j = 3 to 5) are flood buffer areas with aim to buffer flood.
XMj is water target for municipal sector in zone
j (m
3), which is first-stage variable. Similarly,
XEj,
XWj,
XDj,
XFj,
XRj, and
XLj are target of irrigation area for ecological, wet farm, dry farm, fishery, fruit farm, livestock sector in zone
j (ha).
and
are net benefit parameters to municipal sector in zone
j per unit of water being allocated, which have a function relation to first-stage variables (e.g., water targets) to use for tackling nonlinear uncertainties in economic data. Thus, net benefit can be presented as a quadratic programming (QP) expression (
i.e.,
(
)). In the same way,
,
,
,
,
,
,
,
,
,
,
and
are net benefit parameters to ecological, wet farm, dry farm, fishery, fruit farm, livestock sector in zone j per unit of water allocated;
IREj,
IRWj,
IRDj,
URFj,
URRj, and
URLj, are unit water computation of ecological per area (m
3/ha).
where
h denotes probability level of random water availability (
h = 1, 2, …, 7),
h = 1 to 7 represent various water availability levels such as very low (
i.e.,
VL), low (
i.e.,
L), low-medium (
i.e.,
LM) medium (
i.e.,
M), medium-high (
i.e.,
MH), high (
i.e.,
H) and very high (
i.e.,
VH).
phj denotes probability of random water availability
under level
h (%); Water shortages would occur when water availability levels are relative low, which result in losses in water resources system.
YMj is water shortage for municipal sector in zone
j (m
3), which is second-stage variable;
YEj,
YWj,
YDj,
YFj,
YRj and
YLj are water shortages of irrigation areas for ecology, wet farm, dry farm, fishery, fruit farm, livestock in zone
j (ha).
and
are penalties/losses parameters to municipal sector in zone j per unit of water not being allocated. They are used for tackling nonlinear uncertainties in economic data through a function relation to first-stage variables (
i.e.,
) , which reflecting unit system benefit of water being delivered. Similarly,
,
,
,
,
,
,
,
,
,
,
and
are penalties/losses parameters to ecology, wet farm, dry farm, fishery, fruit farm, livestock in zone
j per unit of water allocated.
when water availability levels are very high even flash floods, damages of floods would result in losses in water resources system.
ZMj is water surplus (
i.e., flood water) for municipal sector in zone
j (m
3), which results in losses in flooding seasons.
ZEj,
ZWj,
ZDj,
ZFj,
ZRj and
ZLj are water surplus (
i.e., flood water) for ecology, wet farm, dry farm, fishery, fruit farm, livestock in zone
j (m
3).
DMj,
DEj,
DWj,
DDj,
DFj,
DRj, and
DLj are losses for municipaityl, ecology, wet farm, dry farm, fishery, fruit farm, livestock in zone
j ($/m
3), when flood occurs, which are associated with net system benefits, ratio of water sluice control, direct loss ratio of flood and indirect loss correction coefficient of flood (as shown in Model (4d)).
Constraints include the available water resources, water shortage, flood water, flooding loss, water usage of resident, land use and non-negative as follows:
- (1)
Constraints of water availability:
Constraint (1) presents the mass balance for water resources system. Where water availability (
i.e.,
QDjh) equals water flow (
i.e.,
QFjh) minus evaporation/infiltration loss (
i.e.,
) and normal water requirement of watercourse (
i.e.,
HQjh) (m
3). Since data of water flow is limited,
is a fuzzy number in the Equation (4a), which result in fuzziness in water availability (
i.e.,
).
- (2)
Constraints of water shortage:
Constraints (2) presents water shortages in no-flooding seasons. Since water demand target is pre-regulated at the beginning of year based on empirical value previously, and pre-regulated water target is not equal to current water availability, a recourse problem would occur to optimize water demand target and system benefit. Equation (4b) reflects that a recourse action has to be undertaken to minimize the reduction of system benefit (
i.e., deficiency loss), when the available water resources could not satisfy the water demand.
- (3)
Constraints of flood water:
Constraints (3) present flood water in flooding seasons. When water deluges, the water availability has exceed water demand, the surplus water (
i.e., flood water) would damage benefits of each water users, which results in extensive losses (concluding indirect and direct losses) in study area.
- (4)
Constraints of flooding loss:
Since extents of damage in water flood are influenced by numbers of factors such as water levels, human land-use of region, sluice control in flood discharge, economic development and indirect/direct loss correction coefficient of flood, the values of flooding losses can be estimated by relative impact factors (e.g., net system benefits, ratio of water sluice control, direct/indirect loss ratio of flood) in study regions. There are two steps in the estimation processes: (a) when flood water is less than maximum damaged water, the values of flooding losses equals to sum of one and σ (
i.e., the indirect loss correction coefficient of flood in district
j) multiplied by α (
i.e., the ratio of water sluice control) or β (
i.e., the direct loss ratio of flood in district
j) based on are net benefits of municipality, ecology, wet farm, dry farm, fishery, fruit farm, livestock in zone j per unit of water allocated; (b) when flood water is more than maximum damaged water, the values of flooding losses are estimated by σ, α and β based on are limited unit lost of flood drowning for municipality, ecology, wet farm, dry farm, fishery, fruit farm, livestock in zone
j ($/m
3) (
i.e.,
DMOj,
DEOj,
DWOj,
DDOj,
DFOj,
DROj and
DLOj). Moreover, since floodplain places (
i.e., zone 1 and 2) are deemed as flood diversions during flood time, the ratio of water sluice control would influence damages in these two regions. Under these situations, values of flood losses of fishery, ecology and wet farm (in zone 1 and 2) equal to sum of one and σ (
i.e., the indirect loss correction coefficient of flood in district
j) multiplied by α (
i.e., the ratio of water sluice control) based on net system benefits/limited unit lost of flood drowning for fishery, ecology and wet farm sector in zone j ($/m
3). In contrast, values of flood losses of livestock, fruit farm, resident and dry farm (in zones 3, 4 and 5) equal to sum of one and σ (
i.e., the indirect loss correction coefficient of flood in district
j) multiplied by β (
i.e., the direct loss ratio of flood in district
j) based on net system benefits/limited unit lost of flood drowning for livestock, fruit farm, resident and dry farm.
- (5)
Constraints of water usage of resident:
Constraints (5) is restrictions of water usage of resident, where
is maximum capacity of water usage of resident in study region.
- (6)
Constraints (6) are restrictions of land use, which indicates that target of irrigation area for ecological, wet farm, dry farm, fishery, fruit farm, livestock sector (
i.e.,
XEj,
XWj,
XDj,
XFj and
XRj) are less than maximum capacities of land use (
i.e.,
XMEj,
XMWj,
XMDj,
XMFj and
XMRj) (ha).
- (7)
Constraint (7) is technical constraint.
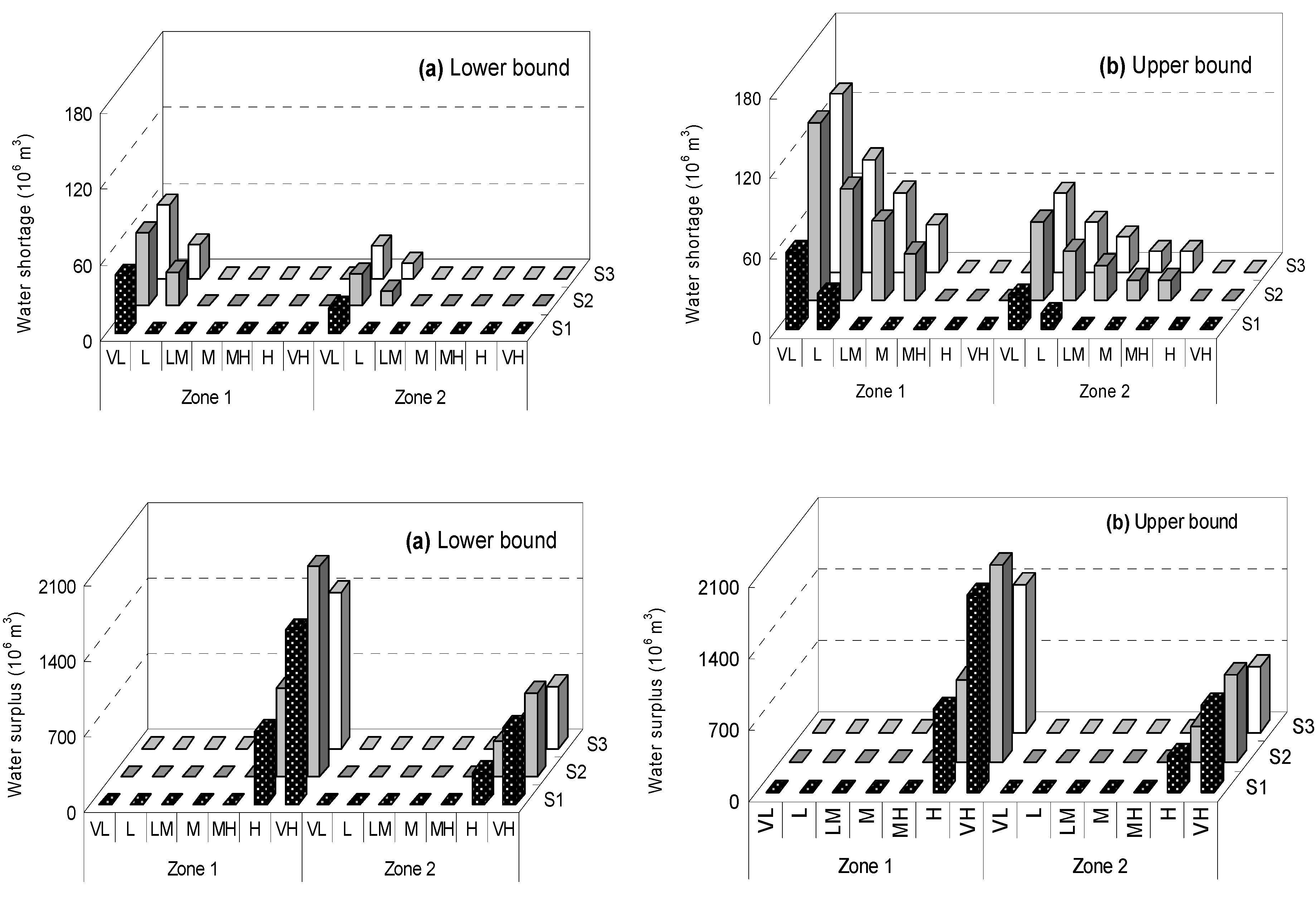
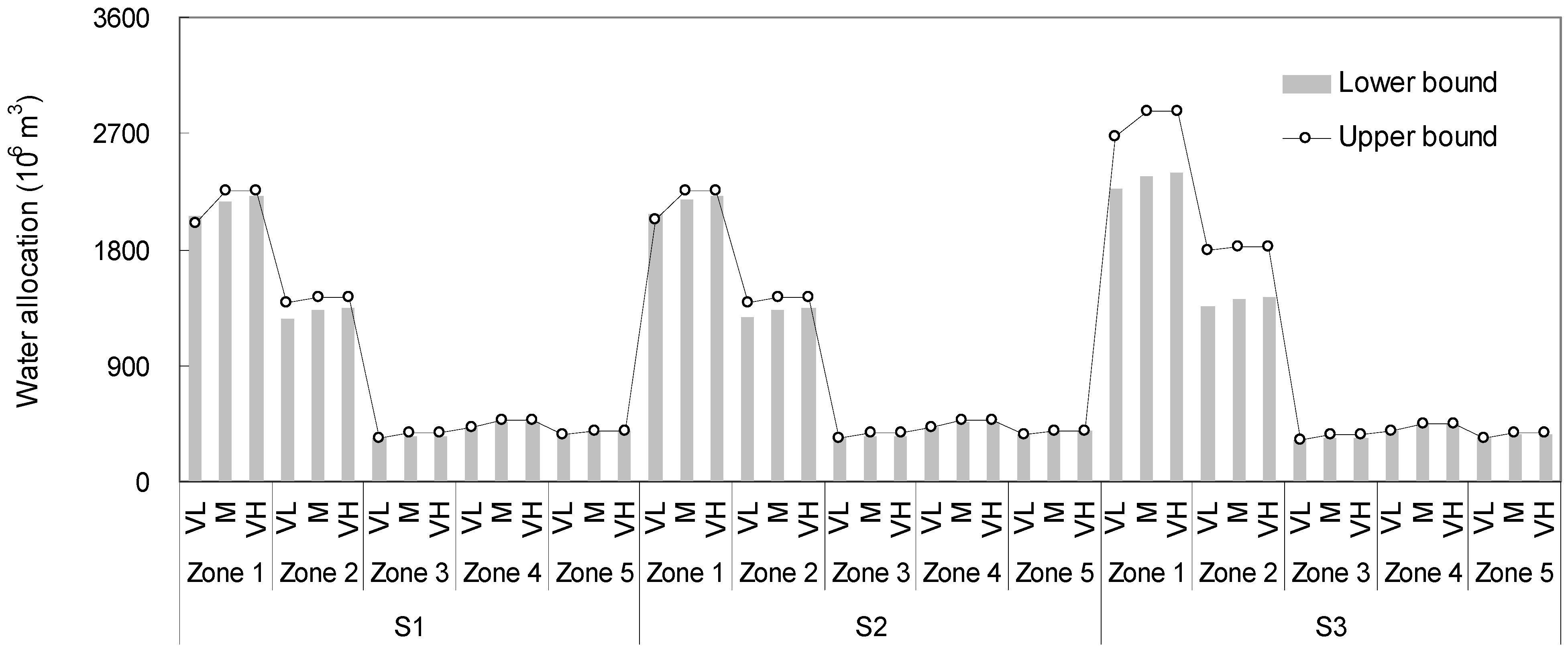
The developed method is applied to a relatively small-scale watershed system where flood water needs to be diverted from a river channel to multiple-diversion regions in a flooding season. In these five regions, water can be delivered to every users to satisfied there pre-regulated water target, shortages and surplus would be occur due to temporal and spatial water inflows. Decision makers desire sound water allocation patterns (no-flooding period) and flood diversion alternatives (flooding period) with both minimized system loss and maximized system safety.
Table 1 provides different water flow levels associated with varied probabilities of occurrences, where the system losses (
i.e., water deficits and flood damages) are varied with water flows temporally and spatially.
Table 1.
Economic data.
| Zone | Water Consumer |
|---|
| Ecology | Fishery | Wet farm | Fruit Farm | Fruit Farm | Livestock | Resident |
|---|
| Net system benefit ($103/103m3) |
| Lower bound | −48.1x + 208.2 | −51.9x + 225.3 | −85.3x + 369.3 | 60.4x − 44.4 | 186.2x − 180.5 | −19.2x + 751.5 | 8.6x + 804.6 |
| Upper bound | −50.7x + 219.1 | −54.7x + 237.1 | −89.8x + 388.8 | 63.6x − 46.6 | 196x − 190 | −20.2x + 791.0 | 9x + 847 |
| Loss of water shortage ($103/103m3) |
| Lower bound | −52.9x + 228.9 | −62.4x + 270.4 | −102.4x + 443.2 | 86.5x − 81.1 | 223.4x − 216.6 | −23.0x + 901.8 | 10.3x + 964.9 |
| Upper bound | −55.8x + 241.0 | −65.7x + 284.6 | −103x + 447.5 | 76.3x − 55.9 | 235.2x − 228 | −33.8x + 968.2 | 10.8x + 1016.4 |
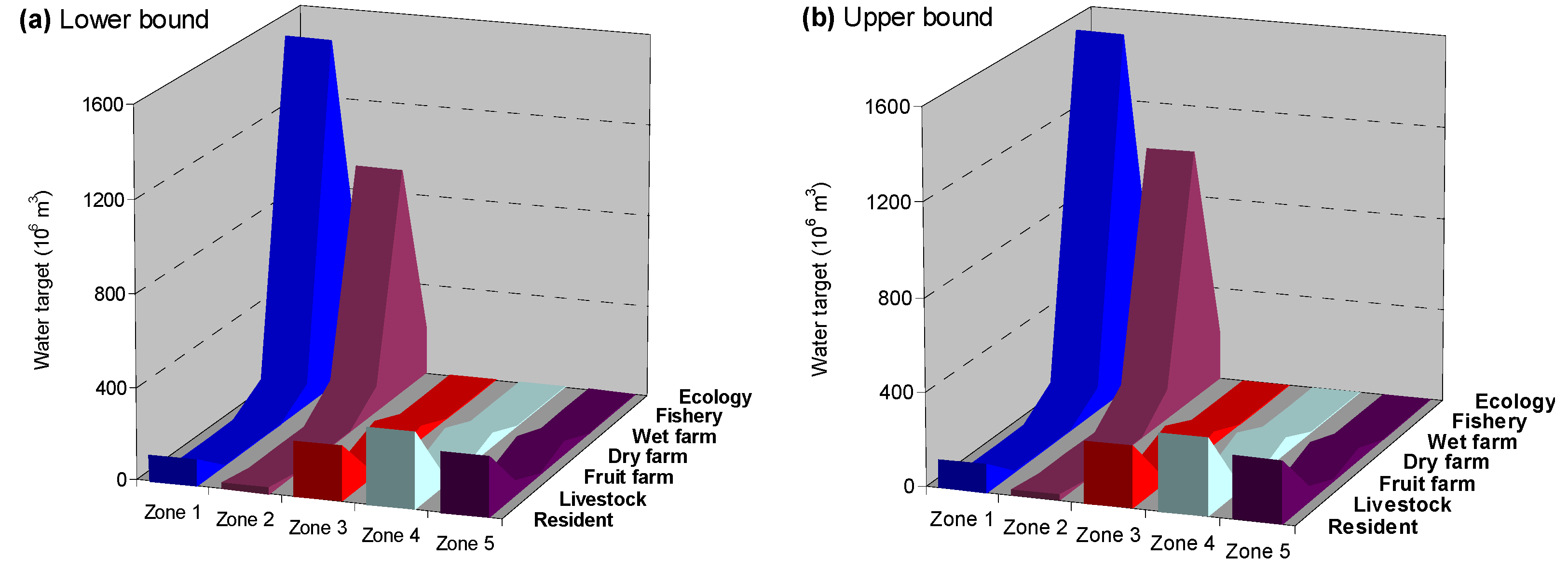
Table 2 shows water demand target based on water resources bulletin of Tianjin 2000–2013, which is estimated by users’ actual water using in recent years while considering the situation of socio-economic development.
Table 2.
Water demand target.
Table 2.
Water demand target.
| Zone | Water Demand Target (106 m3) |
|---|
| Ecology | Fishery | Wet Farm | Dry Farm | Fruit Farm | Livestock | Resident |
|---|
| 1 | [418.3, 464.8] | [1410.8, 1567.5] | [100.8, 112.0] | [0, 0] | [0, 0] | [0, 0] | [107.3, 119.3] |
| 2 | [184.9, 204.6] | [992.6, 1102.9] | [119.0, 132.2] | [0, 0] | [0, 0] | [0, 0] | [24.3, 27.0] |
| 3 | [0, 0] | [0, 0] | [0, 0] | [53.4, 59.3] | [4.5, 4.9] | [45.5, 50.5] | [239.15, 265.7] |
| 4 | [0, 0] | [0, 0] | [0, 0] | [57.1, 63.4] | [6.1, 6.8] | [61.4, 68.2] | [299.3, 332.5] |
| 5 | [0, 0] | [0, 0] | [0, 0] | [48.9, 54.4] | [5.4, 6.1] | [68.3, 75.9] | [243.0, 270.2] |
Table 3 presents economic data concluded net system benefit and loss of water shortage, which are estimated by the statistical yearbook of Tianjin 2000–2013 and the water resources bulletin of Tianjin 2000–2013. When flood water exceed water amount of maximum loss (the losses of flood reach maximum value), the losses of system are estimated by water amount of maximum loss (as shown in
Table 3). Therefore, the objective is to minimize the system losses/maximum system benefits through effectively plans coupling water allocation and flood diversion, while incorporating pre-regulated allocation polices within the planning problems.
Table 3.
Probability levels and water flow of right-side hand fuzzy set.
Table 3.
Probability levels and water flow of right-side hand fuzzy set.
| Level | Probability | Water Flow (106 m3) |
|---|
| | |
|---|
| Very low | 0.05 | 4246.5 | 4340.2 | 4470 |
| Low | 0.10 | 4511.9 | 4628.3 | 4749.4 |
| Low-medium | 0.15 | 4777.4 | 4890 | 5028.8 |
| Medium | 0.40 | 5308.2 | 5400.3 | 5587.5 |
| Medium-high | 0.15 | 6369.8 | 6564.1 | 6705.1 |
| High | 0.10 | 11,678 | 11,998.7 | 12,292.6 |
| Very high | 0.05 | 21,323.7 | 21,986.4 | 22,350.2 |
5. Conclusions
In this study, a mix inexact-quadratic two-stage water resources management of floodplain (IQT-WMMF) has been developed for regional sustainable development under uncertainty and limited data availability, through incorporating techniques of credibility-constrained programming (CP), two-stage programming (TP), interval-parameter programming (IPP) and quadratic programming (QP) within a general framework. The developed IQT-WMMF can deal with multiple uncertainties expressed as probability distributions and fuzzy sets in water resources allocation problems resulting from randomness in water availabilities; it also can promote capacities of fuzzy determination to offer a compromised decision; meanwhile it can resolve imprecise and no-linear economic data in WMF.
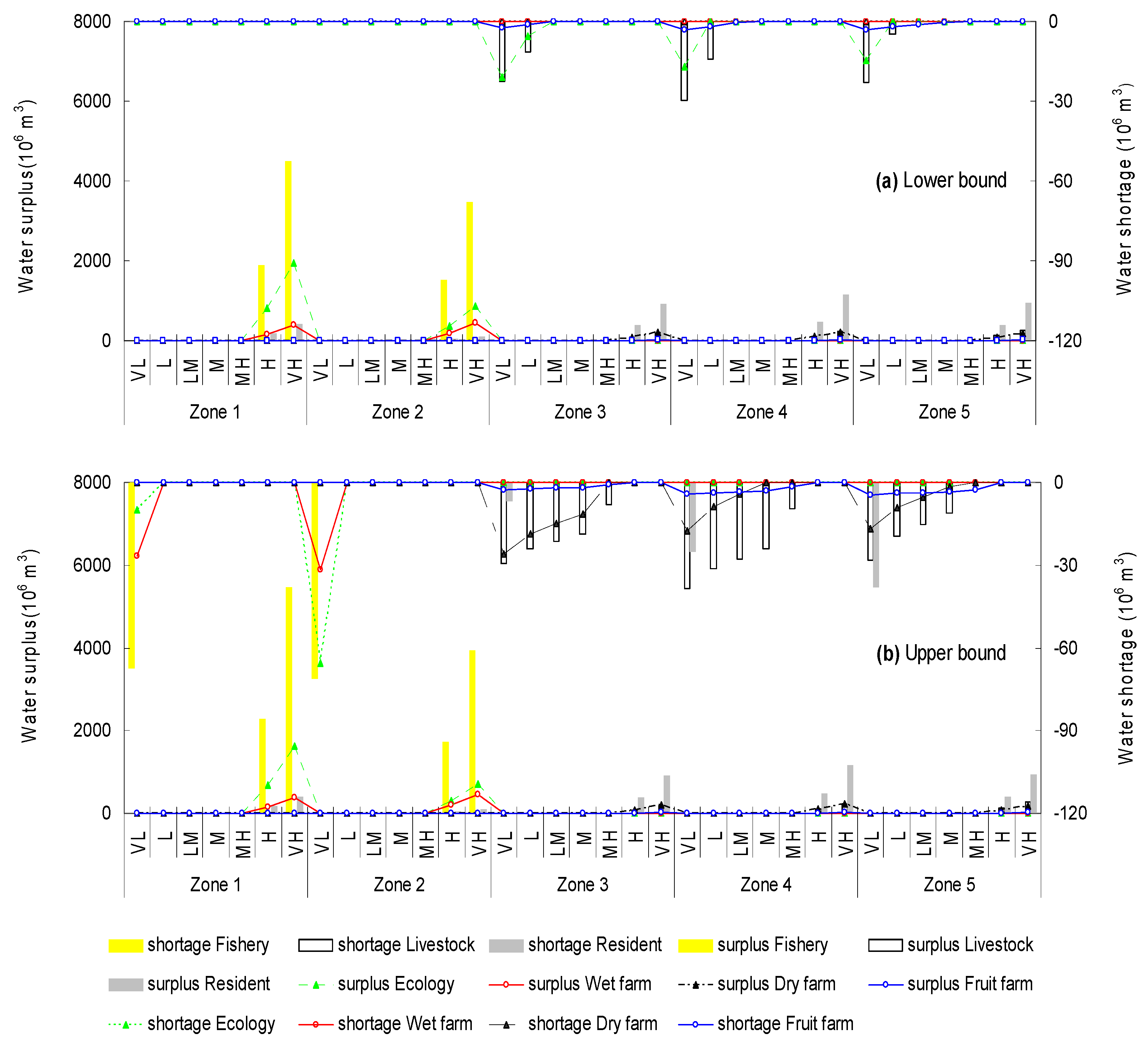
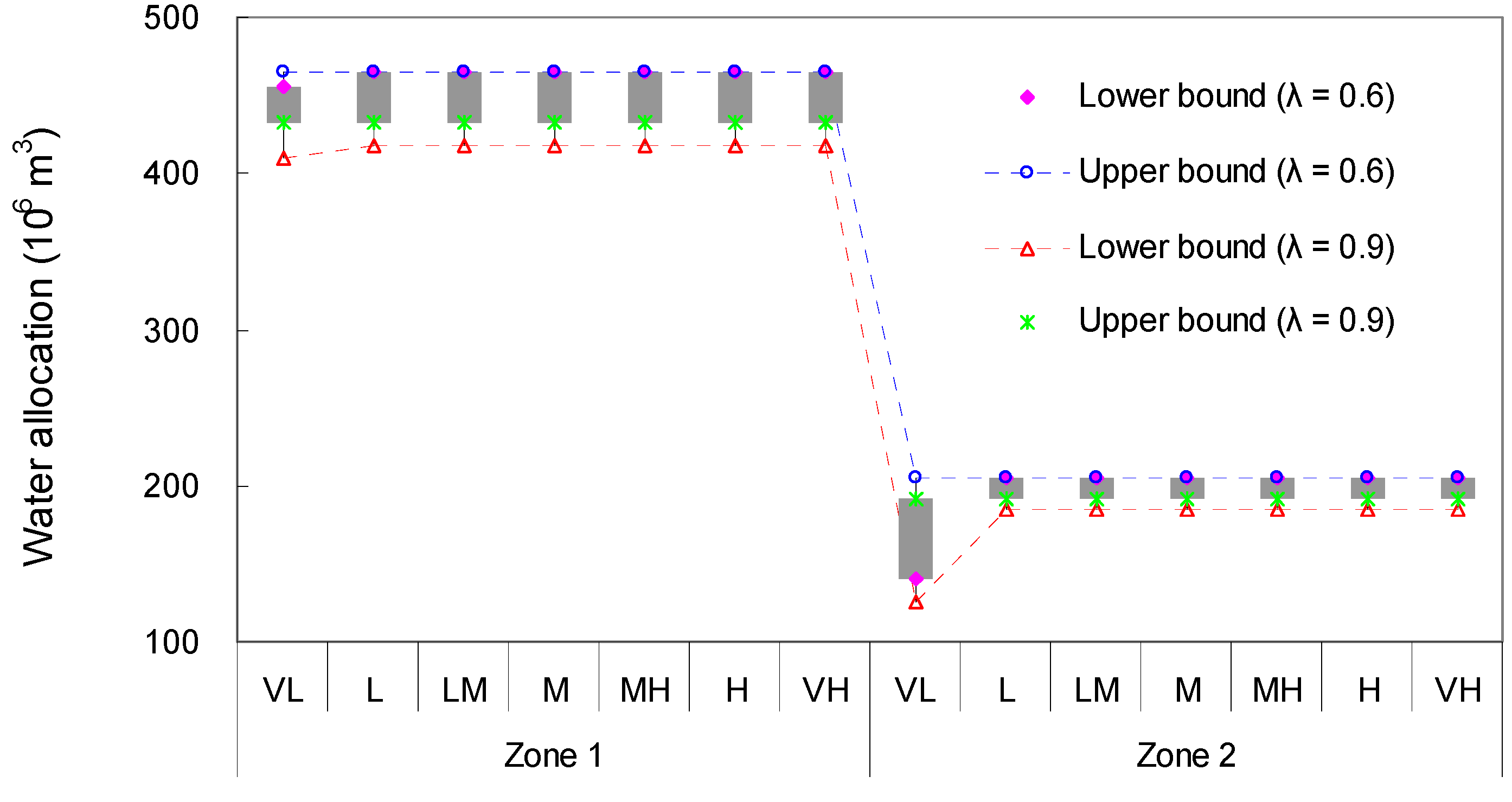
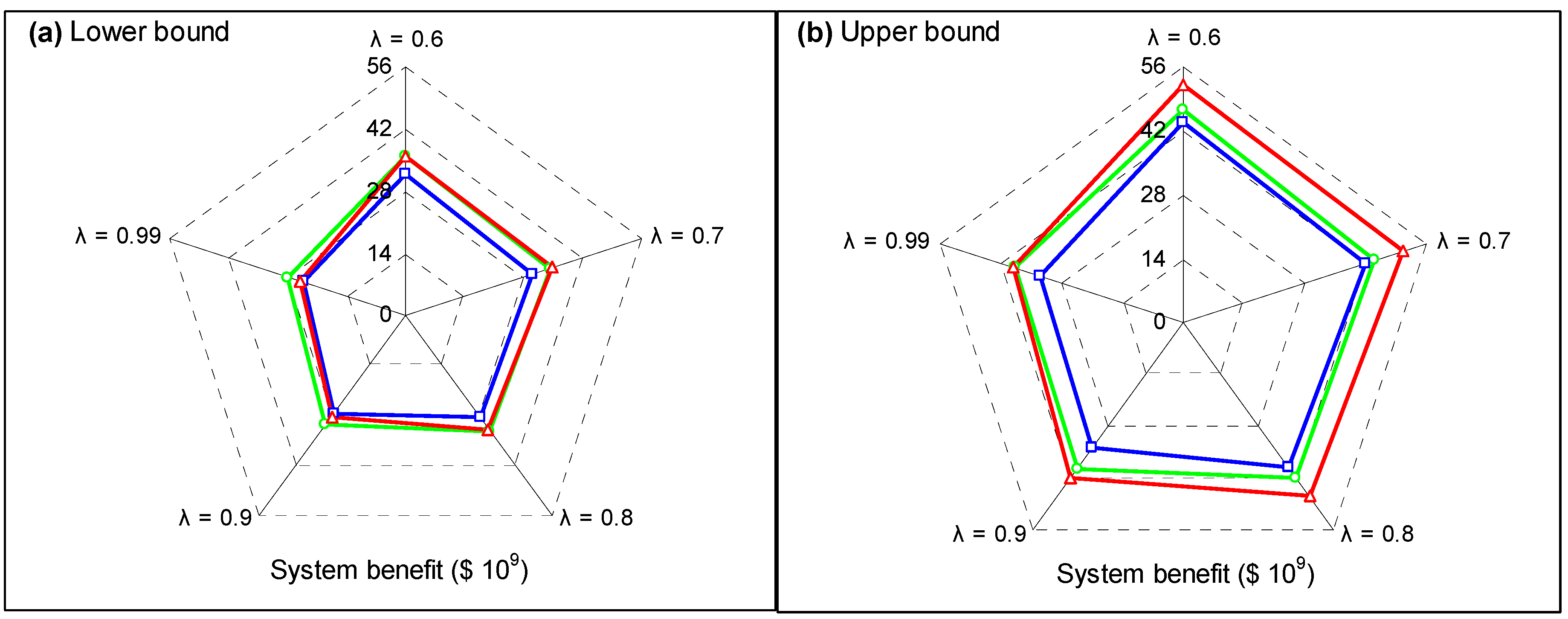
The developed method has been applied to a real case of planning water resources management of Dahuangbaowa floodplain, China. Water flows of the study region would be allocated by water manager to multiple users to satisfy water demand in no-flood seasons, while flood flows would be relived to submerge flood diversions when flood occur. Results indicate that the current water allocation pattern would result in higher water shortages in the flood buffer (i.e., zone 3 to 5) in a no-flooding period, while also resulting in relatively lower shortages in flood diversion (i.e., zone 1 to 2). Meanwhile, in flooding period, about 85% flood water would be adopted by flood diversion, thus, the damages of flood in flood buffer would be relative low. Since the acreage of ecology in flood diversion place (i.e., zone 1 to 2) reaches 68.2%, the role of ecology for mitigating flood water is conspicuous. The results also indicate that net system benefit of ecological sector is lower than other water users, nevertheless, the losses of shortages and surplus are relative lower, which result in its good capacity and most economy when flood occurs. Under these situations, a number of strategies based on ecological expansions (wetland expansions) are assumed to compare, which discovers that scenario 3 would achieved the highest system benefit. Moreover, a number of scenarios based on different satisfaction degrees are listed to compare, which can help generating desired policies for water resources management with maximized economic benefits and minimized system-failure risks. In comparison, a lower credibility measure on constraint (i.e., α = 0.6) leads to a lower water shortage and a higher water allocation, which can reduce shortage of 12.25 × 106 m3 and increase allocation of 137.68 × 106 m3 than those under a higher one (α = 0.9). The results indicate that a lower credibility measure expressed as a lower satisfaction degree and a higher system risk can generate higher in water allocation; while it would lead to a higher risk in such a water resources management system. Therefore, the local decision makers need to adjust water-allocation policy based on the regional situation (e.g., climate change, population growth, economy development, and water demand increase) to balance the tradeoff between the system benefit and water shortage risk.
Although the developed IQT-WMMF model can effectively deal with uncertainties existing in the planning problems for regional sustainable development, there are also several limitations of the proposed method that are subject to further improvement. For example, in the practical water resources management problems, multiple uncertainties (e.g., random in water availability, varied water demand, imprecise economic data, different allocation target) generate complex uncertainties and various risks in water resources system, which affect efficiency of water policies of satisfactions and optimistic/pessimistic criterion for water resources planning. Therefore, IQT-WMMF would be integrated with robust optimization techniques to enhance its capacities in tackling uncertainties presented in multiple formats.