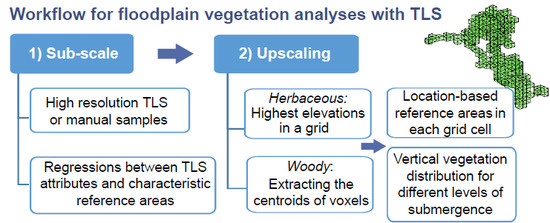
Determining Characteristic Vegetation Areas by Terrestrial Laser Scanning for Floodplain Flow Modeling
Abstract
:1. Introduction
2. Methods
2.1. Herbaceous Vegetation: TLS Campaign and Manual Vegetation Sampling in the Field

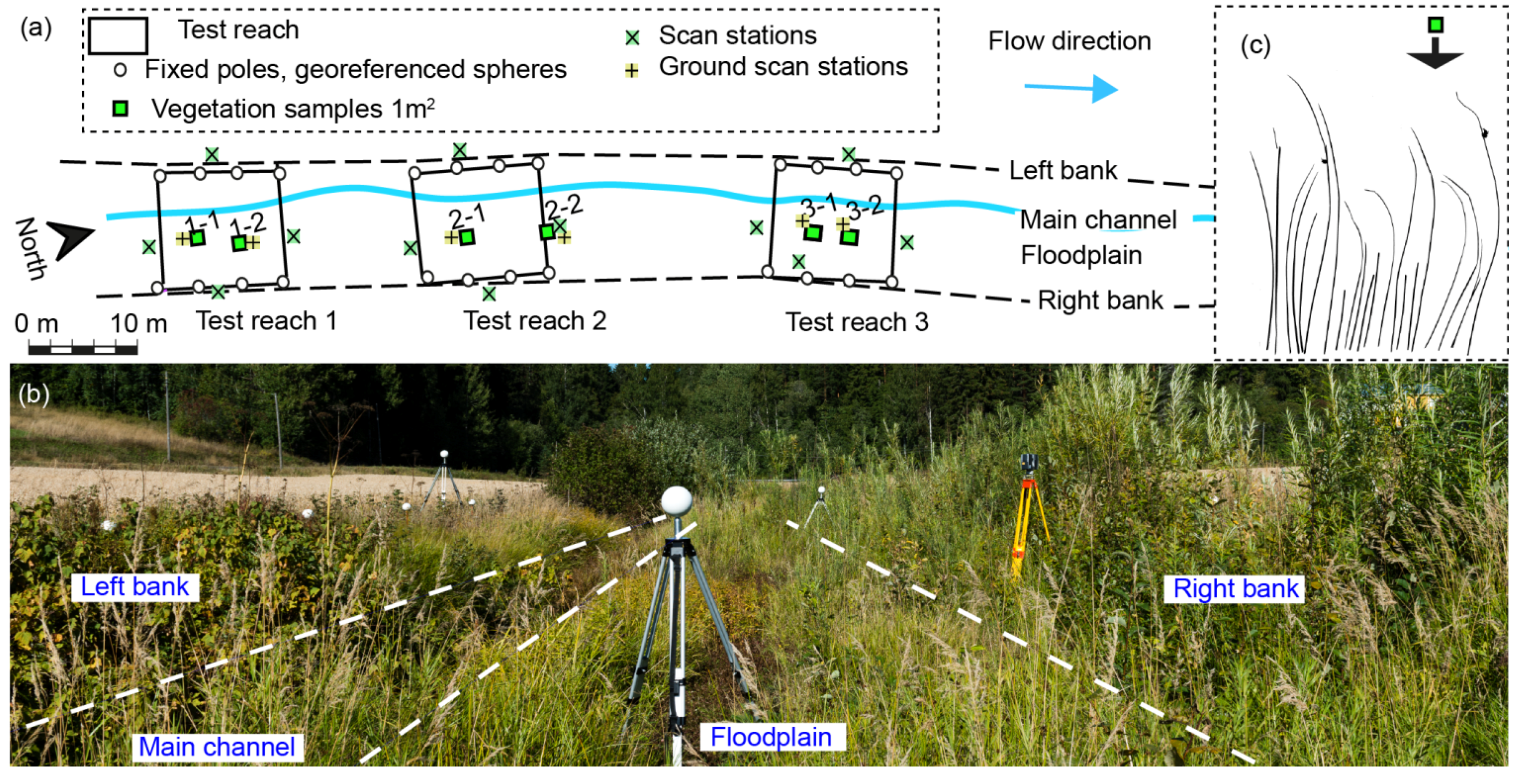
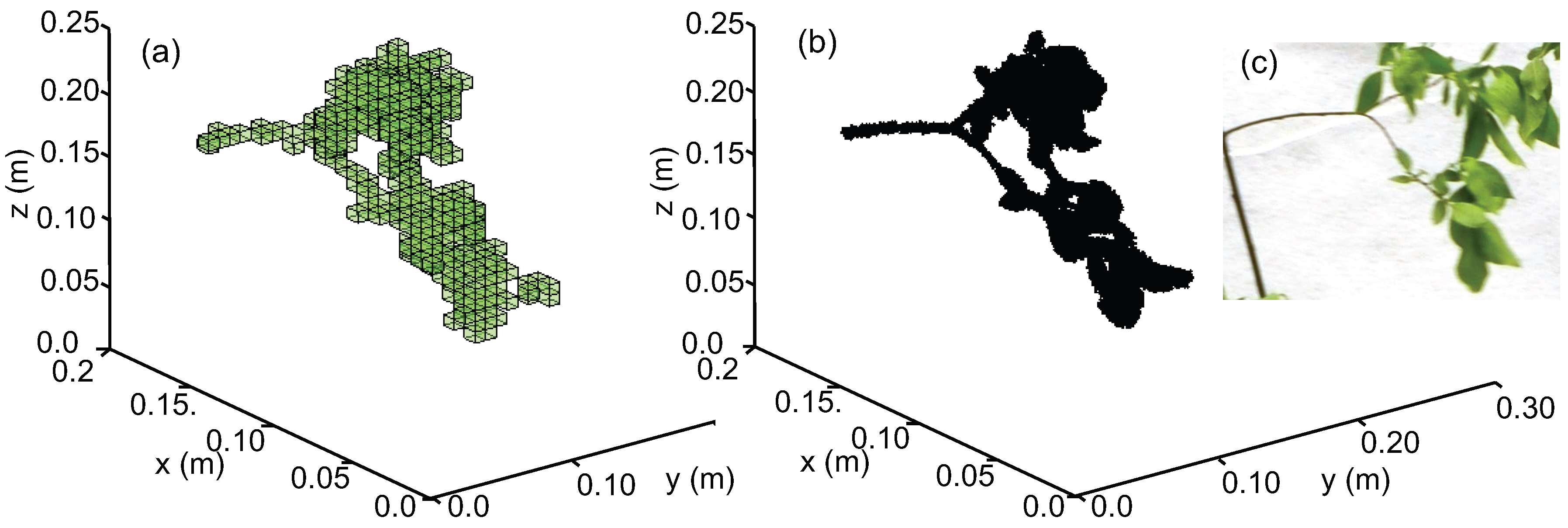
2.2. Woody Vegetation: TLS and Manual Measurements of Trees in the Laboratory
2.3. Characteristic Reference Areas: Regressions between TLS-Based Point Cloud Attributes and Total Plant Area
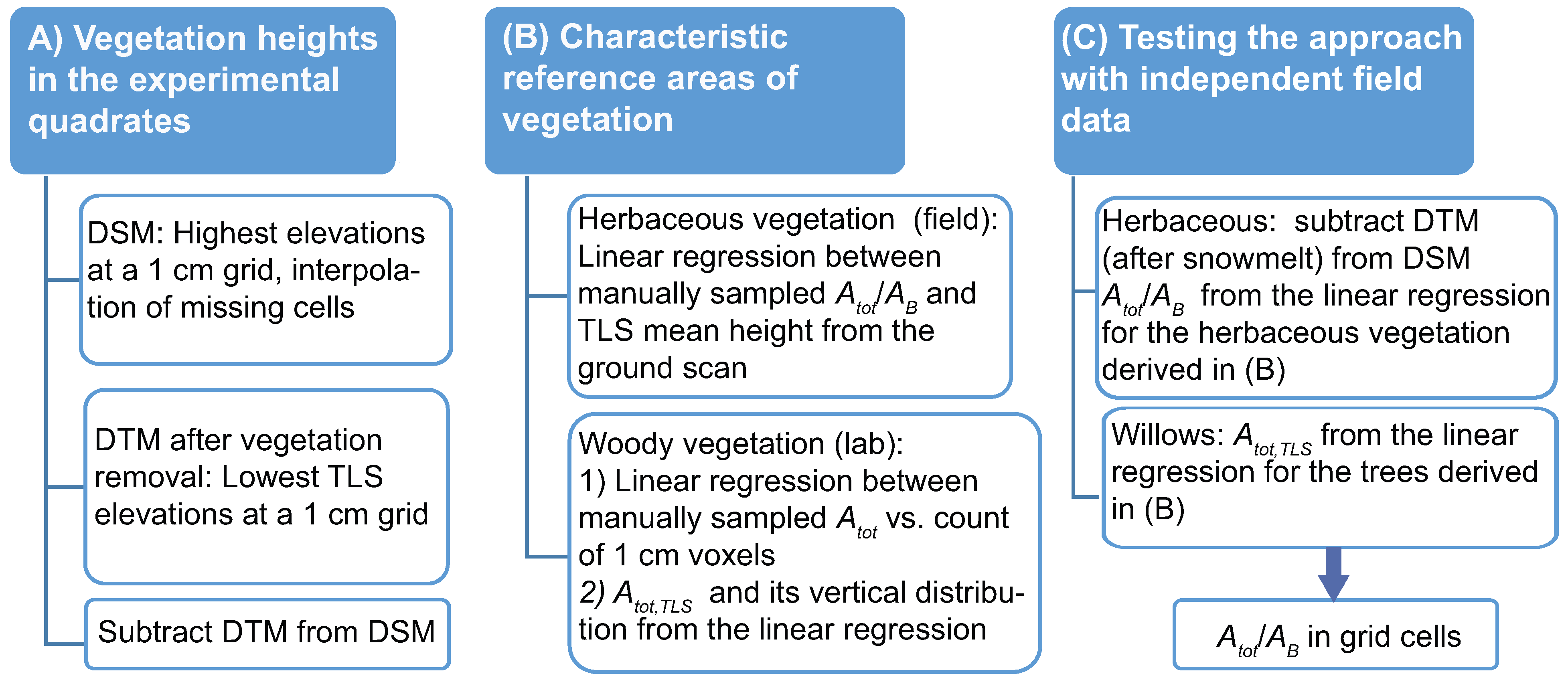
3. Results and Discussion
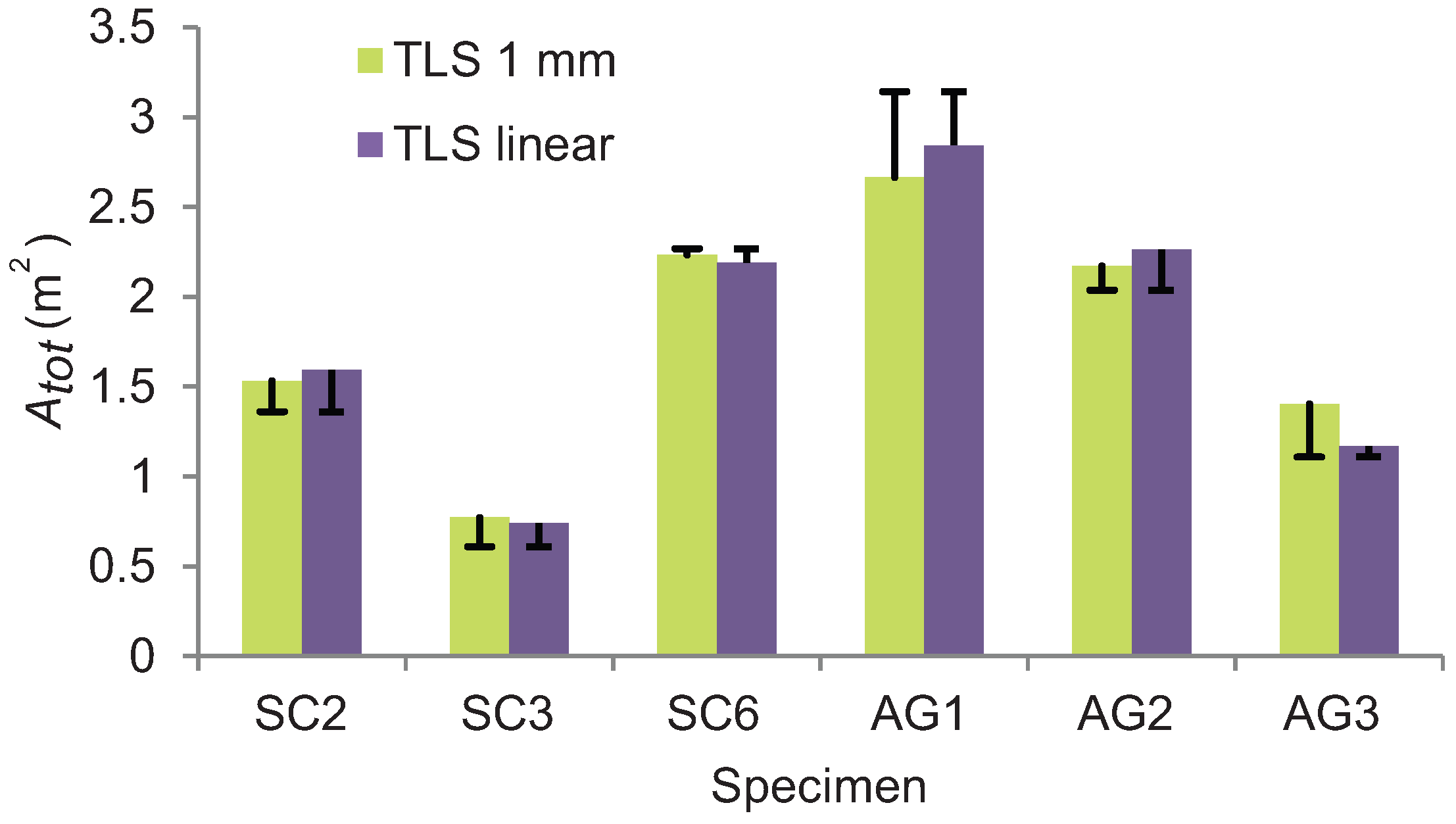
3.1. Woody Vegetation
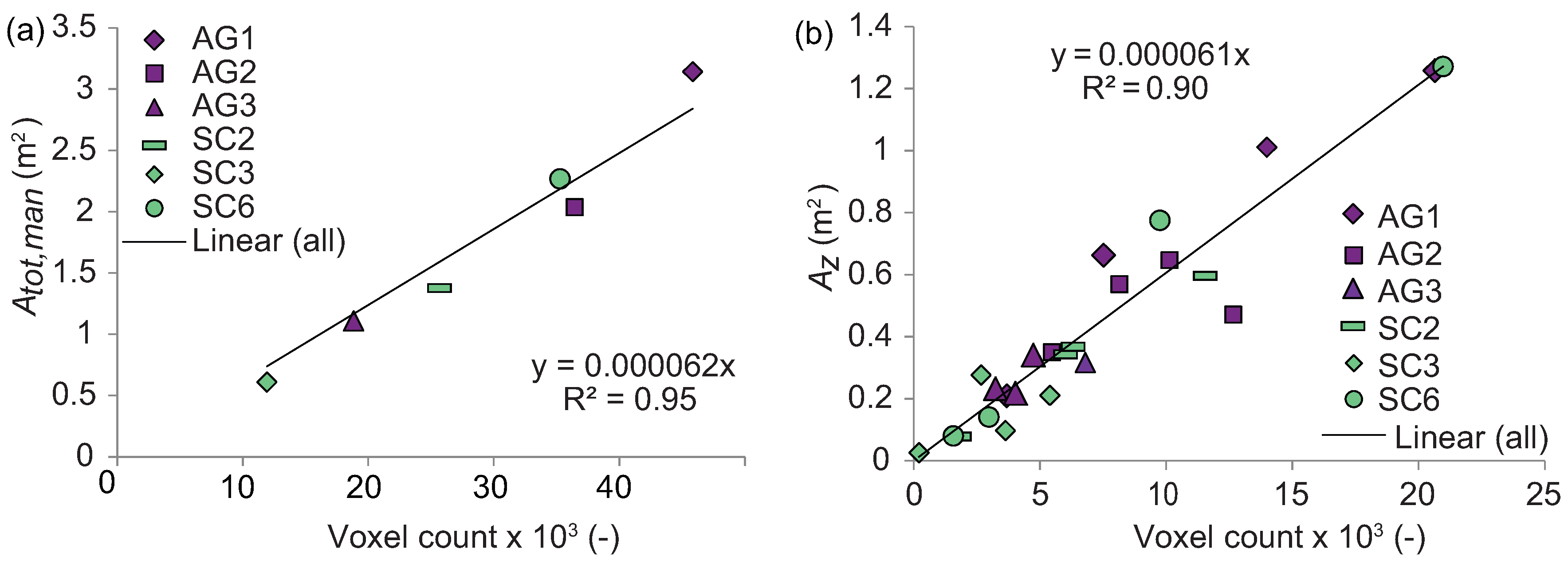
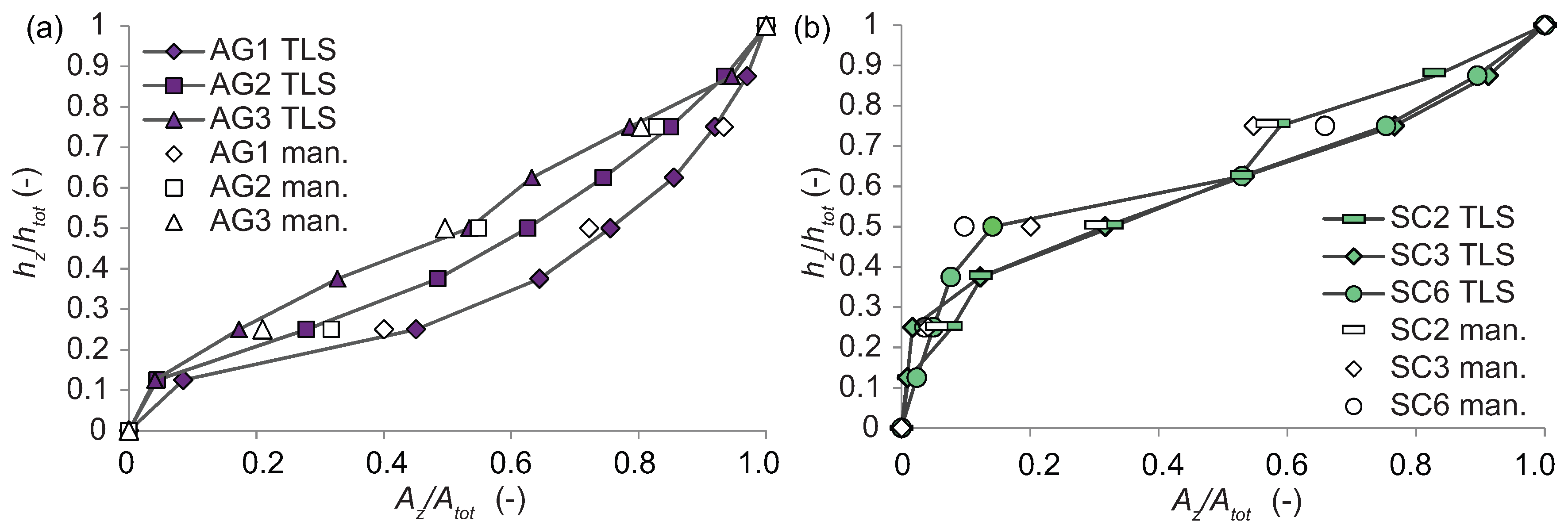
3.2. Herbaceous Vegetation
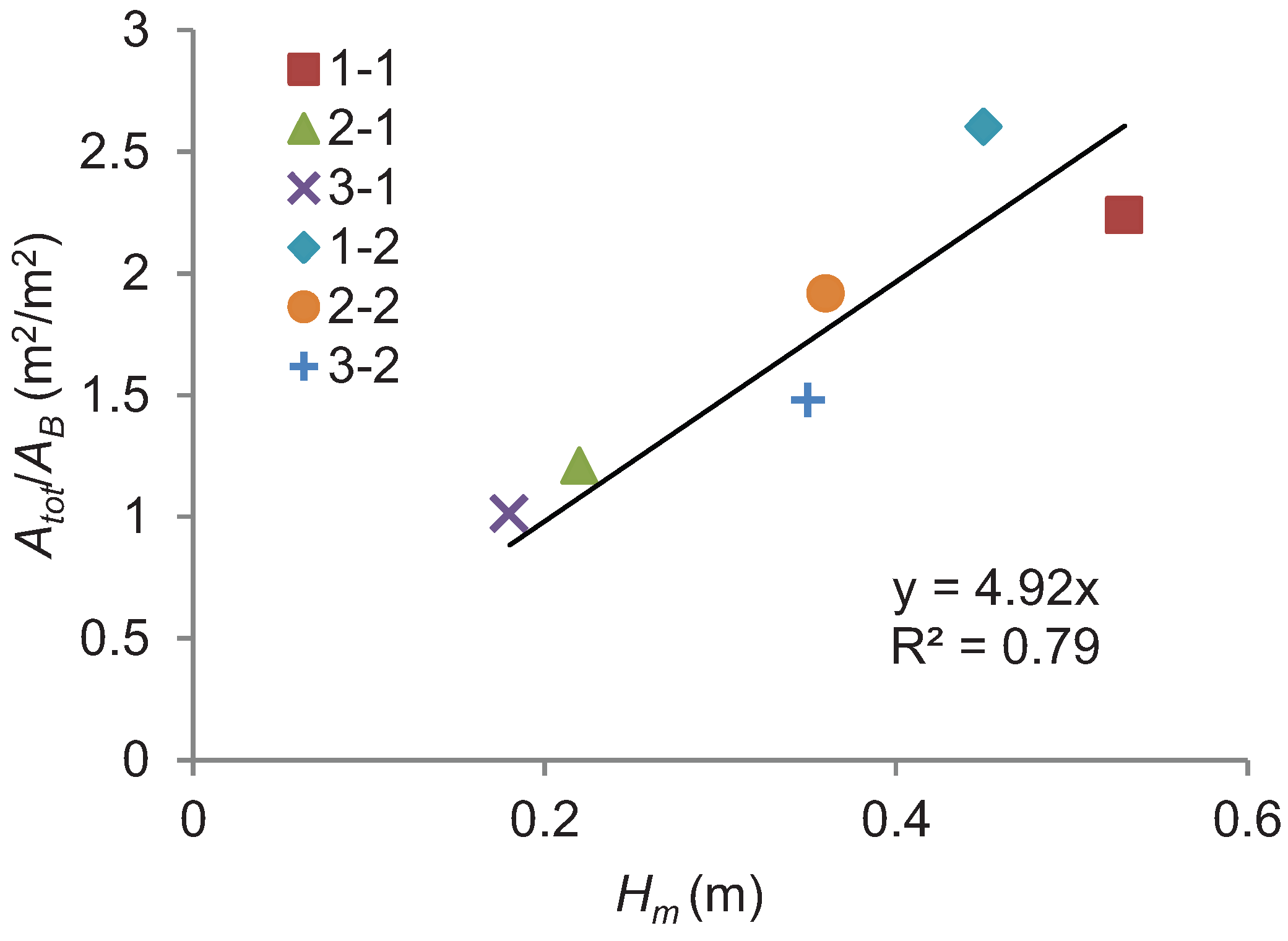
| Sample | Atot/AB (m2/m2) | md/AB (kg/m2) | TLS Density (pts/m2) |
|---|---|---|---|
| 1–1 | 2.16 | 0.23 | 7,377 |
| 1–2 | 2.66 | 0.34 | 13,477 |
| 2–1 | 1.21 | 0.14 | 7,961 |
| 2–2 | 1.74 | 0.19 | 494,952 |
| 3–1 | 0.93 | 0.14 | 135,618 |
| 3–2 | 1.04 | 0.21 | 4,449 |
3.3. Testing of the Proposed TLS Method for the Characteristic Area Determination
| Test Reach | Atot/AB (−) | Atot/AB (−) from TLS | Description | ||
|---|---|---|---|---|---|
| Manual | Mean | Range | St. Dev. | ||
| Grasses-U | 3.51 1 | 1.90 | 0.0–5.4 | 0.91 | Sown pasture grasses, upstream reach |
| Willows-M | 0.29 2 | 0.40 | 0.0–5.1 | 0.50 | Small, young willows with cut grasses, maintained |
| Grasses-D | 3.41 1 | 1.10 | 0.0–3.8 | 0.51 | Sown pasture grasses, downstream reach |
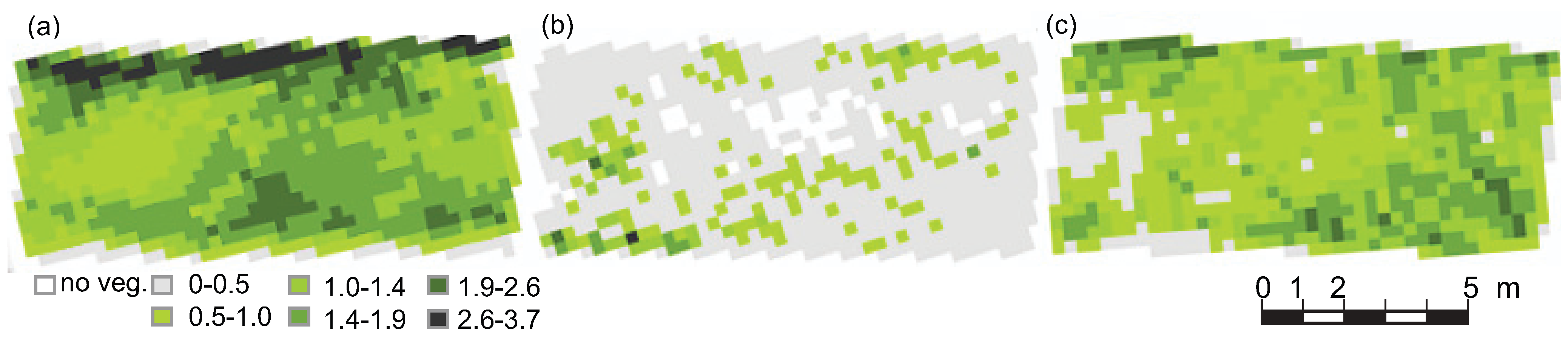
3.4. Summarizing the Process of Characterizing Mixed Floodplain Vegetation from Point Cloud Data
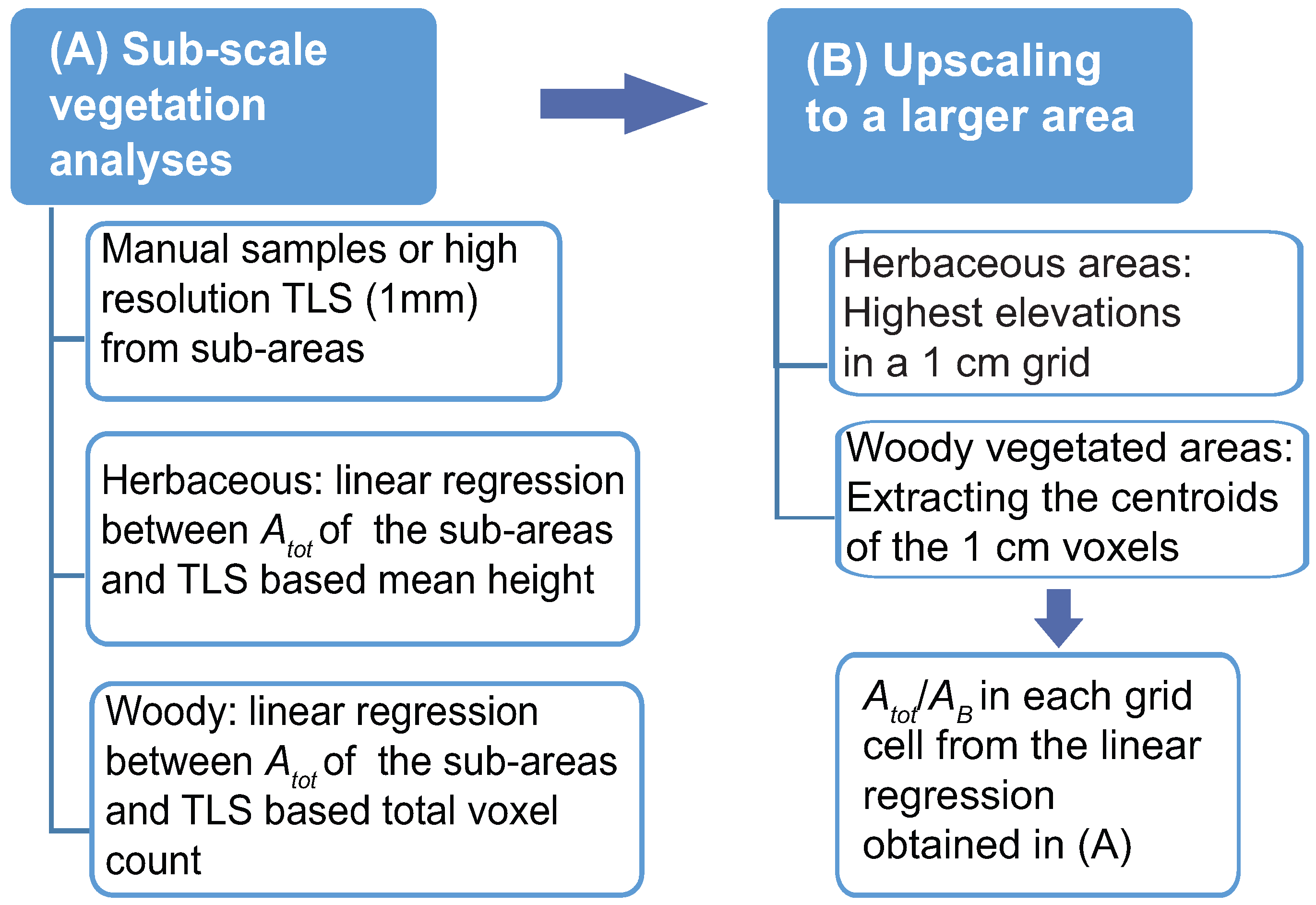
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aberle, J.; Järvelä, J. Hydrodynamics of vegetated channels. In Rivers—Physical, Fluvial and Environmental Processes, GeoPlanet: Earth and Planetary Sciences; Rowinski, P., Radeck-Pawlik, A., Eds.; Springer: Berlin, Germany, 2015. [Google Scholar]
- Gurnell, A. Plants as River System Engineers. Earth Surf. Process. Landf. 2014, 39, 4–25. [Google Scholar]
- Aberle, J.; Järvelä, J. Flow Resistance of Emergent Rigid and Flexible Floodplain Vegetation. J. Hydraul. Res. 2013, 51, 33–45. [Google Scholar] [CrossRef]
- Anderson, B.G.; Rutherfurd, I.D.; Western, A.W. An Analysis of the Influence of Riparian Vegetation on the Propagation of Flood Waves. Environ. Modell. Softw. 2006, 21, 1290–1296. [Google Scholar] [CrossRef]
- Petryk, S.; Bosmajian, G.B. Analysis of Flow through Vegetation. J. Hydraul. Div. 1975, 101, 871–884. [Google Scholar]
- Bunting, D.P.; Kurc, S.; Grabau, M. Long-Term Vegetation Dynamics after High-Density Seedling Establishment: Implications for Riparian Restoration and Management. River Res. Appl. 2013, 29, 1119–1130. [Google Scholar] [CrossRef]
- Västilä, K.; Järvelä, J. Modeling the Flow Resistance of Woody Vegetation using Physically Based Properties of the Foliage and Stem. Water Resour. Res. 2014, 50, 229–245. [Google Scholar] [CrossRef]
- Västilä, K.; Järvelä, J.; Aberle, J. Characteristic Reference Areas for Estimating Flow Resistance of Natural Foliated Vegetation. J. Hydrol. 2013, 492, 49–60. [Google Scholar] [CrossRef]
- Jalonen, J.; Järvelä, J.; Aberle, J. Leaf Area Index as Vegetation Density Measure for Hydraulic Analyses. J. Hydraul. Eng. 2013, 139, 461–469. [Google Scholar] [CrossRef]
- Jalonen, J.; Järvelä, J.; Aberle, J. Vegetated Flows: Drag Force and Velocity Profiles for Foliated Plant Stands. In River Flow 2012, Proceedings of the International Conference on Fluvial Hydraulics, San José, Costa Rica, 5–7 September 2012; pp. 233–239.
- Jalonen, J.; Järvelä, J. Estimation of Drag Forces Caused by Natural Woody Vegetation of Different Scales. J. Hydrodyn. 2014, 26, 608–623. [Google Scholar] [CrossRef]
- Whittaker, P.; Wilson, C.; Aberle, J.; Rauch, H.P.; Xavier, P. A Drag Force Model to Incorporate the Reconfiguration of Full-Scale Riparian Trees under Hydrodynamic Loading. J. Hydraul. Res. 2013, 51, 569–580. [Google Scholar] [CrossRef]
- Green, J.C. Effect of Macrophyte Spatial Variability on Channel Resistance. Adv. Water Resour. 2006, 29, 426–438. [Google Scholar] [CrossRef]
- Nikora, V. Hydrodynamics of Aquatic Ecosystems: An Interface between Ecology, Biomechanics and Environmental Fluid Mechanics. River Res. Appl. 2010, 26, 367–384. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. From the Blade Scale to the Reach Scale: A Characterization of Aquatic Vegetative Drag. Adv. Water Resour. 2013, 51, 305–316. [Google Scholar] [CrossRef]
- Green, J.C. Comparison of Blockage Factors in Modelling the Resistance of Channels Containing Submerged Macrophytes. River Res. Appl. 2005, 21, 671–686. [Google Scholar] [CrossRef]
- Järvelä, J. Determination of Flow Resistance Caused by Non-submerged Woody Vegetation. Int. J. River Basin Manag. 2004, 2, 61–70. [Google Scholar] [CrossRef]
- Katul, G.G.; Poggi, D.; Ridolfi, L. A Flow Resistance Model for Assessing the Impact of Vegetation on Flood Routing Mechanics. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Nepf, H.; Ghisalberti, M. Flow and Transport in Channels with Submerged Vegetation. Acta Geophys. 2008, 56, 753–777. [Google Scholar] [CrossRef]
- Forzieri, G.; Castelli, F.; Preti, F. Advances in Remote Sensing of Hydraulic Roughness. Int. J. Remote Sens. 2012, 33, 630–654. [Google Scholar] [CrossRef]
- Straatsma, M.W.; Baptist, M.J. Floodplain Roughness Parameterization using Airborne Laser Scanning and Spectral Remote Sensing. Remote Sens. Environ. 2008, 112, 1062–1080. [Google Scholar] [CrossRef]
- Straatsma, M.W.; Warmink, J.J.; Middelkoop, H. Two Novel Methods for Field Measurements of Hydrodynamic Density of Floodplain Vegetation using Terrestrial Laser Scanning and Digital Parallel Photography. Int. J. Remote Sens. 2008, 29, 1595–1617. [Google Scholar] [CrossRef]
- Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform Mobile Laser Scanning: Usability and Performance. Sensors 2012, 12, 11712–11733. [Google Scholar] [CrossRef]
- Hodge, R.; Brasington, J.; Richards, K. In situ Characterization of Grain-Scale Fluvial Morphology using Terrestrial Laser Scanning. Earth Surf. Process. Landf. 2009, 34, 954–968. [Google Scholar]
- Brasington, J.; Vericat, D.; Rychkov, I. Modeling River Bed Morphology, Roughness, and Surface Sedimentology using High Resolution Terrestrial Laser Scanning. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Resop, J.; Hession, W. Terrestrial Laser Scanning for Monitoring Streambank Retreat: Comparison with Traditional Surveying Techniques. J. Hydraul. Eng. 2010, 136, 794–798. [Google Scholar] [CrossRef]
- Brodu, N.; Lague, D. 3D Terrestrial Lidar Data Classification of Complex Natural Scenes using a Multi-Scale Dimensionality Criterion: Applications in Geomorphology. ISPRS J Photogramm. Remote Sens. 2012, 68, 121–134. [Google Scholar] [CrossRef]
- Resop, J.P.; Kozarek, J.L.; Hession, W.C. Terrestrial Laser Scanning for Delineating in-Stream Boulders and Quantifying Habitat Complexity Measures. Photogramm. Eng. Remote Sens. 2012, 78, 363–371. [Google Scholar] [CrossRef]
- Smith, M.W.; Vericat, D. Evaluating Shallow-Water Bathymetry from Through-Water Terrestrial Laser Scanning Under a Range of Hydraulic and Physical Water Quality Conditions. River Res. Appl. 2013, 30, 905–924. [Google Scholar] [CrossRef]
- Jalonen, J.; Järvelä, J.; Koivusalo, H.; Hyyppä, H. Deriving Floodplain Topography and Vegetation Characteristics for Hydraulic Engineering Applications by Means of Terrestrial Laser Scanning. J. Hydraul. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Forzieri, G.; Guarnieri, L.; Vivoni, E.R.; Castelli, F.; Preti, F. Spectral-ALS Data Fusion for Different Roughness Parameterizations of Forested Floodplains. River Res. Appl. 2011, 27, 826–840. [Google Scholar]
- Rönnholm, P.; Hyyppä, H.; Hyyppä, J.; Haggrén, H. Orientation of Airborne Laser Scanning Point Clouds with Multi-View, Multi-Scale Image Blocks. Sensors 2009, 9, 6008–6027. [Google Scholar] [CrossRef] [PubMed]
- Manners, R.; Schmidt, J.; Wheaton, J.M. Multiscalar Model for the Determination of Spatially Explicit Riparian Vegetation Roughness. Earth Surf. Process. Landf. 2013, 118, 65–83. [Google Scholar]
- Hosoi, F.; Omasa, K. Voxel-Based 3-D Modeling of Individual Trees for Estimating Leaf Area Density using High-Resolution Portable Scanning Lidar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3610–3618. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.; Fournier, R.A. A Model for Deriving Voxel-Level Tree Leaf Area Density Estimates from Ground-Based LiDAR. Environ. Model. Softw. 2014, 51, 184–189. [Google Scholar] [CrossRef]
- Radtke, P.J.; Bolstad, P.V. Laser Point-Quadrat Sampling for Estimating Foliage-Height Profiles in Broad-Leaved Forests. Can. J. For. Res. 2001, 31, 410–418. [Google Scholar] [CrossRef]
- Antonarakis, A.S.; Richards, K.S.; Brasington, J.; Muller, E. Determining Leaf Area Index and Leafy Tree Roughness using Terrestrial Laser Scanning. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Guarnieri, A.; Vettore, A.; Pirotti, F.; Menenti, M.; Marani, M. Retrieval of Small-Relief Marsh Morphology from Terrestrial Laser Scanner, Optimal Spatial Filtering, and Laser Return Intensity. Geomorphology 2009, 113, 12–20. [Google Scholar] [CrossRef]
- Västilä, K.; Järvelä, J. Cohesive Sediment Dynamics in a Vegetated Two-Stage Drainage Channel: The First Year after Floodplain Excavation. In Proceedings of the 7th International Symposium on River, Coastal and Estuarine Morphodynamics, RCEM, Tsinghua University, Beijing, China, 6–8 September 2011; pp. 1481–1489.
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Dolha, M.; Beetz, M. Towards 3D Point Cloud Based Object Maps for Household Environments. Semant. Knowl. Robot. 2008, 56, 927–941. [Google Scholar]
- Weissteiner, C.; Rauch, H.P.; Jalonen, J.; Järvelä, J. Spatial-Structural Analysis of Woody Riparian Vegetation for Hydraulic Considerations. In Proceedings of the 35th IAHR World Congress, Chengdu, China, 8–13 September 2013.
- Bréda, N.J.J. Ground-Based Measurements of Leaf Area Index: A Review of Methods, Instruments and Current Controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Tilly, N.; Hoffmeister, D.; Cao, Q.; Huang, S.; Lenz-Wiedemann, V.; Miao, Y.; Bareth, G. Multitemporal Crop Surface Models: Accurate Plant Height Measurement and Biomass Estimation with Terrestrial Laser Scanning in Paddy Rice. J. Appl. Remote Sens. 2014, 8. [Google Scholar] [CrossRef]
- Radtke, P.J.; Boland, H.T.; Scaglia, G. An Evaluation of Overhead Laser Scanning to Estimate Herbage Removals in Pasture Quadrats. Agric. For. Meteorol. 2010, 150, 1523–1528. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.; Fournier, R.A.; Côté, J.; Verstraete, M.M. Estimating Leaf Area Distribution in Savanna Trees from Terrestrial LiDAR Measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Saarinen, N.; Vastaranta, M.; Vaaja, M.; Lotsari, E.; Jaakkola, A.; Kukko, A.; Kaartinen, H.; Holopainen, M.; Hyyppä, H.; Alho, P. Area-Based Approach for Mapping and Monitoring Riverine Vegetation using Mobile Laser Scanning. Remote Sens. 2013, 5, 5285–5303. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Lindroos, T.; Hyyppä, J. Toward Hyperspectral Lidar: Measurement of Spectral Backscatter Intensity with a Supercontinuum Laser Source. IEEE Geosci. Remote Sens. Lett. 2007, 4, 211–215. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, Å. Identifying Species of Individual Trees using Airborne Laser Scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J. Automatic Stem Mapping by Merging several Terrestrial Laser Scans at the Feature and Decision Levels. Sensors 2013, 13, 1614–1634. [Google Scholar] [CrossRef] [PubMed]
- Forzieri, G.; Guarnieri, L.; Vivoni, E.R.; Castelli, F.; Preti, F. Multiple Attribute Decision Making for Individual Tree Detection using High-Resolution Laser Scanning. For. Ecol. Manag. 2009, 258, 2501–2510. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Vaaja, M.; Kukko, A.; Kaartinen, H.; Kurkela, M.; Kasvi, E.; Flener, C.; Hyyppä, H.; Hyyppä, J.; Järvelä, J.; Alho, P. Data Processing and Quality Evaluation of a Boat-Based Mobile Laser Scanning System. Sensors 2013, 13, 12497–12515. [Google Scholar] [CrossRef] [PubMed]
- Flener, C.; Vaaja, M.; Jaakkola, A.; Krooks, A.; Kaartinen, H.; Kukko, A.; Kasvi, E.; Hyyppä, H.; Hyyppä, J.; Alho, P. Seamless Mapping of River Channels at High Resolution using Mobile LiDAR and UAV-Photography. Remote Sens. 2013, 5, 6382–6407. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jalonen, J.; Järvelä, J.; Virtanen, J.-P.; Vaaja, M.; Kurkela, M.; Hyyppä, H. Determining Characteristic Vegetation Areas by Terrestrial Laser Scanning for Floodplain Flow Modeling. Water 2015, 7, 420-437. https://doi.org/10.3390/w7020420
Jalonen J, Järvelä J, Virtanen J-P, Vaaja M, Kurkela M, Hyyppä H. Determining Characteristic Vegetation Areas by Terrestrial Laser Scanning for Floodplain Flow Modeling. Water. 2015; 7(2):420-437. https://doi.org/10.3390/w7020420
Chicago/Turabian StyleJalonen, Johanna, Juha Järvelä, Juho-Pekka Virtanen, Matti Vaaja, Matti Kurkela, and Hannu Hyyppä. 2015. "Determining Characteristic Vegetation Areas by Terrestrial Laser Scanning for Floodplain Flow Modeling" Water 7, no. 2: 420-437. https://doi.org/10.3390/w7020420
APA StyleJalonen, J., Järvelä, J., Virtanen, J.-P., Vaaja, M., Kurkela, M., & Hyyppä, H. (2015). Determining Characteristic Vegetation Areas by Terrestrial Laser Scanning for Floodplain Flow Modeling. Water, 7(2), 420-437. https://doi.org/10.3390/w7020420