Benthic Uptake Rate due to Hyporheic Exchange: The Effects of Streambed Morphology for Constant and Sinusoidally Varying Nutrient Loads
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hyporheic Hydraulic Model
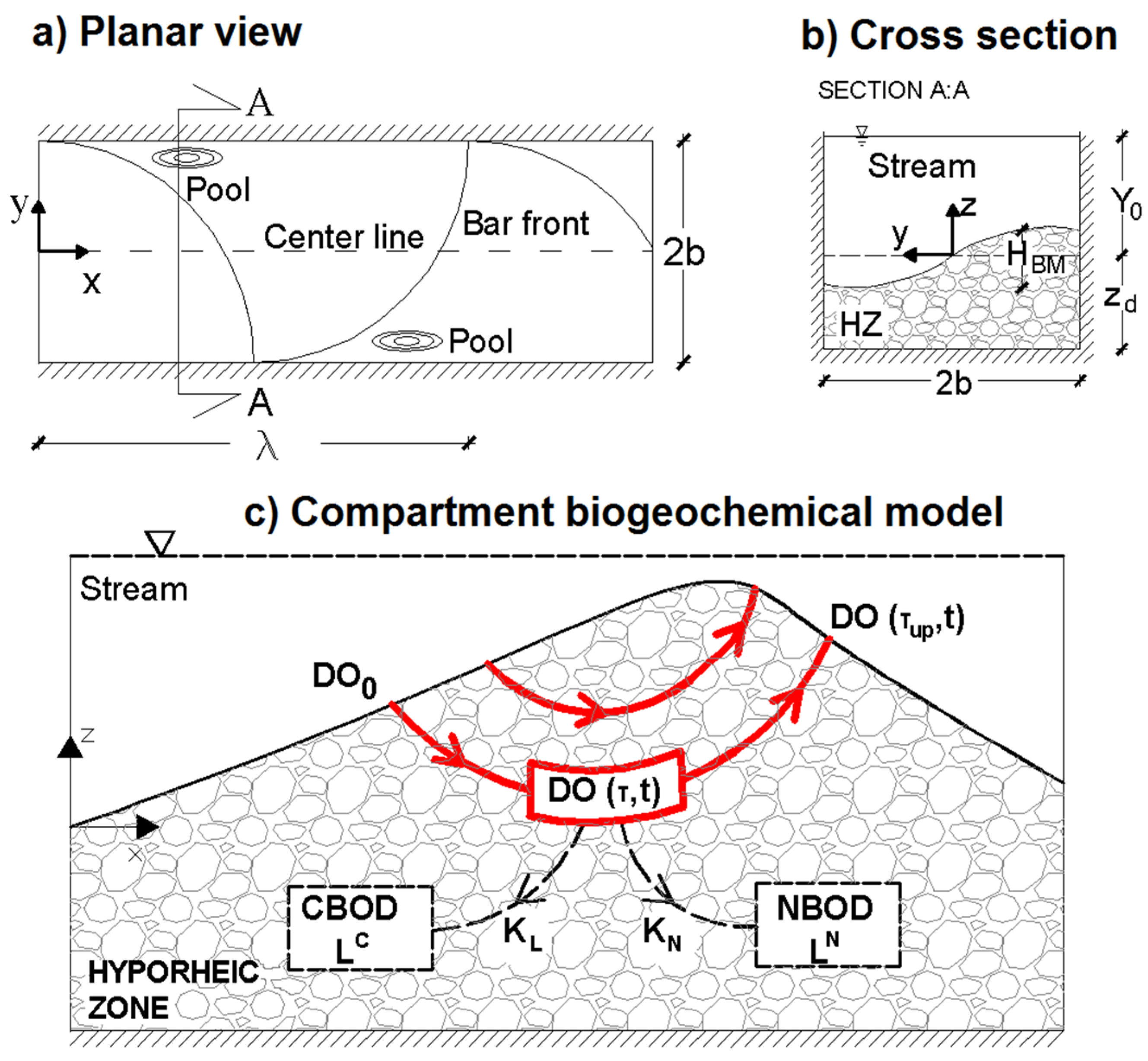
2.2. Biogeochemical Model
2.3. Benthic Uptake Rate
2.4. Field Data
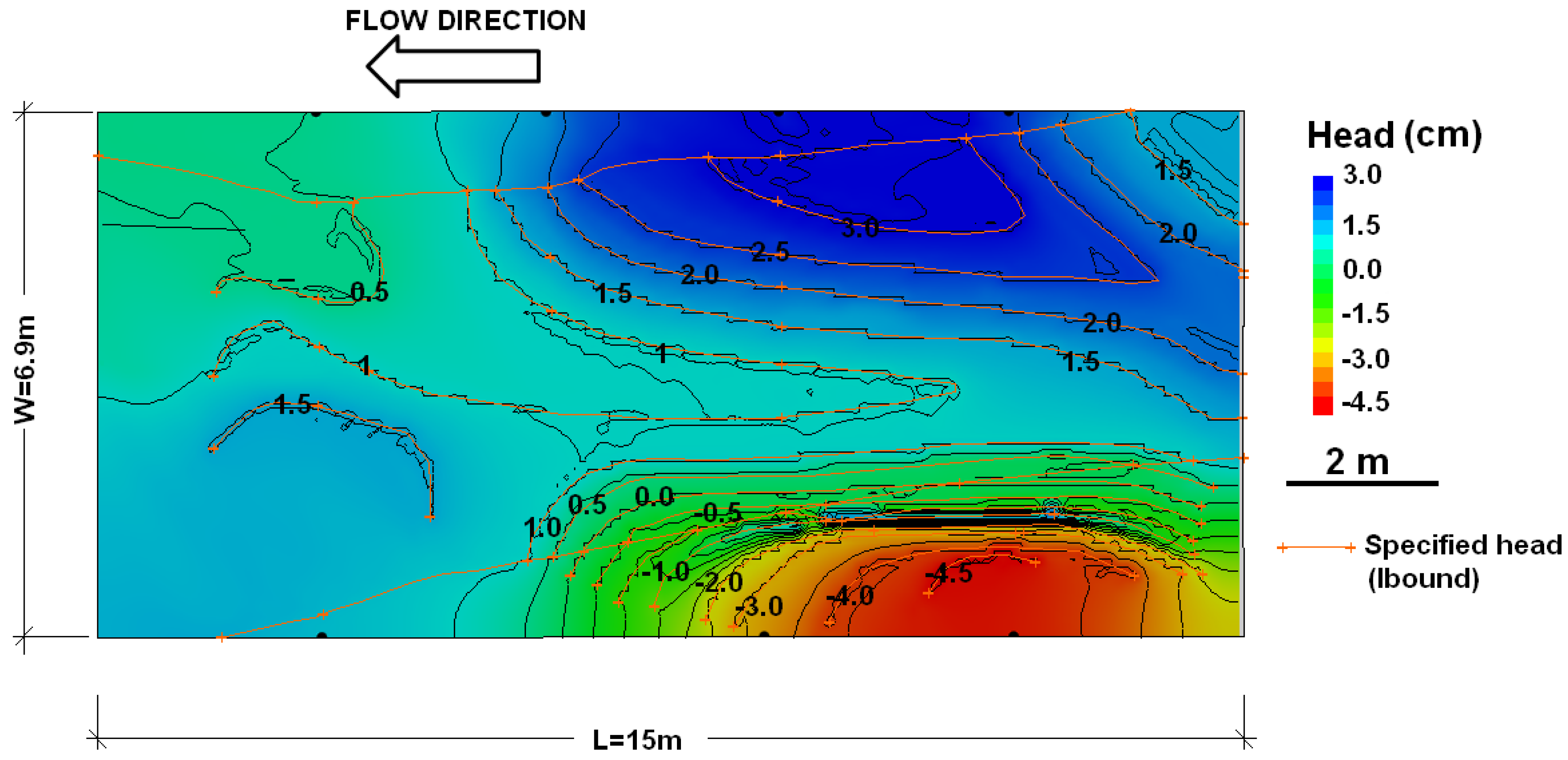
2.5. Numerical Simulations
| Test | β (-) | θ (-) | dS (-) | d50 (m) | (-) | S (%) | HBM (m) | λ (m) | Qstream (m3·s−1) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 13 | 0.08 | 0.200 | 0.01 | 0.33 | 2.64 | 0.15 | 8.76 | 0.057 |
| 2 | 13 | 0.08 | 0.150 | 0.01 | 0.39 | 1.98 | 0.17 | 11.52 | 0.111 |
| 3 | 13 | 0.08 | 0.120 | 0.01 | 0.45 | 1.58 | 0.19 | 14.23 | 0.185 |
| 4 | 13 | 0.08 | 0.105 | 0.01 | 0.48 | 1.39 | 0.20 | 16.16 | 0.251 |
| 5 | 13 | 0.08 | 0.095 | 0.01 | 0.50 | 1.25 | 0.21 | 17.77 | 0.314 |
| 6 | 13 | 0.08 | 0.085 | 0.01 | 0.53 | 1.12 | 0.22 | 19.75 | 0.404 |
| 7 | 13 | 0.08 | 0.075 | 0.01 | 0.56 | 0.99 | 0.23 | 22.26 | 0.537 |
| 8 | 13 | 0.08 | 0.065 | 0.01 | 0.60 | 0.86 | 0.26 | 25.53 | 0.738 |
| 9 | 13 | 0.08 | 0.060 | 0.01 | 0.62 | 0.79 | 0.27 | 27.57 | 0.883 |
| 10 | 13 | 0.08 | 0.055 | 0.01 | 0.65 | 0.73 | 0.28 | 29.98 | 1.072 |
| 11 | 13 | 0.08 | 0.050 | 0.01 | 0.68 | 0.66 | 0.29 | 32.87 | 1.325 |
| 12 | 13 | 0.08 | 0.045 | 0.01 | 0.71 | 0.59 | 0.31 | 36.40 | 1.675 |
| 13 | 13 | 0.08 | 0.040 | 0.01 | 0.75 | 0.53 | 0.33 | 40.82 | 2.174 |
| 14 | 13 | 0.08 | 0.035 | 0.01 | 0.81 | 0.46 | 0.33 | 46.52 | 2.902 |
| 15 | 13 | 0.08 | 0.030 | 0.01 | 0.87 | 0.40 | 0.38 | 54.13 | 4.101 |
| 16 | 13 | 0.08 | 0.025 | 0.01 | 0.96 | 0.33 | 0.42 | 64.82 | 6.121 |
| 17 | 13 | 0.08 | 0.020 | 0.01 | 1.08 | 0.26 | 0.46 | 80.97 | 9.977 |
| 18 | 13 | 0.08 | 0.010 | 0.01 | 1.74 | 0.13 | 0.56 | 163.14 | 45.037 |
| Test | RDO (-) | RBN (-) | L0C (mg/L) | LAC (τ,0) (mg/L) | L0N (mg/L) | LAN (τ,0) (mg/L) | KL (d−1) | KN (d−1) | KR (d−1) |
|---|---|---|---|---|---|---|---|---|---|
| A | 1.2 | 0.5 | 2.78 | 1.11 | 5.56 | 2.22 | 0.33 | 0.26 | 0.16 |
| B | 1.0 | 0.5 | 3.33 | 1.33 | 6.67. | 2.67 | 0.33 | 0.26 | 0.16 |
| C | 0.8 | 0.5 | 4.16 | 1.67 | 8.32 | 3.33 | 0.33 | 0.26 | 0.16 |
| D | 0.5 | 0.5 | 6.67 | 2.67 | 13.33 | 5.33 | 0.33 | 0.26 | 0.16 |
| E | 0.2 | 0.5 | 16.66 | 6.67 | 33.33 | 13.33 | 0.33 | 0.26 | 0.16 |
| F | 1.2 | 2.0 | 5.56 | 2.22 | 2.78 | 1.11 | 0.33 | 0.26 | 0.16 |
| G | 1.0 | 2.0 | 6.67 | 2.67 | 3.33 | 1.33 | 0.33 | 0.26 | 0.16 |
| H | 0.8 | 2.0 | 8.32 | 3.33 | 4.16 | 1.67 | 0.33 | 0.26 | 0.16 |
| I | 0.5 | 2.0 | 13.34 | 5.33 | 6.67 | 2.67 | 0.33 | 0.26 | 0.16 |
| J | 0.2 | 2.0 | 33.33 | 13.33 | 16.67 | 6.67 | 0.33 | 0.26 | 0.16 |
3. Results and Discussion
3.1. Comparison with Field Data
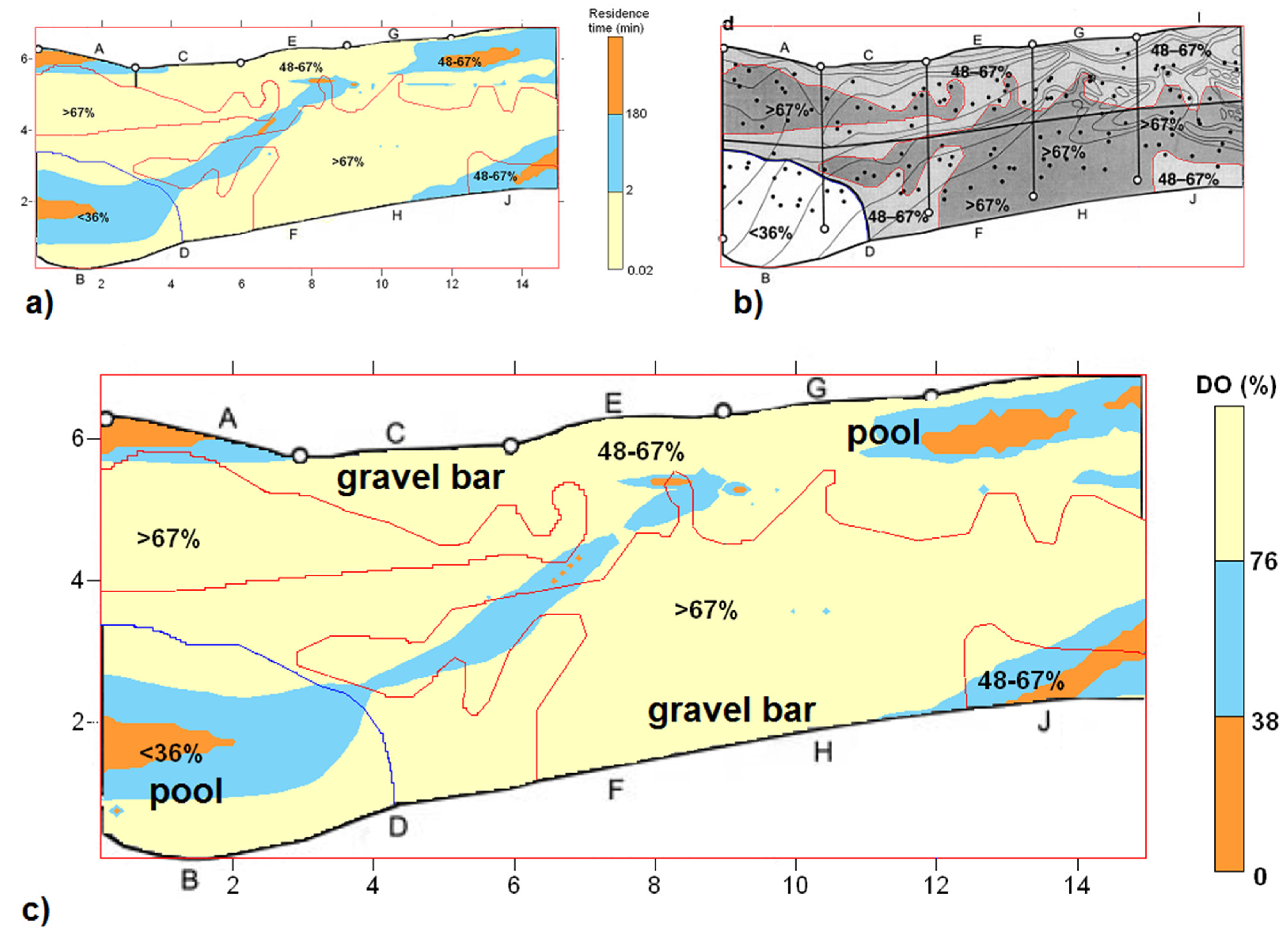
3.2. Effect of Stream Morphology
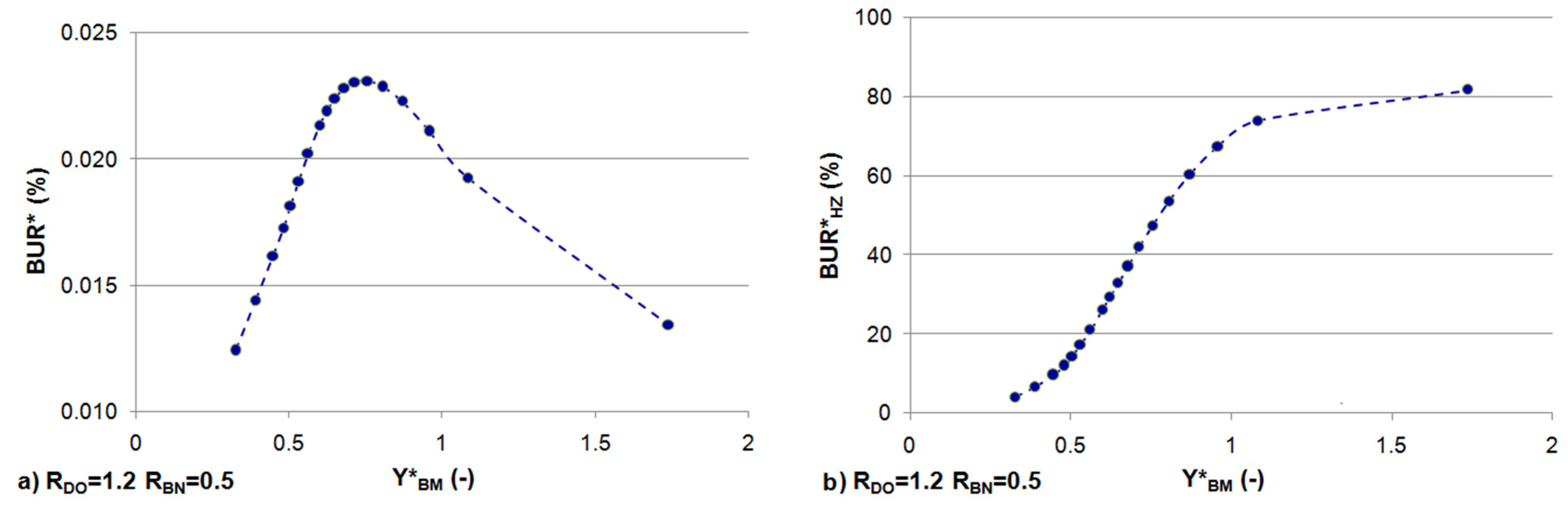
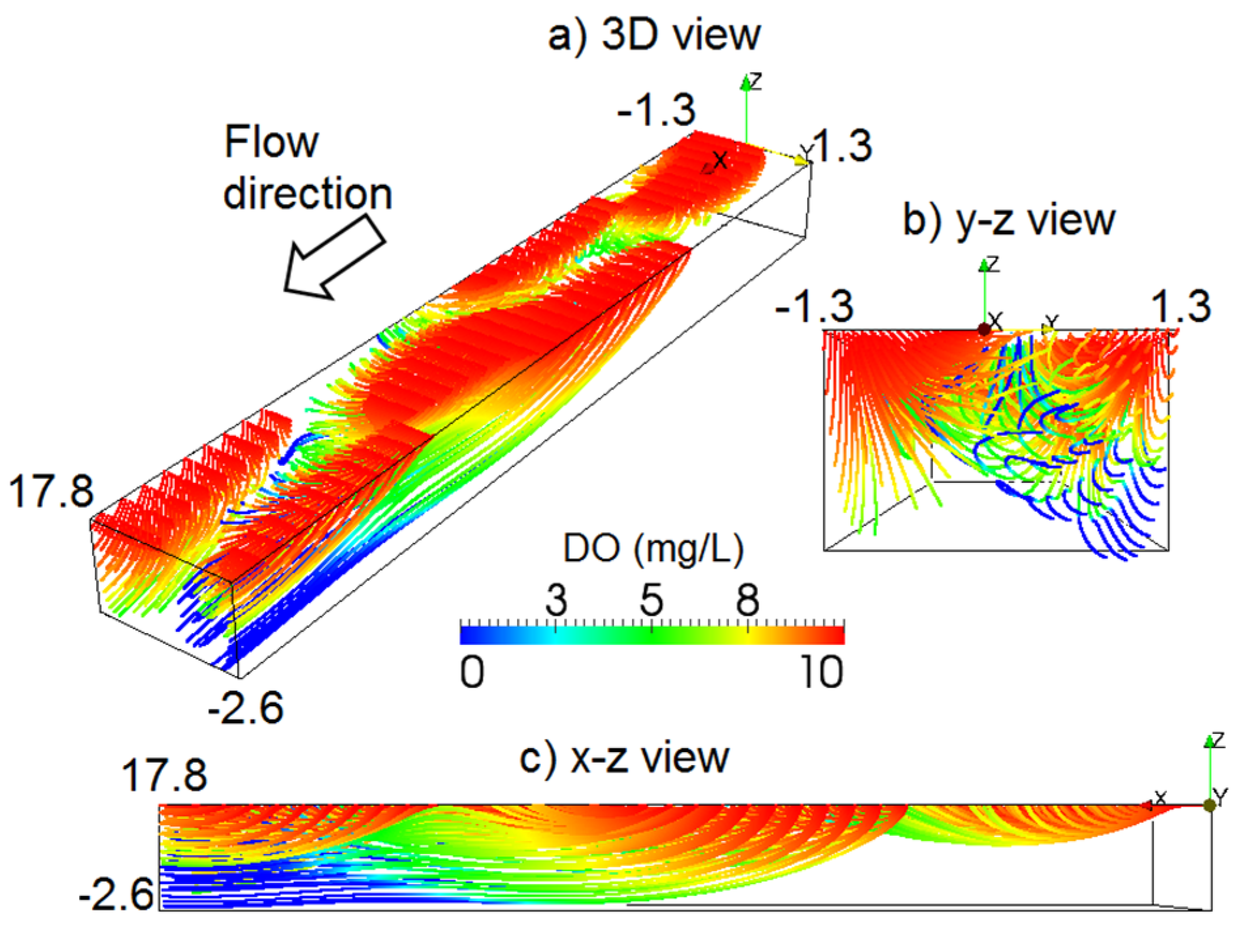
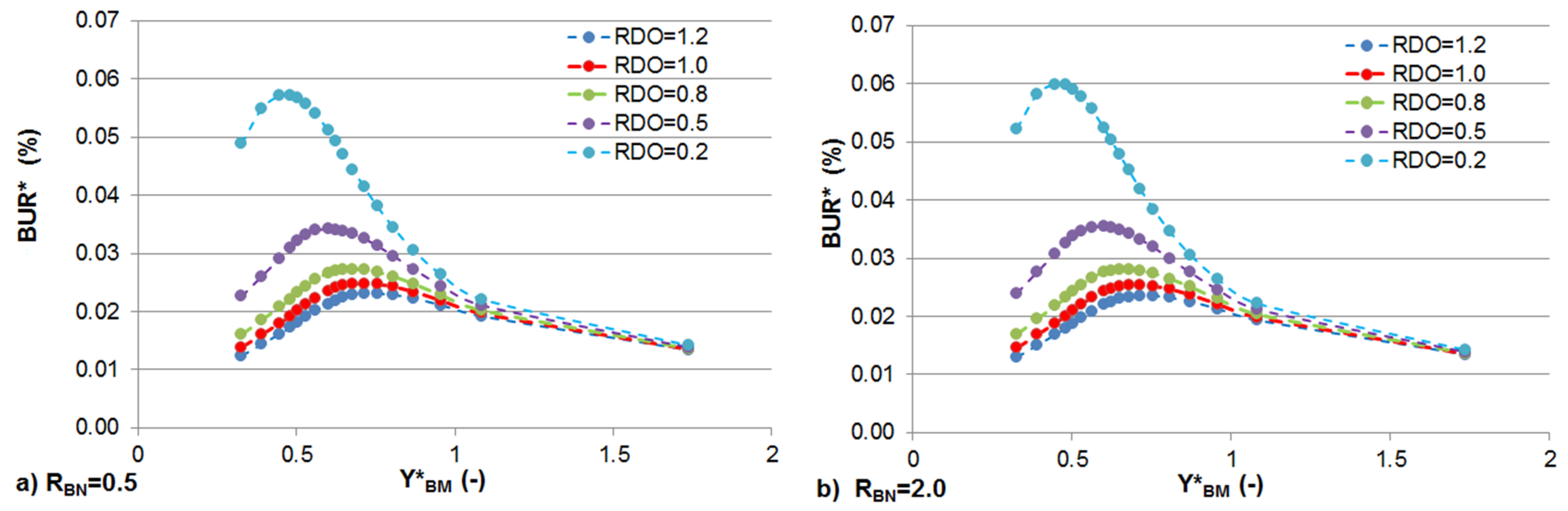
3.3. Effects of Constant BOD and DO Loads
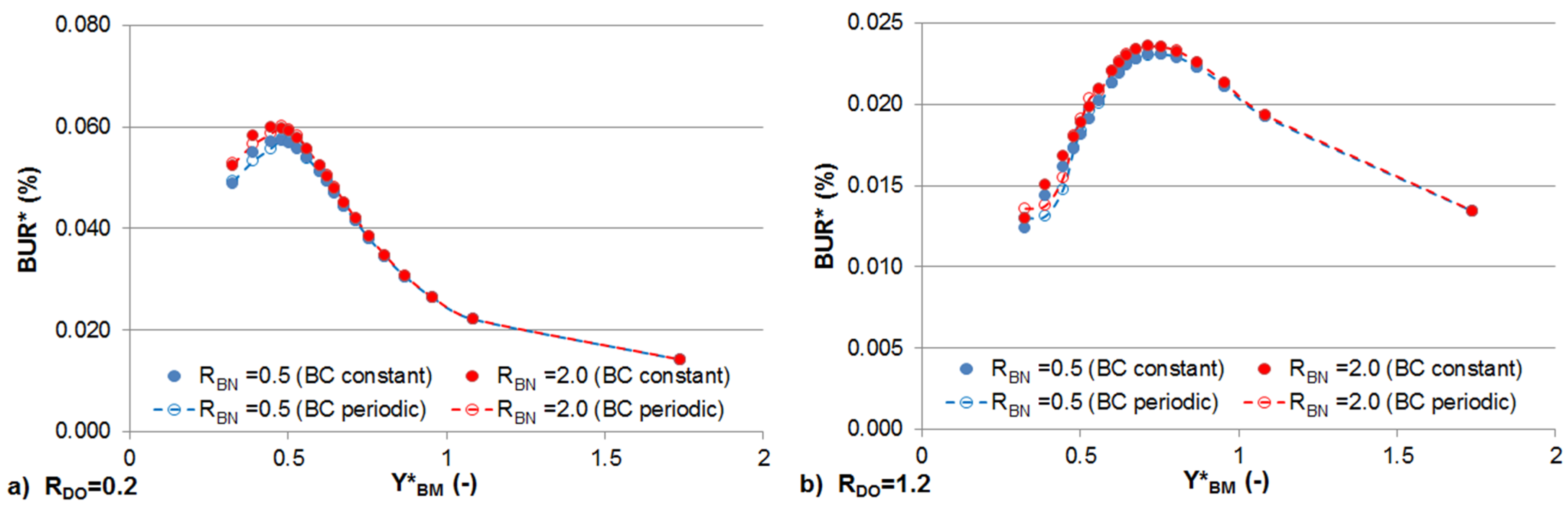
3.4. Effects of Sinusoidally Varying and Constant Stream Solute Concentrations
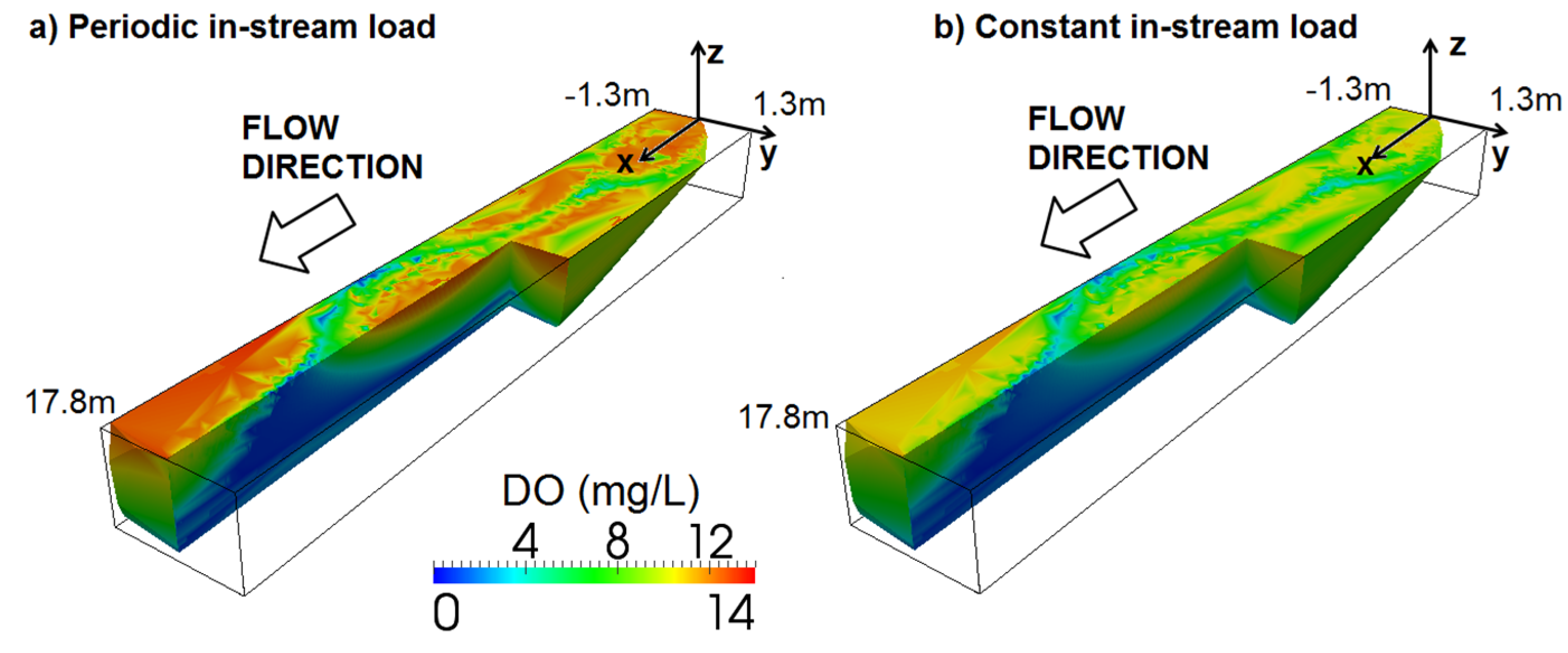
4. Conclusions
Acknowledgments
Appendix
Conflicts of Interest
References
- Galloway, J.N.; Dentener, F.J.; Capone, D.G.; Boyer, E.W.; Howarth, R.W.; Seitzinger, S.P.; Asner, G.P.; Cleveland, C.C.; Green, P.A.; Holland, E.A.; et al. Nitrogen cycles: Past, present, and future. Biogeochemestry 2004, 70, 153–226. [Google Scholar] [CrossRef]
- Galloway, J.N.; Townsend, A.R.; Erisman, J.W.; Bekunda, M.; Cai, Z.; Freney, J.R.; Martinelli, L.A.; Seitzinger, S.P.; Sutton, M.A. Transformation of the nitrogen cycle: Recent trends, questions, and potential solutions. Science 2008, 320, 889–892. [Google Scholar] [CrossRef] [PubMed]
- Jelks, H.; Walsh, S.; Burkhead, N.; Contreras-Balderas, S.; Diaz-Pardo, E.; Hendrickson, D.; Lyons, J.; Mandrak, N.; McCormick, F.; Nelson, J. Conservation status of imperiled north american freshwater and diadromous fishes. Fisheries 2008, 33, 372–407. [Google Scholar] [CrossRef]
- McMahon, P.B.; Tindall, J.A.; Collins, J.A.; Lull, K.J.; Nuttle, J.R. Hydrologic and geochemical effect on oxygen uptake in bottom sediments of an effluent-dominated river. Water Resour. Res. 1995, 31, 2561–2569. [Google Scholar] [CrossRef]
- Paulsen, S.G.; Mayio, A.; Peck, D.; Stoddard, J.; Tarquinio, E.; Holdsworth, S.; Van Sickle, J.; Yuan, L.; Hawkins, C.; Herlihy, A.T. Condition of stream ecosystems in the us: An overview of the first national assessment. J. Inf. 2008, 27, 812–821. [Google Scholar]
- Cooper, A.B. Activities of benthic nitrifiers in streams and their role in oxygen consumption. Microb. Ecol. 1984, 10, 317–334. [Google Scholar] [CrossRef] [PubMed]
- Štambuk-Giljanović, N. The pollution load by nitrogen and phosphorus in the cetina river. Water Air Soil Pollut. 2010, 211, 49–60. [Google Scholar] [CrossRef]
- Pollock, M.S.; Clarke, L.M.J.; Dubé, M.G. The effects of hypoxia on fishes: From ecological relevance to physiological effects. Environ. Rev. 2007, 15, 1–14. [Google Scholar] [CrossRef]
- Yu, F.X.; Adrian, D.D.; Singh, V.P. Modeling river quality by the superposition method. J. Environ. Syst. 1991, 20, 1–16. [Google Scholar]
- Rusjan, S.; Mikoš, M. Seasonal variability of diurnal in-stream nitrate concentration oscillations under hydrologically stable conditions. Biogeochemestry 2010, 97, 123–140. [Google Scholar] [CrossRef]
- Gariglio, F.; Tonina, D.; Luce, C.H. Spatio-temporal variability of hyporheic exchange through a pool-riffle-pool sequence. Water Resour. Res. 2013, 49, 7185–7204. [Google Scholar] [CrossRef]
- Marzadri, A.; Tonina, D.; Bellin, A. Effects of stream morphodynamics on hyporheic zone thermal regime. Water Resour. Res. 2013, 49, 2287–2302. [Google Scholar] [CrossRef]
- Alshawabkeh, A.; Adrian, D.D. Analytical water quality model for a sinusoidally varying bod discharge concentration. Water Resour. Res. 1997, 31, 1207–1215. [Google Scholar]
- Higashino, M.; Gantzer, C.; Stefan, H.G. Unsteady diffusional mass transfer at the sediment/water interface: Theory and significance for sod measurement. Water Res. 2004, 38, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, B.; Revsbech, N. Diffusive boundary layers and the oxygen uptake of sediments and detritus. Limnol. Oceanogr. 1985, 30, 111–122. [Google Scholar] [CrossRef]
- Rutherford, I.C.; Boyle, J.D.; Elliott, A.H.; Hatherell, T.V.J.; Chiu, T.W. Modeling benthic oxygen uptake by pumping. J. Environ. Eng. 1995, 121, 84–95. [Google Scholar] [CrossRef]
- Buffington, J.M.; Tonina, D. Hyporheic exchange in mountain rivers ii: Effects of channel morphology on mechanics, scales, and rates of exchange. Geogr. Compass 2009, 3, 1038–1062. [Google Scholar] [CrossRef]
- Elliott, A.; Brooks, N.H. Transfer of nonsorbing solutes to a streambed with bed forms: Theory. Water Resour. Res. 1997, 33, 123–136. [Google Scholar] [CrossRef]
- Elliott, A.; Brooks, N.H. Transfer of nonsorbing solutes to a streambed with bed forms: Laboratory experiments. Water Resour. Res. 1997, 33, 137–151. [Google Scholar] [CrossRef]
- Tonina, D.; Buffington, J.M. Hyporheic exchange in mountain rivers i: Mechanics and environmental effects. Geogr. Compass 2009, 3, 1063–1086. [Google Scholar] [CrossRef]
- Zarnetske, J.P.; Haggerty, R.; Wondzell, S.M.; Baker, M.A. Dynamics of nitrate production and removal as a function of residence time in the hyporheic zone. J. Geophys. Res. 2011, 116, G01025. [Google Scholar]
- Zarnetske, J.P.; Haggerty, R.; Wondzell, S.M.; Bokil, V.A.; González-Pinzón, R. Coupled transport and reaction kinetics control the nitrate source-sink function of hyporheic zones. Water Resour. Res. 2012, 48, W11508. [Google Scholar]
- Triska, F.J.; Duff, J.H.; Avanzino, R.J. The role of water exchange between a stream channel and its hyporheic zone in nitrogen cycling at the terrestrial-aquatic interface. Hydrobiologia 1993, 251, 167–184. [Google Scholar] [CrossRef]
- Triska, F.J.; Duff, J.H.; Avanzino, R.J. Patterns of hydrological exchange and nutrient transformation in the hyporheic zone of a gravel bottom stream: Examining terrestrial-aquatic linkages. Freshw. Biol. 1993, 29, 259–274. [Google Scholar] [CrossRef]
- Grimaldi, C.; Chaplot, V. Nitrate depletion during within-stream transport: Effects of exchange processes between streamwater, the hyporheic and riparian zones. Water Air Soil Pollut. 2000, 124, 95–112. [Google Scholar] [CrossRef]
- Hlaváčová, E.; Rulík, M.; Čáp, L. Anaerobic microbial metabolism in hyporheic sediment of gravel bar in a small lowland stream. River Res. Appl. 2005, 21, 1003–1011. [Google Scholar] [CrossRef]
- Kasahara, T.; Hill, A.R. Effects of riffle–step restoration on hyporheic zone chemistry in n-rich lowland streams. Can. J. Fish. Aquat. Sci. 2006, 63, 120–133. [Google Scholar] [CrossRef]
- Pinay, G.; O’Keefe, T.C.; Edwards, R.T.; Naiman, R.J. Nitrate removal in the hyporheic zone of a salmon river in alaska. River Res. Appl. 2009, 25, 367–375. [Google Scholar] [CrossRef]
- Krause, S.; Heathwaite, L.; Binley, A.; Keenan, P. Nitrate concentration changes at the groundwater-surface water interface of a small cumbrian river. Hydrol. Process. 2009, 23, 2195–2211. [Google Scholar] [CrossRef]
- Fernald, A.G.; Landers, D.H.; Wigington, P.J. Water quality changes in hyporheic fow paths between a large gravel bed river and off-channel alcoves in oregon, USA. River Res. Appl. 2006, 22, 1111–1124. [Google Scholar] [CrossRef]
- Marzadri, A.; Tonina, D.; Bellin, A. Morphodynamic controls on redox conditions and on nitrogen dynamics within the hyporheic zone: Application to gravel bed rivers with alternate-bar morphology. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Briggs, M.A.; Lautz, L.K.; Hare, D.K. Residence time control on hot moments on net nitrate and uptake in hyporheic zone. Hydrol. Process. 2014, 28, 3741–3751. [Google Scholar] [CrossRef]
- Marzadri, A.; Tonina, D.; Bellin, A.; Tank, J.L. A hydrologic model demonstrates nitrous oxide emissions depend on streambed morphology. Geophys. Res. Lett. 2014, 41, 5484–5491. [Google Scholar] [CrossRef]
- Trauth, N.; Schmidt, J.C.; Vieweg, M.; Maier, U.; Fleckenstein, J.H. Hyporheic transport and biogeochemical reactions in pool-riffle systems under varying ambient groundwater flow conditions. J. Geophys. Res. Biogeosci. 2014, 119, 910–928. [Google Scholar] [CrossRef]
- Marzadri, A.; Tonina, D.; Bellin, A. A semianalytical three-dimensional process-based model for hyporheic nitrogen dynamics in gravel bed rivers. Water Resour. Res. 2011, 47, W11518. [Google Scholar]
- Bardini, L.; Boano, F.; Cardenas, B.M.; Revelli, R.; Ridolfi, L. Nutrient cycling in bedform induced hyporheic zones. Geochim. Cosmochim. Acta 2012, 84, 47–61. [Google Scholar] [CrossRef]
- Hester, E.T.; Young, K.I.; Widdowson, M.A. Controls on mixing-dependent denitrification in hyporheic zones induced by riverbed dunes: A steady state modeling study. Water Resour. Res. 2014, 50, 9048–9066. [Google Scholar] [CrossRef]
- Boano, F.; Demaria, A.; Revelli, R.; Ridolfi, L. Biogeochemical zonation due to intrameander hyporheic flow. Water Resour. Res. 2010, 46, W02511. [Google Scholar]
- Montgomery, D.R.; Buffington, J.M. Channel-reach morphology in mountain drainage basins. Geol. Soc. Am. Bull. 1997, 109, 596–611. [Google Scholar] [CrossRef]
- Tonina, D.; Buffington, J.M. A three-dimensional model for analyzing the effects of salmon redds on hyporheic exchange and egg pocket habitat. Can. J. Fish. Aquat. Sci. 2009, 66, 2157–2173. [Google Scholar] [CrossRef]
- Malard, F.; Tockner, K.; Dole-Olivier, M.-J.; Ward, J.V. A landscape perspective of surface-subsurface hydrological exchanges in river corridors. Freshw. Biol. 2002, 47, 621–640. [Google Scholar] [CrossRef]
- Rouch, R. Sur la répartition spatiale des crustacés dans le sous-écoulement d'un ruisseau des pyrénées. Ann. Limnol. 1988, 24, 213–234. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Cardenas, M.B.; Wilson, J.L. Hydrodynamics of coupled flow above and below a sediment–water interface with triangular bedforms. Adv. Water Resour. 2007, 30, 301–313. [Google Scholar] [CrossRef]
- Marzadri, A.; Tonina, D.; Bellin, A.; Vignoli, G.; Tubino, M. Effects of bar topography on hyporheic flow in gravel-bed rivers. Water Resour. Res. 2010, 46, W07531. [Google Scholar]
- Colombini, M.; Seminara, G.; Tubino, M. Finite-amplitude alternate bars. J. Fluid Mech. 1987, 181, 213–232. [Google Scholar] [CrossRef]
- Tonina, D.; Bellin, A. Effects of pore-scale dispersion, degree of heterogeneity, sampling size, and source volume on the concentration moments of conservative solutes in heterogeneous formations. Adv. Water Resour. 2007, 31, 339–354. [Google Scholar] [CrossRef]
- Marzadri, A.; Tonina, D.; Bellin, A. Effects of Hyporheic Fluxes on Streambed Pore Water Temperature. In Proceedings of the 10th International Conference on Hydroinformatics HIC 2012, Hamburg, Germany, 14–18 July, 2012; International Association of Hydro-Environment Engineering and Research (IAHR): Hamburg, Germany.
- Dagan, G.; Cvetkovic, V.; Shapiro, A.M. A solute flux approach to transport in heterogeneous formations: 1. The general framework. Water Resour. Res. 1992, 28, 1369–1376. [Google Scholar] [CrossRef]
- Marzadri, A.; Tonina, D.; Bellin, A. Quantifying the importance of daily stream water temperature fluctuations on the hyporheic thermal regime: Implication for dissolved oxygen dynamics. J. Hydrol. 2013, 507, 241–248. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999; p. 446. [Google Scholar]
- Marion, A.; Packman, A.I.; Zaramella, M.; Bottacin-Busolin, A. Hyporheic flows in stratified beds. Water Resour. Res. 2008, 44, W09433. [Google Scholar]
- Marion, A.; Zaramella, M.; Bottacin-Busolin, A. Solute transport in rivers with multiple storage zones: The stir model. Water Resour. Res. 2008, 44, W10406. [Google Scholar]
- Tonina, D. Surface water and streambed sediment interaction: The hyporheic exchange. In Fluid Mechanics of Environmental Interfaces; Gualtieri, C., Mihailović, D.T., Eds.; CRC Press, Taylor & Francis Group: London, UK, 2012; pp. 255–294. [Google Scholar]
- Tonina, D.; Buffington, J.M. Effects of stream discharge, alluvial depth and bar amplitude on hyporheic flow in pool-riffle channels. Water Resour. Res. 2011, 47, W08508. [Google Scholar]
- Beaulieu, J.J.; Tank, J.L.; Hamilton, S.K.; Wollheim, W.M.; Hall, R.O.J.; Mulholland, P.J.; Peterson, B.J.; Ashkenas, L.R.; Cooper, L.W.; Dahm, C.N.; et al. Nitrous oxide emission from denitrification in stream and river networks. Proc. Natl. Acad. Sci. USA 2011, 108, 214–219. [Google Scholar] [CrossRef] [PubMed]
- Benjankar, R.; Burke, M.P.; Yager, E.M.; Tonina, D.; Egger, G.; Rood, S.B.; Merz, N. Development of a spatially-distributed hydroecological model to simulate cottonwood seedling recruitment along rivers. J. Environ. Manag. 2014, 145, 277–288. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; Lewis Publishers: Boca Raton, FL, USA, 2008; p. 200. [Google Scholar]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]
- Benjankar, R.; Glenn, N.F.; Egger, G.; Jorde, K.; Goodwin, P. Comparison of field-observed and simulated map output from a dynamic floodplain vegetation model using remote sensing and gis techniques. GIScience Remote Sens. 2010, 47, 480–497. [Google Scholar] [CrossRef]
- Colombini, M. Revisiting the linear theory of sand dune formation. J. Hydraul. Eng. 2004, 502, 1–16. [Google Scholar]
- De Silva, A.M.F.; Zhang, Y. On the steepness of dunes and determination of alluvial stream friction factor. In Proceedings of the XXVIII IAHR Congress, Graz, Austria, 22–27 August 1999; p. 7.
- Van Rijn, L.C. Sediment transport, part iii: Bed forms and alluvial roughness. J. Hydraul. Eng. 1984, 110, 1733–1754. [Google Scholar] [CrossRef]
- Benjankar, R.; Tonina, D.; McKean, J.A. One-dimensional and two-dimensional hydrodynamic modeling derived flow properties: Impacts on aquatic habitat quality predictions. Earth Surf. Process. Landf. 2014. [Google Scholar] [CrossRef]
- Harvey, J.W.; Böhlke, J.K.; Voytek, M.A.; Scott, D.; Tobias, C.R. Hyporheic zone denitrification: Controls on effective reaction depth and contribution to whole-stream mass balance. Water Resour. Res. 2013, 49, 6298–6316. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tonina, D.; Marzadri, A.; Bellin, A. Benthic Uptake Rate due to Hyporheic Exchange: The Effects of Streambed Morphology for Constant and Sinusoidally Varying Nutrient Loads. Water 2015, 7, 398-419. https://doi.org/10.3390/w7020398
Tonina D, Marzadri A, Bellin A. Benthic Uptake Rate due to Hyporheic Exchange: The Effects of Streambed Morphology for Constant and Sinusoidally Varying Nutrient Loads. Water. 2015; 7(2):398-419. https://doi.org/10.3390/w7020398
Chicago/Turabian StyleTonina, Daniele, Alessandra Marzadri, and Alberto Bellin. 2015. "Benthic Uptake Rate due to Hyporheic Exchange: The Effects of Streambed Morphology for Constant and Sinusoidally Varying Nutrient Loads" Water 7, no. 2: 398-419. https://doi.org/10.3390/w7020398
APA StyleTonina, D., Marzadri, A., & Bellin, A. (2015). Benthic Uptake Rate due to Hyporheic Exchange: The Effects of Streambed Morphology for Constant and Sinusoidally Varying Nutrient Loads. Water, 7(2), 398-419. https://doi.org/10.3390/w7020398







