3.1. Description of the Alfeios River Basin
The Alfeios river basin has been extensively described in the past [
35,
36,
37]. This section describes briefly the information for the Alfeios required for the application of the FBISP method, since the thorough analysis of the hydrosystem is included in [
38].
The Alfeios River is a water resources system of great natural, ecological, social and economic importance for Western Greece, since it is the longest watercourse (with a length of 112 km) and has the highest flow-rate (absolute maximum and minimum values recorded 2380 and 13 m3/s) in the Peloponnese region in Greece. The main river and its six tributaries represent a significant source of water supply for the region, aiming at delivering and satisfying the expected demands from a variety of water users, including irrigation, drinking water supply, hydropower production and to a smaller extend recreation. A plethora of environmental stresses were exerted on its river basin the last decades. It drains an area of 3658 km2. Its annual water yield is estimated to be 2100 × 106 m3.
The main water uses in the basin include: (a) the hydropower production at Ladhon hydropower station (HPS) linked with the Ladhon Dam and reservoir situated in the middle mountainous Alfeios; (b) the agricultural demand of the Flokas scheme linked with the diversion Flokas Dam situated almost 20 km before the discharge of Alfeios into the Kyparissiakos Gulf and very close to Ancient Olympia; (c) the hydropower production at the small HPS at Flokas Dam; and (d) the drinking water supply to the Region of Pyrgos and the neighboring communities from Alfeios tributary, Erymanthos.
Beginning with the Ladhon river which is the most important tributary of Alfeios river basin draining almost one third of its total basin area, the operation goals of Ladhon reservoir are specified firstly, as the satisfaction of irrigation demand at the Flokas irrigation scheme, and secondly, as the hydropower production at HPS Ladhon, situated at around 8 km downstream the Ladhon Dam. The general operation rule is to start at the beginning of January with a minimum level of the Ladhon lake and then filling up the lake till May, in order to satisfy mainly irrigation demand. For the application of the FBISP method the upper-and lower-bounds of the optimized hydropower production target
(in MWh) at Ladhon (
Table 1) are required. These bounds are approximated from the statistical analysis of the monthly time series of hydropower production at Ladhon from 1985 to 2011. The ranges between the mean value of the historical timeseries minus its standard deviation (lower-bound) and its mean value plus its standard deviation (upper-bound) are considered as analyzed in [
38].
Proceeding to the Flokas irrigation region, the irrigation scheme is connected to the diversion Flokas Dam, draining an area of 3600 km
2. The irrigation water demand extends officially from May to September, whereas in most years could be further extended from April up to October due to dry climatic conditions. The present monthly irrigation water demand is composed of two parts: (a) a regulated and stable irrigation demand pattern, referring only to the required water volume releases from Ladhon Reservoir, which is derived from the official agreement between Hellenic Public Power Corporation and General Irrigation Organization for the Flokas Irrigation Area; and (b) an extra uncertain irrigation demand at Flokas Dam site based on the actual crop patterns and the water inflows at this position. The total irrigation requirements for the crop pattern of Flokas are estimated for each stochastic hydrologic scenario using the FAO software CROPWAT 8.0. For the application of the FBISP methodology the upper- and lower-bounds of the water allocation targets for irrigation in EUR/m
3 are required. The optimized water allocation target for irrigation (
Table 2) is explored, assuming that the irrigation demand can vary between the maximum demand of the present crop pattern and the maximum demand given in the study of the small HPS at Flokas. Based on this assumption, the lower-bound of the optimized water allocation target is set equal to the maximum of all sets of irrigation water requirements for the fifty hydrologic scenarios as computed by CROPWAT for the present irrigated area and crop pattern.
The small Flokas HPS is situated directly after the diversion of water from the Flokas Dam, and is operated automatically based on the upstream water level. In this way when the river flow rate is between 9 and 90 m
3/s, the entire part of the river flow passes through the Flokas HPS, maintaining the water level of Dam at a stable level. When river flow rate exceeds 90 m
3/s then the surplus flows over the spillways of Flokas Dam. Whereas for flood water volumes exceeding 300 m
3/s the HPS Flokas closes for security reasons and the flood volume passes through the spillways of the dam and the opened gateways. For the application of the FBISP method the upper- and lower-bounds of the optimized hydropower production target
(in MWh) at Flokas small HPS (
Table 3) are required. These bounds are approximated also in this case, from the statistical analysis of the monthly timeseries of hydropower production at Flokas from 2011 to 2015. The ranges between the mean value of the historical timeseries minus its standard deviation (lower-bound) and its mean value plus its standard deviation (upper-bound) are taken into account as specified in [
38].
Finally, a monthly water flow rate of 0.6 m3/s for the drinking water supply system for the north and central part of the Region of Hleias is diverted from Erymanthos to the water treatment plant and then to the neighboring communities extending up to the city of Pyrgos. Due to the short operation period (starting in 2013), this water use is not incorporated in the optimization process as a variable but as a steady and known water abstraction demand.
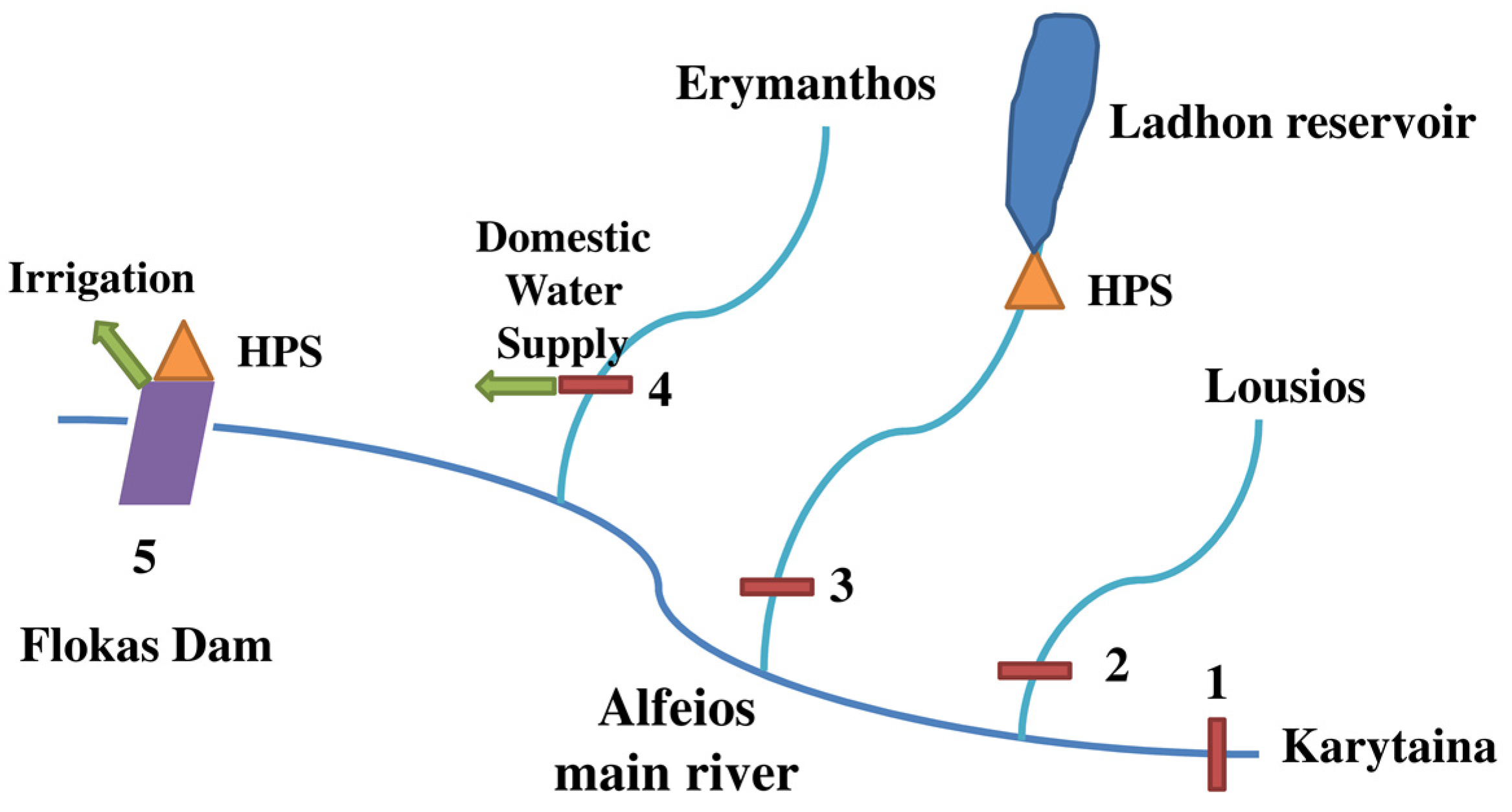
The schematization of the Alfeios river network is depicted as shown in
Figure 1, including the main five water inflow locations, where historical timeseries (rain, temperature and river discharge) are available and the main water users as described above.
Table 1.
Upper- (THydroLadhon+) and lower- (THydroLadhon−) bounds of optimized target for hydropower production at HPS at Ladhon.
Table 1.
Upper- (THydroLadhon+) and lower- (THydroLadhon−) bounds of optimized target for hydropower production at HPS at Ladhon.
| Bounds of Optimized Target | Target Limits for Hydropower Production at Ladhon HPS (MWh) |
|---|
| January | February | March | April | May | June | July | August | September | October | November | December | Annual |
|---|
| THydroLadhon− | 11,857 | 12,553 | 11,810 | 11,046 | 11,081 | 8965 | 9077 | 7613 | 5925 | 7387 | 9427 | 8540 | 115,282 |
| THydroLadhon+ | 37,353 | 38,947 | 48,311 | 35,391 | 23,237 | 15,868 | 15,598 | 14,233 | 13,642 | 17,062 | 17,971 | 24,276 | 301,890 |
Table 2.
Upper- and lower-water allocation targets for irrigation in EUR/m3.
Table 2.
Upper- and lower-water allocation targets for irrigation in EUR/m3.
| Time Stages | Irrigation Water Demand (m3/s) |
|---|
| Lower-Bound of Optimized Allocation Target | Upper-Bound of Optimized Allocation Target |
|---|
| Tirrigation− | Tirrigation+ |
|---|
| t = 1—January | 0 | 0 |
| t = 2—February | 0 | 0 |
| t = 3—March | 0 | 6 |
| t = 4—April | 2.0 | 6 |
| t = 5—May | 5.0 | 6 |
| t = 6—June | 8.9 | 12 |
| t = 7—July | 11.5 | 12 |
| t = 8—August | 9.2 | 12 |
| t = 9—September | 2.7 | 6 |
| t = 10—October | 1.2 | 6 |
| t = 11—November | 0 | 0 |
| t = 12—December | 0 | 0 |
| Annual (m3) | 108,756,934 | 174,700,800 |
Table 3.
Upper- (THydroFlokas+) and lower- (THydroFlokas−) bounds of optimized target for hydropower production at HPS at Flokas.
Table 3.
Upper- (THydroFlokas+) and lower- (THydroFlokas−) bounds of optimized target for hydropower production at HPS at Flokas.
| Bounds of Optimized Target | Target Limits for Hydropower Production at Flokas HPS (MWh) |
|---|
| January | February | March | April | May | June | July | August | September | October | November | December | Annual |
|---|
| THydroFlokas− | 1244 | 1740 | 2450 | 2045 | 1574 | 437 | 219 | 218 | 232 | 395 | 299 | 1129 | 11,982 |
| THydroFlokas+ | 2379 | 2894 | 3435 | 2840 | 1861 | 773 | 251 | 255 | 571 | 1111 | 1397 | 2097 | 19,865 |
Figure 1.
The simplified schematics of the Alfeios river basin
Figure 1.
The simplified schematics of the Alfeios river basin
3.2. Optimization Problem of the Alfeios Hydrosystem
The goal of this optimization problem is to identify an optimal water allocation target with a maximized economic benefit over the planning period for the Alfeios river basin. Different water allocation targets are related not only to different policies for water resources management, but also to different economic implications (probabilistic penalty and opportunity loss). The penalty is associated with the nonproper water allocation/management, and therefore, resulting to shortages and spills for hydropower and for water shortage for irrigation. The optimization problem is structured as follows:
subject to:
Constraints of water-mass balance for the Ladhon reservoir:
Constraints for the minimum and maximum water volume released by turbines at HPS Ladhon:
Constraints of Ladhon reservoir capacity:
Constraints for target of hydropower production at Ladhon:
Constraints of water-mass balance for the Flokas Dam:
Water availability at Flokas dam based on the upstream water inflows:
Water-mass balance at Flokas Dam:
Water-mass balance at the small HPS at Flokas:
Constraints for target of hydropower production at Flokas:
Constraints for the minimum and maximum water volume released by turbines at HPS at Flokas:
Constraints for water allocation target of irrigation at Flokas:
Constraints of upper- and lower-bounds for allocation targets:
Non-negative and technical constrains
where
net system benefit over the planning horizon (EUR);
time period, and t = 1, 2, …, T (T = 12);
surface area of Ladhon reservoir in period t under scenarios k1 ();
slope coefficient from linear regression between surface area of Ladhon reservoir and storage volume;
intercept coefficient from linear regression between surface area of Ladhon reservoir and storage volume;
monthly hydropower production for t = 1, 2, …, T; in period t under scenarios k1 for the water user i with i = 1, 2 corresponding to Ladhon and Flokas, respectively;
annual hydropower production in period t under scenarios k1 for the water user i with i = 1, 2 corresponding to Ladhon and Flokas, respectively;
slope coefficient from linear regression between hydropower production of Ladhon reservoir and water volume released through the turbines;
slope coefficient from linear regression between hydropower production of Ladhon reservoir and water volume released through the turbines;
area-based conversion factor multiplied with each stream discharge to add the contribution of water inflows from intermittent drainage areas;
slope coefficient from linear regression between hydropower production of Flokas and water volume released through the turbines;
slope coefficient from linear regression between hydropower production of Flokas HPS and water volume released through the turbines;
= lower-bound of the optimized target for the water user i in period t (() for irrigation and (MWh) for hydropower;
= upper-bound of the optimized target for the water user i in period t (() for irrigation and (MWh) for hydropower);
average evaporation rate for Ladhon reservoir in period t (m);
evaporation loss of Ladhon reservoir in period t ();
= number of flow scenarios in period t;
= net benefit per unit of water allocated for each water user i—(EUR/) for irrigation and (EUR/ for hydropower;
penalty per unit of water not delivered (EUR/) for each water user i—for irrigation and (EUR/ for hydropower; and ;
= probability of occurrence of scenario in period t, with and ;
water inflow level into stream j in period t under scenario ();
i = 1, 2, 3 for the water users being hydropower production at Ladhon, hydropower production at Flokas and irrigation at Flokas;
j = 1, 2, 3, 4, 5 stream index for the river flows at Karytaina, Lousios, Ladhon, Erymanthos and Flokas;
release flow from the turbines of Ladhon reservoir in period t under scenario ();
spill volume over Ladhon Dam in period t under scenario ();
= maximum storage capacity of Ladhon reservoir ();
= minimum storage capacity of Ladhon reservoir ();
maximum capacity of turbines at Ladhon HPS ();
minimum capacity of turbines at Ladhon HPS ();
maximum capacity of turbines at Flokas HPS ();
minimum capacity of turbines at Flokas HPS ();
= storage level in Ladhon reservoir in period t under scenario ();
= water allocation target that is promised to the user i in period t ();
shortage level by which the water-allocation target is not met in period t under scenarios for the water user i, which is associated with probability of —() for irrigation and MWh for hydropower;
irrigation shortage volume in period t under scenarios ();
water volume left at Flokas after having allocated the irrigation water in period t under scenarios ();
water volume flowing through the fish ladder at Flokas dam in period t under scenarios ();
= water volume flowing through the turbines at Flokas HPS in period t under scenarios ();
spill volume at Flokas dam in period t under scenarios ();
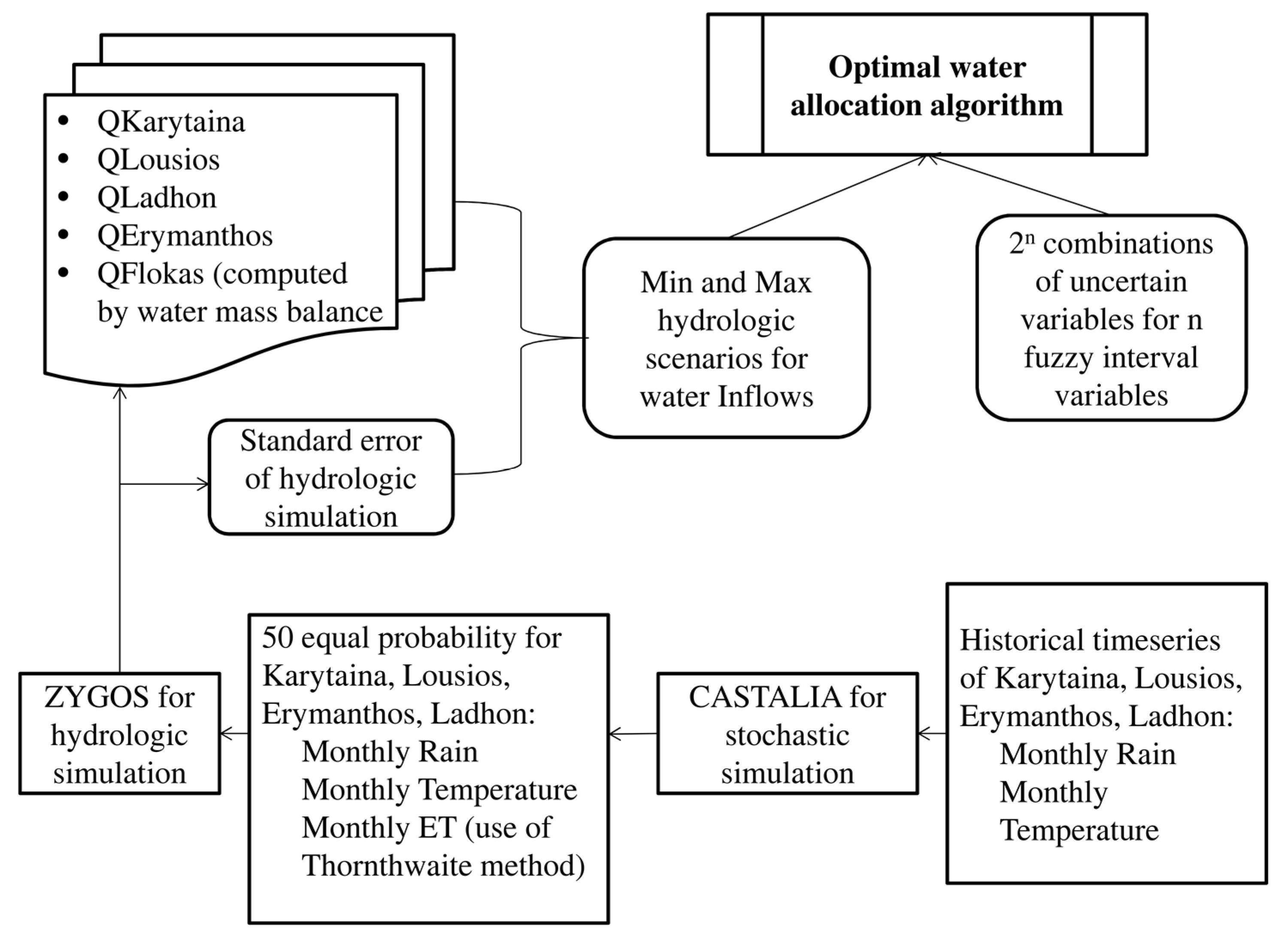
CASTALIA model is applied for the simultaneous stochastic generation of fifty equal-probability scenarios for the hydrologic variables of rain and temperature at the four considered subcatchments (Karytaina, Lousios, Ladhon and Erymanthos) having a time length of ten years (since the future WADI water and agriculture scenarios are projected ten years after the baseline scenario) and monthly time step. The stochastically simulated rain and temperature timeseries are introduced into the calibrated simple lumped conceptual river basin model ZYGOS [
58,
59] for the four subcatchments in order to compute the mean monthly discharges for this ten years period. The uncertainty from the hydrologic model structure and the parametrization is taken into account through the computation of the standard error between the measured and the simulated water discharge timeseries. Based on this standard error, upper-bound water inflows timeseries for all the hydrologic scenarios (which are used in the f
+ model), and lower-bound (which are used in the f
− model) are created. The steps of this process and the software programs used are presented schematically in the form of a flow chart in
Figure 2. The last year of each of the fifty stochastic monthly discharge scenarios (since the future scenarios refer to ten years after the baseline) serves as input inflows into the optimization model for the optimal water allocation of Alfeios river basin. The monthly discharge at Flokas Dam, which is of interest for the optimization process, since at this position the available water is diverted to the irrigation canal, is computed as the sum of the four subcatchments as described in [
38].
In the optimization problem, there are some nonlinear equations, such as the relationship between water flowing through the turbines and the hydropower energy produced. In order to introduce them into the linear programming algorithm their linear regression equations are considered. The uncertainty resulting from this simplification has not been considered in the process, but it is worth mentioning that in all cases the R2 takes values ≥ 0.9.
Figure 2.
Methodological framework for optimal water allocation of Alfeios river basin.
Figure 2.
Methodological framework for optimal water allocation of Alfeios river basin.
The uncertain variables in this case are firstly, the coefficients of the objective function including (a) the unit benefits and penalties from hydropower production of Ladhon (EUR/MWh); (b) the unit benefits and penalties from the hydropower of Flokas (EUR/MWh); and (c) the unit benefits and penalties from Flokas irrigation (EUR/m
3), and secondly, the initial water level of Ladhon reservoir at stage zero (m
3) which is expressed as deterministic-boundary interval (12,362,644.01, 26,783,729.12). A detailed analysis of the estimation of the prementioned unit benefits and penalties is provided in [
38]. Briefly, based on the estimations of the Chief Engineer at Ladhon hydropower station, the upper- and lower- fuzzy-boundary intervals for the unit benefit and penalty of Ladhon are defined as given in
Table 4. The shadow penalty for the hydropower production at Ladhon is composed of two parts: (a) the penalty due to hydropower shortage in comparison to the hydropower production target and (b) the penalty for the water spilled from the Ladhon Dam (if any) and is not available for hydropower production, which intends to express the opportunity loss of hydropower energy production. Based on the monthly selling price data of Flokas HPS, its unit benefit is approximated as a single deterministic interval (and not as a fuzzy-boundary interval) as presented in
Table 4. The unit shadow penalty is approximated as a single deterministic interval and is taken equal to the upper-bound solution of the unit penalty of Flokas HPS, as shown in
Table 4. The unit benefit for water allocated to irrigation is interpreted as the probable net income from agricultural production of the Flokas crop pattern, taking into account the brutto farmer, the cost of production, the cost of the irrigation canal (associated to the water charge to the farmers from the general irrigation organization) and the organizational structure of local irrigation organizations (the charges of the local irrigation organizations). In
Table 5, the lower- and upper- fuzzy-boundaries of the unit benefit of water allocated to the Flokas irrigation scheme is provided for the baseline scenario and the WADI future scenarios. Finally, the unit penalty from the irrigation water deficits is based on the crop yield reduction and the corresponding net farmer income loss. In
Table 6 the lower- and upper- fuzzy-boundaries of the unit penalties for irrigation water deficits of the Flokas irrigation scheme is provided for the baseline scenario and the WADI future scenarios (where as presented in
Section 4 the World agricultural markets scenario is denoted as Future Scenario 1 (FS1), the Global agricultural sustainability scenario as Future Scenario 2 (FS2), the Provincial agriculture scenario as (Future Scenario 3-FS3) and the Local community agriculture as (Future Scenario 4-FS4).
Table 4.
Lower- and upper- fuzzy-boundary intervals for the unit benefit and unit penalty for hydropower production EUR/MWh at Ladhon and at Flokas.
Table 4.
Lower- and upper- fuzzy-boundary intervals for the unit benefit and unit penalty for hydropower production EUR/MWh at Ladhon and at Flokas.
| Variables | NBHP Ladhon | NBHP Flokas | CHP Ladhon | CHP Flokas |
|---|
| EUR/MWh | EUR/MWh | EUR/MWh | EUR/MWh |
|---|
| Lower-Bound—Minimum | 40 | 87.5 | 120 | 140 |
| Lower-Bound—Maximum | 55 | – | 130 | 150 |
| Upper-Bound—Minimum | 60 | 80 | 140 | 140 |
| Upper-Bound—Maximum | 75 | – | 150 | 150 |
Table 5.
Lower- and upper- fuzzy-boundary intervals for the unit benefit from irrigation for the baseline and the WADI future scenarios for Flokas irrigation scheme EUR/m3.
Table 5.
Lower- and upper- fuzzy-boundary intervals for the unit benefit from irrigation for the baseline and the WADI future scenarios for Flokas irrigation scheme EUR/m3.
| Fuzzy-Boundary Intervals | NBIrrigationFlokas EUR/m3 |
|---|
| Baseline | FS 1 | FS 2 | FS 3 | FS 4 |
|---|
| Upper-Bound | Min | 0.166 | 0.127 | 0.189 | 0.191 | 0.221 |
| Max | 0.175 | 0.136 | 0.265 | 0.276 | 0.294 |
| Lower-Bound | Min | 0.187 | 0.190 | 0.266 | 0.277 | 0.295 |
| Max | 0.205 | 0.234 | 0.269 | 0.314 | 0.431 |
Table 6.
Lower- and upper- fuzzy-boundary intervals for the unit penalties for water deficits to irrigation EUR/m3 for the baseline and the future scenarios.
Table 6.
Lower- and upper- fuzzy-boundary intervals for the unit penalties for water deficits to irrigation EUR/m3 for the baseline and the future scenarios.
| Fuzzy-Boundary Intervals | PEIrrigationFlokas EUR/m3 |
|---|
| Baseline | FS 1 | FS 2 | FS 3 | FS 4 |
|---|
| Upper-Bound | Min | 0.989 | 0.748 | 1.052 | 1.035 | 1.043 |
| Max | 1.051 | 1.159 | 1.075 | 1.073 | 1.070 |
| Lower-Bound | Min | 1.715 | 3.361 | 1.537 | 1.552 | 2.184 |
| Max | 1.812 | 3.410 | 1.891 | 1.871 | 2.279 |