Assessing the Feasibility of Managed Aquifer Recharge for Irrigation under Uncertainty

Abstract

Additional storage of water is a potential option to meet future water supply goals. Financial comparisons are needed to improve decision making about whether to store water in surface reservoirs or below ground, using managed aquifer recharge (MAR). In some places, the results of cost-benefit analysis show that MAR is financially superior to surface storage. However, uncertainty often exists as to whether MAR systems will remain operationally effective and profitable in the future, because the profitability of MAR is dependent on many uncertain technical and financial variables. This paper introduces a method to assess the financial feasibility of MAR under uncertainty. We assess such uncertainties by identification of cross-over points in break-even analysis. Cross-over points are the thresholds where MAR and surface storage have equal financial returns. Such thresholds can be interpreted as a set of minimum requirements beyond which an investment in MAR may no longer be worthwhile. Checking that these thresholds are satisfied can improve confidence in decision making. Our suggested approach can also be used to identify areas that may not be suitable for MAR, thereby avoiding expensive hydrogeological and geophysical investigations.

1. Introduction

Water demand continues to grow in order to maintain food security and drinking water supplies, while supplies remain limited from conventional sources. Future water security is threatened in many places, as most suitable locations for large surface storages have already been used [1] and ground water is often being withdrawn at unsustainable rates [2,3,4]. Among other options of water supply augmentation, such as water recycling, desalination etc., storing more water underground appears to be a potential solution to achieve future water supply goals. For many water stressed areas, water security and reliability do not necessarily depend on the absolute amount of precipitation, but on the fraction of water that is efficiently retained as storage for future use [5].

Water shortages can be eased by storing surplus water underground during wet periods for later use during dry periods. Managed aquifer recharge (MAR) has been used successfully in several countries for the storage and treatment of water [6,7,8,9]. Storage of surplus water in aquifers can help minimize evaporative losses and help irrigators to adjust to surface water variability during droughts, provided that MAR is technically feasible and cost effective. The feasibility of MAR and its comparative cost to other alternatives depend on a number of technical and financial factors, such as infiltration, injection and recovery rates, which are dependent on local hydrogeology [10].

A few studies indicate that MAR can achieve more financial value than surface storage and other alternatives [11,12]. However, uncertainty often exists whether it is more cost effective to store water above ground in surface reservoirs or below ground using managed aquifer recharge [13].

Cost-benefit analysis (CBA) provides a comparison of benefits and costs resulting from a proposed policy or investment [14]. Previous studies undertaking CBA of MAR have assumed hydrogeological factors, such as infiltration, injection and recovery rates, to be known [11,12,15]. Overlooking such uncertainties can result in lower than expected operational efficiency and irrigation returns from MAR [16,17]. For example, future returns from MAR may be affected by increases in groundwater pumping cost or reductions in infiltration rates.

An increase in the turbidity of source water due to hydrological variability can significantly increase the cost of infiltration basin maintenance, adding to the cost of water quality treatment for aquifer storage and recovery (ASR) systems. Maliva [16], in this special issue, highlights that assessing such uncertainty is perhaps the most neglected aspect in the economics of MAR.

The primary focus of this paper is to systematically search for conditions under which the requirements for MAR may not be met and failure might occur. Playing such a devil’s advocate role has been shown to improve decision making compared to an exclusively expert-driven approach [18]. The approach used identifies thresholds above which MAR is financially better than surface storage and below which it is not. These thresholds (or cross-over points) describe corresponding values of variables at which the net present value (NPV) from MAR and surface storage become equal. All dollar amounts reported in this study are in Australian dollars. An example of a cross-over point for pumping cost is shown in Figure 1, where basin infiltration (red line) and surface storage (green line) options are compared; and where basin infiltration is initially (dashed vertical line) more profitable than surface storage. A cross-over point between the two compared options is possible when the cost of pumping increases from the best guess value of 35 $/megalitres (ML) to 53.63 $/ML. This increase in the pumping cost will decrease benefits (NPV) from basin infiltration, such that they become equal to the benefits (NPV) obtained from surface storage. However, aquifer storage and recovery (ASR) always result in an inferior NPV regardless of the pumping cost. There is no cross-over point between ASR and the other alternatives.

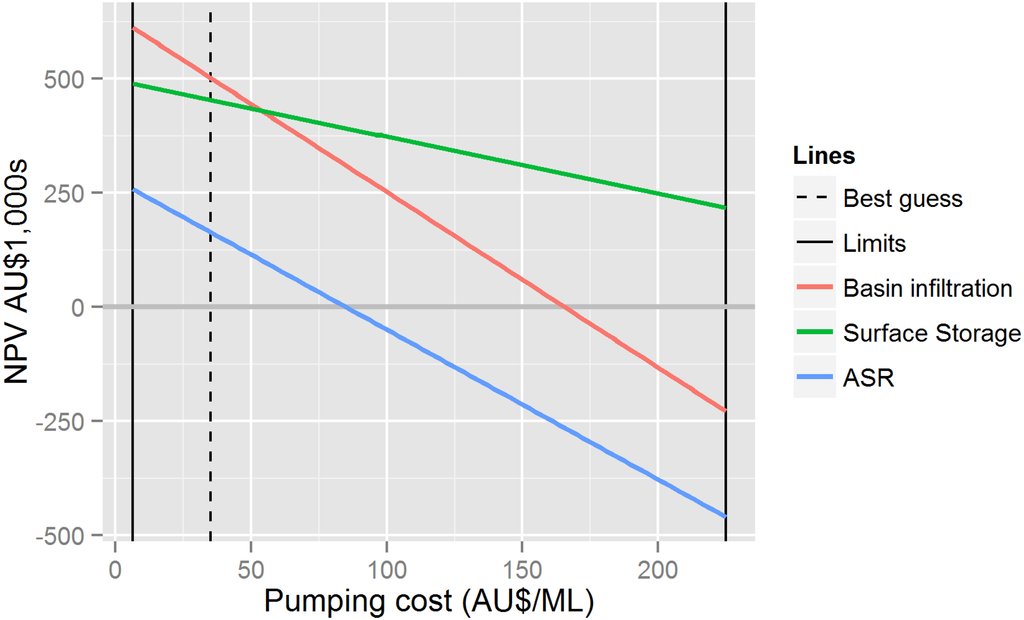
Figure 1. Illustration of identifying cross-over points for pumping cost when comparing basin infiltration, aquifer storage and recovery (ASR) and surface storage of irrigation water.

Figure 1. Illustration of identifying cross-over points for pumping cost when comparing basin infiltration, aquifer storage and recovery (ASR) and surface storage of irrigation water.

At the cross-over point, the decision maker is indifferent to choosing a single option from the two, because their financial returns are equal. In our method, we use computational techniques to identify the cross-over points as values of uncertain variables where the NPV of MAR is exactly equal to the NPV of surface storage of irrigation water. The approach is demonstrated through a case study in a highly developed irrigation region of the lower Namoi catchment in New South Wales, Australia, where irrigation water restrictions motivate the need to consider options to supplement future irrigation supplies, such as MAR.

The suggested approach of identifying cross-over points is beneficial in three ways;

• It can determine minimum hydrogeological and cost requirements under which MAR can be worthwhile;
• It can improve confidence in decision making for MAR investment, by enabling the assessment of conditions that are unfavourable to MAR compared to surface water storage;
• It can substantially lower the cost of geophysical and hydrogeological investigations by targeting only areas that satisfy the minimum requirements, as MAR investigations and trials are shown to be time and resource expensive.

The next section provides an overview of the literature on the feasibility of MAR with a focus on the technical, financial and uncertainty considerations. Section 3 (“Methods”) describes the model and tool used to explore cross-over points. In Section 4, an illustrative study in the lower Namoi catchment evaluates the irrigation-related costs and benefits of storing flood water in aquifers compared to surface storages. The analysis of cross-over points in Section 5 provides a discussion of how cross-over points are reached when only a single variable changes, as well as when many variables interact.

2. Related Work: Feasibility of Managed Aquifer Recharge

Assessing the feasibility of MAR requires the integration of many types of data and information from many disciplines (Figure 2). Although carrying out a comprehensive feasibility assessment is essential, the first step in establishing an MAR scheme requires assessing the feasibility of technical and financial factors, to provide a basis for other investigations to proceed.

An overview of the basic requirements and feasibility guidelines for managed aquifer recharge (MAR) is available in [10] and GHD and AGT [19].

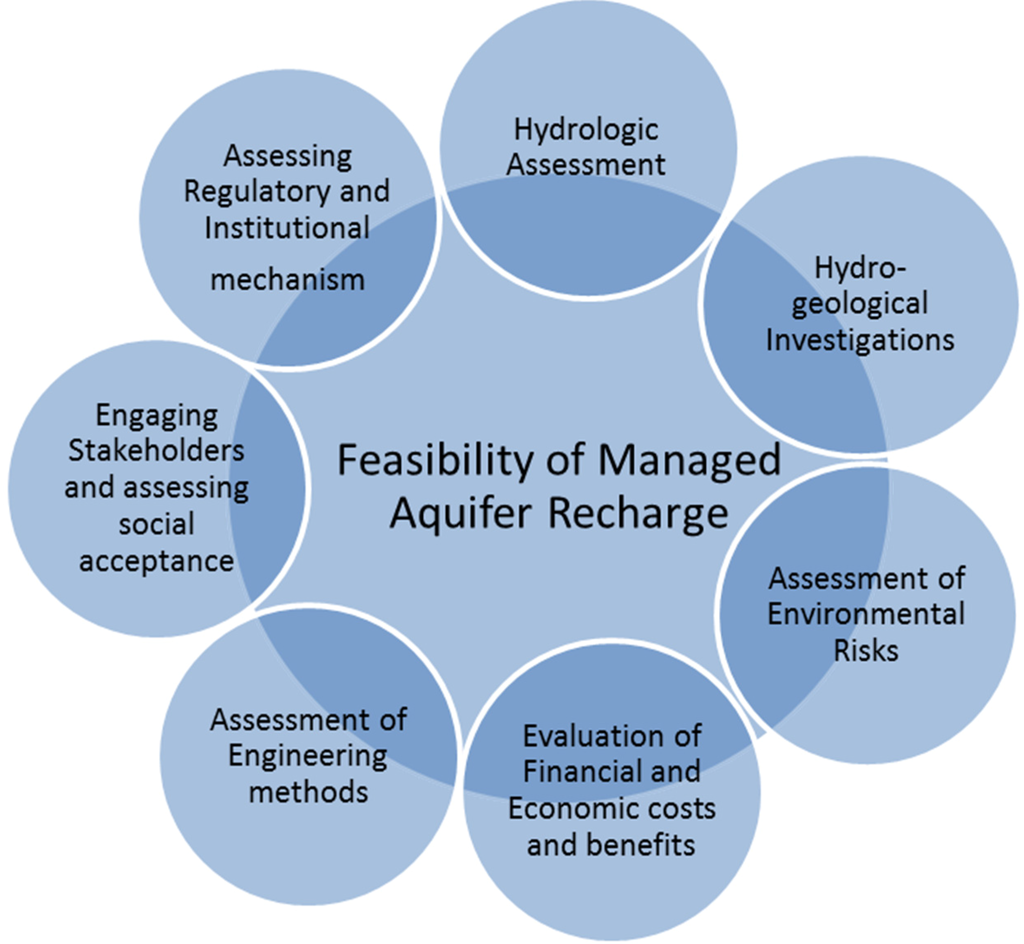
Figure 2. A framework for the feasibility of managed aquifer recharge: adapted from GHD and AGT [19], Dillon et al. [10] and Rawluk et al. [20].

Figure 2. A framework for the feasibility of managed aquifer recharge: adapted from GHD and AGT [19], Dillon et al. [10] and Rawluk et al. [20].

2.1. Technical Considerations

Key technical requirements for MAR include hydrogeological assessment of the target aquifer, the availability of surplus surface water and the means to convey it underground. Relevant hydrogeological factors include aquifer storage size, permeability, infiltration, injection and recovery rates and connections with other aquifers [21,22]. High infiltration rates lower the cost of underground storage; for example, a basin infiltration system with high infiltration rates will require a smaller pond area and can be cheaper to construct and maintain than a pond with low infiltration rates.

There are two main types of MAR methods: basin infiltration and aquifer storage and recovery (ASR), each favourable to different hydrogeological conditions. Basin infiltration is suitable to recharge shallow unconfined aquifers with minimal or no treatment of the recharge water. The methods include deep, large diameter isolated wells, infiltration ponds, infiltration galleries, induced bank filtration, leaky and recharge dams and redirecting floodwaters over the wider landscape to supplement areal recharge [7,9]. Some basin infiltration methods require large surface areas and permeable soils to be effective [21,23].

ASR involves the injection and recovery of water using wells; this has the advantage of targeting a desired aquifer for recharge. Thus, zones of saline water or clay layers can be bypassed. However, ASR systems are costly because of the need for bore well construction and water treatment prior to recharging, and if clogging occurs, they are costly to repair. Passive borehole recharge (under gravity) requires limited mechanical assistance, but the infiltration rate is relatively low. Water injection using pumps can greatly improve the rate of aquifer recharge [24,25]; however, the pumps require constant maintenance and are costly to run. The risk of clogging of the surface or well with fine sediments is common to both MAR methods. Solutions to this issue include stabilization of recharge water through settling ponds and treatment of water before recharge.

2.2. Financial Considerations

When the focus is on estimating the total economic benefits of recharge to a region instead of an individual, the benefits of aquifer storage become complex, as this needs to include public good, socio-economic and environmental benefits to a region, which are more difficult to assess and quantify. Maliva [16] in this special issue provides a greater review of the methods and techniques for assessing total benefits from MAR. With a known target volume of storage and recovery, it is easier to quantify the financial benefits, since the goal is the recovery of the stored water, and the volumes recovered accrue to an identifiable person or water utility for a particular use. The financial feasibility of MAR can then be studied in comparison to other water supply and storage alternatives, including surface storage.

The local situation dictates the costs of MAR options, and large variations may occur between localities [10]. For a fair comparison, it is essential to analyse the benefits and costs of MAR and surface storage in the same location, because the comparison of benefits and costs is complicated by the wide range of biophysical, socio-economic and regulatory conditions in which MAR occurs. There is little published analysis of the economic and financial benefits of MAR. From the few published studies, Ross and Arshad [26] compiled and reported the benefits and costs of surface storage and MAR at multiple locations, showing that the costs and returns of MAR options vary substantially.

2.3. Uncertainty Considerations

A number of methods have been used to address uncertainty in cost-benefit analysis. Sensitivity analysis simulates the impact of changes in financial behaviour, such as the change in NPV of an investment due to a change in an input variable, and identifies variables that are of greater concern [27]. Probabilistic analysis provides the combined effect of variables’ variability on the financial behaviour [17]. Possibility theory assumes that all values within a certain range are possible, with the exact value being treated as unknown [27].

We focus on cross-over points as one possible means of addressing uncertainty in the cost-benefit analysis of MAR. Identification of cross-over points relies solely on the relationship between variables, such that it requires minimal understanding of the uncertainty of variables. The idea of a cross-over point is sufficiently simple that it has a number of widely used variations; it is also known as a break-even point or switch-over point. However, the term break-even in economics specifically applies to the volume of sales at which profit is zero as revenues cover total cost and is therefore used as a tool to calculate the margin of safety of a single investment [28], rather than comparing alternatives. The concept of a cross-over point is fairly simple with only one or two variables, but the complexity increases in the analysis and interpretation of results as the number of input variables increases [29].

3. Methods

The analyses in this paper are carried out in two steps; in the first step, financial analysis compares the net present value of farm benefits to identify the best among the considered options. In the second step, the break-even analysis of cross-over points is carried out; this involves finding values of variables that will provide exactly the same financial returns from the two compared options. The variables were chosen based on an examination of literature concerning the financial feasibility of MAR. Identifying cross-over points allows the user to understand the minimum conditions required for success and allows measures to be taken to ensure they do not occur.

Financial analysis evaluates whether investment in MAR is worthwhile. Analyses of cross-over points help understand the circumstances when MAR is worthwhile. At the most basic level, MAR is worthwhile when net irrigation returns of MAR exceed those of alternatives. In our example, benefits are determined by the agricultural value of the additional water provided, by saving it from non-productive evaporation. This has been referred to as a “vapour shift” [30] from non-productive evaporation to agriculturally-valuable crop transpiration. Costs are composed of additional pumping to recover recharged water and MAR method-specific capital and ongoing costs of implementation during the life of the project.

To enable the break-even analysis, the financial analysis is programmed as a function in R [31]. As a general purpose statistical programming language, R offers a suite of optimization methods, as well as providing tools for visualization and the means to include a user interface. To identify cross-over points of single variables, other variables are set to fixed values, and the R function uniroot [32] is used to identify the value of the variable where the difference in NPV between the two compared options is zero (i.e., ΔNPV(Θ) = 0), meaning that the two options have equal NPV. To identify cross-over points involving many variables, we use optimization to identify a cross-over point (i.e., a point Θ where ΔNPV(Θ) = 0) that is closest to the best guess, in the sense of minimizing the maximum of the distances for each variable, expressed in relative terms using user-defined bounds (max_i|Θ_i-Θ_best,i|/|Θ_bound,i-Θ_best,i|). This is one possible criterion for selecting cross-over points of concern. Other criteria, including probabilistic ones, would be possible and would usually raise different cross-over points for discussion. The code for the analysis is available online [33]. The cross-over points generated are assessed by comparing them to maximum and minimum values of variables that a decision maker thinks might be possible due to physical, climate or policy change over the analysis period. The resulting judgment of a cross-over point is not perfect and is based on the best available knowledge of the decision maker for each variable.

4. The Study Area: Lower Namoi

In many parts of Australia, overdraft of aquifers is resulting in falling groundwater levels in the shallow, unconfined systems and decreasing groundwater pressures in the deep confined and semi-confined systems [34]. In response to the groundwater overdraft, the New South Wales (NSW) government has reduced current groundwater entitlements in its stressed aquifer systems [35]. For the lower Namoi catchment, a highly developed cotton irrigation district in NSW, this cutback translates to a reduction of 21 gigalitres (GL)/year in groundwater entitlements for irrigation by 2015 and beyond. Groundwater in the Namoi River catchment supports an irrigation industry worth in excess of $380 million per annum [36]. All irrigation water is stored and routed from surface storages before application to the field. On-farm water storages within the lower Namoi range from conventional single-cell to advanced multi-cell farm dams. The typical Namoi valley farm holds enough water in storage to complete one full year of irrigation. Conservative estimates suggest that the total capacity of on-farm storages in the cotton industry could be on the order of 3150 gigalitres (GL). Evaporative losses from these surface storages are significant. On average, from surface water storages, evaporative losses range from 1200 to 1800 mm/year [37], which constitute 35% to 50% losses from surface water storage volumes.

To tackle the problem of reduced allocation and evaporative losses, improving water use efficiency at the farm level is an obvious option. This will include installing drip irrigation systems, lining water courses and further improving the design of surface storages to minimize evaporative and seepage losses. Improving water use efficiency needs to be a stepwise approach. Another potential option to reduce evaporative losses is to store water underground in aquifers using managed aquifer recharge. Recently, several studies have highlighted the potential of a regional-scale MAR project in the lower Namoi. Arshad et al. [38] indicated that a significant volume of water could be available from large floods for MAR while still satisfying environmental flow and ecological requirements. Similarly, Rawluk et al. [20] showed a high level of social acceptability for an MAR project in the study area.

4.1. The Analytical Framework for Financial Analysis

The study undertakes an analysis to estimate irrigation-related costs and benefits for a typical irrigation farm in the lower Namoi. The analysis considers a cotton irrigation farm, which has three different scenarios for the storage of flood water: surface storage in farm dams, aquifer storage using basin infiltration and ASR using existing wells. All of the surface water allocations, including flood water, is stored in farm dams before application to the fields. Owing to limited water availability, less than 20% of the available land is irrigated, and irrigated land in each year is variable. Irrigated cotton Bt (Bacillus thuringiensis) and faba bean (Vicia faba L) are the sustainable summer and winter rotations that provide the highest net income per megalitre (ML) of irrigation water applied [39]. It is assumed in the analysis that all required irrigation infrastructure, such as surface storage and the irrigation water delivery network, are already built for the entire irrigation land, as this is a common practice in the study area. The annual irrigation water allocation from all sources for an average cotton farm in the lower Namoi is approximately 1350 ML. However, in this analysis, we only consider and report irrigation costs and returns of 200 ML of flood water, which is only 25% of recent statutory flood water allocations in the study area. The analysis assumes 40% evaporative losses, taking into account current estimates in the study area [37].

Storage and recovery of water underground will require new infrastructure and additional costs, as reported in Section 4.3. Farm economic data, such as the variable cost of farm inputs, cotton prices and gross margins from irrigated and dryland, are adopted from Powell and Scott [39]. The analysis only considers farm-related costs and revenue and does not monetize any socio-economic or environmental cost or revenue that may occur as a result of a change in the water storage option.

4.2. Infiltration and Injection Rates That Can be Possible in Lower Namoi

Infiltration and injection rates can highly affect the usefulness of any aquifer recharge and storage facility. Bouwer [40] provides typical infiltration rates for surface infiltration systems in the range from 0.3 to 3 m per day (m/day) with relatively clean and low turbidity river water. For systems that are operated year-round, long-term infiltration rates vary from 30 m/year to 500 m/year, depending on soil type, water quality and climate. In the lower Namoi, the infiltration rate of 0.2 m/day is considered to be likely achieved in many locations.

ASR can achieve injection rates from 0.5 to 8 megalitres per day (ML/day) per borehole (1 megalitre = 1000 cubic meter = 0.8107 acre foot). In the absence of accurate well injection rates based on field monitoring, Pyne [41] observed that injection rates increased with increasing aquifer transmissivities. For the lower Namoi, Williams et al. [42] reported that the alluvial aquifers that are primarily tapped for irrigation extraction are associated with the semi-confined Gunnedah and Cubbaroo formations and have transmissivities in the range of 1000–2000 square meters per day (m² day⁻¹). The yields from bores tapping these aquifers vary up to 250 litres per second in the Gunnedah Formation at depths of 60–90 m and in the deep Cubbaroo Formation at depths of 80–120 m. The shallow Narrabri Formation has transmissivities less than 250 m² day⁻¹. For this study, an assumed injection rate of 25 L per second (2.2 ML/day) is considered likely for an ASR well.

4.3. Estimation of Costs and Benefits

Cost estimates of aquifer recharge are scarce and can vary considerably with location. Itemized costs for this study were estimated by combining current market rates of earthworks, services and materials for water infrastructure projects in Australia and were adjusted to the local situation in the lower Namoi. Cost estimates were also compared with published data and technical reports of Khan et al. [12], Dillon et al. [10] and Pyne [13].

Capital costs of basin infiltration were estimated by assuming an infiltration rate of 0.2 m/day and calculating the required land area to achieve 2 ML of recharge per day. The target volume of harvested flood water of 200 ML would, on average, appear in four or more events in a flood year. An infiltration pond with a surface area of 1 ha and an infiltration rate of 0.2 m/day would recharge 50 ML of floodwater in a single cycle of 25 days. The size of the basin here has therefore been designed to operate only for 100 days, in 4 cycles of 25 days each, allowing rest and maintenance. The analysis assumed 40% evaporative losses from surface storage and a 5% MAR loss rate. The MAR loss rate is the percent of water lost during aquifer recharge and recovery from basin infiltration and ASR and can be expressed as:

In the base case, surface storage of flood water, the costs considered are the cost of harvesting 200 ML of flood water and the cost of farm dam annual maintenance. The capital cost of basin infiltration includes the cost of earth works and pipes. Ongoing costs include operation and maintenance of water harvesting and recovery and the cost of basin annual maintenance. An existing bore is assumed to be available for recovery after basin infiltration or for injection and recovery in ASR. The capital cost of an ASR facility on existing farms with a bore primarily includes installing a coagulation and filtration pre-treatment facility. Ongoing operation and maintenance costs for ASR include well maintenance, flood water harvesting, water treatment and water recovery. The analysis assumed a 30-year lifespan for surface storage and basin infiltration and 20 years for ASR, with a 7% uniform discount rate for all options. All capital cost estimates are exclusive of land value. Table 1 summarizes the levelised costs of 200 ML of flood water with each water storage option. Levelised costs are annual unit costs obtained by amortising capital cost components over their expected working life, adding the annual operation, maintenance and management cost and dividing by the annual volume of supply, as defined in Dillon et al. [10].

Table 1. Levelised costs ($/ML) of surface storage and MAR methods in lower Namoi. Adapted from Dillon and Arshad [43]. ASR, aquifer storage and recovery; ML, megalitre.

Cost component	Surface storage	Basin infiltration	ASR using existing well
Annual cost of capital items ($/ML)	0.0	32.2	26.0
Annual cost of operation, maintenance and management ($/ML)	22.5	90.5	221.8
Total annual cost ($/ML)	22.5	122.7	247.7

Note: Totals may not match due to rounding.

Table 1. Levelised costs ($/ML) of surface storage and MAR methods in lower Namoi. Adapted from Dillon and Arshad [43]. ASR, aquifer storage and recovery; ML, megalitre.

Cost component	Surface storage	Basin infiltration	ASR using existing well
Annual cost of capital items ($/ML)	0.0	32.2	26.0
Annual cost of operation, maintenance and management ($/ML)	22.5	90.5	221.8
Total annual cost ($/ML)	22.5	122.7	247.7

Note: Totals may not match due to rounding.

With the additional water saved through MAR, farmers in our example have the choice to irrigate additional land with cotton, faba bean or some combination of the two crops that yields the highest returns. Value brought by the MAR water under each option is estimated from the useable volume of flood water, after evaporative and recovery losses, times the gross margin per ML of mixed cropping of cotton and faba bean on equal land areas. On average, for a typical lower Namoi irrigation farm, the average gross margins for cotton and faba bean are estimated as 310 $/ML and 435 $/ML, respectively. It is assumed that cotton and faba bean are planted on the same land area, as they are summer and winter crops, respectively. Allocating the water accordingly yields an average gross margin of 342.3 $/ML and a net margin of 230 $/ML after subtracting overhead costs. In the analysis, we assume that additional irrigation with the saved water is not going to increase the overhead cost, as the farm size is large enough (1200 ha) and irrigated land cropped each year is variable depending on water availability. In this analysis, we use gross margins as the irrigation returns, which is the total revenue minus the variable cost of production. Table 2 presents the value of crop that can be grown with the useable volume in each case.

Table 2. Irrigation benefits: value of the crop under each water storage option. Adapted from Powell and Scott [39] and Arshad et al. [44].

Project component	Surface storage	Basin infiltration	ASR using existing well
Initial volume taken from flooding river ML	200	200	200
Useable volume (after losses) (ML)	120	190	190
Gross value of crop ($/ML)	342.3	342.3	342.3
Irrigation benefits: value of the crop that can be grown with the useable volume in each case ($) (available water times gross margins $/ML)	41,070.6	65,028.4	65,028.4

Note: Totals may not match due to rounding.

Table 2. Irrigation benefits: value of the crop under each water storage option. Adapted from Powell and Scott [39] and Arshad et al. [44].

Project component	Surface storage	Basin infiltration	ASR using existing well
Initial volume taken from flooding river ML	200	200	200
Useable volume (after losses) (ML)	120	190	190
Gross value of crop ($/ML)	342.3	342.3	342.3
Irrigation benefits: value of the crop that can be grown with the useable volume in each case ($) (available water times gross margins $/ML)	41,070.6	65,028.4	65,028.4

Note: Totals may not match due to rounding.

4.4. Results of Financial Cost-Benefit Analysis

A long-term trajectory of the difference of the discounted benefits and discounted costs of the three water storage options is expressed in Figure 3 as net present value using the fixed data in Table 2.

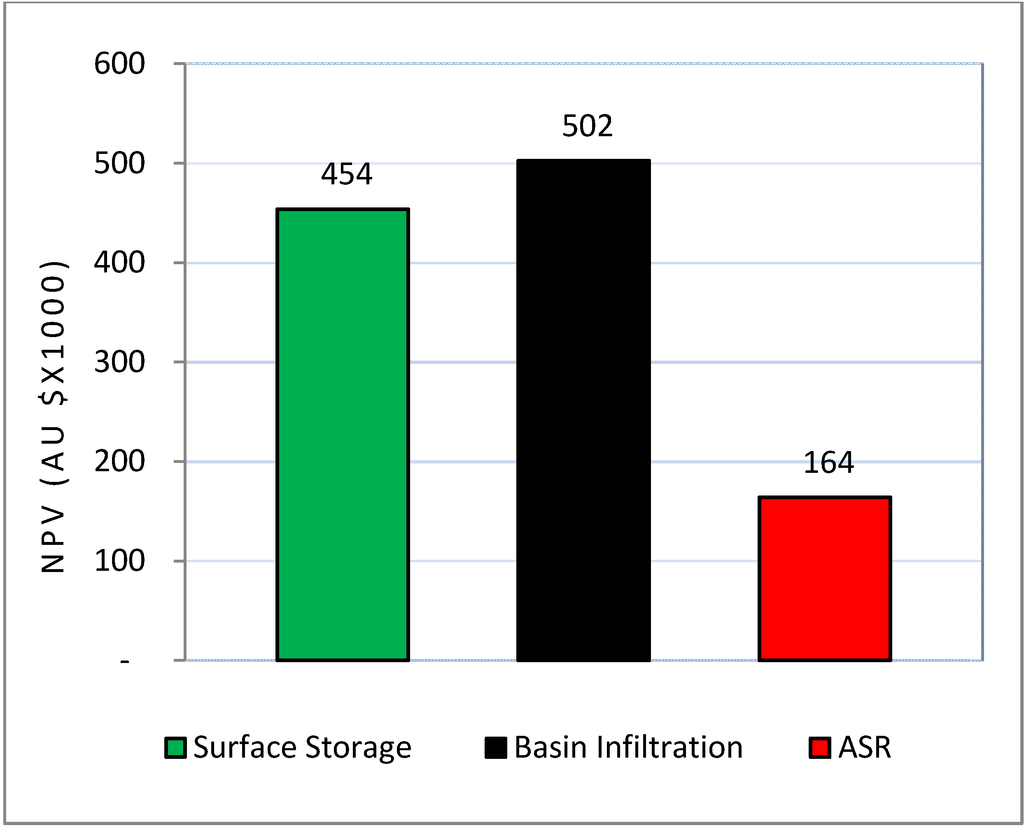
Figure 3. Net present value (NPV) of surface storage, basin infiltration and aquifer storage and recovery options.

Figure 3. Net present value (NPV) of surface storage, basin infiltration and aquifer storage and recovery options.

The results show that MAR using the basin infiltration method will yield 11% more value than surface storage of irrigation water. ASR using existing wells appears to be uneconomical, with 64% less value than surface storage, mainly due to the high capital and water treatment costs required for an ASR system.

The cost and additional value of basin infiltration is highly dependent on the infiltration rates; as infiltration rates increase, the capital costs decrease, and the value of saved water increases. Conversely, as infiltration rates decrease, the capital cost increases, and the additional value of basin infiltration decreases. With a reduction in the infiltration rates, a cross-over point is reached, where the additional value brought by basin infiltration becomes zero and its NPV is exactly equal to that of surface storage. The following section expands the analysis to explore cross-over points of infiltration rates and other variables.

5. Identification of Cross-Over Points in a Single Variable

In single variable analysis, the aim is to identify how far a single variable needs to change to reach a cross-over point for the two compared options. A cross-over point may not always exist; there might be situations where the cross-over point falls outside the minimum or maximum limits considered for the analysis or when the change in the cost or benefit is in the same direction. Such a situation is noted with the use of the acronym, NA, for not applicable, in the tables and following text. A cross-over point for basin infiltration and surface storage occurs when their NPVs are equal; and similarly, for ASR and surface storage, as well as basin infiltration and ASR. Figure 1 showed the cross-over point for pumping cost. Figure 4 illustrates cross-over points for basin capital cost.

Figure 4. NPV for varying basin capital cost in three water storage scenarios, showing cross-over points at intersections between lines.

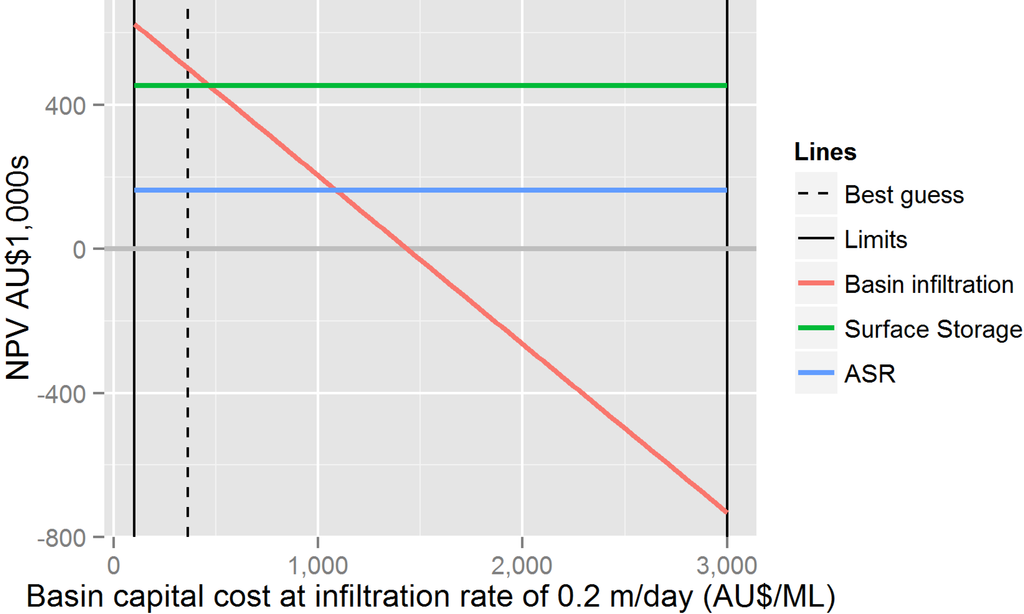
Figure 4. NPV for varying basin capital cost in three water storage scenarios, showing cross-over points at intersections between lines.

A cross-over point between basin infiltration and surface storage is possible when the basin capital cost increases from 363 $/ML to 466.69 $/ML. That increase in the capital cost will equate to the NPV of the two compared options. Similarly, a cross-over point between basin infiltration and ASR is possible when the basin capital cost increases from 363 $/ML to 1085.55 $/ML. No cross-over point is identified between surface storage and ASR (it is NA). The increase in the basin capital cost may result from increases in the price of services and materials or the need to construct a larger pond due to a reduction in infiltration rates. Rather than drawing these curves for every variable, the values of the cross-over points are reported in Table 3 and discussed in the following text.

Table 3 lists cross-over points for 14 variables when each is varied separately. These cross-over points represent the minimum requirements for MAR to be preferred to surface water storage, assuming that the values of other variables listed in the table remain fixed. For example basin infiltration is financially better than surface storage when pumping cost does not exceed 53.63 $/ML or the surface evaporation rate does not fall below 34%, and so on. The variables selected are the most important when undertaking a financial comparison of surface storage with the two MAR options. In the following section, we discuss the basis of how these cross-over points may be reached in reality for each single variable.

Table 3. Single variable cross-over points in three scenarios.

No.	Variable (Unit)	Cross-Over Point
		Best Guess (Modelled) Value	Surface Storage and Basin Infiltration	Surface Storage and ASR	Basin Infiltration and ASR
1	Pumping cost ($/ML)	35	53.63	NA	NA
2	Surface evaporation rate (%)	40	34	74	NA
3	Basin capital cost ($/ML)	363	466.69	NA	1,085.55
4	Basin infiltration rate (m/day)	0.2	0.16	NA	0.07
5	Basin maintenance rate (% of capital cost)	10	15	NA	NA
6	MAR loss rate (% of target storage volume)	5	11	NA	NA
7	ASR water treatment cost ($/ML)	150	NA	13.25	NA
8	ASR maintenance rate (% of capital cost)	0.07	NA	NA	NA
9	Price of cotton ($/bale)	538	475.64	1,155.22	NA
10	Price of faba bean ($/tonne)	348	229.52	NA	NA
11	Discount rate (%)	7	13	NA	NA
12	Lifespan of surface storage (Year)	30	48.16	5.57	NA
13	Lifespan of basin infiltration (Year)	30	23.51	NA	6.69
14	Lifespan ASR (Year)	20	NA	NA	NA

Table 3. Single variable cross-over points in three scenarios.

No.	Variable (Unit)	Cross-Over Point
		Best Guess (Modelled) Value	Surface Storage and Basin Infiltration	Surface Storage and ASR	Basin Infiltration and ASR
1	Pumping cost ($/ML)	35	53.63	NA	NA
2	Surface evaporation rate (%)	40	34	74	NA
3	Basin capital cost ($/ML)	363	466.69	NA	1,085.55
4	Basin infiltration rate (m/day)	0.2	0.16	NA	0.07
5	Basin maintenance rate (% of capital cost)	10	15	NA	NA
6	MAR loss rate (% of target storage volume)	5	11	NA	NA
7	ASR water treatment cost ($/ML)	150	NA	13.25	NA
8	ASR maintenance rate (% of capital cost)	0.07	NA	NA	NA
9	Price of cotton ($/bale)	538	475.64	1,155.22	NA
10	Price of faba bean ($/tonne)	348	229.52	NA	NA
11	Discount rate (%)	7	13	NA	NA
12	Lifespan of surface storage (Year)	30	48.16	5.57	NA
13	Lifespan of basin infiltration (Year)	30	23.51	NA	6.69
14	Lifespan ASR (Year)	20	NA	NA	NA

5.1. Discussion of Single Variables

5.1.1. Pumping Costs and Surface Evaporation Rates

A cross-over point between surface storage and basin infiltration is possible when pumping costs increase by 53% to become 53.63 $/ML; an increase in the cost of pumping will cause an increase in the cost of agricultural production and a decrease in farm benefits (NPV) from basin infiltration. A cross-over point between basin infiltration and ASR is NA, because the rate of increase in pumping cost applies to both aquifer storage options. Similarly, there is no cross-over point between surface storage and ASR, as the lowest possible pumping cost considered in the analysis (6.25 $/ML) will not make ASR financially superior or equal to surface storage.

Low surface evaporation rates will make surface storage financially superior to MAR, as less water will be lost from surface storage, making more water available and resulting in larger benefits. A cross-over point between surface storage and basin infiltration is possible when evaporation rates decrease by 15%, from 40%, to become 34%. For evaporation rates, a cross-over point between surface storage and ASR is possible when evaporation rates increase to 74%, whereas the cross-over point between basin infiltration and ASR is NA.

5.1.2. Basin Capital Cost, Basin Infiltration Rate and Basin Maintenance Rate

An increase in basin capital cost will increase the overall cost and lower the benefits with a concomitant decrease in NPV. For the basin capital cost, a cross-over point between surface storage and basin infiltration is possible when the capital cost of basin infiltration increases from 363 $/ML to 466.69 $/ML.

A decrease in the infiltration rates will recharge less water per unit area of infiltration basin, requiring a large infiltrating pond area with larger capital cost, or with decreased infiltration rates, less water will infiltrate and be stored underground. A cross-over point between surface storage and basin infiltration is possible when infiltration rates drop from 0.2 m/day to 0.16 m/day. Similarly, a cross-over point between basin infiltration and ASR is achieved when infiltration rates drop from 0.2 m/day to 0.07 m/day. An increase in the basin maintenance rates will increase the overall cost of basin infiltration, reducing NPV in comparison to the compared options. A cross-over point between surface storage and basin infiltration is possible when basin maintenance rates increase from 10% to become 15%. The three considered variables do not apply when comparing surface storage and ASR, such that the corresponding cross-over points are NA.

5.1.3. MAR Loss Rate

Increasing the MAR loss rate makes MAR financially less attractive, because it reduces the volume of water recovered and the resulting benefits, though some pumping cost is saved, as less water is recovered with an increase in the MAR loss rate. In other words, a higher MAR loss rate represents a lower recoverability and, therefore, lower useful storage [22,45]. For benefits to be realized, the volume of water that is not recovered from storage must be less than evaporation losses. This applies to both MAR methods when compared to surface storage. A cross-over point between basin infiltration and surface storage is possible when the MAR loss rate reaches 11%. A cross-over point between basin infiltration and ASR is NA.

5.1.4. ASR Water Treatment Cost and ASR Maintenance Rates

A cross-over point for ASR maintenance rate is not possible when ASR is compared with surface storage and basin infiltration. Even its cheapest possible value, when considered alone, does not achieve an NPV equal or superior to basin infiltration and surface storage. The ASR water treatment cost only has a cross-over point if the treatment cost decreases by 91% to 13.25 $/ML. Increases in both variables increase the cost of ASR and, hence, (further) diminish its advantage over the other options.

5.1.5. Price of Cotton and Faba Bean

A decrease in the price of cotton and faba bean will influence the benefits of all three water storage options and lower NPVs for each case. A cross-over point for the price of cotton and the price of faba bean between surface storage and basin infiltration is possible when the price of cotton drops from $538 per bale to $475.64 per bale, and the price of faba bean drops from $348 per tonne to $229.52 per tonne, which are 11% and 34% drops from the best guess values, respectively. A cross-over point for the cotton and faba bean price is possible between surface storage and ASR when the price of cotton rises to $1,155.22 per bale, an increase of 114%. No cross-over point between surface storage and ASR is possible with the highest price considered possible for faba beans.

5.1.6. Discount Rate and Project Lifespan

An increase in the discount rate tends to increase the levelised cost of the two MAR options, in particular through the basin capital cost and the capital cost of establishing an ASR treatment facility. This will result in lower NPVs from the two MAR options. A cross-over point between surface storage and basin infiltration is possible at a discount rate of 13%, while there is no cross-over point between surface storage and ASR. Because ASR is already more expensive than surface storage, a higher discount rate will make ASR even more expensive, while the lowest considered discount rate of 1% will not be able to raise the NPV of ASR to be equal or superior to surface storage. Similarly, a lower discount rate will make basin infiltration more favourable than ASR, so no cross-over point is possible.

Lowering the lifespan of an option increases its levelised cost, such that the NPV of that particular option is lowered. A cross-over point between surface storage and basin infiltration is possible when the lifespan of surface storage increase from 30 years to 48.16 years or the lifespan of the basin infiltration drops from 30 years to become 23.51 years. Similarly, a cross-over point between surface storage and ASR exists when the lifespan of surface storage drops to 5.57 years. A cross-over point between basin infiltration and ASR is possible when the lifespan of the basin infiltration drops to 6.69 years. No cross-over point for the lifespan of ASR is possible when compared with basin infiltration and with surface storage options.

5.2. Changes in Cross-Over Points Due to Interactions between Variables

The values at which cross-over points occur are affected by the values of other variables, so it is important to consider interactions between variables. Every variable that either increases or decreases changes the financial advantage of MAR in comparison to surface storage. We describe the advantage of MAR in terms of change in the position (value) of cross-over points with respect to the best guess. The interaction of two variables can bring a cross-over point closer or further to the best guess. Two variables can interact in a way that they can increase, decrease or balance the effect of each other on the resulting advantage of MAR, depending on whether changes in the variable increase or decrease the financial advantage of MAR.

A cross-over point that moves away from the best guess value indicates increasing financial advantage for MAR. Conversely, when it moves closer to the best guess, the financial advantage decreases. The movement of a cross-over point closer to the best guess reveals situations where the benefits of MAR are reduced and could ultimately have equal benefits to surface storage when the cross-over point coincides with the best guess value.

Figure 5 and Figure 6 illustrate with examples where the advantage of MAR over surface storage changes due to the interaction of variables. This is expressed through changes in the cross-over point of the MAR loss rate.

Given that increased costs reduce the relative benefit of MAR, when costs increase, the cross-over point for the MAR loss rate moves closer to the best guess value (Figure 5). Similarly, lower prices of crops decrease the benefit of MAR, and the cross-over point moves closer to the best guess (middle bar in Figure 6). When costs and prices both increase, the cross-over point can move closer or further from the best guess, depending on the level of change in costs and prices (bottom bar in Figure 6).

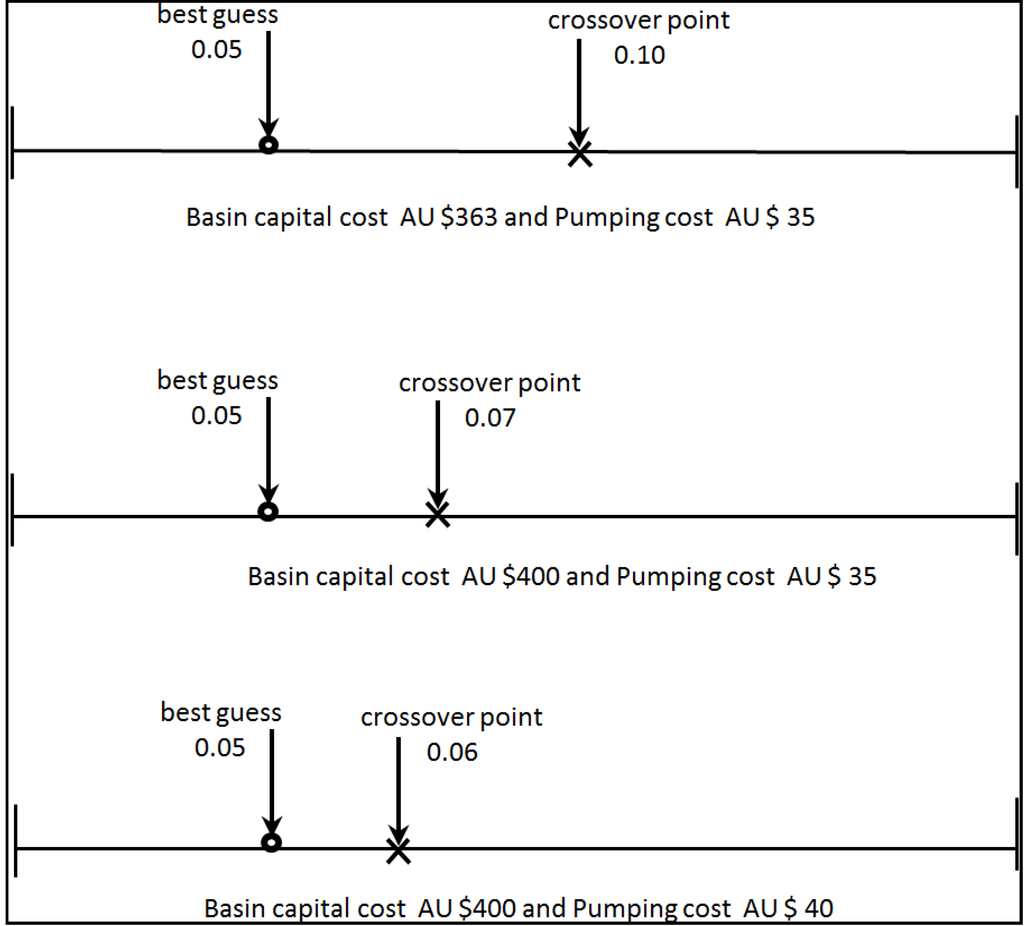
Figure 5. Plot of the MAR loss rate when costs increase. An example of a cross-over point moving toward the best guess.

Figure 5. Plot of the MAR loss rate when costs increase. An example of a cross-over point moving toward the best guess.

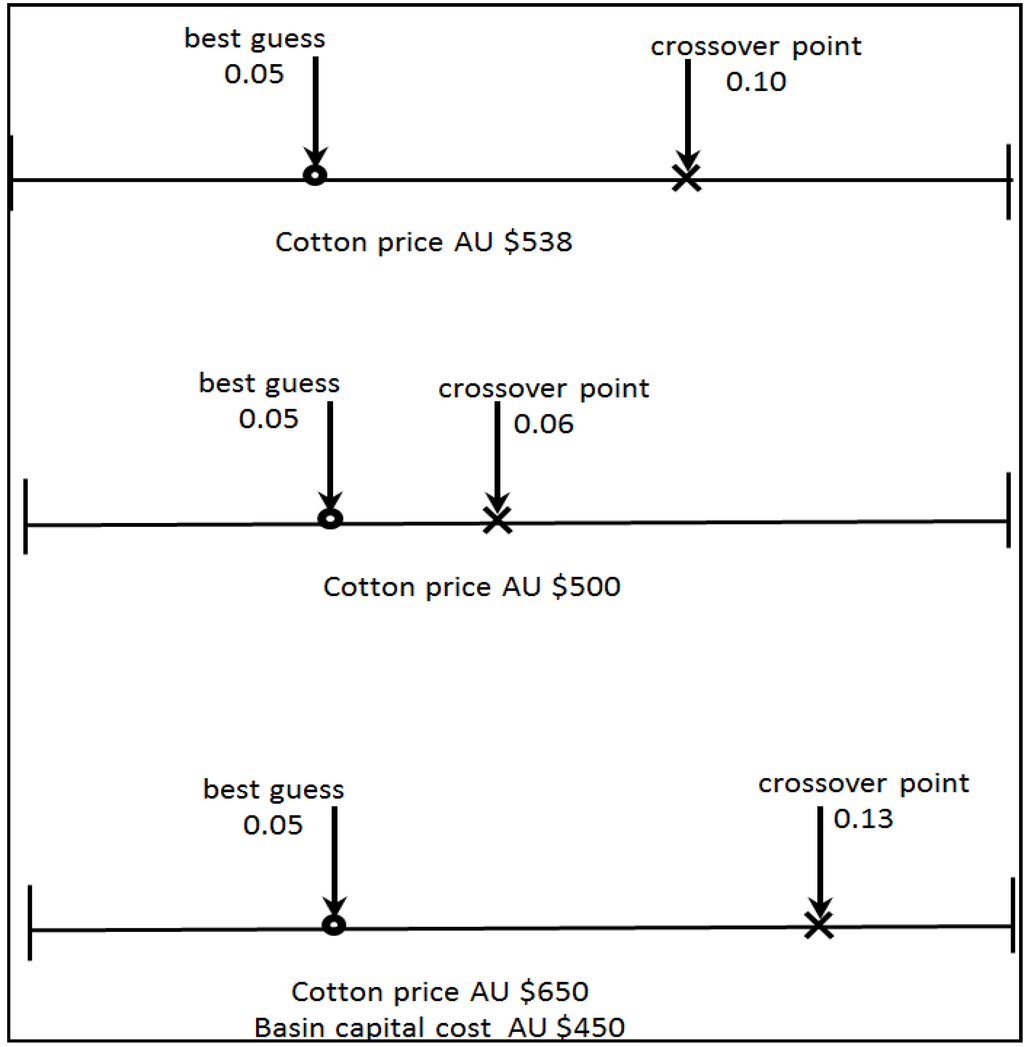
Figure 6. Plot of the MAR lose rate when costs and prices change. An example of the cross-over point changing position when costs and prices both increase.

Figure 6. Plot of the MAR lose rate when costs and prices change. An example of the cross-over point changing position when costs and prices both increase.

5.3. Assessing the Risk of Attaining Cross-Over Points

Uncertainty in the financial assessment of MAR can be assessed by evaluating whether the scenarios described by the cross-over points identified are likely to be experienced in reality. If this occurs, then MAR may not be financially attractive. Alternatively, other measures may need to be taken to avoid situations leading to the cross-over point. Note that initial financial analysis suggests that basin infiltration is a favourable investment. As mentioned in the Introduction, the aim of this analysis is therefore to play the devil’s advocate, that is to systematically search for reasons that requirements may not be met and that failure might occur.

While cross-over points could be assessed probabilistically, a simple approach is to say that a cross-over point is of greater concern if it is closer to the best guess value. This implies that investment in the MAR infrastructure is at greater risk of not making additional profits than surface storage because the return from MAR becomes closer to that of surface storage. On the other hand, the value of a cross-over point may fall outside the bounds (minimum and maximum limits) that are considered to be of concern, in which case, the analysis suggests that the minimum requirements will be met.

Following this approach, Table 4 shows the cross-over point of greatest concern when surface storage and basin infiltration are compared. The point was identified by simultaneously varying all of the variables and searching for a combination where each variable is closest to the best guess, relative to bounds. The bounds were defined by the authors based on an understanding of the factors influencing the variables, taking into account the expected variability, considering the lack of complete the knowledge of hydrogeological variables and the actions that can be taken to manage these concerns. In interpreting the results, the combination of values is assessed, not just each variable separately, and the reasons for the bounds selected are explained.

Table 4. Cross-over point of greatest concern with basin infiltration vs. surface storage, using a subset of variables.

	Variable	Minimum Bound	Maximum Bound	Best Guess	Point of Greatest Concern	Change from Best Guess
1	Pumping cost ($/ML)	6.25	225	35	37.22	2.22
2	Surface evaporation rate (%)	10	100	40	40	0
3	Basin capital cost ($/ML)	100	3,000	363	393.82	30.82
4	Basin infiltration rate (m/day)	0.01	2	0.2	0.2	0
5	Basin maintenance rate (% of capital cost)	1.0	40	10	10	0
6	MAR loss rate (% of target storage volume)	0	85	5	6	1
7	Price of cotton ($/bale)	50	1500	538	532.30	−5.70
8	Price of faba bean ($/tonne)	50	1400	348	344.52	−3.48
9	Discount rate (%)	1	50	7	8	−1
10	Lifespan of surface storage (Year)	2	50	30	30.23	0.23
11	Lifespan of basin infiltration (Year)	2	50	30	29.67	−0.33

Table 4. Cross-over point of greatest concern with basin infiltration vs. surface storage, using a subset of variables.

	Variable	Minimum Bound	Maximum Bound	Best Guess	Point of Greatest Concern	Change from Best Guess
1	Pumping cost ($/ML)	6.25	225	35	37.22	2.22
2	Surface evaporation rate (%)	10	100	40	40	0
3	Basin capital cost ($/ML)	100	3,000	363	393.82	30.82
4	Basin infiltration rate (m/day)	0.01	2	0.2	0.2	0
5	Basin maintenance rate (% of capital cost)	1.0	40	10	10	0
6	MAR loss rate (% of target storage volume)	0	85	5	6	1
7	Price of cotton ($/bale)	50	1500	538	532.30	−5.70
8	Price of faba bean ($/tonne)	50	1400	348	344.52	−3.48
9	Discount rate (%)	1	50	7	8	−1
10	Lifespan of surface storage (Year)	2	50	30	30.23	0.23
11	Lifespan of basin infiltration (Year)	2	50	30	29.67	−0.33

Table 4 shows that the values of cross-over points are very close to the best guess and, hence, are of concern. The point of greatest concern describes a scenario of particularly unfavourable conditions, namely when all of the variables interact and change simultaneously. The scenario of greatest concern describes a situation where pumping costs have increased and the prices of cotton and faba bean have decreased. Basin capital cost turns out to be higher than expected, as well as the MAR loss rate. The lifespan of the basin infiltration project is marginally shorter than that of a surface storage project. Other variables remain at their best guess.

Individually, all variables of the scenario appear to be of great concern. However, in reality it is unlikely that all variables change at once and result in the situation described in Table 4. We analyse groups of variables to assess whether or not the generated scenario is possible, what mitigation options might prevent this cross-over point from occurring and what adaptation actions might be taken if it the scenario described by the cross-over point does occur.

5.3.1. Pumping Costs and Surface Evaporative Rates

The cross-over point of this variable is very close to the best guess value and, hence, may be reached. Based on historical trends, energy costs are expected to increase in the future, despite efficiency improvements in pumping technologies. However, the effect of higher pumping costs may be balanced or outweighed if there is an increase in the price of cotton and faba bean in the future. In addition, if farming becomes uneconomical at some stage, it is possible that government might provide subsidies for pumping to maintain agricultural production and preserve the livelihoods of farmers. Using alternate sources of energy, such as wind and solar, can be cheaper mitigation options in the future. High head gravity feed systems can be designed in certain cases to avoid pumping costs [9].

Surface evaporative rates are expected to increase under climate variability and change [46]. Evaporative rates may also be higher for farms where surface storage is shallow and depending on the water colour and turbidity. Higher evaporative rates will favour MAR, so this is unlikely to be a reason not to proceed with MAR. Reducing evaporative losses from surface storage at costs cheaper than those of setting up a basin infiltration system could have been a reason not to proceed with basin infiltration.

5.3.2. Basin Capital Cost, Infiltration Rate and Basin Maintenance Rate

The increase in the basin capital cost seems likely to occur if the investment is delayed, as the cost of labour, construction materials and energy prices for earth moving machinery are expected to rise due to inflation and other economic factors. Similarly, the values of basin infiltration rates and basin maintenance rates exactly coincide with the current best guess estimates, and hence, the two variables are of great concern. The infiltration rate is a function of a number of variables, with water quality a major factor.

A few mitigation options exist to avoid increases in basin capital cost. Field trials and geophysical investigations can help find suitable sites where high infiltration rates can be achieved. Basin maintenance is related to the amount of silt and other suspended and organic matter contained in the floodwater. Basins can be sized to allow rest and maintenance. In the lower Namoi catchment, floodwater already passes through a de facto two-stage sediment and silt removal process. Firstly, it is retained in large public dams before release, thereby reducing heavy silt loads; secondly, at the farm level, floodwater is kept in farm dams as temporary storage before recharging begins. The two-step sediment removal process can be advantageous in lowering the cost of basin maintenance.

5.3.3. MAR Loss Rate

In the lower Namoi, more than four decades of groundwater pumping have dropped the water levels, and in many places, rivers and streams (naturally) recharge groundwater [47], such that useful storage exists at a large scale. At the farm scale, while water may not physically stay within a farmer’s land and, as such, is not physically stored, the system of surface and groundwater water rights means that injected or infiltrated water could, in principle, be allocated to the farm anyway, in a form of “regulatory storage” [22]. This results in potentially extremely high recovery rates (95%) and low loss rates, as a farmer benefits from contributing water to a common pool rather than being restricted to physically retrieving the water that they recharged. The loss rate determined by regulation could however be affected by a number of broad-scale issues. For example, the MAR loss rate can be of concern for locations where surface water and groundwater connectivity exists and where streams and rivers gain groundwater from aquifers, which is rare in lower Namoi. Low recovery is possible only in aquifers that contain brackish or high salinity water, due to the mixing of fresh recharge water with the native high salinity groundwater. This may occur in some parts of the lower Namoi, particularly areas where drops in groundwater hydraulic heads have resulted in the mixing of saline and freshwater within different layers of aquifers. In areas of excessive groundwater extraction, groundwater hydraulic heads can drop and allow saline water to enter into pumping wells [42], thereby increasing the salinity levels of the recovered water and resulting in less recovery of the volume of freshwater recharged initially.

5.3.4. Price of Cotton and Faba Bean

Cross-over points for the price of cotton and faba bean are not likely to occur, and they are not of greater concern. The future price of cotton is expected to remain stable or increase because of ongoing demand and an established linkage of the Australian cotton industry to overseas markets, where demand exists and can be expected to grow. In the future, with limited irrigation water availability at the global scale, international prices of cotton are expected to rise, rather than decrease. Other cotton producing and competing countries, such as China, Pakistan and Egypt, are likely to become more water stressed in future. Additionally, with world population growth continuing unabated, a higher demand for cotton is expected. The price of faba bean is also expected to increase in the future; however, a drop in the price of faba bean is also possible whenever supply exceeds the local demand. A change in the price of faba bean is not a major concern, because it is a local crop mainly used for cattle and human consumption and has limited potential for export in national and international markets. Faba bean is not a major source of farm revenue, and if at some point, there is an oversupply and a drop in price occurs, faba bean can be replaced with some other high value crop. Any rise in the sale price of both cotton and faba bean would also compensate for increases in pumping costs and other MAR infrastructure costs.

5.3.5. Discount Rate and Lifespan of Projects

A 7% discount rate coincides with the current best guess and is highly likely to occur and is therefore of great concern. Discount rates of more than 7% will make MAR financially un-attractive. As this may occur if the cost of borrowing capital is high, farmers may search for financing at lower rates or governments may assist farmers to set up special MAR grants or loans involving the least possible interest rates. Cross-over points for the lifespan of surface storage and basin infiltration almost coincide with the best guess (30 years) and are of great concern. The lifespan of basin infiltration can be enhanced by drying of basins, frequent scarping of accumulated silt layers and controlling weed growth.

6. Conclusions

Break-even analysis of cross-over points is one way of assessing the financial performance of MAR under uncertainty. Cost-benefit analysis of surface storage and MAR helps to compare options in financial terms, but results cannot be relied upon completely without due consideration of uncertainty. Our approach to addressing uncertainty is to undertake a financial cost-benefit analysis by analysing a range of values for influencing variables and to establish thresholds (cross-over points) where financial returns from surface storage and MAR are equal. Once the thresholds are established, mitigation options can be identified and put in place to avoid variables reaching identified thresholds.

The analysis of cross-over points can be undertaken to identify minimum requirements under which MAR can be more advantageous than surface storage, and this was illustrated for the lower Namoi. For this catchment, MAR using basin infiltration can be financially superior to surface storage, but this depends on the selection of a suitable site where a high infiltration rate, low loss rates and other minimum requirements can be achieved. Further exploration of MAR through field trials and geo-physical investigation is suggested in areas of lower Namoi. MAR can be a potential option to achieve future water supply goals, provided that it is technically feasible and more financially viable than surface storage.