1. Introduction
A water distribution system is an important part of the social infrastructure, facilitating water transport, distribution and supply. Such a system is a highly complicated network that combines pipelines, pumps and valves. Hence, the facilities in any such system should be continuously improved and updated based on specific plans to maintain the stability and safety of the water supply. As the importance of maintaining and managing this water distribution system has increased, projects for repairing and replacing deteriorating water pipes are currently being undertaken throughout Korea. However, the current methods used to deal with deteriorating pipelines involve an evaluation of the degree of deterioration based on empirical means, as well as reactive rehabilitation projects undertaken after accidents, leading to economic losses and failure to improve system functions. The current approach to determining the rehabilitation priority order for pipelines is based only on the year of installation of the pipes, with no clear criteria for evaluating the degree of deterioration. To address these problems, a new approach to determine the rehabilitation priority order for a water distribution system should be developed that overcomes the drawbacks of the existing methods. In addition, the rehabilitation priority order should be determined according to not only the physical deterioration rate of individual pipes, but also the relative importance of those pipes, to increase the overall stability and safety of the system.
Early studies of the methods to determine the rehabilitation priority order for water distribution systems were conducted using rehabilitation models based on empirical determination that use only general guidelines. Subsequent studies on the determination of the rehabilitation priority order can be broadly classified into the categories of analysis of the deterioration rate and failure probability, regression analysis coupled with failure probability analysis and priority order estimation based on economic feasibility analysis. The Guidance Manual-Water Mains Evaluation for Rehabilitation/Replacement published by the American Water Works Association Research Foundation [
1] proposes physical strength, water quality in the pipes, hydraulic conditions and water leakage as criteria for evaluating pipeline functionality. Accordingly, the manual notes that comprehensive management that considers these four criteria is required to effectively maintain and manage water distribution pipelines. The Water Research Centre [
2] of the United Kingdom states that it is reasonable to prioritize the repair and rehabilitation of water distribution pipes that are frequently associated with accidents. K-water [
3] determined pipeline deterioration rates and developed a weighting system for pipeline repair and rehabilitation by collecting and summarizing domestic and international literature, as well as data on large-diameter water distribution pipes in metropolitan water distribution systems. Subsequently, K-water developed a model to estimate the deterioration rate of water pipes using a point-based evaluation method that considers the estimated pipe condition and weight, as well as a model for prioritizing the replacement and rehabilitation of water pipes. However, this model is limited in that the point-based evaluation method does not reflect the hydraulic characteristics of water distribution systems. Kim
et al. [
4] re-calculated the cost function by modifying and complementing the failure rate function proposed by Shamir and Howard [
5]. In addition, they estimated the deterioration rate using a probabilistic neural network (PNN) and proposed a rehabilitation model that prioritizes the rehabilitation and replacement of pipes using a shortest-path model. Studies in which regression analysis and failure probability analysis have been applied to estimating the rate of deterioration of water pipes have been conducted by Marks and Clark [
6,
7], Agbenowosi [
8] and Park and Loganathan [
9,
10]. Marks and Clark [
6,
7] proposed a method for failure modeling based on the deterioration rate of the water distribution pipes. After classifying the deterioration status of water distribution pipes into “early stage”, with a small number of failures, or “later stage”, with a large number of failures, their method applies these stages to each case. Based on their results, they proposed that the deterioration status of a water distribution pipe could be represented by a proportional hazards model in the early stage and a Poisson-type model in the later stage. Deb
et al. [
11] classified water distribution pipes according to their installation year, pipe material, diameter and backfilled soil type. They also developed a probabilistic model called “KANEW” based on this classification to estimate the number of pipes in a water distribution system that should be replaced annually. Agbenowosi [
8] represented the factors related to water distribution pipes in a pipe load model and a pipe break model, so that the factors could be analyzed mathematically and the most economical time at which to replace a water distribution pipe could be determined. Park and Loganathan [
9,
10] proposed a failure estimation model for water distribution pipes using a threshold break rate. Using this model, the economically optimal replacement time is determined as a function of the costs of pipe replacement and rehabilitation, a discount rate and the length and diameter of the pipes.
In general, these models, which determine the rehabilitation priority order of pipes in water distribution systems using regression and failure probability analyses, predict pipe failure through complex formulas and determine the most economical replacement and rehabilitation times through economic feasibility analysis. While these models can predict pipe failure through failure probability analysis, they require a large amount of basic data and complex formulas to produce results. Models for determining the rehabilitation priority order of pipes in water distribution systems on the basis of economic feasibility, which have been examined by Shamir and Howard [
5], Walski [
12] and Luong and Fujiwara [
13], achieve maximum efficiency at minimum cost. Alvisi and Franchini [
14] proposed a near-optimal rehabilitation scheduling method based on a multi-objective genetic algorithm. With reference to a fixed time horizon, the goal is to minimize the overall costs of repairing and/or replacing pipes and to maximize the hydraulic performances of the water network. However, given that these models also require a large amount of basic data and that water distribution pipes are part of social infrastructure networks that directly affect public welfare, cost optimization cannot be an essential condition.
In recent years, computer-aided models and decision support tools, such as Care-W [
15,
16,
17,
18,
19,
20,
21], CASSES [
22] and AWARE-P [
23], have been developed. The CARE-W project aimed to develop methods and software that would enable engineers of the water undertaking to define and implement an effective management of their water supply networks, rehabilitating the right pipelines at the right time. This project was organized in eight work packages (WP), which were the construction of a control panel of performance indicators (WP1), description and validation of technical tools (WP2), elaboration of a decision support system for annual rehabilitation programs (WP3), elaboration of long-term strategic planning and investment (WP4), elaboration of the CARE-W prototype (WP5), testing and validation of the CARE-W prototype (WP6), dissemination (WP7) and project management (WP8). CARE-W used four probabilistic forecast failure models (proportional hazard model, Markov model, Poisson analysis, and non-homogeneous Poisson process) and three mathematical hydraulic reliability assessment models (Aquarel, Failnet-Reliab, Relnet). Among these WPs, WP3 and WP4 focused on the determination of priority and scheduling for rehabilitation according to the target time period (one year and long-term plan). They used multi-criteria techniques, such as scoring and ELETRE TRI methods, to determine relevant procedures during annual rehabilitation programs. In case of long-term rehabilitation strategies, extended KANEW is used. In the continuation of CARE-W, a new break prediction model, called linear extension of the Yule process (LEYP), was developed. It involved a statistical model based on a counting process and relied not only on the pipe’s characteristics and environment, but also its age and previous breaks. This new model was chosen to be used in the development of the break prediction software, CASSES. The main result from this software was the number of breaks for each pipe for a period in the future. The AWARE-P project has been performed for providing water and wastewater utilities with the know-how and the tools needed for efficient decision-making in infrastructural asset management (IAM) of urban water services. The key point of this project is IAM as a management process, based on plan-do-check-act (PDCA) principles and requiring alignments between the organization’s strategic objectives and targets and the actual priorities and actions implemented.
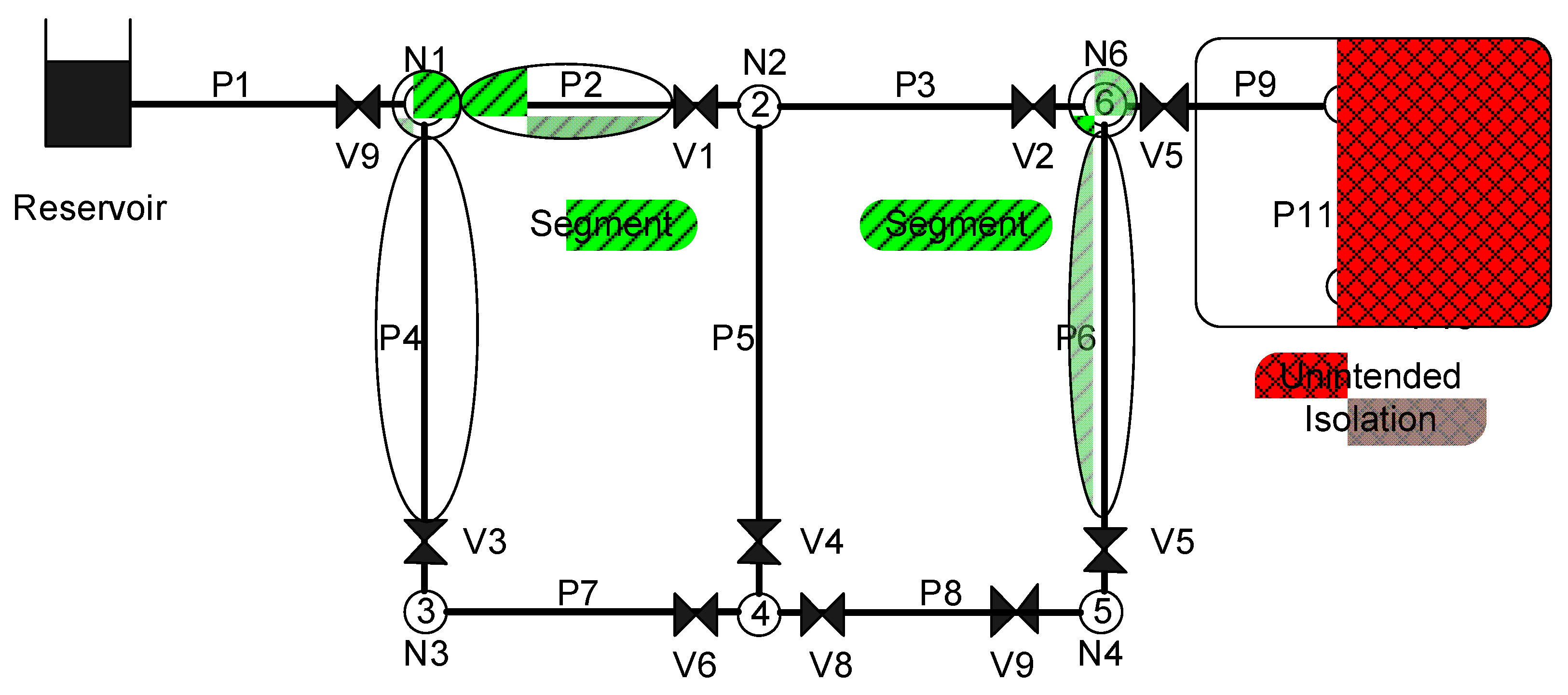
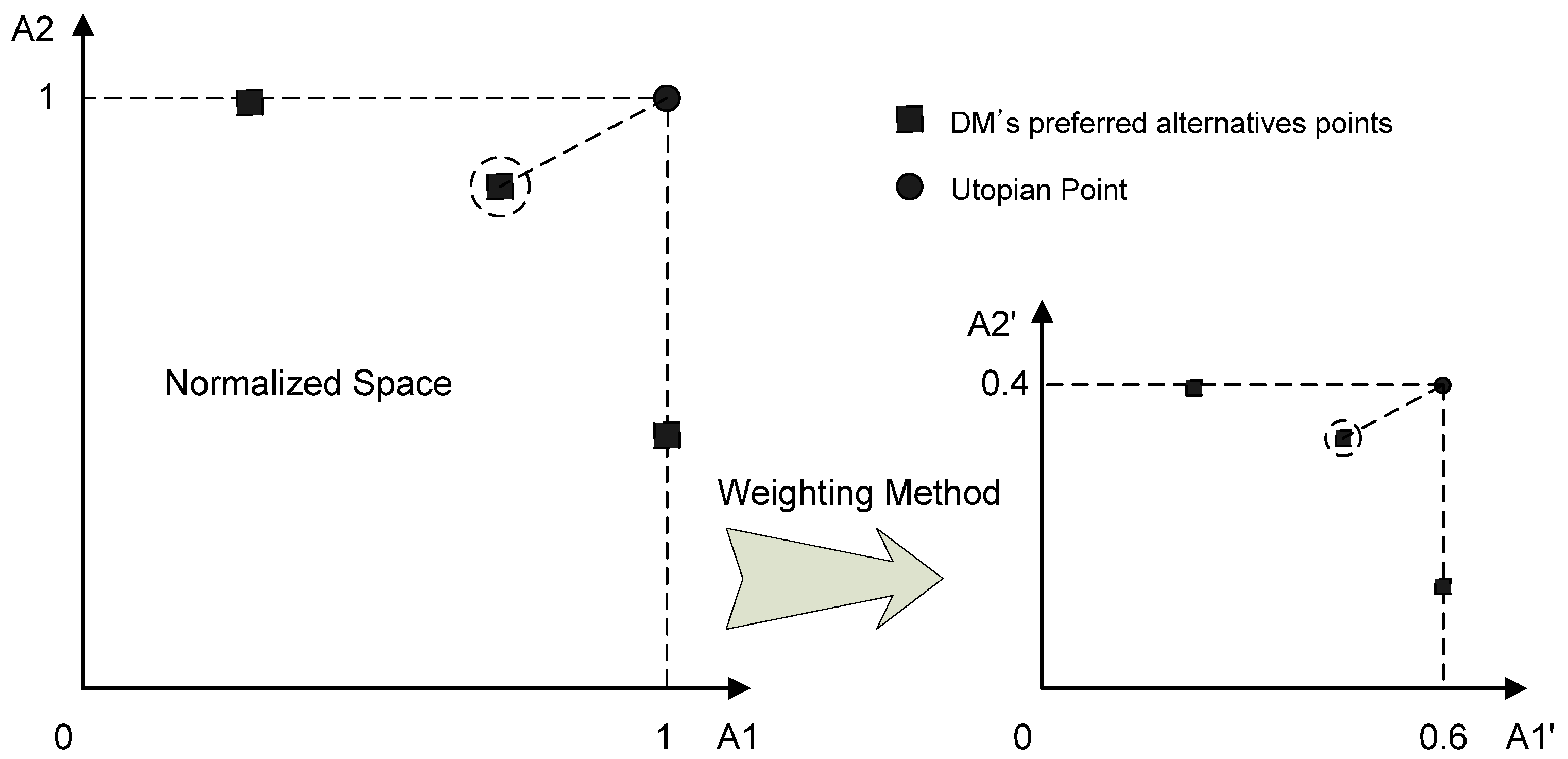
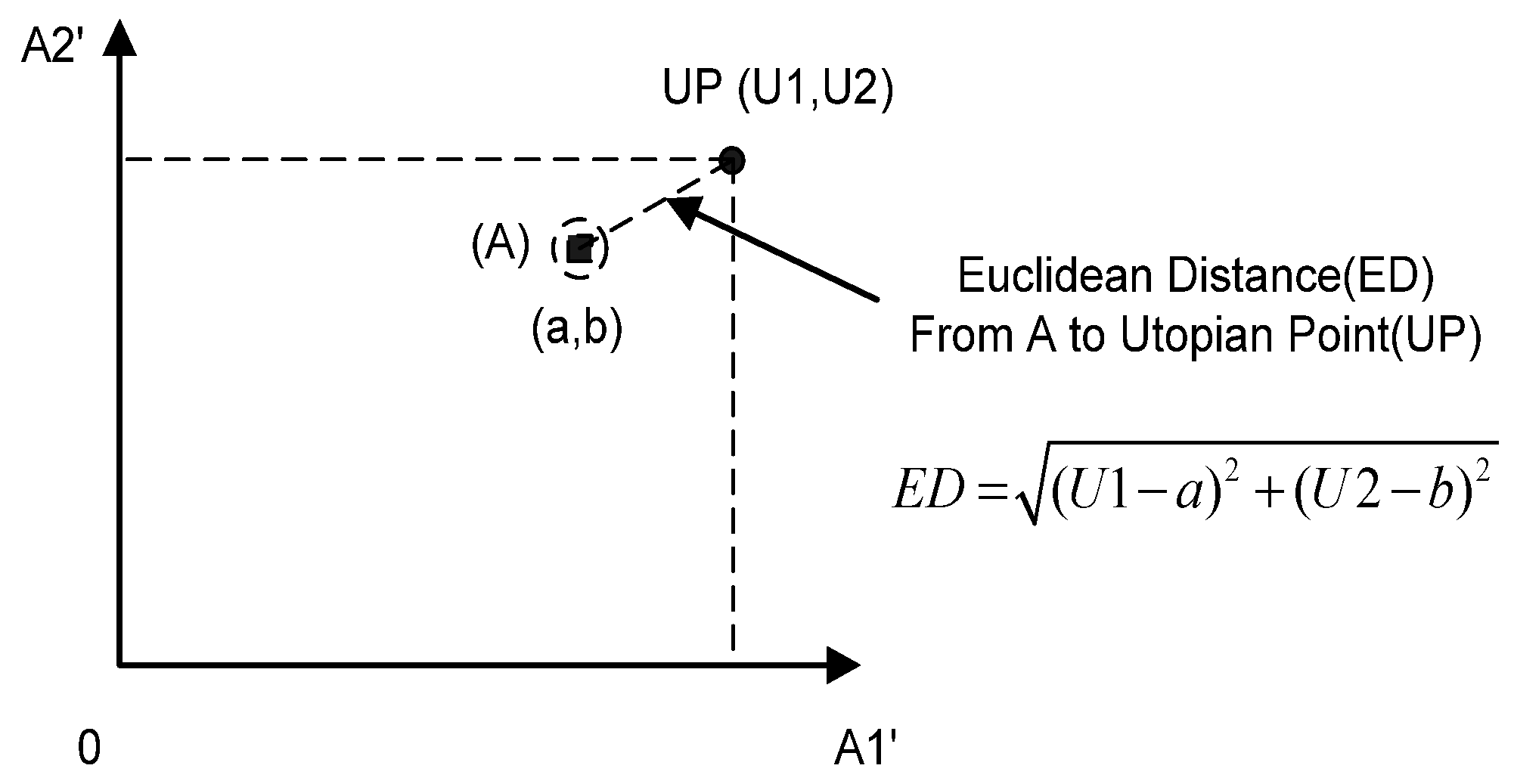
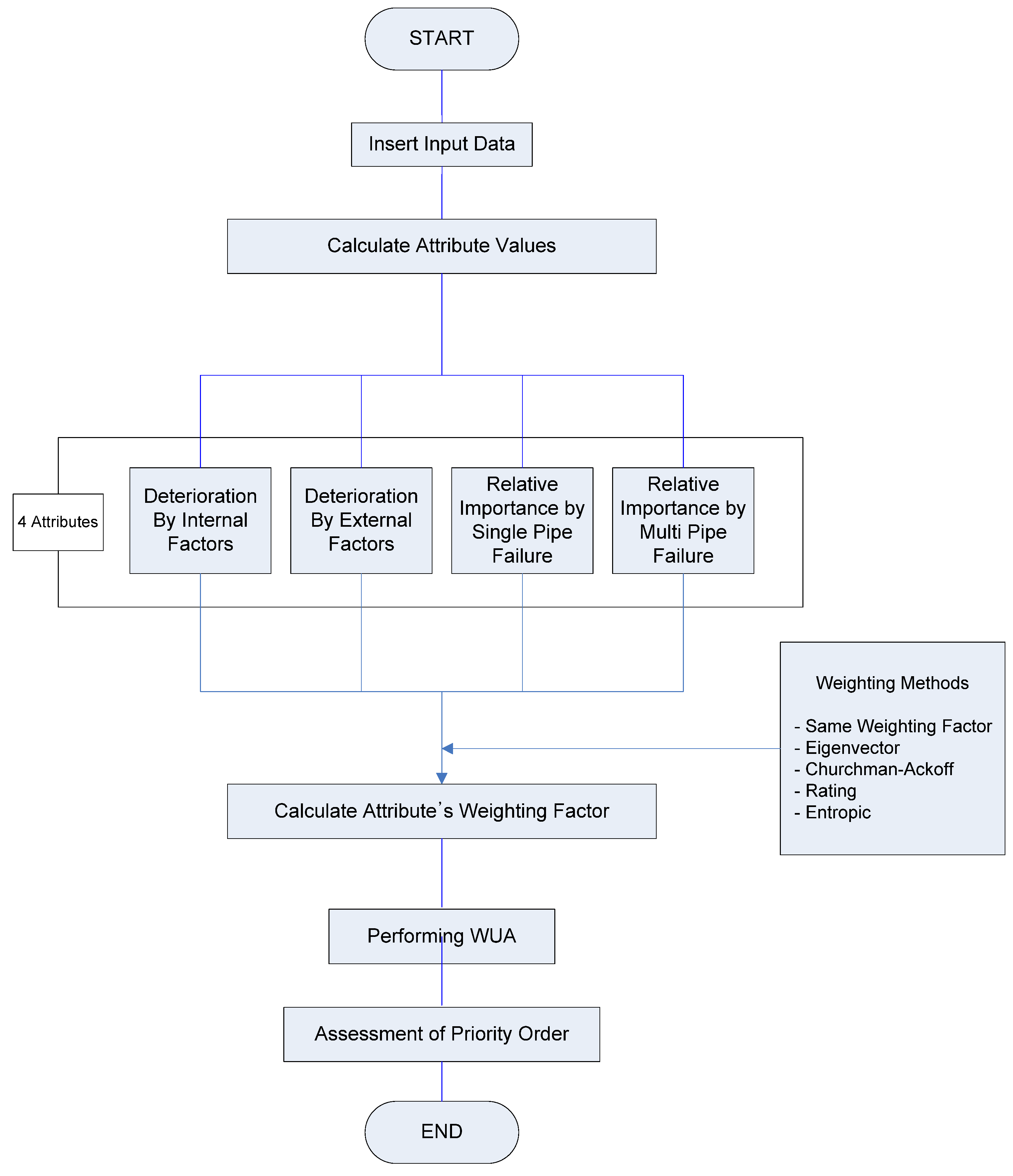
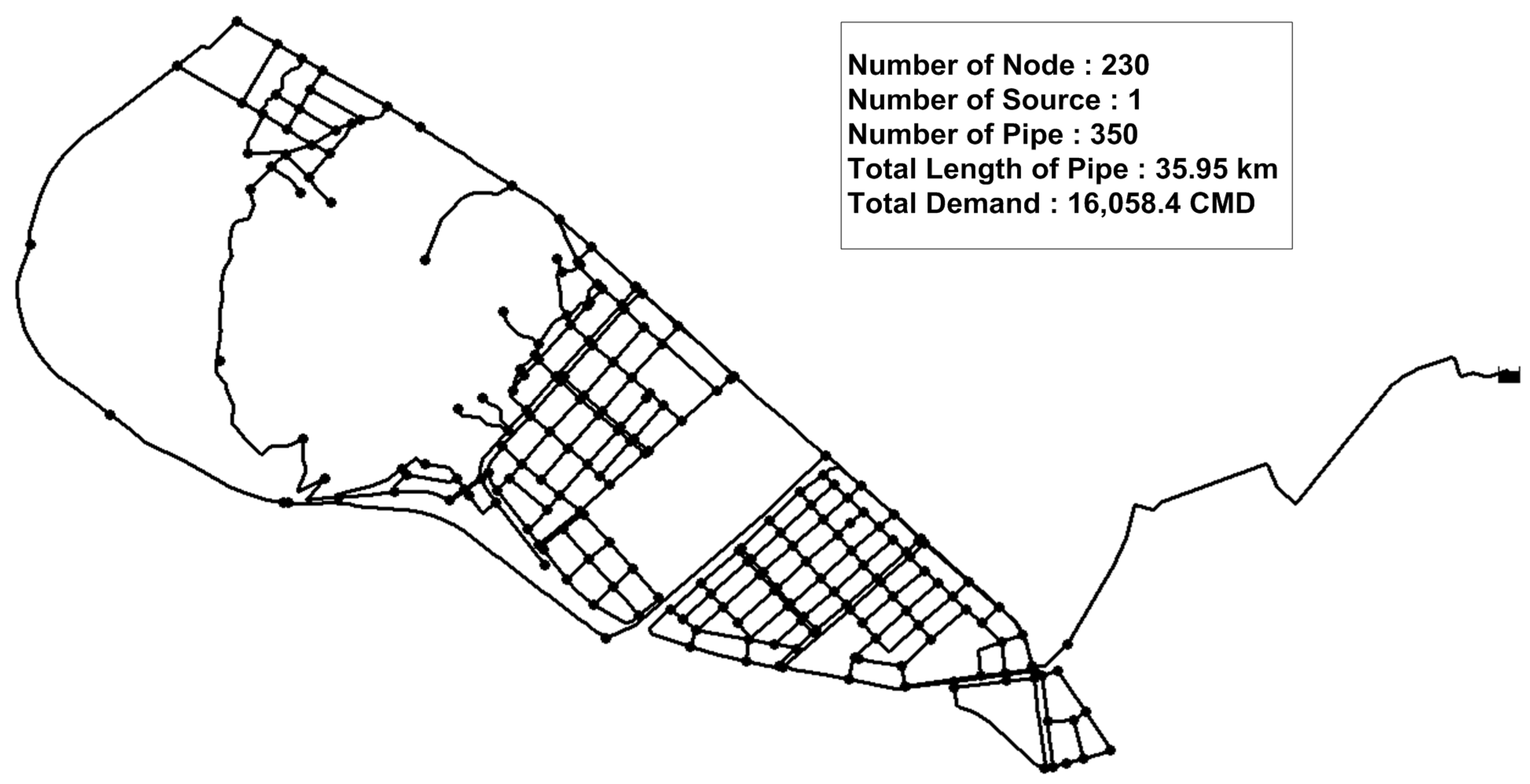
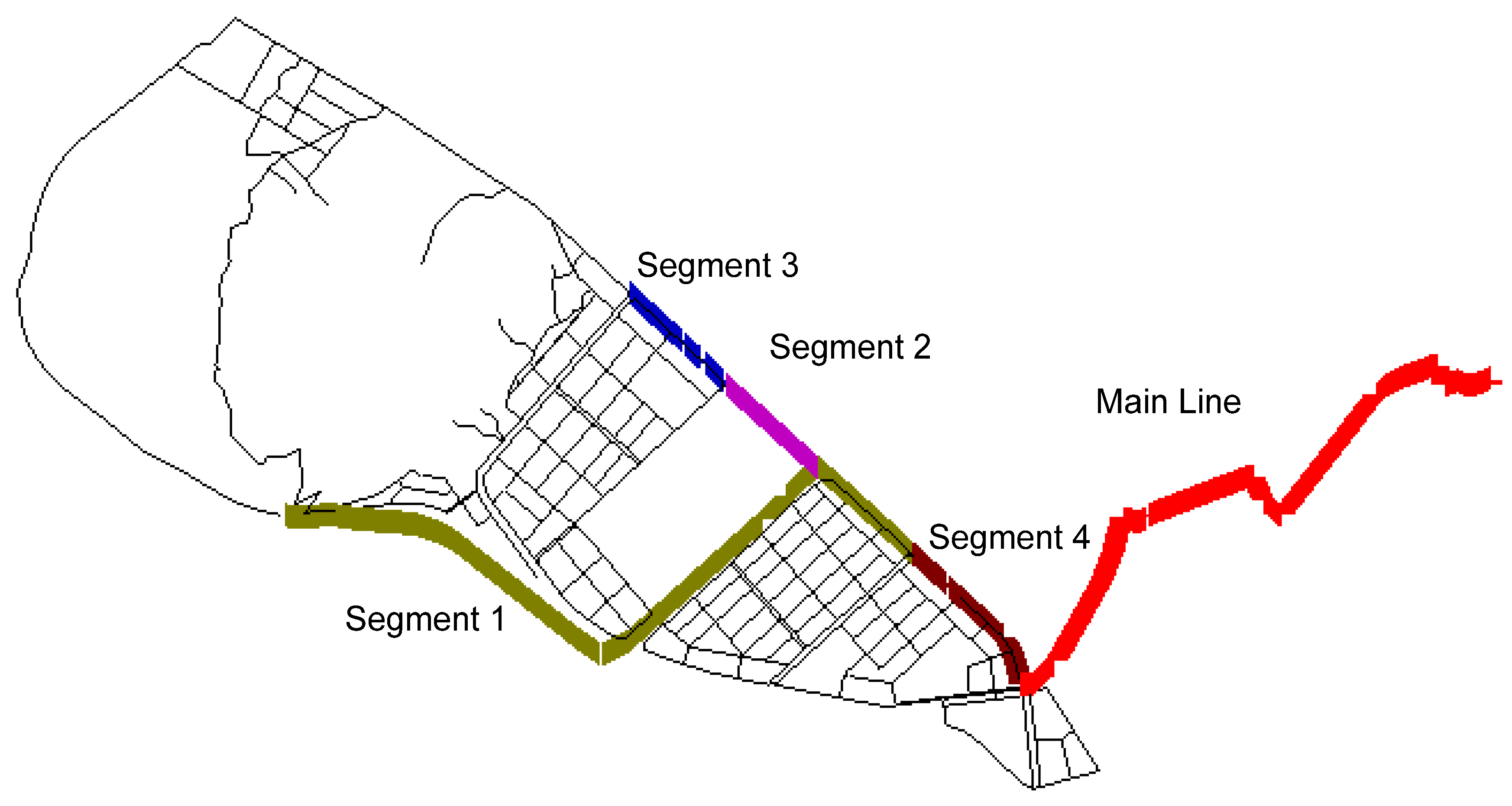
Water distribution pipes can be divided into hydraulically significant or insignificant pipes depending on the installation location, valve location, base demand for water at nodes, variation in demand, pipe flow rates and the population served. Accordingly, the importance of individual water distribution pipes can be termed “hydraulic importance.” This study was conducted to develop a method to determine the rehabilitation priority order of pipes in water distribution systems on the basis of both the deterioration rate of water pipes and their hydraulic importance. Using the method proposed in this paper, pipes are first classified according to their deterioration rate and hydraulic importance according to two different attributes. A multi-criteria decision-making method called a weighted utopian approach, which combines a weighting method and a distance measurement method, is then used to prioritize the pipes’ rehabilitation needs.
4. Conclusions
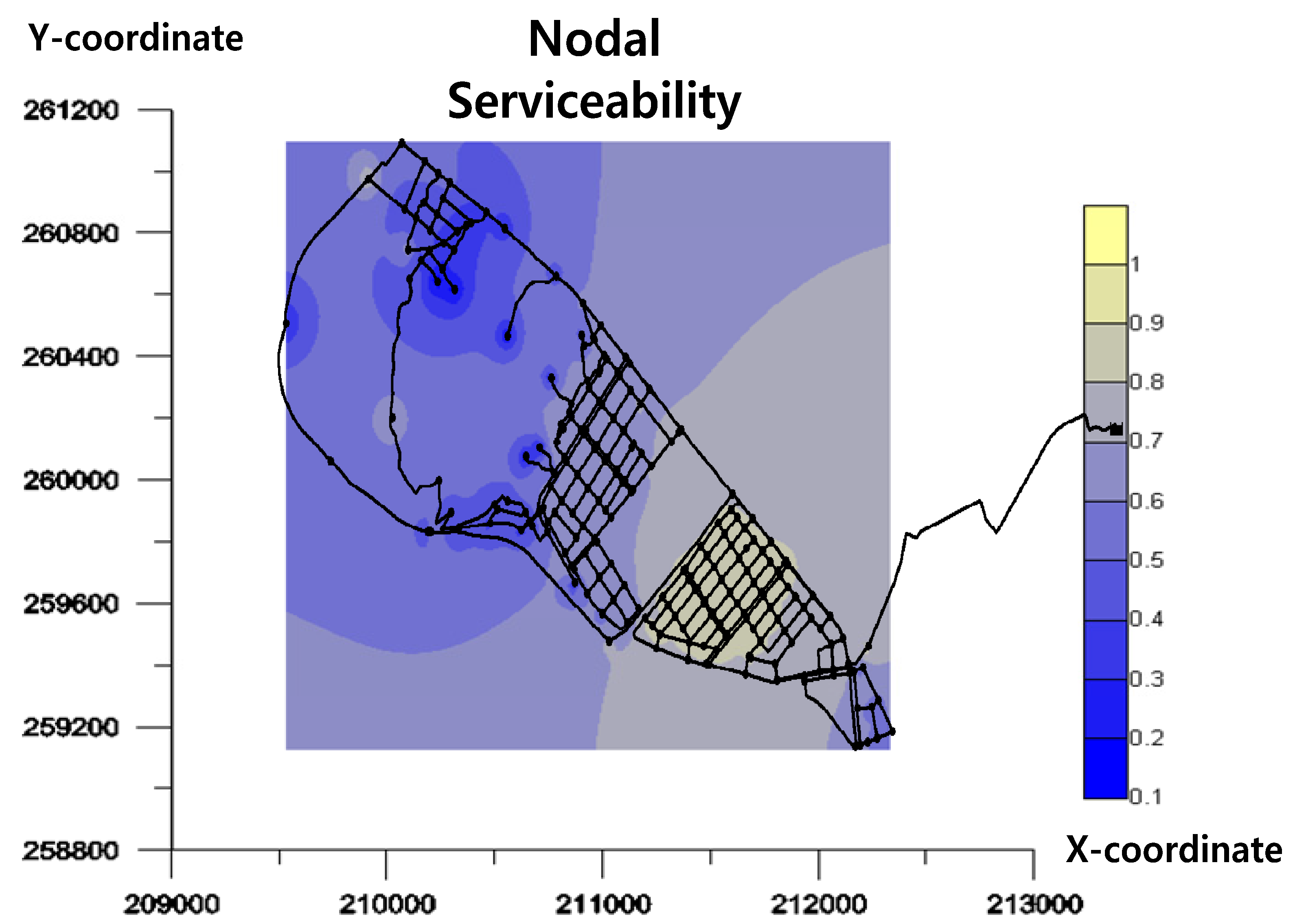
To determine the rehabilitation priority order for pipes in a water distribution system, we developed a new method to address the limitations of existing methods that use only the pipeline deterioration rate. We aimed to determine the priority of pipes for rehabilitation consider normal and abnormal conditions using multi-criteria decision making methods (using compromise of some weighting methods). In this study, we also added single and multiple pipe failures simulation in addition to the deterioration of pipes. These are key points of this manuscript. The proposed method considers the hydraulic importance in addition to the deterioration rate in determining the rehabilitation priority order with higher reliability. The results of this study are significant in that they show how a rehabilitation priority order model can be combined with the concept of the hydraulic importance of water pipes in applying existing deterioration rate calculation methods to determine the rehabilitation priority order. The proposed method was applied to the KA water distribution network of City J to determine the rehabilitation priority order for the pipes in the KA network. The results confirm that the proposed method provides a more realistic determination of the rehabilitation priority order that considers not only the deterioration rate, but also the relative hydraulic importance of each pipe. This model is able to determine the rehabilitation priority order for pipes in a water distribution network and can be applied more easily than existing rehabilitation priority order models that require large amounts of data and involve complex failure probabilities and mathematical models.
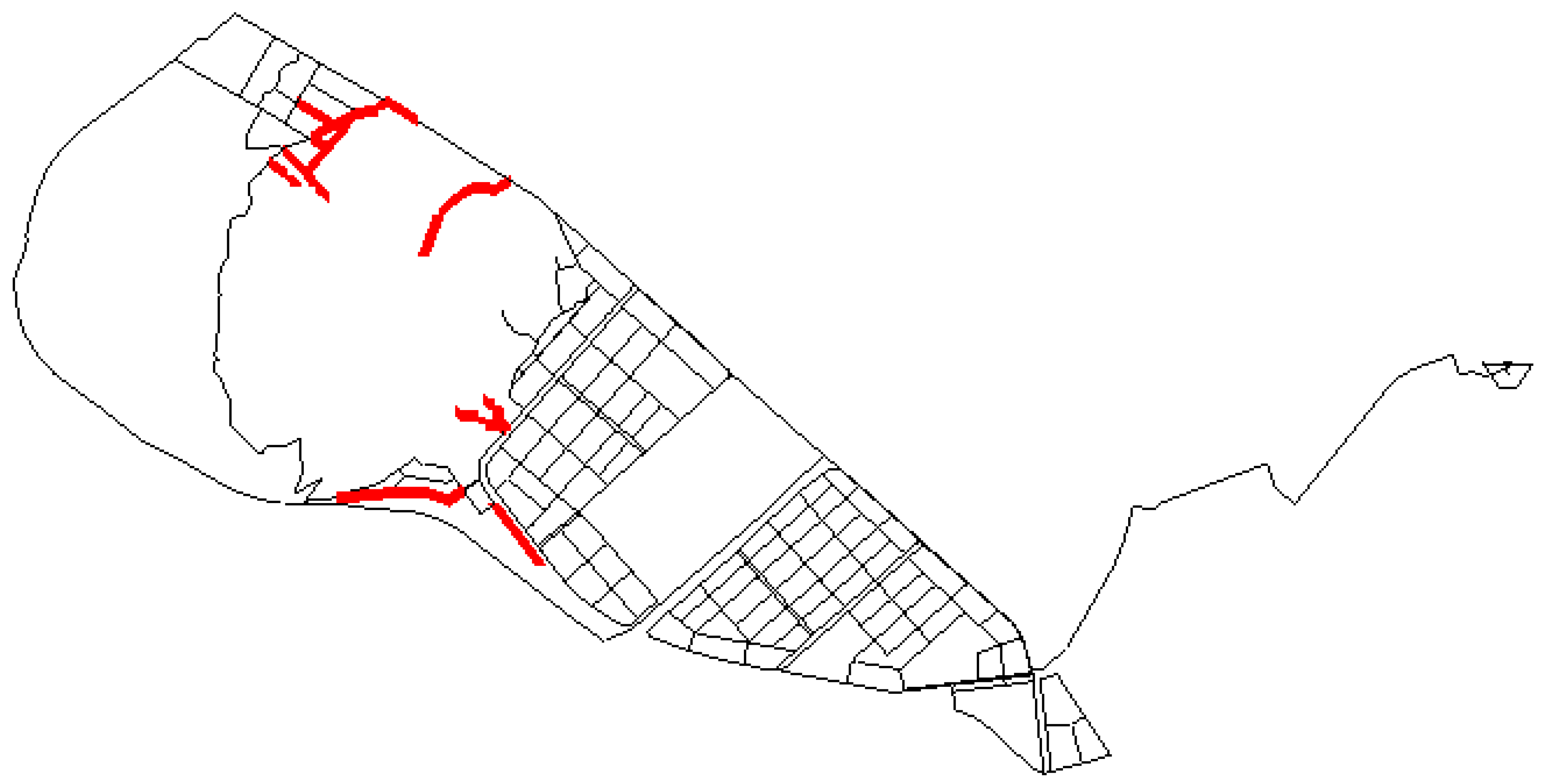
Because large-scale infrastructure networks, such as water distribution systems, require constant maintenance and rehabilitation, the design and reinforcement of water distribution networks to guard against multiple failures in the event of events, such as earthquakes, place huge financial and physical burdens on the water supplier. Korea has never experienced large-scale earthquakes, and most Koreans believe that their country has little to fear in this respect. However, although the probability of a disaster, such as an earthquake in Korea, is low, such an event would cause significant damage if it were to occur. Thus, Korea needs to be prepared for such disasters. Given these circumstances, a method that can determine the level of reliability of a water distribution system in the face of a disaster capable of causing immense damage is necessary within the current framework of maintenance and rehabilitation. The proposed model is also advantageous from this perspective.
The results of this study suggest that further research on this subject is warranted. The proposed method should be compared with other recent methodologies, such as CARE-W, CASSES and AWARE-P. Therefore, a detailed comparative study can be one of the further studies in the near future. The possible malfunction of valves was not considered in calculating the relative importance of structural failures. Because the area in which damage may occur varies depending on the ability to operate the relevant valve, the effect of valve malfunctioning should be studied. In this study, given that water distribution systems are essential social infrastructure networks that directly affect public welfare, an economic feasibility analysis for cost optimization purposes was not performed. Therefore, further studies on rehabilitation prioritization with consideration of economic constraints should be undertaken.