Application of Displacement Height and Surface Roughness Length to Determination Boundary Layer Development Length over Stepped Spillway
Abstract
:1. Introduction
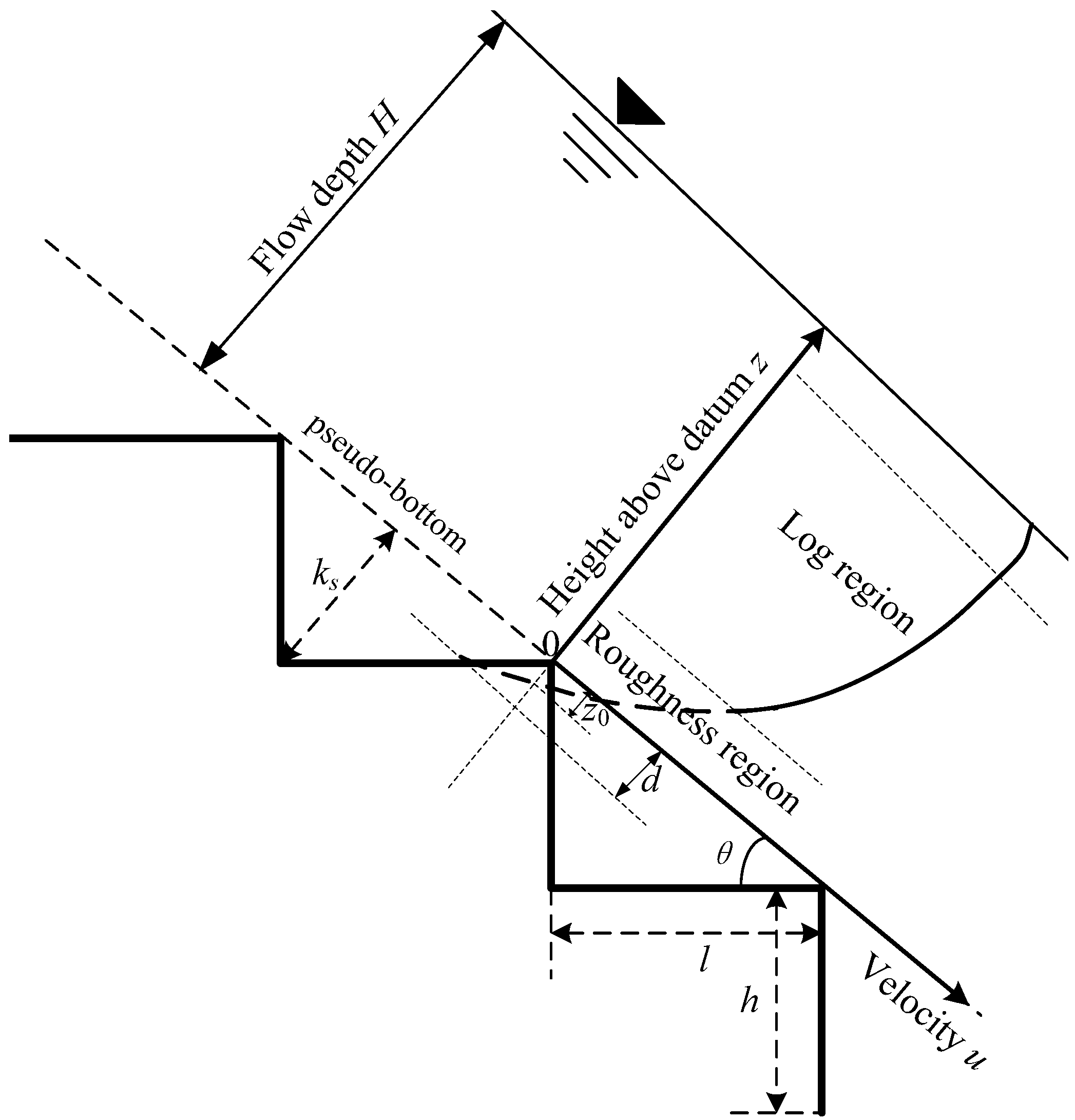
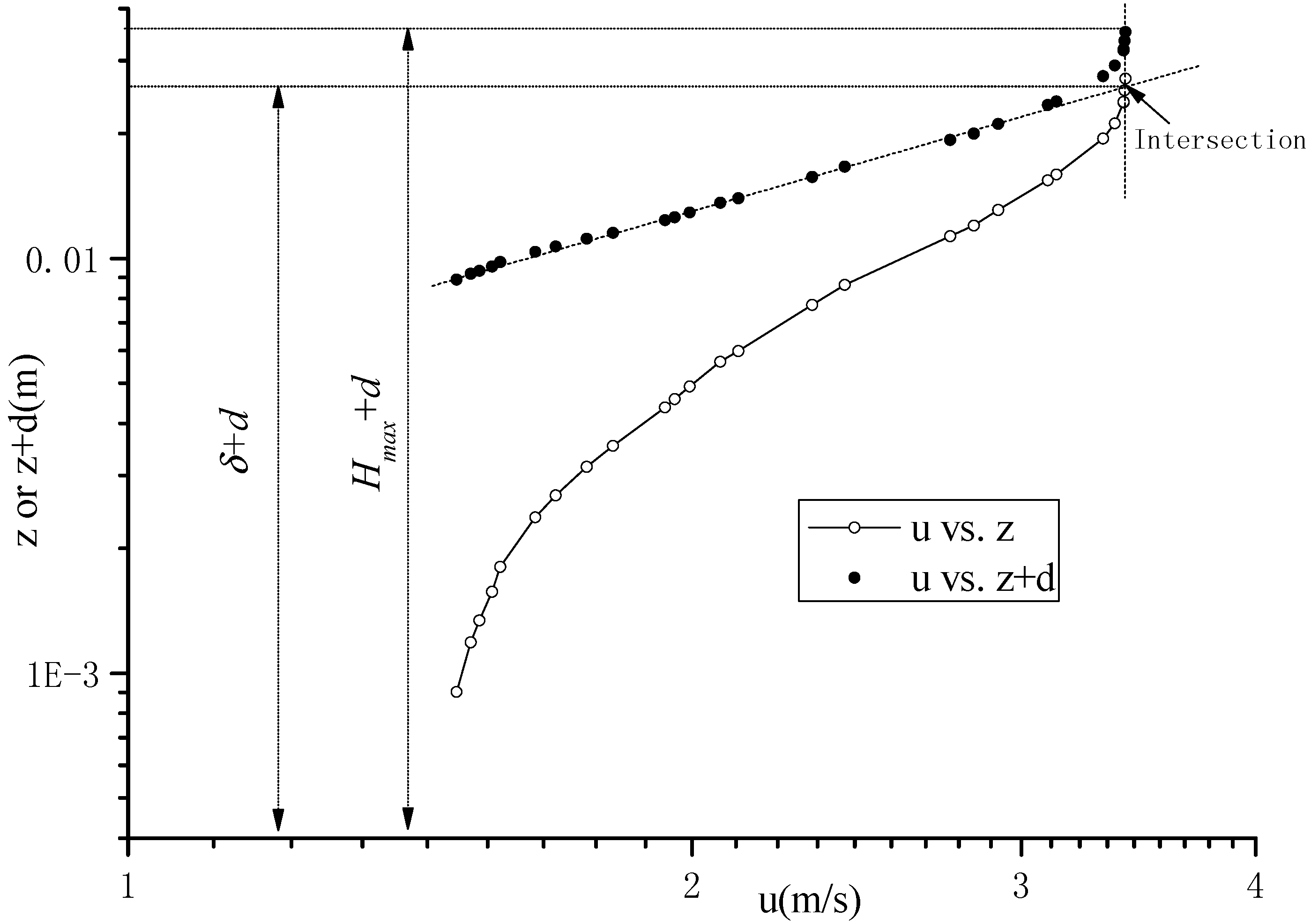
2. Methods to Calculate d and z0 from a Given Velocity Profile
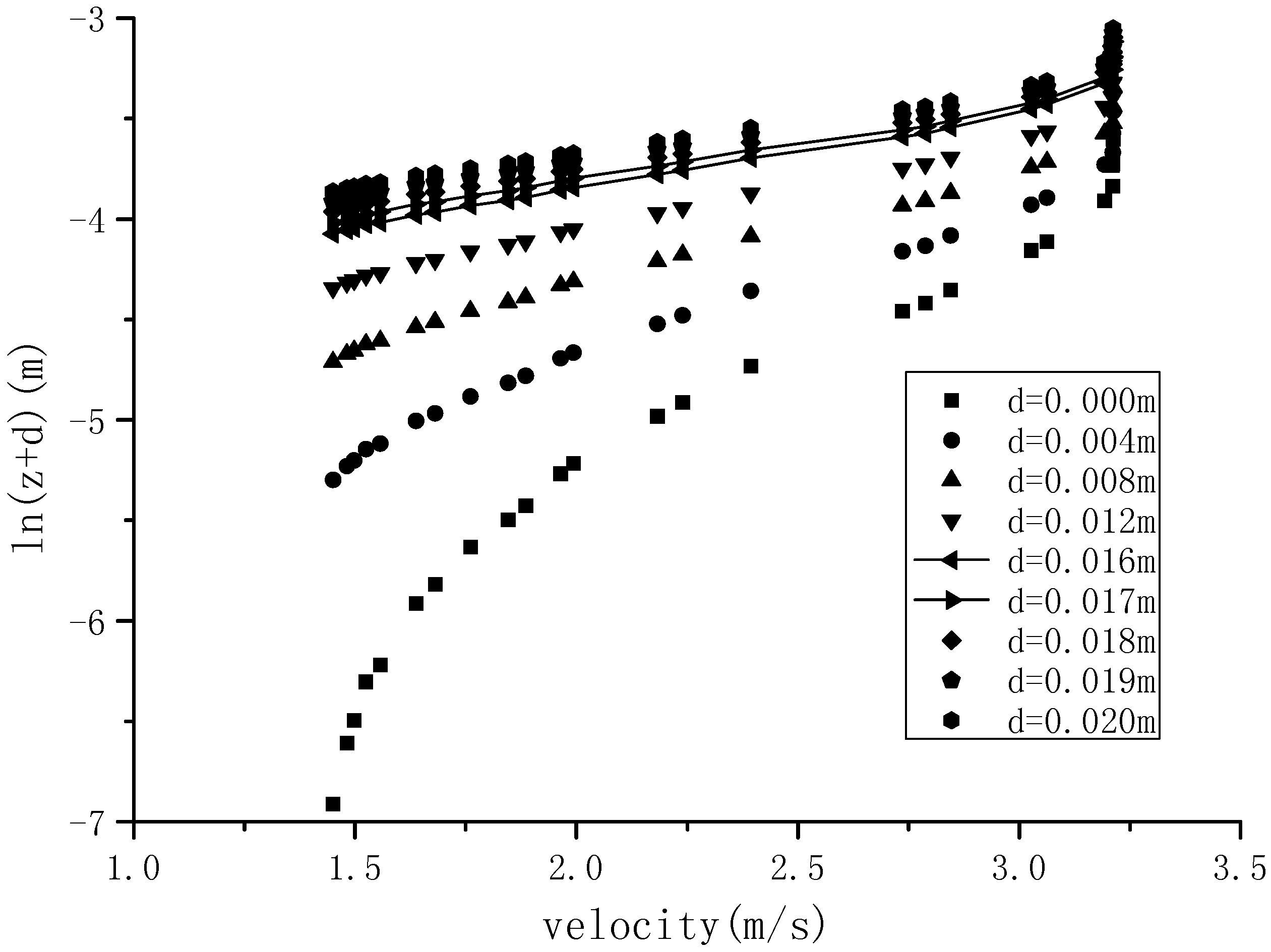

3. Simulation of Velocity Profile on Stepped Spillways
4. Verification of Simulated Velocity Profiles
| Reference | Spillway Geometry Descriptions | Flow Conditions |
|---|---|---|
| [48] | Physical model with an ogee profile was 40.2 m long and 2.74 m wide, consisting of a 23.46 m long rectangular chute at a 2% slope ending with a stepped spillway, which then dropped 2.35 m into a stilling basin. Stepped spillway including 68 steps initially followed a parabolic ogee path and became linear at a slope of 21.8° about half way along the spillway. | Q = 2.46 m3/s |
| No obvious air entrainment over the steps. | ||
| [49] | Physical model was 10.82 m long and 1.8 m wide, consisting of a 2.44 m long broad chute ending with a stepped spillway, which then dropped 1.52 m into a stilling basin. Stepped spillway including 40 identical steps (step height = 3.8 cm, width = 15.2 cm) became at a slope of 14°. | Q = 0.504 m3/s |
| The inception point was located at the distance of 3.44 m from the first step. | ||
| [41] | Physical model with a standard U.S. Army Corps profile consisted of 13 steps. The first five steps were transition steps and the height of each is 2, 2.4, 3, 4, and 5 cm. Below eight steps (height = 6 cm, width = 4.5 cm) continued down to the toe. The spillway slope was 53°. | Q = 0.03 m3/s |
| The location of inception of free-surface aeration was at step 10. |
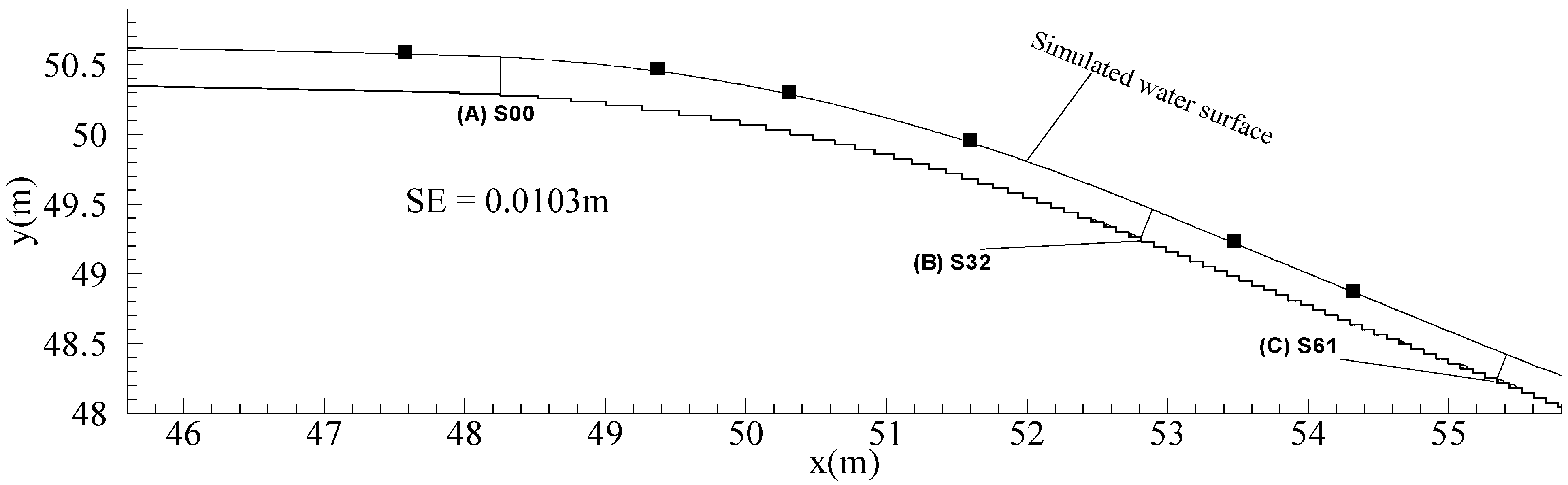
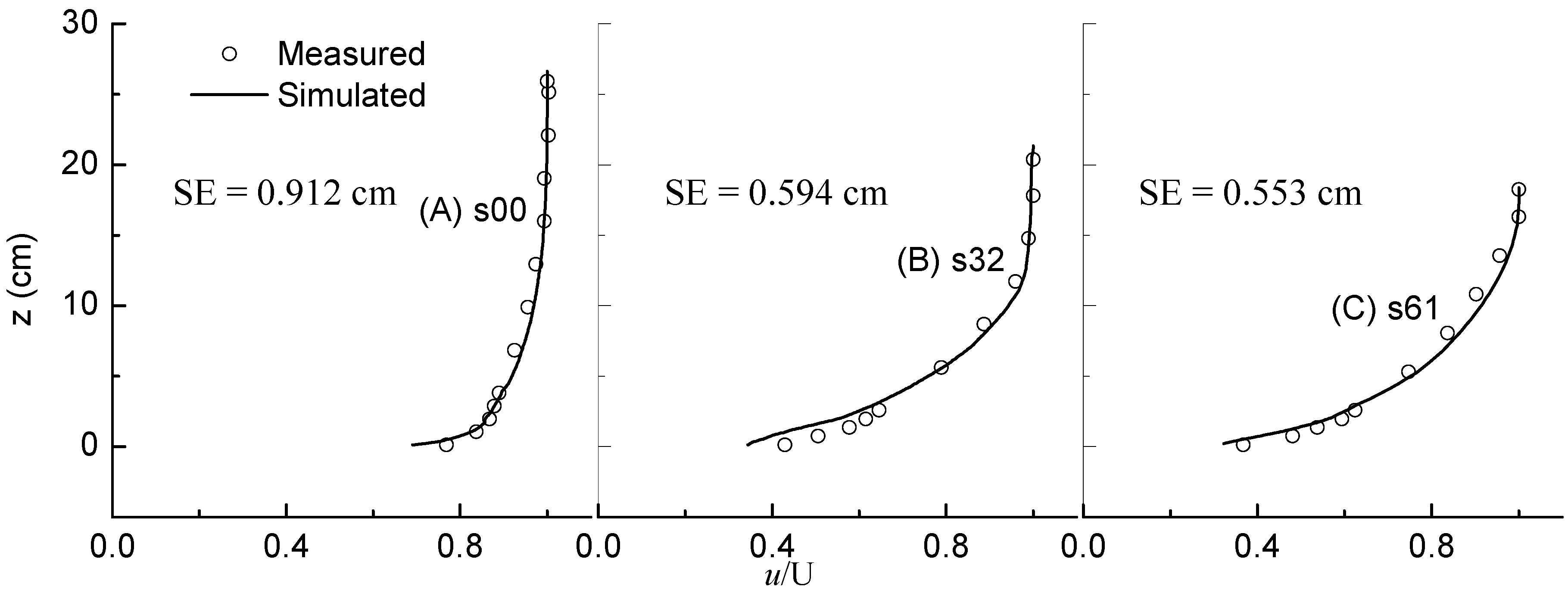
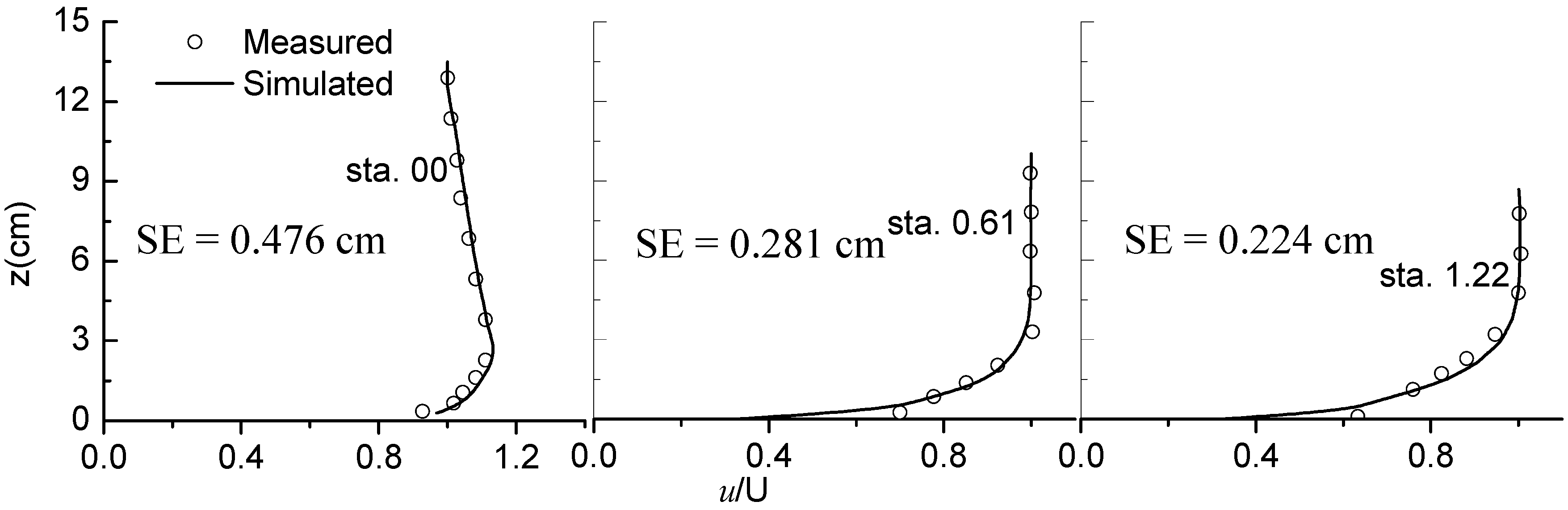
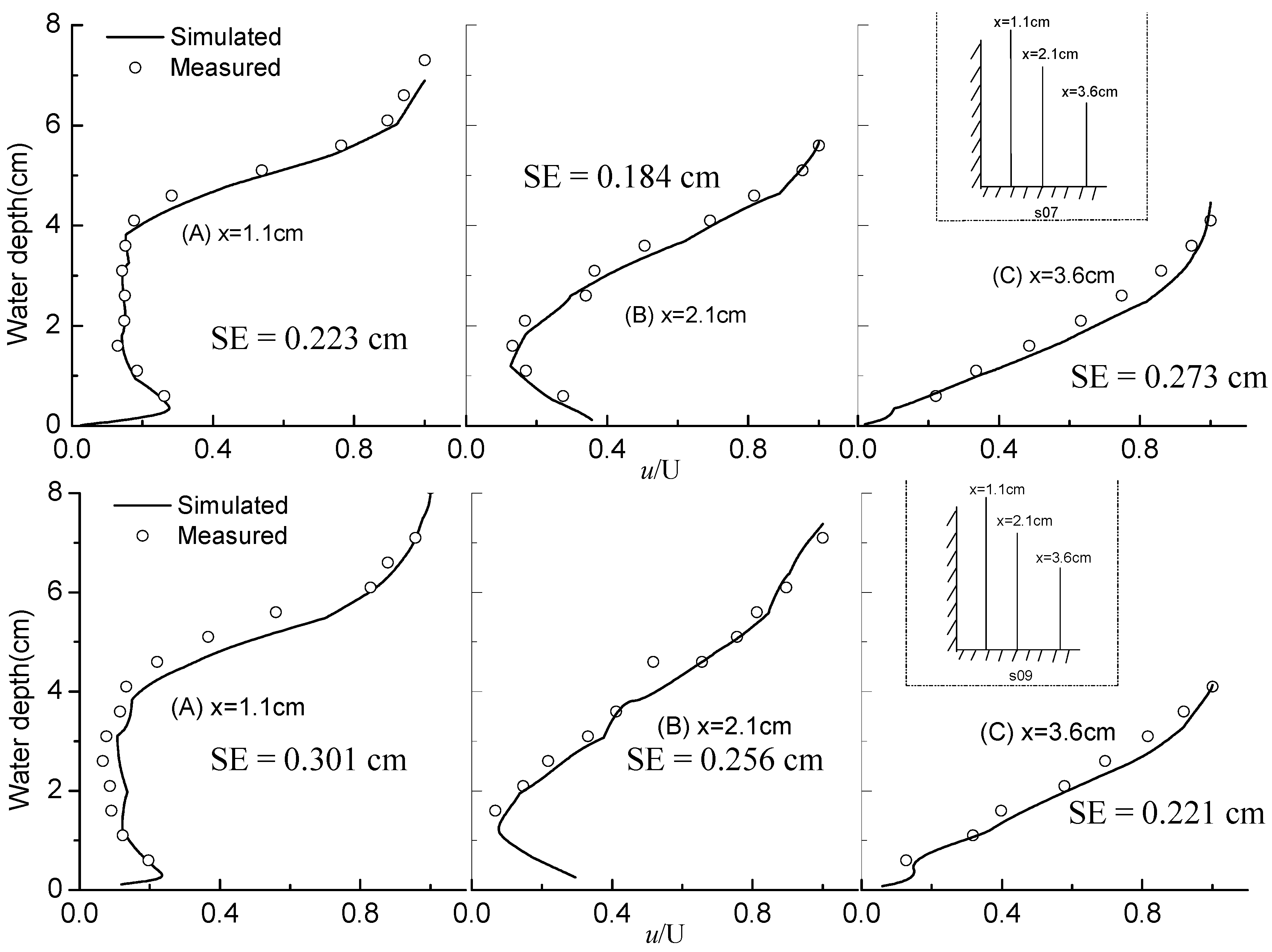
5. Numerical Experiments on Stepped Spillways
| Source | Run No. | h (m) | l (m) | ks (m) | q (m2/s) | θ (deg) | Fr-in | Li-exp (m) | M |
|---|---|---|---|---|---|---|---|---|---|
| [41] | 1 | 0.060 | 0.045 | 0.036 | 0.100 | 53.2 | 0.057 | 0.59 | 12.652 |
| 2 | 0.060 | 0.068 | 0.045 | 0.100 | 41.7 | 0.057 | - | 11.498 | |
| 3 | 0.030 | 0.045 | 0.025 | 0.100 | 33.7 | 0.057 | - | 11.806 | |
| 4 | 0.060 | 0.090 | 0.050 | 0.100 | 33.7 | 0.057 | - | 10.528 | |
| 5 | 0.060 | 0.045 | 0.036 | 0.067 | 53.2 | 0.041 | 0.44 | 11.531 | |
| [49] | 6 | 0.038 | 0.152 | 0.037 | 0.280 | 14.0 | 1 | 3.44 | 15.035 |
| 7 | 0.038 | 0.152 | 0.037 | 0.420 | 14.0 | 1 | 4.54 | 11.673 | |
| 8 | 0.038 | 0.152 | 0.037 | 0.620 | 14.0 | 1 | - | 12.998 | |
| 9 | 0.038 | 0.152 | 0.037 | 0.820 | 14.0 | 1 | - | 13.855 | |
| 10 | 0.076 | 0.304 | 0.074 | 0.820 | 14.0 | 1 | - | 10.205 | |
| 11 | 0.076 | 0.152 | 0.068 | 0.820 | 26.6 | 1 | - | 14.310 | |
| [48] | 12 | 0.035 | 0.087 | 0.032 | 0.899 | 21.8 | 2.26 | - | 19.149 |
| 13 | 0.035 | 0.087 | 0.032 | 0.899 | 21.8 | 1 | - | 19.925 | |
| 14 | 0.035 | 0.087 | 0.032 | 0.899 | 21.8 | 0.674 | - | 18.275 | |
| 15 | 0.035 | 0.137 | 0.034 | 0.899 | 14.3 | 2.26 | - | 18.451 | |
| 16 | 0.035 | 0.227 | 0.035 | 0.899 | 8.7 | 2.26 | - | 18.981 | |
| [51] | 17 | 0.100 | 0.250 | 0.099 | 0.143 | 21.8 | 0.058 | 1.62 | 6.171 |
| [52] | 18 | 0.050 | 0.125 | 0.050 | 0.147 | 21.8 | 0.04 | 2.02 | 8.529 |
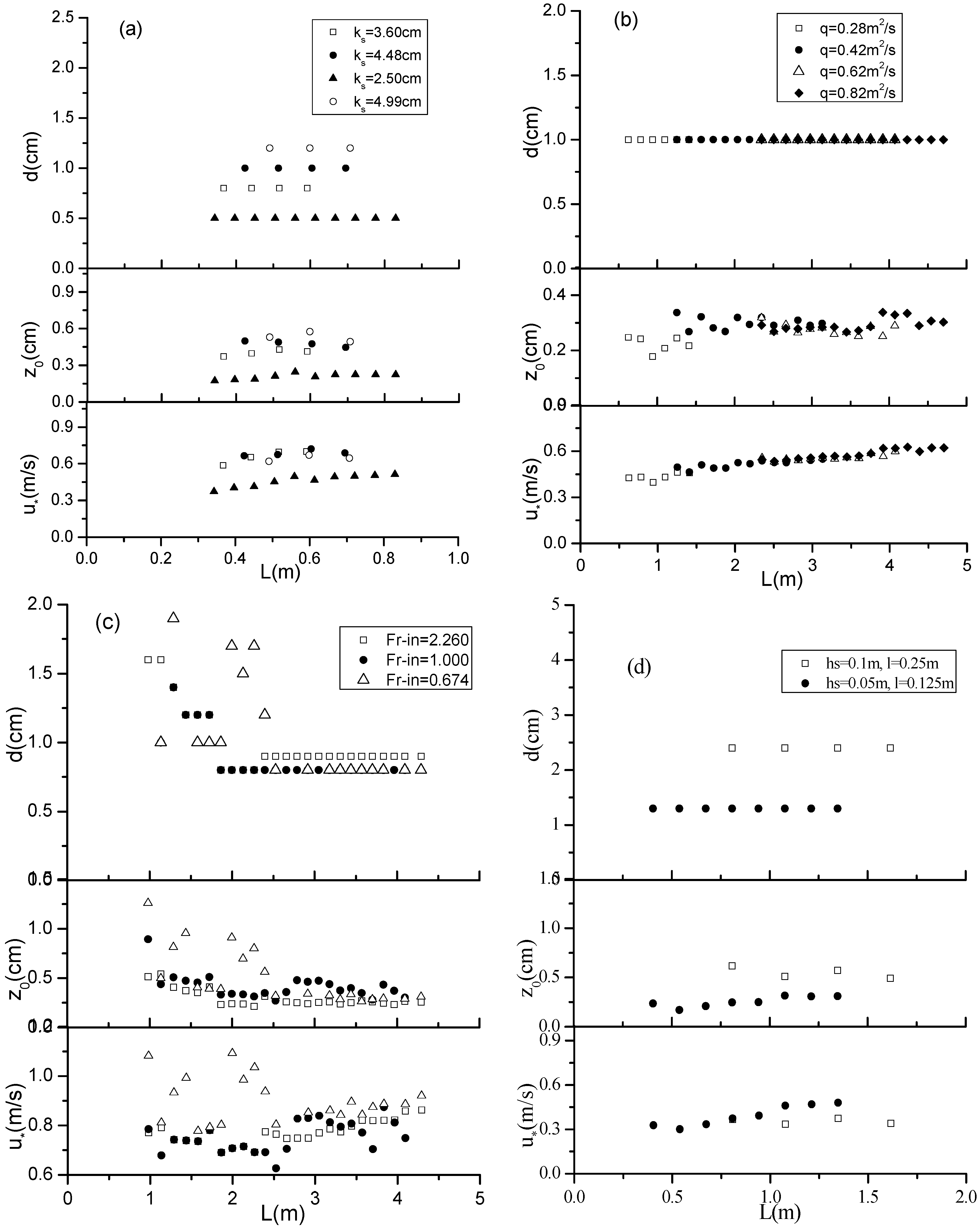
5.1. Estimates of the Displacement Height, Surface Roughness Length and Friction Velocity
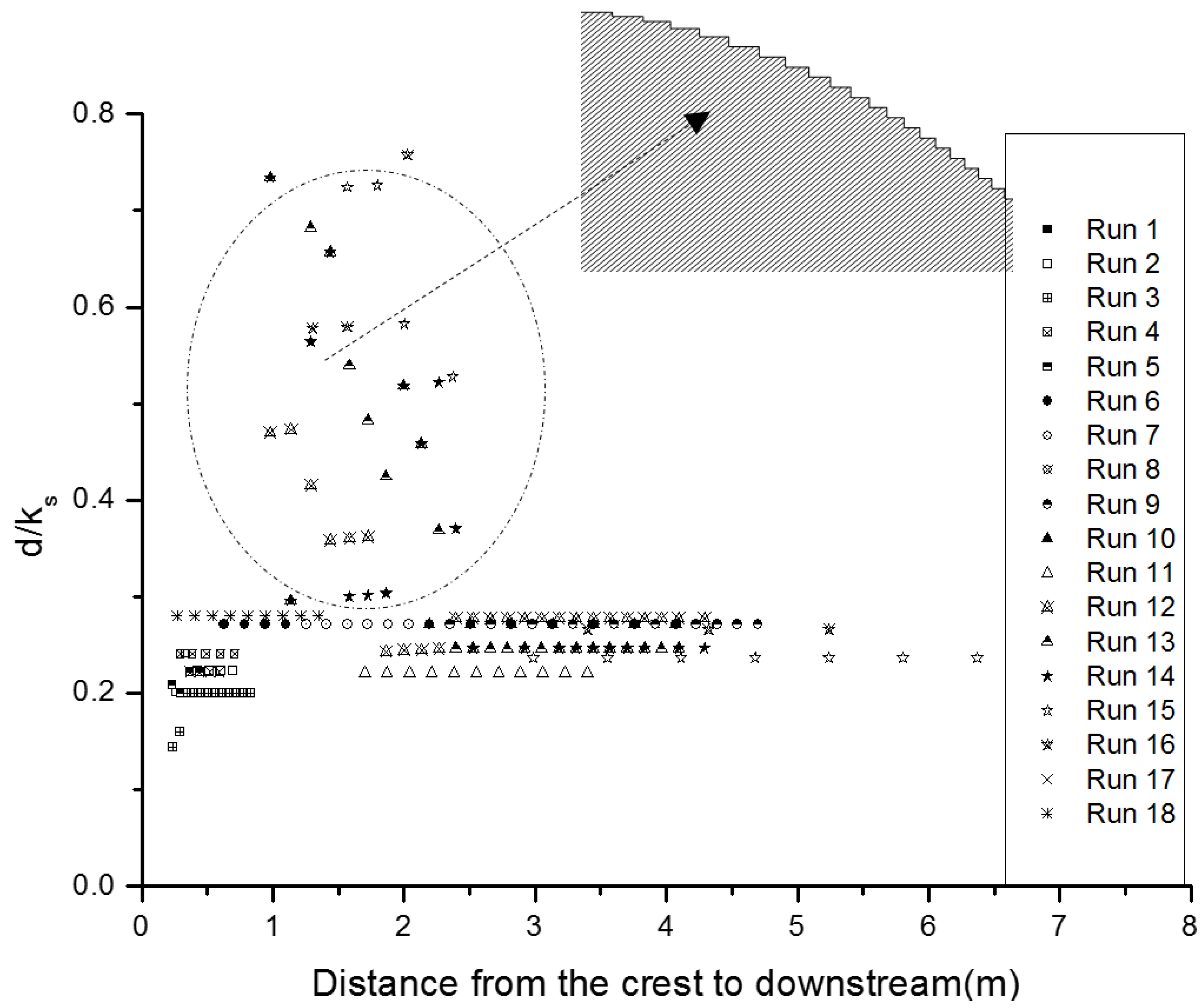
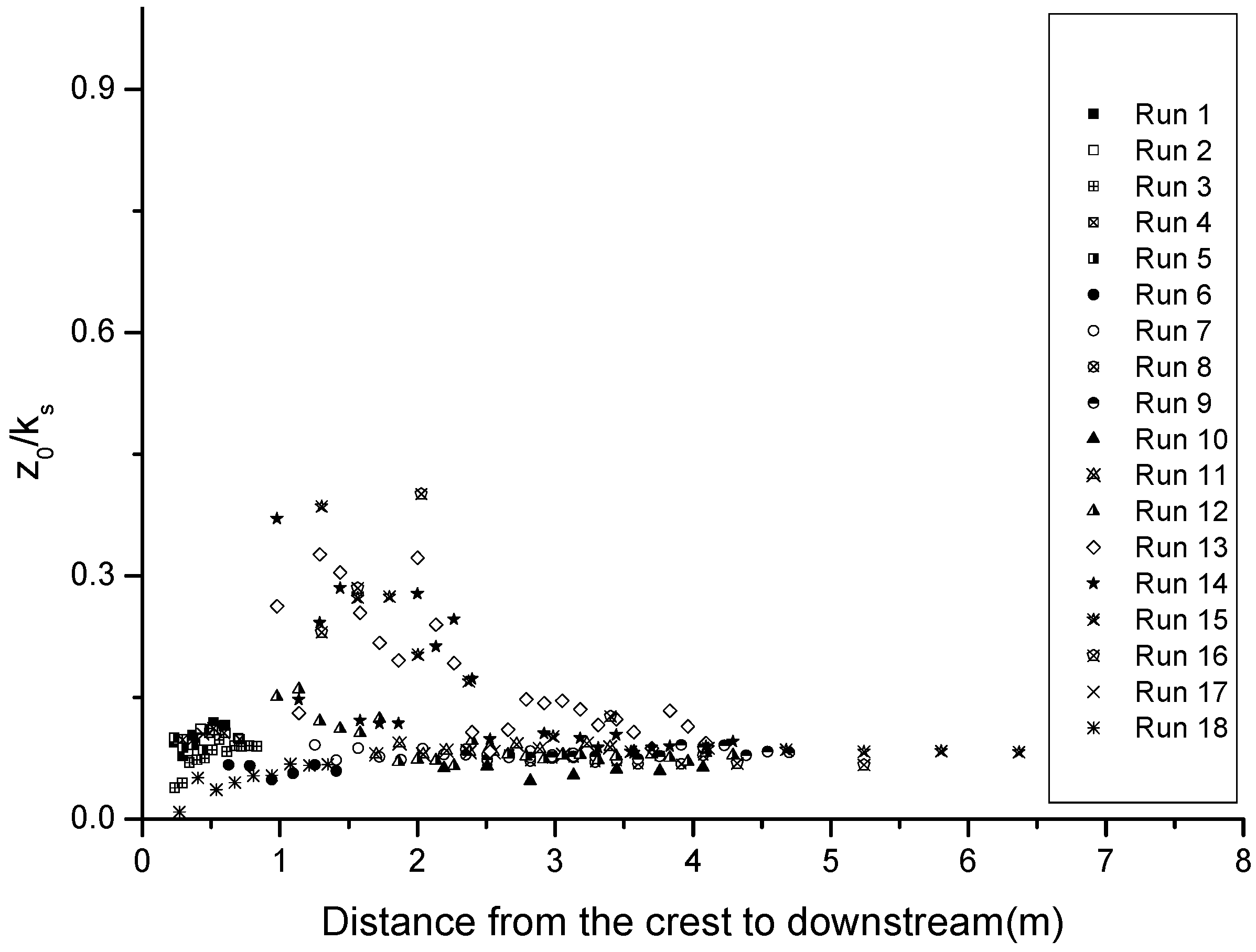
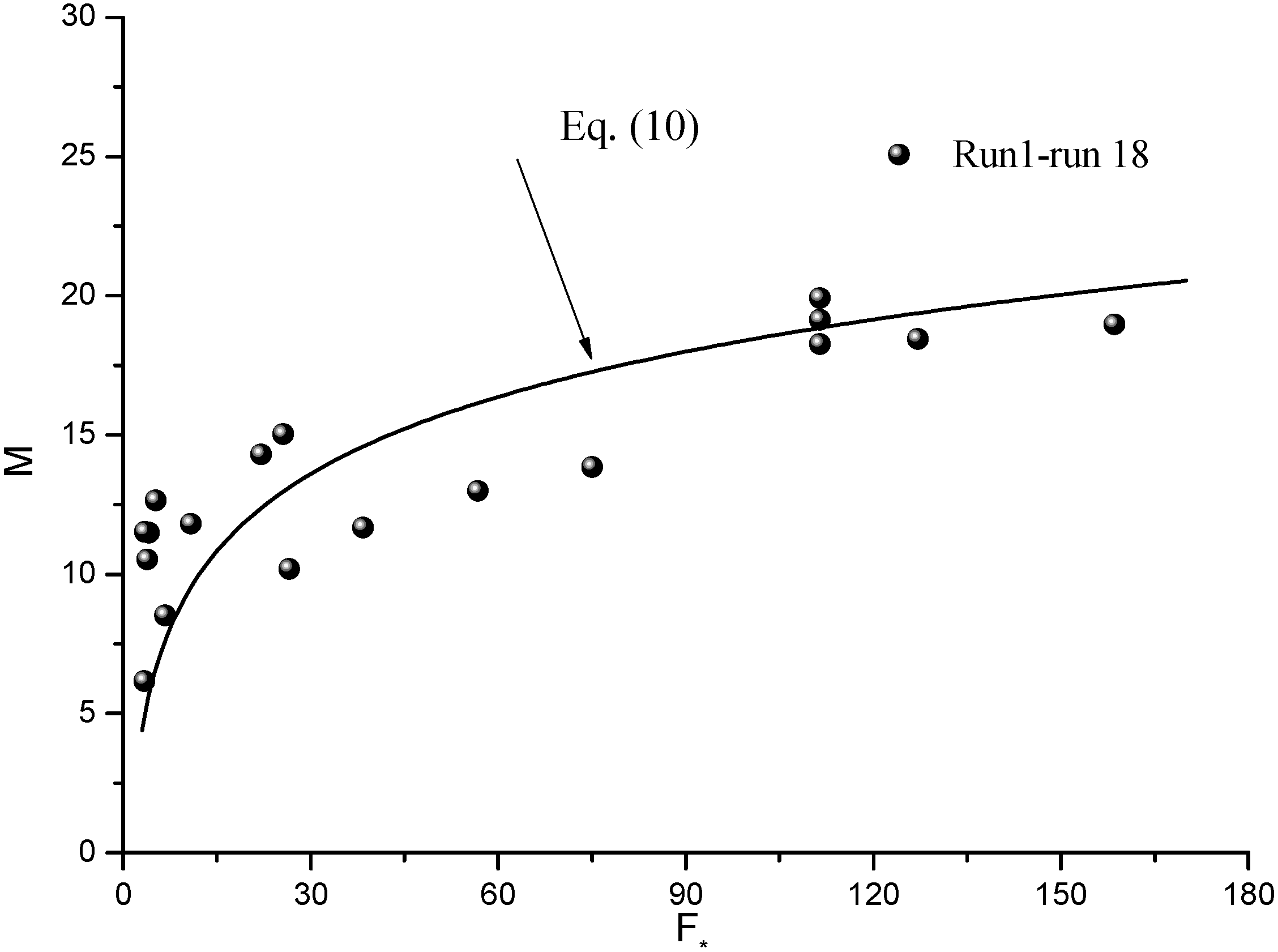
5.2. Estimation of Velocity Profile Parameters

5.3. Application to Boundary Layer Development Length

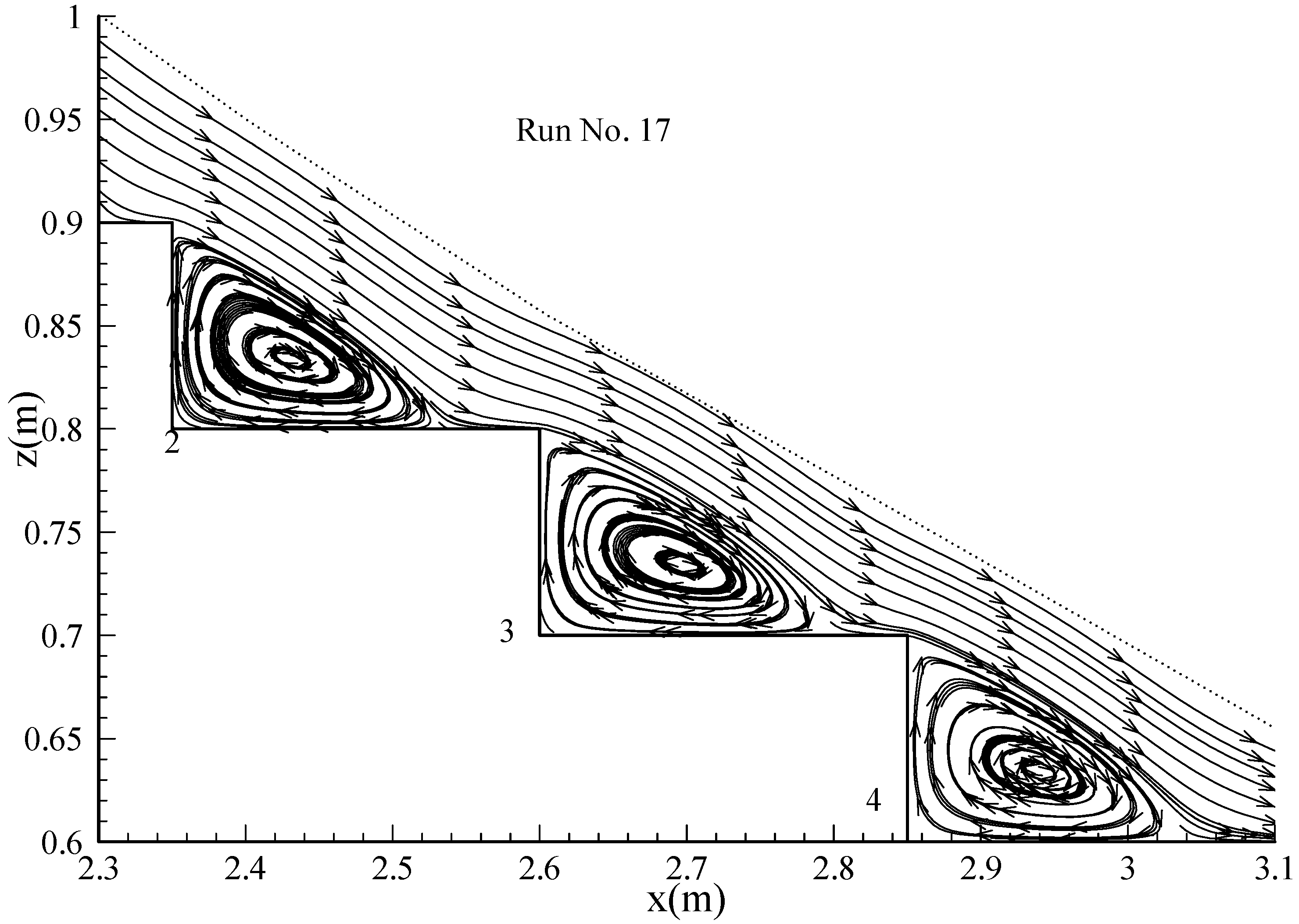
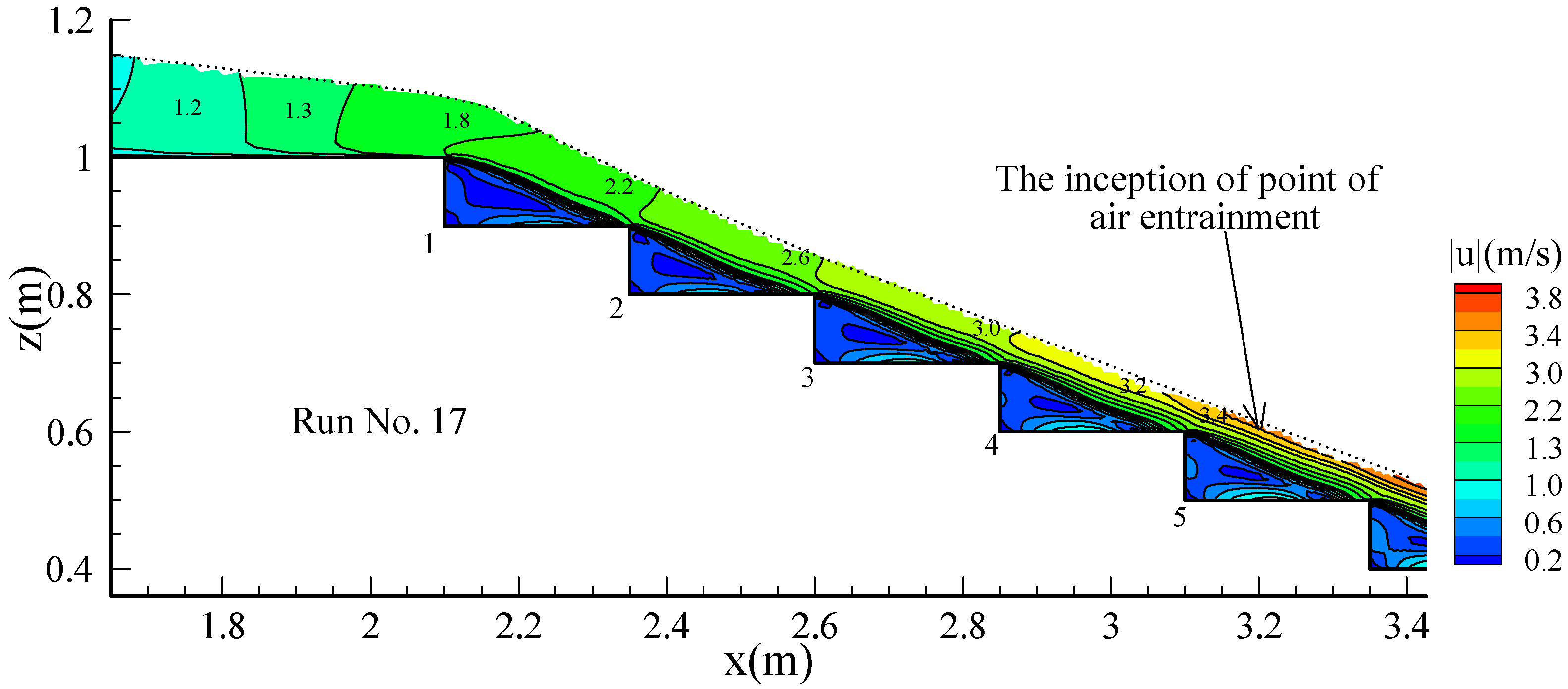
| Run No. | d (m) | δ (m) | Hmax (m) | Li-exp (m) | Li-CFD (m) | (δ + d)/(Hmax + d) |
|---|---|---|---|---|---|---|
| 1 | 0.008 | 0.0173 | 0.027 | 0.60 | 0.66 | 0.72 |
| 5 | 0.008 | 0.0107 | 0.018 | 0.44 | 0.44 | 0.72 |
| 6 | 0.010 | 0.0403 | 0.057 | 3.44 | 3.44 | 0.75 |
| 7 | 0.010 | 0.0713 | 0.099 | 4.38 | 4.28 | 0.75 |
| 17 | 0.023 | 0.0421 | 0.060 | 1.35 | 1.35 | 0.78 |
| 18 | 0.014 | 0.0403 | 0.055 | 2.02 | 2.02 | 0.79 |
| 2 | 0.010 | 0.0177 | 0.025 | - | 0.79 | 0.79 |
| 3 | 0.005 | 0.0173 | 0.026 | - | 0.73 | 0.72 |
| 4 | 0.012 | 0.0203 | 0.029 | - | 0.92 | 0.79 |
| 8 | 0.010 | 0.118 | 0.155 | - | 5.47 | 0.78 |
| 9 | 0.010 | 0.152 | 0.211 | - | 7.90 | 0.73 |
| 10 | 0.020 | 0.153 | 0.203 | - | 6.58 | 0.78 |
| 11 | 0.015 | 0.142 | 0.19 | - | 5.12 | 0.77 |
| 12 | 0.009 | 0.118 | 0.151 | - | 8.42 | 0.79 |
| 13 | 0.009 | 0.104 | 0.142 | - | 8.68 | 0.75 |
| 14 | 0.009 | 0.112 | 0.145 | - | 8.65 | 0.79 |
| 15 | 0.009 | 0.1220 | 0.162 | - | 10.89 | 0.77 |
| 16 | 0.010 | 0.1272 | 0.168 | - | 12.53 | 0.77 |
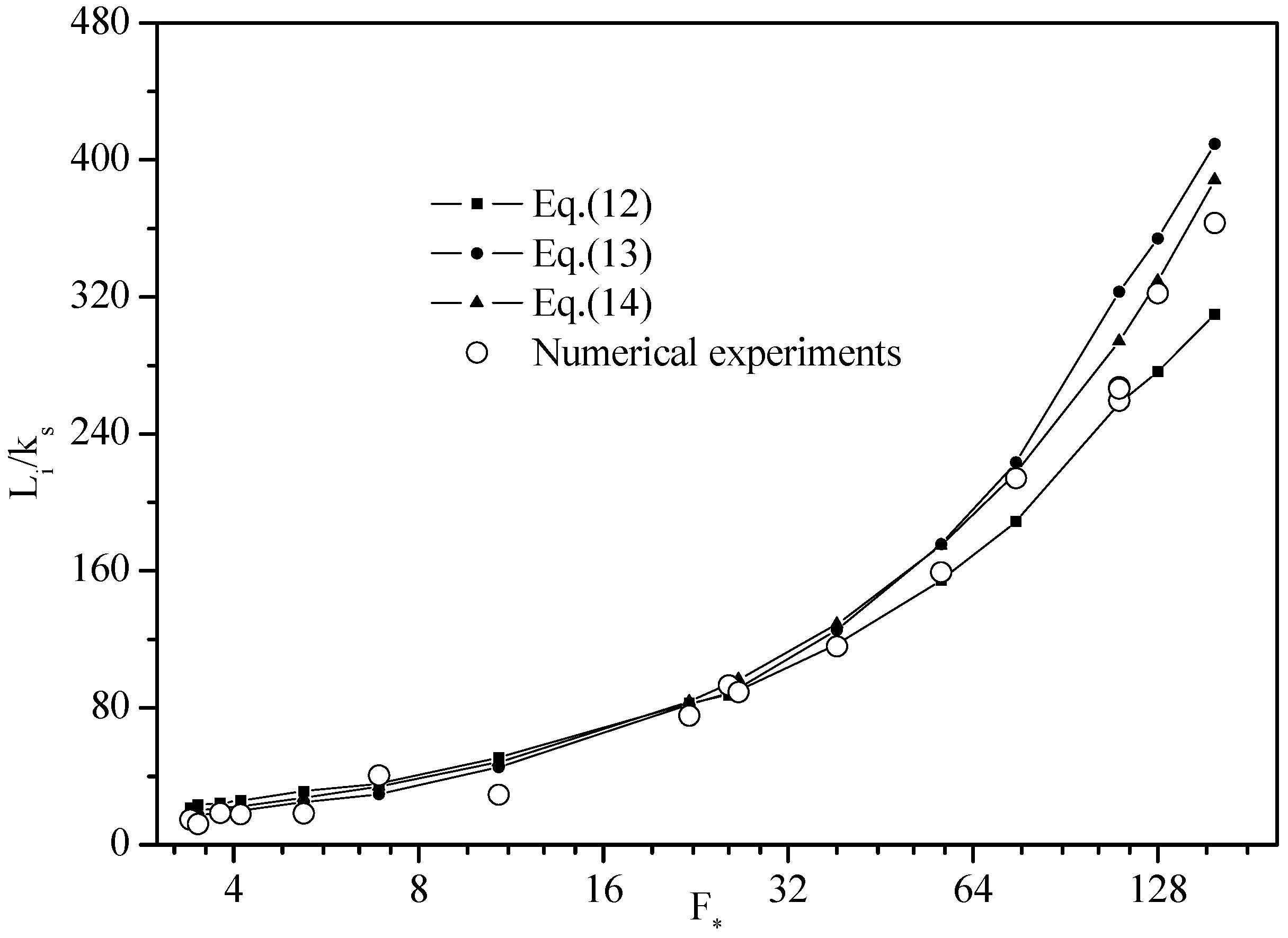
| Run No. | ks | q | θ | F* | Li (m) | Li (m) | Li(m) | Li-CFD |
|---|---|---|---|---|---|---|---|---|
| (cm) | (m2/s) | Equation (12) | Equation (13) | Equation (14) | (m) | |||
| 1 | 3.600 | 0.1 | 53.2 | 5.2 | 1.12 | 0.89 | 0.98 | 0.66 |
| 2 | 4.480 | 0.1 | 41.7 | 4.1 | 1.16 | 0.90 | 1.01 | 0.79 |
| 3 | 2.500 | 0.1 | 33.7 | 10.8 | 1.27 | 1.13 | 1.20 | 0.73 |
| 4 | 4.990 | 0.1 | 33.7 | 3.8 | 1.21 | 0.92 | 1.07 | 0.92 |
| 5 | 3.600 | 0.07 | 53.2 | 3.5 | 0.84 | 0.63 | 0.72 | 0.44 |
| 6 | 3.690 | 0.28 | 14.0 | 25.6 | 3.23 | 3.27 | 3.46 | 3.44 |
| 7 | 3.690 | 0.42 | 14.0 | 38.4 | 4.32 | 4.63 | 4.75 | 4.28 |
| 8 | 3.687 | 0.62 | 14.0 | 56.8 | 5.70 | 6.48 | 6.44 | 5.47 |
| 9 | 3.687 | 0.82 | 14.0 | 75.1 | 6.96 | 8.24 | 8.01 | 7.90 |
| 10 | 7.373 | 0.82 | 14.0 | 26.5 | 6.63 | 6.74 | 7.12 | 6.58 |
| 11 | 6.798 | 0.82 | 26.6 | 22.1 | 5.63 | 5.57 | 5.68 | 5.12 |
| 12 | 3.247 | 1.24 | 21.9 | 110.7 | 8.36 | 10.49 | 9.55 | 8.42 |
| 13 | 3.247 | 1.24 | 21.9 | 110.7 | 8.36 | 10.49 | 9.55 | 8.68 |
| 14 | 3.247 | 1.24 | 21.9 | 110.7 | 8.36 | 10.49 | 9.55 | 8.65 |
| 15 | 3.380 | 1.24 | 14.3 | 128.0 | 9.34 | 11.97 | 11.12 | 10.89 |
| 16 | 3.449 | 1.24 | 8.7 | 158.5 | 10.68 | 14.12 | 13.40 | 12.53 |
| 17 | 9.285 | 0.18 | 21.8 | 3.4 | 1.98 | 1.49 | 1.79 | 1.35 |
| 18 | 5.000 | 0.15 | 21.8 | 6.9 | 1.78 | 1.48 | 1.71 | 2.02 |
6. Conclusions
- (1)
- After validation with experimental data, numerical models and methods were used to simulate flow fields in the nonaerated skimming flow zones on stepped spillways. A two dimensional simulation was successful in simulating velocity profiles on stepped spillways.
- (2)
- In many different step geometries and flow conditions, fixing the origin of vertical coordinate at the tip of the steps, the expressions of d/ks in the range of 0.22 to 0.27, z0/ks in the range of 0.06 to 0.1 and d/z0 from 2.2 to 4 give a good estimate along with the distance down the stepped spillways. It is a precondition that the rough stepped surfaces have a similar density of steps elements, since Figure 9 and Figure 10 illustrate that d and z0 may be strongly dependent on the density of roughness elements.
- (3)
- Equation (10) indicates that hydraulic roughness z0 is proportional to shear stress and the hydraulic roughness Froude number F*, defined in terms of the roughness height ks.
- (4)
- The turbulent boundary layer is seen at the water surface when the Bauer-defined boundary layer thickness is between 0.72 and 0.79 of the flow depth.
- (5)
- The length down the spillway to the inception of air entrainment is best predicted by Equation (13), developed by Hunt and Kadavy [68], especially when the surface roughness F* is equivalent above 64. However, the definition of inception point location in this paper is that the visual observation of the cross section where there is a continuous presence of air within the flow at the sidewalls or within the step cavities, and this conclusion was achieved based on the numerical simulation results under 18 different hydraulic conditions. Further research should expand the range of conditions for the application of these equations.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Meireles, I.; Renna, F.; Matos, J.; Bombardelli, F. Skimming, nonaerated flow on stepped spillways over roller compacted concrete dams. J. Hydraul. Eng. 2012, 138, 870–877. [Google Scholar] [CrossRef]
- Chamani, M.R.; Rajaratnam, N. Jet flow on stepped spillways. J. Hydraul. Eng. 1994, 120, 254–259. [Google Scholar] [CrossRef]
- Chamani, M.R.; Rajaratnam, N. Characteristics of skimming flow over stepped spillways. J. Hydraul. Eng. 1999, 125, 361–368. [Google Scholar] [CrossRef]
- Chanson, H. Stepped spillway flows and air entrainment. Can. J. Civil Eng. 1993, 20, 422–435. [Google Scholar] [CrossRef]
- Chanson, H. Experimental investigations of air entrainment in transition and skimming flows down a stepped chute. Can. J. Civ. Eng. 2002, 29, 145–156. [Google Scholar] [CrossRef]
- Cheng, X.J.; Chen, Y.C.; Luo, L. Numerical simulation of air-water two-phase flow over stepped spillways. Sci. China Ser. E Technol. Sci. 2006, 49, 674–684. [Google Scholar] [CrossRef]
- Cheng, X.J.; Chen, X.W. Numerical simulation of dissolved oxygen concentration in water flow over stepped spillways. Water Environ. Res. 2013, 85, 434–446. [Google Scholar] [CrossRef] [PubMed]
- Meireles, I.; Matos, J. Skimming flow in the nonaerated region of stepped spillways over embankment dams. J. Hydraul. Eng. 2009, 135, 685–689. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of skimming flows on stepped chutes: The effects of inflow conditions. J. Hydraul. Res. 2006, 44, 51–60. [Google Scholar] [CrossRef]
- Bung, D.B. Developing flow in skimming flow regime on embankment stepped spillways. J. Hydraul. Res. 2011, 49, 639–648. [Google Scholar] [CrossRef]
- Amador, A.; Sanchez-Juny, M.; Dolz, J. Characterization of the nonaerated flow region in a stepped spillway by PIV. J. Fluids Eng. 2006, 128, 1266–1273. [Google Scholar] [CrossRef]
- Smart, G.M. Turbulent velocity profiles and boundary shear in gravel bed rivers. J. Hydraul. Eng. 1999, 125, 106–116. [Google Scholar] [CrossRef]
- Franca, M.J.; Ferreira, R.M.; Lemmin, U. Parameterization of the logarithmic layer of double-averaged streamwise velocity profiles in gravel-bed river flows. Adv. Water Resour. 2008, 31, 915–925. [Google Scholar] [CrossRef]
- Wang, J.J.; Dong, Z.N. Open-channel turbulent flow over non-uniform gravel beds. Appl. Sci. Res. 1996, 56, 243–254. [Google Scholar] [CrossRef]
- Perry, A.E.; Schofield, W.H.; Joubert, P.N. Rough wall turbulent boundary layers. J. Fluid Mech. 1969, 37, 383–413. [Google Scholar] [CrossRef]
- Millikan, C.B. A critical discussion of turbulent flow in channels and circular tubes. In Proceedings of the Fifth International Congress for Applied Mechanics, Cambridge, MA, USA, 12–16 September 1938; Den Hartog, J.P., Peter, H., Eds.; Wiley: New York, NY, USA, 1938; pp. 386–392. [Google Scholar]
- Jackson, P.S. On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 1981, 111, 15–25. [Google Scholar] [CrossRef]
- Bridge, J.S.; Jarvis, J. The dynamics of a river bend: A study in flow and sedimentary processes. Sedimentology 1982, 29, 499–541. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; Brookfiel, Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Ferguson, R.I.; Prestegaard, K.L.; Ashworth, P.J. Influence of sand on hydraulics and gravel transport in a braided gravel bed river. Water Resour. Res. 1989, 5, 635–643. [Google Scholar] [CrossRef]
- Stephan, U.; Gutknecht, D. Hydraulic resistance of submerged flexible vegetation. J. Hydrol. 2002, 269, 27–43. [Google Scholar] [CrossRef]
- Klopstra, D.; Barneveld, H.J.; van Noortwijk, J.M.V.; van Velzen, E.H. Analytical model for hydraulic roughness of submerged vegetation. In Managing Water: Coping with Scarcity and Abundance, Proceedings of the 27th Congress of the International Association for Hydraulic Research, San Francisco, CA, USA, 10–15 August 1997.
- Bandyopadhyay, P.R. Rough-wall turbulent boundary layers in the transition regime. J. Fluid Mech. 1987, 180, 231–266. [Google Scholar] [CrossRef]
- Lo, K.L. On the determination of zero-plane displacement and roughness length for flow over forest canopies. Bound. Layer Meteorol. 1990, 51, 255–268. [Google Scholar] [CrossRef]
- Molion, L.C.B.; Moore, C.J. Estimating the zero-plane displacement for tall vegetation using a mass conservation method. Bound. Layer Meteorol. 1983, 26, 115–125. [Google Scholar] [CrossRef]
- Bergeron, N.E.; Abrahams, A.D. Estimating shear velocity and roughness length from velocity profiles. Water Resour. Res. 1992, 28, 2155–2158. [Google Scholar] [CrossRef]
- Yu, G.L.; Tan, S. Errors in the bed shear stress as estimated from vertical velocity profile. J. Irrig. Drain. Eng. 2006, 132, 490–497. [Google Scholar] [CrossRef]
- Bergstrom, D.J.; Kotey, N.A.; Tachie, M.F. The effects of surface roughness on the mean velocity profile in a turbulent boundary layer. J. Fluids Eng. 2002, 124, 664–670. [Google Scholar] [CrossRef]
- Avelino, M.R.; Freire, A.P.S. On the displacement in origin for turbulent boundary layers subjected to sudden changes in wall temperature and roughness. Int. J. Heat Mass Trans. 2002, 45, 3143–3153. [Google Scholar] [CrossRef]
- Chanson, H. The Hydraulics of Stepped Chutes and Spillways; Balkema Publisher: Lisse, The Netherlands, 2002. [Google Scholar]
- Boes, R.M.; Hager, W.H. Two-phase flow characteristics of stepped spillways. J. Hydraul. Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Hydraulic design of stepped spillways. J. Hydraul. Eng. 2003, 129, 671–679. [Google Scholar] [CrossRef]
- Chanson, H.; Toombes, L. Strong interactions between free-surface aeration and turbulence in an open channel flow. Exp. Therm. Fluid Sci. 2003, 27, 525–535. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y.; Takahashi, M. Flow characteristics of skimming flows in stepped channels. J. Hydraul. Eng. 2004, 130, 860–869. [Google Scholar] [CrossRef]
- Gonzalez, C.A.; Takahashi, M.; Chanson, H. An experimental study of effects of step roughness in skimming flows on stepped chutes. J. Hydraul. Res. 2008, 46, 24–35. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Meireles, I.; Matos, J. Laboratory measurements and multi-block numerical simulations of the mean flow and turbulence in the non-aerated skimming flow region of steep stepped spillways. Environ. Fluid Mech. 2011, 11, 263–288. [Google Scholar] [CrossRef]
- Tabbara, M.; Chatila, J.; Awwad, R. Computational simulation of flow over stepped spillways. Comput. Struct. 2005, 83, 2215–2224. [Google Scholar] [CrossRef]
- Carvalho, R.F.; Martins, R. Stepped spillway with hydraulic jumps: Application of a numerical model to a scale model of a conceptual prototype. J. Hydraul. Eng. 2009, 135, 615–619. [Google Scholar] [CrossRef]
- Musavi-Jahromi, H.; Bina, M.; Salmasi, F. Physical and numerical modeling of the Nappe flow in the stepped spillways. J. Appl. Sci. 2008, 8, 1720–1725. [Google Scholar] [CrossRef]
- Tongkratoke, A.; Chinnarasri, C.; Pornprommin, A.; Dechaumphai, P.; Juntasaro, V. Non-linear turbulence models for multiphase recirculating free-surface flow over stepped spillways. Int. J. Comput. Fluid Dyn. 2009, 23, 401–409. [Google Scholar] [CrossRef]
- Chen, Q. Turbulence Numerical Simulation and Model Test of the Stepped Spillway Overflow. Ph.D. Thesis, Sichuan University, Chengdu, China, 2001. [Google Scholar]
- Cheng, X.J.; Luo, L.; Zhao, W.Q.; Li, R. Two-phase flow simulation of aeration on stepped spillway. Prog. Nat. Sci. 2004, 14, 626–630. [Google Scholar] [CrossRef]
- Qian, Z.D.; Hu, X.Q.; Huai, W.X.; Amador, A. Numerical simulation and analysis of water flow over stepped spillway. Sci. China Ser. E Technol. Sci. 2009, 52, 1958–1965. [Google Scholar] [CrossRef]
- André, S.; Dewals, B.J.; Pirotton, M.; Schleiss, A. Quasi 2D-numerical model of aerated flow over stepped chutes. In Proceedings of the 30th International Association for Hydro-Environment Engineering and Research (IAHR) Congress, Thessaloniki, Greece, 24–29 August 2003; Ganoulis, J., Prinos, P., Eds.; IAHR: Thessaloniki, Greece; Volume D, pp. 671–678.
- Dewals, B.J.; André, S.; Schleiss, A.; Pirotton, M. Validation of a quasi-2D model for aerated flows over stepped spillways for mild and steep slopes. In Proceedings of the 6th International Conference of Hydroinformatics, Singapore, 21–24 June 2004; pp. 63–70.
- Fluent User’s Guide. Fluent Incorporated: Lebanon, NH, USA, 2006. Available online: http://www.ansys.com/Products/Simulation+Technology/Fluid+Dynamics/Fluid+Dynamics+Products/ANSYS+Fluent (accessed on 20 September 2014).
- Bijan, D. Experimental study and 3D numerical simulations for a free-overflow spillway. J. Hydraul. Eng. 2006, 132, 899–907. [Google Scholar] [CrossRef]
- Lueker, M.L.; Mohseni, O.; Gulliver, J.S.; Schulz, H.; Christopher, R.A. The Physical Model Study of the Folsom Dam Auxiliary Spillway System; Project Report 511; University of Minnesota, St. Anthony Falls Laboratory: Minneapolis, MI, USA, 2008. [Google Scholar]
- Hunt, S.L.; Kadavy, K.C. Velocities and energy dissipation on a flat-sloped stepped spillway. In Proceedings of the 2008 American Society of Agricultural and Biological Engineers (ASABE) Annual International Meeting, Providence, RI, USA, 29 June–2 July 2008.
- Kiya, M.; Sasaki, K.; Arie, M. Discrete-vortex simulation of a turbulent separation bubble. J. Fluid Mech. 1982, 120, 219–244. [Google Scholar] [CrossRef]
- Carosi, G.; Chanson, H. Air-Water Time and Length Scales in Skimming Flows on a Stepped Spillway, Application to the Spray Characterization; Report CH 59/06; The University of Queensland: Brisbane, Australia, 2006. [Google Scholar]
- Felder, S.; Chanson, H. Turbulence and Turbulent Length and Time Scales in Skimming Flows on a Stepped Spillway, Dynamic Similarity, Physical Modeling and Scale Effects; Report CH64/07; The University of Queensland: Brisbane, Australia, 2007. [Google Scholar]
- Charnock, H. Wind stress on a water surface. Q. J. R. Meteorol. Soc. 1955, 81, 639–640. [Google Scholar] [CrossRef]
- Counihan, J. Wind tunnel determination of the roughness length as a function of the fetch and the roughness density of three dimensional elements. Atmos. Environ. 1971, 5, 637–642. [Google Scholar] [CrossRef]
- Lee, B.E.; Soliman, B.F. An investigation of the forces on three-dimensional bluff bodies in rough wall turbulent boundary layers. Trans. ASME J. Fluids Eng. 1977, 99, 503–510. [Google Scholar] [CrossRef]
- O’Loughlin, E.M.; Annambhotla, V.S. Flow phenomena near rough boundaries. J. Hydraul. Res. 1969, 7, 231–250. [Google Scholar] [CrossRef]
- Blihco, R.G.; Partheniades, E. Turbulence characteristics in free surface flows over smooth and rough boundaries. J. Hydraul. Res. 1971, 9, 43–69. [Google Scholar] [CrossRef]
- Thom, A.S. Momentum absorption by vegetation. Q. J. Roy. Meteorol. Soc. 1971, 97, 414–428. [Google Scholar] [CrossRef]
- Nepf, H.M.; Vivoni, E.R. Flow structure in depth-limited, vegetated flow. J. Geophys. Res. 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Whiting, P.J.; Dietrich, W.E. The roughness of alluvial surfaces and experimental examination of the influence of size heterogeneity and natural packing. EOS Trans. Am. Geophys. Union 1989, 70, 329. [Google Scholar]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History, and Applications; Kluwer Academic: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Chamberlain, A.C. Roughness length of sea, sand, and snow. Bound. Layer Meteorol. 1983, 25, 405–409. [Google Scholar] [CrossRef]
- Keller, R.J.; Rastogi, A.K. Design chart for predicting critical point on spillways. J. Hydraul. Div. 1977, 103, 1417–1429. [Google Scholar]
- Bauer, W.J. Turbulent boundary layer on steep slopes. Trans. Am. Soc. Civ. Eng. 1954, 119, 1212–1233. [Google Scholar]
- Keller, R.J.; Lai, K.K.; Wood, I.R. Developing region in self aerating flows. Proc. ASCE J. Hyd. Div. 1974, 100, 553–568. [Google Scholar]
- Chanson, H. Hydraulics of skimming flows over stepped channels and spillways. J. Hydraul. Res. 1994, 32, 445–460. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C. Inception point relationship for flat-sloped stepped spillways. J. Hydraul. Eng. 2011, 137, 262–266. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C. Inception point for embankment dam stepped spillways. J. Hydraul. Eng. 2013, 139, 60–64. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.; Gulliver, J.S.; Zhu, D. Application of Displacement Height and Surface Roughness Length to Determination Boundary Layer Development Length over Stepped Spillway. Water 2014, 6, 3888-3912. https://doi.org/10.3390/w6123888
Cheng X, Gulliver JS, Zhu D. Application of Displacement Height and Surface Roughness Length to Determination Boundary Layer Development Length over Stepped Spillway. Water. 2014; 6(12):3888-3912. https://doi.org/10.3390/w6123888
Chicago/Turabian StyleCheng, Xiangju, John S. Gulliver, and Dantong Zhu. 2014. "Application of Displacement Height and Surface Roughness Length to Determination Boundary Layer Development Length over Stepped Spillway" Water 6, no. 12: 3888-3912. https://doi.org/10.3390/w6123888
APA StyleCheng, X., Gulliver, J. S., & Zhu, D. (2014). Application of Displacement Height and Surface Roughness Length to Determination Boundary Layer Development Length over Stepped Spillway. Water, 6(12), 3888-3912. https://doi.org/10.3390/w6123888




