The “Puzzle” of Water Behavior at Low Temperature

Abstract

Thermodynamic and transport properties of liquid water are not fully understood despite a large amount of research work both experimental and theoretical. The maximum of density and the enhanced anomalies observed at low temperatures are at the origin of several models that, in some cases, predict specific and unique behavior such as spinodal lines or critical points. We show that a careful analysis of the neutron quasi-elastic scattering data, both the incoherent spectra and the dynamic of the partials, is compatible with a polymer-like model, where the hydrogen bond dynamics explains the behavior of water in the non-accessible temperature region extending from −30° C to the glass transition.

1. Introduction

Apart from a few exceptions, water is the only liquid on the surface of Earth. The total amount of water is of the order of 1.3 × 10⁹ km³, mostly in liquid state but naturally present in all the three states, and transitions between them play a major role in everyday life, in the weather stability and in the “water cycle” allowing the specificity of the physical conditions compatible with the existence of life.

These reasons, among many others, have generated since the Antiquity a unique interest in water, particularly in its liquid state. Firstly it was seen as one of the four or five “elements” of the Universe, later like a “simple” substance, and only at the end of the 18th century it was demonstrated (by A. Lavoisier and H. Cavendish) that the water molecule is formed by one atom of oxygen and two atoms of hydrogen strongly attached by covalent bounds.

With the rapid development of experimental techniques and the advent of industrial demand, the properties of water have been systematically measured and analyzed. As a consequence, water is, by far, the substance better known, at least in the sense that essentially all the properties have been measured with high accuracy [1].

In spite of such a huge amount of information, some fundamental aspects of the physics of water remain object of a few debates, not completely academic. This short paper will focus on one of them, the behavior of liquid water at temperatures and/or pressures where the stable state is solid: supercooled water.

2. The Puzzle of Supercooled Water

Like many other liquids, liquid water can be cooled below 0 °C, at atmospheric pressure, without immediate formation of the stable crystalline phase, the hexagonal form I_h of ice. This situation is even relatively frequent because, if the liquid doesn’t contain nucleation sites, its freezing takes place at temperatures lower than the melting point [2].

This short description of supercooled water needs two additional remarks:

(a)

The degree of supercooling of molecular liquids is very diverse and measured by the difference between the melting temperature T_m and the homogeneous nucleation temperature T_H, normalized by T_m. The ratio (T_m − T_H)/T_m is often of the order of 1/3, while its value for liquid water is 0.15 (T_H = −42 °C) [3].

(b)

Water that does not freeze (does not form a crystal) is very common under different forms of confinement, for example in rocks. This is due to a different structure at the vicinity of the walls, which is thermodynamically stable [4]. We will not speak about this very rich variety of situations but only about “bulk” water.

To say it in the shortest way, the interest for supercooled H₂O is explained by the well known density maximum at 4 °C (11 °C for D₂O, a remarkable and unusual isotopic effect) and associated low density of crystalline ice (the common form I_h). Indeed, a general theory predicts that the specific volume of a substance (solid or liquid) decreases under decreasing temperature. This is generally observed except for alloys or mixtures where changes of coordination explain different behaviors. In the case of liquid water, a complete knowledge of the mechanisms explaining the density maximum is always an object of debate and is directly related to a better knowledge of hydrogen bonds.

What is even more striking in the case of water is that the increase of the specific volume observed below 0 °C is larger at lower temperatures, similar to the behavior of thermodynamic properties at the vicinity of demixtion, spinodals and other critical phenomena. However, in contrast with such situations, the domain of observation of supercooled water is very small: 4 °C in stable conditions, −20 °C to −30 °C in the supercooled domain. This is because at −30 °C the probability of homogeneous nucleation is so high that only microscopic samples can remain liquid, moreover for extremely short times, not compatible with the conditions of an experiment. Consequently, many (if not all) properties of supercooled water have been measured down to −25 °C, in some cases −30 °C, while T_H = −42 °C, as mentioned above.

It is worth noting that in 1976, the apparent criticality of water behavior was the object of an interesting speculative analysis yielding, by extrapolation, a temperature T_s = −45 °C at which all the data apparently would diverge [5]. This behavior is associated with the existence of a “low temperature spinodal line” eventually a counterpart of the real spinodal at high temperature. It is worth noticing that T_s is only 3 °C below T_H and that T_H decreases under applied pressure following (with a stronger dependence) the line of coexisting ice I_h-liquid water [3].

Similar to for other liquids, it is possible to quench water from room temperature to the temperature of liquid nitrogen (77 K) and to obtain a glassy form (now called LDA or low density amorphous ice) [6,7] with a structure similar to that of deeply supercooled water. Finally, an important discovery was made in 1985: the compression of crystalline ice at 77 K generates a total new amorphous state (HDA or high density amorphous ice) with a density almost 30% larger than that of LDA [8,9,10].

The transitions between LDA and HDA forms have been the object of many experiments and controversies, particularly the possible existence of intermediate states. To summarize a complex situation, the transitions are certainly associated with latent heats like in any first order transition. However, they are not reversible: the transition is made from LDA to HDA by compression and from HDA to LDA upon heating. The metastability of both forms is—like for all glasses—related to a frozen dynamics (the temperature T_g of the glass transition of water is 135 K). Today, other denser forms of amorphous ices are known, denoting a very rich polyamorphism [11].

The puzzling problem of supercooled water, the difficulty of the experiments with metastable samples and the development of several “effective potentials” derived for liquid water is at the origin of a parallel research almost totally based on the extrapolation of these potentials to temperatures at the vicinity of T_g. Such studies can give a lot of detailed information when interpreted correctly and within the context of the large amount of available experimental data. However, they suffer from a natural limitation related to the appropriate description of the inter-molecular hydrogen bonds, which play the major role at low temperature. Very schematically, the water molecule, its electronic cloud, even its polarizability, are very close to a perfect sphere, while bonds are formed in well defined directions, forming tetrahedral angles between them. Effective potentials reverse the situation and reproduce the water behavior with a highly asymmetric molecule interacting with its neighbors by spherical (Coulombic) potentials. Concretely, a molecule is represented by an assembly of three to five charges, sometimes an additional dipole, forcing the tetrahedral angle. In contrast, the potentials are spherical and of different nature due to charges of different signs and magnitudes. Despite this ad hoc representation of a more complex reality, the optimization of the parameters done by more than 50 potentials results in a reasonable qualitative description of the thermodynamic properties of water as well as of its structure [12]. However, some potentials optimize the agreement with the atomic structure and reproduce poorly the low temperature properties of water while others reproduce better such properties but with too much of a “solid like” structure. In other words, thermodynamic data such as the position of the maximum of density in the pressure, temperature (P, T) phase diagram, or the reproduction of the pair correlation function and its partials are never satisfied simultaneously [13,14]. Obviously, the parameters of extrapolations to very low temperatures, in regions where experiments are not possible—as pointed out above—cannot be optimized and must be seen with caution.

One astonishing result of such extrapolations is the possible existence of one, two or several critical points at low temperature and different pressures, including negative pressures. This behavior was associated to the two better known polymorphs LDA and HDA. The extrapolation of the curve drawn in a (P, T) diagram separating LDA and HDA could be extended to temperatures above T_g, i.e., in a non-accessible liquid state with a critical end point. In such case, the small water “anomalies” observed between room temperature and −25 °C would be explained by the vicinity of the postulated critical point [15].

This possible explanation of the anomalies of the thermodynamic properties of liquid water highlights a series of problems not solved, namely, the fact that the quenching of the liquid generates always pure LDA and not a mixture of the two (or more) amorphous states. Also, in some cases, it was postulated that in the region beyond the possible critical point, the structure of water would be that of a mixture of two liquids. These interpretations have been ruled out by experiments [16,17].

However, based on such a context of “mixture models”, the self dynamics of water molecules has been interpreted sometimes as a superposition of several processes with a distribution of relaxation times. Formally, this picture is similar to that of a very viscous liquid for which the coupling of viscosity and diffusion generates a global relaxation, described mathematically by the Kohlrausch equation or stretched exponentials. Concretely, a time-dependent property is described by an equation like:

$$I\left(t\right)=A\exp \left[-{\left(\frac{t}{\tau }\right)}^{\beta }\right]$$

where A is a constant, τ is a characteristic time and 0 < β < 1, an exponent that yields the single time relaxation for β = 1. Within this formalism the average relaxation time <τ> is given by <τ> = (τ/β) Г (1/β), where Г is the gamma function [18].

3. The Contribution of Neutron Scattering

Quasi-elastic incoherent neutron scattering (QENS) is particularly well adapted to the study of the self dynamics of water. This is because the very large incoherent cross section of hydrogen nuclei results in an almost unique contribution to the neutron intensity scattered by a hydrogenated sample such as H₂O. In a QENS experiment, one measures the function S(Q,ω) where Q and ω are, respectively, the momentum and energy exchange between the incident neutrons and the sample. It is simply related to the space and time Fourier transform of the function ${\displaystyle \sum }〈\overrightarrow{r_i}\left(0\right)\overrightarrow{r_i}\left(t\right)〉$, where $\overrightarrow{r_i}\left(t\right)$ represents the position of the ith hydrogen atom at time t. Clearly this function, and S(Q,ω), contain intramolecular contributions (called generally “rotations”) and the translational molecular diffusion. Also, in case of aggregation, the presence of some form of clustering, confinement or within the framework of Mode Coupling Theory for very viscous liquids, one may expect several relaxation processes. However, in the case of water at the temperatures accessible to experiment, one may accept a general description with two terms, one due to the motions of hydrogen atoms around the oxygens, another due to the self-diffusion, which can be compared to measurements obtained by other techniques sampling larger spatial domains, such as NMR or tracer methods. This methodology was indeed applied with success to supercooled water, yielding important information about the displacement of hydrogen atoms in the molecule, such large amplitude librations which are certainly the main mechanism for the hydrogen bond breaking taking place over timescales of the order of 1 ps. A remarkable feature of this analysis is that the characteristic time of these “hindered rotations” shows an Arrhenius temperature dependence on temperature and the associated activation energy is, as expected, that of the hydrogen bond [19,20].

The same or similar experiments can be described as well within a more elegant and simplified picture, using stretched exponentials, as emphasized above. This is because, if the two characteristic times of two relaxation processes are not very different, the fitting procedure works as well with a distribution of times [13]. Such an option corresponds to a molecular view for which the molecule is seen as a whole in agreement with the option of a rigid molecule adopted by many, if not all simulations.

Actually, at temperatures low enough, say below −10 °C, the two characteristic times are sufficiently different to avoid a description with a stretched exponential. However, most of the data are restricted to the stable domain of liquid water. In this temperature domain, the two processes have naturally very similar relaxation times because the average number of intact bonds between molecules remains relatively small. Instead, at lower temperatures, even more because of the anomalous temperature dependence of self diffusion, the two times are clearly separated. At −20 °C the ratio of the two times is of the order of 20 [21].

Still, the separation of two relaxation processes from a central line remains naturally an ambiguous procedure. On another hand, the importance of an Arrhenius temperature dependent hydrogen bond lifetime is a main ingredient for a possible interpretation of the low temperature properties of liquid water.

Because of this, a slightly more complex experiment was performed some years ago. Instead of H₂O, a sample of D₂O was used, meaning that the measured S(Q,ω) is the weighed contribution of three pair correlation functions (called partials) that correspond to the pairs OO, DD and OD. A convenient choice of the Q values of the measurements performed both in a triple-axis and a spin-echo spectrometer gives specific information about the dynamics of the pair DD essentially dominated by the hydrogen bond dynamics. In this way, it was possible to demonstrate that the separation of the incoherent S(Q,ω) into two components was based in a real physical background and was not one fitting procedure among others [22].

The purpose of this experiment was to confirm precedent results obtained both by depolarized light scattering [23,24] and by QENS [19,20], showing that the hydrogen bond dynamics has an Arrhenius temperature dependence.

4. Discussion

Within the context of the extrapolation of data (or molecular dynamics simulation) until T_g, it is possible to propose an interpretation based on the two measured relaxation processes.

The “residence time” that is extracted from the diffusion component of S(Q,ω) follows, as expected, the temperature dependence of other transport properties, such as shear viscosity. It is strongly non Arrhenius and, as pointed out above, it diverges apparently around T_s. Instead, the relaxation time extracted from the rotational component depicts a slow, Arrhenius temperature dependence, which demonstrates that, at the level of the hydrogen bonds, there is no anomaly. Actually, the anomalies of the properties of water are due to the increase of the density of intermolecular bonds with decreasing temperature.

The similar values of T_s and T_H constitute a hint for the understanding of the apparent divergence. The very directional bonds formed between molecules generate local arrangements very close to those of ice, as far as the oxygen positions are concerned, meaning that around −30 °C, the freezing in crystalline ice is very easy, implying essentially rotational motions. This explains why T_H is so high as compared with other liquids. Instead, the formation of LDA implies also the freezing of hydrogen bond dynamics, which remains extremely rapid even at T_H, because of its very small temperature dependence. Only a quenching below T_g allows, by definition, the formation of LDA, incidentally accompanied by a small latent heat (see Figure 1).

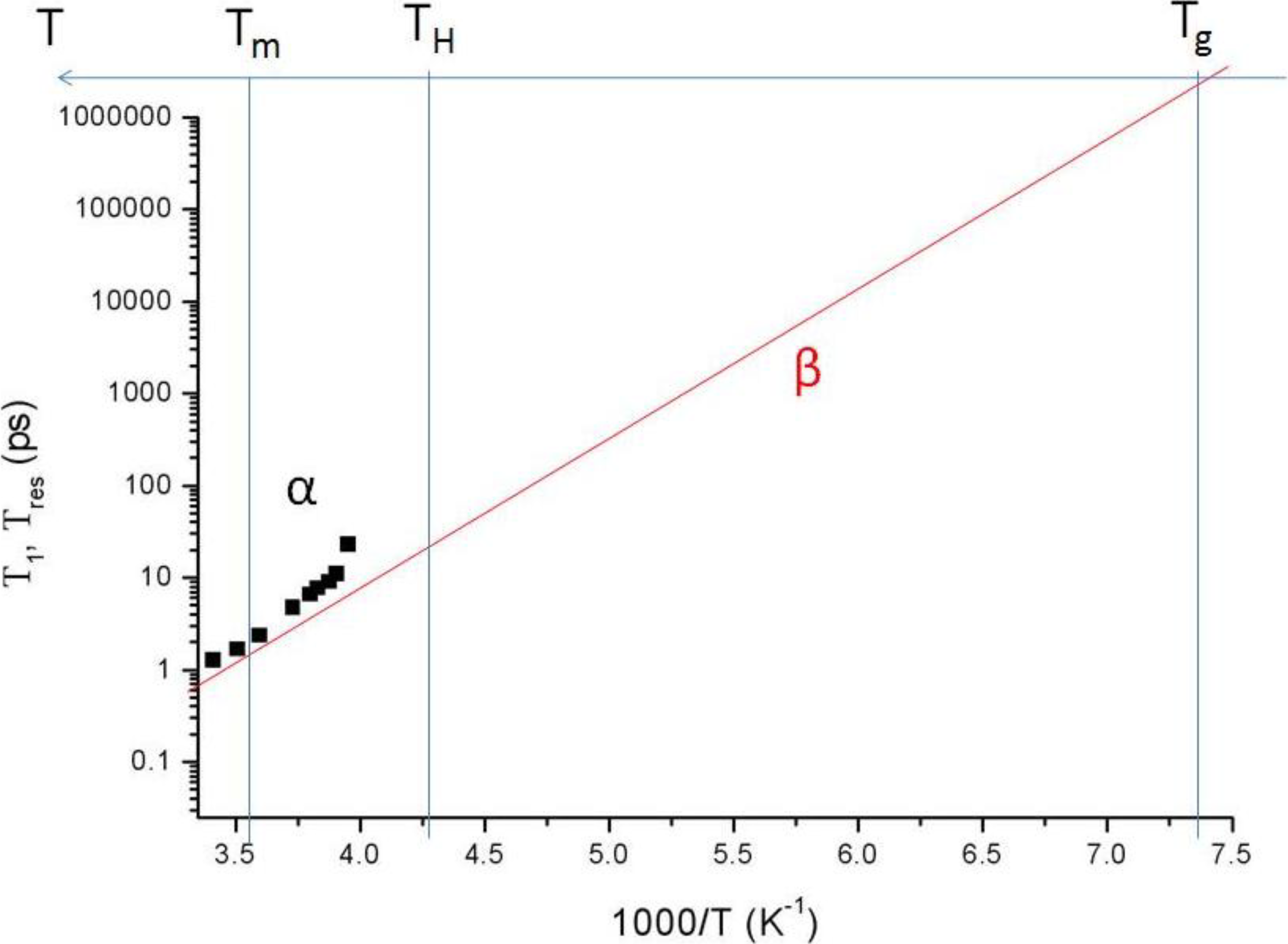
Figure 1. Schematic Arrhenius representation of some dynamic processes in supercooled water. The α line represents the strongly non Arrhenius behavior of the transport properties of water. Squares are residence times, T_res, obtained from neutron scattering experiments at temperatures above −20 °C [19,20,22]. The solid line represents β processes, in this case, the dynamics of hydrogen bond dynamics which follow an Arrhenius temperature dependence. Above −20 °C this characteristic time, T₁, is obtained from the same experimental results. T_m, T_H and T_g are the temperatures of melting, homogeneous nucleation and glass transition, respectively.

Figure 1. Schematic Arrhenius representation of some dynamic processes in supercooled water. The α line represents the strongly non Arrhenius behavior of the transport properties of water. Squares are residence times, T_res, obtained from neutron scattering experiments at temperatures above −20 °C [19,20,22]. The solid line represents β processes, in this case, the dynamics of hydrogen bond dynamics which follow an Arrhenius temperature dependence. Above −20 °C this characteristic time, T₁, is obtained from the same experimental results. T_m, T_H and T_g are the temperatures of melting, homogeneous nucleation and glass transition, respectively.

At room and higher temperatures, the dynamics of translation and rotation take place with the same characteristic time due to a relatively small number of intermolecular bonds. At lower temperatures, the extension of the network of hydrogen bonds drastically limits translational diffusion resulting in a strongly non-Arrhenius dependence of all the transport properties of supercooled water, namely shear viscosity. As explained above, a molecular view can describe this situation by stretched exponentials, as in the Mode Coupling Theory (MCT) derived for very viscous liquids, although loosing the physical meaning of some parameters of MCT. This is because the increasing difference between rotational and diffusion times with decreasing temperature is compatible with phenomenological models where a distribution of times is assumed.

The two relaxation processes are similar to those observed in polymers and called α and β, the first associated with the dynamics of the backbone, the second with that of side chains [25]. At T_g, the transport properties of a polymer are frozen and, macroscopically, it behaves like a solid, despite the motion of side chains that can be measured by appropriate techniques, including neutron scattering. In the case of water, the equivalent β process is that of the hydrogen bonds and the α process is that of the translational dynamics of the water molecules. The crucial difference is that, in the case of water, the β process avoids the macroscopic freezing of the system and T_g is associated with the freezing of the β hydrogen bond dynamics and not with the α molecular diffusion.

The analogy concerns only the microscopic dynamics, more specifically, the coexistence of two times with totally different temperature dependences. In the case of some polymers, side chains show an Arrhenius temperature dependence without important relation to macroscopic properties, namely visco-elastic properties. In the case of water, the dynamics of hydrogen bonds is Arrhenius, as shown by QENS, but the formation of an extended network of intermolecular bonds limits drastically molecular diffusion. With decreasing temperature, the formation of a large number of bonds together with the high directionality of the potential generate a local structure that, a few degrees above T_H, is already similar to that of LDH [26]. This means that within the large temperature domain from T_H to T_g, during a quenching process, only minor molecular arrangements take place. However, the glass transition is not possible because homogeneous nucleation prevails. At the vicinity of T_H, the nucleation rate becomes faster than any relaxation time. As a consequence, it is possible to predict that thermodynamic and transport properties cannot change substantially with temperature in between T_H and T_g as they do not depend directly on the dynamics of the bonds. Also, all the apparent divergences observed around −20 °C must be followed by maxima or minima without particular significance.

The analogy with polymers applies to the anomalous temperature dependence of transport properties, either at the vicinity of T_g for the polymers or at the vicinity of T_H for water. However, the microscopic relaxation time (β relaxation), i.e., motions of side chains in the case of polymers or hydrogen dynamics in the case of water, has very different consequences. In the case of water, it generates the nucleation of ice, because rotations of small amplitude are sufficient to form the crystal, while in polymers the β relaxation has no consequences on the macroscopic properties.

Consequently, the temperature dependence of transport properties of water is similar to that observed in many fragile liquids at the vicinity of a glass transition. In this sense, the behavior of supercooled water at the vicinity of the homogeneous nucleation temperature T_H can be described as a fragile-strong transition, although such a description remains purely phenomenological.

Although speculative and based on inevitable extrapolations, this mechanism appears totally compatible with existing experimental data and useful for the understanding of water behavior in more complex situations.