Research on Mechanical Characteristics of Multi-Stage Centrifugal Pump Rotor Based on Fluid–Structure Interaction

Abstract

This study investigates the mechanical characteristics of a multi-stage centrifugal pump rotor through fluid–structure interaction (FSI) analysis. A two-stage centrifugal pump equipped with back vanes on the trailing impeller is selected as the research object. Numerical simulations are performed based on the continuity equation and Reynolds-averaged Navier–Stokes (RANS) equations, with experimental data utilized to validate the numerical model’s accuracy. The internal flow field mechanisms are analyzed, and the effectiveness of two axial force calculation methods—formula-based and numerical simulation-based—for the rotor system is comprehensively evaluated. Employing an FSI-based modal analysis approach, the governing differential equations of motion are established and decoupled via Laplace transformation to introduce modal coordinates. Modal analysis of the pump rotor system is conducted, revealing the first six natural frequencies and corresponding vibration modes, along with critical speed calculations. The findings demonstrate that when the flow field near the back vanes exhibits complex characteristics, the formula-based axial force calculation shows reduced accuracy. In contrast, without back vanes, the hydraulic motion in the impeller rear chamber remains relatively stable, resulting in higher accuracy for formula-based axial force predictions. The calculation error between the two conditions (with/without back vanes) reaches 27.6%. Based on vibration mode characteristics and critical speed analysis, the pump is confirmed to operate within a safe region. The rotor system exhibits two similar adjacent natural frequencies differing by less than 1 Hz, with perpendicular vibration mode directions. Additionally, rotational speed fluctuations in the rotor system induce alternating critical speed phenomena when operating in this region. This study establishes a coupled analysis framework of “flow field stability–axial force calculation accuracy–rotor dynamic response”, quantifies the axial force calculation error patterns under different flow field conditions of a special pump type, supplements the basic data on axial force calculation accuracy for complex structure centrifugal pumps, and provides new theoretical insights and reference benchmarks for the study of hydraulic–mechanical coupling characteristics of similar fluid machinery. In engineering applications, it avoids over-design or under-design of thrust bearings to reduce manufacturing costs and operational risks. The revealed rotor modal characteristics, critical speed distribution, and frequency alternation phenomena can provide direct technical support for the optimization of operating parameters, vibration control, and structural improvement of pump units in industrial scenarios, thereby reducing rotor imbalance, bearing wear, and other failures.

1. Introduction

As an efficient fluid conveying equipment, the multi-stage centrifugal pump has been widely applied in various fields due to its compact design and excellent head performance. The rotor system of the multi-stage centrifugal pump operates under complex force conditions, which has become one of the main factors affecting the stable operation of the multi-stage pump [1,2,3,4,5].

Shi Lürui et al. [6] conducted in-depth research on the axial force balancing device of large vertical multi-stage pumps and concluded that the axial force of the multi-stage pump and the thrust of the balancing device have an inverse relationship with the flow rate. Li Rennian et al. [7] focused on the mechanism of back blades on the axial force of spiral centrifugal pumps and found that there exists an optimal solution for the number and width of back blades to balance the axial force. Liu Zailun et al. [8] revealed the specific mechanism of back blade parameters on pump performance, liquid pressure distribution in the pump cavity, and axial force by adjusting the width and number of back blades. Zou Pinwen et al. [9] proposed an innovative technology for measuring the impeller axial force during the operation of fuel centrifugal pumps, which can accurately calculate the magnitude of the impeller axial force. Pan Huishan et al. [10] established the physical model and finite element model of the water-lubricated bearing–rotor coupling system. The research results show that the rotor of the seawater de-salination hydraulic turbine booster pump is a rigid rotor; when unbalanced mass excitation is applied to both the turbine impeller and the booster pump impeller simultaneously, the transient response of the turbine end is more obvious and the vibration displacement amplitude is larger compared with the pump end. Teng Xibin et al. [11] studied a domestic 300 MW pump-turbine unit, explored the rotor dynamic characteristics, verified the safety performance between rotors, and provided model support for the analysis of rotors and other dynamics. Liu Baoguo et al. [12] presented the first and second-order perturbation identification results of the reinforcing effect of hot-fitted impellers and shaft sleeves on the rotor stiffness of feedwater pumps, and obtained a modified dynamic calculation model of the feedwater pump rotor system. Zhang Guoyuan et al. [13] realized the four-level functional requirement domain de-composition and design parameter domain mapping for the dynamic design of high-speed turbopumps, obtained a flowchart of the turbopump rotor dynamic design sequence based on multi-source information coupling through the matrix, and completed the dynamic design of a certain turbopump rotor. Arijit et al. [14] studied cast iron ignition engines, calculated the equivalent stress and mode of the rotor system, respectively, compared the calculation results of different materials, and selected the optimal material. Srivastava et al. [15] designed mixed-flow pump impeller blades with two different blade positions in the meridional annular region, and evaluated the stress development of the pump blades using finite element analysis. Ajinkya et al. [16] performed modal analysis of the spiral agitator and agitator arm assembly under the required operating conditions, and optimized the operating speed range. Cao et al. [17] carried out computational aero acoustic fluid–structure interaction and verified the feasibility of the method; the effect of fluid in the band gap and seal is considerable, and the research results are helpful to avoid typical resonant frequencies in design. Huang et al. [18] proposed a simplified method for the blade correction model based on the principle that the mass and moment of inertia remain basically unchanged before and after simplification. Additionally, other scholars have conducted research on the dynamic and static mechanical problems of rotor structures [19,20,21,22].

In this paper, the axial force of a two-stage centrifugal pump with back blades on the final-stage impeller is calculated. The assembly drawing of the two-stage centrifugal pump is shown in Figure 1. The pump parameters are as follows: flow rate Q = 50 m³/h, head H = 450 m, rated speed n = 2800 rpm, outlet setting angle β₂ = 10°, and the final-stage impeller is equipped with back blades. The impeller diameter of the pump is 395 mm. The pump shaft is made of 45# steel, with an elastic modulus E = 2.09 × 10¹¹ Pa, Poisson’s ratio μ = 0.3, density ρ = 7890 kg/m³, shear modulus 8.32 × 10¹⁰ N/m², yield strength 3.55 × 10⁸ N/m², and tensile strength 6.00 × 10⁸ N/m². The impeller is made of QT600-3, with an elastic modulus E = 1.60 × 10¹¹ Pa, Poisson’s ratio μ = 0.286, density ρ = 7120 kg/m³, shear modulus 6.56 × 10¹⁰ N/m², yield strength 3.70 × 10⁸ N/m², and tensile strength 6.00 × 10⁸ N/m².

2. Numerical Simulation

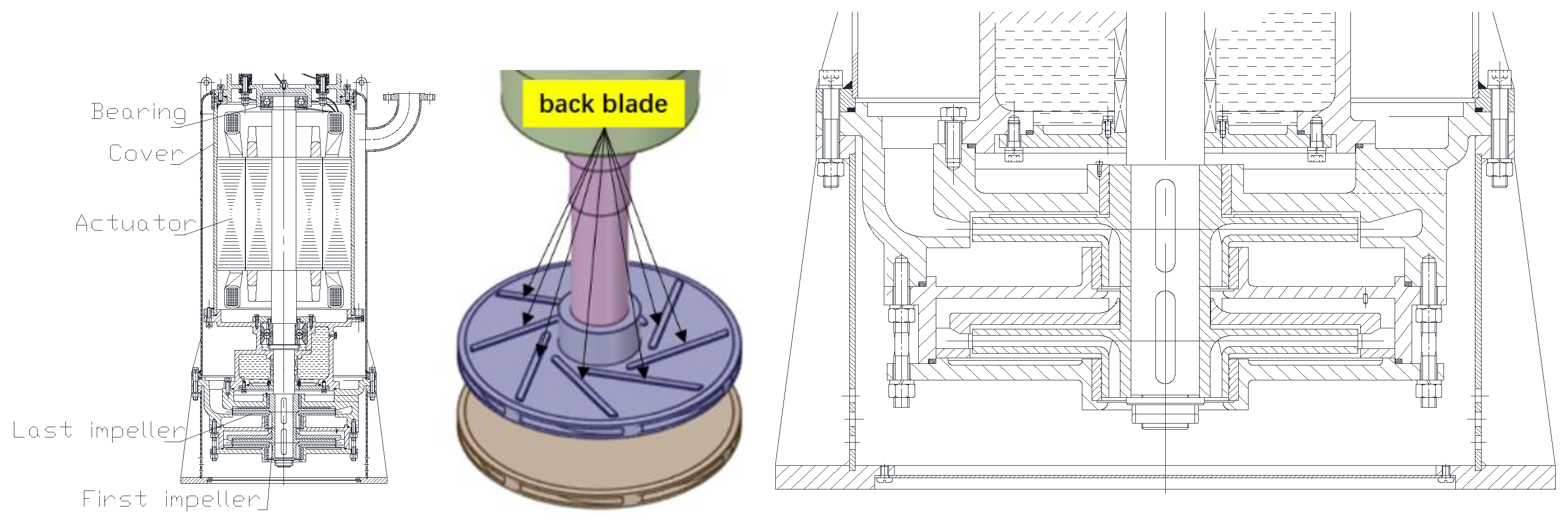
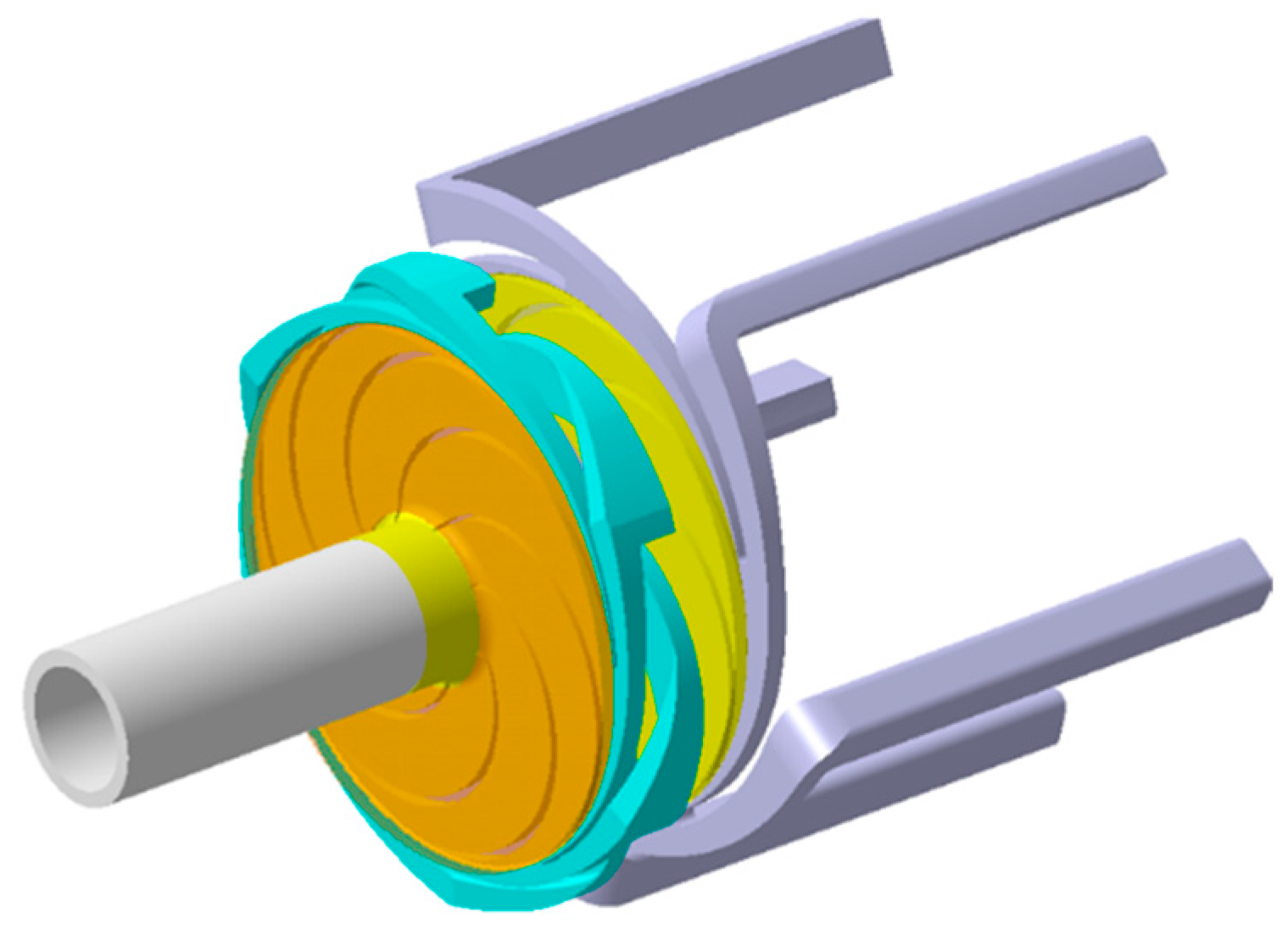
2.1. Computational Modeling

Figure 2 illustrates the water body model within the flow passage components. To ensure the flow stability of the water body at the inlet and outlet ports, extended segments are appended to the water bodies of the inlet section and outlet section, respectively [23]. The medium is clear water at 20 °C, with a density of 998 kg/m³ and a dynamic viscosity of 1.003 × 10⁻³ Pa·s. Initial pressure: The entire water body area is initially set to standard atmospheric pressure (101,325 Pa). The inlet and outlet sections are extended to ensure the stable development of fluid flow and avoid interference of inlet and outlet effects on flow field calculation. The Semi-Implicit Method for Pressure-Linked Equations Consistent (SIMPLEC) is adopted for pressure–velocity coupling solution; the convection term uses a high-resolution scheme, and the time term uses an implicit scheme to ensure calculation accuracy and stability. Convergence criterion: All residual convergence accuracies are set to 1 × 10⁻⁴, and key performance parameters such as pump head and shaft power are monitored simultaneously. The calculation is determined to be convergent when the parameter fluctuation is less than 0.5%. The SST k-ω turbulence model is employed, which combines the stability of the k-ε model in the free-stream region and the calculation accuracy of the k-ω model in the near-wall region, making it suitable for simulating complex rotating flows and separated flows in centrifugal pumps. The standard wall function of the SST k-ω model is applicable to the range of Y⁺ = 30~100. Through grid independence verification in this study, all measured Y⁺ values fall within this optimal interval, and accurate prediction of near-wall flow can be ensured without using extremely fine grids.

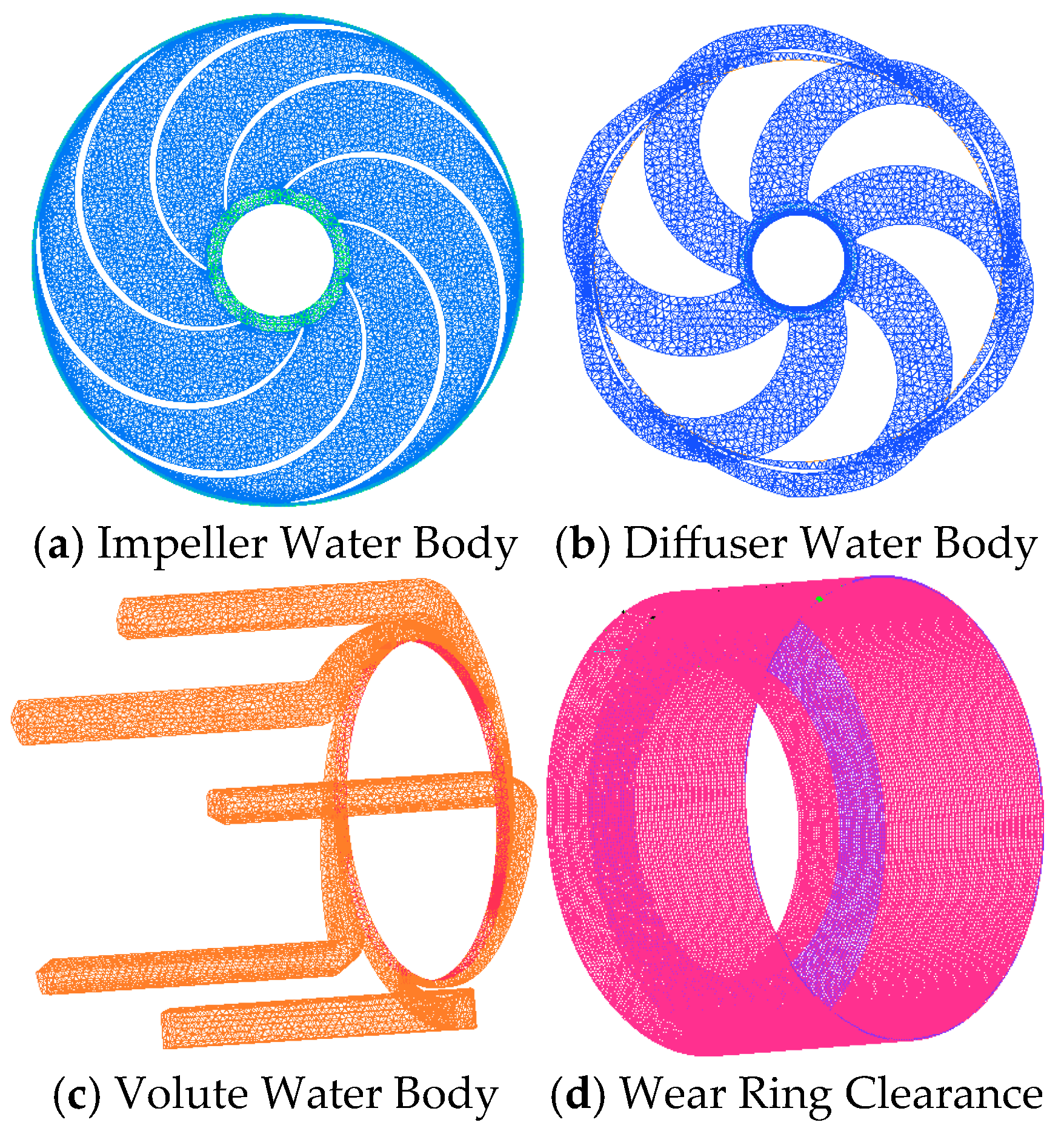
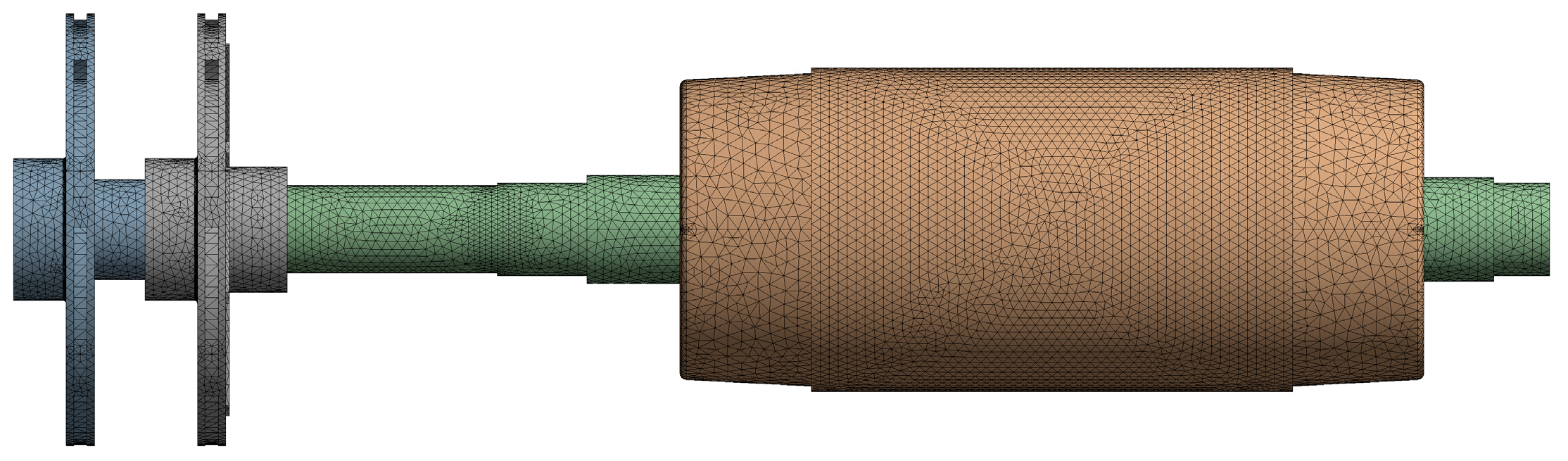
2.2. Mesh Generation

Mesh generation is implemented via ICEM, with the total number of meshes in the water body model reaching 1,883,755. The mesh of the main water body is presented in Figure 3 [24,25]. A combination of structured and unstructured grids is adopted: Wear ring clearance: A structured hexahedral grid is employed for the wear ring clearance to accurately capture the thin-layer flow and reduce numerical diffusion. Other water bodies: Due to the irregular geometric shapes of these components, an unstructured tetrahedral grid is used to adapt to complex boundaries. To ensure computational stability, the grid growth rate between adjacent cells is controlled within 1.2 to avoid abrupt changes in grid size. Three grid density schemes are utilized for grid independence verification (Scheme 1: 1.2 million cells; Scheme 2: 1.88 million cells; Scheme 3: 2.5 million cells), with the pump head as the evaluation index. The results indicate that the relative error of the head between Scheme 2 and Scheme 3 is only 1.2%, demonstrating that the grid density of 1.88 million cells adopted in this study can eliminate grid dependence and guarantee computational accuracy. The standard wall function of the SST k-ω model is applicable to the range of Y⁺ = 30~100. This range does not require the extremely fine grid (Y⁺ < 1) necessary for low-Reynolds-number models, while ensuring the accuracy of near-wall flow prediction. All Y⁺ values measured in this study fall completely within this optimal range, indicating that the grid resolution is sufficient to support the application of the selected turbulence model and can accurately resolve the near-wall flow characteristics.

2.3. Boundary Condition Configuration and Model Selection [26,27,28,29,30,31,32,33]

The numerical simulations are based on the continuity equation and the Reynolds-averaged Navier–Stokes (RANS) equations, which are presented as Equation (1) and Equation (2), respectively. A convergence criterion of 1 × 10⁻⁴ is adopted for the computational iterations.

$${\displaystyle \frac{\partial (u_i)}{\partial x_i}}=0$$

(1)

$$\rho {\displaystyle \frac{\partial (u_i)}{\partial t}}+\rho u_j{\displaystyle \frac{\partial (u_i)}{\partial x_j}}=\rho F_i-{\displaystyle \frac{\partial p}{\partial x_i}}+\mu {\displaystyle \frac{{\partial }^2{u}_i}{\partial x_i\partial x_j}}$$

(2)

where μ_i denotes the instantaneous velocity component in the i direction; x_i represents the coordinate; ρ stands for the fluid density; p denotes the fluid pressure; F_i indicates the body force per unit mass; and μ signifies the kinematic viscosity of the fluid.

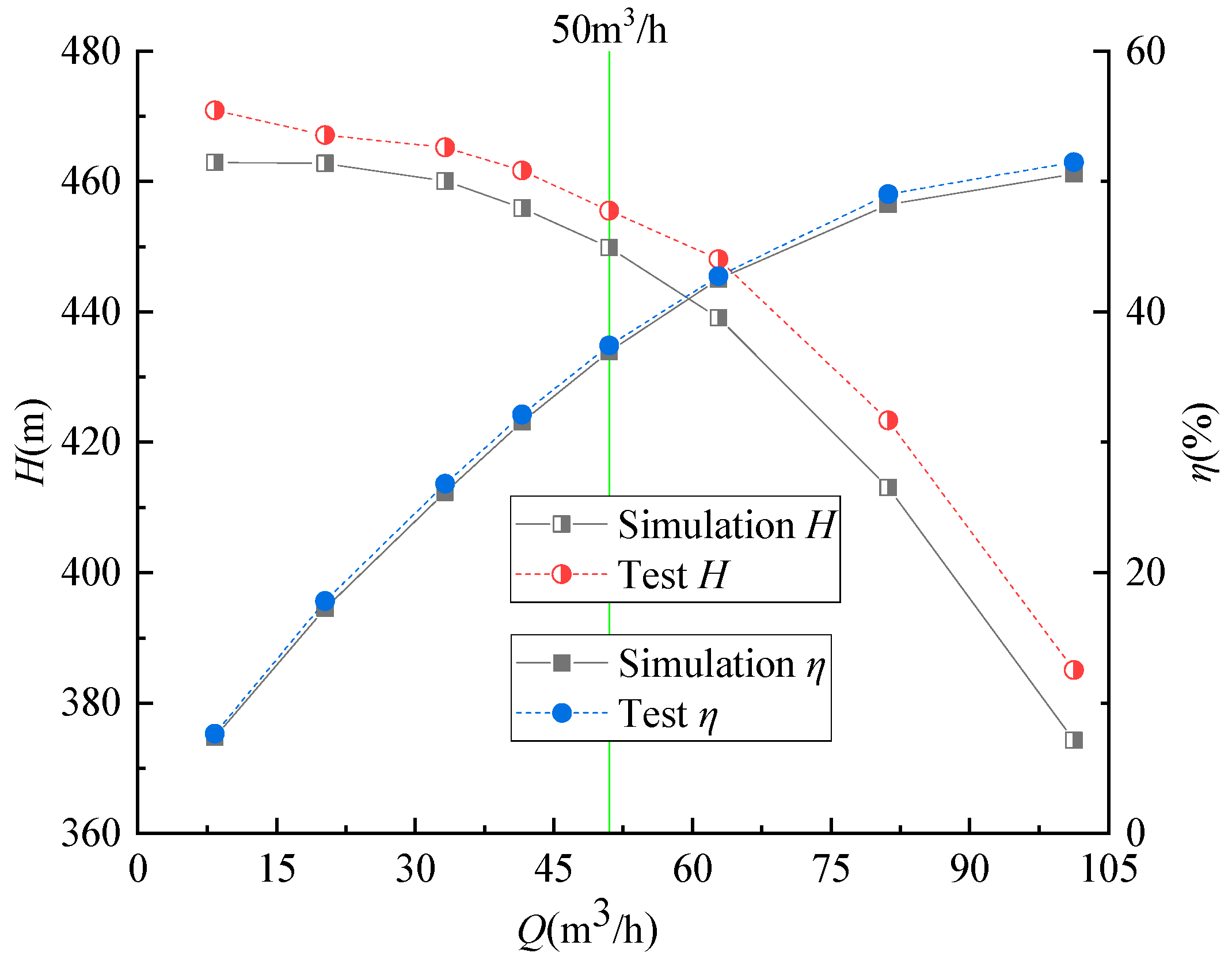
2.4. Validation of Numerical Calculations

Numerical simulations were conducted for the two-stage centrifugal pump based on the CFX software 2020. The calculated data were compared with the experimental data of head and shaft power, and the results are presented in Figure 4. As the flow rate increases, the shaft power of the pump increases while the head decreases, with the variation trend of the numerical results being consistent with that of the experimental results. Near the commonly used operating point of 50 m³/h, the deviation between the simulation results and the experimental results is relatively small; however, the deviation slightly increases under the conditions of large and small flow rates of the pump. Near the commonly used operating point of 50 m³/h, the corresponding head deviation is 1.24%, and the shaft power deviation is 2.5%. This indicates that the numerical calculation exhibits high accuracy near the optimal operating condition, thereby verifying the reliability of the numerical simulation. Consequently, this study focuses on the optimal operating condition of 50 m³/h for predictive analysis.

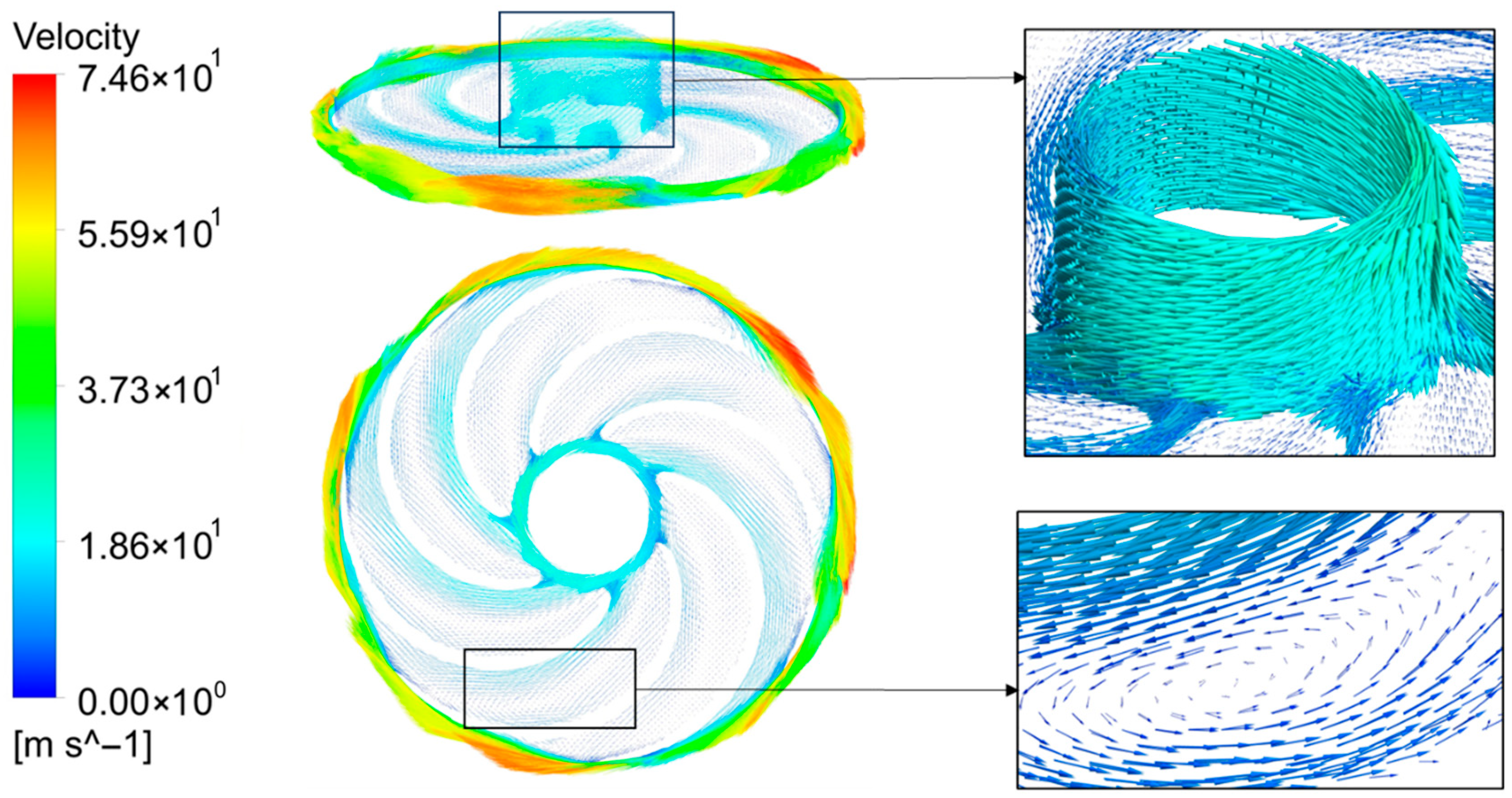
2.5. Analysis of the Internal Flow Field

Figure 5 presents the pressure distribution contour of the entire flow field of the pump under the optimal operating condition. As can be clearly observed from the figure, the pressure exhibits a circumferentially symmetric distribution feature. For each stage of the pump, the increment range of the water pressure is relatively consistent. In the large-area regions at the pump inlet and outlet, since there are no structural components acting on the water, the pressure variation in these regions is not significant. The pressure distribution of the water at the pump’s mid-section is essentially consistent with the overall trend of the pressure distribution of the entire pump’s water. By observing the pressure distribution of the section water, the pressure variation trend of the water at the central part can be more intuitively perceived. There are local regions with relatively low pressure around the impeller axis. After the water is pressurized through the rotational work of the impeller, it is guided by the diffuser into the next-stage pump chamber. Through the multi-stage pressurization process, the water finally flows out from the pump outlet at a relatively high pressure. The pressure at the inlet of the final-stage impeller is non-negative, which is mainly attributed to the pressurization effect of the first-stage impeller. After being pressurized by the first-stage impeller, the pressure is transmitted to the final-stage impeller, resulting in a relatively high pressure in this region.

Figure 6 illustrates the velocity vector distribution of the internal flow field within the final-stage impeller. Influenced by the rotational motion of the fluid in the first-stage impeller, a significant pre-swirl phenomenon is generated at the inlet of the final-stage impeller, where the rotational direction of the pre-swirl is consistent with that of the anti-guide vanes of the diffuser. Subsequently, the fluid flows into the blade passage, and under the action of the blade pressure side, the direction of the velocity vector of the fluid inside the impeller is altered, initiating flow along the direction of the blade pressure side. In the vicinity of the blade pressure side, the fluid streamlines exhibit excellent consistency with negligible turbulent losses, indicating that the guiding effect of the pressure side on the fluid is stable and effective. In contrast, the stability of the streamlines on the blade suction side is relatively weak. Nevertheless, due to the inherent guiding function of the blade suction side, no obvious turbulent phenomenon is formed herein. For the fluid region between two adjacent blades, the guiding effect exerted by the blade pressure side and suction side is relatively insignificant, leading to indirect energy transfer from the blades to the fluid in this region. Consequently, distinct turbulent zones are developed, accompanied by prominent vortex structures at various positions in the middle area. These vortices result in a certain degree of energy dissipation. It is anticipated that the rational addition of blades in this region will significantly mitigate the vortex phenomenon and reduce energy losses.

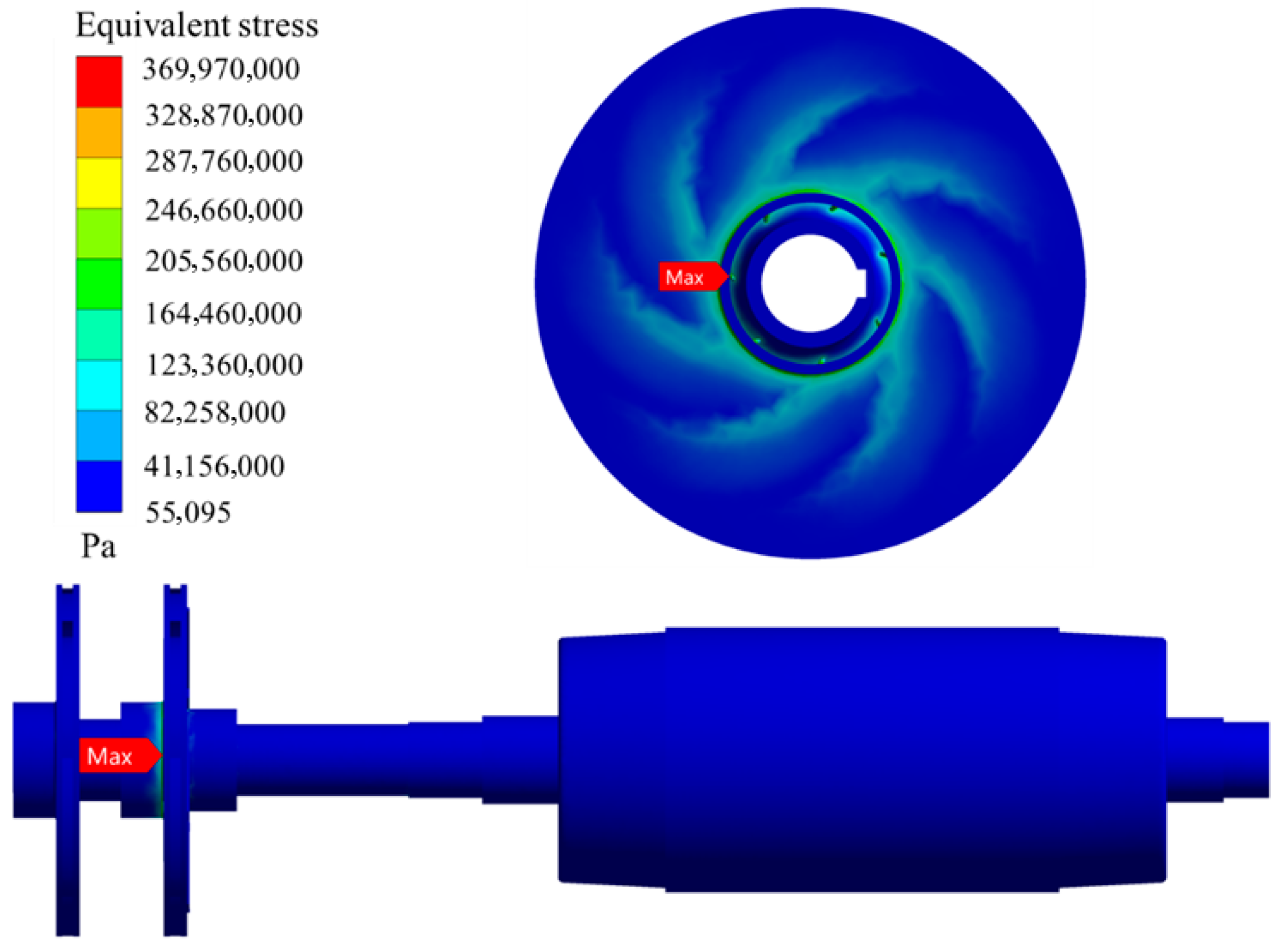
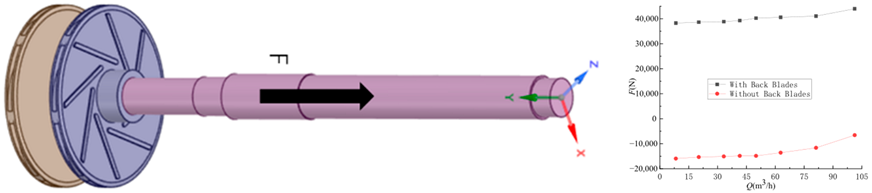
3. Calculation and Analysis of Axial Force [23,24]

3.1. Formula-Based Calculation of Axial Force for Rotor Systems Equipped with Back Blades

According to the classical theory in the pump manual [24], the axial force of the centrifugal pump rotor system is primarily composed of the following five components: cover plate force F₁, hydrodynamic reaction force F₂, axial force F₃ induced by structural factors such as shaft shoulders and shaft ends, axial force G generated by the rotor weight, and other factors F₅ affecting the axial force.

The slip coefficient for a finite number of blades is calculated by Equation (3):

$$y=1-{\displaystyle \frac{\pi }{z}}{\Psi }_2\sin {\beta }_2$$

(3)

where Ψ₂ denotes the blockage factor, and β₂ represents the blade outlet setting angle; the blockage factor is assigned a value of Ψ₂ = 0.836.

Accordingly, the value of y = 0.935 is derived.

The tangential velocity at the impeller outer diameter is u₂ = 60.981 m/s, the impeller outlet width is b₂ = 12 mm, the impeller outer diameter is D₂ = 395 mm, and the impeller outer radius is R₂ = 197.5 mm.

Assuming a volumetric efficiency of 0.9, where Q_t denotes the theoretical flow rate, the theoretical head of a single impeller is calculated by Equation (4):

$$H_t={\displaystyle \frac{u_2}{g}}(y{u}_2-{\displaystyle \frac{Q_t}{\pi D_2{b}_2{\psi }_{2}tg{\beta }_2}})$$

(4)

Consequently, the theoretical head is derived as H_t = 311.024 m.

The potential head (pressure head) of a single impeller is calculated by Equation (5):

$$H_p=H_t(1-{\displaystyle \frac{1}{4}}{\displaystyle \frac{H_t}{{u_2}^2/2g}})$$

(5)

Consequently, the potential head is derived as H_p = 183.558 m.

The cover plate force F₁ denotes the sum of the cover plate forces across all stages. The single-stage cover plate force refers to the pressure difference between the outer surfaces of the front and rear cover plates and the inner surface of the wear ring at the impeller inlet, which is a calculated differential force (Note: not the external force acting on a single front or rear cover plate). This pressure difference represents the state of the pressure differential on the cover plates acting on the impeller without the effect of back blades. For a pump with n stages, the calculated value of the cover plate force F₁ is the product of the single-stage differential force and n. According to Equation (6), the single-stage cover plate force is determined to be 1314 kg, and since the pump is a two-stage unit, F₁ = 2628 kg (direction: downward).

$$F_1=(R_m^2-R_h^2)\pi \rho g\left[H_P-{\displaystyle \frac{{\omega }^2}{8\mathrm{g}}}(R_2^2-{\displaystyle \frac{R_m^2+R_h^2}{2}})\right]$$

(6)

The hydrodynamic reaction force F₂ is calculated in accordance with Equation (7), yielding F₂ = 11 kg (direction: upward).

$$F_2=n{Q}_t\rho v_{m0}$$

(7)

where the axial force F₃ induced by structural factors such as shaft shoulders and shaft ends is not taken into account, and the rotor’s self-weight is G = 350 kg (direction: downward).

The balancing axial force generated by the back blades, which is classified as other factors influencing the axial force, is denoted as F₅. It refers to the pressure reduction on the outer side of the impeller’s rear cover plate after the addition of back blades, and its direction is opposite to that of the pressure acting on the outer side of the rear cover plate. When the single-stage cover plate force of the impeller is subtracted by the balancing axial force F₅ generated by the back blades, the residual single-stage cover plate force of the impeller with back blades is obtained. The balancing axial force generated by the back blades is calculated by Equation (8), where ω = 308.77 rad/m (note: corrected from “rad/m” to standard angular velocity unit “rad/s”), s = 6 mm, t = 3 mm, the outer radius of the back blades R_e = 180 mm, and the inner radius of the back blades R_h = 70 mm. Substituting these parameters into Equation (8) yields F₅ = 1804 kg (direction: upward).

$$F_5={\displaystyle \frac{{\omega }^2}{8}}\rho \left[{\left({\displaystyle \frac{s+t}{s}}\right)}^2-1\right]\left(A_e-A_h\right){\displaystyle \frac{{R_e}^2-{R_h}^2}{2}}$$

(8)

The pump is configured with two stages of impellers, whereas only the final-stage impeller is equipped with back blades. Consequently, in the calculation of the total axial force, the balancing axial force F₅ generated by the back blades is deducted merely once. The total axial force F is defined as follows:

$$F=F_1+F_2+G+F_5=1163 \mathrm{kg}$$

(Direction: downward)

Axial Force of the Rotor System Without Back Blades

$$F=F_1+F_2+G=2967 \mathrm{kg}$$

(Direction: downward)

3.2. Numerical Simulation-Based Calculation of Rotor System Axial Force

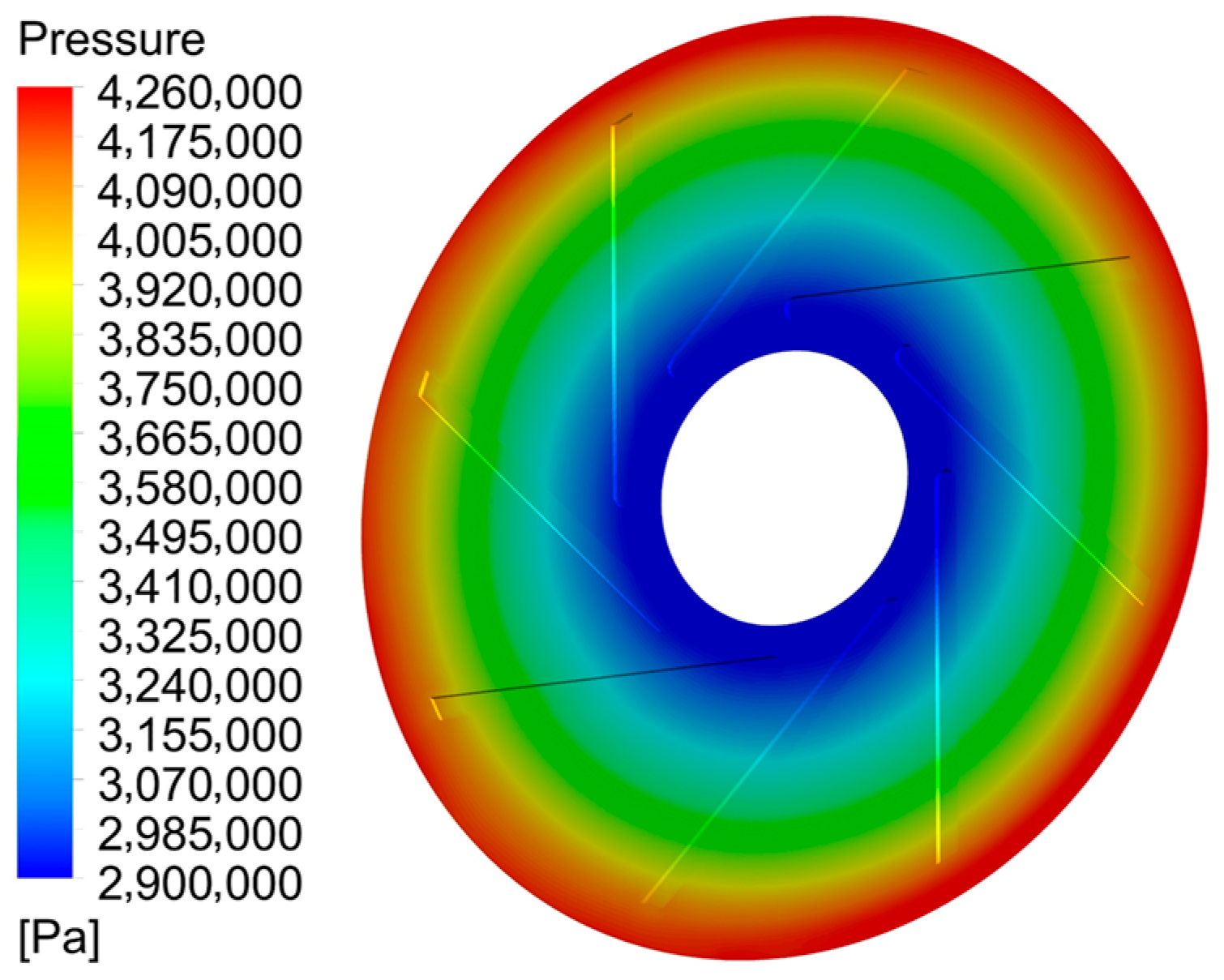
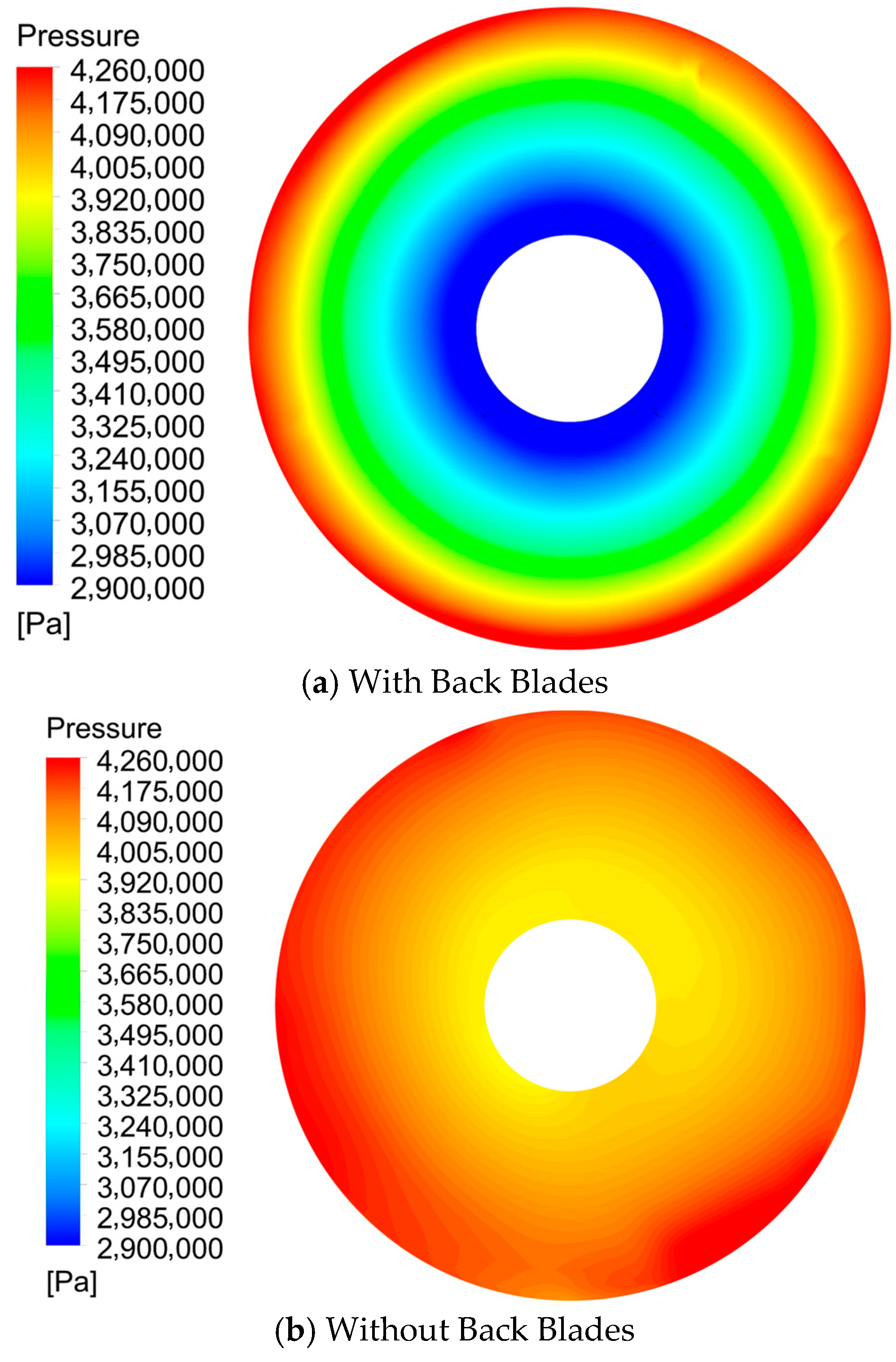
3.2.1. Calculation of Axial Force for Rotor Systems Equipped with Back Blades

Under the mechanical action of fluid flow, the rotor system is subjected to an axial force. Figure 7 presents the pressure distribution contour of the fluid in the rear cavity of the impeller equipped with back blades under design conditions. This contour intuitively reveals the mechanism by which back blades function to reduce the fluid pressure in the impeller rear cavity. When back blades are installed on the final-stage pump, the distribution law of the fluid pressure in its rear cavity differs from that under conventional conditions. Specifically, driven by the rotational motion of the back blades, the fluid pressure in the front cavity is higher than that in the rear cavity. This is attributed to the centrifugal force exerted by the rotating back blades on the fluid in the rear cavity, which ejects the fluid outward, thereby reducing the pressure level in the rear cavity.

The structural design of the back blades offers dual advantages: on one hand, it helps balance the axial force acting on the rotor system, ensuring the stable operation of the pump; on the other hand, it can effectively block impurities from entering the pump interior, extending the pump’s service life. Through numerical simulation calculations, it is determined that under the operating condition of a flow rate of 50 m³/h, the axial force acting on the two-stage centrifugal pump is 40,237 N, with a vertically upward direction. However, there is a significant deviation between this simulation result and that obtained via traditional formula-based calculations. In-depth analysis indicates that this discrepancy primarily stems from the simplification of numerous key factors in the modeling process of traditional calculation methods. Particularly in the axial force calculation of multi-stage pumps, as the number of pump stages increases, the errors arising from each simplification step accumulate and amplify, ultimately leading to a substantial deviation between the calculated results and the actual operating conditions.

Traditional calculation methods often fail to fully consider critical factors such as the balancing and regulating effect of back blades on the axial force, the real-time changes in fluid dynamic characteristics, and the distribution characteristics of the complex internal flow field in multi-stage pumps—all of which are crucial for the accurate calculation of the axial force. In view of this, the calculation method adopted in this study, by incorporating more precise physical models and boundary condition settings, can more truly simulate the internal flow field distribution and mechanical properties of the multi-stage pump. Consequently, it more accurately reflects the axial force distribution of the multi-stage pump under different operating conditions, effectively overcoming the error issues inherent in traditional calculation methods and providing a more re-liable theoretical basis for the design optimization and performance evaluation of multi-stage pumps.

3.2.2. Calculation of Axial Force for Rotor Systems Without Back Blades

Figure 8 presents a comparative analysis of the pressure distribution characteristics on the outer surface of the rear cover plate between impellers with two distinct structural configurations: equipped with back blades and without back blades. In the local region of the impeller rear cavity near the geometric center, the pressure exhibits a significant decreasing trend, and the pressure value even drops to a negative value in some areas, thereby forming a low-pressure region with a considerable scope. For the pump equipped with back blades, a low-pressure region is also formed in the area of the rear cavity fluid near the center, and the pressure value of this low-pressure region is significantly lower than that of the fluid at the same radial position in the rear cavity of the pump without back blades. In terms of the pressure distribution law, as extending radially outward from the center, the pressure value shows a gradual increasing trend. At the outlet position of the rear cavity near the edge, due to the contact with the high-pressure region at the blade outlet, the pressure undergoes an abrupt change, resulting in a pressure jump phenomenon. Comprehensive comparative analysis indicates that the overall pressure level of the fluid in the rear cavity of the pump equipped with back blades is lower than that of the structure without back blades. Based on the analysis of the aforementioned pressure distribution characteristics, it can be inferred that back blades exert a significant influence on the axial force.

Through numerical simulation calculations, it is determined that under the operating condition of a flow rate of 50 m³/h, the axial force borne by the two-stage centrifugal pump without back blades is 14,842 N, with a vertically downward direction. Further comparison reveals that the magnitude of the axial force generated by the impeller without back blades is much smaller than that generated by the impeller with back blades, and the directions of the two are opposite. This result further verifies the effect of the back blade structure on modifying the axial force, providing important data support for the subsequent in-depth investigation into the influence mechanism of back blades on pump performance.

3.2.3. Comparative Analysis of Axial Forces

In the actual operation process, the two-stage centrifugal pump exhibits the following phenomenon: when back blades are adopted to balance the axial force, the bearing near the pump outlet is prone to frequent damage; however, after removing the back blades, the service life of this bearing during pump operation is significantly prolonged. This phenomenon intuitively indicates that the axial force acting on the rotor system is relatively larger when equipped with back blades.

To further investigate the characteristics of the axial force, a comparative analysis was conducted between the numerical simulation results and the axial force results obtained via traditional formula-based calculations, with relevant data detailed in

Table 1. Comparison of Axial Forces.

Axial Force (N) (Negative Values Denote a Downward Direction)
Structure	Formula-Based Explanation	Numerical Simulation	Difference
With Back Blades	11,397	−40,237	51,634
Without Back Blades	29,077	14,842	14,235

. The comparison reveals that when the pump is equipped with back blades, there is a substantial deviation of 51,634 N between the numerical simulation results and the formula-calculated results. In-depth analysis of the underlying reasons indicates that the addition of back blades renders the flow field near the back blades extremely complex, and the fluid dynamic characteristics are influenced by the interaction of multiple factors. Traditional calculation formulas, however, involve simplifications of numerous practical conditions and fail to fully account for the complex characteristics of the flow field adjacent to the back blades. Consequently, they cannot accurately describe the actual flow field conditions in this region, leading to significant calculation deviations.

In contrast, after removing the back blades, the pressure field distribution of the fluid in the rear cavity of the impeller without back blades is relatively simple, and the fluid movement law is more uniform. Under such circumstances, traditional formulas can effectively describe the flow field characteristics, with a calculation deviation of 14,235 N accounting for only 27.6% of the deviation observed in the case with back blades. Thus, these formulas can be utilized for the rapid calculation of axial forces.

Based on the above findings, for multi-stage centrifugal pumps with a back-blade-free structure, the formula-based calculation method is preferred. This avoids the time-consuming numerical simulation process, thereby improving calculation efficiency and providing a convenient and effective technical tool for the de-sign optimization and performance evaluation of pumps.

Table 2. Axial force with and without back blades.

Flow Q (m3/h)	8.34	20.26	33.26	41.55	50	62.83	81.18	101.27
With Back Blades	38,265	38,618	38,847	39,275	40,237	40,579	41,070	43,997
Without Back Blades	−15,926	−15,323	−15,075	−14,849	−14,842	−13,556	−11,648	−6574

presents the axial force data (Unit: N) of multi-stage centrifugal pumps with and without back blades under different flow rate conditions, where the negative sign indicates that the force direction is opposite to the inlet flow velocity direction.

In terms of the data variation trend, for the multi-stage centrifugal pump equipped with back blades, the magnitude of the axial force gradually increases with the rise in flow rate, and the force direction is consistent with the inlet flow velocity direction. In contrast, for the multi-stage centrifugal pump without back blades, the axial force magnitude gradually decreases as the flow rate increases, and the force direction is opposite to the inlet flow velocity direction.

An analysis of the underlying causes of this discrepancy reveals that it primarily stems from the unique mechanism of action of back blades. As the flow rate continuously increases, the upward axial force generated by the back blades becomes increasingly prominent and dominates the composition of the total axial force. Meanwhile, the inherent downward axial force decreases to a certain extent. However, due to the dominant effect of the upward axial force, the overall axial force of the pump exhibits an upward-increasing trend. Based on the aforementioned analysis, it can be concluded that the design of back blades exerts a critical influence on the axial force distribution of multi-stage centrifugal pumps.

Therefore, through the scientific and rational optimization of back blade design parameters—such as blade shape, dimensions, and installation angle—it is possible to effectively regulate the axial force distribution. This not only enhances the operational stability of multi-stage centrifugal pumps, reduces issues such as vibration and noise caused by axial force imbalance, but also improves the pump’s operational efficiency and extends its service life.

4. Rotor Dynamic Calculation and Analysis

For a linear system with N degrees of freedom, its differential equation of motion is given by [34,35,36,37]:

$$[M]\left\{\ddot{x}\right\}+[C]\left\{\dot{x}\right\}+[K]\left\{x\right\}=\left\{F\right\}$$

(9)

where [M] denotes the mass matrix of the system; [C] denotes the damping matrix of the system; [K] denotes the stiffness matrix of the system; {x} denotes the displacement response vector of each point in the system; {F} denotes the excitation force vector of each point in the system.

By applying the Laplace transform to both sides of Equation (9), the following expression is obtained:

$$(s^2[M]+s[C]+[K])\{x(s)\}=\{F(s)\}$$

(10)

Let s = jω, then Equation (10) is transformed into:

$$([K]-{\omega }^2[M]+j\omega [C])\{x(\omega )\}=\{F(\omega )\}$$

(11)

By introducing modal coordinates, let {x} = [φ]{q}, where [φ] denotes the mode shape matrix and {q} denotes the modal coordinates. Then, the following expression is obtained:

$$([K]-{\omega }^2[M]+j\omega [C])[\varphi ]\left\{q\right\}=\left\{F\right\}$$

(12)

According to the orthogonality relations of the mode shape matrix with respect to the mass matrix and stiffness matrix, the following expression holds:

$${\left[\varphi \right]}^T\left[M\right]\left[\varphi \right]=\left(\begin{array}{ccc}\ddots & & \\ & m_i& \\ & & \ddots \end{array}\right)$$

(13)

If the damping matrix is also approximately diagonalized, i.e.,

$${\left[\varphi \right]}^T[C]\left[\varphi \right]=\left(\begin{array}{ccc}\ddots & & \\ & c_i& \\ & & \ddots \end{array}\right)$$

(14)

Then, by pre-multiplying both sides of Equation (12) by [φ]T, the following is obtained

$$([K_i]-{\omega }^2[M]+j\omega [C_i])\left\{q\right\}={\left[\varphi \right]}^T\left\{F\right\}$$

(15)

The i-th decoupled equation is given by:

$$(K_i-{\omega }^2{M}_i+j\omega C_i)q_i={\displaystyle \sum _{j=1}^n{\varphi }_{ji}}{F}_j$$

(16)

where K_i denotes the modal stiffness; M_i denotes the modal mass; C_i denotes the modal damping; φ_i denotes the modal shape.

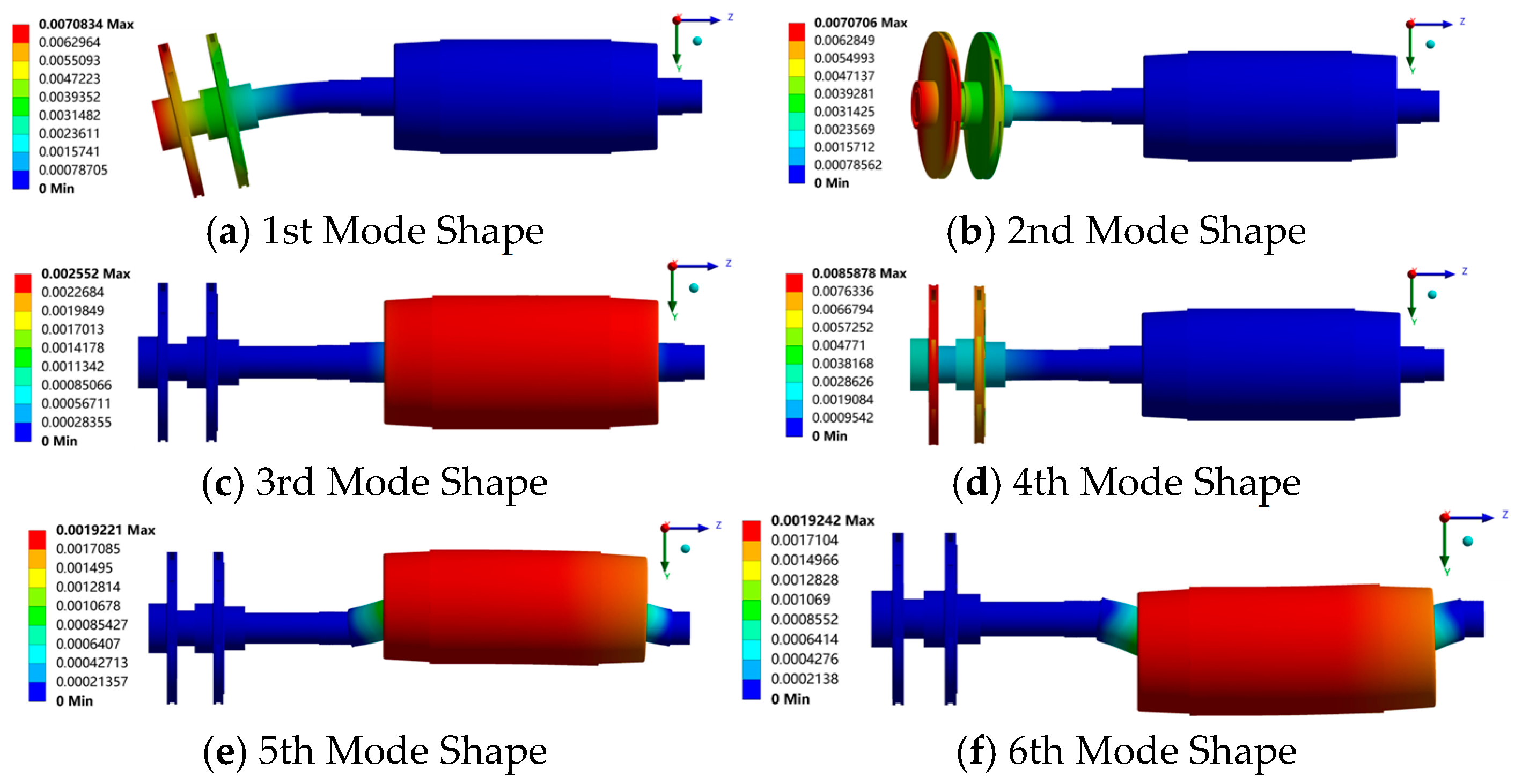
4.1. Modal Analysis of the Pump Rotor System

The pump rotor system consists of components including the pump shaft, keys, impellers, and motor. The three-dimensional model is saved in the *.stp format, with its reference coordinate system consistent with that of the water body model, and subsequently imported into ANSYS Workbench software 2020. The Mesh module within the software is employed, and the 8-node 3D tetrahedral element Solid186 is selected for meshing. The mesh diagram of the pump rotor is presented in Figure 9. Three grid density schemes are constructed for grid independence verification (Scheme 1: 232,080 elements; Scheme 2: 463,198 elements; Scheme 3: 926,092 elements), with the first six natural frequencies compared. The results show that the relative errors of the natural frequencies of each order between Scheme 2 and Scheme 3 are all less than 1.5%, indicating that the grid with 463,198 elements adopted in this study can eliminate grid dependence and ensure the sufficiency of the simulation results. The final total number of elements in the pump rotor system grid generated by the above meshing strategy is 463,198, with 694,916 nodes. Among them, 96% of the elements have an orthogonality greater than 0.85 (minimum orthogonality of 0.78), which meets the requirements of structural modal analysis (orthogonality ≥ 0.7); 97% of the elements have a distortion rate less than 0.25 (maximum distortion rate of 0.32), avoiding deviations in modal frequency calculation caused by element distortion.

To simulate the natural frequencies of the pump under fluid–structure interaction (FSI), the computational results from CFX are imported into ANSYS Workbench. The water pressure derived from the CFX simulation is treated as a known boundary condition, and the modes of the rotor system under prestress are calculated for subsequent comparative analysis. The gravitational acceleration adopts the default value of 9.8006 m/s² in ANSYS Workbench (correcting the non-standard unit “m²/s” to the internationally recognized unit for acceleration), with a direction opposite to the inlet flow velocity. The rotational speed is set to 308.77 rad/s, and the water surface pressure obtained from the CFX simulation is applied to the corresponding surfaces of the rotor. Relevant material parameters are configured, the number of expanded modes is specified as six, and the vibration modes are set to the first six orders.

Based on one-way fluid–structure coupling, The equivalent stress is the maximum under the operating condition of 50 m³/h, with the maximum equivalent stress reaching 36,997,000 Pa. The maximum equivalent stress nephogram is shown in Figure 10, presenting the overall view and the enlarged view of key parts, respectively. It can be observed from the nephogram that as the number of stages increases, the pressure of the internal flow field in the pump also rises, and the equivalent stress of the final stage is higher than that of the first stage. The final-stage impeller is equipped with back vanes, which are relatively large in size. This results in the deformation direction of the final-stage impeller being opposite to that of the first-stage impeller, with a larger deformation amplitude. Stress concentration occurs at the inlet section, leading to a relatively high equivalent stress, and the maximum equivalent stress is located at the inlet of the final-stage impeller.

The Block Lanczos method is employed for the modal analysis of the mining pump rotor. After numerical computation, the first six orders of natural frequencies and corresponding mode shapes of the rotor are obtained. The sixth-order mode shape is illustrated in Figure 11.

As illustrated in the mode shape diagrams of the pump rotor, the 1st and 2nd mode shapes are analogous with closely adjacent natural frequencies, and the deformation directions of the impellers are mutually perpendicular. The vibration direction of the first-order mode shape is along the Y-axis, while that of the second-order mode shape is along the X-axis, with bending concentrated toward a single extreme point. The first-order mode shape is predominantly characterized by deformation at the cantilever tip of the rotor system, with the first-stage impeller exhibiting significant deformation. To enhance the first-order natural frequency, the stiffness of the shaft and impellers can be reinforced, thereby preventing collisions and severe wear between the rotor and other pump components during operation near the first-order critical speed an issue that would otherwise result in pump malfunction. Consequently, the operating frequency of the pump should not exceed the first natural frequency in the design phase.

The third-order mode shape is dominated by motor deformation, featuring an increase in motor diameter with negligible shaft deformation and minimal overall structural change, while the impellers remain relatively stable. Deformation in the fourth-order mode shape primarily occurs in the radial direction of the impellers, with a notable increase in radial deformation magnitude. The shaft segment adjacent to the impellers exhibits slight deformation, and the natural frequency can be improved by enhancing the rigidity of the impellers. The fifth and sixth-order mode shapes are analogous with closely spaced natural frequencies, and de-formation is mainly concentrated in the motor and the shaft segment where the motor is mounted. The deformation tendency of this shaft segment increases significantly, indicating that the rotor system cannot operate reliably within this frequency range.

Through the aforementioned analysis, the rotor system frequently exhibits two consecutive orders of natural frequencies with a frequency difference of less than 1 Hz, characterized by analogous mode shapes and mutually perpendicular vibration directions.

4.2. Critical Speed Analysis of the Rotor

If the rotor operates at its critical speed, severe vibration will be induced. Prolonged operation under such conditions may even lead to the fracture of the rotor, which is composed of the impellers and other components assembled on the shaft.

The relationship between the critical speed of the rotor and its natural frequency is expressed as [38]:

n = 60 × f

(17)

where n denotes the rotor speed (unit: r/min); f represents the rotor natural frequency (unit: Hz), i.e., the number of vibrations per second.

Through modal analysis calculations, the natural frequencies of each order and the corresponding critical speeds of the pump are obtained, as presented in

Table 3. Natural Frequencies and Critical Speeds of the Pump.

No.	1	2	3	4	5	6
Natural Frequencies	119.62	119.75	215.93	228.94	329.00	329.34
Critical Speeds	7177.2	7185	12,955.8	13,736.4	19,740	19,760.4

(frequency unit: Hz; speed unit: r/min).

The rotor system is characterized by circumferentially symmetric blades and a cantilever configuration. Owing to the unbalanced mass distribution within the same local cross-section of the shaft, the product of the mass matrix and acceleration vector undergoes variation during rotor rotation, as derived from the differential equations of motion—consequently inducing changes in the critical speeds of the entire rotor system.

Calculations indicate that the first-order critical speed is 7177.2 r/min, which is higher than the operating speed of 2800 r/min. Thus, the pump operates within a safe range without resonance risks. The first and second-order critical speeds, as well as the fifth and sixth-order critical speeds, are closely adjacent and fall within the allowable speed tolerance of the motor. If the motor operates near this frequency range, mutual fluctuations between the two consecutive natural frequencies may occur. Significant variations are observed in the transition zones between the second and third-order, as well as the fourth and fifth-order critical speeds, corresponding to substantial changes in mode shapes.

5. Conclusions

This study investigates the mechanical characteristics of the rotor of a two-stage centrifugal pump based on fluid–structure interaction (FSI) and establishes a coupled analysis framework of “flow field stability–axial force calculation accuracy–rotor dynamic response”. The presence of back vanes endows the flow field in the rear chamber of the final-stage impeller with complex characteristics such as pre-rotation and vortices, which violates the simplified assumptions of traditional formulas, leading to an axial force calculation error of 27.6%. In contrast, the flow field is stable without back vanes, making the formula-based method more applicable. As a key hydraulic load, the change in the magnitude and direction of the axial force (back vanes reverse and increase the axial force), combined with the cantilever structural characteristics of the rotor, induces dynamic phenomena where two adjacent natural frequencies differ by less than 1 Hz with perpendicular vibration modes. Rotational speed fluctuations further result in alternating critical speeds. Each research link is progressive: flow field analysis explains the differences between calculation methods, axial force provides load input for rotor dynamics, and dynamic characteristics verify the engineering optimization value. These collectively support the central thesis and provide technical references for the design optimization and stable operation of similar pumps. The main conclusions are as follows:

(1)

Under the design conditions, the numerical simulation results of the two-stage centrifugal pump equipped with auxiliary blades are in good agreement with the experimental data, which validates its feasibility for axial force calculation. For the two-stage centrifugal pump with back blades, the flow field in the region adjacent to the back blades is relatively complex, and the numerical simulation method yields more accurate results than the analytical formula method.

(2)

In the absence of back blades, the flow of fluid in the rear cavity of the multi-stage centrifugal pump impeller is relatively stable. The deviation between the numerical simulation results and the analytical formula results is relatively small, accounting for 27.6% of that observed with back blades. Thus, the analytical formula can be employed for rapid calculation to save computational time. After adding back blades, the central pressure of the fluid in the impeller rear cavity decreases significantly, while a distinct high-pressure zone is formed at the outer side. The pressure gradient exhibits a similar trend to that generated by the impeller blades, and the accuracy of the traditional analytical formula for axial force calculation is relatively low under this condition.

(3)

The rotor system of the two-stage centrifugal pump exhibits a phenomenon where two adjacent orders of natural frequencies correspond to similar mode shapes, with a frequency difference of less than 1 Hz. This phenomenon is observed for the first- and second-order, as well as the fifth- and sixth-order natural frequencies. Resonance induced by the first-order natural frequency occurs at the cantilever end of the rotor system. The first-order critical speed can be improved by enhancing the shaft stiffness, thereby enhancing the stability of the rotor system.

(4)

When two adjacent orders of natural frequencies correspond to similar mode shapes, the directions of the two mode shapes are mutually perpendicular. Due to the inherent speed fluctuation and tolerance of the rotor system, alternating critical speeds may occur when the rotor operates near this frequency range. This phenomenon of mutually perpendicular mode shape variations should be considered during the design phase.