A Hybrid PCA-TOPSIS and Machine Learning Approach to Basin Prioritization for Sustainable Land and Water Management

Abstract

Population expansion, urban development, climate change, and precipitation patterns are complicating sustainable natural resource management. Subbasin prioritization enhances the efficiency and cost-effectiveness of resource management. Artificial intelligence and data analytics eradicate the constraints of traditional methodologies, facilitating more precise evaluations of soil erosion, water management, and environmental risks. This research has created a comprehensive decision support system for the multidimensional assessment of sub-basins. The Erosion and Flood Risk-Based Soil Protection (EFR), Socio-Economic Integrated Basin Management (SEW), and Prioritization Based on Basin Water Yield (PBW) functions were utilized to prioritize sustainability objectives. EFR addresses erosion and flood risks, PBW evaluates water yield potential, and SEW integrates socio-economic drivers that directly influence water use and management feasibility. Our approach integrates principal component analysis–technique for order preference by similarity to ideal solution (PCA–TOPSIS) with machine learning (ML) and provides a scalable, data-driven alternative to conventional methods. The combination of machine learning algorithms with PCA and TOPSIS not only improves analytical capabilities but also offers a scalable alternative for prioritization under changing data scenarios. Among the models, support vector machine (SVM) achieved the highest performance for PBW (R² = 0.87) and artificial neural networks (ANNs) performed best for EFR (R² = 0.71), while random forest (RF) and gradient boosting machine (GBM) models exhibited stable accuracy for SEW (R² ~ 0.65–0.69). These quantitative results confirm the robustness and consistency of the proposed hybrid framework. The findings show that some sub-basins are prioritized for sustainable land and water resources management; these areas are generally of high priority according to different risk and management criteria. For these basins, it is suggested that comprehensive local-scale studies be carried out, making sure that preventive and remedial measures are given top priority for execution. The SVM model worked best for the PBW function, the ANN model worked best for the EFR function, and the RF and GBM models worked best for the SEW function. This framework not only finds sub-basins that are most important, but it also gives useful information for managing watersheds in a way that is sustainable even when the climate and economy change.

1. Introduction

Basins are complex ecosystems comprising water, soil, and biological diversity, where natural processes intersect with human activity. Environmental pressures, including population growth, urbanization, climate change, and rainfall events, complicate the sustainable management of natural resources and render watersheds critical to conservation efforts. In this context, watershed management is a crucial instrument for developing soil and water conservation strategies [1,2,3,4].

The sustainable management of resources is essential for the long-term development of basins. Morphometric analyses serve as efficient instruments for the quantitative evaluation of the physical attributes of a drainage basin [5,6]. The analyses, underpinned by Geographic Information System (GIS) and remote sensing, establish a scientific foundation for designing management strategies aimed at conserving water resources [7,8]. Specifically, focusing on sub-basins instead of addressing the entire basin proves to be a more cost-effective and feasible strategy [9,10]. This prioritization process assesses factors including topographic features, hydrological parameters, and land use, employing geographic information systems, the analytic hierarchy process [11,12,13], and remote sensing techniques [14,15,16]. Furthermore, hydro-geomorphological evaluations, improved by morphometric analyses [17], are essential for assessing environmental hazards and establishing the priority ranking of sub-basins [18].

In recent years, the prioritization of sub-basins through morphometric parameters and spatial analyses has proven to be an effective approach for the sustainable management of soil, water, and natural resources, as well as for mitigating erosion and flood risks [4,19,20,21,22,23,24]. This method aids in the preservation of basin resources, specifically by mitigating soil erosion and flood hazards [18]. Furthermore, owing to rising expenses and the necessity for cooperation, benefit–cost-driven prioritization has become increasingly significant in water management [25]. Morphometric analysis, land use and cover (LULC), and principal component analysis (PCA) techniques are proficiently employed to identify erosion-prone areas and prioritize sub-basins [26]. These analyses are essential for prioritizing interventions in sub-basins with elevated erosion risk [27] because soil erosion diminishes the water storage capacity of basins [28] and leads to environmental issues [29]. The examination of parameters including topography, slope, surface runoff, and water potential through GIS and remote sensing aids in the identification of water resources and biophysical challenges within the basin [20,30,31].

In sub-basin prioritization studies, multi-criteria decision-making methods are employed by integrating parameters such as precipitation, slope, drainage intensity, soil, and land use to establish a priority ranking [32]. The incorporation of topographic data and geomorphological parameters enhances the precision of hydrological models in watershed planning and is instrumental in applications like the siting of dams and water collection structures [33,34]. Moreover, models incorporating both morphometric and geo-environmental parameters [35] produce dependable outcomes in assessing environmental hazards such as flooding, erosion, and sediment transport [36]. Sustainable soil and water management can be achieved through diligent micro-level planning [37].

The progression of technology has made machine and deep learning methodologies highly advantageous for modeling environmental processes. Artificial Neural Networks (ANNs) are proficient in analyzing complex data structures [38], whereas deep learning models like Convolutional Neural Network–Deep Neural Network (CNN-DNN) achieve superior accuracy in recognizing more complex patterns [39]. Machine learning techniques are extensively employed in groundwater management [40], soil conservation, and land degradation modeling [41], especially in landslide susceptibility analysis, where Support Vector Machine (SVM) effectively represent spatial variations [42]. Moreover, artificial neural networks and regression models are employed to forecast processes such as surface runoff and sediment loss; however, their applicability may be constrained for each basin [43]. The scarcity of data in sub-basin prioritization studies constrains the application of deep learning techniques; nevertheless, this limitation is expected to be reduced with improved data access [15]. Moreover, although data boosting techniques enhance model efficacy, conventional methods such as linear regression remain prevalent in machine learning [44,45]. Machine learning provides superior accuracy and reduced computational expenses relative to the fuzzy analytic hierarchy process, thus facilitating the assessment of the effectiveness of various [46]. In this context, machine learning algorithms provide effective results in watershed prioritization by accelerating morphometric analyses when integrated with GIS, and they assist decision-makers in analyzing LULC and morphometric data through techniques such as PCA and Weighted Sum Analysis (WSA) [27,47].

The constraint of financial resources necessitates the prioritization of sub-basin in basin management, as simultaneous development programs across all basins cannot be executed. Alongside conventional methods, artificial intelligence and data analytics approaches have gained prominence in basin prioritization in recent years. These methods facilitate a more precise analysis of soil erosion, water resource management, and environmental risks, while providing more comprehensive and dynamic solutions by addressing the constraints of conventional approaches that rely on limited data sets. The combination of artificial intelligence algorithms with multi-criteria decision-making techniques, including WSA, PCA, Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), and the Analytic Hierarchy Process (AHP), enhances the efficacy of basin prioritization processes. Nevertheless, further extensive research is required to assess the error margins of these models. In Türkiye, the application of artificial intelligence algorithms in basin prioritization studies has not yet gained prominence in accordance with sustainable soil and water management objectives, and few examples of such approaches appear in the literature concerning the Susurluk Basin. In most sub-basin prioritization studies, reliance on a restricted set of parameters constrains the precision of the analytical outcomes and the efficacy of decision support. The insufficiency of conventional methods in the thorough assessment of data with varying resolutions and types, as well as their integration into spatial analyses, has increased the demand for innovative approaches. PCA and TOPSIS are robust methodologies in multi-criteria decision-making; however, they predominantly rely on linear assumptions and may inadequately represent the non-linear, multi-dimensional interrelations among hydrological, geomorphological, and socio-economic factors. Consequently, this study integrates machine learning models to enhance the PCA-TOPSIS framework. Machine learning models (i) encapsulate intricate non-linear interactions, (ii) authenticate prioritization outcomes, and (iii) enhance the resilience of predictions across various sub-basins. The proposed methodology is both statistically sound and adaptable to diverse data structures. This offers decision-makers more dependable and generalizable conclusions for sustainable soil and water management practices. Conventional methodologies utilizing AHP, WSA, or PCA-TOPSIS are proficient in sub-basin prioritization; however, they exhibit limitations including linear assumptions, susceptibility to subjective weighting, and restricted ability to validate outcomes on heterogeneous data sets. This study’s innovation lies in its integration of PCA, TOPSIS, and machine learning algorithms within a unified framework. PCA minimizes parameter redundancies, TOPSIS offers systematic ranking, and machine learning enhances the robustness and generalizability of outcomes by uncovering non-linear interactions overlooked by conventional methods. In contrast to conventional methods, this hybrid approach diminishes uncertainty, enhances predictive efficacy, and provides decision-makers with a more dependable foundation for sustainable watershed management. This study employs morphometric parameters and land use/cover data, utilizing PCA, WSA, TOPSIS, and artificial intelligence algorithms to prioritize sub-basins according to erosion, flood risk, water yield, and socio-economic criteria. This study advocates for a methodological framework aimed at enhancing the feasibility and sustainability of water and soil resource management. It addresses environmental issues in relation to the United Nations Sustainable Development Goals, specifically SDG 6 (Clean Water and Sanitation), SDG 11 (Sustainable Cities and Communities), and SDG 15 (Life on Land), providing evidence-based recommendations for decision-makers and practitioners. This research has implications for basin hydrology, flood and erosion risk assessment, water resources planning, and socio-economic aspects of water governance, integrating knowledge and insights from sustainable basin management.

2. Materials and Methods

2.1. Overview of the Study Area

This study was performed in the Susurluk Basin situated in the Marmara Region. The basin, covering an area of approximately 24,035 km², is located between 27°9′50′′ and 29°51′42′′ east longitude and 39°1′8′′ and 40°31′43′′ north latitude (Figure 1). The basin has an average elevation of 631 m, and its slope ranges from 6% to 12%. The Susurluk Basin has a transitional climate is a hybrid of Mediterranean, Black Sea, and continental climates. This leads to predominantly arid summers and erratic precipitation trends year-round [48]. The Susurluk River, discharging into the southern region of the Marmara Sea, influences pollution levels within the sea.

Figure 2 outlines the methodological framework of the study, detailing the steps of data analysis, data preprocessing, weighting, calculation of prioritization indices, and ranking of sub-basins.

2.2. Data Sets

We identified three primary functions for basin prioritization: the Erosion and Flood Risk-Based Soil Protection Function (EFR Function), the Prioritization Based on Basin Water Yield Function (PBW Function), and the Socio-Economic Integrated Basin Management Function (SEW Function). The parameters for these three functions are listed in

Table 1. Formulas for calculation of parameters.

Morphometric and Other Parameters
1. Linear morphometric parameters
ID	Parameters	Symbol	Methods of calculation	Units	References
1.1.	Stream order	U	Hierarchical ranking	Dimensionless	[49]
1.2.	Stream number	Nu	Nu = N1 + N2 + … + Nn	Dimensionless	[50]
1.3.	Stream length	Lu	Lu = L1 + L2 + … + Ln	km	[50]
1.4.	Mean stream length	Lm	Lm = Lu/Nu	km	[49]
1.5.	Stream length ratio	Rl	Rl = Lu/Lu − 1	Dimensionless	[50]
1.6.	Bifurcation ratio	Rb	Rb = Nu/Nu + 1	Dimensionless	[50]
1.7.	Basin length	Lb	Lb = 1.312 * A^0.568	km	[51,52]
2. Shape morphometric parameters
2.1.	Form factor	Ff	Ff = A/Lb2	Dimensionless	[53]
2.2.	Elongation ratio	Re	Re = (1.128 * A^0.5)/Lb	Dimensionless	[51]
2.3.	Circulatory ratio	Rc	Rc = 4πA/P2	Dimensionless	[54]
2.4.	Compactness coefficient	Cc	Cc = P/(2 × (π * A)1/2	Dimensionless	[50,55]
2.5.	Basin of perimeter	P	GIS operation	km	[50]
2.6.	Basin of area	A	GIS operation	km2	[50]
3. Areal morphometric parameters
3.1.	Stream frequency	Fs	Fs = Nu/A	1/km2	[50]
3.2.	Drainage texture	Dt	Dt = Nu/P	1/km2	[50]
3.3.	Drainage density	Dd	Dd = Lu/A	km/km2	[50]
3.4.	Infiltration number	If	If = Dd * Fs	1/km2	[56]
3.5.	Length of overland flow	Lo	Lo = 1/(2 * Dd)	km	[50]
3.6.	Constant of channel maintenance	C	C = 1/Dd	km	[51]
4. Relief morphometric parameters
4.1.	Basin relief	R	R = H − h	Dimensionless	[51]
4.2.	Relief ratio	Rr	Rr = (H − h)/Lb	Dimensionless	[51]
4.3.	Ruggedness number	Rn	Rn = Dd * (H − h)	Dimensionless	[51]
4.4.	Melton’s Rudgedness number	Mrn	Mrn = R/A1/2	Dimensionless	[57]
4.5.	Channel gradient	Cg	Cg = (H − h)/(π/2 * Lb)	Dimensionless	[58]
4.6.	Dissection index	Din	Din = (H − h)/H	Dimensionless	[55]
4.7.	Hypsometric integral	HI	HI = (Emean − Emin)/(Emax − E min)	Dimensionless	[59,60]
4.8.	Mean elevation	Emean	DEM Solutions	m	[61]
4.9.	Minimum elevation	Emin	DEM Solutions	m	[61]
4.10.	Maximum elevation	Emax	DEM Solutions	m	[61]
5. Other parameters
5.1.	Digital Elevation Model	EU-DEM	EU-DEM v1.1	30 m	[61]
5.2.	Land Cover	LC	Corine Land Cover 2018	25 ha/100 m	[62]
5.3.	Settlement Count	Sc	OSM-derived point data filtered by basin boundary in GEE	Number of settlements	[63,64,65]

. Watershed management involves three interconnected sub-functions: the soil conservation function (EFR), which addresses erosion and flood risk; the prioritization function (PBW), which focuses on watershed water yield; and the watershed management function (SEW), which incorporates socio-economic factors. Morphometric indicators, land use variables, and settlement data were used to represent these functions, respectively. Categorization is based on the principles of integrated watershed management. It is essential to identify the sub-basins necessitating priority intervention to manage erosion and flooding, ensure the quantity and quality of water sourced from the basin, and consider socio-economic conditions and the esthetic value of natural resources. This study offers a comprehensive prioritization framework for decision-makers by integrating hydrological processes (EFR and PBW) with socio-economic factors (SEW), in contrast to previous studies that typically concentrated on a singular function. According to their hydrological and management relevance, the parameters were grouped into three functions—EFR, PBW, and SEW—as summarized in

Table A2. Parameters associated with watershed prioritization functions.

Parameters	EFR Function	PBW Function	SEW Function
Elevation (max, min, mean)	✓
Basin relief (R)	✓
Relief ratio (Rr)	✓
Ruggedness number (Rn)	✓
Molten Ruggedness number (Mrn)	✓
Channel gradient (Cg)	✓
Dissection index (Din)	✓
Hypsometric integral (HI)	✓	✓
Drainage density (Dd)	✓	✓
Stream frequency (Fs)	✓	✓	✓
Infiltration number (If)	✓
Bifurcation ratio (Rb)	✓	✓	✓
Basin length (Lb)	✓	✓	✓
Perimeter (P)	✓	✓	✓
Drainage texture (Dt)	✓	✓	✓
Length of overland flow (Lo)	✓
Forest Area (km2)	✓	✓
Agriculture (km2)	✓	✓	✓
Artificial Areas (km2)	✓		✓
Area (A)		✓
Stream length (Lu)		✓
Mean stream length (Lm)		✓
Stream length ratio (Rl)		✓
Constant of channel maintenance (C)		✓
Water (km2)		✓
Wetlands (km2)		✓
Settlement Count			✓
Semi Natural Area (km2)			✓
Stream order (U)			✓
Stream number (Nu)			✓
Form factor (Ff)			✓
Elongation ratio (Re)			✓
Circulatory ratio (Rc)			✓
Compactness coefficient (Cc)			✓

(Appendix A).

2.3. Computational Environment and Tools

All statistical analyses, data manipulation, and visualization were conducted using Python (version 3.11.13) [66] within Google Colab [67], a cloud-based Jupyter notebook environment offered by Google. The Gemini large language model (Google, 2025) [68], integrated with Google Colab, was utilized as an AI-powered resource to generate Python code for specific sections. The libraries utilized for data manipulation and correlation analyses included pandas (version 2.2.2) [69,70], NumPy (version 2.0.2) [71], and scipy.stats (version 1.15.3) [72]. The Shapiro–Wilk normality test was conducted utilizing the shapiro() function from the scipy.stats library (version 1.15.3). Data standardization was performed using the StandardScaler function from the scikit-learn library (version 1.6.1) [73]. The correlation matrix was computed utilizing the corr() function from pandas by selecting numerical columns. PCA was conducted using the Python programming language within the Google Colab [67] environment, employing the scikit-learn, matplotlib, and seaborn libraries for analysis and visualization.

2.4. Data Preprocessing

Initially, a comprehensive correlation analysis was conducted to identify potential relationships within the data set. The parameters were categorized into three functional groups according to the basin prioritization objectives, and the interrelationships among the parameters were comprehensively assessed before this categorization. The Pearson correlation matrix indicated a strong correlation (r ≥ 0.9) between certain parameter pairs. To mitigate multicollinearity concerns, only one variable from each pair was retained in the analyses. The dataset’s normality was assessed via the Shapiro–Wilk test, revealing that the majority of variables significantly deviated from normal distribution (p < 0.05). In addition, z-score standardization was utilized to mitigate the effect of scale differences and guarantee that all variables contributed uniformly to PCA. This procedure facilitated a more rigorous examination of the variance and linear correlations among variables. Furthermore, PCA is a method based on linear correlations, and its applicability was unaffected by the non-normal distribution of the variables.

The standardization formula used was as follows [74]:

$$Z={\displaystyle \frac{X-X\mu }{\sigma }}$$

(1)

where Z is the standardized value (z-score), X is the original data point, Xµ is the mean of the variable, and σ is the standard deviation of the variable.

PCA was initially introduced by Pearson in 1901 [75], subsequently refined by Hotelling in 1933 [76], and established as a standard statistical technique with the advent of computer-assisted analysis, as noted by Anderson (1963) [77], Rao (1964) [78], Gower (1966) [79], and Jeffers (1967) [80]. PCA is extensively utilized in meteorology and oceanography, favored for dimensionality reduction and pattern recognition in multivariate datasets [81]. This technique converts variables into independent components utilizing the eigenvalue decomposition of the correlation or covariance matrix. This study employed PCA to reduce the parameter count, identify predominant variables, and examine the data structure.

Principal Component Weighting and Development of Prioritization Index (EFR, PBW, SEW Function).

2.4.1. Weighting

Weights for each principal component (PC1, PC2, PC3, …, PCn) were determined by calculating the proportion of variance explained by each component relative to the total variance.

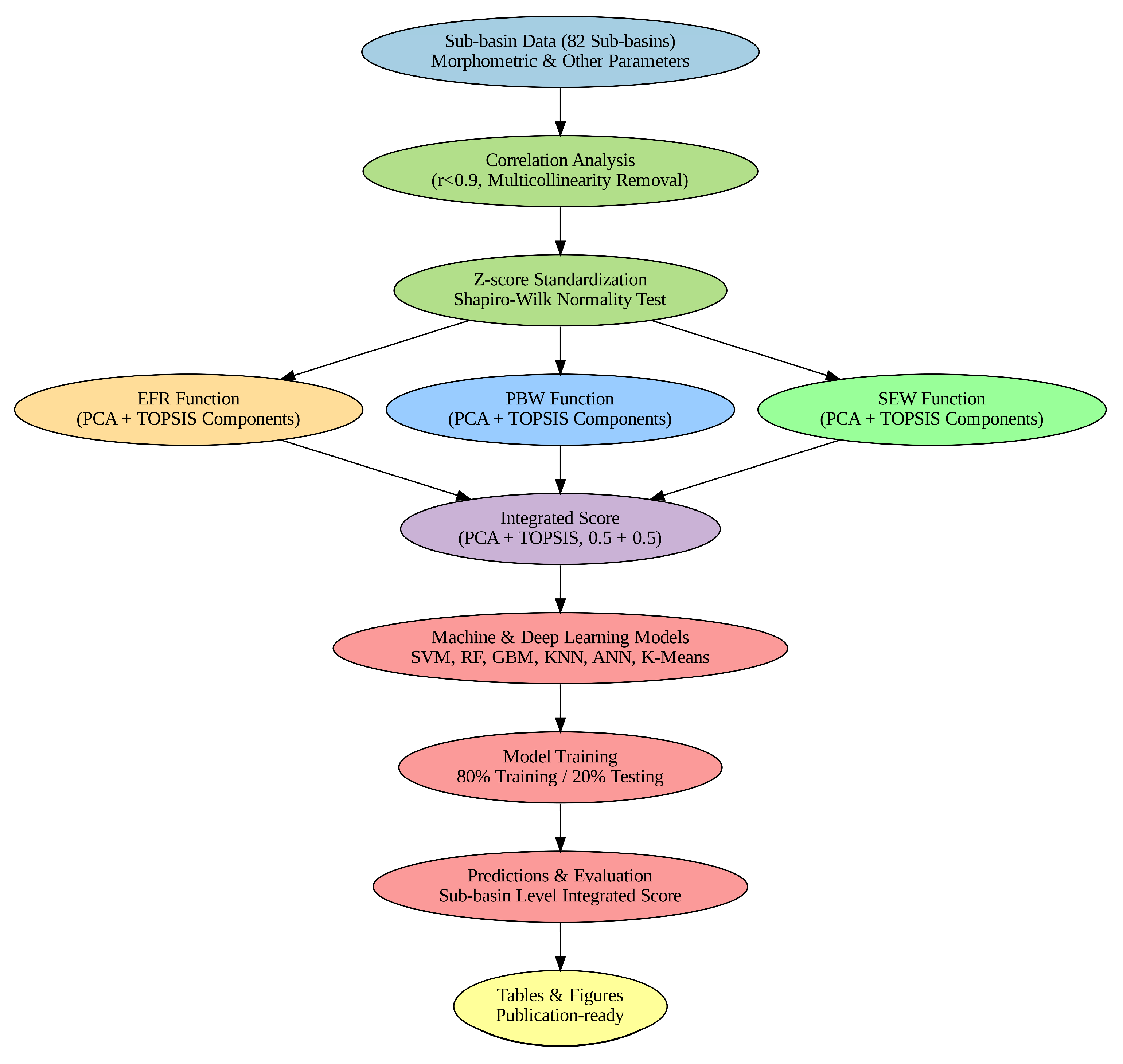
2.4.2. Calculation of the Prioritization Index

The prioritization index for each sub-basin was calculated by summing the products of the principal component values and their corresponding weights. This formulation facilitates the derivation of a composite prioritization index for each basin.

Prioritization Index = (PC1 value × PC1 weight) + (PC2 value × PC2 weight) + … + (PCn value × PCn weight)

(2)

For the prioritization index, typically higher scores signify greater priority. Negative scores, however, could introduce ambiguity and result in inaccurate rankings. This process may distort the semantic framework of negative correlations (anti-correlations) within the data. Consequently, the absolute value method should be employed solely for ranking purposes and should not be utilized for interpreting variables. To address this, the absolute values of the scores were used, transforming them into a positive scale and simplifying the comparison of scores across different components.

The correlation analysis and retained parameters are shown in Supplementary Files such as Table S1 and Figure S1.

2.4.3. Ranking the Sub-Basins

Sub-basins were ranked in descending order based on the computed prioritization indices, with the highest values identified as the areas of greatest priority. The TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) employed in this analysis is a multi-criteria decision-making (MCDM) method developed by Hwang and Yoon in 1981 [82]. The approach ranks each alternative by considering its proximity to both the ideal and anti-ideal solutions. The alternative closest to the ideal solution and furthest from the anti-ideal solution is regarded as the most appropriate alternative. TOPSIS is widely applicable because it effectively balances criteria, compensates for deficiencies in weaker criteria with superior performance in others, and is user-friendly [83]. In all MCDM applications, an m × n decision matrix is created for analysis [84].

TOPSIS Implementation Steps

Step 1: Creating the decision matrix

As a practical step, a decision matrix was created that includes the alternatives (sub-basins) and criteria, specifically the EFR, PBW, and SEW PCA score values.

$$D=Xij$$

(3)

Step 2: Creating the normalized decision matrix

The PCA score criterion values for the EFR, PBW, and SEW functions were normalized to ensure comparability of data across different scales.

$$rij={\displaystyle \frac{xij}{\sqrt{{{\displaystyle \sum }}_{i=1}^m{x}^{2 }ij}}}$$

(4)

where rij is the normalized criteria value, xij is the original decision matrix value, m is the total number of alternatives, and j is the index of a specific criterion.

Step 3: Creating the weighted normalized decision matrix

The weighted normalized decision matrix was created by determining the importance levels (weights) of the criteria for the EFR, PBW, and SEW functions.

$$vij=wj\times rij$$

(5)

where vij is the weighted normalized performance value, wj is the weight of the j-th criterion, and rij is the normalized performance rating for the j-th criterion.

Step 4: Determining ideal and anti-ideal solutions

The ideal (best) and anti-ideal (worst) values were determined.

$$\begin{gathered} A^{+}=(\underset{i}{\max }Vij) for beneficial criteria and \\ {A}^{+}=(\underset{i}{\min }Vij) for non\text{-}beneficial criteria \end{gathered}$$

(6)

$$\begin{gathered} A^{-}=(\underset{i}{\min }Vij) for beneficial criteria and \\ {A}^{-}=(\underset{i}{\max }Vij) for non\text{-}beneficial criteria \end{gathered}$$

(7)

where vij is the weighted normalized performance value. The positive ideal solution takes the best value for each criterion (maximum for beneficial criteria, minimum for non-beneficial criteria). The negative ideal solution takes the worst value for each criterion (minimum for beneficial criteria, maximum for non-beneficial criteria).

Step 5: Calculating distance to ideal and anti-ideal solutions

The distances of each alternative of the EFR, PBW, and SEW functions to the ideal (Di) and anti-ideal (Si) solutions were calculated.

Distance to the ideal solution (Di),

$$Di=\sqrt{{{\displaystyle \sum }}_{j=1}^n(Vij-}{A}_j^{+})2$$

(8)

Distance to the anti-ideal solution (Si),

$$Si=\sqrt{{{\displaystyle \sum }}_{j=1}^n(Vij-}{A}_j^{-})2$$

(9)

where vij is the weighted normalized performance value for alternative i and criterion j, $A_j^{+}$ positive ideal solution for criterion j, $A_j^{-}$ negative ideal solution for criterion j, n number of criteria, Di distance of alternative i to the ideal solution, Si distance of alternative i to the anti-ideal solution.

Step 6: Calculating relative closeness values

The relative closeness value of each alternative of the EFR, PBW, and SEW functions to the ideal solution was calculated.

$$Ci={\displaystyle \frac{Si}{Di+Si}}$$

(10)

where Ci is the relative closeness of alternative i to the ideal solution, Si is the distance of alternative i to the anti-ideal solution, and Di is the distance of alternative i to the ideal solution.

Finally, the sub-basins were ranked based on their relative closeness values, with the highest value assigned as the top priority sub-basin and the lowest as the least priority. For machine and deep learning analyses, the dataset was prepared by integrating the TOPSIS and PCA scores with equal weights of 0.5 each, and this combined score was defined as the target variable. The first column of the dataset represents the sub-basins, the second column contains the integrated TOPSIS + PCA scores, and the subsequent columns include the standardized PCA components derived from each function. These components were used as input variables in the machine and deep learning models (

Table A1. Integrated subbasin scores and clusters—EFR, PBW, and SEW functions.

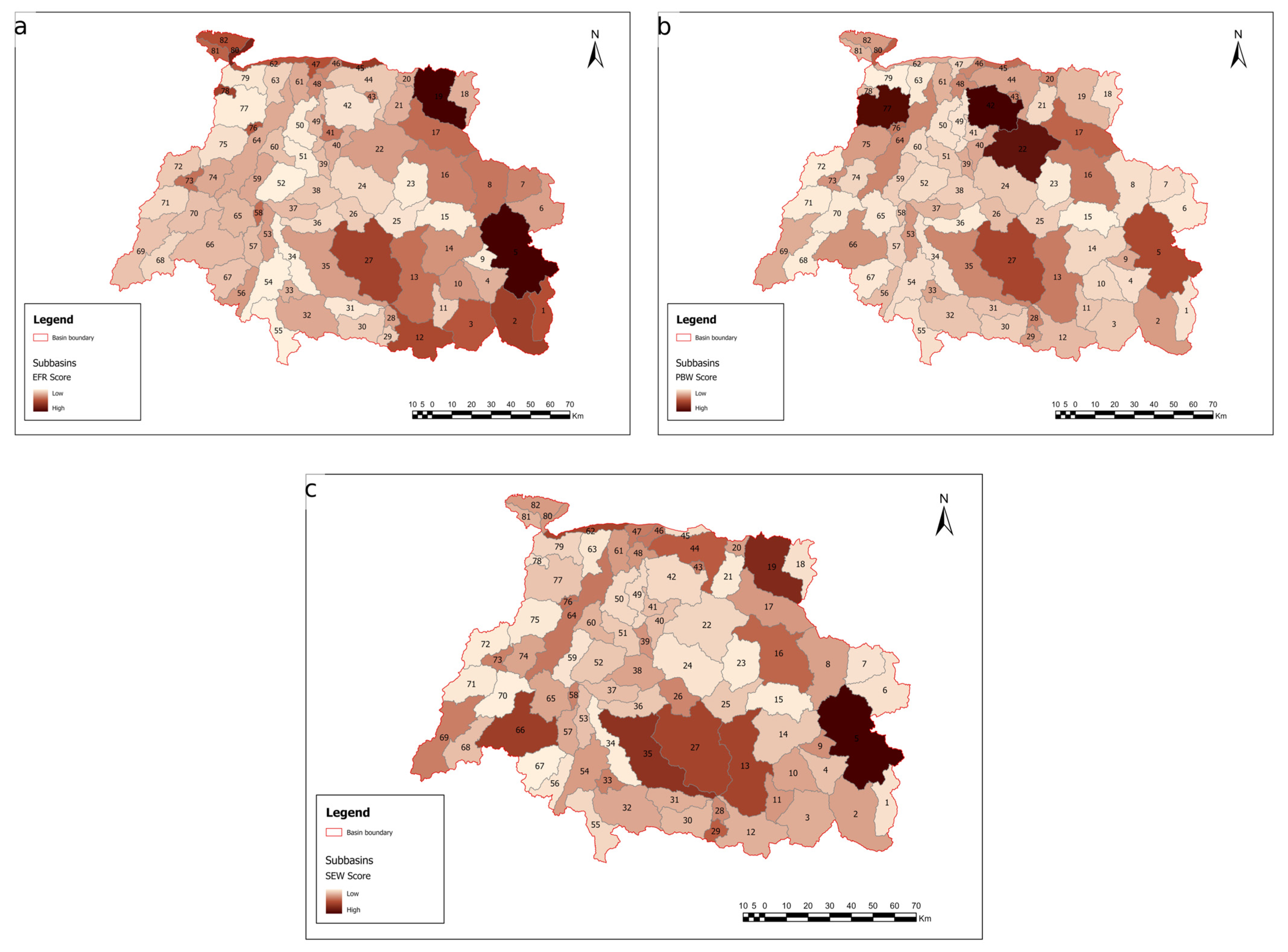
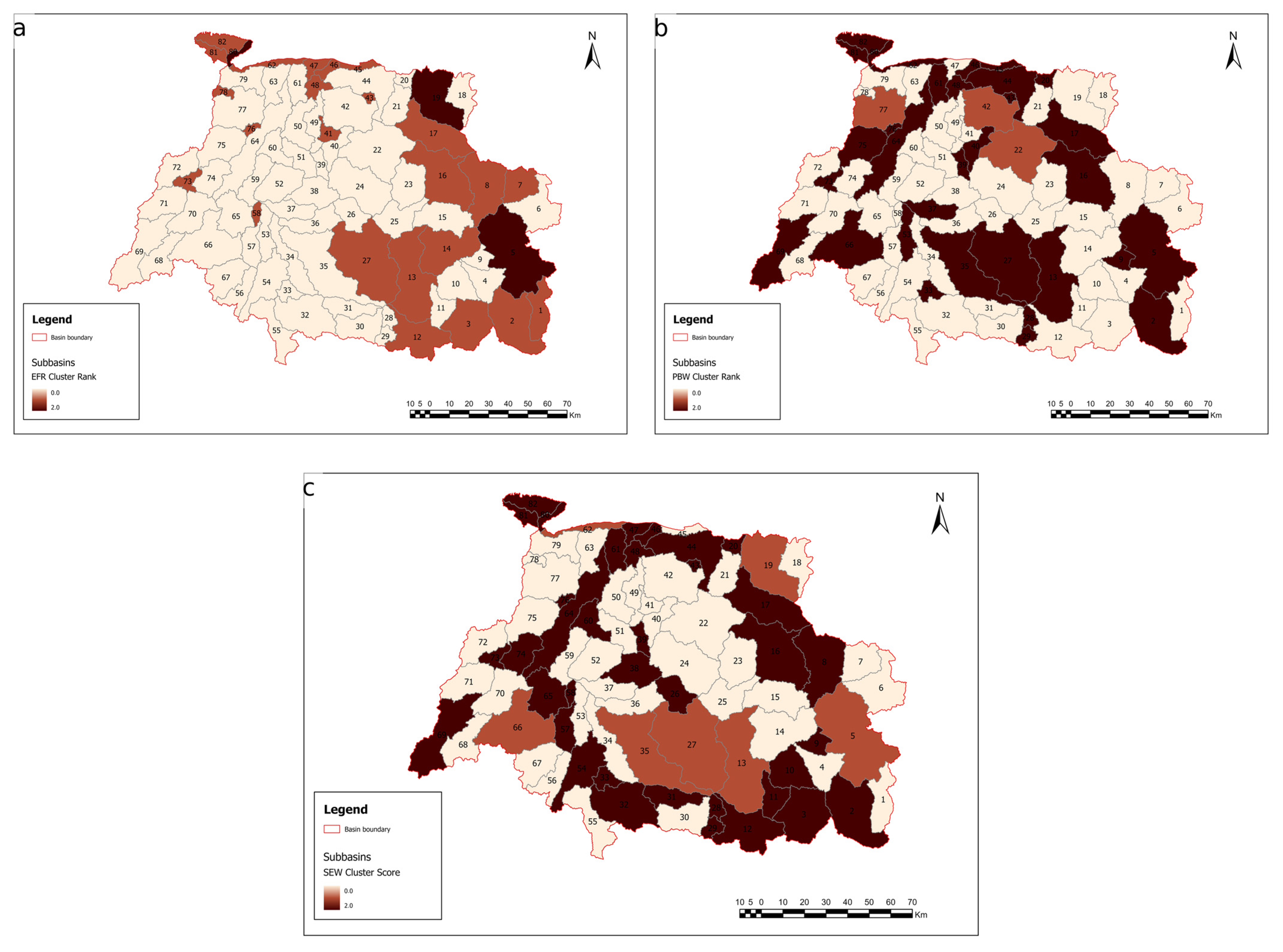
Subbasin	EFR TOPSIS + PCA Integrated Score	EFR Ranking	PBW TOPSIS + PCA Integrated Score	PBW Ranking	SEW TOPSIS + PCA Integrated Score	SEW Ranking	EFR Cluster	EFR Score	PBW Cluster	PBW Score	SEW Cluster	SEW Score
SB1	0.502	10	0.043	69	0.047	68	0.262	1	0.388	0	0.561	0
SB2	0.594	5	0.259	24	0.243	33	0.27	1	0.473	2	0.323	2
SB3	0.48	12	0.118	47	0.209	40	0.477	1	0.879	0	0.48	2
SB4	0.195	44	0.056	62	0.146	51	0.312	0	0.314	0	1.621	0
SB5	1	1	0.537	5	1	1	0.362	2	0.309	2	0.225	1
SB6	0.252	32	0.025	72	0.047	67	0.468	0	0.681	0	0.498	0
SB7	0.339	23	0.054	64	0.044	69	0.417	1	0.512	0	0.546	0
SB8	0.376	20	0.05	66	0.244	32	0.391	1	0.583	0	0.329	2
SB9	0.015	74	0.219	29	0.297	22	0.434	0	0.677	2	0.65	2
SB10	0.274	28	0.074	57	0.241	34	0.433	0	0.65	0	0.404	2
SB11	0.106	61	0.134	42	0.273	26	0.418	0	0.684	0	0.726	2
SB12	0.539	8	0.168	37	0.198	42	0.386	1	0.555	0	0.676	2
SB13	0.398	18	0.355	11	0.563	6	0.444	1	0.439	2	0.344	1
SB14	0.291	27	0.079	56	0.129	55	0.406	1	0.373	0	0.392	0
SB15	0.009	77	0	82	0.011	78	0.409	0	0.444	0	0.662	0
SB16	0.342	22	0.362	10	0.428	10	0.493	1	0.407	2	0.388	2
SB17	0.413	16	0.432	7	0.271	27	0.235	1	0.257	2	0.278	2
SB18	0.201	42	0.055	63	0.051	66	0.246	0	0.431	0	0.412	0
SB19	1	2	0.172	36	0.728	2	0.248	2	0.488	0	0.163	1
SB20	0.22	37	0.324	16	0.246	31	0.488	0	0.482	2	0.48	2
SB21	0.199	43	0.071	58	0.021	74	0.36	0	0.566	0	0.297	0
SB22	0.253	31	0.882	3	0.083	59	0.297	0	0.144	1	0.307	0
SB23	0.014	76	0.02	75	0.014	77	0.539	0	0.43	0	0.318	0
SB24	0.069	68	0.129	45	0.037	72	0.327	0	0.372	0	0.51	0
SB25	0.038	71	0.105	50	0.129	56	0.818	0	0.804	0	0.453	0
SB26	0.111	60	0.162	38	0.328	20	0.455	0	0.476	0	0.495	2
SB27	0.57	7	0.556	4	0.566	5	0.256	1	0.242	2	0.321	1
SB28	0.24	34	0.329	13	0.315	21	0.221	0	0.303	2	0.337	2
SB29	0.105	62	0.26	22	0.456	9	0.362	0	0.521	2	0.707	2
SB30	0.115	59	0.105	49	0.176	45	0.69	0	0.659	0	1.056	0
SB31	0.024	73	0.14	41	0.204	41	0.586	0	1.002	0	0.793	2
SB32	0.223	36	0.133	43	0.226	38	0.732	0	0.858	0	0.629	2
SB33	0.189	45	0.235	27	0.346	17	0.439	0	0.616	2	0.785	2
SB34	0.003	79	0.045	68	0.008	80	0.562	0	0.871	0	0.431	0
SB35	0.256	30	0.327	14	0.669	3	0.41	0	0.438	2	0.324	1
SB36	0.07	66	0.011	79	0.13	53	0.385	0	0.411	0	0.489	0
SB37	0.165	47	0.19	34	0.155	48	0.804	0	1.08	2	0.572	0
SB38	0.124	57	0.104	51	0.239	35	0.47	0	0.495	0	0.531	2
SB39	0.156	50	0.216	30	0.286	23	0.334	0	0.463	2	0.738	2
SB40	0.201	41	0.226	28	0.156	46	0.621	0	0.822	2	0.431	0
SB41	0.375	21	0.09	52	0.155	47	0.354	1	0.317	0	0.412	0
SB42	0.043	70	1	1	0.072	61	0.404	0	0.229	1	0.421	0
SB43	0.33	24	0.349	12	0.356	15	0.299	1	0.341	2	0.22	2
SB44	0.125	56	0.245	26	0.464	8	0.372	0	0.334	2	0.33	2
SB45	0.631	4	0.399	8	0.067	64	0.284	1	0.3	2	0.334	0
SB46	0.32	25	0.324	17	0.378	12	0.359	1	0.385	2	0.305	2
SB47	0.496	11	0.083	54	0.359	14	0.474	1	0.351	0	0.373	2
SB48	0.306	26	0.312	18	0.281	24	0.387	1	0.459	2	0.352	2
SB49	0.155	51	0.04	70	0.07	63	0.394	0	0.271	0	0.357	0
SB50	0.014	75	0.049	67	0.071	62	0.384	0	0.381	0	0.351	0
SB51	0.099	63	0.119	46	0.116	57	0.418	0	0.496	0	0.556	0
SB52	0	81	0.068	60	0.129	54	0.547	0	0.815	0	0.326	0
SB53	0.25	33	0.274	21	0.149	50	0.412	0	0.496	2	0.446	0
SB54	0	80	0.057	61	0.257	30	0.576	0	0.703	0	0.456	2
SB55	0	82	0.05	65	0.076	60	0.787	0	0.817	0	0.373	0
SB56	0.262	29	0.159	39	0.037	71	0.691	0	0.749	0	0.518	0
SB57	0.159	49	0.089	53	0.22	39	0.609	0	0.572	0	0.801	2
SB58	0.404	17	0.132	44	0.338	19	0.345	1	0.338	0	0.29	2
SB59	0.225	35	0.111	48	0.039	70	1.117	0	1.087	0	1.391	0
SB60	0.144	53	0.07	59	0.194	43	0.516	0	0.466	0	0.377	2
SB61	0.214	40	0.192	33	0.261	29	0.748	0	0.788	2	0.346	2
SB62	0.48	13	0.2	32	0.559	7	0.154	1	0.152	2	0.159	1
SB63	0.096	64	0.018	76	0.03	73	0.446	0	0.441	0	0.441	0
SB64	0.216	39	0.325	15	0.372	13	0.38	0	0.27	2	0.22	2
SB65	0.175	46	0.028	71	0.232	37	0.302	0	0.618	0	0.31	2
SB66	0.164	48	0.283	20	0.605	4	0.442	0	0.251	2	0.255	1
SB67	0.142	55	0.023	73	0	82	0.783	0	1.05	0	0.721	0
SB68	0.079	65	0.012	78	0.152	49	0.776	0	0.793	0	0.72	0
SB69	0.143	54	0.207	31	0.352	16	0.743	0	0.71	2	0.466	2
SB70	0.149	52	0.02	74	0.005	81	0.566	0	0.68	0	0.666	0
SB71	0.069	67	0.013	77	0.019	76	0.823	0	0.865	0	0.786	0
SB72	0.121	58	0.008	80	0.01	79	0.747	0	1	0	0.669	0
SB73	0.392	19	0.285	19	0.346	18	0.613	1	0.645	2	0.609	2
SB74	0.22	38	0.082	55	0.235	36	0.766	0	1.063	0	0.691	2
SB75	0.051	69	0.258	25	0.021	75	0.596	0	0.435	2	0.363	0
SB76	0.471	14	0.365	9	0.388	11	0.352	1	0.373	2	0.466	2
SB77	0.007	78	0.936	2	0.132	52	0.253	0	0.273	1	0.297	0
SB78	0.576	6	0.155	40	0.051	65	0.237	1	0.257	0	0.356	0
SB79	0.032	72	0.003	81	0.091	58	0.446	0	0.476	0	0.35	0
SB80	0.77	3	0.446	6	0.277	25	0.226	2	0.216	2	0.271	2
SB81	0.438	15	0.19	35	0.189	44	0.349	1	0.332	2	0.38	2
SB82	0.506	9	0.26	23	0.262	28	0.376	1	0.362	2	0.453	2

). This integration allowed for the elimination of subjective weighting methods and the establishment of an objective, uni-repeatable prioritization index. The deployment of machine learning aimed to determine the effectiveness of data-driven models in sub-basin prioritization, rather than to re-estimate TOPSIS. This method removes subjective weighting and guarantees an equitable contribution of multivariate analysis and multi-criteria decision-making results [85].

Detailed PCA results, including eigenvalues, explained variance ratios, component matrices, and 3D PCA score plots for each function (EFR, PBW, SEW), are provided in the Supplementary Materials (Tables S4–S12; Figures S2–S7).

2.5. Method

Machine and Deep Learning Methods for Sub-Basin Prioritization Analysis

Machine and deep learning methods were employed to prioritize sub-basins using integrated TOPSIS + PCA scores as the target variable. Machine learning algorithms included Support Vector Machine (SVM), Random Forest (RF), Gradient Boosting Machine (GBM), K-Nearest Neighbor (KNN), and K-Means Clustering. Artificial Neural Networks (ANNs) were used as the deep learning method. Additionally, K-Means Clustering was applied to group sub-basins with similar characteristics. Prior to modeling, PCA-derived data were standardized. The dataset was split into 80% training and 20% test subsets (random state = 42). Python libraries such as Pandas and NumPy were used for data preprocessing; Scikit-learn for machine learning, model evaluation, and hyperparameter tuning (Grid search, Randomized search, and/or Optuna Bayesian optimization); TensorFlow (v 2.18.0) [86] and Keras (v 3.8.0) [87] for deep learning; and Matplotlib (v 3.10.0) [88] and Seaborn (v 0.13.2) [89] for visualization. Performance metrics (MSE, R², MAE), cross-validation, and learning curves were also generated using Scikit-learn. In the sub-basin prioritization study, the integrated TOPSIS + PCA score served as the target variable across all models, and machine learning techniques were employed to evaluate the effectiveness of data-driven models in sub-basin prioritization, rather than to re-estimate TOPSIS. Among all hyperparameter combinations tested across all models, the configuration yielding the highest mean cross-validated R² score (based on 5-fold CV) was selected as the best-performing model for each function (EFR, PBW, SEW). Performance metrics (R², MSE, MAE) were evaluated on the testing subset, whereas the mean cross-validated R² scores (5-fold CV) were obtained during the training phase to assess model generalization.

• Support Vector Machine (SVM)

Support Vector Machine (SVM) serve as a technique mainly aimed at classification tasks, adeptly mapping non-linearly separable data into high-dimensional spaces through the application of kernel functions, thereby minimizing the likelihood of overfitting [90]. This study involved selecting the optimal hyperparameter configuration for the Support Vector Regression (SVR) model, culminating in the development of the final model utilizing PCA and integrated score data. The SVM regression model was utilized for the EFR, PBW, and SEW functions. Three distinct hyperparameter optimization techniques were employed to enhance the model’s performance. The optimal hyperparameters were identified using Optuna (EFR) and GridSearchCV (PBW and SEW), optimizing the kernel type (rbf, linear, poly), as well as the C, epsilon, and gamma parameters. Five-fold cross-validation and data standardization using StandardScaler were employed to reduce the risk of model overfitting and accurately identify nonlinear relationships. The generalization capacity of the model was assessed through an analysis of learning curves. Support Vector Machine (SVM) was selected due to its reliable prediction of sub-basin scores, effectively capturing non-linear relationships and modeling complex interactions among variables (

Table 2. Optimal hyperparameter values along with MSE, R², MAE, and the best cross-validated score, as per SVM.

Function	Model	MSE	R2	MAE	Optimal Hyperparameter Values	The Best Cross-Validated Score (R2)
EFR	SVM *	0.063	0.35	0.167	C: 1.3838670221497307 epsilon: 0.006888133398756345 gamma: auto, kernel: rbf	0.42 ± 0.24
PBW	SVM	0.003	0.87	0.045	C: 10, epsilon: 0.01, gamma: scale, kernel: rbf	0.65 ± 0.24
SEW	SVM	0.038	0.46	0.111	C: 10, epsilon: 0.01 gamma: auto, kernel: rbf	0.59 ± 0.22

Note: * The hyperparameter values in the EFR function were determined using the Optuna model.

).

2.

Random Forest (RF)

Random Forest is an ensemble technique comprising numerous independent decision trees [91]. Increasing the quantity of trees diminishes generalization error and aids in feature selection due to the model’s capacity to assess variable significance. RF is effective in both classification and regression tasks. This study identified the optimal hyperparameters for the RF regression model. Performance was assessed through learning curves and metrics. The Random Forest regression model was utilized for three functions: EFR, PBW, and SEW. Hyperparameter optimization was conducted using RandomizedSearchCV for EFR and GridSearchCV for PBW and SEW. The parameters including the number of trees (n_estimators), maximum tree depth (max_depth), minimum number of leaf samples (min_samples_leaf), and minimum number of splitting samples (min_samples_split) were optimized. Overfitting was assessed using five-fold cross-validation and learning curves. Random Forest (RF) effectively predicted sub-basin scores due to its capacity to capture non-linear relationships and evaluate variable importance, thereby enhancing the model’s explanatory power, particularly by clarifying the interactions among attributes in the dataset (

Table 3. Optimal hyperparameter values and MSE, R², MAE, and the best cross-validated score, as per RF.

Function	Model	MSE	R2	MAE	Optimal Hyperparameter Values	The Best Cross- Validated Score (R2)
EFR	RF	0.081	0.16	0.209	max depth: 18, min samples leaf: 1 min samples split: 3, n_estimators: 160	0.08 ± 0.26
PBW	RF	0.008	0.61	0.074	max depth: 26, min samples leaf: 1 min samples split: 2, n_estimators: 67	0.57 ± 0.05
SEW	RF	0.025	0.64	0.114	max depth: none, min samples leaf: 2 min samples split: 2, n_estimators: 50	0.44 ± 0.19

).

3.

Gradient Boosting Machine (GBM)

Gradient Boosting Machine (GBM) is a robust ensemble technique that minimizes error through the iterative application of weak models [92,93]. Hyperparameter optimization was conducted using GridSearchCV for the EFR and PBW functions, and RandomizedSearchCV for the SEW function. The optimized parameters the included learning rate, maximum tree depth, minimum number of leaf samples, minimum number of splitting samples, and number of trees. The model’s performance was assessed through variable significance analysis, five-fold cross-validation, and learning curves. Overfitting was mitigated, non-linear relationships were effectively captured, and predictions for sub-basin scores were made (

Table 4. Optimal hyperparameter values and MSE, R², MAE, and the best cross-validated score, as per GBM.

Function	Model	MSE	R2	MAE	Optimal Hyperparameter Values	The Best Cross- Validated Score (R2)
EFR	GBM	0.084	0.13	0.209	learning rate: 0.01, max depth: 5 min sample leaf: 1, min sample split: 10 n estimators: 200	−0.002 ± 0.232
PBW	GBM	0.007	0.68	0.066	learning rate: 0.1, max depth: 5 min sample leaf: 1, min sample split: 10 n estimators: 200	0.60 ± 0.05
SEW	GBM	0.022	0.69	0.104	learning rate: 0.1331, max depth: 5 min sample leaf: 2, min sample split: 2 n estimators: 177	0.44 ± 0.22

).

4.

K-Nearest Neighbor (KNN)

KNN is a technique employed in classification and regression owing to its straightforward and adaptable framework. Hyperparameter optimization is crucial due to constraints like sensitivity to distance computations and uniform weighting of neighbors [94]. Hyperparameter optimization utilized RandomizedSearchCV for EFR and SEW functions, while GridSearchCV was employed for PBW. The optimization focused on the number of neighbors, distance parameter (p: Manhattan or Euclidean), and weighting method (uniform or distance). A five-fold cross-validation was conducted utilizing data standardized with StandardScaler, minimizing the risk of overfitting and providing reliable estimates of both linear and non-linear relationships (

Table 5. Optimal hyperparameter values and MSE, R², MAE, and the best cross-validated score, as per KNN.

Function	Model	MSE	R2	MAE	Optimal Hyperparameter Values	The Best Cross- Validated Score (R2)
EFR	KNN	0.076	0.21	0.175	n neighbors: 4, p: 1, weights: distance	0.23 ± 0.09
PBW	KNN	0.013	0.39	0.086	n neighbors: 3, p: 1, weights: distance	0.36 ± 0.22
SEW	KNN	0.064	0.09	0.162	n neighbors: 4, p: 2, weights: distance	0.25 ± 0.14

).

5.

Artificial Neural Networks (ANNs)

Artificial Neural Networks (ANNs) are models derived from the architecture of brain neurons, providing adaptable solutions for intricate pattern recognition and classification due to their non-parametric frameworks [95]. Hyperparameter optimization was conducted using RandomizedSearchCV, focusing on hidden layer sizes, activation functions (relu, tanh), the regularization parameter (alpha), and the learning rate. The application of data standardized with StandardScaler, combined with five-fold cross-validation and learning curve analysis, effectively reduced the risk of overfitting, provided reliable estimates of complex nonlinear relationships, and accurately predicted sub-basin scores (

Table 6. Optimal hyperparameter values and MSE, R², MAE, and the best cross-validated score, as per ANN.

Function	Model	MSE	R2	MAE	Optimal Hyperparameter Values	The Best Cross- Validated Score (R2)
EFR	ANN	0.028	0.71	0.127	activation: relu, alpha: 0.00843 hidden layer sizes: [80, 118] learning rate: adaptive	0.31 ± 0.23
PBW	ANN	0.010	0.56	0.079	activation: tanh, alpha: 0.00366 hidden layer sizes: [88, 54] learning rate: constant	−0.39 ± 0.62
SEW	ANN	0.035	0.36	0.128	activation: relu, alpha: 0.001 hidden layer sizes: [80, 118] learning rate: adaptive	0.36 ± 0.38

).

6.

K-Means Clustering

Clustering is a fundamental technique employed to categorize objects within a data set based on their analogous attributes [96]. The K-Means algorithm clusters data according to distances from cluster centroids but is prone to local minima due to its dependence on initial points; this problem is alleviated through multiple re-initializations [96]. The ideal number of clusters for K-Means implemented in Google Colab [67], derived from the TOPSIS and PCA-based scores of the sub-basins, was established via the elbow method (k = 3), and the efficacy of clustering was assessed using the silhouette, Calinski-Harabasz, and Davies-Bouldin indices. Representative power was assessed by calculating distances to cluster centroids, and the groupings facilitated prioritization analyses via the classification of sub-basins. The K-Means clustering algorithm was utilized for the EFR, PBW, and SEW functions. The model served as a complement to the regression models, enhancing the comprehensive interpretation of the sub-basin prioritization results and reinforcing the robustness of the model as a method, thereby mitigating the risk of overfitting.

3. Results

3.1. PCA Results

The PCA results for the EFR function indicate that the first two components (PCA1 and PCA2) accounted for 50.08% of the total variance. PCA1 accounted for 28.02% of the variance, whereas PCA2 accounted for 22.06%. The third component (PCA3) contributed an additional 15.16% to the variance, resulting in an explained total variance of 65.24%. The variance explanation ratios of subsequent components decreased gradually, with PCA10, PCA11, and PCA12 remaining under 1%. Consequently, the first three components in the EFR function significantly represent the data variance. The PCA results for the PBW function indicate that the first two components account for 51.65% of the total variance, with PCA1 explaining 29.24% and PCA2 explaining 22.41% of the variance. PCA3 contributed an extra 12.71% variance, resulting in a total variance of 64.36%. The variance explanation ratios of subsequent components decreased, with PCA10 and PCA11 remaining under 1%. Consequently, it can be asserted that the initial three components adequately represent the variance of the data set for the PBW function. In the PCA for the SEW function, the initial two components accounted for 55.92% of the total variance. PCA1 accounts for 34.68% of the variance, whereas PCA2 explained 21.24%. The third component contributed 14.52% to the variance, increasing the total variance to 70.44%. The variance contribution of later components continued to decrease, with PCA7 and PCA8 remaining under 3%. Consequently, the initial three elements of the SEW function significantly represent the variance.

Upon analysis of the functions in sequence, for EFR, the first three principal components (PC1 = 28%, PC2 = 22%, PC3 = 15%) accounted for approximately 65% of the total variance; for PBW, the first three principal components (PC1 = 29%, PC2 = 22%, PC3 = 13%) accounted for approximately 64% of the total variance; and for SEW, the first three principal componented account for approximately 70% of the total variance, with PC3 alone contributing 15%. Consequently, in each function, the majority of the variability in the dataset was encapsulated by the initial three principal components.

Machine and Deep Learning Methods for Sub-Basin Prioritization Analysis Results

1.

Support Vector Machine (SVM)

The Support Vector Regression (SVR) model was utilized in the Google Colab [67] environment to assess the priority scores of sub-basins. For reducing dimensionality, PCA was employed, and StandardScaler was used to scale the data. GridSearch, RandomizedSearch, and Optuna were employed for hyperparameter optimization, with Optuna’s Bayesian optimization facilitating the rapid and efficient identification of the optimal model configuration. The performance outcomes are displayed in Table 2.

2.

Random Forest (RF)

The RF regression model was utilized with PCA components and composite scores. Following scaling and dimensionality reduction, the hyperparameters (max_depth, min_samples_leaf, min_samples_split, n_estimators) were optimized through GridSearch, RandomizedSearch, and Optuna. Optuna yielded superior outcomes by executing a more rapid and efficient search. The performance metrics are displayed in Table 3.

3.

Gradient Boosting Machine (GBM)

The GBM model has produced effective outcomes in high-dimensional data through the integration of weak learners. Components and integrated scores derived from PCA were employed, data was standardized using StandardScaler, and hyperparameter optimization (learning_rate, max_depth, min_samples_leaf, min_samples_split, n_estimators) was conducted utilizing GridSearch, RandomizedSearch, and Optuna. The performance results are presented in Table 4.

4.

K-Nearest Neighbor (KNN)

The KNN regression model was utilized with PCA components and combined scores, while the data was normalized and dimensionality reduced. GridSearch, RandomizedSearch, and Optuna were employed for hyperparameter optimization. The optimized parameters comprise n_neighbors, p (distance metric), and weights. Performance metrics are presented in Table 5.

5.

Artificial Neural Networks (ANNs)

The ANN regression model was developed utilizing PCA components and integrated scores, with data scaling and dimensionality reduction implemented. Hyperparameters (activation, alpha, hidden_layer_sizes, learning_rate) were optimized through GridSearch, RandomizedSearch, and Optuna. The optimal model configuration was attained through Optuna’s Bayesian optimization. The performance results are displayed in Table 6.

6.

Evaluation of Model Results

The SVM model achieved the highest efficacy with a R² of 0.87 in the PBW function, as indicated in

Table 7. Comprehensive assessment of the models exhibiting optimal performance.

Function	Model	MSE	R2	MAE	Optimal Hyperparameter Values	The Best Cross- Validated Score (R2)
PBW	SVM	0.003	0.87	0.045	C: 10, epsilon: 0.01, gamma: scale, kernel: rbf	0.65 ± 0.24
PBW	RF	0.008	0.61	0.074	max depth: 26, min samples leaf: 1 min samples split: 2, n_estimators: 67	0.57 ± 0.05
SEW	RF	0.025	0.64	0.114	max depth: none, min samples leaf: 2 min samples split: 2, n_estimators: 50	0.44 ± 0.19
PBW	GBM	0.007	0.68	0.066	learning rate: 0.1, max depth: 5 min sample leaf: 1, min sample split: 10 n estimators: 200	0.60 ± 0.05
SEW	GBM	0.022	0.69	0.104	learning rate: 0.1331, max depth: 5 min sample leaf: 2, min sample split: 2 n estimators: 177	0.44 ± 0.22
PBW	KNN	0.013	0.39	0.086	n neighbors: 3, p: 1, weights: distance	0.36 ± 0.22
EFR	ANN	0.028	0.71	0.127	activation: relu, alpha: 0.00843 hidden layer sizes: [80, 118] learning rate: adaptive	0.31 ± 0.23
PBW	ANN	0.010	0.56	0.079	activation: tanh, alpha: 0.00366 hidden layer sizes: [88, 54] learning rate: constant	−0.39 ± 0.62

. The RF and GBM models achieved high performance with R² values of 0.64 and 0.69, respectively, in the SEW function, whereas the KNN model exhibited low performance with a R² of 0.39 in the PBW function. The ANN model produced acceptable outcomes in the EFR function with R² = 0.71; however, its efficacy decreased to R² = 0.56 in the PBW function. Significant variance (e.g., 0.62 standard deviation in PBW function for ANN) was noted in certain models, signifying model inconsistency. In summary, SVM achieved the highest performance in the PBW function, whereas RF and GBM showed an outstanding performance in the SEW function; conversely, KNN consistently demonstrated a poor performance.

All models analyzed (SVM, RF, GBM, KNN, and ANN) exhibited residual plots indicating that the error distribution was predominantly random and devoid of systematic bias. This suggests that the models produce firm predictions. The outliers identified in the lower left and upper right regions indicate that the predictive performance at the model is deficient at extreme values or that there are inaccuracies in the dataset. The learning curves indicate that all models demonstrate strong alignment with the training data; however, substantial declines in cross-validation scores and the occurrence of negative values suggest an overfitting problem and limited generalization ability. To address this, feature scaling using StandardScaler, hyperparameter optimization through GridSearchCV, RandomizedSearchCV, and Optuna, along with five-fold cross-validation, was implemented across all models. The kernel type, C, epsilon, and gamma parameters in the SVM model; the number of trees (n_estimators), maximum depth (max_depth), minimum number of leaf samples (min_samples_leaf), and minimum number of splitting samples (min_samples_split) in the Random Forest model; in the GBM model, the number of trees, learning rate, maximum depth, minimum number of splits, and leaf samples; in the KNN model, the number of neighbors (n_neighbors), weighting method, and distance metric; and in the ANN model, the hidden layer sizes, activation function, alpha, and learning rate strategy were optimized. Nonetheless, early stopping and direct feature selection were not utilized in the present study. The application of these techniques in subsequent research may further mitigate the risk of overfitting. Moreover, ensemble learning and sophisticated data preprocessing methods can enhance the generalization capability and predictive performance of model. The integration of hyperparameter optimization, feature scaling, and cross-validation effectively mitigated the overfitting issue; however, the implementation of supplementary regularization techniques can enhance the models’ generalization ability. The decline in validation performance with an increase in training examples corroborates the hypothesis that the models exhibit high variance. While scatter plots demonstrate overall fit, deviations in extreme values suggest diminished predictive consistency of the models in these crucial areas, indicating a need for performance enhancement (Figure 3). Given these prevalent observations, it is advisable to implement strategies such as hyperparameter optimization, outlier analysis, and alternative modeling techniques to enhance the models’ overall performance.

This study indicates that K-Nearest Neighbor (KNN) and Artificial Neural Networks (ANNs) exhibited suboptimal performance in comparison to other machine learning algorithms. KNN exhibits sensitivity to high-dimensional data and imbalanced sample distributions among classes, potentially diminishing accuracy in datasets characterized by a substantial number of predictive variables and unequal class distributions. Artificial Neural Networks necessitate comprehensive hyperparameter optimization and substantial training datasets to effectively learn intricate nonlinear relationships. Issues such as overfitting or underfitting may arise when working with limited or inaccurate datasets.

In contrast, Support Vector Machine (SVM), Random Forest (RF), and Gradient Boosting Machine (GBM) algorithms demonstrate superior capability in capturing complex relationships within the dataset and achieving more accurate class separation. Support Vector Machine (SVM) are notable for their capacity to classify data in high-dimensional spaces and to delineate class boundaries effectively. Random Forest enhances its accuracy and generalization ability through the integration of multiple decision trees, demonstrating robustness against overfitting. GBM systematically enhances weak models, comprehensively learns variable effects, and attains superior performance. Upon analysis of function-based results:

PBW: The SVM model demonstrated the highest accuracy, with R² = 0.87, MAE = 0.045, and CV = 0.65 ± 0.24. Random Forest (R² = 0.61) and Gradient Boosting Machine (R² = 0.68) exhibited more balanced performance, albeit with lower explanatory power. In contrast, K-Nearest Neighbor demonstrated significantly weaker performance (R² = 0.39). The learning curves and residual diagrams indicate that the generalization performance of SVM is satisfactory.

SEW: GBM and RF demonstrated superior performance (GBM R² = 0.69; RF R² = 0.64), as the implementation of low to medium learning rates and restricted depth configurations mitigated overfitting and resulted in a more balanced error profile. The KNN model exhibited a decline in R² to 0.09, suggesting that neighborhood representations are compromised by heterogeneous inputs.

In the EFR analysis, the ANN model attained the highest R² value of 0.71. The coefficient of variation for variance was notably high at 0.31 ± 0.23, and generalizability exhibited variability. The negative cross-validation score of the Gradient Boosting Model (−0.002 ± 0.232) indicates challenges in the model’s generalization for this function. Random Forest produced a low R² of 0.16, suggesting that individual tree splits are insufficient for adequately representing interactions and nonlinear relationships among parameters.

7.

Evaluation of K-Means Results

The K-Means clustering analysis presented in

Table 8. Clustering metric values.

Function	Silhouette Score	Calinski-Harabasz Score	Davies-Bouldin Score
EFR	0.63	185.20	0.46
PBW	0.64	270.19	0.40
SEW	0.61	207.73	0.49

assessed the clustering performance of the EFR, PBW, and SEW functions utilizing the Silhouette Score, Calinski-Harabasz score, and Davies-Bouldin score metrics. Silhouette score values ranging from 0.61 to 0.64 demonstrate that the clusters are predominantly well delineated across all functions. The PBW function attained the highest Silhouette score (0.64) and Calinski-Harabasz score (270.19), alongside the lowest Davies-Bouldin score (0.40), demonstrating optimal intra-cluster consistency and inter-cluster separation. This signifies that the PBW function can most effectively differentiate the structures within the dataset and that its clustering quality surpasses that of alternative functions. The EFR and SEW functions achieved similar and average performance. Despite being satisfactory regarding Silhouette and Calinski-Harabasz scores, the SEW function’s elevated Davies-Bouldin score suggests that the similarity among clusters surpasses that of PBW, thereby indicating a diminished distinction between clusters. In conclusion, the clustering efficacy of all functions is satisfactory, with the PBW function distinguished by its superior clustering quality based on metrics.

K-Means analysis identified sub-basins sharing similar traits through the unsupervised clustering the integrated TOPSIS + PCA scores. The Elbow method revealed an optimal cluster quantity of k = 3. The Silhouette, Calinski-Harabasz, and Davies-Bouldin indices were employed to assess the clustering outcomes (Table 8). The separation between clusters is at an acceptable level, as evidenced by high Silhouette values, which indicate meaningful structural integrity within the clusters. This approach positions K-Means as a complementary method that highlights the similarity relations among basins, in contrast to supervised regression-based algorithms. Additionally, the scores obtained from cluster identities and distances to cluster centers for each sub-basin are presented in Appendix Table A1 The scores indicate both the similarity-based classification of the clusters and the relative representativeness of the watersheds. For instance, SB25 and SB59 exhibit the highest scores in the EFR function, whereas SB30 and SB59 are notable in the SEW function. The findings indicate that K-Means provides a complementary viewpoint to prioritization analysis by identifying similarities among basins.

The K-Means clustering analysis resulted in the categorization of the sub-basins into three clusters: 0, 1, and 2. The closeness of each sub-basin to the centroid of its cluster was quantified using a “Score” metric derived from inverse distance. This metric quantitatively indicates the proximity of the sub-basin to the cluster center, and higher scores signify that the sub-basin more accurately represents the cluster and its characteristics are more congruent with the cluster’s overall structure. The ranking and prioritization analyses based on these scores facilitate the assessment of sub-basins in relation to their representativeness within the clusters. Consequently, it is feasible to identify which sub-basins are more crucial and essential for that cluster in decision support processes. This method facilitates the efficient allocation of resources and interventions through a data-driven and objective prioritization strategy (Table A1).

Sub-basins were prioritized based on the composite scores derived from the PCA + TOPSIS methodology, focusing on three primary functions: soil protection concerning erosion and flood risk (EFR), water production (PBW), and integrated basin management incorporating socio-economic factors (SEW). Sub-basins with high scores in the EFR function are considered as high-risk zones due to their morphometric attributes, including topographic slope, stream density, and impermeability. This map offers significant insights for decision-makers in the strategic planning of soil conservation structures and flood risk mitigation measures. In the context of the PBW function, sub-basins were evaluated based on hydraulic attributes including water storage capacity, surface runoff, and stream network density. This map serves to identify prospective regions for water management initiatives, including dams, reservoirs, and irrigation, as well as for the incorporation of long-term water resource planning. The SEW function, conversely, emphasizes regions with significant human influence. This map is generated by integrating socio-economic data, including population density, land use, and transportation infrastructure, thereby assisting local governments in optimizing infrastructure investments and development strategies (Figure 4).

The map generated from the K-Means clustering analysis illustrates the classification of sub-basins exhibiting similar characteristics concerning the EFR function. This clustering method enables the implementation of tailored management interventions for each basin and allows for the standardization of regional management strategies concerning engineering solutions. In the context of the PBW function, clustering facilitates the categorization of sub-basins according to morphometric similarities. Clusters exhibiting high efficiency emerge as focal points for water conservation and sustainable utilization, and can facilitate the advancement of integrated water management applications at the regional level. The clustering executed within the SEW function facilitates the aggregation of sub-basins exhibiting analogous socio-economic and environmental traits. This map enables decision-makers to optimize resource allocation by considering social disparities in regions experiencing significant environmental and anthropogenic pressures (Figure 5).

Evaluating Figure 4 alongside Figure 5 reveals notable differences between the sub-basin prioritization maps derived from the TOPSIS + PCA method and those resulting from K-Means clustering. For instance, SB5 and SB19 are identified as high-priority sub-basins in the EFR function (Figure 4a and Table A1); however, they are situated in distinct clusters (Cluster 2 and Cluster 0) as illustrated in Figure 5a. In a similar manner, SB30, categorized as low priority within the SEW function, is situated in high priority clusters (Cluster 0) according to the K-Means clustering results.

The primary cause of these differences is the characteristics of the employed methods. The TOPSIS + PCA approach employs weighted score integration from multi-criteria decision-making methods for prioritization, whereas K-Means functions as an unsupervised clustering method that categorizes basins based on their similarities. Therefore, TOPSIS + PCA approach scores yield a linear ranking, whereas K-Means establishes relative clusters based primarily on data similarities. This may result in variations among clusters with elevated scores, particularly in basins exhibiting heterogeneous socio-economic or morphometric traits.

In summary, the differences illustrated in Figure 4 and Figure 5, and Table A1 do not indicate a contradiction; rather, they highlight distinct methodological perspectives. The TOPSIS + PCA method offers decision makers an objective priority ranking, whereas the K-Means method presents an alternative evaluation perspective by clustering basins with similar characteristics. Detailed PCA- and TOPSIS-based scores and rankings for each sub-basin are provided in the Supplementary Materials (Tables S2 and S3). The combined interpretation of findings from both methods offers an expanded perspective on sub-basin prioritization and enhances the decision support process.

4. Discussion

Recent studies indicate a preference for morphometric parameters in basin prioritization analyses. The parameters include basin area, perimeter, stream order, stream length, bifurcation ratio, drainage density, stream frequency, drainage texture ratio, length of overland flow, infiltration rate, form factor, shape factor, elongation ratio, ruggedness number, compactness coefficient, circularity ratio, basin relief, slope, and hypsometric integral [7,17,22,24,29,35,37,97,98,99,100,101]. Our study employed a multidimensional analytical approach that incorporatedmorphometric data alongside socio-economic variables, including land use and settlement density. Initially, 36 parameters were evaluated, which underwent correlation analysis to mitigate data redundancy and multicollinearity (Table 1). Variables exhibiting a high correlation (r ≥ 0.90) were eliminated from the dataset, thereby obtaining a more representative parameter set for analysis.

Correlation analyses demonstrated robust and significant associations among several key parameters. The basin area exhibited a strong positive correlation (r > 0.90) with parameters including stream number, stream length, basin length, and perimeter. This suggests that larger basins generally possess more intricate and advanced stream networks, as well as extended boundaries. The strong correlation between drainage texture and basin area (r = 0.89) indicates that larger basins may possess more intricate drainage systems. Shekar and Mathew [102] corroborized this finding by highlighting that the basin perimeter affects hydrological processes. Bharath et al. [100] assert that an expansion of basin area will influence surface runoff. The inverse correlation between the form factor and elongation ratio parameters and basin area (r = −0.88 and −0.89, respectively) suggests that larger basins tend to be elongated and narrow i. Bharath et al. [100] also emphasize the inverse correlation among basin perimeter, elongation ratio, and basin area, paralleling our research findings.

Significant correlations were also identified among topographic parameters. The maximum elevation exhibits a strong positive correlation (r = 0.92) with basin relief and ruggedness index. This signifies that topographic elevations are directly correlated with terrain relief and surface irregularity. The strong correlations among average, maximum, and minimum elevations (r ~ 0.87–0.88) indicate that these parameters are inherently complementary. The inverse correlation between minimum elevation and dissection index (r = −0.95) suggests that reduced minimum elevations correspond to more profound valleys and fragmented topographical features.

Significant correlations have been established between stream network parameters and basin shape variables. The stream number demonstrates a strong positive correlation with total stream length, basin length, and drainage texture (r ≥ 0.90), while displaying a negative correlation with form factor and elongation ratio. This suggests that basins characterized by dense stream networks typically exhibit elongated and narrow forms. Comparable results have been documented in the literature, indicating that shape parameters, including circularity ratio, form factor, and elongation ratio, exhibit negative correlations with numerous morphometric variables [37]. A significant correlation was noted between form factor and elongation ratio, suggesting that both parameters provide similar structural information regarding basin shape. The inverse correlation between these two parameters and drainage density and settlement density indicates that elongated and narrow basins exhibit a less dense settlement pattern and a simpler hydrological network.

The correlations between hydrological and socio-economic variables are significant. Positive correlations were noted between drainage density and infiltration rate, whereas negative correlations were identified between length of overland flow and constant of channel maintenance. These relationships indicate that water permeates more readily and surface runoff transpires over shorter distances in basins characterized by dense river networks. The strong correlation between length of overland flow and constant of channel maintenance suggests that these variables should be assessed concurrently. The robust correlations identified among topographic variables, including relief, ruggedness, and channel slope, unequivocally illustrate that topography significantly influences hydrological processes.

Ultimately, positive correlations were identified between the quantity of settlements and both agricultural and water/wetland areas, demonstrating the direct relationship between human settlements and natural water resources. This outcome confirms the evaluations commonly highlighted in the literature that population growth, climate change, and geomorphological processes intensify pressure on water resources, precipitating risks such as drought and water scarcity [102]. Ahmed et al. [24] observed that morphometric parameters, including drainage density, drainage texture ratio, circularity ratio, relief ratio, and ruggedness number, serve as the most reliable indicators of erosion risk. Dofee et al. [101] asserted that linear, areal, and topographic parameters directly influence soil erosion, whereas shape parameters exhibit an inverse relationship with erosion. The findings of this study largely align with the previously mentioned literature and unequivocally illustrate the significance of a multidimensional assessment approach.

Aher et al. [37] highlighted that, alongside remote sensing and GIS methodologies for morphometric characterization and prioritization of sub-basins, classification techniques such as the analytic hierarchy process, fuzzy logic, and clustering can be employed in conjunction with a correlation matrix for the protection planning of critical areas. Our study employed an integrated approach of PCA and TOPSIS to enhance model performance and strengthen the applicability of machine and deep learning methodologies. In contrast to common techniques in the literature, the dimensionality of the features explaining the variance of the dataset was reduced using PCA, followed by the execution of the multi-criteria decision-making process utilizing the TOPSIS method. This integrated approach guarantees more robust and reliable outcomes in the decision-making process by encompassing a significant portion of all parameters and data variance. This integrated approach yields more robust and reliable outcomes in the decision-making process by considering all parameters and data variability. Our study employed equal weighting of PCA and TOPSIS scores as a methodological decision. Nonetheless, the literature underscores the equitable integration of various multi-criteria evaluation methodologies [103]. The equal weighting facilitates the complementary functioning of PCA’s variance explanation and TOPSIS’s ranking mechanism, preventing one from overshadowing the other, thereby enhancing the reliability and generalizability of the index for sub-basin prioritization.

This method provides a versatile framework applicable to diverse data types across multiple disciplines, thereby establishing a robust foundation that will enhance the development of decision support systems in future research. The PCA component matrix analysis indicates that, within the EFR function, the first component (PC1) exhibits a strong positive correlation with ‘Elevation (Mean)’ and ‘Area (km²),’ while demonstrating a weak negative correlation with ‘Stream frequency (Fs)’ and ‘Drainage density (Dd).’ Consequently, PC1 can be construed as the ‘elevation and area’ component. The second component (PC2) exhibits robust positive correlations with ‘Stream frequency’ and ‘Drainage density,’ alongside weak negative correlations with ‘Relief ratio’ and ‘Agricultural area,’ and can be characterized as the ‘stream density’ component. Components PC3 to PC12 exhibit more complex relationships and signify various combinations of variables. Arefin et al. [98] similarly underscored the significance of variables including drainage density, circularity ratio, elongation ratio, and bifurcation ratio in prioritization based on PCA.

In the examination of the PBW function, PC1 exhibits a robust positive correlation with area and elevation, alongside a weak negative correlation with stream frequency and drainage density. This component may also be assessed as the “area and elevation” component. PC2 exhibits robust positive correlations with “stream frequency” and “drainage density,” alongside weak negative correlations with “relief ratio” and “agricultural area,” and can be characterized as the “stream network component.” More complex structures were identified between PC3 and PC11. In the context of the SEW function, PC1 exhibited a robust positive correlation with ‘Settlement count’ and ‘Agriculture area,’ and was classified as the “settlement and agriculture” component. PC2 exhibits a negative correlation with ‘Stream order’ and a positive correlation with ‘Circularity ratio,’ and is interpreted as the ‘stream geometry’ component. PC3 exhibits a strong correlation with the ‘Circularity ratio’ and ‘Stream frequency’ and can be characterized as the ‘hydrographic features’ component. The residual components (PC4-PC8) signify distinct variable groups. Mishra et al. [104] underscore PCA’s capacity to examine interrelated variables within multivariate data frameworks. Madanchian and Taherdoost [83] assert that TOPSIS provides substantial benefits in multi-criteria decision-making due to its capacity to accommodate both qualitative and quantitative criteria, along with its responsiveness to criterion weights and the selection of reference alternatives.

This study conducted basin prioritization through three primary functions: Soil protection function concerning erosion and flood risk (EFR), prioritization based on basin water yield potential (PBW), and socio-economic integrated basin management function (SEW). Each function signifies distinct basin and protection requirements of basin, while the integrated assessment methodology facilitates a more thorough prioritization.

The EFR function indicates that the SB5, SB19, and SB80 basins possess the highest priority concerning erosion and flood risk. This finding aligns significantly with studies conducted using similar methodologies in the literature. Mawarni et al. [105] indicated that erosion rates in the Arjasa sub-basin may attain 184.81 t/(ha/year) on slopes exceeding 40%, a condition correlated with 56% of the morphometric factors. Gezahegn and Mengistu [106] observed that high-priority regions in the Guder Basin exhibited notable variations in parameters including slope, flow intensity, and channel length. Muhammad [107] indicated that stream network density, slope, and basin area are the most significant variables affecting the principal components in PCA-supported TOPSIS analysis. The findings suggest that the criteria for selecting sub-basins with elevated EFR scores in the Susurluk Basin correspond with the parameters emphasized in the literature. In conclusion, the assessment of morphometric parameters through statistical and machine learning methodologies offers a dependable and literature-aligned framework for pinpointing priority regions for erosion and flood risk.

The SB42, SB77, and SB22 sub-basins are notable for their effective water resource management within the PBW function. The results derived from the PBW function indicate that certain sub-basins (e.g., SB42, SB77, and SB22) have a high capacity for water productivity. This can be primarily ascribed to stream density, minimal slope, and significant infiltration rates; likewise, Chen and Chang [108] obtained results in their study that parallel with these findings. Within the SEW function, the SB5, SB19, and SB35 sub-basins were recognized as pivotal regions where social and economic factors intersect. Wang et al. [109] simulated the impact of land use alterations on carbon sink capacity under socio-economic and natural scenarios by integrating the InVEST and GeoSOS-FLUS models in the Bailong River Basin, China. Their findings indicated that the expansion of forest and grassland regions markedly enhanced carbon storage capacity. This situation explains why sub-basins like SB7 and SB12 in our research have high SEW scores, which can be attributable to low settlement pressure and high natural cover ratios. Shiferaw et al. [110] investigated the impact of urbanization in the Gap-Cheon Basin in Korea, revealing that green spaces enhance flood mitigation and water quality, thus promoting socio-economic balance. Zhou et al. [111] assessed the impact of various land use scenarios on the carbon budget and sustainable development in the Yangtze River Delta, observing that these strategies could be incorporated into decision support systems. The results validate that the sub-basins exhibiting high SEW scores in this study demonstrate low anthropogenic effects, favorable ecological condition, and significant carbon sequestration potential. The incorporation of socio-economic variables into morphometric analyses enhances strategic decision-making for risk-based and sustainability-focused approaches.

Upon evaluation of all functions, the SB5 basin attains the highest scores across all three criteria, establishing it as a primary focus for integrated basin management. Basins like SB19 and SB80 are also notable in this context. Conversely, certain basins are prioritized solely for specific functions, whereas others have attained low overall scores and are not prioritized. This comprehensive analysis assesses soil conservation, water resource management, and socio-economic factors in an integrated manner, thereby aiding the formulation of sustainable basin management strategies. The collaborative assessment of various functions in the basin prioritization process provides more efficient and cohesive management and planning strategies. The SB5, SB19, SB80, SB42, SB22, SB27, and SB66 basins are essential for sustainable land and water resource management, given their elevated priority regarding various risk and management parameters. It is advisable to conduct comprehensive studies at the local level for these basins and to prioritize the implementation of preventive and remedial measures.

Our integrated PCA–TOPSIS–ML framework aligns with recent advancements wherein machine learning techniques, including Random Forest, XGBoost, and deep learning approaches, have been successfully employed in water quality evaluation, reservoir performance prediction, and flood vulnerability assessment [112,113,114]. This consistency enhances the importance and adaptability of data-driven approaches for sustainable watershed management.

Since our method is based on open data and a standardized workflow, it is transferable to different basins (semi-arid, humid, mountainous), following the same steps of data preparation, dimensionality reduction with PCA, ranking with TOPSIS and validation with ML. However, peer-reviewed studies that explicitly test transferability between different basin types are limited, indicating a research gap for future out-basin validation and cross-regional comparisons.

This study comprehensively examines the prediction performances of various machine learning models for PBW, EFR, and SEW functions, as well as clustering assessments. The employed models consist of Support Vector Machine (SVM), Random Forest (RF), Gradient Boosting Machine (GBM), K-Nearest Neighbor (KNN), and Artificial Neural Networks (ANNs). Cross-validation scores and error metrics, including R², Mean Squared Error (MSE), and Mean Absolute Error (MAE), were evaluated for each model. The performance of models was assessed individually for each function, and comparative outcomes were provided. These analyses indicate that varying data structures and characteristics of the target variable directly influence model efficacy.

Notably, the SVM model achieved the best performance for the PBW function (R²: 0.87, MSE: 0.003, MAE: 0.045). This high performance illustrates that SVM’s capacity to delineate non-linear decision boundaries confers an advantage in outputs characterized by multiple variables and intricate dependencies, such as PBW. Nonetheless, the performance is markedly low for the EFR (R²: 0.35) and SEW (R²: 0.46) functions. This indicates that SVM may not equally accommodate all functions, especially as the nonlinear complexity of the target variable escalates, requiring model re-optimization. Despite the high variance, the cross-validation outcome for PBW (0.65 ± 0.24) indicates that the model’s generalizability is also within an acceptable range. The findings indicate that the SVM model is an effective predictive instrument, particularly for the PBW function, and that the model’s hyperparameter configurations significantly influence its success.

The RF model produced satisfactory results for both the PBW (R²: 0.61) and SEW (R²: 0.64) functions. Specifically, a low mean squared error (MSE: 0.025) and high stability (coefficient of variation: 0.60 ± 0.18) were attained for SEW. The R² value for the EFR function is merely 0.16, signifying that the model’s predictive capability for this function is inadequate. This indicates that decision trees may insufficiently represent the variance in the EFR variable, suggesting the presence of more intricate non-linear relationships within this function. Enhanced selection of hyperparameters, including depth and tree quantity, may augment model performance.

In a study by Chen and Chang [108], Support Vector Regression (SVR) and Random Forest (RF) models were evaluated for their efficacy in predicting the impact of wildfires on water quality. The study demonstrated that SVR effectively manages high-dimensional data; however, it has been demonstrated that the RF model can capture nonlinear complex relationships more effectively. This finding supports the efficacy of the RF model in the SEW function and the enhanced performance of SVM in the PBW function in this study. The literature indicates that the RF model produces effective results with multivariate environmental data. Bushara et al. [115] employed the RF algorithm in their investigation of the correlation between agricultural productivity and water availability, attaining high accuracy in their findings and illustrating that this methodology is a valuable instrument in both agriculture and water management planning. Yan et al. [116] demonstrated low error rates and high model consistency through the application of RF and Bagging models to long-term time series data. The findings indicate the effectiveness of the RF model in the SEW function within this study and highlight the model’s capacity to accommodate the intricate nature of environmental systems.

The GBM model exhibited comparable strong performance for the PBW and SEW functions. The R² value for SEW was 0.69, positioning it at the higher end relative to comparable applications in the literature. Performance regarding EFR estimates was suboptimal (R²: 0.13). A low learning rate (0.01–0.1331) mitigated overfitting in the model, thereby benefiting balanced functions like SEW. The negative cross-validation results for EFR (–0.002) suggest that the GBM model exhibits very low generalizability for this function.

The KNN model exhibited the lowest performance among all evaluated functions. The R² values recorded were 0.39 for PBW, 0.21 for EFR, and 0.09 for SEW. The findings suggest that KNN is insufficient for accurately representing neighborhood relationships in high-dimensional and heterogeneous datasets. The optimal hyperparameter configurations for the model typically maintained the number of nearest neighbors within the range of 3 to 4 and favored the distance-based weighting approach. The KNN model exhibits limited explanatory power for the three functions, particularly demonstrating low predictive performance for the SEW function. The application of the KNN model is constrained in complex hydrogeological and morphometric data.

The ANN model has received attention due to its significant explanatory power (R²: 0.71), particularly concerning the EFR function. This finding demonstrates that deep learning architectures offer benefits in addressing nonlinear and multivariate relationships. The model’s cross-validation success (0.31 ± 0.23) indicates significant variance and challenges in generalizability. The results for PBW and SEW are moderate, with PBW exhibiting a negative cross-validation result (–0.39 ± 0.62), suggesting that the model overfits the training data. It is essential to optimize the network architecture and the training procedure at this stage. Derakhshani et al. [38] employed an Artificial Neural Network (ANN) methodology, integrating basin morphometric parameters with the FAHP method to assess tectonic movements, resulting in a high accuracy (R² = 0.97). The results indicate that high accuracy is attainable with artificial neural networks, highlighting that the model’s potential is contingent upon appropriate configuration.

This study utilizes a dataset comprising a singular integrated target score for each sub-basin, derived from TOPSIS and PCA, in addition to a varying quantity of PCA components determined by the functions applied. The model operates with a heterogeneous input structure characterized by varying dimensions, rather than being constrained to a limited set of observations. The prediction performance of the model may be impacted, particularly regarding PCA components characterized by high dimensionality yet limited explanatory power. The low R² values and high CV variance produced by data structure sensitive algorithms like KNN and ANN indicate a structural limitation. Algorithms including SVM, RF, and GBM demonstrated greater stability across functions, with SVM achieving R² = 0.87 in PBW and RF/GBM yielding R² values of approximately 0.65–0.69 in SEW. The primary aim is to offer decision support in the basin prioritization process through the comparison of alternative scenarios generated by various algorithms, rather than developing a single, deterministic model deemed “correct.” Consequently, while low R² values present a relative limitation, the comparative performance differences among the models and the presence of robust algorithms yield scientifically valid outputs.

Machine learning techniques applied to the EFR function, specifically Artificial Neural Networks (ANNs, R² = 0.71) and Support Vector Regression (SVR, R² = 0.35), have produced moderately successful outcomes in forecasting erosion and flood risks. In contrast, the lower performance of the Random Forest (RF) model may result from restricted interactions among the utilized parameters. The variability of hydro-morphological structures within the sub-basins complicates the consistent functioning of these data-intensive models. It is advisable to assess hybrid approaches that enhance both accuracy and model stability for the EFR function.

Comparative analysis on a function-by-function basis indicates that the most appropriate model for the PBW function is SVM. RF and GBM models provide a more balanced approach, though with comparatively low explanatory power. Artificial Neural Networks (ANNs) produce optimal outcomes for Event Frequency Response (EFR); however, their applicability in other functions is constrained by low generalizability. The observed differences indicate that the data structures, inter-variable relationships, and distributions of each function vary in their suitability for the models. The PBW function exhibits a more nonlinear, separable structure, whereas EFR encompasses more intricate nonlinear relationships. In the context of the PBW function, SVR demonstrates significant efficacy in regression tasks involving high-dimensional data, whereas RF is distinguished by its capacity to identify complex interactions among variables. The comparatively low performance of certain models, including KNN and ANN, indicates a propensity for these algorithms to overfit high-variance data. Ensemble-based models, particularly, yield more balanced and reliable outputs when predicting complex hydrological processes such as PBW.

The K-Means algorithm employed in this study differs from supervised machine learning methods by clustering sub-basins with analogous characteristics without the necessity of a target variable. The performance evaluation relies on indices that assess the structural integrity of the clusters, rather than on accuracy or error rate. The Silhouette, Calinski-Harabasz, and Davies-Bouldin scores indicate that the separation between clusters is statistically consistent (Table 8). The sensitivity of the method’s parameters, such as the selection of the k-value, along with its reliance on data preprocessing, must be considered when interpreting the results. In conclusion, K-Means is presented in this study not as a tool for comparison with predictive models, but as a complementary analysis method that clarifies structural similarities among sub-basins. Clustering analyses have yielded significant insights for the indirect assessment of the models’ classification capabilities. Silhouette scores exceeding 0.6 across all functions signify that the clusters are predominantly coherent. The highest score of 0.64 was recorded for PBW, signifying that the spatial patterns linked to PBW exhibit more pronounced clustering. The Calinski-Harabasz and Davies-Bouldin scores corroborate this observation, indicating that the PBW function exhibits a more stable clustering structure than the alternatives.

SVM models are distinguished for the PBW function, whereas ANN models stand out for EFR. The RF and GBM models produced more equitable outcomes for the SEW function. The efficacy of a model is contingent not only upon the employed algorithm but also on the configuration of the target variable, the dataset’s magnitude, the interrelations among variables, and the hyperparameter configurations of the model. Future research may enhance these results through model combinations (ensemble learning), hyperparameter optimization, and data preprocessing techniques (scaling, selection, feature engineering). The study findings indicate that the EFR function can facilitate the implementation of strategic approaches and the prioritization of basin areas to mitigate soil erosion and flash floods. The PBW function serves as a numerical prioritization criterion in hydrology, intended to assess the potential water yield capabilities of basins. This model assesses the spatial and relative water yield potential based on the physical characteristics of sub-basins. The parameters encompass stream length, slope, drainage density, and infiltration coefficient, with the process directed by PCA-based analysis. The SEW function considers morphometric, hydrological, and socio-economic variables, including settlement density, land use, carbon sink capacity, and agricultural productivity, when prioritizing sub-basins. This comprehensive approach provides substantial benefits for sustainable and enduring water resource management. Similarly, in recent years, there has been a growing interest in multi-criteria evaluation methods, which are extensively employed, especially in analyses related to land use and ecosystem services.

5. Conclusions

Conventional techniques employed in basin prioritization encompass manual digitization of river networks and the computation of morphometric parameters. This procedure is time-consuming and expensive. Conversely, employing GIS to compute morphometric parameters facilitates faster, cost-effective, and efficient basin prioritization processes. This study presents a comprehensive decision-support framework that amalgamates physical, hydrological, and socio-economic factors for the efficient prioritization of sub-basins. The three developed functions—EFR, SEW, and PBW—facilitate a comprehensive assessment that addresses natural hazard mitigation while aligning with the overarching goals of sustainable development. The integration of statistical methods like PCA and the TOPSIS approach, alongside machine learning algorithms, improves the analytical robustness and spatial relevance of the model.

The proposed multi-criteria prioritization approach provides a comprehensive perspective on sustainable basin management by integrating socio-economic vulnerabilities with environmental risks. The SEW function enhances decision-making by incorporating indicators like population density, land use attributes, and carbon sequestration potential, whereas the PBW function detects spatial discrepancies in potential water yield, aiding in climate-adaptive water resource planning. The model’s flexible architecture allows for easy adaptation to various basin contexts and integration into current decision-support systems. Moreover, it directly advances global sustainability goals, specifically SDG 6 (Clean Water and Sanitation), SDG 11 (Sustainable Cities and Communities), and SDG 15 (Life on Land).

The primary limitation of the study is that the prioritization analysis relied solely on morphometric and land use data. The combination of PCA and TOPSIS methodologies with machine and deep learning techniques provides a robust and holistic framework for basin prioritization studies from analytical and practical viewpoints. The exceptional performance outcomes indicate that the proposed methods can be effectively utilized across various geographical and data frameworks. The K-Means method was favored as an alternative to regression-based approaches due to its unsupervised nature, enhancing other models by uncovering structural similarities among sub-basins. The integration of PCA and TOPSIS methods with machine learning and deep learning techniques provides a comprehensive approach to watershed prioritization studies, addressing both analytical and practical aspects. The obtained high-performance results indicate that the proposed methods are applicable across various geographical and data structures. The performance of various algorithms exhibits variability; however, comparative analysis offers decision-makers multiple scenarios and functions as a dependable decision support tool in watershed prioritization.

The proposed model appears to be a strategic, flexible instrument to support an interdisciplinary approach, covering water resource governance, land use optimization, and disaster risk mitigation. Calibration of the model in different climatic or land use scenarios may benefit future applications by increasing the model adaptability and relevance to decision-making in changing environmental settings.

Future incorporation of hydrometeorological data such as water quality, flow regime, and climatic variables will help enhance the prioritization accuracy and model prediction. Within this framework, the study offers decision support capacity not just for academia but also for its applications in watershed management, flood risk reduction, and land use planning. PCA+TOPSIS integrated approach is an innovative methodological framework in assessing the interoperability between machine learning, deep learning, and clustering analysis.

The integrated priority grid which was suggested here can have a policy implication regarding decision making processes by jointly considering, to consider together Hydrological Processes (EFR, PBW) and socio-economic Drivers (SEW) in basin management. This is a practical roadmap for resource allocation, adaptive measure design, and balancing water use and governance challenges in the context of increasing uncertainty.

The main conclusion of this study is not solely the comparative effectiveness of individual models, but rather the demonstration that the amalgamation of PCA, TOPSIS, and machine learning produces a transferable, objective, and comprehensive decision-support framework for prioritizing sub-basins. This mixed method reduces subjectivity, enhances the reliability of predictions, and ensures alignment between scientific analysis and practical watershed governance. With this framework as a guide, sustainable land and water management is possible in a wide range of hydro-climatic conditions, not only in the Susurluk Basin.