Grading Evaluation of Grouting Seal Quality for Recharge Channels in Water-Hazardous Aquifers of Extremely Complex Mines

Abstract

Grouting to seal the recharge channels of water-bearing aquifers is an effective method for reducing mine water inflow. Evaluating effectiveness and establishing a hierarchical classification system are crucial for assessing project quality. Taking the grouting seal project of the Cambrian limestone aquifer recharge channels at Mine No.7 in the Pingdingshan Coalfield as a case study, this paper first comprehensively evaluates the grouting seal effectiveness based on the difference in dynamic water recharge to goaf before and after grouting, derived from long-term pumping test data. Further, six indicator factors—grout volume, grout volume per unit time, grout volume per unit thickness, final borehole pressure, penetration depth into Cambrian limestone, and variation in rock mechanical strength—were selected. Weights for these factors were determined by integrating the Analytic Hierarchy Process, entropy weight method, and composite weighting method. The TOPSIS model was applied to classify and rank the grouting seal effectiveness in six recharge channels. Results indicate that post-grouting water recharge from goaf decreased by 240.78 m³/h during dry season and 878.57 m³/h during wet season, confirming high-quality grouting seal. The grouting seal quality of the six recharge channels was ranked from highest to lowest as follows: NO.3 > NO.2 > NO.6 > NO.1 > NO.5 > NO.4. The evaluation results corresponded with the actual karst fissure development and distribution of goaf in the exposed recharge channels.

1. Introduction

Water hazards in coal mines represent a common environmental and safety challenge for the global mining industry. In recent years, the number of closed coal mines has increased annually in major coal-producing regions such as China, Europe, and India. Following mine closure, the cessation of groundwater pumping leads to a rapid increase in groundwater levels, posing a significant threat to the regional ecological environment and adjacent operational mines [1,2,3,4,5]. Curtain grouting involves injecting cementitious slurry into rock and soil strata through boreholes to fill fractures and voids, thereby forming a continuous impermeable barrier. This effectively blocks groundwater flow pathways, achieving rock mass reinforcement or seepage prevention. The curtain formed by grouting constitutes a concealed engineering feature. Construction parameters alone cannot guarantee the continuity of the grout curtain. Consequently, evaluating the effectiveness of curtain grouting is a core element in ensuring the safety, economy, and technical reliability of the project.

Conventional methods for evaluating curtain grouting effectiveness include field testing, water quality and water level analysis, physical and mechanical parameter testing, and geophysical exploration. Komine [6] utilized high-density electrical surveys and discovered that the electrical resistivity of the grouting slurry is significantly lower than that of groundwater or the ground. Based on this, a calculation method for formation resistivity before and after grouting was proposed to evaluate the grouting effectiveness. Lynch et al. [7] applied 3D seismic tomography technology to achieve a volumetric assessment of grouting reinforcement effects by comparing the 3D distribution of compressional wave velocities in the subsurface medium before and after grouting. Zhao [8] studied groundwater level variations and influencing factors during grouting operations in the water-filled goaf of Jining Daizhuang Coal Mine. Results indicated that sustained grouting reduced conductive fractures in the overlying rock, significantly decreasing permeability and progressively improving the seal. Borehole water levels were closely correlated with grouting effectiveness in the goaf. Li [9] employed multiple methodologies to evaluate grouting effectiveness in the mine’s curtain grouting project, acoustic testing of rock blocks determined the degree of fissure development in strata during each sequence of borehole grouting within the test section. This enabled comparative analysis of grouting effectiveness before and after each sequence, as well as between all sequences across all boreholes.

In recent years, with the advancement of science and technology, numerous scholars have applied modern mathematical methods and machine learning algorithms to engineering practice. Based on the grouting projects at the 8901 working face of Baizhuang Coal Mine and the D3, D10, D11, and D12 surface borehole groups at Qiuji Coal Mine in Shandong Province, Chen [10] and Yuan [11] respectively established a grouting effectiveness evaluation model. This model was based on a combined weighting method, using the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) for ranking and the Rank Sum Ratio (RSR) method for auxiliary classification. The results showed that the model possesses high accuracy and rationality, aligning well with engineering practice. To address the influence of multiple factors on the reinforcement effectiveness of grouting in fractured coal-rock masses, Wang [12] established a GRA and IAHP integrated evaluation system. It was found that after grouting, sidewall convergence was reduced by 606 mm, achieving a reduction ratio of 86.57%; floor heave was reduced by 928 mm, with a reduction ratio of 84.36%, thereby achieving the remediation objectives. Zadhesh et al. [13] constructed an Artificial Neural Network (ANN) model for the consolidation grouting project of the Cheraghvays Dam in Iran. To assess the secondary permeability of the foundation after grouting, they used initial permeability, cement take, and depth as input parameters. The results demonstrated that, compared to traditional linear regression methods, the ANN model could predict secondary permeability more accurately. Based on the on-site grouting project at Qiuji Coal Mine in the Huanghebei Coalfield, Li [14] analyzed the effectiveness of directional grouting in limestone using four algorithms: XGBoost, Support Vector Machine, K-Nearest Neighbors, and BP Artificial Neural Network. The study ultimately demonstrated the feasibility and accuracy of the BP Artificial Neural Network for evaluating grouting effectiveness, realizing an intelligent and rapid assessment.

Taking the grouting project on the floor of the working face at Anhui Banji Coal Mine as an example, Tang et al. [15] proposed a combined weighting method that integrates the Preference Chart (PC) method with the CRITIC method. They simultaneously employed the TOPSIS-RSR method for comprehensive evaluation and further verified the results by comparing the on-site actual water inflow with that from exploration boreholes. The results indicated that this model possesses high accuracy and reliability. Taking the coal seam floor grouting project at Rongkang Coal Mine in Shanxi as a background, Gao et al. [16] utilized Geographic Information System (GIS) and Monte Carlo Analytic Hierarchy Process (MAHP) to establish a comprehensive evaluation model for the effectiveness of coal seam floor grouting, which classified the grouting effectiveness into three segments: poor, qualified, and good. The results showed that the model’s predictions had a high degree of consistency with the actual on-site conditions, verifying the model’s reliability. Taking five mines under Zhengzhou Coal Group as case studies, Li et al. [17] compared the evaluation results of the game theory combined weighting-TOPSIS comprehensive evaluation model with those from the fuzzy analytic hierarchy process and the improved composite weighting-TOPSIS model. The results demonstrated that the evaluation results of the game theory combined weighting-TOPSIS method were basically consistent with the actual safety status of the coal mines, reflecting the model’s superiority and practicality. Against the backdrop of the directional drilling grouting modification of the limestone aquifer at Qiuji Coal Mine, Li et al. [18] established a “dual-process, multi-parameter, multi-factor” indicator system. They employed eight high-performance machine learning models and three parameter optimization algorithms to develop an evaluation model for the effectiveness of directional grouting in the limestone aquifer. The results showed that, compared to traditional methods, the AdaBoost machine learning model optimized by a genetic algorithm exhibited superior performance and more accurate evaluation results.

In summary, although modern mathematical methods and machine learning algorithms—such as numerical simulation, TOPSIS, RSR, AHP, CRITIC, and Fuzzy AHP—have provided diversified tools for grouting effectiveness evaluation, existing research still suffers from issues including unreasonable determination of indicators and weights, reliance on single evaluation methods, and results that occasionally deviate from actual engineering conditions. Conventional mathematical methods and machine learning algorithms each have their pros and cons in the field of grouting effectiveness evaluation. The advantage of machine learning algorithms lies in their ability to learn and capture non-linear relationships and interaction effects within grouting data and to analyze the patterns among indicators. In contrast, conventional mathematical methods require less data than machine learning algorithms. These methods typically rely on expert experience or a limited set of key indicators, utilize mathematical logic for deduction, offer greater interpretability, and are more suitable for small-dataset problems such as grouting effectiveness evaluation. Furthermore, traditional methods for weight selection of various factors often adopt subjective or objective weighting methods separately. Subjective weighting methods consider expert experience but possess subjective arbitrariness, while objective weighting only considers the internal connections of data and ignores the relative importance of certain factors. The combinational weighting method is a technique that determines indicator weights by combining multiple weighting methods. Its advantage lies in combining the merits of both subjective and objective methods, avoiding the bias that may be caused by a single method, thereby improving the accuracy and reliability of decision-making [19,20].

Therefore, this paper focuses on the grouting seal project for the Cambrian limestone aquifer’s recharge channel at Mine No.7 of the Pingdingshan Coalfield. It selects grout volume, grout volume per unit time, grout volume per unit thickness, final borehole pressure, penetration depth into the Cambrian strata, and the variation in rock mechanical strength as indicator factors. The study employs the Analytic Hierarchy Process, the Entropy Weight Method, and a combined weighting method to determine the subjective, objective, and comprehensive weights of these factors. It then applies the TOPSIS model to quantitatively identify the grouting effectiveness and validates the evaluation results by comparing geophysical survey results and drainage volumes from before and after grouting. This research is of great significance for guiding the precise identification of grouting seal effectiveness.

2. Project Background and Implementation

2.1. Project Background

Mine No.7 of the Pingdingshan Coalfield primarily extracted coal from the Carboniferous Geng Formation and the Permian Ji Formation. The location map of the Mine No.7 and the Mine No.5 is shown in Figure 1. On the southern side of the mining area, Cambrian limestone outcrops in a strip-like pattern, receiving recharge from atmospheric precipitation and surface water (Figure 2). The recharged groundwater flows along the dip of the Cambrian limestone strata or through fault fracture zones, moving from shallow to deep areas to form water-rich anomaly zones and high-pressure zones. Under mining disturbance conditions, these zones become the primary sources of water recharge to Mine No.7. With the depletion of coal resources, Mine No.7 ceased operations in June 2016. Prior to closure, the mine’s water inflow ranged from 1040 to 1656 m³/h, with a maximum of 3500 m³/h, classifying it as a hydrogeologically extremely complex mine.

Mine No.5 is an operating mine located to the west of Mine No.7 (Figure 3). To mitigate the threat of goaf water to the operational safety of Mine No.5, pumping of goaf water from the main shaft of Mine No.7 was continued. Despite this measure, the water inflow at Mine No.5 still increased by a net amount of 206 to 1278 m³/h (Figure 4); moreover, in August 2021, its inflow reached 2232 m³/h, approaching its maximum drainage capacity. Calculations show that the combined annual drainage costs for Mine No.7 and Mine No.5 total 32.66 million yuan. Therefore, to eliminate the water hazard threat from the goaf and reduce drainage expenses, it is of great significance to implement a grouting seal project on the recharge channels of the Cambrian limestone aquifer, which is the main recharge source for the goaf water of Mine No.7.

2.2. Project Implementation

To investigate the recharge from the Wujiang River into the Cambrian limestone aquifer, rectangular weirs were used on 3 December and 10 December 2021, to measure the cross-sectional flow rate of the river. Six monitoring cross-sections were established at Jiaodian Bridge, Xihuan Road Bridge, Yaozhong Road Bridge, the Daotian Gou Inlet, the Railway Bridge, and the Zhanhe Arch Bridge (Figure 3). Two separate measurements of flow loss per unit length along the Wujiang River yielded values of 0.0765 m³/h·m and 0.1343 m³/h·m respectively, which indicates seepage through the riverbed. Given this seepage, the grouting seal project for the goaf water recharge channels should be implemented on the north bank of the river.

To determine the spatial location of the groundwater recharge channels within the Cambrian limestone, transient electromagnetic (TEM) and high-density electrical resistivity surveys were conducted along the northern bank of the Wujiang River in November 2021. By integrating the mine’s geological and hydrogeological data with previous geophysical findings, a total of six recharge channels were delineated within the range from the top interface of the Cambrian limestone aquifer down to a depth of 150 m (Figure 5).

For each Cambrian limestone recharge channel, two rows of grouting plugging boreholes were designed, with a total of 40 boreholes deployed across six channels, numbered A1–A24 and B1–B16, as shown in

Table 1. Grouting borehole numbers for recharge channels.

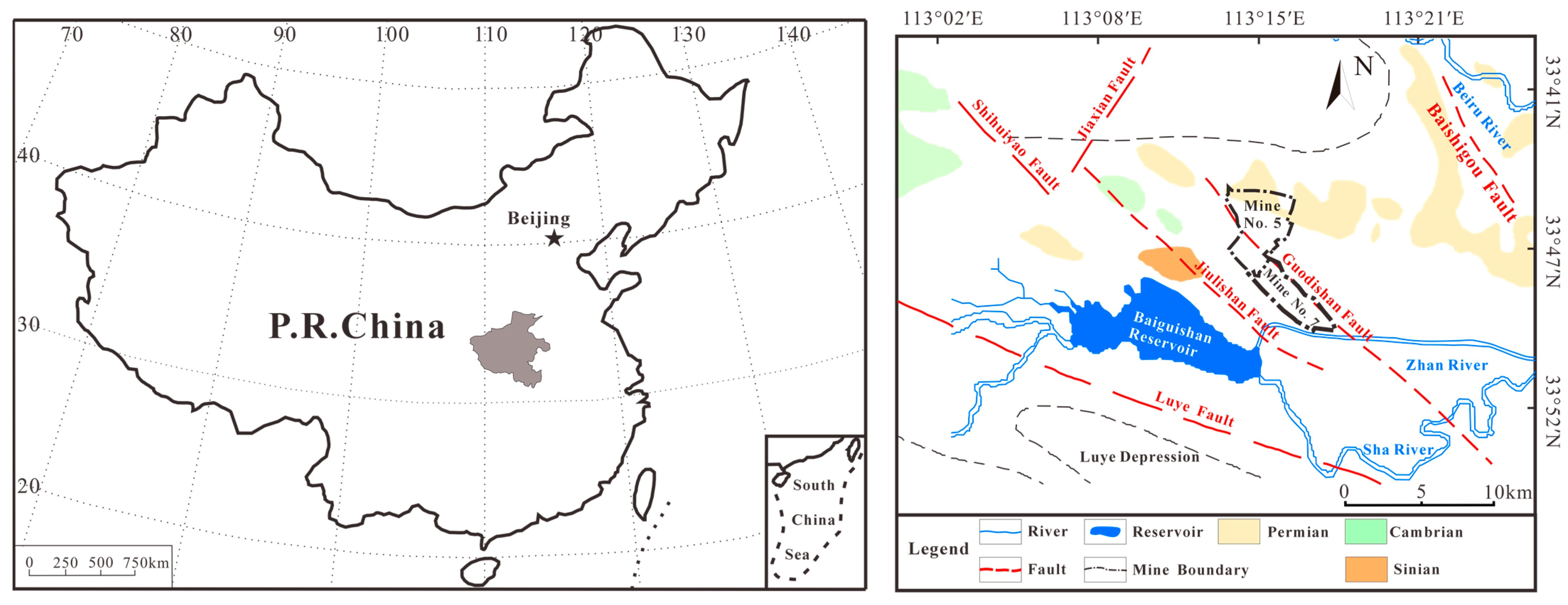
Recharge Channel	No.1	No.2	No.3	No.4	No.5	No.6
Borehole Numbers	A1~A3, B1~B2	A4~A6, B3~B4	A7~A12, B5~B8	A13~A15, B9~B10	A16~A18, B11~B12	A19~A24, B13~B16
Number of Boreholes	5	5	10	5	5	10

. From July 2022 to June 2023, drilling and grouting plugging operations were sequentially implemented across the 40 boreholes. Individual borehole depths ranged from 50.56 to 255.7 m, with a total drilling depth of 5494.94 m. The depth range penetrating the Cambrian limestone varied between 50 and 164.76 m, totalling 2694.39 m. Individual grout volumes ranged from 136 to 2054.4 tonnes, with a total grout volume of 28,552.21 tonnes.

2.3. Project Outcomes

The effectiveness of the grouting project for sealing the goaf water recharge channels can be evaluated based on changes in the dynamic recharge volume. In this study, the definitions of “dry season” and “wet season” are primarily based on long-term hydrological observation data from the Pingdingshan area. Generally, the dry season spans from November to June of the following year, while the wet season occurs from July to October. Notably, June serves as a transitional month; its first half typically exhibits hydrological characteristics closer to the dry season, whereas the second half marks the transition toward the wet season. To calculate the dynamic recharge volume for the goaf of Mine No.7 during dry and wet seasons before and after the grouting, unsteady-state pumping tests were conducted in the main shaft of Mine No.7. Tests for the dry season were carried out from 14 to 27 June 2022 (before grouting) and from 27 March to 5 April 2023 (after grouting), as shown in Figure 6. Similarly, tests for the wet season were conducted from 23 July to 26 August, 2020 (before grouting) and from 21 June to 14 August 2023 (after grouting), as detailed in Figure 7.

Based on the principle of water balance, the relationship between pumping volume, recharge volume, and water level fluctuation can be established as:

$$Q_{\mathit{pump}} = Q_{\mathit{supplement}} + {\mu }^{\mathrm{*}}F\frac{\Delta h}{\Delta t}$$

(1)

where Q_pump denotes groundwater pump discharge, m³/h; Q_supplement is the dynamic water recharge, m³/h; Δt is the pumping period, h; Δh is the water level fluctuation within Δt (positive for decline, negative for rise), m; ${\mu }^{\mathrm{*}}$ is the storage coefficient, a parameter related to the overburden lithology, coal seam thickness, degree of compaction, and coal seam dip angle of the goaf; $F$ is the area of the water accumulation zone, m².

Using the pumping test data from the main shaft of Mine No.7 during the dry season before grouting, periods with similar water level fluctuations and pumping flow rates were selected to precisely analyze the changes in dynamic water recharge before and after grouting. The test data are shown in

Table 2. Data from three pumping tests.

Pumping Test	Time Period	Duration (h)	Pumping Volume $({\mathbf{m}}^3/\mathbf{h})$	Water Level (m)	Fluctuation (Decline)
First	17 June 2022 16:54~25 June 15:50	190.93	696.93	−121.9$\to$−122.6	0.7
Second	11 January 2023 10:10~14 January 11:55	73.75	683.89	−121.3$\to$−122.6	1.3
Third	27 March 2023 11:05~28 March 1:23	14.3	683.89	−123.5$\to$−123.9	0.4

.

To eliminate the influence of variations in pumping volume as much as possible, based on the data in Table 2 where the pumping volume and water level fluctuation ranges in the main shaft of Mine No.7 are basically the same, Equation (1) was used to calculate ${\mu }^{\mathrm{*}}F$ for different water level intervals. The results are shown in

Table 3. Calculated parameters ${\mu }^{\mathrm{*}}F$ from pumping tests in mine No.7 goaf.

No.	June 2022		January 2023		March 2023
	Water Level (m)	${\mathit{\mu }}^{\mathbf{*}}\mathit{F}$	Water Level (m)	${\mathit{\mu }}^{\mathbf{*}}\mathit{F}$	Water Level (m)	${\mathit{\mu }}^{\mathbf{*}}\mathit{F}$
1	−122.6~−122.5	29.44	−122.6~−122.5	11,910.48	−123.5~−123.6	8370.34
2	−122.5~−122.4	29.37	−122.5~−122.4	11,910.48	−123.6~−123.7	8370.34
3	−122.4~−122.3	407.65	−122.4~−122.3	8360.24	−123.7~−123.8	8370.34
4	−122.3~−122.2	409.26	−122.3~−122.2	986.38	−123.8~−123.9	8370.34
5	−122.2~−122.1	642.56	−122.2~−122.1	562.88	N/A	N/A
6	−122.1~−122.0	4592.59	−122.1~−122.0	6089.03	N/A	N/A
7	−122.0~−121.9	6110.87	−122.0~−121.9	4777.11	N/A	N/A
8	−121.9~−121.8	5671.63	N/A	N/A	N/A	N/A
9	−121.8~−121.7	6944.09	N/A	N/A	N/A	N/A
10	−121.7~−121.6	9972.46	N/A	N/A	N/A	N/A
11	−121.6~−121.5	14,032.39	N/A	N/A	N/A	N/A
12	−121.5~−121.4	13,534.86	N/A	N/A	N/A	N/A
13	−121.4~−121.3	11,281.20	N/A	N/A	N/A	N/A
Mean		1745.96		8156.40		8370.34

Note: N/A indicates not applicable or no data available.

.

Based on the mean values of ${\mu }^{\mathrm{*}}F$ at different times provided in Table 3, the corresponding dynamic water recharge Q_supplement for the goaf water can be calculated using Equation (1) as 690.53 m³/h.

Similarly, the dynamic water recharge volumes for Mine No.7 in other periods can be obtained, as shown in

Table 4. Dynamic water recharge in goaf before and after grouting (m³/h).

Time	Dry Season		Wet Season
	Before Grouting	After Grouting	Before Grouting	After Grouting
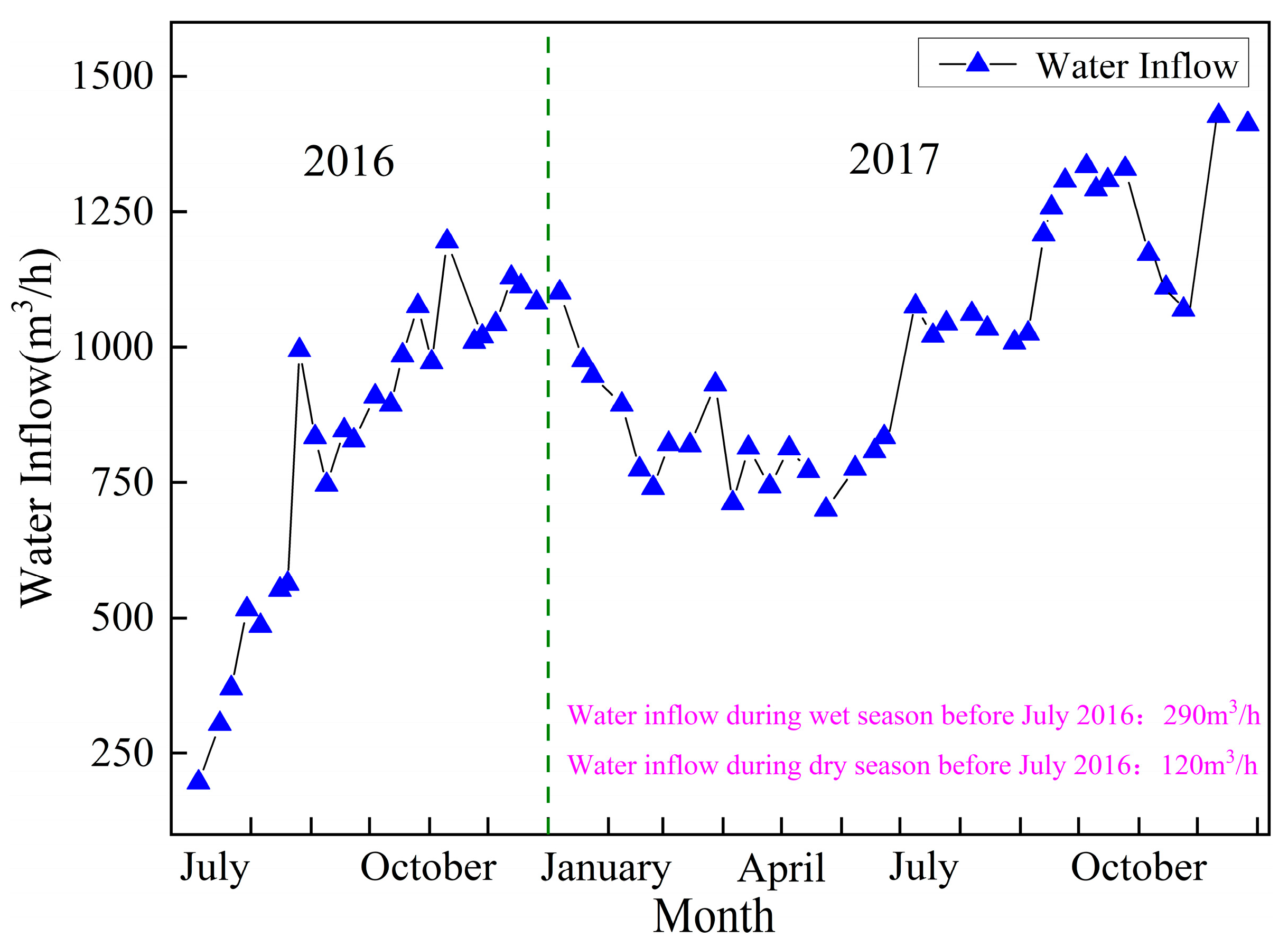
Mine No.7 Dynamic Recharge	690.53	449.75	1500	621.43

. Specifically, for the wet season before grouting, as shown in Figure 7, the pumping flow rate in the main shaft of Mine No.7 was maintained at 1500 m³/h, yet the water level still showed an upward trend. Therefore, the dynamic water recharge of Mine No.7 was greater than 1500 m³/h. For calculation convenience, 1500 m³/h is taken as the dynamic water recharge of the goaf of Mine No.7 during the wet season before grouting.

The calculations show that the dynamic water recharge of Mine No.7 during the dry season was 690.53 m³/h before grouting and 449.75 m³/h after grouting. The water volume decreased by 240.78 m³/h, a reduction of 34.87%, indicating a distinct water-blocking effect of the curtain grouting.

During the wet season, the dynamic water recharge of Mine No.7 was 1500 m³/h before grouting and 621.43 m³/h after grouting. The water volume decreased by 878.57 m³/h, a reduction of 58.57%, confirming the distinct water-blocking effect of the curtain grouting.

3. Development of an Evaluation Indicator System

Establishing an indicator system is key to accurately evaluating grouting quality. Due to complex influencing factors and uncertain, fuzzy relationships, the selection of indicators must consider both reasonableness and accessibility to ensure the objectivity and consistency of the evaluation results. Based on borehole data, geological conditions, and expert judgment, the quality evaluation indicators for the grouting seal project at Mine No.7 were determined as follows: grout volume, grout volume per unit time, grout volume per unit of thickness, final borehole pressure, penetration depth into the Cambrian limestone, and variation in rock mechanical strength.

3.1. Establishment of the Indicator System

3.1.1. Grout Volume

The grout volume affects the penetration depth of the material and the ground improvement effectiveness within the target strata. Generally, a higher grout volume leads to more effective void filling.

Across the 40 boreholes, the grout volume ranged from 136 to 2054.4 tonnes, with a mean of 713.81 tonnes. This wide variation indicates non-uniform development of karst fractures within the Neogene marlstone, Carboniferous limestone, and Cambrian limestone across different recharge paths and boreholes. Eight of these boreholes (22.2%) had a grout volume exceeding 1000 tonnes and were primarily located near karst cave zones or goaf areas in the coal-bearing strata.

3.1.2. Grout Volume per Unit Time

The grout volume per unit time reflects the stability and continuity of the grouting process. A higher volume suggests good grout flow, allowing for thorough filling of the target strata and the formation of a uniform consolidated zone, thereby enhancing the stability and strength of the surrounding rock mass.

The grout volume per unit time for the 40 curtain grouting boreholes was calculated from the recorded grout volume and duration. This value ranged from 5.73 to 12.15 m³/h, with a mean of 8.68 m³/h.

3.1.3. Grout Volume per Unit Thickness

The grout volume per unit thickness determines the diffusion range and degree of filling within the formation. A higher value corresponds to a greater improvement in the strength and stability of the rock mass.

For the 40 boreholes, the grout volume per unit thickness varied significantly, ranging from 1.25 to 32.76 t/m with a mean of 9.79 t/m. This indicates non-uniform groutability of the rock layers, with higher values observed near karst cave zones or goaf areas within the coal-bearing strata.

3.1.4. Final Borehole Pressure

In addition to the grout’s properties and materials, the effectiveness of grouting is also highly dependent on the grouting pressure. The pressure directly governs the flow of grout within the pores and fractures of the medium, determining its penetration capacity and distance under given conditions and thus influencing the overall filling effectiveness.

The final borehole pressure for the 40 boreholes ranged from 0 to 3.9 MPa, with a mean of 2.35 MPa.

3.1.5. Penetration Depth into Cambrian Limestone

Greater penetration depth reveals more information about the strata, potentially involves a thicker target layer and a longer grouting section, and consequently leads to a better water-blocking outcome.

The final depth of all 40 boreholes penetrated more than 50 m into the Cambrian limestone, with depths ranging from 50 to 164.76 m and a mean of 67.36 m. This work volume exceeded the design requirements, laying a solid foundation for the successful completion of the grouting project.

3.1.6. Variation in Rock Mechanical Strength

A comparative analysis of rock mechanical strength was conducted by collecting core samples from reference and inspection boreholes both before (baseline state) and after grouting. Using the RMT-150C Rock Mechanics Testing System, systematic laboratory tests—including uniaxial compressive strength (UCS) tests and Brazilian splitting (indirect tensile) tests—were performed on these cores to determine key mechanical parameters.

The quantitative indicator values for the six channels were determined based on the variation in tensile strength of rock cores from the same lithological layer and sampling horizon. If the post-grouting test results show a statistically significant increase in compressive or tensile strength compared to the baseline state (i.e., the strength ratio is greater than 1), this improvement in mechanical properties is considered direct evidence that the grouting has effectively reinforced the rock mass and enhanced its engineering performance, thus confirming a successful grouting outcome.

3.2. Quantification of Indicator Factors

The quantitative values for the grouting seal effectiveness identification indicators are presented in

Table 5. Quantification of evaluation indicators.

Recharge Channel	Borehole No.	Grout Volume (t)	Grout Volume per Unit Time (m3/h)	Grout Volume per Unit Thickness (t/m)	Final Borehole Pressure (Mpa)	Penetration Depth into Cambrian Limestone (m)	Variation in Rock Mechanical Strength ([-])
No.1	A1	452.41	6.96	8.32	1.5	51.9	1.0173
	A2	895.38	7.39	16.87	1.5	50.35	1.0173
	A3	569.35	6.69	10.58	1.5	50.59	1.0173
	B1	863.67	8.43	15.33	1.6	53.33	1.0173
	B2	136	9.75	2.52	1.7	50.7	1.0173
No.2	A4	412.79	9.6	7.35	3.5	94.17	1.2594
	A5	455.6	8.99	8.22	3.9	50	1.2594
	A6	522.22	9.17	3.07	3	164.76	1.2594
	B3	1509.43	8.94	27.39	3.1	50.5	1.2594
	B4	652.68	9.75	11.16	3.1	50.49	1.2594
No.3	A7	241.09	7.79	4.50	1.6	56.72	1.3109
	A8	1174.8	8.62	25.48	2	53.6	1.3109
	A9	1055.86	10.56	20.78	1.7	53.8	1.3109
	A10	911.26	10.43	17.27	1.5	55.76	1.3109
	A11	645.49	7.80	12.63	1.5	54.8	1.3109
	A12	519.8	11.55	9.92	1.7	55.9	1.3109
	B5	728.66	8.88	14.44	1.8	53.8	1.3109
	B6	1408.76	9.44	32.76	1.5	54.8	1.3109
	B7	463.76	8.90	9.45	1.6	52.5	1.3109
	B8	958.40	12.15	19.36	2.1	53.4	1.3109
No.4	A13	212	7.16	1.84	3.1	54.56	1.355
	A14	176	6.56	1.25	3.2	83	1.355
	A15	536	10.53	4.69	3.3	52	1.355
	B9	224	9.40	1.94	3.2	63.05	1.355
	B10	480	8.74	4.20	3.5	53	1.355
No.5	A16	853.56	8.69	8.09	2.1	108.5	1.0701
	A17	413.18	8.04	8.11	1.5	55.06	1.0701
	A18	318.86	9.84	6.31	1.6	54.4	1.0701
	B11	489.95	8.19	9.76	1.6	55.4	1.0701
	B12	388.85	7.57	7.73	1.6	54.6	1.0701
No.6	A19	986	8.82	4.96	3	85.3	1.3074
	A20	980	9.45	5.69	3.2	57	1.3074
	A21	2054.4	9.76	9.96	0	90.62	1.3074
	A22	1638	10.04	8.77	3	87.87	1.3074
	A23	616	5.97	6.34	3.2	88.3	1.3074
	A24	264	5.73	2.61	3	89.75	1.3074
	B13	1050	9.42	5.25	3	86.81	1.3074
	B14	1174	8.31	5.61	3	84	1.3074
	B15	424	7.20	4.22	3.2	90.3	1.3074
	B16	696	6.17	6.98	3.1	89	1.3074

.

4. Quality Assessment Method for Sealing

4.1. Analytic Hierarchy Process

The Analytic Hierarchy Process (AHP) [21,22] is a systematic decision-making modeling tool based on hierarchical decomposition. Its core principle is the transformation of unstructured subjective judgments within a complex system into quantifiable weight sequences through the construction of a judgment matrix. By systematically deconstructing the target problem and establishing scales for comparing the relative importance of elements, this method provides an explicit mathematical representation of implicit experience in multi-criteria decision-making scenarios. The specific steps are as follows:

4.1.1. Judgment Matrix Construction

The evaluation criteria are then compared pairwise, with their relative importance quantified using the 1–9 scale (

Table 6. Scaling of Factors in the AHP Judgment Matrix.

Scale	Meaning of the Scale
1	Factor i is as important as factor j.
3	Factor i is slightly more important than factor j.
5	Factor i is moderately more important than factor j.
7	Factor i is strongly more important than factor j.
9	Factor i is extremely more important than factor j.
2, 4, 6, 8	Intermediate values between the above judgments.

) to construct the judgment matrix R.

$$R={\left[r_{ij}\right]}_{n\times n}=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \dots & r_{1j}\\ r_{21}& r_{22}& \dots & r_{2j}\\ ⋮& ⋮& r_{ij}& ⋮\\ r_{i1}& r_{i2}& \dots & r_{nn}\end{array}\right]$$

(2)

where $r_{ij} > 0$, $r_{ij} \times r_{ji} = 1$, and $r_{ii} = 1$.

4.1.2. Consistency Test

First, the eigenvector is approximated by calculating the relative weights of the factors in the judgment matrix R. This involves normalizing the values in each column of the matrix and then averaging the results across each row to obtain the subjective weights.

Once the subjective weights are determined, a consistency test is performed to check if the weights assigned at this level are reasonable. If the Consistency Ratio (CR) ≤ 0.1, the matrix has an acceptable level of consistency, and the weights can be used for the application. If the CR > 0.1, the judgments in the matrix or the hierarchical model must be reconsidered, and the preceding calculation steps must be repeated.

$$CR={\displaystyle \frac{CI}{RI}}$$

(3)

$$CI={\displaystyle \frac{{\lambda }_{\max }-n}{n-1}}$$

(4)

where $CI$ denotes the consistency index; $RI$ denotes the random consistency index, whose values are shown in

Table 7. Random consistency index $RI$ values.

$$\mathbf{Order} \mathit{n}$$	1	2	3	4	5	6	7	8	9
RI	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45

.

4.2. Entropy Weight Method

The Entropy Weight Method (EWM) [23,24] serves as an objective approach for weight determination. It operates on the principle that indicators with lower entropy values—indicating higher variability and thus greater discriminatory power—should be assigned higher weights. In the context of the selected indicators, while Grout Volume, Grout Volume per Unit Time, and Grout Volume per Unit Thickness share mathematical links, they characterize distinct engineering dimensions: cumulative magnitude, construction efficiency, and spatial distribution intensity, respectively. Statistical analysis supports their distinctness, with the maximum coefficient of determination ($R^2$) reaching only 0.34. Moreover, a key advantage of EWM is its ability to reduce the bias caused by redundant information; it naturally assigns lower weights to indicators with limited variability. Therefore, retaining all three indicators allows for a comprehensive assessment of the complementary characteristics of grouting behavior [25,26,27]. The specific steps are as follows:

4.2.1. Construction of the Judgment Matrix

Assuming an object to be classified, where each sample possesses $n$ evaluation indicators, construct the judgment matrix $X$:

$$X=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \dots & x_{1n}\\ x_{21}& x_{22}& \dots & x_{2n}\\ ⋮& ⋮& x_{ij}& ⋮\\ x_{m1}& x_{m2}& \dots & x_{mn}\end{array}\right]$$

(5)

where $x_{ij}$ denotes the value of the $j$th criterion for the $i$th object under evaluation, with $i=1,2,\dots ,m$ and $j=1,2,\dots ,n$.

Normalize the judgment matrix $X$ to obtain the normalized matrix $Y$:

$$Y=\left[\begin{array}{cccc}{y}_{11}& y_{12}& \dots & y_{1n}\\ y_{21}& y_{22}& \dots & y_{2n}\\ ⋮& ⋮& y_{ij}& ⋮\\ y_{m1}& y_{m2}& \dots & y_{mn}\end{array}\right]$$

(6)

$$y_{ij}=(x_{ij}-x_{\min })/(x_{\max }-x_{\min })$$

(7)

where $x_{\min }$ and $x_{\max }$ denote the minimum and maximum values of the $j$th criterion, respectively.

4.2.2. Weight Determination

The entropy value $E_j$ for the $j$th indicator may be calculated according to entropy weight theory:

$$E_j=-{\displaystyle \frac{{\displaystyle \sum _{i=1}^m{P}_{ij}\cdot \ln P_{ij}}}{\ln m}}$$

(8)

$$P_{ij}={\displaystyle \frac{y{i}_j}{{\displaystyle \sum _{i=1}^m{y}_{ij}}}},\left(i=1,2,\dots ,m; j=1,2,\dots ,n\right)$$

(9)

where $P_{ij}$ denotes the characteristic weight of the indicator. When $P_{ij}=0$, let $\ln P_{ij}=0$.

Based on the entropy value given by Equation (9), the difference coefficient $G_j$ for the jth indicator can be calculated:

$$G_j=1-E_j$$

(10)

The weighting factor $W_j$ for the jth indicator is determined using the difference coefficient:

$$W_j={\displaystyle \frac{G_j}{{\displaystyle \sum _{j=1}^n{G}_j}}}$$

(11)

4.3. Combination Weighting Method

The AHP [28] calculates weights based on the perceived relative importance among evaluation criteria, making it highly subjective. In contrast, the EWM relies on the inherent properties of the indicator data, which provides strong objectivity. Therefore, this paper proposes an optimized combined weighting model. In this model, the combined weight $W_j$ is determined by applying the Principle of Minimum Relative Information Entropy and the Lagrange Multiplier Method, thereby mitigating the drawbacks of both methods to a certain extent [29,30].

$$W_j={\displaystyle \frac{{\left(W_j^{\prime }\times W_j^{″}\right)}^{0.5}}{{\displaystyle \sum _{j=1}^n{\left(W_j^{\prime }\times W_j^{″}\right)}^{0.5}}}}$$

(12)

where $W_j^{\prime }$ represents the subjective weight determined by the AHP; $W_j^{″}$ represents the objective weight determined by the entropy weight method.

Determining the combined weights is critical for balancing expert experience with data-driven information. The AHP reflects the long-term cognitive understanding of domain experts regarding factors influencing grouting effectiveness, whereas the EWM is based entirely on the dispersion characteristics of actual construction data. To avoid biases potentially arising from an over-reliance on a single perspective, this study adopts a balanced weighting strategy, assigning equal contributions (0.5 each) to both subjective and objective weights.

4.4. TOPSIS Model

The TOPSIS model [31,32] is a multi-attribute decision evaluation method based on geometric principles. Due to its computational simplicity and clear methodology, this approach is widely applied in assessing the interrelationships between entities.

4.4.1. Matrix Construction

Normalizing the judgment matrix expressed in Equation (5) yields the target matrix $B={\left(b_{ij}\right)}_{m\times n}$:

$$B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \dots & b_{1n}\\ b_{21}& b_{22}& \dots & b_{2n}\\ ⋮& ⋮& b_{ij}& ⋮\\ b_{m1}& b_{m2}& \dots & b_{m3}\end{array}\right]$$

$${b_{ij}={\displaystyle \frac{x_{ij}}{\sqrt{{\displaystyle \sum _{i=1}^m{x_{ij}}^2}}}}}_{\left(i=1,2,\dots m; j =1,2,\dots n\right)}$$

(13)

Construct the weight vector matrix $w={\left[w_1,w_2,\dots ,w_n\right]}^T$, and further construct the weighted normalized matrix $Z={\left(Z_{ij}\right)}_{m\times n}$, then:

$$Z_{ij}=w_j\times b_{ij},i=1,2,\dots ,m;j=1,2,\dots n$$

(14)

4.4.2. Determination of Ideal Solutions

In the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method, the globally optimal and worst-case states of an evaluation object are defined as the Positive Ideal Solution (PIS) and Negative Ideal Solution (NIS), respectively. However, in engineering practice, evaluation objects are often influenced by dynamic spatiotemporal variations and the coupling of multiple factors, making it highly challenging to achieve an absolute PIS. Consequently, the relative closeness of a model solution to the PIS has become a standard criterion for assessing the reliability of decision outcomes.

For the six evaluation indicators considered in this study, all are benefit-type attributes, meaning a higher value indicates better grouting performance. Based on this characteristic, the vector of maximum values from each indicator column in the decision matrix is designated as the Positive Ideal Solution ($Z^{+}$), representing the most desirable state of grouting effectiveness. Correspondingly, the vector of minimum values is designated as the Negative Ideal Solution ($Z^{-}$), representing the least desirable state. $Z^{+}$ and $Z^{-}$ thus serve as the theoretical benchmarks within the multi-dimensional evaluation space for measuring grouting performance. The formulae for the positive and negative ideal solutions are, respectively:

$$Z^{+}=\left(\max \left\{z_{11},z_{22},\dots ,z_{m1}\right\},\max \left\{z_{12},z_{22},\dots ,z_{m2}\right\},\dots ,\max \left\{z_{1n},z_{2n},\dots ,z_{mn}\right\}\right)=\left(Z_1^{+},Z_2^{+},\dots ,Z_n^{+}\right)$$

(15)

$$Z^{-}=\left(\min \left\{z_{11},z_{22},\dots ,z_{m1}\right\},\min \left\{z_{12},z_{22},\dots ,z_{m2}\right\},\dots ,\min \left\{z_{1n},z_{2n},\dots ,z_{mn}\right\}\right)=\left(Z_1^{-},Z_2^{-},\dots ,Z_n^{-}\right)$$

(16)

4.4.3. Weighted Distance Calculation

For the $i$th object to be classified, the weighted (Euclidean) distance between the model solution and the ideal solution is:

$$D_i^{+}=\sqrt{{\displaystyle \sum _{j=1}^n{\left(Z_j^{+}-z_{ij}\right)}^2}},D_i^{-}=\sqrt{{\displaystyle \sum _{j=1}^n{\left(Z_j^{-}-z_{ij}\right)}^2}}$$

(17)

4.4.4. Adherence Calculation

From Equation (17), it can be observed that the smaller the value of $D^{+}$, the larger the value of $D^{-}$, indicating that the model solution is closer to the positive ideal value. Conversely, the larger the value of $D^{+}$, the smaller the value of $D^{-}$, indicating that the model solution deviates further from the positive ideal value.

For the $i$th object to be classified, the closeness of its model solution to the positive ideal value can be calculated using the following equation:

$$C_i={\displaystyle \frac{D_i^{-}}{D_i^{+}+D_i^{-}}}$$

(18)

where $C_i$ represents the proximity of the model solution to the positive ideal value, i.e., the quantitative measure of the effectiveness of the borehole grouting. Its value range is [0,1]. A larger $C_i$ indicates that the model solution is closer to the positive ideal solution, i.e., the borehole grouting is more effective.

5. Classification of Sealing Effectiveness

5.1. Weighting of Indicator Factors

5.1.1. Subjective Weighting

Considering the characteristics and actual conditions of the study area, a judgment matrix $R$ can be constructed for secondary indicators such as grouting volume characteristics, grouting parameters, final hole stratum, and formation characteristics.

$$R=\left[\begin{array}{cccc}1& 2& 4& 5\\ 1/2& 1& 2& 3\\ 1/4& 1/2& 1& 2\\ 1/5& 1/3& 1/2& 1\end{array}\right]$$

The calculated feature vector $w=\left(0.5056,0.2642,0.1434,0.0868\right)$ yields $CR=0.0157<0.1$ from Equation (3), satisfying consistency testing and confirming the matrix’s validity. Similarly, the weights for tertiary indicators at the scheme layer are presented in

Table 8. Subjective Weights Determined by the AHP Method.

Secondary Indicators	Weight	Third-Level Indicators	Weight
Grouting Volume Characteristics	0.5056	Grouting Volume	0.1798
		Grout volume per unit time	0.0427
		Grout volume per unit thickness	0.2831
Grouting parameters	0.2642	Final borehole pressure	0.2642
Final hole stratum	0.1434	Depth of Cambrian limestone	0.1434
Stratigraphic characteristics	0.0868	Variation in Rock Mechanical Strength	0.0868

.

5.1.2. Objective Weighting

Based on the judgment matrix $X$ and Equations (6)–(9), the entropy values $E_j$ for each indicator are calculated as follows:

$$E_j=\left(E_1,E_2,E_3,E_4,E_5,E_6\right)=\left(0.9549,0.9962,0.9358,0.9784,0.9864,0.9987\right)$$

The coefficient of variation for each indicator is obtained from Equation (10): $G_j$:

$$G_j=\left(G_1,G_2,G_3,G_4,G_5,G_6\right)=\left(0.0451,0.0038,0.0642,0.0216,0.0136,0.0013\right)$$

Finally, the weights for each indicator $W_j$ are obtained from Equation (11):

Wi = (W₁, W₂, W₃, W₄, W₅, W₆) = (0.3017, 0.0257, 0.4293, 0.1442, 0.0906, 0.0085)

5.1.3. Combined Weight

Based on the weights obtained separately via the AHP method and EWM ($W^{\prime }$ and $W^{″}$ respectively), the composite weights for each indicator were determined using Equation (12). The results are presented in

Table 9. Comprehensive weighting table.

Evaluation Indicator	Grout Volume	Grout Volume per Unit Time	Grout Volume per Unit Thickness	Final Borehole Pressure	Depth of Cambrian limestone	Variation in Rock Mechanical Strength
Combined weighting	0.2453	0.0348	0.3667	0.2051	0.1197	0.0283

.

5.2. Grouting Effectiveness Evaluation

Based on the TOPSIS theoretical model, an evaluation was conducted for 40 boreholes across six channels. The TOPSIS evaluation parameters were determined as follows: the indicator weighted standardization matrix $Z$, the positive and negative ideal solutions $Z^{+}$ and $Z^{-}$, the Euclidean distance $D$, and the proximity of the borehole grouting effectiveness to the ideal solution $C$.

The weighted standardization matrix $Z$ is derived from Equations (13) and (14):

Determine the positive and negative ideal solution $Z$ through Equations (15) and (16):

$$Z=\left[\begin{array}{cccccc}0.0211& 0.0043& 0.0397& 0.0195& 0.0138& 0.0037\\ 0.0415& 0.0046& 0.0801& 0.0195& 0.0134& 0.0037\\ 0.0267& 0.0042& 0.0507& 0.0195& 0.0135& 0.0037\\ 0.0402& 0.0053& 0.0731& 0.0208& 0.0142& 0.0037\\ 0.0070& 0.0061& 0.0133& 0.0221& 0.0135& 0.0037\\ 0.0192& 0.0060& 0.0349& 0.0454& 0.0251& 0.0046\\ 0.0212& 0.0056& 0.0392& 0.0506& 0.0133& 0.0046\\ 0.0245& 0.0057& 0.0147& 0.0389& 0.0439& 0.0046\\ 0.0709& 0.0056& 0.1318& 0.0402& 0.0134& 0.0046\\ 0.0304& 0.0061& 0.0532& 0.0402& 0.0134& 0.0046\\ 0.0112& 0.0049& 0.0214& 0.0208& 0.0151& 0.0046\\ 0.0547& 0.0054& 0.1215& 0.0260& 0.0143& 0.0048\\ 0.0492& 0.0066& 0.0991& 0.0221& 0.0143& 0.0048\\ 0.0424& 0.0065& 0.0823& 0.0234& 0.0149& 0.0048\\ 0.0301& 0.0049& 0.0602& 0.0195& 0.0146& 0.0048\\ 0.0242& 0.0072& 0.0473& 0.0195& 0.0149& 0.0048\\ 0.0339& 0.0055& 0.0688& 0.0221& 0.0143& 0.0048\\ 0.0656& 0.0059& 0.1562& 0.0234& 0.0146& 0.0048\\ 0.0216& 0.0056& 0.0450& 0.0195& 0.0140& 0.0048\\ 0.0446& 0.0076& 0.0923& 0.0208& 0.0142& 0.0048\\ 0.0099& 0.0045& 0.0088& 0.0273& 0.0145& 0.0049\\ 0.0082& 0.0041& 0.0059& 0.0402& 0.0221& 0.0049\\ 0.0250& 0.0066& 0.0224& 0.0415& 0.0138& 0.0049\\ 0.0104& 0.0059& 0.0093& 0.0428& 0.0168& 0.0049\\ 0.0224& 0.0056& 0.0200& 0.0415& 0.0141& 0.0049\\ 0.0397& 0.0076& 0.0386& 0.0454& 0.0289& 0.0039\\ 0.0192& 0.0045& 0.0387& 0.0273& 0.0147& 0.0039\\ 0.0148& 0.0041& 0.0301& 0.0402& 0.0145& 0.0039\\ 0.0228& 0.0066& 0.0465& 0.0415& 0.0148& 0.0039\\ 0.0181& 0.0059& 0.0369& 0.0428& 0.0145& 0.0039\\ 0.0459& 0.0055& 0.0236& 0.0415& 0.0227& 0.0047\\ 0.0456& 0.0050& 0.0271& 0.0454& 0.0152& 0.0047\\ 0.0957& 0.0061& 0.0475& 0.0273& 0.0241& 0.0047\\ 0.0763& 0.0063& 0.0418& 0.0195& 0.0234& 0.0047\\ 0.0287& 0.0037& 0.0302& 0.0208& 0.0235& 0.0047\\ 0.0123& 0.0036& 0.0125& 0.0208& 0.0239& 0.0047\\ 0.0489& 0.0059& 0.0250& 0.0208& 0.0231& 0.0047\\ 0.0547& 0.0052& 0.0268& 0.0389& 0.0224& 0.0047\\ 0.0197& 0.0045& 0.0201& 0.0415& 0.0240& 0.0047\\ 0.0324& 0.0039& 0.0333& 0.0402& 0.0237& 0.0047\end{array}\right]$$

$$Z_i^{+}=(Z_1^{+},Z_2^{+},Z_3^{+},Z_4^{+},Z_5^{+},Z_6^{+})=(0.0957,0.0076,0.1562,0.0506,0.0439,0.0049)$$

$$Z_i^{-}=(Z_1^{-},Z_2^{-},Z_3^{-},Z_4^{-},Z_5^{-},Z_6^{-})=(0.0070,0.0036,0.0059,0.0013,0.0133,0.0037)$$

The Euclidean distance $D$ for each sample is calculated using Equation (17). The complexity proximity value $C$ is obtained from Equation (18).

To capture the overall governance level, the arithmetic mean is adopted to bridge the scale from discrete boreholes to continuous channels. In the absence of explicit parameters defining individual hydraulic contribution, equal weighting serves as the most objective and reproducible baseline [33]. The quantified grouting effectiveness values for the 40 boreholes across six channels are presented in

Table 10. TOPSIS Model Quantification of Grouting Quality.

Recharge Channel	Borehole No.	${\mathit{D}}_{\mathit{i}}^{+}$	${\mathit{D}}_{\mathit{i}}^{-}$	${\mathit{C}}_{\mathit{i}}$	Mean	Recharge Channel	Borehole No.	${\mathit{D}}_{\mathit{i}}^{+}$	${\mathit{D}}_{\mathit{i}}^{-}$	${\mathit{C}}_{\mathit{i}}$	Mean
NO.1	A1	0.1452	0.0416	0.223	0.298	NO.4	A13	0.1737	0.0404	0.189	0.212
	A2	0.1029	0.0848	0.452			A14	0.1758	0.0424	0.194
	A3	0.1339	0.0526	0.282			A15	0.1548	0.0495	0.242
	B1	0.1086	0.0781	0.418			B9	0.1725	0.0419	0.196
	B2	0.1750	0.0229	0.116			B10	0.1579	0.0501	0.241
NO.2	A4	0.1448	0.0566	0.281	0.387	NO.5	A16	0.1334	0.0563	0.297	0.231
	A5	0.1422	0.0623	0.305			A17	0.1468	0.0402	0.215
	A6	0.1592	0.0533	0.251			A18	0.1558	0.0330	0.175
	B3	0.0484	0.1460	0.751			B11	0.1383	0.0485	0.260
	B4	0.1263	0.0666	0.345			B12	0.1486	0.0391	0.208
NO.3	A7	0.1646	0.0264	0.138	0.434	NO.6	A19	0.1439	0.0590	0.291	0.308
	A8	0.0662	0.1281	0.659			A20	0.1419	0.0610	0.301
	A9	0.0844	0.1051	0.554			A21	0.1216	0.0993	0.450
	A10	0.1006	0.0869	0.463			A22	0.1186	0.0884	0.427
	A11	0.1241	0.0624	0.335			A23	0.1447	0.0540	0.272
	A12	0.1367	0.0503	0.269			A24	0.1681	0.0412	0.197
	B5	0.1144	0.0727	0.388			B13	0.1415	0.0616	0.303
	B6	0.0523	0.1630	0.757			B14	0.1382	0.0661	0.324
	B7	0.1403	0.0469	0.250			B15	0.1576	0.0470	0.230
	B8	0.0902	0.0985	0.522			B16	0.1404	0.0561	0.286

.

Based on the quantitative grouting effectiveness scores, higher values indicate superior grouting performance. Therefore, as shown in Table 9, the effectiveness ranking for the five boreholes in Recharge Channel 1 is: A2, B1, A3, A1, B2; the effectiveness ranking for the five boreholes in Recharge Channel 2 is: B3, B4, A5, A4, A6; the effectiveness ranking for the ten boreholes in Recharge Channel 3 is: B6, A8, A9, B8, A10, B5, A11, A12, B7, A7. the effectiveness ranking for the five boreholes in Recharge Channel 4 is: A15, B10, B9, A14, A13. the effectiveness ranking for the five boreholes in Recharge Channel 5 is: A16, B11, A17, B12, A18; the effectiveness ranking for the ten boreholes in Recharge Channel 6 is: A21, A22, B14, B13, A20, A19, B16, A23, B15, A24. Based on the average quantitative values of grouting effectiveness across all channels, the comprehensive ranking of the six channels is as follows: 3rd, 2nd, 6th, 1st, 5th, 4th.

5.3. Discussion

Generally speaking, once the specific patterns of karst development have been ascertained and appropriate grouting materials and techniques are employed, the more developed the karst in the target layer, the higher the quality of the grouting in sealing the aquifer recharge channels. The degree of karst development in the six recharge channels is shown in

Table 11. Degree of karst development in recharge channels.

Recharge Channel	No.1	No.2	No.3	No.4	No.5	No.6
Borehole exposure rate (%)	20	100	50	0	20	0
Cave height (m)	1.17	4.99	4.71	N/A	4.51	N/A
Cambrian limestone exposure rate (%)	2.7	8.66	13.26	N/A	8.19	N/A
Old voids rate (%)	0	0	0	0	0	100

Note: N/A indicates not applicable or no data available.

.

Evidently, the degree of karst development in the Cambrian limestone: Channels 2 and 3 are well-developed, Channels 1 and 5 are moderately developed, while Channels 4 and 6 show no development. However, as Channel 6 encountered a goaf during drilling, coal mining disturbance has resulted in relatively well-developed fractures in the strata of the coal seam’s roof and floor. In summary, the evaluation results align with the observed karst fissure development and goaf distribution in the exposed recharge channels, demonstrating the reliability of the assessment model.

Both the AHP and EWM employed in this study are standard approaches. To explore the rationale behind the combined weighting approach, the performance of individual methods was compared with that of the combined method, as detailed in

Table 12. Comparison of evaluation scores and rankings under different weighting methods.

Channel	AHP Score	AHP Rank	EWM Score	EWM Rank	Combined Score	Combined Rank
NO.3	0.425227	2	0.437869	1	0.433854	1
NO.2	0.441987	1	0.351323	2	0.386961	2
NO.6	0.360964	3	0.279225	4	0.308139	3
NO.1	0.308547	4	0.290784	3	0.298432	4
NO.5	0.258220	6	0.217675	5	0.231217	5
NO.4	0.300994	5	0.150189	6	0.212955	6

.

As shown in Table 12, when using AHP alone, the channel ranking was: NO.2 > NO.3 > NO.6 > NO.1 > NO.4 > NO.5. When using only the EWM, the ranking was: NO.3 > NO.2 > NO.1 > NO.6 > NO.5 > NO.4. The ranking obtained from the combined weighting method was: NO.3 > NO.2 > NO.6 > NO.1 > NO.5 > NO.4.

Correlation analysis indicated that the ranking from the combined weighting method showed the highest consistency with that from the EWM (Spearman correlation coefficient ρ = 0.9429, p = 0.0048), though differences existed with the individual methods. For example, for Channel 4, the score given by AHP alone (0.300994) was significantly higher than that from the combined weighting method (0.212955), resulting in its ranking being subjectively overestimated to the 5th position. In contrast, the combined result adjusted it to a more reasonable last place (6th), revealing potential bias in relying solely on subjective weighting. Conversely, using only the EWM may excessively suppress indicators with low variation due to its complete reliance on the statistical characteristics of the data.

Therefore, the combined weighting method adopted in this study effectively integrates subjective experience and objective data. It not only retains the data-driven ranking structure of the EWM but also reasonably corrects for extreme cases through the integration of AHP. The final evaluation ranking (NO.3 > NO.2 > NO.6 > NO.1 > NO.5 > NO.4) aligns with the actual development of karst fissures and the distribution of goaf areas as revealed by drilling, verifying the reliability and robustness of the assessment model.

In terms of practical engineering implications, this study serves not only as a “post-project evaluation” of completed works but, more crucially, provides guidance for future “pre-design” and “in-process control.” During the design phase, the findings reveal a direct correlation between geological conditions (specifically karst and fissure development) and grouting effectiveness. For projects with similar hydrogeological conditions, the “injectability” of different zones can be predicted based on preliminary geological exploration, enabling differentiated and refined grouting designs; for instance, in karst-developed zones (e.g., Channels 2 and 3), the design grout volume and borehole density should be increased, whereas in areas dominated by structural fissures (e.g., Channel 6), greater attention should be paid to grouting pressure and grout penetrability. Regarding construction control, the weight analysis identifies “Grout Volume per Unit Thickness” as a critical sensitivity indicator, suggesting that construction managers should not focus solely on the total grout volume but must also monitor the distribution intensity of the grout within the target strata in real-time to ensure effective sealing. Finally, in terms of effectiveness evaluation, the proposed model offers a rapid, low-cost quantitative assessment tool; by comparing the TOPSIS scores of different boreholes or zones, weak links in the grouting process can be quickly identified, providing a scientific basis for subsequent supplementary grouting or decision-making in the next stage of the project.

6. Conclusions and Future Work

(1) Grouting seal operations were sequentially implemented across 40 boreholes targeting the six Cambrian limestone aquifer recharge channels. The total drilling advance reached 5494.94 m, with cumulative penetration into the Cambrian limestone of 2694.39 m. The total grout volume injected amounted to 28,552.21 tonnes, providing substantial support for reducing dynamic water recharge.

(2) Based on four long-duration unsteady flow pumping tests, the dynamic water recharge volume to the goaf was calculated. Compared to pre-grouting conditions, post-grouting seal reduced dynamic water recharge by 240.78 m³/h during the dry season and 878.57 m³/h during the wet season, demonstrating the significant effectiveness of grouting in sealing recharge channels.

(3) Key indicators were selected: grout volume, grout volume per unit time, grout volume per unit thickness, final borehole pressure, penetration depth into Cambrian limestone, and variation in rock mechanical strength. Subjective, objective, and comprehensive weights for these indicator factors were determined, establishing a foundation for quantitatively evaluating grout sealing quality.

(4) An evaluation model for assessing the effectiveness of grouting in sealing aquifer recharge channels was established based on TOPSIS theory. This model quantitatively evaluates the sealing effectiveness of curtain grouting. The comprehensive ranking of sealing effectiveness across the six channels was, NO.3 > NO.2 > NO.6 > NO.1 > NO.5 > NO.4, consistent with the actual extent of karst fissure development revealed by drilling and the distribution of goaf areas.

(5) The practical significance of this study lies in providing a systematic and objective quantitative evaluation method for highly concealed underground grouting projects. It realizes a transition from a binary “qualified/unqualified” judgment to a refined grading system (e.g., excellent, good, fair, poor). This transformation facilitates the precise identification of weak links in the project, thereby providing a scientific basis for decision-making regarding supplementary grouting.

However, this study also presents certain limitations. First, although the evaluation indicator system is representative, its universality requires validation and refinement through more engineering cases; for example, economic and material indicators such as grouting cost and grout mix ratio could be incorporated in future iterations. Second, the AHP weighting component relies on expert experience; future research could introduce multi-round scoring by a larger panel of experts (e.g., the Delphi method) to further reduce subjectivity. Finally, this study currently provides a relative ranking of effectiveness among channels but has not yet established a definitive quantitative relationship between the evaluation scores and the absolute water-blocking rate.

(6) The proposed evaluation framework possesses significant potential for broader application. It is applicable not only to water hazard control in coal mines but also serves as a valuable reference for evaluating grouting curtain effectiveness in other domains, such as reservoir dams and tunnel engineering. Future research efforts should focus on (1) integrating this evaluation model with real-time monitoring data to develop a dynamic, intelligent system for grouting process control and assessment and (2) combining the model with numerical simulation methods to explore the mapping relationship between TOPSIS scores and physical parameters, such as the reduction rate of regional permeability coefficients, thereby achieving a more absolute quantification of grouting effectiveness.