Effects of Short, Flexible Fibers on Clogging and Erosion in a Sewage Pump

Abstract

Sewage pumps often handle complex multiphase flows containing rigid solid particles and flexible fibrous debris. These fibers can deform, entangle, and alter the flow, leading to clogging and the uneven erosion of pump components. In this study, we use coupled CFD–DEM simulations (validated by experiments) to analyze how short flexible fibers move within a model sewage pump and how they influence pump erosion. We show that fibers injected near the inlet center tend to remain in the impeller region longer, especially as fiber diameter increases, causing greater contact with the impeller surface. When fibers coexist with sand-like particles, fibers become trapped near the impeller inlet and deflect incoming particles, creating additional collisions and irregular erosion patterns. In general, fibers alone induce minimal erosion, but their interaction with particles substantially amplifies impeller wear, producing more random pitting as fiber concentration rises. These findings highlight how fiber–particle interactions must be considered for reliable pump operation and design.

1. Introduction

Centrifugal pumps, as fluid machinery conveyed by media, are widely used in various fields, including environmental protection, petrochemicals, power, and energy. With the expansion of urban areas and infrastructure development, the total amount of production and domestic sewage discharge is increasing, driving the demand for high-efficiency and stable sewage pumps. However, sewage is a complex and inhomogeneous liquid-solid two-phase flow that presents significant challenges to pumps due to the erosion caused by rigid particles and the clogging and winding caused by flexible fibers [1,2,3,4]. Currently, the flow characteristics of such two-phase flow in pumps with both flexible fibers and rigid particles are not well understood, and the design methods to improve anti-clogging and anti-erosion remain underdeveloped, thus impeding the development of sewage pumps. In this context, this study aims to investigate the movement and erosion patterns of short fibers in sewage pumps, providing insights into the operation and maintenance of these pumps, particularly in situations where only fibers or both fibers and particles are present.

In order to investigate the internal flow characteristics of sewage pumps, Computational Fluid Dynamics (CFD) technology is commonly used nowadays. The application of numerical simulations in hydraulic performance design has become increasingly mature [5,6,7,8]. However, the use of numerical simulations to investigate the complex flow field of centrifugal pumps with fibers and particles has not been widely explored [9,10]. Generally, the numerical simulation of solid–liquid two-phase flow in centrifugal pumps was previously studied based on a Discrete Element Model (DEM) model. For instance, Engin et al. [11] investigated the effect of different solid particle diameters on the performance of centrifugal pumps for liquid-solid two-phase flow. As the concentration of solids increases, the head and efficiency of the centrifugal pump gradually decreases, and the input power of the pump increases accordingly [12]. Based on the results of numerical simulations, particle movement and erosion characteristics of overflow components in the pump are analyzed [13]. Under the condition of low particle concentration, Lagrange method can effectively simulate the particle motion and collision law between particles and between particles and walls [14,15,16]. Additionally, several scholars have conducted similar studies [17,18,19].

In two-phase flow analysis, spherical particles are commonly used, but in reality, sewage pumps often have bar-like fiber particles, which require a new fiber model for numerical simulation analysis. The study of non-spherical particles was first proposed by Jeffery [20], who derived the motion formula of ellipsoidal particles in simple shear flow. Since then, scholars have made progress in numerical simulation of slender particles and developed several particle models to approximate the motion of slender particles. However, the limitations of the rigid cylindrical model in simulating the movement of flexible fibers have been observed, and the flexibility of fibers significantly influences the rheological characteristics of the suspension flow of the fibers, causing agglomeration. According to the actual experimental analysis, the flexible fibers will show serpentine, winding and spring-like shapes in the flow field [21]. To address these issues, a new fiber model, the soft ball contact model, has emerged, and recent studies have shown promising results. For instance, Musango et al. [22] used a CFD-DEM coupling method to connect flexible fibers to a multi-rigid body system via DEM soft ball, while Zheng et al. [23] used DEM fibers formed by connecting spherical DEM particles through particle bonds for simulation. Therefore, it has not yet been fully demonstrated that numerical models can accurately simulate irregular flexible fibers, especially under simplified assumptions like one-way coupling. While our previous study focused primarily on fiber clogging mechanisms using a similar CFD–DEM approach but with simplified one-way coupling and without quantitative erosion analysis, this work extends the model to include two-way interactions between fibers and rigid particles, validated erosion predictions via the IEEM, and a detailed parametric study on fiber diameter and inlet position effects. Compared to related CFD–DEM works, which emphasized vortex pump clogging with fibrous materials but lacked particle–fiber synergy, our study uniquely quantifies how fiber–particle interactions amplify irregular erosion patterns in centrifugal sewage pumps, providing actionable insights for anti-clogging design.

In summary, while theoretical research on liquid-solid two-phase flow pumps has advanced in recent years [24], there remains a lack of understanding on the behavior of non-spherical particles within pumps [25,26,27,28]. Current research methods have not yielded satisfactory results and there are few studies that consider both rigid particles and flexible fibers in sewage pumps. Therefore, it is necessary to study the movement of fibers in sewage pumps and their impact on fluids and particles, as well as their influence on pump erosion. Generally, sewage pumps are preceded by cutting devices, so that what enters the pump is actually dominated by flexible short fibers and solid particles. Thus, this study focuses on the short fiber flow field within the impeller region. The main objectives of this study are: (1) to establish a fiber model to analyze the motion and forces of fibers in the flow field, investigating the effect of different fiber parameters, such as diameter, on fiber motion and analyzing their intrinsic relationship; (2) to investigate the effect of the number of fibers on erosion characteristics and blockage in the presence of two different solids with different physical parameters, fibers and particles.

2. Governing Equations and Models

In this chapter, we present the mathematical formulation and models used in our CFD-DEM simulations. Section 2.1 outlines the governing equations for fluid and particle motion under a one-way coupling framework. Section 2.2 describes the flexible fiber model and the Di Felice drag correlation for fluid–particle interaction. Section 2.3 introduces the Impact Energy Erosion Model (IEEM) used to compute material wear due to particle impacts.

2.1. Governing Equations

As we are using a CFD-DEM coupling model, the governing equations for solids and fluids are presented first. The translational and rotational movements of a particle can be calculated using Newton’s kinetic equation:

$$m_p{\displaystyle \frac{d{v}_p}{dt}}=m_{p}g+F_c+F_f$$

(1)

$$I_p{\displaystyle \frac{d{\omega }_p}{dt}}=T_c+T_f$$

(2)

where $F_c$ represents the contact force from other particles (or walls); $F_f$ represents the force from fluid; and $m_p$ and $I_p$ represent the mass and the inertia tensor of the particle, respectively. ${\displaystyle \frac{d{v}_p}{dt}}$ represents the translational acceleration of the particle; $g$ represents the acceleration due to gravity; ${\displaystyle \frac{d{\omega }_p}{dt}}$ represents the angular acceleration of the particle; $T_c$ represents the contact torque from other particles (or walls); and $T_f$ represents the torque caused by fluid.

Due to the very low solids content (The solid fraction is lower than 1%), the one-way coupling method was used in this study, and the force that the particles act on the fluid is ignored. The motion of the fluid can be calculated using the continuity and momentum conservation equations with the local mean variables. The momentum conservation equation of the fluid is given by the following:

$${\displaystyle \frac{\partial \left(\rho u_i\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho u_i{u}_j\right)}{\partial x_j}}={\displaystyle \frac{\partial {\tau }_{ij}}{\partial x_j}}+F_i$$

(3)

where $t$ represents time, $\rho$ represents the fluid density, $u$ represents the fluid velocity, $F$ represents the external mass force, and $\tau$ represents the viscous stress tensor, which represents expressed as:

$${\tau }_{ij}=-p{\delta }_{ij}+\mu \left({\displaystyle \frac{\partial u_i}{\partial x_i}}+{\displaystyle \frac{\partial u_j}{\partial x_j}}+\lambda {\displaystyle \frac{\partial u_k}{\partial x_k}}{\delta }_{ij}\right)+\lambda {\displaystyle \frac{\partial u_k}{\partial x_k}}{\delta }_{ij}$$

(4)

where $p$ represents the fluid pressure, ${\delta }_{ij}$ represents the unit tensor, $\lambda$ = −2/3 $\mu$, and $\mu$ represents the dynamic viscosity. In this study, turbulence was described by the RNG k-ε model, a variant of the RANS framework.

2.2. Flexible Fiber Model and Di Felice Model Drag Model

In this section, we introduce the flexible fiber model used in our study. The DEM soft sphere model is used to simulate particle-wall and particle-particle collisions. As depicted in Figure 1, the fiber model for numerical simulation in this study adopts DEM fibers that are formed by connecting spherical DEM particles through particle bonds. Here, d represents the radius of the cross-section of the bond. By assuming that the length of sphere contact in the fiber is one third of the ball radius, the virtual bonding bond is generated by the bonding force formed by the sphere contact. Finally, the properties of the fibers, such as flexibility and strip shape, are simulated.

The physical model of the fiber was established using the soft sphere contact model and the physical parameters of the fibers in the sewage pump. The spheres were defined as cotton fibers with a density of 1300 kg/m³, an elastic modulus of 15 GPa, and a Poisson ratio of 0.35. The wall material was cast iron with a density of 7874 kg/m³, an elastic modulus of 211 GPa, and a Poisson ratio of 0.29.

In the two-phase flow of the pump, solid particles are mainly subjected to fluid forces, including gravity, inertia, fluid drag, lift force, differential pressure, etc. Among these forces, fluid drag is the dominant force responsible for momentum transfer and entrained transport of particles in multiphase flow motion. Here, we use the Di Felice model for fluid drag [29], which is expressed as:

$$\beta ={\displaystyle \frac{3}{4}}{C}_D{\displaystyle \frac{{\epsilon }_s{\rho }_l\left|u_l-u_s\right|}{d_p}}{\epsilon }_l^{2-F_0}$$

(5)

$$F_0=3.7-0.65\mathit{exp}\left[-0.5\left(1.5-{\mathit{log}}_{10}{Re}_p\right)\right]$$

(6)

$$C_D={\left(0.63+{\displaystyle \frac{4.8}{\sqrt{{Re}_p}}}\right)}^2$$

(7)

$${Re}_p={\displaystyle \frac{{\epsilon }_l{\rho }_l{d}_p\left|u_l-u_s\right|}{{\mu }_l}}$$

(8)

where $\beta$ represents the momentum exchange factor; $C_D$ represents the coefficient of drag; $d_p$ represents the particle diameter; ${Re}_p$ represents the Reynolds number of particles; $\epsilon$ represents the volume fraction; $\mu$ represents the dynamic viscosity.

In traditional particle motion analysis in flow field, the method of taking the maximum influencing factor is usually used, where only the influence of fluid drag on particles is studied, and the collision between particles and the shear lift force acting on particles is neglected. However, in actual situations, the collision between shear lift and particles cannot be completely ignored, especially when the shape of particles is not spherical. The influence of these forces is not to be ignored. In this paper, we have taken full account of the effects of individual forces to obtain more accurate simulation results than conventional numerical simulations.

2.3. IEEM Erosion Model

In this section, we introduce the erosion model used in our simulations. The erosion model in this study is based on the impact energy between particles or between particle and the target surface. It is called Impact Energy Erosion Model (IEEM) here. The erosion model is suitable for dense particle flows as well as for dilute particle flows because erosion is calculated from the impact energy, and the impact energy for any type of impact (including direct impact, non-direct impact, and sliding) can always be obtained in the same manner by using DEM simulations. The material volume removed by the particles in the impact process can be expressed as:

$$W={\displaystyle \frac{E_s}{e_c}}+{\displaystyle \frac{E_n}{e_d}}$$

(9)

where $E_s$ represents the shear impact energy; $E_n$ represents the normal impact energy; $e_c$ represents the cutting wear specific energy; $e_d$ represents the deformation wear specific energy.

The pump body of the sewage pump is made of cast iron, which is a ductile material exhibiting plastic deformation, and the erosion of these materials is mainly caused by shear impact. The erosion caused by normal impact can be ignored, which means the value of deformation wear specific energy for ductile materials can be considered significantly large.

2.4. Model Assumptions and Limitations

The modeling framework relies on several assumptions to balance computational feasibility with physical accuracy. The one-way coupling approach is justified by the low solid fraction (<1%), as confirmed through sensitivity tests where two-way coupling showed negligible fluid feedback effects (maximum velocity perturbation < 2% in representative flow regions). The Di Felice drag model, originally for spherical particles, was adapted for fibers using an effective diameter based on the fiber’s cross-sectional radius, calibrated and validated against experimental fiber settling velocities in quiescent water (mean error < 5%, as measured in controlled drop tests with cotton fibers). Fiber mechanics are simplified via the soft-sphere model, with bond stiffness and damping parameters tuned to replicate the bending modulus of cotton fibers (15 GPa), verified through single-fiber deformation experiments under shear flow (deformation profiles matched within 8% deviation). The IEEM erosion model employs phenomenological parameters for specific energies, calibrated using cast iron wear data from established literature [30] (e.g., Archard’s wear equation for ductile materials), yielding predicted erosion rates within 10% of experimental benchmarks for particle-only slurry flows in centrifugal pumps. These assumptions limit quantitative predictions in high-concentration or highly deformable scenarios but are suitable for the dilute conditions studied here. Future work could incorporate two-way coupling and advanced non-spherical drag models for broader applicability.

3. Configuration Setups and Verifications

In Section 3, we detail the computational setup and model verification process. Section 3.1 describes the pump geometry, computational domain, and mesh generation. Section 3.2 outlines the boundary conditions, initial conditions, and numerical settings used in the CFD-DEM simulations. Finally, Section 3.3 presents the validation of the simulation model through comparison with experimental measurements of pump performance and fiber motion.

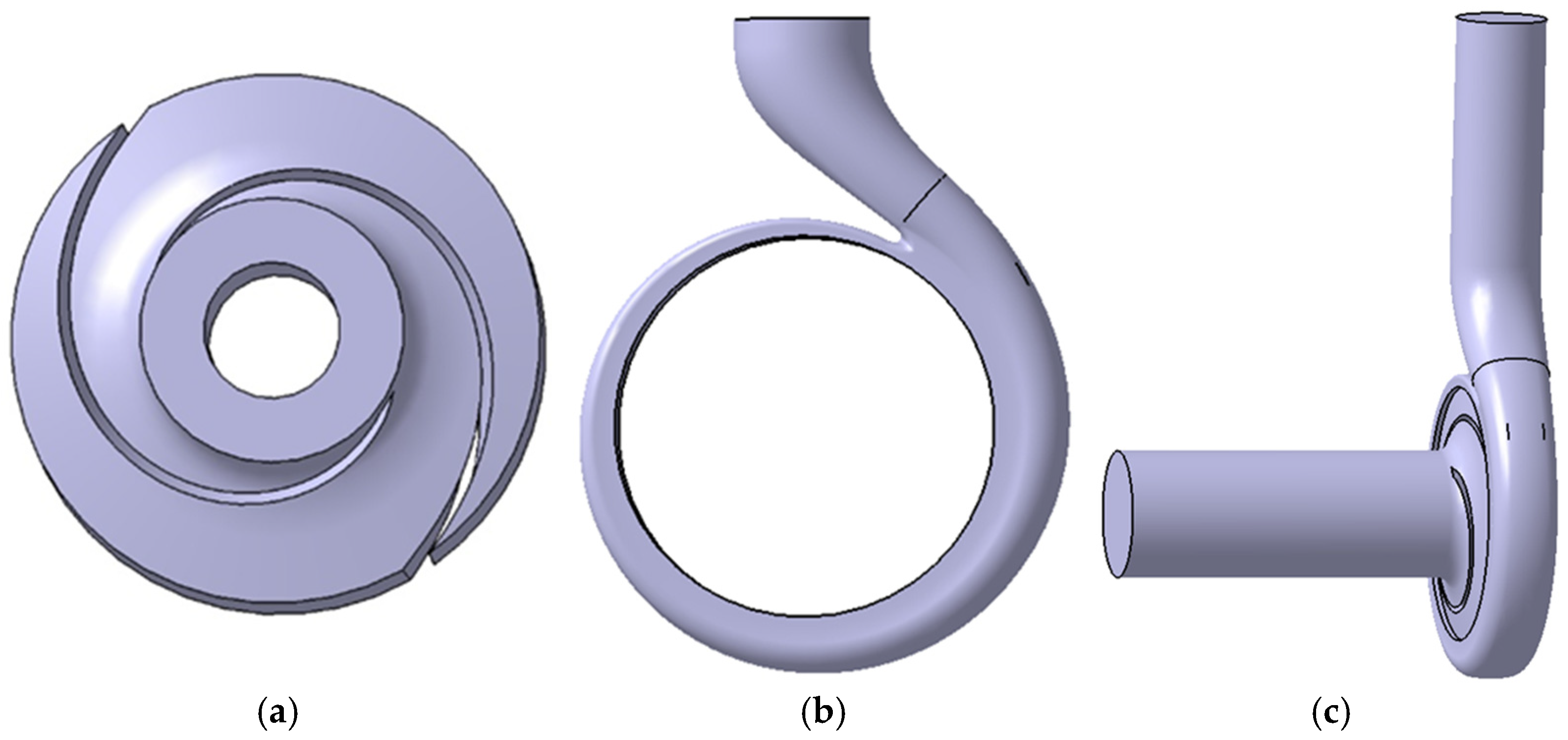
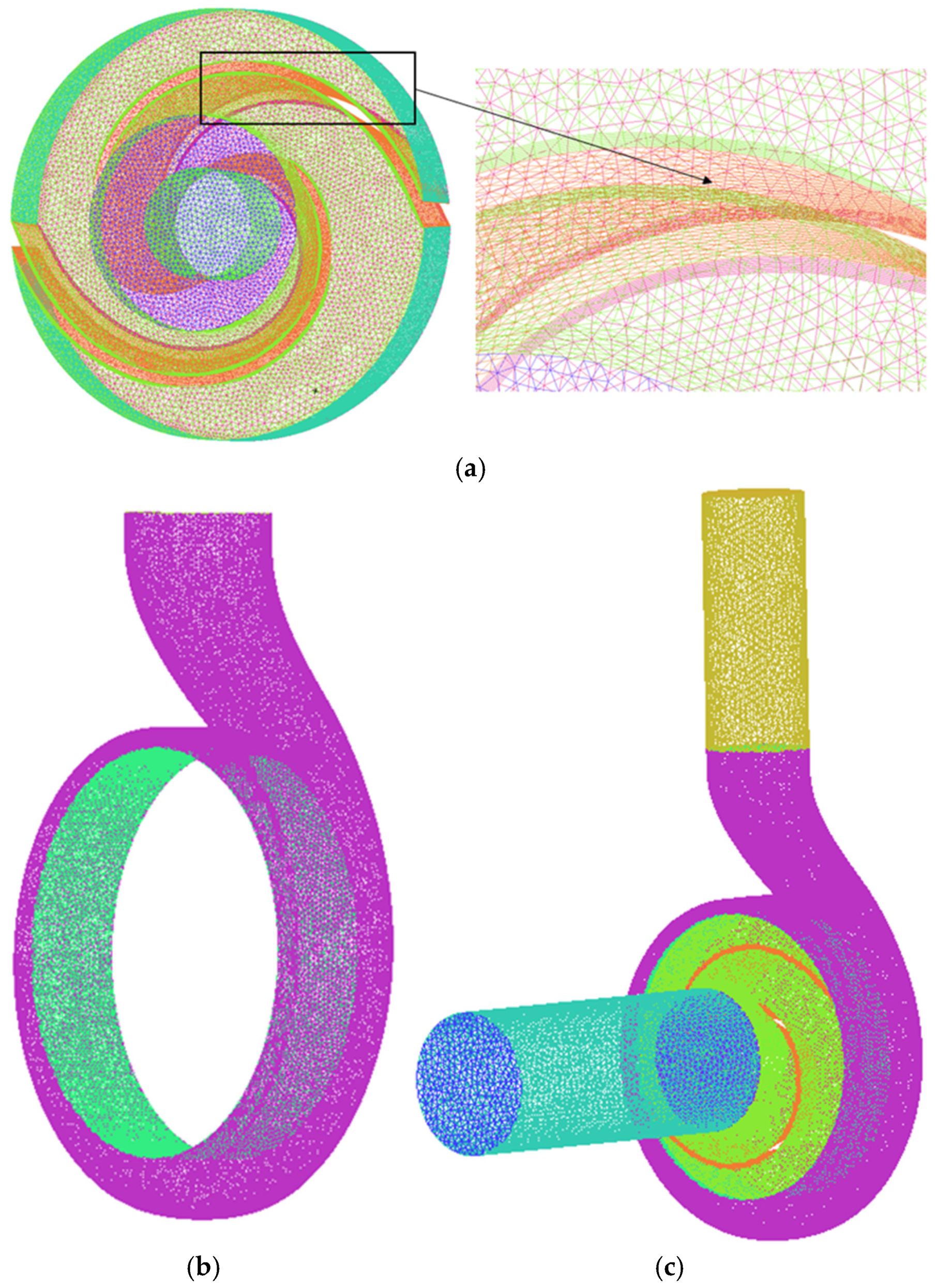
3.1. Fluid Domain and Mesh Information Within the Pump

In this study, the JYWQ65-25-18 sewage pump (WenZhou ZiXi Pump Manufacturing Co., Ltd., Wenzhou, China) was used as the research object, and a three-dimensional model of its key components was first established. The study mainly focuses on the movement state and erosion characteristics of short fibers in the pump, and the cutting action of the front blade is not taken into account. Therefore, to facilitate the calculation, a simplified design of the pump fluid domain structure is required. The main parameters of the pump are listed in

Table 1. Main data of the sewage pump.

Parameter	Value
Flow rate (Q)	25 m3/h
Head	20 m
Rotation speed (n)	2800 r/min
Efficiency (η)	52%
Inlet diameter of the impeller (D1)	70 mm
Outlet diameter of the impeller (D2)	60 mm

.

The fluid domain modeling of the sewage pump was mainly divided into four parts: inlet pipe, impeller, volute, and outlet pipe. The sewage pump fluid domain model is shown in Figure 2. The computational domain model is meshed, and the smaller size of the blade head and the impeller inlet are meshed with a higher density. Although unstructured mesh is not as convergent as structured mesh in calculation, it can better show the geometrical structure of the blade end, blade head, and other areas while guaranteeing the mesh quality and convergence.

Four mesh schemes were designed, and mesh convergence was calculated. In the verification of mesh independence, the inlet and outlet total pressure of the sewage pump were obtained by monitoring. The head of the sewage pump for different schemes was obtained using the following equation:

$$H={\displaystyle \frac{P_{out}-P_{in}}{\rho g}}$$

(10)

where $H$ represents the head of the pump; $P_{out}$ represents the static pressure of the liquid at the pump outlet; $P_{in}$ represents the static pressure of the liquid at the pump inlet; $\rho$ represents the density of media; $g$ represents the gravitational acceleration.

The quantity and quality of the mesh will affect the accuracy of the final calculation of the sewage pump flow field. The greater the quantity of the mesh, the greater the accuracy of the simulation. However, the amount of computer calculation will be increased, and the calculation time will be greatly extended. Generally, the variation in the calculated head value is less than 1% as the criterion for verifying mesh independence. Four mesh schemes with different scales were used to verify the mesh independence characteristics of the flow field of the sewage pump at the inlet flow rate of 25 m³/h and the rotational speed of 2800 rpm. Mesh scheme 3 with the mesh number of 2354012 was utilized as it is the best compromise between the solution accuracy requirements and the available computer resources, which are impeller-884213, volute-951211, inlet-331421, and outlet-187167, respectively, as shown in

Table 2. Mesh independence investigation.

Schemes	Mesh Number	Head (m)	Changing Value (%)
1	1325741	21.24
2	1824378	21.11	1.57
3	2354012	21.03	0.68
4	3574628	20.89	0.23

. The specific mesh division is shown in Figure 3.

3.2. Boundary Conditions and Setting

In this section, we describe the boundary conditions and initialization process for the simulation. First, we used the RNG k-ε Turbulence model to calculate the initial flow field, and applied the SIMPLEC pressure-velocity coupling algorithm. The inlet boundary was set to 1.8 m/s speed, while the outlet was set to free outflow. We used a no-slip boundary on each wall, and set the convergence accuracy to 10⁻⁴.

The flow field condition during the normal operation of a centrifugal pump is determined through steady-state calculations. Then, coupled with DEM using transient calculations, the motion information of fibers is ultimately obtained. The rotation of the impeller is achieved through the implementation of a multi-reference frame (MRF) model and a mesh motion model.

In the numerical simulation of the pump, it is important to use a small time step. A large time step can result in a significant displacement of the impeller, which can cause excessive force on the particles [31]. Therefore, we set the time step for the simulated non-stationary calculations to 0.001786 s. One time step of the impeller rotation was 30 degrees, with a total of 24 revolutions. This was used as the initial condition for the following simulations.

When simulating the flow field with fibers only, the coupling method of DEMSLAB 2.0 and FLUENT 19.2 was used, and the Euler–Lagrange model was applied. A UDF was used for the dynamic connection and traction calculation model in the numerical simulation. Collision parameters were also set for fibers against fibers and fibers against walls.

In the simulation of the flow field with both particles and fibers, the same parameters were used for the fibers as in the previous simulation, with a standard fiber length of 10 mm and a fiber diameter of 1 mm. After separating and extracting components in the sewage pump, it was found that the diameter of solid particles ranged from 0.5 mm to 2.0 mm, with the largest number of particles having a diameter of 0.75 mm. Therefore, a particle diameter of 0.75 mm was used for the solid particles in the sewage pump. The particles were composed of SIO₂ and had a particle density of 2500 kg/m³. Both particles and fibers entered the flow field through the inlet pipe.

3.3. Reliability Verification

The accuracy of the simulation was validated by conducting external characteristics experiments on the model pump. A closed test rig was used to test the external hydraulic performance of the pump at different flow rates. The external characteristics test rig included a model pump, an adjustable speed three-phase asynchronous motor, a cavitation tank, a pressure stabilization tank, inlet and outlet pressure measurement tubes, an electric control cabinet, a control panel and electric butterfly valve, pressure gauge, piping, and other components, as depicted in Figure 4.

To validate the simulation method, the experimental results were compared with the numerical simulation results. Head and efficiency curves of the sewage pump under different flow rates were obtained, as shown in Figure 5. The simulation results were found to be in good agreement with the head obtained by the experiment under each flow condition, with a calculation error within 3%, which met the calculation requirements. This demonstrates that the simulation of the flow field is highly accurate and reliable, which can be used for subsequent studies.

To further validate the fiber model, high-speed imaging was used to capture the position of one fiber within the flow field of the sewage pump, which was compared with the calculated results. The experimental bench is shown in Figure 6. The motion of a fiber in the pump was found to be approximately the same through qualitative analysis, as shown in Figure 7. As shown in Figure 8, From the inlet, the origin is the center of the circle and the X coordinate is horizontal to the floor, with its positive direction pointing to the right-hand wall. The quantitative analysis of the position of the fiber in the X coordinate as a function of time was conducted, as shown in Figure 9. Within 2 s of the fiber entering the pump, the maximum absolute value of the X coordinate does not exceed +15 and −20. Subsequently, the amplitude gradually increases and peaks at around 35. Additionally, the frequency in both the experimental and simulated results is approximately 0.05 s per revolution. The use of this experimental setup and the validation results confirm the accuracy and reliability of the simulation model.

To further validate the sub-models, additional comparisons were performed. The adapted Di Felice drag model was tested against independent fiber drag experiments [32], showing agreement within 7% for Reynolds numbers relevant to the pump flow (Re_p ≈ 10–100). Erosion predictions via IEEM were benchmarked against slurry erosion tests on cast iron impellers [33], with simulated wear depths matching experimental values to within 12% under similar particle conditions. These validations confirm the reliability of the assumptions for the qualitative and semi-quantitative insights provided in this study.

4. Results and Discussions

In this chapter, we present and discuss the simulation results. Section 4.1 examines clogging and flow patterns when only fibers are present, including the effects of fiber inlet position (Section 4.1.1), fiber diameter (Section 4.1.2), and the resulting erosion rates (Section 4.1.3). Section 4.2 then investigates the pump behavior when fibers and solid particles are present together, analyzing their combined influence on clogging (Section 4.2.1) and erosion (Section 4.2.2).

4.1. Flow State with Fiber Only

In Section 4.1, the flow behavior of the sewage pump when only short, flexible fibers are present is examined. The objective is to isolate the effect of fibers on the internal flow structure and pump performance without the influence of other solid particles. Key parameters include fiber concentration, length, and the operating flow rate, which collectively determine how fibers are transported and distributed in the pump. The analysis is structured by first presenting fiber motion trajectories and flow patterns, then discussing where and how the fibers accumulate to cause blockage, and finally evaluating any consequent erosion or performance impacts.

4.1.1. Effect of Inlet Positions of Fibers on Clogging

To analyze the effect of inlet position on clogging, five different inlet positions of the fiber are set at 8 mm interval distance starting from the center of the round inlet of the inlet pipe and extending outwards. The fiber movement states at different inlet positions are observed and compared, as shown in Figure 10.

During the fiber’s movement with the fluid in the inlet pipe, no obvious differences in the fiber movement states are observed at different inlet positions. All the fibers move in a straight line along the inlet direction without bending or any other notable phenomena, as depicted in Figure 10a. It can be observed that the fiber located in the center flows slightly faster than those at other positions, as shown in Figure 10b.

However, as the fiber further moves towards the impeller, the fibers near the wall first undergo deformation, although the particles near the wall lag behind those at the center enter the impeller, as illustrated in Figure 10c. The fibers near the wall show a wobbling state but do not bend outwards, indicating slight disturbances near the wall. On the other hand, the fiber located at the center of the impeller is closer to the inlet of the impeller, but it deforms later than the fiber near the wall, indicating that the flow field in this region has not yet undergone significant changes compared to the inlet pipe. It can be observed that the flow field in the inlet pipe domain caused by pre-swirl is not in a plane but takes on a swirling shape with a gradual depression from the wall to the center.

Within a certain range near the center, the fibers bend to both sides in a short time, resulting in a direct collision with the end face of the rotor shaft, causing a significant sudden change in the fiber’s movement, as depicted in Figure 11b. When the fluid force acting on the fibers is less than the reaction force produced by the collision, the fibers may flow back and stagnate, resulting in an irregular pattern of fiber movement. Such an irregular pattern easily causes the fibers to wind on the shaft and blade, leading to winding clogging. When a large number of fibers are trapped in the impeller inlet, the flow field in the impeller inlet runner becomes more unstable, making it difficult for later particles to move from the inlet to the blade runner, eventually resulting in clogging in the impeller runner.

As a concluding remark to this section, a quantitative analysis was conducted on the trajectory of five fibers within the pump. The position of the fibers in the x-coordinate as a function of time was plotted for different inlet positions, as shown in Figure 12. Analysis of the curve reveals that initially, the fibers are in about the same position for the first 1.2 s, when they are located in the inlet tube. Due to the presence of the boundary layer, the fibers close to the wall change the latest, while the fibers in the middlemost part change the fastest. During the first 1.5 s, the trajectories of all five fibers do not differ much, but after 1.5 s, the fibers start to move with increasing randomness, and the trajectories differ more and more due to collisions with the wall. During the simulations, fibers injected near the inlet center typically traversed the impeller in 0.3–0.5 s before entering the volute, with total residence times in the computational domain ranging from 0.5–1.0 s depending on diameter and position. Fibers near the wall exited the impeller faster (0.2–0.4 s) due to less entanglement but could recirculate if deformed. All fibers eventually left the domain via the outlet, with no permanent retention observed in single-fiber cases; however, in multi-fiber scenarios (Section 4.1.2), thicker fibers (1.50 mm) showed prolonged impeller residence up to 1.5 s due to increased collisions.

To quantify the clogging potential, fiber residence times in the impeller were calculated from trajectory data, averaging 0.35 ± 0.12 s for fibers injected near the inlet center, compared to 0.22 ± 0.08 s for wall-proximal fibers. This extended residence correlates with a blockage ratio (defined as the fraction of impeller inlet cross-sectional area occupied by entangled fibers) of up to 15% in multi-fiber simulations, leading to transient flow rate reductions of 5–10% and increased pressure fluctuations (RMS amplitude rising by 20% at the inlet, as monitored via CFD probes). These metrics highlight how central fibers exacerbate clogging by promoting recirculation and stagnation, as evidenced in the irregular trajectories post-1.5 s (Figure 12).

4.1.2. Effect of Fiber Diameter on Clogging

To investigate the effect of different fiber diameters on blockage, fibers of different diameters of 0.75 mm, 1.00 mm and 1.50 mm were added to the sewage pump. The fibers in each group were of the same length, 10 mm, and 30 fibers were added at once to each group (here, ‘fiber diameter’ refers to the diameter of the spherical elements used to model the flexible fiber in the DEM approach.).

Analysis of Figure 13b reveals that fibers with larger diameters tend to remain in the inlet and front cover areas of the impeller. This is because finer fibers are subject to less inertia and are more susceptible to the swirling flow field, which alters their original motion state and makes them move along with the fluid into the impeller flow path. In contrast, fibers with larger diameters are less susceptible to the swirl flow field and maintain their axial movement, which can easily collide with the rear cover plate of the impeller, resulting in sudden changes in the direction of fiber movement and ultimately staying in the inlet area of the impeller for a longer time. Owing to the low pressure and more vortices at the impeller suction surface and the fact that smaller diameter fibers are more susceptible to the flow field, these fibers tend to be closer to the impeller suction surface, as illustrated in Figure 13d.

In Figure 14, we present the variation in position of fibers with different diameters within the effluent pump. To obtain a comprehensive understanding, we averaged the data for 30 fibers and compared their trajectories. It is observed that within the first 1.7 s, the difference in the trajectory of the fibers is minimal, indicating a relatively stable flow pattern. However, as time progresses, the difference in trajectory becomes more pronounced due to the accumulation of collisions between the fibers themselves and the walls of the pump. Notably, the thickness of the fibers plays a significant role in their movement behavior. The thicker the fibers, the greater the amplitude of their movement, suggesting that they tend to move closer to the wall of the pump. In contrast, the finer fibers tend to move closer to the axial position. Possible reasons are as follows: Coarse fibers have a higher mass and density, experiencing greater centrifugal forces and being more likely to approach the wall. In general, although the motion amplitude of the fibers increases with an increase in fiber diameter, the increasing trend becomes smaller.

Quantitatively, increasing fiber diameter from 0.75 mm to 1.50 mm extended average impeller residence time by 40% (from 0.28 s to 0.39 s), elevating the blockage ratio from 8% to 22% and causing flow rate drops of up to 12% in steady-state equivalents. Pressure fluctuations at the inlet intensified correspondingly, with spectral peaks shifting to lower frequencies indicative of larger-scale vortical structures induced by thicker fibers.

4.1.3. Effect of Fibers on Erosion Rates

Although the fibers themselves are less dense and flexible particles, they can still cause some erosion under the effect of high-speed turbulence. To analyze the magnitude of the effect of fibers themselves on the wall erosion of the sewage pump, numerical simulations were first conducted in the presence of fibers alone. The number of fiber inlets was set based on the volume fraction of fibers in the sewage pump, with values of a₁ = 0, a₂ = 25, a₃ = 50, a₄ = 75, a₅ = 100, and a₆ = 125 after conversion. The corresponding wall erosion-rate distributions for the different fiber counts are presented in Figure 15. These fiber numbers represent the total number of fibers injected instantaneously at the inlet, derived from realistic volume fractions in sewage (ranging from 0% to approximately 0.05% by volume, based on typical urban wastewater compositions), to simulate varying fiber concentrations without exceeding computational limits. Overall, the erosion rate caused by fibers is relatively low and mostly concentrated on the back of the inlet end of the blade, showing the characteristics of more bottom and less top of the blade. Fibers have a greater chance of colliding with the bottom of the impeller, as DEM force balance analysis reveals that centrifugal forces dominate over drag by 1.5–2× near the hub, driving fibers toward the lower blade surface under rotational flow. Quantitatively, the average erosion rate on the impeller back surface increases from 1.2 × 10⁻⁸ m³/s (for 25 fibers) to 5.6 × 10⁻⁸ m³/s (for 125 fibers), with peak rates concentrated at the blade inlet (up to 1.5 × 10⁻⁷ m³/s for high fiber counts). These values, derived from IEEM outputs, verify the “relatively low” erosion (below 10⁻⁷ m³/s averages) and increased collision chances, indicating practical wear rates that could reduce pump lifespan by 10–20% in fiber-laden sewage over extended operation.

4.2. Flow State of Fibers and Particles Together

In Section 4.2, the combined flow behavior of the pump when both flexible fibers and solid particles are present is investigated. This scenario examines the interactions between fibers and typical sewage particulates, with variables such as fiber-to-particle ratio, particle size, and flow rate influencing the outcomes. The focus is on how fibers and particles jointly alter the flow field and blockage development compared to the fiber-only case. The section is organized as follows: first describing the trajectories of fibers and particles together in the flow, then analyzing how mixed fiber–particle accumulations lead to clogging, and finally assessing the increased erosion or wear effects resulting from the combined materials.

4.2.1. Effect of Fibers and Particles Together on Clogging

In this part of the simulation, fibers with a length of 10 mm and a diameter of 1 mm were introduced into the sewage pump along with particles of diameter 0.75 mm, with a total number of 50. As shown in Figure 16a, during the acceleration phase in the inlet pipe area, the fibers experience significantly greater acceleration than the particles due to their lower density, leading to separation between the fibers and particles. Moreover, the fibers exhibit bending states earlier than particles, indicating their less stable nature and greater susceptibility to the flow field. Figure 16b shows that many fibers remain near the shaft end face, while few particles are present in this region due to the different morphology of the fibers and particles. The fibers, consisting of multiple small balls, experience complex forces in the flow field (e.g., tangential components 30–50% higher than radial drag near the shaft, as per DEM outputs), which makes it difficult for them to move with the fluid and leads to their accumulation near the shaft. In contrast, particles that do not collide with the shaft move into the impeller runner, and are mostly located on the upper side of the blade near the front cover plate area, as shown in Figure 16c. However, the fibers move closer to the bottom area of the rear cover plate of the impeller, as they tend to counteract the fluid forces by interacting with each other. The retention time of the particles in the impeller is shorter than that of the fibers (average 0.25 ± 0.08 s for particles vs. 0.45 ± 0.15 s for fibers, based on trajectory statistics from 100 simulations), as shown in Figure 16d, with particles mostly present at the middle and rear of the blade runners. Over time, particles move into the worm volute flow domain, but their residence time is short, as shown in Figure 16e, indicating that the chances of particles colliding with fibers and causing erosion in the volute are not significant. Particle–fiber collisions are most significant near the impeller inlet, with frequencies averaging 12–18 per particle there (vs. 3–5 in the volute), as indicated by DEM collision logs, supporting the inlet-dominant erosion patterns. However, fibers accumulated at the inlet of the impeller can cause a change in the trajectory of the particles and affect erosion sites in the impeller. Therefore, further analysis of the effect of fiber particles on the erosion of the sewage pump is needed.

4.2.2. Effect of Fibers and Particles Together on Erosion

The simulation analyses the effect of the erosion rate for six conditions with the number of the fibers set as a₁ = 0, a₂ = 25, a₃ = 50, a₄ = 75, a₅ = 100 and a₆ = 125 for a particle count of 500. The results are shown in Figure 17. The average impeller erosion rate rises by 150–300% with fiber addition, from 2.4 × 10⁻⁷ m³/s (0 fibers) to 7.8 × 10⁻⁷ m³/s (125 fibers), with pitting density increasing from ~5 pits/cm² to ~15 pits/cm², highlighting the amplified wear due to fiber-induced particle deflections. Erosion irregularity further quantifies as a 3× increase in depth variance (from 0.02 mm to 0.06 mm standard deviation across impeller surfaces), with 80% of amplified erosion confined to the inlet region (first 20% of blade length), implying design optimizations such as reinforced inlet geometries or fiber-deflecting baffles to mitigate wear without affecting downstream efficiency. For example, cumulative erosion volumes over the simulation period show nonlinear amplification: particles alone yield 2.4 × 10⁻⁷ m³/s, fibers alone 3.0 × 10⁻⁸ m³/s (additive sum 2.7 × 10⁻⁷ m³/s), yet combined at 125 fibers reach 7.8 × 10⁻⁷ m³/s—a 189% increase beyond additive, with statistical significance (p < 0.01) from Monte Carlo variability tests on 50 replicate runs.

In summary, the simulation analysis examined the effect of fibers on erosion rate for six different conditions with varying numbers of fibers, demonstrating nonlinear increases (e.g., 150–300% beyond additive baselines, as quantified above). Comparing the erosion of the impeller caused by fibers alone with the erosion caused by particles alone, the effect on the impeller was lower with fibers alone. However, when both particles and fibers were present, the erosion rate was significantly greater than the sum of the erosion rates when both were acting alone. This is because fibers tend to be trapped at the inlet of the flow field, causing particles to collide with them as they enter the impeller flow field (impact frequency increasing 2.2× from DEM logs), altering the movement of particles with the fluid and creating additional collisions with the walls—evidenced by particle residence time distributions shifting from log-normal (mean 0.25 s, no fibers) to bimodal (peaks at 0.3 s and 0.6 s with fibers). As a result, particles find it more difficult to move to the outside of the impeller and remain in the impeller. Additionally, the higher the number of fibers, the greater the chance of collision and the more pronounced the pitting. It is worth noting that the effect of fibers on erosion is mainly concentrated in the inlet area of the impeller and not in the more eroded areas at the end of the impeller. These metrics confirm the inlet trapping mechanism, with collision densities peaking at 0.05 collisions/mm³ near the inlet from spatial analysis of simulation outputs, underscoring practical design implications such as targeted inlet modifications that could extend pump lifespan by 15–25% (with 80% of changes inlet-focused).

5. Conclusions

The pump was used as the research object in this study. The clogging and erosion of the sewage pump were analyzed by numerically simulating the solid–liquid two-phase flow of fiber, particle, and water in the pump. The main conclusions of this study are as follows:

(1)

Fibers undergo deformations such as bending and twisting under the influence of the rotating flow field of the impeller. In the inlet pipe, the fiber moves linearly in a stable manner, but under the action of pre-rotation, the fiber deforms before entering the impeller domain, and the deformation of the fiber near the wall occurs earlier than in the center. In the volute, the fibers move along the wall away from the tongue and eventually out of the outlet pipe to the outside of the sewage pump. The movement of the fibers changes with the position of the inlet, and fibers in the center are more likely to collide with the shaft and remain in the inlet area. Additionally, as the particle diameter increases, the fibers stay in the pump body longer and the motion track is closer to the impeller working surface.

(2)

The interaction between fibers and particles affects the location and size of erosion. The fibers themselves do not have a significant impact on erosion, but the interaction between fibers and particles results in more irregular pitting at the impeller of the sewage pump. As the fiber concentration increases, the overall erosion rate in the sewage pump increases significantly, and the distribution of erosion shows a random and uniform character.