Study on the Coordinated Regulation of Storage and Discharge Mode in Plain Cities Under Extreme Rainfall: A Case Study of a Southern Plain City
Abstract
1. Introduction
- Section 2 details the data sources and hydrological model construction for the case study area, introduces the CRSD framework, including its evaluation system, regional mode allocation rules, and optimization objectives.
- Section 3 analyzes the performance of CRSD under different rainfall return periods, compares optimization objectives, and evaluates waterlogging reduction effects through spatial distribution and downstream pressure metrics.
- Section 4 examines the applicability of CRSD strategies, interprets hydraulic mechanisms behind optimization outcomes, and discusses limitations in balancing regional priorities and infrastructure constraints.
- Section 5 summarizes the effectiveness of CRSD in enhancing urban flood resilience, highlights its innovation in cross-regional coordination, and proposes future research directions.
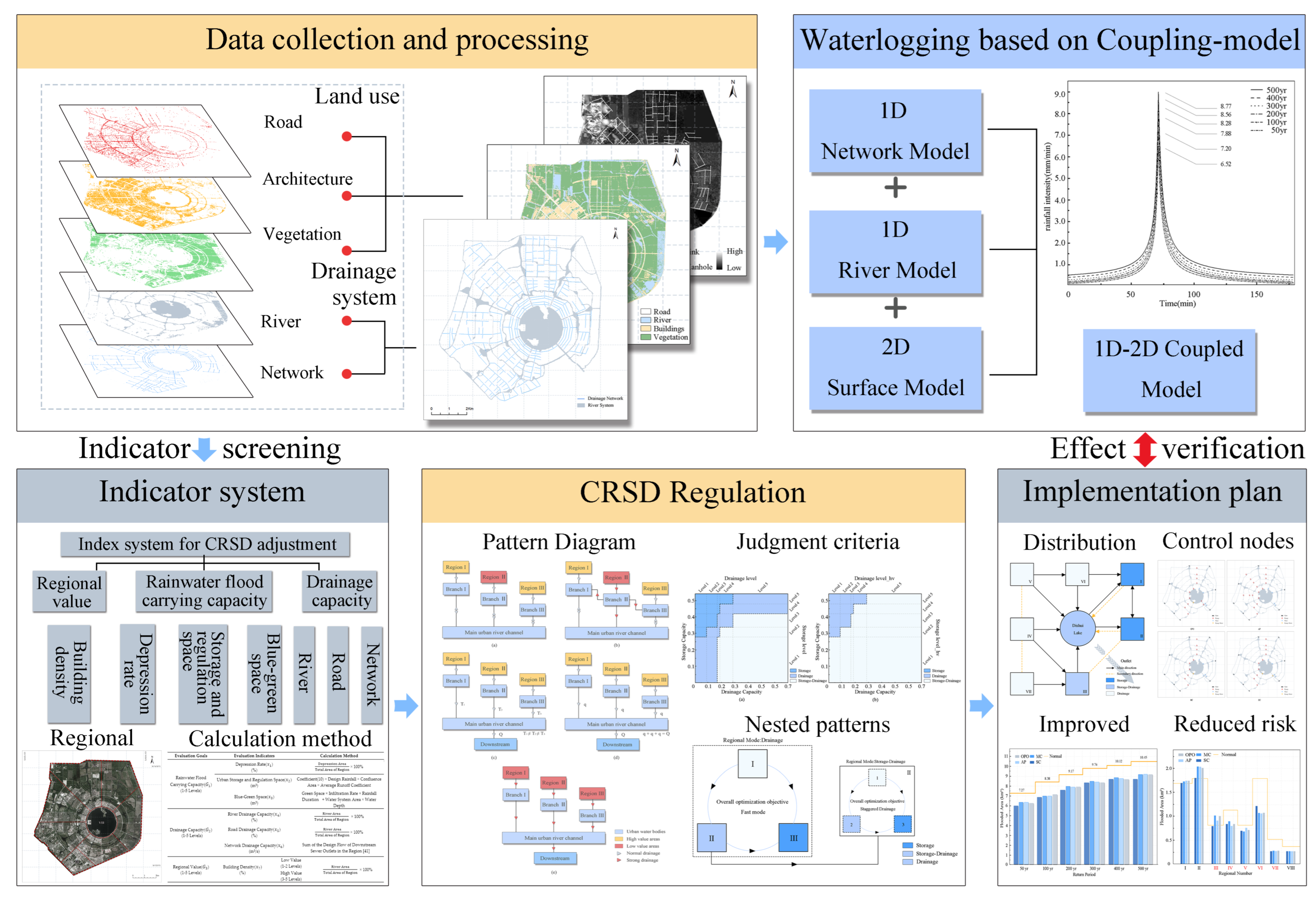
2. Materials and Methods
2.1. Regional Model Construction
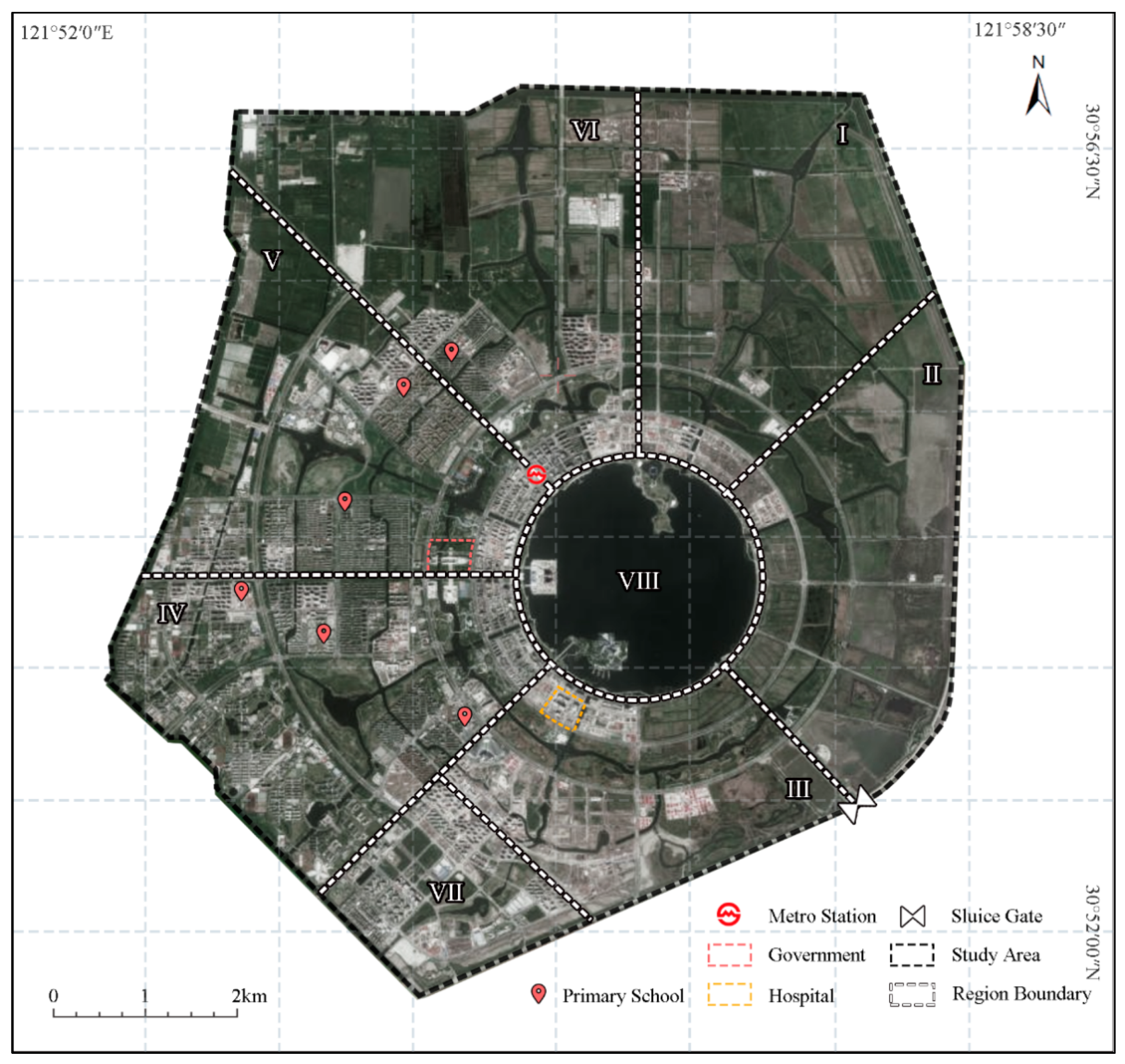
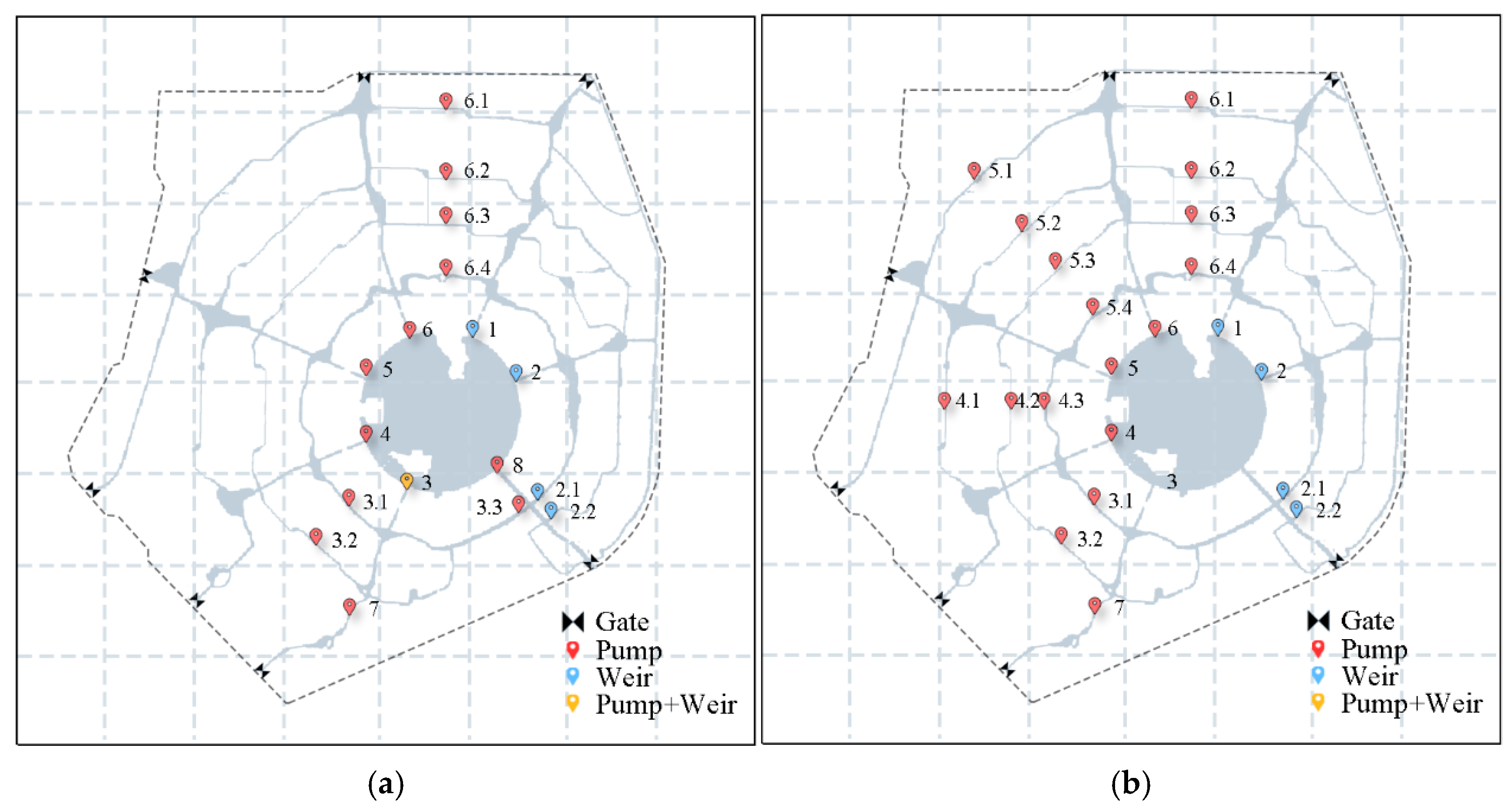
2.1.1. Regional Overview
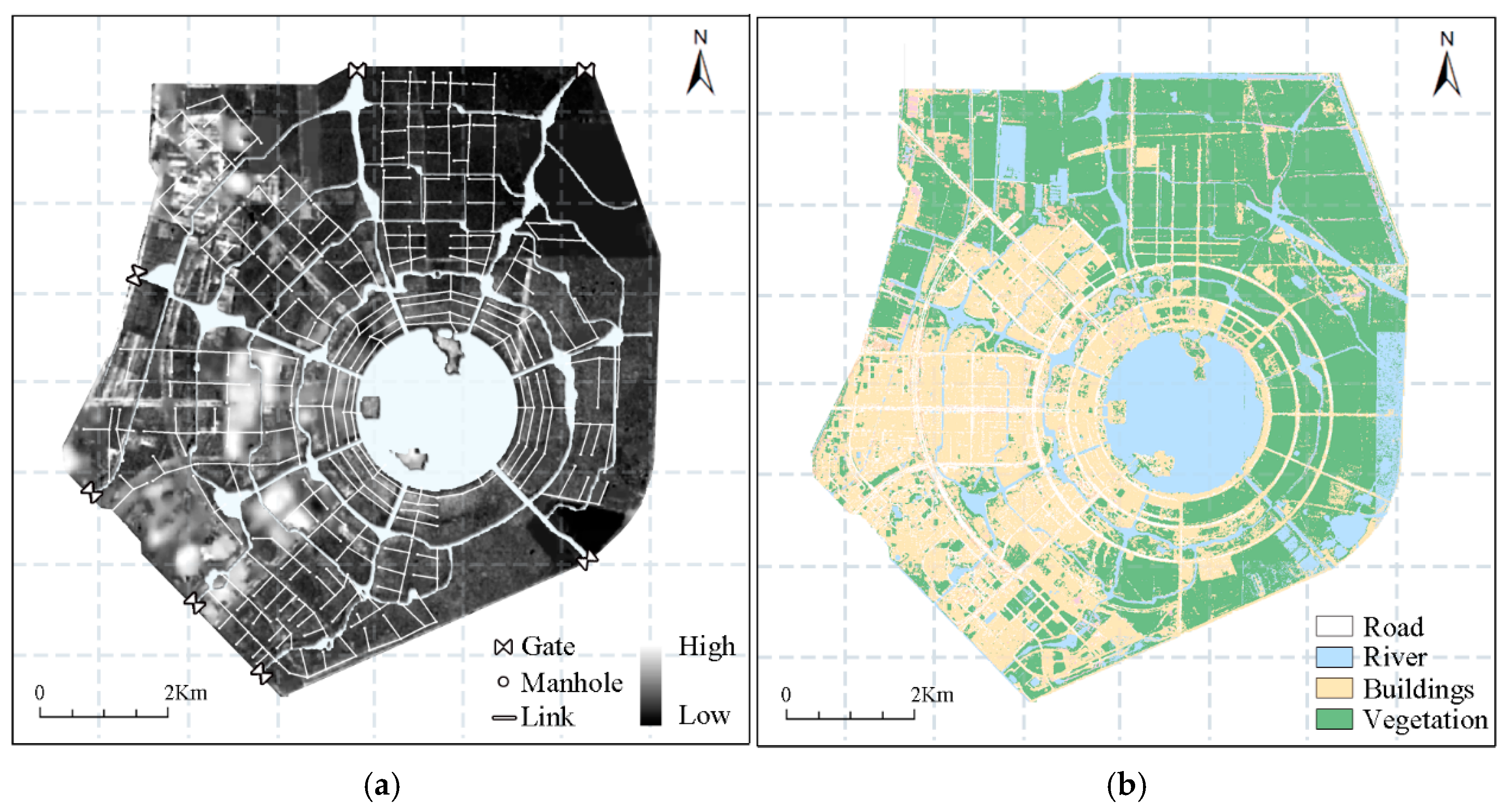
2.1.2. Data Sources
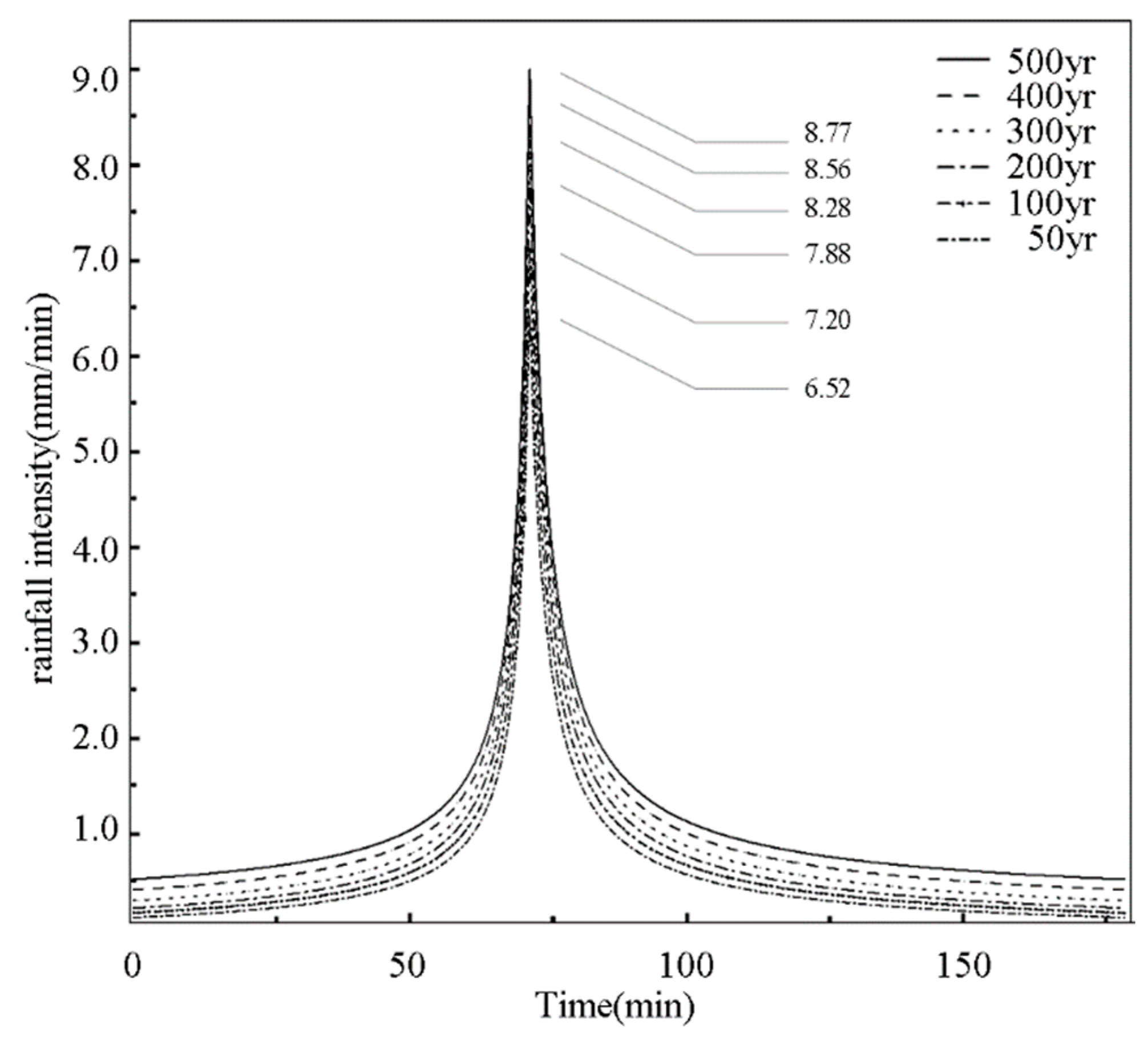
2.1.3. Design Rainfall
2.2. Establishment of CRSD
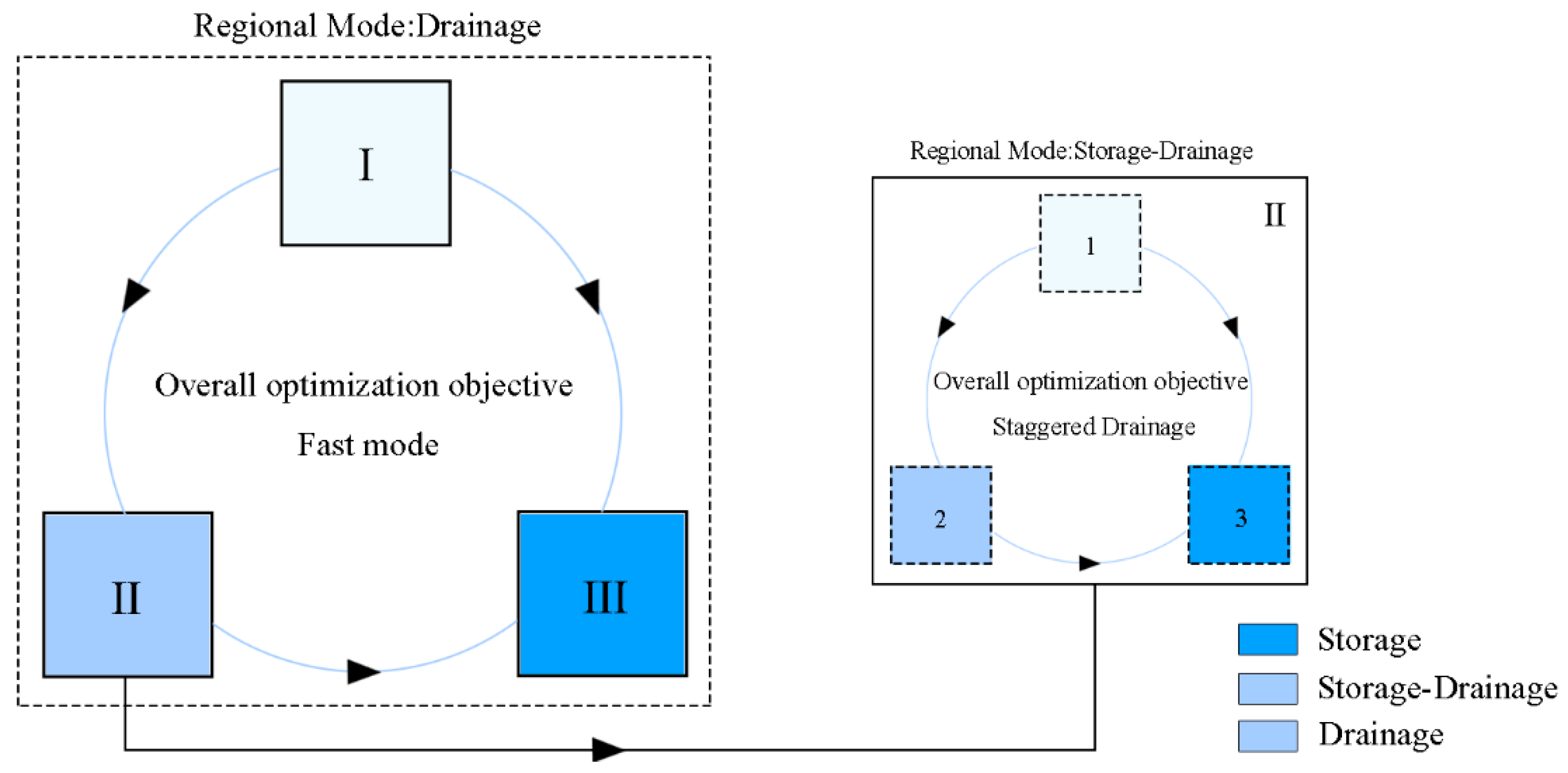
2.2.1. Regional Allocation of CRSD
2.2.2. Scheduling Rules of CRSD
- Watershed Principle: CRSD implementation is only allowed within the same watershed.
- Upstream–Downstream Principle: Water from upstream regions can be preferentially stored and regulated into downstream regions;
- Value Principle: High-value regions should prioritize drainage to low-value regions;
- Mode Principle: The drainage priority among different modes is priority drainage > combined storage and drainage > priority storage.
- Carrying Capacity Principle: Regions with lower rainwater flood carrying capacity can drain into regions with higher carrying capacity.
- Rule Priority: The priority of the rules is: Mode Principle > Value Principle > Carrying Capacity Principle > Upstream–Downstream Principle
- When the drainage priorities of regions are the same, they can drain into each other.
2.2.3. Optimization Objective of CRSD
- Maximum Consumption (MC): Maximize the retention of excess rainfall within the urban river network system, which may increase waterlogging risks in high-value regions;
- Safe Consumption (SC): Prioritize the safety of high-value regions, using low-value regions for storage and regulation;
- Off-Peak Outflow (OPO): Through mutual cooperation between regions, avoid runoff peaks occurring simultaneously in downstream discharge areas;
- Average Pressure (AP): Adjust the storage and discharge ratio between regions to ensure that the river levels in regions with the same mode are consistent;
- Rapid Drainage (RD): Achieve rapid rainwater discharge by improving the convergence capacity of sewer networks and lowering upstream water levels, thereby mitigating the damming effect.
2.2.4. Control Methods of CRSD
2.3. Evaluation Indicators for CRSD Effectiveness
3. Results
3.1. Results of CRSD
3.1.1. Indicator Weights and Regional Modes
3.1.2. Water Allocation of CRSD
3.1.3. Optimization Objective Control Scheme
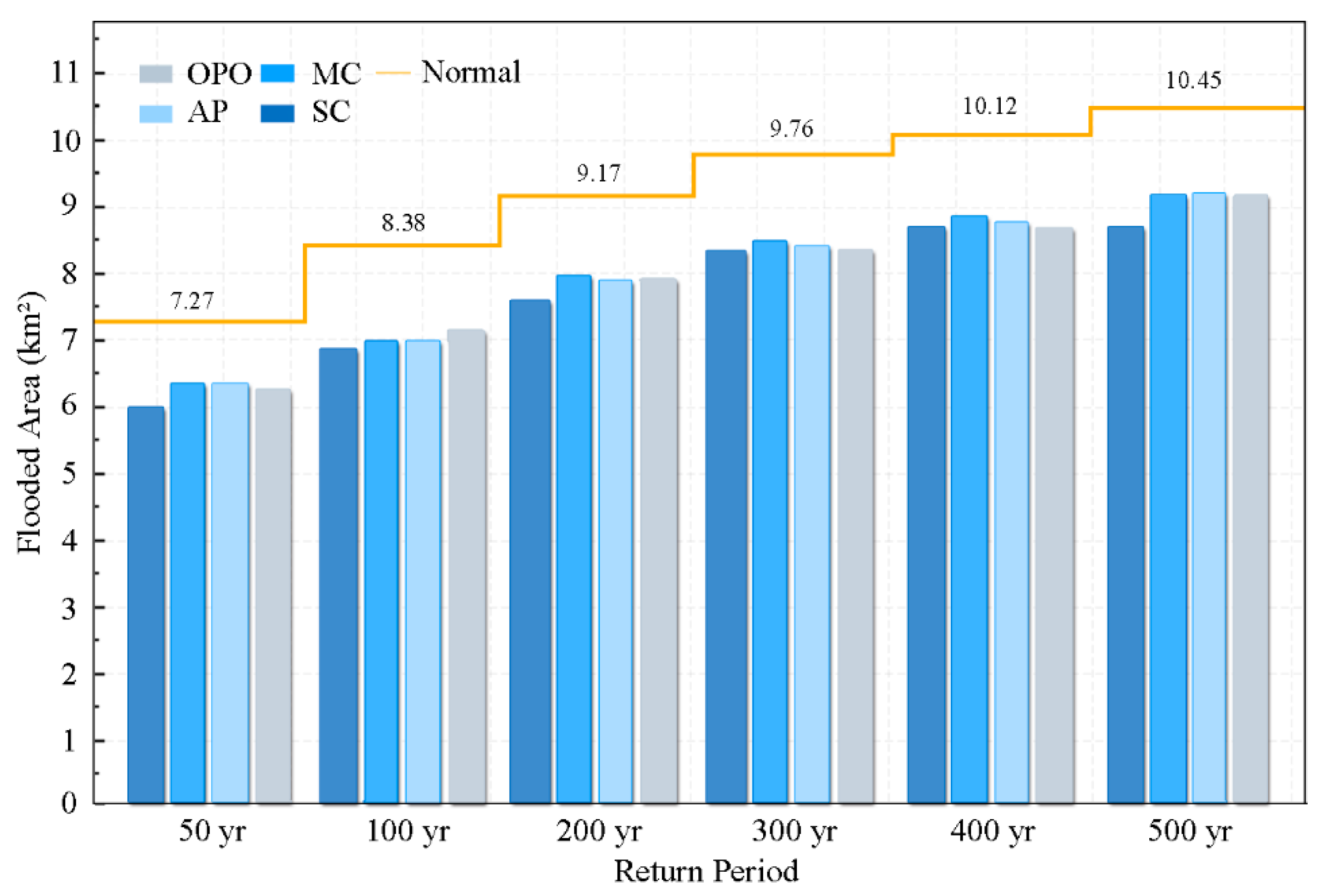
3.2. Mode Effect Evaluation Under Different Return Periods
3.2.1. Regional Waterlogging Situation
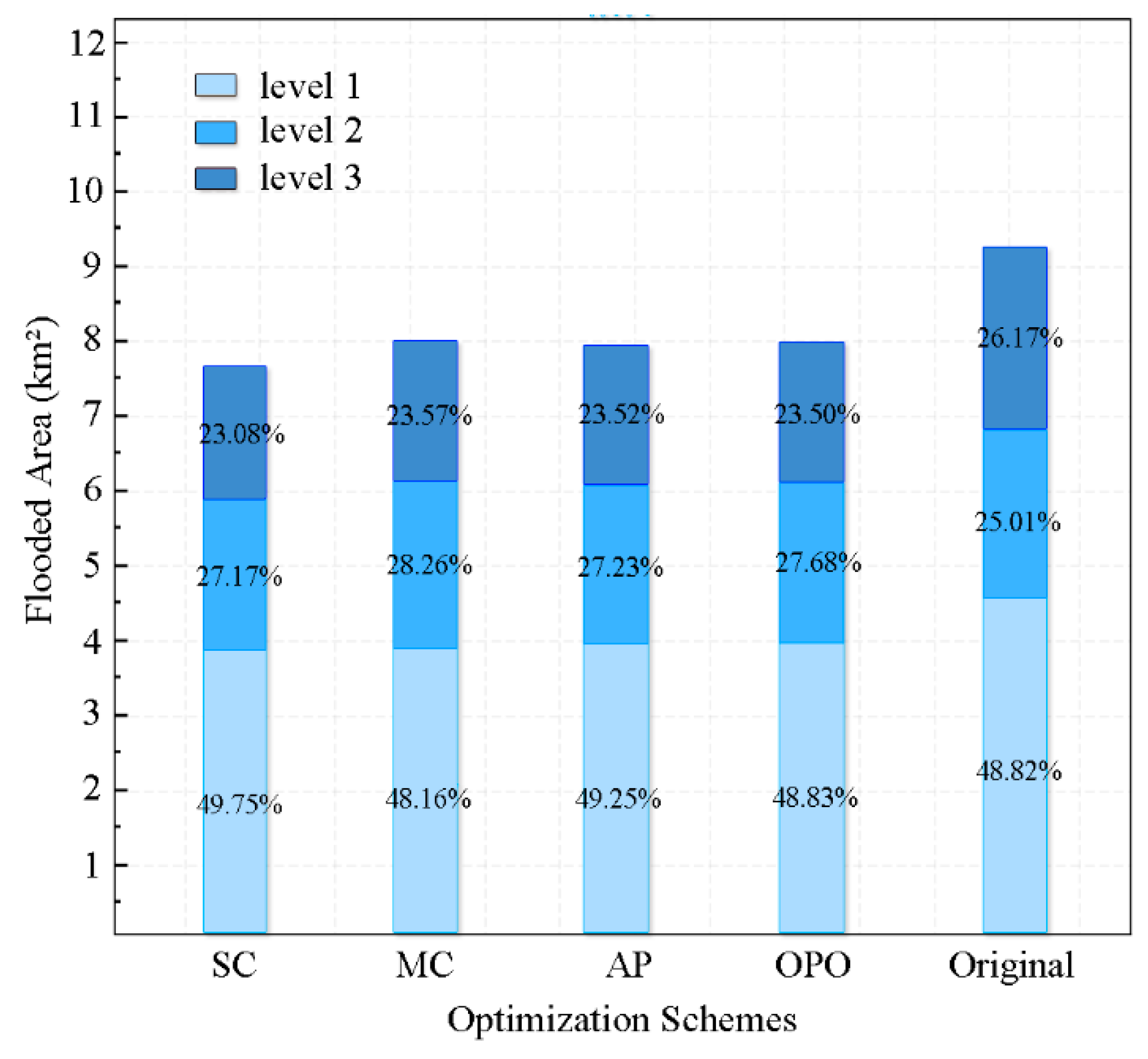
3.2.2. Drainage Capacity Improvement
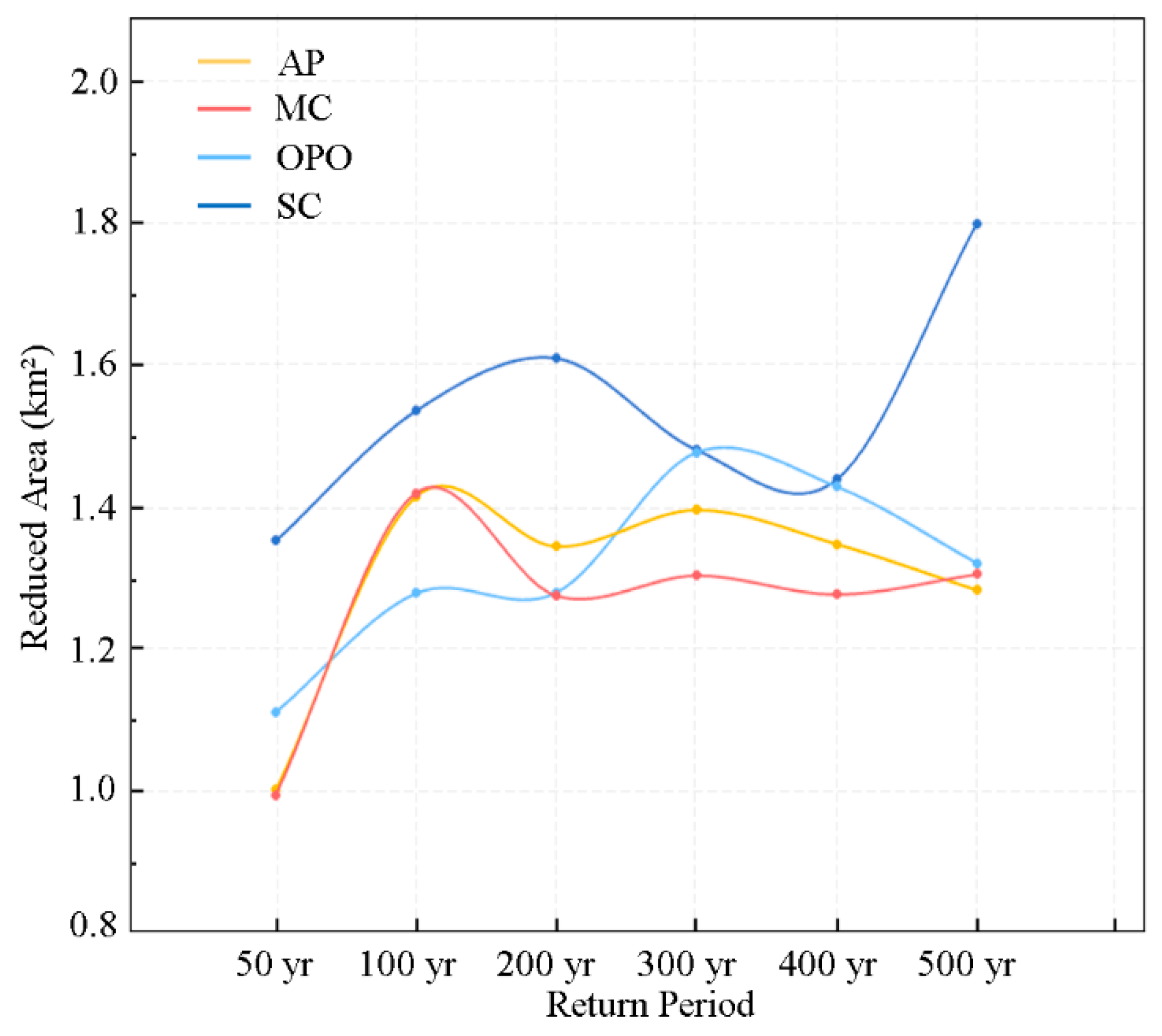
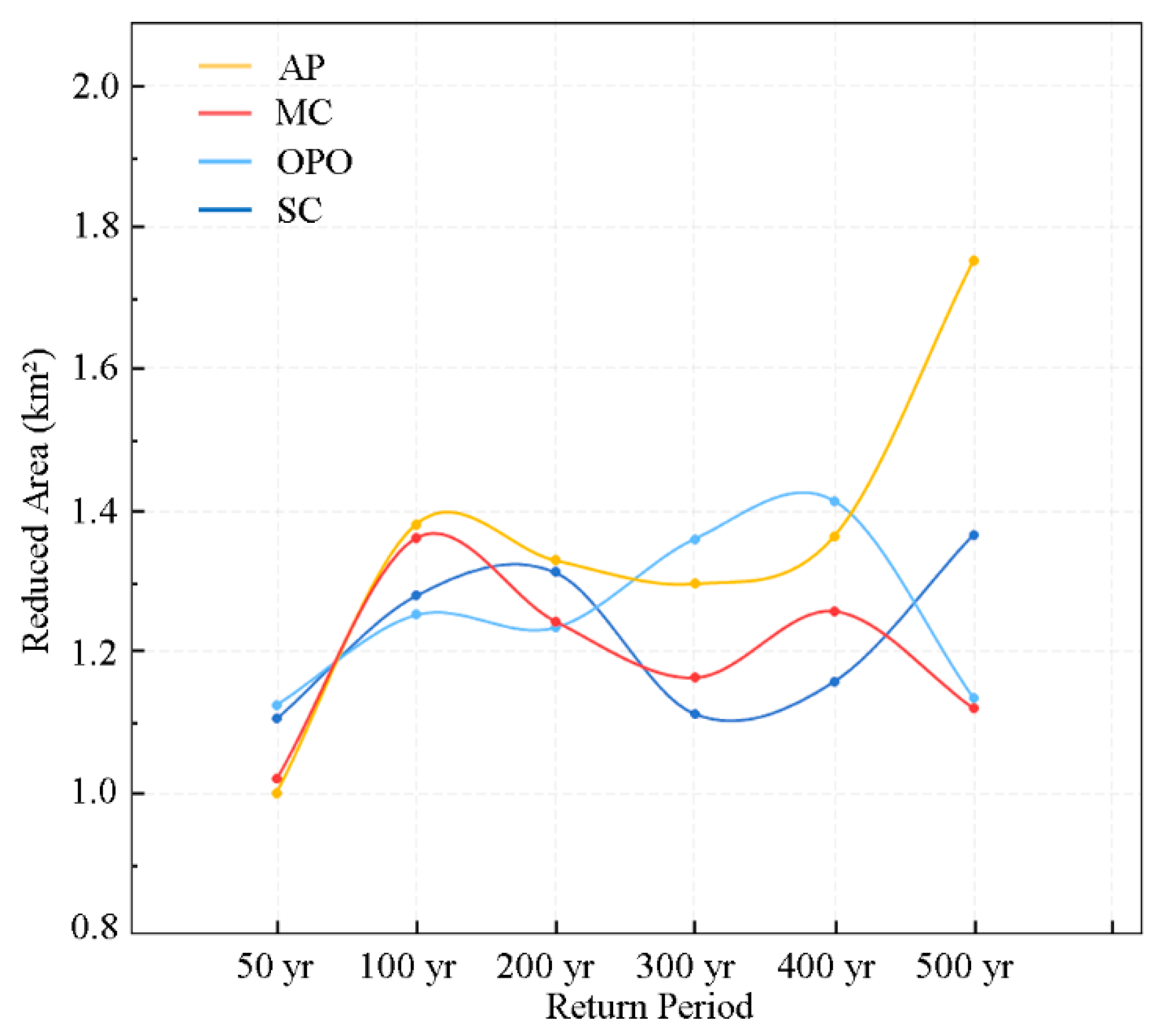
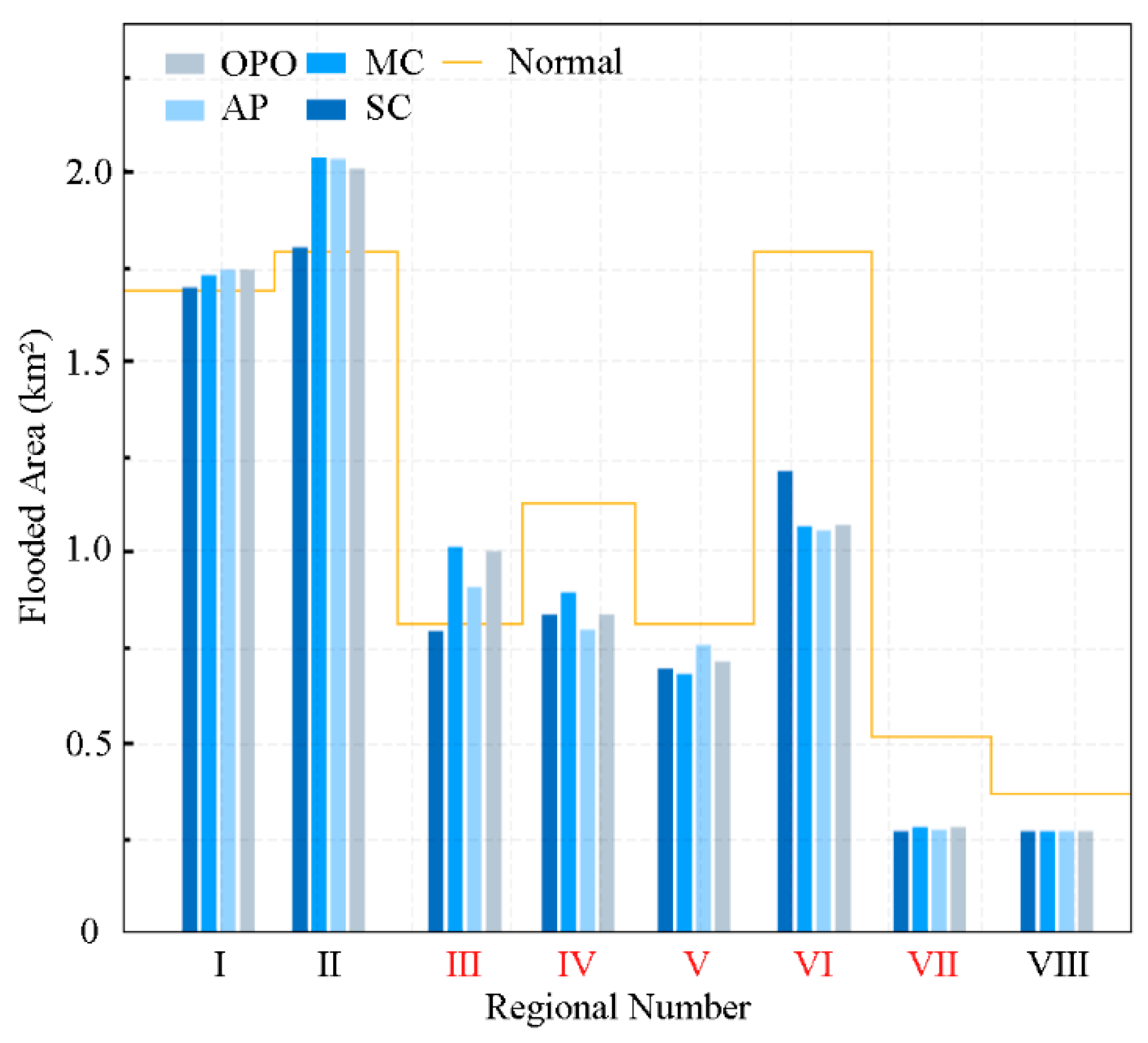
3.2.3. Comparison of Optimization Objectives’ Effects
3.3. Evaluation of Mode Effects Under the Same Return Period—200 Yr
3.3.1. Comparison of Mode Effects
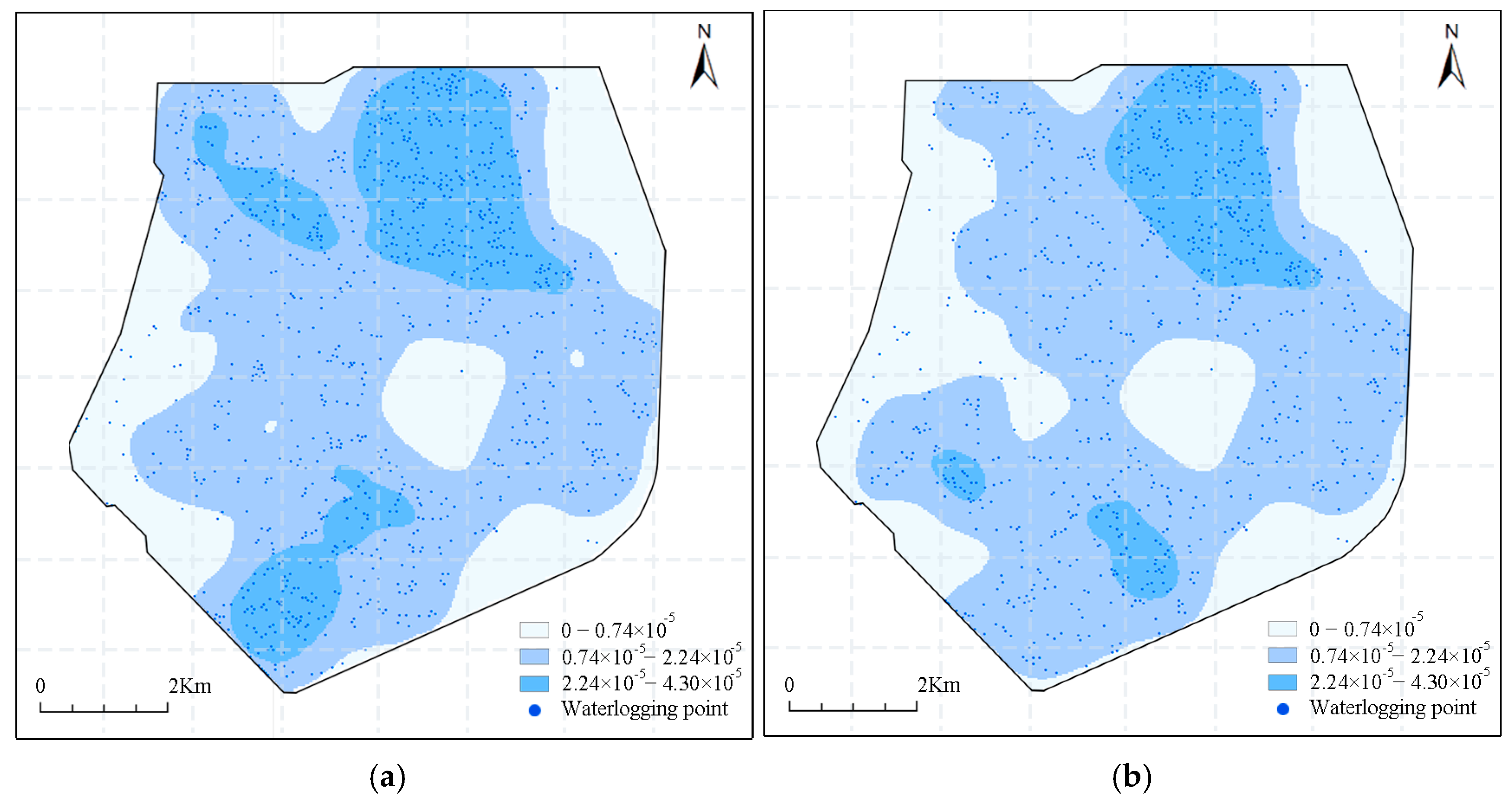
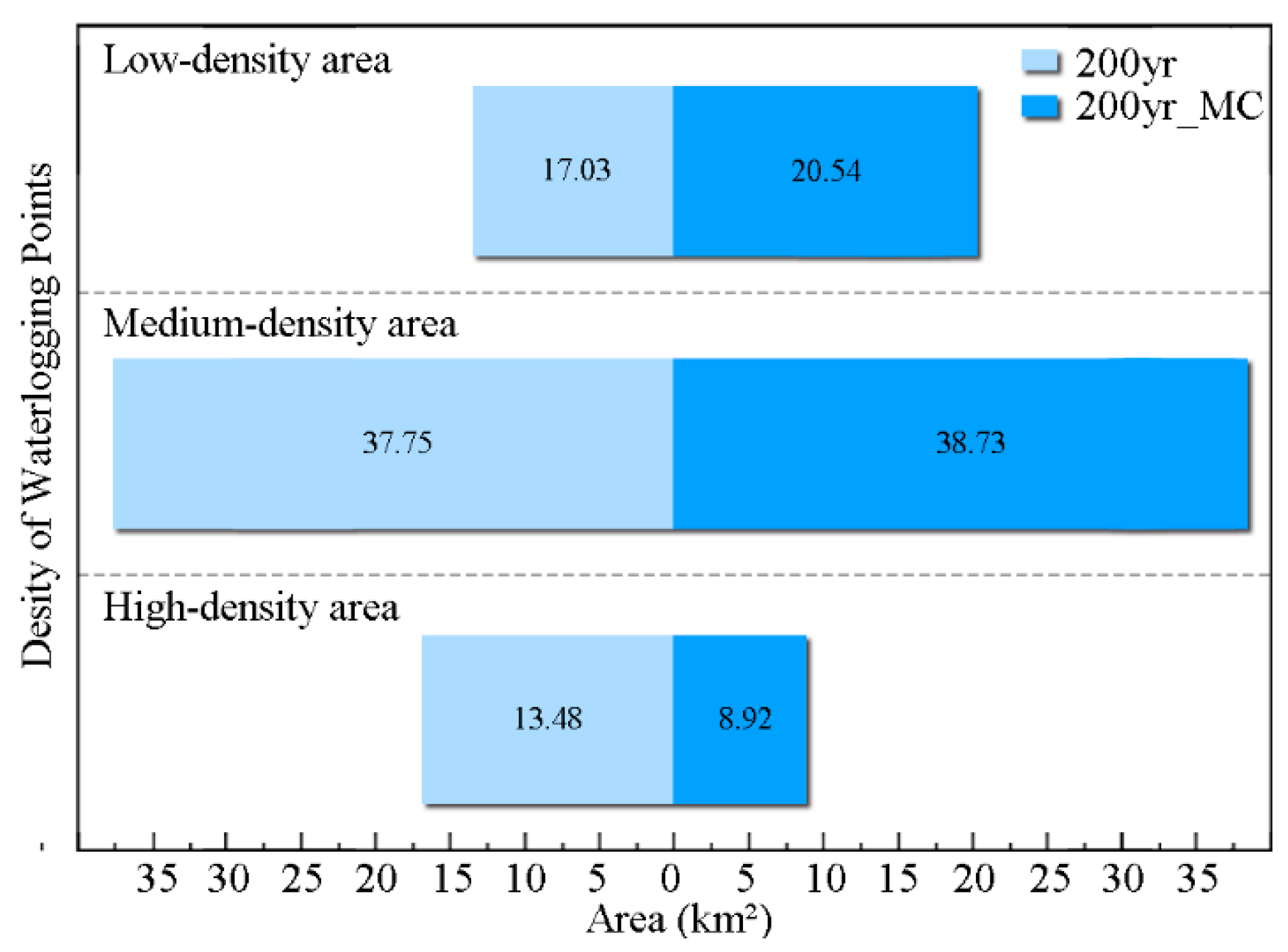
3.3.2. Waterlogging Point Density Distribution
3.3.3. Comparison of Outlet Pressure
4. Discussion
4.1. Evolution Characteristics of Urban Waterlogging Under EREs and Validation of CRSD Optimization System
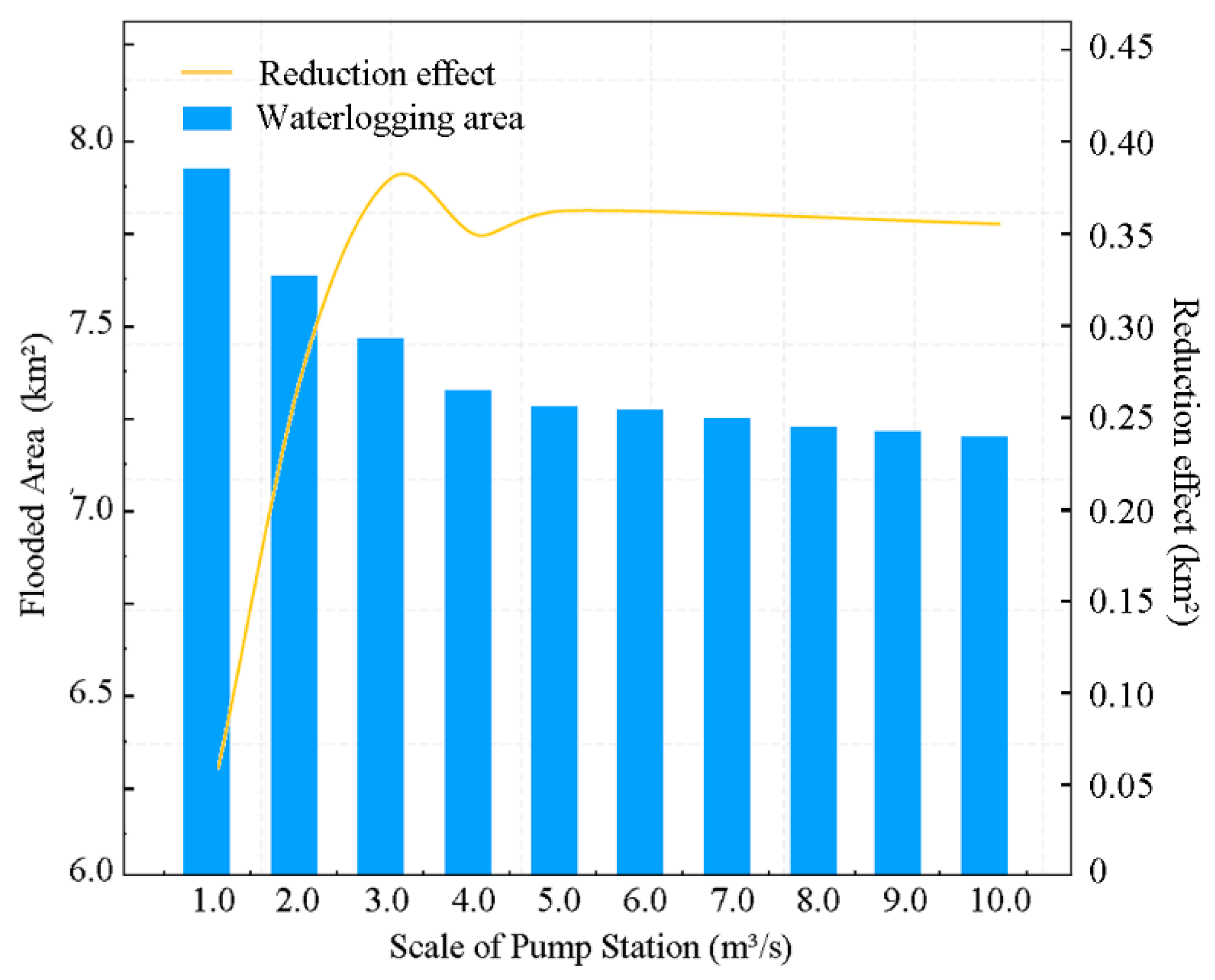
4.2. Hydraulic Explanation of Response Curves
4.3. Applicable Scenarios for Optimization Objectives
- SC prioritizes the protection of high-value areas while using low-value areas for water storage. Although the overall performance is good, this model results in a peak water level of 3.3 m at the downstream outlet, which increases the flood risk downstream. This model is suitable for urban areas with limited rainwater flood carrying capacity, where modifications are challenging, and the downstream flood risk is relatively low.
- MC maximizes the absorption of excess water by prioritizing water storage areas and the urban river network. However, due to the limited overall rainwater flood carrying capacity of the region, the model performs poorly under higher return periods. This model is suitable for urban areas with a higher rainwater flood carrying capacity.
- OPO reduces downstream flood pressure by implementing peak-shifting drainage; however, it sacrifices drainage efficiency during EREs. This model is suitable for urban areas with significant flood risk.
- AP balances the drainage pressure between high-value areas, reducing the waterlogged area in high-value zones by 1.96 km2 and showing better performance under higher rainfall return periods. However, this model requires multi-region and multi-device coordinated scheduling, which increases system complexity. It is suitable for urban areas with a multi-center structure and good connectivity between regions.
- RD, though not discussed in this paper due to specific constraints, is expected to perform well in mitigating regional waterlogging. Its main disadvantage is the need for extensive hydraulic infrastructure, which increases costs. This model is suitable for cities with well-connected water systems and high-value areas.
5. Conclusions
- In response to EREs, the study reveals a significant drainage deficit in the study area, with the drainage capacity falling short by over 64%. As the return period of rainfall increases, the waterlogged area develops in three distinct phases: a rapid rise, followed by a leveling off, and, ultimately, reaching a state of deep saturation. The implementation of CRSD can substantially mitigate urban waterlogging caused by EREs, with the capacity to absorb at least 0.98 km2 of waterlogged area. Specifically, under a 500 yr return scenario, the waterlogged area is reduced to the level typically seen at 200 yr, and in the case of 300 yr, it is brought down to 100 yr.
- The CRSD evaluation system performs excellently in regional model assessments, as demonstrated by the waterlogging simulation results. The system identifies priority drainage areas, which are typically high-value regions with more severe waterlogging and weaker drainage capacity. In contrast, priority storage areas experience less severe waterlogging and are better equipped to manage excessive rainfall, highlighting the system’s ability to target and regulate critical areas effectively.
- CRSD model significantly improves urban waterlogging control by dynamically coordinating cross-regional water resource allocation with blue–green–grey infrastructure. In the scenario of a 500 yr return period, SC reduces waterlogged areas by 1.80 km2, while AP reduces waterlogging by 1.96 km2, particularly in high-value areas. This supports the effectiveness of regional differentiated regulation. The study also uncovers notable differences in the response mechanisms of various optimization objectives: SC optimizes conditions globally by prioritizing the safety of high-value areas, AP enhances resilience in high-risk zones by balancing pressure, and OPO alleviates downstream pressure through peak-shifting drainage techniques.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EREs | Extreme rainfall events |
| CRSD | Coordinated regulation of storage and discharge mode |
References
- Kong, F.; Sun, S.; Lei, T.J. Understanding China’s Urban Rainstorm Waterlogging and Its Potential Governance. Water 2021, 13, 891. [Google Scholar] [CrossRef]
- Ardiclioglu, M.; Hadi, A.; Periku, E.; Kuriqi, A. Experimental and Numerical Investigation of Bridge Configuration Effect on Hydraulic Regime. Int. J. Civ. Eng. 2022, 20, 981–991. [Google Scholar] [CrossRef]
- Hosseini, F.S.; Choubin, B.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Darabi, H.; Haghighi, A.T. Flash-Flood Hazard Assessment Using Ensembles and Bayesian-Based Machine Learning Models: Application of the Simulated Annealing Feature Selection Method. Sci. Total Environ. 2020, 711, 135161. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Bai, Z.J.; Yang, Y.H. Linking Trends in Urban Extreme Rainfall to Urban Flooding in China. Int. J. Climatol. 2017, 37, 4586–4593. [Google Scholar] [CrossRef]
- Kumar, S.; Kant, S.; Ahmed, R. Assessment of an Extreme Heavy Rainfall over Meghalaya, India on 16th & 17th June 2022: A Case Study Using Meteorological and Remote Sensing Observations. Trop. Cyclone Res. Rev. 2025, 14, 60–70. [Google Scholar] [CrossRef]
- Saufina, E.; Trismidianto; Satiadi, D.; Harjupa, W.; Risyanto; Purwaningsih, A.; Fathrio, I.; Praja, A.S.; Juaeni, I.; Witono, A.; et al. The role of Madden-Julian Oscillation, Westerly Wind Bursts, and Kelvin Waves in Triggering Extreme Rainfall Through Mesoscale Convective Systems: A Case Study of West Sumatra, March 7–8, 2024. Atmos. Res. 2025, 318, 107993. [Google Scholar] [CrossRef]
- Xie, C.; Xu, C.; Huang, Y.; Liu, J.; Shao, X.; Xu, X.; Gao, H.; Ma, J.; Xiao, Z. Advances in the Study of Natural Disasters Induced by the “23.7” Extreme Rainfall Event in North China. Nat. Hazards Res. 2025, 5, 1–13. [Google Scholar] [CrossRef]
- Yazdanfar, Z.; Sharma, A. Urban Drainage System Planning and Design—Challenges with Climate Change and Urbanization: A Review. Water Sci. Technol. 2015, 72, 165–179. [Google Scholar] [CrossRef]
- Tavakol-Davani, H.; Burian Steven, J.; Devkota, J.; Apul, D. Performance and Cost-Based Comparison of Green and Gray Infrastructure to Control Combined Sewer Overflows. J. Sustain. Water Built Environ. 2016, 2, 04015009. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Wang, E.S.; Gong, Y.W. A Structural Optimization of Urban Drainage Systems: An Optimization Approach for Mitigating Urban Floods. Water 2024, 16, 1696. [Google Scholar] [CrossRef]
- Anwer, A.A.; Soliman, A.H.; Radwan, H.G. Hydraulic-Based Optimization Algorithm for the Design of Stormwater Drainage Networks. Appl. Water Sci. 2024, 14, 139. [Google Scholar] [CrossRef]
- Ngamalieu-Nengoue, U.A.; Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Mora-Meliá, D.; Valderrama, J.G.S. Urban Drainage Network Rehabilitation Considering Storm Tank Installation and Pipe Substitution. Water 2019, 11, 515. [Google Scholar] [CrossRef]
- Mark, O.; Weesakul, S.; Apirumanekul, C.; Aroonnet, S.B.; Djordjević, S. Potential and Limitations of 1D Modelling of Urban Flooding. J. Hydrol. 2004, 299, 284–299. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, H.; Liu, Y.; Lei, X. Urban Waterlogging Structure Risk Assessment and Enhancement. J. Environ. Manag. 2024, 352, 120074. [Google Scholar] [CrossRef]
- Lu, P.; Sun, Y.; Steffen, N. Scenario-Based Performance Assessment of Green-Grey-Blue Infrastructure for Flood-Resilient Spatial Solution: A Case Study of Pazhou, Guangzhou, Greater Bay Area. Landsc. Urban Plan. 2023, 238, 104804. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Wang, H.; Shao, W.; Mei, C.; Ding, X. Matching Analysis of Investment Structure and Urban Inundation Control Function of Sponge Cities in China. J. Clean. Prod. 2020, 266, 121850. [Google Scholar] [CrossRef]
- Wu, J.; Xu, J.; Lu, M.; Ming, H. An Integrated Modelling Framework for Optimization of the Placement of Grey-Green-Blue Infrastructure to Mitigate and Adapt Flood Risk: An Application to the Upper Ting River Watershed, China. J. Hydrol. Reg. Stud. 2025, 57, 102156. [Google Scholar] [CrossRef]
- Chen, W.; Wang, W.; Huang, G.; Wang, Z.; Lai, C.; Yang, Z. The Capacity of Grey Infrastructure in Urban Flood Management: A Comprehensive Analysis of Grey Infrastructure and the Green-Grey Approach. Int. J. Disaster Risk Reduct. 2021, 54, 102045. [Google Scholar] [CrossRef]
- Green, D.; O’Donnell, E.; Johnson, M.; Slater, L.; Thorne, C.; Zheng, S.; Stirling, R.; Chan, F.K.S.; Li, L.; Boothroyd, R.J. Green Infrastructure: The Future of Urban Flood Risk Management? Wiley Interdiscip. Rev. Water 2021, 8, e1560. [Google Scholar] [CrossRef]
- Qin, Y. Urban Flooding Mitigation Techniques: A Systematic Review and Future Studies. Water 2020, 12, 3579. [Google Scholar] [CrossRef]
- Wickenberg, B. Collaborating for Nature-Based Solutions: Bringing Research and Practice Together. Local Environ. 2024, 29, 118–134. [Google Scholar] [CrossRef]
- Yin, D.; Zhang, X.; Cheng, Y.; Jia, H.; Jia, Q.; Yang, Y. Can Flood Resilience of Green-Grey-Blue System Cope with Future Uncertainty? Water Res. 2023, 242, 120315. [Google Scholar] [CrossRef] [PubMed]
- Omori, Y.; Kuriyama, K.; Tsuge, T.; Onuma, A.; Shoji, Y. Coastal Infrastructure Typology and People’s Preference-Based Grey-Green-Hybrid Infrastructure Classifications Using a Latent Class Model: A Case Study of Japan. Int. J. Disaster Risk Reduct. 2024, 114, 104992. [Google Scholar] [CrossRef]
- Sarkar, S.K.; Rahman, M.A.; Esraz-Ul-Zannat, M.; Islam, M.F. Simulation-Based Modeling of Urban Waterlogging in Khulna City. J. Water Clim. Change 2021, 12, 566–579. [Google Scholar] [CrossRef]
- Alves, A.; Vojinovic, Z.; Kapelan, Z.; Sanchez, A.; Gersonius, B. Exploring Trade-Offs Among the Multiple Benefits of Green-Blue-Grey Infrastructure for Urban Flood Mitigation. Sci. Total Environ. 2020, 703, 134980. [Google Scholar] [CrossRef]
- Zhi-Yong, H.; Xiao-Yan, H.E.; Jin-Chi, H.; Hui-Rang, W. Studing on Non-Engineering Flood Control Strategies Abroad (I): Disaster Reduction Measures. J. Nat. Disasters 2002, 5, 52–56. [Google Scholar]
- Huang, X.; Shen, J.; Li, S.; Chi, C.; Guo, P.; Hu, P. Sustainable Flood Control Strategies Under Extreme Rainfall: Allocation of Flood Drainage Rights in the Middle and Lower Reaches of the Yellow River Based on a New Decision-Making Framework. J. Environ. Manag. 2024, 367, 122020. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Liu, L.; Shen, J.; Zhang, D.; Sun, F. Necessity and Feasibility of Allocation and Trading of Drainage Rights in Jiangsu Province. Water Resour. Prot. 2019, 35, 25–28. [Google Scholar]
- Liu, Q.; Yang, H.; Liu, M.; Sun, R.; Zhang, J. An Integrated Flood Risk Assessment Model for Cities Located in the Transitional Zone between Taihang Mountains and North China Plain: A Case Study in Shijiazhuang, Hebei, China. Atmosphere 2019, 10, 104. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.; Zhang, H.; Dalla Fontana, G.; Tarolli, P. Identifying Dominant Factors of Waterlogging Events in Metropolitan Coastal Cities: The Case Study of Guangzhou, China. J. Environ. Manag. 2020, 271, 110951. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Mei, C.; Wang, H.; Lu, J. A Multi-Objective Optimization Model for Synergistic Effect Analysis of Integrated Green-Gray-Blue Drainage System in Urban Inundation Control. J. Hydrol. 2022, 609, 127725. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Liu, J.; Wang, Y.; Jia, H.; Tao, S. A Flood Resilience Assessment Method of Green-Grey-Blue Coupled Urban Drainage System Considering Backwater Effects. Ecol. Indic. 2025, 170, 113032. [Google Scholar] [CrossRef]
- Joyce, J.; Chang, N.-B.; Harji, R.; Ruppert, T. Coupling Infrastructure Resilience and Flood Risk Assessment via Copulas Analyses for a Coastal Green-Grey-Blue Drainage System Under Extreme Weather Events. Environ. Model. Softw. 2018, 100, 82–103. [Google Scholar] [CrossRef]
- Lintsen, H. Two Centuries of Central Water Management in the Netherlands. Technol. Cult. 2002, 43, 549–568. [Google Scholar] [CrossRef]
- Guo, J. Urban Flood Mitigation and Stormwater Management; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Yau, W.K.; Radhakrishnan, M.; Liong, S.-Y.; Zevenbergen, C.; Pathirana, A. Effectiveness of Abc Waters Design Features for Runoff Quantity Control in Urban Singapore. Water 2017, 9, 577. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, M.; Wang, Z.; Lai, C. Assessment of the Vulnerability of Road Networks to Urban Waterlogging Based on a Coupled Hydrodynamic Model. J. Hydrol. 2021, 603, 127105. [Google Scholar] [CrossRef]
- Martínez, C.; Vojinovic, Z.; Price, R.; Sanchez, A. Modelling Infiltration Process, Overland Flow and Sewer System Interactions for Urban Flood Mitigation. Water 2021, 13, 2028. [Google Scholar] [CrossRef]
- GB 51222-2017; Technical Code for Urban Flooding Prevention and Control. Ministry of Housing and Urban-Rural Development: Beijing, China, 2017.
- Wang, Y.; Li, Y.; Li, H.; Dang, W.; Zheng, A. Study on the Correlation Between Soil Resistivity and Multiple Influencing Factors Using the Entropy Weight Method and Genetic Algorithm. Electr. Power Syst. Res. 2025, 246, 111692. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J. A Maximum-Entropy-Based Method for Alarm Flood Prediction. J. Process Control 2021, 107, 58–69. [Google Scholar] [CrossRef]
- Zhang, D.; Shen, J.; Liu, P.; Zhang, Q.; Sun, F. Use of Fuzzy Analytic Hierarchy Process and Environmental Gini Coefficient for Allocation of Regional Flood Drainage Rights. Int. J. Env. Res. Public Health 2020, 17, 2063. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Analytical Solution of Gradually Varied Flow Equation in Circular Channels Using Variable Manning Coefficient. Flow Meas. Instrum. 2015, 43, 53–58. [Google Scholar] [CrossRef]
- Zhang, D.; Shen, J.; Sun, F.; Liu, B.; Wang, Z.; Zhang, K.; Li, L. Research on the Allocation of Flood Drainage Rights of the Sunan Canal Based on a Bi-level Multi-Objective Programming Model. Water 2019, 11, 1769. [Google Scholar] [CrossRef]
- Al-busaltan, S.; Kadhim, M.; Basim, K.; Alshammaa, G. Evaluating Porous Pavement for the Mitigation of Stormwater Impacts; IOP Publishing: Bristol, UK, 2021; Volume 1067. [Google Scholar]
- Barreiro, J.; Santos, F.; Ferreira, F.; Neves, R.; Saldanha Matos, J. Development of a 1D/2D Urban Flood Model Using the Open-Source Models SWMM and MOHID Land. Sustainability 2022, 15, 707. [Google Scholar] [CrossRef]






| Composition | Name | Estuary Width (m) | Riverbed Width (m) | Riverbed Elevation (m) | Control Width (m) | Remarks |
|---|---|---|---|---|---|---|
| One Lake | Dishui Lake | -- | -- | -- | -- | Area: 4.5 km2 |
| Four Rivers | Chunlian | 43 | 15 | −1 | 20 | Partial Expansion Water level: 2.0–3.3 m |
| Xialian | 25–43 | 5–15 | −1 | 20 (10) | ||
| Qiulian | 25–43 | 5–15 | −1 | 20 (30) | ||
| Donglian | 25–43 | 5–15 | −1 | 20 (6) | ||
| Seven Channels | Chifeng Channel | 70 | 40 | −1 | 30 | -- |
| Chenghe Channel | 30–45 | 15 | −1 | 6–30 | Partial Expansion Water level: 2.0–3.3 m | |
| Huangri Channel | 45 | 15 | −1 | 6–30 | ||
| L1ha Channel | 45 | 15 | −1 | 6–30 | ||
| Qingxiang Channel | 45–90 | 15–60 | −1 | 6–30 | ||
| Lanyun Channel | 45 | 15 | −1 | 30 (15) | ||
| Zifei Channel | 45 | 15 | −1 | 30 | ||
| Discharge Sluice | Dishui Lake Sluice | -- | -- | -- | -- | Maximum flow rate: 40 m3/s |
| Evaluation Goals | Evaluation Indicators | Calculation Method | |
|---|---|---|---|
(1–5 Levels) | ) (%) | × 100% | |
(m3) | Coefficient (10) × Design Rainfall × Confluence Area × Average Runoff Coefficient | ||
| ) (m3) | Green Space × Infiltration Rate × Rainfall Duration + Water System Area × Water Depth | ||
| ) (1–5 Levels) | ) (%) | × 100% | |
| ) (%) | × 100% | ||
| ) (m3/s) | Sum of the Design Flow of Downstream Sewer Outlets in the Region [43] | ||
| ) (1–5 Levels) | ) (%) | Low Value (1–2 Levels) | × 100% |
| High Value (3–5 Levels) | |||
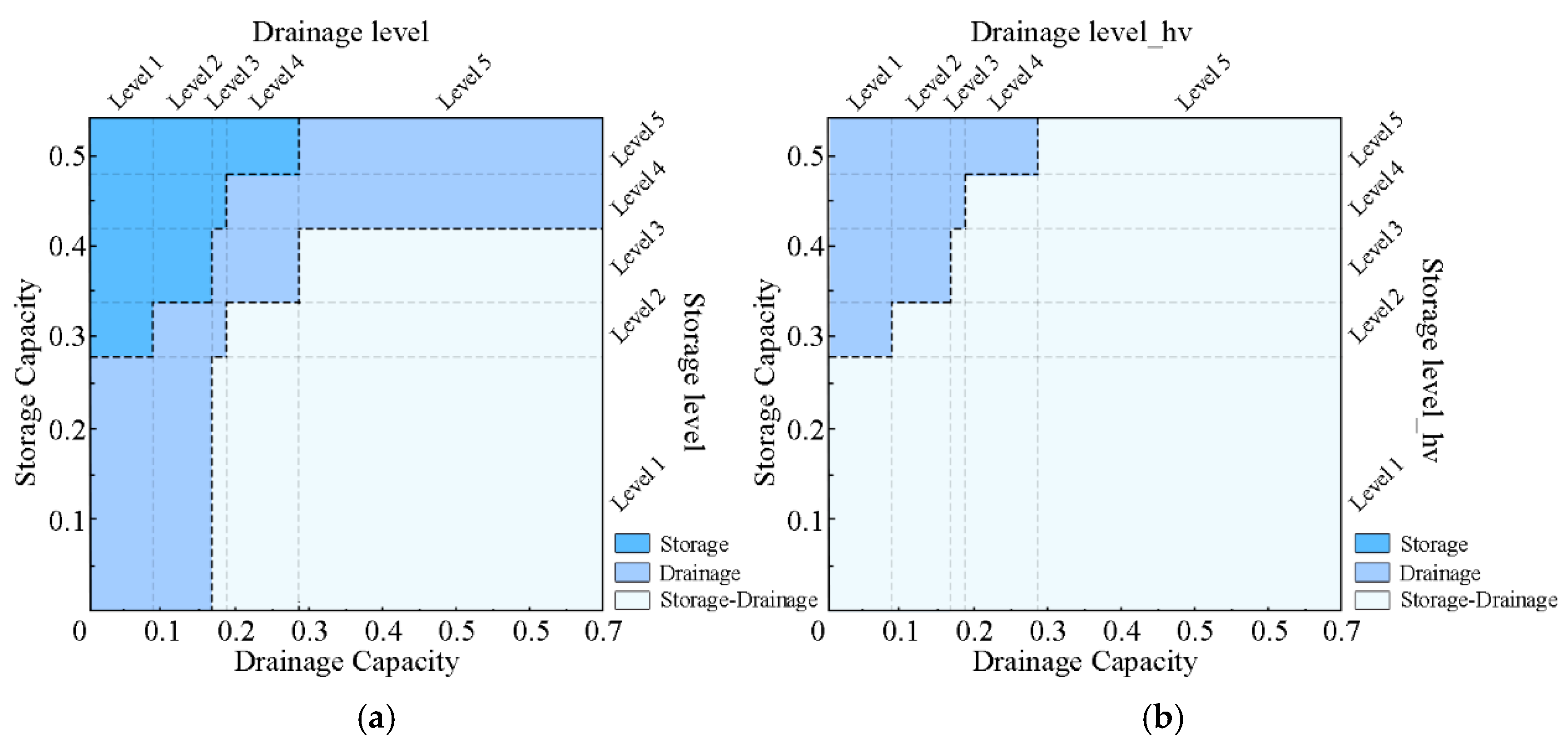
| Evaluation Goals | Level 1 | Level 2 | Level 3 | Level4 | Level 5 |
|---|---|---|---|---|---|
| 0–0.28 | 0.28–0.34 | 0.34–0.42 | 0.42–0.48 | 0.48–0.52 | |
| 0–0.09 | 0.09–0.17 | 0.17–0.19 | 0.19–0.29 | 0.29–0.71 | |
| 0–0.11 | 0.11–0.25 | 0.25–0.32 | 0.32–0.64 | 0.64–1.11 |
| Evaluation Goals | Evaluation Indicators | Weight |
|---|---|---|
| 0.21 | ||
| 0.27 | ||
| 0.15 | ||
| 0.70 | ||
| 0.21 | ||
| 0.09 | ||
| 1 |
| Region No. | Regional Mode | |||
|---|---|---|---|---|
| I | Level 2 | Level 1 | Level 2 | Priority Storage |
| II | Level 4 | Level 3 | Level 2 | Priority Storage |
| III | Level 3 | Level 2 | Level 4 | Storage Discharge |
| IV | Level 3 | Level 4 | Level 5 | Priority Discharge |
| V | Level 3 | Level 4 | Level 5 | Priority Discharge |
| VI | Level 3 | Level 3 | Level 3 | Priority Discharge |
| VII | Level 1 | Level 2 | Level 3 | Priority Discharge |
| VIII | Level 5 | Level 5 | Level 1 | Storage Discharge |
| Source Region | Target Region | Flow Type |
|---|---|---|
| I | II | Free Flow |
| VIII | Opportunistic Drainage | |
| II | III | Disconnected |
| VIII | Opportunistic Drainage | |
| III | VIII | Priority Drainage |
| IV | III | Priority Drainage |
| VIII | Priority Drainage | |
| V | IV | Free Flow/Opportunistic Drainage |
| VI | Free Flow/Opportunistic Drainage | |
| VIII | Priority Drainage | |
| VI | I | Priority Drainage |
| VIII | Priority Drainage | |
| VII | III | Priority Drainage |
| VIII | I | Priority Drainage |
| II | Priority Drainage | |
| Outlet | Priority Drainage |
| Optimization Objective | Facility Type | Location ID | Control Method |
|---|---|---|---|
| OPO | Pump | 6.1–6.4 | Open if the water level before the pump in Region VI is greater than 2.1 m and the water level in Region I is less than 3.3 m, otherwise close. |
| 4–7 | Open if the water level before the pump in Region IV-VII is greater than 2.1 m, otherwise close. | ||
| 3.1–3.2 | Open if the water level before the pump in Region IV is greater than 2.1 m and the water level in Region III is less than 3.3 m, otherwise close. | ||
| 3 | Open if the water level in Region III is greater than 3.2 m, otherwise close. | ||
| 8 | Keep open to maintain downstream water level around 2.6 m. | ||
| Gate | 3.3 | Keep open to maintain downstream water level around 2.6 m. | |
| Weir | All | Open during rainfall, with a height restriction of 3.3 m. | |
| AP | Pump | 6.1–6.4 | Open if the water level before the pump in Region VI is greater than 2.1 m and the water level in Region I is less than 3.3 m, otherwise close. |
| 4–7 | Open if the water level before the pump in Region IV–VII is greater than 2.1 m, otherwise close. | ||
| 4.1–4.3, 5.1–5.4 | Maintain consistent water levels in Regions IV–VI. | ||
| 3.1–3.2 | Open if the water level before the pump in Region IV is greater than 2.1 m and the water level in Region III is less than 3.3 m, otherwise close. | ||
| Weir | All | Open during rainfall, with a height restriction of 3.3 m. | |
| MC | Pump | 6.1–6.4 | Open if the water level before the pump in Region VI is greater than 2.1 m and the water level in Region I is less than 3.3 m, otherwise close. |
| 4–7 | Open if the water level before the pump in Region IV–VII is greater than 2.1 m, otherwise close. | ||
| 3 | Open if the water level in Region III is greater than 3.2 m, otherwise close. | ||
| 3.1–3.2 | Open if the water level before the pump in Region IV is greater than 2.1 m and the water level in Region III is less than 3.3 m, otherwise close. | ||
| Weir | All | Open during rainfall, with a height restriction of 3.3 m. | |
| SC | Pump | 6.1–6.4 | Open if the water level before the pump in Region VI is greater than 2.1 m, the water level in Region I is less than 3.3 m, and the water level in Dripping Water Lake is greater than 3.3 m, otherwise close. |
| 4–7 | Open if the water level before the pump in Region IV–VII is greater than 2.1 m, otherwise close. | ||
| 3, 3.3 | Open if the water level in Region III is greater than 2.1 m, and close when the water level in Dripping Water Lake is greater than 3.3 m. | ||
| 3.1–3.2 | Open if the water level before the pump in Region IV is greater than 2.1 m and the water level in Region III is less than 3.3 m, otherwise close. | ||
| Weir | All | Open during rainfall, with a height restriction of 3.3 m. |
| Return Period | Level 1 (km2) | Proportion (%) | Level 2 (km2) | Proportion (%) | Level 3 (km2) | Proportion (%) | Total (km2) | Waterlogging Area in High-Value (km2) |
|---|---|---|---|---|---|---|---|---|
| 50 yr | 3.58 | 49.18 | 1.86 | 25.57 | 1.83 | 25.25 | 7.27 | 4.24 |
| 100 yr | 4.10 | 48.96 | 2.13 | 25.48 | 2.14 | 25.56 | 8.38 | 4.90 |
| 200 yr | 4.48 | 48.82 | 2.29 | 25.01 | 2.40 | 26.17 | 9.17 | 5.32 |
| 300 yr | 4.73 | 48.45 | 2.48 | 25.41 | 2.55 | 26.14 | 9.76 | 5.55 |
| 400 yr | 4.78 | 47.38 | 2.64 | 26.18 | 2.67 | 26.44 | 10.09 | 5.80 |
| 500 yr | 4.99 | 47.71 | 2.68 | 25.67 | 2.78 | 26.62 | 10.45 | 5.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhang, Z.; Liu, Q.; Yang, L. Study on the Coordinated Regulation of Storage and Discharge Mode in Plain Cities Under Extreme Rainfall: A Case Study of a Southern Plain City. Water 2025, 17, 1385. https://doi.org/10.3390/w17091385
Wang Z, Zhang Z, Liu Q, Yang L. Study on the Coordinated Regulation of Storage and Discharge Mode in Plain Cities Under Extreme Rainfall: A Case Study of a Southern Plain City. Water. 2025; 17(9):1385. https://doi.org/10.3390/w17091385
Chicago/Turabian StyleWang, Zhe, Zhiming Zhang, Qianting Liu, and Liangrui Yang. 2025. "Study on the Coordinated Regulation of Storage and Discharge Mode in Plain Cities Under Extreme Rainfall: A Case Study of a Southern Plain City" Water 17, no. 9: 1385. https://doi.org/10.3390/w17091385
APA StyleWang, Z., Zhang, Z., Liu, Q., & Yang, L. (2025). Study on the Coordinated Regulation of Storage and Discharge Mode in Plain Cities Under Extreme Rainfall: A Case Study of a Southern Plain City. Water, 17(9), 1385. https://doi.org/10.3390/w17091385







