Simulating Anomalous Migration of Radionuclides in Variably Saturation Zone Based on Fractional Derivative Model
Abstract
1. Introduction
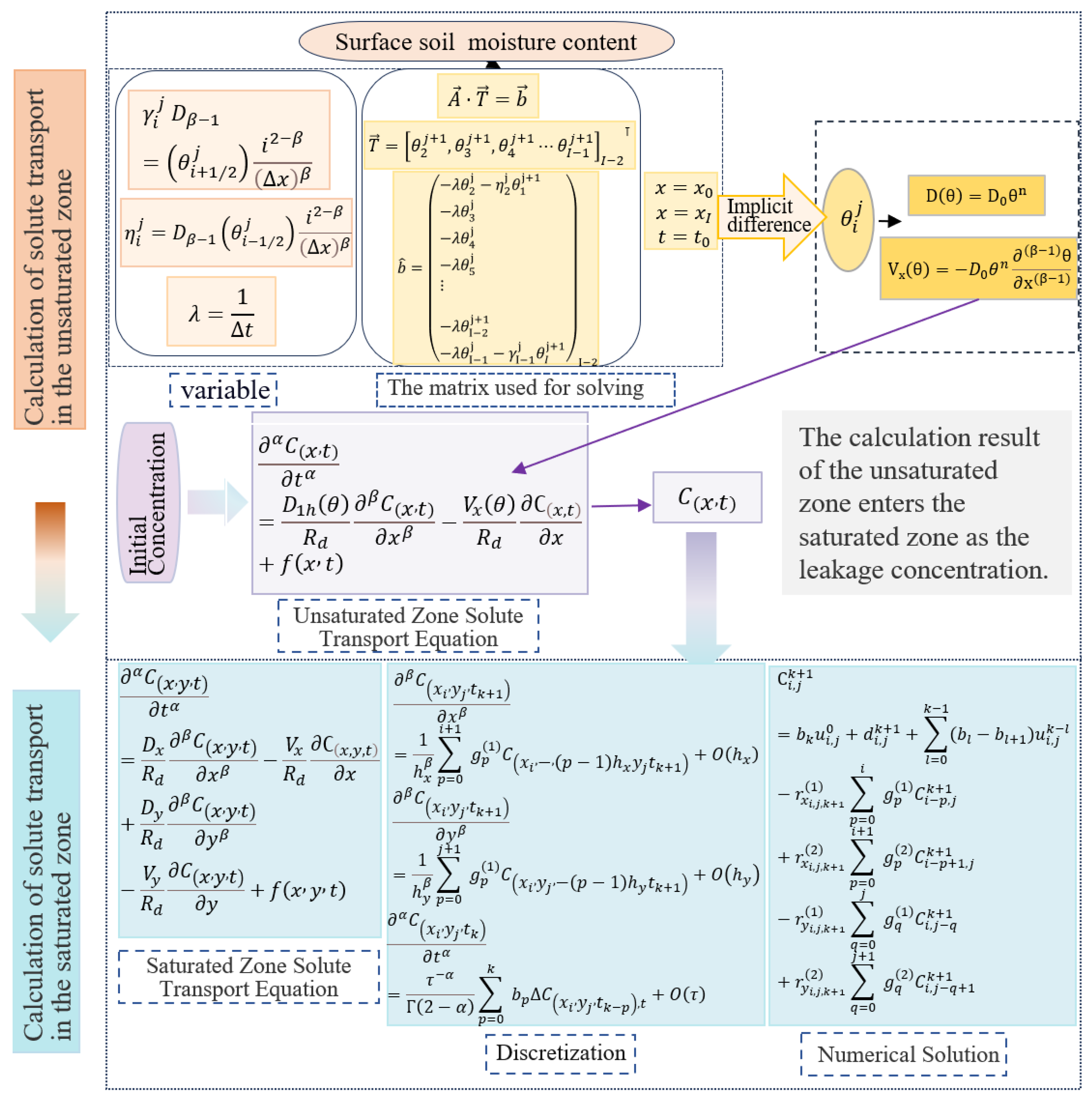
2. Methodology Development
2.1. Fractional Derivative Equation for Saturated Zone
2.2. Unsaturated-Fractional Derivative Model Development
2.2.1. Seepage Velocity in the Unsaturated Zone
2.2.2. Solute Hydrodynamic Dispersion Coefficient
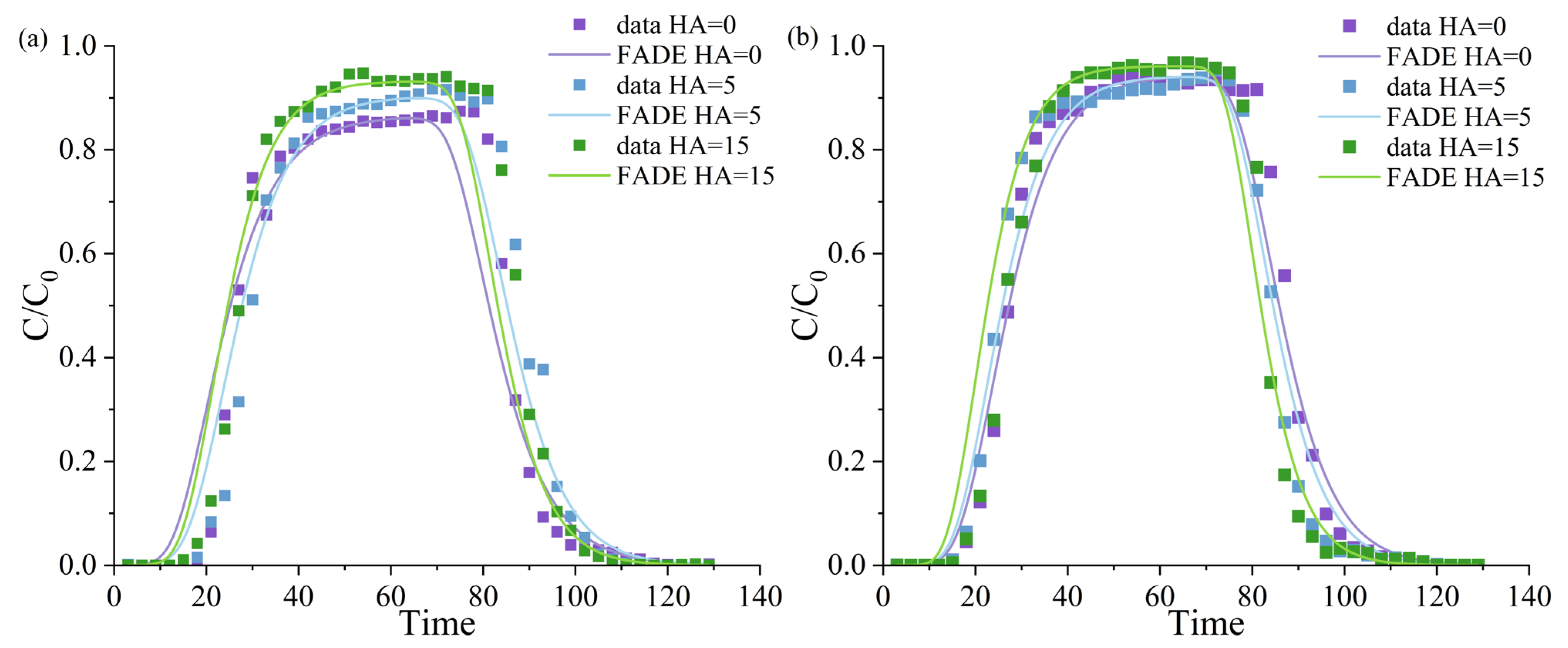
3. Methodology Validations
4. Field Application
4.1. Natural Conditions of the Study Area
4.2. Parameter Configuration
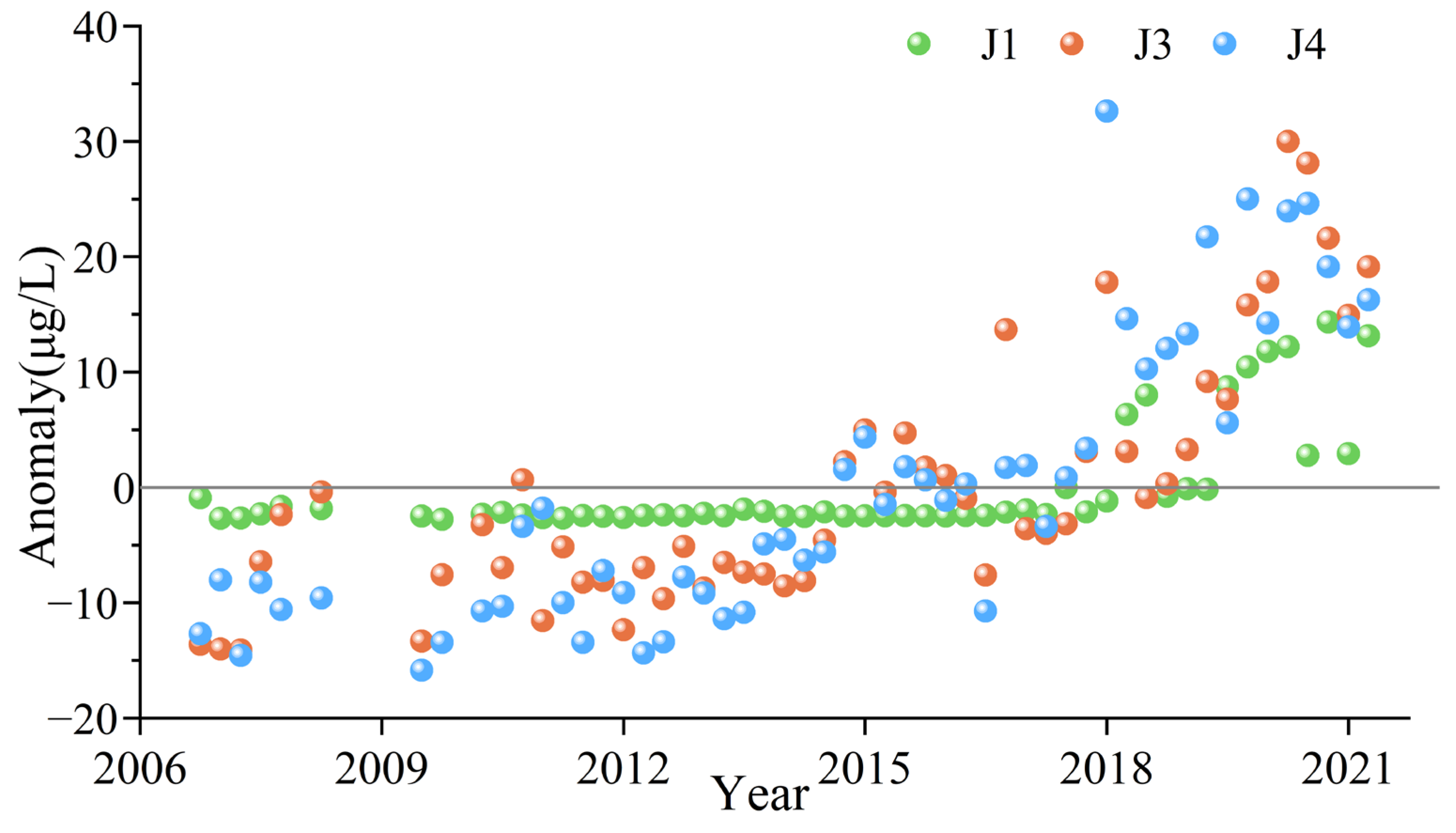
4.2.1. Analysis of Measured Data
4.2.2. Release Scenario Determination
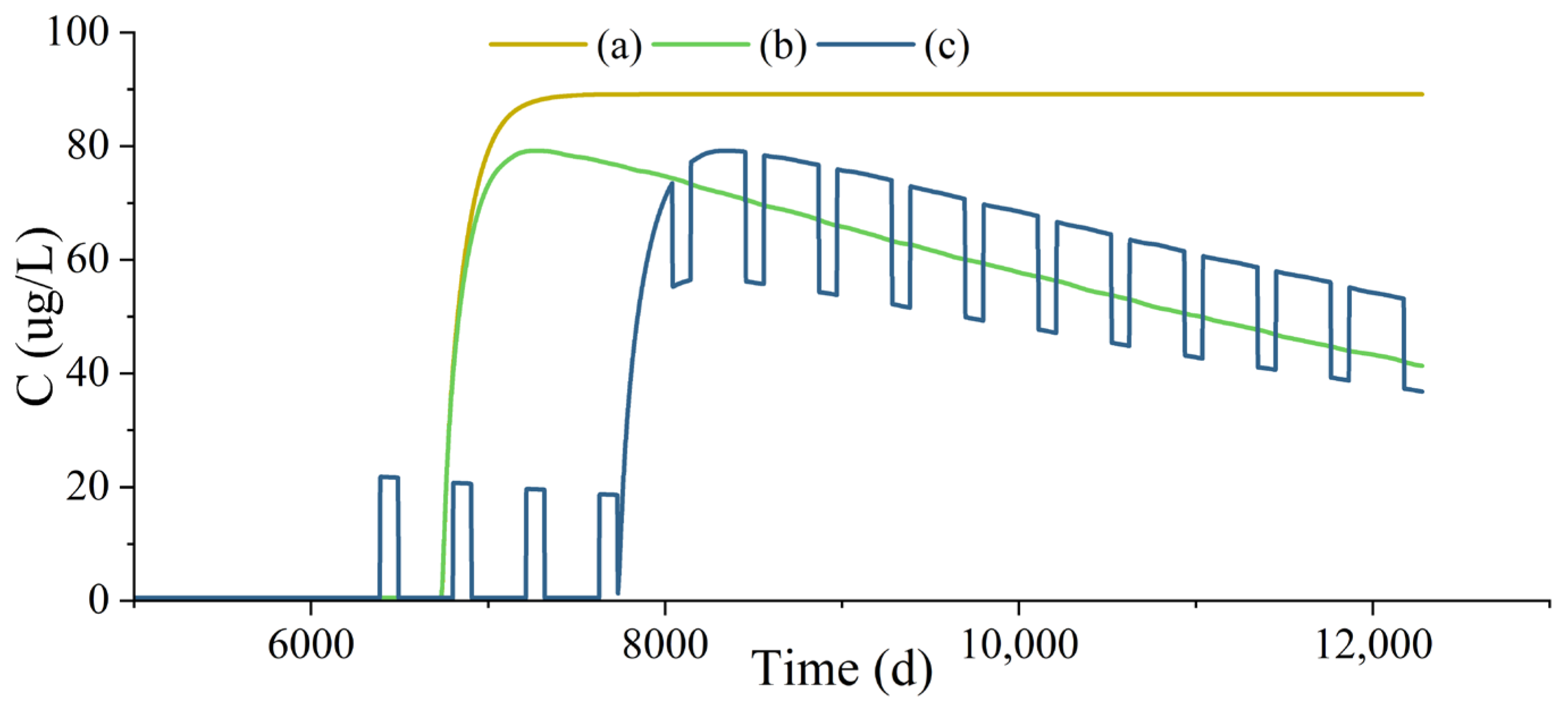
4.3. Simulated Results
4.3.1. Radionuclide Migration in the Unsaturated Zone
4.3.2. The Fitting Result of Nuclide Migration in the Observation Well
4.4. Sensitivity Analysis
5. Discussion
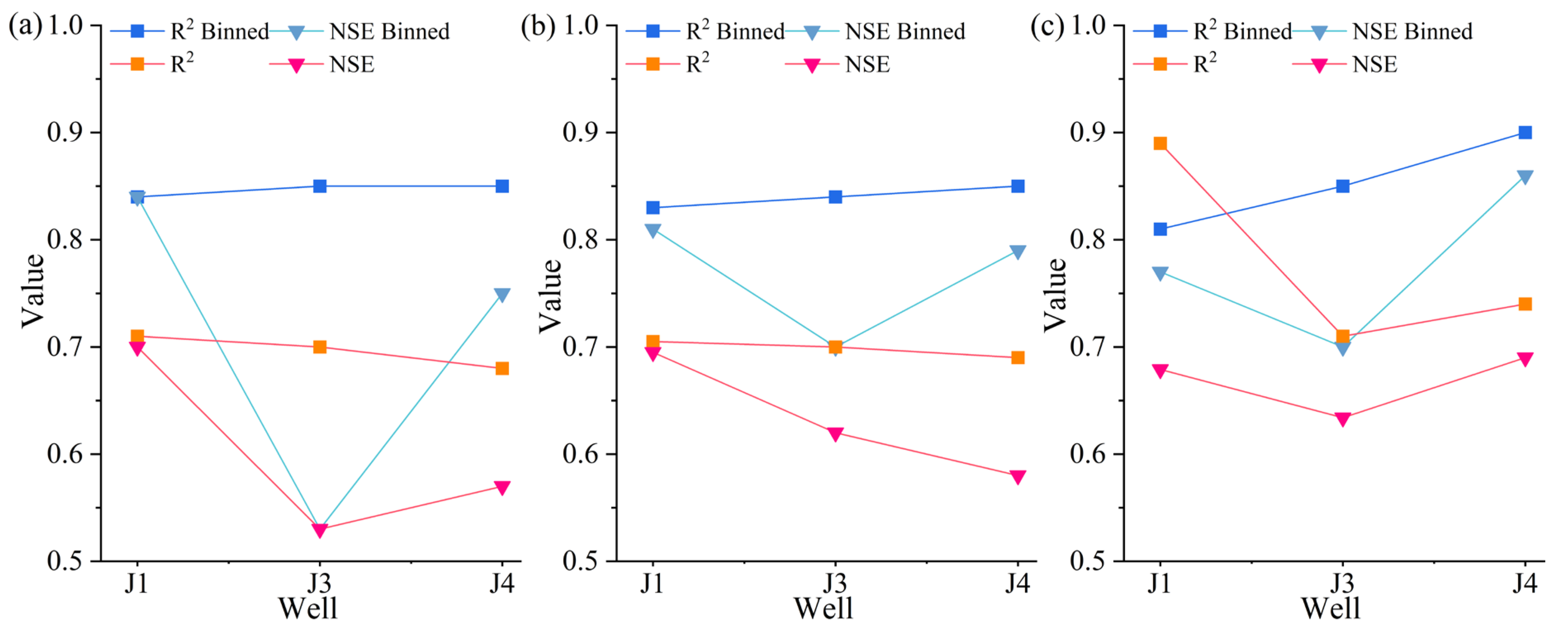
5.1. Model Fitting Performance
5.2. Advantages and Disadvantages of the Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ferguson, C. Do Not Phase out Nuclear Power—Yet. Nature 2011, 471, 411. [Google Scholar] [CrossRef]
- Wang, X.; Tan, X.; Chen, C.; Chen, L. The concentration and pH dependent diffusion of 137Cs in compacted bentonite by using capillary method. J. Nucl. Mater. 2005, 345, 184–191. [Google Scholar] [CrossRef]
- Li, Z.; Ding, Z.B.; Fu, B.F.; Wang, X.C.; Liu, D.X. Calculation of radionuclide migration based on generalized integral transform technique. Atomic Energy Sci. Technol. 2017, 51, 1500–1508. [Google Scholar]
- Wang, Y.; Pan, J. Building Ecological Security Patterns Based on Ecosystem Services Value Reconstruction in an Arid Inland Basin: A Case Study in Ganzhou District, NW China. J. Clean. Prod. 2019, 241, 118337. [Google Scholar] [CrossRef]
- Robinson, B.A.; Li, C.; Ho, C.K. Performance Assessment Model Development and Analysis of Radionuclide Transport in the Unsaturated Zone, Yucca Mountain, Nevada. J. Contam. Hydrol. 2003, 62–63, 249–268. [Google Scholar] [CrossRef]
- Cho, W.-J.; Lee, J.-O.; Choi, H.-J. Radionuclide Migration through an Unsaturated Clay Buffer under Thermal and Hydraulic Gradients for a Nuclear Waste Repository. Ann. Nucl. Energy 2012, 50, 71–81. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Hu, J.; Zhang, X.; Zhang, X.; Ma, Y.; Zhang, P. A Case Study on the Soil-Water Characteristics of the Vadose Zone and the Migration of Intermediate-Level Nuclides in a Planned Spent-Fuel Reprocessing Plant Site. J. Clean. Prod. 2020, 284, 124743. [Google Scholar] [CrossRef]
- Jakimavičiūtė-Maselienė, V.; Cidzikienė, V. Modelling of Tritium Transport in the Underground Water from Hypothetical Reactor at the New NPP Site in Lithuania. Prog. Nucl. Energy 2015, 80, 1–6. [Google Scholar] [CrossRef]
- Birdsell, K.H.; Wolfsberg, A.V.; Hollis, D.; Cherry, T.A.; Bower, K.M. Groundwater Flow and Radionuclide Transport Calculations for a Performance Assessment of a Low-Level Waste Site. J. Contam. Hydrol. 2000, 46, 99–129. [Google Scholar] [CrossRef]
- Fares, A.; Deb, S.K.; Fares, S. Review of Vadose Zone Soil Solution Sampling Techniques. Environ. Rev. 2009, 17, 215–234. [Google Scholar] [CrossRef]
- Fomin, S.; Chugunov, V.; Hashida, T. The Effect of Non-Fickian Diffusion into Surrounding Rocks on Contaminant Transport in a Fractured Porous Aquifer. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2923–2939. [Google Scholar] [CrossRef]
- Gerke, H.H. Preferential Flow Descriptions for Structured Soils. J. Plant Nutr. Soil Sci. 2006, 169, 382–400. [Google Scholar] [CrossRef]
- Li, L.; Gawande, N.; Kowalsky, M.B.; Steefel, C.I.; Hubbard, S.S. Physicochemical Heterogeneity Controls on Uranium Bioreduction Rates at the Field Scale. Environ. Sci. Technol. 2011, 45, 9959–9966. [Google Scholar] [CrossRef]
- Friedly, J.C.; Davis, J.A.; Kent, D.B. Modeling Hexavalent Chromium Reduction in Groundwater in Field-Scale Transport and Laboratory Batch Experiments. Water Resour. Res. 1995, 31, 2783–2794. [Google Scholar] [CrossRef]
- Cushman, J.H. Development of Stochastic Partial Differential Equations for Subsurface Hydrology. Stoch. Hydrol. Hydraul. 1987, 1, 241–262. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Wierenga, P.J. Mass Transfer Studies in Sorbing Porous Media I. Analytical Solutions. Soil Sci. Soc. Am. J. 1976, 40, 473–480. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling Non-Fickian Transport in Geological Formations as a Continuous Time Random Walk. Rev. Geophys. 2006, 44, RG2003. [Google Scholar] [CrossRef]
- Zhang, Y.; Benson, D.A.; Reeves, D.M. Time and space nonlocalities underlying fractional-derivative models: Distinction and literature review of field applications. Adv. Water Resour. 2009, 32, 561–581. [Google Scholar] [CrossRef]
- Benson, D.A.; Meerschaert, M.M.; Revielle, J. Fractional calculus in hydrologic modeling: A numerical perspective. Adv. Water Resour. 2013, 51, 479–497. [Google Scholar] [CrossRef]
- Tian, J.; Tong, D. The Flow Analysis of Fiuids in Fractal Reservoir with the Fractional Derivative. J. Hydrodyn. 2006, 18, 287–293. [Google Scholar] [CrossRef]
- Xu, M.; Tan, W. Intermediate Processes and Critical Phenomena: Theory, Method and Progress of Fractional Operators and Their Applications to Modern Mechanics. Sci. China Ser. G Phys. Mech. Astron. 2006, 49, 257–272. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Chen, W.; Reeves, D.M. Use of a Variable-Index Fractional-Derivative Model to Capture Transient Dispersion in Heterogeneous Media. J. Contam. Hydrol. 2014, 157, 47–58. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, J.; Zhao, Z.; Chen, S.; Liu, G.; Zhao, X.; Wang, J.; Lin, T.; Liu, B. Numerical Modeling on Nuclide Transport around a Nuclear Waste Repository under Coupled Thermo-Hydro-Mechanical Condition. Comput. Geotech. 2023, 164, 105776. [Google Scholar] [CrossRef]
- Trinchero, P.; Iraola, A. Models for the Assessment of Transport of Naturally-Occurring Nuclides in Fractured Media. J. Hydrol. 2020, 580, 124322. [Google Scholar] [CrossRef]
- Benson, D.A. The Fractional Advection-Dispersion Equation: Development and Application. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 1998. [Google Scholar]
- Zech, A.; Attinger, S.; Bellin, A.; Cvetkovic, V.; Dagan, G.; Dietrich, P.; Fiori, A.; Teutsch, G. Evidence Based Estimation of Macrodispersivity for Groundwater Transport Applications. Groundwater 2022, 61, 346–362. [Google Scholar] [CrossRef]
- Padilla, I.Y.; Yeh, T.-C.J.; Conklin, M.H. The Effect of Water Content on Solute Transport in Unsaturated Porous Media. Water Resour. Res. 1999, 35, 3303–3313. [Google Scholar] [CrossRef]
- Dagan, G. Theory of Solute Transport by Groundwater. Annu. Rev. Fluid Mech. 1987, 19, 183–213. [Google Scholar] [CrossRef]
- Labolle, E.M.; Fogg, G.E. Role of Molecular Diffusion in Contaminant Migration and Recovery in an Alluvial Aquifer System; Springer eBooks: Berlin/Heidelberg, Germany, 2001; pp. 155–179. [Google Scholar] [CrossRef]
- Sun, H. Modeling and Application of Anomalous Diffusion in Complex Media. Ph.D. Thesis, Hohai University, Nanjing, China, 2012. (In Chinese). [Google Scholar]
- Lu, C.; Lin, Y.; Zhang, Y.; Qin, W.; Wu, C.; Liu, P.; Shu, L. Simulation of solute transport in the hyporheic zone based on a spatiotemporal fractional derivative model. South-North Water Div. Water Sci. Technol. 2022, 20, 506–515. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Y.; Green, C.T.; LaBolle, E.M.; Neupauer, R.M.; Sun, H. Bounded Fractional Diffusion in Geological Media: Definition and LAgrangian Approximation. Water Resour. Res. 2016, 52, 8561–8577. [Google Scholar] [CrossRef]
- Huang, J.; Goltz, M.N. Analytical Solutions for a Soil Vapor Extraction Model That Incorporates Gas Phase Dispersion and Molecular Diffusion. J. Hydrol. 2017, 549, 452–460. [Google Scholar] [CrossRef]
- Mao, R.; Luo, X.; Jiao, J.J.; Li, H. Molecular Diffusion and Pore-Scale Mechanical Dispersion Controls on Time-Variant Travel Time Distribution in Hillslope Aquifers. J. Hydrol. 2023, 616, 128798. [Google Scholar] [CrossRef]
- Ozdemir, O.N.; Buyruk, T.; Ucaner, E. Calculation of Chlorine and Fluoride Diffusion/Dispersion Coefficients in Water Supply Pipes. J. Water Resour. Plan. Manag. 2021, 147, 04021041. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, D.; Hu, L. Numerical simulations of hydrodynamic dispersion based on an equivalent pore network model. Tsinghua Sci. Technol. 2022, 62, 1906–1914. [Google Scholar] [CrossRef]
- Ahn, J.; Cho, C.-K.; Kang, S. An Efficient Numerical Parameter Estimation Scheme for the Space-Dependent Dispersion Coefficient of a Solute Transport Equation in Porous Media. Math. Comput. Model. 2010, 51, 167–176. [Google Scholar] [CrossRef]
- Xu, X.; Lewis, C.; Liu, W.; Albertson, J.D.; Kiely, G. Analysis of Single-Ring Infiltrometer Data for Soil Hydraulic Properties Estimation: Comparison of BEST and Wu Methods. Agric. Water Manag. 2012, 107, 34–41. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, H.; Zhuo, Z.; Xue, D.; Yang, S. Finite difference method for spatial fractional seepage model in unsaturated soil. Chin. J. Geotech. Eng. 2020, 42, 6. (In Chinese) [Google Scholar] [CrossRef]
- Diao, Y. Study on the Migration Mechanism of Aged Microplastics in Porous Media. Ph.D. Thesis, Donghua University, Shanghai, China, 2022. (In Chinese) [Google Scholar] [CrossRef]
- Tran, T.H.H.; Kim, S.H.; Kim, H.-B.; Kwon, M.J.; Chung, J.; Lee, S. Prediction of Arsenic Retention in Vadose Zone Based on Empirical Relationship between Soil Properties and Segmented Retardation Factors. J. Hazard. Mater. 2024, 476, 134990. [Google Scholar] [CrossRef]
- Gelhar, L.W.; Welty, C.; Rehfeldt, K.R. A Critical Review of Data on Field-Scale Dispersion in Aquifers. Water Resour. Res. 1992, 28, 1955–1974. [Google Scholar] [CrossRef]
- Zhou, K. Experimental Study on the Release of Uranium Elements in Uranium Tailings of Different Particle Sizes Under Water Medium Conditions. Ph.D. Thesis, Nanhua University, Taiwan, China, 2015. (In Chinese). [Google Scholar]
- He, Y.; Zhang, Q.; Wang, W.; Hua, J.; Li, H. The Multi-Media Environmental Behavior of Heavy Metals around Tailings under the Influence of Precipitation. Ecotoxicol. Environ. Saf. 2023, 266, 115541. [Google Scholar] [CrossRef]
- Yu, X.; Sui, Q.; Lyu, S.; Zhao, W.; Wu, D.; Yu, G. Rainfall Influences Occurrence of Pharmaceutical and Personal Care Products in Landfill Leachates: Evidence from Seasonal Variations and Extreme Rainfall Episodes. Environ. Sci. Technol. 2021, 55, 4822–4830. [Google Scholar] [CrossRef]
- Schumer, R.; Benson, D.A.; Meerschaert, M.M.; Baeumer, B. Multiscaling Fractional Advection-Dispersion Equations and Their Solutions. Water Resour. Res. 2003, 39, 1022–1032. [Google Scholar] [CrossRef]
- Samper, J.; Dai, Z.; Molinero, J.; García-Gutiérrez, M.; Missana, T.; Mingarro , M. Mingarro Inverse Modeling of Tracer Experiments in FEBEX Compacted Ca-Bentonite. Phys. Chem. Earth Parts A/B/C 2006, 31, 640–648. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Collenteur, R.A.; Jasechko, S.; Jaramillo, F.; Luijendijk, E.; Moeck, C.; van der Velde, Y.; Allen, S.T. Groundwater Recharge Is Sensitive to Changing Long-Term Aridity. Nat. Clim. Change 2024, 14, 357–363. [Google Scholar] [CrossRef]
- Guo, Z.; Ma, R.; Zhang, Y.; Zheng, C. Contaminant Transport in Heterogeneous Aquifers: A Critical Review of Mechanisms and Numerical Methods of Non-Fickian Dispersion. Sci. China Earth Sci. 2021, 64, 1224–1241. [Google Scholar] [CrossRef]




| Paraments | HA = 0 mg/L | HA = 5 mg/L | HA = 15 mg/L | ||||
|---|---|---|---|---|---|---|---|
| Types of Microplastics | α | β | α | β | α | β | |
| Pristine microplastics | 1 | 1.83 | 1 | 1.81 | 1 | 1.89 | |
| Aged microplastics | 1 | 1.88 | 1 | 1.89 | 1 | 1.96 | |
| Data | α | β | Rd | Bulk Density |
|---|---|---|---|---|
| 1 | 1 | 1.9 | 5 | 1.16 |
| 2 | 1 | 1.9 | 6 | 1.26 |
| 3 | 1 | 1.88 | 6 | 1.36 |
| 4 | 1 | 1.7 | 6 | 1.46 |
| Well | J1 | J3 | J4 | |
|---|---|---|---|---|
| Paraments | Release scenarios | Stable groundwater level: Uniform release | ||
| Vx|Vy/(m· d−1) | 0.65|0.002 | 7|0.06 | 10|0.08 | |
| Dx |Dy/(m2·d−1) | 22.68|0.22 | 22.68|0.22 | 22.68|0.22 | |
| Rd | 6 | 6 | 8 | |
| α | 1 | 1 | 1 | |
| βx|βy | 1.9|2 | 1.4|2 | 1.4|2 | |
| Paraments | Release scenarios | Stable groundwater level: Decrease release | ||
| Vx|Vy/(m · d−1) | 1|0.002 | 7|0.06 | 10|0.08 | |
| Dx |Dy/(m2·d−1) | 22.68|0.22 | 22.68|0.22 | 22.68|0.22 | |
| Rd | 7 | 6 | 8 | |
| α | 1 | 1 | 1 | |
| βx|βy | 1.9|2 | 1.4|2 | 1.4|2 | |
| Paraments | Release scenarios | Fluctuating groundwater levels | ||
| Vx|Vy/(m · d−1) | 1|0.002 | 9|0.06 | 10| 0.08 | |
| Dx |Dy/(m2 · d−1) | 22.68|0.22 | 22.68|0.22 | 22.68|0.22 | |
| Rd | 7 | 6 | 8 | |
| α | 1 | 1 | 1 | |
| βx|βy | 1.9|2 | 1.4|2 | 1.4|2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Liu, J.; Li, Y.; Sun, H.; Lu, C. Simulating Anomalous Migration of Radionuclides in Variably Saturation Zone Based on Fractional Derivative Model. Water 2025, 17, 1337. https://doi.org/10.3390/w17091337
Zhang M, Liu J, Li Y, Sun H, Lu C. Simulating Anomalous Migration of Radionuclides in Variably Saturation Zone Based on Fractional Derivative Model. Water. 2025; 17(9):1337. https://doi.org/10.3390/w17091337
Chicago/Turabian StyleZhang, Mengke, Jingyu Liu, Yang Li, Hongguang Sun, and Chengpeng Lu. 2025. "Simulating Anomalous Migration of Radionuclides in Variably Saturation Zone Based on Fractional Derivative Model" Water 17, no. 9: 1337. https://doi.org/10.3390/w17091337
APA StyleZhang, M., Liu, J., Li, Y., Sun, H., & Lu, C. (2025). Simulating Anomalous Migration of Radionuclides in Variably Saturation Zone Based on Fractional Derivative Model. Water, 17(9), 1337. https://doi.org/10.3390/w17091337







