Next Article in Journal
Coupling Coordination Relationships Between Water Resource–Water Environment–Social Economy Resilience and Ecosystem Services in Five Provinces of Northwest China
Next Article in Special Issue
Making Different Decisions: Demonstrating the Influence of Climate Model Uncertainty on Adaptation Pathways
Previous Article in Journal
The Patterns of Dissolved N2O Concentrations Are Driven by Nutrient Stoichiometry Related to Land Use Types in the Yiluo River Basin, China
Previous Article in Special Issue
Evaluation of Historical Dry and Wet Periods over Lake Kyoga Basin in Uganda
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 17
Issue 8
10.3390/w17081171
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Understanding Climate Change Impacts on Streamflow by Using Machine Learning: Case Study of Godavari Basin

by
Ravi Ande
1,*,
Chandrashekar Pandugula
2,
Darshan Mehta
3,
Ravikumar Vankayalapati
4,
Prashant Birbal
5,
Shashikant Verma
6,
Hazi Mohammad Azamathulla
5 and
Nisarg Nanavati
3
1
Department of Fabric and Apparel Science, Lady Irwin College, University of Delhi, New Delhi 110001, Delhi, India
2
Lowe’s Inc., 1000 Lowe’s Blvd., Mooresville, NC 28117, USA
3
Department of Civil Engineering, Dr. S. & S. S. Ghandhy Government Engineering College, Surat 395001, Gujarat, India
4
Equinix Inc., Dallas, TX 75207, USA
5
Department of Civil and Environmental Engineering, University of the West Indies, St. Augustine 330110, Trinidad and Tobago
6
Department of Civil Engineering, National Institute of Technology, Raipur 492010, Chhattisgarh, India
*
Author to whom correspondence should be addressed.
Water 2025, 17(8), 1171; https://doi.org/10.3390/w17081171
Submission received: 7 March 2025 / Revised: 8 April 2025 / Accepted: 9 April 2025 / Published: 14 April 2025
(This article belongs to the Special Issue Climate Change and Hydrological Processes, 2nd Edition)
Browse Figures
Versions Notes

Abstract

:
The study aims to assess future streamflow forecasts in the Godavari basin of India under climate change scenarios. The primary objective of the Coupled Model Inter-comparison Project Phase 6 (CMIP6) was to evaluate future streamflow forecasts across different catchments in the Godavari basin, India, with an emphasis on understanding the impacts of climate change. This study employed both conceptual and machine learning models to assess how changing precipitation patterns and temperature variations influence streamflow dynamics. Seven satellite precipitation products CMORPH, Princeton Global Forcing (PGF), Tropical Rainfall Measuring Mission (TRMM), Climate Prediction Centre (CPC), Infrared Precipitation with Stations (CHIRPS), and Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks (PERSIANN-CDR) were evaluated in a gridded precipitation evaluation over the Godavari River basin. Results of Multi-Source Weighted-Ensemble Precipitation (MSWEP) had a Nash–Sutcliffe efficiency (NSE), coefficient of determination (R2), and root mean square error (RMSE) of 0.806, 0.831, and 56.734 mm/mon, whereas the Tropical Rainfall Measuring Mission had 0.768, 0.846, and 57.413 mm, respectively. MSWEP had the highest accuracy, the lowest false alarm ratio, and the highest Peirce’s skill score (0.844, 0.571, and 0.462). Correlation and pairwise correlation attribution approaches were used to assess the input parameters, which included a two-day lag of streamflow, maximum and minimum temperatures, and several precipitation datasets (IMD, EC-Earth3, EC-Earth3-Veg, MIROC6, MRI-ESM2-0, and GFDL-ESM4). CMIP6 datasets that had been adjusted for bias were used in the modeling process. R, NSE, RMSE, and R2 assessed the model’s effectiveness. RF and M5P performed well when using CMIP6 datasets as input. RF demonstrated adequate performance in testing (0.4 < NSE < 0.50 and 0.5 < R2 < 0.6) and extremely good performance in training (0.75 < NSE < 1 and 0.7 < R < 1). Likewise, M5P demonstrated good performance in both training and testing (0.4 < NSE < 0.50 and 0.5 < R2 < 0.6). While RF was the best performer for both datasets, Indian Meteorological Department outperformed all CMIP6 datasets in streamflow modeling. Using the Indian Meteorological Department gridded precipitation, RF’s NSE, R, R2, and RMSE values during training were 0.95, 0.979, 0.937, and 30.805 m3/s. The test results were 0.681, 0.91, 0.828, and 41.237 m3/s. Additionally, the Multi-Layer Perceptron (MLP) model demonstrated consistent performance across both the training and assessment phases, reinforcing the reliability of machine learning approaches in climate-informed hydrological forecasting. This study underscores the significance of incorporating climate change projections into hydrological modeling to enhance water resource management and adaptation strategies in the Godavari basin and similar regions facing climate-induced hydrological shifts.

1. Introduction

Hydrological models, integral to understanding and simulating natural hydrological processes, serve as decision-making tools, particularly in data-scarce contexts with numerous options [1]. They maximize available data but do not replace field observations. These models require inputs like climatic variables (e.g., precipitation, temperature), watershed characteristics (e.g., drainage network, topography), and more, with complexity depending on the model’s design [1,2]. Historically, hydrological modeling has evolved from Mulvany’s 1850 Rational Method to contemporary grid-based physically distributed models [3]. Sherman’s (1932) Unit Hydrograph (UH) model marked a turning point, predicting flood hydrographs by assuming uniform rainfall at fixed intervals [4]. Later, models like Instantaneous Unit Hydrographs (IUH) and Finite Period Unit Hydrographs (TUH) emerged [5]. Some IUH models were physically based, while others, like the Clark Unit Hydrograph, relied on historical data [6]. The study of the hydrological cycle and its transformations, as well as the prospective consequences for water resources, holds great importance in the areas of sustainable development and the management of water resources [7].
It is crucial to comprehend river hydrology and how it may evolve under future climatic conditions. Nevertheless, it is imperative to recognize that although several studies conducted on a global scale offer valuable insights, they frequently employ spatial resolutions that are insufficient to capture localized climate events [8]. In recent years, the field of streamflow forecasting has witnessed a surge in the popularity of data-driven models, owing to their swift development, minimal data prerequisites, and ease of real-time application [9]. These models encompass diverse approaches, including Linear Time Series Models such as autoregressive moving average (ARMA), autoregressive integrated moving average (ARIMA), and seasonal autoregressive integrated moving average (SARIMA), which presume a probabilistic distribution for streamflow [10]. Nonlinear Time Series Models, particularly chaos-based models, have been employed to capture the intricate nonlinear dynamics inherent in streamflow data [11]. ANNs have demonstrated effectiveness in handling large, dynamic, and nonlinear time series data, especially when the underlying physical processes are not fully understood.
Furthermore, the adoption of machine learning models, particularly using CMIP6 data, represents an innovative approach poised to enhance predictive capabilities in hydrology. In summary, this study’s holistic approach aims to advance our understanding of hydrological processes and their responses to climate change, acknowledging the regional variations and specific relevance to the Godavari River basin. Against the backdrop of the 21st century’s environmental challenges, understanding the impacts of climate change on hydrological extremes is paramount [12]. The accelerated emission of greenhouse gases has significantly influenced the hydrological cycle, notably altering extreme precipitation patterns and temperature regimes [13]. These climatic shifts have profound repercussions on hydrological extremes, with manifestations varying spatially and temporally across different regions [14]. Environmental alteration is a global phenomenon characterized by a multitude of interconnected factors, including land degradation, loss of biodiversity, shifts in climate patterns, and alterations in hydrology [15]. The consequences of these changes are far-reaching and extend to various aspects of our natural environment, including the hydrological cycle. Studies indicate that while climate change has been linked to phenomena such as reduced water-resource quantity and intensified tropical cyclones, the manifestation of these hydrological extremes is influenced by complex atmospheric, land, and water interactions [16]. The impact of environmental change on hydrology is a critical concern in today’s world. Anthropogenic activities have replaced approximately 41% of global natural vegetation with land cover such as croplands and pastures [17]. This transformation, coupled with the escalating emissions of greenhouse gases, has led to alarming levels of global warming, resulting in a steady increase in global temperatures [18].
Physical, conceptual, and data-driven models are the three primary categories of streamflow models that are frequently employed. Physical models, sometimes referred to as process-driven models, include lumped, semi-distributed, and distributed hydrological models. Given the profound socio-economic and environmental implications of these extremes, there is an urgent need for nuanced, region-specific research to devise adaptive and informed strategies for the future [18]. Climate models project changes in precipitation patterns, with some regions expected to receive more precipitation while others receive less. These changes in precipitation are likely to be mirrored in future variations in runoff. The escalating trend in temperature has the potential to lead to increased flooding in various regions worldwide, including South Asia, which is particularly vulnerable to the adverse impacts of climate change.
Streamflow forecasting models are essential in hydrology for predicting the behavior of hydrologic systems. These models are broadly categorized into three types: physical-based models, conceptual models, and black-box models [19]. Physical-Based Models: These models, also known as white-box or process-based models, provide detailed descriptions of hydrological characteristics by solving differential equations based on physical laws. They account for the physical processes governing mass, energy, and momentum conservation [20]. However, they require extensive physical data and complex mathematical representations. Streamflow Modelling and Prediction: The hydrological cycle and the management of water resources depend heavily on streamflow. We can learn more about flood risk and water availability by modelling and forecasting streamflow, which will help with sustainable water resource management. Creative Uses of Machine Learning: The use of machine learning models to estimate streamflow, particularly with CMIP6 data as input, offers a novel strategy that could greatly improve the precision of hydrological forecasts. Studies in India and other countries have used these machine learning models in hydrological research worldwide. They have shown promise in enhancing runoff forecasting, sediment estimation, infiltration modeling, and streamflow predictions [21,22]. Overall, the use of machine learning methods in hydrological modeling offers useful information and resources for the efficient management of water resources and disaster prevention. Examples of literature from various parts of the world that have used AI models in hydrological investigations include the following. Examples of literature from various parts of the world that have applied these machine learning approaches for many uses in hydrological modeling, such as managing water resources, forecasting floods and droughts, and creating water management strategies, demonstrate that precise streamflow prediction is essential. Researchers and decision-makers can evaluate how human activity, climate change, and land use changes affect water availability using streamflow models [22]. These models, which mimic hydrological processes within a catchment region, include IHACRE, HBV, NRECA, and MIKE-SHE. They frequently call for a large amount of input data [23,24]. These models can be difficult to calibrate and validate, and their simplistic architecture and inaccurate data may add uncertainty. However, data-driven models have become more widely used in streamflow forecasting because of their quick iteration cycles, lower data needs, and ability to be implemented in real time [25,26,27]. Without specifically outlining the underlying hydrological processes, these models can make accurate predictions about streamflow [28,29]. Hydrological modeling has made use of several machine learning approaches, including ANNs, SVMs, Random Forest (RF), Multilayer Perceptron (MLP), and M5P. ANNs, sometimes known as “black-box models”, have demonstrated promise in identifying intricate and nonlinear correlations in streamflow data. They need very few input parameters [30,31,32,33].

1.1. Research Gap of the Study Area

The focus on the Godavari River basin, where little research has been carried out on the effects of climate change, highlights how special this place is in dealing with its complexities. Additionally, the use of machine learning models specifically with CMIP6 data represents a novel strategy positioned to improve hydrology’s forecasting capacities. There is not much research on how climate change affects streamflow; therefore, the study’s primary focus on streamflow modeling offers insights into managing and controlling water resources [34]. The paper also addresses the urgent problem of excessive runoff rates, which exacerbate erosion and flooding, and highlights the usefulness of precise runoff forecasting in disaster mitigation. In conclusion, the holistic approach of this study recognizes regional variability and the particular importance of the Godavari River basin while working to improve our understanding of hydrological processes and their responses to climate change [35,36].

1.2. Objectives of the Research Work

Apply conceptual rainfall-runoff models to several sub-basins of the Godavari River basin using the meteorological and bias-corrected CMIP6 datasets. Examine gridded precipitation products in the Godavari River basin of India in comparison to meteorological data. Using CMIP6 data for scenarios SSP126, SSP245, SSP370, and SSP585, examine Extreme Precipitation indices across India using spatial and temporal analysis, using Ranking and Trend assessments [37,38,39]. Forecast streamflow in the Godavari River basin’s numerous sub-basins by using machine learning models using Indian Meteorological Development and bias-corrected CMIP6 datasets. Using CMIP6 data, combine conceptual models and machine learning techniques to forecast future streamflow across various sub-basins in the Godavari basin [40].

2. Materials and Methods

In this section, the selection of data sources, the application of specialized tools such as Climate Data Operators 26.4 (CDO) (https://www.unidata.ucar.edu/software/netcdf/workshops/2012/third_party/CDO.html, accessed on 7 April 2025), Geographic Information System (GIS 10.4) software (https://www.esri.com/, accessed on 7 April 2025), and Python 3.9 programming (https://docs.python.org/release/3.9.22/whatsnew/3.9.html, accessed on 7 April 2025), and the logical flow of activities tailored to the unique objectives of this study. Using CMIP6 data, the combination of conceptual models and machine learning approaches improves the precision of future streamflow forecasts across several sub-basins within the Godavari River basin. The Godavari River basin’s gridded precipitation data demonstrate greater accuracy and dependability in comparison to Indian Meteorological Department (IMD) data [41,42].

2.1. Location

Smaller parts of Karnataka, Madhya Pradesh, Odisha, Telangana, Chhattisgarh, and Andhra Pradesh are included in the Godavari River basin, which spans 312,812 km2 [43]. It makes up around 9.5% of the country’s total land area and is located between latitudes 16°19′ N and 22°34′ N and longitudes 73°24′ E to 83°4′ E. The Godavari River runs 1465 km from its source to its drainage into the Bay of Bengal [44]. The basin is bounded to the east and west by the Eastern and Western Ghats, to the north by the Satmala hills, and to the south by the Mahadeo hills and Ajanta range [45]. The monsoon season (June to September) provides almost 85% of the basin’s annual rainfall, contributing to its tropical climate. In the Godavari, rainfall in the research area, divided into 12 sub-basins, rises from Trimbakeshwar in the Nashik area of Maharashtra [46]. Rainfall in the basin varies significantly by place and time each year, ranging from 600 to 3000 mm (Figure 1)

2.2. Data Collection and Sources

The data collection process forms the foundation of the study. Essential climate data were gathered from multiple sources to comprehensively assess climate change impacts in the Godavari River basin. Primary data sources include the CMIP6 climate model data, which simulates Earth’s climate under various greenhouse gas concentration scenarios [47]. These scenarios, specifically SSP126, SSP245, SSP370, and SSP585, allow investigation of climate change effects. Additionally, historical precipitation records from the Indian Meteorological Department and gridded satellite precipitation datasets were acquired for validation and complementary analysis, as streamflow datasets [48].

2.2.1. CMIP6 Model Data

The eight extreme precipitation indices created by the ETCCDI for the historical period of 1950–2024 were evaluated using the 17 CMIP6 models used in this study. Due to CMIP6 Model Data, only 17 of the available models were processed for study. The 17 CMIP6 models were employed in this study to assess the eight extreme precipitation indices developed by the ETCCDI for the historical period of 1950–2024. Due to insufficient data, only 17 of the available models were processed for analysis over the selected research region for any of the baseline scenarios. Out of 17 models only five were selected for the subsequent stage, and the SSP126, SSP245, SSP370, and SSP585 models for the near (2015–2040), medium (2041–2070), and far future (2071–2100) were evaluated for future extreme precipitation indices for all baseline scenarios [49]. The archives kept by the ESGF contain these CMIP6 models for inspection. Bilinear interpolation was used to spatially remap all general circulation models and data to a latitude and longitude grid that was like 0.25°*0.25° (Table 1) [50,51].

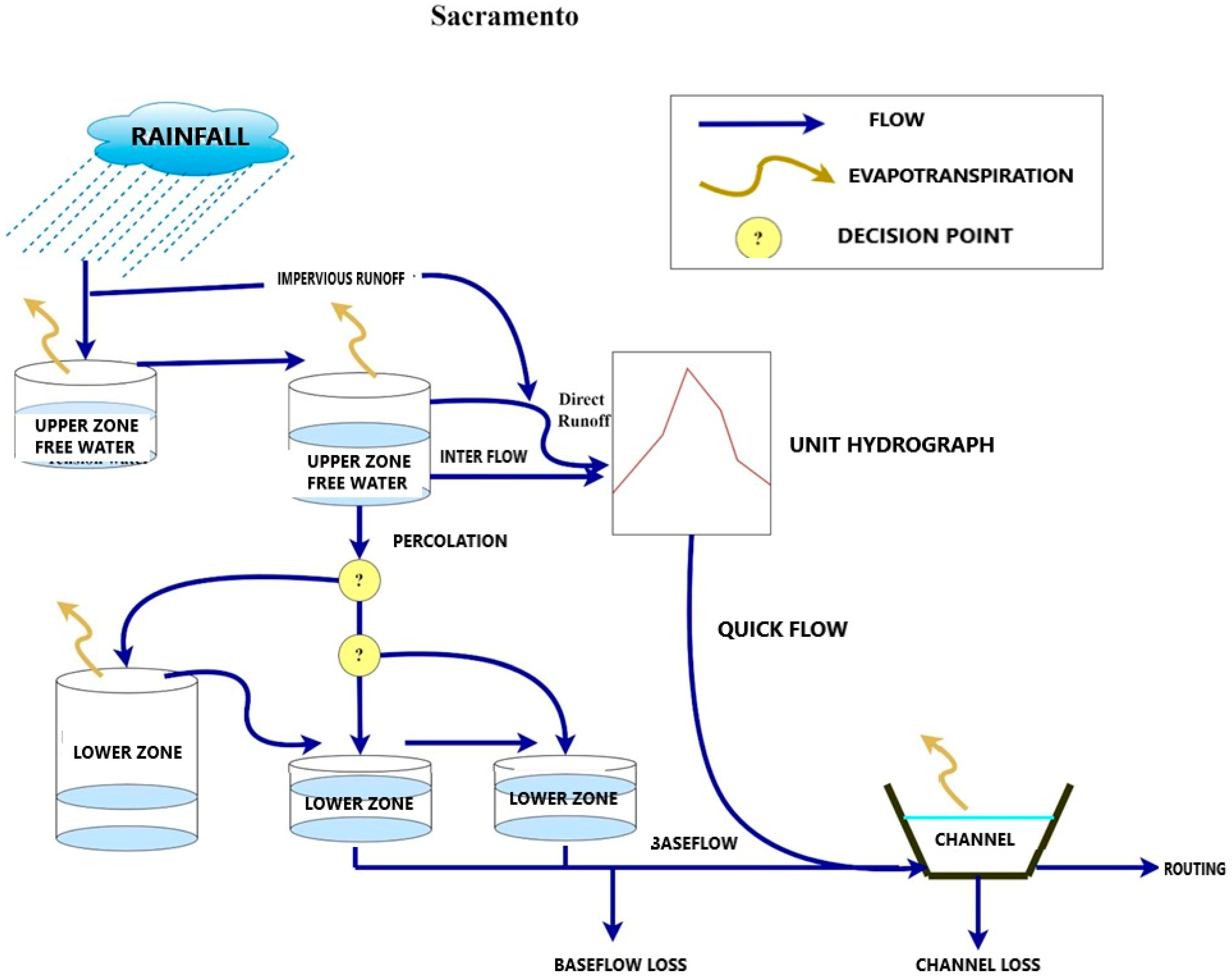
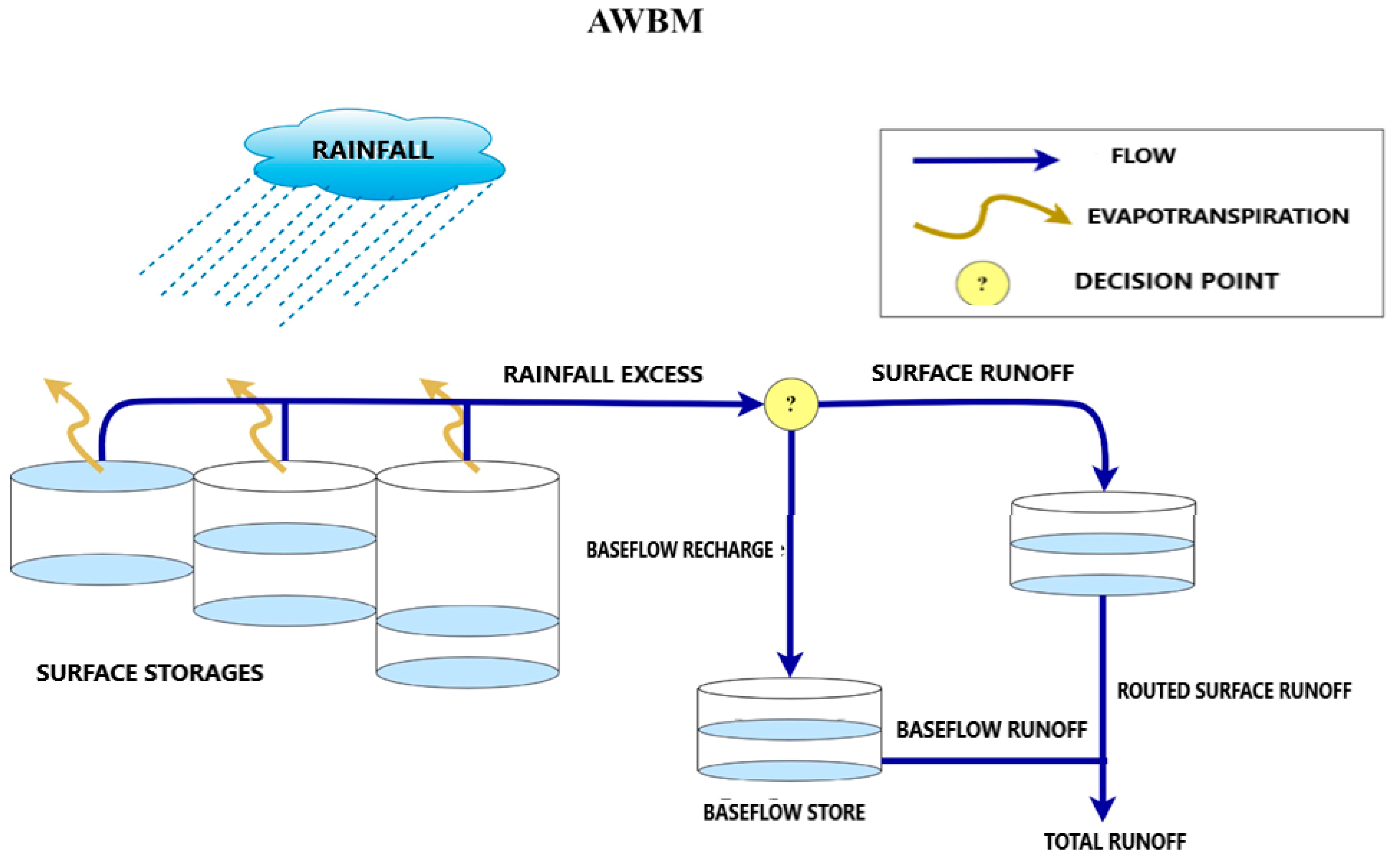
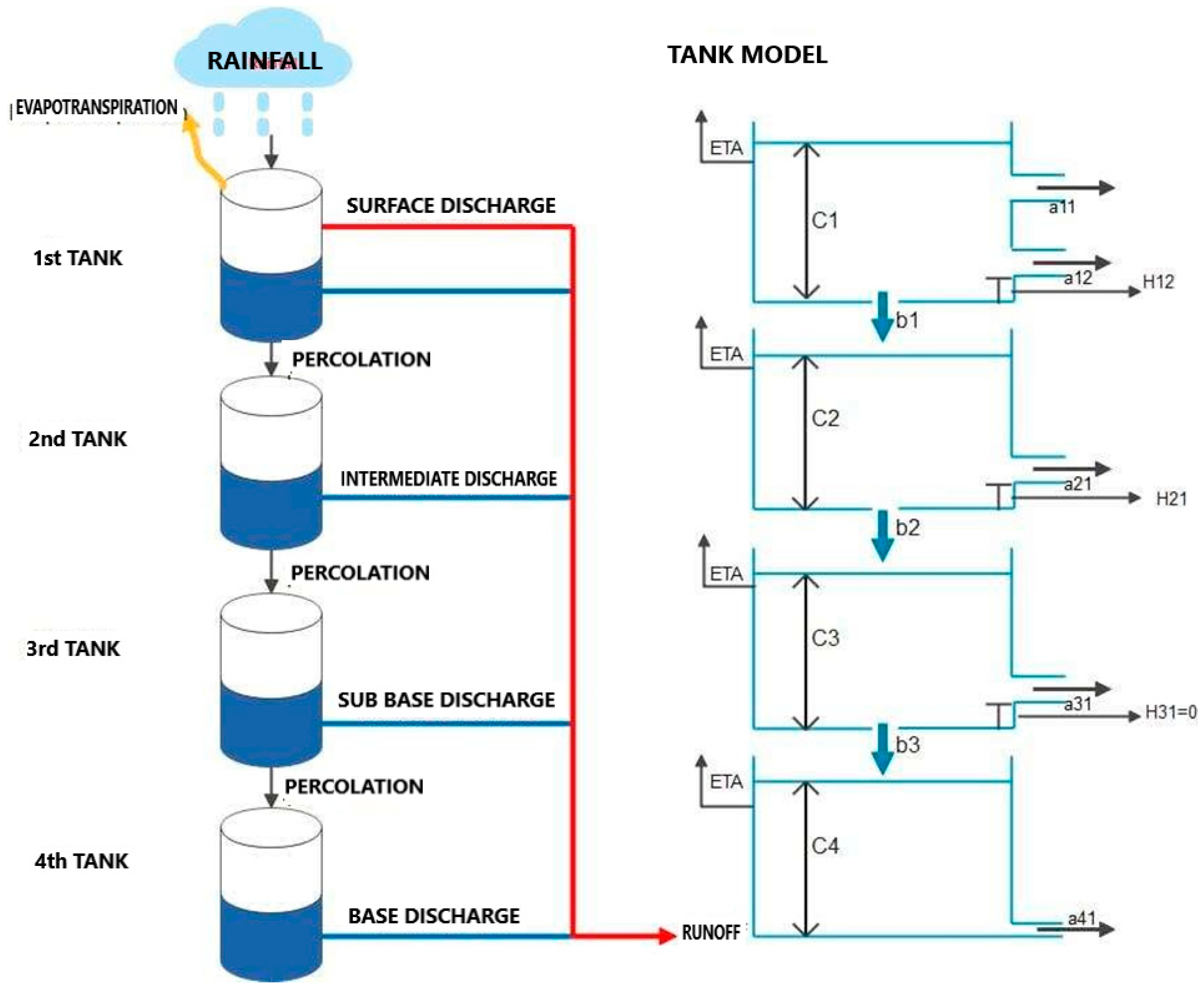
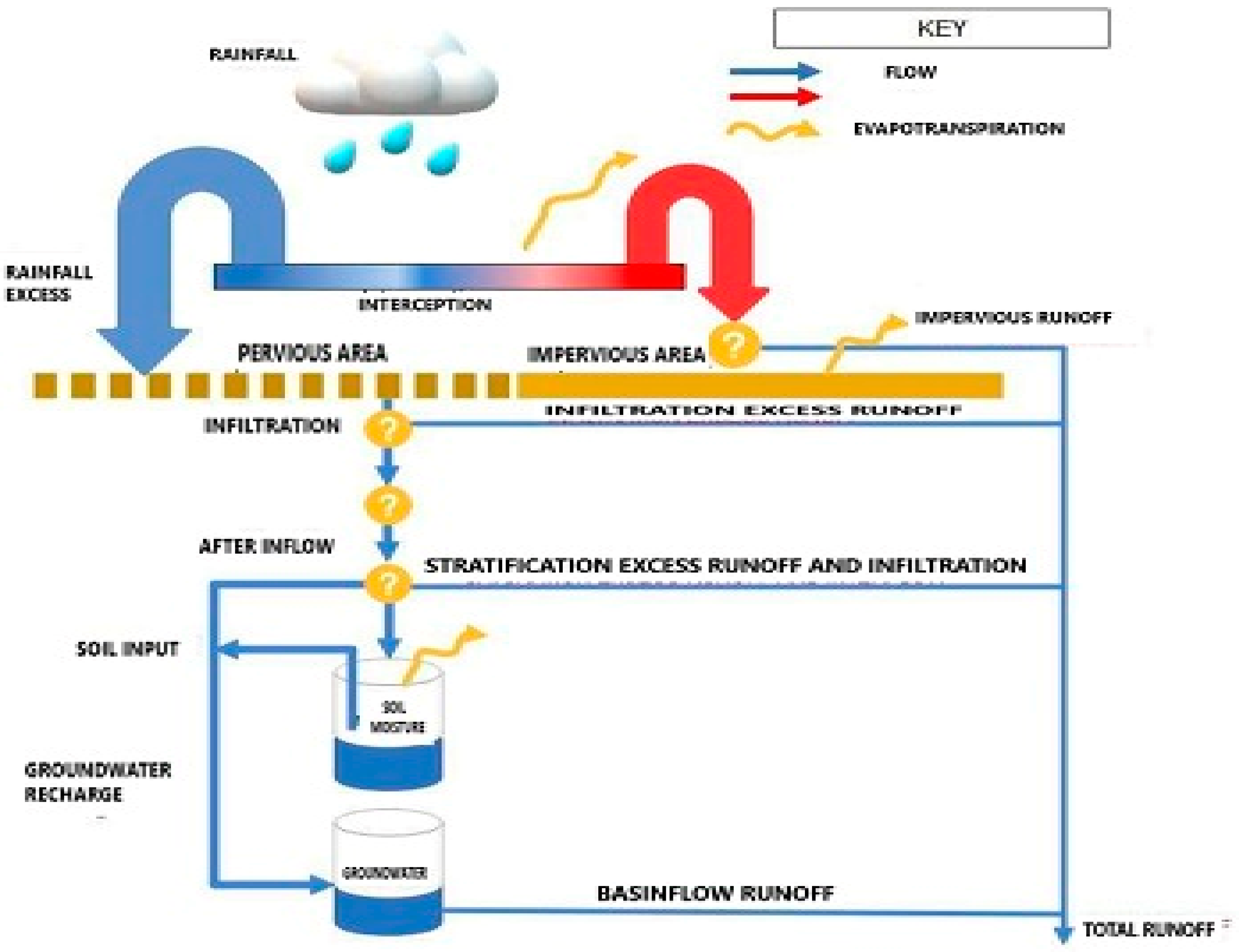
2.2.2. Conceptual Models

Sacramento

Using daily rainfall and PET data, the Sacramento model is a hydrological model that calculates streamflow daily. The model replicates the catchment region’s hydrological balance by incorporating soil moisture [52]. The Sacramento model differs from the AWBM model in that it is more complicated, with a total of five stores and twenty-two distinct attributes [53,54]. The Sacramento model uses the genetic algorithm (GA) to optimize its maximum, minimum, and default parameters. The Sacramento soil’s hydrologically active zone is made up of two distinct layers: Figure 2 shows the Sacramento model’s schematic form. Surface tension in tension water reservoirs helps to retain water within the soil profile. The only mechanism responsible for the outflow of water from this stratum is evapotranspiration [55]. Water can flow both horizontally and vertically within a free water store before being released as interflow (upper zone) or base flow (lower zone). The Sacramento model separates the catchment into impermeable and pervious groups according to its permeability [56]. Lakes, rivers, and other bodies of water, as well as non-porous surfaces like pavement that are directly connected to the river system, make up the impermeable area. Making use of the Rainfall-Runoff Library’s features to model runoff in a particular catchment region by using evapotranspiration and daily rainfall, Manual’s Sacramento model is guided by Podger’s (2003) extensive instructions (Table 2) [29].

The Australian Water Balance Model

In hydrological management, the Australian Water Balance Model (AWBM) is a theoretical framework used to evaluate rainfall losses and ascertain the interdependencies among daily rainfall, evapotranspiration, and runoff at the watershed scale. Five separate stores make up the model: a base flow store, a surface runoff routing shop, and three surface stores that mimic partial runoff regions [14]. It has been observed that the Pranhita sub-basin simulates daily streamflow by utilizing the characteristics of the Rainfall-Runoff Library to model runoff in a specific catchment area, utilizing daily rainfall and evapotranspiration. Each storage unit is given a unique storage capacity, and the water balance of each partial surface area of the AWBM is calculated independently, as shown in the schematic model in Figure 3 and Table 3 [21].

TANK

This model is easy to use and effective. As seen in Figure 4, the highest tank is where rainwater is collected. The water level gradually decreases due to evaporation; water is taken from the tank beneath it to compensate until all the tanks are empty [12]. The side outlets then release the calculated runoff, with the top tank output representing surface runoff, the second tank output representing intermediate runoff, the third tank output representing sub-base runoff, and the fourth tank output representing base flow [13]. Even though the TANK model is simple, its behavior is intricate, and the contents of each tank have a big influence on how well the model works. Notably, depending on the tanks’ storage capacities, the same rainstorm might produce very varied amounts of runoff [15]. The tank model is a widely used method for simulating diurnal streamflow patterns. It is based on daily inputs of evapotranspiration and rainfall and does not require accounting for the initial rainfall loss as the model’s nonlinear structure already accounts for its impact [16]. The TANK model’s parameters are listed in Table 4 and Figure 4, along with their lowest, maximum, and default values.

SIMHYD

The SIMHYD model predicts the daily discharge at a selected gauging station using daily rainfall and PET data [31]. A more straightforward version of the HYDROLOG model, created in 1972, is SIMHYD. A conceptual model that mimics the physics of rainwater runoff is called HYDROLOG. Furthermore, another model known as MODHYDROLOG [24] exists. HYDROLOG and MODHYDROLOG have seventeen and nineteen parameters, respectively, while SIMHYD only has seven (Table 5 and Figure 5). A system that uses the daily rainfall to replenish the interception storage, which is released daily, is part of the SIMHYD concept. The extra rainfall is subsequently subjected to an infiltration capacity assessment function. Infiltration excess runoff is the term used to describe any additional rainfall that is beyond the infiltration capacity.

3. Results and Discussion

3.1. Findings and Talks

In addition to categorical measures like accuracy, POD, FAR, POFD, and PSS, which are calculated daily using the rainfall threshold of 2.5 mm/day that the Indian Meteorological Department uses to identify a wet day, continuous metrics include NSE, R2, MBE, MAE, and RMSE. These metrics were computed using monthly rainfall accumulation for each dataset from 1998 to 2020. The entire basin was compared using 427 Indian Meteorological Department gridded points with a spatial precision of 0.25°*0.25°. The average yearly rainfall for several datasets is shown in Figure 6 [25]. The yearly average precipitation varied less in other models; however, TRMM, PERSIANN CDR, and MSWEP nearly matched data from the Indian Meteorological Department [26]. In terms of spatial extent, MSWEP and CHIRPS nearly matched the Indian Meteorological Department, whereas Figure 6 shows the average yearly precipitation over all eight datasets. Except for PGF, CPC, and CMORPH, all products faithfully captured the well-known precipitation features, such as high precipitation areas on the north and east boundaries of the study area. According to the Indian Meteorological Department, the east side of the basin receives the most rainfall on average each year (1887.04 mm), while the western side receives the lowest amount (553.46 mm). From west to east, the average annual rainfall tends to rise [28].
The average monthly precipitation for the entire basin from 1998 to 2024 is shown in Table 6 and Figure 6. The monsoon months of June, July, August, and September bring the majority of the basin’s rainfall (around 85%). Monsoon precipitation over the basin was estimated with 83% to 86% accuracy by almost all precipitation products [4]. The findings indicate that TRMM and PERSIANN_CDR were overstated for every month throughout the monsoon season [15]. The data from the Indian Meteorological Department and PERSIANN_CDR differed significantly. PERSIANN_CDR and CHIRPS overestimated precipitation by up to about 350 mm [18]. Moderate precipitation (200–300 mm), CMORPH and CPC were subtitled [32].
The Indian Meteorological Department’s seven-satellite precipitation estimates served as the basis for the CDFs. The Indian Meteorological Department gridded dataset was used as a reference for the CDF comparison [24]. MSWEP and the Indian Meteorological Department matched pretty well when compared to the other datasets. However, Figure 7a–d exhibits a slight overestimation of positive bias, particularly for low (between 10 and 65 mm) and moderate (between 110 and 180 mm) precipitation amounts. TRMM displayed a favorable bias for most of the events between 100 and 420 mm; it also matched Indian Meteorological Department data for the remaining section [32].
The gridded dataset from the Indian Meteorological Department served as a source for the CDF comparison. When juxtaposed with the other datasets, Figure 7a–d displays the CDFs based on seven satellite precipitation estimates from the Indian Meteorological Department’s gridded precipitation. MSWEP and the Indian Meteorological Department matched quite well. Even so, Figure 7d shows a small positive bias (overestimates), especially for moderate precipitation (110 to 180 mm) and light precipitation (10 to 65 mm) [19]. TRMM had a favorable bias for most of the events that occurred between 100 and 420 mm; for the remaining, it also coincided with Indian Meteorological Department data. PERSIANN CDR data showed a significant disparity from Indian Meteorological Department data. Up to roughly 350 mm of precipitation, PERSIANN CDR and CHIRPS were overestimated. For moderate precipitation (200–300 mm), CMORPH and CPC were understated [22].

3.1.1. Ongoing Metrics Assessment

The monthly precipitation for each grid cell of the seven datasets was computed and compared to the monthly precipitation data from the Indian Meteorological Department, and statistical characteristics such as NSE, R2, MBE, MAE, and RMSE were evaluated. Continuous measurements for the study area between 1998 and 2024 were used [15]. The NSE coefficients between each precipitation product and the Indian Meteorological Department reference dataset suggest that there might be a conflict of interest between the precipitation products and the Indian Meteorological Department product. MSWEP has higher NSE values over the study area, especially in the western section (Upper Godavari, Pravara, and some portions of Purna), while the other products have low or negative NSE values [23]. The eastern component of the study area includes extremely elevated locations and a few areas of Pranhita, on the northern side. Higher accuracy is indicated by an NSE value greater than 0.7, which was present in 389 out of 427 stations. Comparable to the second-most accurate precipitation dataset after MSWEP, TRMM has 367 stations with an NSE value greater than 0.7 [24]. The lack of rainfall and the large spatial variance at all-time scales are the primary reasons for this notable performance drop. The regional variability of the R2 along the basin is depicted in Table 7, where all precipitation datasets apart from PGF show robust connections. In particular, MSWEP and TRMM showed the highest correlation among the 427 stations, with R2 values over 0.8 for 336 and 357 stations, respectively [26].
The mountainous landscapes of the eastern, western, and northern regions did not correlate well. Figure 8 displays the spatial variance of MBE for the study region. All datasets in the eastern portion had negative MBE, suggesting a comparable underestimation of precipitation, especially in extremely and moderately dense woodlands [32]. There was little to no positive bias in the central and northern regions, suggesting that the judgment was accurate. Due to the infrequent rainfall, TRMM and PERSIANN_CDR provide accurate results up to 76° E from the east; nevertheless, the remaining region displays subpar data with negative NSE. The Upper Godavari region receives 800 mm of rainfall annually, which may have been influenced by the leeward side of the Western Ghats [33].
For the TANK, SIMHYD, AWBM, and Sacramento hydrological models, the standard deviation values of the predicted values are 324.74, 288.44, 296.36, and 332.98, respectively, as shown in Figure 8b. Confidence intervals (CC) for the observed and expected values are 0.87, 0.84, 0.86, and 0.86, respectively [13]. The Taylor diagram also shows the RMSE values, which are 202.61, 226.35, 216.85, and 211.99 m3/s. Since the Sacramento model is the closest to the observed value, it seems to perform the best based on the standard deviation values. Additionally, the Sacramento model is demonstrated to be the most effective of the daily streamflow simulation models according to the RMSE and CC values during the validation period [15].
However, when compared to the other models, the AWBM and TANK models display smaller standard deviation values, which may indicate that they have a propensity to underestimate the variability of the actual data. Nonetheless, the Sacramento model’s standard deviation values of 308.59 were quite similar [19]. In terms of absolute errors, the Sacramento model corresponds with the real data the best, as evidenced by it displaying the lowest RMSE score. The RMSE values for each model fall between 168.04 and 181.44 m3/s. Figure 8a–d compares observed data for daily streamflow modeling with several hydrological models (TANK, SIMHYD, AWBM, and Sacramento) throughout both the calibration process and validation using Taylor’s diagram [22]. A graphical tool called Taylor’s diagram is used to compare models to the observed data in Table 8 and Figure 8. It offers a rapid visual evaluation of a model’s ability to represent the volatility of and pattern in the data. As seen in Figure 8a, the calibration CC for each model ranged from 0.83 to 0.86, indicating that the model outputs and the observed data have a respectable level of agreement [24].

3.1.2. Evaluation of Categorical Metrics

To assess each precipitation product’s capacity to predict a rainy day, five category metrics were calculated. As per the rules set by the Indian Meteorological Department, a day is deemed rainy if it records 2.5 mm or more of precipitation. Evaluations of five categorical criteria for seven products of precipitation between 1998 and 2016 were carried out [12]. With values of 0.844, 0.571, and 0.462, MSWEP had the lowest FAR, the highest accuracy, and the lowest PSS. With accuracy, POD, and PSS of 0.821, 0.705, and 0.549, respectively, PERSIANN_CDR was the second-most dependable precipitation product to identify wet days. With a maximum MBE of 9.332 mm/month, PERSIANN_CDR was likely overestimating the entire research region, which is how rainy days were found [14].
In the eastern Godavari basin (Sabari, parts of lower Godavari), the accuracy of all precipitation products is poorer. When it comes to counting hits within the research region, MSWEP was operating effectively, ignoring false alarms, which ranged from 0.59 to 0.89 [24]. In terms of hit detection, PERSIANN_CDR also outperformed other datasets. In areas with higher yearly precipitation, both of these datasets made accurate predictions in some areas of Sabari and the lower Godavari. Moreover, CHIRPS demonstrated strong performance in identifying rainy days, with 0.823 accuracy, 0.613 POD, and 0.497 PSS. When it comes to predicting wet days, MSWEP performs somewhat better than the other precipitation programs [26].
The average for July will increase significantly in the near future, from 277.41 m3/s to 481.75 m3/s. Furthermore, it will increase to 619.29 m3/s in the medium future and 847.14 m3/s in the distant future. While the intermediate and far future averages will be 724.62 m3/s and 965.38 m3/s, respectively, this will soon increase to 757.67 m3/s. The historical average for August is 374.57 m3/s. It will shortly rise to 402.71 m3/s, with the historical average for September at 252.30 m3/s [11]. The averages are 528.45 m3/s in the intermediate future and 433.63 m3/s in the remote future. Last but not least, the October average is 60.68 m3/s historically, rising to 85.57 m3/s in the middle and 118.46 m3/s in the long term. However, in the near future, it drops somewhat to 58.89 m3/s [14].
This study rigorously assessed seven satellite precipitation products against Indian Meteorological Department gridded data in the Godavari River basin from 1998 to 2024. The findings revealed that spatial correlations were generally strong, but performance varied with climate regimes. Notably, MSWEP and TRMM stood out, delivering exceptional accuracy, high NSE and R2 values, and low MAE and RMSE in monthly evaluations. These datasets performed remarkably well during the monsoon and post-monsoon seasons, making them valuable for precipitation detection. However, the spatial assessment showed limitations in elevated, forested, and low-rainfall regions. Overall, MSWEP and TRMM emerged as top performers, especially in data-scarce areas, offering significant potential for hydrological studies and climate scenario downscaling in the future. Further research should consider bias correction and finer-resolution datasets for enhanced accuracy in various water resource applications.
To estimate the monthly and daily precipitation over the Godavari River basin using the Indian Meteorological Department gridded data with 427 grid stations, this paper provides a comprehensive assessment of seven satellite precipitation products from 1998 to 2016: CHIRPS, PGF, TRMM, CPC, CMORPH, PERSIANN_CDR, and MSWEP. The evaluation period was established at 27 years due to the availability and quality. All seven products were interpolated (distance-weighted average remapping) using a comparable geographic resolution of 0.25° and contrasted with gridded data from the Indian Meteorological Department.
Several parameters, including calibrated connections between sensor reflectivity and projected rain rate and sampling error derived from satellite overpass time, were used to evaluate rainfall product category metrics. The algorithms and procedures used in the product created their relationship, and they were connected in some manner. The monthly average streamflow forecasts for the SSP585 scenario were calculated. It will shortly rise to 5.23 m3/s, which is higher than the historical average for January at 3.94 m3/s. In the intermediate and distant futures, it will rise to 1.32 m3/s and 30.34 m3/s, respectively. The historical average for June will soon rise from 22.67 m3/s to 39.00 m3/s. In the intermediate and distant future, it will continue to rise to 98.20 m3/s and 15.08 m3/s.
The models were created using data for the years between 1987 and 2024, with 30% going towards validation and 70% going towards calibration. The evaluation metrics used showed that all four conceptual models performed satisfactorily in modeling streamflow. In contrast to the other models, the Sacramento model produced noticeably superior results. The most notable variations in rainfall patterns across various periods are displayed in the SSP585 scenario. The region with the largest relative change in rainfall in the far future is SSP585 (55.02%), followed by SSP370 (46.09%) [18], SSP245 (25.78%), and SSP126 (22.64%). The SSP585 scenario predicts the far future to have the biggest absolute change in annual mean temperature, 3.29 °C. Bias-corrected EC-Earth3 datasets have been used to forecast future streamflow using the Sacramento model. Depending on the situation and time frame, the monthly streamflow changed. Q95 is predicted to rise by 40.09% to 127.06% in the mid-future and 73.90% to 215.13% in the distant future during the wettest July [14].
In terms of evaluation measures, RF and M5P performed well when using CMIP6 datasets as input. RF demonstrated adequate performance in testing (0.4 < NSE < 0.50 and 0.5 < R2 < 0.6) and extremely good performance in training (0.75 < NSE < 1 and 0.7 < R < 1). Likewise, M5P demonstrated good performance in both training and testing (0.4 < NSE < 0.50 and 0.5 < R2 < 0.6). The input precipitation dataset for CMIP6 was determined to be MIROC6 for the RF model and MRI-ESM2-0 for the M5P model. Daily estimates: The streamflow estimates for the Kanhargaon, Nowrangpur, and Wairagarh regions show a trend of rising water flow across several SSP scenarios, suggesting both potential flooding difficulties and opportunities in terms of water supply [16]. An average streamflow of 74.16 m3/s is anticipated at Kanhargaon under the more severe SSP585 scenario, with peaks possibly reaching 10,915.63 m3/s. Extreme water flows, indicated by this high value, could result in flooding and pose serious problems for flood control. Nowrangpur, which has historically seen larger flows, is also about to undergo significant changes. SSP585 predicts extremely high levels of 11,548.50 m3/s, which would pose a serious risk of flooding during peak hours. Wairagarh is susceptible to significant changes, even though it began with very small flows in the SSP126 scenario at 48.92 m3/s. Highs of 6691.33 m3/s are predicted by the SSP585 scenario, indicating that even regions with normally moderate flows may experience significant flooding difficulties.

4. Conclusions

The seven satellite precipitation products CHIRPS, PGF, TRMM, CPC, CMORPH, PERSIANN_CDR, and MSWEP are thoroughly evaluated in this study. The monthly and daily precipitation over the Godavari River basin is estimated using data from 427 grid stations collected by the Indian Meteorological Department between 1998 and 2024. The availability and quality of the data led to the establishment of the evaluation period at 27 years. Using a similar geographic resolution of 0.25°, all seven products were interpolated (distance-weighted average remapping) and compared to gridded data from the Indian Meteorological Department. The assessment was conducted using both continuous and categorical variables at multiple temporal (daily, monthly, and seasonal) and geographical (basin and grid) resolutions. The following are the key findings:
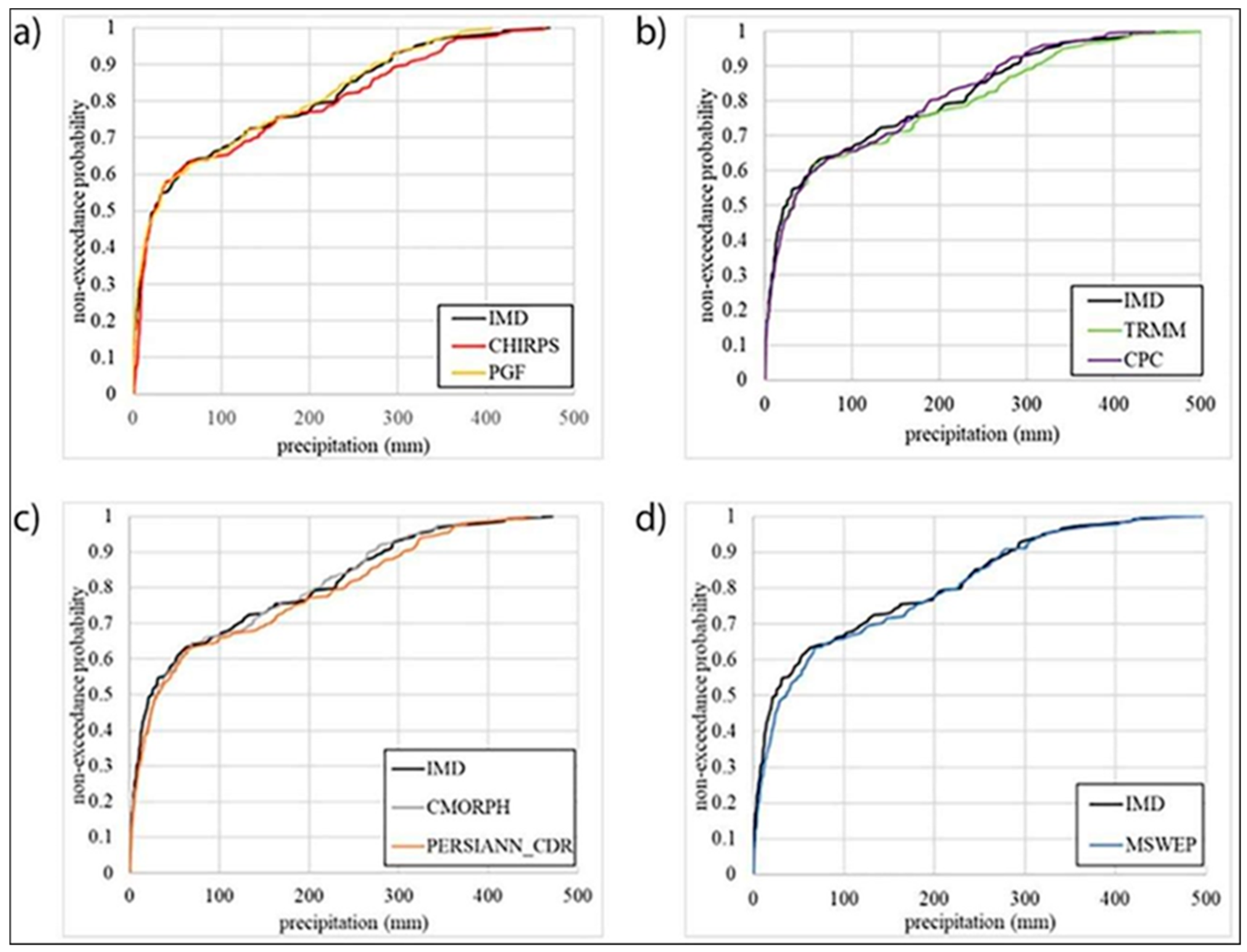
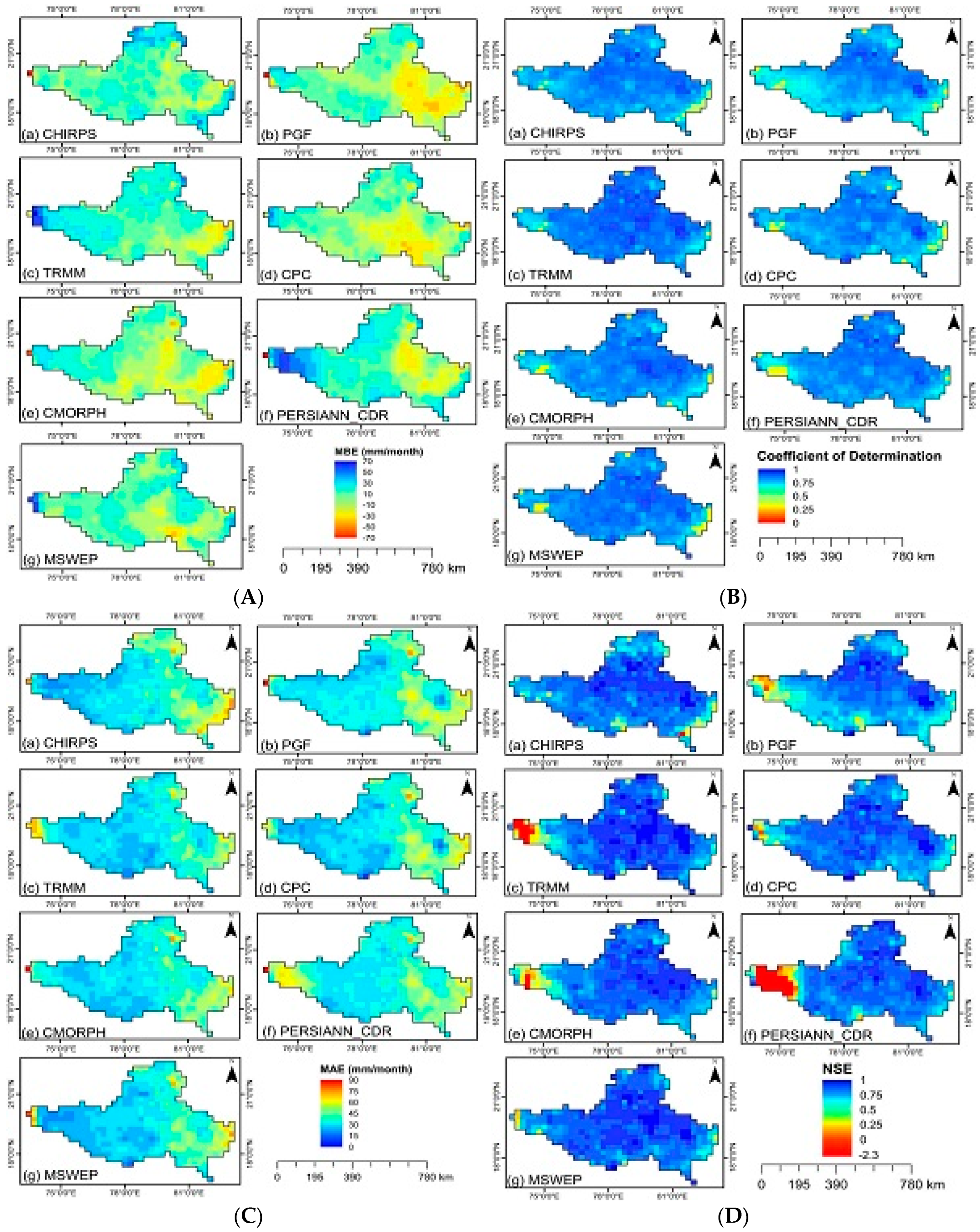
  • Geographic Correlation: The satellite precipitation products showed excellent geographic correlation, although the degree of accuracy varied depending on the climate regime and evolving weather patterns influenced by climate change.
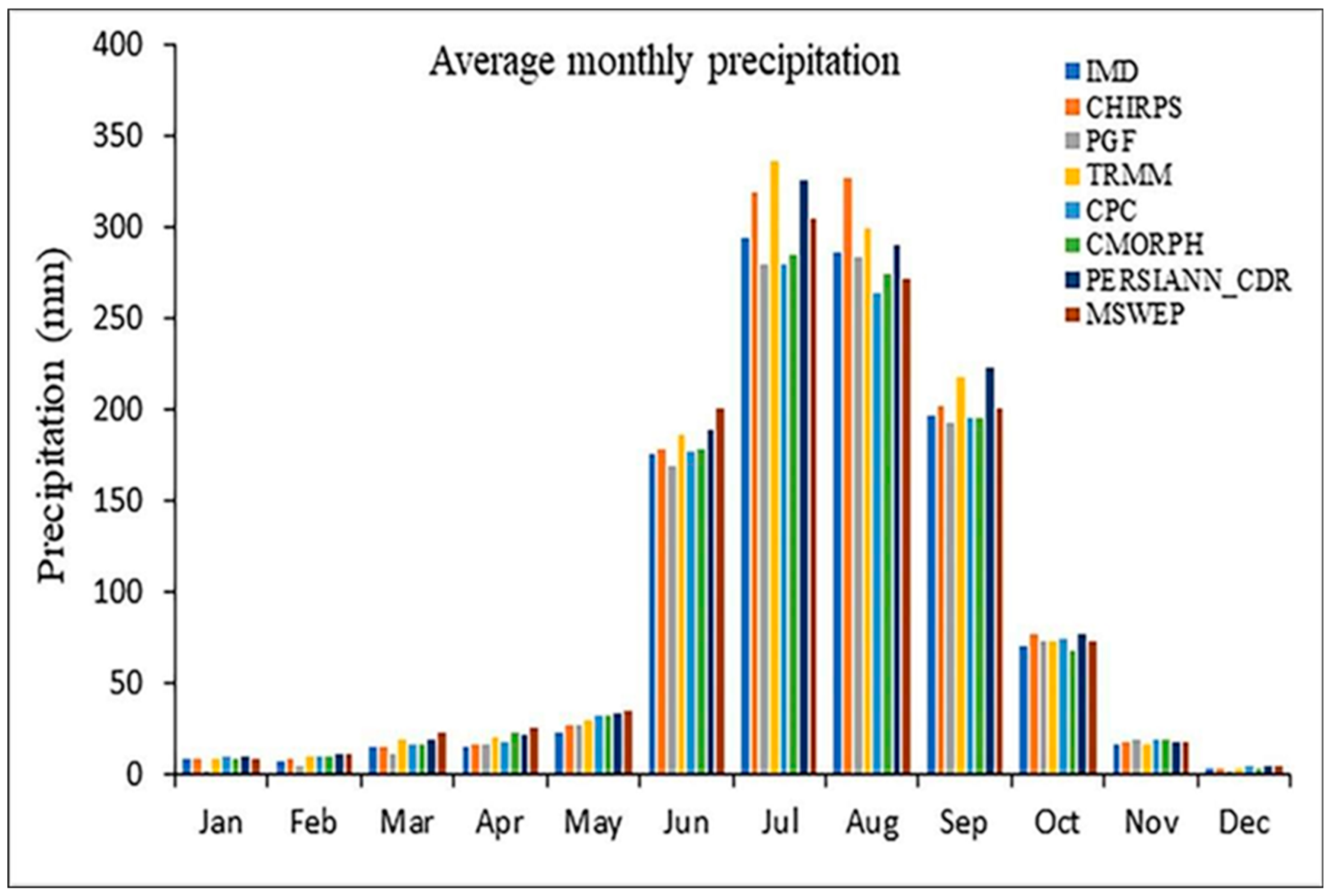
  • Monsoon Dominance: The monsoon season (June to September) remains the dominant precipitation period, accounting for approximately 85% of the basin’s total rainfall. This trend aligns with projections of intensified monsoon activities due to climate change, potentially increasing flood risks and altering water resource availability.
  • Seasonal Performance Variations: Except for MSWEP and TRMM, none of the datasets accurately captured precipitation during the pre-monsoon (March–May) and winter (January–February) seasons. This gap is critical under climate change scenarios, where shifts in seasonal precipitation patterns are expected to intensify.
  • Performance Under Monsoon and Post-Monsoon Conditions: MSWEP and TRMM outperformed the other datasets during the monsoon and post-monsoon seasons, exhibiting lower Mean Bias Error (MBE), Mean Absolute Error (MAE), and Root Mean Square Error (RMSE), along with higher Nash–Sutcliffe Efficiency (NSE) and coefficient of determination (R2). The MSWEP dataset, in particular, achieved an NSE of 0.806, R2 of 0.831, an MAE of 31.79 mm/month, and an RMSE of 56.73 mm/month, indicating robust performance in tracking precipitation trends amidst climate variability.
  • Accuracy in Precipitation Event Detection: MSWEP demonstrated the highest accuracy, with a Peirce’s Skill Score (PSS) of 0.571, a False Alarm Ratio (FAR) of 0.462, and an overall accuracy of 0.844. Additionally, CHIRPS and PERSIANN_CDR successfully detected rainfall occurrences, proving their utility as reliable backup data sources for identifying extreme precipitation events under changing climate conditions.
These findings highlight the importance of selecting the most reliable precipitation datasets to enhance hydrological modeling and climate adaptation strategies in the Godavari basin. As climate change continues to alter precipitation patterns, such evaluations are crucial for improving flood forecasting, water resource management, and resilience planning in vulnerable regions.

Author Contributions

Conceptualization, R.A. and C.P.; methodology, D.M. and S.V.; software, R.V.; validation, H.M.A. and N.N.; formal analysis, R.A. and C.P.; investigation, D.M. and S.V.; resources, R.V.; data curation, H.M.A. and P.B.; writing—original draft preparation, N.N.; writing—review and editing, R.A.; visualization, D.M.; supervision, R.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

Author Chandrashekar Pandugula was employed by the company Lowe’s Inc., author Ravikumar Vankayalapati was employed by the company Equinix Inc. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Agridiotis, V.; Forster, C.F.; Carliell-Marquet, C. Addition of Al and Fe salts during treatment of paper mill effluents to improve activated sludge settlement characteristics. Bioresour. Technol. 2007, 98, 2926–2934. [Google Scholar] [CrossRef] [PubMed]
  2. Akar, Ö.; Saralioğlu, E.; Güngör, O.; Bayata, H.F. Semantic segmentation of very-high spatial resolution satellite images: A comparative analysis of 3D-CNN and traditional machine learning algorithms for automatic vineyard detection. Int. J. Eng. Geosci. 2024, 9, 12–24. [Google Scholar] [CrossRef]
  3. Al-Shannag, M.; Al-Qodah, Z.; Bani-Melhem, K.; Qtaishat, M.R.; Alkasrawi, M. Heavy metal ions removal from metal plating wastewater using electrocoagulation: Kinetic study and process performance. Chem. Eng. J. 2015, 260, 749–756. [Google Scholar] [CrossRef]
  4. Anselmo, L. The long-term evolution of the Italian satellites in the GEO region and their possible interaction with the orbital debris environment. In Proceedings of the 54th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law, Bremen, Germany, 29 September–3 October 2003. IAC-03-IAA.5.2.05. [Google Scholar] [CrossRef]
  5. Aydın, V.A. Comparison of CNN-based methods for yoga pose classification. Turk. J. Eng. 2024, 8, 65–75. [Google Scholar] [CrossRef]
  6. Akgül, V.; Görmüş, K.S.; Kutoğlu, Ş.H.; Jin, S. Performance analysis and kinematic test of the BeiDou Navigation Satellite System (BDS) over coastal waters of Türkiye. Adv. Eng. Sci. 2024, 4, 1–14. [Google Scholar]
  7. Baudhanwala, D.; Mehta, D.; Kumar, V. Machine learning approaches for improving precipitation forecasting in the Ambica River basin of Navsari District, Gujarat. Water Pract. Technol. 2024, 19, 1315–1329. [Google Scholar] [CrossRef]
  8. Briffa, J.; Sinagra, E.; Blundell, R. Heavy metal pollution in the environment and their toxicological effects on humans. Heliyon 2020, 6, e04691. [Google Scholar] [CrossRef]
  9. Bakar, A.F.A.; Halim, A.A. Treatment of automotive wastewater by coagulation-flocculation using poly-aluminum chloride (PAC), ferric chloride (FeCl3) and aluminum sulfate (alum). AIP Conf. Proc. 2013, 1571, 524–529. [Google Scholar] [CrossRef]
  10. Camaj, A.; Haziri, A.; Nuro, A.; Ibrahimi, A.C. Levels of BTEX and Chlorobenzenes in water samples of White Drin River, Kosovo. Adv. Eng. Sci. 2024, 4, 45–53. Available online: https://publish.mersin.edu.tr/index.php/ades/article/view/1326 (accessed on 12 February 2024).
  11. Capizzi, G.; Lo Sciuto, G.; Napoli, C.; Tramontana, E.; Wozniak, M. Automatic classification of fruit defects based on co-occurrence matrix and neural networks. In Proceedings of the 2015 Federated Conference on Computer Science and Information, Lodz, Poland, 13–16 September 2015; pp. 861–867. [Google Scholar] [CrossRef]
  12. Çetin Taş, İ.; Bozdoğan, A.M.; Arıca, S. Application of Convolutional Neural Networks for Watermelon Detection in UAV Aerial Images: A Case Study. Turk. J. Eng. 2025, 9, 1–11. [Google Scholar] [CrossRef]
  13. Chang, S.; Ahmad, R.; Kwon, D.E.; Kim, J. Hybrid ceramic membrane reactor combined with fluidized adsorbents and scouring agents for hazardous metal-plating wastewater treatment. J. Hazard. Mater. 2020, 388, 121777. [Google Scholar] [CrossRef] [PubMed]
  14. Dursun, S.; Qasim, M.N. Measurements and modelling of PM2.5 level in summertime period in Novada Main Shopping Centre Konya, Turkey. Eng. Appl. 2022, 1, 19–32. Available online: https://publish.mersin.edu.tr/index.php/enap/article/view/314 (accessed on 15 January 2023).
  15. Demirgül, T.; Yılmaz, C.B.; Zıpır, B.N.; Kart, F.S.; Pehriz, M.F.; Demir, V.; Sevimli, M.F. Investigation of Turkey’s climate periods in terms of precipitation and temperature changes. Eng. Appl. 2022, 1, 80–90. Available online: https://publish.mersin.edu.tr/index.php/enap/article/view/320 (accessed on 18 June 2022).
  16. Daberdini, A.; Basholli, F.; Metaj, N. Simulation with the Mirone application for the construction of marine mechanical waves generated by possible seismic events in the territory of the Adriatic and Ionian seas. Adv. Eng. Sci. 2023, 3, 46–54. Available online: https://publish.mersin.edu.tr/index.php/ades/article/view/856 (accessed on 13 February 2023).
  17. Dursun, S.; Sarcan, A. Determination of water quality in Hadim District of Konya (Turkey) and the investigation of disinfection efficiency. Adv. Eng. Sci. 2022, 2, 101–108. Available online: https://publish.mersin.edu.tr/index.php/ades/article/view/89 (accessed on 16 January 2022).
  18. Ekiz, A.; Arica, S.; Bozdogan, A.M. Classification and Segmentation of Watermelon in Images Obtained by Unmanned Aerial Vehicle. In Proceedings of the ELECO 2019—11th International Conference on Electrical and Electronics Engineering, Bursa, Turkey, 28–30 November 2019; pp. 619–622. [Google Scholar] [CrossRef]
  19. El Gaayda, J.; Rachid, Y.; Titchou, F.E.; Barra, I.; Hsini, A.; Yap, P.S.; Akbour, R.A. Optimizing removal of chromium (VI) ions from water by coagulation process using central composite design: Effectiveness of grape seed as a green coagulant. Sep. Purif. Technol. 2023, 307, 122805. [Google Scholar] [CrossRef]
  20. Ezquerro, O.; Ortiz, G.; Pons, B.; Tena, M.T. Determination of benzene, toluene, ethylbenzene and xylenes in soils by multiple headspace solid-phase microextraction. J. Chromatogr. A 2004, 1035, 17–22. [Google Scholar] [CrossRef]
  21. Fen, İ.Ü.; Enst, B.; Der, K. Kadir SABANCI ve Ark. Available online: http://www.tuik.gov.tr/bitkiselapp/ (accessed on 30 June 2022).
  22. Fu, S.Y.; Wang, Z.R.; Shi, H.L.; Ma, L.H. The application of decommissioned GEO satellites to CAPS. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kitakyushu City, Japan, 10–13 April 2018; Volume 372, p. 012033. [Google Scholar] [CrossRef]
  23. Gangani, P.; Mangukiya, N.K.; Mehta, D.J.; Muttil, N.; Rathnayake, U. Evaluating the efficacy of different DEMs for application in flood frequency and risk mapping of the Indian Coastal River Basin. Climate 2023, 11, 114. [Google Scholar] [CrossRef]
  24. Gholami, A. Exploring drone classifications and applications: A review. Int. J. Eng. Geosci. 2024, 9, 418–442. [Google Scholar] [CrossRef]
  25. Gordani, O.; Simoni, A. Leveraging SVD for efficient image compression and robust digital watermarking. Adv. Eng. Sci. 2024, 4, 103–112. Available online: https://publish.mersin.edu.tr/index.php/ades/article/view/1496 (accessed on 3 September 2024).
  26. Gohil, M.; Mehta, D.; Shaikh, M. An integration of geospatial and fuzzy-logic techniques for multi-hazard mapping. Results Eng. 2024, 21, 101758. [Google Scholar] [CrossRef]
  27. Hosseini, S.S.; Bringas, E.; Tan, N.R.; Ortiz, I.; Ghahramani, M.; Shahmirzadi, M.A.A. Recent progress in development of high performance polymeric membranes and materials for metal plating wastewater treatment: A review. J. Water Process Eng. 2016, 9, 78–110. [Google Scholar] [CrossRef]
  28. Huang, J.; Yuan, F.; Zeng, G.; Li, X.; Gu, Y.; Shi, L.; Liu, W.; Shi, Y. Influence of pH on heavy metal speciation and removal from wastewater using micellar-enhanced ultrafiltration. Chemosphere 2017, 173, 199–206. [Google Scholar] [CrossRef] [PubMed]
  29. Ilhan, F.; Ulucan-Altuntas, K.; Avsar, Y.; Kurt, U.; Saral, A. Electrocoagulation process for the treatment of metal-plating wastewater: Kinetic modeling and energy consumption. Front. Environ. Sci. Eng. 2019, 13, 1–8. [Google Scholar] [CrossRef]
  30. Kocalar, A.C. Sinkholes caused by agricultural excess water using and administrative traces of the process. Adv. Eng. Sci. 2023, 3, 15–20. Available online: https://publish.mersin.edu.tr/index.php/ades/article/view/756 (accessed on 18 January 2023).
  31. Kalay, E.; Sarıoğlu, H.; Özkul, I. Design parameters of sand filtration systems in wastewater treatment process. Adv. Eng. Sci. 2021, 1, 34–42. Available online: https://publish.mersin.edu.tr/index.php/ades/article/view/23 (accessed on 24 August 2021).
  32. Mehta, D.; Prajapati, K.; Islam, M.N. Watershed delineation and land use land cover (LULC) study of Purna River in India. In India II: Climate Change Impacts, Mitigation and Adaptation in Developing Countries; Springer International Publishing: Cham, Switzerland, 2021; pp. 169–181. [Google Scholar]
  33. Mukasa, P.; Wakoli, C.; Faqeerzada, M.A.; Amanah, H.Z.; Kim, H.; Joshi, R.; Suh, H.K.; Kim, J.; Lee, H.; Kim, M.S.; et al. Nondestructive discrimination of seedless from seeded watermelon seeds by using multivariate and deep learning image analysis. Comput. Electron. Agric. 2022, 194, 106799. [Google Scholar] [CrossRef]
  34. Mehta, D.; Hadvani, J.; Kanthariya, D.; Sonawala, P. Effect of land use land cover change on runoff characteristics using curve number: A GIS and remote sensing approach. Int. J. Hydrol. Sci. Technol. 2023, 16, 1–16. [Google Scholar] [CrossRef]
  35. Reddy, N.M.; Saravanan, S.; Almohamad, H.; Al Dughairi, A.A.; Abdo, H.G. Effects of Climate Change on Streamflow in the Godavari Basin Simulated Using a Conceptual Model including CMIP6 Dataset. Water 2023, 15, 1701. [Google Scholar] [CrossRef]
  36. Nguyen, M.K.; Tran, V.S.; Pham, T.T.; Pham, H.G.; Hoang, B.L.; Nguyen, T.H.; Nguyen, T.H.; Tran, T.H.; Ngo, H.H. Fenton/ozone-based oxidation and coagulation processes for removing metals (Cu, Ni)-EDTA from plating wastewater. J. Water Process Eng. 2021, 39, 101836. [Google Scholar] [CrossRef]
  37. Oymak, A.; Tür, M.R.; Bouchiba, N. PV connected pumped-hydro storage system. Eng. Appl. 2022, 1, 46–54. Available online: https://publish.mersin.edu.tr/index.php/enap/article/view/316 (accessed on 18 June 2022).
  38. Öz, İ.; Yılmaz, Ü.C. Determination of coverage oscillation for inclined communication satellite. Sak. Univ. J. Sci. 2020, 24, 973–983. [Google Scholar] [CrossRef]
  39. Oz, I. Salınımlı yörünge haberleşme uydularında 2 eksen düzeltmeli kapsama alanı stabilizasyonu. J. Fac. Eng. Archit. Gazi Univ. 2022, 38, 219–229. [Google Scholar] [CrossRef]
  40. Palansooriya, K.N.; Yang, Y.; Tsang, Y.F.; Sarkar, B.; Hou, D.; Cao, X.; Meers, E.; Rinklebe, J.; Kim, K.H.; Ok, Y.S. Occurrence of contaminants in drinking water sources and the potential of biochar for water quality improvement: A review. Crit. Rev. Environ. Sci. Technol. 2020, 50, 549–611. [Google Scholar] [CrossRef]
  41. Pfaff, K.; Hildebrandt, L.H.; Leach, D.L.; Jacob, D.E.; Markl, G. Formation of the Wiesloch Mississippi Valley-type Zn-Pb-Ag deposit in the extensional setting of the Upper Rhinegraben, SW Germany. Miner. Deposita 2010, 45, 647–666. [Google Scholar] [CrossRef]
  42. Qasem, N.A.; Mohammed, R.H.; Lawal, D.U. Removal of heavy metal ions from wastewater: A comprehensive and critical review. Npj Clean Water 2021, 4, 36. [Google Scholar] [CrossRef]
  43. Raaj, S.; Gupta, V.; Singh, V.; Shukla, D.P. A novel framework for peak flow estimation in the Himalayan river basin by integrating SWAT model with machine learning based approach. Earth Sci. Inform. 2024, 17, 211–226. [Google Scholar] [CrossRef]
  44. Sattari, M.T.; Kamrani, Y.; Javidan, S.; Fathollahzadeh Attar, N.; Apaydın, H. Groundwater quality mapping based on the Wilcox Classification method for agricultural purposes: Qazvin Plain aquifer case. Turk. J. Eng. 2025, 9, 116–128. [Google Scholar] [CrossRef]
  45. Salamon, J.; Bello, J.P. Deep Convolutional Neural Networks and Data Augmentation for Environmental Sound Classification. IEEE Signal Process. Lett. 2017, 24, 279–283. [Google Scholar] [CrossRef]
  46. Tchounwou, P.B.; Yedjou, C.G.; Patlolla, A.K.; Sutton, D.J. Heavy metal toxicity and the environment. In Molecular, Clinical and Environmental Toxicology: Volume 3: Environmental Toxicology; Springer: Berlin/Heidelberg, Germany, 2012; Volume 3, pp. 133–164. [Google Scholar] [CrossRef]
  47. Verma, S.; Verma, M.K.; Prasad, A.D.; Mehta, D.; Azamathulla, H.M.; Muttil, N.; Rathnayake, U. Simulating the hydrological processes under multiple land use/land cover and climate change scenarios in the mahanadi reservoir complex, Chhattisgarh, India. Water 2023, 15, 3068. [Google Scholar] [CrossRef]
  48. Verma, S.; Kumar, K.; Verma, M.K.; Prasad, A.D.; Mehta, D.; Rathnayake, U. Comparative analysis of CMIP5 and CMIP6 in conjunction with the hydrological processes of reservoir catchment, Chhattisgarh, India. J. Hydrol. Reg. Stud. 2023, 50, 101533. [Google Scholar] [CrossRef]
  49. Verma, S.; Verma, M.K.; Prasad, A.D.; Mehta, D.J.; Islam, M.N. Modeling of uncertainty in the estimation of hydrograph components in conjunction with the SUFI-2 optimization algorithm by using multiple objective functions. Model. Earth Syst. Environ. 2024, 10, 61–79. [Google Scholar] [CrossRef]
  50. Wan Nurazwin Syazwani, R.; Muhammad Asraf, H.; Megat Syahirul Amin, M.A.; Nur Dalila, K.A. Automated image identification, detection and fruit counting of top-view pineapple crown using machine learning. Alex. Eng. J. 2022, 61, 1265–1276. [Google Scholar] [CrossRef]
  51. Witkowska, D.; Słowik, J.; Chilicka, K. Heavy metals and human health: Possible exposure pathways and the competition for protein binding sites. Molecules 2021, 26, 6060. [Google Scholar] [CrossRef] [PubMed]
  52. Yalçın, C.; Canlı, H. IP/Resistivity methods for Pb-Zn deposit exploration: A case study in Sudöşeği, (Simav-Kütahya, Türkiye). Eng. Appl. 2024, 3, 27–35. Available online: https://publish.mersin.edu.tr/index.php/enap/article/view/1503 (accessed on 15 February 2024).
  53. Yalçın, C. Geochemical and geological approach to the carbonate-hosted barite deposits in Dadağlı (Kahramanmaraş), Turkey. Eng. Appl. 2022, 1, 55–62. Available online: https://publish.mersin.edu.tr/index.php/enap/article/view/317 (accessed on 19 June 2022).
  54. Yoshioka, K.; Zhdanov, M.S. Three-dimensional nonlinear regularized inversion of the induced polarization data based on the Cole–Cole model. Phys. Earth Planet. Inter. 2005, 150, 29–43. [Google Scholar] [CrossRef]
  55. Zamora-Ledezma, C.; Negrete-Bolagay, D.; Figueroa, F.; Zamora-Ledezma, E.; Ni, M.; Alexis, F.; Guerrero, V.H. Heavy metal water pollution: A fresh look about hazards, novel and conventional remediation methods. Environ. Technol. Innov. 2021, 22, 101504. [Google Scholar] [CrossRef]
  56. Zhu, Y.; Fan, W.; Zhou, T.; Li, X. Removal of chelated heavy metals from aqueous solution: A review of current methods and mechanisms. Sci. Total Environ. 2019, 678, 253–266. [Google Scholar] [CrossRef]
Water 17 01171 g001
Figure 1. Godavari River basin’s geographic location of the study area.
Figure 1. Godavari River basin’s geographic location of the study area.
Water 17 01171 g001
Water 17 01171 g002
Figure 2. The Sacramento model’s schematic representation.
Figure 2. The Sacramento model’s schematic representation.
Water 17 01171 g002
Water 17 01171 g003
Figure 3. Schematic representation of the Australian Water Balance Model (AWBM).
Figure 3. Schematic representation of the Australian Water Balance Model (AWBM).
Water 17 01171 g003
Water 17 01171 g004
Figure 4. Schematic representation of the TANK model.
Figure 4. Schematic representation of the TANK model.
Water 17 01171 g004
Water 17 01171 g005
Figure 5. Schematic representation of the SIMHYD model.
Figure 5. Schematic representation of the SIMHYD model.
Water 17 01171 g005
Water 17 01171 g006
Figure 6. CHIRPS, PGF, TRMM, CPC, CMORPH, PERSIANN_CDR, MSWEP, and the Indian Meteorological Department’s monthly average precipitation.
Figure 6. CHIRPS, PGF, TRMM, CPC, CMORPH, PERSIANN_CDR, MSWEP, and the Indian Meteorological Department’s monthly average precipitation.
Water 17 01171 g006
Water 17 01171 g007
Figure 7. A comparison of the non-exceedance probability of the Indian Meteorological Department with seven-satellite precipitation estimates. (a) The precipitation estimates from the IMD and CHIRPS data, (b) Matched with IMD data for the remaining portion of TRMM, (c) PERSIANN_CDR had a high discrepancy compared to IMD data, (d) MSWEP was closely matched with IMD as compared to the remaining datasets.
Figure 7. A comparison of the non-exceedance probability of the Indian Meteorological Department with seven-satellite precipitation estimates. (a) The precipitation estimates from the IMD and CHIRPS data, (b) Matched with IMD data for the remaining portion of TRMM, (c) PERSIANN_CDR had a high discrepancy compared to IMD data, (d) MSWEP was closely matched with IMD as compared to the remaining datasets.
Water 17 01171 g007
Water 17 01171 g008
Figure 8. The coefficient of determination of datasets from 1998 to 2024: (A) POD of the seven-satellite precipitation estimation, (B) NSE of the seven datasets estimation, (C) FAR of the seven-satellite precipitation estimation, (D) the seven datasets estimation of precipitation.
Figure 8. The coefficient of determination of datasets from 1998 to 2024: (A) POD of the seven-satellite precipitation estimation, (B) NSE of the seven datasets estimation, (C) FAR of the seven-satellite precipitation estimation, (D) the seven datasets estimation of precipitation.
Water 17 01171 g008
Table 1. An overview of the 17 CMIP6 models used in the research.
Table 1. An overview of the 17 CMIP6 models used in the research.
ModelAtmospheric
Resolution		Institution
ACCESS-ESM1-51.9° × 1.2°The Commonwealth Scientific and Industrial Research Organization (CSIRO) and the Australian Bureau of Meteorology
ACCESS-CM21.87° × 1.25°The Commonwealth Scientific and Industrial Research Organization (CSIRO) and the Australian Bureau of Meteorology (BOM)
CanESM52.81° × 2.79°Canada’s Centre for Climate Modelling and Analysis, The Centre for Climate Change in Europe and the Mediterranean
EC-Earth31.3° × 0.9°Consortium EC-EARTH
EC-Earth3-Veg0.7° × 0.7°Consortium EC-EARTH
EC-Earth3-Veg-LR0.7° × 0.7°Consortium EC-EARTH
GFDL-ESM41.1° × 1.1°Geophysical Fluid Dynamics Laboratory
INM-CM5-01.3° × 1°The Institute of Numerical Mathematics
IPSL-CM6A-LR2° × 1.5°Institute of Pierre-Simon Laplace
MIROC61.41° × 1.41°R-CCS, AORI, NIES, and JAMSTEC
MPI-ESM1-2-HR0.93° × 0.93°The Max Planck Institute of Meteorology (MPI-M)
MPI-ESM1-2-LR0.93° × 0.93°The Max Planck Institute of Meteorology (MPI-M)
MRI-ESM2-00.9° × 1.3°Meteorological Research Institute
NorESM2-LM0.9° × 1.3°Meteorological Research Institute
NorESM2-MM1.3° × 1°The Taiwan Earth System Model, Version 1
Table 2. The Sacramento model parameters by default.
Table 2. The Sacramento model parameters by default.
ParameterDescriptionDefaultMinMax
LZPKThe proportion of water in LZFPM that drains daily as base flow.ZoneFreeWater
LZSKThe proportion of water in LZFSM that drains daily as base flow.6040600
UZKThe percentage of water in UZFWM that drains as daily interflow.0.0600.5
UZTWMMaximum Water Tension in the Upper Zone.103
UZFWMThe storage that serves as the source of water for interflow and the impetus for moving water to greater depths is known as the Upper Zone Free Water Maximum.40080
LZTWMWater Maximum for Lower Zone Tension.000.8
LZFSMMaximum Free Water Supplement in the Lower Zone.0.010.0010.015
LZFPMPrimary Maximum for Lower Zone Free Water.0.050.030.2
PFREERecharging the lower zone’s free water reservoirs requires a minimum percentage of percolation from the upper zone to the lower zone.0.30.20.5
REXPAn exponent that calculates how quickly the percolation rate changes as the lower zone water storage changes5025125
ZPERCThe maximal percolation rate is determined by the proportionate increase in Pbase401075
SIDEThe non-channel base flow ratio.13075300
Table 3. The Australian Water Balance Model’s parameter values by default.
Table 3. The Australian Water Balance Model’s parameter values by default.
ParameterDescriptionDefaultMinMax
KSurfRecession constant of surface flow1500500
KBaseRecession constant for base flow700200
C3Surface store capacity 3 (in mm)7050
C2Surface store capacity 2 (in mm)0.3501
C1Surface store capacity 1 (in mm)0.9501
BFIIndex of base flow0.13401
A2Surface storage 2’s partial area0.3501
A1Surface store 1’s partial area0.3501
KSurfRecession constant of surface flow0.43301
Table 4. Parameter values by default for the TANK model.
Table 4. Parameter values by default for the TANK model.
ParameterMinimumDefault ValueMaximum
First outlet height of the first tank (H11) (in mm)00500
Second outlet height of first tank (H12) (in mm)00300
First outlet height of the second, third, and fourth
tanks (H21, H31, and H41) (in mm)		00100
Coefficient of runoff from various tank outlets
(a11, a12, a21, a31, and a41)		00.21
Coefficient of Evaporation (α)00.11
Coefficient of infiltration in tanks 1, 2, and 3 (b1, b2, and b3)00.21
Tank’s water level (C1, C2, C3, and C4) (in mm)020100
Table 5. SIMHYD’s default model parameter values.
Table 5. SIMHYD’s default model parameter values.
ParameterMinimumDefault ValueMaximum
Baseflow coefficient0.00.91.0
Unaffected Threshold0.01.55.0
Infiltration Coefficient0.00.21.0
Infiltration Form1320500
Interflow Coefficient0.00.31.0
Prior Fraction015
Capacity of the Rainfall Interception Store0200400
Recharge Coefficient 0310
Soil Moisture Store Capacity0.00.11.0
Table 6. Various gridded precipitation datasets used in this study area.
Table 6. Various gridded precipitation datasets used in this study area.
DATA Temporal Resolution Availability Link
IMD 0.25° and D 1951–2024 The website https://www.imdpune.gov.in/, accessed on 7 April 2025
CHIRPS 0.05° and D and M 1981–present CHIRPS 2.0: https://data.chc.ucsb.edu/products/, accessed on 7 April 2025
PGF 0.25° and D 1948–2020 https://hydrology.soton.ac.uk/, accessed on 7 April 2025
TRMM 0.25° and 3H, D and M 1998–2023 The summary can be seen at https://disc.gsfc.nasa.gov/datasets/TRMM_3B42_Daily_7, accessed on 7 April 2025
CPC 0.5° and D 1979–present Balprecip.html https://psl.noaa.gov/data/gridded/data.cpc.glo, accessed on 7 April 2025
CMORPH 0.25° and 30 min, 1H and D 1998–2024https://www.ncei.noaa.gov/products/climate-data-records, accessed on 7 April 2025
PERSIA NN_CDR 0.25° and D and M1983–Present https://chrsdata.eng.uci.edu/, accessed on 7 April 2025
MSWEP0.1° and 3H, D and M 1979–2024 Gloh2o.org/mswep/’s website
Table 7. Monthly precipitation was calculated for each of the seven dataset’s grid cells.
Table 7. Monthly precipitation was calculated for each of the seven dataset’s grid cells.
DATANSER2MBEMAERMSE
CHIRPS0.7680.8127.50534.32461.519
PGF0.720.768−2.43335.50266.775
TRMM0.7680.8469.12631.52857.413
CPC0.7720.801−0.77433.24761.58
CMORPH0.7670.8150.15732.66360.16
PERSIANN_CDR0.6670.8159.33235.93465.177
MSWEP0.8060.8315.53131.79456.734
Table 8. All conceptual models’ parameters were calibrated.
Table 8. All conceptual models’ parameters were calibrated.
SacramentoAWBMTANKSIMHYD
ADIM 0.031A1 0.014H11 119.60base flow Coefficient 0.373
LZFP 49.608A2 0.433 a11 0.169 Impervious Threshold 4.431
LZFS M 49.608 BFI 0.298 a12 0.204 Infiltration Coefficient 371.76
LZPK 0.118 C1 1.569 a21 0.812 Infiltration Shape 0.196
LZSK 0.729 C2 130.1 96 a31 0.847 Interflow Coefficient 0.000
LZTW M 117.647 C3 252.9 41 a41 0.478 previous Fraction 1.000
PCTI M 0.000 KBase 0.561 alpha 1.000 rainfall Interception Capacity 4.569
PFREE 0.184 KSurf 0.627 b1 0.031 Recharge Coefficient 0.741
REXP 1.529 b2 0.337Soil Moisture Store Capacity 169.29 0
RSERV 0.300 b3 0.027
SARVA 0.010 C1 51.765
SIDE 0.000 C2 18.824
SSOUT 0.001 C3 52.549
UZFWM 79.373 C4 26.667
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ande, R.; Pandugula, C.; Mehta, D.; Vankayalapati, R.; Birbal, P.; Verma, S.; Azamathulla, H.M.; Nanavati, N. Understanding Climate Change Impacts on Streamflow by Using Machine Learning: Case Study of Godavari Basin. Water 2025, 17, 1171. https://doi.org/10.3390/w17081171

AMA Style

Ande R, Pandugula C, Mehta D, Vankayalapati R, Birbal P, Verma S, Azamathulla HM, Nanavati N. Understanding Climate Change Impacts on Streamflow by Using Machine Learning: Case Study of Godavari Basin. Water. 2025; 17(8):1171. https://doi.org/10.3390/w17081171

Chicago/Turabian Style

Ande, Ravi, Chandrashekar Pandugula, Darshan Mehta, Ravikumar Vankayalapati, Prashant Birbal, Shashikant Verma, Hazi Mohammad Azamathulla, and Nisarg Nanavati. 2025. "Understanding Climate Change Impacts on Streamflow by Using Machine Learning: Case Study of Godavari Basin" Water 17, no. 8: 1171. https://doi.org/10.3390/w17081171

APA Style

Ande, R., Pandugula, C., Mehta, D., Vankayalapati, R., Birbal, P., Verma, S., Azamathulla, H. M., & Nanavati, N. (2025). Understanding Climate Change Impacts on Streamflow by Using Machine Learning: Case Study of Godavari Basin. Water, 17(8), 1171. https://doi.org/10.3390/w17081171

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop