Evaluation of Leaf Water Content in Watermelon Based on Hyperspectral Reflectance
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Culture
2.2. Hyperspectral Reflectance Measurements
2.3. Determination of Plant Leaf Water Content (LWC)
2.4. Calculation of Spectral Vegetation Indices
2.5. Model Training and Evaluation
3. Results
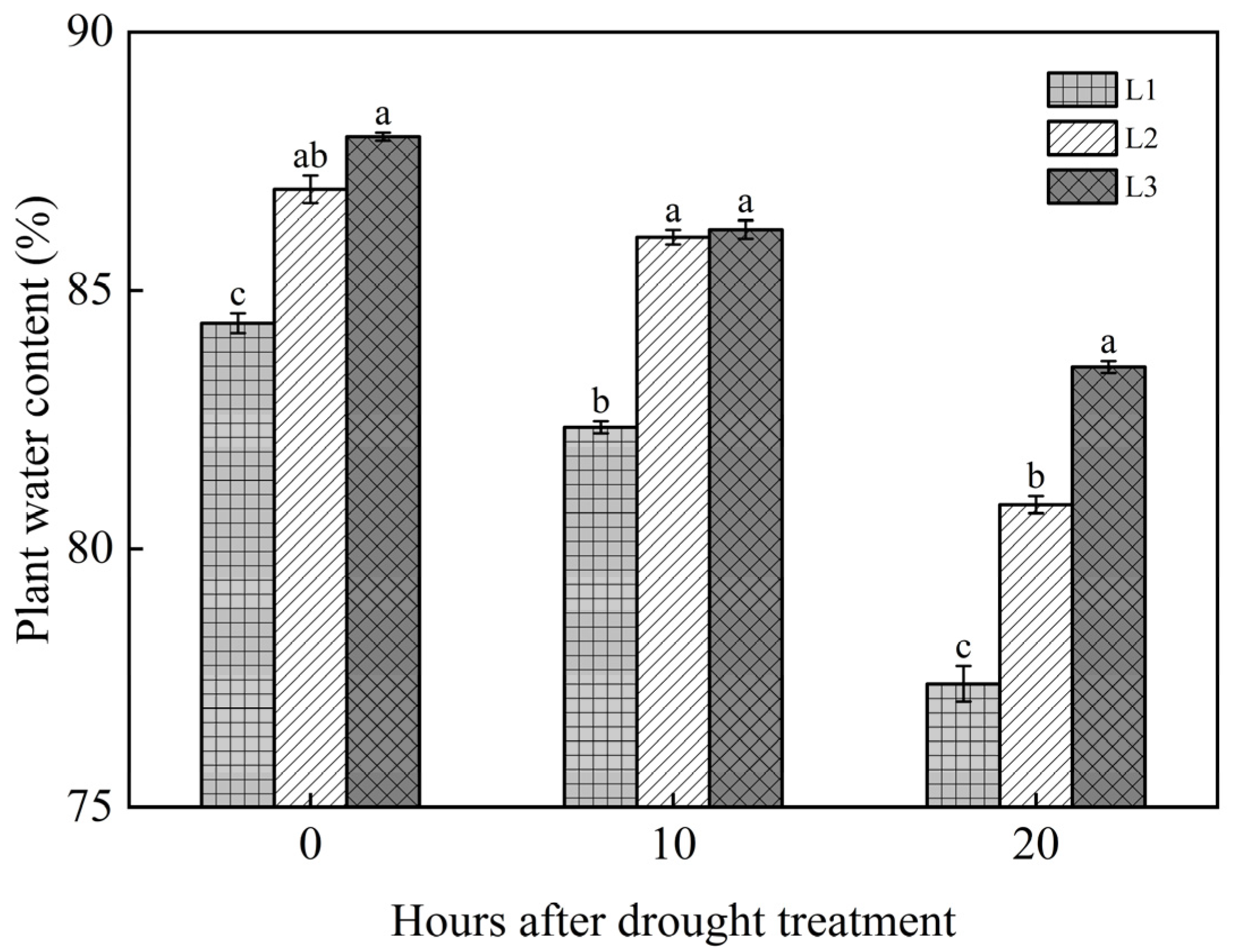
3.1. Dynamic Changes of LWC in Watermelon Plants at Different Leaf Layers
3.2. Spectral Reflectance of Watermelon Leaf Under Different Drought Treatments
3.3. Relationships Between Watermelon Plant LWC and Spectral Indices
3.4. Simple Linear Regression Modeling Based on Single Spectral Index
3.5. Machine Learning Modeling Based on Eleven Spectral Indices
3.6. Machine Learning Modeling Based on Full Wavelength
4. Discussion
4.1. Changes of LWC Under Different Drought Treatments
4.2. Changes in Leaf Hyperspectral Reflectance Under Different Drought Treatments
4.3. Relationships Between LWC of Watermelon Plant and Spectral Indices
4.4. The Optimal Leaf Layer for the LWC Prediction of Watermelon Plants
4.5. Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SWIR | short-wave infrared |
| VNIR | visible and near-infrared |
| LWC | leaf water content |
| FW | fresh weight |
| DW | dry weight |
| ML | machine learning |
| RF | Random Forest |
| AdaBoost | Adaptive Boosting |
| Catboost | Categorical Boosting |
| GBDT | Gradient Boosting Decision Tree |
| RMSE | root mean square error |
| MAE | mean absolute error |
| RWC | relative water content |
References
- Junttila, S.; Hölttä, T.; Saarinen, N.; Kankare, V.; Yrttimaa, T.; Hyyppä, J.; Vastaranta, M. Close-Range hyperspectral spectroscopy reveals leaf water content dynamics. Remote Sens. Environ. 2022, 277, 113071. [Google Scholar] [CrossRef]
- Boyer, J.S. Plant productivity and environment. Science 1982, 218, 443–448. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Lin, S.; Zhang, B.; Wei, Z.; Liu, L.; Han, N.; Cai, J.; Chen, H. Winter wheat canopy water content monitoring based on spectral transforms and “three-edge” parameters. Agric. Water Manag. 2020, 240, 106306. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, J.R.; Riaño, D.; Carlisle, E.; Ustin, S.; Smart, D.R. Evaluation of hyperspectral indexes to detect grapevine water status in vineyards. Am. J. Enol. Vitic. 2007, 58, 302–317. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Bozzolo, A.; Wilkins, J.L.; Kwasniewski, M.T. Early detection of plant physiological responses to different levels of water stress using reflectance spectroscopy. Remote Sens. 2017, 9, 745. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Wang, A.Z. Comparison of various approaches for estimating leaf water content and stomatal conductance in different plant species using hyperspectral data. Ecol. Indic. 2022, 142, 109278. [Google Scholar] [CrossRef]
- Rallo, G.; Minacapilli, M.; Ciraolo, G.; Provenzano, G. Detecting crop water status in mature olive groves using vegetation spectral measurements. Biosyst. Eng. 2014, 128, 52–68. [Google Scholar] [CrossRef]
- Thomas, J.R.; Namken, L.N.; Oerther, G.F.; Brown, R.G. Estimating leaf water content by reflectance measurements. Agron. J. 1971, 63, 845–847. [Google Scholar] [CrossRef]
- Carter, G.A. Primary and secondary effects of water content on the spectral reflectance of leaves. Am. J. Bot. 1991, 78, 916–924. [Google Scholar] [CrossRef]
- Pôças, I.; Rodrigues, A.; Gonçalves, S.; Costa, P.M.; Gonçalves, I.; Pereira, L.S.; Cunha, M. Predicting grapevine water status based on hyperspectral reflectance vegetation indices. Remote Sens. 2015, 7, 16460–16479. [Google Scholar] [CrossRef]
- Holben, B.N.; Schutt, J.B.; McMurtrey, J. Leaf water stress detection utilizing thematic mapper bands 3, 4 and 5 in soybean plants. Int. J. Remote Sens. 1983, 4, 289–297. [Google Scholar] [CrossRef]
- Inoue, Y.; Morinaga, S.; Shibayama, M. Non-destructive estimation of water status of intact crop leaves based on spectral reflectance measurements. Jpn. J. Crop Sci. 1993, 62, 462–469. [Google Scholar]
- Peñuelas, J.; Inoue, Y. Reflectance indices indicative of changes in water and pigment contents of peanut and wheat leaves. Photosynthetica 1999, 36, 355–360. [Google Scholar] [CrossRef]
- Peñuelas, J.; Pinol, J.; Ogaya, R.; Filella, I. Estimation of plant water concentration by the reflectance water index WI (900/970). Int. J. Remote Sens. 1997, 18, 2869–2875. [Google Scholar] [CrossRef]
- Khan, A.; Vibhute, A.D.; Mali, S.; Patil, C.H. A systematic review on hyperspectral imaging technology with a machine and deep learning methodology for agricultural applications. Ecol. Inform. 2022, 69, 101678. [Google Scholar] [CrossRef]
- Shoko, C.; Mutanga, O.; Dube, T.; Slotow, R. Characterizing the spatio-temporal variations of C3 and C4 dominated grasslands aboveground biomass in the Drakensberg, South Africa. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 51–60. [Google Scholar]
- Das, B.; Sahoo, R.N.; Pargal, S.; Krishna, G.; Verma, R.; Chinnusamy, V.; Sehgal, V.K.; Gupta, V.K. Comparison of different uni- and multi-variate techniques for monitoring leaf water status as an indicator of water-deficit stress in wheat through spectroscopy. Biosyst. Eng. 2017, 160, 69–83. [Google Scholar] [CrossRef]
- Mirzaie, M.; Darvishzadeh, R.; Shakiba, A.; Matkan, A.A.; Atzberger, C.; Skidmore, A. Comparative analysis of different uni- and multi-variate methods for estimation of vegetation water content using hyper-spectral measurements. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 1–11. [Google Scholar]
- Li, H.; Yang, X.; Chen, H.; Cui, Q.; Yuan, G.; Han, X.; Wei, C.; Zhang, Y.; Ma, J.; Zhang, X. Water requirement characteristics and the optimal irrigation schedule for the growth, yield, and fruit quality of watermelon under plastic film mulching. Sci. Hortic. 2018, 241, 74–82. [Google Scholar]
- Wang, X.C.; Liu, R.; Luo, J.; Zhu, P.; Wang, Y.; Pan, X.C.; Shu, L.Z. Effects of water and NPK fertigation on watermelon yield, quality, irrigation-water, and nutrient use efficiency under alternate partial root-zone drip irrigation. Agric. Water Manage. 2022, 271, 107785. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the Third ERTS Symposium, Washington, DC, USA, 10–14 December 1973; NASA: Washington, DC, USA, 1974; pp. 310–317. [Google Scholar]
- Demetriades-Shah, T.H.; Steven, M.D.; Clark, J.A. High resolution derivative spectra in remote sensing. Remote Sens. Environ. 1990, 33, 55–64. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar]
- Kim, M.S.; Daughtry, C.S.T.; Chappelle, E.W.; Mcmurtrey, J.E.; Walthall, C.L. The use of high spectral resolution bands for estimating absorbed photosynthetically active radiation. In Proceedings of the 6th International Symposium on Physical Measurements and Signatures in Remote Sensing, Val D’Isere, France, 17–21 January 1994; pp. 299–306. [Google Scholar]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar]
- Wang, Z.J.; Wang, J.H.; Liu, L.Y.; Huang, W.J.; Zhao, C.J.; Wang, C.Z. Prediction of grain protein content in winter wheat (Triticum aestivum L.) using plant pigment ratio (PPR). Field Crops Res. 2004, 90, 311–321. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1996, 55, 119–139. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of feature selection and CatBoost for prediction: The first application to the estimation of aboveground biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Ding, L.; Li, Y.; Li, Y.; Sheng, Q.; Guo, S. Effects of drought stress on photosynthesis and water status of rice leaves. Chin. J. Rice Sci. 2014, 28, 65–70. [Google Scholar]
- Wang, F.; He, Q.; Zhou, G. Leaf water content at different positions and its relationship with photosynthesis when consecutive drought treatments are applied to summer maize from the 3-leaf stage. Acta Ecol. Sin. 2019, 39, 254–264. [Google Scholar]
- Tian, Y.; Cao, W.; Wang, S.; Zhu, Y. Variation of water and nitrogen contents & photosynthesis at different position leaves of rice under different soil water and nitrogen conditions. Acta Agron. Sin. 2004, 30, 1129–1134. [Google Scholar]
- Zhou, S.L.; Xie, R.Z.; Jiang, H.R.; Wang, J.H. Study on the relationship between canopy relative depth index and water content in different leaf layers of maize. Crops 2005, 5, 13–15. [Google Scholar]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar]
- Thomas, J.R.; Gausman, H.W. Leaf reflectance vs. leaf chlorophyll and carotenoid concentrations for eight crops. Agron. J. 1977, 69, 799–802. [Google Scholar] [CrossRef]
- Bowman, W.D. The relationship between leaf water status, gas exchange, and spectral reflectance in cotton leaves. Remote Sens. Environ. 1989, 30, 249–255. [Google Scholar]
- Gausman, H.W.; Allen, W.A. Optical parameters of leaves of 30 plant species. Plant Physiol. 1973, 52, 57–62. [Google Scholar]
- Jacquemoud, S.; Baret, F. Prospect: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Ustin, S.L.; Verdebout, J.; Schmuck, G.; Andreoli, G.; Hosgood, B. Estimating leaf biochemistry using the PROSPECT leaf optical properties model. Remote Sens. Environ. 1996, 56, 194–202. [Google Scholar] [CrossRef]
- Carter, G.A. Responses of leaf spectral reflectance to plant stress. Am. J. Bot. 1993, 80, 239–243. [Google Scholar] [CrossRef]
- Sun, P.; Grignetti, A.; Liu, S.; Casacchia, R.; Salvatori, R.; Pietrini, F.; Centritto, M. Associated changes in physiological parameters and spectral reflectance indices in olive (Olea europaea L.) leaves in response to different levels of water stress. Int. J. Remote Sens. 2008, 29, 1725–1743. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, Q.; Zheng, C. Best hyperspectral indices for tracing leaf water status as determined from leaf dehydration experiments. Ecol. Indic. 2015, 54, 96–107. [Google Scholar] [CrossRef]
- Tian, Y.C.; Zhu, Y.; Cao, W.X.; Dai, Y.B. Relationship between canopy reflectance and plant water status of wheat. Chin. J. Appl. Ecol. 2004, 11, 2072–2076. [Google Scholar]
- Liu, C.; Sun, P.S.; Liu, S.R. A comparison of spectral reflectance indices in response to water: A case study of Quercus aliena var. acuteserrata. Chin. J. Plant Ecol. 2017, 41, 850–861. [Google Scholar]
- Han, G. Monitoring Water Status with Hyperspectral Sensing in Wheat. Master’s Thesis, Nanjing Agricultural University, Nanjing, China, 2011; pp. 41–49. [Google Scholar]
- Xiang, J.L.; Yao, X.F.; Liu, Q.; Huang, D.F.; Chang, L.Y. Hyperspectral based monitoring of leaf water content in different leaf positions of muskmelon in greenhouse. Jiangsu Agric. Sci. 2018, 46, 105–109. [Google Scholar]




| Vegetation Index | Equation | References |
|---|---|---|
| Normalized difference vegetation index (NDVI) | (RNIR − RRed)/(RNIR + RRed) | [21] |
| Difference vegetation index (DVI) | RNIR − RRed | [22] |
| Enhance vegetation index (EVI) | 2.5(RNIR − RRed)/(RNIR + 6RRed − 7.5RBlue + 1) | [23] |
| Chlorophyll absorption ratio index (CARI) | [|(670a + R670 + b)|/(a2 + 1)0.5](R700/R670) | [24] |
| Photochemical reflectance index (PRI) | (R531 − R570)/(R531 + R570) | [25] |
| Renormalized difference vegetation index (RDVI) | (NDVI × DVI)0.5 | [26] |
| Ratio vegetation index (RVI) | RNIR/RRed | [27] |
| Soil adjusted vegetation index (SAVI) | 1.5(RNIR − RGreen)/(RNIR + RGreen + 0.5) | [28] |
| Structure insensitive pigment index (SIPI) | (R800 − R451)/(R800 + R680) | [29] |
| Triangular vegetation coefficient (TVI) | 0.5[120(R750 − R550) − 200(R670 − R550)] | [30] |
| Water index (WI) | R900/R970 | [15] |
| LWC | NDVI | DVI | EVI | CARI | PRI | RDVI | RVI | SAVI | SIPI | TVI | WI | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LWC | 1.000 | |||||||||||
| NDVI | −0.024 | 1.000 | ||||||||||
| DVI | 0.358 * | 0.736 *** | 1.000 | |||||||||
| EVI | 0.105 | −0.016 | 0.232 | 1.000 | ||||||||
| CARI | 0.368 * | −0.302 | −0.151 | −0.067 | 1.000 | |||||||
| PRI | −0.205 | −0.19 | −0.484 ** | −0.804 *** | 0.424 * | 1.000 | ||||||
| RDVI | 0.184 | 0.928 *** | 0.936 *** | 0.12 | −0.241 | −0.366 * | 1.000 | |||||
| RVI | −0.021 | 0.998 *** | 0.743 *** | −0.021 | −0.303 | −0.183 | 0.93 *** | 1.000 | ||||
| SAVI | 0.128 | 0.962 *** | 0.894 *** | 0.084 | −0.261 | −0.322 | 0.995 *** | 0.963 *** | 1.000 | |||
| SIPI | −0.029 | 0.084 | −0.098 | −0.976 *** | −0.024 | 0.695 *** | −0.01 | 0.092 | 0.016 | 1.000 | ||
| TVI | 0.433 ** | 0.643 *** | 0.932 *** | 0.275 | 0.193 | −0.372 * | 0.85 *** | 0.648 *** | 0.805 *** | −0.179 | 1.000 | |
| WI | 0.595 *** | −0.2 | 0.072 | 0.051 | 0.13 | −0.082 | −0.065 | −0.185 | −0.104 | −0.023 | 0.051 | 1.000 |
| Spectral Indices | Leaf Layers | R2 (Training) | R2 (Testing) | RMSE (%) (Training) | RMSE (%) (Testing) | Modeling Equations | Test Equations |
|---|---|---|---|---|---|---|---|
| NDVI | L1 | 0.0074 | 0.0166 | 2.19 | 1.77 | y = −0.1613x + 0.9503 | y = 0.1782x + 0.7126 |
| L2 | 0.0259 | 0.0479 | 3.13 | 3.63 | y = −0.3867x + 1.1137 | y = 0.6296x + 0.3865 | |
| L3 | 0.0049 | 0.1057 | 3.31 | 2.98 | y = −0.2172x + 0.9562 | y = −1.4048x + 1.7923 | |
| DVI | L1 | 0.0010 | 0.0239 | 2.19 | 1.78 | y = −0.0469x + 0.8658 | y = 0.1710x + 0.7327 |
| L2 | 0.1370 | 0.1402 | 2.88 | 3.45 | y = 1.0591x + 0.2054 | y = 1.0026x + 0.2178 | |
| L3 | 0.0314 | 0.0269 | 3.26 | 2.90 | y = 0.4050x + 0.5602 | y = −0.3813x + 1.0391 | |
| EVI | L1 | 0.0209 | 0.3693 | 2.18 | 1.47 | y = 0.4096x + 0.7034 | y = 1.6896x + 0.2859 |
| L2 | 0.0682 | 0.0596 | 3.25 | 3.60 | y = 1.0146x + 0.5125 | y = −1.1967x + 1.2145 | |
| L3 | 0.0075 | 0.1273 | 3.30 | 2.75 | y = 0.3193x + 0.6994 | y = −1.3808x + 1.2623 | |
| CARI | L1 | 0.0344 | 0.0344 | 2.18 | 1.78 | y = 0.0694x + 0.7978 | y = 0.0487x + 0.8068 |
| L2 | 0.1957 | 0.0465 | 2.81 | 3.50 | y = 0.2059x + 0.7239 | y = 0.1454x + 0.7388 | |
| L3 | 0.0792 | 0.0046 | 3.14 | 2.91 | y = 0.2733x + 0.6554 | y = −0.0808x + 0.8561 | |
| PRI | L1 | 0.0357 | 0.1448 | 2.16 | 1.71 | y = −0.4821x + 0.8130 | y = −0.7617x + 0.8004 |
| L2 | 0.0699 | 0.0101 | 3.17 | 3.71 | y = −1.002x + 0.7953 | y = −0.4076x + 0.8035 | |
| L3 | 0.0269 | 0.0001 | 3.25 | 2.94 | y = −0.6457x + 0.7722 | y = −0.0088x + 0.8100 | |
| RDVI | L1 | 0.0033 | 0.0228 | 2.19 | 1.77 | y = −0.0983x + 0.9014 | y = 0.1921x + 0.7118 |
| L2 | 0.0122 | 0.0979 | 3.11 | 3.53 | y = 0.3166x + 0.6396 | y = 0.8882x + 0.2484 | |
| L3 | 0.0082 | 0.0622 | 3.31 | 2.91 | y = 0.2597x + 0.6356 | y = −0.8325x + 1.3492 | |
| RVI | L1 | 0.0116 | 0.0142 | 2.18 | 1.77 | y = −0.0091x + 0.8894 | y = 0.0076x + 0.794 |
| L2 | 0.0235 | 0.0463 | 3.14 | 3.64 | y = −0.0168x + 0.9384 | y = 0.0287x + 0.6639 | |
| L3 | 0.0022 | 0.0926 | 3.31 | 2.97 | y = −0.0064x + 0.8407 | y = −0.0585x + 1.1411 | |
| SAVI | L1 | 0.0043 | 0.0217 | 2.19 | 1.76 | y = −0.1163x + 0.9148 | y = 0.1933x + 0.7084 |
| L2 | 0.0011 | 0.0841 | 3.11 | 3.56 | y = 0.0907x + 0.7847 | y = 0.8293x + 0.2751 | |
| L3 | 0.0029 | 0.0789 | 3.31 | 2.89 | y = 0.1604x + 0.6977 | y = −1.0247x + 1.4889 | |
| SIPI | L1 | 0.0168 | 0.3689 | 2.19 | 1.44 | y = −0.0692x + 0.8898 | y = −0.2953x + 1.0609 |
| L2 | 0.0391 | 0.1146 | 3.25 | 3.54 | y = −0.1365x + 0.9477 | y = 0.2978x + 0.5984 | |
| L3 | 0.0028 | 0.1609 | 3.31 | 2.70 | y = −0.0367x + 0.8317 | y = 0.3053x + 0.5826 | |
| TVI | L1 | 0.0005 | 0.0508 | 2.19 | 1.74 | y = −0.0005x + 0.857 | y = 0.0042x + 0.6693 |
| L2 | 0.2288 | 0.1469 | 2.78 | 3.42 | y = 0.0201x + 0.0593 | y = 0.0187x + 0.091 | |
| L3 | 0.0315 | 0.0676 | 3.27 | 2.94 | y = 0.006x + 0.5707 | y = −0.0101x + 1.2033 | |
| WI | L1 | 0.0415 | 0.1537 | 2.19 | 1.86 | y = 0.7306x + 0.0746 | y = 1.4071x − 0.6413 |
| L2 | 0.2939 | 0.4524 | 2.59 | 2.76 | y = 2.5300x − 1.7951 | y = 3.4248x − 2.7426 | |
| L3 | 0.0488 | 0.0292 | 3.24 | 2.99 | y = −1.7114x + 2.5663 | y = −1.1966x + 2.0416 |
| Algorithms | Leaf Layers | R2 (Training) | R2 (Testing) | RMSE (%) (Training) | RMSE (%) (Testing) | MAE (%) (Training) | MAE (%) (Testing) | Cross-Validation Scores (R2) |
|---|---|---|---|---|---|---|---|---|
| RF | L1 | 0.7367 | 0.7582 | 2.04 | 1.94 | 1.27 | 1.52 | 0.4099 |
| L2 | 0.8576 | 0.8290 | 1.62 | 2.12 | 1.26 | 1.76 | 0.6324 | |
| L3 | 0.8033 | 0.7995 | 1.32 | 1.63 | 0.88 | 1.22 | 0.5792 | |
| AdaBoost | L1 | 0.8816 | 0.7797 | 1.37 | 1.85 | 0.94 | 1.40 | 0.4913 |
| L2 | 0.9504 | 0.8760 | 0.96 | 1.80 | 0.78 | 1.49 | 0.6953 | |
| L3 | 0.9475 | 0.8433 | 0.68 | 1.44 | 0.51 | 1.03 | 0.6266 | |
| GBDT | L1 | 0.4706 | 0.3101 | 2.89 | 3.27 | 2.43 | 2.59 | 0.2280 |
| L2 | 0.6763 | 0.5790 | 2.45 | 3.33 | 1.97 | 2.96 | 0.3705 | |
| L3 | 0.6318 | 0.5720 | 1.81 | 2.38 | 1.34 | 2.01 | 0.2972 | |
| Catboost | L1 | 0.6893 | 0.6481 | 2.21 | 2.34 | 1.68 | 1.80 | 0.6003 |
| L2 | 0.7916 | 0.7114 | 1.96 | 2.75 | 1.60 | 2.40 | 0.7485 | |
| L3 | 0.7554 | 0.6638 | 1.47 | 2.11 | 1.10 | 1.77 | 0.6907 |
| Algorithms | Leaf Layers | R2 (Training) | R2 (Testing) | RMSE (%) (Training) | RMSE (%) (Testing) | MAE (%) (Training) | MAE (%) (Testing) | Cross-Validation Scores (R2) |
|---|---|---|---|---|---|---|---|---|
| L1 | 0.8280 | 0.7864 | 1.65 | 1.82 | 1.00 | 1.33 | 0.4276 | |
| RF | L2 | 0.9695 | 0.9555 | 0.75 | 1.08 | 0.60 | 0.87 | 0.9022 |
| L3 | 0.9303 | 0.9048 | 0.79 | 1.12 | 0.52 | 0.87 | 0.8087 | |
| L1 | 0.9479 | 0.8166 | 0.91 | 1.69 | 0.61 | 1.32 | 0.5004 | |
| AdaBoost | L2 | 0.9927 | 0.9787 | 0.37 | 0.75 | 0.31 | 0.60 | 0.9636 |
| L3 | 0.9892 | 0.9417 | 0.31 | 0.88 | 0.24 | 0.57 | 0.8154 | |
| L1 | 0.6589 | 0.6379 | 2.32 | 2.37 | 1.87 | 1.93 | 0.1651 | |
| GBDT | L2 | 0.8230 | 0.7785 | 1.81 | 2.41 | 1.44 | 2.15 | 0.6002 |
| L3 | 0.7511 | 0.7227 | 1.49 | 1.92 | 0.99 | 1.48 | 0.5292 | |
| L1 | 0.7575 | 0.7007 | 1.96 | 2.16 | 1.45 | 1.69 | 0.6372 | |
| Catboost | L2 | 0.9039 | 0.8556 | 1.33 | 1.95 | 1.03 | 1.68 | 0.8817 |
| L3 | 0.8447 | 0.7923 | 1.17 | 1.66 | 0.77 | 1.29 | 0.8030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Wang, P.; Chen, B.; Yi, L.; Dai, Z.; Xiao, B. Evaluation of Leaf Water Content in Watermelon Based on Hyperspectral Reflectance. Water 2025, 17, 1142. https://doi.org/10.3390/w17081142
Wu D, Wang P, Chen B, Yi L, Dai Z, Xiao B. Evaluation of Leaf Water Content in Watermelon Based on Hyperspectral Reflectance. Water. 2025; 17(8):1142. https://doi.org/10.3390/w17081142
Chicago/Turabian StyleWu, Dan, Penghui Wang, Bing Chen, Licong Yi, Zhaoyi Dai, and Bo Xiao. 2025. "Evaluation of Leaf Water Content in Watermelon Based on Hyperspectral Reflectance" Water 17, no. 8: 1142. https://doi.org/10.3390/w17081142
APA StyleWu, D., Wang, P., Chen, B., Yi, L., Dai, Z., & Xiao, B. (2025). Evaluation of Leaf Water Content in Watermelon Based on Hyperspectral Reflectance. Water, 17(8), 1142. https://doi.org/10.3390/w17081142






