Robust Wetting and Drying with Discontinuous Galerkin Flood Model on Unstructured Triangular Meshes
Abstract
1. Introduction
2. Shallow-Water Equations
3. Robust RKDG Flood Model on Unstructured Triangular Meshes
3.1. Second-Order RKDG Method
3.2. Source Terms Discretization
3.3. Preserving Positivity and Wetting and Drying
- Evaluate the local flow variables and at each Gaussian point, , , , , , and , via Equation (3) in order to evaluate the Riemann fluxes at the interfaces.
- Evaluate the associated velocities:However, if the water depth is below , the velocities are set to zero to prevent unphysical high velocities that can occur in very shallow-water.
- Produce a locally continuous topography at each interface as follows:
- Reconstruct the water depths and at cell interfaces as follows:to maintain the positivity of the water depth.
- Compute the associated Riemann states of the flow discharge according to the depth in a way that is positivity-preserving:
- Finally, solve the friction term using a semi-implicit scheme as proposed in [55] to mitigate numerical instabilities that may arise during rapid changes in flow depth or velocity.
4. Model Validation
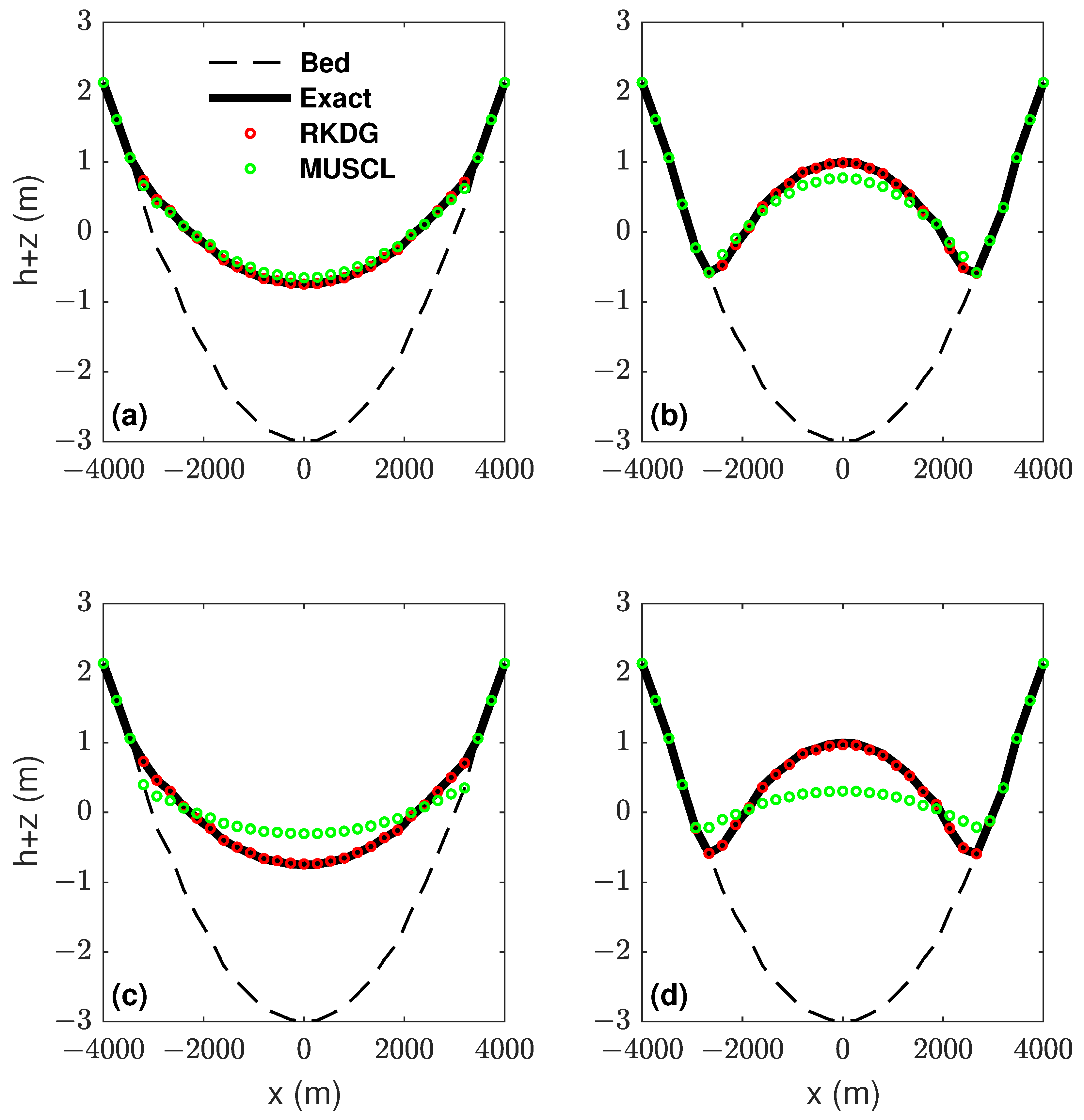
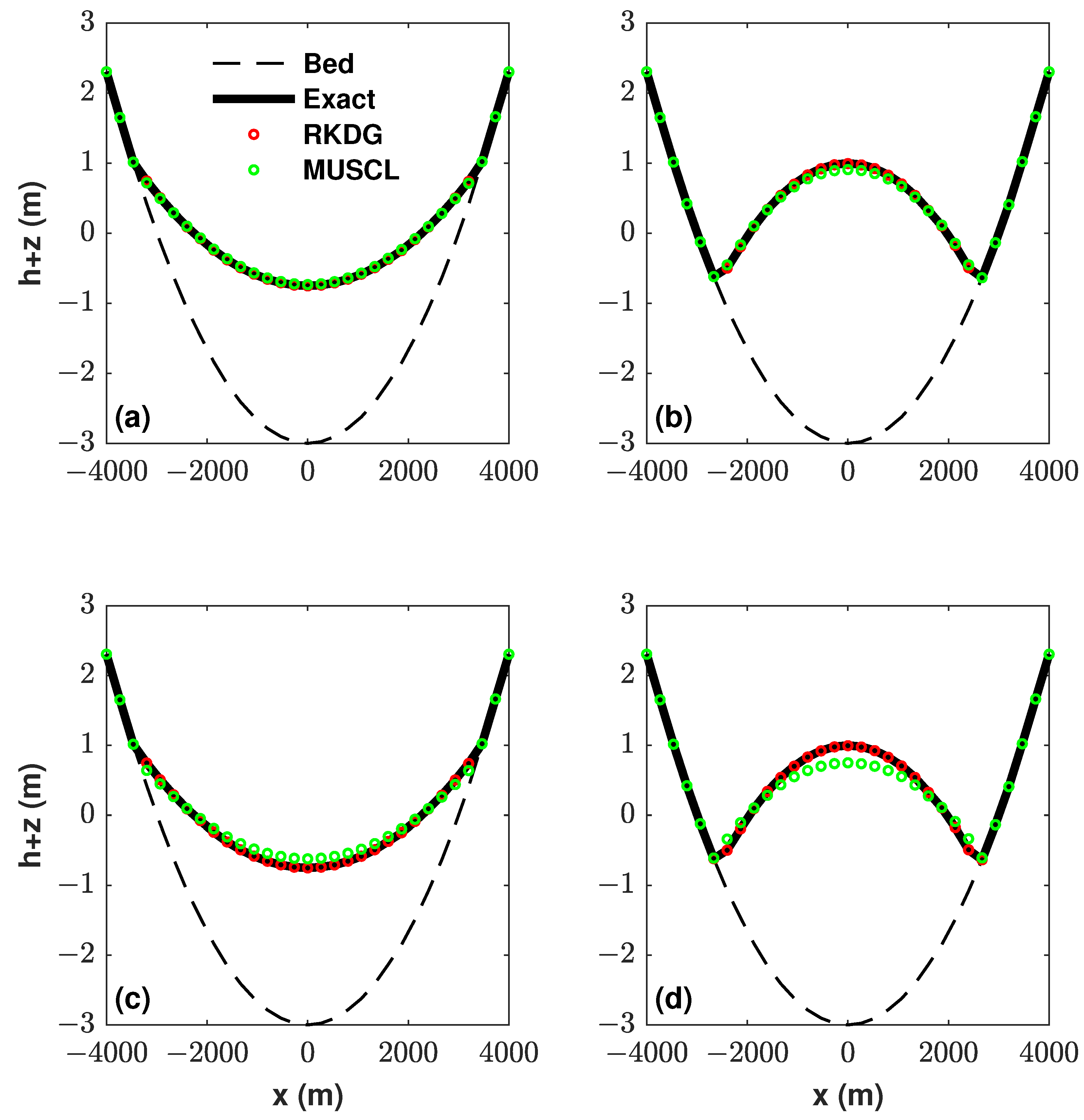
4.1. Curved Flow in Parabolic Bowl
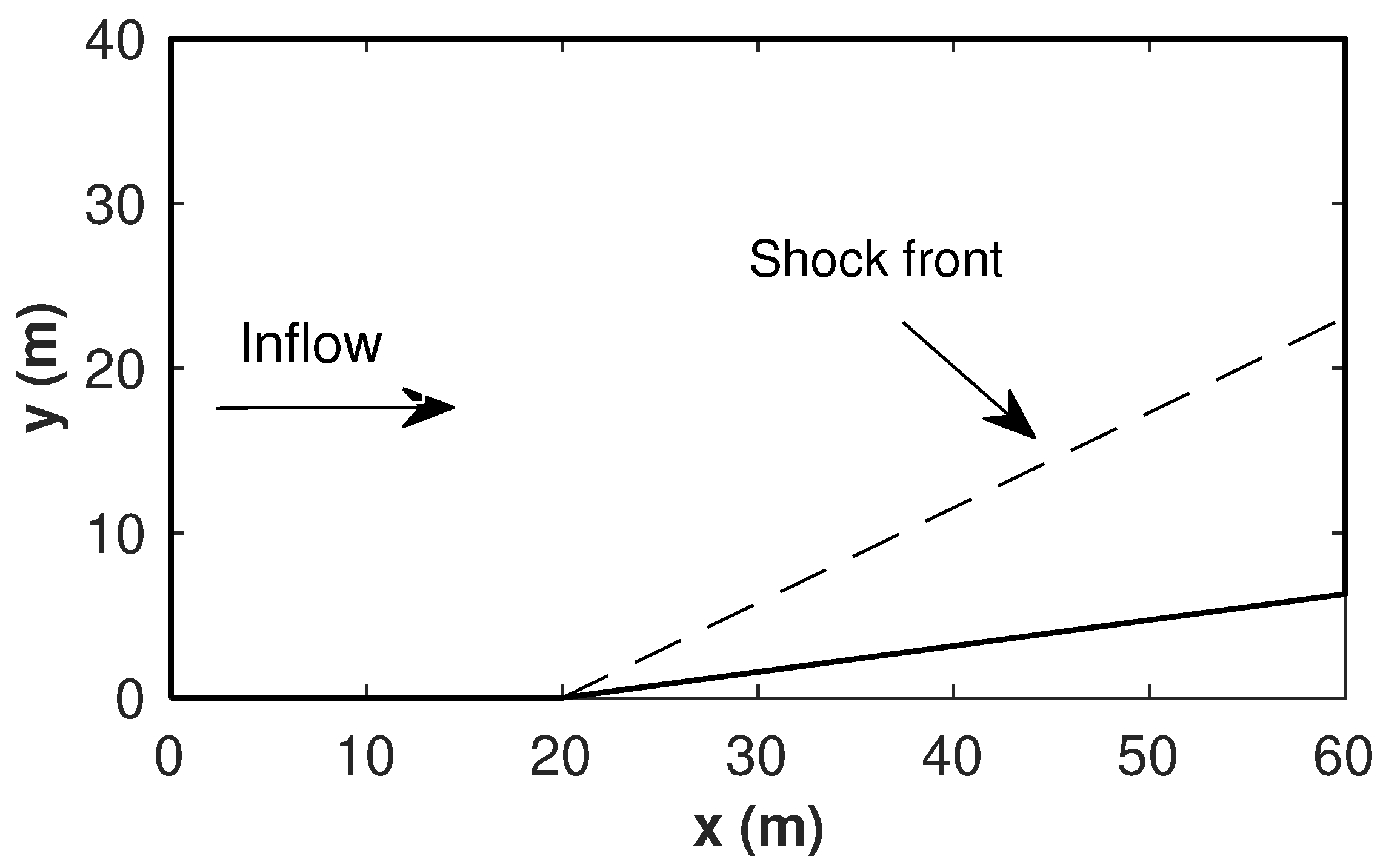
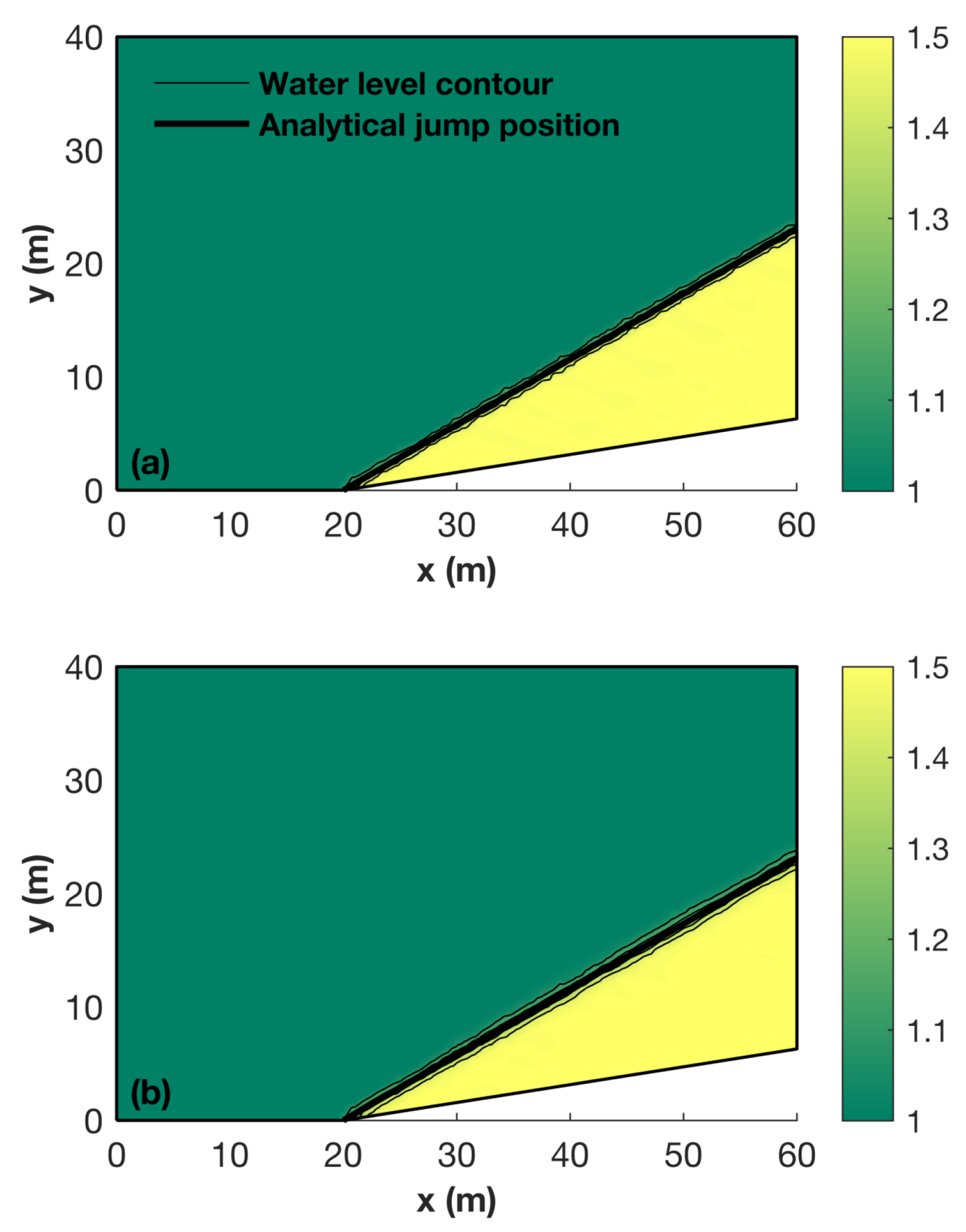
4.2. Oblique Hydraulic Jump
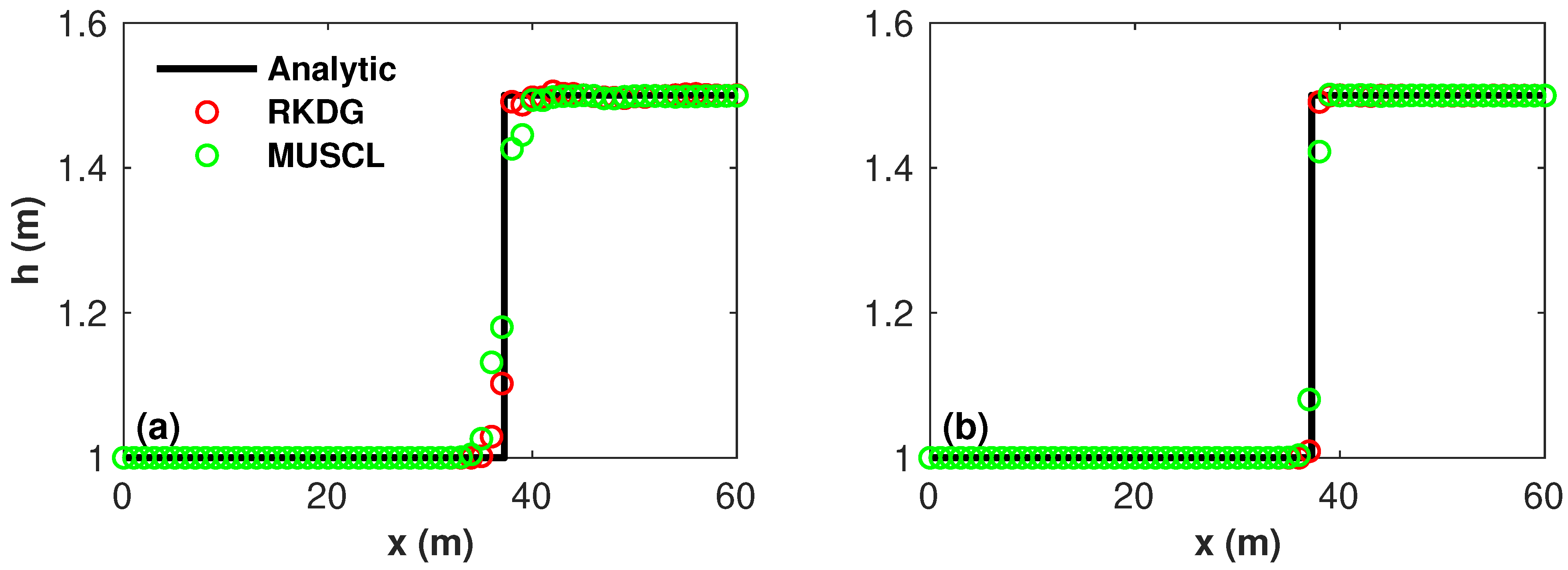
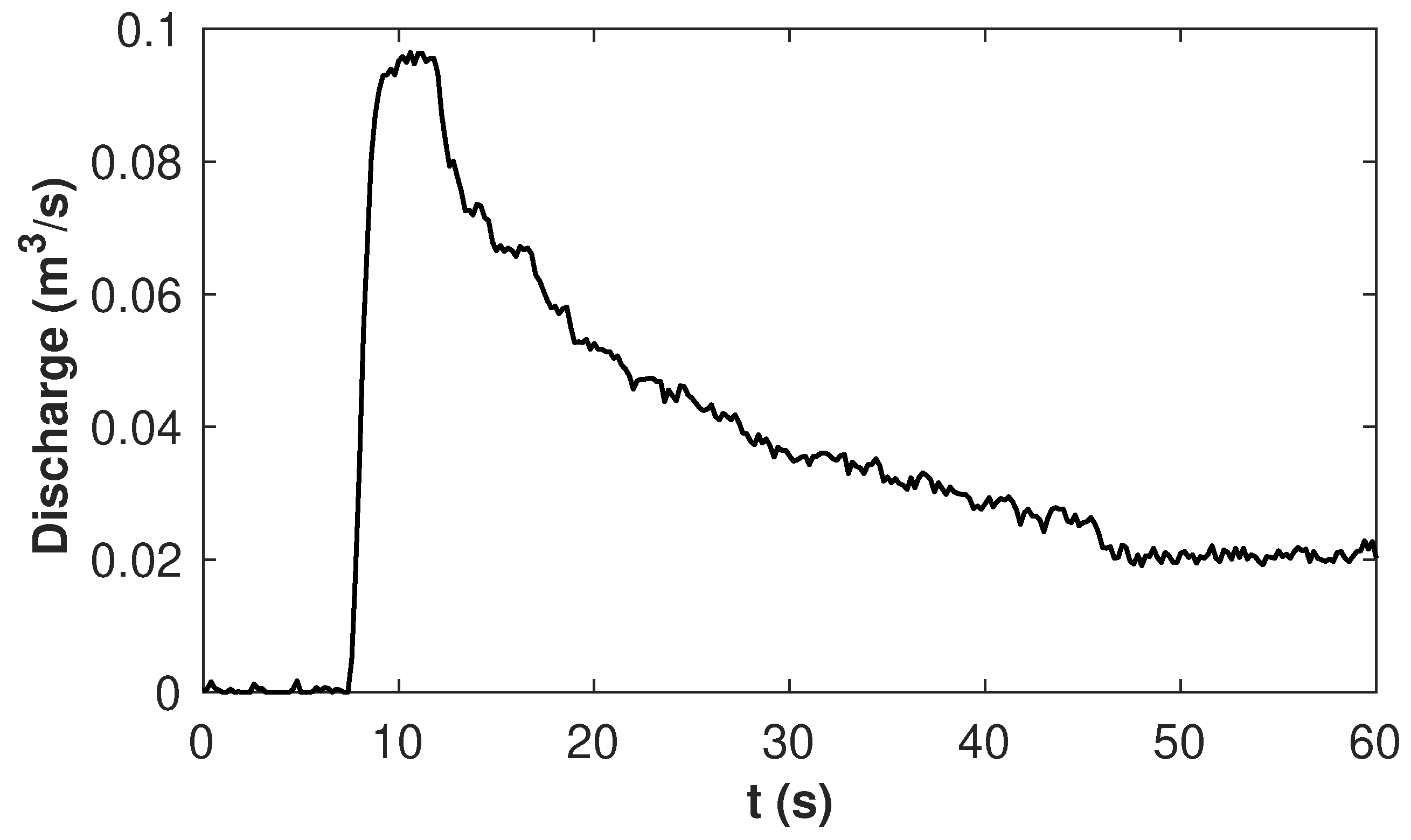
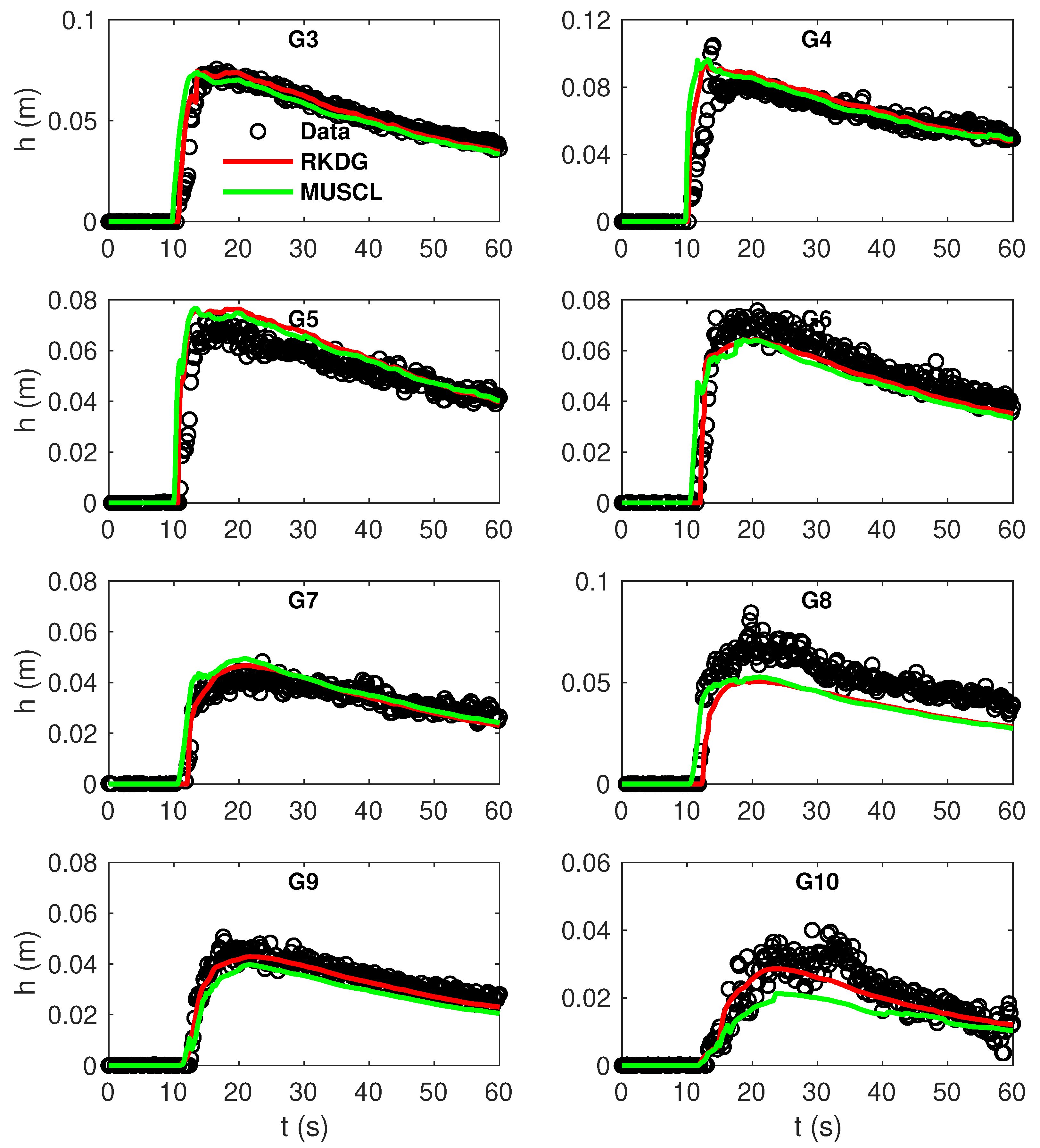
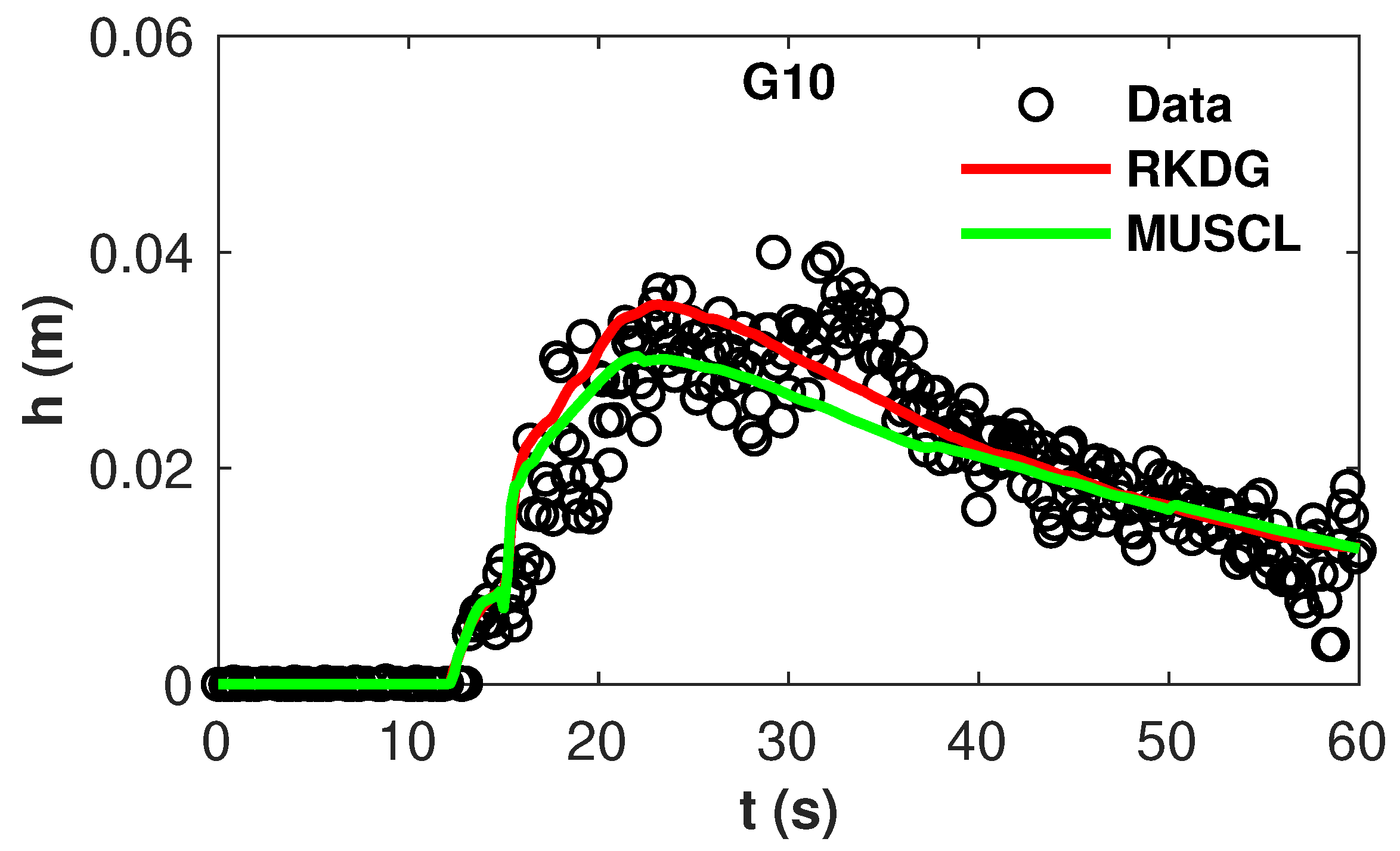
4.3. Toce River Test Case
4.4. Malpasset Dam-Break
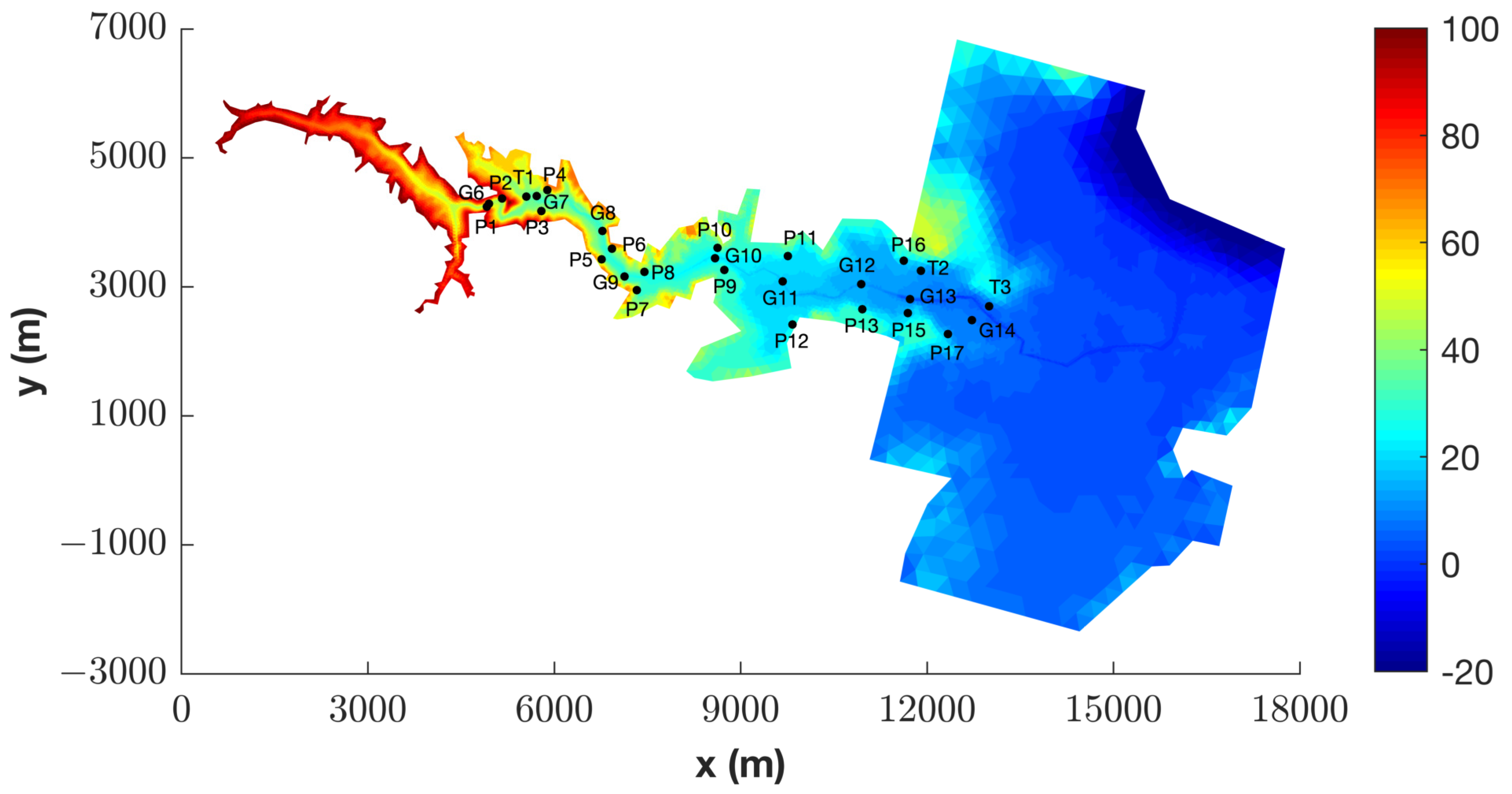
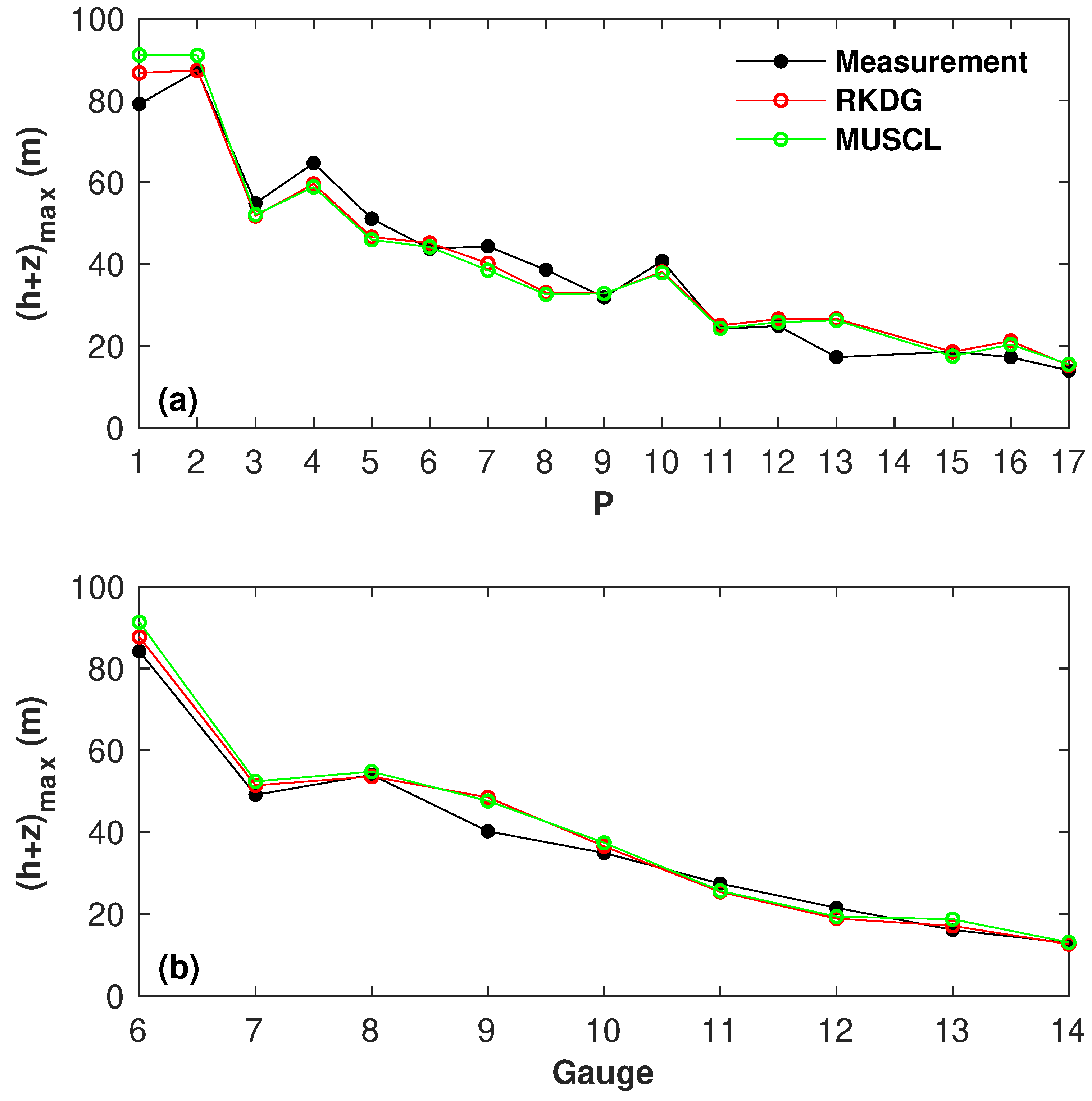
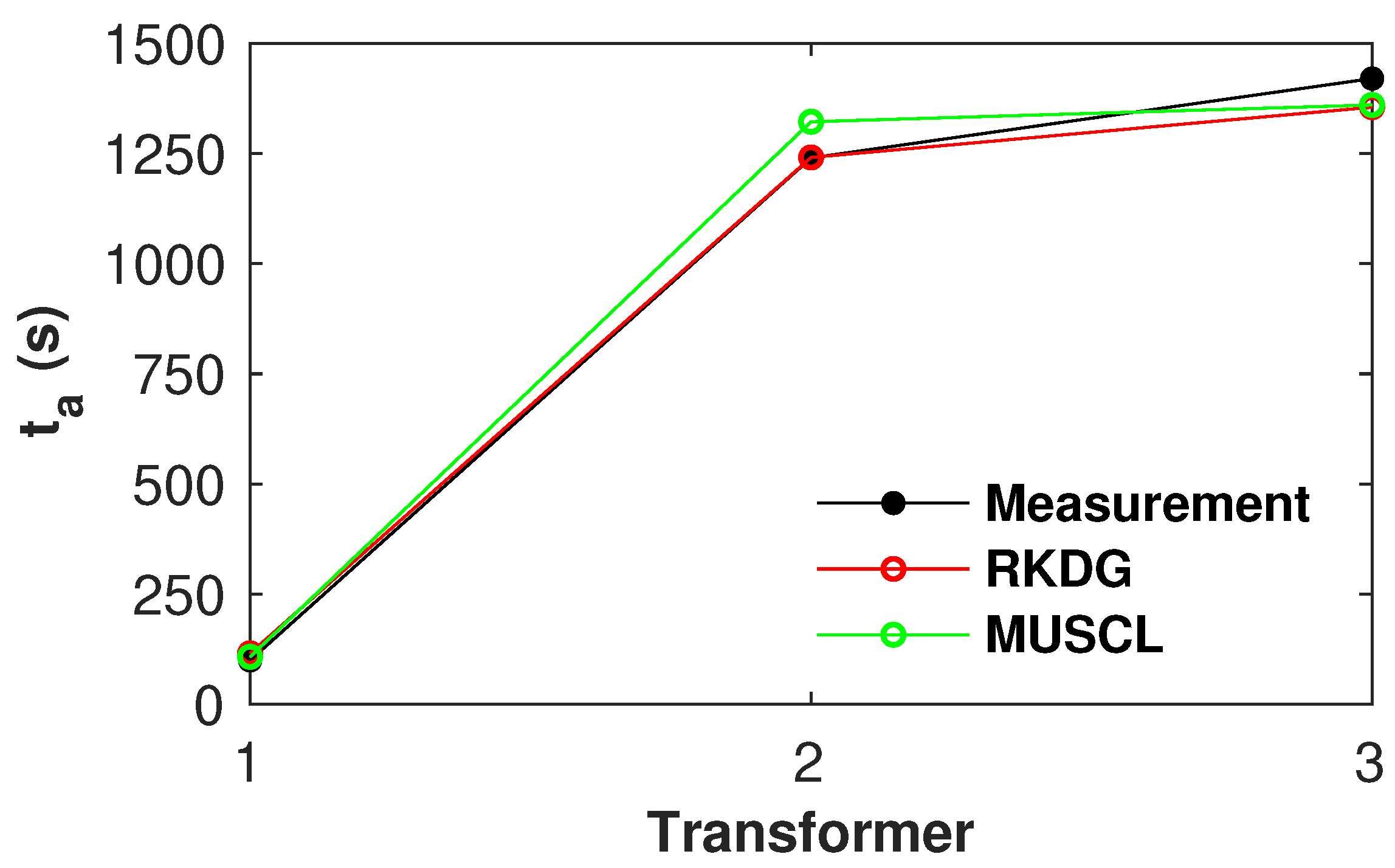
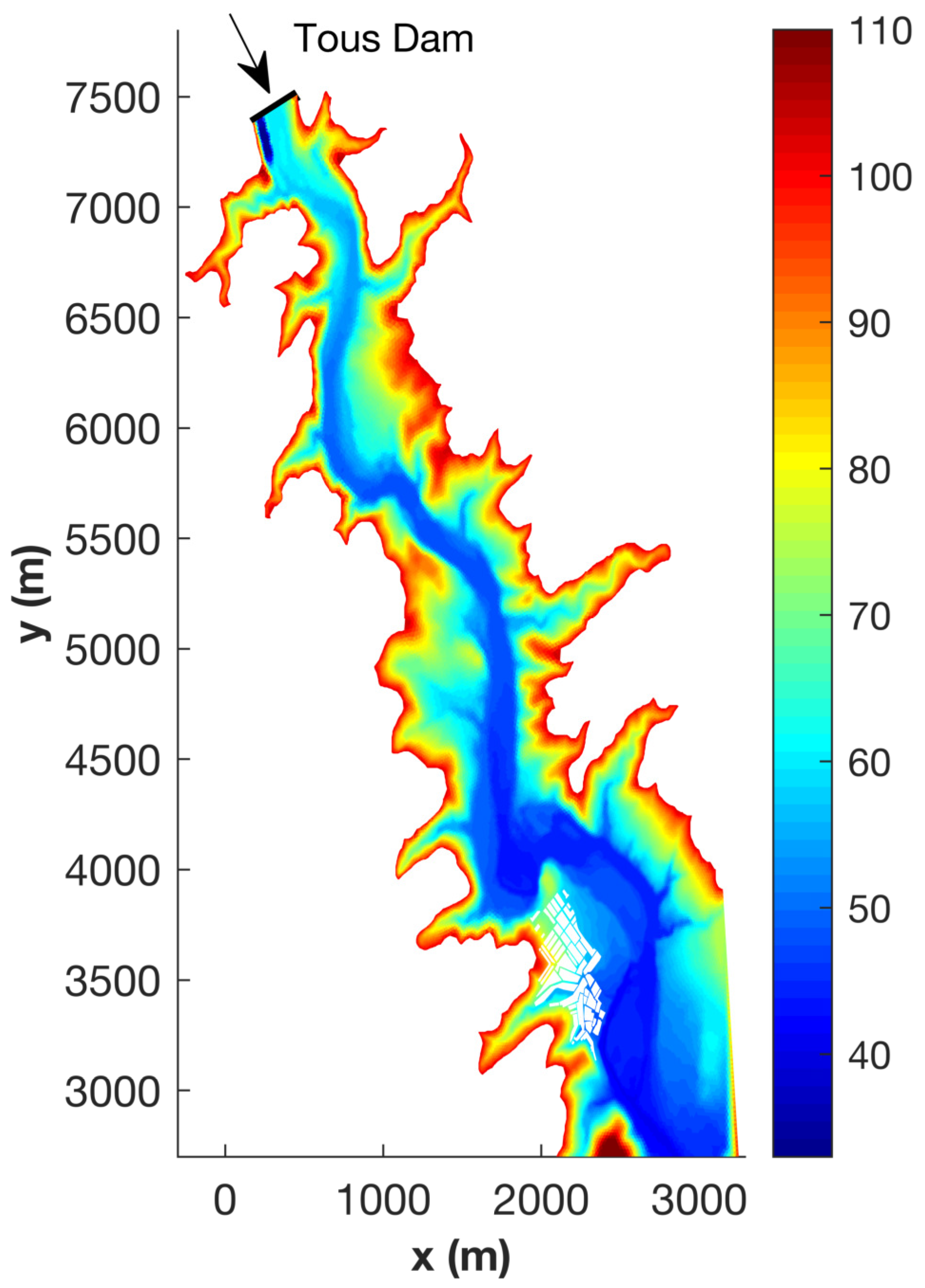
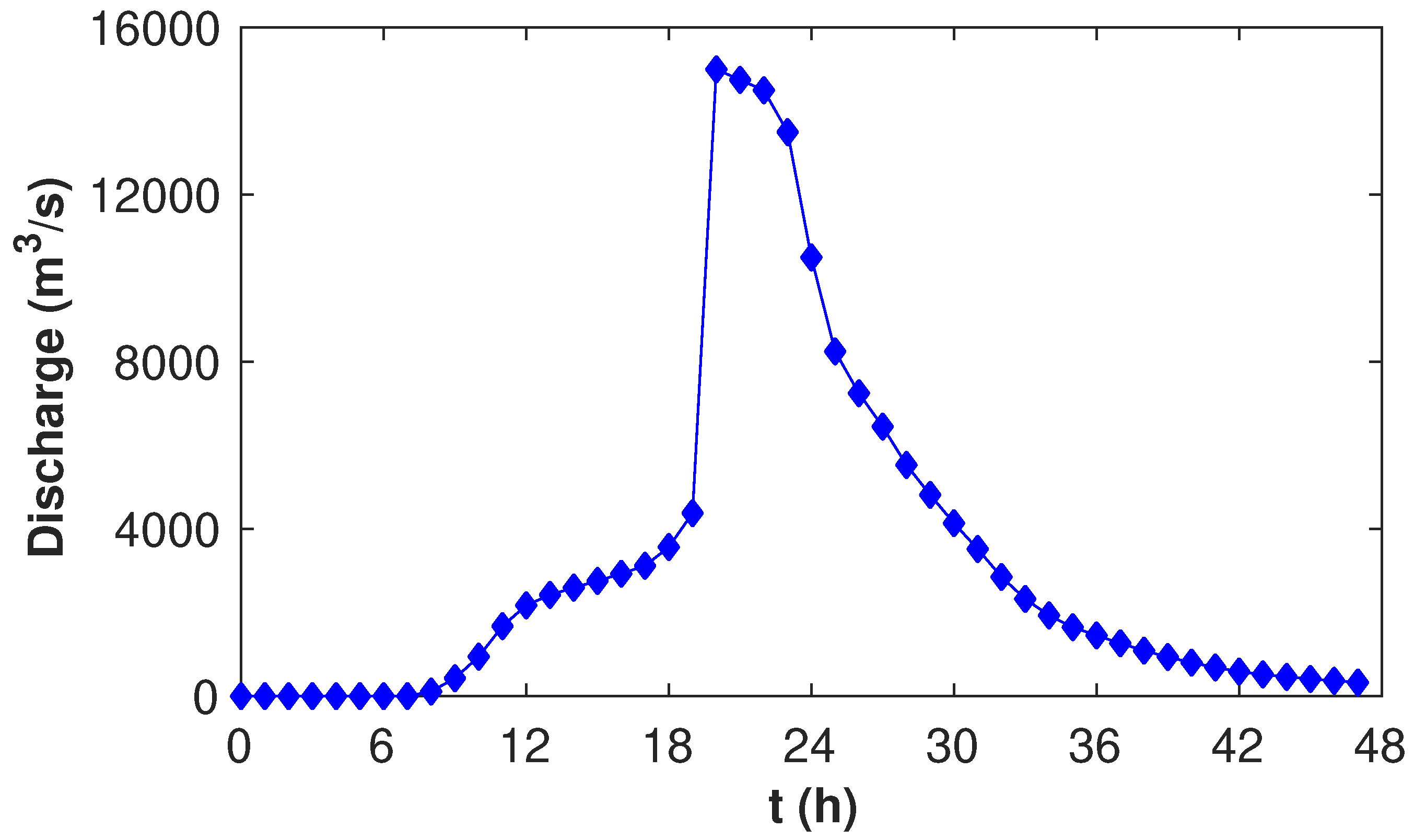
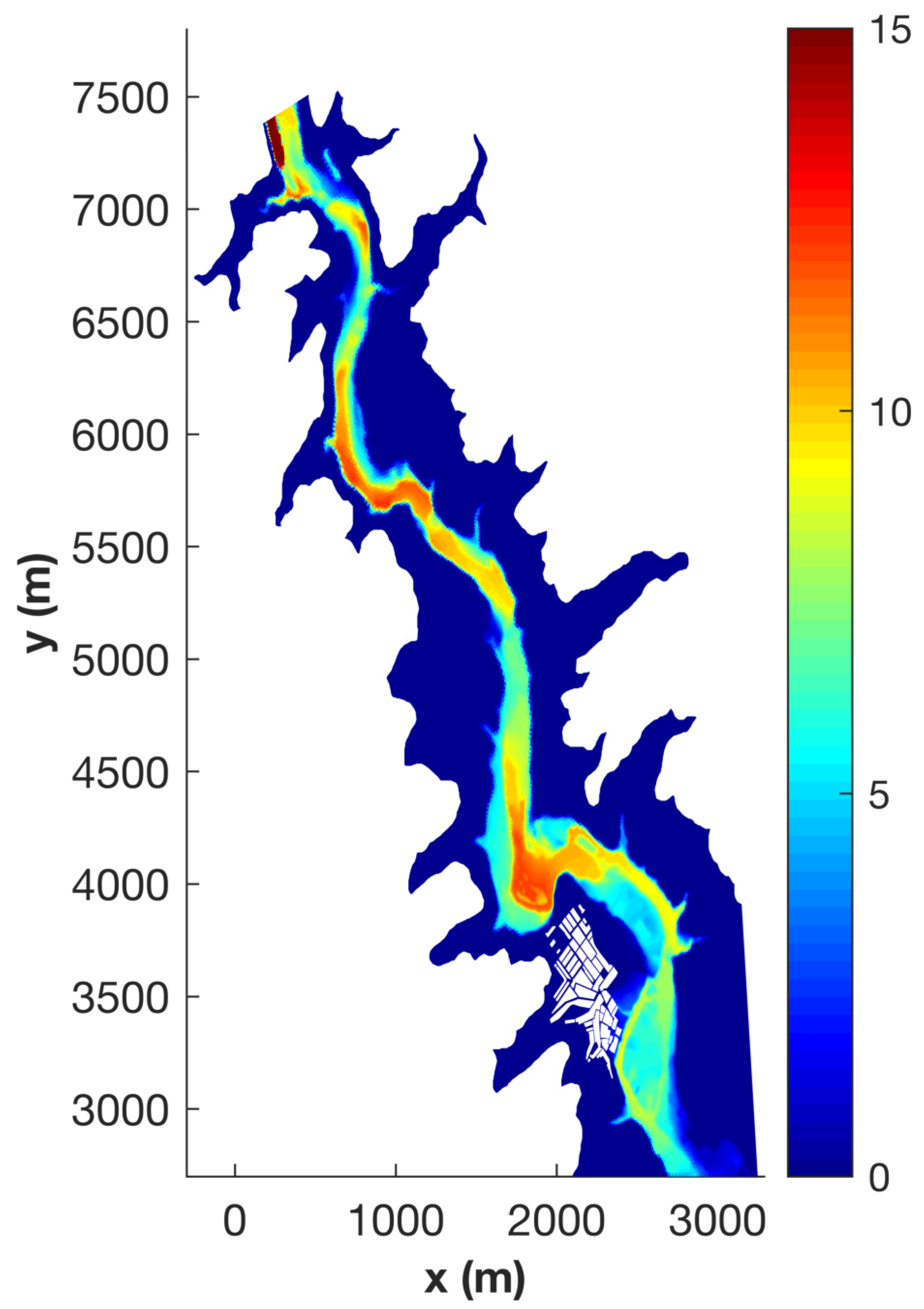
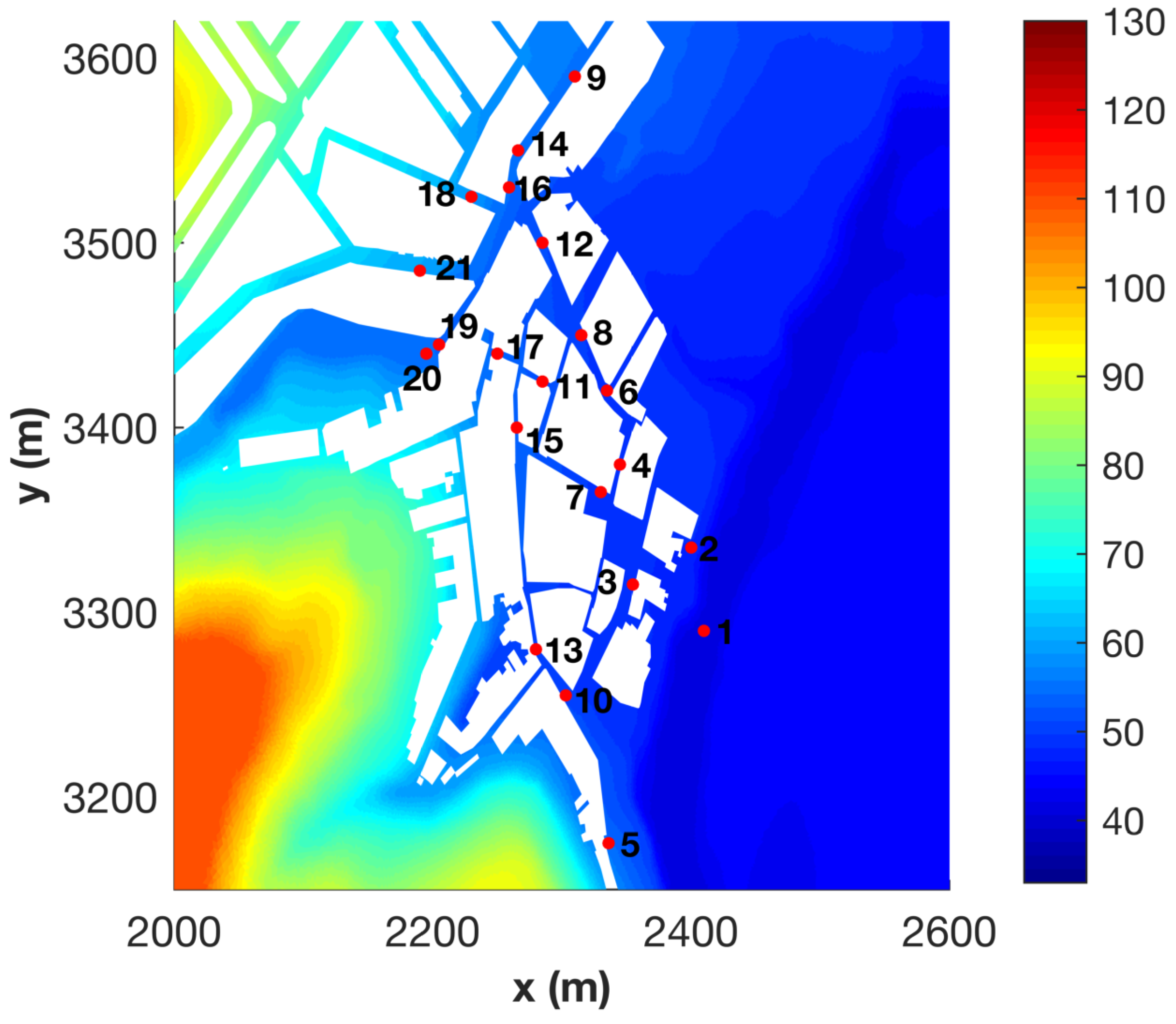
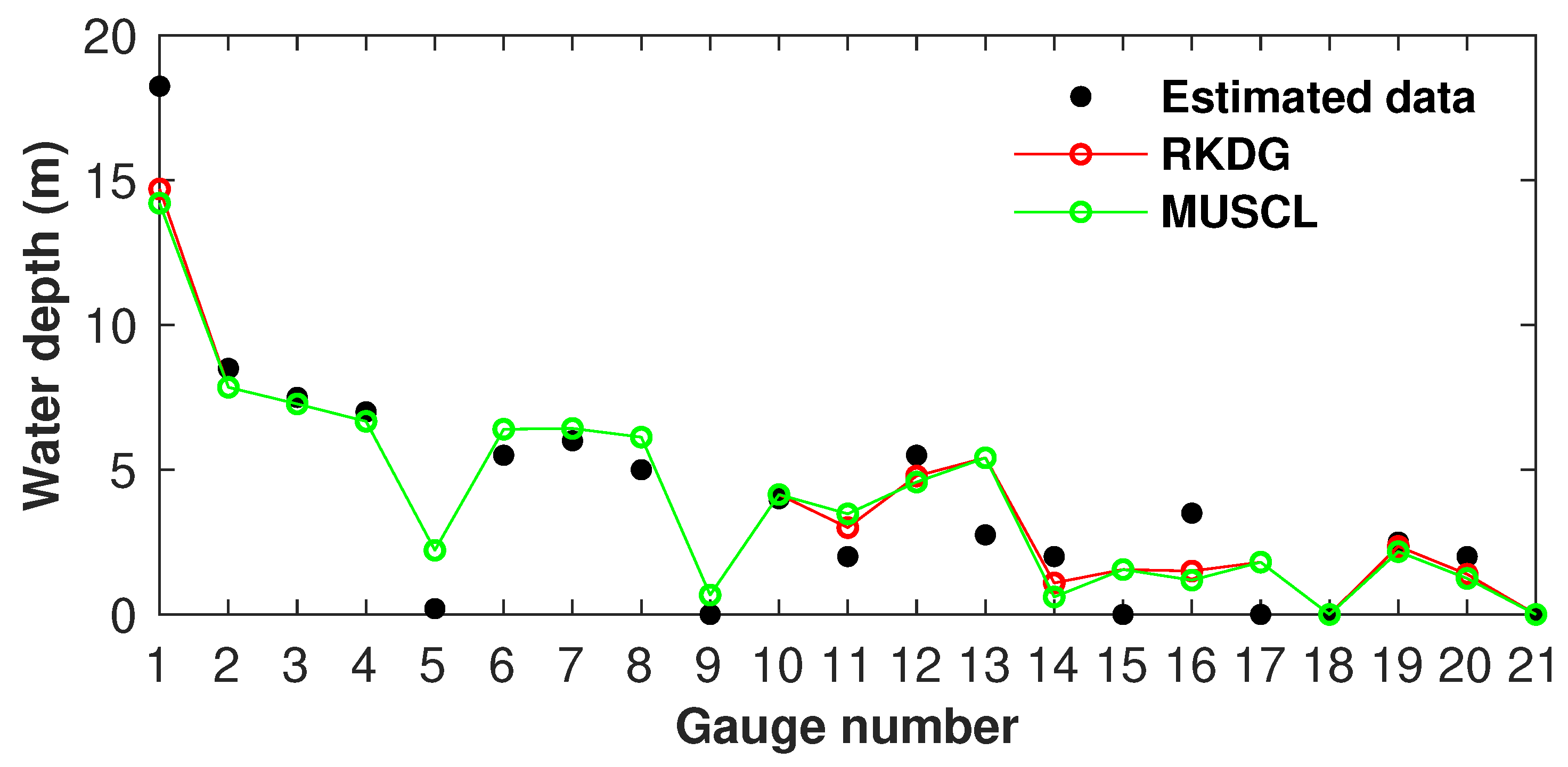
4.5. Tous Dam-Break
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dottori, F.; Mentaschi, L.; Bianchi, A.; Alfieri, L.; Feyen, L. Cost-effective adaptation strategies to rising river flood risk in Europe. Nat. Clim. Chang. 2023, 13, 196–202. [Google Scholar] [CrossRef]
- Lhomme, J.; Gutierrez-Andres, J.; Weisgerber, A.; Davison, M.; Mulet-Marti, J.; Cooper, A.; Gouldby, B. Testing a new two-dimensional flood modelling system: Analytical tests and application to a flood event. J. Flood Risk Manag. 2010, 3, 33–51. [Google Scholar] [CrossRef]
- Neal, J.; Villanueva, I.; Wright, N.; Willis, T.; Fewtrell, T.; Bates, P. How much physical complexity is needed to model flood inundation? Hydrol. Process. 2012, 26, 2264–2282. [Google Scholar] [CrossRef]
- Mungkasi, S.; Roberts, S. Validation of ANUGA hydraulic model using exact solutions to shallow water wave problems. J. Phys. Conf. Ser. 2013, 423, 012029. [Google Scholar] [CrossRef]
- BMT-WBM. TUFLOW Classic/HPC User Manual Build 2018-03-AD; WBM Pty Ltd.: Bangalow, NSW, Australia, 2018. [Google Scholar]
- Wang, Z.J.; Fidkowski, K.; Abgrall, R.; Bassi, F.; Caraeni, D.; Cary, A.; Deconinck, H.; Hartmann, R.; Hillewaert, K.; Huynh, H.T.; et al. High-order CFD methods: Current status and perspective. Int. J. Numer. Methods Fluids 2013, 72, 811–845. [Google Scholar] [CrossRef]
- Özgen-Xian, I.; Xia, X.; Liang, Q.; Hinkelmann, R.; Liang, D.; Hou, J. Innovations towards the next generation of shallow flow models. Adv. Water Resour. 2021, 149, 103867. [Google Scholar] [CrossRef]
- Kim, B.; Sanders, B.F.; Schubert, J.E.; Famiglietti, J.S. Mesh type tradeoffs in 2D hydrodynamic modeling of flooding with a Godunov-based flow solver. Adv. Water Resour. 2014, 68, 42–61. [Google Scholar] [CrossRef]
- Abderrezzak, K.E.K.; Paquier, A.; Mignot, E. Modelling flash flood propagation in urban areas using a two-dimensional numerical model. Nat. Hazards 2009, 50, 433–460. [Google Scholar] [CrossRef]
- Gallegos, H.A.; Schubert, J.E.; Sanders, B.F. Two-dimensional, high-resolution modeling of urban dam-break flooding: A case study of Baldwin Hills, California. Adv. Water Resour. 2009, 32, 1323–1335. [Google Scholar] [CrossRef]
- Sanders, B.F.; Schubert, J.E.; Detwiler, R.L. ParBreZo: A parallel, unstructured grid, Godunov-type, shallow-water code for high-resolution flood inundation modeling at the regional scale. Adv. Water Resour. 2010, 33, 1456–1467. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment. Adv. Water Resour. 2013, 52, 107–131. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q.; Ming, X. A full-scale fluvial flood modelling framework based on a high-performance integrated hydrodynamic modelling system (HiPIMS). Adv. Water Resour. 2019, 132, 103392. [Google Scholar] [CrossRef]
- Coulibaly, G.; Leye, B.; Tazen, F.; Mounirou, L.A.; Karambiri, H. Urban flood modeling using 2D shallow-water equations in Ouagadougou, Burkina Faso. Water 2020, 12, 2120. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; De Lorenzo, G.; Macchione, F. Is local flood hazard assessment in urban areas significantly influenced by the physical complexity of the hydrodynamic inundation model? J. Hydrol. 2020, 580, 124231. [Google Scholar] [CrossRef]
- Liu, D.; Tang, J.; Wang, H.; Cao, Y.; Bazai, N.A.; Chen, H.; Liu, D. A new method for wet-dry front treatment in outburst flood simulation. Water 2021, 13, 221. [Google Scholar] [CrossRef]
- Zhao, J.; Liang, Q. Novel variable reconstruction and friction term discretisation schemes for hydrodynamic modelling of overland flow and surface water flooding. Adv. Water Resour. 2022, 163, 104187. [Google Scholar] [CrossRef]
- Maranzoni, A.; Tomirotti, M. New formulation of the two-dimensional steep-slope shallow water equations. Part II: Numerical modeling, validation, and application. Adv. Water Resour. 2023, 177, 104403. [Google Scholar] [CrossRef]
- Peng, F.; Hao, X.; Chai, F. A GPU-Accelerated Two-Dimensional Hydrodynamic Model for Unstructured Grids. Water 2023, 15, 1300. [Google Scholar] [CrossRef]
- Vallés, P.; Echeverribar, I.; Mairal, J.; Martínez-Aranda, S.; Fernández-Pato, J.; García-Navarro, P. 2D numerical simulation of floods in Ebro river and analysis of boundary conditions to model the Mequinenza reservoir dam. GeoHazards 2023, 4, 136–156. [Google Scholar] [CrossRef]
- Ferrari, A. A parallel porosity model for large-scale modelling of river floods in urban areas. J. Hydrol. 2024, 635, 131232. [Google Scholar] [CrossRef]
- Wang, J.; Hou, J.; Li, S.; Sun, J.; Jing, J.; Wang, J. Advancements in enhancing flood evolution and urban inundation predictions: A study of local time stepping algorithm and GPU-accelerated hydrodynamic model. J. Hydrol. 2024, 641, 131744. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Ayog, J.L.; Kesserwani, G.; Shaw, J.; Sharifian, M.K.; Bau, D. Second-order discontinuous Galerkin flood model: Comparison with industry-standard finite volume models. J. Hydrol. 2021, 594, 125924. [Google Scholar] [CrossRef]
- Ghostine, R.; Kesserwani, G.; Vazquez, J.; Rivière, N.; Ghenaim, A.; Mose, R. Simulation of supercritical flow in crossroads: Confrontation of a 2D and 3D numerical approaches to experimental results. Comput. Fluids 2009, 38, 425–432. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, X.; Shu, C.W. Positivity-preserving high order well-balanced discontinuous Galerkin methods for the shallow water equations. Adv. Water Res. 2010, 33, 1476–1493. [Google Scholar] [CrossRef]
- Duran, A.; Marche, F. Recent advances on the discontinuous Galerkin method for shallow water equations with topography source terms. Comput. Fluids 2014, 101, 88–104. [Google Scholar] [CrossRef]
- Wirasaet, D.; Kubatko, E.; Michoski, C.; Tanaka, S.; Westerink, J.; Dawson, C. Discontinuous Galerkin methods with nodal and hybrid modal/nodal triangular, quadrilateral, and polygonal elements for nonlinear shallow water flow. Comput. Methods Appl. Mech. Eng. 2014, 270, 113–149. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; Kesserwani, G. Benchmarking a multiresolution discontinuous Galerkin shallow water model: Implications for computational hydraulics. Adv. Water Resour. 2015, 86, 14–31. [Google Scholar] [CrossRef]
- Kesserwani, G.; Ayog, J.L.; Bau, D. Discontinuous Galerkin formulation for 2D hydrodynamic modelling: Trade-offs between theoretical complexity and practical convenience. Comput. Methods Appl. Mech. Eng. 2018, 342, 710–741. [Google Scholar] [CrossRef]
- Faghih-Naini, S.; Kuckuk, S.; Zint, D.; Kemmler, S.; Köstler, H.; Aizinger, V. Discontinuous Galerkin method for the shallow water equations on complex domains using masked block-structured grids. Adv. Water Resour. 2023, 182, 104584. [Google Scholar] [CrossRef]
- Kesserwani, G.; Wang, Y. Discontinuous Galerkin flood model formulation: Luxury or necessity? Water Resour. Res. 2014, 50, 6522–6541. [Google Scholar] [CrossRef]
- Samii, A.; Michoski, C.; Dawson, C. A parallel and adaptive hybridized discontinuous Galerkin method for anisotropic nonhomogeneous diffusion. Comput. Methods Appl. Mech. Eng. 2016, 304, 118–139. [Google Scholar] [CrossRef]
- Fuhry, M.; Giuliani, A.; Krivodonova, L. Discontinuous Galerkin methods on graphics processing units for nonlinear hyperbolic conservation laws. Int. J. Numer. Methods Fluids 2014, 76, 982–1003. [Google Scholar] [CrossRef]
- Brus, S.; Wirasaet, D.; Westerink, J.J.; Dawson, C. Performance and scalability improvements for discontinuous Galerkin solutions to conservation laws on unstructured grids. J. Sci. Comput. 2017, 70, 210–242. [Google Scholar] [CrossRef]
- Ern, A.; Piperno, S.; Djadel, K. A well-balanced Runge–Kutta discontinuous Galerkin method for the shallow-water equations with flooding and drying. Int. J. Numer. Methods Fluids 2008, 58, 1–25. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, X. Positivity-preserving well-balanced discontinuous Galerkin methods for the shallow water equations on unstructured triangular meshes. J. Sci. Comput. 2013, 57, 19–41. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, Y.; Shu, C.W. Maximum-principle-satisfying and positivity-preserving high order discontinuous Galerkin schemes for conservation laws on triangular meshes. J. Sci. Comput. 2012, 50, 29–62. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q. A new vertex-based limiting approach for nodal discontinuous Galerkin methods on arbitrary unstructured meshes. Comput. Fluids 2017, 159, 316–326. [Google Scholar] [CrossRef]
- Vater, S.; Beisiegel, N.; Behrens, J. A limiter-based well-balanced discontinuous Galerkin method for shallow-water flows with wetting and drying: Triangular grids. Int. J. Numer. Methods Fluids 2019, 91, 395–418. [Google Scholar] [CrossRef]
- Dutt, K.; Krivodonova, L. A high-order moment limiter for the discontinuous Galerkin method on triangular meshes. J. Comput. Phys. 2021, 433, 110188. [Google Scholar] [CrossRef]
- Bunya, S.; Kubatko, E.J.; Westerink, J.J.; Dawson, C. A wetting and drying treatment for the Runge–Kutta discontinuous Galerkin solution to the shallow water equations. Comput. Methods Appl. Mech. Eng. 2009, 198, 1548–1562. [Google Scholar] [CrossRef]
- Brufau, P.; García-Navarro, P.; Vázquez-Cendón, M. Zero mass error using unsteady wetting–drying conditions in shallow flows over dry irregular topography. Int. J. Numer. Methods Fluids 2004, 45, 1047–1082. [Google Scholar] [CrossRef]
- Kärnä, T.; De Brye, B.; Gourgue, O.; Lambrechts, J.; Comblen, R.; Legat, V.; Deleersnijder, E. A fully implicit wetting–drying method for DG-FEM shallow water models, with an application to the Scheldt Estuary. Comput. Methods Appl. Mech. Eng. 2011, 200, 509–524. [Google Scholar] [CrossRef]
- Audusse, E.; Bouchut, F.; Bristeau, M.O.; Klein, R.; Perthame, B. A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. J. Sci. Comput. 2004, 25, 2050–2065. [Google Scholar] [CrossRef]
- Kesserwani, G.; Sharifian, M.K. (Multi) wavelets increase both accuracy and efficiency of standard Godunov-type hydrodynamic models: Robust 2D approaches. Adv. Water Resour. 2020, 144, 103693. [Google Scholar] [CrossRef]
- Shaw, J.; Kesserwani, G.; Neal, J.; Bates, P.; Sharifian, M.K. LISFLOOD-FP 8.0: The new discontinuous Galerkin shallow water solver for multi-core CPUs and GPUs. Geosci. Model Dev. 2020, 14, 3577–3602. [Google Scholar] [CrossRef]
- Lai, W.; Khan, A.A. Modeling dam-break flood over natural rivers using discontinuous Galerkin method. J. Hydrodyn. 2012, 24, 467–478. [Google Scholar] [CrossRef]
- Filippini, A.G.; Arpaia, L.; Perrier, V.; Pedreros, R.; Bonneton, P.; Lannes, D.; Marche, F.; De Brye, S.; Delmas, S.; Lecacheux, S.; et al. An operational discontinuous Galerkin shallow water model for coastal flood assessment. Ocean Model. 2024, 192, 102447. [Google Scholar] [CrossRef]
- Wichitrnithed, C.; Valseth, E.; Kubatko, E.J.; Kang, Y.; Hudson, M.; Dawson, C. A discontinuous Galerkin finite element model for compound flood simulations. Comput. Methods Appl. Mech. Eng. 2024, 420, 116707. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Cockburn, B.; Shu, C.W. The Runge–Kutta discontinuous Galerkin method for conservation laws V: Multidimensional systems. J. Comput. Phys. 1998, 141, 199–224. [Google Scholar] [CrossRef]
- Xing, Y.; Shu, C.W. A new approach of high order well-balanced finite volume WENO schemes and discontinuous Galerkin methods for a class of hyperbolic systems with source terms. Commun. Comput. Phys. 2006, 1, 100–134. [Google Scholar]
- Begnudelli, L.; Sanders, B.F. Unstructured grid finite-volume algorithm for shallow-water flow and scalar transport with wetting and drying. J. Hydraul. Eng. 2006, 132, 371–384. [Google Scholar] [CrossRef]
- Alcrudo, F.; Garcia-Navarro, P. A high-resolution Godunov-type scheme in finite volumes for the 2D shallow-water equations. Int. J. Numer. Methods Fluids 1993, 16, 489–505. [Google Scholar] [CrossRef]
- Testa, G.; Zuccala, D.; Alcrudo, F.; Mulet, J.; Soares-Frazão, S. Flash flood flow experiment in a simplified urban district. J. Hydraul. Res. 2007, 45, 37–44. [Google Scholar] [CrossRef]
- Valiani, A.; Caleffi, V.; Zanni, A. Case study: Malpasset dam-break simulation using a two-dimensional finite volume method. J. Hydraul. Eng. 2002, 128, 460–472. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, N.; Pei, Y. Well-balanced finite volume scheme for shallow water flooding and drying over arbitrary topography. Eng. Appl. Comput. Fluid Mech. 2013, 7, 40–54. [Google Scholar] [CrossRef][Green Version]
- Biscarini, C.; Di Francesco, S.; Ridolfi, E.; Manciola, P. On the simulation of floods in a narrow bending valley: The malpasset dam break case study. Water 2016, 8, 545. [Google Scholar] [CrossRef]
- Wu, G.f.; He, Z.g.; Zhao, L.; Liu, G.h. A well-balanced positivity preserving two-dimensional shallow flow model with wetting and drying fronts over irregular topography. J. Hydrodyn. 2018, 30, 618–631. [Google Scholar] [CrossRef]
- Goutal, N. The Malpasset dam failure. An overview and test case definition. In Proceedings of the 4th CADAM Meeting, Zaragoza, Spain, 18–19 November 1999. [Google Scholar]
- Alcrudo, F.; Mulet, J. Description of the Tous Dam break case study (Spain). J. Hydraul. Res. 2007, 45, 45–57. [Google Scholar] [CrossRef]
- Mulet, J.; Alcrudo, F. Uncertainty analysis of Tous flood propagation case study. In Proceedings of the 4rd IMPACT Project Workshop, Málaga, Spain, 10–12 November 2004. [Google Scholar]




| Mesh | MUSCL | RKDG | |||
|---|---|---|---|---|---|
| Coarse | Fine | Coarse | Fine | ||
| 7.6 × | 2.1 × | 5.2 × | 7.5 × | ||
| 2.3 × | 7.7 × | 8.1 × | 1.0 × | ||
| MUSCL | RKDG | |
|---|---|---|
| Coarse | 12.37 s | 29.94 s |
| Fine | 157.51 s | 366.68 s |
| Mesh | MUSCL | RKDG | |||
|---|---|---|---|---|---|
| RMSE | Runtime | RMSE | Runtime | ||
| Coarse | 3.1 × | 6.78 s | 1.5 × | 24.81 s | |
| Fine | 1.4 × | 72.25 s | 1.6 × | 278.56 s | |
| G3 | G4 | G5 | G6 | G7 | G8 | G9 | G10 | |
|---|---|---|---|---|---|---|---|---|
| RKDG | 0.54 | 1.01 | 1.07 | 0.65 | 0.64 | 1.54 | 0.49 | 1.21 |
| MUSCL | 0.98 | 1.31 | 1.17 | 0.99 | 0.95 | 1.48 | 0.97 | 2.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghostine, R.; Kesserwani, G.; Hoteit, I. Robust Wetting and Drying with Discontinuous Galerkin Flood Model on Unstructured Triangular Meshes. Water 2025, 17, 1141. https://doi.org/10.3390/w17081141
Ghostine R, Kesserwani G, Hoteit I. Robust Wetting and Drying with Discontinuous Galerkin Flood Model on Unstructured Triangular Meshes. Water. 2025; 17(8):1141. https://doi.org/10.3390/w17081141
Chicago/Turabian StyleGhostine, Rabih, Georges Kesserwani, and Ibrahim Hoteit. 2025. "Robust Wetting and Drying with Discontinuous Galerkin Flood Model on Unstructured Triangular Meshes" Water 17, no. 8: 1141. https://doi.org/10.3390/w17081141
APA StyleGhostine, R., Kesserwani, G., & Hoteit, I. (2025). Robust Wetting and Drying with Discontinuous Galerkin Flood Model on Unstructured Triangular Meshes. Water, 17(8), 1141. https://doi.org/10.3390/w17081141








