Insights into the Hydraulic Characteristics of Critical A-Jumps for Energy Dissipator Design
Abstract
1. Introduction
| No. | Projects | Dam Height (m) | Design Discharge (m3/s) | Step Height (m) | Country |
|---|---|---|---|---|---|
| 1 | Xiangjiaba | 162.0 | 41,200 | 9.0 | China |
| 2 | Huangjinping | 95.5 | 5650 | - | China |
| 3 | Jin’anqiao | 160.0 | 11,668 | - | China |
| 4 | Guanyinyuan | 159.0 | 16,900 | 7.5 | China |
| 5 | Liyuan | 155.0 | 11,361 | 15.8 | China |
| 6 | Guandi | 168.0 | 14,000 | 6.5 | China |
| 7 | Tingzikou | 110.0 | 34,500 | 8.0 | China |
| 8 | Myitsone | 139.5 | - | 8.0 | Burma |
| 9 | Sayano-Shushenskaya | 242 | - | 4.2–6.0 | Russia |
| 10 | TaSang Dam | 227.5 | - | - | Burma |
2. Numerical Model
2.1. Governing Equations
2.2. Numerical Setting
2.3. Numerical Experiment Design
3. Results
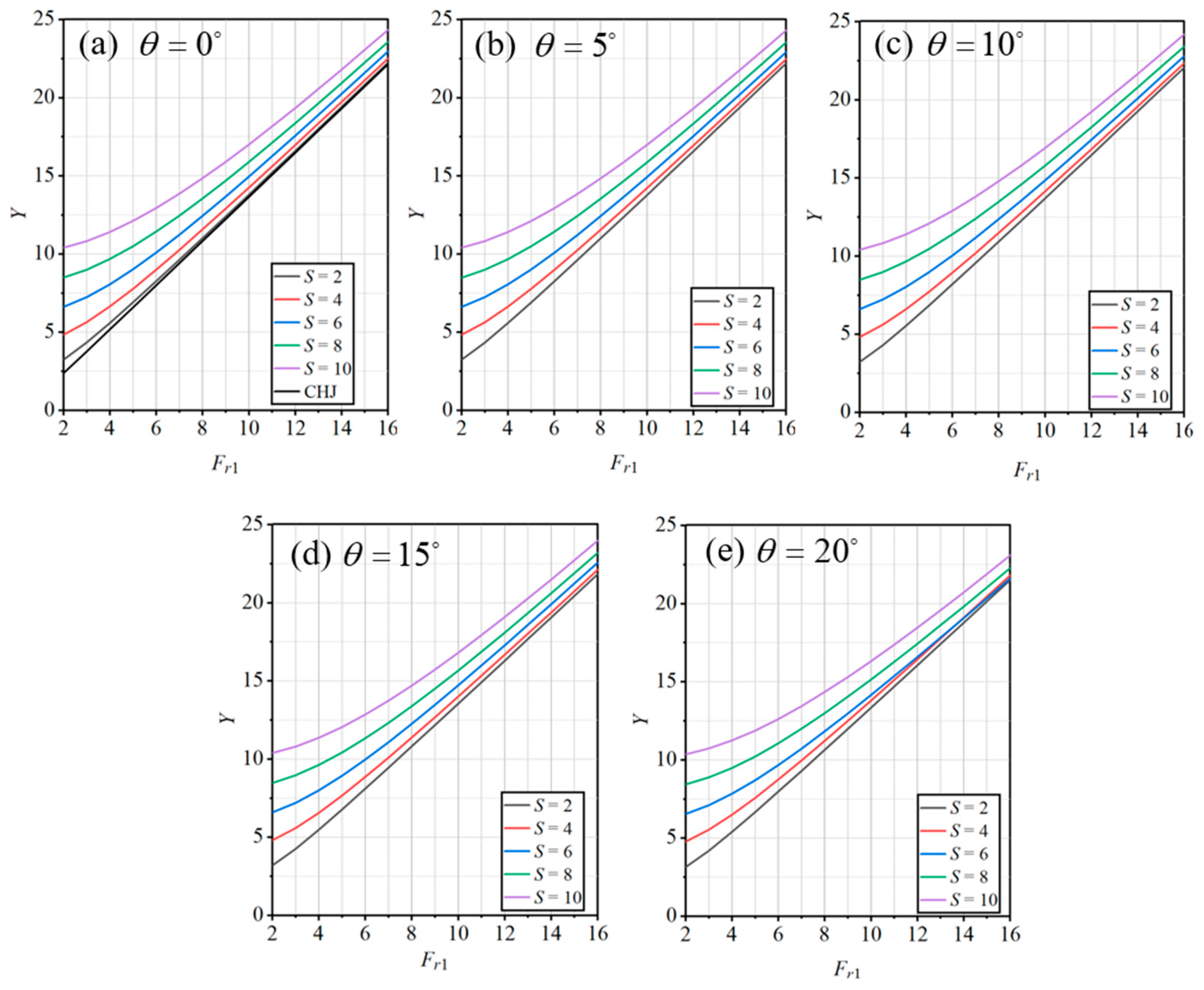
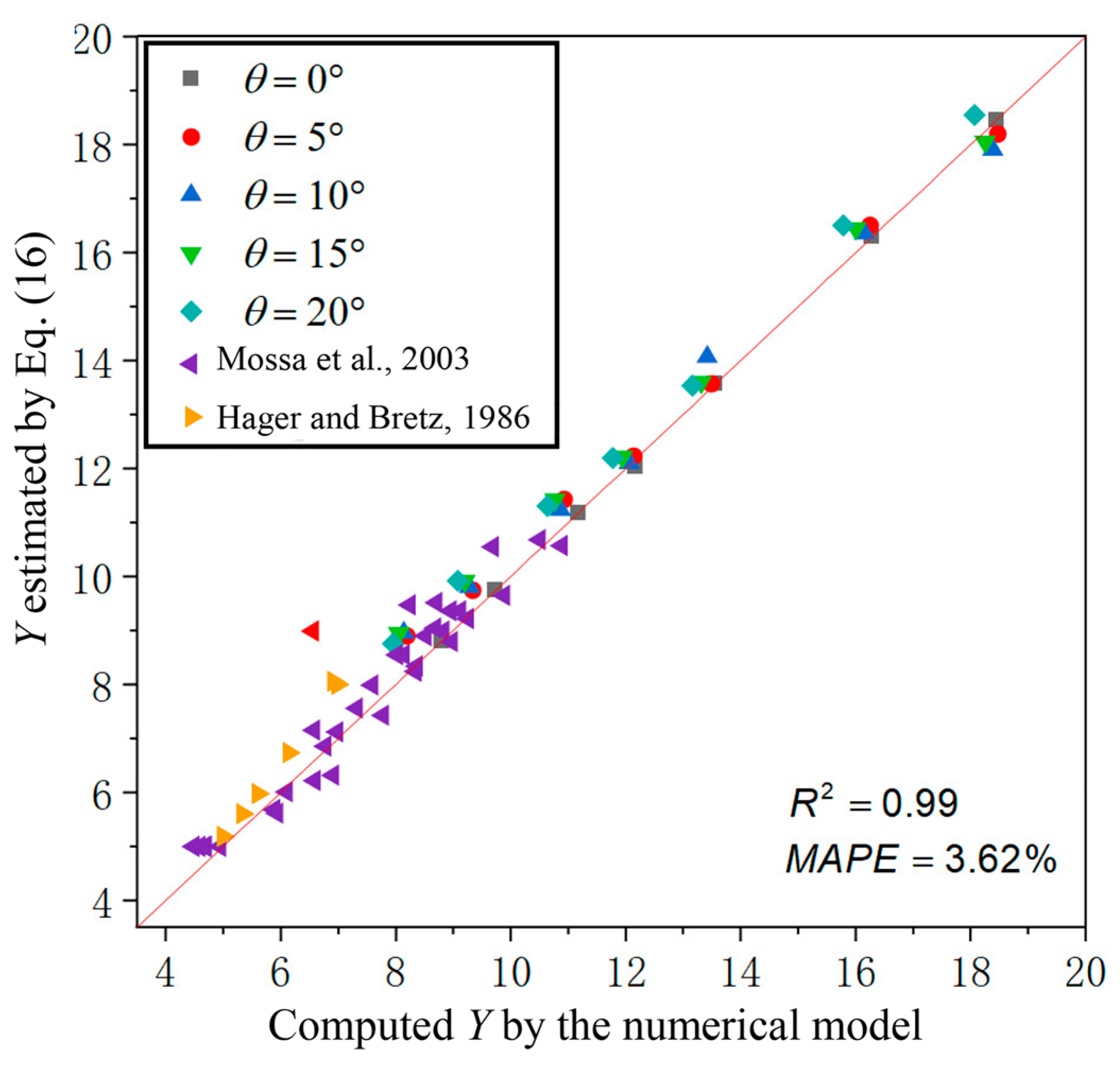
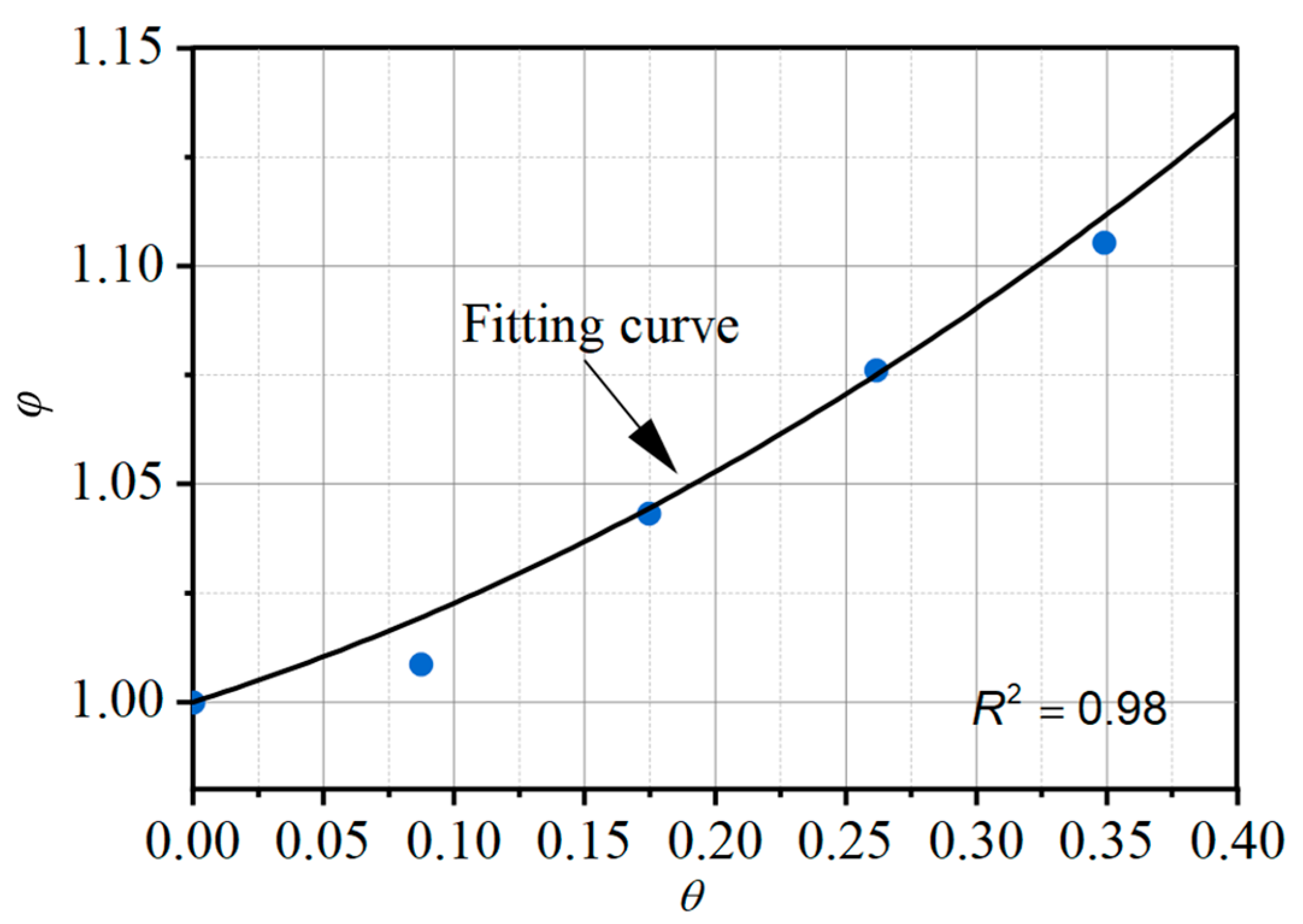
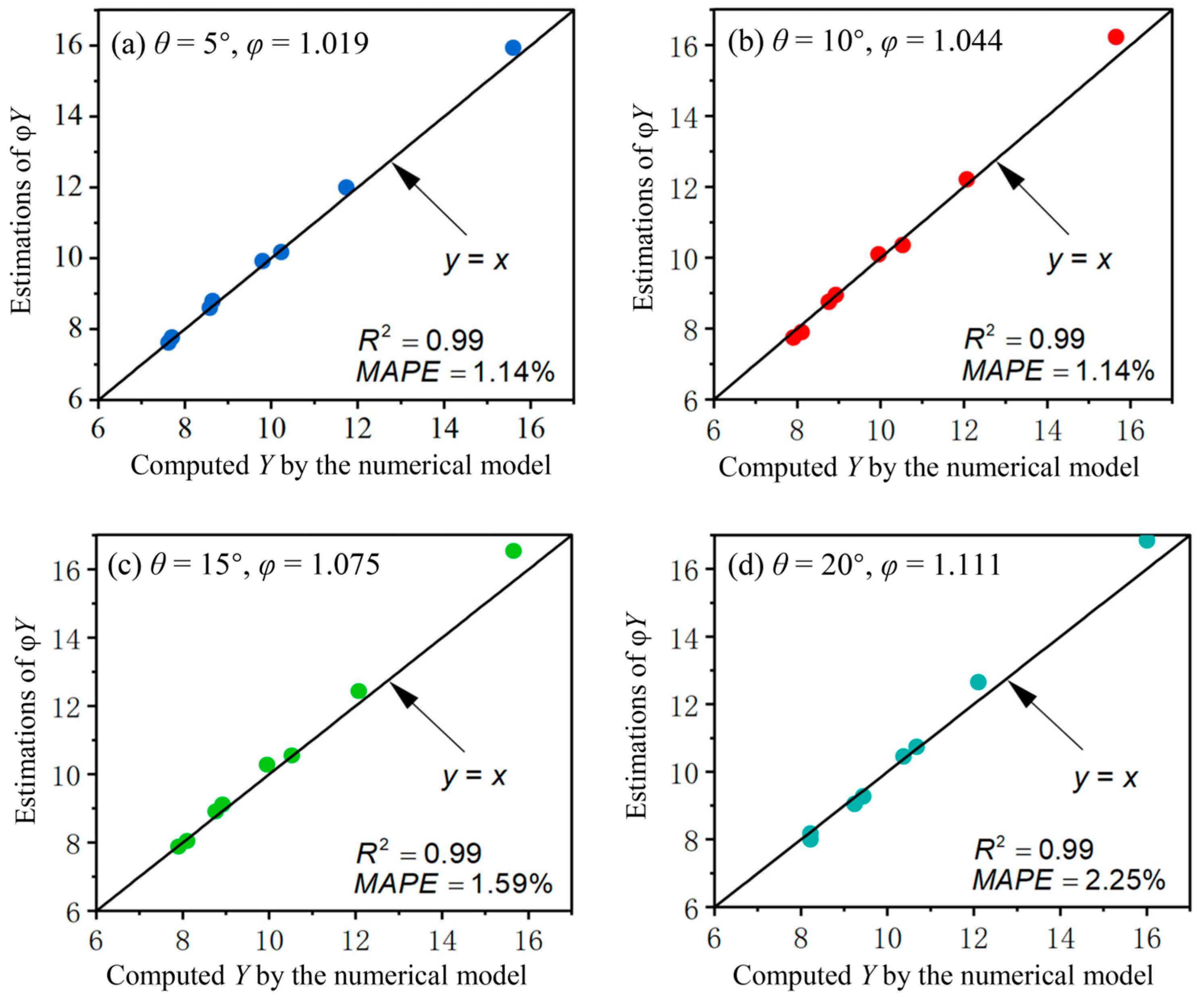
3.1. Sequent Depth Ratio
3.2. Energy Dissipation Rate
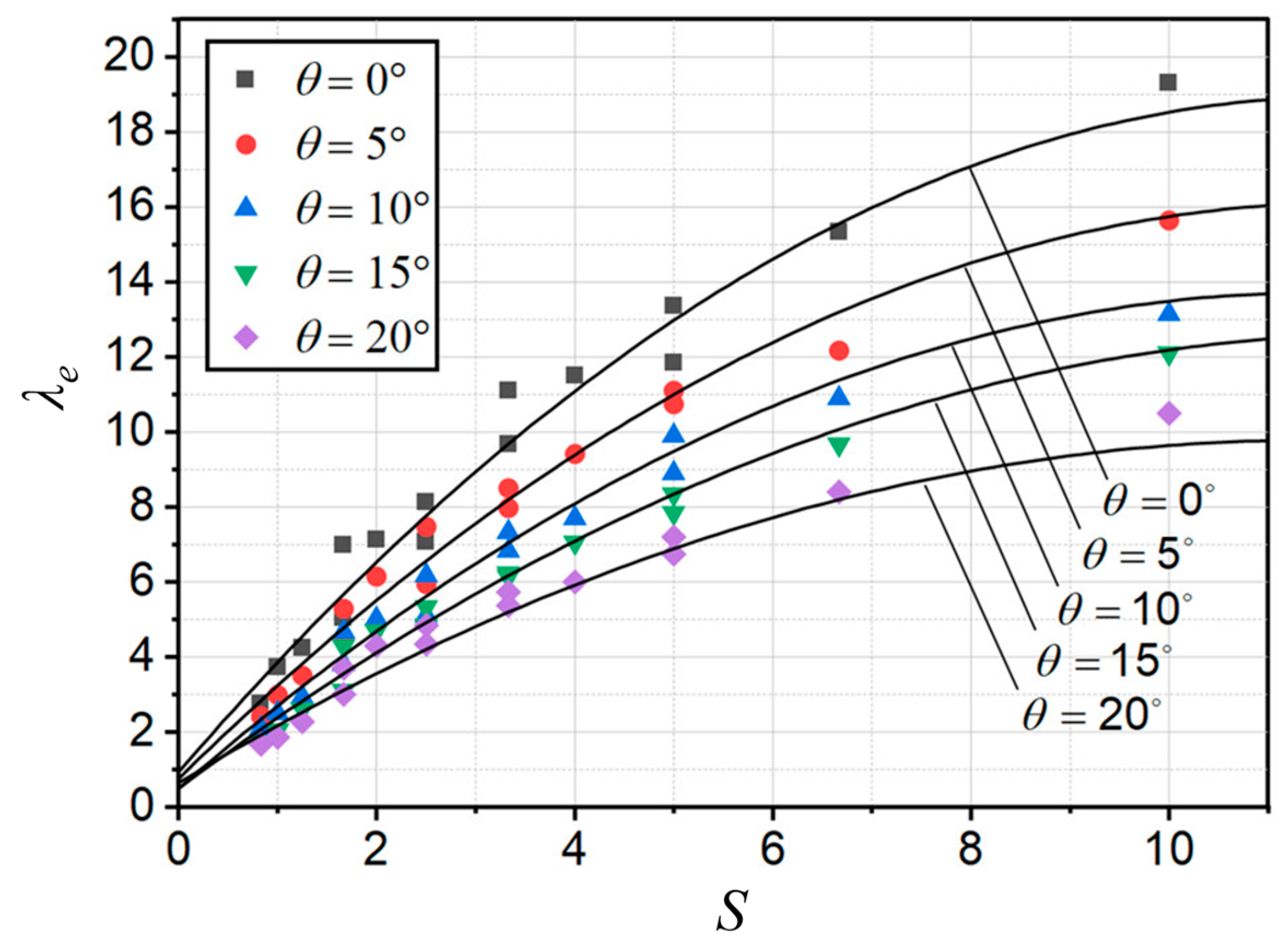
3.3. Roller Length
3.4. Reattachment Length
4. Discussion
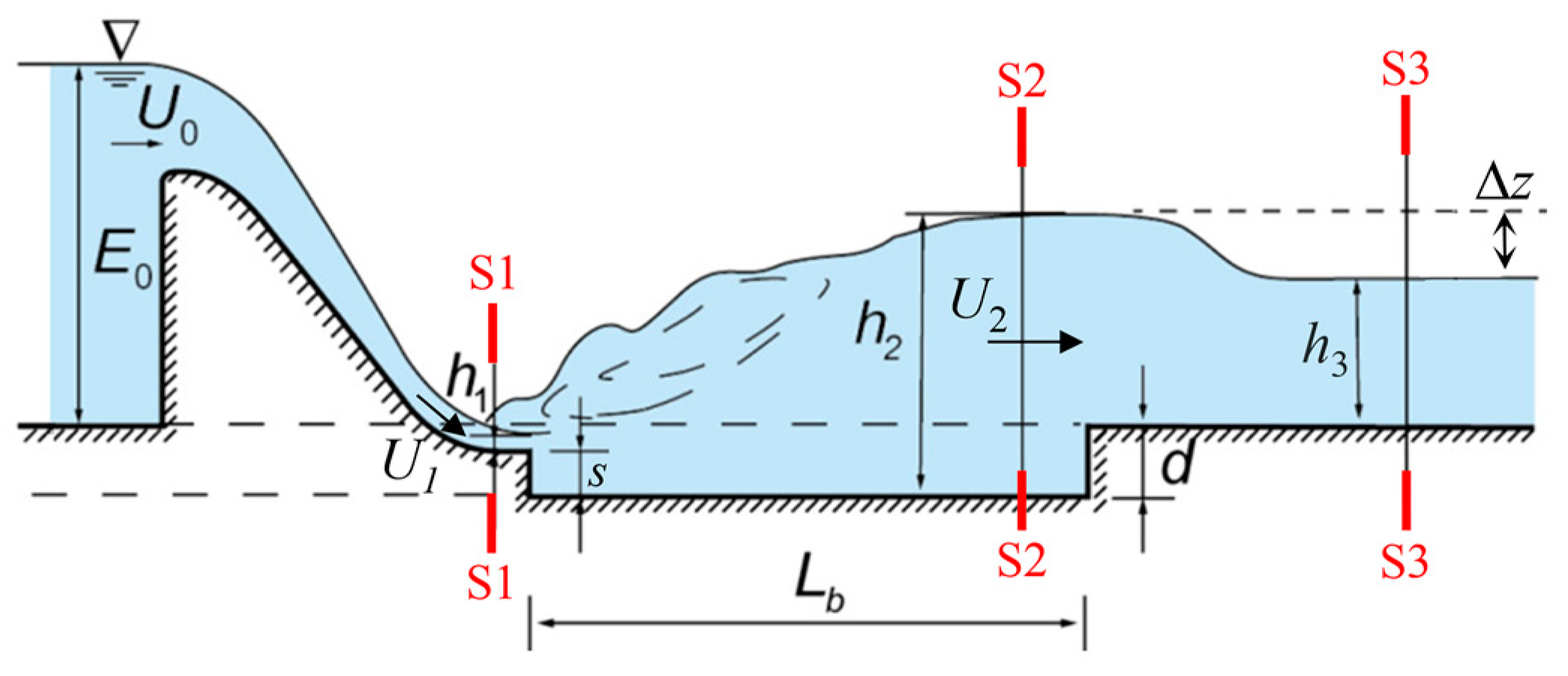
4.1. A Case Study on Stilling Basin Design
- (1)
- Estimate the negative step height (S).
- (2)
- Determining the depth of the stilling basin (d).
- (3)
- Determining the length of the stilling basin (Lb).
- (4)
- Estimating the energy dissipation rate (ER).
- (5)
- Estimating characteristic lengths of the generated critical A-jump.
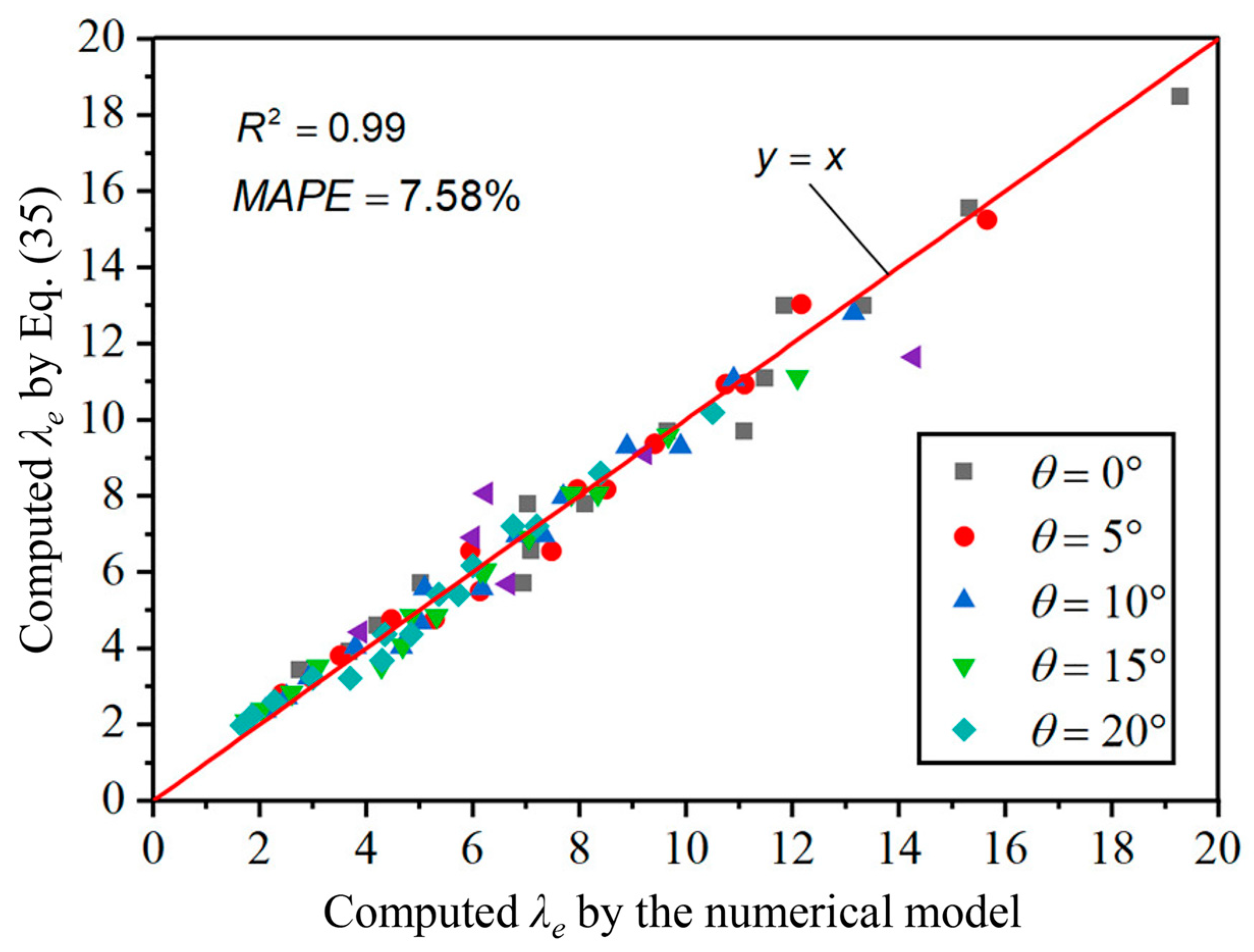
4.2. Validation
5. Conclusions
- (1)
- The relationship between the sequent depth ratio (Y) of the critical A-jumps and the inflow Froude (Fr1) number with the varying negative step height (S) and incident angle (θ) were derived based on the momentum equation. This formula was further revised by adding a correction coefficient (φ) to consider the significant influence of θ on Y when S stays at a low level with 0.833 ≤ S ≤ 2.5, based on the numerical results. The theoretical sequent depth ratio was first calculated using the following formula based on momentum conservation:Then, the value was revised to , which provided an estimated sequent depth ratio for critical A-jumps, considering a wide range of negative step heights and the influence of the incident angle.
- (2)
- Based on the numerical results and regression analysis, an estimation for the dimensionless roller length was proposed, incorporating the influence of the incident angle. A reasonable roller length for A-jumps helps to control hydraulic jumps within the stilling basin, ensuring stable outflows and preventing undesirable flow patterns.
- (3)
- An estimation for the dimensionless reattachment length was proposed, as it plays a crucial role in protecting the basin floor. The estimations were presented as follows:
- (4)
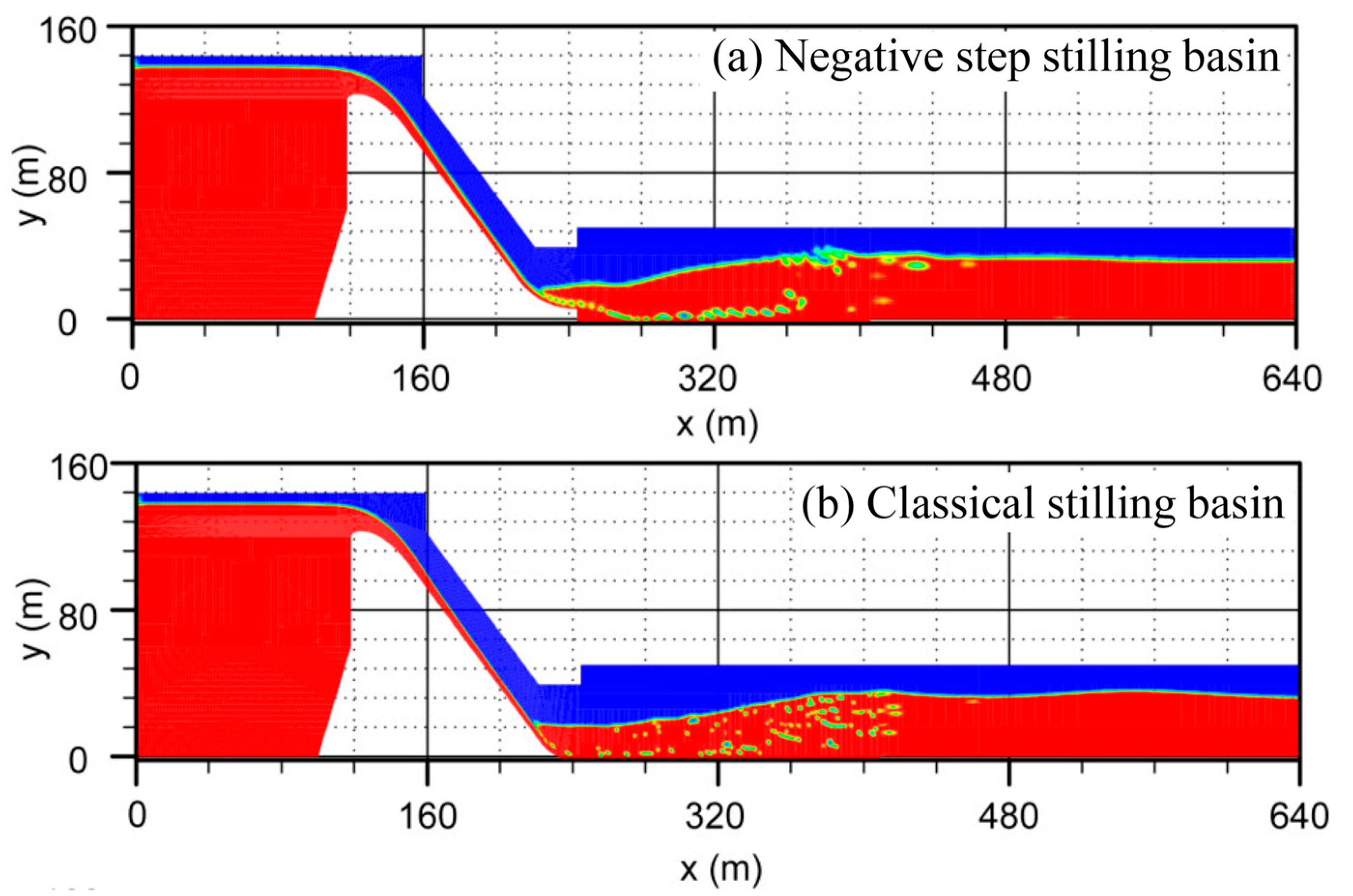
- To validate the proposed estimations, a case study was conducted on a negative step stilling basin designed according to the Design Specification Manual and the proposed estimation methods. The results demonstrated that the estimated key hydraulic characteristics of A-jumps closely aligned with the numerical predictions. The designed stilling basin effectively enhanced the energy dissipation efficiency, stabilized outflows, and significantly reduced the near-bottom flow velocity, thereby preventing impact damage to the basin floor. Compared to the classical stilling basin, the proposed design achieved superior performance. This case study underscored the practical applicability and engineering significance of the proposed estimations.
- (5)
- Estimations of the key characteristic parameters for A-jumps were derived based on scenarios where the dimensionless step height (S = s/h1) ranged from 0.83 to 10.00, the incident angle (θ) varied between 0° and 20°, and the inflow Froude number (Fr1) spanned from 5.6 to 11.3. Although these ranges covered the parameter space of current high dam and large reservoir spillways as comprehensively as possible, the applicability and accuracy of the estimation method must be further verified if variables exceed this range.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| NO. | (cm) | ) | q (m2/s) | h1 (m) | U1 (m/s) | (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 0 | 0.100 | 0.020 | 5.000 | 11.3 | 15.60 | 62.35 | 7.05 | 77.2 |
| 2 | 5 | 0 | 0.140 | 0.030 | 4.667 | 8.6 | 11.70 | 45.57 | 5.03 | 71.2 |
| 3 | 5 | 0 | 0.180 | 0.040 | 4.500 | 7.2 | 9.70 | 38.85 | 4.23 | 66.4 |
| 4 | 5 | 0 | 0.220 | 0.050 | 4.400 | 6.3 | 8.44 | 32.10 | 3.70 | 62.4 |
| 5 | 5 | 0 | 0.260 | 0.060 | 4.333 | 5.6 | 7.57 | 30.75 | 2.75 | 59 |
| 6 | 5 | 5 | 0.100 | 0.020 | 5.000 | 11.3 | 15.60 | 64.65 | 5.95 | 77.1 |
| 7 | 5 | 5 | 0.140 | 0.030 | 4.667 | 8.6 | 11.73 | 49.67 | 4.47 | 71 |
| 8 | 5 | 5 | 0.180 | 0.040 | 4.500 | 7.2 | 9.80 | 39.65 | 3.50 | 65.9 |
| 9 | 5 | 5 | 0.220 | 0.050 | 4.400 | 6.3 | 8.58 | 34.58 | 2.98 | 61.6 |
| 10 | 5 | 5 | 0.260 | 0.060 | 4.333 | 5.6 | 7.62 | 30.95 | 2.42 | 58.6 |
| 11 | 5 | 10 | 0.100 | 0.020 | 5.000 | 11.3 | 15.65 | 67.10 | 5.10 | 76.8 |
| 12 | 5 | 10 | 0.140 | 0.030 | 4.667 | 8.6 | 12.07 | 52.27 | 3.80 | 69.8 |
| 13 | 5 | 10 | 0.180 | 0.040 | 4.500 | 7.2 | 9.95 | 39.73 | 2.93 | 65 |
| 14 | 5 | 10 | 0.220 | 0.050 | 4.400 | 6.3 | 8.76 | 35.44 | 2.50 | 60.3 |
| 15 | 5 | 10 | 0.260 | 0.060 | 4.333 | 5.6 | 7.90 | 32.80 | 2.10 | 56.4 |
| 16 | 5 | 15 | 0.100 | 0.020 | 5.000 | 11.3 | 15.70 | 69.85 | 4.85 | 76.3 |
| 17 | 5 | 15 | 0.140 | 0.030 | 4.667 | 8.6 | 12.30 | 53.90 | 3.10 | 68.6 |
| 18 | 5 | 15 | 0.180 | 0.040 | 4.500 | 7.2 | 10.10 | 40.48 | 2.60 | 63.8 |
| 19 | 5 | 15 | 0.220 | 0.050 | 4.400 | 6.3 | 9.04 | 36.14 | 2.04 | 58.3 |
| 20 | 5 | 15 | 0.260 | 0.060 | 4.333 | 5.6 | 8.15 | 33.33 | 1.75 | 54.2 |
| 21 | 5 | 20 | 0.100 | 0.020 | 5.000 | 11.3 | 16.00 | 72.10 | 4.35 | 75.1 |
| 22 | 5 | 20 | 0.140 | 0.030 | 4.667 | 8.6 | 12.10 | 54.40 | 3.00 | 68.4 |
| 23 | 5 | 20 | 0.180 | 0.040 | 4.500 | 7.2 | 10.38 | 41.23 | 2.28 | 61.8 |
| 24 | 5 | 20 | 0.220 | 0.050 | 4.400 | 6.3 | 9.24 | 37.88 | 1.86 | 56.2 |
| 25 | 5 | 20 | 0.260 | 0.060 | 4.333 | 5.6 | 8.22 | 33.70 | 1.67 | 52.7 |
| 26 | 10 | 0 | 0.100 | 0.020 | 5.000 | 11.3 | 16.29 | 67.85 | 11.85 | 77 |
| 27 | 10 | 0 | 0.140 | 0.030 | 4.667 | 8.6 | 12.03 | 50.80 | 9.67 | 71.5 |
| 28 | 10 | 0 | 0.180 | 0.040 | 4.500 | 7.2 | 9.93 | 41.73 | 8.13 | 67 |
| 29 | 10 | 0 | 0.220 | 0.050 | 4.400 | 6.3 | 8.64 | 33.60 | 7.10 | 63.2 |
| 30 | 10 | 0 | 0.260 | 0.060 | 4.333 | 5.6 | 7.67 | 33.00 | 6.97 | 60.3 |
| 31 | 10 | 5 | 0.100 | 0.020 | 5.000 | 11.3 | 16.50 | 70.65 | 10.75 | 76.6 |
| 32 | 10 | 5 | 0.140 | 0.030 | 4.667 | 8.6 | 12.23 | 51.13 | 8.50 | 70.9 |
| 33 | 10 | 5 | 0.180 | 0.040 | 4.500 | 7.2 | 10.23 | 43.63 | 7.48 | 65.8 |
| 34 | 10 | 5 | 0.220 | 0.050 | 4.400 | 6.3 | 8.64 | 35.80 | 6.14 | 63 |
| 35 | 10 | 5 | 0.260 | 0.060 | 4.333 | 5.6 | 7.70 | 33.10 | 5.28 | 60 |
| 36 | 10 | 10 | 0.100 | 0.020 | 5.000 | 11.3 | 16.35 | 70.80 | 9.90 | 76.6 |
| 37 | 10 | 10 | 0.14 | 0.030 | 4.667 | 8.6 | 12.10 | 52.60 | 7.33 | 70.9 |
| 38 | 10 | 10 | 0.180 | 0.040 | 4.500 | 7.2 | 10.53 | 45.68 | 6.18 | 64.4 |
| 39 | 10 | 10 | 0.220 | 0.050 | 4.400 | 6.3 | 8.92 | 39.80 | 5.02 | 61.4 |
| 40 | 10 | 10 | 0.260 | 0.060 | 4.333 | 5.6 | 8.10 | 34.28 | 4.67 | 57.3 |
| 41 | 10 | 15 | 0.100 | 0.020 | 5.000 | 11.3 | 16.45 | 71.10 | 8.35 | 76 |
| 42 | 10 | 15 | 0.140 | 0.030 | 4.667 | 8.6 | 12.22 | 54.30 | 6.23 | 70.1 |
| 43 | 10 | 15 | 0.180 | 0.040 | 4.500 | 7.2 | 10.70 | 45.80 | 5.33 | 63.2 |
| 44 | 10 | 15 | 0.220 | 0.050 | 4.400 | 6.3 | 9.22 | 40.00 | 4.68 | 59.3 |
| 45 | 10 | 15 | 0.260 | 0.060 | 4.333 | 5.6 | 8.17 | 34.37 | 4.28 | 56.2 |
| 46 | 10 | 20 | 0.100 | 0.020 | 5.000 | 11.3 | 16.50 | 75.40 | 6.75 | 75.3 |
| 47 | 10 | 20 | 0.140 | 0.030 | 4.667 | 8.6 | 12.20 | 60.03 | 5.37 | 69.4 |
| 48 | 10 | 20 | 0.180 | 0.040 | 4.500 | 7.2 | 10.68 | 46.20 | 4.85 | 62.4 |
| 49 | 10 | 20 | 0.220 | 0.050 | 4.400 | 6.3 | 9.44 | 43.40 | 4.30 | 57.3 |
| 50 | 10 | 20 | 0.260 | 0.060 | 4.333 | 5.6 | 8.22 | 36.33 | 3.70 | 54.9 |
| 51 | 20 | 0 | 0.100 | 0.020 | 5.000 | 11.3 | 18.45 | 69.80 | 19.30 | 75.6 |
| 52 | 20 | 0 | 0.140 | 0.030 | 4.667 | 8.6 | 13.57 | 53.47 | 15.33 | 70.1 |
| 53 | 20 | 0 | 0.180 | 0.040 | 4.500 | 7.2 | 11.18 | 42.05 | 13.35 | 65.5 |
| 54 | 20 | 0 | 0.220 | 0.050 | 4.400 | 6.3 | 9.74 | 37.94 | 11.50 | 61.5 |
| 55 | 20 | 0 | 0.260 | 0.060 | 4.333 | 5.6 | 8.80 | 33.33 | 11.10 | 57.6 |
| 56 | 20 | 5 | 0.100 | 0.020 | 5.000 | 11.3 | 18.20 | 72.75 | 15.65 | 75.8 |
| 57 | 20 | 5 | 0.140 | 0.030 | 4.667 | 8.6 | 13.57 | 53.77 | 12.17 | 70 |
| 58 | 20 | 5 | 0.180 | 0.040 | 4.500 | 7.2 | 11.43 | 45.55 | 11.10 | 64.6 |
| 59 | 20 | 5 | 0.220 | 0.050 | 4.400 | 6.3 | 9.74 | 38.30 | 9.42 | 61.3 |
| 60 | 20 | 5 | 0.260 | 0.060 | 4.333 | 5.6 | 8.90 | 34.63 | 7.97 | 57 |
| 61 | 20 | 10 | 0.100 | 0.020 | 5.000 | 11.3 | 17.90 | 74.65 | 13.15 | 76 |
| 62 | 20 | 10 | 0.140 | 0.030 | 4.667 | 8.6 | 14.07 | 54.70 | 10.90 | 68.5 |
| 63 | 20 | 10 | 0.180 | 0.040 | 4.500 | 7.2 | 11.23 | 45.73 | 8.90 | 64.9 |
| 64 | 20 | 10 | 0.220 | 0.050 | 4.400 | 6.3 | 9.80 | 41.06 | 7.70 | 60.8 |
| 65 | 20 | 10 | 0.260 | 0.060 | 4.333 | 5.6 | 8.95 | 36.67 | 6.83 | 56.4 |
| 66 | 20 | 15 | 0.100 | 0.020 | 5.000 | 11.3 | 18.05 | 76.75 | 12.10 | 75.4 |
| 67 | 20 | 15 | 0.140 | 0.030 | 4.667 | 8.6 | 13.60 | 54.77 | 9.67 | 69.1 |
| 68 | 20 | 15 | 0.180 | 0.040 | 4.500 | 7.2 | 11.43 | 46.98 | 7.85 | 63.7 |
| 69 | 20 | 15 | 0.220 | 0.050 | 4.400 | 6.3 | 9.92 | 41.50 | 7.06 | 59.6 |
| 70 | 20 | 15 | 0.260 | 0.060 | 4.333 | 5.6 | 8.95 | 37.68 | 6.15 | 55.7 |
| 71 | 20 | 20 | 0.100 | 0.020 | 5.000 | 11.3 | 18.55 | 76.85 | 10.50 | 74.1 |
| 72 | 20 | 20 | 0.140 | 0.030 | 4.667 | 8.6 | 13.53 | 57.47 | 8.40 | 68.6 |
| 73 | 20 | 20 | 0.180 | 0.040 | 4.500 | 7.2 | 11.30 | 47.30 | 7.20 | 63.3 |
| 74 | 20 | 20 | 0.220 | 0.050 | 4.400 | 6.3 | 9.92 | 44.50 | 6.00 | 58.8 |
| 75 | 20 | 20 | 0.260 | 0.060 | 4.333 | 5.6 | 8.75 | 38.82 | 5.73 | 55.9 |
References
- Luo, M.; Wang, H.; Zheng, X.; Wüthrich, D.; Bai, R.; Liu, S. Air Entrainment and Free-Surface Fluctuations in A-Type Hydraulic Jumps with an Abrupt Drop. J. Hydraul. Res. 2023, 61, 720–734. [Google Scholar]
- Jiang, L.; Diao, M.; Wang, C. Investigation of a Negative Step Effect on Stilling Basin by Using CFD. Entropy 2022, 24, 1523. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Teng, P.; Xie, Q.; Li, S. Understanding Water Flows and Air Venting Features of Spillway—A Case Study. Water 2020, 12, 2106. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Ma, X.; Li, X. Flow Features in a Pooled Fishway with V-Shaped Weir Formation. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1337–1350. [Google Scholar] [CrossRef]
- Wang, T.; Guo, X.; Guo, G.; Fu, H.; Yang, K. New Energy Dissipation Structures for Storm Discharge in Coastal Cities. In Proceedings of the International Conference on Hydraulics, Berlin, Germany, 2–4 November 2015. [Google Scholar]
- Yin, F.; Zhang, Y.; Nie, S.; Ji, H.; Ma, Z. A system-level CFD simulation model for investigating the energy dissipation mechanism of seawater pump and rotary energy recovery device in SWRO desalination system. Desalination 2024, 587, 117947. [Google Scholar]
- Grace, J.L.; Pickering, G.A. Evaluation of Three Energy Dissipators for Storm-Drain Outlets: Hydraulic Laboratory Investigation. J. Hydraul. Res. 1971, 9, 37–42. [Google Scholar]
- Hager, W.H.; Bretz, M. Hydraulic Jumps at Positive and Negative Steps. J. Hydraul. Res. 1986, 24, 237–253. [Google Scholar]
- Wang, H.; Ni, C.; Lyu, W.; Tang, L. A-Type Hydraulic Jumps Over a Negative Step: Numerical Investigation Based on Composite Modeling and Validation. Phys. Fluids 2023, 35, 105–121. [Google Scholar]
- Ohtsu, I.; Yasuda, H. Transition from Supercritical to Subcritical Flow at an Abrupt Drop. J. Hydraul. Res. 1991, 29, 309–328. [Google Scholar]
- Retsinis, E.; Papanicolaou, P. Supercritical Flow over a Submerged Vertical Negative Step. Hydrology 2022, 9, 74. [Google Scholar] [CrossRef]
- Quraishi, A.A.; Al-Brahim, A.M. Hydraulic Jump in Sloping Channel with Positive or Negative Step. J. Hydraul. Res. 1992, 30, 769–782. [Google Scholar] [CrossRef]
- Eroğlu, N.; Taştan, K. Local Energy Losses for Wave-Type Flows at Abrupt Bottom Changes. J. Irrig. Drain. Eng. 2020, 146, 04020029. [Google Scholar] [CrossRef]
- Bai, R.; Wang, H.; Tang, R.; Liu, S.; Xu, W. Roller Characteristics of Preaerated High-Froude-Number Hydraulic Jumps. J. Hydraul. Eng. 2021, 147, 04021008. [Google Scholar] [CrossRef]
- Negm, A.A.M. Hydraulic Jumps at Positive and Negative Steps on Sloping Floors. J. Hydraul. Res. 1996, 34, 409–420. [Google Scholar] [CrossRef]
- Mossa, J.; Petrillo, A.; Chanson, H. Tailwater Level Effects on Flow Conditions at an Abrupt Drop. J. Hydraul. Res. 2003, 40, 13. [Google Scholar] [CrossRef]
- Nasr Esfahani, M.J.; Shafai Bajestan, M. Dynamic Force Measurement of Roughened Bed B-Jump at an Abrupt Drop. Arch. Sci. J. 2012, 65, 47–54. [Google Scholar]
- Nyantekyi-Kwakye, B.; Clark, S.P.; Tachie, M.F.; Malenchak, J.; Muluye, G. Flow Characteristics within the Recirculation Region of Three-Dimensional Turbulent Offset Jet. J. Hydraul. Res. 2015, 53, 230–242. [Google Scholar] [CrossRef]
- Bayón-Barrachina, A.; Valero, E.; García-Bartual, R.; Vallés-Morán, F.; López-Jiménez, P. Performance Assessment of OpenFOAM and FLOW-3D in the Numerical Modeling of a Low Reynolds Number Hydraulic Jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Helal, A.; Elshenawy, Y. Numerical Assessment of the Performance of Bed Water Jets in Submerged Hydraulic Jumps. J. Irrig. Drain. Eng. 2020, 146, 04020014. [Google Scholar] [CrossRef]
- Macián-Pérez, J.F.; Bayón, A.; García-Bartual, R.; López-Jiménez, P.A.; Vallés-Morán, F.J. Characterization of Structural Properties in High Reynolds Hydraulic Jump Based on CFD and Physical Modeling Approaches. J. Hydraul. Eng. 2020, 146, 04020079. [Google Scholar] [CrossRef]
- Huang, G.; Diao, M.; Jiang, L.; Wang, C.; Jia, W. Experimental Study on Wave Characteristics of Stilling Basin with a Negative Step. Entropy 2022, 24, 445. [Google Scholar] [CrossRef] [PubMed]
- Kirkgoz, M.S.; Akoz, M.S.; Oner, A.A. Numerical Modeling of Flow over a Chute Spillway. J. Hydraul. Res. 2009, 47, 790–797. [Google Scholar] [CrossRef]
- Akoz, M.S.; Gumus, V.; Kirkgoz, M.S. Numerical Simulation of Flow over a Semicylinder Weir. J. Irrig. Drain. Eng. 2014, 140, 04014016. [Google Scholar] [CrossRef]
- Bayón-Barrachina, A.; López-Jiménez, P.A. Numerical Analysis of Hydraulic Jumps Using OpenFOAM. J. Hydroinform. 2015, 17, 662–678. [Google Scholar] [CrossRef]
- Spalding, B.E.; Launderd, B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar]
- Yakhot, V.; Orszag, S.A. Renormalization Group Analysis of Turbulence. I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar]
- Koutsourakis, N.; Bartzis, J.G.; Markatos, N.C. Evaluation of Reynolds Stress, k-ε, and RNG k-ε Turbulence Models in Street Canyon Flows Using Various Experimental Datasets. Environ. Fluid Mech. 2012, 12, 379–403. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar]
- Simsek, O.; Soydan, N.G.; Gümü, V.; Akz, M.S.; Kirkgz, M.S. Numerical Modeling of B-Type Hydraulic Jump at an Abrupt Drop. Tek. Dergi 2015, 26, 7215–7240. [Google Scholar]
- Issa, R.I. Solution of the Implicitly Discretised Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar]
- Hager, W.H. B-Jumps at Abrupt Channel Drops. J. Hydraul. Eng. 1985, 111, 861–866. [Google Scholar]
- Hager, W.H.; Sinniger, R. Flow characteristics of the hydraulic jump in a stilling basin with an abrupt bottom rise. J. Hydraul. Res. 1985, 23, 101–113. [Google Scholar]
- Hager, W.H.; Bremen, L.; Kawagoshi, N. Classical Hydraulic Jump: Length of Roller. J. Hydraul. Res. 1990, 28, 591–608. [Google Scholar]
- Guan, X.; Hu, K.; Chen, X.; Gao, J.; Shi, H. Investigating the intense sediment load by dam-break floods using a meshless two-phase mathematical model. Water Resour. Res. 2024, 60, e2023WR035399. [Google Scholar]
- National Energy Administration. Design Guidelines for Energy Dissipation and Scour Prevention of Hydraulic Structures in Hydropower Projects; China Electric Power Press: Beijing, China, 2019.
- Li, W. Hydraulic Calculation Manual; China Water Power Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Sichuan University Key Laboratory of Hydraulics and Mountain River Development & Protection. Hydraulics; Higher Education Press: Beijing, China, 2016; Volume, I. (In Chinese) [Google Scholar]

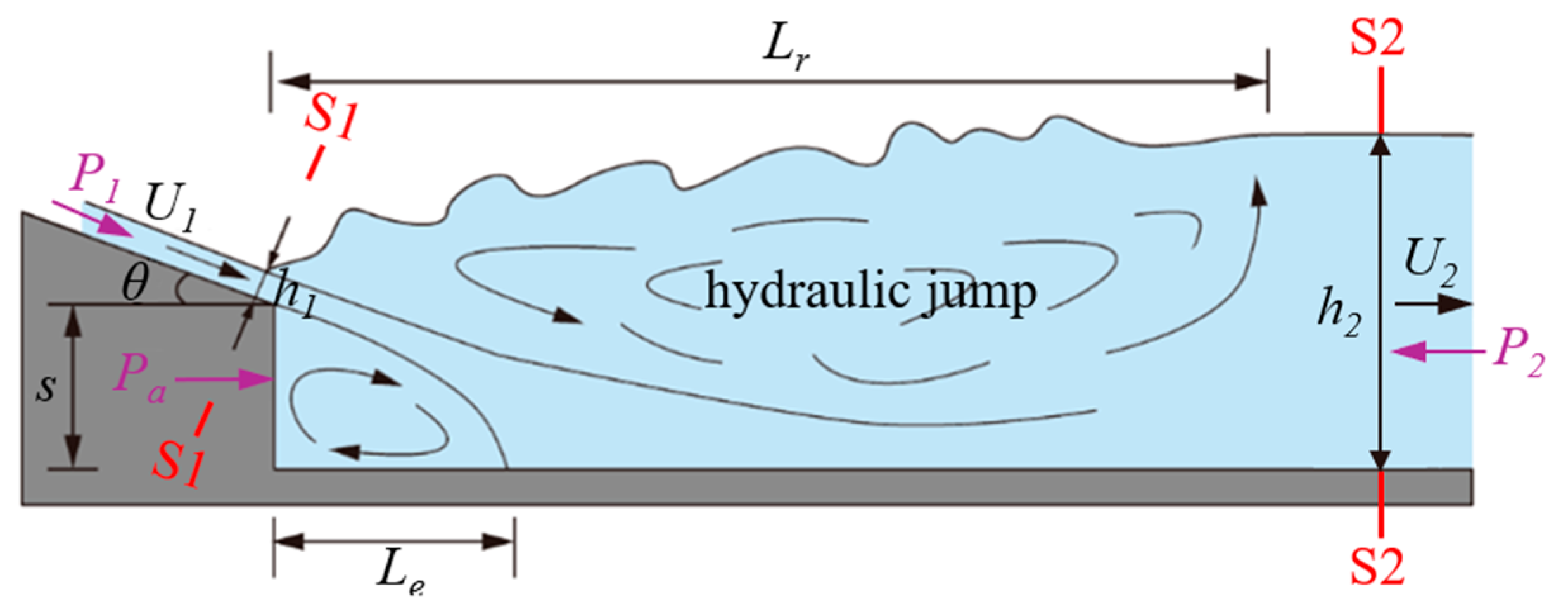
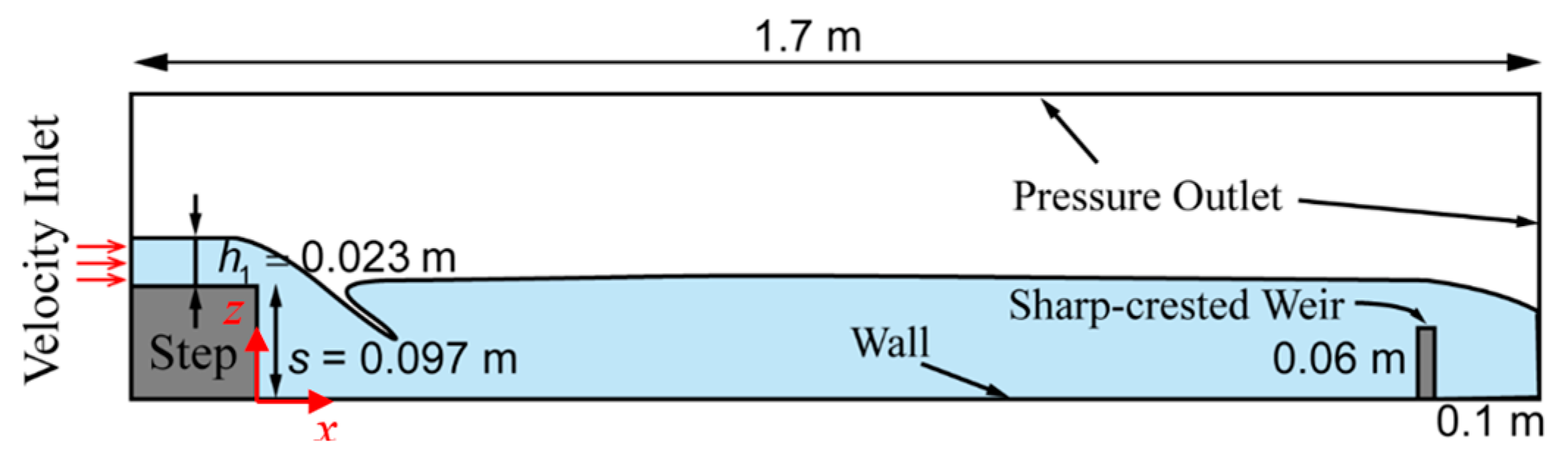
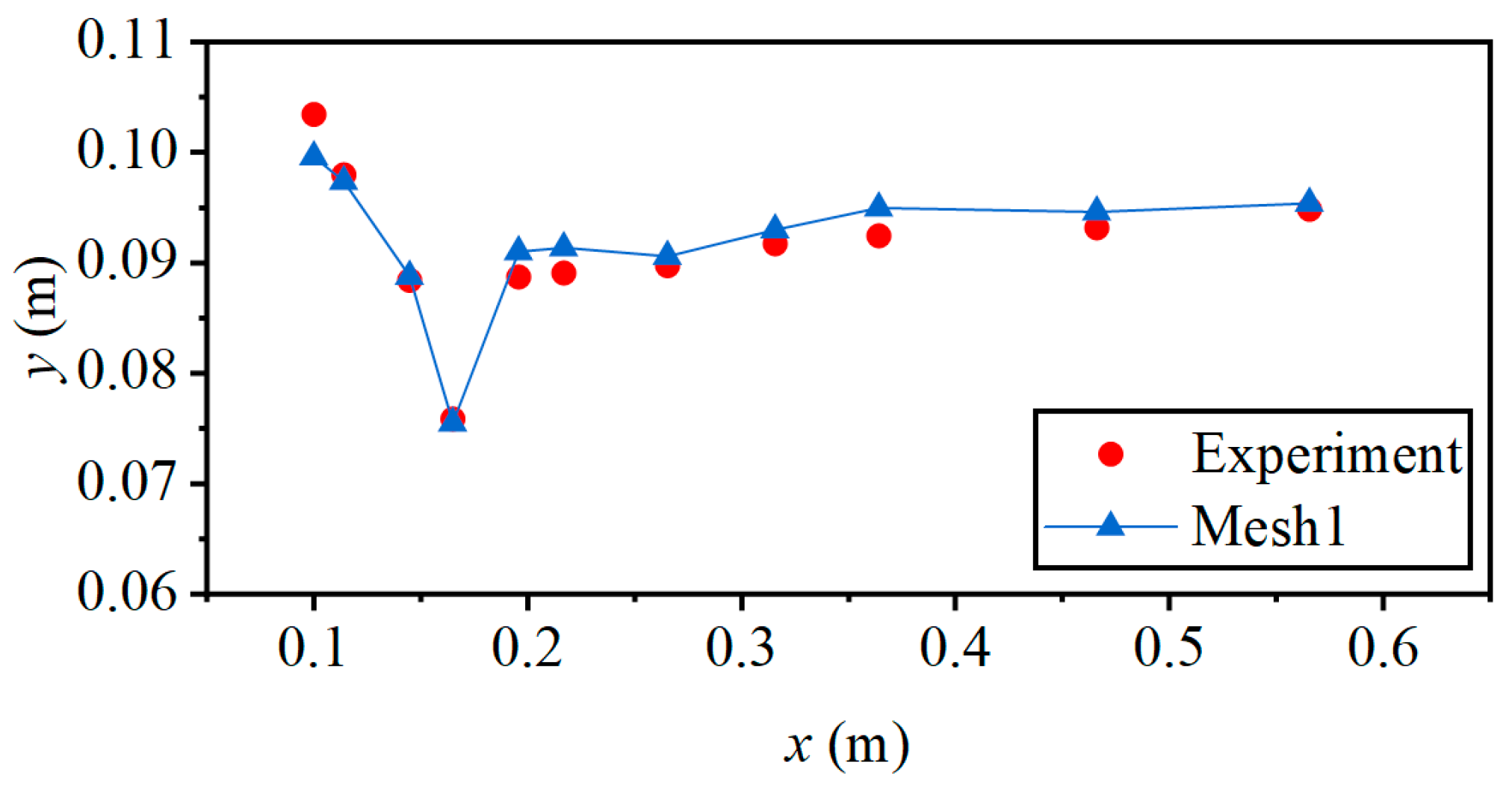

| x (m) | (m) | (m) | (m) | (m) | |||
|---|---|---|---|---|---|---|---|
| 0.100 | 0.100 | 0.097 | 0.096 | 0.103 | −2.91% | −5.83% | −6.80% |
| 0.114 | 0.097 | 0.095 | 0.096 | 0.098 | −1.02% | −3.06% | −2.04% |
| 0.145 | 0.089 | 0.087 | 0.085 | 0.088 | 1.14% | −1.14% | −3.41% |
| 0.165 | 0.075 | 0.074 | 0.074 | 0.076 | −1.32% | −2.63% | −2.63% |
| 0.196 | 0.091 | 0.094 | 0.095 | 0.088 | 3.41% | 6.82% | 7.95% |
| 0.217 | 0.091 | 0.092 | 0.095 | 0.089 | 2.25% | 3.37% | 6.74% |
| 0.265 | 0.091 | 0.095 | 0.096 | 0.09 | 1.11% | 5.56% | 6.67% |
| 0.316 | 0.093 | 0.095 | 0.096 | 0.092 | 1.09% | 3.26% | 4.35% |
| 0.364 | 0.095 | 0.095 | 0.096 | 0.092 | 3.26% | 3.26% | 4.35% |
| 0.466 | 0.095 | 0.095 | 0.096 | 0.093 | 2.15% | 2.15% | 3.23% |
| 0.566 | 0.095 | 0.095 | 0.096 | 0.095 | 0.00% | 0.00% | 1.05% |
| Parameters | Estimations | Estimated Value | Adopted Value |
|---|---|---|---|
| ) | Equation (36) | 8.75 m | 8.0 m |
| ) | Equations (16), (18), (37)–(39) | 2.57 m | 2.57 m |
| Inflow depth () | Equations (16), (18), (37)–(39) | 2.78 m | 2.78 m |
| Sequent depth () | Equations (16), (18), (37)–(39) | 34.11 m | 34.11 m |
| ) | Equations (40) and (41) | 161.7 m | 161.0 m |
| ) | Equation (23) | 70.4% | - |
| ) | Equation (29) | 50.46 | - |
| ) | Equation (35) | 8.63 | - |
| Values | (%) | (m) | (m) | |
|---|---|---|---|---|
| Estimated by the proposed formula | 12.3 | 70.4 | 140.3 | 24.0 |
| Computed by the numerical model | 14.6 | 72.5 | 173.2 | 23.2 |
| Relative error | −15.75% | −2.90% | −19.00% | 3.45% |
| Type | (m) | (m) | Lb (m) | (%) | (m/s) | (m) | (m) |
|---|---|---|---|---|---|---|---|
| Negative step stilling basin | 8.0 | 2.57 | 161.0 | 72.5 | 26.6 | 173.2 | 23.2 |
| Classical stilling basin | 0.0 | 2.09 | 164.0 | 73.2 | 46.2 | 187.9 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Deng, Y.; Liu, Y.; Fang, L.; Guan, X. Insights into the Hydraulic Characteristics of Critical A-Jumps for Energy Dissipator Design. Water 2025, 17, 960. https://doi.org/10.3390/w17070960
Jiang L, Deng Y, Liu Y, Fang L, Guan X. Insights into the Hydraulic Characteristics of Critical A-Jumps for Energy Dissipator Design. Water. 2025; 17(7):960. https://doi.org/10.3390/w17070960
Chicago/Turabian StyleJiang, Lei, Yao Deng, Yangrong Liu, Lindong Fang, and Xiafei Guan. 2025. "Insights into the Hydraulic Characteristics of Critical A-Jumps for Energy Dissipator Design" Water 17, no. 7: 960. https://doi.org/10.3390/w17070960
APA StyleJiang, L., Deng, Y., Liu, Y., Fang, L., & Guan, X. (2025). Insights into the Hydraulic Characteristics of Critical A-Jumps for Energy Dissipator Design. Water, 17(7), 960. https://doi.org/10.3390/w17070960





