Probability Distribution Functions of Velocity Fluctuations and Quadrant Analysis on Turbulent Flow Around a Horizontal Cylinder Across a Channel Bed

Abstract

An experiment is conducted to investigate the turbulent flow field close to a wall-fastened horizontal cylinder. The evolution of the flow field is analyzed by evaluating turbulent flow characteristics and fluid dynamics along the lengthwise direction. The approach flow velocity retards in the immediate upstream area of the cylinder. At the crest level of the cylindrical pipe, the turbulence characteristics such as Reynolds stresses and turbulence intensities are attaining their peaks. Gram–Charlier (GC) series-based Hermite polynomials yield probability density functions that better match experimental data than those from Gram–Charlier (GC) series-based exponential distributions, demonstrating the superiority of the Hermite polynomial method. Quadrant analysis reveals that sweeps (Q4) dominate intermediate and free-surface zones, while ejections (Q2) prevail near the bed, both being primary contributors to Reynolds shear stress (RSS). The stress component remains minimal or zero for all events when $\mathrm{hole} \mathrm{size} \left(\mathrm{H}\right)\ge \mathrm{six}$. Larger hole sizes (≥five) drastically reduced the stress fraction, approaching zero. The stress fraction was highest near the cylinder, decreasing with distance and eventually plateauing. The study enhances the understanding of flow hydraulics around cylindrical objects in rough-bed natural streams.

1. Introduction

The study of flow interactions with cylindrical structures remains a fundamental focus in fluid mechanics, structural engineering, hydrodynamics, and geophysical and environmental flow dynamics [1,2].

A pipeline installed on an erodible bed results in sediment erosion around it, leading to its partial suspension. The scouring process induces vortex shedding, generating unsteady hydrodynamic forces, including lift and drag, which compromise pipeline stability and may cause structural damage. A comprehensive understanding of the flow dynamics around the pipeline is essential to mitigate these issues. The authors have shown the exposed cylindrical pipeline in a lined and unlined channel across the width of the drainage system. Their impact and erosion under the pipes are observed in both channels, as shown in Figure 1.

The cylindrical pipeline causes erosion and degradation surrounding both channels while a channel bed is dry. This cylindrical wall significantly impacts the velocity distribution, turbulence, vortex formation, etc. [2,3]. The flow past a circular cylinder adjacent to the plane boundary has undergone extensive study due to its significant engineering applications [1,2,3,4]. Akoz et al. [1] investigated the flow behavior of a circular cylinder positioned on a free surface in a wide open channel, and quantitatively analyzed it using PIV. Around the cylinder, flow structures remain dynamic due to the continuous evolution of shear flow phenomena. The high circulatory motion of vorticial structures significantly enhances entrainment, forming wake flow patterns. Magnier et al. [4] investigated turbulence behavior near two wall-mounted obstacles arranged in tandem, simulating seabed obstruction in greater Reynolds number (R_e) flow. Taye et al. [5] carried out an experiment at the center of the sinuous bend and investigated the variation of various parameters such as time mean flow velocity, Reynolds shear stress, and turbulence intensity, and performed quadrant analysis to characterize the turbulence flow.

Devi et al. [2] analyzed the turbulence characteristics and mean flow with a spoiler attachment of pipe and without a spoiler attachment. They observed that the length of the recirculation region extends with the presence of a spoiler on the pipe and turbulence characteristics attained their peak near the spoiler crest, as well as the switching of ejection and sweep events occurred near the crest of the spoiler.

To elucidate primary flow mechanisms across different planes, 2D planar PIV measurements were conducted. The results indicated that the upstream cube markedly alters the wake dynamics of the downstream cylinder by suppressing the formation of large-scale flow structures typically observed around an isolated wall-fastened cylinder under similar flow conditions.

Fluid flow turbulence is defined by the chaotic, erratic motion of the fluid particles, whose velocities alter quickly in space and time [6,7]. Three-dimensional velocity fluctuations caused by the disordered motion of fluid particles are superimposed on the mean value of each velocity component, known as velocity fluctuations. When turbulence is generated, flow velocity fluctuations are primarily associated with large vortices, the turbulent energy is then transferred to small-scale vortices through a process known as the energy cascade, where it remains until it is converted into heat by the molecular viscosity in the viscous subrange [8,9,10]. The reattachment point, and recirculation region behind the cylindrical pipe in the time average velocity vector $\overline{U}={\left({\overline{u}}^2+{\overline{w}}^2\right)}^{0.5}$ plot in the direction of flow, where the zone has been divided into three segments, are depicted in Figure 2. The separation line (dash line) has been obtained such that Reynolds shear stress is zero on the separation line.

A random variable’s probability density function (PDF) describes the likelihood that the random variable will deal with a specific value. The methods representing PDFs, such as Gaussian distribution and log-normal distribution, are characterized by the finite convergence period.

Understanding the relevant turbulent parameters is aided by having working information on the PDF of turbulent variables like velocity fluctuation and Reynolds shear stress [11,12]. For the investigation of joint PDFs of velocity fluctuation obtained by inverting Gaussian-based characteristics functions, (Feriet and Kampe, [8]; and Antonia and Atkinson, [13]) GC-series expansion was used. The shear layer may be severely deformed in the reattachment region, invalidating the standard thin layer estimates. To explore the effects of additional strains caused by separation and reattachment on the flow characteristics and the subsequent reconstruction to an equilibrium state, separated and reattaching turbulent flows can be utilized as prototype flows in this regard. Geometry-induced separated turbulent flows have been broadly examined in the past due to their wide range of practical and theoretical importance. Sharma and Kumar [14] found that the GC series exponential distribution-based PDFs are relevant for both seepage flow and no seepage; Figure 3 exhibits the side view of the experimental set.

Dey et al. [6,7,8] provided the theoretical formulation for the PDFs of velocity fluctuation and Reynolds shear stress. A curved cross-section alluvial channel’s PDFs were experimentally explored [15], and it was found that the PDFs they produced followed the theoretical curves based on the GC series exponential variation. A similar study carried out by Gurugubelli et al. [16] in the asymmetric sinuous alluvial channel examined the turbulent structures and PDF distribution based on the GC series expansion of turbulence. A Gaussian distribution has zero skewness; any nonzero value indicates temporal asymmetry in velocity fluctuations linked to the bursting process.

The bursting phenomena consist of a series of quasi-cyclic occurrences, the most significant of which are ejections and sweeps. Raupach [17] found that skewness and diffusion in streamwise and vertical velocity fluctuations correlate with ejection and sweep contributions to RSS.

The current study aims to thoroughly investigate the turbulence in the wake region of a horizontal wall-fastened pipe by analyzing key characteristics, including mean flow, turbulence intensities, RSS, TKE, velocity fluctuation probability distribution, a comparison of joint PDFs using GC series-based exponential, and quadrant analysis.

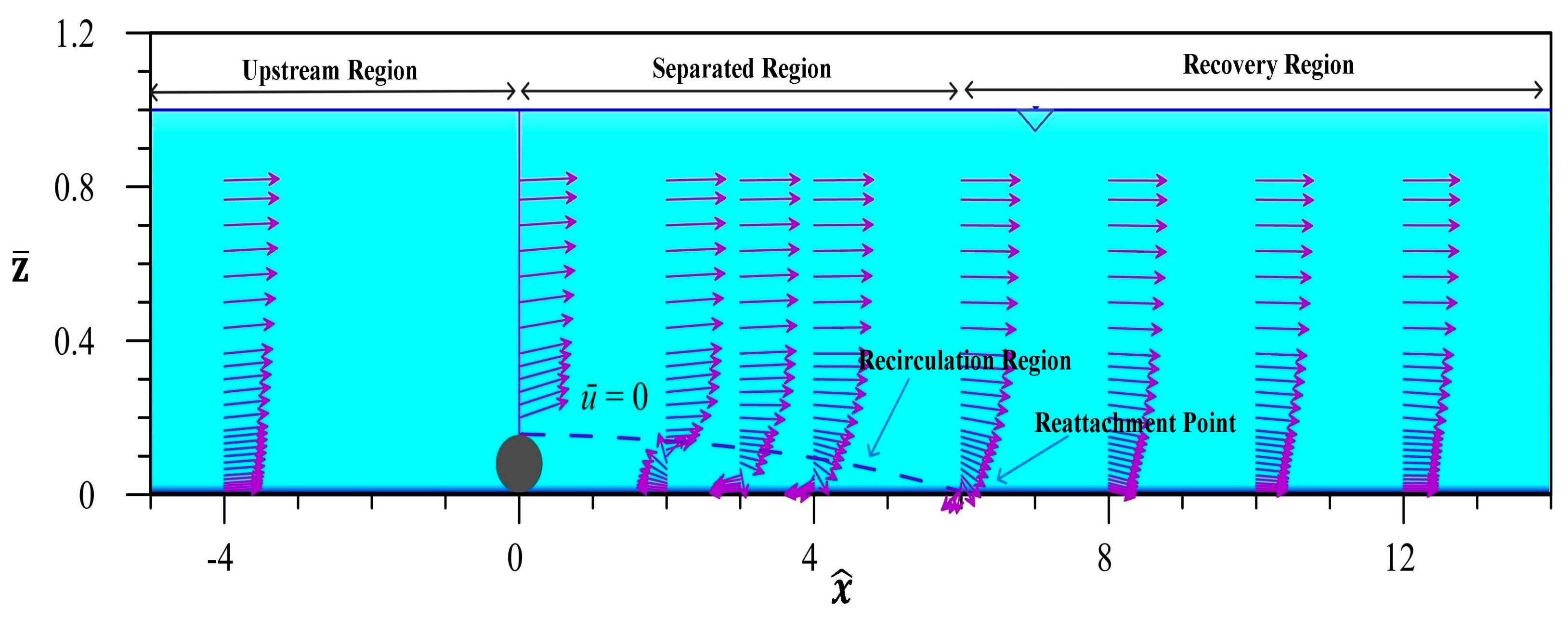
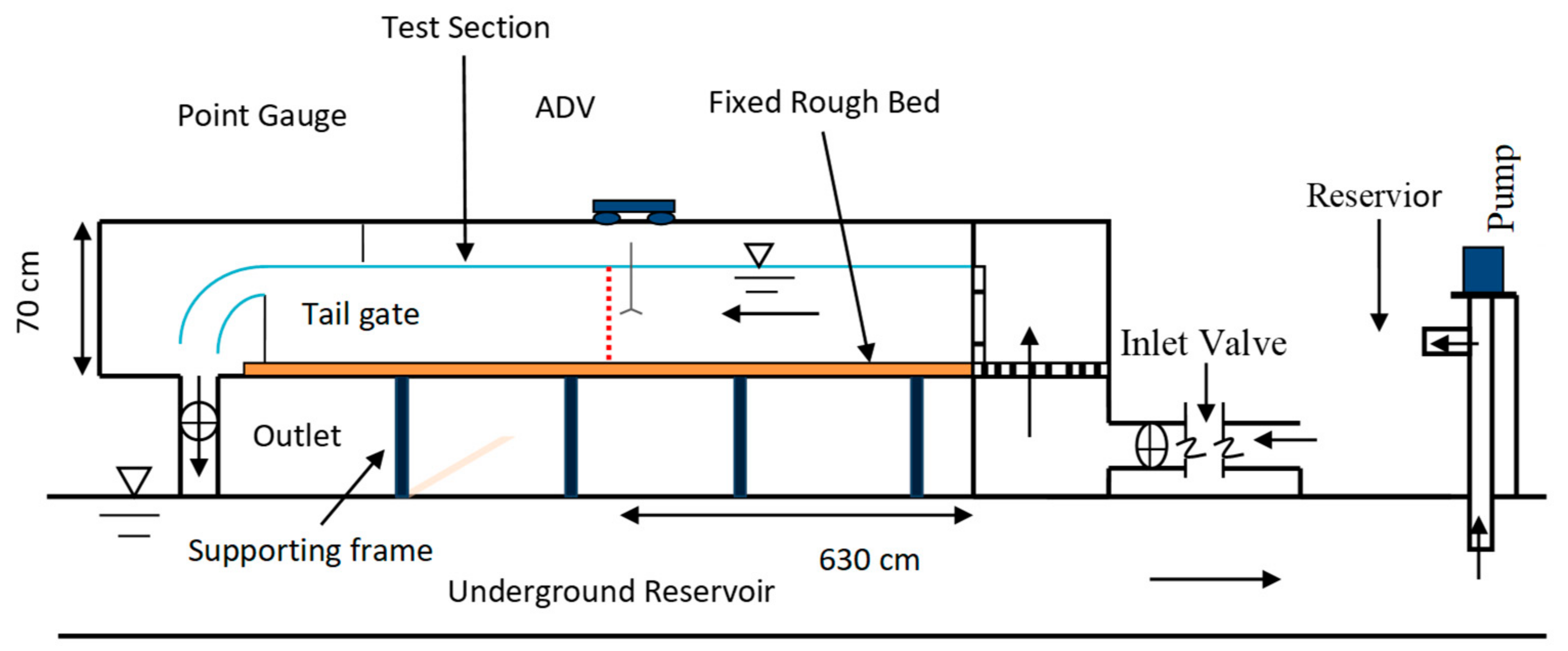
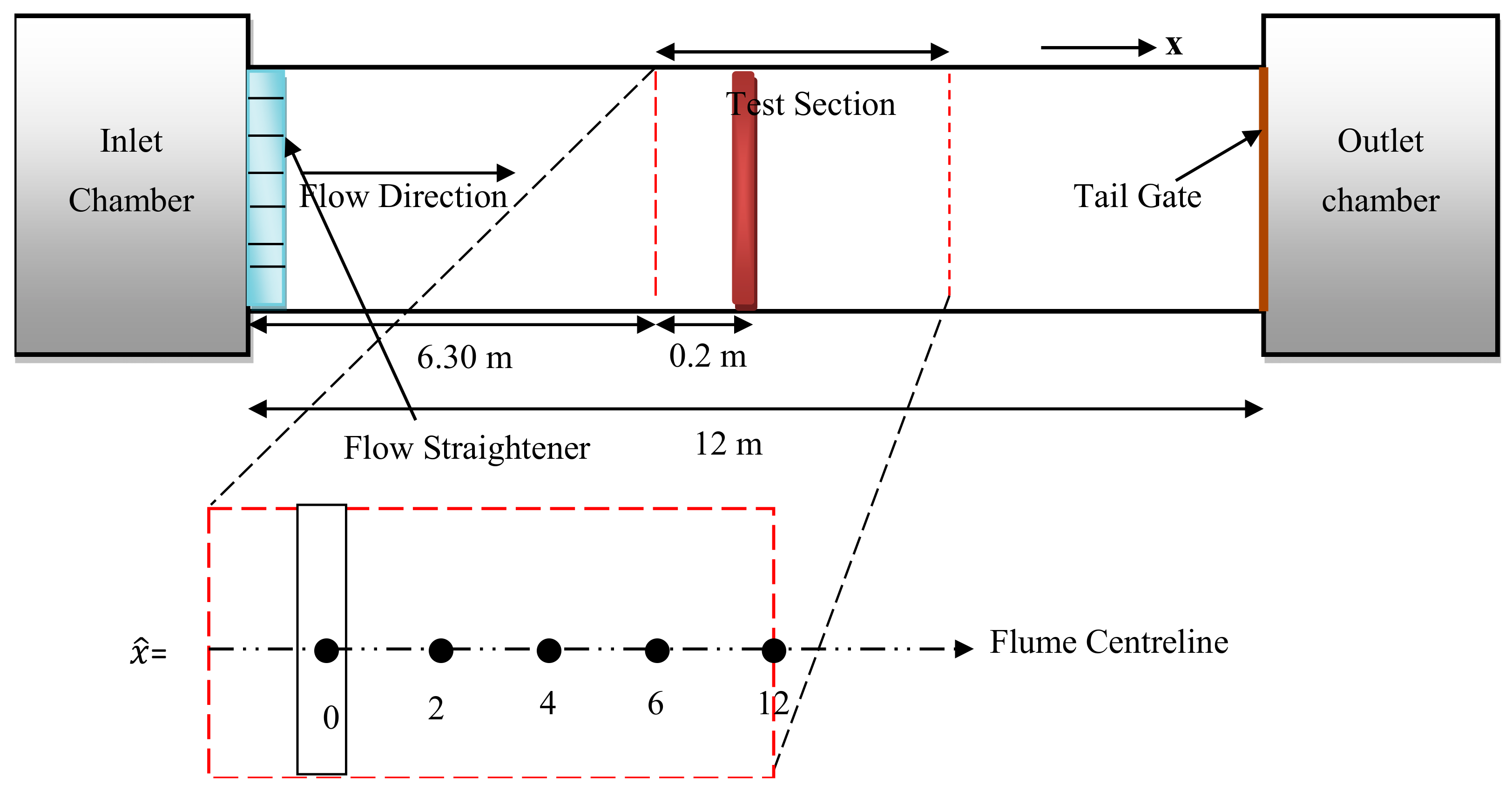
2. Experimental Procedure and Methodology

The experiments were conducted in a narrow open channel in the Civil Engineering Department at the IIT, Kharagpur, India, using a recirculating rectangular laboratory flume (0.91 m wide, 0.7 m deep, and 12 m long) with a bed slope of 0.002.

A centrifugal pump was installed to transfer water from an underground sump to the laboratory’s overhead reservoir. Upstream, a stilling basin receives water from the overhead tank. To regulate the flow rate into the flume, a valve is placed between the overhead tank and the stilling basin. For the stabilization of flow, the inlet consists of a honeycomb. An adjustable tailboard was employed at the flume’s downstream end to obtain appropriate flow depth.

Water was released into a sump tank through a vertical pipeline, and a rough bed was created by adhering uniformly sized sand particles (d₅₀ = 2.25 mm) to make a smooth channel bottom. The test section, considered 630 cm from the inlet, ensured a fully developed rough flow. The 3D velocities were measured using a Nortek Vectrino Plus four-arms probe (10 MHz) (Nortek AS, Rud, Norway), with a sampling rate of 100 Hz and an interval of 5 min, to obtain time-independent turbulence statistics. Doppler signal correlations exceeded 80%, and the signal-to-noise ratio was kept above 17. Raw data from the Vectrino + ADV was filtered for spikes using Gonzalez-Castro and Muste’s [18] and Goring and Nikora’s [19] phase space threshold method. Low-frequency spikes can result from interference between the incoming acoustic signal and its reflected pulses [20].

Velocity profiles were measured at different streamwise locations, using a 300-s sampling period for each measurement. The geometric standard deviation (d₈₄/d₁₆) of the sand was 1.1, indicating uniform sand with a gradation coefficient of 1.10 (<1.4). The experiment was carried out with a flow depth (h) of 0.3 m, and the approach flow shear velocity (u*) was calculated from the RSS distribution curve by extrapolating it to the flume bed.

The hydraulic and physical parameters for the present experimental run are given in

Table 1. The summary of two experiments.

Runs	D (cm)	h (cm)	U (cm/s)	${\mathit{u}}_{*}$ (cm/s)	${\mathit{F}}_{\mathit{r}}$	$\mathit{R}{\mathit{e}}_{\mathit{D}}$
1	8	30	15	0.71	0.087	12,000
2	8	30	19	0.92	0.111	15,200

. Froude number (Fr) is based on the approach flow depth (h) and cross-sectional area-averaged velocity (U) and is equal to ${\displaystyle \frac{v}{\sqrt{gh}}}$, and R_e of the flow (4RU/υ), where R is a hydraulic radius. With a point gauge and a Vernier scale attachment, the flow depth was measured with an accuracy of 0.1 mm. All the experimental data was collected in the channel’s central wall-normal plane (xz), and under two distinct R_e, Run_1 and Run_2 (Table 1). The correlation between transmitted and received signals, along with the signal-to-noise ratio (SNR), was utilized as a filtering criterion for velocity data. ADV measurements often contain spurious outliers, which were removed to mitigate noise using a MATLAB-based despiking algorithm (MATLAB version is R2024b). This algorithm employs the phase-space threshold method, a technique previously developed by other researchers [19].

A pipe model with a diameter of 8 cm was used for all four runs. Throughout the whole experiment, approach area-averaged velocities (U) of 15 and 19 cm/s were kept consistent for the depth of flow 30 cm.

The value of $F_r$ shows that subcritical flow conditions exist. The data were collected at three lengthwise locations ($\widehat{x}$ = 2, 7.25, and 12) for each run. Here, $\widehat{x}$ is the non-dimensional lengthwise distance. The rest of the data measurement locations are in the pipe’s wake zone, with $\widehat{x}$ = 0 designating the area directly above the pipe. Data were gathered for each measurement location at three wall-normal positions with z values of 0.9, 0.6, and 19 cm, as shown in Figure 4.

3. Theoretical Background

The probability density function (PDF) defines the distribution of a continuous random variable within a specified range [6]. It quantifies the likelihood of the variable assuming particular values. The GC series is employed for probability distributions in this study. The GC series is useful for series with intervals across which the application of convergence is infinite [20].

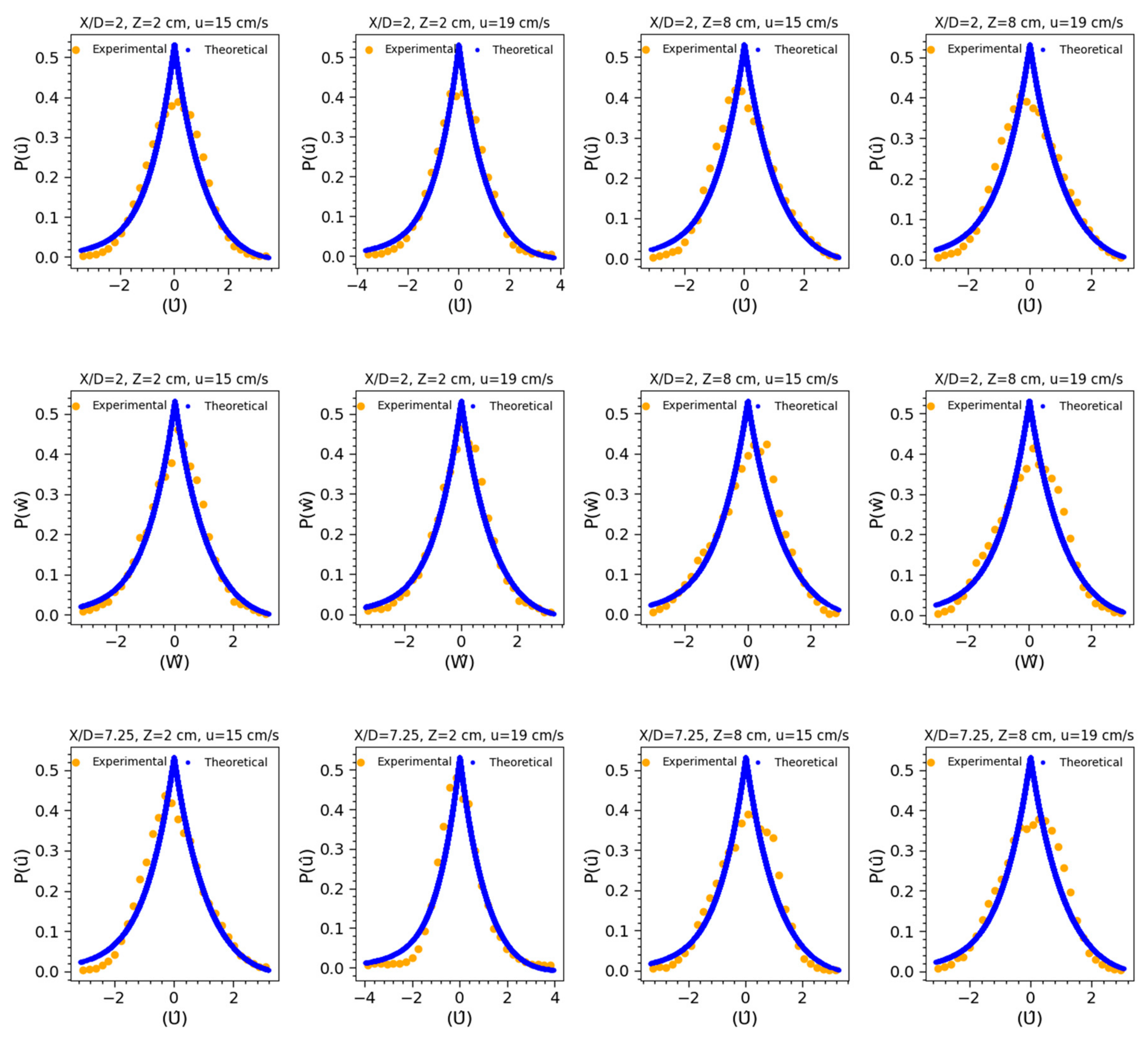
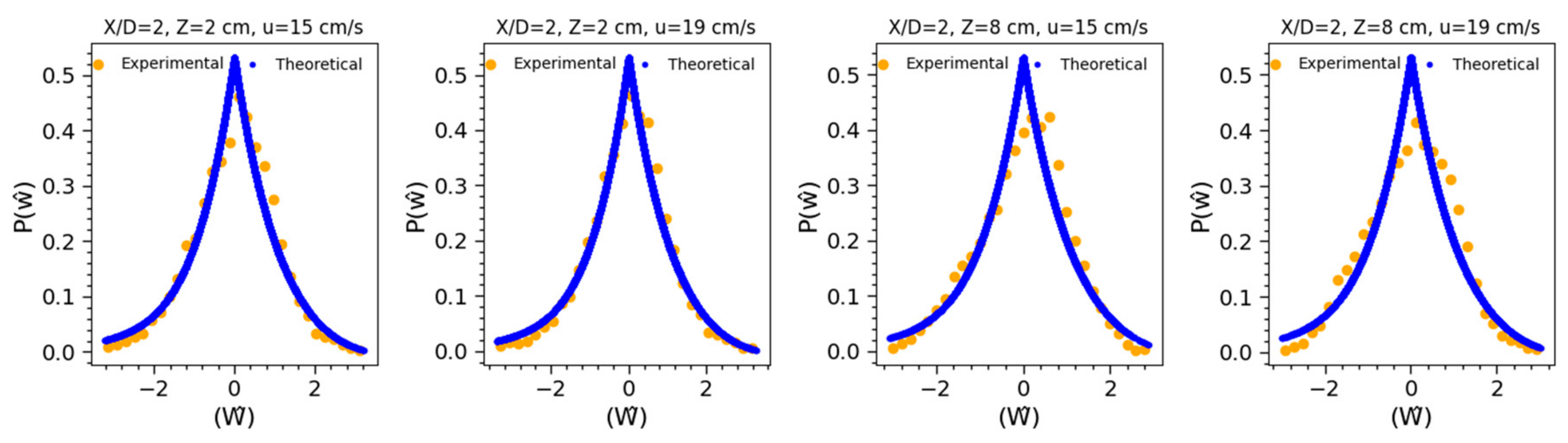
3.1. Probability Function for Velocity Fluctuation

Velocity fluctuation (u′, w′) follows the exponential distribution-based GC series [2,16]. For normalizing u′ and w′ to get $\hat{\mathrm{u}}$ and $\hat{\mathrm{w}}$, the ${\mathsf{\sigma }}_{\mathrm{u}}$ and ${\mathsf{\sigma }}_{\mathrm{w}}$ are computed from the root-mean-square values of u′ and w′, which are written as $\hat{\mathrm{u}}=u^{\prime }/{\sigma }_u$ and $\hat{\mathrm{w}}=w^{\prime }/{\sigma }_w$ where ${\mathsf{\sigma }}_{\mathrm{u}}$ and ${\mathsf{\sigma }}_{\mathrm{w}}$ are the lengthwise and vertical turbulence intensity; their PDF is represented by [6,17].

$${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}=\left[\begin{array}{c}{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{4}}{ \mathrm{C}}_{10} \hat{\mathrm{u}}-{\displaystyle \frac{1}{16}}{ \mathrm{C}}_{20 }\left(1+\left|\hat{\mathrm{u}}\right|-{\hat{\mathrm{u}}}^2\right)\\ -{\displaystyle \frac{1}{96}}{ \mathrm{C}}_{30} \hat{\mathrm{u}}\left(3+3 \left|\hat{\mathrm{u}}\right|-{\hat{\mathrm{u}}}^2\right)\\ +{\displaystyle \frac{1}{768}}{ \mathrm{C}}_{40} \hat{\mathrm{u}} \left(9+9 \left|\hat{\mathrm{u}}\right|-3{\hat{\mathrm{u}}}^2-6 {\left|\hat{\mathrm{u}}\right|}^3+{\hat{\mathrm{u}}}^4\right)+--- \end{array}\right] \exp \left(-\left|\hat{\mathrm{u}}\right|\right)$$

(1)

$${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}=\left[\begin{array}{c}{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{4}}{ \mathrm{C}}_{01} \hat{\mathrm{w}}-{\displaystyle \frac{1}{16}}{ \mathrm{C}}_{02 }\left(1+\left|\hat{\mathrm{w}}\right|-{\hat{\mathrm{w}}}^2\right)\\ -{\displaystyle \frac{1}{96}}{ \mathrm{C}}_{03} \hat{\mathrm{w}} \left(3+3 \left|\hat{\mathrm{w}}\right|-{\hat{\mathrm{w}}}^2\right)\\ +{\displaystyle \frac{1}{768}}{ \mathrm{C}}_{04}\hat{\mathrm{w}} \left(9+9 \left|\hat{\mathrm{w}}\right|-3 {\hat{\mathrm{w}}}^2-6 {\left|\hat{\mathrm{w}}\right|}^3+{\hat{\mathrm{w}}}^4\right)+---\end{array}\right] \exp \left(-\left|\hat{\mathrm{w}}\right|\right)$$

(2)

where,

$${ \mathrm{C}}_{10}={\mathrm{m}}_{10}, {\mathrm{C}}_{20}={\displaystyle \frac{1}{2}}{\mathrm{m}}_{20}-1, {\mathrm{C}}_{30}={\displaystyle \frac{1}{6}}{\mathrm{m}}_{30}-2{\mathrm{m}}_{10}, {\mathrm{C}}_{40}={\displaystyle \frac{1}{24}}{\mathrm{m}}_{40}-{\displaystyle \frac{3}{2}}{\mathrm{m}}_{20}+2$$

(3)

Similarly,

$${\mathrm{C}}_{01}={\mathrm{m}}_{01},{ \mathrm{C}}_{02}={\displaystyle \frac{1}{2}}{\mathrm{m}}_{02}-1,{ \mathrm{C}}_{03}={\displaystyle \frac{1}{6}}{\mathrm{m}}_{03}-2{\mathrm{m}}_{01}, {\mathrm{C}}_{04}={\displaystyle \frac{1}{24}}{\mathrm{m}}_{04}-{\displaystyle \frac{3}{2}}{\mathrm{m}}_{02}+2$$

(4)

The coefficients ${\mathrm{C}}_{\mathrm{jk}}$ of the order j + k > 4 in Equations (3) and (4) are not indicated as moments up to order four are considered, and the estimation of moments ${\mathrm{m}}_{\mathrm{jk}}$ is done using the experimental data.

Where

$${\mathrm{m}}_{\mathrm{j}0}=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\widehat{u}}^{\mathrm{j}}{ \mathrm{p}}_{\hat{\mathrm{u}}}\left(\hat{\mathrm{u}}\right) \mathrm{d}\hat{\mathrm{w}}, {\mathrm{m}}_{0\mathrm{k}}=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{\hat{\mathrm{w}}}^{\mathrm{j}}{ \mathrm{p}}_{\hat{\mathrm{w}}}\left(\hat{\mathrm{w}}\right) \mathrm{d}\hat{\mathrm{w}}$$

(5)

The coefficients ${\mathrm{C}}_{\mathrm{j}0}$ and ${\mathrm{C}}_{0\mathrm{k}}$ come into sight in the PDFs, ${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$, rely on the boundary resistance. Therefore, if the relative frequency $f_{ {\widehat{u}}^{\left( \widehat{u}\right)}}$ of the random variable $\hat{\mathrm{u}}$ calculated from the experimental data at a specific location z, then from Equation (5), the ${\mathrm{m}}_{\mathrm{j}0}$ are determined by relating ${\mathrm{p}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$ by $f_{ {\widehat{w}}^{\left( \widehat{w}\right)}}$. Similarly, the ${\mathrm{m}}_{0\mathrm{k}}$ are estimated from $f_{ {\widehat{u}}^{\left( \widehat{u}\right) }}$ of the random variable w. Therefore, using Equations (3) and (4), ${\mathrm{C}}_{\mathrm{j}0}$ and ${\mathrm{C}}_{0\mathrm{k}}$ are calculated, and the corresponding PDFs are determined to derive the theoretical curves for ${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$.

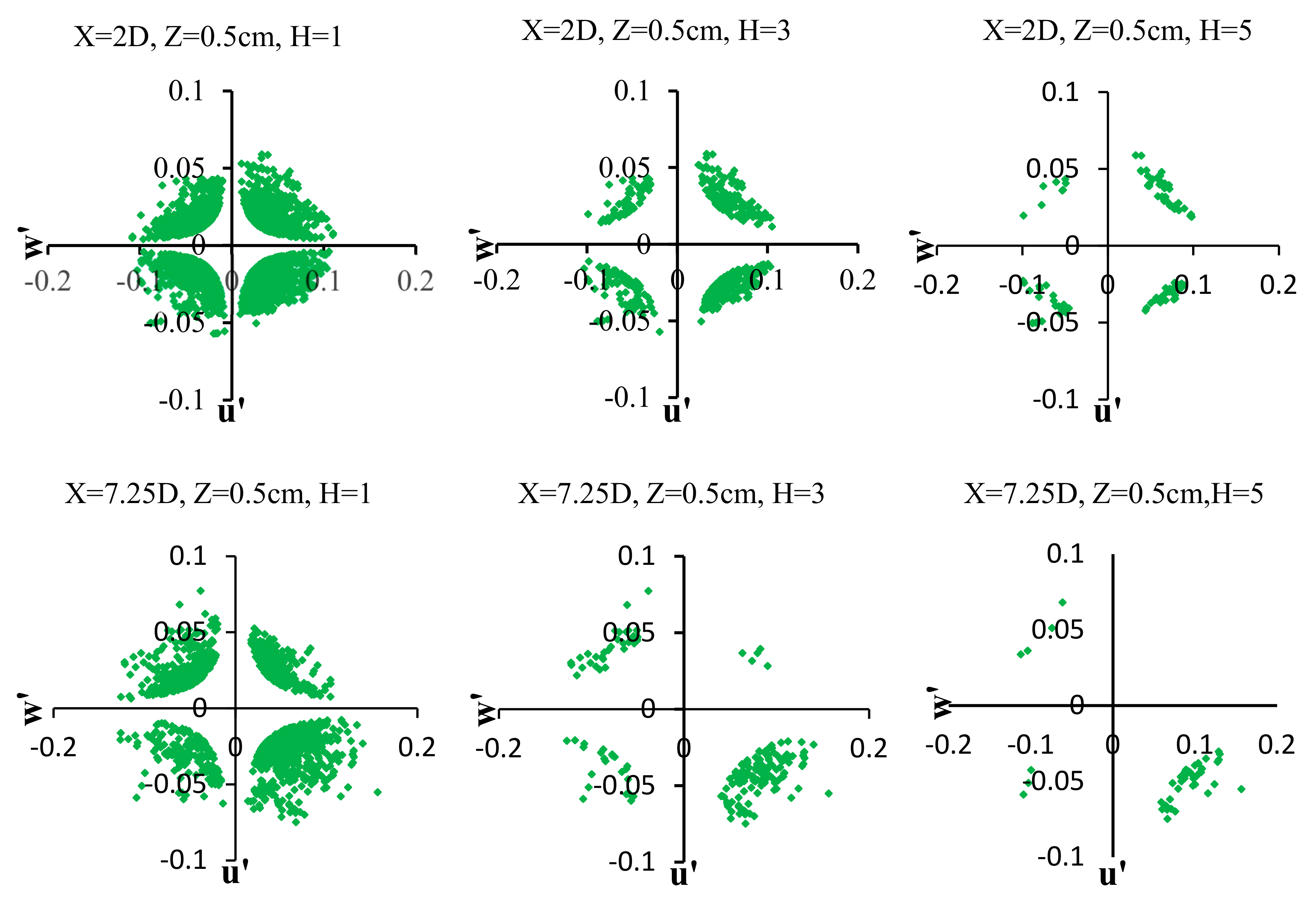
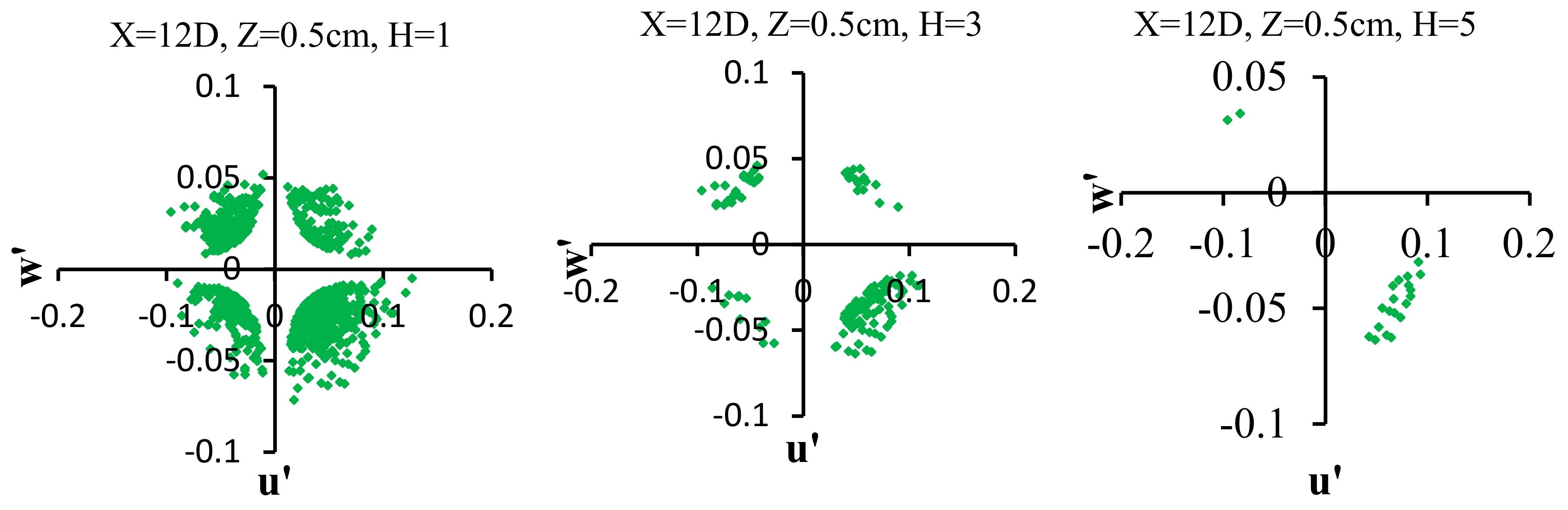
3.2. Quadrant Analysis

The conditional statistics of velocity variations (u′, w′) quantify bursting events, which play a crucial role in sediment transport (Willmarth and Lu, [12]; Nakagawa and Nezu, [21]; Lu and Willmarth, [22]). It is typical to plot the variations of velocity components (u′, w′)d based on the quadrant in a u′w′ plane to determine the overall $-\rho \overline{u^{\prime }{w}^{\prime }},$ as shown in Figure 5.

A hyperbolic zone is a region enclosed by the curve |u′w′| = constant. According to [21], who introduced a parameter H called hole size that stands for the threshold level, the curve determines the hole’s size $\left|u^{\prime }{w}^{\prime }\right|=H{\left(\overline{u^{\prime }{u}^{\prime }}\right)}^{0.5}{\left(\overline{w^{\prime }{w}^{\prime }}\right)}^{0.5}$. When the hole size H is small, it is possible to differentiate between strong and weak events, but only strong events are viable for large values of the hole size. Bursting events are characterized by the four quadrants, i.e., (i =1, 2, 3, and 4). They are (1) the outward interactions Q1 (i = 1, u′ > 0, w > 0), (2) the ejections Q2 (i = 2, u′ < 0, w′ > 0), (3) the inward interactions Q3 (i = 3, u′ < 0, w′ < 0), and (4) the sweeps Q4 (i = 4, u′ > 0, w′ < 0) [16,23,24]. Due to the local and temporal adverse pressure gradient, low-speed fluid streaks from the wall (channel bed) enter the outer layer and cause ejection events. When a low-velocity fluid streak eventually loses its coherence, a high-speed fluid streak sweeps away residual ejected fluid, which propels it toward the wall, known as a sweep event. When the hole size H = 0, all data from u′ and w′ are considered. The analysis of conditional statistics is another name for quadrant analysis, which offers a quadrant-wise examination of velocity fluctuation data by adjusting the hole size to omit weak occurrences. The examination of conditional statistics can be done by providing a detention function ${\lambda }_{i,H}\left(t\right)$ expressed as [24]:

$$\begin{array}{l}{\mathsf{\lambda }}_{\mathrm{i},\mathrm{H}}\left(\mathrm{z},\mathrm{t}\right)\\ =\left\{\begin{array}{l}1, \mathrm{i}\mathrm{f} {\mathrm{u}}^{\prime }{\mathrm{w}}^{\prime } \mathrm{i}\mathrm{s} \mathrm{i}\mathrm{n} \mathrm{q}\mathrm{u}\mathrm{a}\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{t} \mathrm{i} \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{i}\mathrm{f} \left| {\mathrm{u}}^{\prime }{\mathrm{w}}^{\prime }\right|\ge \mathrm{H}{\overline{\left({\mathrm{u}}^{\prime }{\mathrm{u}}^{\prime }\right)}}^{0.5}{\overline{\left({\mathrm{w}}^{\prime }{\mathrm{w}}^{\prime }\right)}}^{0.5}\\ 0, \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.\end{array}$$

(6)

where t is time, from the quadrant, i is outside of the hyperbolic hole region of size H, the contribution to the overall RSS is expressed at any position by:

$${\left(u^{\prime }{w}^{\prime }\right)}_{i,H}=\underset{T\to \infty }{\lim }{\displaystyle \frac{1}{T}}{{\displaystyle \int }}_0^T{u}^{\prime }\left(t\right)w^{\prime }\left(t\right){\lambda }_{i,H}\left(z,t\right)dt$$

(7)

where T is the sampling period. The RSS fractional contribution from each event is shown by:

$${\mathrm{S}}_{\left(\mathrm{i},\mathrm{H}\right)}={\displaystyle \frac{{\left({\mathrm{u}}^{\prime }{\mathrm{w}}^{\prime }\right)}_{\mathrm{i},\mathrm{H}}}{\overline{{\mathrm{u}}^{\prime }{\mathrm{w}}^{\prime }}}}$$

(8)

From Equation (8), ${\mathrm{S}}_{\left(\mathrm{i},\mathrm{H}\right)}>0$ when i = 2 and 4 (ejections and sweeps) and ${\mathrm{S}}_{\left(\mathrm{i},\mathrm{H}\right)}<0$ when i = 1 and 3 (outward and inward interactions). Hence,

$${\displaystyle \sum }_{i=0}^{i=4}{S}_{i,H}{|}_{H=0}=1$$

(9)

4. Results and Discussion

To understand the flow physics in the wake region of a cylindrical pipe, the key variables governing flow behavior, structure, and turbulence are analyzed, as they play a crucial role in the mechanisms driving scouring and erosion around the pipe.

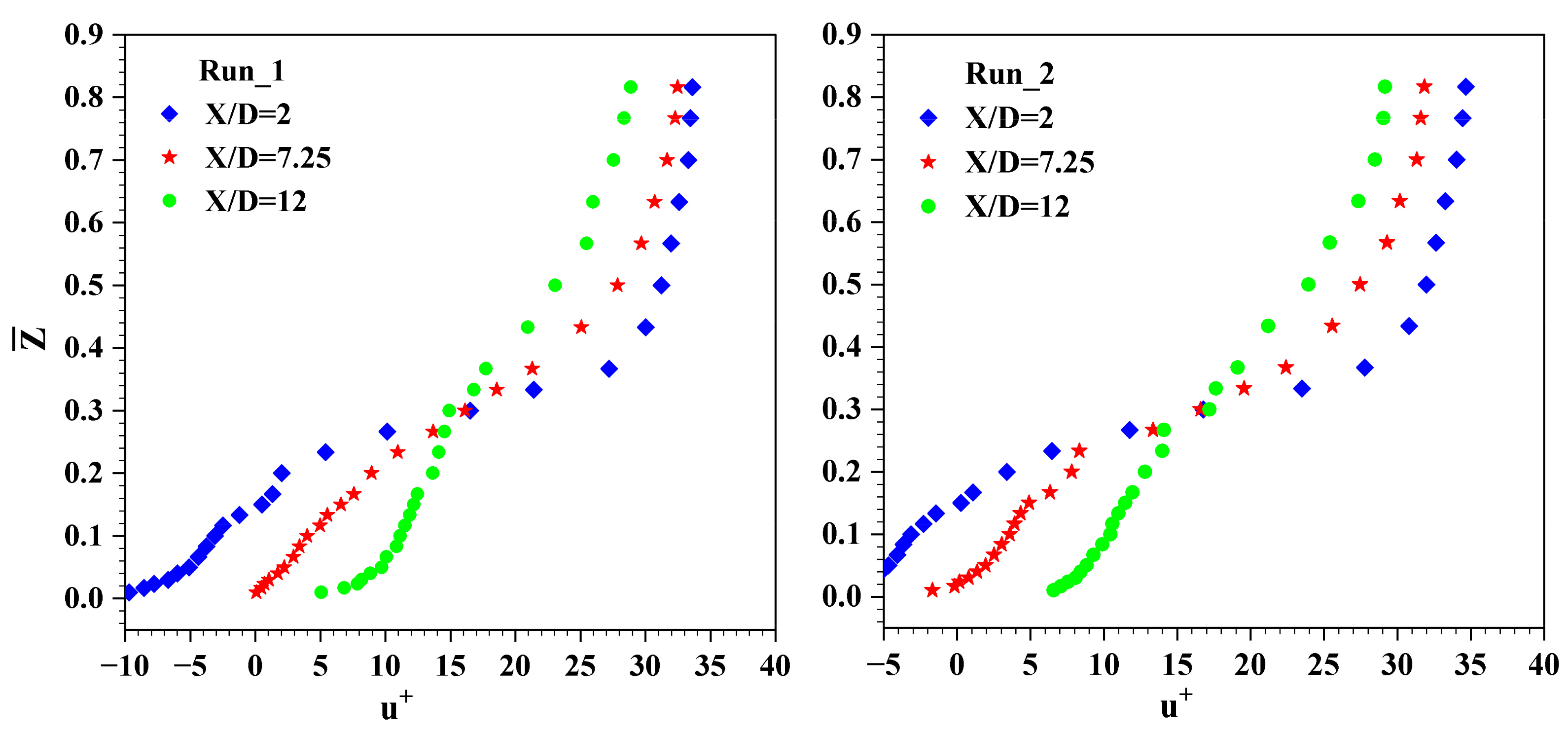
4.1. Mean Velocity

The non-dimensional time-averaged lengthwise velocity, ${\mathrm{U}}^{+}=\left({\displaystyle \raisebox{1ex}{$\overline{u} $}\!\left/ \!\raisebox{-1ex}{$u_{*}$}\right.}\right)$ in the wake region of the pipe at various lengthwise distances, $\hat{x}$ = 2, 7.25, and 12 for Run_1 and Run_2 are shown in Figure 5. From Figure 5, for all streamwise locations, $\widehat{x}$ the lengthwise velocity reached its maximum near the free surface. Along the flow direction, the magnitude of streamwise velocity increased up to $\overline{Z}$ = six before declining as x continues to increase. The wall-wake effects induced the upward concavity observed in the velocity ($u^{+})$ profiles, within the wake zone. The presence of the pipe influences velocity in the free-surface region, though its magnitude differs from the approach flow velocity in the same zone. Due to reduced near-bed velocities in the recirculation region, which adhere to mass conservation, the free-surface velocity within the free surface exceeds the undisturbed upstream velocity at the same altitude.

In the wake region, the velocity profiles exhibited substantial distortion near the bed, characterized by an ejection event. The velocity becomes positive as they ascend, signifying an outward flow phenomenon. These mean velocity profiles intersect vertically at a point known as the point of intersection, and each velocity profile has an inflection point. Beyond this point, the mean velocity values are increased notably closer to the wake region. As the flow moves past the cylinder in the flow direction, the velocity profiles gradually achieve greater uniformity in their distribution from the bed to the top. The pressure gradient prevails near the bed and within the wake region, significantly influencing the recirculating flow, which is exhibited to a greater extent in both runs.

4.2. Reynolds Shear Stress (RSS)

The non-dimensional RSS wall-normal profiles, ${\tau }^{+}$_uw at a various lengthwise distance in the pipe’s wake region, $\widehat{x}$, for Run_1 and Run_2 are exhibited in Figure 6. The RSS is expressed as ${\tau }_{uw}=-\left({\mathrm{u}}^{\prime }{\mathrm{w}}^{\prime }\right)$. Figure 6 shows that the RSS increased significantly with an ascend in the wall-normal distance, z, initiating at the bed, where it has a tiny positive value. The ${\tau }^{+}$_uw exhibits a peak near the pipe’s upper boundary (z/D = 1). Beyond this point, the ${\tau }^{+}$_uw gradually decreases with increasing height (z), eventually stabilizing at negligible levels in the free-surface region due to enhanced turbulent mixing. The turbulence intensity and TKE followed a similar pattern with different ranges. The distribution of RSS, TKE, and turbulence intensity exhibited a maximum peak near the wake region, i.e., at X/D =2 and 7.25. Along the streamwise direction, the peak magnitudes increase until the reattachment point, after which they decline due to boundary layer expansion and turbulence-induced dissipating large eddies.

The maximum absolute value of ${\tau }^{+}$_uw was found in the recirculation region along the flow direction up to the reattachment point. Beyond this point, ${\tau }^{+}$_uw decreases with a further rise in X/D due to the mixing and dispersion of the new shear layer, leading to the dissipation of large-scale eddies. The ${\tau }^{+}$_uw approaches an insignificant value and remains nearly invariant concerning the wall-normal distance z in the free-surface region. The point of inflection is where the RSS reaches its maximum $\left({\displaystyle \frac{d^2\overline{u}}{d{z}^2}}=0\right)$ in the velocity profiles. The ${\tau }^{+}$_uw is uniform above the $\overline{Z}$ > 0.6 in both run scenarios. In both run scenarios, ${\tau }^{+}$_uw has a maximum peak in the case of $\widehat{x}$ = 7.25.

4.3. Turbulence Intensity

Due to fluctuations in instantaneous flow velocity induced by pipe and bed roughness, turbulence develops downstream of the pipe. The streamwise, non-dimensional turbulence intensities, ${\sigma }_u$⁺ and wall-normal directions, ${\sigma }_w$⁺ are exhibited as ${{\sigma }_u}^{+}={\displaystyle \raisebox{1ex}{${\sigma }_u$}\!\left/ \!\raisebox{-1ex}{$u_{*}$}\right.}$ and ${{\sigma }_w}^{+}={\displaystyle \raisebox{1ex}{${\sigma }_w$}\!\left/ \!\raisebox{-1ex}{$u_{*}$}\right.}$, respectively [5]. The streamwise ${\sigma }_u=\sqrt{\overline{u^{\prime }{u}^{\prime }}}$, and the wall-normal ${\sigma }_w=\sqrt{\overline{w^{\prime }{w}^{\prime }}}$. Turbulence intensity quantifies the strength of turbulence and is defined as the root mean square (RMS) of velocity fluctuations along respective directional components. The wall-normal profiles of the non-dimensional streamwise ${\sigma }_u$⁺ and wall-normal turbulence intensities ${\sigma }_w$⁺ in the wake region of the pipe at various streamwise distances, $\widehat{x}$ for Run_1 and Run_2, are shown in Figure 7 and Figure 8. Similar to RSS distributions, at the bed, ${\sigma }_u$⁺ and ${\sigma }_w$⁺ represent the high-velocity fluctuations caused by heightened turbulence mixing at that level. The turbulence intensity initially exhibits slightly positive values in both runs before increasing sharply with rising z, peaking at the pipe’s uppermost level (z/D = 1). For z/D > 1, turbulence intensities decrease as z rises. The peak of turbulence intensities along the streamwise direction $\widehat{x}$ exhibit increasing trends in the near-wake region and diminish in the far-wake region. The former region’s increased and the latter region’s decreased turbulence is responsible for these patterns, respectively. Due to reduced turbulence mixing with decreasing z, the turbulence intensities below the pipe’s top level, where z/D < 1, diminished as z decreased. Turbulence intensities exhibited lower magnitudes and stabilized approximately along the z-axis in the free-surface region. Along lengthwise distance, all of the turbulence intensity profiles exhibit good collapse, with $\widehat{x}$ for the wall-normal domain of the study, z/D < 2. This result indicated that the free-surface region is largely unaffected by the influences of the cylinder and the bed.

4.4. Turbulent Kinetic Energy (TKE)

TKE is a significant factor in determining how much turbulence is present [9]. According to one study, the turbulent kinetic energy per unit mass is Equation (10).

$$k=\left({\displaystyle \frac{\overline{{u^{\prime }}^2}+\overline{{v^{\prime }}^2}+\overline{{w^{\prime }}^2}}{2}}\right)$$

(10)

where ${\mathrm{k}}^{+}={\displaystyle \frac{\mathrm{k}}{{\mathrm{u}}_{*}}}$.

Figure 9 demonstrates a sharp rise in the size of the kinetic energy profiles of turbulent flow just downstream of the pipe. However, as x increases, the TKE peak increases in the wake region up to the reattachment point and decreases in the redevelopment zone. In both the separated shear layer and near-bed flow zone, TKE levels for z < 2D significantly improve with an increase in D/h. However, when z > 2D, the TKE profiles for all runs coincide. TKE is at its minimum just above the cylinder. Further, as the flow shifts downstream, away from the cylinder, the previously accelerating flow transitions into a decelerating flow.

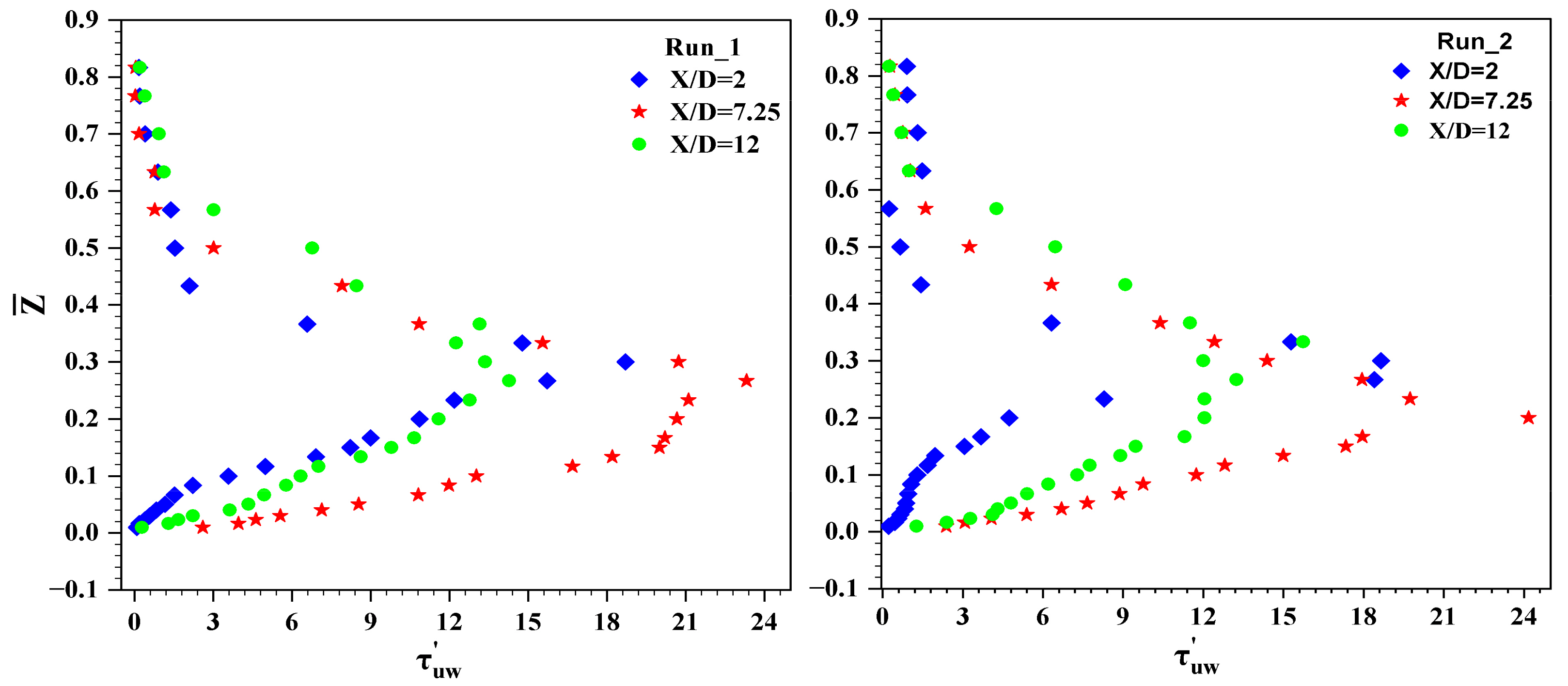
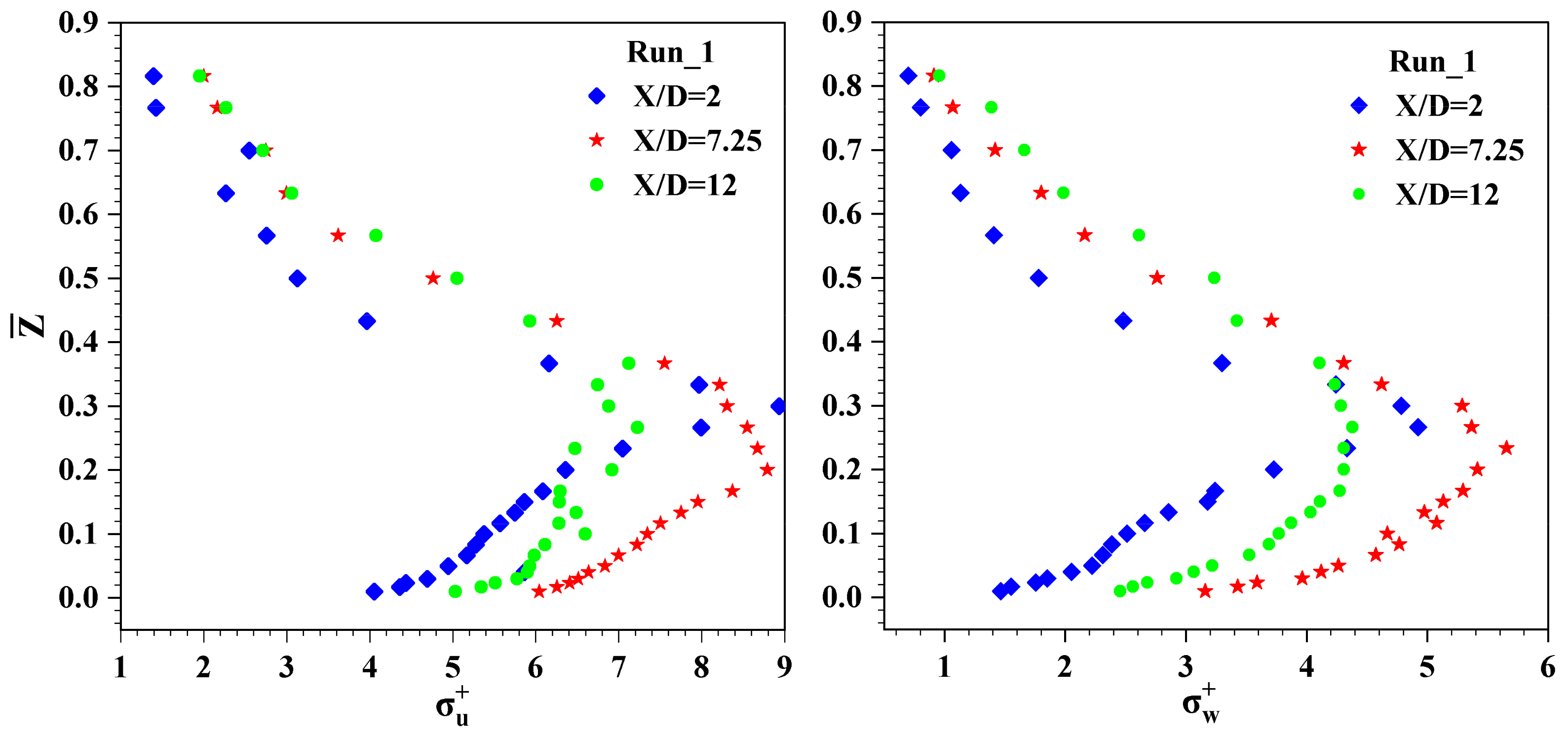
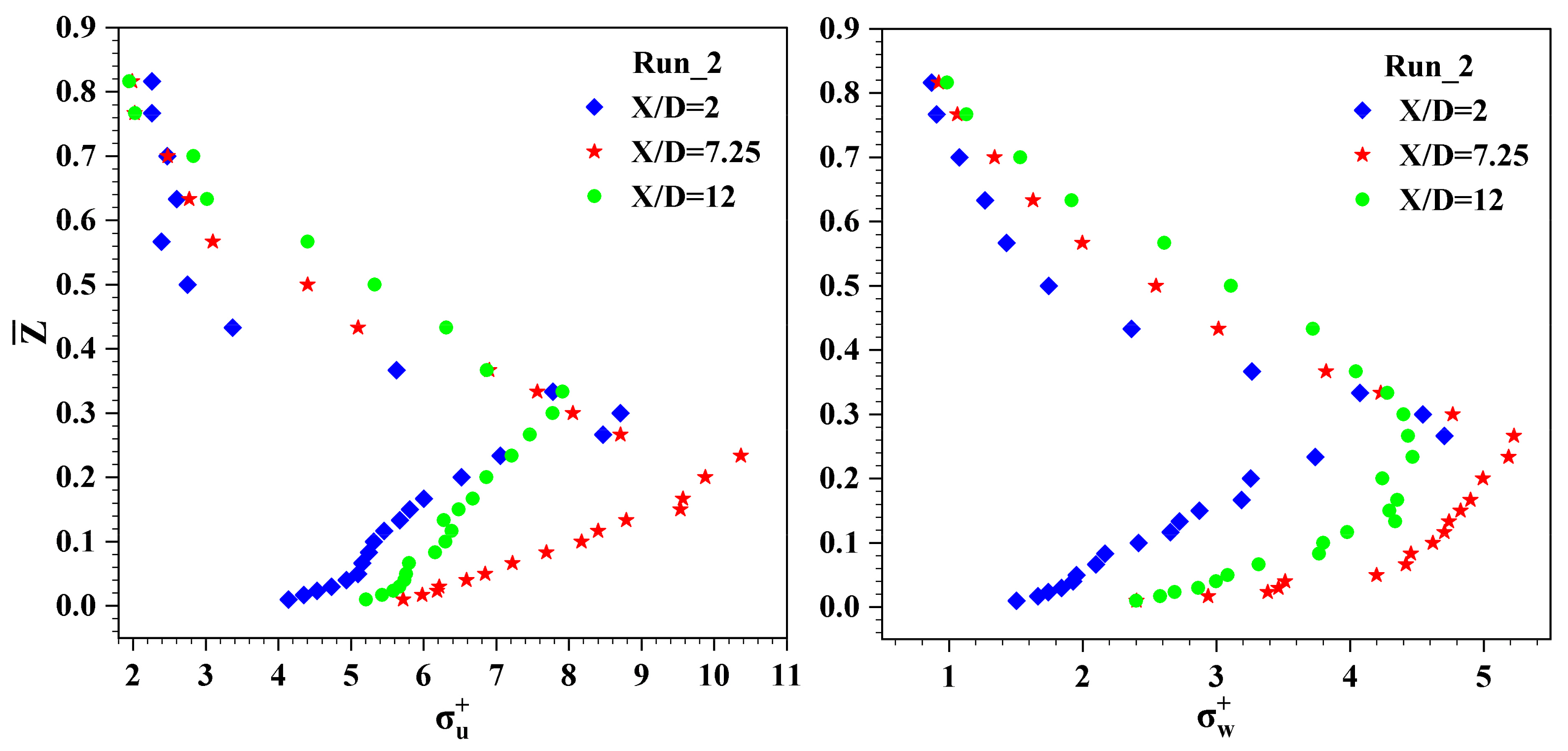
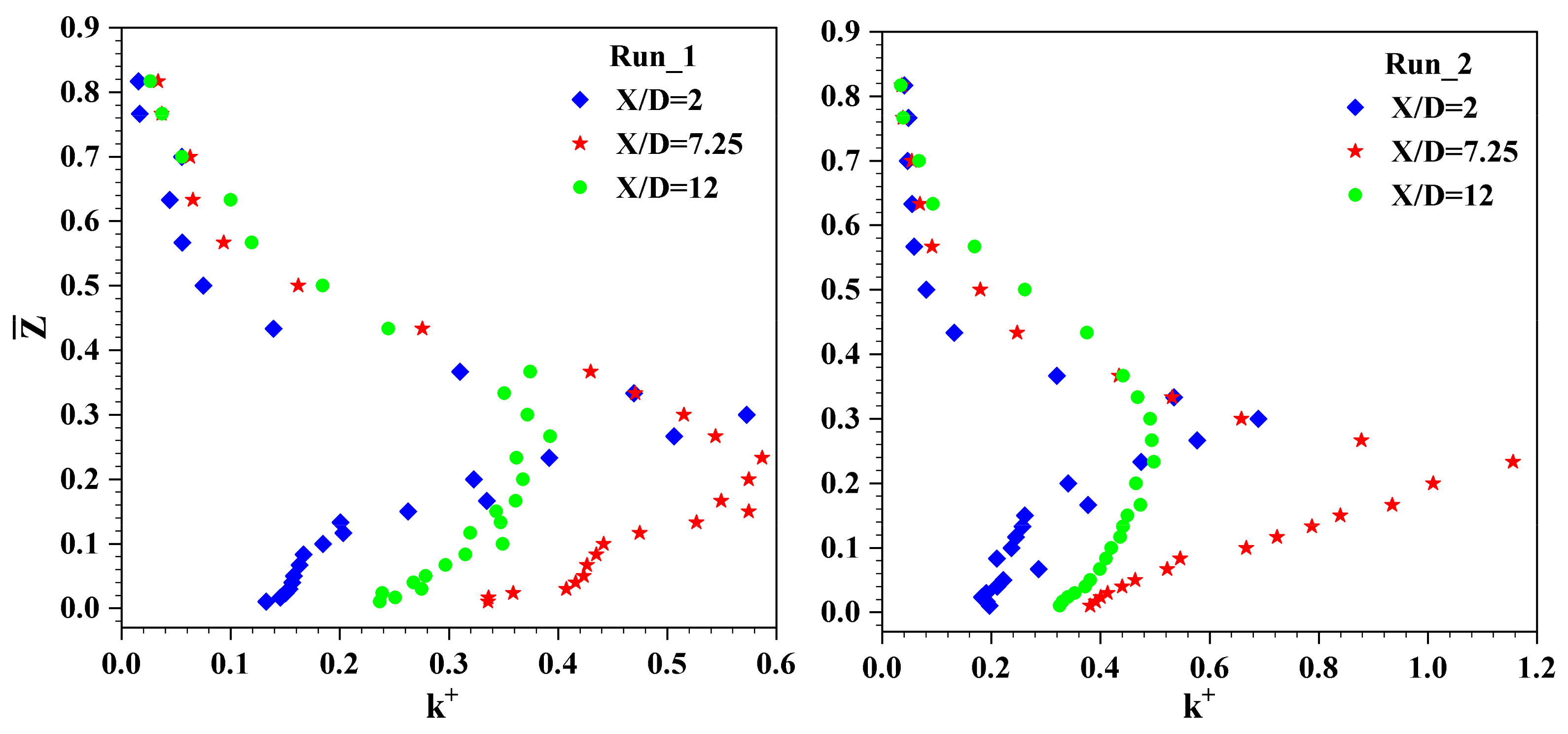
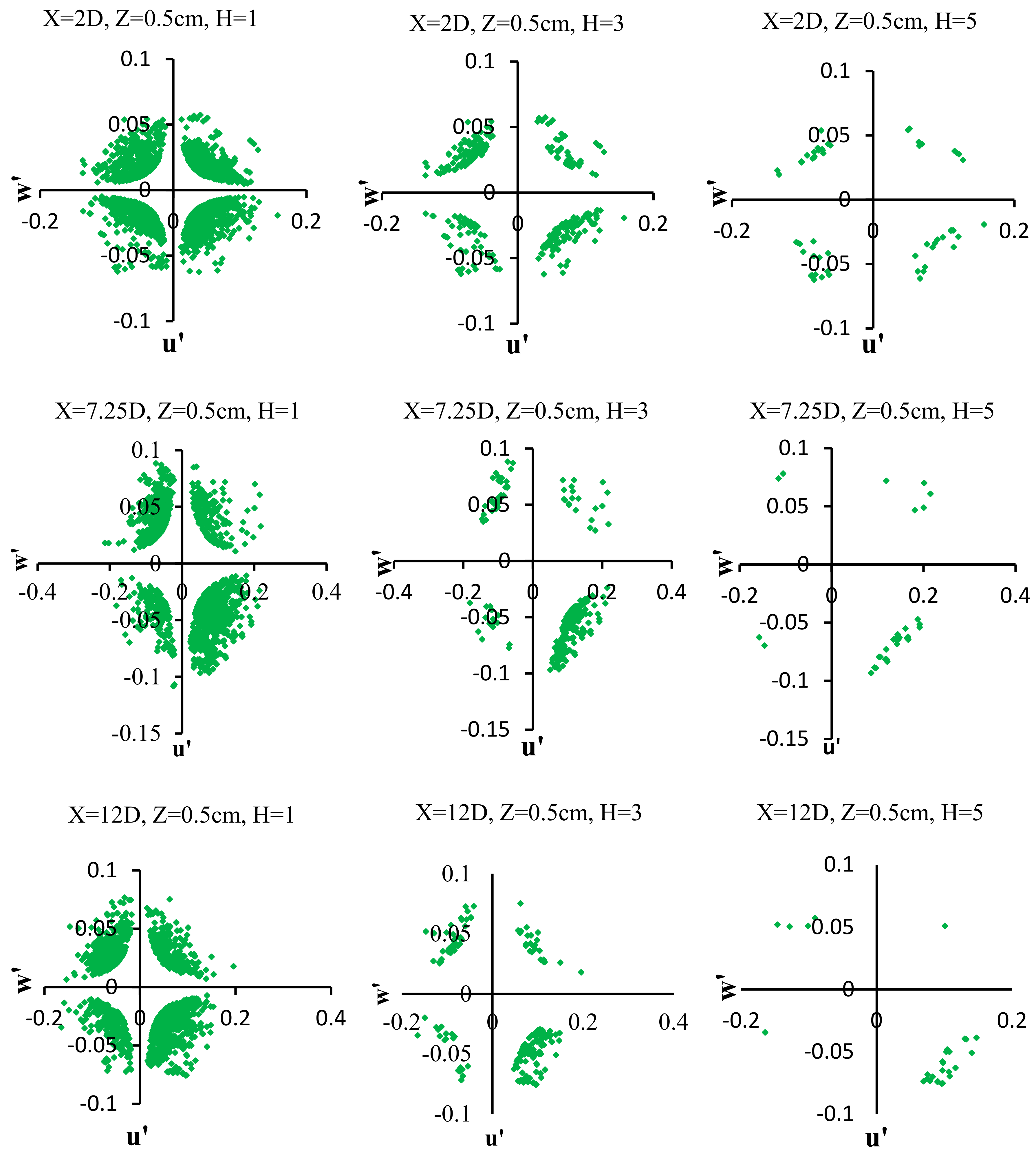
4.5. PDF of Velocity Fluctuations

The experimental data were utilized to compute the coefficient ${\mathrm{C}}_{\mathrm{j}0}$ and ${\mathrm{C}}_{0\mathrm{k}}$, defined in Equations (3) and (4). The relative frequencies ${\mathrm{f}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{f}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$ of the random variables $\hat{\mathrm{u}}$ and $\hat{\mathrm{w}}$ were derived from the experimental data at a specified flow depth z to construct the theoretical curves for PDFs of ${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$. To evaluate the moment ${ \mathrm{m}}_{\mathrm{j}0}$ and ${ \mathrm{m}}_{0\mathrm{k}}$, the PDF ${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$ is approximated by ${\mathrm{f}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{f}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$, respectively.

To study PDFs, two vertically oriented locations were chosen for ${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$, i.e., z = 2 cm and 8 cm. These sections exhibit locations near the bed and crest level of the cylinder, as near to the crest zone, a greater extent of alterations in u⁺, ${\sigma }_u$⁺, ${\tau }^{+}$_uw, ${\sigma }_w$⁺, and ${\mathrm{k}}^{+}$ were observed. Figure 10 shows ${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$ variations at the proposed depth at a distance of X/D=2 and X/D= 7.25 from the cylinder for the F_r, 0.087 and 0.111 in the wake zone.

Experimental data leading to ${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$ was calculated for each of these scenarios, with the estimated curves reasonably collapsing on the experimental data. Therefore, the conclusion is that the ${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$ exponential distribution-based GC series follows the closer alignment with experimental data, although initially, both are significantly aligned, and the absolute values of the experimental pdf were less than those of the theoretical pdf. The theoretical probability density functions (PDFs) of ${\mathrm{p}}_{{\hat{\mathrm{u}}}^{\left(\hat{\mathrm{u}}\right)}}$ and ${\mathrm{P}}_{{\hat{\mathrm{w}}}^{\left(\hat{\mathrm{w}}\right)}}$ exhibit near symmetry around their expected values, corresponding to the distribution mode. However, in particular experimental cases, the observed PDFs in some plots deviated from this symmetry. A similar observation was made by finding the skewness of probability distribution functions [25,26].

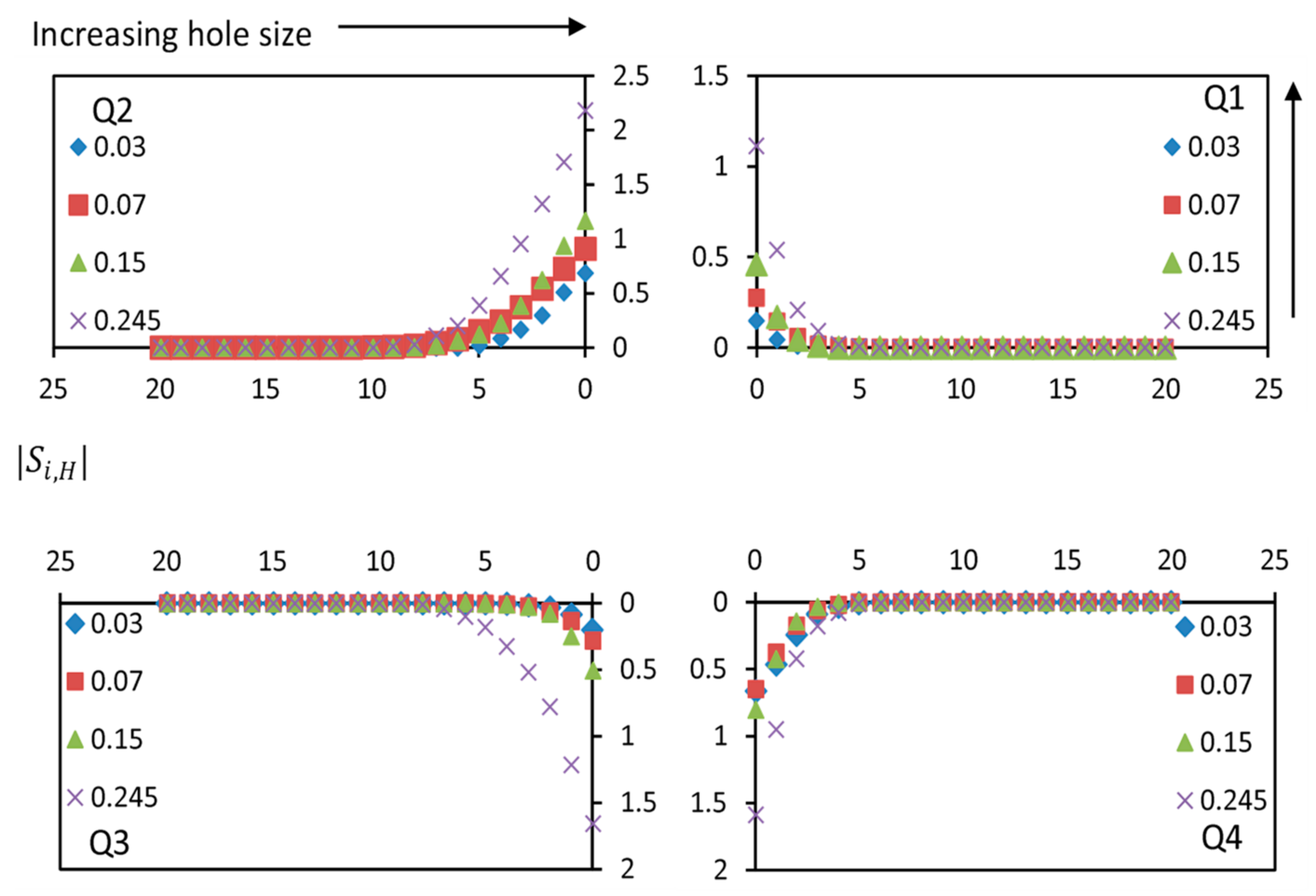
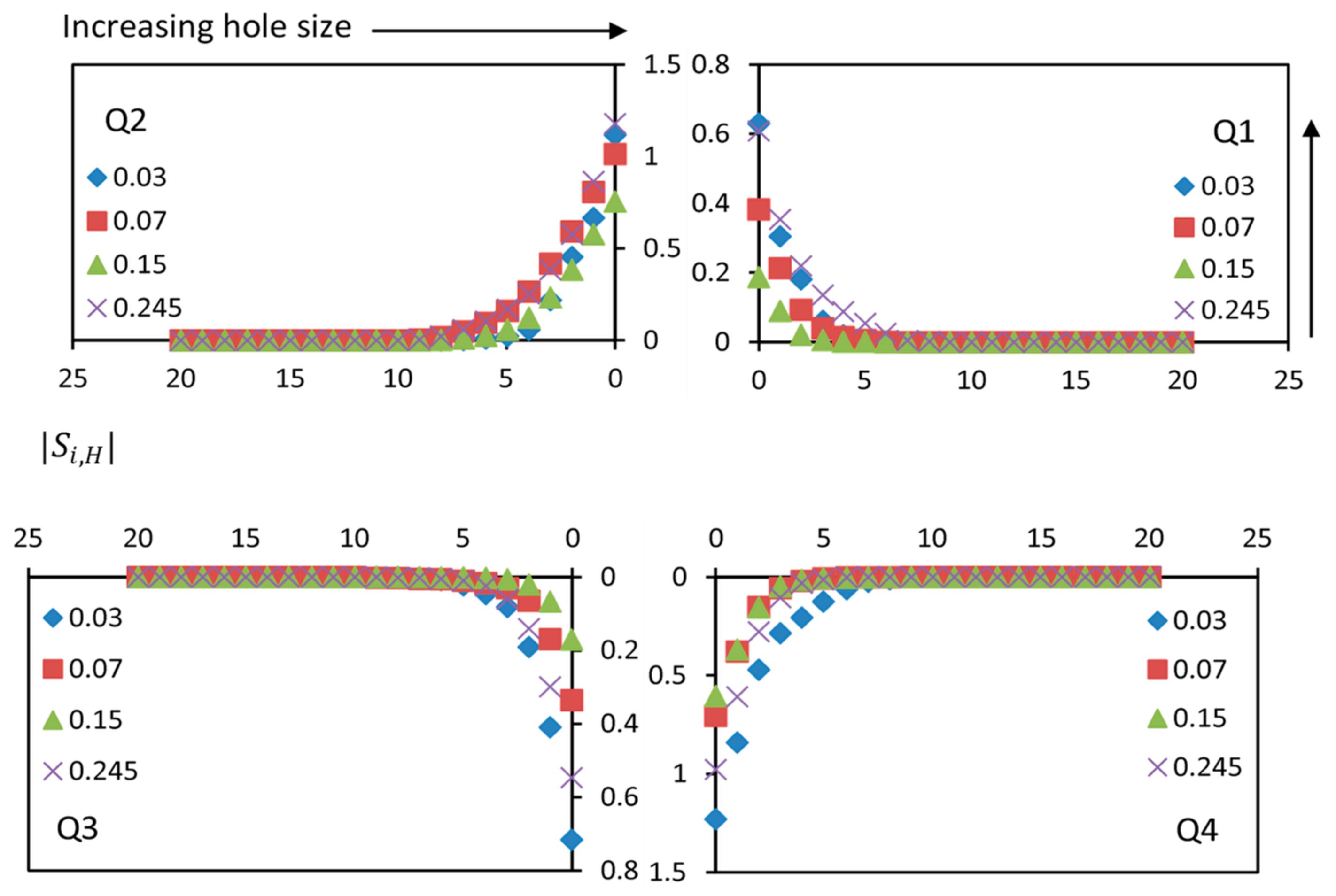
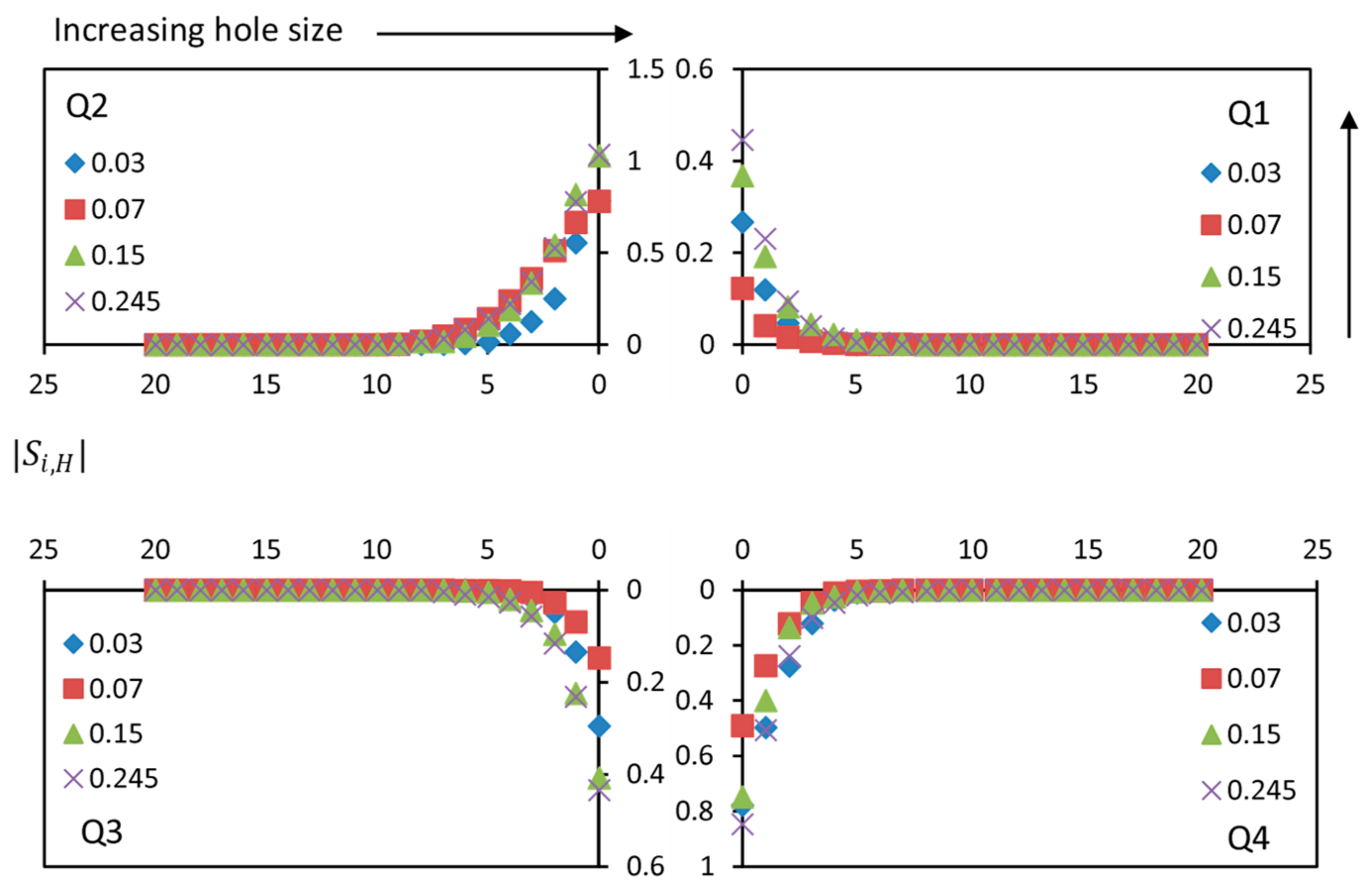
4.6. Quadrant Analysis

As bursting events are crucial for sediment transport (Willmarth and Lu, [12]; Nakagawa and Nezu, [21]; Lu and Willmarth, [22]), quantifying them is the primary goal of the quadrant analysis. RSS controls the momentum transfer arising from the instantaneous velocity fluctuations ${\mathrm{u}}^{\prime }$ and ${\mathrm{w}}^{\prime }$. A quadrant analysis of fluctuating velocity components in the streamwise ${\mathrm{u}}^{\prime }$ and vertical ${\mathrm{w}}^{\prime }$ directions is conducted to elucidate the underlying momentum transport mechanisms.

Intense ejection events close to the bed exhibit neither deposition nor erosion. Sweep events are crucial in bedload transport, regardless of bedform presence. Inward and outward events are prominent in non-equilibrium mobile dunes [23].

The u′-w′ scatter plots at different locations, i.e., X = 2D, 7.25 D, 12D, where D is the diameter of the cylinder for Run_1 ($F_r$ = 0.087) and Run_2 ($F_r$ = 0.111), are depicted in Figure 11 and Figure 12, having hole sizes H = 1, 3, and 5, respectively.

From these figures, we can infer that as the hole size increases, the cluster of data points also reduces with an increase in a gap from the cylinder, which implies the attenuation of turbulent mixing that causes a significant decrease in fluctuation.

In the 2nd and 4th quadrants, greater velocity points exist, showing that sweeps (Q4) prevail in the intermediate and free-surface flow zones and that the ejections (Q2) are the strong bursting event close to the bed flow zone.

At X = 2D, 7.25D, and 12D in both runs, the probability of occurrence of bursting events at H = 1 is extremely greater. Among X = 2D, 7.25D, and 12D at X = 2D, the bursting events are more predominant than all sections in the wake region.

At X = 12D in all the runs, the ejections and sweeps have a cluster of fluctuating velocity values compared to inward and outward interactions, implying that the ejections and sweeps are stronger events. Additionally, as the distance from the cylinder increases, the number of data points for u′ and w′ decreases and sweep events are more frequent in all cases than other events.

Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 depict the distribution of the fractional contribution $S_{i,H}$ for H = 1, 3, and 5 of the RSS at locations X = 2D, 7.25D, and 12D for Run_1 and Run_2, in the wake region. The stress fraction shows the strength of each event ${\mathrm{S}}_{\mathrm{i},\mathrm{H}}$ which measures each event’s proportionate contribution to the total RSS.

In all the runs and at every measurement location, the stress fraction values for Q1 (outward interactions) and Q3 (inward interactions) are negative, while Q2 (ejections) and Q4 (sweeps) are positive.

With an increase in the gap from X = 2D to X = 12D, the magnitude of the RSS fraction also increases but with a minimal magnitude in all the runs.

The stress fraction values are slightly higher for ejections and sweeps than for outward and inward interactions across the flow depth at the mentioned locations in the wake region for both run scenarios. The stress fraction ${\mathrm{S}}_{\mathrm{i};\mathrm{H}}$ for the first and third quadrants nearly disappeared at H = 3 as the distance from the cylinder increased. This behavior was observed at X = 7.25D and X = 12D in both run scenarios, while for the second and fourth quadrants, the stress fraction persisted, extending up to H = 4.

The stress fraction $S_{i;H}$ for the first and third quadrants exhibited minimal variation, ranging between H = 2–4, as observed at X/D = 2 in both run scenarios, while the second and fourth quadrants extended to H = 5 and demonstrated greater variability, particularly beyond X/D =2. The $S_{i;H}$ in a specific quadrant decreased as H increased. Moreover, a comparison of stress fractions across various H reveals that as H increases from zero to five, the ${\mathrm{S}}_{\mathrm{i};\mathrm{H}}$ for each event drops significantly. This trend indicates that the contribution of stronger events to the total RSS is minimal. The $S_{i;H}$ dropped sharply as the hole size increased, becoming nearly zero or negligible for H = 5 or larger across all quadrants, although, in the second and fourth quadrants, the variation is much greater than in the first and third quadrants, i.e., sweeps and ejections are predominant.

At each selected location in the wake region, four points, each at a various vertical distance from the bed, have been considered. Those four points are vertically considered at a distance from the bed of 0.03, 0.07, 0.15 and 0.245 cm. The ${\mathrm{S}}_{\mathrm{i};\mathrm{H}}$ is utmost near the cylinder, and as it moves away, the stress fraction decreases and becomes constant after a distance. In the free-surface flow region, ${\mathrm{S}}_{\mathrm{i};\mathrm{H}}$ is increased drastically along x directions for both run scenarios. For all cases, the ${\mathrm{S}}_{\mathrm{i};\mathrm{H}}$ diminished to negligible levels or zero when H reached six or more. In the inner and intermediate layers, sweeps were the predominant bursting events, whereas ejections dominated the outer layer of the wake region.

5. Conclusions

The points of inflection $\left({\displaystyle \frac{d^{2}u}{d{z}^2}}\right)$ in the individual $u^{+}$ profiles were observed near the top level of the pipe at (z/D ≈ 1). Consequently, both the Reynolds shear stress and turbulence intensities reach their peak values at this location. At the boundary, turbulence is minimal but rapidly intensifies, reaching its maximum within a short distance (z/D = 1) from the boundary. Beyond this point, turbulence decreases and remains nearly constant in the main flow region. Close to the boundary, turbulence intensity is affected by boundary roughness, with increased roughness reducing streamwise turbulence intensity and enhancing vertical turbulence intensity. However, this influence diminishes in the main flow region farther from the boundary.

The probability density function (PDF) distributions derived from GC series-based exponential distribution show a closer alignment with experimental data.

The vertical extent of the recirculation region reduces as the streamwise distance from the cylinder increases because the flow is bending towards the flume bed.

Quadrant analysis reveals that sweeps (Q4) dominate intermediate and free-surface zones, while ejections (Q2) prevail near the bed, both being primary contributors to Reynolds shear stress (RSS). The stress component remains minimal or zero for all events when $\mathrm{H}\ge \mathrm{six}$. In the inner and intermediate layers of the wake zone, sweeps dominate as the primary bursting events, while ejections predominate in the outer layer. The stress fraction in the first and third quadrants showed minimal variation between H = two and four at X/D = two, while in the second and fourth quadrants, it extended to H = five with greater variability, significantly beyond X/D = two. As H increased, the stress fraction dropped sharply, approaching zero for sizes ≥ five. Therefore, the stress fraction is the highest near the cylinder, and as it moves away from the cylinder, the stress fraction decreases and becomes constant after a distance.