Numerical Simulation of the Hydrodynamic Behavior of Immersed Tunnel in Waves
Abstract
1. Introduction
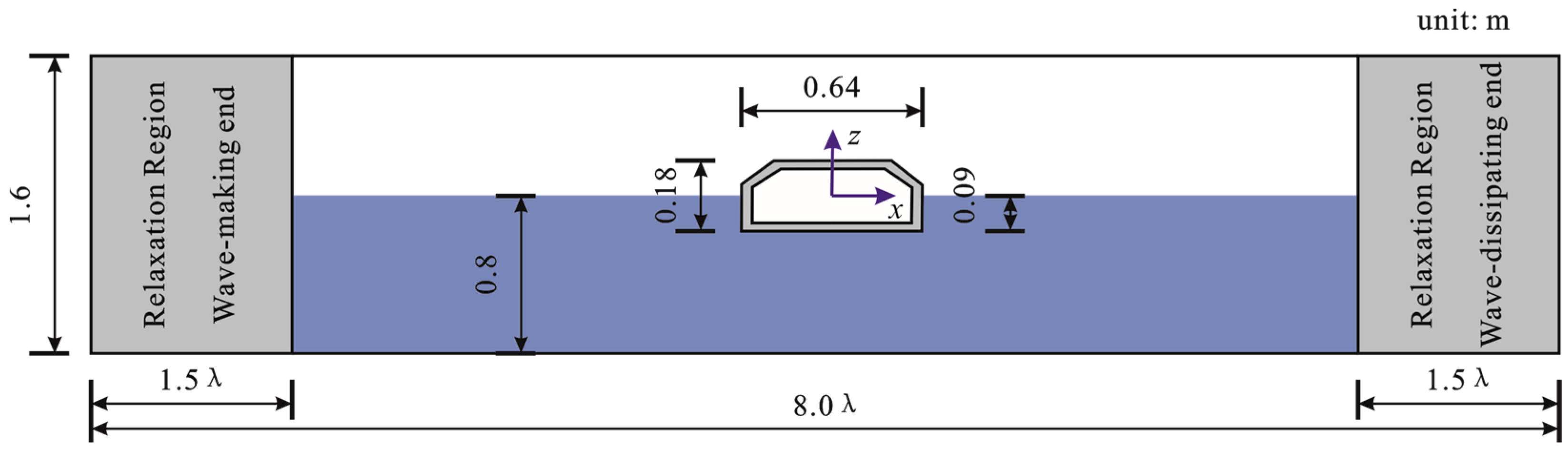
2. Numerical Model
2.1. Governing Equations
2.2. Floating Body Motion Equation
2.3. Wave Generation and Absorption
3. Experimental Validation
3.1. Mesh Convergence Analysis
3.2. Floating Body Motion Response Verification
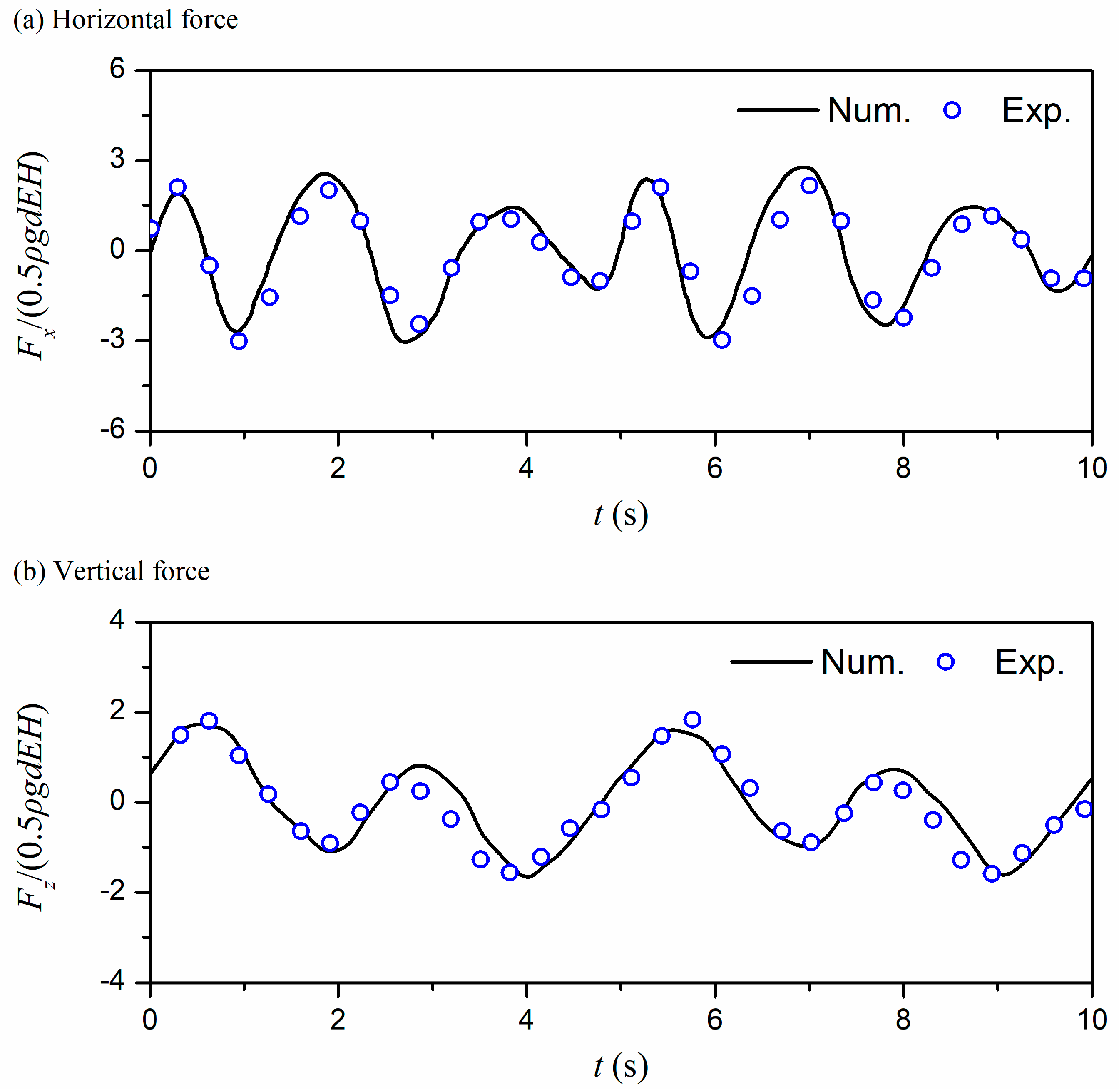
3.3. Wave Force Verification
4. Results and Discussion
4.1. Hydrodynamic Characteristics of the Immersed Tunnel in Regular Waves
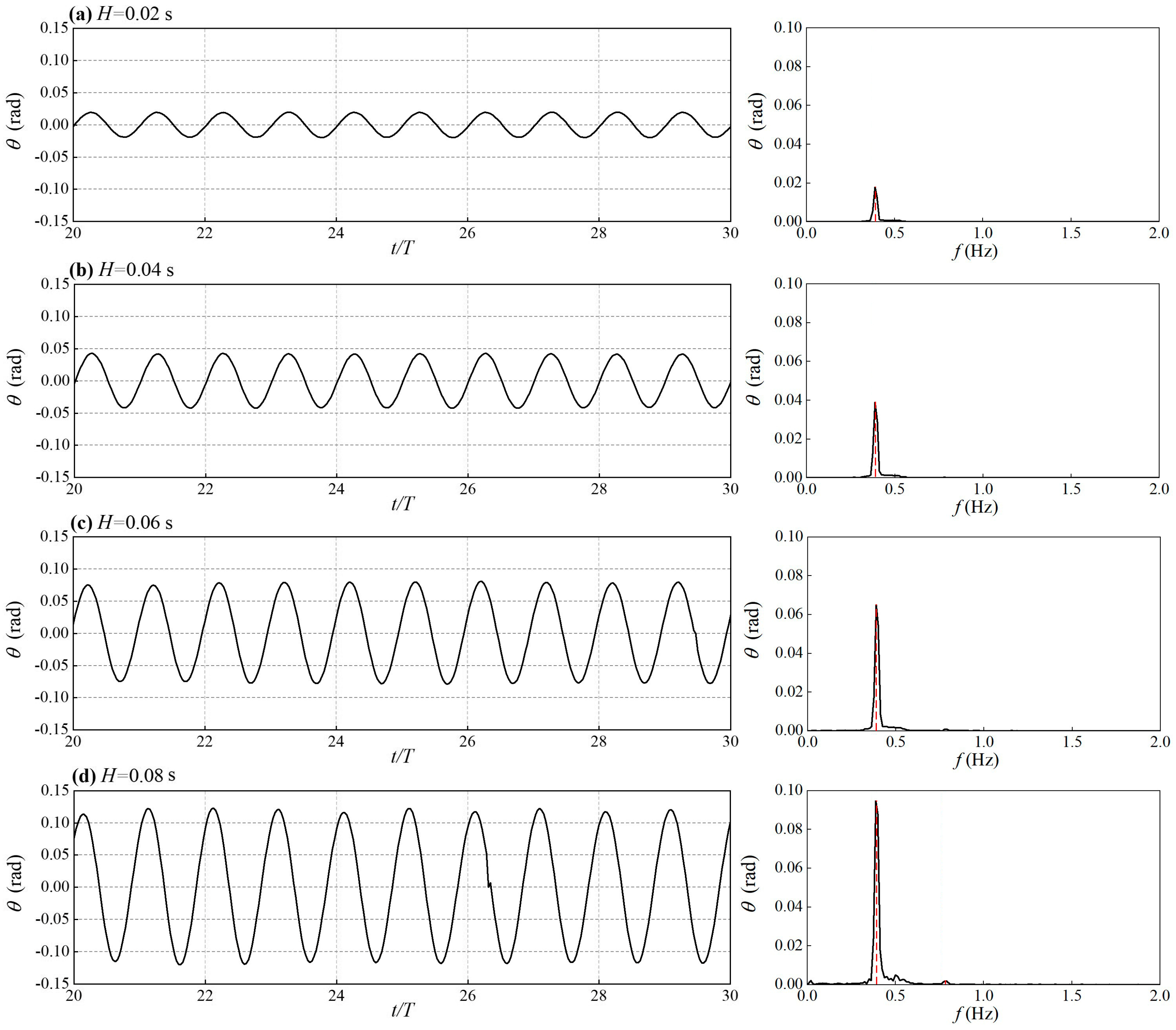
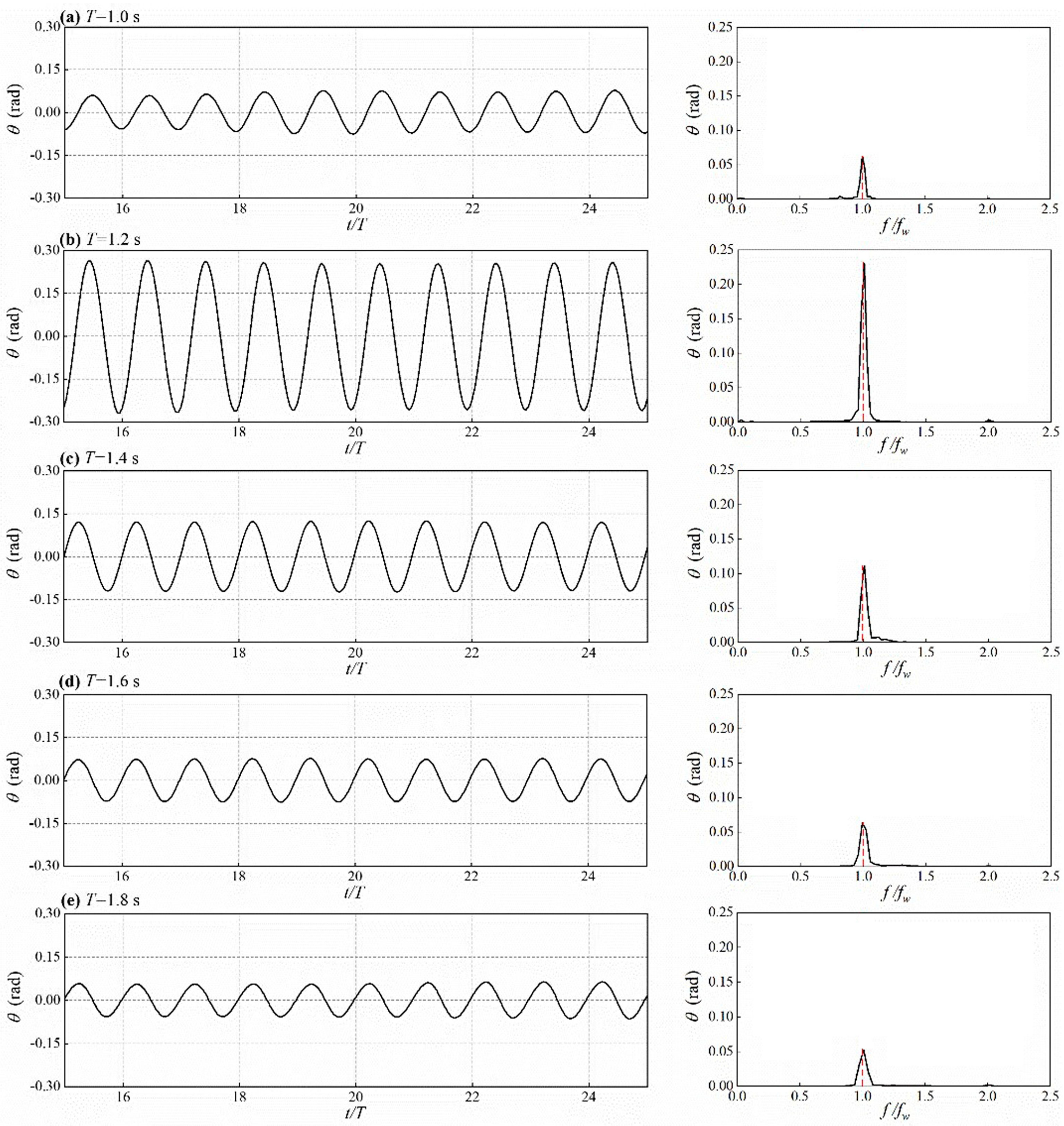
4.1.1. Analysis of Roll Motion Response
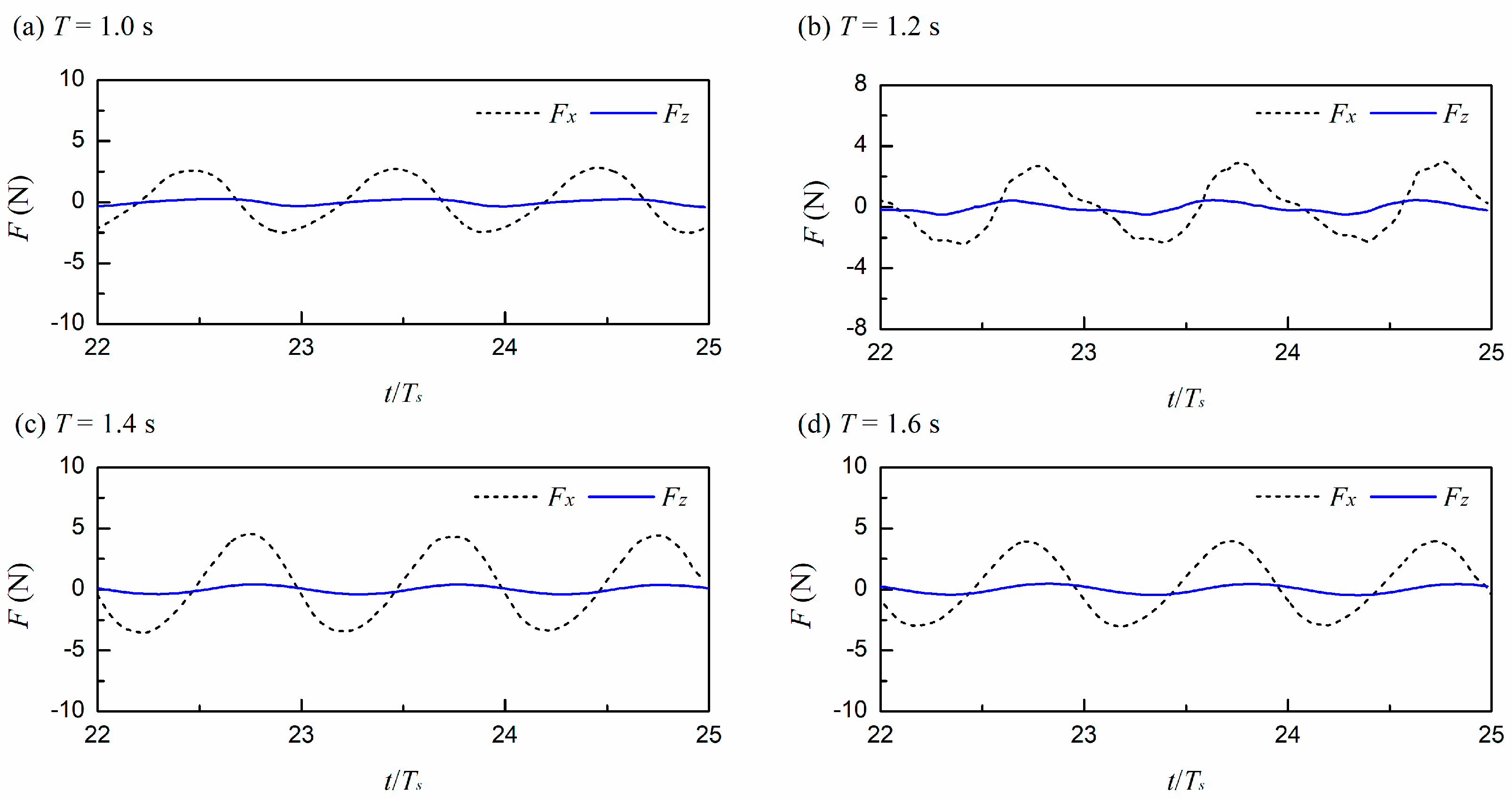
4.1.2. Analysis of Wave Forces
4.2. Hydrodynamic Characteristics of the Immersed Tunnel in Irregular Waves
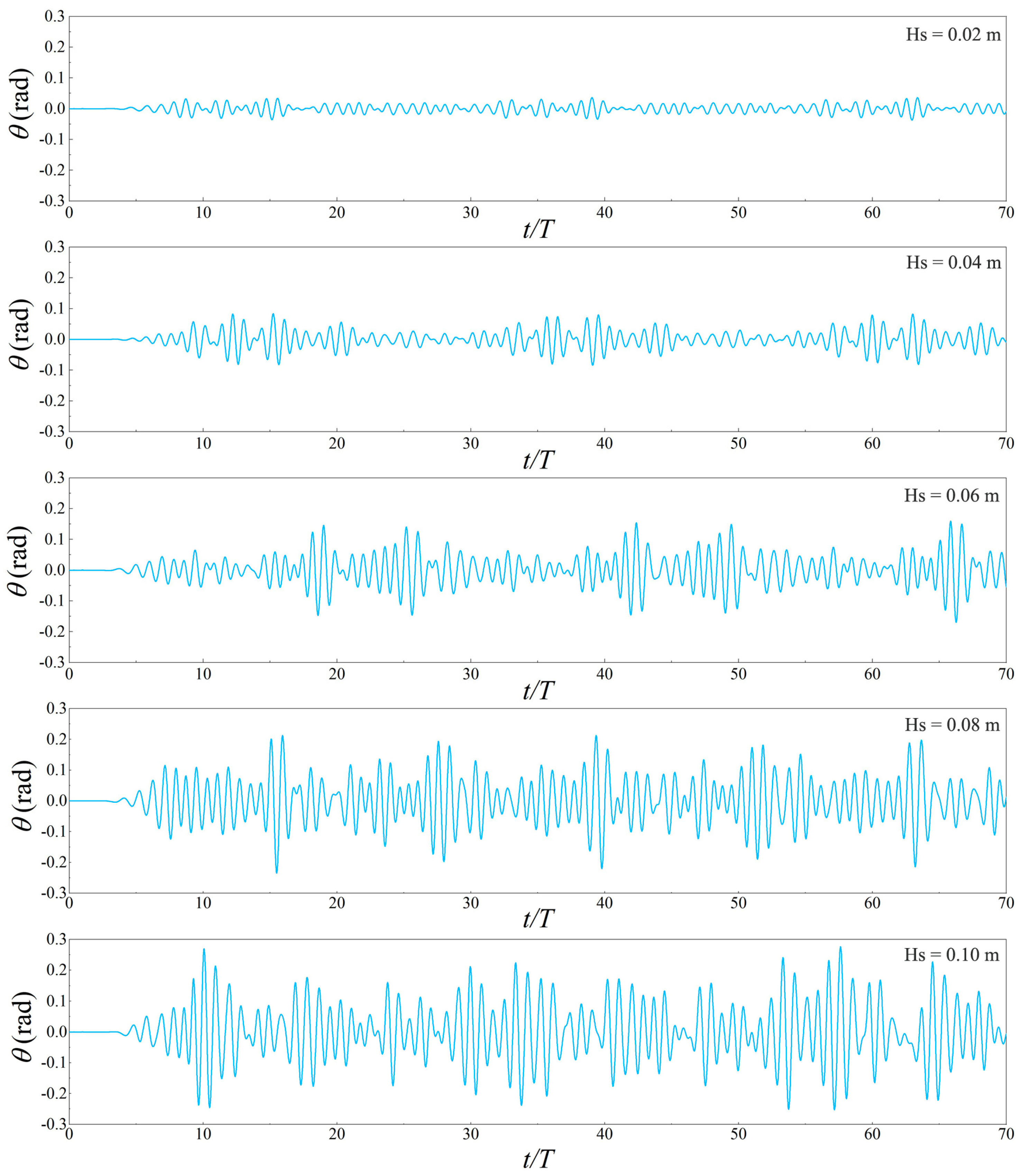
4.2.1. Analysis of Roll Motion Response
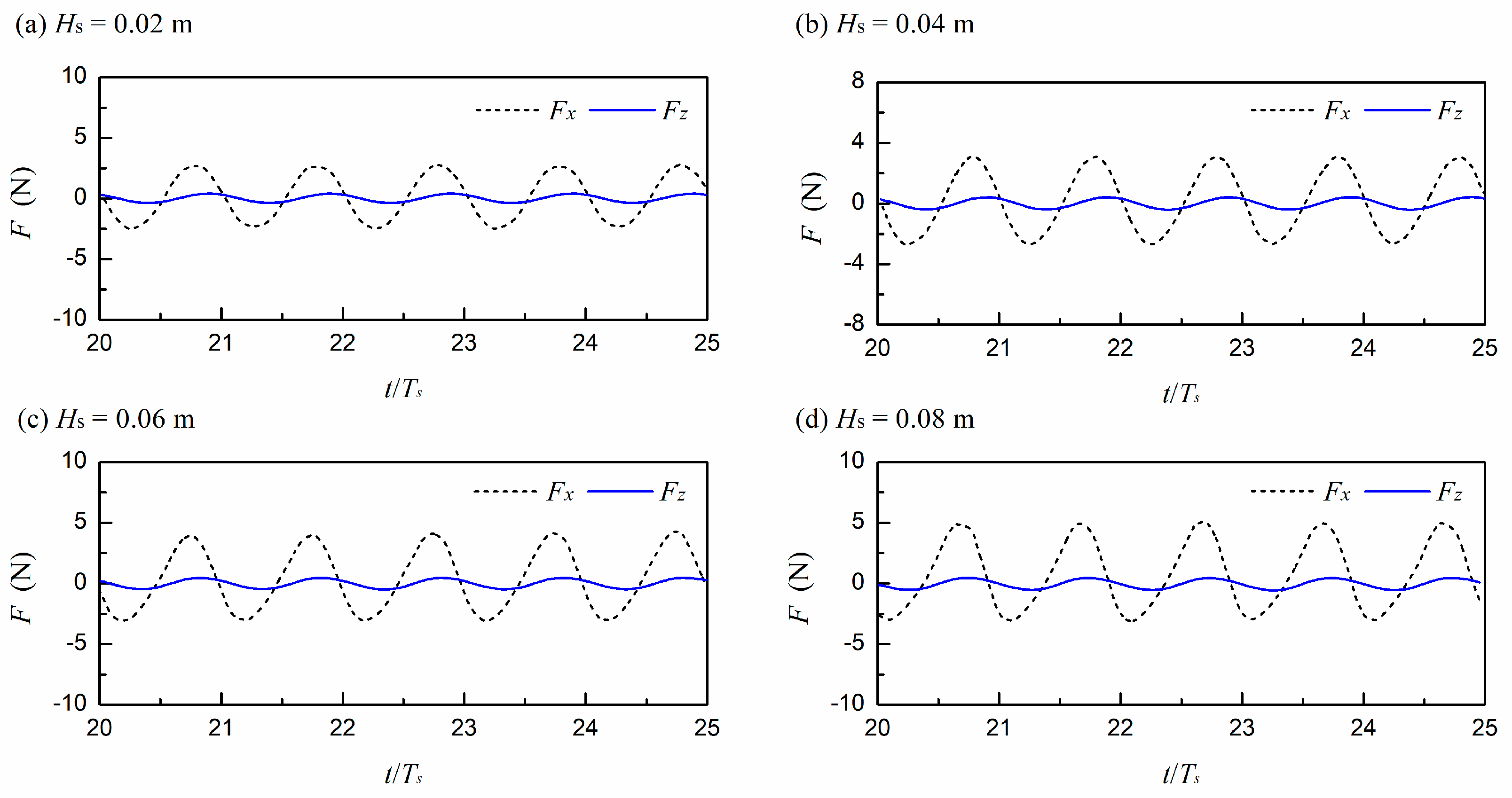
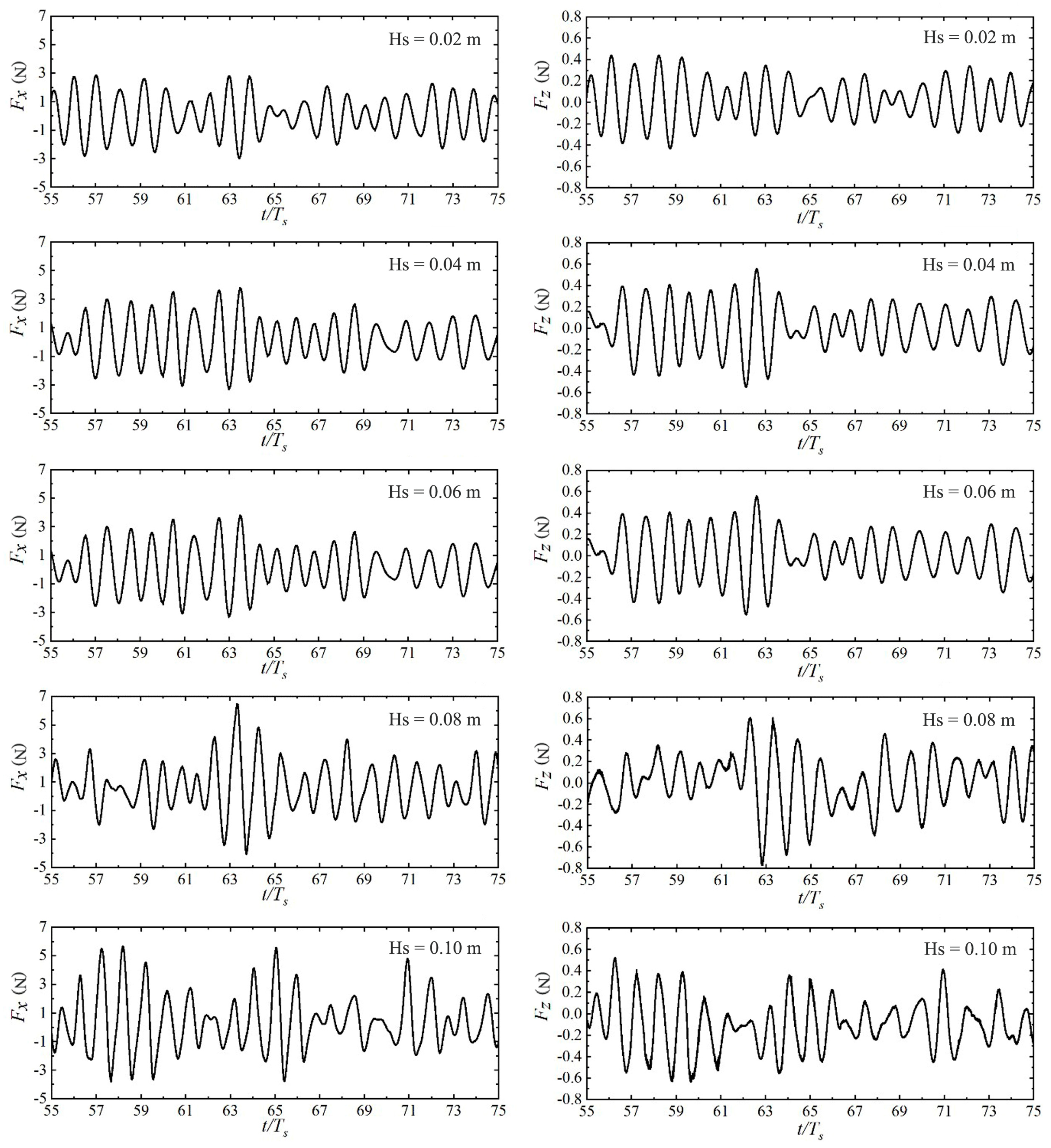
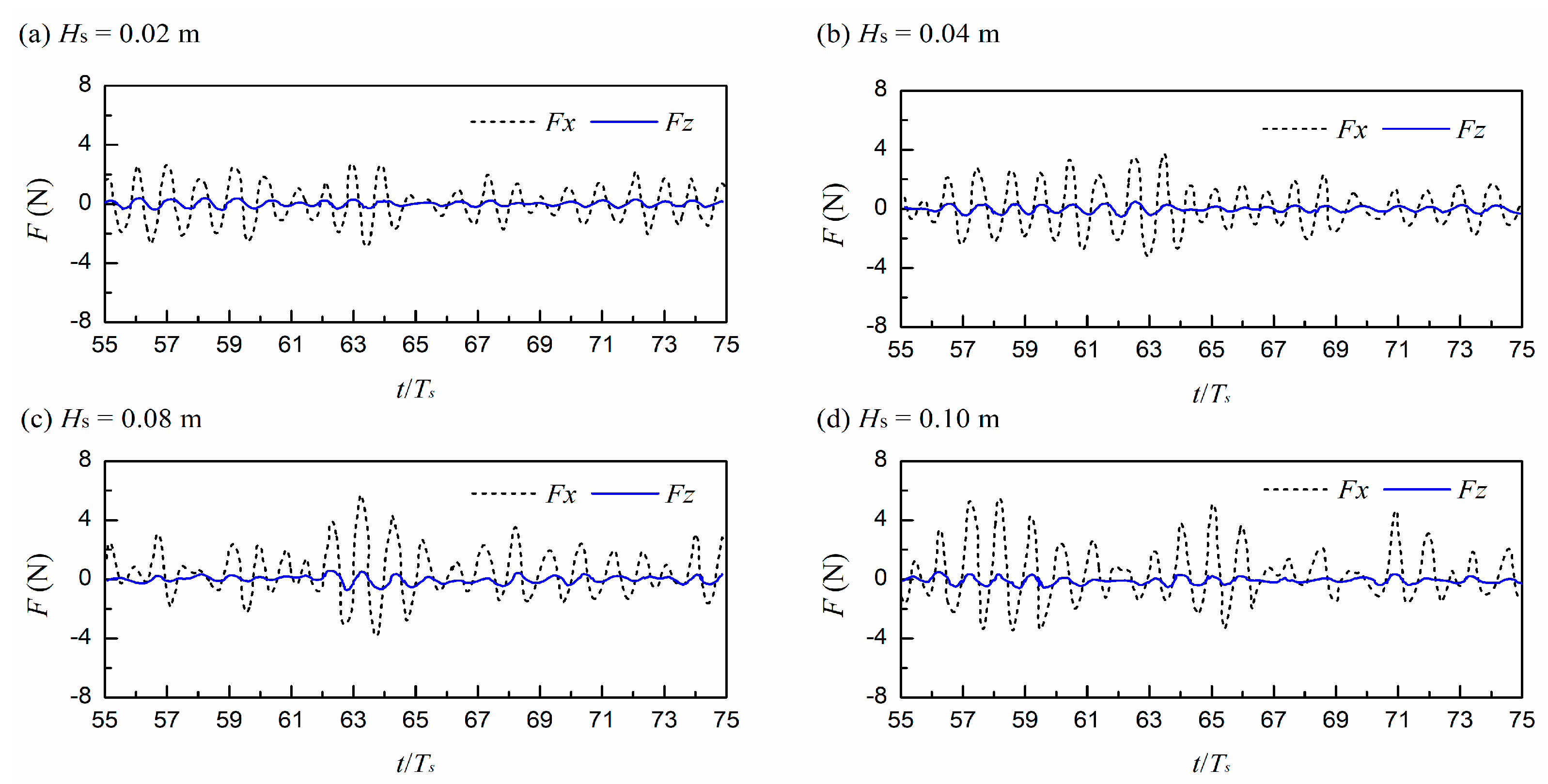
4.2.2. Analysis of Wave Forces
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, K.; Peng, S.; Wu, W. Model test of immersed tunnel element in towing tank in winds, waves and currents. In Proceedings of the 22nd International Offshore and Polar Engineering Conference, Rhodes, Greece, 17 June 2012. [Google Scholar]
- Peng, S.; Wu, W.; Chen, K. Experimental Investigation on Element Immersing Process of Immersed Tube Tunnel of Hong Kong-Zhuhai-Macao Bridge. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1 July 2012. [Google Scholar]
- Wu, R.D.; Ying, Z.Q.; Wang, Z. Model Test for Hydrodynamic Parameters of Immersed Tube Tunnel in Static Water. Appl. Mech. Mater. 2014, 477, 754–758. [Google Scholar]
- Cozijn, H.; Heo, J.W. Analysis of the tunnel immersion for the Busan-Geoje Fixed Link Project through scale model tests and computer simulations. In Proceedings of the 8th International Conference on Ocean, Offshore and Arctic Engineering-OMAE 2009, Honolulu, HI, USA, 31 May 2009. [Google Scholar]
- Partha, C.; Subrata, K.C.; Tommy, O.; Koo, I.S. Dynamic simulation of immersion of tunnel elements for Busan-Geoje Fixed Link Project. In Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering 2008, San Francisco, CA, USA, 25 June 2008; Volume 4. [Google Scholar]
- Jensen, O.P.; Olsen, T.H.; Kim, C.; Heo, J.W.; Yang, B. Construction of immersed tunnel in offshore wave conditions Busan-Geoje project South Korea. Tunn. Undergr. Space Technol. 2006, 21, 333. [Google Scholar] [CrossRef]
- Hakkaart, C.J.A. Transport of tunnel elements from Baltimore to Boston, over the Atlantic Ocean. Tunn. Undergr. Space Technol. 1996, 11, 479–483. [Google Scholar] [CrossRef]
- Gong, S.K.; Gao, J.L.; Yan, M.Y.; Song, Z.W.; Shi, H.B. Effects of floater motion on wave loads during steady-state gap resonance occurring between two non-identical boxes. Ocean. Eng. 2025, 323, 120649. [Google Scholar] [CrossRef]
- Aono, T.; Sumida, K.; Fujiwara, R. Rapid stabilization of the immersed tunnel element. In Proceedings of the Coastal Structures 2003 Conference, Portland, OR, USA, 26–30 August 2003. [Google Scholar]
- Kasper, T.; Steenfelt, J.S.; Pedersen, L.M. Stability of an immersed tunnel in offshore conditions under deep water wave impact. Coast. Eng. 2008, 55, 753–760. [Google Scholar]
- Wu, Z.W.; Liu, J.K.; Liu, Z.Q. Nonlinear wave forces on large-scale submerged tunnel element. Mar. Struct. 2016, 45, 133–156. [Google Scholar] [CrossRef]
- Bhatt, R.B.; Dukkipati, R.V. Advanced Dynamics; Alpha Science International, Ltd.: Oxford, UK, 2001; pp. 213–219. [Google Scholar]
- Goda, Y. A comparative review on the functional forms of directional wave spectrum. Coast. Eng. J. 1999, 41, 1–20. [Google Scholar] [CrossRef]
- Charkrabarti, S.K. Offshore Structure Modeling; World Scientific Publishing: Singapore, 1994. [Google Scholar]
- He, M. Study on the Dynamic Response of a New Type of Floating Combined Structure Under Wave Action. Doctoral Dissertation, Dalian University of Technology, Dalian, China, 2016. (In Chinese). [Google Scholar]
- Wang, D.G.; Zou, Z.L. Study of non-linear wave motions and wave forces on ship sections against vertical quay in a harbor. Ocean. Eng. 2007, 34, 1245–1256. [Google Scholar] [CrossRef]
- Yang, Z.W.; Li, J.Z.; Xu, Y.W.; Ji, X.R.; Sun, Z.X.; Ouyang, Q.N.; Zhang, H.Q. Experimental study on the wave-induced dynamic response and hydrodynamic characteristics of a submerged floating tunnel with elastically truncated boundary condition. Mar. Struct. 2023, 88, 103339. [Google Scholar]
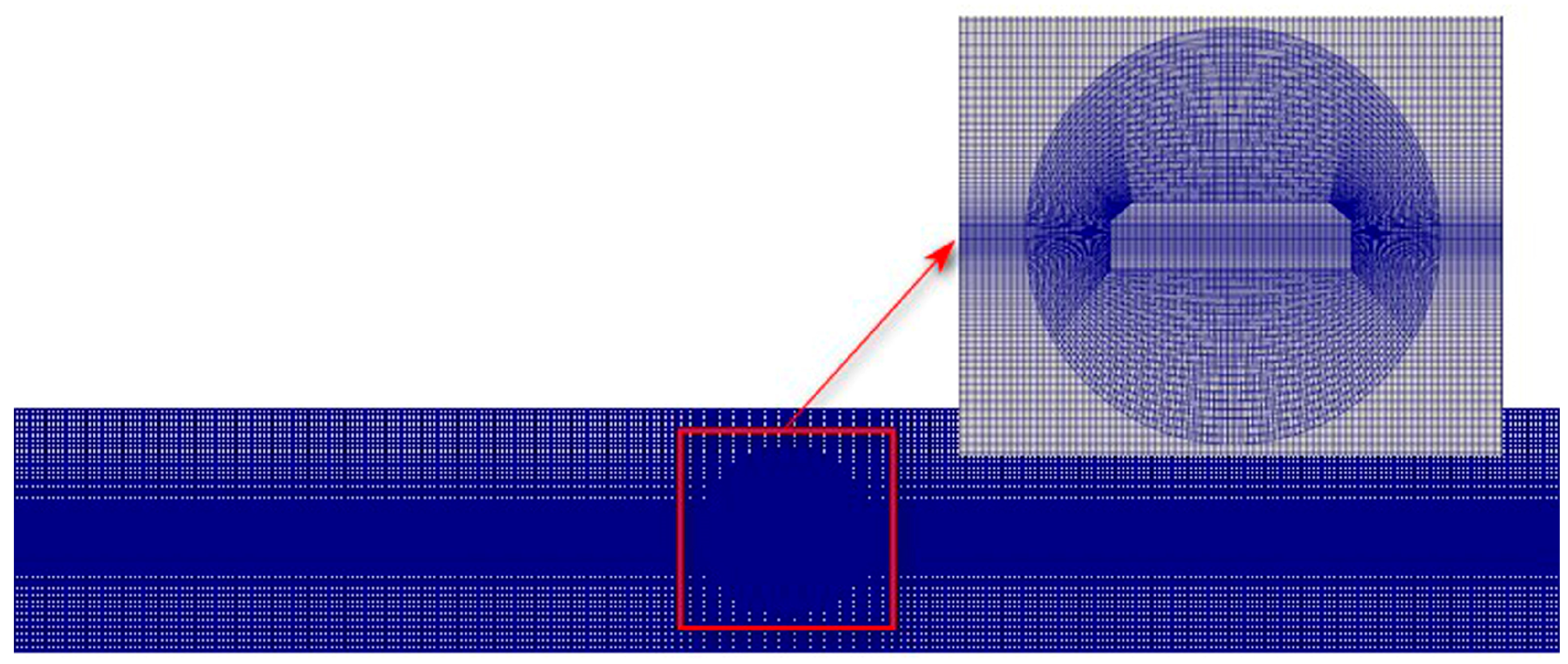
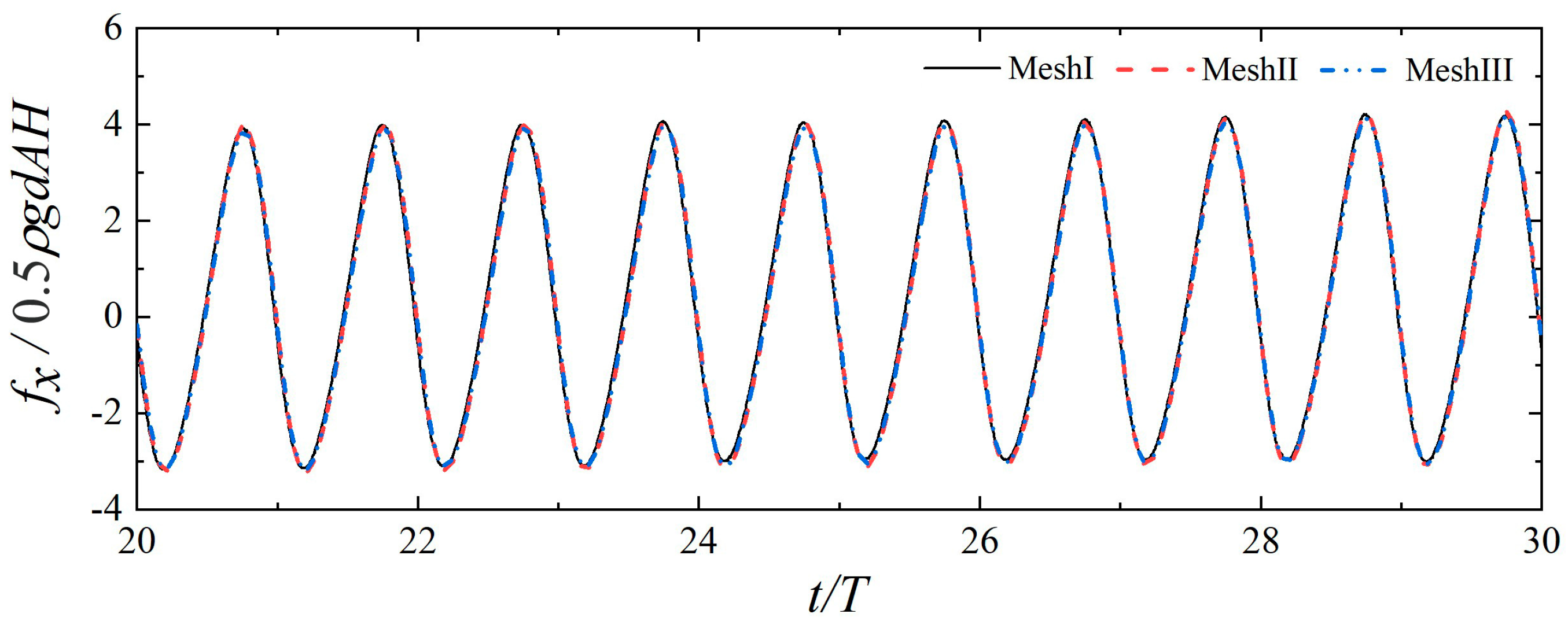
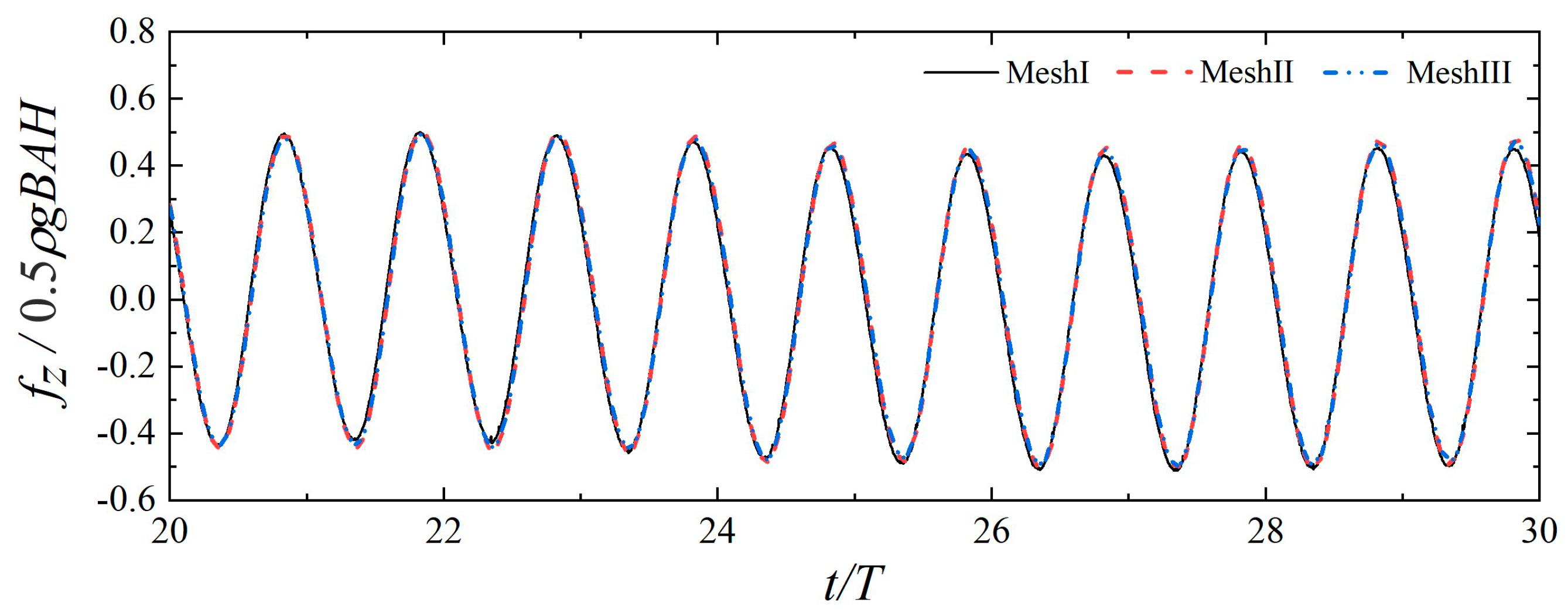
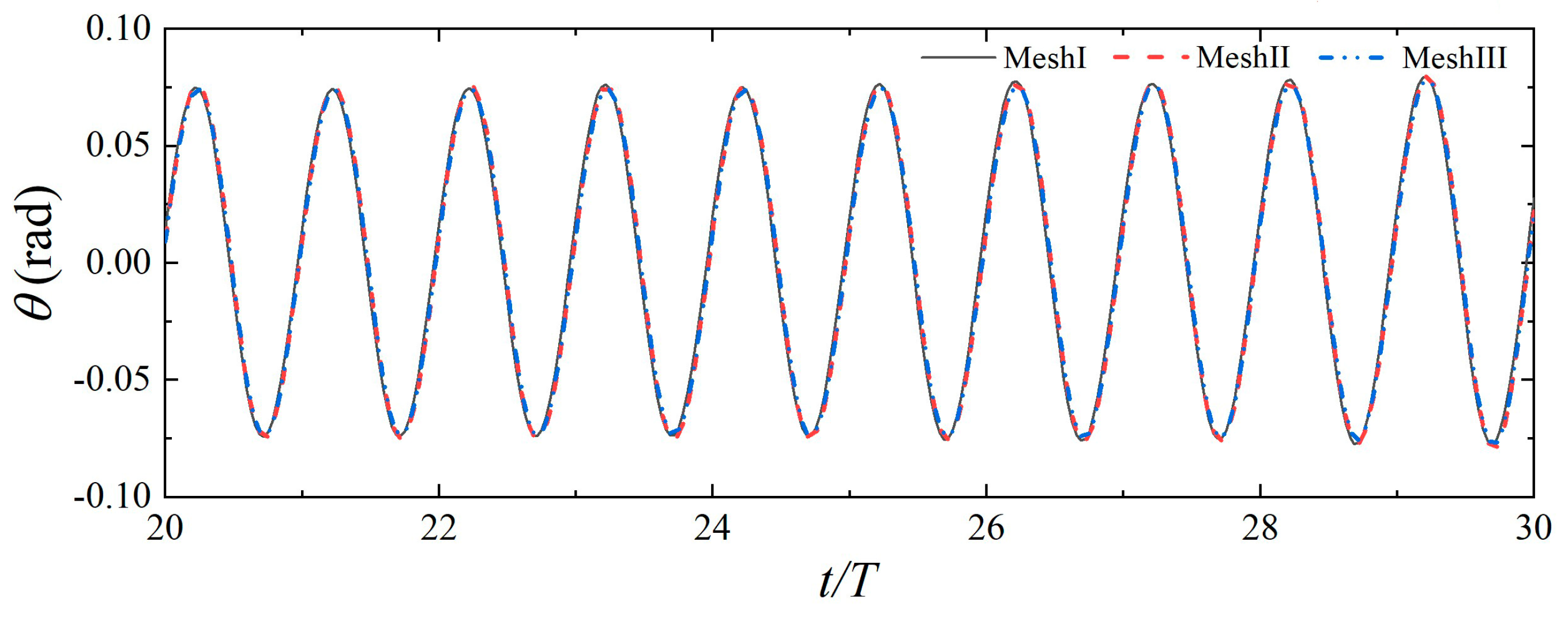
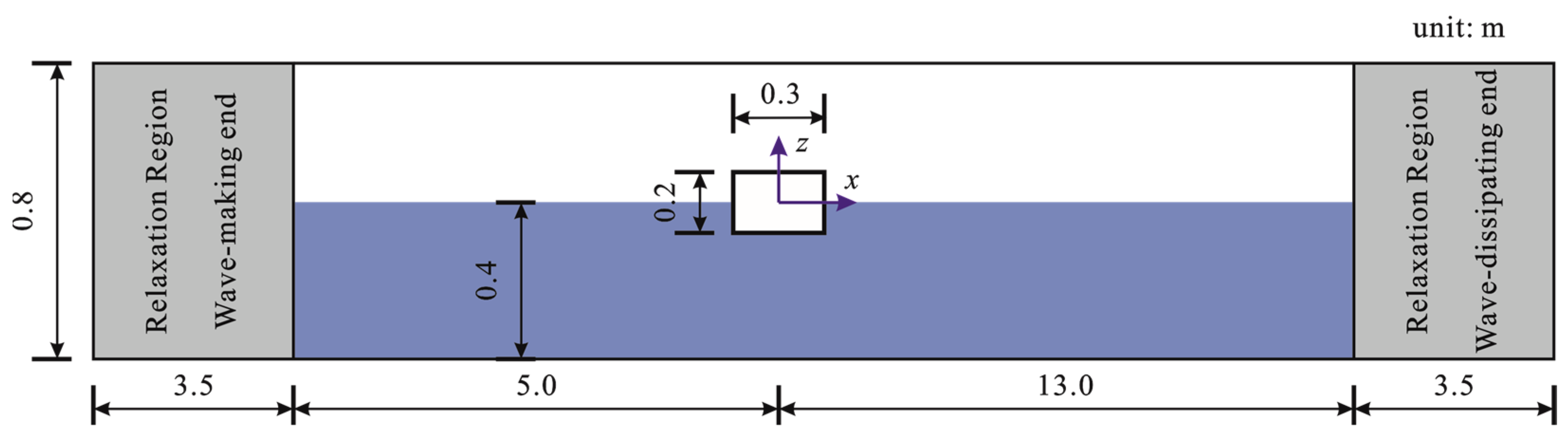
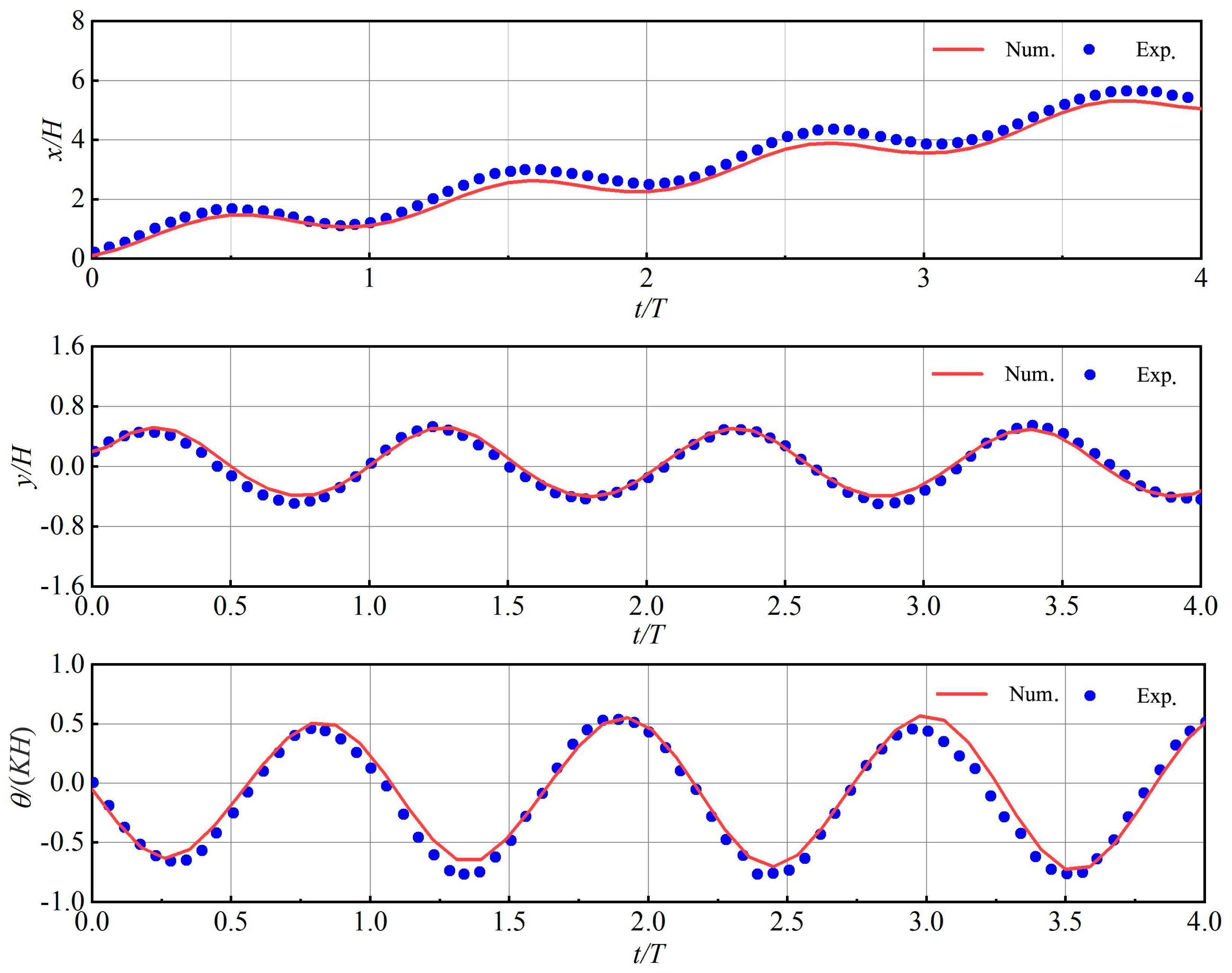
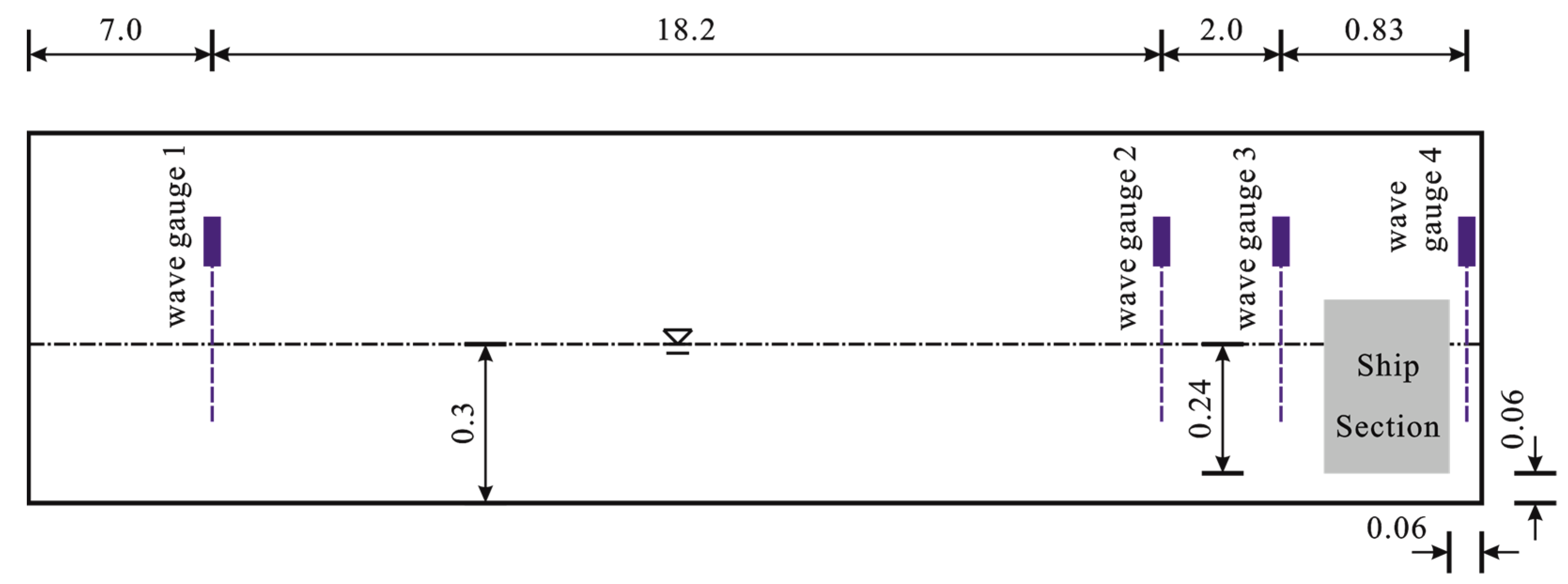


| λ/Δx | H/Δz | Number of Meshes | |
|---|---|---|---|
| Mesh I | 60 | 16 | 69,187 |
| Mesh II | 80 | 18 | 79,615 |
| Mesh III | 100 | 20 | 90,041 |
| No. | Draft (m) | Wave Period (s) | Wave Height H (m) |
|---|---|---|---|
| 1 | 0.09 | 1.6 | 0.02 |
| 2 | 0.09 | 1.6 | 0.04 |
| 3 | 0.09 | 1.6 | 0.06 |
| 4 | 0.09 | 1.6 | 0.08 |
| 5 | 0.09 | 1.0 | 0.06 |
| 6 | 0.09 | 1.2 | 0.06 |
| 7 | 0.09 | 1.4 | 0.06 |
| 8 | 0.09 | 1.6 | 0.06 |
| 9 | 0.09 | 1.8 | 0.06 |
| No. | Draft d (m) | Significant Wave Period Ts (s) | Significant Wave Height Hs (m) |
|---|---|---|---|
| 1 | 0.09 | 1.6 | 0.02 |
| 2 | 0.09 | 1.6 | 0.04 |
| 3 | 0.09 | 1.6 | 0.06 |
| 4 | 0.09 | 1.6 | 0.08 |
| 5 | 0.09 | 1.6 | 0.10 |
| Wave Type | Wave Height | |||
|---|---|---|---|---|
| 0.02 m | 0.04 m | 0.06 m | 0.08 m | |
| Regular wave | −0.02~0.02 | −0.04~0.04 | −0.07~0.07 | −0.09~0.09 |
| Irregular wave | −0.05~0.05 | −0.08~0.10 | −0.18~0.16 | −0.24~0.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, H.; Jia, X.; Xu, T.; Zhang, W. Numerical Simulation of the Hydrodynamic Behavior of Immersed Tunnel in Waves. Water 2025, 17, 1094. https://doi.org/10.3390/w17071094
Shi H, Jia X, Xu T, Zhang W. Numerical Simulation of the Hydrodynamic Behavior of Immersed Tunnel in Waves. Water. 2025; 17(7):1094. https://doi.org/10.3390/w17071094
Chicago/Turabian StyleShi, Hang, Xianlin Jia, Tiaojian Xu, and Wo Zhang. 2025. "Numerical Simulation of the Hydrodynamic Behavior of Immersed Tunnel in Waves" Water 17, no. 7: 1094. https://doi.org/10.3390/w17071094
APA StyleShi, H., Jia, X., Xu, T., & Zhang, W. (2025). Numerical Simulation of the Hydrodynamic Behavior of Immersed Tunnel in Waves. Water, 17(7), 1094. https://doi.org/10.3390/w17071094






