Abstract
Bayesian methods have revolutionised hydrological modelling by providing a framework for managing uncertainty, improving model calibration, and enabling more accurate predictions. This paper reviews the evolution of Bayesian methods in hydrology, from their initial applications in flood-frequency analysis to their current use in streamflow forecasting, flood risk assessment, and climate-change adaptation. It discusses the development of key Bayesian techniques, such as Markov Chain Monte Carlo (MCMC) methods, hierarchical models, and approximate Bayesian computation (ABC), and their integration with remote sensing and big data analytics. The paper also presents simulated examples demonstrating the application of Bayesian methods to flood, drought, and rainfall data, showcasing the potential of these methods to inform water-resource management, flood risk mitigation, and drought prediction. The future of Bayesian hydrology lies in expanding the use of machine learning, improving computational efficiency, and integrating large-scale datasets from remote sensing. This review serves as a resource for hydrologists seeking to understand the evolution and future potential of Bayesian methods in addressing complex hydrological challenges.
1. Introduction
1.1. Overview
Bayesian methods, based on Bayes’ theorem, have become a cornerstone of modern hydrological modelling due to their capacity to handle uncertainty in data and model parameters. Hydrology, the study of water in the environment, is inherently uncertain due to the complex and dynamic interactions between climatic, topographic, and hydrological variables. Understanding the behaviour of water bodies, whether rivers, lakes, or groundwater, requires models that can predict future events such as floods, droughts, and rainfall, while accounting for the uncertainty in the data and parameters. Bayesian methods provide a probabilistic framework to incorporate this uncertainty into hydrological models, making them more transparent and reliable.
The origins of Bayesian methods in hydrology can be traced back to the late 20th century, where early applications focused on flood risk analysis and hydrological parameter estimation. Over the years, the adoption of computational advancements such as Markov Chain Monte Carlo (MCMC) methods has allowed for more complex and robust modelling techniques. Today, Bayesian methods are widely used in areas such as flood forecasting, drought prediction, and rainfall modelling, where traditional deterministic models often fall short in handling the inherent variability and uncertainty.
The need for Bayesian methods in hydrology has grown as climate change, urbanisation, and other global changes introduce new challenges to water management. These changes have made hydrological systems more unpredictable, requiring models that can not only forecast and estimate hydrological extremes but also quantify the associated uncertainties. This paper seeks to explore the historical development, current applications, and future directions of Bayesian methods in hydrology, with a focus on flood, drought, rainfall modelling and other hybrid approaches. The next section provides an outline of the key equations used in Bayesian analysis, as applied in this study. These equations form the foundation for the Bayesian methods implemented in the various hydrological applications discussed in this manuscript.
1.2. Fundamental Bayes’ Theorem
At its core, Bayes’ theorem provides a way to update the probability for a hypothesis (or parameter) θ in light of new data D. The theorem is written as:
where
- is the posterior probability distribution of the parameter after observing the data D.
- is the likelihood, which represents the probability of observing data D given the parameter .
- P(θ) is the prior probability distribution of θ before the data are observed.
- P(D) is the marginal likelihood (or evidence), acting as a normalising constant, calculated by integrating over all possible parameter values:
Because P(D) does not depend on θ, it is common to write the relationship in proportional form:
1.3. Liklihood Function
In many hydrological applications, the likelihood function is chosen based on the statistical characteristics of the data. For example, if the observed runoff y is assumed to be normally distributed with mean μ(θ) (which depends on the parameters θ) and known variance σ2, then the likelihood is given by:
When multiple independent observations y = {y1, y2, …, yn} are available, the joint likelihood becomes:
1.4. Prior Distribution
The prior P(θ) encapsulates our knowledge about the parameter θ before observing the data. Priors can be informative (based on previous studies or expert judgement) or non-informative (designed to have minimal influence). For example, a common non-informative prior for a parameter that can take any real value is the uniform prior:
Alternatively, if previous information suggests that θ is normally distributed with mean μ0 and variance τ2, the prior might be:
1.5. Posterior Distribution and Bayesian Updating
Combining the likelihood and the prior via Bayes’ theorem yields the posterior distribution:
In practice, the denominator (the evidence) is often difficult to compute directly, particularly for complex models or high-dimensional parameter spaces. As a result, numerical methods such as Markov Chain Monte Carlo (MCMC) are used to sample from the posterior distribution without having to calculate the normalising constant explicitly.
1.6. Bayesian Estimation
A common point of estimate from the posterior distribution is the posterior mean:
This estimate can be used as a input in predictive models, though it is often more informative to consider the full posterior distribution when quantifying uncertainty.
1.7. Predictive Distribution
To predict a new observation ynew given the data y, the predictive distribution is computed by integrating over the uncertainty in θ:
This equation underscores one of the key advantages of the Bayesian framework—uncertainty in parameter estimates is naturally propagated to the predictions.
1.8. Practical Application in Hydrology
In hydrological modelling, such as in rainfall–runoff prediction or flood-frequency analysis, Bayesian methods allow for:
- Integration of Diverse Data Sources: Prior information from regional studies can be combined with local observations.
- Uncertainty Quantification: The full posterior distribution gives insights into the range of possible outcomes rather than a single deterministic prediction.
- Adaptive Learning: As new data become available (e.g., during a flood event), the posterior can be updated, leading to improved and dynamic forecasting.
For example, when estimating flood quantiles, the use of a Bayesian framework might involve specifying a likelihood function for the observed peak flows, choosing an appropriate prior based on historical records, and using MCMC techniques to obtain a posterior distribution for flood quantiles. The resulting credible intervals provide decision-makers with a clear measure of the uncertainty associated with flood predictions.
The next section provides an outline of the methods employed in the literature review. This includes the theoretical foundations of Bayesian inference as well as the systematic approach used to identify, evaluate, and synthesise relevant studies in the field of hydrological modelling.
2. Methodology and Literature Review
2.1. Databases and Timeframes
Searches were conducted in Scopus, Web of Science, and Google Scholar to cover both multidisciplinary and domain-specific journals. Publications from 1975 to the present were considered. This period captures the formative years of Bayesian applications in hydrology (notably in flood-frequency analysis and parameter estimation) as well as more recent innovations (e.g., hybrid Bayesian–machine learning models).
2.2. Search Strategy and Keywords
Keywords: The following terms were used in various combinations:
- (i)
- Core Bayesian Terms: “Bayesian”, “Bayes”, “Markov Chain Monte Carlo”, “hierarchical Bayesian”, “Bayesian network”, “approximate Bayesian computation”.
- (ii)
- Hydrology Keywords: “hydrology”, “flood forecasting”, “flood frequency”, “drought prediction”, “rainfall modelling”, “water quality”, “streamflow”, “runoff”, “groundwater”, “hydraulic”. Advanced Topics: “machine learning”, “data assimilation”, “uncertainty quantification”, “dynamic Bayesian networks”, “spatio-temporal modelling”.
- (iii)
- Boolean Operators: Queries combined these keywords with AND, OR, and NOT to refine results. For example:
(“Bayesian” OR “Bayes”) AND (“hydrology” OR “flood forecasting” OR “rainfall modelling”)
(“Bayesian network” OR “hierarchical Bayesian”) AND (“uncertainty” OR “uncertainty quantification”)
2.3. Initial Screening and Eligibility Criteria
- (i)
- Title and Abstract Screening:
- Articles were initially filtered based on relevance to Bayesian methods in hydrology. Titles and abstracts mentioning Bayesian approaches, hydrological modelling, or related topics were retained.
- (ii)
- Language and Publication Type:
- Only English-language peer-reviewed articles, conference proceedings, and book chapters were considered to ensure the quality of the materials and feasibility of analysis.
- (iii)
- Inclusion Criteria:
- Explicit use or discussion of Bayesian methods in hydrological contexts.
- Sufficient methodological detail, allowing for an assessment of how Bayesian inference was applied (e.g., parameter estimation, flood-frequency analysis, model calibration).
- (iv)
- Exclusion Criteria:
- Studies focusing purely on statistical theory without hydrological application.
- Non-academic literature, short news articles, or publications lacking methodological details.
2.4. Full- and Partial-Text Review and Quality Appraisal
- (i)
- Full-Text Retrieval:
- Potentially relevant articles were downloaded and reviewed, some partially and some in full.
- (ii)
- Quality Assessment:
- Studies were assessed on the clarity of Bayesian methodology, data availability, and rigour of results.
- Articles that did not provide enough detail on Bayesian model construction or uncertainty analysis were excluded.
- (iii)
- Reference Checking and the Snowball Approach:
- Reference lists of key articles were scanned to identify additional relevant publications. This iterative process helped capture important works that might not have surfaced in the initial database queries.
- (iv)
- Data Extraction and Categorising Information:
- For each article, the following information was recorded in a spreadsheet.
- Study objective and hydrological domain (flood, drought, water quality, rainfall–runoff, etc.).
- Type of Bayesian method used (MCMC, hierarchical Bayesian, Bayesian network, etc.).
- Key findings, especially regarding uncertainty quantification and parameter estimation.
- Articles were organised into histograms reflecting historical development, current applications, advancements and innovations, and challenges in Bayesian hydrology.
- Overlapping themes (e.g., flood forecasting plus machine learning) were cross-referenced to avoid duplication and to highlight interdisciplinary links.
- (v)
- Final Selection and Synthesis
- Final Dataset: After removing duplicates and non-relevant items, the final list comprised the core references used in this review.
- Synthesis Approach: Literature findings were summarised in narrative form, highlighting the evolution of Bayesian methods in hydrology, their current state-of-the-art applications, and the outstanding challenges.
- Tables and figures (e.g., Table 1 (a), (b), (c), timeline diagrams) were developed to provide a structured overview of major contributions, authorship networks, and emerging trends.
 Table 1. (a) Historical development of Bayesian methods in hydrological modelling. (b) Current applications of Bayesian methods in hydrological modelling. (c) Advancements, innovations, and challenges in Bayesian hydrology.
Table 1. (a) Historical development of Bayesian methods in hydrological modelling. (b) Current applications of Bayesian methods in hydrological modelling. (c) Advancements, innovations, and challenges in Bayesian hydrology.
- (vi)
- Limitations in the Overall Search
- While multiple databases and a broad range of keywords were used, some relevant studies may not have been retrieved (e.g., non-English publications or grey literature).
- The chosen timeframe (1975–present) aimed to capture seminal works and current research but may exclude earlier formative studies not widely digitised.
This multi-step, systematic search strategy helped ensure a comprehensive and unbiased coverage of Bayesian hydrology research. By integrating keyword-based database queries, careful eligibility screening, quality assessment, and iterative reference checking, it helped identify the most relevant and methodologically robust studies. These selected works form the basis of the review and inform the discussions on historical development, current applications, and future directions in Bayesian hydrological modelling.
3. Evolution of Bayesian Methods in Hydrology
The following section traces the evolution of Bayesian methods in hydrology, highlighting key developments from their early theoretical foundations to modern applications in flood-frequency analysis and forecasting, drought prediction, and hydrological modelling.
Table 1 (a), (b), and (c) present a comprehensive overview of the historical development, current applications, advancements, and challenges related to Bayesian methods in hydrology, while Figure 1 succinctly summarises the Bayesian hydrology evolution timeline. The historical development section traces the evolution of Bayesian approaches in hydrology, from the early contributions by [1,2,3,4,5,6,7,8,9] to the adoption of geostatistical methods e.g., [40]. Current applications highlight how Bayesian frameworks are used in flood risk assessment [51], rainfall modelling [111] and drought forecasting [158]. Advancements include the integration of machine learning with Bayesian methods [159] and dynamic Bayesian networks [110], which address complex hydrological dynamics. The challenges section identifies issues such as data quality [33], computational intensity [105], and parameter uncertainty [142,146,147,148,160,161].
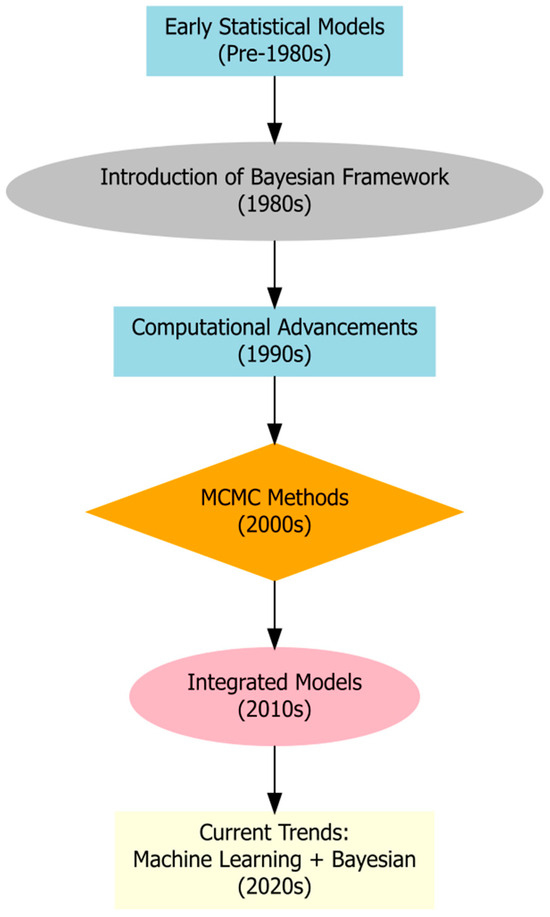
Figure 1.
Evolution of Bayesian methods in hydrology.
The flowchart in Figure 1 provides an overview of the evolution of Bayesian methods in hydrology, showcasing its development and increasing complexity over time. Beginning with foundational applications in uncertainty quantification for basic hydrological processes, these methods evolved to address spatial dependencies using hierarchical models and geostatistical approaches. The integration of temporal dynamics enabled the improved modelling of seasonal and inter-annual hydrological variability, particularly under the influence of climate phenomena such as ENSO.
Recent advancements have focused on coupling Bayesian frameworks with machine learning techniques, such as Bayesian neural networks, to enhance predictive accuracy and account for non-linear relationships. Additionally, modern Bayesian methods now facilitate multi-hazard risk assessment and decision making under uncertainty, offering probabilistic insights critical for sustainable water-resource management. This evolution underscores the transformative impact of Bayesian approaches on hydrology, supporting more robust and informed modelling across diverse contexts.
Figure 2 depicts the key contributions used in Bayesian hydrology from 1975 to 2024. To develop this figure a combination of keywords, Boolean operators, and truncations were used to capture the breadth of relevant studies in Scopus, Web of Science, and Google Scholar. Detailed steps regarding this approach are discussed in Section 2. For Bayesian methods in hydrology, the following was considered in summary:
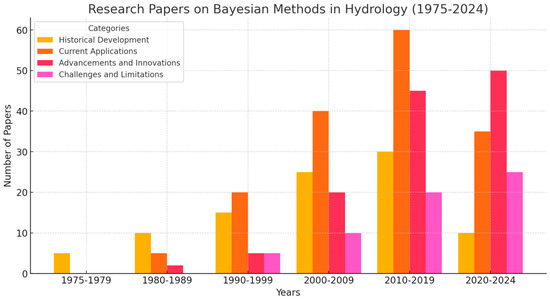
Figure 2.
Papers on Bayesian methods in hydrology based on Table 1’s (a), (b), and (c) categories.
Core keywords:
General: Bayesian; Bayes; hydrology; hydrological
Applications: flood; drought; water quality; groundwater; streamflow; hydraulic
Advancements: Bayesian network; hierarchical Bayesian; Markov Chain Monte Carlo (MCMC); copula Bayesian; Bayesian geostatistics
Challenges: uncertainty; bias; model validation; interdisciplinary
Since the 1990s, the number of publications based on the different categories as per Table 1 and Figure 2 has gradually increased, with the highest number of publications starting in 2009 and 2010. As shown in Figure 2, Bayesian methods in the current application subcategory has been the most popular, followed by the advancements and innovations subcategory. However, the popularity of challenges in Bayesian methods in hydrology has been increasing in recent years, particularly from 2008 onwards.
Figure 3 shows a network diagram map of authorship of papers on Bayesian methods in hydrology and the network of co-authorships. Here, the bigger the node (in blue), the greater the number of papers published by the country. It can be seen that the US, UK, Canada, and Australia have published the highest number of articles in this research field, which is followed by China, Germany, and France. It can also be seen that US has the strongest network of co-authorship (linked with UK, Canada, and Australia), followed by UK (linked with USA, Germany, France, and Greece).
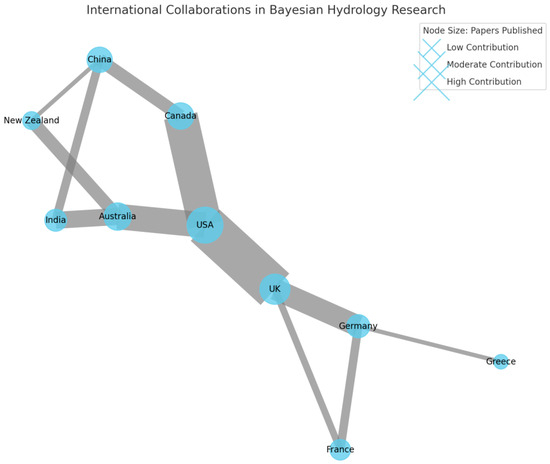
Figure 3.
Network diagram illustrating international collaborations in Bayesian hydrology research—node sizes in blue represent the number of papers published, while edge widths in grey indicate collaboration strength.
4. Historical Development of Bayesian Methods in Hydrology
The use of Bayesian methods in hydrology began with early attempts to quantify uncertainty in the estimation of hydrological parameters. In the 1980s and 1990s, the development of Bayesian models in hydrology was initially focused on flood-frequency analysis, where they were used to estimate the probability of extreme flood events based on limited historical data. One of the major advantages of Bayesian methods is their ability to incorporate prior knowledge, such as expert judgement or physical principles, into the analysis. This was particularly valuable in flood modelling, where data scarcity often limits the reliability of traditional methods. A number of influential papers using Bayesian empirical methods for flood-frequency analysis were by [4,5,6]. Kuczera [4] evaluates the performance of flood-frequency estimators under varying conditions, focusing on the robustness and efficiency of empirical Bayes estimators. He introduces hybrid models that combine regional and site-specific data, demonstrating their superiority for short record lengths. The models are designed to balance resistance to bias with efficiency, ensuring reliable flood-quantile estimates even under adverse data conditions. This work emphasised the importance of robust modelling techniques to enhance flood risk assessments. Kuczera [5] addresses the challenge of integrating site-specific and regional data for flood analysis. The incorporation of spatial correlation into an empirical Bayes framework, showed improved estimates under sampling uncertainty. This method reduced bias by leveraging shared regional characteristics, advancing reliability in flood predictions. Kuczera [6] also introduced a Bayesian approach to model regional skew in flood-frequency analysis. By treating regional skew as a prior distribution, he was able to create a surrogate that reduces the sensitivity of flood-quantile estimates to localised data, providing robust and consistent results.
Gelman et al. [162] introduced Markov Chain Monte Carlo (MCMC) methods, which would later become the cornerstone of modern Bayesian analysis in hydrology. This breakthrough allowed for more efficient sampling from posterior distributions and laid the groundwork for Bayesian methods to be applied to more complex hydrological models.
Another key milestone in Bayesian hydrology was the development of the Bayesian methodology for model calibration by [163]. Their study examined the relationship between data characteristics and the precision of parameter estimates in hydrologic models. It highlighted how the quality and quantity of data influence model parameter uncertainty. The study used sensitivity analysis to show that data with greater variability and better alignment with model predictions lead to more precise parameter estimates. The work presented by [163] here complemented and extended the work of [5,6] who presented a Bayesian approach for the evaluation of flood-frequency models.
One of the most significant contributions to Bayesian hydrology came from [164], who extended Bayesian methods to address uncertainty in hydrological model predictions. Beven’s work on the Topmodel framework demonstrated how Bayesian inference could be used to quantify uncertainty in runoff predictions, particularly in the context of spatial variability and limited observational data. As Bayesian methods gained popularity, researchers began to apply it to other areas of hydrology, such as parameter estimation for rainfall–runoff models. Early work in this area involved using Bayesian inference to estimate parameters in lumped models, which treat the catchment as a single entity—[165]. However, this approach was soon expanded to distributed models, which account for spatial variations in rainfall and runoff across a catchment. With the advent of more powerful computing resources in the late 1990s and early 2000s, Bayesian methods became increasingly sophisticated. The development of MCMC techniques allowed for more efficient sampling from complex posterior distributions, enabling Bayesian inference in more computationally demanding models [146,147]. Hierarchical Bayesian models, which allow for the incorporation of multi-level data (e.g., temporal and spatial data), climate-change impacts on extremes, also became more common [166,167,168,169]. These advancements allowed Bayesian methods to be applied to more complex hydrological systems, such as river basins and groundwater flow models.
5. Current Applications of Bayesian Methods in Hydrology
5.1. Flood Risk Assessment
Flood risk assessment is one of the most prominent areas where Bayesian methods are applied in hydrology. Flood models typically rely on historical data to estimate the frequency and magnitude of extreme flood events. However, the uncertainty inherent in these estimates can be significant due to the limited length of the historical record and the complex nature of flood processes. Bayesian methods help address these challenges by providing a probabilistic framework that accounts for uncertainty in both the data and model parameters.
For example, a Bayesian framework can be used to estimate flood hazard maps that predict the probability of flood events at various locations. This is particularly useful in flood-prone regions where flood mitigation measures need to be prioritised. Bayesian models can also incorporate spatially and temporally varying information, such as climate data, land-use patterns, and river flow characteristics, to provide more accurate flood predictions.
Little et al. [63] explored Bayesian approaches to classify extreme rainfall events across the UK for flood risk management. By using a Bayesian objective classification system, the study evaluated the probability of extreme rainfall events and their associated risks. This methodology allows for dynamic updates as new data become available, enhancing the precision and adaptability of flood risk predictions. The Bayesian framework in this application provided a structured way to incorporate uncertainties and offers probabilistic outputs that are particularly valuable for decision-making in flood risk management.
Parkes & Demeritt [18] developed a Bayesian statistical model for flood-frequency analysis that integrates historic flood data with annual maximum flow data. By applying Bayesian methods, the model effectively combines disparate data sources to reduce uncertainties in estimating rare flood events, such as the 100-year flood. The authors demonstrate that including historical data significantly narrows confidence intervals by as much as 50% for certain return periods as compared to traditional frequency analysis methods. They applied the model to the River Eden in the United Kingdom (UK) and highlighted the importance of addressing uncertainties related to historical channel changes and discharge estimates. This Bayesian framework provided a robust tool for flood risk assessment by leveraging both systematic and historical information. Supplementary Example S1 illustrates a typical Bayesian model setup in R and JAGS (Just Another Gibbs Sampler), implementing a Bayesian MCMC framework to estimate the parameters of the Log Normal distribution (location and scale). It also shows the setting up of priors based on expert knowledge and historical data with the graphing of flood-frequency curves with credible limits and a boxplot comparison of observed vs. posterior flood-quantile estimation.
Cai & Wang [170] examined the uncertainty in precipitation forecasts using the TIGGE (THORPEX Interactive Grand Global Ensemble) database. It combines fuzzy probability with Bayesian theory to improve the modelling and quantification of forecast uncertainty. The Bayesian component of the study focused on probabilistically estimating forecast distributions and updating these estimates as new observational data become available. This hybrid approach improved the reliability of precipitation forecasts, which is crucial for managing flood risks and other hydrological applications.
Overall, it can be seen how Bayesian methods provide a versatile and robust framework for addressing uncertainties inherent in hydrological and meteorological data. These studies also highlighted the value of integrating historical data, probabilistic reasoning, and adaptive learning in enhancing predictive models for water-resource and flood risk management.
5.2. Drought Prediction
Drought prediction is another key area where Bayesian methods are becoming increasingly popular. Droughts, defined by prolonged periods of abnormally low rainfall, are difficult to predict due to their dependence on complex climate patterns. Bayesian models are well-suited for this task because they can integrate information from different sources, such as past drought events, climate indices (e.g., ENSO), and atmospheric conditions. Bayesian hierarchical models have been used to predict drought severity based on regional and global climatic factors. These models allow for the estimation of uncertainty in both short-term and long-term drought predictions, providing decision-makers with more reliable forecasts.
Madadgar & Moradkhani [29,30] introduced a comprehensive Bayesian framework for seasonal drought forecasting. Bayesian inference was utilised to integrate historical hydrologic data with dynamic climate model outputs. The methodology incorporated prior knowledge of drought characteristics and updated it with new information, enabling probabilistic forecasts of drought indices. The Bayesian framework provided a mechanism to quantify uncertainty in seasonal drought forecasts, offering a robust tool for water-resource management and planning.
Madadgar et al. [171] developed a hybrid approach combining statistical and dynamical models for drought prediction in the southwestern United States (U.S). Bayesian methods were employed to estimate probabilistic drought predictions by assimilating diverse sources of uncertainty from the climate models and observational data. Bayesian inference helped calibrate and validate the statistical–dynamical model ensemble, enabling robust seasonal drought forecasting. The framework highlighted the importance of Bayesian approaches for decision support by addressing the variability and uncertainty in climate predictors and improving the prediction of drought indices such as the Standardised Precipitation Index (SPI).
Ali et al. [33] proposed a Bayesian network approach to regional drought monitoring. The methodology involved integrating diverse drought indicators (e.g., precipitation deficits and soil moisture) within a probabilistic framework. Bayesian inference was used to evaluate the likelihood of drought conditions based on observed data and model predictions. The approach was particularly effective in handling data sparsity and provided a robust regional drought index that combined multiple seasonal factors, enhancing the reliability of drought-monitoring efforts. These studies highlight the versatility of Bayesian methods in handling uncertainties, integrating multi-source data, and providing probabilistic predictions for drought management and decision making. In Supplementary Example S2, a simple Bayesian linear regression model to predict future drought indices based on historical data is illustrated, incorporating uncertainty in the predictions based on the Palmer Drought Severity Index. The developed model can be used as a basis to predict future drought occurrences and quantify the risk of extreme drought events and a probabilistic assessment of drought severity under different scenarios.
5.3. Rainfall Modelling
Rainfall modelling is a core application of Bayesian methods in hydrology. Rainfall data are often sparse, particularly in regions with limited monitoring stations or unreliable data sources [61]. Bayesian methods can help integrate various sources of information to improve rainfall predictions [172,173]. By using priors based on historical rainfall patterns and incorporating data from remote sensing technologies (e.g., satellite-based rainfall estimates), Bayesian models can offer more accurate rainfall forecasts. For instance, Bayesian networks have been used to model the spatiotemporal distribution of rainfall, taking into account spatial correlations between rainfall stations and temporal dependencies [174,175]. This approach has been applied in various parts of the world, including tropical regions where rainfall patterns exhibit significant variability. Bayesian methods have been extensively applied to rainfall–runoff modelling, especially in the context of model calibration [143,176,177]. By using Bayesian inference, hydrologists can estimate parameters such as soil moisture retention, evapotranspiration, and runoff coefficients. In Australia, a Bayesian hierarchical model was presented by [178] to improve rainfall prediction by integrating data from ground-based stations and satellite observations. The results showed that the Bayesian model outperformed traditional models in terms of both accuracy and uncertainty quantification. Previous studies have also showed similar results e.g., [61,179].
Supplementary Examples S3 and S4 illustrate comprehensive examples of a Bayesian rainfall–runoff model using R and JAGS. The Bayesian rainfall–runoff model estimates the relationship between rainfalls, evaporation, and temperature inputs (while taking into account the dependences between the covariates) and runoff output, and the Bayesian framework in both examples quantifies the uncertainty in the parameters.
6. Advancements and Innovations in Bayesian Methods for Hydrology
6.1. Machine Learning and Bayesian Methods
The integration of machine learning (ML) with Bayesian methods is a growing trend in hydrology. Traditional Bayesian models rely on prior distributions and likelihood functions, but machine learning algorithms can learn patterns directly from data [180,181,182]. Combining these two approaches allows for the creation of more flexible models that can handle large and complex datasets.
For instance, Bayesian neural networks (BNNs) combine the flexibility of neural networks with the probabilistic framework of Bayesian inference. BNNs can be used to model non-linear relationships between hydrological variables, such as the impact of climate factors on river flow or rainfall. By estimating the uncertainty in model predictions, BNNs provide a more reliable tool for flood and drought prediction. In a study by [183], they show that hybrid modelling that combines hydrological models, BNNs, and uncertainty analysis improves streamflow prediction in alpine regions influenced by rainfall, snow, and glacier melt and also achieves higher precision and more reliable uncertainty intervals than traditional approaches. Tested in the Yarkant River basin, this hybrid approach outperforms alternative methods, making it a robust tool for global alpine streamflow prediction.
Vasheghani et al. [184] used the BNN model integrated with atmospheric teleconnection patterns to predict monthly dam inflows in Iran, showing superior performance compared to Artificial Neural Networks (ANN). By leveraging teleconnection indices and local variables, the BNN model achieved lower normalised root mean square errors across three major dams, demonstrating enhanced predictive accuracy and probabilistic reliability. While both models struggled with peak flow predictions, BNN’s ability to incorporate large-scale climate patterns into hydrological forecasting represents a significant advancement in water-resource management. Supplementary Example S5 illustrates the combination of Bayesian methods and ML in hydrology. This example focuses on a scenario where we model streamflow (runoff) based on multiple covariates (e.g., rainfall, temperature, and evaporation), using a Bayesian approach for parameter estimation and a machine learning technique, such as Random Forest, to improve predictions.
6.2. Integration of Remote Sensing and Big Data
The availability of big data and remote sensing technologies has revolutionised hydrological modelling. Satellite-based measurements of rainfall, temperature, and soil moisture are now widely used to supplement ground-based observations. These data sources can be incorporated into Bayesian models to improve predictions of hydrological extremes. Bayesian models can handle the vast amount of data generated by remote sensing technologies and use it to update model parameters in real time. For example, satellite-based rainfall estimates can be used to update flood risk models during a storm event, providing more accurate and timely predictions. Weather forecasting plays a crucial role in various sectors like agriculture, transportation, and emergency planning, all of which can be affected by flooding. A study by [185] introduced a Bayesian model that improves weather predictions by integrating remote sensing data from sources such as satellites, radar, and ground observations. The model employs data pre-processing, Bayesian probability frameworks, and ensemble predictions to provide probabilistic forecasts, enhancing reliability and capturing uncertainties. Preliminary results demonstrated improved accuracy for both short- and long-term forecasts, particularly for extreme weather events. By offering probabilistic insights, this approach supports smarter decision-making across industries and highlights the benefits of incorporating remote sensing data into weather prediction models.
6.3. Hybrid Models
Hybrid models, which combine physical models with data-driven approaches, are gaining increasing attention in hydrology due to their ability to integrate the strengths of both methodologies. These models typically use physical laws (e.g., conservation of mass and energy) to represent hydrological processes and combine them with data-driven methods (e.g., machine learning or Bayesian networks) to estimate unknown parameters or improve prediction accuracy. Example: Bayesian inference with hydrological simulation models: One of the leading examples of hybrid models in hydrology is the integration of Bayesian inference with hydrological simulation models like SWAT (Soil and Water Assessment Tool) or HEC-HMS (Hydrologic Engineering Center’s Hydrologic Modelling System). In these models, Bayesian techniques are applied to optimise parameters that cannot be directly measured, such as soil permeability or vegetation parameters. These parameters are often inferred by Bayesian methods based on available observational data, which improves the model’s predictive power and provides a rigorous measure of uncertainty.
A recent example of hybrid modelling for flood forecasting is the combination of Bayesian methods with ensemble machine learning techniques can be read in [186]. This study introduced an advanced ensemble learning model, combining a Bayesian Belief Network with an extreme learning machine and a back-propagation structure optimised by a genetic algorithm. Using a dataset of 194 flood locations and ten conditioning factors, the model outperformed benchmark established methods. The findings demonstrate the hybrid model that combines genetic algorithms and Bayesian Belief Networks has potential as a robust tool for managing flood risks globally. Han & Coulibaly [83,182] also provide good examples of Bayesian flood-forecasting hybrid methods.
6.4. Data Assimilation
Data assimilation, the process of combining model predictions with observational data, is another area where Bayesian methods have led to significant advancements. By incorporating real-time observations into hydrological models, data assimilation methods improve model forecasts and reduce uncertainty. The Kalman filter, a recursive Bayesian estimation technique, has been widely used in hydrological modelling for data assimilation [187,188,189]. It is particularly effective in real-time forecasting, where observations become available at different time steps and need to be incorporated into ongoing model predictions. The Kalman filter has been applied in flood-forecasting models to assimilate streamflow observations and adjust the model’s parameters accordingly, improving flood prediction accuracy [53,190]. For non-linear and non-Gaussian systems, particle filters offer a more flexible alternative to Kalman filters. Particle filters approximate the posterior distribution by using a set of random samples or “particles” to represent the distribution. This method has been successfully applied in hydrological models to assimilate data from multiple sources, such as rainfall and streamflow measurements, leading to improved forecasts in flood and drought prediction [191,192,193].
6.5. Spatial and Temporal Modelling
The growing complexity of hydrological systems and their interactions with climatic and anthropogenic factors have underscored the critical importance of spatial–temporal modelling in hydrology. These models provide a framework for capturing the variability and interdependence of hydrological processes across space and time [194], which is vital for informed water-resource management. Spatial–temporal modelling allows researchers to better understand and predict phenomena such as rainfall distribution, runoff patterns, and flood events by incorporating location-specific features such as topography, land use, and soil characteristics [65]. Bayesian models have emerged as a powerful tool for modelling spatial correlations in hydrology, offering a probabilistic approach that quantifies uncertainty while accounting for inter-site dependencies [195]. For instance, Gaussian Process models and Bayesian hierarchical models are commonly used to analyse spatial rainfall patterns, estimate runoff in ungauged basins, and predict flood risks by leveraging spatially distributed data and covariates such as elevation and land cover [44].
Bayesian methods are particularly well-suited for capturing spatial correlations in hydrological data due to their flexibility and ability to incorporate prior information. Bayesian spatial models, such as those using Gaussian–Markov Random Fields (GMRFs) or spatial autoregressive priors, enable the explicit modelling of dependencies between measurements taken at different locations [196,197]. These models can integrate diverse data sources, such as satellite precipitation estimates and ground-based measurements, to provide more robust and comprehensive insights into spatial hydrological processes. In the context of rainfall, Bayesian kriging has been used to interpolate rainfall data over large areas [44], while Bayesian copulas have been applied to model joint distributions of flood peaks across multiple sites [198]. Such spatially aware Bayesian frameworks allow hydrologists to make predictions in data-scarce regions, assess risks more comprehensively, and optimise infrastructure design in the face of spatially variable hydrological inputs.
In addition to spatial correlations, Bayesian methods are invaluable for modelling temporal dependencies in hydrological processes, particularly under the influence of climate variability and periodic patterns, [62,199,200]. These models enable the incorporation of temporal covariates such as El Niño–Southern Oscillation (ENSO) indices, seasonal cycles, and long-term climate trends, allowing researchers to understand how hydrological processes evolve over time. For example, Bayesian state-space models are often used to analyse streamflow time series, while dynamic linear models capture shifting relationships between rainfall and runoff in response to ENSO events. By integrating historical and real-time data, Bayesian frameworks help assess the impacts of changing climate regimes on hydrological processes, providing probabilistic forecasts of droughts, floods, and water availability [201,202,203]. This ability to quantify uncertainty and infer temporal dynamics makes Bayesian methods an essential tool for developing adaptive strategies to manage water resources in the face of climate change.
7. Challenges in Bayesian Hydrology
7.1. Current Trends
Bayesian methods are now widely used in hydrology, particularly for assessing uncertainty in model predictions, model calibration, and data assimilation. One of the major developments has been the application of Markov Chain Monte Carlo (MCMC) methods, which have made Bayesian methods more feasible for complex hydrological systems. The availability of open-source software packages like R version 4.4.0, Python version 3.12.2, JAGS version 4.31, WinBUGS (Windows Bayesian Inference Using Gibbs Sampling) version 1.4.3, and Stan version 2.35.0 has significantly lowered the barriers to applying Bayesian methods in hydrology.
7.2. Advancements in Computational Tools and Software
The development of more efficient MCMC algorithms and parallel computing has made Bayesian analysis more accessible for hydrologists. Integrated Nested Laplace Approximation (INLA), a method that provides approximate Bayesian inference, has also gained traction due to its speed and efficiency, especially in spatial modelling contexts [204]. Additionally, the rise in high-performance computing and cloud-based solutions has further accelerated the adoption of Bayesian methods.
Despite the considerable advancements in Bayesian methods for hydrology, there remain several challenges that limit their widespread adoption in practice. These challenges range from issues related to data and model complexity to computational demands and the interpretation of results [205].
The advancements in Bayesian hydrology have been significantly influenced by computational tools like R version 4.4.0, Python version 3.12.2, JAGS version 4.31, WinBUGS version 1.4.3, and Stan version 2.35.0 These tools have revolutionised how researchers approach uncertainty, spatial–temporal modelling, and predictive analysis in hydrology, offering both flexibility and efficiency in implementing Bayesian methods. Stan has been transformative in Bayesian hydrology due to its high-performance Hamiltonian Monte Carlo (HMC) algorithm, which allows researchers to tackle complex, high-dimensional models with faster convergence and improved accuracy. Its gradient-based approach makes it particularly suitable for handling spatial-temporal data in hydrology, such as rainfall–runoff modelling or groundwater flow simulations [206]. Stan’s integration with R and Python through packages like rstan and pystan has made it a cornerstone for hydrologists seeking advanced hierarchical modelling capabilities [207].
JAGS and WinBUGS remain popular choices for Bayesian hydrology due to their simplicity and effectiveness in modelling smaller datasets and moderate complexity problems. These tools leverage Gibbs Sampling, which, while slower than HMC, provides an intuitive framework for parameter estimation and hierarchical modelling [208,209]. JAGS, in particular, have advanced hydrology research through its seamless integration with R (via rjags), enabling flexible scripting and visualisation [210]. WinBUGS, with its graphical interface, has been instrumental in the early adoption of Bayesian methods for flood-frequency analysis and parameter uncertainty studies [127]. R and Python, as programming environments, have further propelled Bayesian hydrology by offering diverse libraries for Bayesian computation, data manipulation, and visualisation. R packages like brms (which interfaces with Stan), rjags, and coda simplify Bayesian analysis and provide tools for model diagnostics and posterior summaries [211]. Python’s libraries such as PyMC3 [212] mirror these functionalities, offering dynamic options for building Bayesian models with custom workflows.
Collectively, these tools have allowed hydrologists to develop more realistic models that capture the uncertainty inherent in hydrological processes. They support advanced applications like spatial correlation modelling, probabilistic flood forecasting, and climate impact assessment, cementing Bayesian analysis as a fundamental approach in modern hydrology. Table 2, below, compares these computational tools on specific features from ease of use to speed and performance, while also comparing how well they integrate with other software. Overall, Table 2 illustrates that each tool has its strengths, and the choice software depends on the complexity of the model, computational needs, and user familiarity.

Table 2.
Comparison of computational tools for Bayesian hydrology.
7.3. Prior Selection and Subjectivity
One of the main challenges in applying Bayesian methods is the selection of appropriate priors. In Bayesian inference, the choice of prior distribution reflects prior knowledge or beliefs about the model parameters. However, the selection of priors can be subjective, and different priors can lead to significantly different posterior distributions, especially when data are sparse.
Commonly used priors in hydrological applications include non-informative priors (e.g., uniform or Jeffreys’ prior) when minimal prior knowledge exists, or informative priors derived from historical data and expert judgement. For example, [213] provides tools to investigate prior distributions in Bayesian hydrology, while [214] demonstrate the application of empirical Bayes estimation in peak over threshold modelling. The selection of a prior can influence the posterior results, particularly when data are scarce, and thus must be justified based on physical reasoning or historical evidence.
In at-site and regional flood-frequency analysis, the choice of prior distribution for the parameters of a flood-frequency distribution (e.g., Generalised Extreme Value and Log-Pearson type 3 distributions) can heavily influence the resulting risk estimates [12,22,49,51,215,216]. If the prior is chosen poorly or without sufficient justification, it may lead to biased flood risk assessments, which could have significant implications for flood management decisions. To address this challenge, empirical Bayes methods have been proposed as a way to estimate priors directly from the data [4,49,61,160,161,217,218,219]. However, even these methods require careful consideration, as they may still introduce biases, particularly in the case of complex models with many parameters.
The practical implementation of Bayesian methods in this study demonstrates that the choice of prior distributions can influence the posterior results and subsequent uncertainty quantification. In the examples provided in the Supplementary Materials, the selection of priors has been tailored to the specific requirements of each hydrological application, as detailed below.
Example 1.
Bayesian Flood Risk Assessment
Let Y denote the annual maximum streamflow. We assume that log(Y) ∼ N (μ, σ2). The priors for the parameters are chosen as follows:
For the location parameter (μ): μ ∼ N (0,τμ−1), with τu = 0.0001, meaning that μ has a very wide Gaussian prior. For the scale parameter (σ):
σ ∼ U (0,10). In this formulation, the precision is defined as τ = 1/σ2
Example 2.
Bayesian Drought Prediction
Let D denote the drought index (e.g., Palmer Drought Severity Index). We assume that D ∼ N (μ, σ2).
The priors are specified as: For μ: μ ∼ N (0, 106) (using a precision of 1.0 × 10−6), providing a very uninformative prior. For σ: σ ∼ Gamma (0.1, 0.1), where the Gamma distribution is used to model the precision indirectly.
Example 3.
Bayesian Rainfall–Runoff Modelling
Consider the linear regression model: Q = β0 + β1R + β2E + β3T + ε, ε ∼ N (0, σ2), where Q is the runoff, and R, E, and T represent rainfall, evaporation, and temperature, respectively. The priors are defined as: For the regression coefficients (β0, β1, β2, β3): βi ∼ N (0, 103) for i = 0, 1, 2, 3 (using a precision of 0.001). For the precision (τ): τ ∼ Gamma (0.1, 0.1), and the standard deviation is recovered as σ = .
Example 4.
Parameter Uncertainty Via GLUE Framework
For a simple rainfall–runoff model defined as Q = aPb, where Q is runoff and P is precipitation, the parameters are assumed to have uniform priors: For a: a ∼ U (0.1, 1).
For b: b ∼ U (0.5, 1.5). This approach reflects uncertainty by allowing a broad range of plausible values for both parameters.
Example 5.
Combining Bayesian and machine learning for rainfall–runoff modelling: The Bayesian component of this example employs the same linear regression model as in Example 3: Q = β0 + β1R + β2E + β3T + ε, ε ∼ N (0, σ2), with priors: for each βᵢ: βi ∼ N (0, 103) for i = 0, 1, 2, 3. For τ: τ ∼ Gamma (0.1, 0.1), and σ = . The machine learning (Random Forest) component does not involve an explicit prior.
Example 6.
Bayesian hydrology with an interdisciplinary objective: in the interdisciplinary example, where agricultural yield (Y) is modelled as a function of rainfall (X1) and streamflow (X2), we consider the linear model
Y = β0 + β1X1 + β2X2 + ε, ε ∼ N (0, σ2)
The priors in this example are slightly more informative: for the coefficients (β0, β1, β2): βi ∼ N (0, 102) for i = 0, 1, 2 (using a precision of 0.01).
For σ: σ ∼ U (0, 50), with the precision defined as τ = 1/σ2.
Therefore, in summarising mathematically:
Normal (Gaussian) priors are used for regression coefficients in Examples 3, 5, and 6, with varying degrees of informativeness (precision of 0.001 vs. 0.01).
Uniform priors are applied for σ in Example 1 and Example 6, as well as for parameters a and b in Example 4.
Gamma priors are chosen for τ in Examples 2, 3, and 5. These choices reflect the need to accommodate data sparsity, capture the skewed nature of hydrological variables, and provide flexibility in uncertainty quantification.
It is important to acknowledge that some degree of subjectivity is inevitable in the selection of priors.
7.4. High-Dimensional Parameter Estimation
Many hydrological models, particularly those used for flood forecasting or climate-change impact assessment, involve high-dimensional parameter spaces. Estimating the posterior distributions of these parameters using Bayesian inference can be computationally expensive, especially when using methods like MCMC. For large-scale models such as those used in global flood or drought forecasting, the parameter spaces may involve hundreds or even thousands of parameters. The computational burden of estimating these parameters, particularly with MCMC or other sampling methods can make Bayesian inference impractical for many real-world applications [220,221,222,223]. Recent advances in variational inference and approximate Bayesian computation (ABC) offer promising alternatives to MCMC. These techniques allow for faster computation by approximating the posterior distribution, though they may sacrifice some of the accuracy of the results [224,225,226].
7.5. Data Limitations and Uncertainty and Computational Demands
Another significant challenge in applying Bayesian methods in hydrology is the inherent uncertainty in the available data. Hydrological data are often sparse, particularly in remote regions or in the context of extreme events like floods and droughts. Additionally, data may be noisy, biased, or incomplete, which can further complicate the modelling process. In regions where streamflow data are sparse, Bayesian methods are often used to estimate parameters by integrating prior knowledge and expert judgement [227,228]. However, the limited number of observations can lead to high uncertainty in model predictions, which can affect decision making in water-resource management. Bayesian methods, particularly MCMC and particle filters, can be computationally expensive, especially when applied to large-scale models or complex systems with many parameters. This is particularly problematic in operational settings, where real-time predictions are needed [229,230,231,232]. In operational flood forecasting, where predictions need to be updated in real time based on incoming data, the computational cost of Bayesian methods may limit their feasibility. Hybrid approaches that combine Bayesian methods with faster machine learning algorithms are increasingly being explored to address this challenge [232,233].
7.6. Interdisciplinary Integration in Bayesian Hydrology
Bayesian hydrology has increasingly embraced interdisciplinary approaches to address the multifaceted challenges posed by climate change, water scarcity, and environmental management. By integrating insights from disciplines such as climatology, ecology, social sciences, and data science, Bayesian methods provide a holistic framework for understanding complex hydrological systems. For instance, climatological inputs, including sea surface temperatures, atmospheric pressure indices, and global circulation models, are commonly incorporated into Bayesian hydrological models to improve predictions of rainfall and streamflow patterns under varying climate scenarios [234,235]. Additionally, coupling Bayesian frameworks with ecological models helps evaluate the impacts of hydrological variability on aquatic ecosystems, such as fish habitats and wetland dynamics [236,237]. This interdisciplinary integration enables the simultaneous consideration of natural variability and anthropogenic influences, improving decision making in water-resource management. Supplementary Example S6 illustrates an interdisciplinary objective where Bayesian hydrology is integrated with agriculture to assess flood risks and their impact on agricultural yield, focusing on the joint modelling of extreme rainfall and streamflow using copulas and Bayesian inference.
Advances in computational science and machine learning have further expanded the interdisciplinary applications of Bayesian hydrology. Techniques like Bayesian neural networks and hierarchical Bayesian models are increasingly used to merge hydrological data with socioeconomic factors, enabling the assessment of water availability, agricultural productivity, and flood risk in a socio-environmental context [238,239,240]. Moreover, Bayesian decision analysis frameworks integrate stakeholder inputs to balance competing objectives in water-resource planning, such as flood protection and ecosystem preservation [241]. These approaches underscore the strength of Bayesian methods in synthesising diverse datasets and perspectives, providing probabilistic insights that align with interdisciplinary goals. By bridging domains, Bayesian hydrology is poised to address urgent global water challenges with robust, data-driven, and integrative solutions.
7.7. Limitations of the Current Study and the Way Forward
Despite the strengths of Bayesian methods, several limitations remain. The computational demands of advanced Bayesian models, especially when using MCMC techniques for high-dimensional problems, can be significant. Additionally, the subjectivity involved in selecting prior distributions may influence the results, particularly in data-sparse situations. This review focuses on the methodological aspects and literature trends, yet future work should aim at developing more efficient algorithms and objective criteria for prior selection to enhance reproducibility.
8. Conclusions
In this review, we have traced the historical development of Bayesian methods in hydrology, highlighting key contributions, advancements, and the challenges that have shaped their application. From their origins in parameter estimation and uncertainty quantification to their current use in advanced predictive modelling, Bayesian methods have proven to be invaluable tools in hydrological research and practice. The ability to incorporate prior knowledge, update predictions with new data, and quantify uncertainty allows hydrologists to make more informed decisions, particularly in contexts where data are sparse or uncertain.
However, as has been discussed, there are still several challenges that must be addressed for Bayesian methods to be more widely adopted in operational hydrology. These include the subjective nature of prior selection, high-dimensional parameter estimation, data limitations, and the significant computational resources required for real-time forecasting. Overcoming these challenges will require continued research into alternative methods for prior selection, as well as advancements in computational techniques such as variational inference, parallel computing, and hybrid models that integrate machine learning with traditional hydrological models. Moreover, R has emerged as a powerful tool for implementing Bayesian methods in hydrology, with applications spanning parameter estimation, flood-frequency analysis, drought prediction, rainfall–runoff modelling, sediment transport analysis, and uncertainty quantification. The six examples presented in the Supplementary Materials demonstrate how Bayesian frameworks can address a wide range of hydrological challenges effectively.
Looking to the future, the integration of big data, machine learning, and real-time data assimilation with Bayesian methods is set to be a major area of growth. With the increasing availability of high-resolution data from remote sensing, sensor networks, and other sources, there is a growing opportunity to combine data-driven insights with physical models, improving the accuracy of predictions while maintaining the rigorous uncertainty quantification provided by Bayesian inference. Hybrid models, which leverage the strengths of both physical and data-driven approaches, will likely become more prevalent, providing a powerful framework for addressing complex hydrological challenges. Furthermore, as climate change continues to affect water resources and hydrological extremes, the need for robust uncertainty quantification in climate-change modelling will only grow. Bayesian methods offer a powerful approach to capturing the uncertainty associated with future climate projections, making them indispensable in water-resource management and flood risk assessment.
In conclusion, the future of Bayesian hydrology is bright, with many exciting opportunities for innovation and advancement. As computational capabilities continue to improve and as new data sources become available, Bayesian methods will remain at the forefront of hydrological research, helping scientists and engineers tackle some of the most pressing water-related challenges of our time. Whether in flood forecasting, flood-frequency analysis, drought prediction, water quality monitoring, or climate-change impact assessment, Bayesian methods will continue to offer critical insights that improve our understanding of hydrological processes and inform better decision making.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/w17071095/s1, Example S1: Simulated Examples to Highlight Current Applications Bayesian Flood Risk Assessment; Example S2: Simulated Example to Highlight Current Applications: Bayesian Drought Prediction; Example S3: Simulated Example to Highlight Bayesian Rainfall-Runoff Model; Example S4: Simulated Example to Highlight Parameter Uncertainty; Example S5: Simulated Example to Highlight the Combining of Bayesian + Machine Learning for a Rainfall-Runoff Model; Example S6: Simulated Example to Highlight Bayesian Hydrology Combining an Interdisciplinary Objective—Specific Focus on Hydrology and Agriculture. Figure S1: Histogram of simulated annual maximum data following a lognormal distribution—Example 1; Figure S2: Flood frequency curve with 95% credible intervals (from posterior distribution) using simulated annual maximum data—Example 1; Figure S3: Traceplot and density plots for the posterior distributions of μ (mean)—Example 1; Figure S4: Traceplot and density plots for the posterior distributions of σ (standard deviation)—Example 1; Figure S5: Boxplot comparison of True Quantiles vs. Posterior Quantiles for ARIs 2–100 years—Example 1; Figure S6: Traceplots and density plots for the posterior distributions of μ (mean) and σ (standard deviation)—Example 2; Figure S7: Observed vs. Predicted for values Drought Severity Index—Example 2; Figure S8: Rainfall vs. Runoff with 95% Credible Intervals—Example 3; Figure S9: Predicted Runoff vs. Observed Runoff—Example 3; Figure S10: Traceplots and Density Plots for β0, β1, β2, β3 and σ—Example 3; Figure S11. Wide uncertainty bounds underscore the difficulty of making precise predictions in hydrology with parameter uncertainty—Example 4; Figure S12: Observed vs. Predicted Streamflow—Bayesian and Machine Learning Methods–Example 5; Figure S13: Traceplots and Density Plots for β0, β1, β2, β3 and σ—Example 5; Figure S14: Variable Importance Plot for Random Forest Model—Example 5; Figure S15: Rainfall vs. Yield with Bayesian 95% Credible Limits from Posterior Distribution—Example 6; Figure S16: Yield Variability due to Rainfall and Streamflow—Example 6; Figure S17: Yield Comparison: Simulated vs. Observed—Example 6.
Funding
This research received no external funding.
Data Availability Statement
The datasets used in this study can be obtained from Scopus, Google Scholar, and Web of Science. The R code used to develop the figures in this study can be provided upon request by emailing the author. The R code used in the examples can be found in the Supplementary Materials.
Acknowledgments
I would like to acknowledge the contributions of hydrologists, statisticians, and data scientists around the world who have advanced the field of Bayesian hydrology. Their work in integrating Bayesian methods into hydrological modelling has paved the way for more robust and reliable flood, drought, and rainfall predictions. Additionally, I would like to thank the organisations and agencies around the world that provide open access to hydrological data and statistical software (e.g., Australian Bureau of Meteorology (BOM), United States Geological Survey (USGS), European Environment Agency (EEA), National Oceanic and Atmospheric Administration (NOAA), World Meteorological Organization (WMO), Global Runoff Data Centre (GRDC), R Project for Statistical Computing, Python Software Foundation, Stan, JAGS (Just Another Gibbs Sampler), WinBUGS (Bayesian Analysis Using Gibbs Sampling), and HydroPlatform (Deltares)), which have been invaluable in conducting the simulations and analyses presented in this paper. The author would like to thank the three anonymous reviewers for their constructive comments, which helped improve the quality of the manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Box, G.E.; Tiao, G.C. Bayesian Inference in Statistical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1973. [Google Scholar]
- Vicens, G.J.; Rodriguez-Iturbe, I.; Schaake, J.C., Jr. A Bayesian framework for the use of regional information in hydrology. Water Resour. Res. 1975, 11, 405–414. [Google Scholar] [CrossRef]
- Sorooshian, S.; Dracup, J.A. Stochastic parameter estimation procedures for hydrologie rainfall-runoff models: Correlated and heteroscedastic error cases. Water Resour. Res. 1980, 16, 430–442. [Google Scholar] [CrossRef]
- Kuczera, G. A Bayesian surrogate for regional skew in flood frequency analysis. Water Resour. Res. 1983, 19, 821–832. [Google Scholar] [CrossRef]
- Kuczera, G. Improved parameter inference in catchment models: 1. Evaluating parameter uncertainty. Water Resour. Res. 1983, 19, 1151–1162. [Google Scholar] [CrossRef]
- Kuczera, G. Improved parameter inference in catchment models: 2. Combining different kinds of hydrologic data and testing their compatibility. Water Resour. Res. 1983, 19, 1163–1172. [Google Scholar] [CrossRef]
- Pericchi, L.R.; Rodriguez-Iturbe, I. On some problems in Bayesian model choice in hydrology. J. R. Stat. Soc. Ser. D (Stat.) 1983, 32, 273–278. [Google Scholar] [CrossRef]
- Kitanidis, P.K. Parameter uncertainty in estimation of spatial functions: Bayesian analysis. Water Resour. Res. 1986, 22, 499–507. [Google Scholar] [CrossRef]
- Kuczera, G. Prediction of water yield reductions following a bushfire in ash-mixed species eucalypt forest. J. Hydrol. 1987, 94, 215–236. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Cohn, T.A. Flood frequency analysis with historical and paleoflood information. Water Resour. Res. 1986, 22, 785–793. [Google Scholar] [CrossRef]
- Merz, B.; Thieken, A.H. Separating natural and epistemic uncertainty in flood frequency analysis. J. Hydrol. 2005, 309, 114–132. [Google Scholar] [CrossRef]
- Reis, D.S., Jr.; Stedinger, J.R.; Martins, E.S. Bayesian generalized least squares regression with application to log Pearson type 3 regional skew estimation. Water Resour. Res. 2005, 41, W10419. [Google Scholar] [CrossRef]
- Seidou, O.; Ouarda, T.B.; Barbet, M.; Bruneau, P.; Bobée, B. A parametric Bayesian combination of local and regional information in flood frequency analysis. Water Resour. Res. 2006, 42, W11408. [Google Scholar] [CrossRef]
- Micevski, T.; Kuczera, G. Combining site and regional flood information using a Bayesian Monte Carlo approach. Water Resour. Res. 2009, 45, W04405. [Google Scholar] [CrossRef]
- Gaume, E.; Gaál, L.; Viglione, A.; Szolgay, J.; Kohnová, S.; Blöschl, G. Bayesian MCMC approach to regional flood frequency analyses involving extraordinary flood events at ungauged sites. J. Hydrol. 2010, 394, 101–117. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Regional flood frequency analysis in eastern Australia: Bayesian GLS regression-based methods within fixed region and ROI framework—Quantile Regression vs. Parameter Regression Technique. J. Hydrol. 2012, 430, 142–161. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A.; Stedinger, J.R. Regional flood frequency analysis using Bayesian generalized least squares: A comparison between quantile and parameter regression techniques. Hydrol. Process. 2012, 26, 1008–1021. [Google Scholar] [CrossRef]
- Parkes, B.; Demeritt, D. Defining the hundred year flood: A Bayesian approach for using historic data to reduce uncertainty in flood frequency estimates. J. Hydrol. 2016, 540, 1189–1208. [Google Scholar] [CrossRef]
- Gaume, E. Flood frequency analysis: The Bayesian choice. Wiley Interdiscip. Rev. Water 2018, 5, e1290. [Google Scholar] [CrossRef]
- Mehmood, A.; Jia, S.; Mahmood, R.; Yan, J.; Ahsan, M. Non-stationary Bayesian modeling of annual maximum floods in a changing environment and implications for flood management in the Kabul River Basin, Pakistan. Water 2019, 11, 1246. [Google Scholar] [CrossRef]
- Qu, C.; Li, J.; Yan, L.; Yan, P.; Cheng, F.; Lu, D. Non-stationary flood frequency analysis using cubic B-spline-based GAMLSS model. Water 2020, 12, 1867. [Google Scholar] [CrossRef]
- Reis, D.S., Jr.; Veilleux, A.G.; Lamontagne, J.R.; Stedinger, J.R.; Martins, E.S. Operational Bayesian GLS regression for regional hydrologic analyses. Water Resour. Res. 2020, 56, e2019WR026940. [Google Scholar]
- Shang, X.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Liu, J.; Zou, Y.; He, R. Effect of uncertainty in historical data on flood frequency analysis using bayesian method. J. Hydrol. Eng. 2021, 26, 04021011. [Google Scholar]
- Jarajapu, D.C.; Rathinasamy, M.; Agarwal, A.; Bronstert, A. Design flood estimation using extreme Gradient Boosting-based on Bayesian optimization. J. Hydrol. 2022, 613, 128341. [Google Scholar] [CrossRef]
- Barna, D.M.; Engeland, K.; Thorarinsdottir, T.L.; Xu, C.Y. Flexible and consistent Flood–Duration–Frequency modeling: A Bayesian approach. J. Hydrol. 2023, 620, 129448. [Google Scholar]
- Lei, G.; Yin, J.; Wang, W.; Wang, H.; Liu, C. Hydrological frequency analysis in changing environments based on empirical mode decomposition and metropolis-hastings sampling Bayesian models. J. Hydrol. Eng. 2023, 28, 04023027. [Google Scholar] [CrossRef]
- Alexandre, D.A.; Chaudhuri, C.; Gill-Fortin, J. Continental Scale Regional Flood Frequency Analysis: Combining Enhanced Datasets and a Bayesian Framework. Hydrology 2024, 11, 119. [Google Scholar] [CrossRef]
- Lucas, M.; Lang, M.; Renard, B.; Le Coz, J. A comprehensive uncertainty framework for historical flood frequency analysis: A 500-year-long case study. Hydrol. Earth Syst. Sci. 2024, 28, 5031–5047. [Google Scholar]
- Madadgar, S.; Moradkhani, H. A Bayesian framework for probabilistic seasonal drought forecasting. J. Hydrometeorol. 2013, 14, 1685–1705. [Google Scholar]
- Madadgar, S.; Moradkhani, H. Spatio-temporal drought forecasting within Bayesian networks. J. Hydrol. 2014, 512, 134–146. [Google Scholar]
- Avilés, A.; Célleri, R.; Solera, A.; Paredes, J. Probabilistic forecasting of drought events using Markov chain-and Bayesian network-based models: A case study of an Andean regulated river basin. Water 2016, 8, 37. [Google Scholar] [CrossRef]
- Kim, K.; Lee, S.; Jin, Y. Forecasting quarterly inflow to reservoirs combining a copula-based Bayesian network method with drought forecasting. Water 2018, 10, 233. [Google Scholar] [CrossRef]
- Ali, Z.; Hussain, I.; Grzegorczyk, M.A.; Ni, G.; Faisal, M.; Qamar, S.; Shoukry, A.M.; Sharkawy, M.A.; Gani, S.; Al-Deek, F.F. Bayesian network based procedure for regional drought monitoring: The seasonally combinative regional drought indicator. J. Environ. Manag. 2020, 276, 111296. [Google Scholar] [CrossRef]
- Raza, A.; Hussain, I.; Ali, Z.; Faisal, M.; Elashkar, E.E.; Shoukry, A.M.; Al-Deek, F.F.; Gani, S. A seasonally blended and regionally integrated drought index using Bayesian network theory. Meteorol. Appl. 2021, 28, e1992. [Google Scholar]
- Wu, H.; Su, X.; Singh, V.P.; Zhang, T. Predicting hydrological drought with Bayesian model averaging ensemble vine copula (BMAViC) model. Water Resour. Res. 2022, 58, e2022WR033146. [Google Scholar]
- Wu, H.; Su, X.; Singh, V.P.; Niu, J. Predicting compound agricultural drought and hot events using a Cascade Modeling framework combining Bayesian Model Averaging ensemble with Vine Copula (CaMBMAViC). J. Hydrol. 2024, 642, 131901. [Google Scholar]
- Diggle, P.J.; Tawn, J.A.; Moyeed, R.A. Model-based geostatistics. J. R. Stat. Soc. Ser. C Appl. Stat. 1998, 47, 299–350. [Google Scholar] [CrossRef]
- Renard, B.; Garreta, V.; Lang, M. An application of Bayesian analysis and Markov chain Monte Carlo methods to the estimation of a regional trend in annual maxima. Water Resour. Res. 2006, 42, W12422. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Leblois, E.; Thyer, M.; Kuczera, G.; Franks, S.W. Toward a reliable decomposition of predictive uncertainty in hydrological modeling: Characterizing rainfall errors using conditional simulation. Water Resour. Res. 2011, 47, W11516. [Google Scholar] [CrossRef]
- Nowak, W.; De Barros, F.P.J.; Rubin, Y. Bayesian geostatistical design: Task-driven optimal site investigation when the geostatistical model is uncertain. Water Resour. Res. 2010, 46, W03535. [Google Scholar] [CrossRef]
- Verdin, A.; Rajagopalan, B.; Kleiber, W.; Funk, C. A Bayesian kriging approach for blending satellite and ground precipitation observations. Water Resour. Res. 2015, 51, 908–921. [Google Scholar]
- Gupta, A.; Kamble, T.; Machiwal, D. Comparison of ordinary and Bayesian kriging techniques in depicting rainfall variability in arid and semi-arid regions of north-west India. Environ. Earth Sci. 2017, 76, 1–16. [Google Scholar] [CrossRef]
- Yang, P.; Ng, T.L. Fast Bayesian regression kriging method for real-time merging of radar, rain gauge, and crowdsourced rainfall data. Water Resour. Res. 2019, 55, 3194–3214. [Google Scholar]
- Lima, C.H.; Kwon, H.H.; Kim, Y.T. A Bayesian Kriging model applied for spatial downscaling of daily rainfall from GCMs. J. Hydrol. 2021, 597, 126095. [Google Scholar]
- Senoro, D.B.; de Jesus, K.L.M.; Mendoza, L.C.; Apostol, E.M.D.; Escalona, K.S.; Chan, E.B. Groundwater quality monitoring using in-situ measurements and hybrid machine learning with empirical Bayesian kriging interpolation method. Appl. Sci. 2021, 12, 132. [Google Scholar] [CrossRef]
- Zaresefat, M.; Derakhshani, R.; Griffioen, J. Empirical Bayesian Kriging, a robust method for spatial data interpolation of a large groundwater quality dataset from the Western Netherlands. Water 2024, 16, 2581. [Google Scholar] [CrossRef]
- Fill, H.D.; Stedinger, J.R. Using regional regression within index flood procedures and an empirical Bayesian estimator. J. Hydrol. 1998, 210, 128–145. [Google Scholar]
- Marshall, L.; Nott, D.; Sharma, A. Hydrological model selection: A Bayesian alternative. Water Resour. Res. 2005, 41, W10422. [Google Scholar] [CrossRef]
- Reis, D.S., Jr.; Stedinger, J.R. Bayesian MCMC flood frequency analysis with historical information. J. Hydrol. 2005, 313, 97–116. [Google Scholar] [CrossRef]
- Ribatet, M.; Sauquet, E.; Grésillon, J.M.; Ouarda, T.B. A regional Bayesian POT model for flood frequency analysis. Stoch. Environ. Res. Risk Assess. 2007, 21, 327–339. [Google Scholar]
- Viglione, A.; Merz, R.; Salinas, J.L.; Blöschl, G. Flood frequency hydrology: 3. A Bayesian analysis. Water Resour. Res. 2013, 49, 675–692. [Google Scholar] [CrossRef]
- Šraj, M.; Viglione, A.; Parajka, J.; Blöschl, G. The influence of non-stationarity in extreme hydrological events on flood frequency estimation. J. Hydrol. Hydromech. 2016, 64, 426–437. [Google Scholar] [CrossRef]
- Liu, R.; Chen, Y.; Wu, J.; Gao, L.; Barrett, D.; Xu, T.; Li, L.; Huang, C.; Yu, J. Assessing spatial likelihood of flooding hazard using naïve Bayes and GIS: A case study in Bowen Basin, Australia. Stoch. Environ. Res. Risk Assess. 2016, 30, 1575–1590. [Google Scholar] [CrossRef]
- Naseri, K.; Hummel, M.A. A Bayesian copula-based nonstationary framework for compound flood risk assessment along US coastlines. J. Hydrol. 2022, 610, 128005. [Google Scholar] [CrossRef]
- Rampinelli, C.G.; Smith, T.J.; Araújo, P.V. Addressing Uncertainty in Flood Hazard Mapping under a Bayesian Approach. J. Hydrol. Eng. 2024, 29, 04024004. [Google Scholar] [CrossRef]
- Kuczera, G. Estimation of runoff-routing model parameters using incompatible storm data. J. Hydrol. 1990, 114, 47–60. [Google Scholar] [CrossRef]
- Khan, M.S.; Coulibaly, P. Bayesian neural network for rainfall-runoff modeling. Water Resour. Res. 2006, 42, W07409. [Google Scholar] [CrossRef]
- Martina, M.L.V.; Todini, E.; Libralon, A. A Bayesian decision approach to rainfall thresholds based flood warning. Hydrol. Earth Syst. Sci. 2006, 10, 413–426. [Google Scholar] [CrossRef]
- Smith, T.J.; Marshall, L.A. Bayesian methods in hydrologic modeling: A study of recent advancements in Markov chain Monte Carlo techniques. Water Resour. Res. 2008, 44, W00B05. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Lall, U. Hierarchical Bayesian modeling of multisite daily rainfall occurrence: Rainy season onset, peak, and end. Water Resour. Res. 2009, 45, W07422. [Google Scholar] [CrossRef]
- Haddad, K.; Johnson, F.; Rahman, A.; Green, J.; Kuczera, G. Comparing three methods to form regions for design rainfall statistics: Two case studies in Australia. J. Hydrol. 2015, 527, 62–76. [Google Scholar] [CrossRef]
- Molina, J.L.; Zazo, S.; Rodríguez-Gonzálvez, P.; González-Aguilera, D. Innovative analysis of runoff temporal behavior through bayesian networks. Water 2016, 8, 484. [Google Scholar] [CrossRef]
- Little, M.A.; Rodda, H.J.; McSharry, P.E. Bayesian objective classification of extreme UK daily rainfall for flood risk applications. Hydrol. Earth Syst. Sci. Discuss. 2008, 5, 3033–3060. [Google Scholar]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K.L. Retrospective analysis and Bayesian model averaging of CMIP6 precipitation in the Nile River Basin. J. Hydrometeorol. 2021, 22, 217–229. [Google Scholar]
- Ossandón, Á.; Rajagopalan, B.; Kleiber, W. Spatial-temporal multivariate semi-Bayesian hierarchical framework for extreme precipitation frequency analysis. J. Hydrol. 2021, 600, 126499. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Le, X.H.; Anh, D.T.; Kim, S.H.; Bae, D.H. Hourly streamflow forecasting using a Bayesian additive regression tree model hybridized with a genetic algorithm. J. Hydrol. 2022, 606, 127445. [Google Scholar]
- Zorzetto, E.; Canale, A.; Marani, M. A Bayesian non-asymptotic extreme value model for daily rainfall data. J. Hydrol. 2024, 628, 130378. [Google Scholar]
- Gronewold, A.D.; Qian, S.S.; Wolpert, R.L.; Reckhow, K.H. Calibrating and validating bacterial water quality models: A Bayesian approach. Water Res. 2009, 43, 2688–2698. [Google Scholar]
- Jin, X.; Xu, C.Y.; Zhang, Q.; Singh, V.P. Parameter and modeling uncertainty simulated by GLUE and a formal Bayesian method for a conceptual hydrological model. J. Hydrol. 2010, 383, 147–155. [Google Scholar]
- Haddad, K.; Egodawatta, P.; Rahman, A.; Goonetilleke, A. Uncertainty analysis of pollutant build-up modelling based on a Bayesian weighted least squares approach. Sci. Total Environ. 2013, 449, 410–417. [Google Scholar] [CrossRef][Green Version]
- Egodawatta, P.; Haddad, K.; Rahman, A.; Goonetilleke, A. A Bayesian regression approach to assess uncertainty in pollutant wash-off modelling. Sci. Total Environ. 2014, 479, 233–240. [Google Scholar]
- Zhao, Y.; Sharma, A.; Sivakumar, B.; Marshall, L.; Wang, P.; Jiang, J. A Bayesian method for multi-pollution source water quality model and seasonal water quality management in river segments. Environ. Model. Softw. 2014, 57, 216–226. [Google Scholar]
- Liang, S.; Jia, H.; Xu, C.; Xu, T.; Melching, C. A Bayesian approach for evaluation of the effect of water quality model parameter uncertainty on TMDLs: A case study of Miyun Reservoir. Sci. Total Environ. 2016, 560, 44–54. [Google Scholar]
- Peng, Z.; Hu, Y.; Liu, G.; Hu, W.; Zhang, H.; Gao, R. Calibration and quantifying uncertainty of daily water quality forecasts for large lakes with a Bayesian joint probability modelling approach. Water Res. 2020, 185, 116162. [Google Scholar] [PubMed]
- Perera, T.; McGree, J.; Egodawatta, P.; Jinadasa, K.B.S.N.; Goonetilleke, A. A Bayesian approach to model the trends and variability in urban stormwater quality associated with catchment and hydrologic parameters. Water Res. 2021, 197, 117076. [Google Scholar]
- Jackson-Blake, L.A.; Clayer, F.; Haande, S.; Sample, J.E.; Moe, S.J. Seasonal forecasting of lake water quality and algal bloom risk using a continuous Gaussian Bayesian network. Hydrol. Earth Syst. Sci. 2022, 26, 3103–3124. [Google Scholar] [CrossRef]
- Chowdhury, A.; Egodawatta, P. Automatic model calibration of combined hydrologic, hydraulic and stormwater quality models using approximate Bayesian computation. Water Sci. Technol. 2022, 86, 321–332. [Google Scholar]
- Spezia, L.; Gibbs, S.; Glendell, M.; Helliwell, R.; Paroli, R.; Pohle, I. Bayesian analysis of high-frequency water temperature time series through Markov switching autoregressive models. Environ. Model. Softw. 2023, 167, 105751. [Google Scholar]
- Zhang, C.; Nong, X.; Behzadian, K.; Campos, L.C.; Chen, L.; Shao, D. A new framework for water quality forecasting coupling causal inference, time-frequency analysis and uncertainty quantification. J. Environ. Manag. 2024, 350, 119613. [Google Scholar]
- Nadiri, A.A.; Chitsazan, N.; Tsai, F.T.C.; Moghaddam, A.A. Bayesian artificial intelligence model averaging for hydraulic conductivity estimation. J. Hydrol. Eng. 2014, 19, 520–532. [Google Scholar]
- Camacho, R.A.; Martin, J.L.; McAnally, W.; Díaz-Ramirez, J.; Rodriguez, H.; Sucsy, P.; Zhang, S. A comparison of Bayesian methods for uncertainty analysis in hydraulic and hydrodynamic modeling. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 1372–1393. [Google Scholar]
- Shrestha, R.; Kozlowski, T. Inverse uncertainty quantification of input model parameters for thermal-hydraulics simulations using expectation–maximization under Bayesian framework. J. Appl. Stat. 2016, 43, 1011–1026. [Google Scholar] [CrossRef]
- Han, S.; Coulibaly, P. Bayesian flood forecasting methods: A review. J. Hydrol. 2017, 551, 340–351. [Google Scholar] [CrossRef]
- Liu, Z.; Merwade, V. Accounting for model structure, parameter and input forcing uncertainty in flood inundation modeling using Bayesian model averaging. J. Hydrol. 2018, 565, 138–149. [Google Scholar] [CrossRef]
- Garcia, R.; Costa, V.; Silva, F. Bayesian rating curve modeling: Alternative error model to improve low-flow uncertainty estimation. J. Hydrol. Eng. 2020, 25, 04020012. [Google Scholar] [CrossRef]
- Yin, J.; Medellín-Azuara, J.; Escriva-Bou, A.; Liu, Z. Bayesian machine learning ensemble approach to quantify model uncertainty in predicting groundwater storage change. Sci. Total Environ. 2021, 769, 144715. [Google Scholar] [CrossRef]
- Badjadi, M.A.; Zhu, H.; Zhang, C.; Safdar, M. A Bayesian Network Model for Risk Management during Hydraulic Fracturing Process. Water 2023, 15, 4159. [Google Scholar] [CrossRef]
- Pourahari, A.; Amini, R.; Yousefi-Khoshqalb, E. Advancing Nodal Leakage Estimation in Decentralized Water Networks: Integrating Bayesian Optimization, Realistic Hydraulic Modeling, and Data-Driven Approaches. Sustain. Cities Soc. 2024, 112, 105612. [Google Scholar] [CrossRef]
- Humphrey, G.B.; Gibbs, M.S.; Dandy, G.C.; Maier, H.R. A hybrid approach to monthly streamflow forecasting: Integrating hydrological model outputs into a Bayesian artificial neural network. J. Hydrol. 2016, 540, 623–640. [Google Scholar] [CrossRef]
- Alexander, R.B.; Schwarz, G.E.; Boyer, E.W. Advances in quantifying streamflow variability across continental scales: 2. Improved model regionalization and prediction uncertainties using hierarchical Bayesian methods. Water Resour. Res. 2019, 55, 11061–11087. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Regional flood frequency analysis: Evaluation of regions in cluster space using support vector regression. Nat. Hazards 2020, 102, 489–517. [Google Scholar] [CrossRef]
- Cheng, S.Y.; Hsu, K.C. Bayesian integration using resistivity and lithology for improving estimation of hydraulic conductivity. Water Resour. Res. 2021, 57, e2020WR027346. [Google Scholar] [CrossRef]
- Xu, H.; Song, S.; Li, J.; Guo, T. Hybrid model for daily runoff interval predictions based on Bayesian inference. Hydrol. Sci. J. 2023, 68, 62–75. [Google Scholar] [CrossRef]
- Sheikh, M.R.; Coulibaly, P. Review of Recent Developments in Hydrologic Forecast Merging Techniques. Water 2024, 16, 301. [Google Scholar] [CrossRef]
- Sattari, A.; Jafarzadegan, K.; Moradkhani, H. Enhancing streamflow predictions with machine learning and Copula-Embedded Bayesian model averaging. J. Hydrol. 2024, 643, 131986. [Google Scholar] [CrossRef]
- George, J.; Athira, P. Bayesian Framework for Uncertainty Quantification and Bias Correction of Projected Streamflow in Climate Change Impact Assessment. Water Resour. Manag. 2024, 38, 4499–4516. [Google Scholar] [CrossRef]
- Ponce Romero, J.M.; Hallett, S.H.; Jude, S. Leveraging big data tools and technologies: Addressing the challenges of the water quality sector. Sustainability 2017, 9, 2160. [Google Scholar] [CrossRef]
- Fer, I.; Kelly, R.; Moorcroft, P.R.; Richardson, A.D.; Cowdery, E.M.; Dietze, M.C. Linking big models to big data: Efficient ecosystem model calibration through Bayesian model emulation. Biogeosciences 2018, 15, 5801–5830. [Google Scholar] [CrossRef]
- Monrat, A.A.; Islam, R.U.; Hossain, M.S.; Andersson, K. Challenges and opportunities of using big data for assessing flood risks. In Applications of Big Data Analytics: Trends, Issues, and Challenges; Springer: Cham, Switzerland, 2018; pp. 31–42. [Google Scholar]
- Marcot, B.G.; Penman, T.D. Advances in Bayesian network modelling: Integration of modelling technologies. Environ. Model. Softw. 2019, 111, 386–393. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, Y.; Feng, J. SMOTE-Boost-based sparse Bayesian model for flood prediction. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 78. [Google Scholar] [CrossRef]
- Donratanapat, N.; Samadi, S.; Vidal, J.M.; Tabas, S.S. A national scale big data analytics pipeline to assess the potential impacts of flooding on critical infrastructures and communities. Environ. Model. Softw. 2020, 133, 104828. [Google Scholar] [CrossRef]
- Gaffoor, Z.; Pietersen, K.; Jovanovic, N.; Bagula, A.; Kanyerere, T. Big data analytics and its role to support groundwater management in the southern African development community. Water 2020, 12, 2796. [Google Scholar] [CrossRef]
- Yuan, F.; Fan, C.; Farahmand, H.; Coleman, N.; Esmalian, A.; Lee, C.C.; Patrascu, F.I.; Zhang, C.; Dong, S.; Mostafavi, A. Smart flood resilience: Harnessing community-scale big data for predictive flood risk monitoring, rapid impact assessment, and situational awareness. Environ. Res. Infrastruct. Sustain. 2022, 2, 025006. [Google Scholar]
- Tanguy, M.; Eastman, M.; Chevuturi, A.; Magee, E.; Cooper, E.; Johnson, R.H.; Facer-Childs, K.; Hannaford, J. Optimising ensemble streamflow predictions with bias-correction and data assimilation techniques. Hydrol. Earth Syst. Sci. Discuss. 2024, 2024, 1–41. [Google Scholar]
- Leu, S.S.; Bui, Q.N. Leak prediction model for water distribution networks created using a Bayesian network learning approach. Water Resour. Manag. 2016, 30, 2719–2733. [Google Scholar]
- Xue, J.; Gui, D.; Lei, J.; Sun, H.; Zeng, F.; Feng, X. A hybrid Bayesian network approach for trade-offs between environmental flows and agricultural water using dynamic discretization. Adv. Water Resour. 2017, 110, 445–458. [Google Scholar]
- Jäger, W.S.; Christie, E.K.; Hanea, A.M.; Den Heijer, C.; Spencer, T. A Bayesian network approach for coastal risk analysis and decision making. Coast. Eng. 2018, 134, 48–61. [Google Scholar]
- Chen, J.; Zhong, P.A.; An, R.; Zhu, F.; Xu, B. Risk analysis for real-time flood control operation of a multi-reservoir system using a dynamic Bayesian network. Environ. Model. Softw. 2019, 111, 409–420. [Google Scholar]
- Mihunov, V.V.; Lam, N.S. Modeling the dynamics of drought resilience in South-Central United States using a Bayesian Network. Appl. Geogr. 2020, 120, 102224. [Google Scholar]
- Das, P.; Chanda, K. Bayesian Network based modeling of regional rainfall from multiple local meteorological drivers. J. Hydrol. 2020, 591, 125563. [Google Scholar]
- Ma, Y.; Zhang, Z.; Kang, Y.; Özdoğan, M. Corn yield prediction and uncertainty analysis based on remotely sensed variables using a Bayesian neural network approach. Remote Sens. Environ. 2021, 259, 112408. [Google Scholar]
- Xie, X.; Huang, L.; Marson, S.M.; Wei, G. Emergency response process for sudden rainstorm and flooding: Scenario deduction and Bayesian network analysis using evidence theory and knowledge meta-theory. Nat. Hazards 2023, 117, 3307–3329. [Google Scholar]
- Albert, C.G.; Callies, U.; von Toussaint, U. A Bayesian approach to the estimation of parameters and their interdependencies in environmental modeling. Entropy 2022, 24, 231. [Google Scholar] [CrossRef]
- Martina, M.L.V.; Todini, E.; Libralon, A. Rainfall thresholds for flood warning systems: A Bayesian decision approach. In Hydrological Modelling and the Water Cycle: Coupling the Atmospheric and Hydrological Models; Springer: Berlin/Heidelberg, Germany, 2009; pp. 203–227. [Google Scholar]
- Pagano, A.; Giordano, R.; Portoghese, I.; Fratino, U.; Vurro, M. A Bayesian vulnerability assessment tool for drinking water mains under extreme events. Nat. Hazards 2014, 74, 2193–2227. [Google Scholar]
- Bertone, E.; Sahin, O.; Richards, R.; Roiko, A. Extreme events, water quality and health: A participatory Bayesian risk assessment tool for managers of reservoirs. J. Clean. Prod. 2016, 135, 657–667. [Google Scholar] [CrossRef]
- Madadgar, S.; AghaKouchak, A.; Farahmand, A.; Davis, S.J. Probabilistic estimates of drought impacts on agricultural production. Geophys. Res. Lett. 2017, 44, 7799–7807. [Google Scholar]
- Roozbahani, A.; Ebrahimi, E.; Banihabib, M.E. A framework for ground water management based on bayesian network and MCDM techniques. Water Resour. Manag. 2018, 32, 4985–5005. [Google Scholar]
- Phan, T.D.; Smart, J.C.; Stewart-Koster, B.; Sahin, O.; Hadwen, W.L.; Dinh, L.T.; Tahmasbian, I.; Capon, S.J. Applications of Bayesian networks as decision support tools for water resource management under climate change and socio-economic stressors: A critical appraisal. Water 2019, 11, 2642. [Google Scholar] [CrossRef]
- Kostyuchenko, Y.V.; Yuschenko, M.; Kopachevsky, I.; Artemenko, I. Bayes Decision-Making Systems for Quantitative Assessment of Hydrological Climate-Related Risk using Satellite Data. In Mathematical Modelling of System Resilience; River Publishers: Rome, Italy, 2022; pp. 113–141. [Google Scholar]
- Garzon, J.L.; Ferreira, Ó.; Zózimo, A.C.; Fortes, C.J.E.M.; Ferreira, A.M.; Pinheiro, L.V.; Reis, M.T. Development of a Bayesian networks-based early warning system for wave-induced flooding. Int. J. Disaster Risk Reduct. 2023, 96, 103931. [Google Scholar]
- Huang, T.; Merwade, V. Uncertainty analysis and quantification in flood insurance rate maps using Bayesian model averaging and hierarchical BMA. J. Hydrol. Eng. 2023, 28, 04022038. [Google Scholar]
- Lu, Y.; Zhai, G.; Zhou, S. An integrated Bayesian networks and Geographic information system (BNs-GIS) approach for flood disaster risk assessment: A case study of Yinchuan, China. Ecol. Indic. 2024, 166, 112322. [Google Scholar]
- Tanim, A.H.; Smith-Lewis, C.; Downey, A.R.; Imran, J.; Goharian, E. Bayes_Opt-SWMM: A Gaussian process-based Bayesian optimization tool for real-time flood modeling with SWMM. Environ. Model. Softw. 2024, 179, 106122. [Google Scholar] [CrossRef]
- Xue, C.; Zhang, Q.; Jia, Y.; Tang, H.; Zhang, H. Attribution of hydrological droughts in large river-connected lakes: Insights from an explainable machine learning model. Sci. Total Environ. 2024, 952, 175999. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010, 46, W05521. [Google Scholar] [CrossRef]
- Rode, M.; Arhonditsis, G.; Balin, D.; Kebede, T.; Krysanova, V.; Van Griensven, A.; Van der Zee, S.E. New challenges in integrated water quality modelling. Hydrol. Process. 2010, 24, 3447–3461. [Google Scholar] [CrossRef]
- Liu, Y.; Engel, B.A.; Flanagan, D.C.; Gitau, M.W.; McMillan, S.K.; Chaubey, I.; Singh, S. Modeling framework for representing long-term effectiveness of best management practices in addressing hydrology and water quality problems: Framework development and demonstration using a Bayesian method. J. Hydrol. 2018, 560, 530–545. [Google Scholar] [CrossRef]
- Hernández, F.; Liang, X. Hybridizing Bayesian and variational data assimilation for high-resolution hydrologic forecasting. Hydrol. Earth Syst. Sci. 2018, 22, 5759–5779. [Google Scholar] [CrossRef]
- DeChant, C.M.; Moradkhani, H. Toward a reliable prediction of seasonal forecast uncertainty: Addressing model and initial condition uncertainty with ensemble data assimilation and sequential Bayesian combination. J. Hydrol. 2014, 519, 2967–2977. [Google Scholar] [CrossRef]
- Qamar, S.; Khalique, A.; Grzegorczyk, M.A. On the Bayesian network based data mining framework for the choice of appropriate time scale for regional analysis of drought Hazard. Theor. Appl. Climatol. 2021, 143, 1677–1695. [Google Scholar] [CrossRef]
- Wu, X.; Marshall, L.; Sharma, A. Quantifying input error in hydrologic modeling using the Bayesian error analysis with reordering (BEAR) approach. J. Hydrol. 2021, 598, 126202. [Google Scholar] [CrossRef]
- Yoon, H.N.; Marshall, L.; Sharma, A.; Kim, S. Bayesian model calibration using surrogate streamflow in ungauged catchments. Water Resour. Res. 2022, 58, e2021WR031287. [Google Scholar] [CrossRef]
- Zou, H.; Marshall, L.; Sharma, A. Characterizing Errors Using Satellite Metadata for Eco-Hydrological Model Calibration. Water Resour. Res. 2023, 59, e2022WR033978. [Google Scholar] [CrossRef]
- Liu, Y.; Weerts, A.H.; Clark, M.; Hendricks Franssen, H.J.; Kumar, S.; Moradkhani, H.; Seo, D.J.; Schwanenberg, D.; Smith, P.; Van Dijk, A.I.; et al. Advancing data assimilation in operational hydrologic forecasting: Progresses, challenges, and emerging opportunities. Hydrol. Earth Syst. Sci. 2012, 16, 3863–3887. [Google Scholar] [CrossRef]
- Sadegh, M.; Vrugt, J.A. Approximate bayesian computation using markov chain monte carlo simulation: Dream(ABC). Water Resour. Res. 2014, 50, 6767–6787. [Google Scholar] [CrossRef]
- Kavetski, D.; Fenicia, F.; Reichert, P.; Albert, C. Signature-domain calibration of hydrological models using approximate Bayesian computation: Theory and comparison to existing applications. Water Resour. Res. 2018, 54, 4059–4083. [Google Scholar] [CrossRef]
- Moges, E.; Demissie, Y.; Larsen, L.; Yassin, F. Sources of hydrological model uncertainties and advances in their analysis. Water 2021, 13, 28. [Google Scholar] [CrossRef]
- Gupta, A.; Govindaraju, R.S. Uncertainty quantification in watershed hydrology: Which method to use? J. Hydrol. 2023, 616, 128749. [Google Scholar] [CrossRef]
- Saha, S.; Bradley, J.R. Incorporating Subsampling into Bayesian Models for High-Dimensional Spatial Data. arXiv 2023, arXiv:2305.132213, 11–13. [Google Scholar] [CrossRef]
- Ulzega, S.; Albert, C. Bayesian parameter inference in hydrological modelling using a Hamiltonian Monte Carlo approach with a stochastic rain model. Hydrol. Earth Syst. Sci. 2023, 27, 2935–2950. [Google Scholar] [CrossRef]
- Andraos, C. Breaking Uncertainty Barriers: Approximate Bayesian Computation Advances in Rainfall–Runoff Modeling. Water 2024, 16, 3499. [Google Scholar] [CrossRef]
- Nizeyimana, P.; Lee, K.E.; Kim, G. Bayesian Estimation of Neyman–Scott Rectangular Pulse Model Parameters in Comparison with Other Parameter Estimation Methods. Water 2024, 16, 2515. [Google Scholar] [CrossRef]
- Kuczera, G. Comprehensive at-site flood frequency analysis using Monte Carlo Bayesian inference. Water Resour. Res. 1999, 35, 1551–1557. [Google Scholar] [CrossRef]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resour. Res. 2006, 42, W03407. [Google Scholar] [CrossRef]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian analysis of input uncertainty in hydrological modeling: 2. Application. Water Resour. Res. 2006, 42, W03408. [Google Scholar] [CrossRef]
- Kuczera, G.; Kavetski, D.; Franks, S.; Thyer, M. Towards a Bayesian total error analysis of conceptual rainfall-runoff models: Characterising model error using storm-dependent parameters. J. Hydrol. 2006, 331, 161–177. [Google Scholar] [CrossRef]
- Thyer, M.; Renard, B.; Kavetski, D.; Kuczera, G.; Franks, S.W.; Srikanthan, S. Critical evaluation of parameter consistency and predictive uncertainty in hydrological modeling: A case study using Bayesian total error analysis. Water Resour. Res. 2009, 45, W00B14. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, F.; Yu, B.; Zong, Z. Explicitly integrating parameter, input, and structure uncertainties into Bayesian Neural Networks for probabilistic hydrologic forecasting. J. Hydrol. 2011, 409, 696–709. [Google Scholar] [CrossRef]
- Ouarda, T.B.; El-Adlouni, S. Bayesian nonstationary frequency analysis of hydrological variables. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 496–505. [Google Scholar] [CrossRef]
- Gui, Z.; Zhang, F.; Yue, K.; Lu, X.; Chen, L.; Wang, H. Identifying and Interpreting Hydrological Model Structural Nonstationarity Using the Bayesian Model Averaging Method. Water 2024, 16, 1126. [Google Scholar] [CrossRef]
- van Dam, A.A.; Kipkemboi, J.; Rahman, M.M.; Gettel, G.M. Linking hydrology, ecosystem function, and livelihood outcomes in African papyrus wetlands using a Bayesian Network model. Wetlands 2013, 33, 381–397. [Google Scholar] [CrossRef]
- Kumari, N.; Pandey, S. Sustainability assessment of jumar river in Ranchi district of Jharkhand using river sustainability Bayesian network (RSBN) model Approach. In Ecological Significance of River Ecosystems; Elsevier: Amsterdam, The Netherlands, 2022; pp. 407–428. [Google Scholar]
- Kneier, F.; Woltersdorf, L.; Peiris, T.A.; Döll, P. Participatory Bayesian Network modeling of climate change risks and adaptation regarding water supply: Integration of multi-model ensemble hazard estimates and local expert knowledge. Environ. Model. Softw. 2023, 168, 105764. [Google Scholar] [CrossRef]
- Dubbert, M.; Couvreur, V.; Kübert, A.; Werner, C. Plant water uptake modelling: Added value of cross-disciplinary approaches. Plant Biol. 2023, 25, 32–42. [Google Scholar] [CrossRef]
- Rampinelli, C.G.; Knack, I.; Smith, T. Flood mapping uncertainty from a restoration perspective: A practical case study. Water 2020, 12, 1948. [Google Scholar] [CrossRef]
- Achite, M.; Banadkooki, F.B.; Ehteram, M.; Bouharira, A.; Ahmed, A.N.; Elshafie, A. Exploring Bayesian model averaging with multiple ANNs for meteorological drought forecasts. Stoch. Environ. Res. Risk Assess. 2022, 36, 1835–1860. [Google Scholar] [CrossRef]
- Hsu, S.H.; Ho, Y.F.; Hsu, T.H.; Lee, M.T. Constructing a Risk Assessment Model for Marine Protected Areas Using Bayesian Network. 2024. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4846408 (accessed on 5 December 2024). [CrossRef]
- Kuczera, G. Correlated rating curve error in flood frequency inference. Water Resour. Res. 1996, 32, 2119–2127. [Google Scholar] [CrossRef]
- Kuczera, G. Uncorrelated measurement error in flood frequency inference. Water Resour. Res. 1992, 28, 183–188. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 1995. [Google Scholar]
- Sorooshian, S.; Gupta, V.K. The analysis of structural identifiability: Theory and application to conceptual rainfall-runoff models. Water Resour. Res. 1985, 21, 487–495. [Google Scholar] [CrossRef]
- Beven, K. How far can we go in distributed hydrological modelling? Hydrol. Earth Syst. Sci. 2001, 5, 1–12. [Google Scholar] [CrossRef]
- Engeland, K.; Gottschalk, L. Bayesian estimation of parameters in a regional hydrological model. Hydrol. Earth Syst. Sci. 2002, 6, 883–898. [Google Scholar] [CrossRef]
- Wu, W.; Clark, J.S.; Vose, J.M. Assimilating multi-source uncertainties of a parsimonious conceptual hydrological model using hierarchical Bayesian modeling. J. Hydrol. 2010, 394, 436–446. [Google Scholar] [CrossRef]
- Lima, C.H.; Lall, U. Spatial scaling in a changing climate: A hierarchical bayesian model for non-stationary multi-site annual maximum and monthly streamflow. J. Hydrol. 2010, 383, 307–318. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H. A hierarchical Bayesian approach for the analysis of climate change impact on runoff extremes. Hydrol. Process. 2014, 28, 6292–6308. [Google Scholar]
- Smith, T.; Marshall, L.; Sharma, A. Modeling residual hydrologic errors with Bayesian inference. J. Hydrol. 2015, 528, 29–37. [Google Scholar]
- Cai, C.; Wang, J.; Li, Z. Assessment and modelling of uncertainty in precipitation forecasts from TIGGE using fuzzy probability and Bayesian theory. J. Hydrol. 2019, 577, 123995. [Google Scholar]
- Madadgar, S.; AghaKouchak, A.; Shukla, S.; Wood, A.W.; Cheng, L.; Hsu, K.L.; Svoboda, M. A hybrid statistical-dynamical framework for meteorological drought prediction: Application to the southwestern United States. Water Resour. Res. 2016, 52, 5095–5110. [Google Scholar]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall spatial estimations: A review from spatial interpolation to multi-source data merging. Water 2019, 11, 579. [Google Scholar]
- Wu, Y.B.; Xue, L.Q.; Liu, Y.H. Local and regional flood frequency analysis based on hierarchical Bayesian model in Dongting Lake Basin, China. Water Sci. Eng. 2019, 12, 253–262. [Google Scholar]
- Bayat, B.; Hosseini, K.; Nasseri, M.; Karami, H. Challenge of rainfall network design considering spatial versus spatiotemporal variations. J. Hydrol. 2019, 574, 990–1002. [Google Scholar]
- Das, P.; Chanda, K. A Bayesian network approach for understanding the role of large-scale and local hydro-meteorological variables as drivers of basin-scale rainfall and streamflow. Stoch. Environ. Res. Risk Assess. 2023, 37, 1535–1556. [Google Scholar] [CrossRef]
- Smith, J.D.; Lamontagne, J.R.; Jasek, M. Considering uncertainty of historical ice jam flood records in a Bayesian frequency analysis for the Peace-Athabasca Delta. Water Resour. Res. 2024, 60, e2022WR034377. [Google Scholar] [CrossRef]
- Costa, V.; Fernandes, W. Bayesian estimation of extreme flood quantiles using a rainfall-runoff model and a stochastic daily rainfall generator. J. Hydrol. 2017, 554, 137–154. [Google Scholar]
- Kou, L.; Mao, Y.; Lin, Z.; Gao, H.; Chu, Z.; Chen, A. Error modeling and hierarchical Bayesian fusion for spaceborne and ground radar rainfall data. J. Hydrol. 2024, 629, 130599. [Google Scholar]
- Sreeparvathy, V.; Srinivas, V.V. A Bayesian Fuzzy Clustering Approach for Design of Precipitation Gauge Network Using Merged Remote Sensing and Ground-Based Precipitation Products. Water Resour. Res. 2022, 58, e2021WR030612. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble machine learning paradigms in hydrology: A review. J. Hydrol. 2021, 598, 126266. [Google Scholar]
- Li, D.; Marshall, L.; Liang, Z.; Sharma, A.; Zhou, Y. Bayesian LSTM with stochastic variational inference for estimating model uncertainty in process-based hydrological models. Water Resour. Res. 2021, 57, e2021WR029772. [Google Scholar]
- Quilty, J.; Jahangir, M.S.; You, J.; Hughes, H.; Hah, D.; Tzoganakis, I. Bayesian extreme learning machines for hydrological prediction uncertainty. J. Hydrol. 2023, 626, 130138. [Google Scholar]
- Ren, W.W.; Yang, T.; Huang, C.S.; Xu, C.Y.; Shao, Q.X. Improving monthly streamflow prediction in alpine regions: Integrating HBV model with Bayesian neural network. Stoch. Environ. Res. Risk Assess. 2018, 32, 3381–3396. [Google Scholar]
- Vasheghani Farahani, E.; Massah Bavani, A.R.; Roozbahani, A. Enhancing reservoir inflow forecasting precision through Bayesian Neural Network modeling and atmospheric teleconnection pattern analysis. Stoch. Environ. Res. Risk Assess. 2025, 39, 205–229. [Google Scholar] [CrossRef]
- Nair, P.S.; Ezhilarasan, G. Bayesian Models for Weather Prediction: Using Remote Sensing Data to Improve Forecast Accuracy. In International Conference on Machine in Telligence for Research & Innovations; Springer Nature: Singapore, 2023; pp. 327–343. [Google Scholar]
- Shirzadi, A.; Asadi, S.; Shahabi, H.; Ronoud, S.; Clague, J.J.; Khosravi, K.; Pham, B.T.; Ahmad, B.B.; Bui, D.T. A novel ensemble learning based on Bayesian Belief Network coupled with an extreme learning machine for flash flood susceptibility mapping. Eng. Appl. Artif. Intell. 2020, 96, 103971. [Google Scholar]
- Sun, L.; Seidou, O.; Nistor, I.; Liu, K. Review of the Kalman-type hydrological data assimilation. Hydrol. Sci. J. 2016, 61, 2348–2366. [Google Scholar]
- Khaki, M.; Ait-El-Fquih, B.; Hoteit, I.; Forootan, E.; Awange, J.; Kuhn, M. Unsupervised ensemble Kalman filtering with an uncertain constraint for land hydrological data assimilation. J. Hydrol. 2018, 564, 175–190. [Google Scholar]
- Ghorbanidehno, H.; Kokkinaki, A.; Lee, J.; Darve, E. Recent developments in fast and scalable inverse modeling and data assimilation methods in hydrology. J. Hydrol. 2020, 591, 125266. [Google Scholar] [CrossRef]
- Maxwell, D.H.; Jackson, B.M.; McGregor, J. Constraining the ensemble Kalman filter for improved streamflow forecasting. J. Hydrol. 2018, 560, 127–140. [Google Scholar] [CrossRef]
- Abbaszadeh, P.; Moradkhani, H.; Yan, H. Enhancing hydrologic data assimilation by evolutionary particle filter and Markov chain Monte Carlo. Adv. Water Resour. 2018, 111, 192–204. [Google Scholar] [CrossRef]
- Jamal, A.; Linker, R. Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology. Water 2022, 14, 3606. [Google Scholar] [CrossRef]
- García-Alén, G.; Hostache, R.; Cea, L.; Puertas, J. Joint assimilation of satellite soil moisture and streamflow data for the hydrological application of a two-dimensional shallow water model. J. Hydrol. 2023, 621, 129667. [Google Scholar] [CrossRef]
- Lima, C.H.; Lall, U. Climate informed monthly streamflow forecasts for the Brazilian hydropower network using a periodic ridge regression model. J. Hydrol. 2010, 380, 438–449. [Google Scholar] [CrossRef]
- Bracken, C.; Holman, K.D.; Rajagopalan, B.; Moradkhani, H. A Bayesian hierarchical approach to multivariate nonstationary hydrologic frequency analysis. Water Resour. Res. 2018, 54, 243–255. [Google Scholar] [CrossRef]
- Prates, M.O.; Dey, D.K.; Willig, M.R.; Yan, J. Transformed Gaussian Markov random fields and spatial modeling of species abundance. Spat. Stat. 2015, 14, 382–399. [Google Scholar] [CrossRef]
- Ferreira, M.A. Proper Gaussian Markov Random Fields. In Modeling Spatio-Temporal Data; Chapman and Hall/CRC: Boca Raton, FL, USA, 2024; pp. 1–23. [Google Scholar]
- Wen, Y.; Yang, A.; Kong, X.; Su, Y. A Bayesian-model-averaging copula method for bivariate hydrologic correlation analysis. Front. Environ. Sci. 2022, 9, 744462. [Google Scholar] [CrossRef]
- Das, M.; Ghosh, S.K. FB-STEP: A fuzzy Bayesian network based data-driven framework for spatio-temporal prediction of climatological time series data. Expert Syst. Appl. 2019, 117, 211–227. [Google Scholar] [CrossRef]
- Santos-Fernandez, E.; Ver Hoef, J.M.; Peterson, E.E.; McGree, J.; Isaak, D.J.; Mengersen, K. Bayesian spatio-temporal models for stream networks. Comput. Stat. Data Anal. 2022, 170, 107446. [Google Scholar]
- Dehghani, M.; Saghafian, B.; Rivaz, F.; Khodadadi, A. Monthly stream flow forecasting via dynamic spatio-temporal models. Stoch. Environ. Res. Risk Assess. 2015, 29, 861–874. [Google Scholar]
- Takeshita, K.M.; Iwasaki, Y. Application of a Bayesian structural time series model for evaluating 11-year variation in pH in the headwaters of the Tama River, Japan. Limnology 2023, 24, 227–234. [Google Scholar]
- McEachran, Z.P.; Kietzmann, J.; Johnston, M. Parsimonious streamflow forecasting system based on a dynamical systems approach. J. Hydrol. 2024, 641, 131776. [Google Scholar]
- Martino, S.; Riebler, A. Integrated nested Laplace approximations (INLA). arXiv 2019, arXiv:1907.01248. [Google Scholar]
- Reichert, P.; Ammann, L.; Fenicia, F. Potential and challenges of investigating intrinsic uncertainty of hydrological models with stochastic, time-dependent parameters. Water Resour. Res. 2021, 57, e2020WR028400. [Google Scholar] [CrossRef]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.; Guo, J.; Li, P.; Riddell, A. Stan: A probabilistic programming language. J. Stat. Softw. 2017, 76, 1–32. [Google Scholar]
- Gelman, A.; Vehtari, A.; Simpson, D.; Margossian, C.C.; Carpenter, B.; Yao, Y.; Kennedy, L.; Gabry, J.; Bürkner, P.C.; Modrák, M. Bayesian workflow. arXiv 2020, arXiv:2011.01808. [Google Scholar]
- Lunn, D.; Spiegelhalter, D.; Thomas, A.; Best, N. The BUGS project: Evolution, critique and future directions. Stat. Med. 2009, 28, 3049–3067. [Google Scholar]
- Lunn, D.; Jackson, C.; Best, N.; Thomas, A.; Spiegelhalter, D. The BUGS Book. A Practical Introduction to Bayesian Analysis; Chapman Hall: London, UK, 2013. [Google Scholar]
- Thyer, M.; Leonard, M.; Kavetski, D.; Need, S.; Renard, B. The open source RFortran library for accessing R from Fortran, with applications in environmental modelling. Environ. Model. Softw. 2011, 26, 219–234. [Google Scholar]
- Bürkner, P.C. brms: An R package for Bayesian multilevel models using Stan. J. Stat. Softw. 2017, 80, 1–28. [Google Scholar]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar]
- Tang, Y.; Marshall, L.; Sharma, A.; Smith, T. Tools for investigating the prior distribution in Bayesian hydrology. J. Hydrol. 2016, 538, 551–562. [Google Scholar]
- Madsen, H.; Rosbjerg, D. Generalized least squares and empirical Bayes estimation in regional partial duration series index-flood modeling. Water Resour. Res. 1997, 33, 771–781. [Google Scholar]
- Haddad, K.; Rahman, A. Development of a Large Flood Regionalisation Model Considering Spatial Dependence—Application to Ungauged Catchments in Australia. Water 2019, 11, 677. [Google Scholar] [CrossRef]
- Tian, D.; Wang, L. BLP3-SP: A Bayesian Log-Pearson type III model with spatial priors for reducing uncertainty in flood frequency analyses. Water 2022, 14, 909. [Google Scholar] [CrossRef]
- Maranzano, C.J.; Krzysztofowicz, R. Identification of likelihood and prior dependence structures for hydrologic uncertainty processor. J. Hydrol. 2004, 290, 1–21. [Google Scholar] [CrossRef]
- Frey, M.P.; Stamm, C.; Schneider, M.K.; Reichert, P. Using discharge data to reduce structural deficits in a hydrological model with a Bayesian inference approach and the implications for the prediction of critical source areas. Water Resour. Res. 2011, 47, W12529. [Google Scholar] [CrossRef]
- Herrera, P.A.; Marazuela, M.A.; Hofmann, T. Parameter estimation and uncertainty analysis in hydrological modeling. Wiley Interdiscip. Rev. Water 2022, 9, e1569. [Google Scholar]
- Raje, D.; Krishnan, R. Bayesian parameter uncertainty modeling in a macroscale hydrologic model and its impact on Indian river basin hydrology under climate change. Water Resour. Res. 2012, 48, W08522. [Google Scholar] [CrossRef]
- Fenicia, F.; Kavetski, D.; Reichert, P.; Albert, C. Signature-domain calibration of hydrological models using approximate Bayesian computation: Empirical analysis of fundamental properties. Water Resour. Res. 2018, 54, 3958–3987. [Google Scholar] [CrossRef]
- Liu, S.; She, D.; Zhang, L.; Xia, J. An improved Approximate Bayesian Computation approach for high-dimensional posterior exploration of hydrological models. Hydrol. Earth Syst. Sci. Discuss. 2023, 2023, 1–46. [Google Scholar]
- Sharma, A.; Wang, H.; Zhang, J.; Lu, M.; Wu, C. Constructing multivariate distribution of rainfall characteristics: A Bayesian vine algorithm. J. Hydrol. 2024, 637, 131392. [Google Scholar] [CrossRef]
- Zhan, X.; Qin, H.; Liu, Y.; Yao, L.; Xie, W.; Liu, G.; Zhou, J. Variational Bayesian neural network for ensemble flood forecasting. Water 2020, 12, 2740. [Google Scholar] [CrossRef]
- Li, D.; Marshall, L.; Liang, Z.; Sharma, A. Hydrologic multi-model ensemble predictions using variational Bayesian deep learning. J. Hydrol. 2022, 604, 127221. [Google Scholar] [CrossRef]
- Ma, J.; Li, R.; Zheng, H.; Li, W.; Rao, K.; Yang, Y.; Wu, B. Multivariate adaptive regression splines-assisted approximate Bayesian computation for calibration of complex hydrological models. J. Hydroinform. 2024, 26, 503–518. [Google Scholar] [CrossRef]
- Mohajerani, H.; Kholghi, M.; Mosaedi, A.; Farmani, R.; Sadoddin, A.; Casper, M. Application of Bayesian decision networks for groundwater resources management under the conditions of high uncertainty and data scarcity. Water Resour. Manag. 2017, 31, 1859–1879. [Google Scholar] [CrossRef]
- Siqueira, P.G.; das Chagas Moura, M.; Duarte, H.O. A Bayesian population variability based method for estimating frequency of maritime accidents. Process Saf. Environ. Prot. 2022, 163, 308–320. [Google Scholar] [CrossRef]
- Biondi, D.; De Luca, D.L. A Bayesian approach for real-time flood forecasting. Phys. Chem. Earth Parts A/B/C 2012, 42, 91–97. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Z.; Jiang, X.; Li, B.; Chen, L. Bayesian theory based self-adapting real-time correction model for flood forecasting. Water 2016, 8, 75. [Google Scholar] [CrossRef]
- Barbetta, S.; Coccia, G.; Moramarco, T.; Todini, E. Real-time flood forecasting downstream river confluences using a Bayesian approach. J. Hydrol. 2018, 565, 516–523. [Google Scholar] [CrossRef]
- Bai, H.; Li, G.; Liu, C.; Li, B.; Zhang, Z.; Qin, H. Hydrological probabilistic forecasting based on deep learning and Bayesian optimization algorithm. Hydrol. Res. 2021, 52, 927–943. [Google Scholar] [CrossRef]
- Xu, C.; Zhong, P.A.; Zhu, F.; Xu, B.; Wang, Y.; Yang, L.; Wang, S.; Xu, S. A hybrid model coupling process-driven and data-driven models for improved real-time flood forecasting. J. Hydrol. 2024, 638, 131494. [Google Scholar] [CrossRef]
- Westra, S.; Thyer, M.; Leonard, M.; Kavetski, D.; Lambert, M. A strategy for diagnosing and interpreting hydrological model nonstationarity. Water Resour. Res. 2014, 50, 5090–5113. [Google Scholar] [CrossRef]
- Beven, K. Environmental Modelling: An Uncertain Future? CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Hallouin, T.; Bruen, M.; Christie, M.; Bullock, C.; Kelly-Quinn, M. Challenges in using hydrology and water quality models for assessing freshwater ecosystem services: A review. Geosciences 2018, 8, 45. [Google Scholar] [CrossRef]
- Bruen, M.; Hallouin, T.; Christie, M.; Matson, R.; Siwicka, E.; Kelly, F.; Bullock, C.; Feeley, H.B.; Hannigan, E.; Kelly-Quinn, M. A Bayesian modelling framework for integration of ecosystem services into freshwater resources management. Environ. Manag. 2022, 69, 781–800. [Google Scholar] [CrossRef]
- Gelman, A.; Hwang, J.; Vehtari, A. Understanding predictive information criteria for Bayesian models. Stat. Comput. 2014, 24, 997–1016. [Google Scholar] [CrossRef]
- Vehtari, A.; Gelman, A.; Sivula, T.; Jylänki, P.; Tran, D.; Sahai, S.; Blomstedt, P.; Cunningham, J.P.; Schiminovich, D.; Robert, C.P. Expectation propagation as a way of life: A framework for Bayesian inference on partitioned data. J. Mach. Learn. Res. 2020, 21, 1–53. [Google Scholar]
- Hao, Y.; Baik, J.; Tran, H.; Choi, M. Quantification of the effect of hydrological drivers on actual evapotranspiration using the Bayesian model averaging approach for various landscapes over Northeast Asia. J. Hydrol. 2022, 607, 127543. [Google Scholar] [CrossRef]
- Kuczera, G.; Parent, E. Monte Carlo assessment of parameter uncertainty in conceptual catchment models: The Metropolis algorithm. J. Hydrol. 1998, 211, 69–85. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).