A Numerical Study on the Effect of the Coriolis Force on the Sediment Exchange Between the Yangtze River Estuary and Hangzhou Bay
Abstract
1. Introduction
2. Model Description
2.1. Model Control Equations
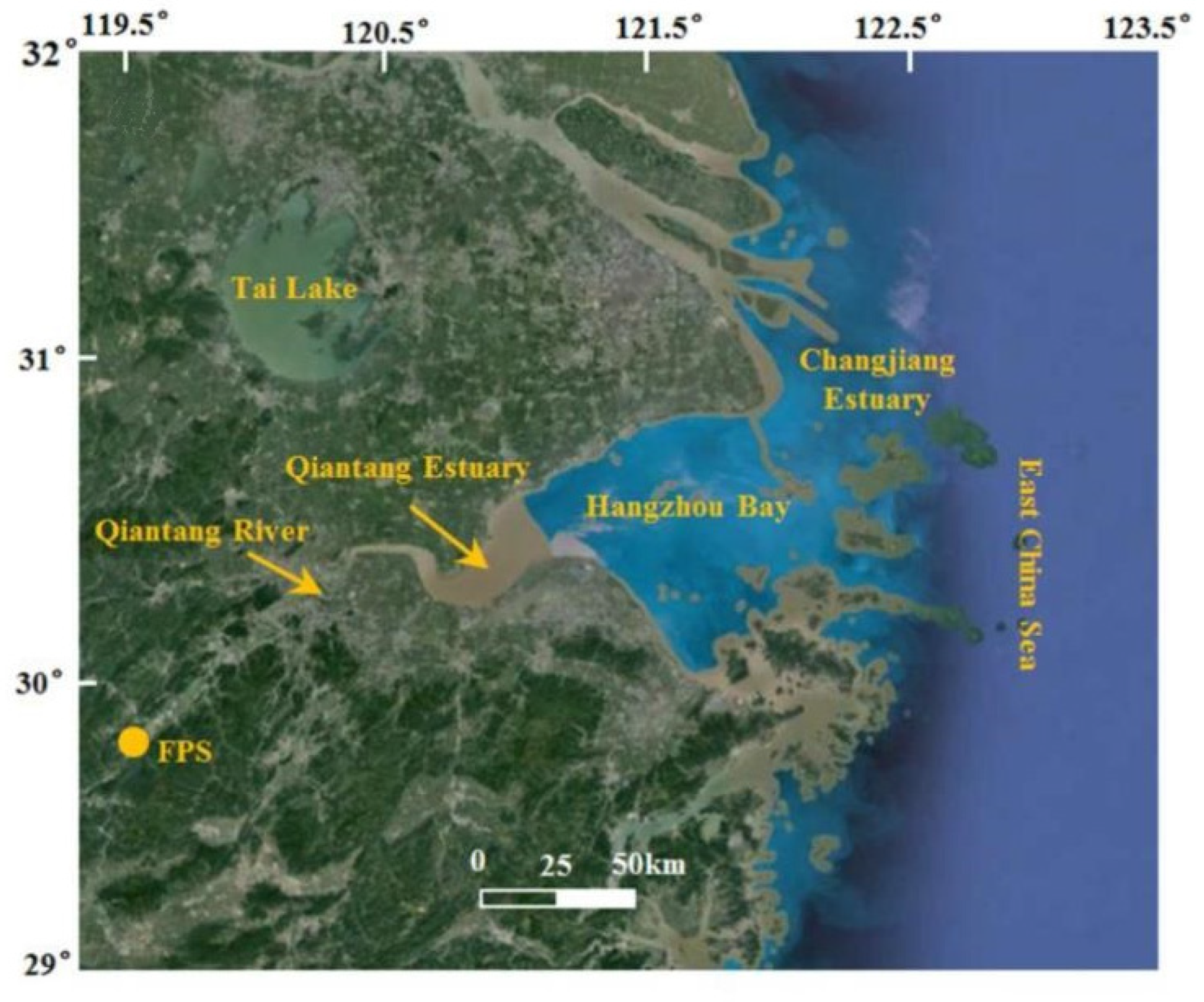
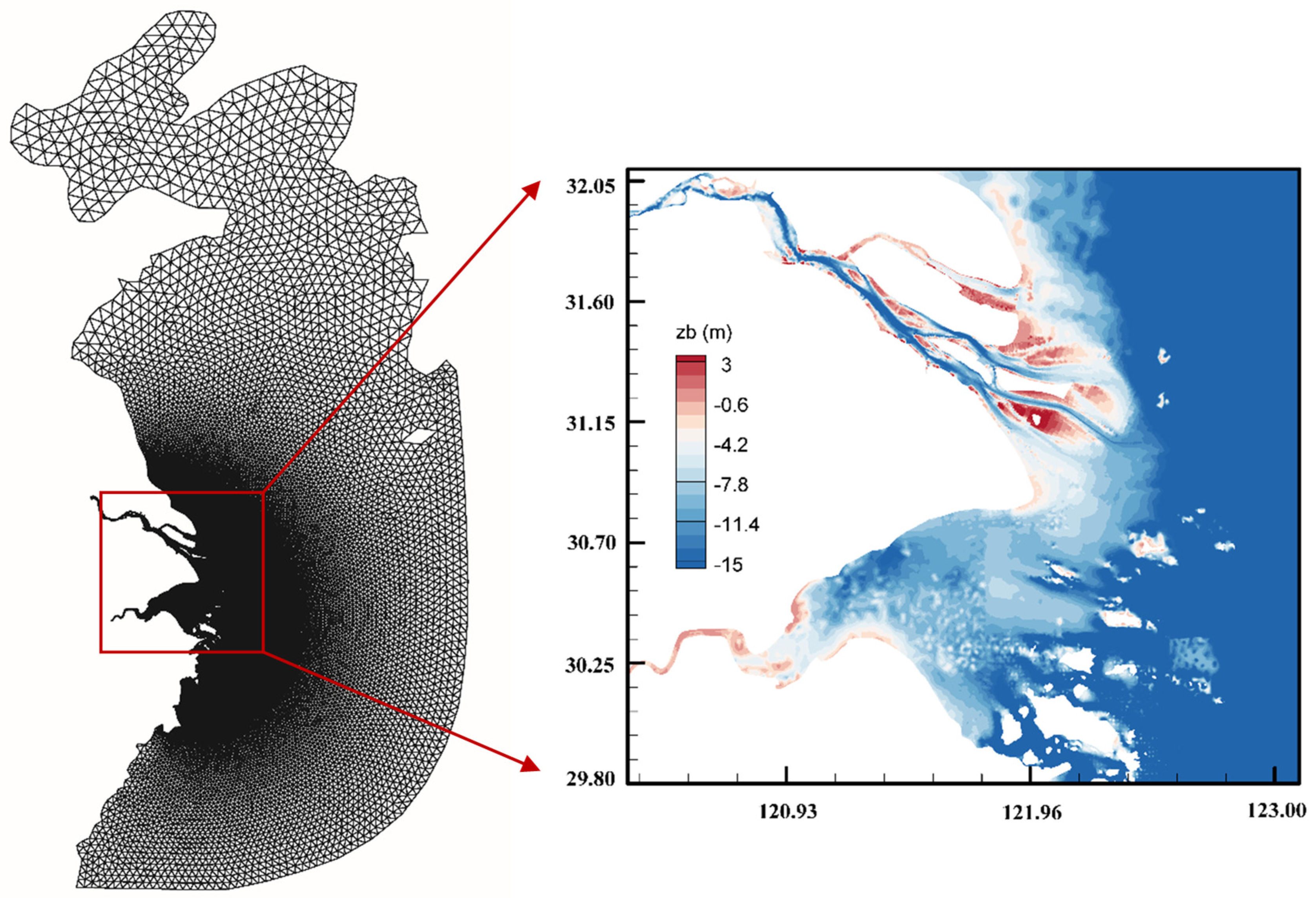
2.2. Numerical Algorithm and Model Model Study Area
2.3. Model Parameter Settings
2.4. Computational Efficiency
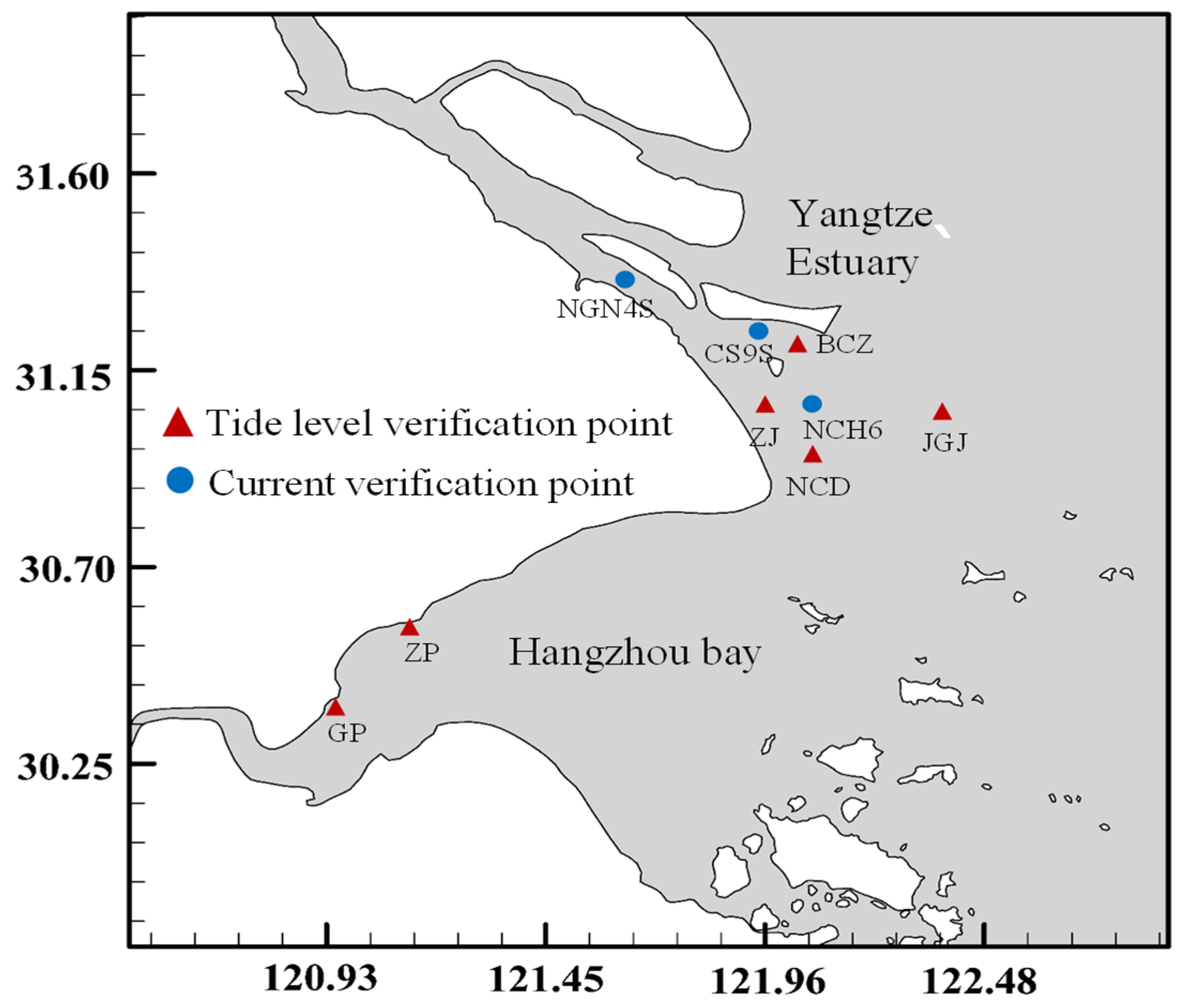
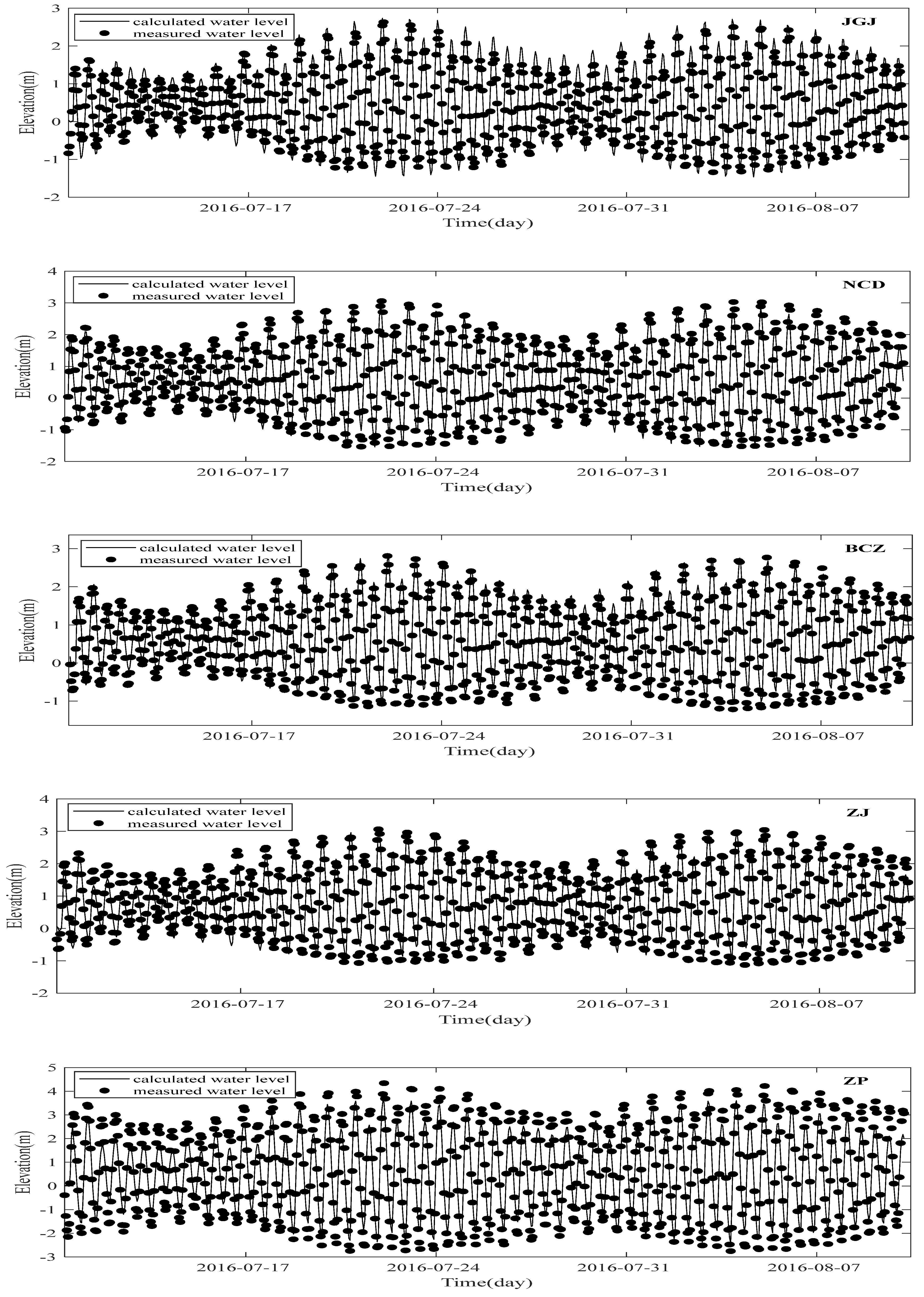
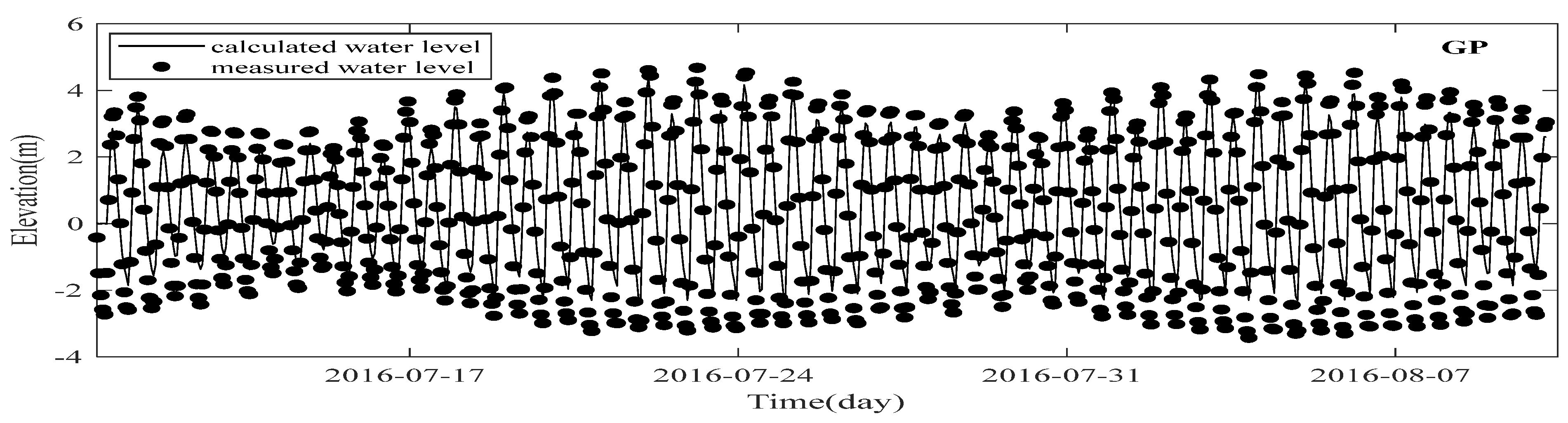
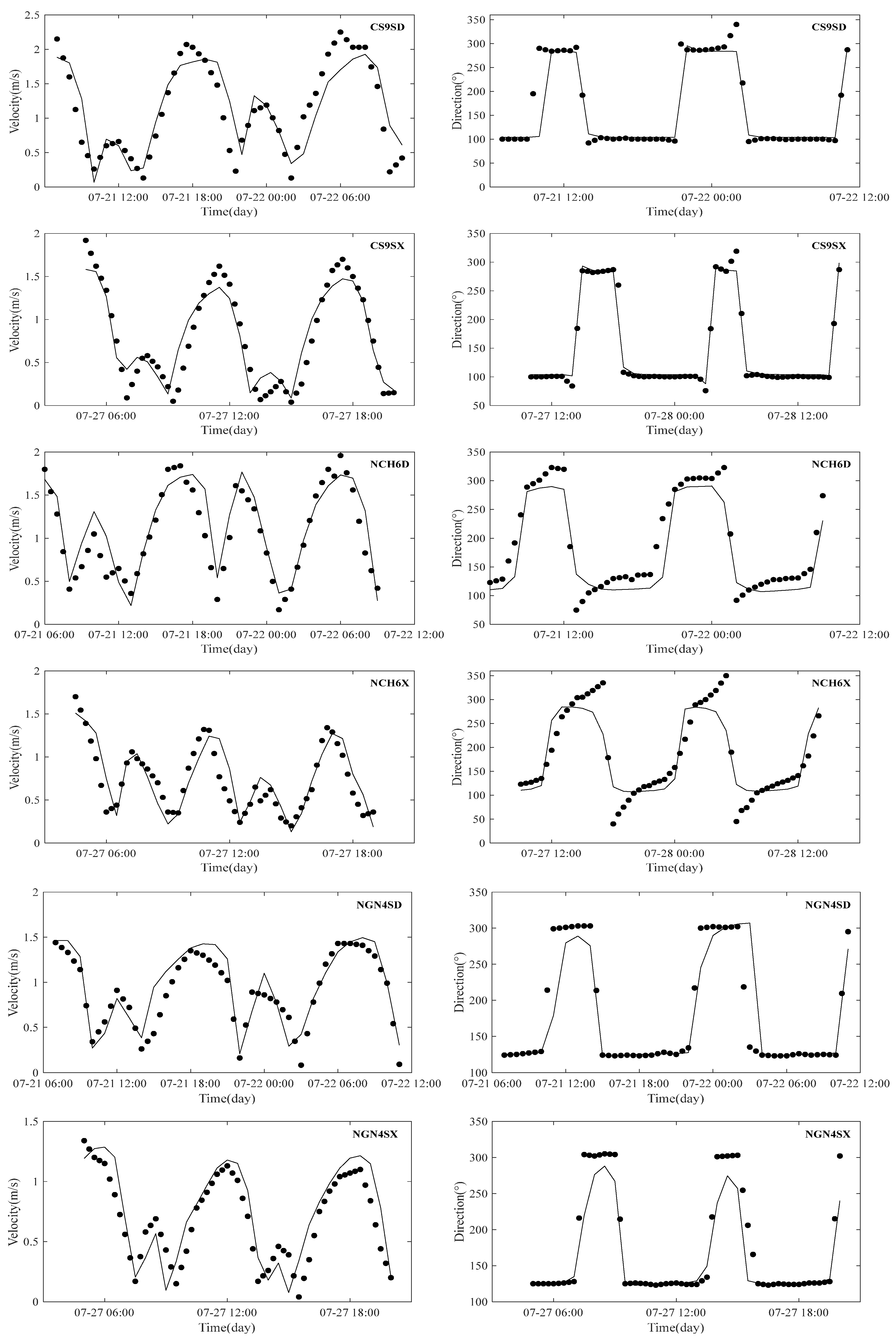
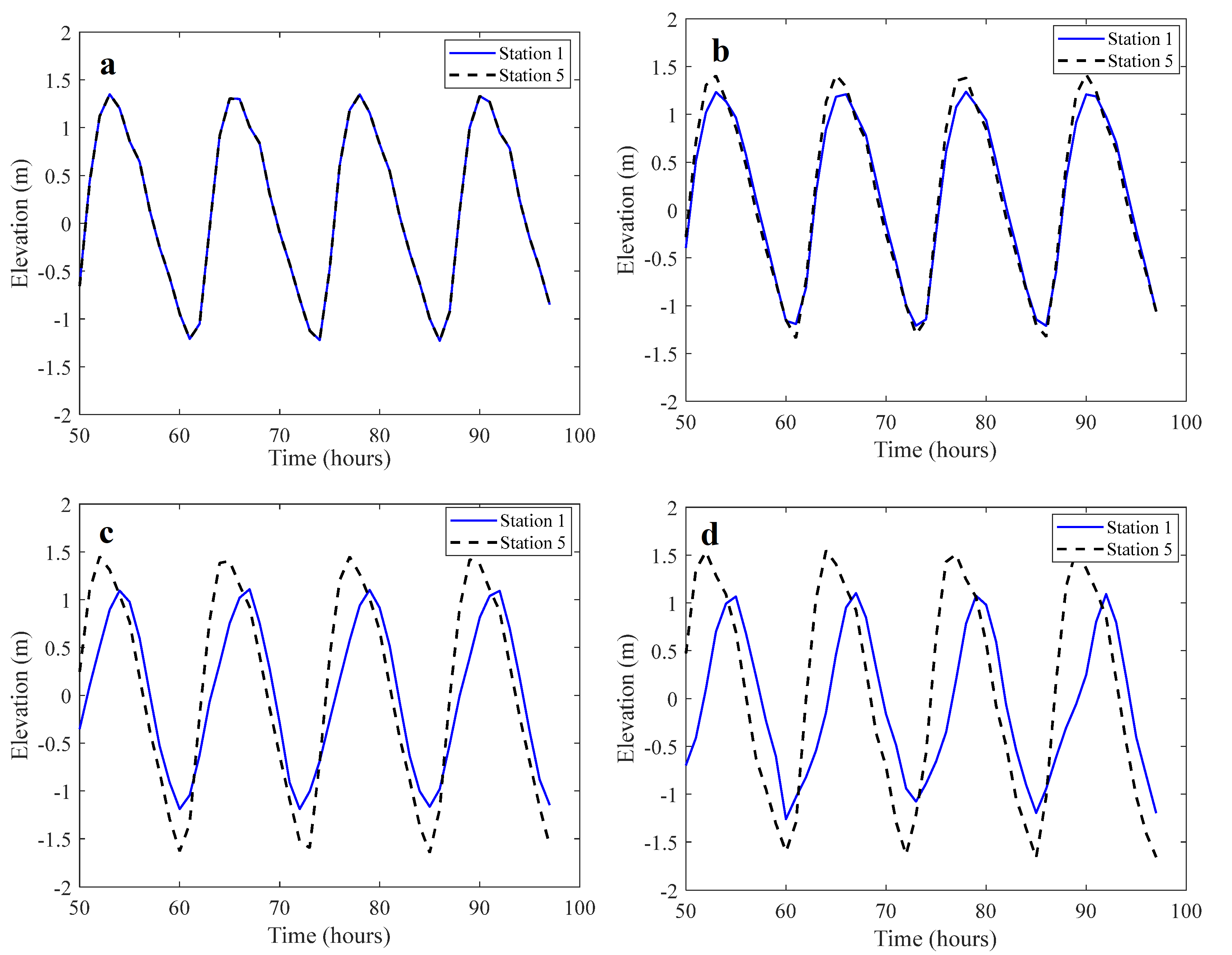
3. Quantitative Accuracy
4. Generalized Model and Case Settings
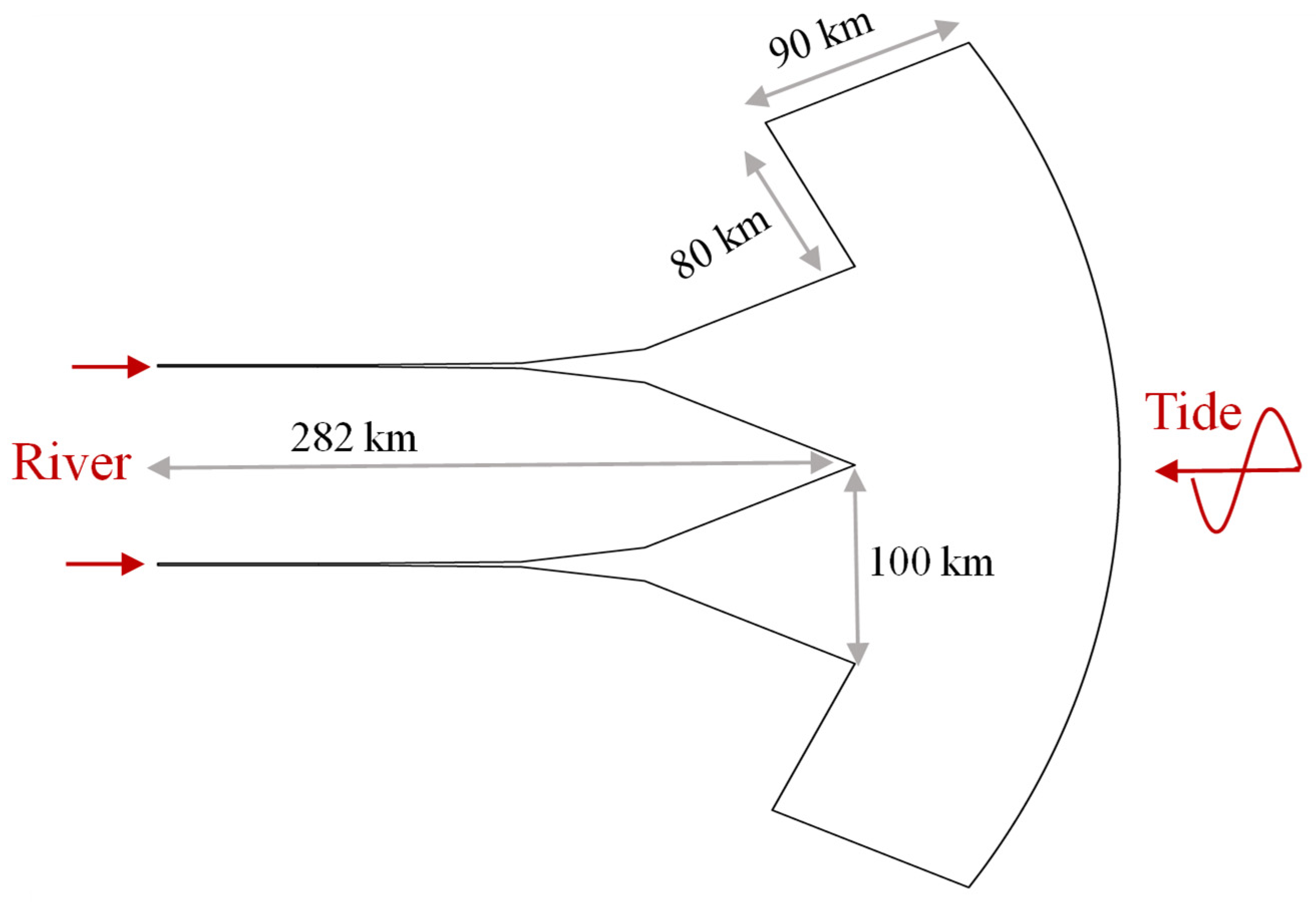
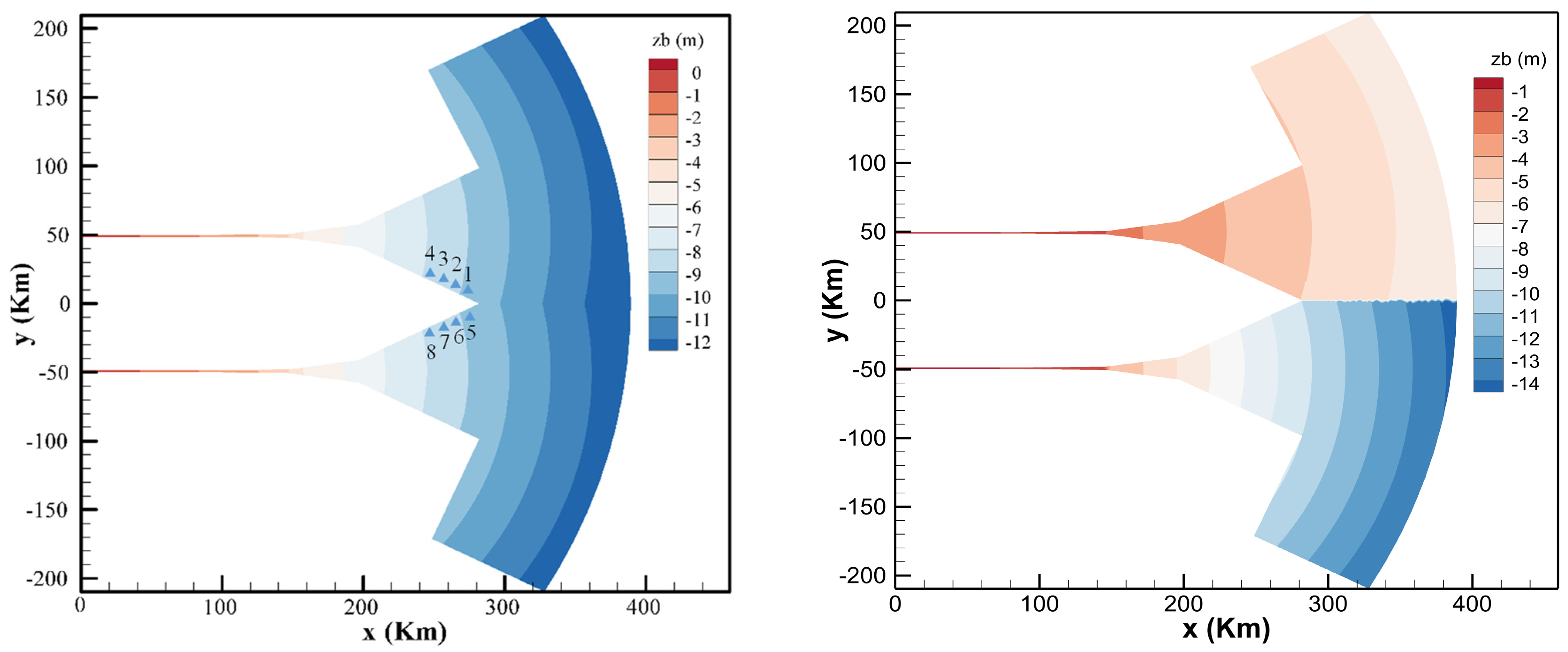
4.1. Adjacent Estuary Idealized Model
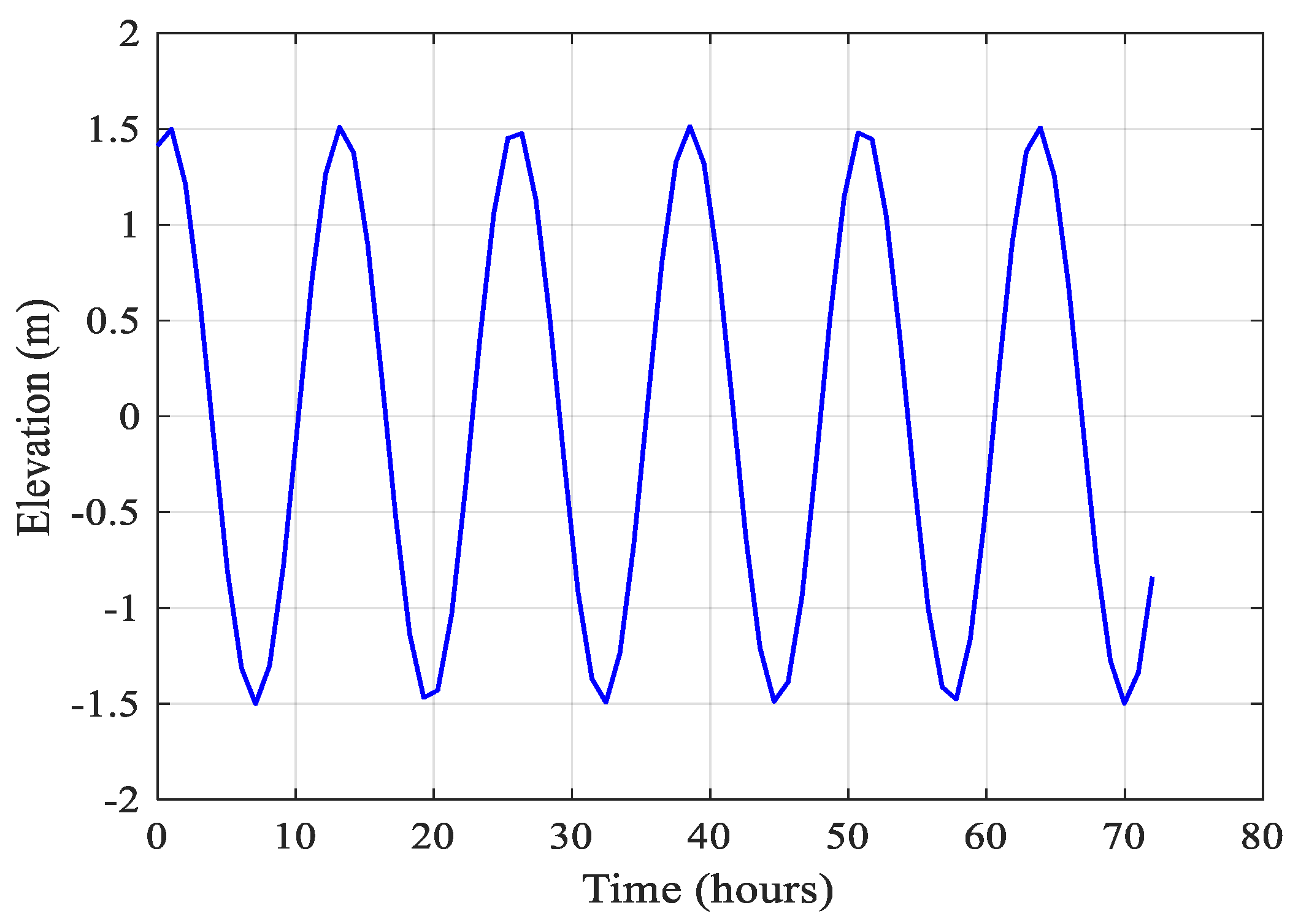
4.2. Case Condition Settings
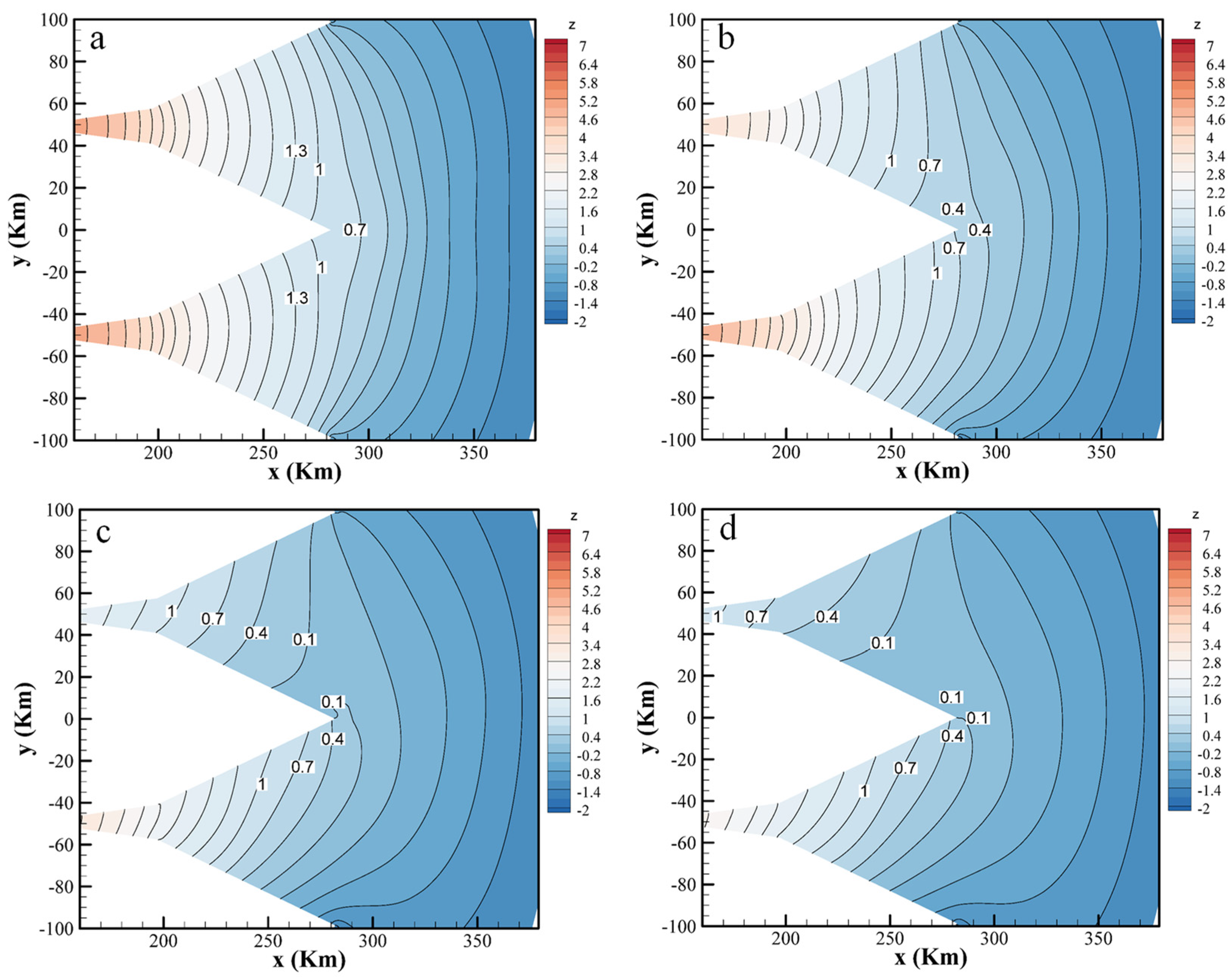
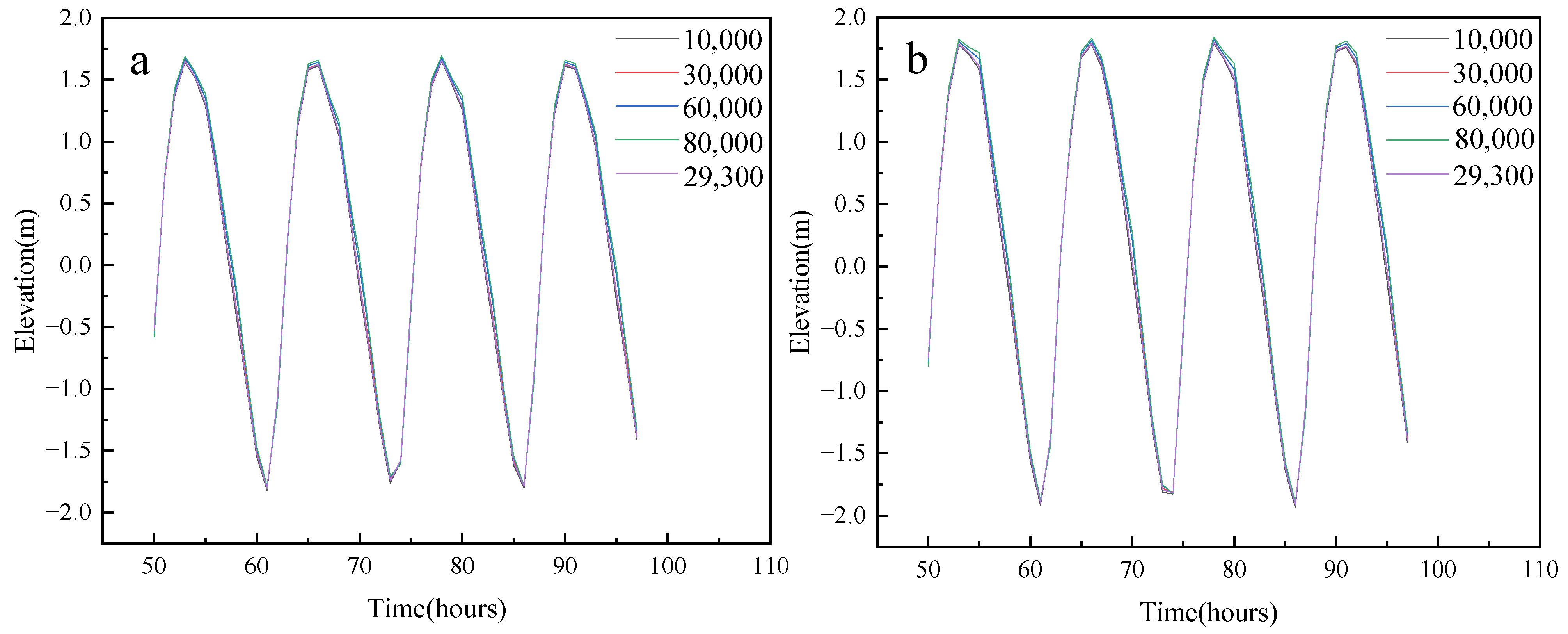
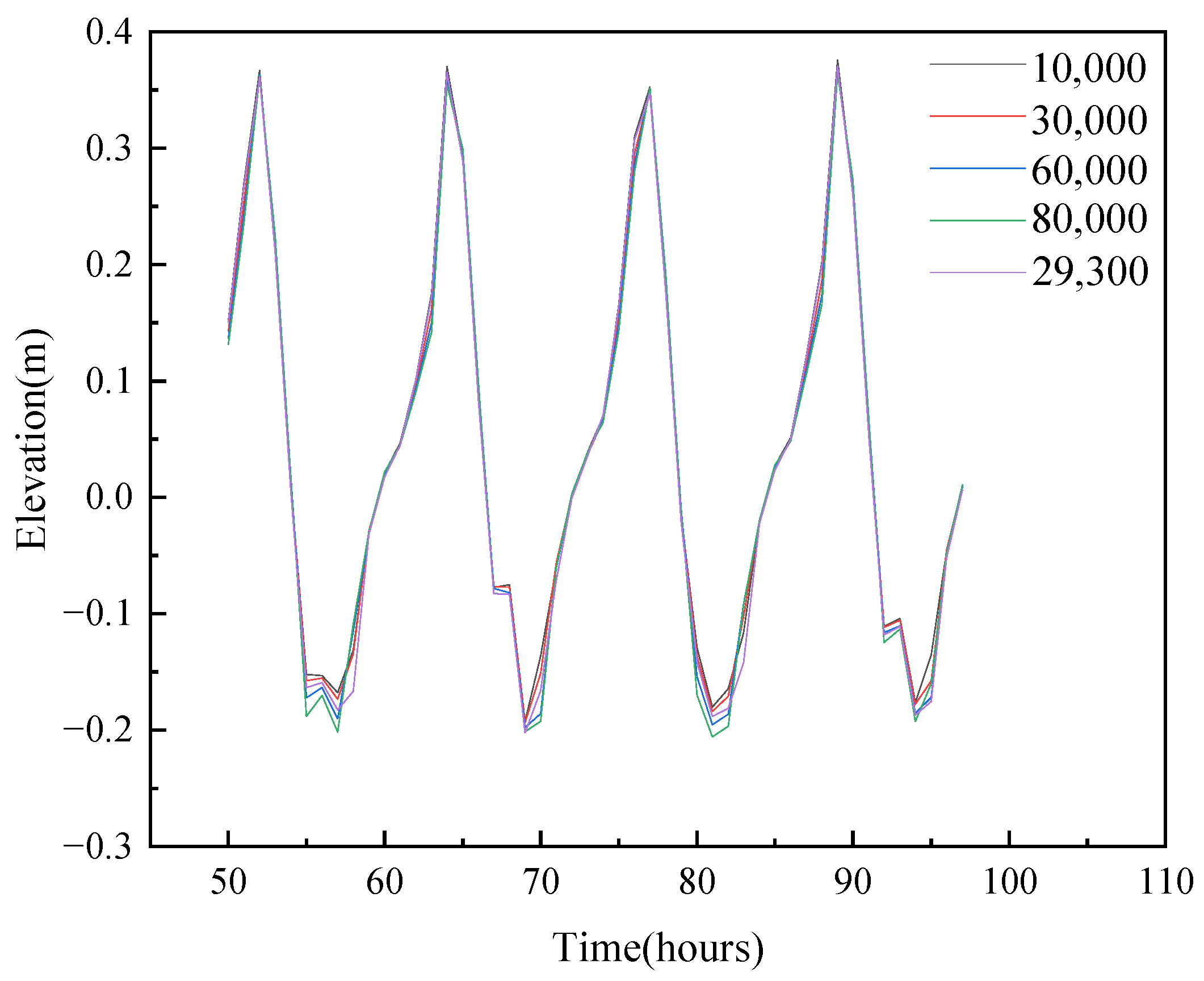
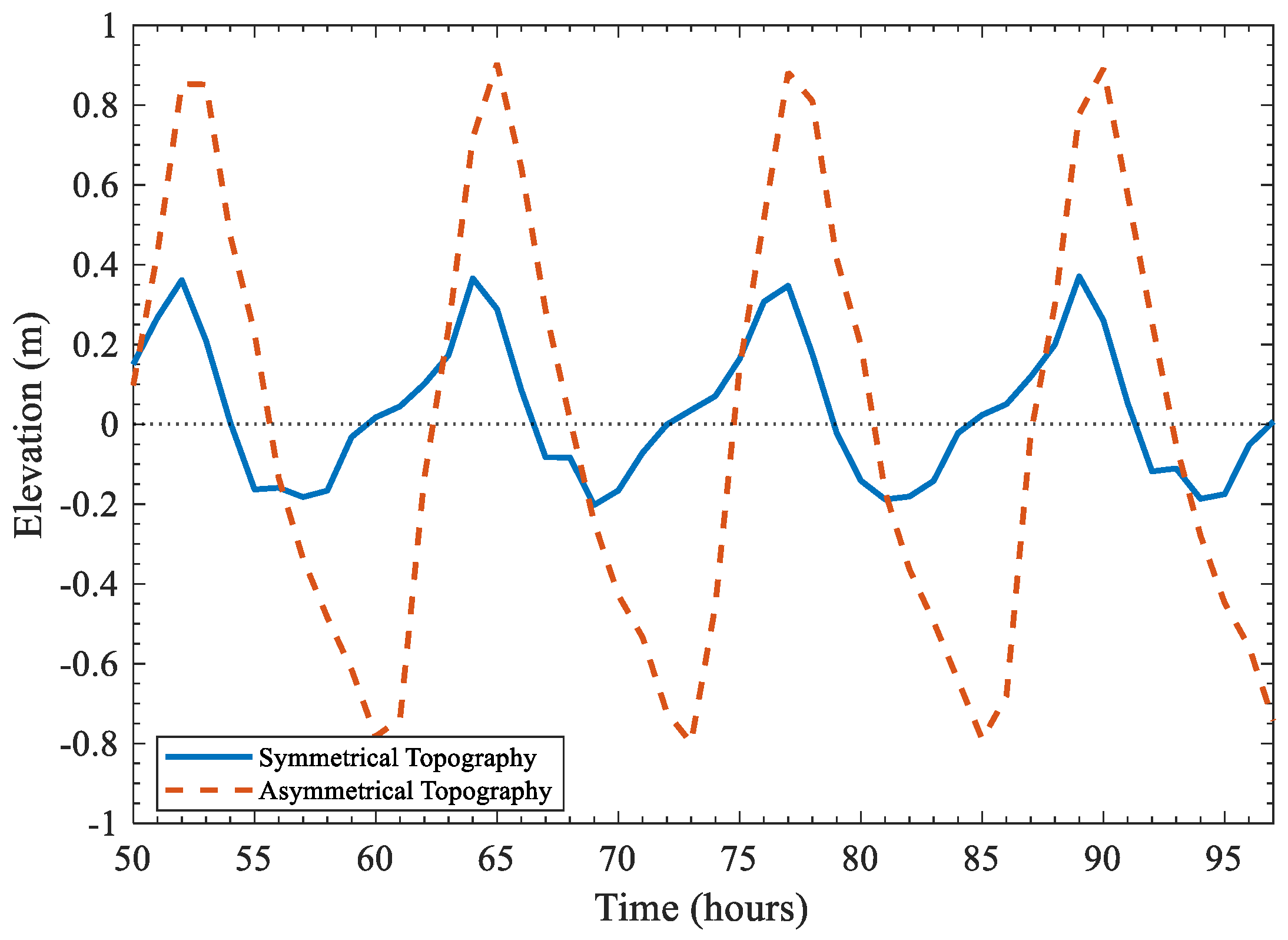
5. Results
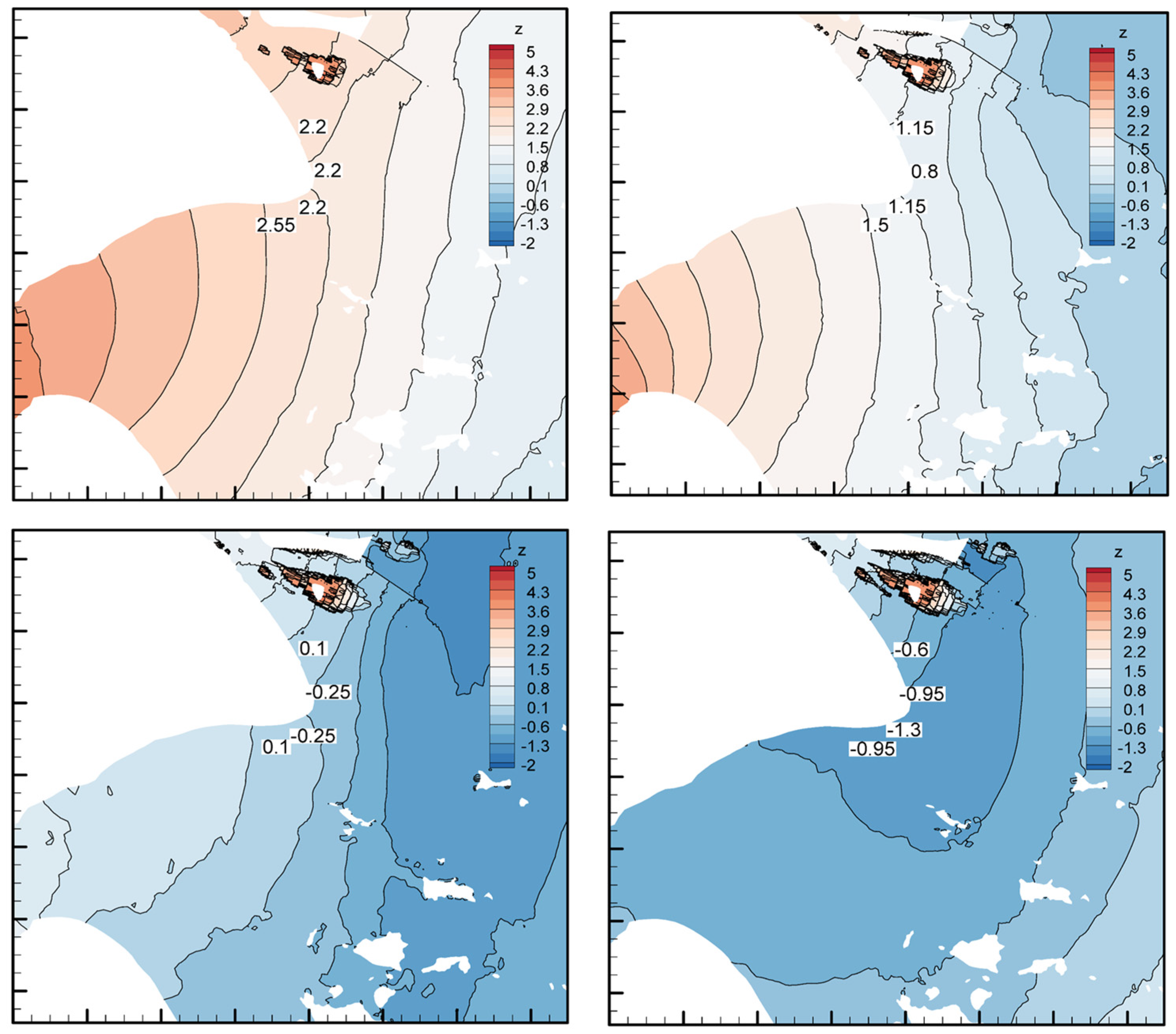
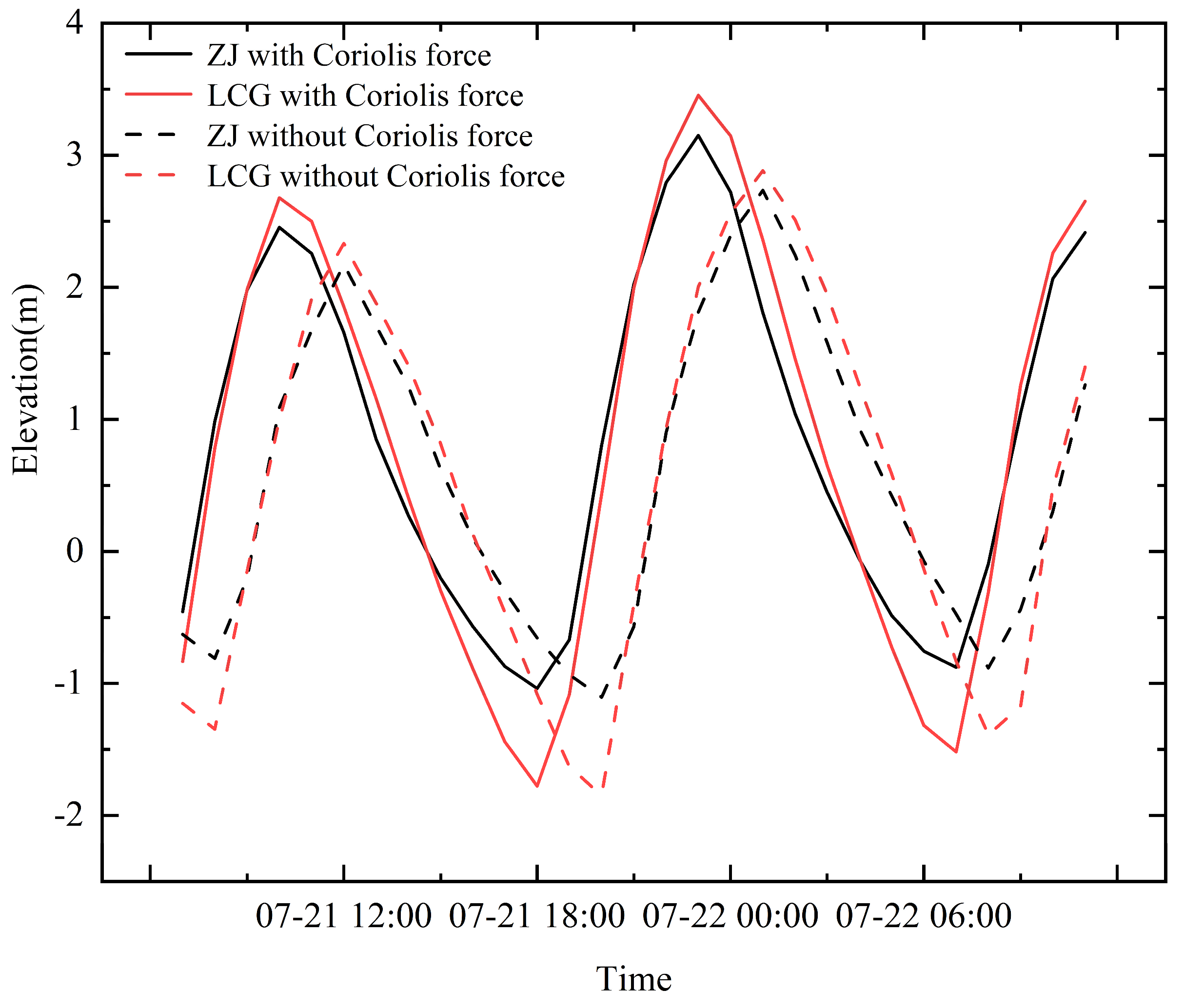
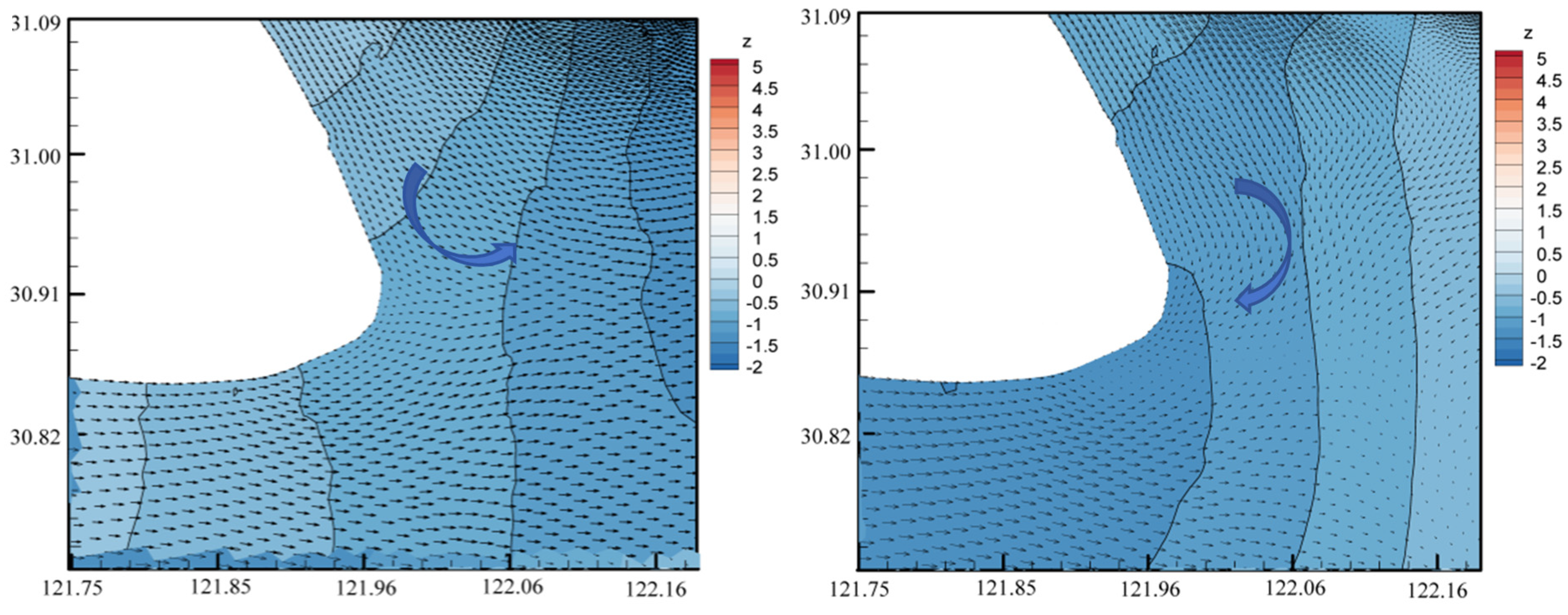
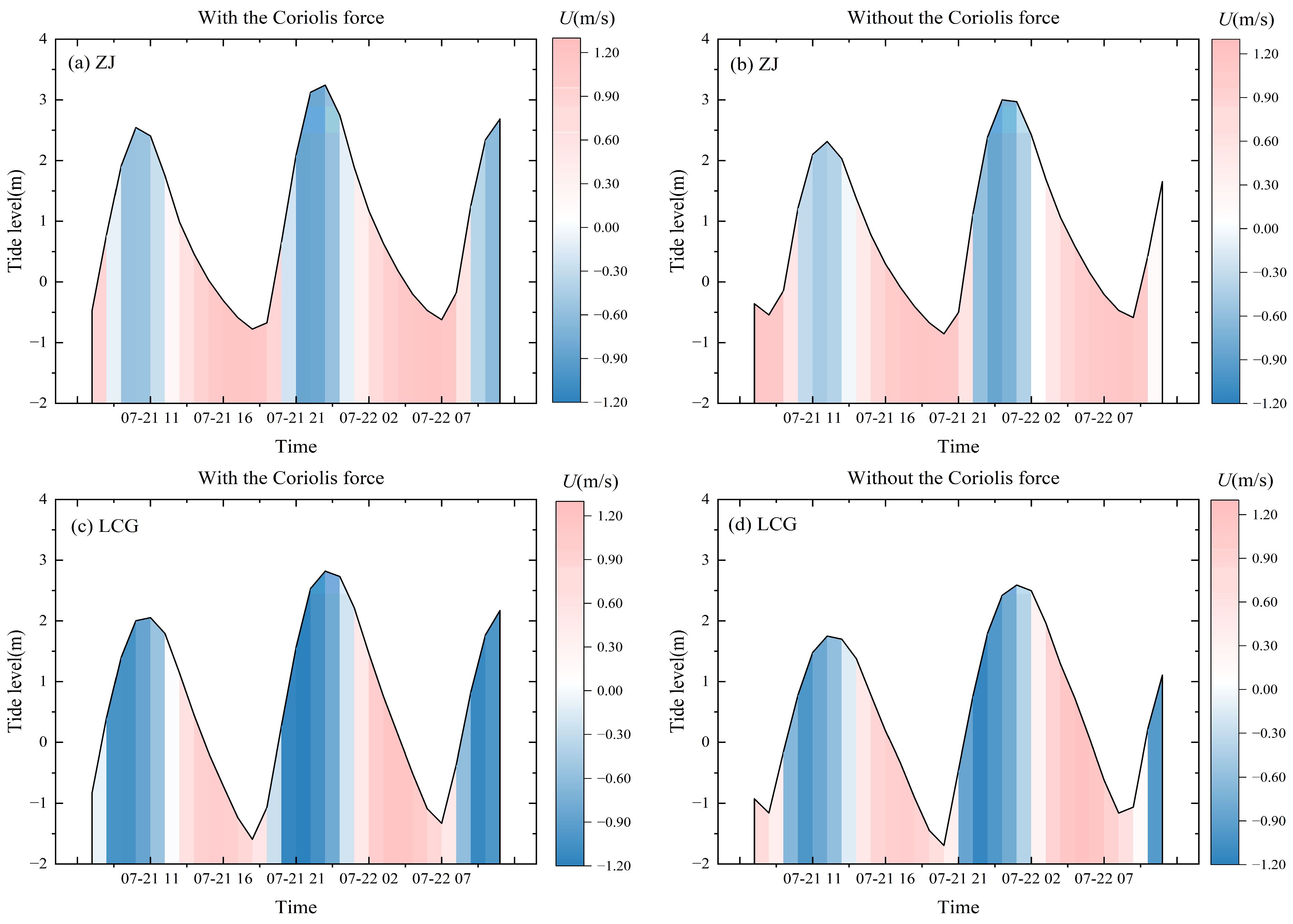
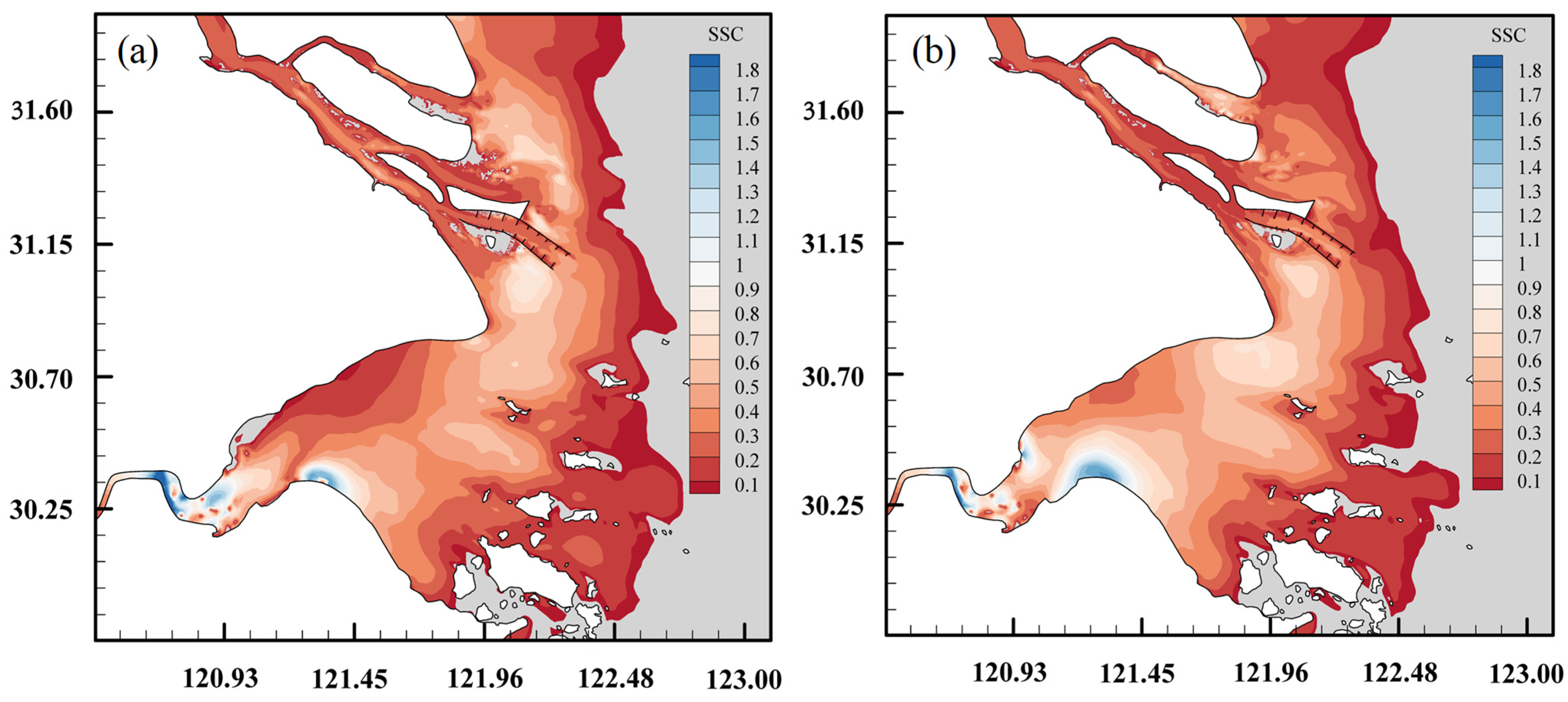
5.1. Effect of the Coriolis Force on Hydrodynamics in Actual Models
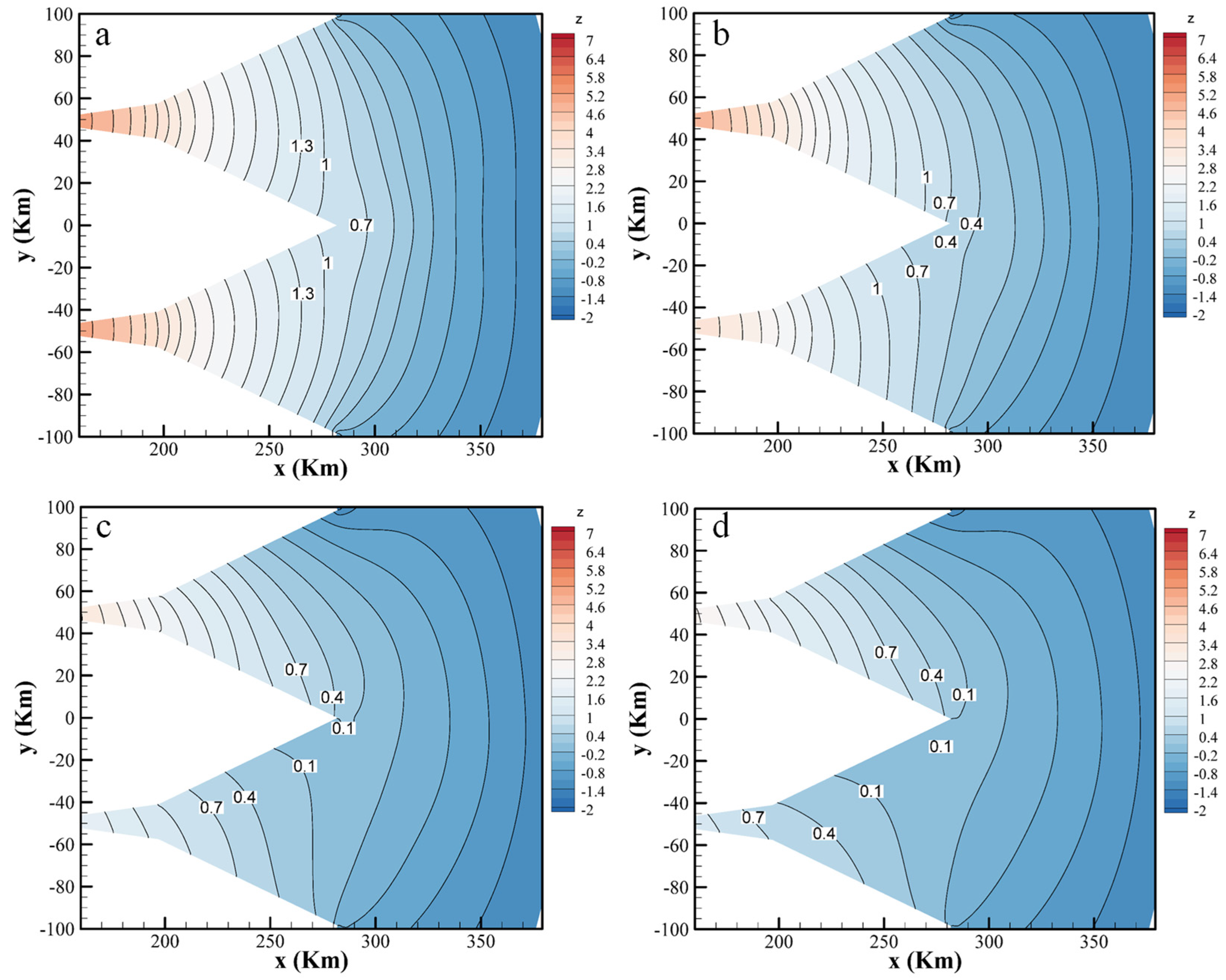
5.2. Analysis of the Arithmetic Results of the Idealized Generalized Model
6. Conclusions
- Quantify the relative contributions of tidal asymmetry and the Coriolis force to sediment transport in the Yangtze River estuary and Hangzhou Bay system.
- Investigate the long-term impacts of sea-level rise and anthropogenic activities on tidal asymmetry and sediment dynamics.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, J.Y.; Chen, S.L.; Ding, P.X. Sediment transport pathways in the nearshore waters of Nan-huizui, Yangtze River Estuary. Resour. Environ. Yangtze Basin. 2001, 10, 166–172. (In Chinese) [Google Scholar]
- Yang, S.L.; Milliman, J.D.; Li, P.; Xu, K. 50,000 dams later: Erosion of the Yangtze River and its delta. Glob. Planet. Change 2011, 75, 14–20. [Google Scholar] [CrossRef]
- Dai, Z.; Fagherazzi, S.; Mei, X.; Gao, J. Decline in suspended sediment concentration delivered by the Changjiang (Yangtze) River into the East China Sea between 1956 and 2013. Geomorphology 2016, 268, 123–132. [Google Scholar] [CrossRef]
- Li, P.; Yang, S.; Milliman, J.D.; Xu, K.; Qin, W.; Wu, C.; Chen, Y.; Shi, B. Spatial, temporal, and human-induced variations in suspended sediment concentration in the surface waters of the Yangtze estuary and adjacent coastal areas. Estuaries Coasts 2012, 35, 1316–1327. [Google Scholar] [CrossRef][Green Version]
- Dai, Z.; Liu, J.T.; Xie, H.; Shi, W. Sedimentation in the Outer Hangzhou Bay, China: The influence of Changjiang sediment load. J. Coast. Res. 2014, 30, 1218–1225. [Google Scholar] [CrossRef]
- Dai, Z.; Liu, J.T.; Wei, W.; Chen, J. Detection of the Three Gorges Dam influence on the Changjiang (Yangtze River) submerged delta. Sci. Rep. 2014, 4, 6600. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.M. Davies A G. Flood/ebb tidal asymmetry in a shallow sandy estuary and the impact on net sand transport. Geomorphology 2010, 114, 431–439. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, J.; Li, L. Analysis of the dynamic causes of flood-ebb asymmetry in the Yangtze River Estuary. Acta Oceanol. Sin. 2011, 33, 19–27. (In Chinese) [Google Scholar]
- Pan, C.; Zheng, J.; Chen, G.; He, C.; Tang, Z. Spatiotemporal variations and causes of tidal characteristics in Hangzhou Bay. Ocean Eng. 2019, 37, 11. (In Chinese) [Google Scholar]
- Suh, S.W.; Lee, H.Y.; Kim, H.J. Spatio-Temporal Variability of Tidal Asymmetry Due to Multiple Coastal Constructions along the West Coast of Korea. Estuar. Coast. Shelf Sci. 2014, 151, 336–346. [Google Scholar] [CrossRef]
- Suh, S.W. Tidal Asymmetry and Energy Variation Due to Sea-Level Rise in a Macro Tidal Bay. J. Coast. Res. 2016, 75, 765–769. [Google Scholar] [CrossRef]
- Ji, X.; Huang, L.; Zhang, W.; Yao, P. On the Mechanism behind the Variation of the Tidal Current Asymmetry in Response to Reclamations in Lingding Bay, China. J. Mar. Sci. Eng. 2022, 10, 951. [Google Scholar] [CrossRef]
- Feng, X.; Feng, H. On the Role of Anthropogenic Activity and Sea-Level-Rise in Tidal Distortion on the Open Coast of the Yellow Sea Shelf. J. Geophys. Res. Oceans 2021, 126, e2020JC016583. [Google Scholar] [CrossRef]
- Li, J. Study on sediment transport patterns in the Nanhui tidal flat of the Yangtze River Estuary. Acta Oceanol. Sin. 1990, 75–82. (In Chinese) [Google Scholar]
- Cao, P.; Yan, S. Suspended sediment front in the Yangtze River Estuary and its impact on material transport. J. East China Norm. Univ. (Nat. Sci.) 1996, 85–94. (In Chinese) [Google Scholar]
- Kong, J.; Ye, R.; Xue, X.; Zhou, Y. Impact of Nanhui East Shoal on sediment exchange between the Yangtze Estuary and Hangzhou Bay. Waterw. Port. 2009, 30, 77–81. (In Chinese) [Google Scholar]
- Huang, G. Study on Water and Sediment Exchange and Transport Characteristics Between the Yangtze Estuary and Hangzhou Bay. Ph.D. Thesis, East China Normal University, Shanghai, China, 2007. (In Chinese). [Google Scholar]
- Huang, J.; Zhu, J.; Su, J.; Han, X.; Cai, L. Suspended sediment exchange between the Changjiang Estuary and Hangzhou Bay and their key driving mechanisms. Estuar. Coast. Shelf Sci. 2024, 305, 108876. [Google Scholar] [CrossRef]
- Sassi, M.G.; Hoitink, A.J.F. River flow controls on tides and tide-mean water level profiles in a tidal freshwater river. J. Geophys. Res. Oceans 2013, 118, 4139–4151. [Google Scholar] [CrossRef]
- Guo, L.; van der Wegen, M.; Roelvink, J.A.; He, Q. The role of river flow and tidal asymmetry on 1D estuarine morphodynamics. J. Geophys. Res. Earth Surf. 2014, 119, 2315–2334. [Google Scholar] [CrossRef]
- Guo, L.; van der Wegen, M.; Roelvink, D.; He, Q. Exploration of the impact of seasonal river discharge variations on long-term estuarine morphodynamic behavior. Coast. Eng. 2015, 95, 105–116. [Google Scholar] [CrossRef]
- Hu, P.; Han, J.; Li, W.; Sun, Z.; He, Z. Numerical investigation of a sandbar formation and evolution in a tide-dominated estuary using a hydro-morphodynamic model. Coast. Eng. J. 2018, 60, 466–483. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment. Adv. Water Resour. 2013, 52, 107–131. [Google Scholar] [CrossRef]
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Zhang, R.; Xie, J.; Wang, M.; Huang, J. River Sediment Dynamics; Water Resources and Electric Power Press: Beijing, China, 1989. (In Chinese) [Google Scholar]
- Crossley, A.J.; Wright, N.G. Time accurate local time stepping for the unsteady shallow water equations. Int. J. Numer. Meth. Fluids 2005, 48, 775–799. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Dal Palù, A.; Mignosa, P. A local time stepping algorithm for GPU-accelerated 2D shallow water models. Adv. Water Resour. 2018, 111, 274–288. [Google Scholar] [CrossRef]
- Dazzi, S.; Maranzoni, A.; Mignosa, P. Local time stepping applied to mixed flow modelling. J. Hydraul. Res. 2016, 54, 145–157. [Google Scholar] [CrossRef]
- Hu, P.; Lei, Y.; Han, J.; Cao, Z.; Liu, H.; He, Z. Computationally efficient modeling of hydro-sediment-morphodynamic processes using a hybrid local time step/global maximum time step. Adv. Water Resour. 2019, 127, 26–38. [Google Scholar] [CrossRef]
- Hu, P.; Lei, Y.; Han, J.; Cao, Z.; Liu, H.; He, Z.; Yue, Z. Improved local time step for 2D shallow-water modeling based on unstructured grids. J. Hydraul. Eng. 2019, 145, 06019017. [Google Scholar] [CrossRef]
- Hu, P.; Zhao, Z.; Ji, A.; Li, W.; He, Z.; Liu, Q.; Li, Y.; Cao, Z. A GPU-accelerated and LTS-based finite volume shallow water model. Water 2022, 14, 922. [Google Scholar] [CrossRef]
- Vacondio, R.; Dal Palù, A.; Ferrari, A.; Mignosa, P.; Aureli, F.; Dazzi, S. A non-uniform efficient grid type for GPU-parallel shallow water equations models. Environ. Model. Softw. 2017, 88, 119–137. [Google Scholar] [CrossRef]
- Lacasta, A.; Morales-Hernández, M.; Murillo, J.; García-Navarro, P. An optimized GPU implementation of a 2D free surface simulation model on unstructured meshes. Adv. Eng. Softw. 2014, 78, 1–15. [Google Scholar] [CrossRef]
- Brodtkorb, A.R.; Sætra, M.L.; Altinakar, M. Efficient shallow water simulations on GPUs: Implementation, visualization, verification, and validation. Comput. Fluids 2012, 55, 1–12. [Google Scholar] [CrossRef]
- Lacasta, A.; Morales-Hernández, M.; Murillo, J.; García-Navarro, P. GPU implementation of the 2D shallow water equations for the simulation of rainfall/runoff events. Environ. Earth Sci. 2015, 74, 7295–7305. [Google Scholar] [CrossRef]
- Castro, M.J.; Ortega, S.; de la Asunción, M.; Mantas, J.M.; Gallardo, J.M. GPU computing for shallow water flow simulation based on finite volume schemes. Comptes Rendus Mec. 2010, 339, 165–184. [Google Scholar] [CrossRef]
- de la Asunción, M.; Castro, M.J. Simulation of tsunamis generated by landslides using adaptive mesh refinement on GPU. J. Comput. Phys. 2017, 345, 91–110. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, H. SMS Hydrodynamic Software. Waterw. Harbor. 2006, 1, 57–59. (In Chinese) [Google Scholar]
- Scientific Software Group Surface Water Modeling System (SMS). In Encyclopedia of Hydrological Sciences; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; pp. 154–196. [CrossRef]
- Wu, Z.; Xu, X. Modeling of the Yangtze River Estuary-Hangzhou Bay Waters Based on SMS. China Water Transp. (Second. Half Mon.) 2013, 13, 125–126. (In Chinese) [Google Scholar]
- Dou, X.; Li, L.; Dou, G. Study on the Total Sediment Mathematical Model of the Yangtze River Estuary. J. Hydraul. Eng. Water Resour. Res. 1999, 2, 32–41. (In Chinese) [Google Scholar]
- Warner, J.C.; Geyer, W.R.; Lerczak, J.A. Numerical modeling of an estuary: A comprehensive skill assessment. J. Geophys. Res. Oceans 2005, 110, C05001. [Google Scholar] [CrossRef]
- Allen, J.I.; Somerfield, P.J.; Gilbert, F.J. Quantifying uncertainty in high-resolution coupled hydrodynamic-ecosystem models. J. Mar. Syst. 2007, 64, 3–14. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, X.; Pan, C.; Zhang, J. Numerical simulation of the tidal flow and suspended sediment transport in the Qiantang Estuary. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 192–202. [Google Scholar] [CrossRef]
- Yu, D. Analysis on Impact of the Coriolis Forces on Flow in the Yangtze River Estuary. In Proceedings of the Third Chinese-German Joint Symposium on Coastal and Ocean Engineering National, Tainan, Taiwan, 8–16 November 2006. [Google Scholar]
- Osadchiev, A.; Alfimenkov, I.; Rogozhin, V. Influence of the Coriolis force on spreading of river plumes. Remote Sens. 2023, 15, 3397. [Google Scholar] [CrossRef]
- Li, M.; Chen, Z.; Yin, D.; Chen, J.; Wang, Z.; Sun, Q. Morphodynamic characteristics of the dextral diversion of the Yangtze River mouth, China: Tidal and the Coriolis force controls. Earth Surf. Process. Landf. 2011, 36, 641–650. [Google Scholar] [CrossRef]
- Xie, D.; Gao, S.; Wang, Z.B.; Pan, C.; Wu, X.; Wang, Q. Morphodynamic modeling of a large inside sandbar and its dextral morphology in a convergent estuary: Qiantang Estuary, China. J. Geophys. Res. Earth Surf. 2017, 122, 1553–1572. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, H.; Li, J. Nonlinear advection, Coriolis force, and frictional influence in the South Channel of the Yangtze Estuary, China. Sci. China Earth Sci. 2015, 58, 429–435. [Google Scholar] [CrossRef]
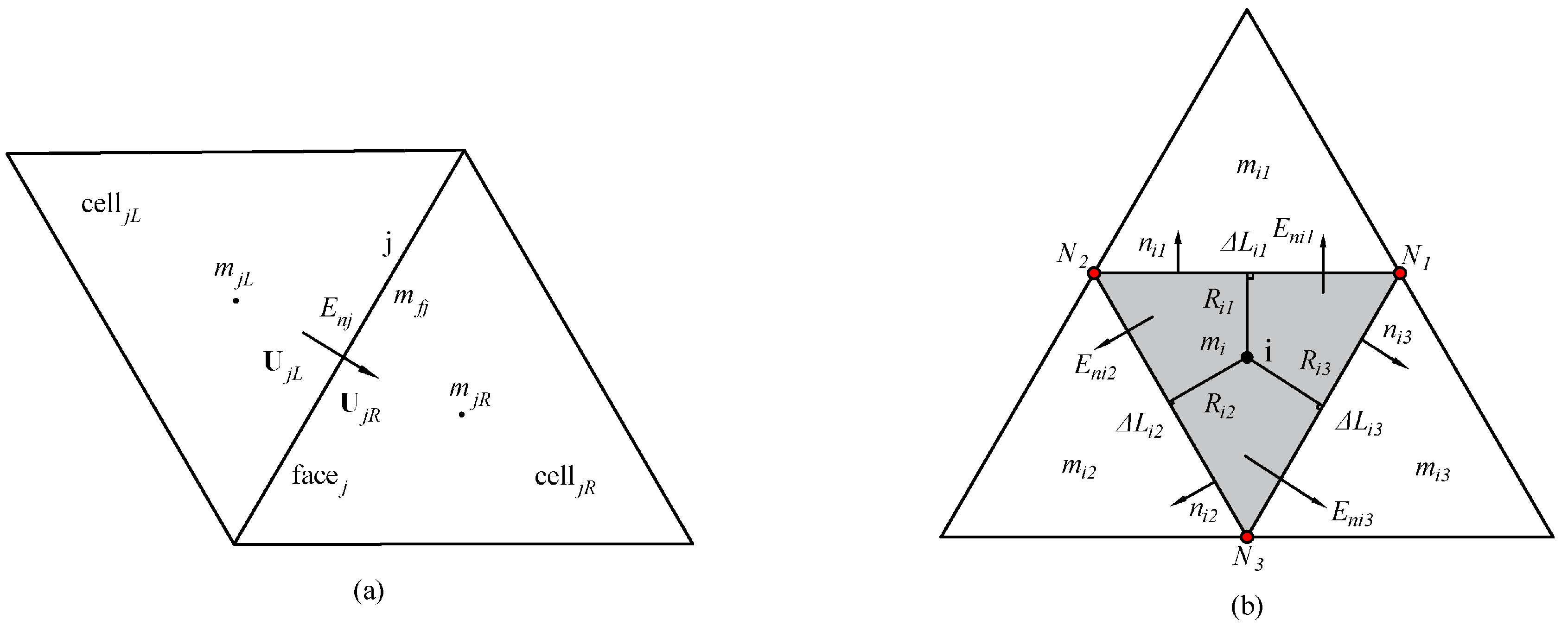
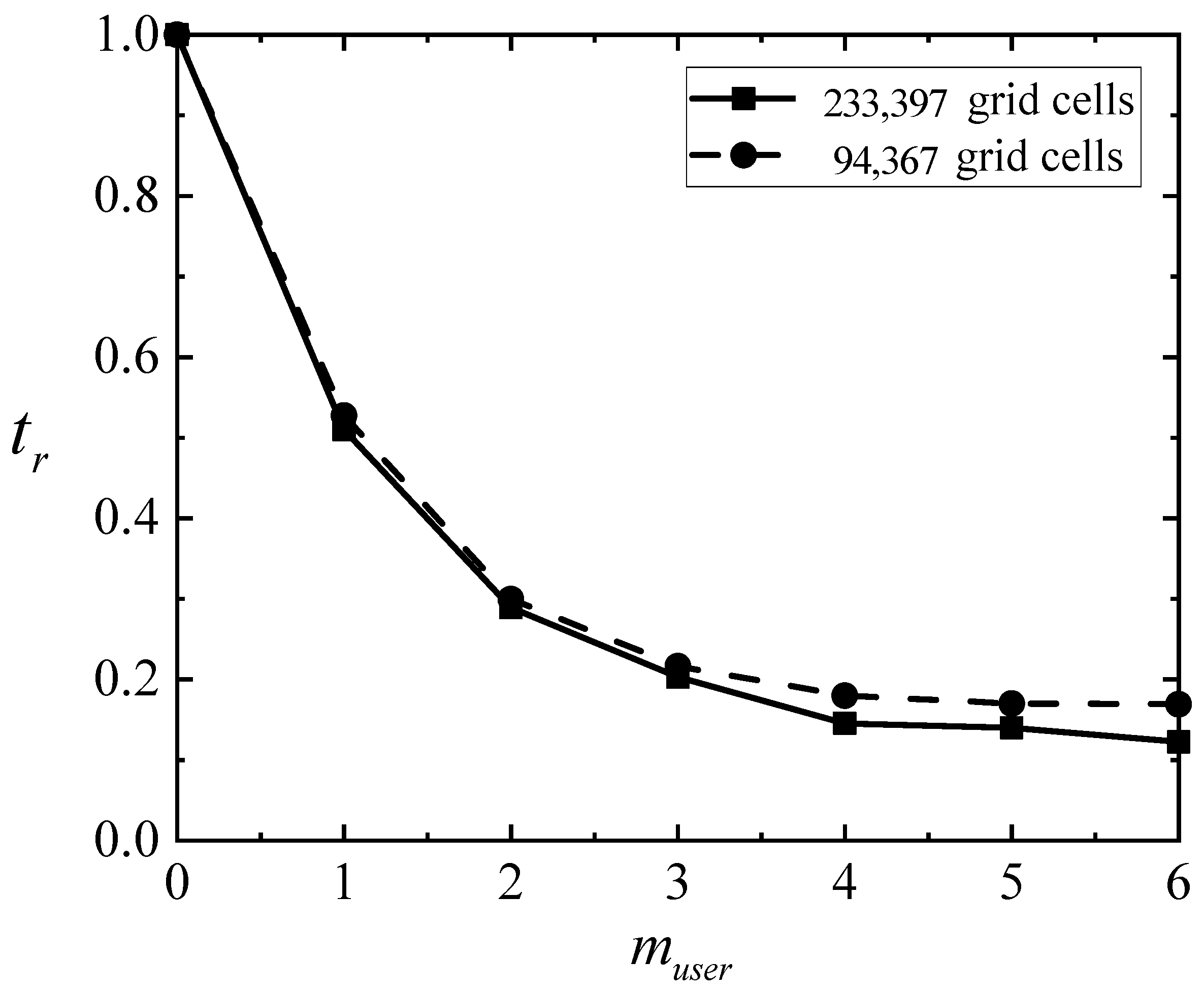

| PC Platform | Method | muser | 94,367 Grid Cells | 233,397 Grid Cells | ||
|---|---|---|---|---|---|---|
| Time/s | tr | Time/s | tr | |||
| PC: GTX 1660 | GPU | 0 | 53.353 | 1.00 | 574.481 | 1.00 |
| GPU + LTS | 1 | 28.143 | 0.53 | 292.986 | 0.51 | |
| 2 | 15.991 | 0.30 | 166.113 | 0.29 | ||
| 3 | 11.549 | 0.22 | 116.608 | 0.20 | ||
| 4 | 9.597 | 0.18 | 83.538 | 0.15 | ||
| 5 | 9.068 | 0.17 | 80.517 | 0.14 | ||
| 6 | 9.028 | 0.17 | 70.384 | 0.12 | ||
| Stations | Hydrodynamics | SS | RMSE | Level |
|---|---|---|---|---|
| JGJ | Water level | 0.9122 | 0.2760 m | Excellent |
| BCZ | 0.9223 | 0.2796 m | ||
| NCD | 0.9144 | 0.3714 m | ||
| ZJ | 0.8607 | 0.4033 m | ||
| ZP | 0.9239 | 0.4642 m | ||
| GP | 0.8998 | 0.5314 m | ||
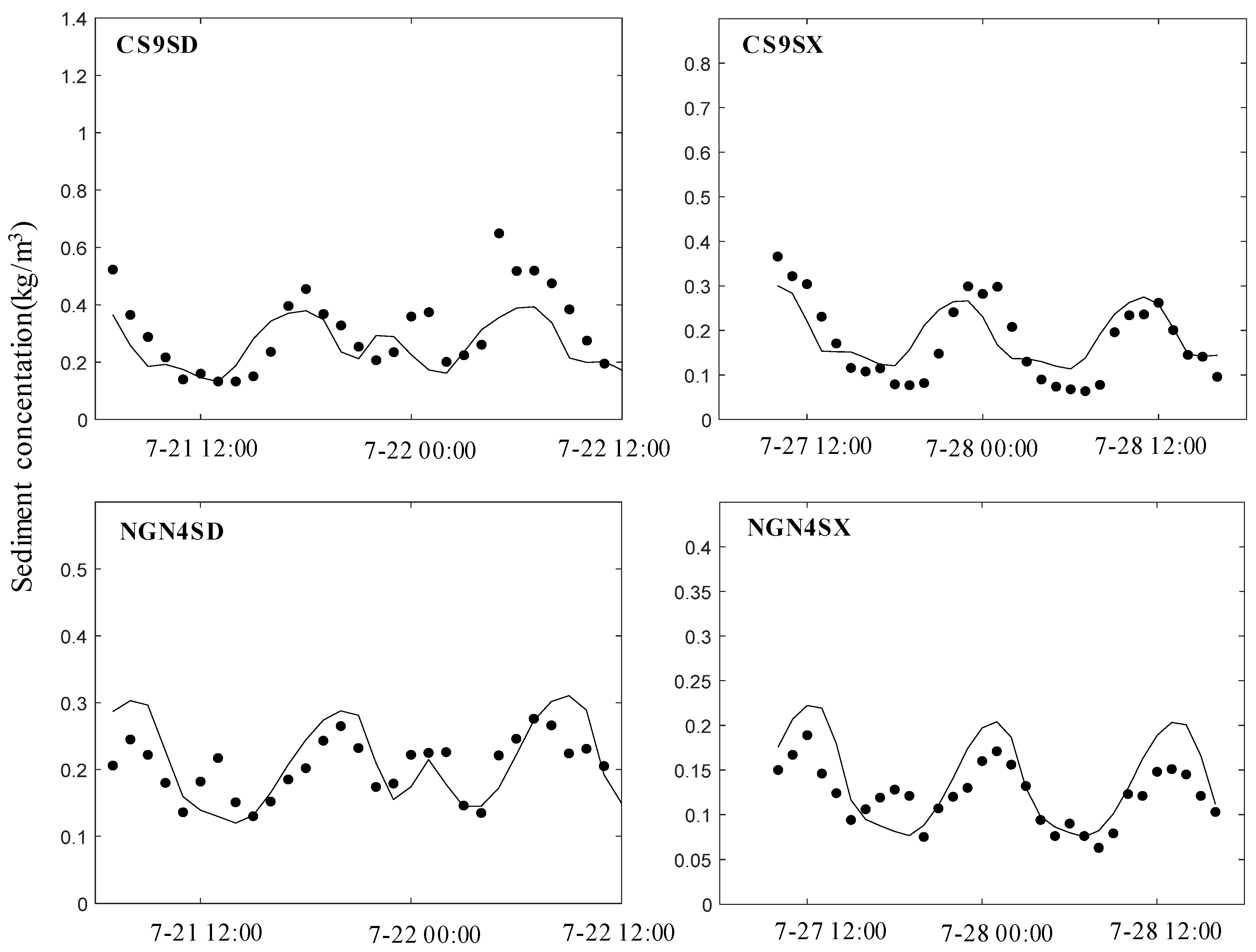
| CS9SD | Tidal current velocity | 0.7934 | 0.2940 m/s | |
| NCH6D | 0.8265 | 0.2097 m/s | ||
| NGN4SD | 0.8198 | 0.1667 m/s | ||
| CS9SX | 0.8793 | 0.1983 m/s | ||
| NCH6X | 0.7718 | 0.1778 m/s | ||
| NGN4SX | 0.7469 | 0.1748 m/s | ||
| CS9SD | Tidal current direction | 0.8525 | 34° | |
| NCH6D | 0.8609 | 31° | ||
| NGN4SD | 0.7720 | 36° | ||
| CS9SX | 0.9817 | 11° | ||
| NCH6X | 0.8161 | 38° | ||
| NGN4SX | 0.8695 | 26° |
| Case | Model | Boundary 1 (m3/s) | Boundary 2 (m3/s) | Boundary 3 | Coriolis | Topography |
|---|---|---|---|---|---|---|
| 1 | Actual model | Measured flow process | 1000 | TPXO modeling process for calculating tide levels | With (actual) | Actual Topography |
| 2 | Without | |||||
| 3 | Idealized generalized model | 10,000 | 3 m | Without | Symmetrical Topography | |
| 4 | 30° N | |||||
| 5 | 60° N | |||||
| 6 | 85° N | |||||
| 7 | 30° S | |||||
| 8 | 60° S | |||||
| 9 | 85° S | |||||
| 10 | 30,000 | 30° N | ||||
| 11 | 60,000 | |||||
| 12 | 80,000 | |||||
| 13 | 29,300 | 950 | ||||
| 14 | Asymmetrical Topography | |||||
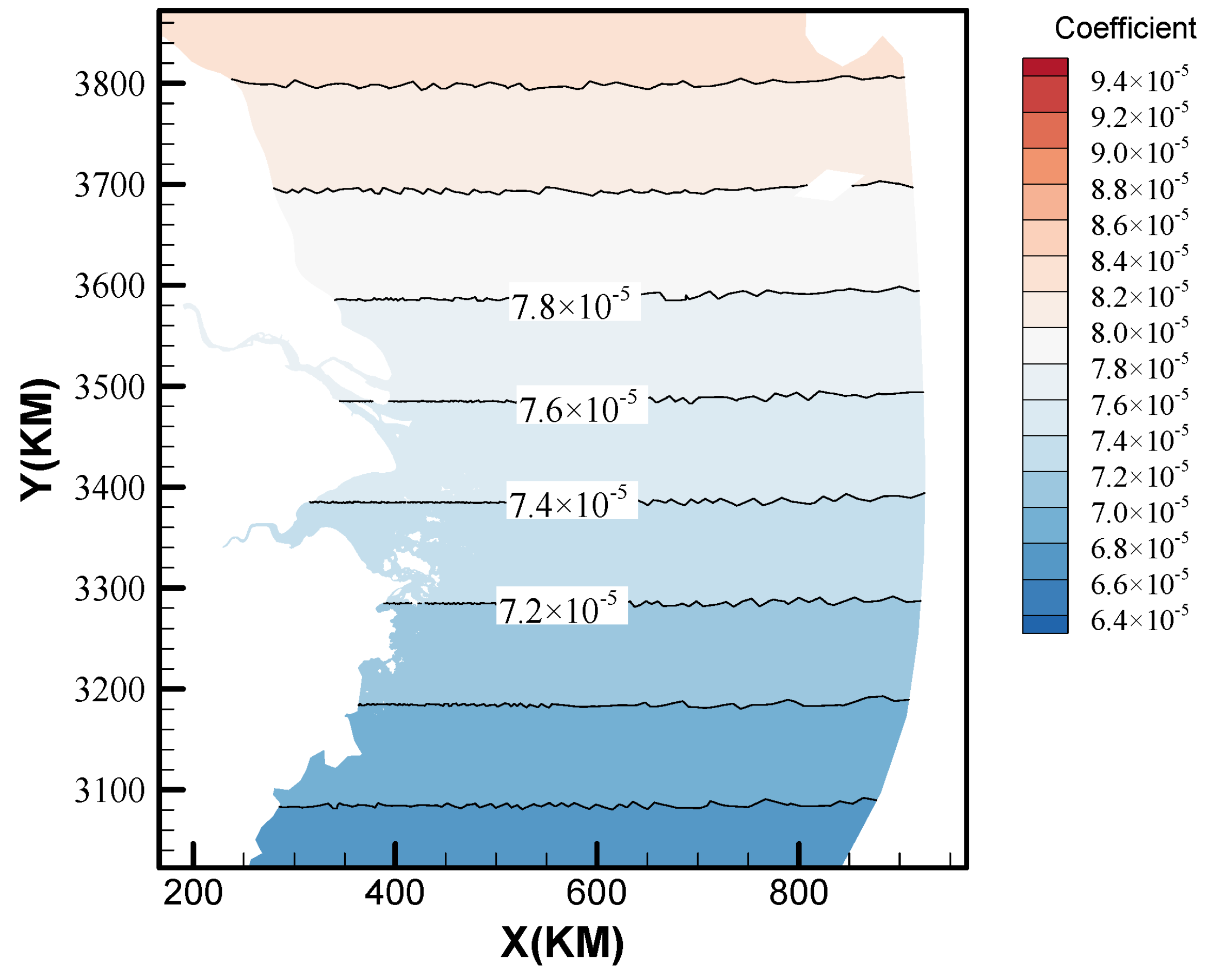
| Station | Longitude | Coefficient of Force |
|---|---|---|
| ZJ | 31.0895 | 0.0000751038 |
| LCG | 30.8181 | 0.0000745131 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Hu, P.; Zhao, Z.; Tao, J.; Ji, A.; Feng, Z.; Dai, L. A Numerical Study on the Effect of the Coriolis Force on the Sediment Exchange Between the Yangtze River Estuary and Hangzhou Bay. Water 2025, 17, 1011. https://doi.org/10.3390/w17071011
Tang J, Hu P, Zhao Z, Tao J, Ji A, Feng Z, Dai L. A Numerical Study on the Effect of the Coriolis Force on the Sediment Exchange Between the Yangtze River Estuary and Hangzhou Bay. Water. 2025; 17(7):1011. https://doi.org/10.3390/w17071011
Chicago/Turabian StyleTang, Jia, Peng Hu, Zixiong Zhao, Junyu Tao, Aofei Ji, Zihao Feng, and Linwei Dai. 2025. "A Numerical Study on the Effect of the Coriolis Force on the Sediment Exchange Between the Yangtze River Estuary and Hangzhou Bay" Water 17, no. 7: 1011. https://doi.org/10.3390/w17071011
APA StyleTang, J., Hu, P., Zhao, Z., Tao, J., Ji, A., Feng, Z., & Dai, L. (2025). A Numerical Study on the Effect of the Coriolis Force on the Sediment Exchange Between the Yangtze River Estuary and Hangzhou Bay. Water, 17(7), 1011. https://doi.org/10.3390/w17071011






