Reliability Performance Indices for Planning and Operational Evaluation of Main Tanks in Water Distribution Networks
Abstract
1. Introduction
2. Literature Review
2.1. Water Distribution System
2.2. Tanks in Water Distribution Networks
2.3. Optimization of Water Distribution Systems
2.4. Behaviour Simulation (BS)
2.5. Summary of the Literature Review
3. Methodology
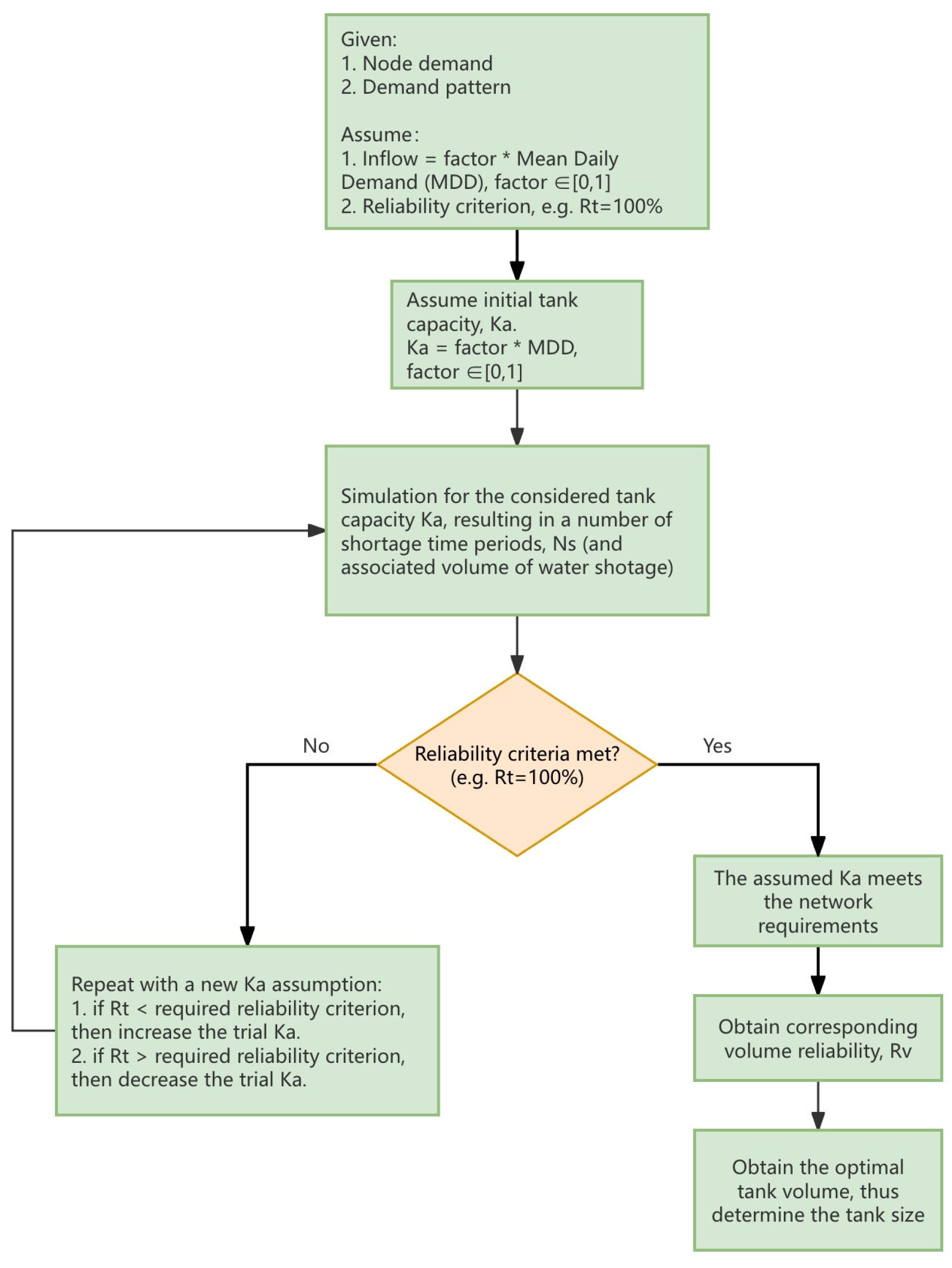
3.1. Behaviour Simulation
- Insufficient water is available to the system, i.e., Wt < Dt;
- 2.
- Sufficient water is available, and the tank is not filled, i.e., Dt ≤ Wt < Dt + Ka.
- 3.
- Sufficient water is available, and the tank is full, i.e., Wt ≥ Dt + Ka.
3.2. Vulnerability
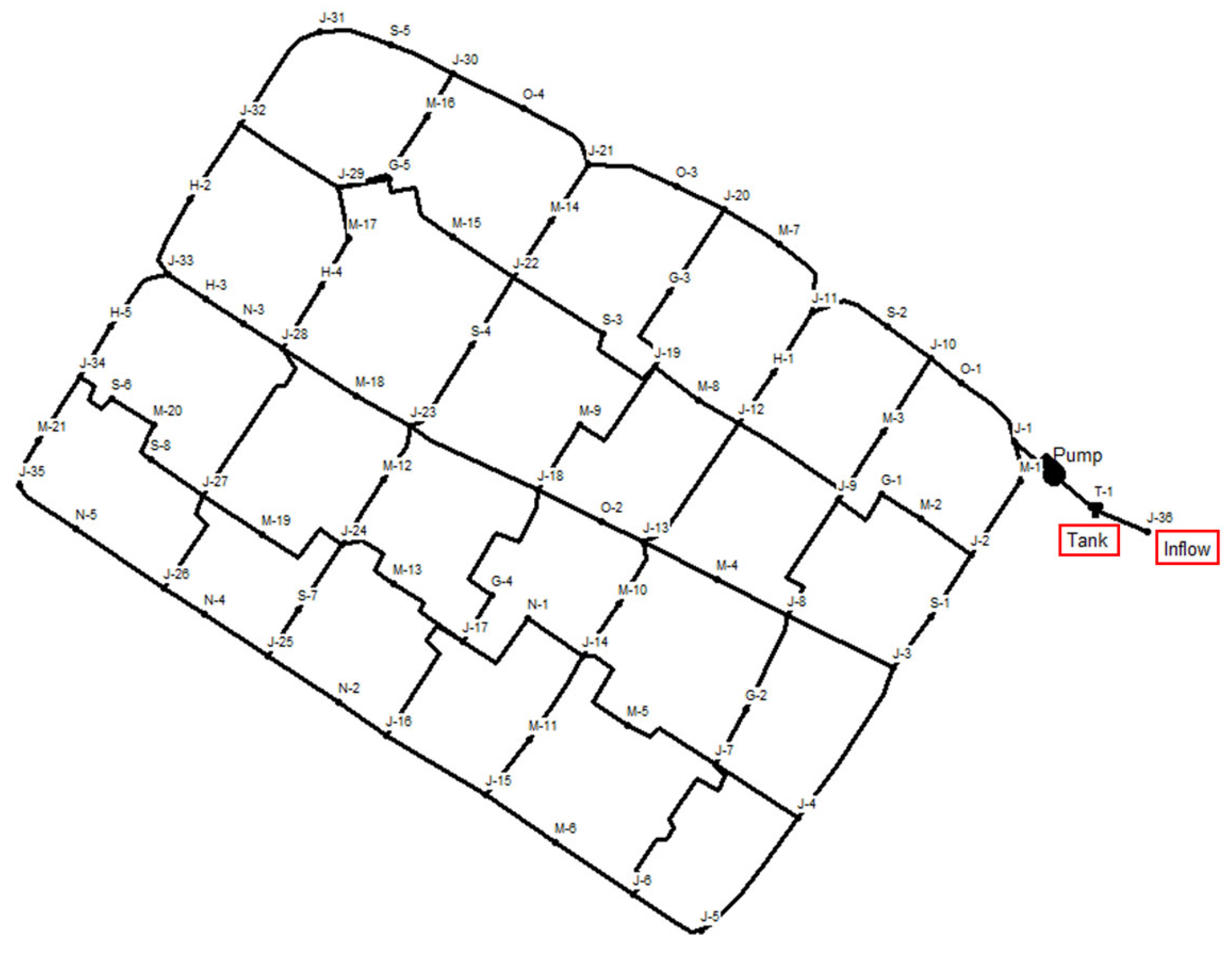
4. Case Study
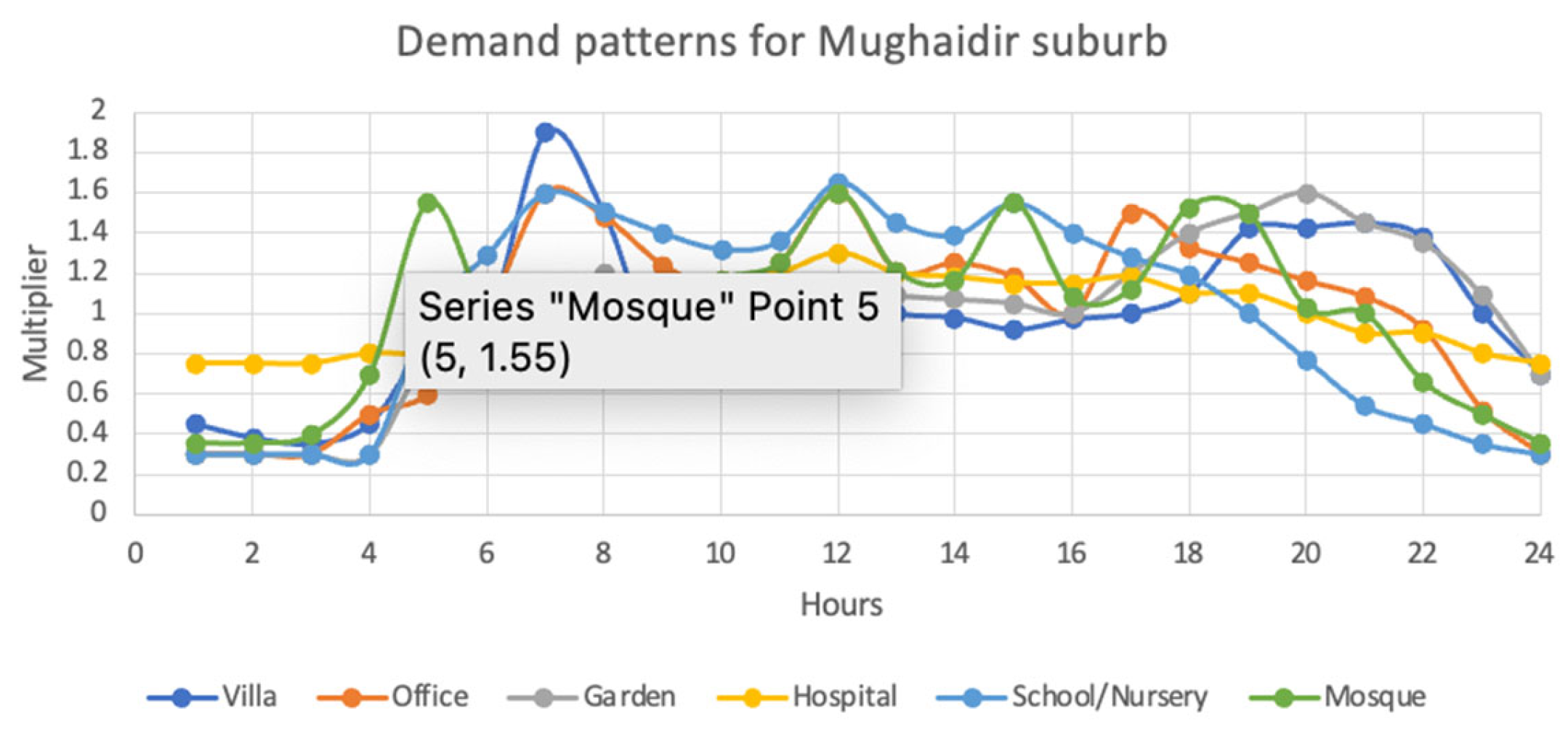
4.1. Case Study #1: Sharjah Mughaidir Suburb
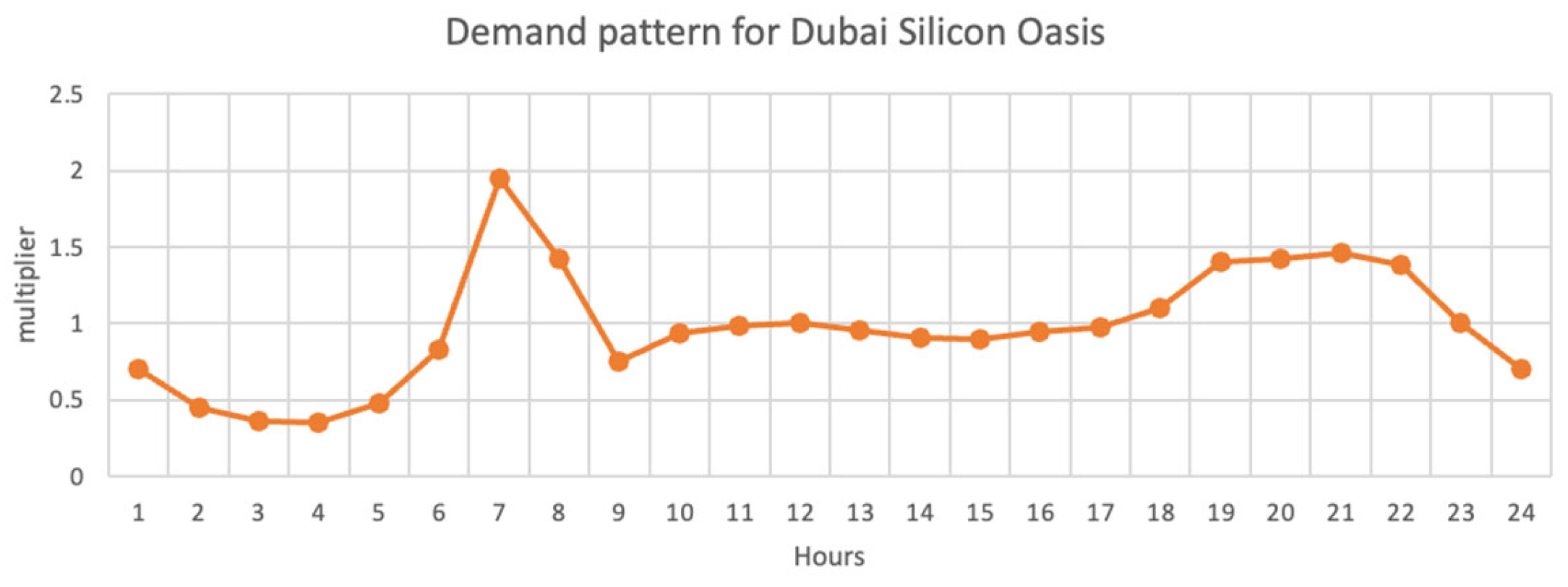
4.2. Case Study #2: Dubai Silicon Oasis
4.3. Extended Period Simulation (EPS)
4.4. Modelling
- Step 1: Network preparation:
- Step 2: Grading of inflow and Ka:For a clearer comparison of the design options, the inflow and Ka are graded on a 10% gradient. The specific grading is as follows:
- Inflow is defined as
- Tank capacity (Ka) is defined as
- Step 3: Implementation of BS:
- Step 4: Reliability calculations:
- Step 5: Simulation in EPANET:
- Step 6: Comparison and analysis of results
5. Results and Discussion
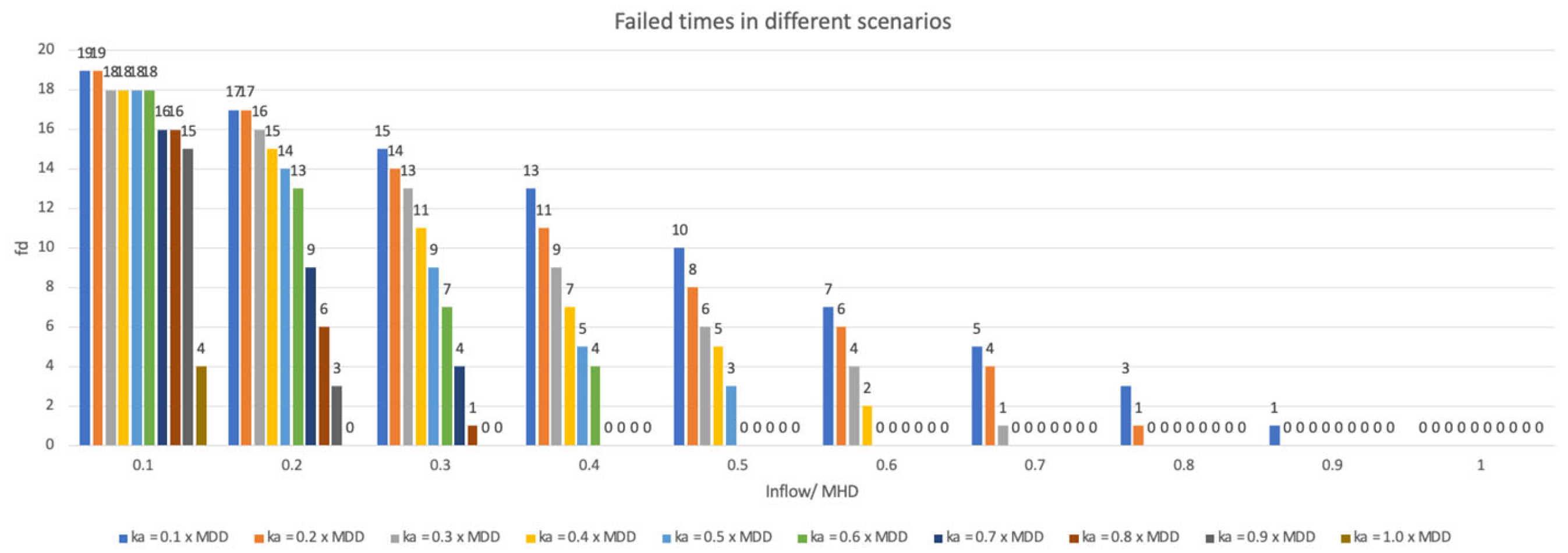
5.1. Network Failure
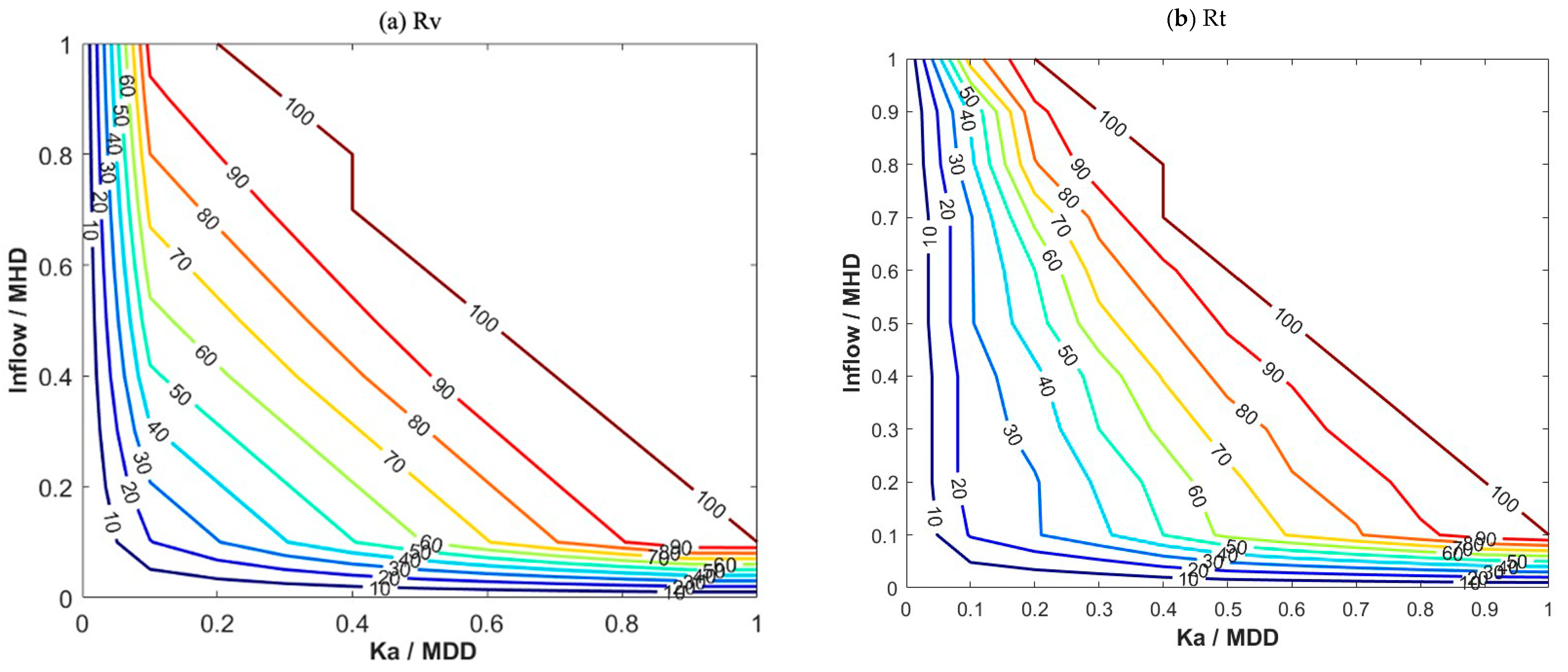
5.2. System Reliability
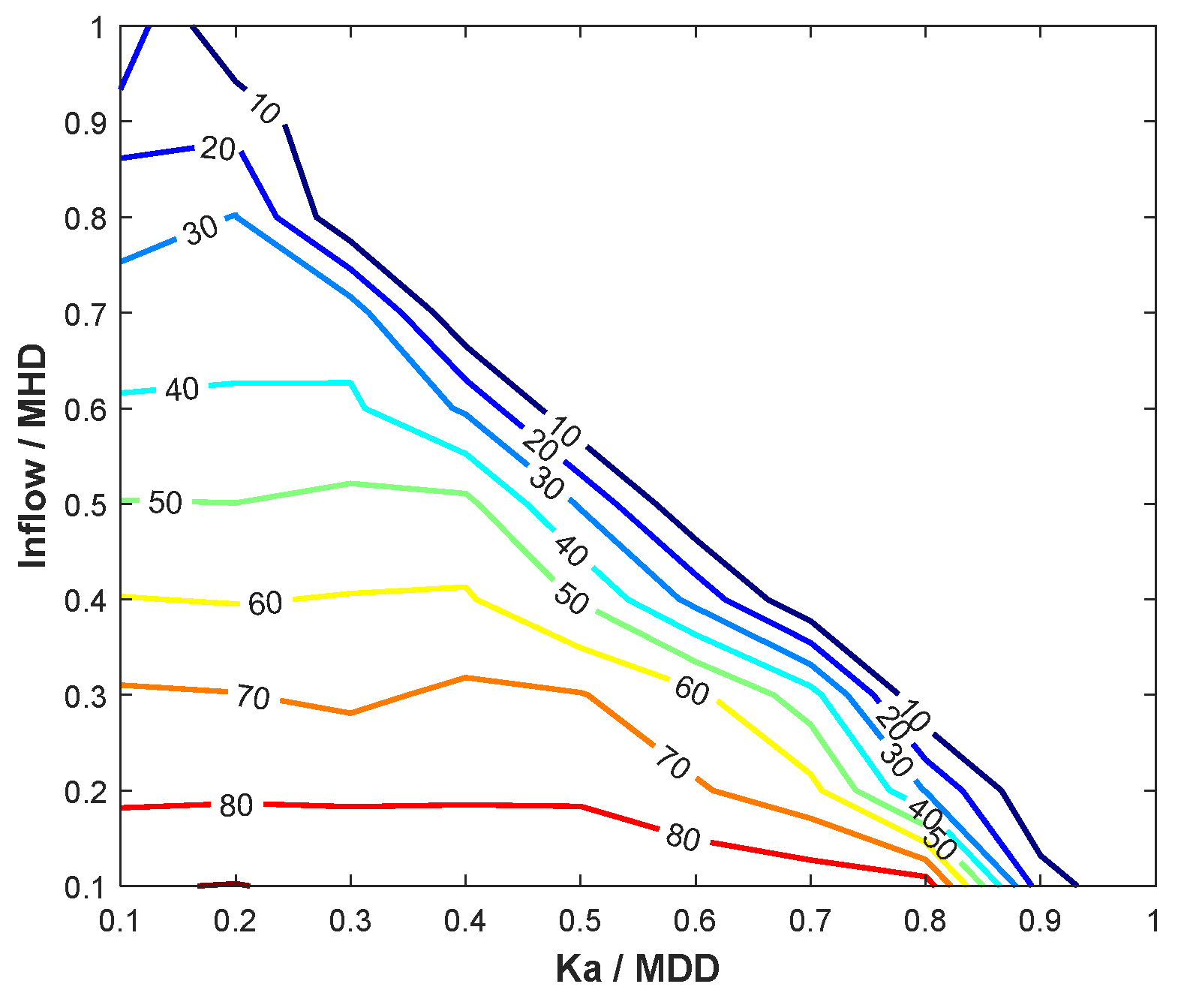
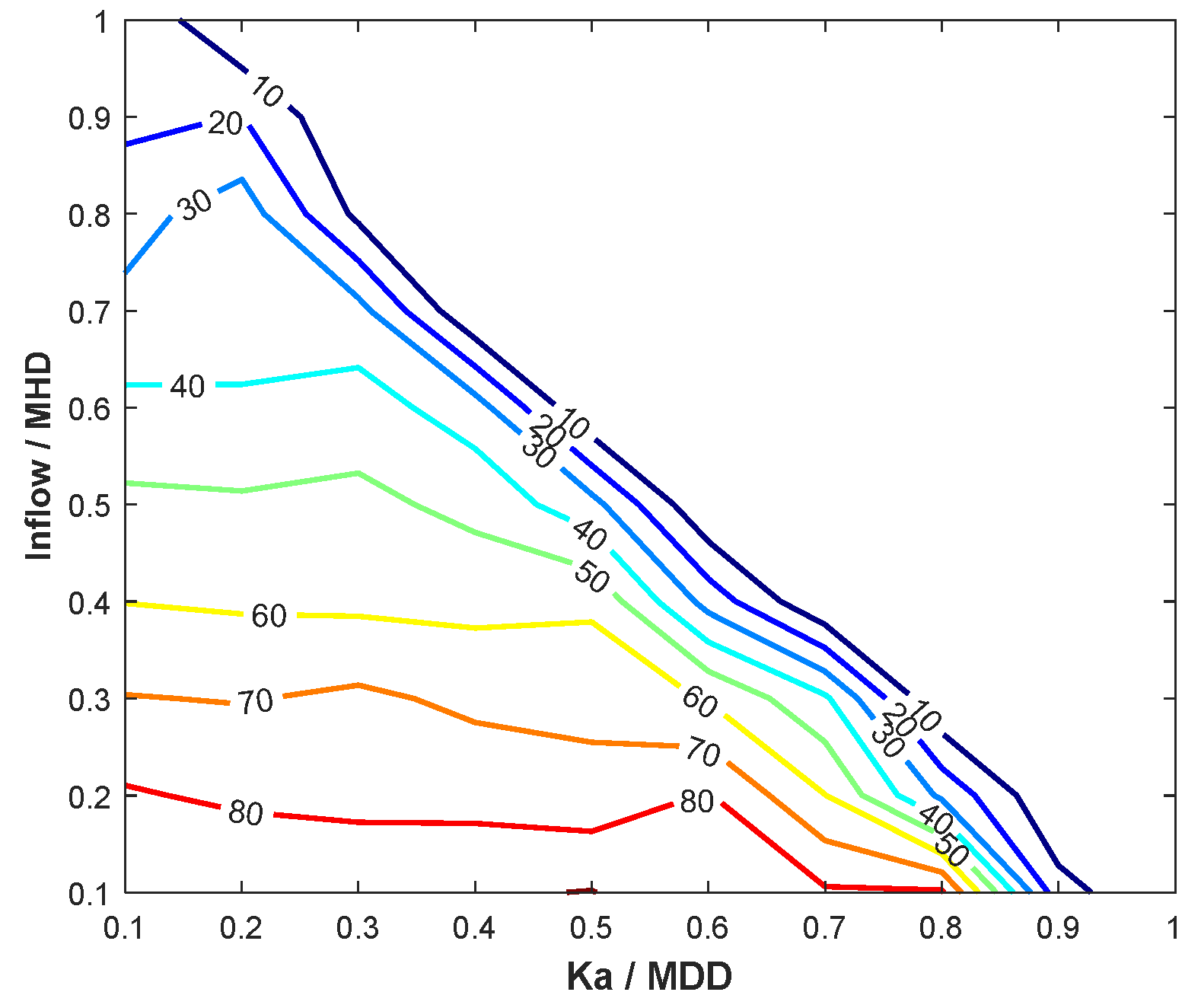
5.3. Vulnerability Assessment
5.4. EPANET Modelling Result Comparison
5.5. Comparison with the Literature
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- van Zyl, J.E.; Piller, O.; le Gat, Y. Sizing Municipal Storage Tanks Based on Reliability Criteria. J. Water Resour. Plan. Manag. 2008, 134, 548–555. [Google Scholar] [CrossRef]
- Gupta, A.D.; Bokde, N.; Marathe, D.; Kulat, K. Optimization techniques for leakage management in urban water distribution networks. Water Sci. Technol. Water Supply 2017, 17, 1638–1652. [Google Scholar] [CrossRef]
- Zhang, J. Approaches for estimating mixing time in a water storage tank. Water Sci. Technol. Water Supply 2022, 22, 3769–3783. [Google Scholar] [CrossRef]
- Batchabani, E.; Fuamba, M. Optimal Tank Design in Water Distribution Networks: Review of Literature and Perspectives. J. Water Resour. Plan. Manag. 2014, 140, 136–145. [Google Scholar] [CrossRef]
- Abrha, B.; Ostfeld, A. Analytical Solutions to Conservative and Non-Conservative Water Quality Constituents in Water Distribution System Storage Tanks. Water 2021, 13, 3502. [Google Scholar] [CrossRef]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Sherali, H.D.; Totlani, R.; Loganathan, G.V. Enhanced lower bounds for the global optimization of water distribution networks. Water Resour. Res. 1998, 34, 1831–1841. [Google Scholar] [CrossRef]
- Puleo, V.; Morley, M.; Freni, G.; Savić, D. Multi-stage linear programming optimization for pump scheduling. Procedia Eng. 2014, 70, 1378–1385. [Google Scholar] [CrossRef]
- Fujiwara, O.; Khang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Pandey, S.; Singh, R.P.; Mahar, P.S. Optimal Pipe Sizing and Operation of Multistage Centrifugal Pumps for Water Supply. J. Pipeline Syst. 2020, 11, 4020007. [Google Scholar] [CrossRef]
- Maskit, M.; Ostfeld, A. Multi-Objective Operation-Leakage Optimization and Calibration of Water Distribution Systems. Water 2021, 13, 1606. [Google Scholar] [CrossRef]
- Murphy, L.J.; Dandy, G.C.; Simpson, A.R. (Eds.) Optimum design and operation of pumped water distribution systems. In Proceedings of the National Conference Publication-Institution of Engineers Australia NCP, Melbourne, Australia, 13–16 April 1994; p. 149. [Google Scholar]
- Prasad, T.D. Design of Pumped Water Distribution Networks with Storage. J. Water Resour. Plan. Manag. 2010, 136, 129–132. [Google Scholar] [CrossRef]
- Luna, T.; Ribau, J.; Figueiredo, D.; Alves, R. Improving energy efficiency in water supply systems with pump scheduling optimization. J. Clean. Prod. 2019, 213, 342–356. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, P.; Pu, Y.; Lei, H.; Zheng, X. Unit Operation Combination and Flow Distribution Scheme of Water Pump Station System Based on Genetic Algorithm. Appl. Sci. 2023, 13, 11869. [Google Scholar] [CrossRef]
- Ostfeld, A.; Tubaltzev, A. Ant Colony Optimization for Least-Cost Design and Operation of Pumping Water Distribution Systems. J. Water Resour. Plan. Manag. 2008, 134, 107–118. [Google Scholar] [CrossRef]
- Hajibandeh, E.; Nazif, S. Pressure Zoning Approach for Leak Detection in Water Distribution Systems Based on a Multi Objective Ant Colony Optimization. Water Resour. Manag. 2018, 32, 2287–2300. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mansoori, B.; Aghamajidi, R. Optimization of chlorine consumption in water distribution networks by using the new ant colony optimization (ACOR) algorithm. Int. J. Environ. Sci. Technol. 2024, 22, 3199–3212. [Google Scholar] [CrossRef]
- Wegley, C.; Eusuff, M.; Lansey, K. Determining pump operations using particle swarm optimization. In Building Partnerships; American Society of Civil Engineers: Reston, VA, USA, 2000; pp. 1–6. [Google Scholar]
- Sheikholeslami, R.; Talatahari, S. Developed Swarm Optimizer: A New Method for Sizing Optimization of Water Distribution Systems. J. Comput. Civ. Eng. 2016, 30, 04016005. [Google Scholar] [CrossRef]
- Jafari-Asl, J.; Sami Kashkooli, B.; Bahrami, M. Using particle swarm optimization algorithm to optimally locating and controlling of pressure reducing valves for leakage minimization in water distribution systems. Sustain. Water Resour. Manag. 2020, 6, 64. [Google Scholar] [CrossRef]
- Adeloye, A.J.; Soundharajan, B.-S.; Mohammed, S. Harmonisation of Reliability Performance Indices for Planning and Operational Evaluation of Water Supply Reservoirs. Water Resour. Manag. 2017, 31, 1013–1029. [Google Scholar] [CrossRef]
- Adeloye, A.J.; Dau, Q.V. Hedging as an adaptive measure for climate change induced water shortage at the Pong reservoir in the Indus Basin Beas River, India. Sci. Total Environ. 2019, 687, 554–566. [Google Scholar] [CrossRef] [PubMed]
- Anirbid, S.; Kriti, Y.; Kamakshi, R.; Namrata, B.; Hemangi, O. Application of machine learning and artificial intelligence in oil and gas industry. Pet. Res. 2021, 6, 379–391. [Google Scholar]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water Distribution Reliability: Simulation Methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef]
- McMahon, T.A.; Adeloye, A.J. Water Resources Yield; McMahon, T.A., Adeloye, A.J., Eds.; Water Resources Publication: Littleton, CO, USA, 2005. [Google Scholar]
- Adeloye, A. Hydrological sizing of water supply reservoirs. In Encyclopedia of Lakes and Reservoirs; Bengtsson, L., Herschy, R.W., Fairbridge, R.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 346–355. [Google Scholar]
- Perelman, L.; Ostfeld, A. Topological clustering for water distribution systems analysis. Environ. Model. Softw. Environ. Data News 2011, 26, 969–972. [Google Scholar] [CrossRef]
- Steinebach, G.; Rosen, R.; Sohr, A.; Morsi, A.; Oberlack, M.; Klamroth, K.; Leugering, G.; Lang, J.; Martin, A.; Ostrowski, M. Modeling and Numerical Simulation of Pipe Flow Problems in Water Supply Systems. In Mathematical Optimization of Water Networks; Birkhäuser: Basel, Switzerland, 2012; pp. 3–15. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, K.; Bharanidharan, B.; Matial, N.; Dey, E.; Singh, M.; Thakur, V.; Sharma, S.; Malhotra, N. Design of water distribution system using EPANET. Int. J. Adv. Res. 2015, 3, 789–812. [Google Scholar]
- Hooda, N.; Damani, O. JalTantra: A System for the Design and Optimization of Rural Piped Water Networks. INFORMS J. Appl. Anal. 2019, 49, 447–458. [Google Scholar] [CrossRef]
- Marlim, M.S.; Jeong, G.; Kang, D. Identification of critical pipes using a criticality index in water distribution networks. Appl. Sci. 2019, 9, 4052. [Google Scholar] [CrossRef]
- Albarakati, A.; Tassaddiq, A.; Srivastava, R. Assessment of the Water Distribution Networks in the Kingdom of Saudi Arabia: A Mathematical Model. Axioms 2023, 12, 1055. [Google Scholar] [CrossRef]
- Janzen, J.G.; Freire, I.L. Evaluation of Disinfection Cost for Different Flow Regimes in Water Storage Tanks. J. Water Resour. Plan. Manag. 2021, 147, 06021004. [Google Scholar] [CrossRef]
- Pinheiro, A.; Monteiro, L.; Carneiro, J.; do Céu Almeida, M.; Covas, D. Water Mixing and Renewal in Circular Cross-Section Storage Tanks as Influenced by Configuration and Operational Conditions. J. Hydraul. Eng. 2021, 147, 04021050. [Google Scholar] [CrossRef]
- Ortega-Ballesteros, A.; Muñoz-Rodríguez, D.; Perea-Moreno, A.-J. Advances in Leakage Control and Energy Consumption Optimization in Drinking Water Distribution Networks. Energies 2022, 15, 5484. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system operation. Environ. Model. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef]
- Muwini, R.; Mulayi, S.A.M. Simulation-optimization model for design of water distribution system using ant based algorithms. J. Eng. Res. (Print) 2018, 15, 42–60. [Google Scholar] [CrossRef]
- Sulianto; Setiono, E.; Yasa, I.W. Optimization model the pipe diameter in the drinking water distribution network using multi-objective genetic algorithm. J. Water Land Dev. 2021, 48, 55–64. [Google Scholar] [CrossRef]
- Sulianto, S.; Darmawan, A.A.; Andardi, F.R.; Sumadi, F.D.S.; Rahmandhika, A.; Setyawan, N.; Utama, D.M.; Rahim, R. Optimization model of pipe diameter in drinking water distribution network using a combination of the Newton Raphson method and the Codeq algorithm. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2024; Volume 2927. [Google Scholar] [CrossRef]
- Carpitella, S.; Brentan, B.; Montalvo, I.; Izquierdo, J.; Certa, A. Multi-criteria analysis applied to multi-objective optimal pump scheduling in water systems. Water Sci. Technol. Water Supply 2019, 19, 2338–2346. [Google Scholar] [CrossRef]
- Martin-Candilejo, A.; Santillán, D.; Garrote, L. Pump Efficiency Analysis for Proper Energy Assessment in Optimization of Water Supply Systems. Water 2020, 12, 132. [Google Scholar] [CrossRef]
- Hajgató, G.; Paál, G.; Gyires-Tóth, B. Deep Reinforcement Learning for Real-Time Optimization of Pumps in Water Distribution Systems. J. Water Resour. Plan. Manag. 2020, 146, 04020079. [Google Scholar] [CrossRef]
- Shao, Y.; Zhou, X.; Yu, T.; Zhang, T.; Chu, S. Pump scheduling optimization in water distribution system based on mixed integer linear programming. Eur. J. Oper. Res. 2024, 313, 1140–1151. [Google Scholar] [CrossRef]
- Farmani, R.; Savic, D.; Walters, G. The Simultaneous Multi-Objective Optimization of Anytown Pipe Rehabilitation, Tank Sizing, Tank Siting, and Pump Operation Schedules; American Society of Civil Engineers: Reston, VA, USA, 2004; pp. 1–10. [Google Scholar]
- Basile, N.; Fuamba, M.; Barbeau, B. Optimization of Water Tank Design and Location in Water Distribution Systems. In Water Distribution Systems Analysis 2008; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 1–13. [Google Scholar]
- Miller-Moran, D.; Trifunović, N.; Kennedy, M.; Kapelan, Z. Optimisation of pumping and storage design through iterative hydraulic adjustment for minimum energy consumption. Urban Water J. 2024, 21, 113–130. [Google Scholar] [CrossRef]
- Walski, T.M.; Chase, D.V.; Savic, D.A.; Grayman, W.; Beckwith, S.; Koelle, E. (Eds.) Advanced Water Distribution Modeling and Management; Haestad Press: Waterbury, CT, USA, 2003. [Google Scholar]
- Bai, Y.; Bai, Q. Subsea Engineering Handbook; Gulf Professional Publishing: Houston, TX, USA, 2018. [Google Scholar] [CrossRef]
- Ting, D. Thermofluids: From Nature to Engineering; Academic Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Curtin, B. Optimizing Storage Tank Design for Efficient Potable Water Supply; Worcester Polytechnic Institute: Worcester, MA, USA, 2024. [Google Scholar]
- Ajitha, T.; Viji, R. Site suitability analysis of water tank in Athivilai village of India using an analytical hierarchy process and a geographical information system. Water Supply 2023, 23, 3805–3818. [Google Scholar] [CrossRef]
- Urrea, C.; Páez, F. Design and Comparison of Strategies for Level Control in a Nonlinear Tank. Processes 2021, 9, 735. [Google Scholar] [CrossRef]
- Rizvi, S.A.H. Studying the Effects of Integrating Private Water Tanks on the Performance of Water Distribution Networks. Ph.D. Thesis, Heriot-Watt University, Dubai, United Arab Emirates, 2024. [Google Scholar]
- Clark, R.M.; Abdesaken, F.; Boulos, P.F.; Mau, R.E. Mixing in Distribution System Storage Tanks: Its Effect on Water Quality. J. Environ. Eng. 1996, 122, 814–821. [Google Scholar] [CrossRef]
- Trifunovic, N.; Abunada, M.; Babel, M.; Kennedy, M. The role of balancing tanks in optimal design of water distribution networks. J. Water Supply Res. Technol.—AQUA 2015, 64, 610–628. [Google Scholar] [CrossRef]
- Government of ABU Dhabi. The Water Distribution Code; Government of ABU Dhabi: ABU Dhabi, United Arab Emirates, 2018. Available online: https://jawdah.qcc.abudhabi.ae/en/Registration/QCCServices/Services/STD/ISGL/ISGL-LIST/WA-710.pdf (accessed on 20 November 2024).
- Brière, F.G. Drinking-Water Distribution, Sewage, and Rainfall Collection; Presses Inter Polytechnique: Paris, France, 2014. [Google Scholar]
- Sayl, K.N.; Muhammad, N.S.; El-Shafie, A. Optimization of area–volume–elevation curve using GIS–SRTM method for rainwater harvesting in arid areas. Environ. Earth Sci. 2017, 76, 368. [Google Scholar] [CrossRef]
- Venkatesan, V.; Balamurugan, R.; Krishnaveni, M. Establishing Water Surface Area-Storage Capacity Relationship of Small Tanks Using SRTM and GPS. Energy Procedia 2012, 16, 1167–1173. [Google Scholar] [CrossRef]
- Dourado, G.F.; Hestir, E.L.; Viers, J.H. Establishing Reservoir Surface Area-Storage Capacity Relationship Using Landsat Imagery. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 863–866. [Google Scholar] [CrossRef]
- Liu, H.; Yin, J.; Feng, L. The Dynamic Changes in the Storage of the Danjiangkou Reservoir and the Influence of the South-North Water Transfer Project. Sci. Rep. 2018, 8, 8710–8712. [Google Scholar] [CrossRef]
- Li, W.; Qin, Y.; Sun, Y.; Huang, H.; Ling, F.; Tian, L.; Ding, Y. Estimating the relationship between dam water level and surface water area for the Danjiangkou Reservoir using Landsat remote sensing images. Remote Sens. Lett. 2016, 7, 121–130. [Google Scholar] [CrossRef]
- Zhu, W.; Zhao, S.; Qiu, Z.; He, N.; Li, Y.; Zou, Z.; Yang, F. Monitoring and Analysis of Water Level–Water Storage Capacity Changes in Ngoring Lake Based on Multisource Remote Sensing Data. Water 2022, 14, 2272. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, F.; Duan, H.-F.; Zhang, Q. Multi-objective optimal design of water distribution networks accounting for transient impacts. Water Resour. Manag. 2020, 34, 1517–1534. [Google Scholar] [CrossRef]
- Sangroula, U.; Han, K.-H.; Koo, K.-M.; Gnawali, K.; Yum, K.-T. Optimization of Water Distribution Networks Using Genetic Algorithm Based SOP–WDN Program. Water 2022, 14, 851. [Google Scholar] [CrossRef]
- Singh, M.K.; Kekatos, V. Optimal Scheduling of Water Distribution Systems. IEEE Trans. Control Netw. Syst. 2020, 7, 711–723. [Google Scholar] [CrossRef]
- Dini, M.; Asadi, A. Optimal Operational Scheduling of Available Partially Closed Valves for Pressure Management in Water Distribution Networks. Water Resour. Manag. 2020, 34, 2571–2583. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in Optimisation of Water Distribution Systems? A Literature Review of System Design. Water 2018, 10, 307. [Google Scholar] [CrossRef]
- Parvaze, S.; Kumar, R.; Khan, J.N.; Al-Ansari, N.; Parvaze, S.; Vishwakarma, D.K.; Elbeltagi, A.; Kuriqi, A. Optimization of Water Distribution Systems Using Genetic Algorithms: A Review. Arch. Comput. Methods Eng. 2023, 30, 4209–4244. [Google Scholar] [CrossRef]
- Elsheikh, M.A.; Saleh, H.I.; Rashwan, I.M.; El-Samadoni, M.M. Hydraulic modelling of water supply distribution for improving its quantity and quality. Sustain. Environ. Res 2013, 23, 403–411. [Google Scholar]
- Lence, B.J.; Moosavian, N.; Daliri, H. Fuzzy Programming Approach for Multiobjective Optimization of Water Distribution Systems. J. Water Resour. Plan. Manag. 2017, 143, 04017020. [Google Scholar] [CrossRef]
- Jung, D.; Kim, J.H. Water Distribution System Design to Minimize Costs and Maximize Topological and Hydraulic Reliability. J. Water Resour. Plan. Manag. 2018, 144, 06018005. [Google Scholar] [CrossRef]
- Nair, S.S.; Neelakantan, T.R. Review of reliability indices of the water distribution system. J. Integr. Sci. Technol. 2022, 10, 120–125. [Google Scholar]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Sandoval-Solis, S.; McKinney, D.C.; Loucks, D.P. Sustainability Index for Water Resources Planning and Management. J. Water Resour. Plan. Manag. 2011, 137, 381–390. [Google Scholar] [CrossRef]
- Fujiwara, O.; Tung, H.D. Reliability improvement for water distribution networks through increasing pipe size. Water Resour. Res. 1991, 27, 1395–1402. [Google Scholar] [CrossRef]
- McMahon, T.A.; Adeloye, A.J.; Zhou, S.-L. Understanding performance measures of reservoirs. J. Hydrol. 2006, 324, 359–382. [Google Scholar] [CrossRef]
- Lifang, M. D21WA Water Supply System Analysis Water Distribution Network Design Project Report; Heriot-Watt University: Edinburgh, UK, 2022. [Google Scholar]
- Rossman, L.A. EPANET 2: Users Manual; Risk Reduction Engineering Laboratory, US Environmental Protection Agency: Cincinnati, OH, USA, 2000.
- Ramana, G.V.; Sudheer, C.V.; Rajasekhar, B. Network analysis of water distribution system in rural areas using EPANET. Procedia Eng. 2015, 119, 496–505. [Google Scholar] [CrossRef]
- da Costa, D.M. Simulation of Contaminant Concentrations in Drinking-Water Distribution Systems. Master’s Thesis, Universidade do Porto, Porto, Portugal, 2008. [Google Scholar]
- Grayman, W.M.; Rossman, L.A.; Deininger, R.A.; Smith, C.D.; Arnold, C.N.; Smith, J.F. Mixing and aging of water in distribution system storage facilities. J.—Am. Water Work. Assoc. 2004, 96, 70–80. [Google Scholar] [CrossRef]



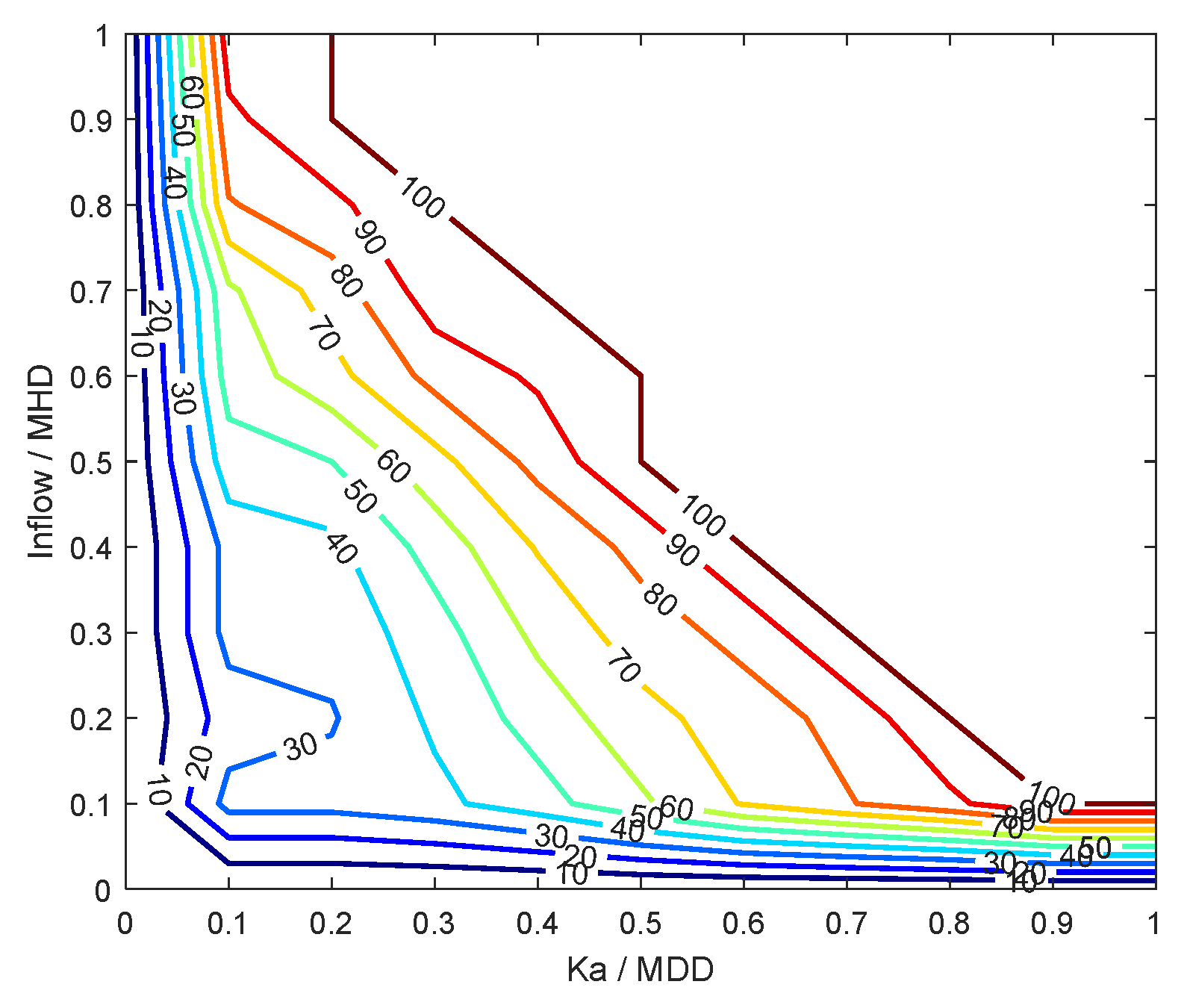
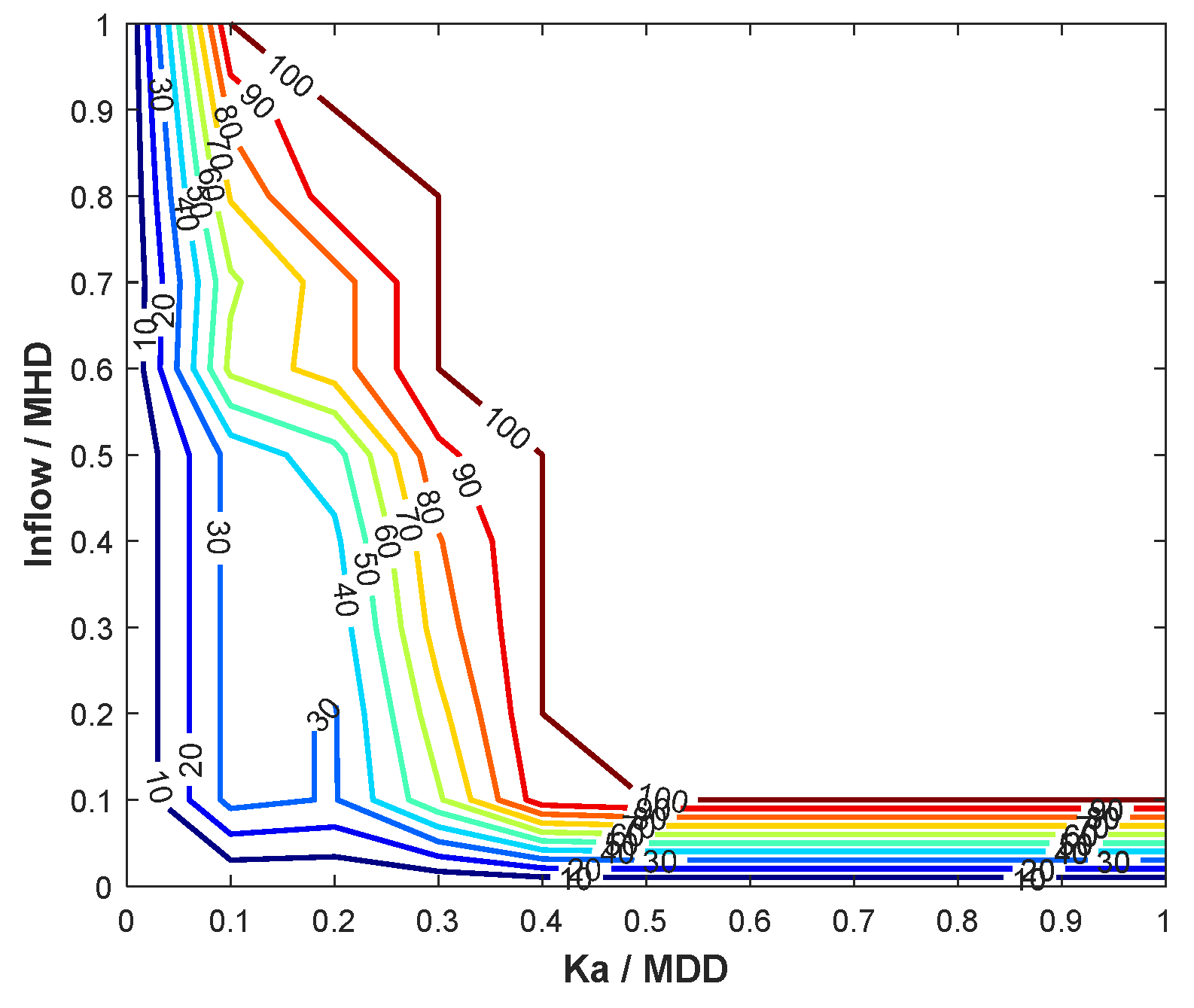
| Time (Hours) | Flow (m3/h) |
|---|---|
| 00:00 | 391.536 |
| 01:00 | 338.616 |
| 02:00 | 316.728 |
| 03:00 | 416.664 |
| 04:00 | 727.956 |
| 05:00 | 824.688 |
| 06:00 | 1557.792 |
| 07:00 | 1251.468 |
| 08:00 | 702.972 |
| 09:00 | 841.284 |
| 10:00 | 883.080 |
| 11:00 | 979.632 |
| 12:00 | 885.168 |
| 13:00 | 866.484 |
| 14:00 | 831.708 |
| 15:00 | 855.396 |
| 16:00 | 878.508 |
| 17:00 | 956.844 |
| 18:00 | 1192.968 |
| 19:00 | 1180.728 |
| 20:00 | 1182.708 |
| 21:00 | 1119.672 |
| 22:00 | 819.540 |
| 23:00 | 583.344 |
| ∑ | 20,585.484 |
| Average | 857.729 |
| Inflow/MHD | Inflow (m3/h) |
|---|---|
| 0.1 | 85.774 |
| 0.2 | 171.547 |
| 0.3 | 257.317 |
| 0.4 | 343.091 |
| 0.5 | 428.864 |
| 0.6 | 514.638 |
| 0.7 | 600.412 |
| 0.8 | 686.182 |
| 0.9 | 771.955 |
| 1 | 857.729 |
| Ka/MDD | Ka (m3) |
|---|---|
| 0.1 | 2058.548 |
| 0.2 | 4117.097 |
| 0.3 | 6175.645 |
| 0.4 | 8234.194 |
| 0.5 | 10,292.742 |
| 0.6 | 12,351.29 |
| 0.7 | 14,409.839 |
| 0.8 | 16,468.387 |
| 0.9 | 18,526.936 |
| 1 | 20,585.484 |
| Time (Hours) | Flow (m3/h) |
|---|---|
| 00:00 | 1211.328 |
| 01:00 | 778.680 |
| 02:00 | 622.944 |
| 03:00 | 605.664 |
| 04:00 | 830.628 |
| 05:00 | 1436.292 |
| 06:00 | 3374.460 |
| 07:00 | 2457.324 |
| 08:00 | 1297.836 |
| 09:00 | 1626.696 |
| 10:00 | 1695.924 |
| 11:00 | 1730.484 |
| 12:00 | 1661.256 |
| 13:00 | 1574.748 |
| 14:00 | 1557.468 |
| 15:00 | 1643.976 |
| 16:00 | 1678.536 |
| 17:00 | 1903.500 |
| 18:00 | 2422.656 |
| 19:00 | 2457.324 |
| 20:00 | 2526.552 |
| 21:00 | 2388.096 |
| 22:00 | 1730.484 |
| 23:00 | 1211.328 |
| ∑ | 40,424.184 |
| Average | 1684.341 |
| Inflow/MHD | Inflow (m3/h) |
|---|---|
| 0.1 | 168.433 |
| 0.2 | 336.870 |
| 0.3 | 505.303 |
| 0.4 | 673.736 |
| 0.5 | 842.170 |
| 0.6 | 1010.606 |
| 0.7 | 1179.040 |
| 0.8 | 1347.473 |
| 0.9 | 1515.906 |
| 1 | 1684.343 |
| Ka/MDD | Ka (m3) |
|---|---|
| 0.1 | 4042.418 |
| 0.2 | 8084.837 |
| 0.3 | 12,127.255 |
| 0.4 | 16,169.674 |
| 0.5 | 20,212.092 |
| 0.6 | 24,254.510 |
| 0.7 | 28,296.929 |
| 0.8 | 32,339.347 |
| 0.9 | 36,381.766 |
| 1 | 40,424.184 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, L.; Rustum, R.; Adeloye, A.J. Reliability Performance Indices for Planning and Operational Evaluation of Main Tanks in Water Distribution Networks. Water 2025, 17, 847. https://doi.org/10.3390/w17060847
Mo L, Rustum R, Adeloye AJ. Reliability Performance Indices for Planning and Operational Evaluation of Main Tanks in Water Distribution Networks. Water. 2025; 17(6):847. https://doi.org/10.3390/w17060847
Chicago/Turabian StyleMo, Lifang, Rabee Rustum, and Adebayo J. Adeloye. 2025. "Reliability Performance Indices for Planning and Operational Evaluation of Main Tanks in Water Distribution Networks" Water 17, no. 6: 847. https://doi.org/10.3390/w17060847
APA StyleMo, L., Rustum, R., & Adeloye, A. J. (2025). Reliability Performance Indices for Planning and Operational Evaluation of Main Tanks in Water Distribution Networks. Water, 17(6), 847. https://doi.org/10.3390/w17060847







