Reactive Transport Modeling of Uranium in Subsurface: Impact of Field-Scale Heterogeneity and Biogeochemical Dynamics
Abstract
1. Introduction
1.1. Physical and Chemical Heterogeneity
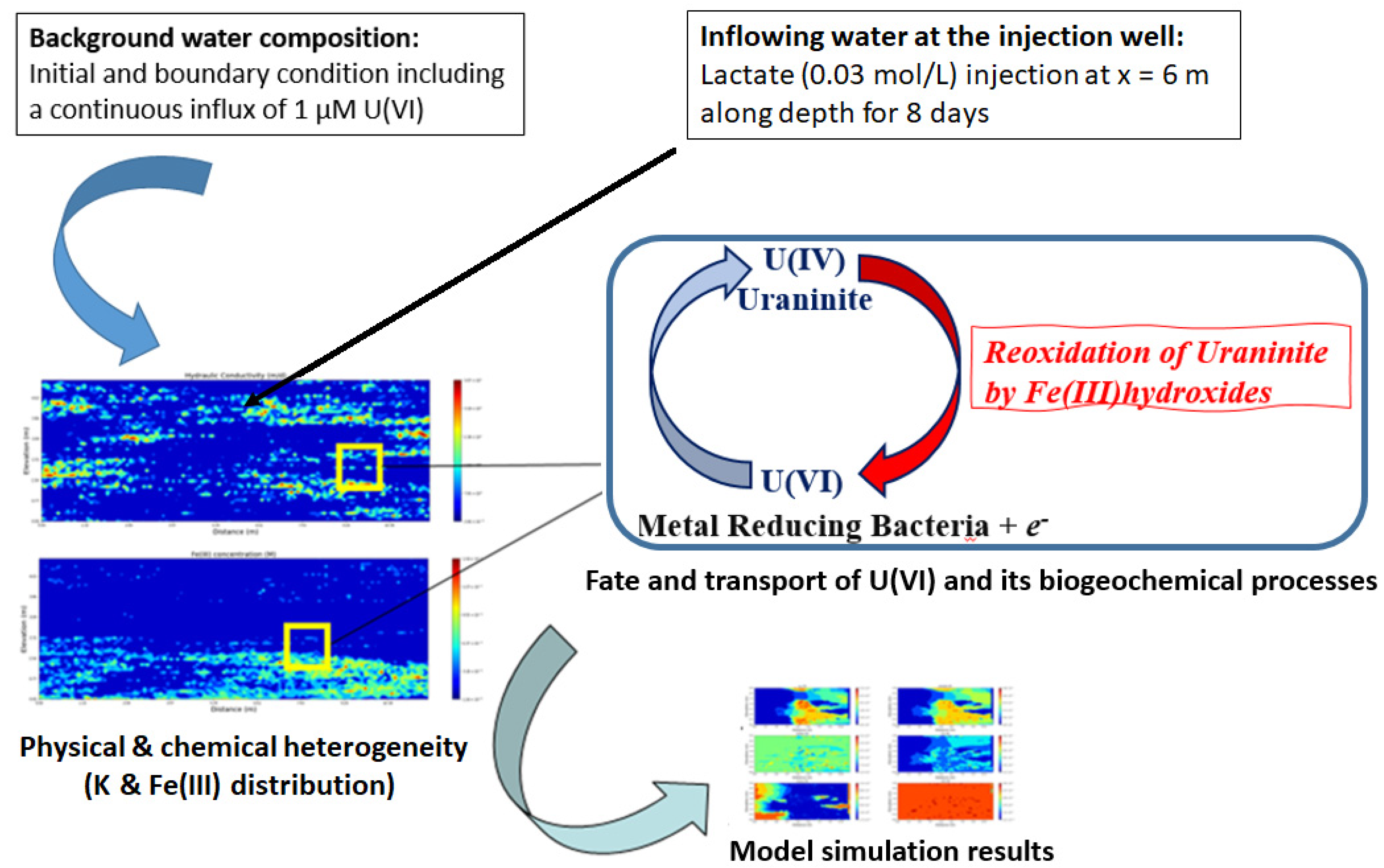
1.2. Biogeochemical Processes and Reoxidation: An Example of Uranium
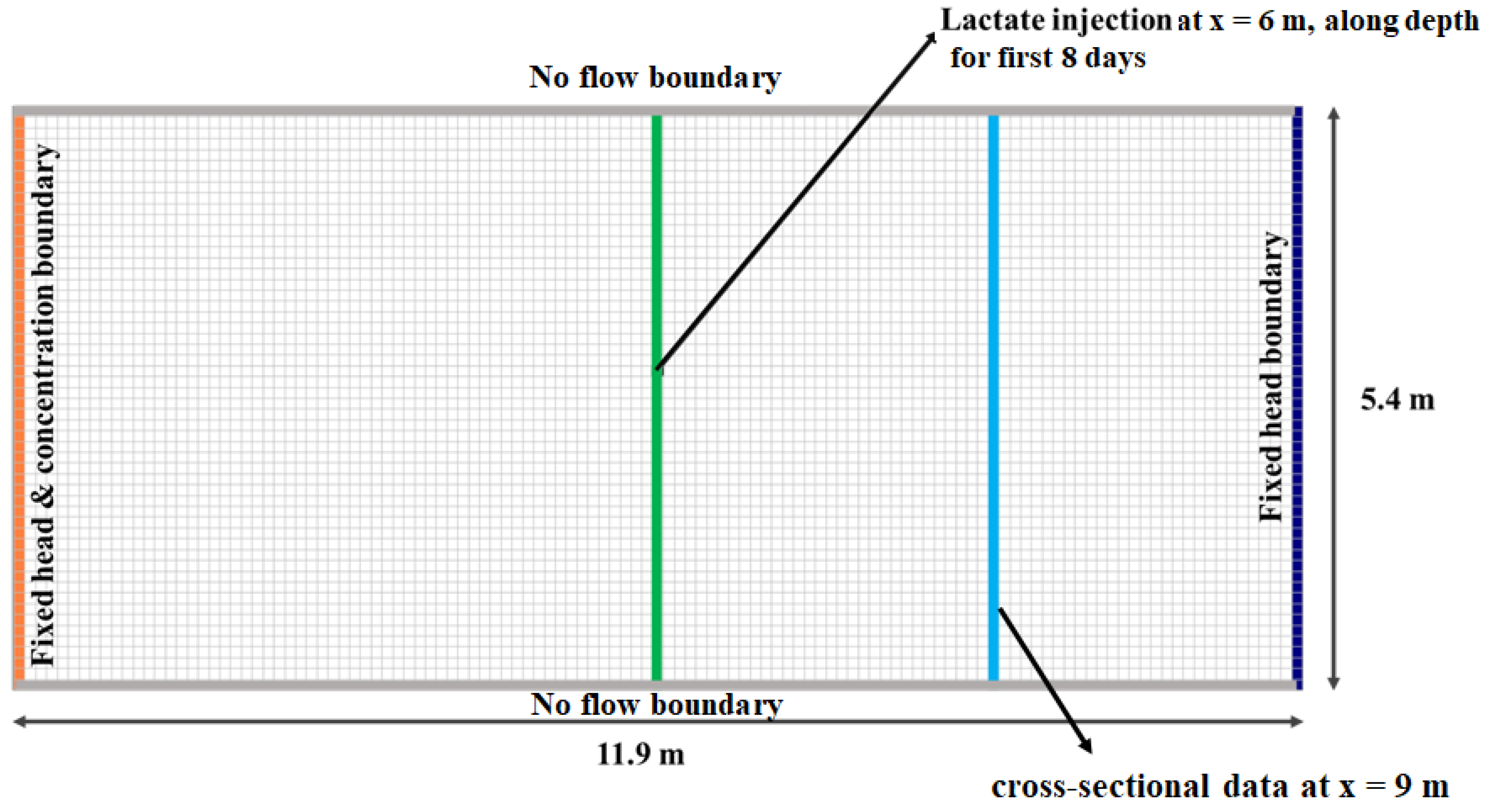
2. Model Structure and Parameters
2.1. Modeling Approach
- Reactive transport simulations are carried out with both physical and chemical heterogeneities (i.e., heterogeneous K and a heterogeneous Fe case);
- Reactive transport simulations are carried out with physical heterogeneity but not with chemical heterogeneity (i.e., heterogeneous K and a homogeneous Fe case);
- Reactive transport simulations are carried out with no physical or chemical heterogeneity (i.e., homogeneous K and a homogeneous Fe case).
2.2. Description of the Site
2.3. Key Input Parameters
2.4. Biogeochemical Reactions
2.5. Transport Processes
3. Results and Discussion
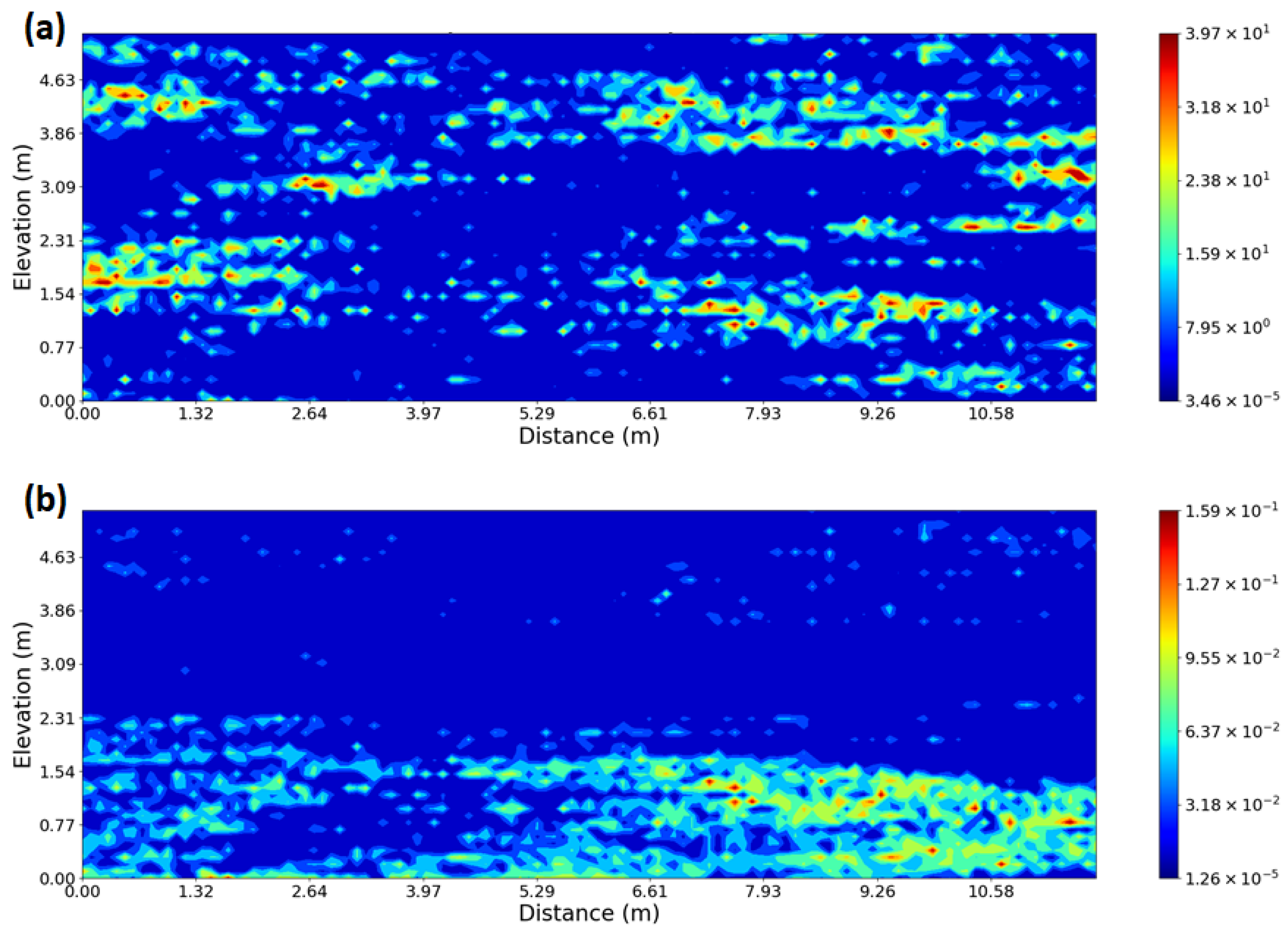
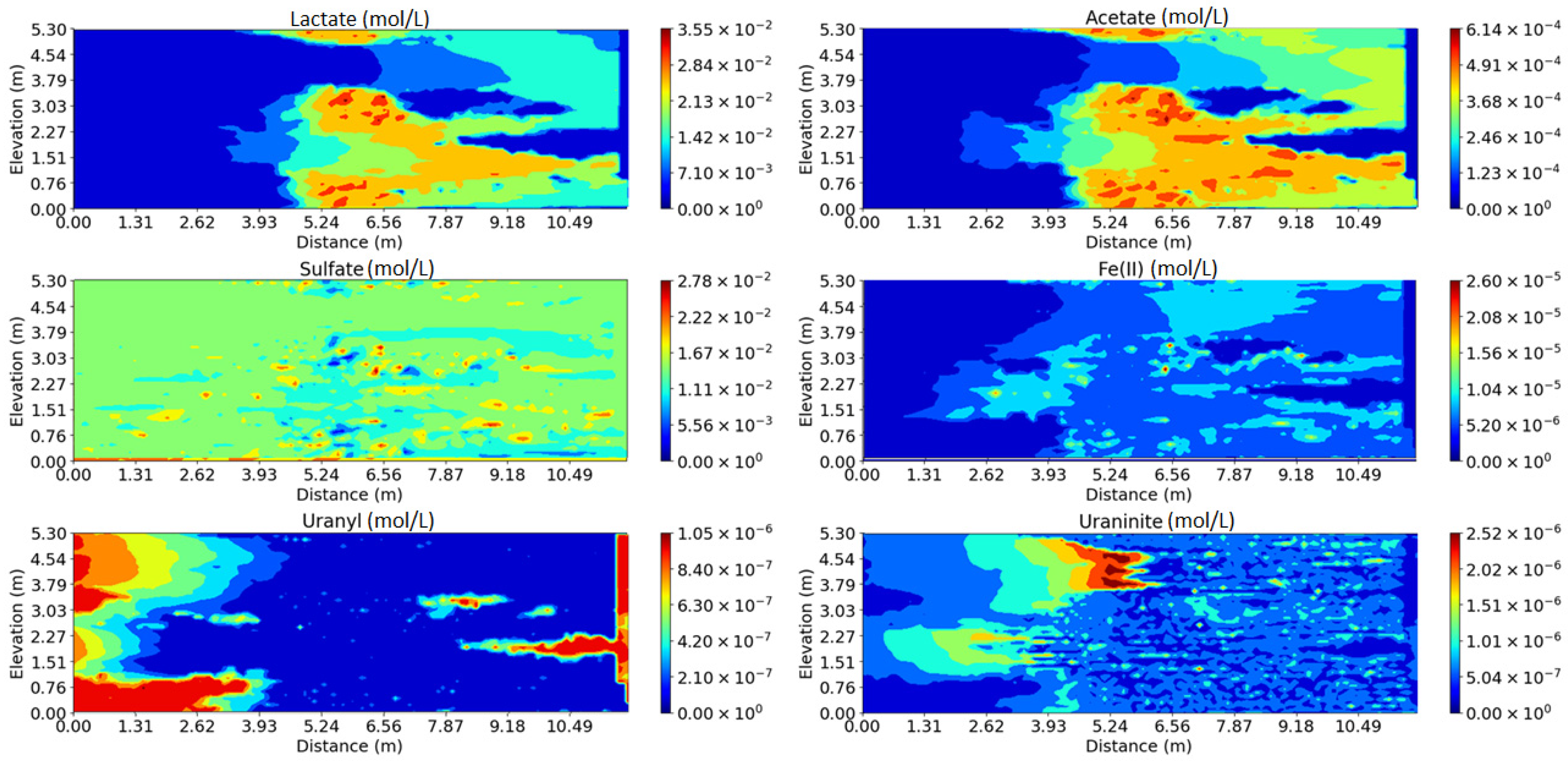
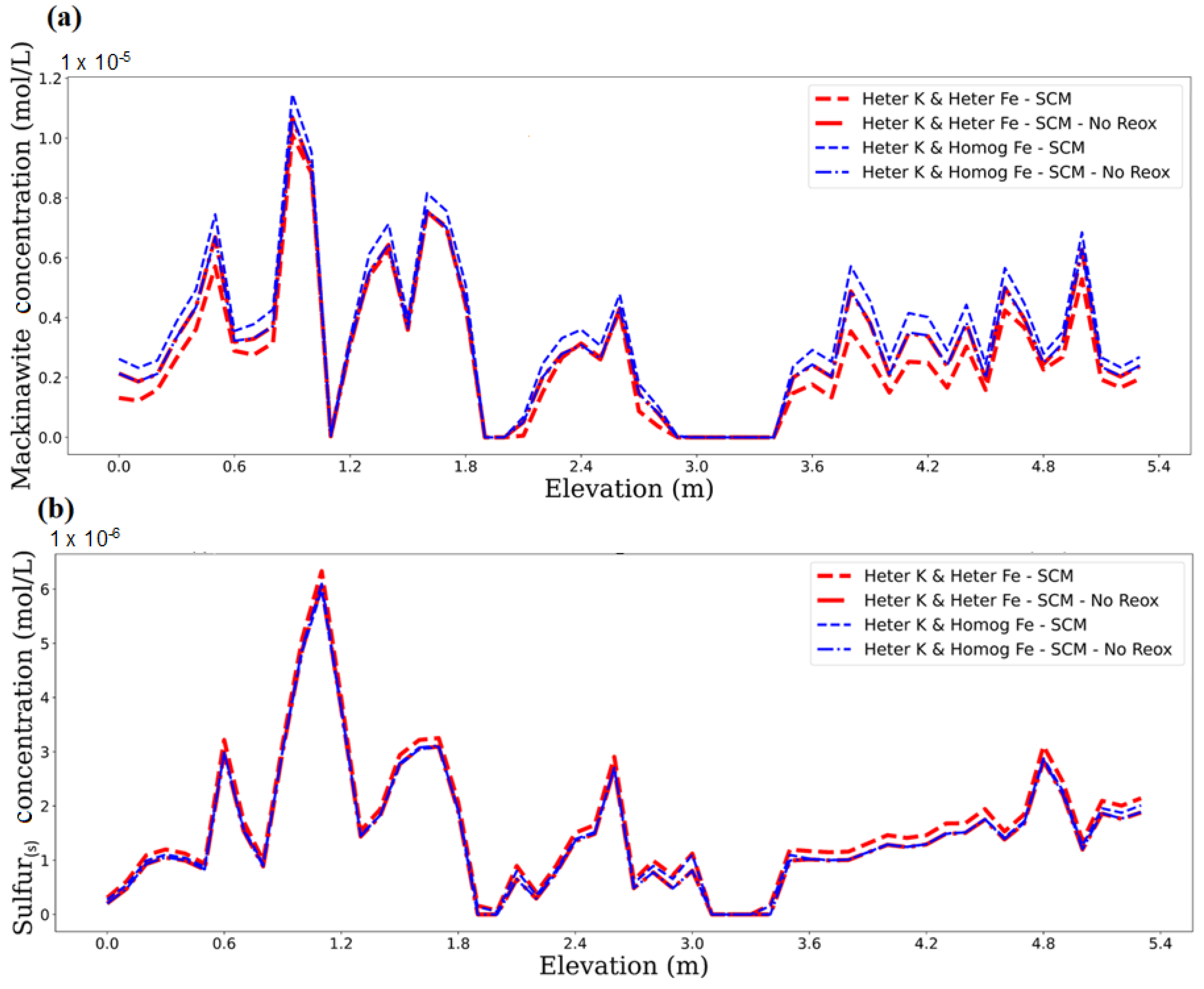
3.1. Impact of Physical and Chemical Heterogeneity on the Biogeochemical Dynamics of the Reactive Transport Model
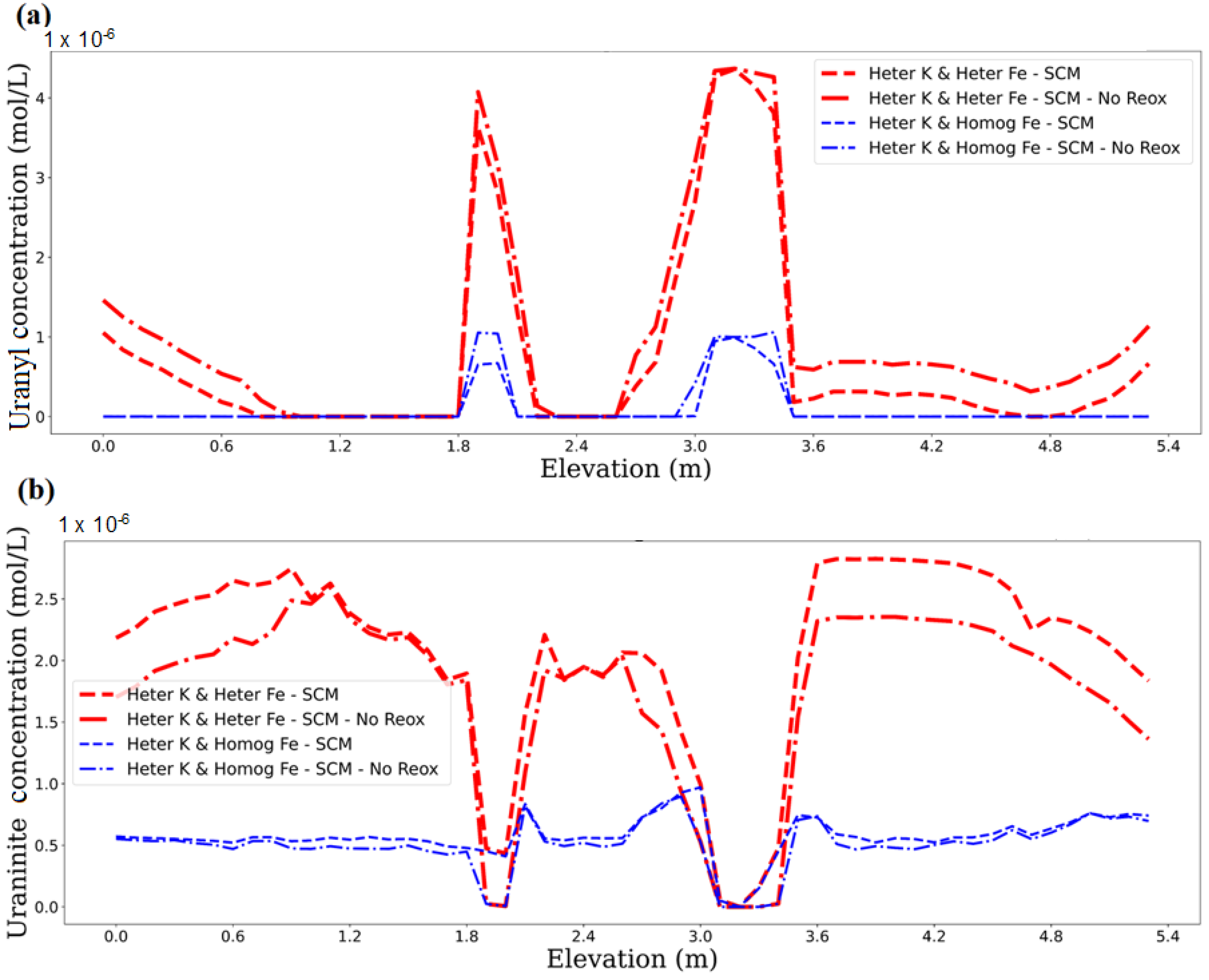
3.2. Impact of Physical and Chemical Heterogeneity on the Biogeochemical Dynamics of the Reactive Transport Model with the Surface Complexation of U(VI)
3.3. Impact of Physical and Chemical Heterogeneity on the Biogeochemical Dynamics of the Reactive Transport Model Without the U(IV) Reoxidation Reaction
4. Summary and Conclusions
- Reactive transport simulations are carried out with no physical or chemical heterogeneity (i.e., the homogeneous K and homogeneous Fe case);
- Reactive transport simulations are carried out with physical but no chemical heterogeneity (i.e., the heterogeneous K and homogeneous Fe case);
- Reactive transport simulations are carried out with both physical and chemical heterogeneities (i.e., the heterogeneous K and heterogeneous Fe case).
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cozzarelli, I.M.; Herman, J.S.; Baedecker, M.J.; Fischer, J.M. Geochemical heterogeneity of a gasoline-contaminated aquifer. J. Contam. Hydrol. 1999, 40, 261–284. [Google Scholar] [CrossRef]
- Cunningham, J.A.; Fadel, Z.J. Contaminant degradation in physically and chemically heterogeneous aquifers. J. Contam. Hydrol. 2007, 94, 293–304. [Google Scholar] [CrossRef] [PubMed]
- Fakhreddine, S.; Lee, J.; Kitanidis, P.K.; Fendorf, S.; Rolle, M. Imaging geochemical heterogeneities using inverse reactive transport modeling: An example relevant for characterizing arsenic mobilization and distribution. Adv. Water Resour. 2016, 88, 186–197. [Google Scholar] [CrossRef]
- Maliva, R.G. Aquifer Characterization and Properties. In Aquifer Characterization Techniques; Springer Hydrogeology; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Jang, E.; He, W.; Savoy, H.; Dietrich, P.; Kolditz, O.; Rubin, Y.; Schüth, C.; Kalbacher, T. Identifying the influential aquifer heterogeneity factor on nitrate reduction processes by numerical simulation. Adv. Water Resour. 2017, 99, 38–52. [Google Scholar] [CrossRef]
- Berg, S.J.; Illman, W.A. Capturing aquifer heterogeneity: Comparison of approaches through controlled sandbox experiments. Water Resour. Res. 2011, 47, 1–17. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Kitanidis, P.K.; Roberts, P.V. Analysis of one-dimensional solute transport through porous media with spatially variable retardation factor. Water Resour. Res. 1990, 26, 437–446. [Google Scholar] [CrossRef]
- Uçankuş, T.; Ünlü, K. The effect of aquifer heterogeneity on natural attenuation rate of BTEX. Environ. Geol. 2008, 54, 759–776. [Google Scholar] [CrossRef]
- Sarris, T.S.; Close, M.E.; Moore, C. Uncertainty assessment of nitrate reduction in heterogeneous aquifers under uncertain redox conditions. Stoch. Environ. Res. Risk Assess. 2019, 33, 1609–1627. [Google Scholar] [CrossRef]
- Wang, Z.W.; Chen, H.W.; Li, F.L. Identifying spatial heterogeneity of groundwater and its response to anthropogenic activities. Environ. Sci. Pollut. Res. 2019, 26, 29435–29448. [Google Scholar] [CrossRef]
- Aksoy, A.; Culver, T.B. Impacts of physical and chemical heterogeneities on aquifer remediation design. J. Water Resour. Plan. Manag. 2004, 130, 311–320. [Google Scholar] [CrossRef]
- Haberer, C.M.; Rolle, M.; Cirpka, O.A.; Grathwohl, P. Impact of Heterogeneity on Oxygen Transfer in a Fluctuating Capillary Fringe. Groundwater 2015, 53, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Harvey, R.W.; Kinner, N.E.; MacDonald, D.; Metge, D.W.; Bunn, A. Role of physical heterogeneity in the interpretation of small-scale laboratory and field observations of bacteria, microbial-sized microsphere, and bromide transport through aquifer sediments. Water Resour. Res. 1993, 29, 2713–2721. [Google Scholar] [CrossRef]
- Edwards, E.C. What lies beneath? Aquifer heterogeneity and the economics of groundwater management. J. Assoc. Environ. Resour. Econ. 2016, 3, 453–491. [Google Scholar] [CrossRef]
- Englert, A.; Hubbard, S.S.; Williams, K.H.; Li, L.; Steefel, C.I. Feedbacks between hydrological heterogeneity and bioremediation induced biogeochemical transformations. Environ. Sci. Technol. 2009, 43, 5197–5204. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, L.; Steefel, C.I.; Kowalsky, M.B.; Englert, A.; Hubbard, S.S. Effects of physical and geochemical heterogeneities on mineral transformation and biomass accumulation during biostimulation experiments at Rifle, Colorado. J. Contam. Hydrol. 2010, 112, 45–63. [Google Scholar] [CrossRef]
- Mohamed, M.; Hatfield, K.; Hassan, A.; Klammler, H. Stochastic evaluation of subsurface contaminant discharges under physical, chemical, and biological heterogeneities. Adv. Water Resour. 2010, 33, 801–812. [Google Scholar] [CrossRef]
- Tompson, A.F.B.; Schafer, A.L.; Smith, R.W. Impacts of physical and chemical heterogeneity on cocontaminant transport in a sandy porous medium. Water Resour. Res. 1996, 32, 801–818. [Google Scholar] [CrossRef]
- Atchley, A.L.; Navarre-Sitchler, A.K.; Maxwell, R.M. The effects of physical and geochemical heterogeneities on hydro-geochemical transport and effective reaction rates. J. Contam. Hydrol. 2014, 165, 53–64. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, F.; Yin, S.; Wallace, C.D.; Soltanian, M.R.; Dai, Z.; Ritzi, R.W.; Ma, Z.; Zhan, C.; Lü, X. Application of upscaling methods for fluid flow and mass transport in multi-scale heterogeneous media: A critical review. Appl. Energy 2021, 303, 117603. [Google Scholar] [CrossRef]
- Zhan, C.; Dai, Z.; Soltanian, M.R.; Zhang, X. Stage-wise stochastic deep learning inversion framework for subsurface sedimentary structure identification. Geophys. Res. Lett. 2022, 49, e2021GL095823. [Google Scholar] [CrossRef]
- Scheibe, T.D.; Fang, Y.; Murray, C.J.; Roden, E.E.; Chen, J.; Chien, Y.J.; Brooks, S.C.; Hubbard, S.S. Transport and biogeochemical reaction of metals in a physically and chemically heterogeneous aquifer. Geosphere 2006, 2, 220–235. [Google Scholar] [CrossRef]
- Roh, Y.; Lee, S.Y.; Elless, M.P.; Cho, K.S. Electro-enhanced remediation of radionuclide-contaminated groundwater using zero-valent iron. J. Environ. Sci. Health Part A Toxic/Hazard. Subst. Environ. Eng. 2000, 35, 1043–1059. [Google Scholar] [CrossRef]
- Baba, A.; Tayfur, G. Groundwater contamination and its effect on health in Turkey. Environ. Monit. Assess. 2011, 183, 77–94. [Google Scholar] [CrossRef]
- Waseem, A.; Ullah, H.; Rauf, M.K.; Ahmad, I. Distribution of natural uranium in surface and groundwater resources: A review. Crit. Rev. Environ. Sci. Technol. 2015, 45, 2391–2423. [Google Scholar] [CrossRef]
- You, W.; Peng, W.; Tian, Z.; Zheng, M. Uranium bioremediation with U(VI)-reducing bacteria. Sci. Total Environ. 2021, 798, 149107. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.T.; Vrionis, H.A.; Ortiz-Bernad, I.; Resch, C.T.; Long, P.E.; Dayvault, R.; Karp, K.; Marutzky, S.; Metzler, D.R.; Peacock, A.; et al. Stimulating the In Situ Activity of Geobacter Species to Remove Uranium from the Groundwater of a Uranium-Contaminated Aquifer. Appl. Environ. Microbiol. 2003, 69, 5884–5891. [Google Scholar] [CrossRef]
- Gihring, T.M.; Zhang, G.; Brandt, C.C.; Brooks, S.C.; Campbell, J.H.; Carroll, S.; Criddle, C.S.; Green, S.J.; Jardine, P.; Kostka, J.E.; et al. A limited microbial consortium is responsible for extended bioreduction of uranium in a contaminated aquifer. Appl. Environ. Microbiol. 2011, 77, 5955–5965. [Google Scholar] [CrossRef]
- Wufuer, R.; Wei, Y.; Lin, Q.; Wang, H.; Song, W.; Liu, W.; Zhang, D.; Pan, X.; Gadd, G.M. Chapter Four—Uranium Bioreduction and Biomineralization. Adv. Appl. Microbiol. 2017, 101, 137–168. [Google Scholar] [CrossRef]
- Yabusaki, S.B.; Şengör, S.S.; Fang, Y. A uranium bioremediation reactive transport benchmark. Comput. Geosci. 2015, 19, 551–567. [Google Scholar] [CrossRef]
- Gu, B.; Wu, W.M.; Ginder-Vogel, M.A.; Yan, H.; Fields, M.W.; Zhou, J.; Fendorf, S.; Criddle, C.S.; Jardine, P.M. Bioreduction of uranium in a contaminated soil column. Environ. Sci. Technol. 2005, 39, 4841–4847. [Google Scholar] [CrossRef]
- Renshaw, J.C.; Butchins, L.J.C.; Livens, F.R.; May, I.; Charnock, J.M.; Lloyd, J.R. Bioreduction of uranium: Environmental implications of a pentavalent intermediate. Environ. Sci. Technol. 2005, 39, 5657–5660. [Google Scholar] [CrossRef] [PubMed]
- Şengör, S.S.; Mayer, K.U.; Greskowiak, J.; Wanner, C.; Su, D.; Prommer, H. A reactive transport benchmark on modeling biogenic uraninite re-oxidation by Fe(III)-(hydr)oxides. Comput. Geosci. 2015, 19, 569–583. [Google Scholar] [CrossRef]
- Hyun, S.P.; Davis, J.A.; Hayes, K.F. Abiotic U(VI) reduction by aqueous sulfide. Appl. Geochem. 2014, 50, 7–15. [Google Scholar] [CrossRef]
- Senko, J.M.; Istok, J.D.; Suflita, J.M.; Krumholz, L.R. In-situ evidence for uranium immobilization and remobilization. Environ. Sci. Technol. 2002, 36, 1491–1496. [Google Scholar] [CrossRef]
- Vrionis, H.A.; Anderson, R.T.; Ortiz-Bernad, I.; O’Neill, K.R.; Resch, C.T.; Peacock, A.D.; Dayvault, R.; White, D.C.; Long, P.E.; Lovley, D.R. Microbiological and geochemical heterogeneity in an in situ uranium bioremediation field site. Appl. Environ. Microbiol. 2005, 71, 6308–6318. [Google Scholar] [CrossRef]
- Sani, R.K.; Peyton, B.M.; Amonette, J.E.; Geesey, G.G. Reduction of uranium(VI) under sulfate-reducing conditions in the presence of Fe(III)-(hydr)oxides. Geochim. Cosmochim. Acta 2004, 68, 2639–2648. [Google Scholar] [CrossRef]
- Komlos, J.; Moon, H.S.; Jaffé, P.R. Effect of Sulfate on the Simultaneous Bioreduction of Iron and Uranium. J. Environ. Qual. 2008, 37, 2058–2062. [Google Scholar] [CrossRef]
- Spycher, N.F.; Issarangkun, M.; Stewart, B.D.; Sevinç Şengör, S.; Belding, E.; Ginn, T.R.; Peyton, B.M.; Sani, R.K. Biogenic uraninite precipitation and its reoxidation by iron(III) (hydr)oxides: A reaction modeling approach. Geochim. Cosmochim. Acta 2011, 75, 4426–4440. [Google Scholar] [CrossRef]
- Prommer, H.; Barry, D.A.; Zheng, C. MODFLOW/MT3DMS-Based Reactive Multicomponent Transport Modeling. Groundwater 2003, 41, 247–257. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, P.P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide, Contract Report SERDP-99-1; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 1999. [Google Scholar]
- Parkhurst, D.L.; Appelo, C.A.J. User’s Guide to PHREEQC (Version 2)—A Computer Program for Speciation, Batch-Reaction, one Dimensional Transport, and Inverse Geochemical Calculations; USGS Report; United States Geological Survey: Denver, CO, USA, 1999. [Google Scholar]
- Harbaugh, A.W.; Langevin, C.D.; Hughes, J.D.; Niswonger, R.N.; Konikow, L.F. MODFLOW-2005 Version 1.12.00, the U.S. Geological Survey Modular Groundwater Model; U.S. Geological Survey Software Release; United States Geological Survey: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- USEPA. Radionuclides Rule: A Quick Reference Guide; Office of Water (4606). In EPA 816 F-01-003; USEPA: Washington, DC, USA, 2001. [Google Scholar]
- Bao, C.; Wu, H.; Li, L.; Newcomer, D.; Long, P.E.; Williams, K.H. Uranium bioreduction rates across scales: Biogeochemical hot moments and hot spots during a biostimulation experiment at Rifle, Colorado. Environ. Sci. Technol. 2014, 48, 10116–10127. [Google Scholar] [CrossRef]
- Dzombak, D.A.; Morel, F.M.M. Surface Complexation Modeling Hydrous Ferric Oxide; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Li, L.; Gawande, N.; Kowalsky, M.B.; Steefel, C.I.; Hubbard, S.S. Physicochemical heterogeneity controls on uranium bioreduction rates at the field scale. Environ. Sci. Technol. 2011, 45, 9959–9966. [Google Scholar] [CrossRef] [PubMed]
- Amde, M.; Liu, J.; Tan, Z.-Q.; Bekana, D. Transformation and bioavailability of metal oxide nanoparticles in aquatic and terrestrial environments: A review. Environ. Pollut. 2017, 230, 250–267. [Google Scholar] [CrossRef]
- Michael, H.A.; Khan, M.R. Impacts of physical and chemical aquifer heterogeneity on basin-scale solute transport: Vulnerability of deep groundwater to arsenic contamination in Bangladesh. Adv. Water Resour. 2016, 98, 147–158. [Google Scholar] [CrossRef]
- Chen, W.; Dai, Z.; Samper, J.; Ling, H.; Zhan, C.; Ma, F.; Yang, Z.; Zhang, X.; Soltanian, M.R. Impact of reactive mineral facies distributions on radionuclide sorption properties in multiscale heterogeneous granite rocks. Hydrogeol. J. 2023, 31, 1581–1597. [Google Scholar] [CrossRef]

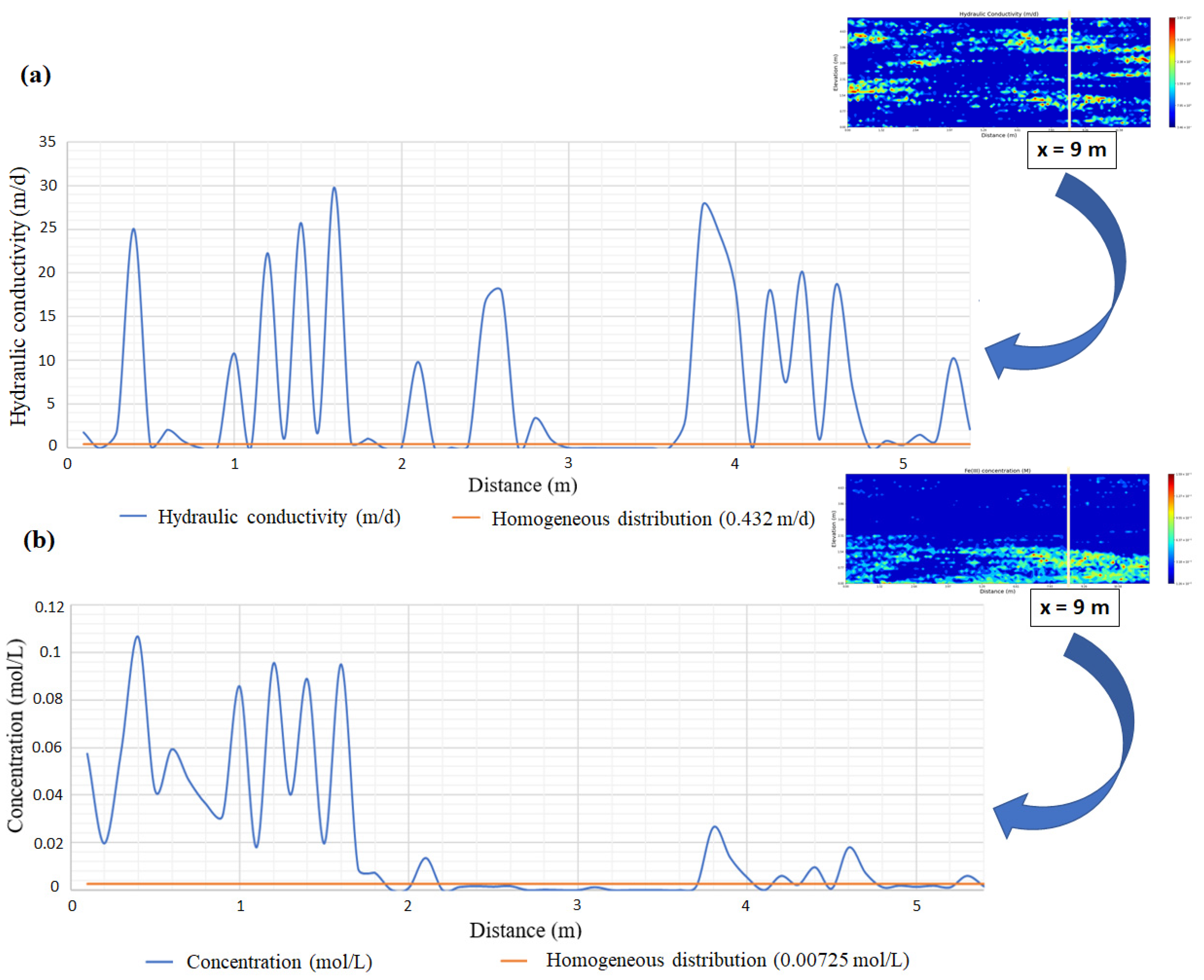

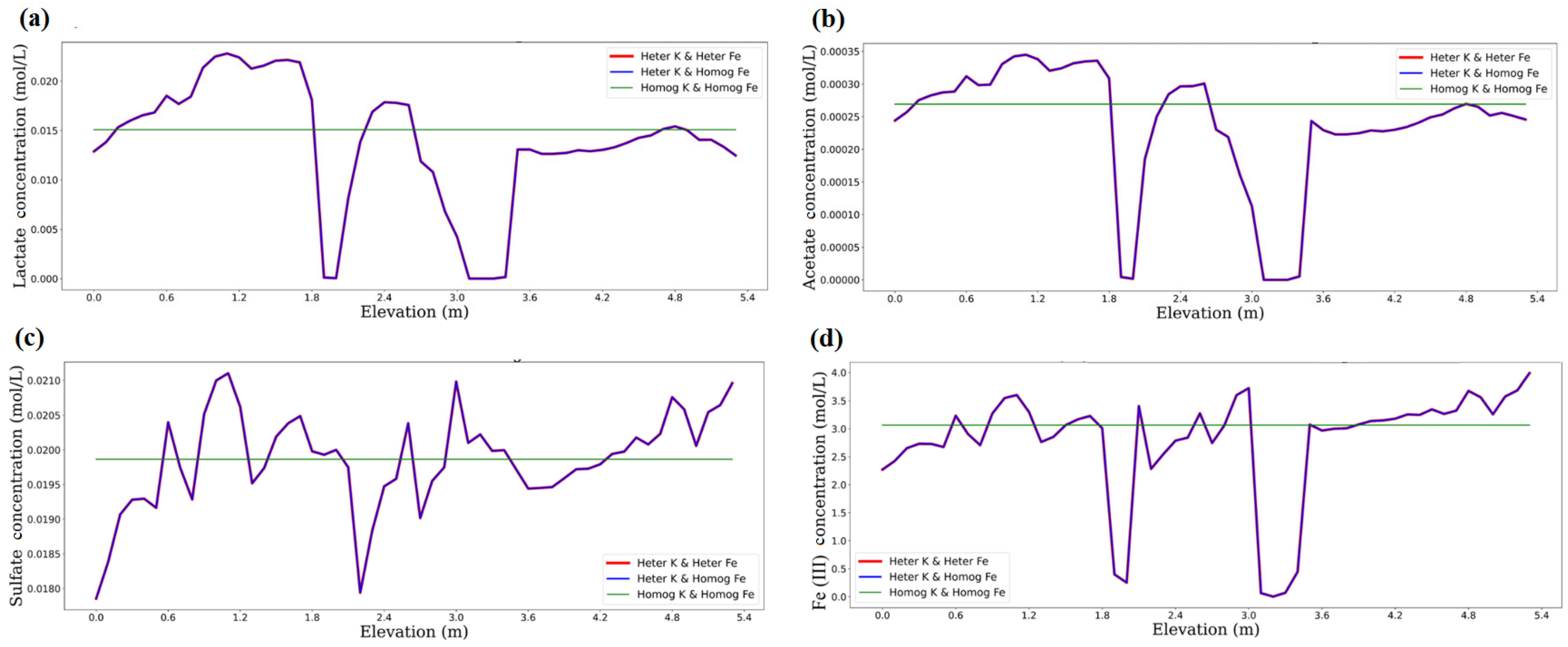
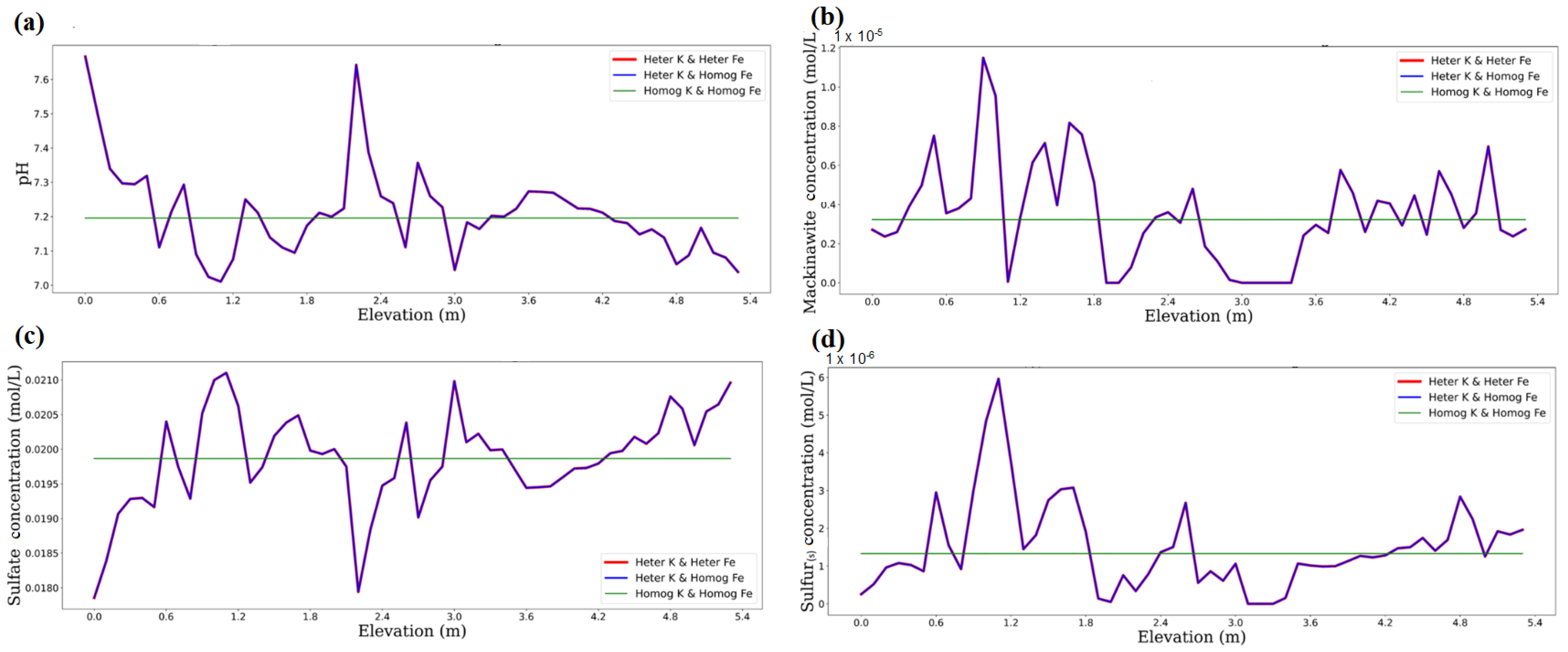
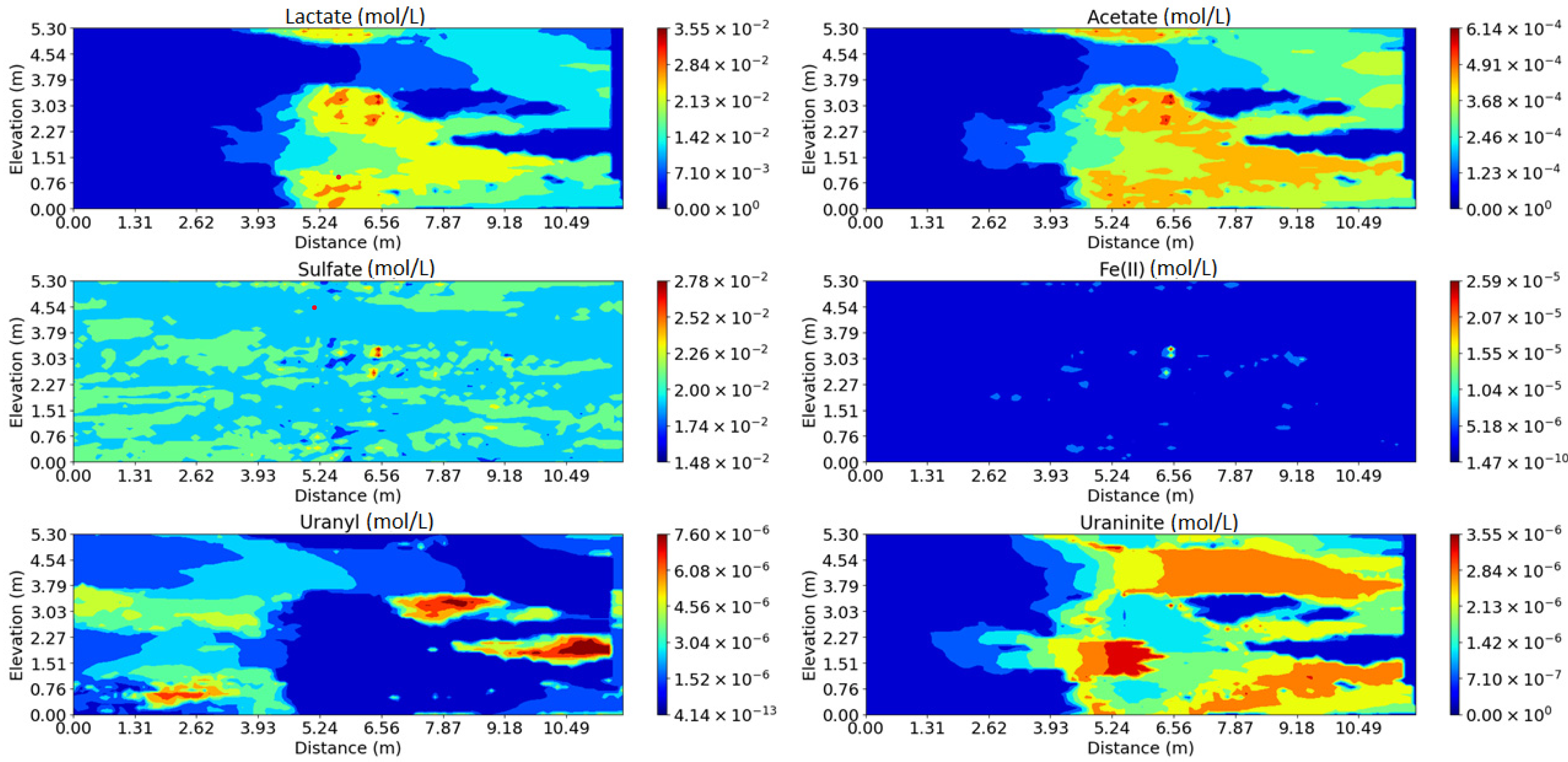



| Chemical Species | Initial Water Composition | Inflowing Water Composition |
|---|---|---|
| Concentration (mol/L) | Concentration (mol/L) | |
| Lactate | 3 × 10−7 (a) | 0.03 (b) |
| Acetate | 1 × 10−23 | 1 × 10−23 |
| Sulfate (SO42−) | 0.02 | 0.02 |
| Sulfide (S2−) | 1 × 10−8 | 1 × 10−23 |
| Fe(II) | 1 × 10−23 | 1 × 10−23 |
| Fe (III) | 1 × 10−11 | 1.3 × 10−12 |
| Uranyl (U(VI) or (UO22+) | 1 × 10−6 (c) | 1 × 10−23 |
| Ca | 0.00042 | 0.00042 |
| Mg | 0.004 | 0.004 |
| Inorganic carbon (C4+) | 1.7 × 10−7 | 1.187 × 10−4 (d) |
| U(IV) | 1 × 10−23 | 1 × 10−23 |
| Na | 0.06 | 0.07914 (e) |
| Cl | 8.2 × 10−4 | 8.2 × 10−4 |
| Pip | 0.03 (f) | 0.03 |
| Reaction No | Process and Reaction | Rate Law | q (mol/s/mgcells) or r (mol/s) | kD (mol/L) | kA (mol/L) | Yb (mgcells/mol) | kdec (1/s) |
|---|---|---|---|---|---|---|---|
| 1 | Sulfate bioreduction (lactate degradation, biotic): 2C3H5O3− + SO42− → 2CH3COO− + 2 CO32− + HS− + 3H+ | Equations (1)–(3) | 10−8/100 | 2 × 10−2 | 2 × 10−2 | 1600 | 10−8/100 |
| 2 | Fe(III) bioreduction (lactate degradation, biotic): C3H5O3− + 4Fe3+ + 2H2O → CH3COO− + CO32− + 4Fe2+ +6H+ | Equations (1)–(3) | 10−11/100 | 2 × 10−2 | 10 −20 (a) | 1600 | 10−8/100 |
| 3 | U(VI) bioreduction (abiotic and biotic): 4UO22+ + HS− + 7H+ → 4U 4+ + SO42− + 4H2O | Equation (4) | 8 × 10 −11/100 | 4 × 10−2 | |||
| 4 | U(IV) reoxidation by Fe(III) (abiotic) U4+ + 2Fe 3+ + 2H2O → UO22+ + 2Fe2+ + 4H+ | Equation (5) | 0.45 × 10−11/100 | ||||
| 5 | Sulfide reoxidation by Fe(III) (abiotic) 8Fe 3+ + HS− + 4H2O → 8Fe2+ + SO42− + 9H+ | Equation (5) | 2 × 10 −11/100 | ||||
| 6 | Precipitation of sulfur: (b) 2Fe 3+ + HS− → 2Fe2+ +S(s) + H+ | Equation (5) | 2 × 10 −11/100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gökçe, S.; Şengör, S.S. Reactive Transport Modeling of Uranium in Subsurface: Impact of Field-Scale Heterogeneity and Biogeochemical Dynamics. Water 2025, 17, 514. https://doi.org/10.3390/w17040514
Gökçe S, Şengör SS. Reactive Transport Modeling of Uranium in Subsurface: Impact of Field-Scale Heterogeneity and Biogeochemical Dynamics. Water. 2025; 17(4):514. https://doi.org/10.3390/w17040514
Chicago/Turabian StyleGökçe, Selin, and S. Sevinç Şengör. 2025. "Reactive Transport Modeling of Uranium in Subsurface: Impact of Field-Scale Heterogeneity and Biogeochemical Dynamics" Water 17, no. 4: 514. https://doi.org/10.3390/w17040514
APA StyleGökçe, S., & Şengör, S. S. (2025). Reactive Transport Modeling of Uranium in Subsurface: Impact of Field-Scale Heterogeneity and Biogeochemical Dynamics. Water, 17(4), 514. https://doi.org/10.3390/w17040514






