Next Article in Journal
Experimental Study on Alternating Vacuum–Electroosmosis Treatment for Dredged Sludges
Previous Article in Journal
Enhancing Methane Production in a Sidestream Bioelectrochemical Anaerobic Digestion of Sewage Sludge: Focusing on Energy Efficiency and Tradeoffs
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 17
Issue 24
10.3390/w17243498
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comparison of Process-Based and Machine Learning Models for Streamflow Simulation in Typical Basins in Northern and Southern China

by
Rui Ye
1,
Feng Zhang
1,
Jiaxue Ren
2,
Tao Wu
3,* and
Haitao Chen
2,4,*
1
Anhui Water Conservancy Technical College, Hefei 231603, China
2
College of Water Conservancy, Jiangxi University of Water Resources and Electric Power, Nanchang 330099, China
3
Chinese Research Academy of Environmental Sciences, Beijing 100012, China
4
College of Environmental Science and Engineering, Nankai University, Tianjin 300350, China
*
Authors to whom correspondence should be addressed.
Water 2025, 17(24), 3498; https://doi.org/10.3390/w17243498
Submission received: 11 November 2025 / Revised: 30 November 2025 / Accepted: 7 December 2025 / Published: 10 December 2025
(This article belongs to the Special Issue New Technologies for Hydrological Forecasting and Modeling)
Browse Figures
Versions Notes

Abstract

Accurate streamflow forecasting is vital for sustainable water resource management but remains challenging due to pronounced spatiotemporal variability. This study evaluates two process-based models, the SWAT (comprehensive) and the GWLF (parsimonious), and a data-driven random forest (RF) model for monthly streamflow simulations in two contrasting Chinese basins: the humid southern basin (SSB) and the semi-arid northern basin (SRB). Using four statistical metrics (NSE, R2, MAE, RMSE), we assess model accuracy, robustness in capturing extremes, and sensitivity to hydrological characteristics and data availability. The results reveal consistently superior performance in the SSB across all models, with SWAT demonstrating the highest overall accuracy—especially for peak flows—due to its physically based structure. The GWLF provides acceptable simulations with minimal data requirements, offering a practical alternative in data-limited regions, like the SRB. RF performs well in the SSB under zero-lag conditions but requires hydrologically informed lag structures in the SRB. However, it consistently underestimates high flows due to its lack of physical constraints. The findings underscore that model selection must, therefore, be guided not only by predictive performance but also by the underlying hydrological context, data availability, and the need for physical realism in decision-making.

1. Introduction

Accurate streamflow forecasting is vital for effective water allocation, planning, and management [1,2]. However, streamflow exhibits high spatiotemporal variability due to uneven water distribution and the combined effects of precipitation, evapotranspiration, landscape characteristics, topography, climate change, and human activities [3,4,5,6]. This complexity introduces significant uncertainty in hydrological simulations across regions. Consequently, selecting modeling tools that align with local hydrological characteristics is critical to accurately represent streamflow dynamics [7,8,9,10].
Process-based hydrological models have long been used to simulate watershed-scale streamflow by explicitly representing key hydrological processes [11,12,13]. These models vary widely in structural complexity and data requirements. For instance, the Soil and Water Assessment Tool (SWAT) is among the most widely applied models in water resources management, demonstrating robust performance across diverse physical and climatic conditions [14,15]. However, its complex structure and extensive data demands often hinder its application in data-limited regions [16]. In contrast, the Generalized Watershed Loading Function (GWLF) model offers a more parsimonious alternative, requiring fewer inputs and offering greater operational flexibility [17,18], making it suitable for areas with constrained data availability [19,20]. Thus, the choice between these models involves a trade-off between process representation and practical feasibility.
In recent years, machine learning (ML) approaches have gained prominence in hydrology, driven by advances in big data and computational power [21,22,23]. Unlike process-based models, ML methods do not explicitly encode physical relationships; instead, they rely on mathematical functions to map inputs to outputs, thereby identifying complex, nonlinear patterns in data [24]. Models such as random forest (RF), Support Vector Machine (SVM), and Artificial Neural Networks (ANNs) have been widely applied across hydrological tasks [23,25]. Among these, RF excels at handling high-dimensional datasets and automatically selecting relevant features, making it particularly effective for streamflow forecasting [26]. Nevertheless, ML models are frequently regarded as “black boxes” owing to poor interpretability, and their performance is strongly influenced by the underlying data and feature selection, warranting further evaluation of their applicability in regions with high data heterogeneity.
As the world’s largest developing country, China faces significant challenges related to water pollution and severe spatial imbalance in water resources—northern regions account for only 19% of the nation’s total water endowment despite hosting a large share of its population and economic activity [27,28]. Accurate hydrological prediction is, therefore, critical for understanding pollution dynamics and enabling equitable water allocation. While both process-based and ML models have achieved satisfactory performance in Chinese watersheds, few studies have systematically compared their applicability across regions with stark hydrological contrasts—particularly between water-rich southern and water-scarce northern basins.
This study selects two representative watersheds in northern and southern China to evaluate the performance of two process-based models of differing complexity—the SWAT and the GWLF—and a machine learning model (RF model) in monthly streamflow simulations. Model performance is assessed using four statistical metrics. The primary objective is to compare the applicability of these approaches across contrasting hydroclimatic regions. Specifically, the study includes (1) calibration of the SWAT and the GWLF for streamflow simulation; (2) training of the RF model; (3) streamflow prediction using the calibrated/trained models; and (4) comparative analysis of model performance and regional suitability.

2. Materials and Methods

2.1. Study Area

This study was conducted in two contrasting watersheds: the Shahe River Basin (SRB) in northern China and the Shuai Shui Basin (SSB) in southern China. Although the two basins have similar elevation ranges and drainage areas, they exhibit a significant difference in water resources (Figure 1a). The SRB is located in the upstream area of the Yuqiao Reservoir in Tianjin city (117°30′–118°0′ E, 40°0′–42°20′ N) and constitutes a key part of the Yuqiao Reservoir watershed, with a total drainage area of 905.2 km2. Land use is dominated by forest land (44.06%) and agricultural land (37.78%). The basin’s topography is higher in the northeast and lower in the southwest, with a maximum elevation of 1100 m (Figure 1b,c). The long-term average annual precipitation and temperature are 650.7 mm and 12.9 °C, respectively, with rainfall concentrated during the summer months (July–September), marking a distinct wet season [17].
In contrast, the SSB is situated in southern Anhui Province (117°30′–118°10′ E, 29°30′–29°50′ N) and forms an important part of the upstream watershed of Qiandao Lake, covering a drainage area of 880.4 km2. Land use is overwhelmingly dominated by forest land (90.4%), with only a small proportion of agricultural land (6.7%). The basin is characterized by mountainous and hilly terrain, with elevations ranging from 140 to 1614 m (Figure 1d,e). The long-term average annual precipitation is approximately 1700 mm, and the mean annual temperature is 15.6 °C. Precipitation is unevenly distributed throughout the year, with the majority occurring during spring and summer [29].

2.2. Data Source

Both the SRB and SSB are equipped with a meteorological station and a hydrological station, as well as several rainfall stations (Figure 1b,d). The meteorological station data (including precipitation, maximum and minimum temperatures, average temperatures, relative humidity, wind speed, and solar radiation) were obtained from the National Weather Science Data Center (http://data.cma.cn/ (accessed on 15 May 2023)). The rainfall station data (including precipitation) and streamflow data from the hydrological station were obtained from the local hydrological bureau. The monthly evapotranspiration data were available from the Institute of Tibetan Plateau Research, Chinese Academy of Sciences, and all these data were used to construct a hydrological model (including the SWAT and GWLF models) and an RF model. In addition, spatial data, including the digital elevation model (DEM), land use, and soils, are also required in the hydrological model. The DEM is derived from the Geospatial Data Cloud (https://www.gscloud.cn/ (accessed on 15 May 2023)) with a resolution of 30 m × 30 m, and the land use and soil are derived from the Resource and Environmental Science and Data Center (https://www.resdc.cn/ (accessed on 15 May 2023)), with a scale of 1:1,000,000. The description of the datasets are list in Table 1.

2.3. Model Description

2.3.1. SWAT Model Description

The SWAT model is a process-based, semi-distributed hydrological model developed by the USDA Agricultural Research Center, characterized by robust physical mechanisms. This model divides the watershed into hydrological response units (HRUs) based on land use types, soil types, and slopes within the study area. It conducts water quantity and quality simulations based on the hydrological response units and their water balances. The SWAT model employs the curve number method for runoff calculation and utilizes the Muskingum method for channel routing. Independently, the SWAT calculates water yield for each HRU and then consolidates these values at the sub-basin level. Since its development, the SWAT model has been widely applied in streamflow and water quality simulations, making it one of the most extensively used hydrological models [30,31].

2.3.2. GWLF Model Description

The GWLF model, developed by Cornell University and Pennsylvania State University, is a combined distributed/lumped parameter, continuous watershed model [32]. Over the past decades, the GWLF model has been secondarily developed on different platforms. Here, we use the modified GWLF model (ReNuMa model) for streamflow simulations. The model is not spatially conceptualized, and each area is considered uniformly in terms of soil and cover [19]. Soil moisture contains unsaturated zone, shallow saturated zone, and deep saturated zone parameters. The model uses a daily time step and the curve number method to simulate daily hydrologic water balance [33,34]. Compared with the SWAT model, this model has more moderate data requirements and a more flexible mode of operation and has been widely used around the world.

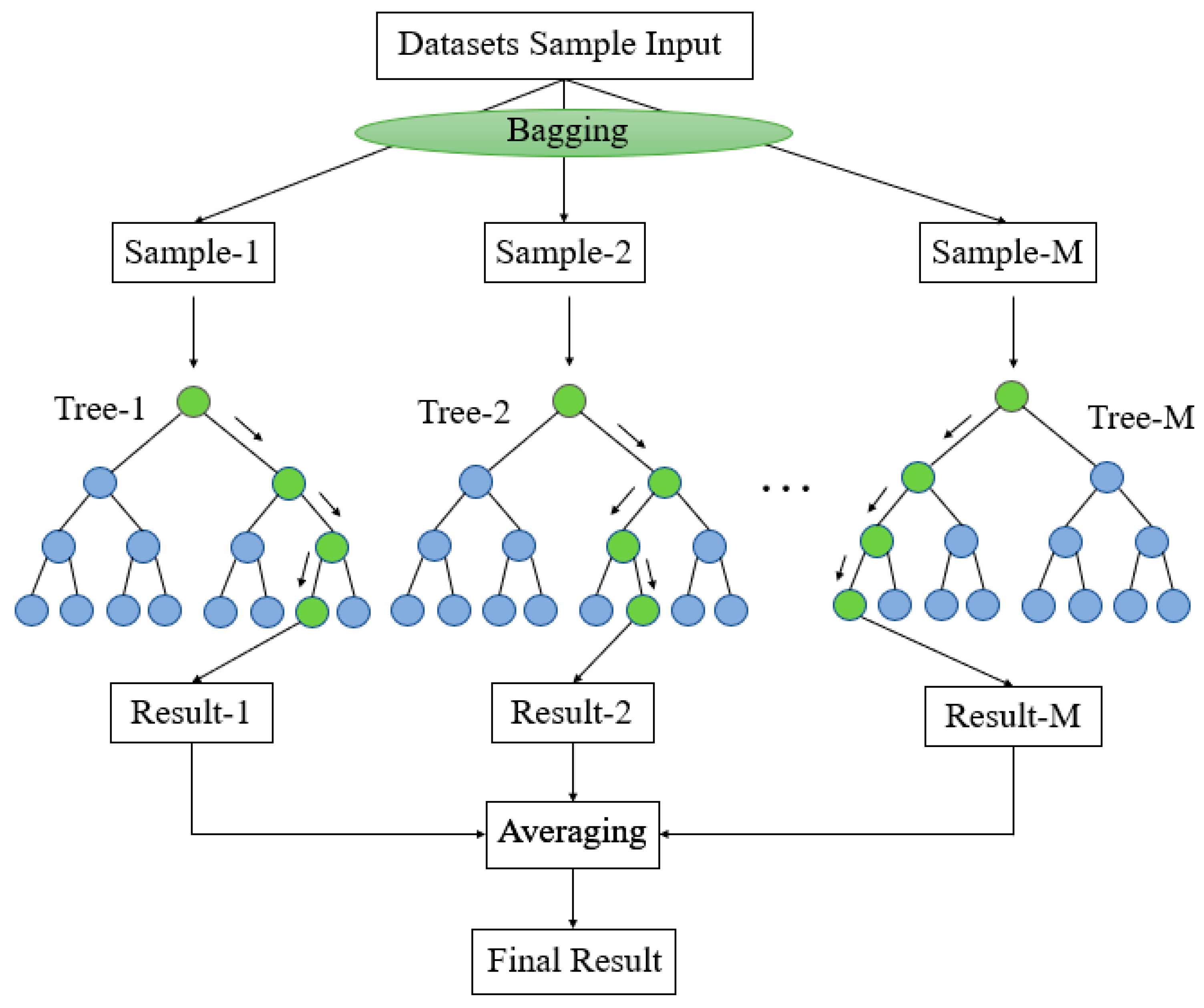
2.3.3. RF Model Description

The RF model is an integrated learning model, which is a classifier method combining bagging integrated learning theory with random subspaces and has been widely used to deal with classification and regression issues [7,35]. The RF model mainly consists of two parts: the training sample subset and the subclassification model. Each tree of the RF model is drawn from a random subset of the original sample set. Based on the extracted M sets of training samples, M sub-prediction models can be constructed, and based on each sub-prediction model, a corresponding forecast result can be obtained (Figure 2). The final forecast value is determined by voting (for categorical variables) or averaging (for continuous numerical variables) among the M sub-prediction models. The streamflow simulation mainly involves the application of the RF model in regression.

2.4. Model Settings and Evaluation

2.4.1. SWAT Model

By setting the stream definition thresholds in the SWAT model, the SSB and SRB were divided into 15 and 19 sub-basins, respectively, with 89 and 116 HURs (Figure 1). The Penman–Monteith equation and the SCS curve number method were applied in the model to calculate potential evapotranspiration and rainfall–runoff. The SWAT-CUP with the SUFI-2 algorithm was adopted to calibrate the hydrological parameters in the SWAT model, and fifteen parameters were selected for five hundred simulation iterations twice. The periods 2007–2013 and 2001–2007 were assigned for calibration in the SSB and SRB, both with a one-year period for warming up, and 2014–2016 and 2008–2010 were used for validating streamflow, respectively. The chosen parameters were calibrated using monthly time steps, and the accuracy of the streamflow simulation results is judged by the Nash efficiency coefficient (NSE) and R2 value.

2.4.2. GWLF Model

The streamflow simulation in the GWLF model typically requires meteorological data (including watershed-averaged precipitation and temperature), observed streamflow records, and spatially distributed land use information. In this study, the Thiessen polygon method in ArcGIS 10.2 was used to compute the basin-wide average precipitation and temperature from multiple rainfall and meteorological stations. The modified GWLF model, known as the ReNuMa model, was applied, and its built-in calibration function was used to calibrate the model using streamflow data. The model uses a programming solver method to keep the simulated values as close as possible to the predicted values. As well, the time settings for the warm-up, calibration, and validation periods in the SSB and SRB are consistent with those in the SWAT model, and the reliability of the model is based on the values of NSE and R2.

2.4.3. RF Model

The RF model was performed using the “RandomForest” package in R. Six variables were selected as independent variable inputs to the model, including precipitation (P), evapotranspiration (ET), average temperature (AT), relative humidity (RH), wind speed (WS), and solar radiation (SR), and all these variables were processed into the form of a monthly scale. Based on the established hydrological principle that antecedent precipitation influences soil moisture and subsequently contributes to runoff generation, we assume that watershed discharge is influenced not only by concurrent rainfall (Pt) but also by rainfall from preceding days. To account for this dependence, we first performed a cross-correlation analysis to identify the relevant rainfall lag time. Several modeling scenarios were then constructed and tested to estimate monthly streamflow (Table 2). These scenarios consider the effect of different rainfall’s lag days on streamflow simulation, with the 1st, 2nd, and 3rd day’s lagged rainfall along with the streamflow.

2.4.4. Performance Evaluation Indicators

Four statistical indicators were chosen to evaluate the fits of the models during the calibration and the validation period, including the coefficient of determination (R2), Nash efficiency coefficient (NSE), mean absolute error (MAE), and root mean square error (RMSE).
The corresponding formulas are provided in Table 3, where Ot denotes the observed streamflow value, Oavg represents the average observed value of the streamflow, Pt indicates the predicted value, and Pavg represents the average predicted value of the streamflow. R2 measures the linear relationship between the simulated and observed data, and NSE is used to characterize the variance between observed and simulated data. The closer the R2 and NSE values are to 1, the better the model performance. In contrast, the MAE and RMSE measure the average magnitude of prediction errors, reflecting the overall deviation between predicted and observed values. Both metrics range from 0 to ∞.

3. Results and Discussion

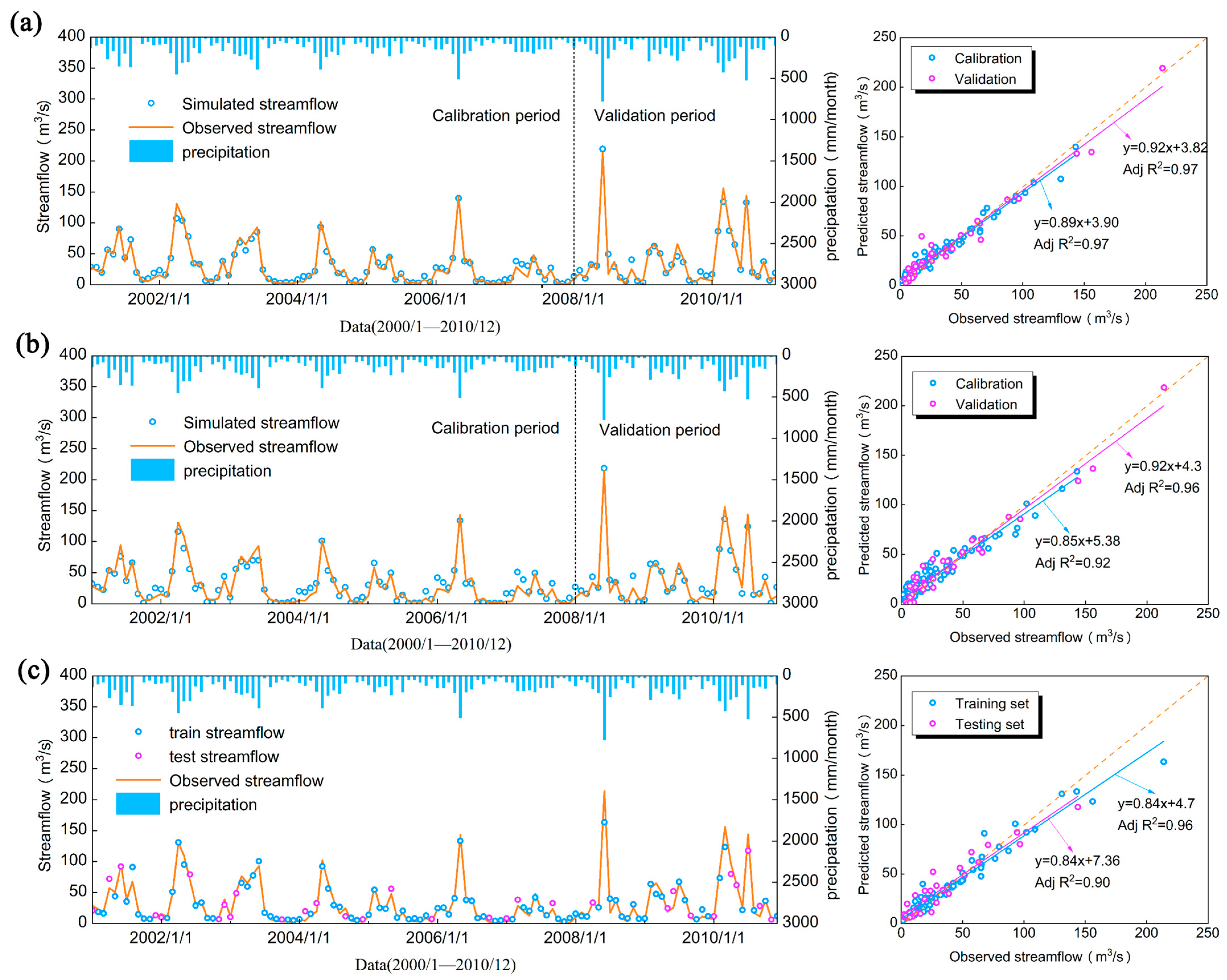
3.1. SWAT and GWLF Calibration

Fifteen and four frequently used streamflow calibration parameters were selected for model calibration in the SWAT and GWLF models, respectively. The parameter descriptions, default value ranges, and final calibration values are listed in Table 4.
The calibrated parameter values exhibit significant spatial variability across the mechanistic models applied for streamflow simulation in the southern and northern basins of China. In the SWAT model, the CN2 value of the SSB was higher than that of the SRB, indicating a greater potential for surface runoff generation in the south. Conversely, the SRB exhibits a high SOL_AWC value of 0.88, reflecting typical characteristics of watersheds in northern China, where arid conditions lead to a higher soil available water capacity [36]. ALPHA_BF governs the rate at which groundwater contributes to streamflow; a larger ALPHA_BF value indicates more stable baseflow. Since the SSB is located in a humid southern region with consistently high rainfall and sustained high soil moisture, its groundwater discharge is more stable compared to the drier northern SRB. LAT_TTIME and SURLAG values reflect the retention effect of streamflow to some extent, with longer retention times for the SRB and shorter retention times for the SSB [37].
In the GWLF model, the CN2 values and SOL_AWC for the SSB and SRB exhibit patterns consistent with those observed in the SWAT model. These similarities are primarily attributed to watershed-specific soil properties. The SSB is predominantly underlain by red soils, while the SRB is dominated by brown soils. Compared to red soils, brown soils typically have lower permeability but greater water-holding capacity [38]. The recession coefficient and seepage coefficient are the most critical parameters governing groundwater processes [39]. The higher values of these parameters in the SSB indicate more active and intense groundwater dynamics. Overall, the variability in model parameters across catchments reflects fundamental differences in their underlying hydrological processes.

3.2. RF Training and Testing

In the RF model, input variables significantly influence forecasting outcomes. In this study, we selected six readily available, continuous variables that are closely related to streamflow to construct the RF model and we considered different scenarios based on varying runoff retention periods (i.e., lag days). The dataset was split into training and testing subsets, with 75% allocated for training and 25% for testing. A larger training sample was used to ensure the model captures the majority of the underlying data patterns and variability. Model performance was evaluated across all scenarios, with the RF hyperparameters fixed at 200 trees and maximum depth allowed for tree expansion. The results show that the RF model achieves low computational time across all scenarios, demonstrating its efficiency for streamflow forecasting under different retention day configurations.

3.3. Analysis and Comparison of the Model Performance in the SRB and SSB

The model calibration and validation performance metrics in the SRB and SSB are presented in Table 5. It is evident that the values of the four statistical metrics differ slightly between the calibration and validation periods in both watersheds. Overall, the models perform significantly better in the SSB than in the SRB. In the SSB, all three models achieve R2 and NSE values exceeding 0.85 during both calibration and validation, along with low MAE and RMSE values, indicating reliable and accurate monthly streamflow predictions.
Among the three models, the SWAT demonstrates the best performance in the SSB, yielding the highest R2 and NSE values and the lowest MAE and RMSE across both calibration and validation periods. For the RF model, Scenario I (i.e., zero lag or shortest retention period) yields the best validation performance, suggesting that the rainfall–streamflow response in the SSB exhibits a weak retention effect, with streamflow reacting rapidly to precipitation inputs.
In contrast, model performance in the SRB shows greater variability. The SWAT outperforms the GWLF consistently in both calibration and validation phases, while the RF model performs well during training but only moderately during testing—reflecting the more complex, nonlinear rainfall–runoff dynamics characteristic of semi-arid regions. For the RF model in the SRB, Scenario III (i.e., incorporating a multi-day runoff lag) achieves the best predictive performance, which can be attributed to the presence of a discernible time lag between rainfall and runoff response in the watershed.
Figure 3 and Figure 4 present the monthly streamflow simulations for the SRB and SSB, respectively, using the SWAT, the GWLF, and the RF model under their optimal scenarios. Both process-based models and the data-driven RF model effectively capture the temporal dynamics of streamflow, demonstrating their general applicability. However, visual inspection of hydrographs and scatter plots reveals markedly better agreement between observed and simulated streamflow in the SSB than in the SRB. This discrepancy is consistent with the climatic contrasts between the two basins. Monthly precipitation ranges from 0 to 500 mm in the SRB versus 0 to 1000 mm in the SSB, while corresponding streamflow ranges from 0 to 30 m3/s to 0 to 250 m3/s, respectively. These differences underscore the strong influence of regional climate on model performance.
Furthermore, in the SRB, observed monthly streamflow hydrographs do not align closely with precipitation timing in the SWAT and GWLF simulations, whereas in the SSB, a tighter correspondence is evident. This observation aligns with the model parameterization results, indicating a more pronounced rainfall–runoff retention effect in the semi-arid northern watershed. The disparity arises from fundamental differences in runoff generation mechanisms. The SRB, situated in an arid to semi-arid climate zone, experiences predominantly short-duration, high-intensity storms that generate infiltration-excess runoff [40]. In contrast, the SSB, located in a humid to semi-humid region with more sustained rainfall, is dominated by saturation-excess runoff [41]. This hydroclimatic contrast is also reflected in the optimal configurations of the RF model. Scenario I, which assumes minimal lag between rainfall and runoff, performs best in the SSB, while Scenario III, incorporating a multi-day lag, yields superior results in the SRB—highlighting the differing temporal dynamics of the rainfall–runoff response in the two basins.
Additionally, the process-based models (SWAT and GWLF) demonstrate a greater capacity to capture peak flow events, whereas the RF model exhibits markedly reduced accuracy under high-flow extremes (Figure 3 and Figure 4)—a pattern consistent with the findings from other studies on data-driven hydrological modeling [42]. This discrepancy arises because the SWAT and GWLF are grounded in explicit physical equations that represent key hydrological processes, such as overland flow, interflow, and baseflow, enabling them to physically extrapolate beyond observed conditions and respond plausibly to extreme rainfall events. In contrast, the RF model is a data-driven, black box approach that effectively learns nonlinear input–output relationships, including those between precipitation, temperature, and streamflow, but it is fundamentally constrained by the scope and representativeness of its training data. When extreme high-flow events are scarce or absent in the training set, RF lacks a physical mechanism to generalize to unprecedented conditions, often resulting in systematic underestimation of peak flows [42]. Such underestimation is further exacerbated by the inherent rarity of extreme events in historical records, which leads to insufficient sampling of high-intensity rainfall scenarios [43]. Consequently, when input variables, such as rainfall intensity, fall outside the range of observed training data, data-driven models tend to produce smoothed or averaged responses, further compromising their ability to capture the true magnitude of peak flows.

3.4. Model Insights and Implications for Future Water Management

Driven by the combined effects of climate change and intensifying anthropogenic activities, natural runoff processes have become highly nonlinear and increasingly complex, posing significant challenges for traditional hydrological models to fully capture their dynamics [44,45,46,47,48]. Machine learning methods offer a promising new pathway for hydrological forecasting. However, their performance is critically dependent on the scientific selection of input variables and the rational optimization of model architecture—precise feature engineering and structural design are essential prerequisites for achieving reliable predictions [43].
In this context, a comparative assessment of process-based models (SWAT and GWLF) and data-driven approaches (RF model) across northern and southern Chinese watersheds yields critical insights for future water resource management. Process-based models consistently outperformed the RF model in simulating peak flow events under extreme hydrological conditions, particularly in southern basins where intensified rainfall extremes linked to climate change are more prevalent. This advantage stems from their mechanistic representation of key hydrological processes—including overland flow, interflow, and baseflow—which enables physically plausible extrapolation beyond the range of observed data [49].
In contrast, the RF model systematically underestimated peak flows in both regions, especially when confronted with non-stationary conditions arising from rapid urbanization, reservoir regulation, and groundwater depletion in the north or unprecedented rainfall intensities in the south—scenarios that are typically underrepresented or absent in historical training datasets [42]. While the RF model demonstrated reasonable accuracy for moderate flows in data-rich and relatively stable environments, its predictive reliability deteriorated sharply under anthropogenic non-stationarity and climate regime shifts, underscoring its inherent vulnerability to extrapolation beyond the limits of training data.
These findings affirm that process-based models remain indispensable for long-term planning under evolving climate and land use scenarios, particularly in regions characterized by complex human–water interactions. Meanwhile, data-driven approaches can become robust tools only when augmented with explicit physical constraints or integrated into hybrid modeling frameworks [50].
From a management perspective, these results suggest that water resource strategies must be regionally differentiated [51]. In northern watersheds, where human interventions dominate hydrological trends, the SWAT and GWLF should be prioritized to evaluate the long-term impacts of policies such as groundwater recharge programs, irrigation efficiency upgrades, and reservoir operation rules. In southern watersheds, where flood risk is escalating due to climate-driven extreme rainfall, process-based models are essential for designing resilient infrastructure, updating flood hazard maps, and informing early warning systems under future climate scenarios. The RF model, despite its limitations in extreme event prediction, holds value in operational settings for short-term flow forecasting and real-time monitoring, particularly when calibrated with high-frequency observational data and constrained by physical bounds—for example, the maximum possible runoff under given antecedent conditions [52].
We, therefore, advocate for an integrated modeling strategy: deploying process-based models as the backbone for scenario analysis and policy evaluation while integrating machine learning for adaptive, data-driven refinement of forecasts, and residual error correction [53]. This hybrid paradigm not only enhances predictive accuracy but also ensures scientific credibility, enabling water managers to make informed, resilient, and adaptive decisions in an era of accelerating environmental uncertainty.

4. Conclusions

This study systematically evaluates the regional applicability of two process-based models (SWAT and GWLF) and a data-driven machine learning model (RF) for monthly streamflow simulation across two hydroclimatically contrasting basins in China: the humid southern basin (SSB) and the semi-arid northern basin (SRB). The results indicate that all models perform markedly better in the SSB, achieving high Nash–Sutcliffe efficiency (NSE) and coefficient of determination (R2) values (>0.85) along with a low mean absolute error (MAE) and root mean square error (RMSE). The SWAT yields the highest overall accuracy in both basins, particularly in simulating peak flows, which can be attributed to its comprehensive physics-based representation of hydrological processes. The GWLF, despite its lower complexity and reduced input requirements, produces reasonably accurate simulations, making it particularly useful in data-limited contexts, such as the SRB, though it exhibits limitations in capturing extreme flow events. RF performs well in the SSB under zero-lag conditions, reflecting a rapid rainfall–runoff response, but it necessitates the incorporation of multi-day lags in the SRB to account for delayed infiltration-excess runoff. However, RF consistently underestimates high-flow events, especially in the SRB, owing to its reliance on training data and absence of embedded physical mechanisms. The pronounced performance disparity between the two basins underscores the critical influence of regional hydrological characteristics—such as precipitation regimes, soil properties, and dominant runoff generation mechanisms (saturation-excess versus infiltration-excess)—on model suitability. We conclude that SWAT is the more reliable choice for physically consistent, extreme event forecasting in heterogeneous environments; the GWLF provides a practical, low-data footprint alternative for regional-scale applications; and RF serves as an efficient, high-accuracy tool in data-rich basins, but it requires more nuanced consideration of rainfall–runoff processes and their underlying physical logic. Therefore, model selection should be guided not only by predictive performance but also by the underlying hydrological context, data availability, and the need for physical realism in decision-making.

Author Contributions

H.C.: conceptualization, data curation, formal analysis, and original draft. R.Y.: methodology, supervision, and writing (reviewing and editing). F.Z.: methodology, supervision, software, and writing (review and editing). J.R.: methodology, supervision, software, and writing (review and editing). T.W.: supervision and writing (reviewing and editing). All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Anhui Province of China (Grant No. 2208085US06) and the Jiangxi Province High-level and High-skilled Leading Talents Cultivation Project (2025).

Data Availability Statement

The data that support the findings of this study are available upon request from the corresponding author (H.C.).

Acknowledgments

The constructive comments and suggestions by the journal referees are gratefully acknowledged.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Luo, X.; Yuan, X.; Zhu, S.; Xu, Z.; Meng, L.; Peng, J. A hybrid support vector regression framework for streamflow forecast. J. Hydrol. 2019, 568, 184–193. [Google Scholar] [CrossRef]
  2. Reis, G.B.; da Silva, D.D.; Fernandes Filho, E.I.; Moreira, M.C.; Veloso, G.V.; de Souza Fraga, M.; Pinheiro, S.A.R. Effect of environmental covariable selection in the hydrological modeling using machine learning models to predict daily streamflow. J. Environ. Manag. 2021, 290, 112625. [Google Scholar] [CrossRef]
  3. Sarah, S.; Shah, W.; Ahmed, S. Modeling and comparing streamflow simulations in two different montane watersheds of western himalayas. Groundw. Sustain. Dev. 2021, 15, 100689. [Google Scholar] [CrossRef]
  4. Shi, R.; Wang, T.; Yang, D.; Yang, Y. Streamflow decline threatens water security in the upper Yangtze river. J. Hydrol. 2022, 606, 127448. [Google Scholar] [CrossRef]
  5. Wu, L.; Zhang, X.; Hao, F.; Wu, Y.; Li, C.; Xu, Y. Evaluating the contributions of climate change and human activities to runoff in typical semi-arid area, China. J. Hydrol. 2020, 590, 125555. [Google Scholar] [CrossRef]
  6. Feng, Z.K.; Liu, S.; Niu, W.J.; Li, B.J.; Wang, W.C.; Luo, B.; Miao, S.M. A modified sine cosine algorithm for accurate global optimization of numerical functions and multiple hydropower reservoirs operation. Knowl.-Based Syst. 2020, 208, 106461. [Google Scholar] [CrossRef]
  7. Abbasi, M.; Farokhnia, A.; Bahreinimotlagh, M.; Roozbahani, R. A hybrid of Random Forest and Deep Auto-Encoder with support vector regression methods for accuracy improvement and uncertainty reduction of long-term streamflow prediction. J. Hydrol. 2021, 597, 125717. [Google Scholar] [CrossRef]
  8. Liu, Y.; Ji, C.; Wang, Y.; Zhang, Y.; Hou, X.; Ma, H. Consideration of streamflow forecast uncertainty in the development of short-term hydropower station optimal operation schemes: A novel approach based on mean-variance theory. J. Clean. Prod. 2021, 304, 126929. [Google Scholar] [CrossRef]
  9. Lorenzo-Lacruz, J.; Morán-Tejeda, E.; Vicente-Serrano, S.M.; Hannaford, J.; García, C.; Peña-Angulo, D.; Murphy, C. Streamflow frequency changes across western Europe and interactions with North Atlantic atmospheric circulation patterns. Glob. Planet. Change 2022, 212, 103797. [Google Scholar] [CrossRef]
  10. Teutschbein, C.; Grabs, T.; Karlsen, R.H.; Laudon, H.; Bishop, K. Hydrological response to changing climate conditions: Spatial streamflow variability in the boreal region. Water Resour. Res. 2015, 51, 9425–9446. [Google Scholar] [CrossRef]
  11. Sadler, J.M.; Appling, A.P.; Read, J.S.; Oliver, S.K.; Jia, X.; Zwart, J.A.; Kumar, V. Multi-Task Deep Learning of Daily Streamflow and Water Temperature. Water Resour. Res. 2022, 58, e2021WR030138. [Google Scholar] [CrossRef]
  12. Yuan, Y.; Koropeckyj-Cox, L. SWAT model application for evaluating agricultural conservation practice effectiveness in reducing phosphorous loss from the Western Lake Erie Basin. J. Environ. Manag. 2022, 302, 114000. [Google Scholar] [CrossRef]
  13. Cho, K.H.; Pachepsky, Y.A.; Oliver, D.M.; Muirhead, R.W.; Park, Y.; Quilliam, R.S.; Shelton, D.R. Modeling fate and transport of fecally-derived microorganisms at the watershed scale: State of the science and future opportunities. Water Res. 2016, 100, 38–56. [Google Scholar] [CrossRef]
  14. Chen, L.; Wei, G.; Zhong, Y.; Wang, G.; Shen, Z. Targeting priority management areas for multiple pollutants from non-point sources. J. Hazard. Mater. 2014, 280, 244–251. [Google Scholar] [CrossRef]
  15. Shen, Z.; Zhong, Y.; Huang, Q.; Chen, L. Identifying non-point source priority management areas in watersheds with multiple functional zones. Water Res. 2015, 68, 563–571. [Google Scholar] [CrossRef]
  16. Tan, M.L.; Gassman, P.W.; Yang, X.; Haywood, J. A review of SWAT applications, performance and future needs for simulation of hydro-climatic extremes. Adv. Water Resour. 2020, 143, 103662. [Google Scholar] [CrossRef]
  17. Sha, J.; Liu, M.; Wang, D.; Swaney, D.P.; Wang, Y. Application of the ReNuMa model in the Sha He river watershed: Tools for watershed environmental management. J. Environ. Manag. 2013, 124, 40–50. [Google Scholar] [CrossRef]
  18. Frederiksen, R.R.; Molina-Navarro, E. The importance of subsurface drainage on model performance and water balance in an agricultural catchment using SWAT and SWAT-MODFLOW. Agric. Water Manag. 2021, 255, 107058. [Google Scholar] [CrossRef]
  19. Niraula, R.; Kalin, L.; Srivastava, P.; Anderson, C.J. Identifying critical source areas of nonpoint source pollution with SWAT and GWLF. Ecol. Model. 2013, 268, 123–133. [Google Scholar] [CrossRef]
  20. Dos Santos, F.M.; de Oliveira, R.P.; Mauad, F.F. Evaluating a parsimonious watershed model versus SWAT to estimate streamflow, soil loss and river contamination in two case studies in Tietê river basin, São Paulo, Brazil. J. Hydrol. Reg. Stud. 2020, 29, 100685. [Google Scholar] [CrossRef]
  21. Chu, H.; Wei, J.; Wu, W.; Jiang, Y.; Chu, Q.; Meng, X. A classification-based deep belief networks model framework for daily streamflow forecasting. J. Hydrol. 2021, 595, 125967. [Google Scholar] [CrossRef]
  22. Kumar, A.; Ramsankaran, R.; Brocca, L.; Muñoz-Arriola, F. A simple machine learning approach to model real-time streamflow using satellite inputs: Demonstration in a data scarce catchment. J. Hydrol. 2021, 595, 126046. [Google Scholar] [CrossRef]
  23. Niu, W.J.; Feng, Z.K. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management. Sustain. Cities Soc. 2021, 64, 102562. [Google Scholar] [CrossRef]
  24. Jimeno-Sáez, P.; Martínez-España, R.; Casalí, J.; Pérez-Sánchez, J.; Senent-Aparicio, J. A comparison of performance of SWAT and machine learning models for predicting sediment load in a forested Basin, Northern Spain. CATENA 2022, 212, 105953. [Google Scholar] [CrossRef]
  25. Ferreira, R.G.; da Silva, D.D.; Elesbon, A.A.A.; Fernandes-Filho, E.I.; Veloso, G.V.; de Souza Fraga, M.; Ferreira, L.B. Machine learning models for streamflow regionalization in a tropical watershed. J. Environ. Manag. 2021, 280, 111713. [Google Scholar] [CrossRef]
  26. Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
  27. Jiang, J.; Li, S.; Hu, J.; Huang, J. A modeling approach to evaluating the impacts of policy-induced land management practices on non-point source pollution: A case study of the Liuxi River watershed, China. Agric. Water Manag. 2014, 131, 1–16. [Google Scholar] [CrossRef]
  28. Yuan, F.; Wei, Y.D.; Gao, J.; Chen, W. Water crisis, environmental regulations and location dynamics of pollution-intensive industries in China: A study of the Taihu Lake watershed. J. Clean. Prod. 2019, 216, 311–322. [Google Scholar] [CrossRef]
  29. Chen, H.; Wang, C.; Ren, Q.; Liu, X.; Ren, J.; Kang, G.; Wang, Y. Long-term water quality dynamics and trend assessment reveal the effectiveness of ecological compensation: Insights from China’s first cross-provincial compensation watershed. Ecol. Indic. 2024, 169, 112853. [Google Scholar] [CrossRef]
  30. Li, M.; Di, Z.; Duan, Q. Effect of sensitivity analysis on parameter optimization: Case study based on streamflow simulations using the SWAT model in China. J. Hydrol. 2021, 603, 126896. [Google Scholar] [CrossRef]
  31. Jeyrani, F.; Morid, S.; Srinivasan, R. Assessing basin blue–green available water components under different management and climate scenarios using SWAT. Agric. Water Manag. 2021, 256, 107074. [Google Scholar] [CrossRef]
  32. Evans, B.M.; Lehning, D.W.; Corradini, K.J.; Petersen, G.W.; Robillard, P.D. A Comprehensive GIS-Based Modeling Approach for Predicting Nutrient Loads in Watersheds. J. Spat. Hydrol. 2002, 2, 1–18. [Google Scholar]
  33. Sharifi, A.; Yen, H.; Boomer, K.M.B.; Kalin, L.; Li, X.; Weller, D.E. Using multiple watershed models to assess the water quality impacts of alternate land development scenarios for a small community. CATENA 2017, 150, 87–99. [Google Scholar] [CrossRef]
  34. Wu, R.-S.; Lin, I.W. Modification of generalized watershed loading functions (GWLF) for daily flow simulation. Paddy Water Environ. 2014, 13, 269–279. [Google Scholar] [CrossRef]
  35. Zhang, L.; Abbasi, M.; Yang, X.; Ren, L.; Hosseini-Moghari, S.-M.; Döll, P. Estimation of the prevalence of non-perennial rivers and streams in anthropogenically altered river basins by random Forest modeling: A case study for the Yellow River basin. J. Hydrol. 2025, 656, 132910. [Google Scholar] [CrossRef]
  36. Saedi, J.; Sharifi, M.R.; Saremi, A.; Babazadeh, H. Assessing the impact of climate change and human activity on streamflow in a semiarid basin using precipitation and baseflow analysis. Sci. Rep. 2022, 12, 9228. [Google Scholar] [CrossRef]
  37. Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
  38. Qi, Z.; Kang, G.; Chu, C.; Qiu, Y.; Xu, Z.; Wang, Y. Comparison of SWAT and GWLF Model Simulation Performance in Humid South and Semi-Arid North of China. Water 2017, 9, 567. [Google Scholar] [CrossRef]
  39. Sha, J.; Swaney, D.P.; Hong, B.; Wang, J.; Wang, Y.; Wang, Z.-L. Estimation of watershed hydrologic processes in arid conditions with a modified watershed model. J. Hydrol. 2014, 519, 3550–3556. [Google Scholar] [CrossRef]
  40. Huang, M.; Gallichand, J. Use of the SHAW model to assess soil water recovery after apple trees in the gully region of the Loess Plateau, China. Agric. Water Manag. 2006, 85, 67–76. [Google Scholar] [CrossRef]
  41. Ren-Jun, Z. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
  42. Hodson, T.O.; Over, T.M.; Foks, S.S. Mean Squared Error, Deconstructed. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002681. [Google Scholar] [CrossRef]
  43. Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
  44. Long, H.; Wang, L.X.; Zhang, J.W.; Liu, Z.; Yang, C. Hydrological simulation and prediction of the Jinghe River Basin based on CMIP6 climate scenario. Water Resour. Hydropower Eng. 2025, 56, 89–103. [Google Scholar]
  45. Wang, X.Y.; Jia, W.H.; Wang, S.; Feng, Z.; Qin, Y.; Zhang, K.; Liu, X.; Li, J. Research on the variation trends of precipitation and runoff in the Pearl River Basin based on innovative trend analysis method. Water Resour. Hydropower Eng. 2025, 56, 52–69. [Google Scholar]
  46. Wang, B.; Xia, C.L.; Song, Z.; Wu, Y.; Zhang, G.; Dai, C. Characteristics of extreme hydrological evolution in Nenjiang River Basin under future climate change scenarios. Water Resour. Hydropower Eng. 2025, 56, 109–123. [Google Scholar]
  47. Zhai, R.; Liu, Z.W.; Dai, H.C.; Liang, L.L.; Jiang, D.G.; Xu, Z.; Yin, Z.K.; Yang, H.; Lv, Z.Y. Characteristic and prediction of runoff change in the Yangtze River Basin. Water Resour. Hydropower Eng. 2023, 54, 87–97. [Google Scholar]
  48. Wen, X.; Sun, Y.; Li, Y.; Tang, S.W.; Shu, X.S. Analysis of annual runoff forecasting methods and the influence of factors in watersheds. Water Resour. Hydropower Eng. 2023, 54, 113–123. [Google Scholar]
  49. Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
  50. Bohl, J.P.; Wood, R.R.; Frank, C.; Astagneau, P.C.; Peters, J.; Brunner, M.I. Hybrid models generalize better to warmer climate conditions than process-based and purely data-driven models. EGUsphere 2025, preprint. [Google Scholar] [CrossRef]
  51. Tapas, M.R.; Howard, G.; Etheridge, R.; Mair, M.; Peralta, A.L. Integrating human decision-making into a hydrological model to accurately estimate the impacts of agricultural policies. Commun. Earth Environ. 2025, 6, 412. [Google Scholar] [CrossRef]
  52. Pham, L.T.; Luo, L.; Finley, A. Evaluation of random forests for short-term daily streamflow forecasting in rainfall- and snowmelt-driven watersheds. Hydrol. Earth Syst. Sci. 2021, 25, 2997–3015. [Google Scholar] [CrossRef]
  53. Altarawneh, E.S.; Sharil, S.; Razali, S.F.M.; Ahmed, A.N.; El-Shafie, A. Hybrid hydrological modeling: Integration of machine learning and conventional hydrology. Phys. Chem. Earth Parts A/B/C 2025, 141, 104150. [Google Scholar] [CrossRef]
Water 17 03498 g001
Figure 1. (a) Location of the SRB and SSB in China; (b) digital elevation model and sub−basin and (c) land use of the SRB; (d) digital elevation model and sub−basin and (e) land use of the SSB. The abbreviations for land use types adhere to those specified in the SWAT model documentation.
Figure 1. (a) Location of the SRB and SSB in China; (b) digital elevation model and sub−basin and (c) land use of the SRB; (d) digital elevation model and sub−basin and (e) land use of the SSB. The abbreviations for land use types adhere to those specified in the SWAT model documentation.
Water 17 03498 g001
Water 17 03498 g002
Figure 2. Schematic diagram of the random forest regression model. The gree dots represent nodes in a decision tree, and the arrows: indicate the flow direction of data or prediction results.
Figure 2. Schematic diagram of the random forest regression model. The gree dots represent nodes in a decision tree, and the arrows: indicate the flow direction of data or prediction results.
Water 17 03498 g002
Water 17 03498 g003
Figure 3. Comparison of observed and simulated streamflow for the SRB using the SWAT (a), GWLF (b), and RF (c) models.
Figure 3. Comparison of observed and simulated streamflow for the SRB using the SWAT (a), GWLF (b), and RF (c) models.
Water 17 03498 g003
Water 17 03498 g004
Figure 4. Comparison of observed and simulated streamflow for the SSB using the SWAT (a), GWLF (b), and RF (c) models.
Figure 4. Comparison of observed and simulated streamflow for the SSB using the SWAT (a), GWLF (b), and RF (c) models.
Water 17 03498 g004
Table 1. Type, source, resolution, and description of the model datasets.
Table 1. Type, source, resolution, and description of the model datasets.
Data TypeData SourceResolution Description
Meteorological dataNational Weather Science Data Center
(http://data.cma.cn/ (accessed on 15 May 2023))		dailyPrecipitation, temperatures, relative humidity, wind speed, solar radiation
Rainfall station dataLocal hydrological bureaudailyPrecipitation
Evapotranspiration dataInstitute of Tibetan Plateau Research, Chinese Academy of Sciences
(http://data.tpdc.ac.cn/zh-hans/ (accessed on 15 May 2023))		monthlyEvapotranspiration
Hydrological dataLocal hydrological bureaudailyStreamflow
DEMGeospatial Data Cloud
(https://www.gscloud.cn/ (accessed on 15 May 2023))		30 mDigital elevation model
Land useResource and Environmental Science and Data Center (https://www.resdc.cn/ (accessed on 15 May 2023))1:1,000,000Land use type
SoilResource and Environmental Science and Data Center (https://www.resdc.cn/ (accessed on 15 May 2023))1:1,000,000Soil type
Table 2. Independent and dependent variables in various scenarios of the streamflow simulation.
Table 2. Independent and dependent variables in various scenarios of the streamflow simulation.
ScenariosIndependent VariableDependent Variable
IPt, ET, AT, RH, WS, SRQt
IIPt-1, ET, AT, RH, WS, SRQt
IIIPt-2, ET, AT, RH, WS, SRQt
IVPt-3, ET, AT, RH, WS, SRQt
Table 3. Model performance statistical metrics.
Table 3. Model performance statistical metrics.
Statistical MetricsFormulaRange
R2 R 2 = ∑ t = 1 n ( O t − O a v g ) ( P t − P a v g ) 2 ∑ t = 1 n ( O t − O a v g ) 2 ∑ t = 1 n ( P t − P a v g ) 2 [0, 1]
NSE N S E = 1 − ∑ t = 1 n ( O t − P t ) 2 ∑ t = 1 n ( O t − O a v g ) 2 [–∞, 1]
MAE M A E = ∑ t = 1 n O t − P t n [0, ∞]
RMSE R M S E = 1 n ∑ t = 1 n ( O t − P t ) 2 [0, ∞]
Table 4. The SWAT and GWLF model parameter selection for calibration in the SRB and SSB.
Table 4. The SWAT and GWLF model parameter selection for calibration in the SRB and SSB.
ModelParameterDescriptionDefault Value RangeCalibrated Value
SRBSSB
SWATv__CN2.mgtSCS runoff curve number35~9846.4780.06
v__ESCO.hruSoil evaporation compensation factor0~10.620.91
v__SOL_AWC.solAvailable water capacity of the soil layer0~10.880.36
v__GW_REVAP.gwGroundwater “revap” coefficient0.02~0.20.040.07
v__GWQMN.gwThreshold depth of water in the shallow aquifer required for return flow to occur0~5000102.5848.87
v__REVAPMN.gwThreshold depth of water in the shallow aquifer for “revap” to occur0~500210.48373.4
v__ALPHA_BF.gwBaseflow alpha factor 0~10.590.88
v__SOL_K.solSaturated hydraulic conductivity0~200023.510
v__SFTMP.bsnSnowfall temperature−20~2010.5913.4
v__RCHRG_DP.gwDeep aquifer percolation fraction0~10.470.23
v__LAT_TTIME.hruLateral flow travel time0~301.860.67
v__SOL_ALB.solMoist soil albedo0~0.250.180.11
v__SURLAG.bsnSurface runoff lag coefficient0.05~2414.875.27
v__SMTMP.bsnSnowmelt base temperature−20~207.034.28
v__SOL_BD.solMoist bulk density0.9~2.51.571.74
GWLFCN2SCS runoff curve number0~100VariesVaries
(40–100) a(45–100) a
Recess coefficientGroundwater discharge coefficient0.10.0040.158
Seepage coefficientGroundwater seepage constant00.0080.02
Unsat Avail WatAvailable soil water capacity-14.059.65
a varies with land use.
Table 5. The performance metrics of various models and scenarios in the SRB and SSB.
Table 5. The performance metrics of various models and scenarios in the SRB and SSB.
WatershedModelScenarioModel Performance Metrics Calibration (Validation)
R2NSEMAERMSE
SRBSWAT-0.870.861.021.35
(0.86)(0.60)(1.09)(1.29)
GWLF-0.830.821.071.53
(0.60)(0.58)(1.24)(1.58)
RF I0.900.801.500.88
(0.44)(0.67)(2.00)(1.53)
II0.900.810.851.43
(0.44)(0.48)(1.55)(2.03)
III0.890.790.941.59
(0.63)(0.66)(1.06)(1.36)
IV0.910.790.921.62
(0.53)(0.56)(1.31)(1.75)
SSBSWAT-0.970.974.085.72
(0.96)(0.96)(6.08)(9.05)
GWLF-0.930.926.848.87
(0.96)(0.96)(7.40)(9.66)
RF I0.960.945.218.58
(0.91)(0.90)(7.82)(10.37)
II0.960.964.678.26
(0.85)(0.89)(8.69)(12.68)
III0.970.964.447.65
(0.89)(0.88)(8.71)(11.84)
IV0.970.964.527.59
(0.90)(0.89)(8.53)(11.33)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ye, R.; Zhang, F.; Ren, J.; Wu, T.; Chen, H. Comparison of Process-Based and Machine Learning Models for Streamflow Simulation in Typical Basins in Northern and Southern China. Water 2025, 17, 3498. https://doi.org/10.3390/w17243498

AMA Style

Ye R, Zhang F, Ren J, Wu T, Chen H. Comparison of Process-Based and Machine Learning Models for Streamflow Simulation in Typical Basins in Northern and Southern China. Water. 2025; 17(24):3498. https://doi.org/10.3390/w17243498

Chicago/Turabian Style

Ye, Rui, Feng Zhang, Jiaxue Ren, Tao Wu, and Haitao Chen. 2025. "Comparison of Process-Based and Machine Learning Models for Streamflow Simulation in Typical Basins in Northern and Southern China" Water 17, no. 24: 3498. https://doi.org/10.3390/w17243498

APA Style

Ye, R., Zhang, F., Ren, J., Wu, T., & Chen, H. (2025). Comparison of Process-Based and Machine Learning Models for Streamflow Simulation in Typical Basins in Northern and Southern China. Water, 17(24), 3498. https://doi.org/10.3390/w17243498

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop