Effects of SDS Surfactant on Oxygen Transfer in a Fine-Bubble Diffuser Aeration Column

Abstract

Aeration is one of the most energy-intensive operations in wastewater treatment plants, with its efficiency strongly affected by the presence of surfactants. This study investigates the impact of Sodium Dodecyl Sulphate (SDS) on oxygen mass transfer using a commercial fine-bubble diffuser. Oxygen transfer experiments were performed under varying air flow rates and SDS concentrations. Key parameters, including the volumetric mass transfer coefficient ($k_{L}a$), gas holdup, bubble size, and interfacial area, were experimentally measured and analysed. SDS reduces the average bubble diameter by up to 50%; above 4 mg/L, further increases in concentration do not change the bubble size. Gas holdup increases by approximately 2% per mg L⁻¹ of SDS, and a new empirical correlation was proposed to predict gas holdup as a function of air flow rate and surfactant concentration, achieving an R² of 0.97 with deviations below 10%. Despite the increase in interfacial area, SDS strongly suppresses interfacial turbulence, reducing the liquid-side mass transfer coefficient ($k_L$) by up to 70%, which ultimately leads to a significant loss of overall oxygen transfer efficiency. The Sardeing model, originally developed for single bubbles, successfully predicted $k_L$ within ±15% of the experimental values, demonstrating its potential as a practical tool for estimating oxygen transfer in aeration systems. These findings highlight the substantial impact of surfactants on fine-bubble aeration performance and underscore the need to account for their effects in the design and operation of industrial aeration systems.

1. Introduction

Wastewater treatment plants (WWTPs) play a strategic role in protecting the environment, safeguarding public health, and promoting the sustainable use of water resources [1]. Among the various unit operations in WWTPs, aeration is one of the most energy-intensive processes, accounting for up to 70% of the total energy consumption in a typical plant [2]. Over the past three decades, fine-bubble aeration has become widely adopted in activated sludge systems due to its high oxygen transfer efficiency in clean water. However, a major limitation of this system is the significant reduction in oxygen transfer efficiency when operating in wastewater, which can decrease by 40% to 70% compared to clean water [3].

One of the main factors contributing to this reduction is the presence of surfactants. Surfactants are surface-active agents commonly used in soaps and cleaning products. These amphiphilic molecules tend to accumulate at gas–liquid interfaces, where they significantly reduce interfacial tension as their concentration increases [4]. However, this reduction continues only up to a point, the Critical Micelle Concentration (CMC), beyond which additional surfactant does not further decrease the interfacial tension. Surfactants accumulate at the bubble interface, influencing mass transfer through two opposing mechanisms: (i) increasing the interfacial area by promoting the formation of smaller bubbles, and (ii) reducing the liquid-side mass transfer coefficient ($k_L$) by decreasing bulk fluid disturbance through resistance to interfacial motion [5,6,7].

Numerous experimental studies have investigated the effects of surfactants on single-bubble behaviour, with some focusing specifically on the kinetics of surfactant adsorption at the bubble interface and the transient nature of this process [5,8]. In such systems, several key phenomena have been observed: (i) a reduction in terminal velocity due to increased interfacial rigidity [9]; (ii) a decrease in bubble size resulting from changes in bubble formation dynamics [10,11]; and (iii) a reduction in the liquid-side mass transfer coefficient [6,12]. Local-scale measurements obtained in these studies are crucial, as they provide direct insight into the underlying physicochemical mechanisms that govern bubble motion and mass transfer. These detailed observations form the basis for developing predictive models that estimate parameters such as the mass transfer coefficient [13,14,15], bubble drag coefficient [16,17], and bubble generation size [18] in the presence of surfactants under single-bubble conditions.

While single-bubble investigations offer valuable fundamental understanding, they inherently simplify the complex hydrodynamics of practical systems. To overcome these limitations, several researchers have investigated the behaviour of surfactants in multi-bubble systems [19,20,21,22,23], where bubble interactions and coalescence inhibition become more significant [24,25,26,27,28]. Some research has specifically focused on the impact of surfactants on fine-bubble diffusers used in aeration systems for WWTPs, showing that mass transfer efficiency can decrease by more than 50% [3,4,29]. Chen et al. [29] developed a correlation to predict the $k_L$ in a commercial fine-bubble diffuser operating with surfactants; however, their study was limited to a single airflow rate and did not include bubble size measurements, which are essential for accurately characterizing mass transfer behaviour [13,20,30,31]. A promising approach is the general model proposed by Sardeing et al. [13] for single bubbles, which predicts the $k_L$ in the presence of any surfactant, based on models developed for bubbles with rigid [32] and free interfaces [33]. Although this model has been tested in multi-bubble systems, such as bubble columns [19], it has not yet been validated for use in commercial diffusers.

This study aims to build on previous work by experimentally investigating the effect of SDS on oxygen mass transfer using a commercial fine-bubble diffuser under conditions representative of wastewater treatment applications. A comprehensive database was compiled, including measurements of volumetric mass transfer coefficient ($k_{L}a$), gas holdup, bubble size distribution, interfacial area concentration and $k_L$, all of which govern the overall mass transfer process and were systematically analysed. In addition, a correlation was developed to describe gas holdup as a function of airflow rate and surfactant concentration. Finally, the experimental results were compared with the different models to evaluate their ability to predict the $k_L$ behaviour of a commercial diffuser operating in the presence of surfactants.

2. Materials and Methods

2.1. Materials

For the experiments, deionized water was obtained using the TW40-1812-50 unit (ALPSPRING, Inc., Hsinchu, Taiwan), which produces water with a conductivity of 40 μS/cm. This system was used to minimize the natural hardness of the local water supply. The surfactant used is SDS [CAS No: 151-21-3, molecular weight 288.38 g/mol], which was supplied by Thermo Fisher Scientific (Waltham, MA, USA) with a purity of 97.4%. In this study, surfactant concentrations of 0, 2, 4, 6, and 8 mg/L were used, which are commonly applied in similar research [3,29,34]. These concentrations cover the typical range of surfactants found in raw municipal wastewater [35]. The surface tension values obtained for the different surfactant concentrations were 73.0, 69.9, 62.8, 61.1, and 57.7 mN/m for 0, 2, 4, 6, and 8 mg/L, respectively. In this study, these values were determined using the pendant-drop method, following the protocol described by Berry et al. [36] and were analysed using the software developed by Huang et al. [37].

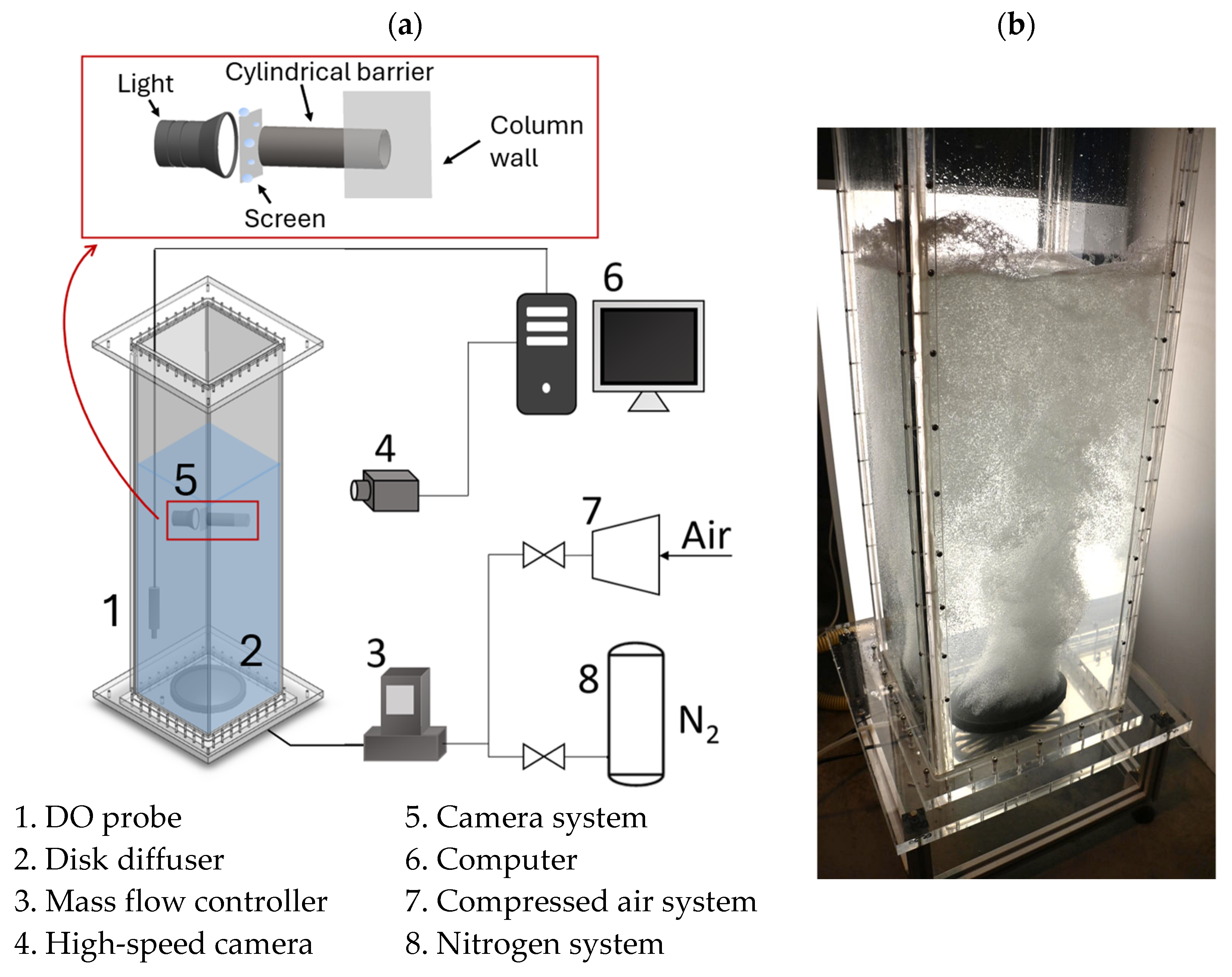
2.2. Experimental Setup

Figure 1a shows a schematic of the experimental setup, which consists of a square column with dimensions of 0.4 m × 0.4 m × 0.8 m. A fine-pore rubber diffuser (D-Rex model with a Flexnorm membrane from OTT Group, Langenhagen, Germany) with a pore size of 1 mm was installed at the base of the column. The airflow rate is controlled using a mass flow controller (EL-FLOW F-203AV, Bronkhorst, Vorden, The Netherlands). An image of the column in operation can be seen in Figure 1b.

Oxygen transfer tests were conducted using an OXYPro PSt7 sensor from PreSens (Regensburg, Germany). To remove dissolved oxygen from the water, nitrogen gas was supplied through the diffuser. The gas holdup was determined by recording the increase in the liquid–gas interface height ($∆h$) with a camera.

Bubble characteristics, including size and aspect ratio, were analysed using a high-speed CCD camera (NR4-S2, IDT Vision, Pasadena, CA, USA). Because bubbles rising near the walls are not representative of the bulk flow, the camera system was designed to capture only those in the central region of the column. Its schematic layout was shown in Figure 1a. The system includes a cylindrical barrier placed along the inner wall and extending halfway across the column (0.2 m). This barrier prevented peripheral bubbles from entering the observation area, ensuring that only bubbles from the central flow zone were recorded. Beyond the end of the barrier, a translucent panel (screen) was mounted on the opposite side of the column and back-illuminated, providing uniform lighting for clear visualization of the bubbles.

2.3. Methods

Oxygen transfer and bubble characteristics were evaluated for five different surfactant concentrations (0, 2, 4, 6, and 8 mg/L) and five gas flow rates (20, 40, 60, 80, and 100 L/min). For each combination of surfactant concentration and flow rate, several key parameters were determined: the volumetric mass transfer coefficient, bubble size and shape, gas holdup, interfacial area, and the liquid-side mass transfer coefficient. All experiments were conducted at a water temperature of 13 ± 1 °C, which is typical of wastewater conditions during winter [38], when contaminant loads are generally higher.

The methodology applied to obtain each of these parameters is described in detail in the following subsections.

2.3.1. Volumetric Mass Transfer Coefficient

Oxygen transfer experiments were performed in accordance with the ASCE standard method [39]. Prior to aeration, the dissolved oxygen concentration was reduced to below 0.5 mg/L. Air was then introduced, and the temporal evolution of oxygen concentration was measured. The volumetric mass transfer coefficient ($k_{L}a$) and the equilibrium oxygen concentration (${\mathrm{C}}_{\mathrm{\infty }}^{\mathrm{*}}$) were obtained by fitting Equation (1) to the oxygenation curve.

$$\mathrm{C}={\mathrm{C}}_{\mathrm{\infty }}^{\mathrm{*}}-\left({\mathrm{C}}_{\mathrm{\infty }}^{\mathrm{*}}-{\mathrm{C}}_0\right)\mathrm{e}\mathrm{x}\mathrm{p}(-k_{L}a·\mathrm{t})$$

(1)

where ${\mathrm{C}}_0$ and $\mathrm{C}$ are the concentrations at time zero and at time $\mathrm{t}$, respectively. The adjusted parameters are corrected to standard conditions, and with these, the SOTE is calculated (2).

$$\mathrm{S}\mathrm{O}\mathrm{T}\mathrm{E}={\displaystyle \frac{k_L{a}_{20} C_{\infty 20}^{*} V}{W_{O_2}}}$$

(2)

where $k_L{a}_{20}$ is the volumetric mass transfer coefficient corrected to standard conditions, $C_{\mathrm{\infty }20}^{*}$ is the equilibrium oxygen concentration corrected to standard conditions, $V$ is the aerated liquid volume, and $W_{O_2}$ is the mass flow rate of oxygen supplied per unit time.

2.3.2. Bubble Equivalent Diameter

A high-speed CCD camera was used to determine the average bubble equivalent diameter. To ensure that only bubbles from the centre of the plume were recorded, the cylindrical barrier described in the experimental setup was employed. Images were acquired at 20 cm and 70 cm above the diffuser membrane to evaluate bubble size evolution caused by coalescence and breakup. Example images of the bubbles captured with the high-speed camera are shown in Figure 2. Bubble dimensions were obtained through manual image analysis. Four points were selected along the bubble contour to fit the major and minor axes of each bubble.

From the major and minor axes of each bubble, the bubble diameter was determined. In mass transfer studies, there are several ways to define a global equivalent bubble diameter, and one of the most commonly used is the Sauter diameter, which corresponds to the diameter of a sphere with the same volume-to-surface ratio as the total population of bubbles. The method described by Vasconcelos et al. [20] was applied to obtain this diameter. First, an equivalent diameter for each bubble was determined by fitting its shape according to Equation (3).

$$d_{eq,i}=\sqrt[3]{E_i^2{e}_i}$$

(3)

where $E$ and $e$ represent the major and minor axes, respectively, of the ellipsoidal bubble in a two-dimensional projection. Subsequently, the Sauter mean diameter ($d_{32}$) was determined using Equation (4), as defined by Shah et al. [40], based on the number of bubbles $n_i$ with equivalent diameters $d_{eq,i}$.

$$d_{32}={\displaystyle \frac{{\sum }_i{n}_i{d}_{eq,i}^3}{{\sum }_i{n}_i{d}_{eq,i}^2}}$$

(4)

2.3.3. Gas Holdup

Gas holdup plays an important role in mass transfer processes, as it is required to estimate the interfacial area between the gas and liquid phases, a key parameter governing oxygen transfer efficiency. In this study, gas holdup was determined from the variation in liquid column height ($∆h$) and the total column height ($H$), according to Equation (5).

$$\epsilon ={\displaystyle \frac{∆h}{∆h+H}}$$

(5)

To measure the variation in column height, recordings were captured using a camera, as surface oscillations required analysis of multiple frames. For each experimental condition, a total of 20 images were analysed. The interface was manually traced by selecting several equally spaced points along it in each image, and a straight line was fitted to these points to determine the column height in that frame. Figure 3a shows the manually selected points at the interface, along with the fitted line (solid red) and the 3σ limit (dashed red).

Figure 3b shows the relationship between flow rate and the increase in interface level for clean water, along with the standard deviation of the interface position at each flow rate. Despite the relatively high variability, the mean values follow a clear trend. From these data, it is possible to estimate the gas holdup.

2.3.4. Interfacial Area

The interfacial area, $a$, is estimated from the gas holdup and the average Sauter diameter using Equation (6) [41].

$$a={\displaystyle \frac{6 \epsilon }{d_{32}(1-\epsilon )}}$$

(6)

This expression is derived under the assumption that the bubbles are spherical and uniformly distributed within the liquid phase. In this context, the Sauter diameter provides an equivalent measure that preserves the interfacial area per unit volume. Gómez-Díaz et al. [30] reported good agreement between this approach and the chemical method for determining interfacial area.

2.3.5. Mass Transfer Coefficient

The mass transfer coefficient ($k_L$) is determined using Equation (7), by dividing the volumetric mass transfer coefficient ($k_{L}a$) by the interfacial area ($a$).

$$k_L={\displaystyle \frac{k_{L}a}{a}}$$

(7)

2.3.6. Experimental Uncertainty

To contextualize the magnitude of the observed surfactant effects, we estimated the repeatability/uncertainty of the main experimental quantities. Based on repeated oxygen-transfer runs, the variability of $k_{L}a$was on the order of 5%. Bubble-size statistics were obtained from the measured bubble-size distributions; the associated uncertainty in the $d_{32}$was estimated to be below 6%. The uncertainty of gas holdup/void fraction was likewise estimated to be below 6%. Overall, the changes reported in this work are larger than these uncertainty levels, supporting the robustness of the observed trends.

3. Results

This section presents experimental results on the effects of SDS surfactant concentration and airflow rate on the key parameters governing oxygen transfer in a bubble column equipped with a membrane diffuser. By analysing these parameters both individually and in combination, a comprehensive understanding of the mechanisms controlling oxygen transfer efficiency in the presence of surfactants can be achieved. The analysis focuses on the volumetric mass transfer coefficient, bubble size and shape, gas holdup, interfacial area, and the liquid-side mass transfer coefficient.

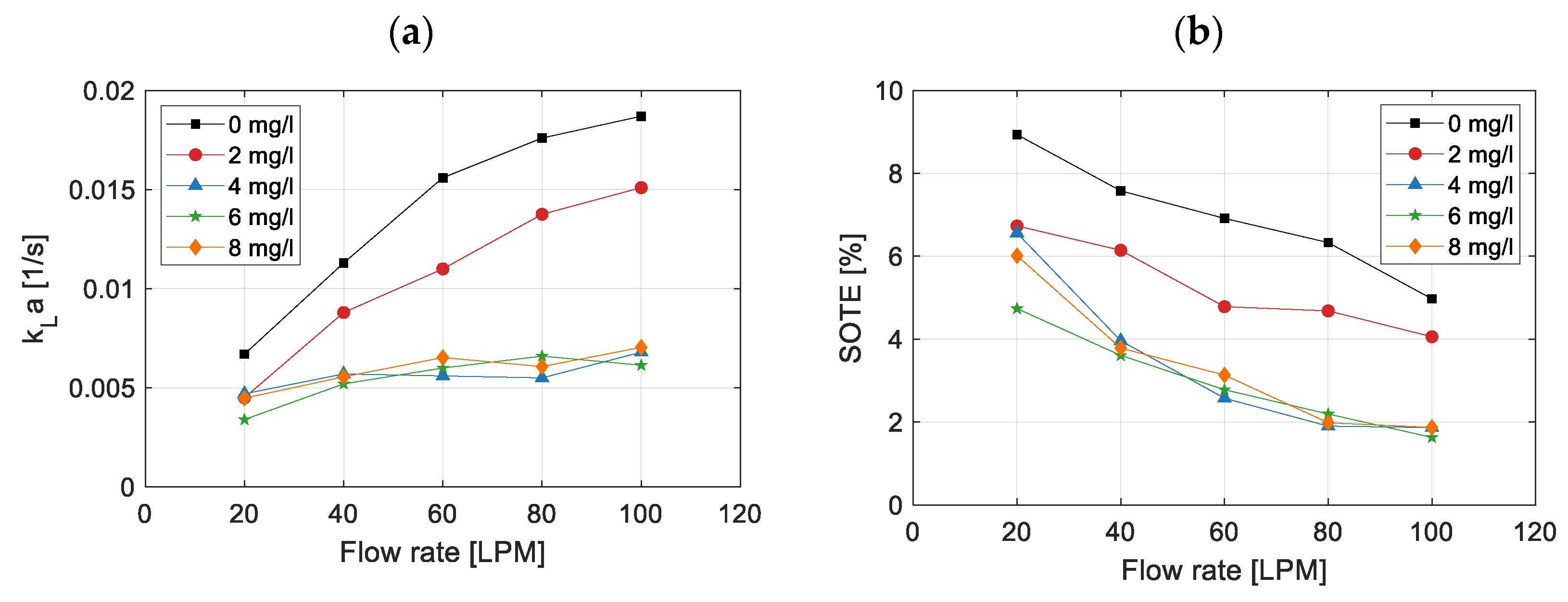
3.1. Effect on Volumetric Mass Transfer Coefficient

Figure 4a shows how the $k_{L}a$ varies with airflow rate for different SDS concentrations. As expected, $k_{L}a$ increases with increasing airflow rate, mainly due to the enlargement of the gas–liquid interfacial area. Conversely, higher surfactant concentrations result in a decrease in $k_{L}a$. A significant reduction is observed when comparing clean water with solutions containing 2 mg/L and 4 mg/L of surfactant. However, beyond 4 mg/L, further increases in surfactant concentration have a minimal additional effect on $k_{L}a$, suggesting a saturation effect at the interface. This trend was also reported by Chen et al. [29], who found that the most significant decline in $k_{L}a$ occurred within the 0–5 mg/L range of SDS concentration.

The increase of $k_{L}a$ with air flow rate means a decrease of the efficiency of oxygen transfer. This trend clearly appears by plotting the SOTE as a function of flow rate (Figure 4b). This indicates that although more oxygen is transferred at higher flow rates, the process becomes less efficient. A decrease in SOTE is also observed with increasing surfactant concentration.

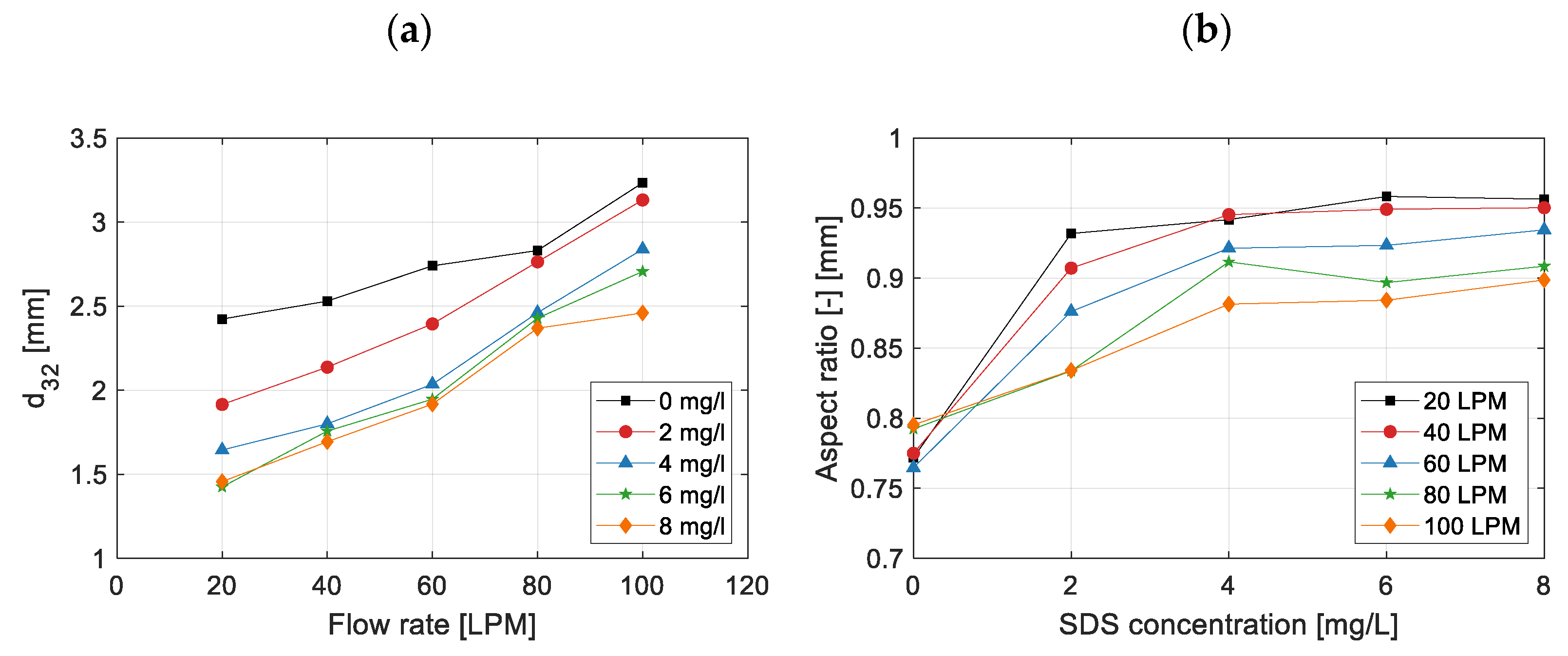
3.2. Effect on Bubble Size and Shape

Figure 5a shows the variation in the mean Sauter diameter within the reactor, calculated as the average value between 20 cm and 70 cm from the diffuser membrane, across different flow rates and SDS concentrations. The data reveal two main trends. First, the bubble Sauter diameter decreases as the surfactant concentration increases, until it reaches a nearly constant value, where further increases have little effect. Second, higher flow rates result in larger bubble diameters. Both effects directly influence the interfacial area concentration and, consequently, the mass transfer behaviour.

According to Liu et al. [34], the reduction in bubble size due to surfactant addition can be attributed to two primary mechanisms: bubble generation and coalescence inhibition. At a certain concentration, coalescence would be completely inhibited; this concentration is known as the Critical Coalescence Concentration (CCC) [42]. To observe this reduction, the variation in the bubble size distribution (BSD) for different flow rates and surfactant concentrations is plotted in Figure 6, measured at 20 cm and 70 cm from the diffuser membrane. For the first mechanism, it is particularly evident at 20 cm that the BSD decreases with increasing surfactant concentration, primarily due to the reduction in surface tension, which controls bubble growth and detachment [10,12,13,14]. This occurs because the presence of surfactant reduces surface tension, promoting the formation of smaller bubbles, as the detachment size is governed by the balance between buoyancy and surface tension forces [12]. Loubière and Hébrard [10] suggest that at low flow rates, bubble size is controlled by dynamic surface tension through surfactant adsorption-diffusion, whereas at high flow rates static surface tension dominates.

The second mechanism is related to bubble coalescence, as surfactants accumulate at the gas–liquid interface, generating repulsive forces between adjacent bubbles and thereby preventing coalescence [26,43]. However, this effect is not clearly observed in the Bubble Size Distribution (BSD) shown in Figure 6, as the variation between the two heights is minimal. This could be due to coalescence primarily occurring during the early stages of bubble formation, particularly near the diffuser. Despite this, a slight increase in bubble size can still be observed between 20 cm and 70 cm in the clean water cases.

In addition to the effect of surfactants on bubble size, increasing the gas flow rate also results in larger bubbles, as shown in Figure 5a. This occurs due to changes in bubble formation dynamics, enhanced coalescence, and variations in the hydrodynamic conditions. The increase in flow rate alters the overall hydrodynamics of the column, intensifying the liquid circulation and increasing the number of bubbles that recirculate along the walls, all of which influence the resulting bubble size. At higher gas flow rates, the influence of the surfactant on bubble size becomes less significant. The BSD data in Figure 6 further illustrate the impact of flow rate, with larger bubbles becoming more abundant as the gas flow rate increases.

Finally, the Marangoni effect induced by surfactants reduces bubble surface mobility, driving the aspect ratio toward unity and resulting in more spherical bubbles [44], as illustrated in Figure 5b. Additionally, the reduction in bubble size, as previously discussed, also contributes to this change in aspect ratio.

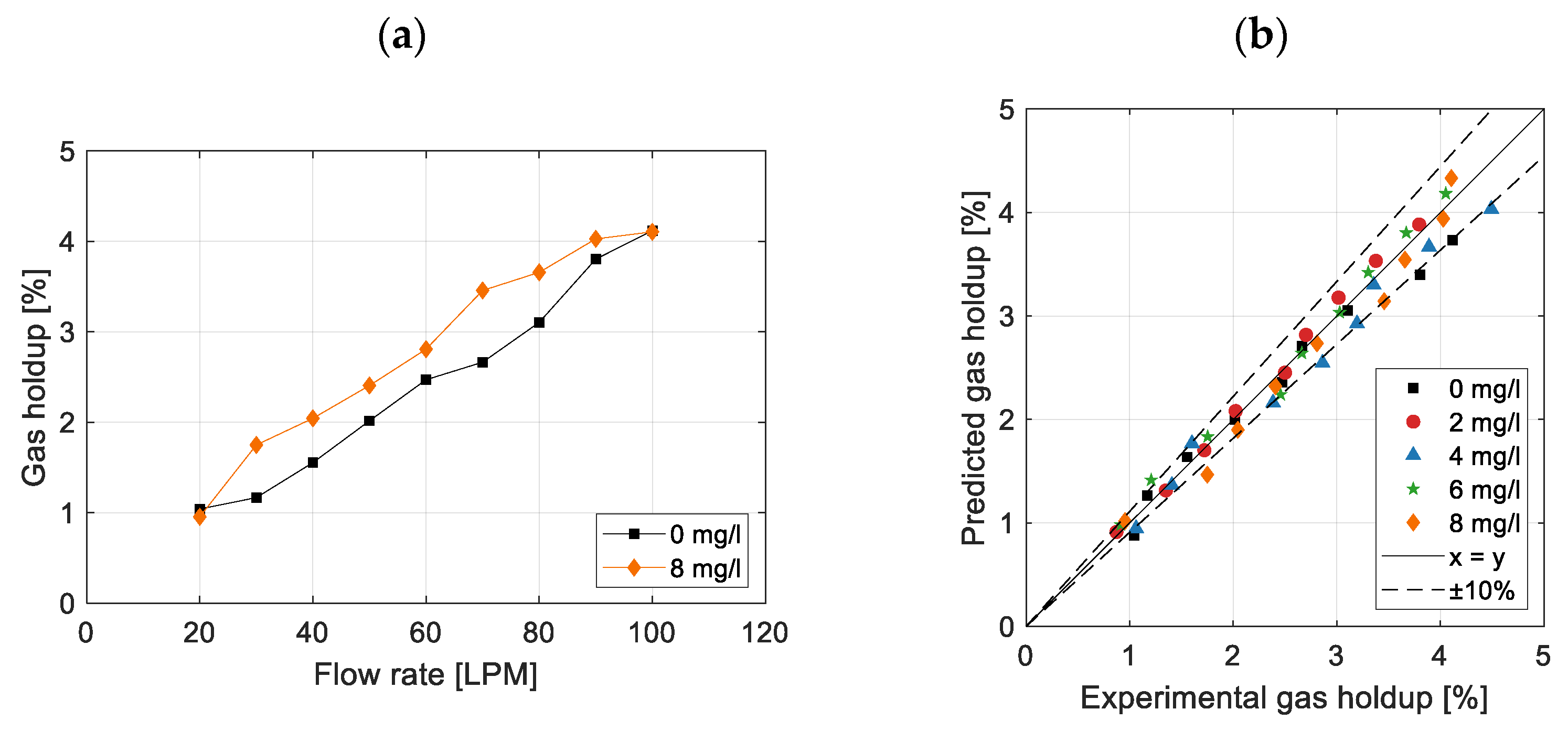
3.3. Effect on Gas Holdup

As illustrated in Figure 7a, an increase in flow rate results in higher gas holdup. Another observed effect is that increasing the surfactant concentration also leads to an increase in holdup, a trend consistent with previous reports in the literature [45,46,47]. For clarity, the cases corresponding to 2, 4, and 6 mg/L of surfactant were omitted from Figure 7a to better illustrate this variation. The observed increase in holdup is attributed to a reduction in bubble rise velocity, which prolongs bubble residence time within the liquid phase. According to Li et al. [48], the decrease in bubble rise velocity arises from two main factors: (i) the reduction in bubble size, and (ii) the asymmetric accumulation of surfactants on the bubble surface, which induces surface tension gradients and enhances drag force, a phenomenon known as the Marangoni effect. Consequently, bubbles remain suspended in the liquid for a longer period, leading to an overall increase in gas holdup.

Inspired by Moraveji et al. [45], who correlated gas holdup with superficial gas velocity and surfactant concentration in an airlift reactor, the experimental data were fitted using these two parameters, with the original equation modified to account for the effect of zero surfactant concentration. The experimental data were used to fit Equation (8).

$$\epsilon =0.036U_G^{0.9}(1+0.02C_S)$$

(8)

where $U_G$ is expressed in cm/s, $C_s$ in mg/L, and $\epsilon$ is dimensionless. Note that the coefficient of determination (R² = 0.97) indicates an excellent agreement between the experimental and predicted values. Most of the experimental data fall within ± 10% of the fitted correlation. According to this equation, the gas holdup increases by approximately 2% for each additional milligram per litre of SDS within the studied range.

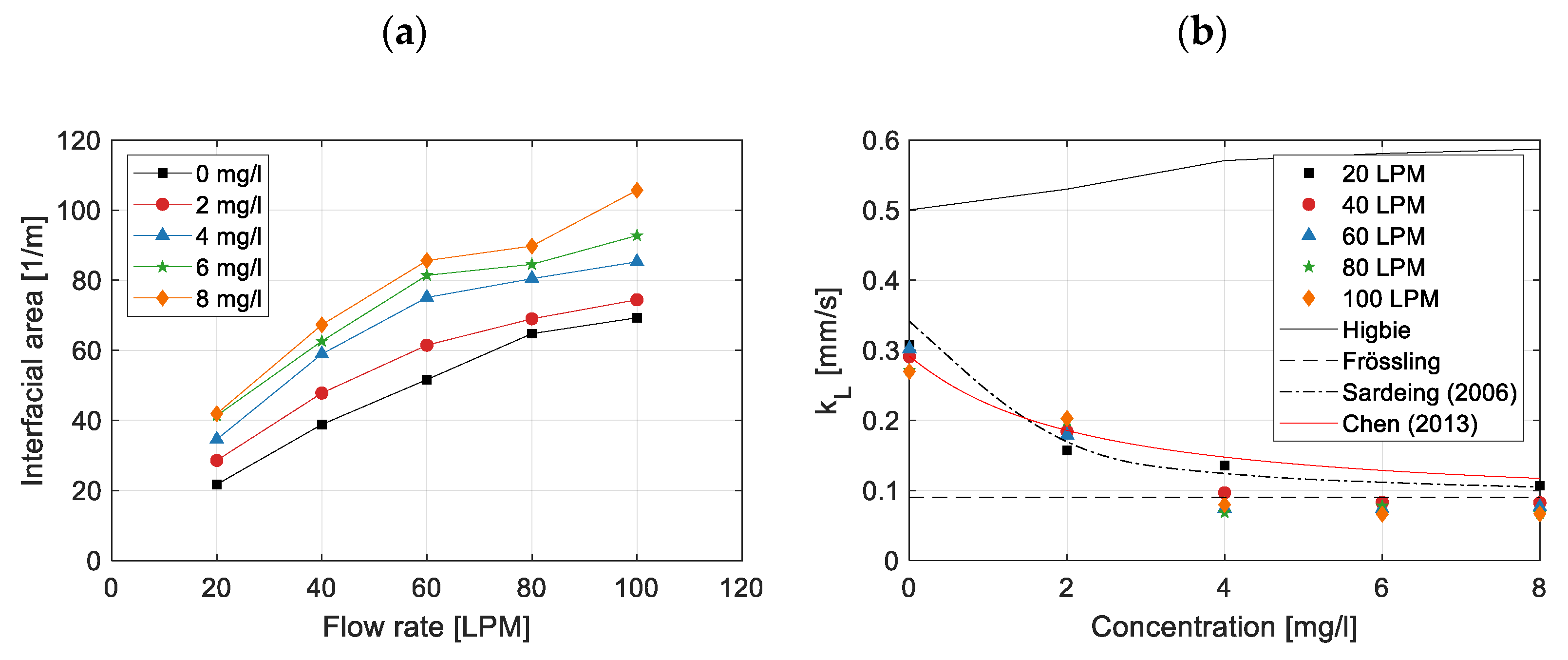
3.4. Effect on Interfacial Area

Figure 8a shows how the interfacial area varies with gas flow rate and surfactant concentration. To minimize uncertainty in the calculation of interfacial area, gas holdup was obtained from the correlation in Equation (8). As expressed in Equation (6), the interfacial area reflects the competition between bubble size and gas holdup. Increasing the gas flow rate tends to produce larger bubbles, which reduces interfacial area; at the same time, it increases gas holdup, which enhances interfacial area. The observed trend results from the balance of these opposing effects. Under these conditions, the increase in gas hold-up generally dominates, yielding a net rise in interfacial area with flow rate.

Surfactants also have a marked impact. In their presence, the gas holdup increases slightly while bubble size decreases significantly; both effects contribute to a clear increase in interfacial area. With increasing surfactant concentration, the interfacial area grows more slowly and eventually reaches a plateau. Because overall oxygen transfer depends on the product $a · k_L$, the increase in interfacial area discussed above must be interpreted together with possible changes in the liquid-side mass transfer coefficient $k_L$. The analysis of $k_L$ is presented next.

3.5. Effect on Mass Transfer Coefficient

Although Figure 8a indicates that surfactants enlarge the interfacial area, Figure 8b reveals that the liquid-side mass transfer coefficient $k_L$ remains nearly constant with flow rate (with a slight deviation at 20 LPM) and decreases systematically with surfactant addition. This decrease is attributed to the adsorption of surface-active molecules at the gas–liquid interface, which suppresses surface renewal and interfacial turbulence [5,6,7], thereby hindering molecular diffusion. Consequently, despite the growth in interfacial area, the drop in $k_L$ dominates and leads to a net reduction in oxygen transfer. A pronounced reduction in $k_L$ is observed between 0 and 4 mg/L—on the order of 70%. Beyond this point, the increase from 4 to 8 mg/L results in only minimal changes, with $k_L$ remaining essentially constant. This behaviour is consistent with previous studies [29,34], which reported a reduction of approximately 60% from 0 to 4 mg/L, followed by a tendency to stabilize. Furthermore, in a study using wastewater with added SDS, a substantial decrease in mass transfer was observed for surfactant concentrations between 0 and 5 mg/L, after which the values remained nearly constant up to 12 mg/L [49].

To interpret these trends, several models were compared with the $k_L$ data obtained in this study. Predictions used the mean Sauter bubble diameter evaluated for the five gas flow rates at each surfactant concentration; the bubble slip velocity was estimated with Tomiyama’s correlation [50] for partially contaminated water.

The limiting cases of interfacial mobility are first analysed, providing upper and lower bounds for $k_L$. The clean, fully mobile limit is represented by the penetration theory result of Higbie [33], which assumes rapid surface renewal and negligible interfacial shear resistance. In that idealised scenario, $k_L$ scales with the square root of the contact (or renewal) time and depends on the bubble slip velocity and size as

$$k_L^{\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{b}\mathrm{i}\mathrm{e}}=2\sqrt{{\displaystyle \frac{D{u}_r}{\pi d_b}}}$$

(9)

where D is the diffusion coefficient of oxygen in water, $u_r$ is the bubble slip velocity and $d_b$ is the bubble diameter. In this study, the Sauter diameter was used. The opposite extreme corresponds to a rigid, fully contaminated interface that suppresses motion at the surface and eliminates internal circulation; the classical Frössling correlation [32] captures this behaviour:

$$k_L^{Frössling}={\displaystyle \frac{D}{d_b}}(2+0.6R{e}^{1/2}S{c}^{1/3})$$

(10)

with $Re$ and $Sc$ the Reynolds and Schmidt numbers, respectively, evaluated from $u_r$, $d_b$, and the fluid properties. As shown in Figure 8b, the measurements lie well below Higbie even for deionized water, which is consistent with partial interfacial contamination by trace impurities that produce Marangoni stresses and reduce surface mobility. At high surfactant concentrations, the data approach the rigid limit, and the Frössling correlation aligns more closely. Nevertheless, the Frössling correlation slightly overpredicts $k_L$, as observed in previous studies, which has been attributed to a decrease in the diffusion coefficient and oxygen saturation [47,51].

The models developed by Higbie and Frössling do not account for the effect of surfactant concentration; rather, they represent the limiting cases of mass transfer for a clean (free) and a fully contaminated (rigid) bubble interface, corresponding to the maximum and minimum $k_L$ values, respectively. To better describe the intermediate conditions that occur in the presence of surfactants, several models have been proposed that express $k_L$ as a function of surfactant concentration. In this work, two of these correlations are analysed. The first one, proposed by Chen et al. [29], describes the decrease in $k_L$ for SDS solutions using a ceramic diffuser. The second, developed by Sardeing et al. [13], is a more general model for single bubbles that incorporates the effects of surfactant type and concentration, and is based on the limiting cases represented by the Higbie and Frössling models.

The model presented by Chen et al. [29] is useful for comparing the results with other experimental data obtained using the same surfactant (SDS) and a porous diffuser. Equation (11) shows the correlation proposed by Chen et al. for SDS, which relates the mass transfer coefficient in the presence of surfactants ($k_L^{\mathrm{C}\mathrm{h}\mathrm{e}\mathrm{n}}$) to that obtained with tap water ($k_L^{Water}$).

$$k_L^{\mathrm{C}\mathrm{h}\mathrm{e}\mathrm{n}}=k_L^{Water}(1.23-0.22{\mathrm{e}}^{\mathrm{S}\mathrm{e}/0.67})$$

(11)

The correlation is expressed as a function of ${\mathrm{S}}_{\mathrm{e}}$, the dimensionless interfacial coverage ratio, which is defined by Equation (12).

$${\mathrm{S}}_{\mathrm{e}}={\displaystyle \frac{\mathrm{K}·\mathrm{C}}{1+\mathrm{K}·\mathrm{C}}}$$

(12)

where K is the adsorption constant at equilibrium, which is obtained from the data presented by Chen et al. [29], and C is the surfactant concentration. In this framework, ${\mathrm{S}}_{\mathrm{e}}$ condenses the chemistry (adsorption strength and concentration) into a single mobility parameter that attenuates $k_L$ relative to the water baseline. When applied to the data (Figure 8b), the 20 LPM condition exhibits the closest agreement with Chen’s correlation, which is plausible because Chen’s superficial gas velocity (~0.06 cm/s) is nearest to the lowest-velocity case (20 LPM, ~0.21 cm/s). A clear similarity in trend is observed between Chen’s correlation and the experimental data presented, with the remaining deviations likely arising from differences in diffuser type and experimental conditions, particularly the superficial gas velocity. Two practical notes arise when transporting Chen’s correlation to another industrial diffuser. First, the baseline $k_L^{Water}$ should be defined consistently with the reference water quality and bubble dynamics, and in this study, the experimentally determined value for clean water was used. Second, since the model was developed for a specific surfactant (SDS), it may not be directly applicable to other surfactant types.

In contrast, Sardeing et al. [13] developed a model for $k_L$ that accounts for the effects of surfactant type, surfactant concentration, bubble size, slip velocity, and other parameters. They structured the influence of surfactants on the liquid-side mass transfer coefficient, $k_L$, around the bubble diameter, $d_b$, which serves as a reference parameter describing how interfacial mobility, wake structure, and internal circulation contribute to mass transfer.

• For bubble diameters smaller than 1.5 mm. In this range, $k_L$ is independent of surfactant concentration and corresponds to the mass transfer coefficient for rigid bubbles. In this regime, $k_L$ can be described using the Calderbank and Moo-Young’s correlation [52] or the Frössling correlation (Equation (10)).
• For bubble diameters between 1.5 mm and 3.5 mm. In this range, $k_L$ increases with bubble diameter, but in the presence of surfactants, this increase is significantly reduced. Consequently, $k_L$ varies approximately linearly between the limits corresponding to bubbles smaller than 1.5 mm and larger than 3.5 mm. This study falls within this range, which is the most critical due to the variability of $k_L$ with the bubble diameter. For this reason, it is essential to accurately measure the bubble diameter.
• For bubble diameters larger than 3.5 mm. For this range, $k_L$ does not depend on bubble diameter. The constant $k_L$ is determined by the interfacial coverage (${\mathrm{S}}_{\mathrm{e}}$), the mass transfer coefficient for a clean (surfactant-free) interface ($k_L^0$, given by Higbie’s correlation, Equation (9)), and the mass transfer coefficient for a fully surfactant-saturated interface ($k_L^1$, given by Equation (13)).

$$k_L^1=1.7440K^{-0.0837}{k}_L^{Frössling}$$

(13)

As shown in Figure 8b, the single-bubble model proposed by Sardeing et al. [13] can predict $k_L$ for a membrane diffuser in a bubble column within ±15% of the experimental values. The best agreement is obtained for the 20 LPM case, which corresponds to the lowest flow rate and therefore most closely resembles single-bubble conditions. The model presented by Sardeing et al. [13] shows great promise, demonstrating its potential as a practical tool for estimating oxygen mass transfer in fine-bubble diffusers.

This information is highly valuable for improving and controlling aeration in WWTP reactors because surfactants do not act as a simple efficiency penalty: they alter the bubble size distribution and gas holdup (and thus the interfacial area) while also reducing the $k_L$. Consequently, modelling and design efforts should move beyond a single global correction factor and incorporate surfactant-dependent descriptions of bubble size, gas holdup/interfacial area, and $k_L$, to avoid compensating errors when predicting oxygen transfer. From an operational standpoint, measures that lower the effective surfactant loading at the diffuser—e.g., staged aeration in which a first stage promotes surfactant removal/conditioning and a second stage is optimized for oxygen uptake—can help shift operation toward regimes where oxygen transfer is less inhibited [53].

4. Conclusions

In this work, the influence of SDS on mass transfer in a fine-bubble diffuser was investigated across different airflow rates, analysing the key parameters governing this process. Surfactants produce smaller bubbles and increase gas holdup—thus enhancing a—but they also suppress interfacial turbulence, reducing $k_L$ by up to 70%. Consequently, surfactants significantly decrease overall oxygen transfer, underscoring their strong impact on aeration systems.

Regarding the available interfacial area a, the two main contributing factors, bubble size and gas holdup, were examined separately. Surfactants reduced the average bubble diameter by up to 50%, and their effect became less pronounced at higher airflow rates. Gas holdup increased by approximately 2% per mg/L of SDS, leading to the development of a new empirical correlation that accurately predicts holdup as a function of airflow rate and surfactant concentration (R² = 0.97; deviations <10%).

For $k_L$, airflow rate had little effect, whereas SDS caused substantial reductions. Two predictive models were evaluated: the correlation by Chen et al. [29] reproduced general trends but presented limitations, while the model by Sardeing et al. [13]—a more general approach combining correlations for rigid and mobile bubble interfaces—predicted $k_L$ within ±15% of the experimental values.

Overall, the study highlights the significant role of surfactants in oxygen transfer performance and the need to account for their effects in aeration system design. The strong predictive capability of the Sardeing model demonstrates its potential as a practical tool for estimating oxygen transfer under surfactant-affected conditions.