Characterization of a Multi-Diffuser Fine-Bubble Aeration Reactor: Influence of Local Parameters and Hydrodynamics on Oxygen Transfer

Abstract

Fine-bubble aeration is a core process in wastewater treatment plants (WWTPs). However, the physical mechanisms linking bubble plume hydrodynamics to oxygen transfer performance remain insufficiently quantified under configurations representative of full-scale installations. This study presents a local multi-sensor experimental characterization of a multiple bubble plume system using a 4 × 4 array of commercial membrane diffusers in a pilot-scale aeration tank (2 m³), emulating WWTP diffuser density and geometry. Airflow rate was varied to analyze its effects on mixing and oxygen transfer efficiency. The experimental methodology combines three complementary measurement approaches. Oxygen transfer performance is quantified using a dissolved oxygen probe. Liquid-phase velocity fields are then mapped using Acoustic Doppler Velocimetry (ADV). Finally, local two-phase measurements are obtained using dual-tip Conductivity Probe (CP) arrays, which provide bubble size, bubble velocity, void fraction, and Interfacial Area Concentration (IAC). Based on these observations, a zonal hydrodynamic model is proposed to describe plume interaction, wall-driven recirculation, and the formation of a collective plume core at higher airflows. Quantitatively, the results reveal a 29% reduction in Standard Oxygen Transfer Efficiency (SOTE) between 10 and 40 m³/h, driven by a 41% increase in bubble size and an 18% rise in bubble velocity. Bubble chord length also increased with height, by 33%, 19%, and 15% over 0.8 m for 10, 20, and 40 m³/h, respectively. These trends indicate that increasing airflow enhances turbulent mixing but simultaneously enlarges bubbles and accelerates their ascent, thereby reducing residence time and negatively affecting oxygen transfer. Overall, the validated multiphase datasets and mechanistic insights demonstrate the dominant role of diffuser interaction in dense layouts, supporting improved parameterization and experimental benchmarking of fine-bubble aeration systems in WWTPs.

1. Introduction

Aeration systems are used in many industrial applications, such as aquaculture, chemical processes, and wastewater treatment. In wastewater treatment, fine bubble aeration systems are commonly used in the activated sludge process due to the advantages, including less noise, fewer odors, and higher aeration efficiencies in comparison to mechanical aeration systems [1,2]. Aeration represents the most energy-demanding process in wastewater treatment plants, accounting for approximately 50–90% of the total energy consumption [3]. For this reason, it is important to focus efforts on improving the efficiency of these systems.

The mass transfer process is determined by the volumetric mass transfer coefficient ($k_{L}a$), which is a measure of the rate at which oxygen is transferred from the gas phase to the liquid phase per unit volume of the liquid, obtained by multiplying the liquid-phase mass transfer coefficient ($k_L$) and the gas–liquid interface area ($a$). The first parameter, $k_L$, is the rate of particle transport from the bulk to the edge of the adsorption layer, which depends on the relative velocity of the bubbles, bubble size, water properties, etc. There are various theories that explain $k_L$ (i.e., the film theory; Higbie’s penetration theory; Kolmogoroff’s turbulence theory) [4]. The second factor, the gas–liquid interface area ($a$), is the interface area between phases per volume unit, which depends on bubble size, bubble shape, and the number of bubbles. A precise understanding of bubble motion is necessary to estimate the $k_L$ and $a$ parameter separately, which involves many factors, including bubble size, contact time, and the liquid velocity field—all of which depend on plume dynamics.

One of the earliest and most significant works on modelling a classical plume was carried out by Morton, Taylor, and Turner [5]. The difference between plume and liquid ambient density accelerates the plume. An important parameter of this model is the entrainment of surrounding fluid to the plume, which is proportional to some characteristic velocity at height. The first significant model for air-bubble plumes was developed by Cederwall et al. [6], with important subsequent contributions of other authors [7,8,9]. However, most studies focus on single plumes and do not account for the higher complexity of real, multi-diffuser reactors, where liquid-phase dynamics affect the gas phase distribution. Comparing aeration systems in terms of hydrodynamics or local flow parameters is complex. To simplify the analysis of these systems, the standard of the American Society of Civil Engineers [10] focuses on the calculation, based on the $k_{L}a$, of a series of parameters that characterize overall transfer efficiency, including the Standard Oxygen Transfer Efficiency (SOTE). These parameters allow comparison of the efficiency difference between systems, but do not give information about the causes of this efficiency variation.

SOTE is defined as the ratio between the oxygen introduced into the system and the oxygen transferred. Understanding both SOTE and $k_{L}a$ is essential for designing and optimizing systems where efficient gas–liquid mass transfer is critical. SOTE allows direct comparison between systems; meanwhile, $k_{L}a$ provides a more specific description of the determined system. Various factors affect SOTE in fine bubble diffuser systems, including gas flow rate, diffuser density, and submergence depth. There is a large body of work that studies the influence of these parameters on the efficiency of the aeration system [1,11,12,13,14]. These studies demonstrate that increasing the diffuser density and reducing the airflow rate generally enhances the SOTE. Behnisch et al. [15] have provided conclusions of three decades of oxygen transfer tests in clear water, presenting a new favorable SOTE per meter range between 8.5 and 9.8% m⁻¹, higher than the one presented by Wagner et al. [1] between 4.3 and 5.7%∙m⁻¹. This variation shows the improvement of these systems over the last three decades. On the other hand, Johnson et al. [16] show that velocity gradient, airflow rate per unit aeration volume, and diffuser density are the factors that have the most influence on $k_{L}a$ and then on aeration efficiency. Other experimental models have been developed for aeration efficiency [17,18,19]; all these models show an important dependence on the flow rate.

Many studies, rather than focusing solely on mass transfer, have investigated the hydrodynamic characterization of diffusers and their relationship with mass transfer. Different studies examine bubble size in diffusers, either in bubble generation or in their evolution due to coalescence or break-up phenomena [20,21]. Pöpel and Wagner [22] early on attempted to predict the oxygen transfer rate based on simple measurements of bubble characteristics. Other works have studied the characteristics of plumes in detail, obtaining profiles of void fraction, entrainment coefficients, or the evolution of plume width [23,24,25,26]. However, only a few studies have addressed multiple bubble plumes, and these works generally do not consider aeration applications [27,28], highlighting a clear gap in the literature for multi-plume systems relevant to wastewater treatment.

Many sensors have been used over the years for the characterization of these systems. For the characterization of the liquid phase, particle image velocimetry (PIV) is used for small reactors [24,25], and ADV is used for large reactors [23]. For the characterization of the gas phase, techniques are generally divided into intrusive and non-intrusive methods. Image analysis is a common non-intrusive technique [8,23,29,30], but it is difficult to use at high void fractions. Among non-intrusive sensors, optical and CP are widely used for the characterization of these systems [22,25,26,31,32].

Although extensive research has been conducted on single plumes, far fewer studies address the hydrodynamics of multiple interacting plumes under realistic WWTP conditions. This gap limits our understanding of how plume interactions govern mass transfer and oxygen transfer efficiency. This study aims to characterize a multiple plume system, focusing on the interaction between these plumes. The effect of airflow rate variation is examined, investigating the physical reasons behind this variation, and providing experimental data to evaluate the influence of different factors, such as local flow parameters (chord length, interfacial velocity, void fraction, IAC, etc.). To achieve this objective, multiple velocity and gas phase profiles were measured in the reactor using ADV and CP sensors, obtaining the hydrodynamic characterization and local flow parameters. A conceptual model has been presented, dividing the system into zones with different hydrodynamic characteristics, which allows for a better understanding of the system.

From a practical standpoint, understanding the hydrodynamics of interacting fine-bubble plumes is essential for improving process control in full-scale WWTPs. Aeration already accounts for 50–90% of the total energy consumption of a plant, so any improvement in diffuser layout or airflow distribution that enhances oxygen transfer without increasing blower power has a direct impact on operating costs. In particular, a mechanistic description of multi-plume behavior provides guidance for selecting diffuser density and spacing, for identifying operating windows that maximize SOTE at a given air supply, and for designing dissolved oxygen control strategies that avoid inefficient regimes dominated by recirculation or excessive bubble coalescence. The present work addresses this need by experimentally linking the local hydrodynamics of a dense multi-diffuser array to its global oxygen transfer efficiency.

2. Materials and Methods

2.1. Experimental Setup

The experimental setup consists of a nearly cylindrical reactor with a diameter of 2 m and a height of 2 m (REACT-UJI). One of the reactor walls is flat with transparent glass, allowing optical measurements from the outside (Figure 1a). Inside the reactor, there is a system of transparent acrylic walls, enabling the experiments to be conducted in a rectangular system that measures 1.3 × 1.3 m with a water level of 1.2 m. The rectangular system was created to simulate the behavior of a rectangular biological reactor in a wastewater treatment plant and to obtain symmetrical measurements, since the reactor’s asymmetry made measurements more difficult to characterize.

A homogeneous array of 4 × 4 commercial diffusers was used to carry out the tests (Figure 1b). The diffusers are 9-inch D-Rex model units from OTT Group (Langenhagen, Germany), equipped with Flexnorm^® membranes. They are evenly distributed, covering approximately 40% of the total basin area. Each diffuser has a diameter of 28 cm, and the distance between the centers of adjacent diffusers is 32.5 cm, arranged in a perfectly square pattern. The distance from the center of the nearest diffusers to the basin walls is 16.25 cm.

In Figure 2, a P&ID schematic of the experimental setup is shown. The diffusers can be supplied with either air or nitrogen, the latter being used to deoxygenate the system. The total flow supplied to the diffusers is controlled by a mass flow meter (EL-FLOW F-203AV, Bronkhorst, Vorden, The Netherlands). Line losses to each diffuser have been adjusted to ensure that flow differences at the same feeding pressure are less than 5%. In-line solenoid valves are installed for each diffuser to allow independent control. In

Table 1. Main features of the elements in the P&ID diagram.

Code	Name	Characteristics
F-01	Air source	${\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ = 8 bar
F-02	${\mathrm{N}}_2 \mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}$	${\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ = 200 bar
FC-01 & FV-01	Flow meter controller (Bronkhorst EL-FLOW F-203AV)	${\mathrm{Q}}_{\mathrm{m}\mathrm{a}\mathrm{x}} = 1400 \mathrm{L}/\mathrm{m}\mathrm{i}\mathrm{n}$ $\mathrm{M}\mathrm{a}\mathrm{x}.∆\mathrm{P} = 20 \mathrm{b}\mathrm{a}\mathrm{r}$ Accuracy $\to$±0.5% RD plus ±0.1% FS
PG-01	Pressure sensor	Range $\to -1 \mathrm{b}\mathrm{a}\mathrm{r} \mathrm{t}\mathrm{o} +9 \mathrm{b}\mathrm{a}\mathrm{r}$ Accuracy $\to \pm 0.25\%$
SOV-0X	Solenoid valve (SMC EVT317)	${\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ = 9 bar
TG-01	Temperature sensor (NTC)	Range $\to 0 °\mathrm{C} \mathrm{t}\mathrm{o} 50 °\mathrm{C}$ Accuracy $\to \pm 1 °\mathrm{C}$
F-02	REACT-UJI Reactor	Capacity $\approx 6000 \mathrm{L}$

, the main features of the P&ID diagram elements are shown.

A 3D positioning system is used for automatic mapping of the reactor with different sensors: ADV to measure liquid velocity; CP to measure local two-phase flow parameters; HSC to validate the CP; and Dissolved Oxygen Probes (DOP) to study mass transfer. The system allows positioning of any sensor at arbitrary spatial locations within the reactor. The entire system is autonomously controlled using custom LabVIEW^® 2016 software (National Instruments, Austin, TX, USA), which collects data from spatial mapping sensors as well as from reactor state sensors, including measurements of temperature, pressure, and flow rate.

Table 2. Experimental conditions.

Parameter	Value	Unit
Pit dimensions	1.3 × 1.3	m2
Water depth	1.2	m
Diffuser depth	1.15	m
Diffuser diameter	0.23	m
Released gas	Atmospheric air	—
Water density (20 °C)	998	Kg m−3
Water temperature	15–20	°C
Water conductivity	1040	$\mathsf{\mu }$ S/cm
Total gas flow rates	{10, 20, 40}	Nm3/h

summarizes the experimental conditions. The tests were conducted using tap water with an average conductivity of 1040 μS/cm, while the temperature was maintained between 15 and 20 °C throughout the experiments. Atmospheric air was used as the injected gas. The selected range of 15–20 °C is representative of the typical water temperatures found in the biological reactors of wastewater treatment plants (WWTPs) in the Mediterranean arc, which is the relevant geographical context for this study. This is supported by operational data and scientific literature [33].

2.2. Experimental Methodology

SOTE values were determined for total flow rates ranging from 2 to 40 Nm³/h, equally distributed among each diffuser, and used to generate the relationship curve between SOTE and flow rate. Furthermore, three scenarios were studied in detail to analyze their hydrodynamic parameters and how they affect the system’s oxygen transfer: 10 Nm³/h, 20 Nm³/h, and 40 Nm³/h, equating to 0.625, 1.25, and 2.5 Nm³/h per diffuser, respectively.

To better understand how flow structure affects SOTE, we analyzed both the liquid and gas phases separately. Liquid velocity profiles were measured using ADV. Gas phase parameters—including void fraction, interfacial velocity, bubble chord length, and IAC—were measured using CP.

As illustrated in Figure 3, measurements using CP and ADV focused on the radial profile across two diffusers (Profile A), sampled at multiple heights depending on the sensor type. This radial profiling approach enables a detailed characterization of plume morphology and its interaction with the surrounding flow. A full characterization of the diffuser (i.e., not only a radial profile) was not feasible within the available time, further constrained by the frequent replacement required for the conductivity probes. Therefore, taking advantage of the system’s symmetry, a radial profile was selected for measurement.

For a comprehensive understanding of the system hydrodynamics, additional ADV measurements were collected along profiles: between diffusers (Profile B), near the reactor wall (Profile C), and at the corner of the system (Profile D). These additional profiles help to clarify patterns of liquid recirculation and the influence of boundaries on the flow within the reactor.

2.2.1. Oxygen Transfer

To compare the oxygen transfer efficiency for different flow rates, oxygen tests were conducted following the American Society of Civil Engineers standard [10]. To perform the mass transfer tests, the dissolved oxygen concentration is reduced to below 0.5 mg/L by purging with nitrogen. The oxygen probe used is the OXYPro PSt7 model from PreSens (Regensburg, Germany). The $k_{L}a$ and ${\mathrm{C}}_{\mathrm{\infty }}^{\ast }$ are obtained by adjusting Equation (1) to the oxygenation curve data.

$$\mathrm{C}={\mathrm{C}}_{\mathrm{\infty }}^{\ast }-\left({\mathrm{C}}_{\mathrm{\infty }}^{\ast }-{\mathrm{C}}_0\right)\mathrm{e}\mathrm{x}\mathrm{p}(-k_{L}a·\mathrm{t})$$

(1)

where $\mathrm{C}$ is the DO concentration at time $\mathrm{t}$, ${\mathrm{C}}_{\mathrm{\infty }}^{\ast }$ is the determination point value of the steady-state DO saturation concentration as time approaches infinity, ${\mathrm{C}}_0$ is the DO concentration at time zero, and $k_{L}a$ is the determination point value of the apparent volumetric mass transfer coefficient. The adjusted parameters are corrected to standard conditions, and with these, the SOTE is calculated from Equation (2).

$$\mathrm{S}\mathrm{O}\mathrm{T}\mathrm{E}={\displaystyle \frac{k_L{a}_{20}{\mathrm{C}}_{\mathrm{\infty }20}^{\ast }V}{W_{O_2}}}$$

(2)

where $V$ is the liquid volume of water in the test tank with aerators turned off and $W_{O_2}$ is the mass flow of oxygen in the air stream.

2.2.2. Acoustic Doppler Velocimetry (ADV)

Due to the nature of the experiments, full optical access is not an option because there is only one window; the ADV has been chosen over PIV. ADV is a non-intrusive measurement technique that uses the Doppler effect to measure fluid velocity. It works by emitting a high-frequency sound wave into the fluid through a transmitter probe, which is then scattered by particles or suspended solids present in the fluid. The scattered sound wave is detected by a receiver probe, and the frequency shift caused by the moving particles is measured. Fluid velocity is then calculated by analyzing the frequency shift and the angle between the transmitter and receiver probes. ADV is widely used for obtaining three-dimensional velocity measurements and offers the advantages of being inherently drift-free and not requiring routine calibration.

ADV reliably measures velocities in single-phase flows. But in two-phase flows, gas bubbles create spike noise, which can be misinterpreted as turbulence. This issue has been widely studied [34,35,36]. At high void fractions, the presence of bubbles renders velocity measurements nearly impossible. Nevertheless, for lower void fractions, signal filtering techniques can be employed to recover meaningful data. Goring and Nikora [37] proposed several algorithms for filtering ADV signals contaminated by bubble-induced noise, including RC Filters, Tukey 53H, Acceleration Thresholding, Wavelet Thresholding, and Phase-Space Thresholding. In this study, we opted for the Acceleration Thresholding Method, which offers several advantages over other approaches, including robustness and the ability to filter dynamic flows effectively.

For these experiments, a Vectrino Profiler (Nortek^®, Vangkroken, Norway) was employed. Velocity data were collected at various points over a 5-min period using the ADV, with an acquisition frequency of 25 Hz. The Profiles A, B, C, and D shown in Figure 3 were measured. The liquid velocity was analyzed in relation to factors such as plume morphology and bubble motion. Finally, the velocity fields obtained with the ADV were compared across different flow rates to evaluate the influence of velocity on mass transfer processes.

2.2.3. Dual-Tip Conductivity Probe

To characterize local two-phase flow parameters, such as bubble size, bubble velocity, void fraction, and interfacial area, this study employs CP. Needle probe sensors have been extensively used in the characterization of two-phase flows [38,39,40,41,42,43,44,45,46,47,48,49,50]. The sensor electrodes are made of two copper wires with an outer diameter of 0.2 mm, which are glued with epoxy resin, ensuring that the distance between the tips is approximately 1 mm. The copper wires are coated with enamel to ensure that only the wire ends are electrically exposed to the surrounding environment. In Figure 4b, an image of the sensor is shown.

Figure 4a shows a schematic of the sensor’s operation along with the electronics used. The resistance Rf represents the resistance between the sensor shielding, which is connected to ground (GND), and the sensor tip. This resistance mainly depends on the presence of air or gas at the needle tip. Ultimately, the voltage at the positive terminal of the operational amplifier depends on the ratio of the resistances Rf/Rc. When air is present, the voltage is approximately 5 V, and when water is at the tip, the voltage is approximately 0 V. A buffer is used at the end to measure without altering the reading.

Ideally, probe signals are binary: low voltage for liquid, high for gas. In reality, the signals are continuous and must be processed to extract local flow parameters. The procedure is as follows. First, the signal is filtered and normalized. Then, the start of the bubbles must be recognized; two different methods can be used: a recursive fitting algorithm or a threshold (if the signal noise near the rise point is too high). Finally, to recognize the end of the bubbles, the maxima of the signal are identified before a fall in the signal.

Figure 5a shows an example of a bubble detection event with a vertical velocity $v_b$, displaying the signals recorded by needle 1 (S1) and needle 2 (S2), together with their corresponding binarized signals. The start and end times of the bubble for each needle ($t_{s1}$, $t_{s2}$, $t_{e1}$ & $t_{e2}$) are indicated. The delay time ($T_d$) between the penetration in each needle tip and the bubble contact time with the tip of the needle 1 ($T_c$) are also marked. Figure 5b presents a schematic representation of the bubble and the sensor, including the start and end times of each tip shown in Figure 5a.

The mean local volume fraction is defined as the volume occupied by the gas phase divided by the total volume; the plume dynamics are greatly influenced by this parameter. With Equation (3), the mean local volume fraction ($\overline{\alpha }$) is estimated by the fraction of time that the sensor is exposed to the gas phase over the total sampling time ($T$). The total time that the sensor is exposed to the gas phase corresponds to the sum of the exposure times for each individual bubble ($T_{c,i}=t_{e1,i}-t_{s1,i}$)

$$\overline{\alpha }={\displaystyle \frac{1}{T}}\sum _{i=1}^N{T}_{c,i}$$

(3)

The interfacial velocity of a bubble ($v_{b,i}$) is obtained from the time delay between paired signals ($T_{d,i} = t_{s2,i}-t_{s1,i}$) from the front and rear needles and the distance between tips ($d_t$) (Equation (4)).

$$v_{b,i}={\displaystyle \frac{d_t}{T_{d,i}}}$$

(4)

The chord length of a bubble ($c_{b,i}$) can be estimated using the interfacial velocity ($v_{b,i}$) and the bubble contact time ($T_{c,i}$), which is the time between the bubble’s start and end in the front needle (Equation (5)).

$$c_{b,i}=v_{b,i}·T_{c,i}$$

(5)

The total interfacial area ($a$) can be calculated based on the local Interfacial Area Concentration (IAC), which is estimated using CP and Equation (6) as outlined by Kim et al. [51]. The local IAC is then determined using the bubble frequency ($N_t$) and bubble velocity ($v_{b,i}$).

$$IAC=4N_t\overline{{\displaystyle \frac{1}{v_{b,i}}}}$$

(6)

To ensure that the bubble velocity and size measurements obtained with the CP accurately represent the flow, a performance check was carried out using HSC measurements, previously employed to calibrate other sensors [52]. The measurements were taken 10 cm from the diffuser membrane. Bubble velocities were determined from the HSC recordings using frame-to-frame cross-correlation, while bubble sizes were obtained by fitting the bubble outlines to ellipses and then calculating the equivalent diameter using Equation (7), where $E$ and $e$ are the major and minor axes, respectively.

$$d_{eq}=\sqrt[3]{E^{2}e}$$

(7)

The conductivity probes required frequent replacement, as they typically became fouled—through oxidation or particle deposition—within roughly one day.

3. Results and Discussion

To analyze the performance of a multi-diffuser system and the relationship between local flow parameters and mass transfer, it is first necessary to describe the hydrodynamics of bubble plumes. We can take the classical and well-established study of the isolated air-water plume as a reference [6,7,8,9,53,54]. As depicted in Figure 6a, injection of gas through a single diffuser into a quiescent fluid generates a buoyant plume whose ascending bubbles entrain ambient liquid. This entrainment, characterized by a coefficient that governs the linear increase of plume volume with height, establishes both the axial velocity field and the radial spreading of the plume. Under unconfined laboratory conditions, measurements have consistently shown that the transverse profiles of liquid velocity and void fraction conform closely to Gaussian distributions. In contrast, when multiple diffusers operate in proximity or when wall boundaries intervene, these ideal Gaussian profiles deteriorate. Interactions among neighboring plumes and confinement effects produce more complex flow structures, underscoring the need for a complete, system-scale hydrodynamic characterization to predict SOTE in realistic aeration configurations.

In our experimental arrangement, the diffuser spacing precludes treating the plumes as independent. Instead, plume–plume interactions, together with confinement and corner effects, govern the resulting flow field. The proximity of the diffusers, and of the diffusers to the reactor walls, renders the isolated-plume assumption inapplicable, necessitating that the system be analyzed with explicit consideration of both plume–plume and plume–wall interactions.

To understand the established flow regions and their behavior, the system’s hydrodynamic response has been categorized into distinct zones, as shown in Figure 6b:

• Zone 1 corresponds to the region immediately above each diffuser, where the plume rises freely until, at a given height, it meets its neighbors and thus enters Zone 3. Close to the diffuser, the plume’s behavior resembles that of an isolated plume, but as it ascends, it entrains fluid from Zone 2. This entrainment adds complexity to the flow and causes the plume to diverge from isolated-plume behavior before it reaches Zone 3.
• Zone 2 encompasses the region between diffusers and is characterized by highly complex, oscillatory flow. The upward liquid comes from the lower region of the diffusers and from the tank walls and is entrained into the plume by the motion of the rising bubbles. However, the lateral oscillations of neighboring plumes disrupt this entrainment, rendering the flow chaotic and inducing partial downward recirculation. Time-averaged velocity measurements in many parts of Zone 2 approach zero, reflecting the alternation of upward and downward motions. The close spacing of the diffusers, combined with plume oscillations, imposes a highly turbulent, unsteady flow structure that defies the definition of steady or mean conditions. In the current setup with a high number of diffusers and high diffuser density, recirculation occurs primarily along the walls, and there is little recirculation between the diffusers. However, as the distance between diffusers increases, these recirculation zones become more significant in the downward flows.
• Zone 3 is formed when the plumes have merged and become indistinguishable from one another, creating a homogeneous void fraction region. The liquid rise velocity in this zone decreases due to the increased cross-sectional area of ascent and the reduced number of areas available for downward flow, which hinders recirculation. The behavior in Zone 3 is characterized by a more stable and homogenized state, where recirculation occurs primarily at the peripheries, especially along the walls and corners of the reactor. This transition marks a shift from the chaotic, oscillatory flow seen in Zone 2 to a more steady, uniform flow pattern.
• Zone 4 is the region where liquid descends in areas near the walls. The plumes move away from the walls due to these currents. Some of the ascending bubbles get trapped in this downward flow, causing the floating bubbles observed on the walls. This recirculating flow travels through the area beneath the diffusers and ascends to enter the plume (entrainment).

In summary, increasing the air flow rate causes the individual plumes to spread more rapidly, to merge closer to the diffusers, and to form a nearly homogeneous core where upward liquid velocities are reduced, and most recirculation is displaced towards the walls and corners. Near the diffusers (Zone 1), the liquid and bubble velocities increase with flow rate, while in the merged region (Zone 3), the axial velocity tends to saturate, i.e., reaching terminal velocity, as the cross-sectional area of the plume grows. These hydrodynamic changes give rise to two opposing effects that both act on the interfacial area, and therefore on oxygen transfer: increased gas hold-up and mixing tend to enlarge the interfacial area, while the formation of larger, faster-rising bubbles tends to reduce it.

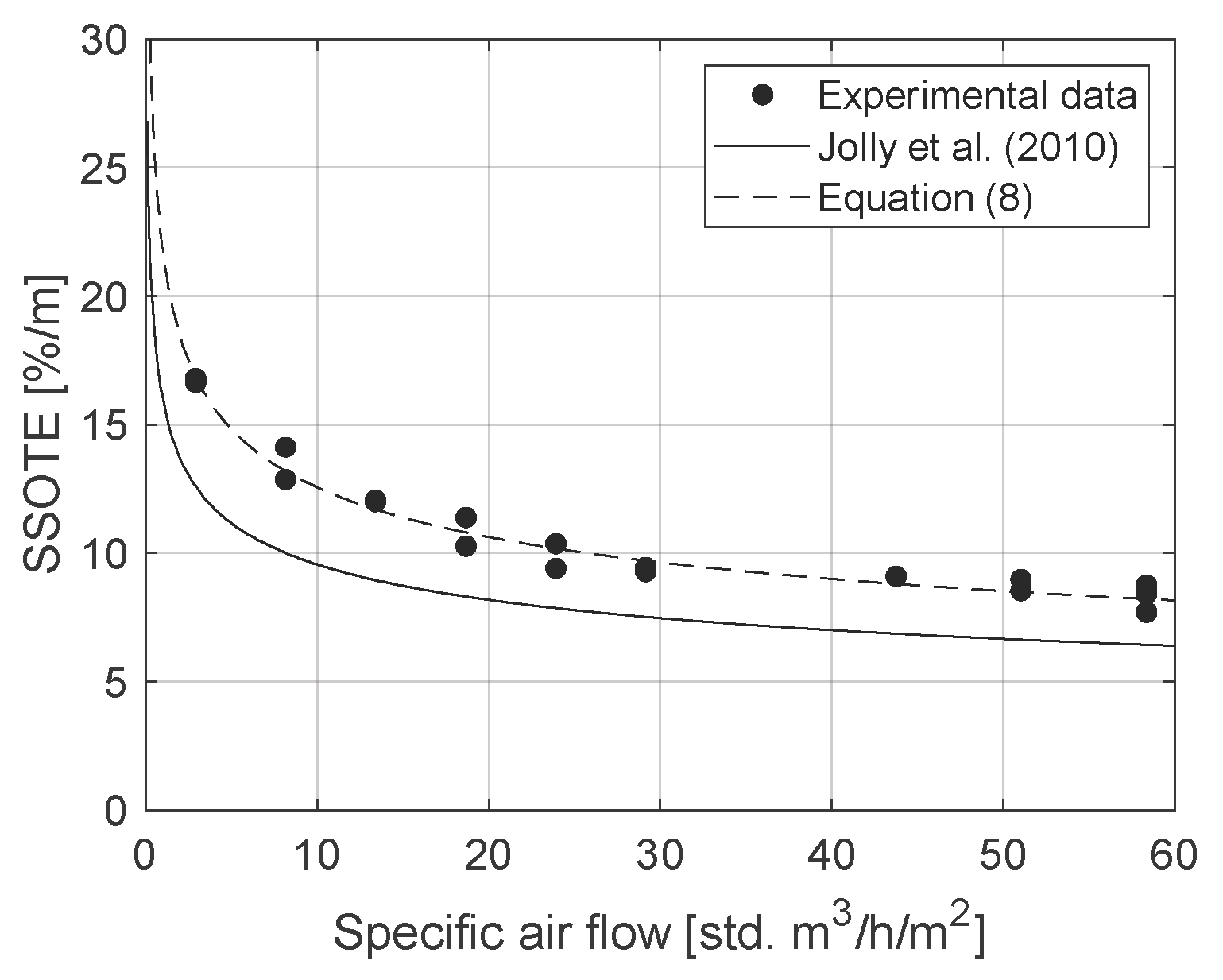
3.1. Oxygen Transfer Results

The SOTE data in Figure 7 summarizes the overall oxygen transfer performance of the reactor for the range of air flow rates considered. In the remainder of Section 3, we interpret this trend using the hydrodynamic picture established above, examining how plume spreading, plume merging, bubble velocities, and bubble coalescence jointly determine the effective interfacial area and contact time.

In Figure 7, it can be observed that the SSOTE decreases with increasing specific air flow rate. The experimental data follow the same trend as the correlation proposed by Jolly et al. [12], although the experimental values in this study are approximately 30% higher. This discrepancy may be attributed to differences in the diffusers used by Jolly et al. compared to those used in the present study. Additionally, the improvements in system design over the past fifteen years, as noted by Behnisch et al. [15], may contribute to this variation. Using the model presented by Jolly et al. [12], a fit of the experimental data was performed, yielding the expression of Equation (8), which provides an excellent representation of the data (R² = 0.977).

$$\mathrm{S}\mathrm{S}\mathrm{O}\mathrm{T}\mathrm{E}=21.8·{\mathrm{Q}}_{\mathrm{s}}^{-0.24}$$

(8)

The specific air flow rate is defined as the flow rate divided by the diffuser-covered area, thereby indirectly accounting for both diffuser density and basin area. Another relevant parameter is the standardized SOTE per meter (SSOTE), which expresses the SOTE normalized by reactor depth and thus indirectly incorporates the effect of reactor height. The observed decrease in SSOTE can be attributed to multiple factors influencing bubble size, liquid and bubble flow patterns, and phase velocities. In the following sections, these factors are examined in detail to evaluate their impact on interphase mass transfer. We focus on three specific air flow rates (10, 20, and 40 Nm³/h) and, for each case, analyze the void fraction distribution, bubble size, bubble rise velocity, and liquid velocity at various heights above line A in Figure 3, which spans two adjacent diffusers.

3.2. Hydrodynamics

Figure 8 shows the evolution of the void fraction profiles across the two diffusers as a function of height for the three flow rates. Near the diffuser membrane, each profile exhibits two distinct Gaussian peaks corresponding to the individual plumes. As the plumes rise, the profiles broaden and eventually merge, forming a homogeneous void fraction zone. At 10 Nm³/h (Figure 8a), the plumes remain separate throughout the measurement domain. At 20 Nm³/h (Figure 8b) and 40 Nm³/h (Figure 8c), merging occurs at approximately 70 cm and 50 cm above the membrane, respectively, marking the transition from Zone 1 to Zone 3 in Figure 6b. The merging height is not straightforward to determine and depends on factors such as flow rate, basin geometry, and diffuser layout.

It is important to note that the plumes undergo lateral oscillations that are difficult to resolve when multiple plumes interact in a confined geometry. The profiles in Figure 8 are time-averaged void fraction distributions obtained from long-duration measurements with CP probes. Instantaneously, each plume is narrower than the averaged profile suggests, but plume wandering broadens the time-averaged distribution. Beelen et al. [26] demonstrated that plume-center oscillations increase with flow rate, so at low flow rates, the time-averaged and instantaneous profiles are very similar. In this study, our local flow parameter profiles likewise represent averaged rather than instantaneous plume shapes, which can lead to an overestimation of plume diameter compared with instantaneous measurements obtained using a high-speed camera.

In the lowest-flow case (10 Nm³/h, Figure 8a), the profile at $\mathrm{h} = 10$ cm exhibits a minimum void fraction at the center of the diffuser. This feature remains, though less pronounced, at 20 Nm³/h (Figure 8b) and disappears at 40 Nm³/h (Figure 8c). This central dip arises because the diffuser has an unperforated region in its middle where no bubbles form. At higher flow rates, bubble spreading quickly fills this zone.

The void fraction profiles for the three flow rates exhibit similar trends (Figure 8), as the plumes behave independently near the diffuser and progressively merge until forming a homogeneous void fraction. The observed differences arise mainly from two factors: (i) variations in plume half-width, governed by the spreading ratio and flow rate, which determine the transition from Zone 1 to Zone 3; and (ii) the increase in void fraction values with flow rate. The following sections analyze these flow rate-dependent parameters and their implications for oxygen transfer.

Figure 9a shows the evolution of plume half-width with height, obtained from Gaussian fits of the void fraction profiles. This behavior is consistent with the spreading rate model for a classical bubble plume, which follows a linear trend (9).

$${\displaystyle \frac{db}{\mathrm{d}z}}=\beta$$

(9)

Linear fits were performed to determine the slope (β) for each flow rate (

Table 3. Fitted slope for the different flow rates.

Flow Rates	$\mathit{\beta }$	R2
10 m3/h	0.05	0.892
20 m3/h	0.15	0.991
40 m3/h	0.18	0.971

). For a classical plume, β is typically around 0.1 [55]. In our case, β increases with flow rate, which can be attributed to interactions between adjacent diffusers. As the flow rate rises, neighboring plumes reduce the local velocity, promoting lateral spreading to conserve the total flow rate, and thereby increasing the slope β.

Since the distance between diffusers is 0.325 m, it can be assumed that at the midpoint (0.1625 m from each diffuser), the adjacent plumes merge. When the plume half-width reaches this value, the plumes can be considered merged, as indicated by the dashed line in Figure 9a. This point is reached earlier at higher flow rates: around 0.67 m for 20 m³/h and 0.52 m for 40 m³/h. In contrast, for 10 m³/h, this condition is never reached. This behavior is also observable in Figure 8. At 10 m³/h (Figure 8a), the profiles remain distinct across the column height, whereas at 20 and 40 m³/h (Figure 8b,c), the void fraction becomes nearly homogeneous. As previously mentioned, this defines the transition from Zone 1 to Zone 3.

An important observation is that even when the plume merging point shown in Figure 9a is satisfied, the plume profiles continue to broaden. This occurs because the superposition of two Gaussian distributions with widths much larger than their separation still produces residual valleys in the void fraction profile. As a result, the curves exhibit further growth, even though the combined profile already appears homogeneous.

Figure 9b shows the evolution of the void fraction at the center of the plume with height, along with the fitted curve given by $\epsilon = c_1{z}^{-2} + c_2$, where ε and $z$ represent the void fraction and height, respectively, and $c_1$ and $c_2$ are the fitting constants. It can be observed that the void fraction at the center of the plumes exhibits a more pronounced decrease near the diffusers, gradually approaching a constant value with increasing height, as it enters Zone 3 of homogenization, where the plumes merge, and the void fraction profile becomes uniformly distributed within the plume zone. This behavior is not observed in the case of 10 m³/h, where, as already seen in Figure 9a, the plume spread is significantly lower and grows very slowly, resulting in a very gradual evolution of the void fraction at the center, which remains nearly constant throughout the height.

The liquid velocity, Figure 10, has been characterized using ADV equipment, as explained in Section 2.2.2, in Profile A in Figure 3. As can be seen in Figure 10, the profiles can be explained by looking at the behavior of the plumes and are consistent with the results presented for the behavior of the void fraction.

For the three studied flow rates, the plume liquid velocity profiles have been characterized. Figure 10 shows the liquid velocity profiles for the three studied flow rates; these profiles are consistent with the void fraction profile results. At 10 m³/h, the liquid plumes remain independent with height and do not merge, unlike what is observed at 20 m³/h and 40 m³/h. At 40 m³/h, liquid plume merging is observed around 20 cm, whereas at 20 m³/h, it is observed around 30 to 40 cm. This difference is due to the plume’s spreading ratio, which depends on the flow rate, as shown in Figure 9a. In a total floor coverage system, plume merging reduces liquid currents, increasing bubble contact time and thereby increasing the SOTE. Predicting plume behavior is crucial for understanding its impact on mass transfer. Despite being a system of multiple interacting plumes, the behavior of the spreading ratio is linear and in the range of simple plumes. Although in these systems, it is important to consider the significant impact of liquid circulation.

A velocity minimum point is observed in the center of the diffuser (Figure 10). This is explained by two reasons: the central area of the diffuser lacks pores, and the plume acceleration due to entrainment occurs laterally. It is also observed that the maximum plume velocities are reached at the lowest flow rate (10 m³/h). This is due to the combination of plume oscillation and the calculation of temporal average values. When temporally averaging the velocity of a point in an oscillating plume, the obtained values are the mean between the velocity when the plume is present and when it is absent.

To quantitatively assess the interaction between phases, Figure 11 presents the void fraction field obtained with the CP, along with the velocity field obtained with the ADV and the plume half-width derived from the Gaussian fit of the void fraction curves. At all three flow rates, the region near the diffuser exhibits liquid entrainment towards the center of the plume. Clear differences are observed between the three flow rates studied. For the 10 m³/h case, the plumes do not merge and remain independent; at 60 cm, the velocity between the diffusers is lower than at the center of the plume, indicating a still visible velocity profile. For the 20 m³/h case, the plumes merge around 70 cm, and the velocity profile becomes constant by 60 cm. Finally, for the 40 m³/h case, the plumes merge around 50 cm, resulting in a constant liquid velocity profile at 40 cm.

Figure 11 illustrates some of the regions described in Figure 6. Before the plumes merge, plumes corresponding to Zone 1 and Zone 2 that remain independent are observed. Zone 1 is the area covered by diffusers with positive ascent velocity and liquid entrainment into the plume ($\mathrm{X}\approx \left[-10, 10\right]\cup [-22.5, 42.5]$). Zone 2 corresponds to the region between diffusers and has nearly zero average velocity values ($\mathrm{X}\approx \left[-18, -10\right]\cup \left[10, 22.5\right]\cup [42.5, 52.5]$). As the plume ascends, the spreading ratio causes lateral expansion until the plumes merge, marking the beginning of Zone 3. In this zone, the entire liquid flow rises at the same velocity, and the void fraction becomes homogeneous. The onset of Zone 3 depends on the merging of the plumes and, consequently, on the flow rate.

Figure 12 presents polar histograms of the plume angle, with 0° representing positive velocity in the X direction and 90° representing positive velocity in the vertical direction. At X = −12 cm and height = 10 cm (Figure 12a), both inlet and ascent velocities are observed, with velocity oscillations ranging from 0° to 90°. At X = 12 cm and height = 10 cm (Figure 12b), entrainment towards the diffuser is also visible, and the oscillations increase with higher flow rates. At X = 0 cm and height = 20 cm (Figure 12c), an ascent velocity with oscillations that increase with flow rate is observed. Finally, at this same point, but with radial dispersion (Figure 12d), where 0° denotes positive velocity in the X direction and 90° denotes positive velocity perpendicular to both X and height, the plume shows oscillations in all directions.

To conduct a detailed analysis of mass transfer, it is essential to link the distributions of local flow parameters with hydrodynamics. The merging point of the plumes leads to a reduction in plume velocity, resulting in an increase in SOTE. The spreading ratio of the plumes near recirculation zones generates descending bubbles, which enhance the system’s efficiency.

For the 40 m³/h case, certain areas of interest have been characterized to obtain the general hydrodynamics of the system (Figure 13). The data obtained justify the behavior of the areas explained in Figure 6. In the area near the diffuser, the liquid primarily ascends through the regions covered by diffusers (Zone 1), as observed in Profile A. In the areas between diffusers (Zone 2), the velocities oscillate due to plume motion. Although the average velocity is zero near the diffuser, as observed in Figure 13 (Profile B at 100 mm), non-zero velocities begin to appear with increasing height, as seen in Figure 13 (Profile B at 200 mm). The behavior of Profile B, corresponding to Zone 2, is strongly influenced by the distance between diffusers. In an isolated plume, this zone exhibits downward velocity. However, in this multi-plume scenario, the high diffuser density shifts the preferential recirculation towards the walls.

In the area far from the diffuser, the plumes merge and rise together, with the descending currents also occurring along the walls. This descending region corresponds to Zone 4, which can be observed in Profiles C and D in Figure 13. All the liquid that rises through the plumes due to entrainment and gas acceleration mainly descends along the system’s perimeter. This makes the relationship between the perimeter and the reactor area important for systems with a high diffuser density.

This behavior has been observed in simulations by various authors. Gresch et al. [56] noted that in a multi-plume system, the plumes tended to converge, creating a region of homogeneous void fraction, with recirculation occurring mainly at the corners. When diffusers were placed at the corners, it was observed that these recirculating currents were diminished. Bari et al. [57] observed that for a reactor with three diffusers, bringing the diffusers closer together while moving them away from the walls caused the currents along the sides and the merging of plumes to induce recirculation, which reduced the void fraction and consequently reduced the interfacial area. Conversely, when the diffusers were positioned further apart and distributed homogeneously, a reduction in recirculating currents was observed, leading to an increase in the void fraction.

3.3. Local Flow Parameters and Their Effect on Mass Transfer

In this section, key parameters that directly affect mass transfer are examined. First, bubble velocity, which is inversely proportional to the contact time; second, the chord length, which is related to bubble size; finally, the interfacial area, which is correlated with the other two key parameters. The measurement points are the same as those where the void fraction was measured.

3.3.1. Bubble Interfacial Velocity

Figure 14 shows the bubble velocity profiles obtained for the three flow rates at different heights. Zero velocity values correspond to areas where no bubbles are detected, indicating regions with almost zero void fraction. An increase in bubble velocity with flow rate is observed, rising from approximately 0.5 m/s at 10 m³/h (Figure 14a) to around 0.6 m/s at 40 m³/h (Figure 14b). Additionally, as the flow rate increases, the velocity variation with height becomes more pronounced, with greater dispersion observed in the case of 40 m³/h (Figure 14c).

Figure 15 shows the average bubble velocity at different heights for the three flow rates studied. As expected, higher flow rates result in greater bubble velocities due to the increased induced liquid velocity. From a mass transfer perspective, one reason for the reduction in SOTE at higher flow rates is the shorter bubble contact time caused by faster-rising bubbles.

Additionally, Figure 15 reveals that bubble velocity varies with height. Near the diffuser (Zone 1), the flow accelerates and increases the liquid velocity until the plumes merge (Zone 3), where the velocity begins to decrease. The transition from Zone 1 to Zone 3 depends on the flow rate: at 10 m³/h, the plumes do not merge for the depth considered. However, the 20 and 40 m³/h flow rate cases show a distinctive bubble velocity profile, caused by plume merging, as depicted in Figure 11. At 40 m³/h, once the plumes merge, the velocity decreases to levels similar to those at 20 m³/h. Although higher flow rates initially produce higher velocities, beyond Zone 3, the velocity tends to be saturated, as observed in the 40 m³/h and 20 m³/h cases.

Therefore, one possible reason for the increase in SOTE with diffuser density is the reduction in velocity when plumes merge, as observed in other works [1,15]. The importance of avoiding recirculation currents that lower SOTE has been extensively studied. For example, Gong et al. [58] examined bubble injection in bubble plumes and found that uniform injection induces significantly less flow than concentrated injection. Extrapolating these findings to the present work, considering plume merging, the uniform gas profiles observed reduce the induced flow, thereby improving SOTE.

3.3.2. Bubble Chord Length

Figure 16 presents the chord length profiles along the plumes. Similar to the velocity data, not all data points are averaged over the same number of bubbles. The bubble size distribution appears largely homogeneous, although some degree of dispersion is observed. The chord length increases with flow rate, with an average of approximately 1.5 mm at 10 m³/h and 2 mm at 40 m³/h. Additionally, a noticeable increase in chord length with height is observed, which can be attributed to a combination of bubble coalescence and decompression effects.

Using the chord length profiles obtained with CP, the evolution of the average chord length with height is analyzed, as shown in Figure 17a. The chord length at 0.1 m from the diffuser increases with flow rate: from 10 m³/h to 40 m³/h, it rises by approximately 45%, leading to a theoretical reduction in the interfacial area of around 20%. This increase in chord length contributes to the observed decrease in SSOTE with higher flow rates. The variation in initial chord length with flow rate may be attributed to bubble formation at the membrane [59].

Figure 17a shows an increase in bubble size with height. Although the chord length increases by approximately 20% with height, decompression alone would account for less than a 3% variation. This discrepancy indicates that the observed increase is predominantly attributable to bubble coalescence, a phenomenon previously reported in similar systems [20,21]. For flow rates of 20 m³/h and 40 m³/h, the chord length increases up to about 0.5 m, after which it begins to stabilize. This stabilization is likely due to the homogenization of the void fraction, a decrease in velocity, and an increase in bubble size, all of which contribute to reduced coalescence. The subsequent decrease in chord length at 0.7 and 0.8 m for the 40 m³/h flow rate may be the result of lateral bubble velocities or measurement deviations.

To closely observe the evolution of the chord length population, Figure 17b shows the cumulative distribution function of the chord length at 10 cm and 80 cm from the diffuser membrane for the three flow rates studied. A reduction in the population of smaller bubbles and a corresponding increase in larger ones is observed with increasing flow rate and height. The variation in bubble sizes at 10 cm from the diffuser is attributed to bubble generation phenomena, while the differences observed from 10 cm to 80 cm across the three flow rates are primarily due to coalescence.

3.3.3. Interfacial Area

The IAC is a local measurement defined as the area of gas–liquid interface per unit volume of the two-phase flow. This parameter integrates the various factors that influence the available mass transfer area, including bubble chord length, bubble velocity, and gas void fraction. Figure 18 shows the IAC profiles for the three flow rates studied. It can be observed that, since bubble velocity and chord length are nearly constant along the radial direction, the local IAC profiles closely resemble the void fraction profiles. The same Gaussian-shaped distributions are seen, which merge and become more uniform with increasing height. Additionally, the IAC increases with flow rate. Although larger bubble diameters tend to reduce the IAC, the effect of increased gas void fraction predominates, leading to an overall increase in interfacial area. This does not result in an increase in mass transfer efficiency, as the increase in IAC is smaller, causing the systems to become less efficient as the flow rate increases.

In this section, the IAC results obtained with the CP are correlated with the SOTE values measured using the DOP. The interfacial area serves as the connecting parameter between local hydrodynamic variables—such as bubble size, bubble and liquid velocities, and gas void fraction—and the overall mass transfer performance. To establish this link, the local IAC must be converted into a global interfacial area ($a$) through a volumetric averaging process of the local quantities. The average interfacial area within the reactor is evaluated using three different approaches:

1.

Radial integration of the CP’s IAC profiles (RI-CP). The reactor’s average interfacial area ($a$) is obtained from the profiles measured with the CP. The integral in Equation (10) is evaluated up to the midpoint between the diffusers ($R_{\mathrm{eq}}=0.1625$ m). By computing this integral at each height, a mean interfacial area, $a$, is obtained for each vertical position, representing the average interfacial area at that height. Finally, a correction is applied to account for the volume below the diffusers, where the local IAC is zero, yielding the reactor’s average interfacial area ($a).$

$$a={\displaystyle \frac{\left({\int }_0^{R_{eq}}IAC\left(r\right)2\pi rdr\right)}{\pi r^2}}$$

(10)

2.

Using the bubble size and the bubble velocity obtained with CP (Vel-CP). This method assumes that at a given height, all bubbles rise at the same velocity and are the same size, which is consistent with the results obtained in Figure 14 and Figure 16. The values used for this calculation are taken from Figure 15 and Figure 17a. The calculation is based on Equation (11), where $N_b$ is the number of bubbles, $A_b$ is the area of a bubble, and $V$ is the volume of the reactor. The IAC is determined as a function of the flow rate ($Q$), bubble velocity ($v_b$), reactor area ($A$), and bubble diameter ($d_b$), under these assumptions. The bubble diameter used in this calculation is assumed to be the chord length.

$$a={\displaystyle \frac{N_b{A}_b}{V}}={\displaystyle \frac{6Q}{v_{b}A{d}_b}}$$

(11)

3.

Using the bubble size and the void fraction obtained from the variation of the interface height in the reactor. This method (Void-Level) uses Equation (12) [60], which is a variation of the previous expression and has been employed in many earlier studies. In this equation, $\epsilon$ represents the mean void fraction in the reactor, and $d_b$ is the mean bubble diameter:

$$a={\displaystyle \frac{6\epsilon }{d_b(1-\epsilon )}}$$

(12)

This method for calculating $a$ has been previously tested [61]. In this approach, the void fraction is determined by measuring the increase in the liquid column height, as described by Herrman-Heber et al. [62]. To determine the gas void fraction, Equation (13) is used, which accounts for the relationship between the liquid level without gas injection ($H_0$) and with gas injection ($H_a$), with the interface height measured using a camera.

$$\overline{\alpha }=1-{\displaystyle \frac{H_0}{H_a}}$$

(13)

To verify the consistency of the data trend, the void fraction was fitted using a common correlation between gas flow rate and gas void fraction [63]. The resulting fit, $\alpha = 0.02 Q^{1.3}$, where $Q$ is the flow rate (m³/h) and $\alpha$ is the void fraction (%), showed excellent agreement with the experimental data, yielding $R^2 = 0.997$.

Using the first and second methods, the variation of a with height can be determined. Figure 19a illustrates this evolution of $a$ with height for the three flow rates studied. Although some differences exist between the two methods, they ultimately yield comparable values. The $a$ values obtained using the first method (RI-CP) are influenced by errors arising from the assumptions made during the radial integration of the IAC profile derived from CP measurements. In contrast, the second method (Vel-CP) is particularly useful for analysing mass transfer, as it provides a single parameter that captures the combined effects of velocity and chord length, thereby facilitating the investigation of these two factors.

Analyzing the data obtained using the second method (Vel-CP), it can be observed in Figure 19a that for the 10 m³/h case, the interfacial area decreases with height due to the increase in bubble size. In contrast, for the 20 and 40 m³/h cases, a minimum interfacial area occurs when the bubbles reach their maximum velocity. As the plumes merge and bubble velocity decreases, the interfacial area increases. Notably, in the 40 m³/h case, the variation in bubble velocity has a greater influence than the change in bubble size, resulting in an overall increase in interfacial area with height.

The mass transfer coefficient values were obtained by dividing $k_{L}a$, determined from the mass transfer experiments, by the mean interfacial area of the reactor. To calculate this mean interfacial area, in the first and second methods, the average of the $a$ values measured at different heights was taken, after applying a correction for the lower region below the diffusers, where no bubbles are present, and the interfacial area is therefore zero. In the third method, the interfacial area was obtained directly using Equation (12), assuming that the chord length corresponds to the mean value for the reactor.

There is a notable difference between the three methods. The first two methods estimate the interfacial area based solely on bubbles rising through the plume, disregarding any bubbles that may recirculate along the reactor walls. In contrast, the third method, which calculates the gas void fraction based on the total reactor height, inherently accounts for the contribution of bubbles recirculating near the walls and corners. The discrepancy in interfacial areas between the first two methods and the third increases with flow rate, as bubble recirculation becomes more prominent at higher gas flow rates. The differences are 11%, 39%, and 55% for flow rates of 10, 20, and 40 m³/h, respectively.

Figure 19b presents the $k_L$ values obtained using the three different methods, which are then compared with four different $k_L$ correlations: Higbie [64], representing pure water with a perfectly mobile bubble interface; Frössling [65], representing a perfectly rigid interface; Clift et al. [66], representing clean water similar to the Higbie case; and Brauer [67], representing partially contaminated water, intermediate between the Higbie and Frössling limits.

Figure 19. (a) Interfacial area as a function of height for two different methods (RI-CP and Vel-CP). (b) Comparison between $k_L$ for the different flow rates obtained using the three different methods (RI-CP, Vel-CP, and Void-Level), and compared with the different $k_L$ correlations for clean water (Higbie [64]), partly contaminated water (Clift [66] and Brauer [67]), and contaminated water (Frössling [65]).

Figure 19. (a) Interfacial area as a function of height for two different methods (RI-CP and Vel-CP). (b) Comparison between $k_L$ for the different flow rates obtained using the three different methods (RI-CP, Vel-CP, and Void-Level), and compared with the different $k_L$ correlations for clean water (Higbie [64]), partly contaminated water (Clift [66] and Brauer [67]), and contaminated water (Frössling [65]).

The differences in interfacial area observed between the methods are reflected in the $k_L$ values as well, since $k_{L}a$ is the same for all three methods. For the 10 m³/h case, the $k_L$ values are more similar across the methods because the effect of recirculating bubbles is less pronounced. However, as the flow rate increases to 20 and 40 m³/h, the $k_L$ values diverge significantly due to the increased gas hold-up caused by recirculating bubbles. This divergence is attributed to downward-moving bubbles near the walls and corners, which increase the total number of bubbles in the reactor.

Assuming the $k_L$ values obtained using the third method are correct, they fall within the range expected for clear or partially contaminated water, aligning closely with the Brauer [67] correlation. This is consistent with the type of water used in this study—deionized tap water. Since deionized water is not pure, the maximum $k_L$ values predicted by Higbie’s correlation are not reached.

Bringing together these local observations allows a mechanistic interpretation of the global SOTE trend in Figure 7. When the air flow rate is increased from 10 to 40 Nm³/h, the mean bubble chord length near the diffusers grows by about 45% and continues to increase with height due to coalescence, which alone reduces the specific interfacial area by roughly 20%. At the same time, the mean bubble rise velocity increases by approximately 18%, shortening the single-pass contact time of individual bubbles. In parallel, plume spreading and earlier plume merging lead to a more homogeneous void fraction core, where the liquid velocity partially saturates, and a larger fraction of the gas holdup is associated with bubbles recirculating along the walls and in the corners. These two opposing effects—shorter single-pass contact times but longer overall residence times due to recirculation—result in only moderate variations in the mass transfer coefficient $k_L$, whereas the effective interfacial area decreases because of the coarsening of the bubble population. The combination of a reduced a and a slightly lower $k_L$ therefore explains the observed 29% decrease in SOTE with increasing specific air flow rate, despite the higher gas holdup.

Overall, these results highlight the importance of the $a$ and ${\mathrm{k}}_{\mathrm{L}}$ as the key parameters governing global mass transfer. While the $a$ integrates local hydrodynamic effects—such as bubble size, bubble velocity, and gas void fraction—the coefficient ${\mathrm{k}}_{\mathrm{L}}$ reflects the efficiency of the exchange at the gas–liquid interface. The combination of these two parameters establishes a direct link between local phenomena and the overall reactor performance, emphasizing the need to address mass transfer from both local and global perspectives to better understand and optimize the operation of aerated systems at realistic scales.

3.4. Validation of Dual-Tip Conductivity Probes

The mean deviations of the bubble chord length, velocity, and void fraction data points from their respective profiles are 5.5%, 6.5%, and 8%, respectively. To maintain clarity in the graphical representation of trends across multiple flow rates and heights, error bars were omitted from the figures; however, the complete dataset, including all uncertainty values, is provided in the repository cited in the Data Availability Statement section.

To ensure accurate measurements with the dual-tip conductivity probe (CP), a validation was performed using the High-Speed Camera (HSC) for an external zone of the diffuser at 0.1 m above the diffuser membrane. Figure 20a compares the Probability Density Functions (PDFs) of the velocity distributions measured using the CP and the HSC. The two methods yield very similar velocity populations, with a difference in the median of less than 2%. Figure 20b shows the comparison of the chord length distributions obtained from the CP and the equivalent diameters with the HSC. Again, a consistent trend is observed, with the median differing by less than 5%. The close agreement between chord length and equivalent diameter arises from the small bubble size. Bubbles that hit the probe off-axis are not detected, so only those passing fully along the main axis are measured, ensuring that the recorded chord lengths reliably represent bubble diameters.

Finally, to generally validate the data obtained with the CP probes, the flow rate is integrated at different heights for the three flow rates studied. The integration is performed by obtaining the profile resulting from multiplying the bubble velocity by the void fraction, and this profile is numerically integrated over the plume radius (Equation (14)). Radial symmetry is assumed, so the integration is valid only when the plumes remain separate, and there are null void fraction values between diffusers.

$$Q={\int }_0^R\alpha \left(r\right) v\left(r\right) 2\pi r dr$$

(14)

Figure 21 shows the conservation of flow rate for different flow rates at heights where the plumes remain independent. The shaded areas indicate a 15% deviation from the average. Thus, the differences in flow rate conservation are in the order of this magnitude.

4. Conclusions

This work provides a detailed experimental insight into the hydrodynamics and oxygen transfer performance of a multi-diffuser fine-bubble aeration reactor representative of full-scale wastewater treatment systems. By combining local two-phase measurements using ADV and CP sensors, a consistent and validated description of the liquid velocity field and bubble dynamics was achieved. The accuracy of the CP measurements was confirmed through complementary high-speed imaging and flow-rate conservation analysis.

The results show that the interaction between neighboring plumes strongly governs reactor hydrodynamics and, consequently, oxygen transfer performance. In the region close to the diffusers, plumes behave independently, increasing their half-width with height until they eventually merge, forming a zone with a nearly homogeneous void fraction. In systems with high diffuser density, liquid recirculation occurs mainly along the corners and walls. As the airflow rate increases, plume merging occurs at lower elevations, leading to a reduction in liquid velocity that increases the interfacial area and, therefore, enhances oxygen transfer.

Local two-phase flow factors, together with hydrodynamics, have a major influence on mass transfer. The 29% decrease in SOTE observed between 10 and 40 m³/h is primarily attributed to a 41% increase in bubble size and an 18% increase in bubble rise velocity, the latter resulting from enhanced liquid motion. Nevertheless, several effects were found to mitigate this loss of efficiency, such as plume merging, which reduces liquid velocity and increases bubble residence time, and bubble recirculation along the walls, which can account for up to 50% of the local void fraction. A progressive increase in bubble size with height was also detected; over 0.8 m, the bubble chord length increased by 33%, 19%, and 15% for 10, 20, and 40 m³/h, respectively. Finally, the combined analysis of the local parameters enabled the experimental estimation of both the $a$ and the $k_L$. The resulting $k_L$ values showed good agreement with Brauer’s partially contaminated water model, validating the consistency of the dataset.

Overall, this study shows the dominant role of local two-phase flow parameters, hydrodynamics, and plume interaction in governing gas–liquid mass transfer, providing new experimental evidence to better characterize multi-plume bubble dynamics. The novelty of this work lies in the detailed experimental characterization of interacting plumes in a dense diffuser configuration, offering a comprehensive dataset that captures local hydrodynamics and mass transfer simultaneously. The validated dataset provides a robust benchmark for the development and calibration of multiphase flow models and supports future simulation, design, and optimization of fine-bubble aeration systems. These results also point to promising research directions, including the development of predictive tools for reactor design based on the hydrodynamic criteria identified in this study.