Seepage Modeling in Filled Tortuous Fractures Coupled with Porous Media Matrix: Influence of Filling Material Properties
Abstract
1. Introduction
2. Materials and Methods
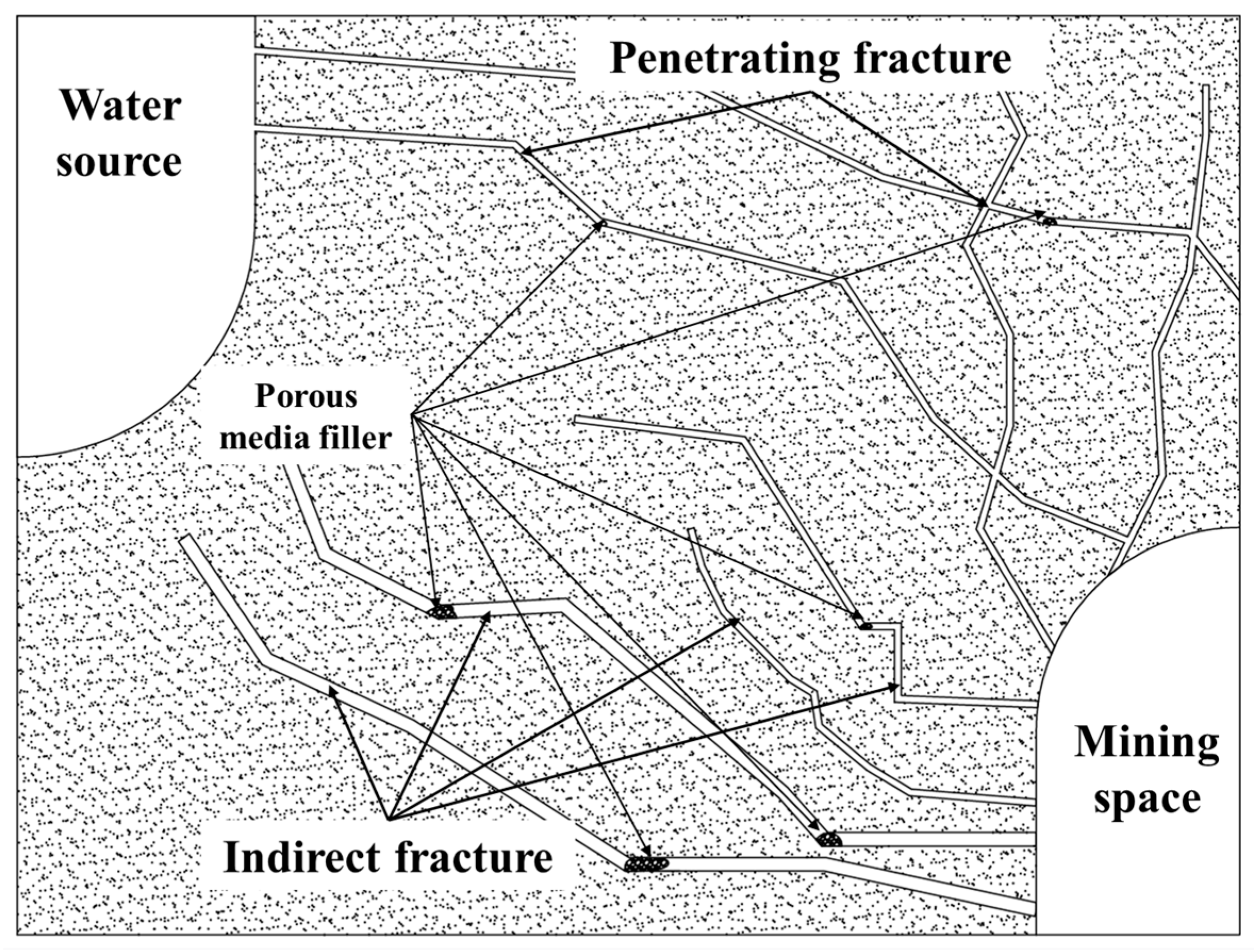
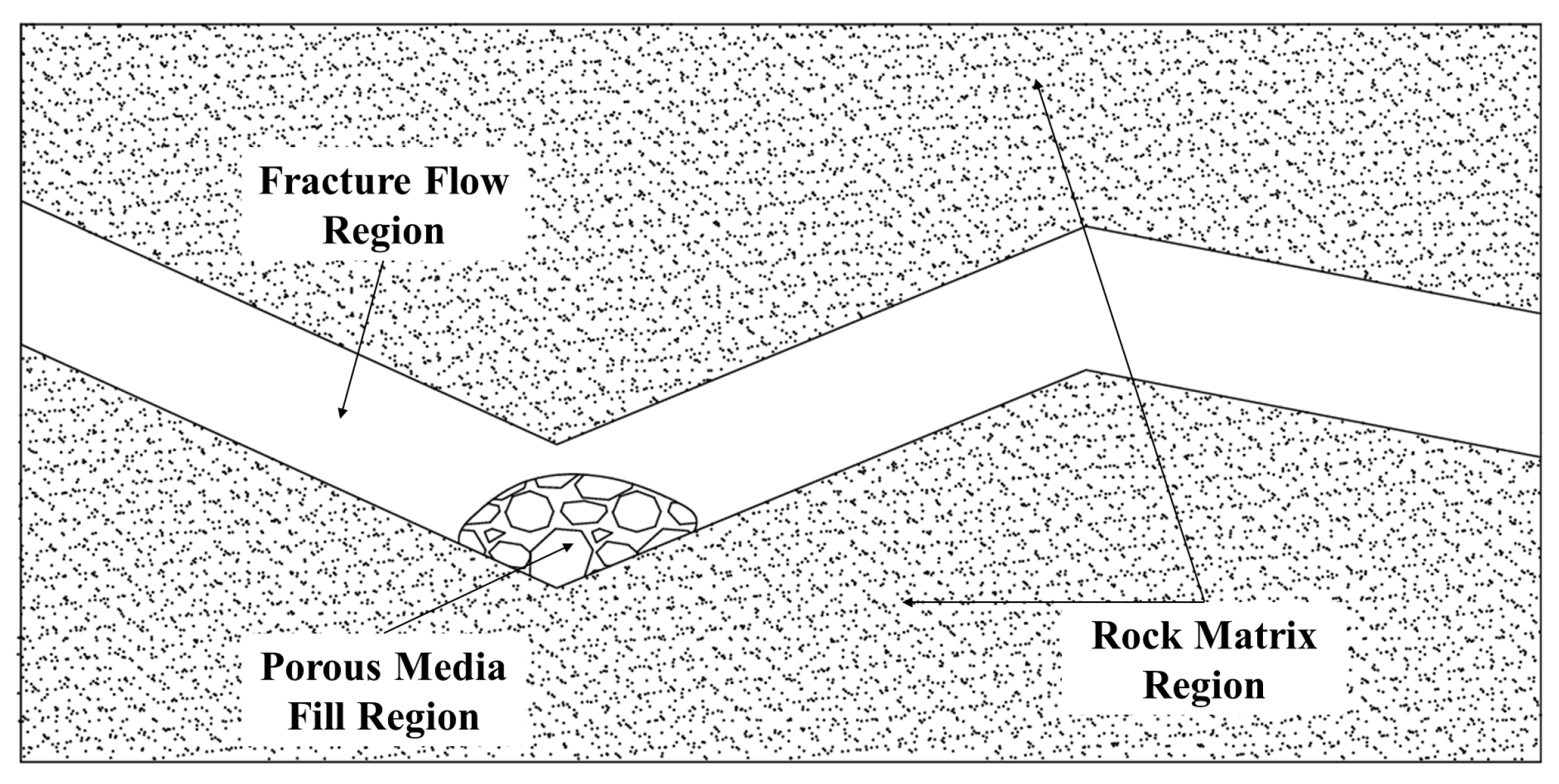
2.1. Engineering Context
2.2. Nonlinear Seepage Theory
2.3. Simulation Parameters
3. Analysis of Seepage Characteristics in Horizontal Fractures
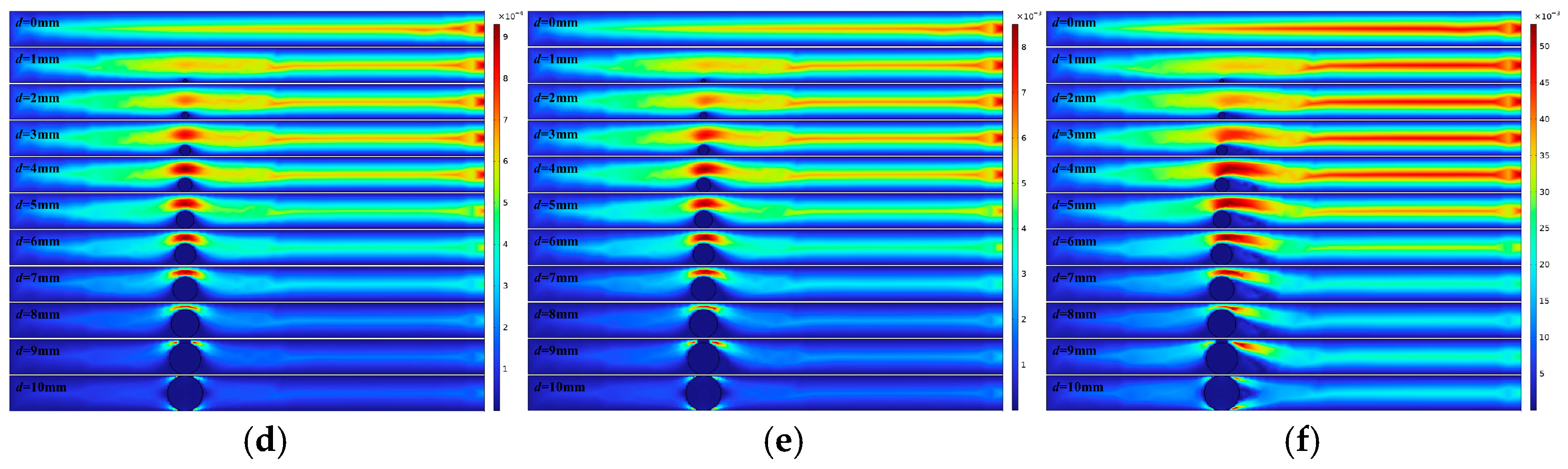
3.1. Flow Field Architectures of Horizontal Fractures Simulation
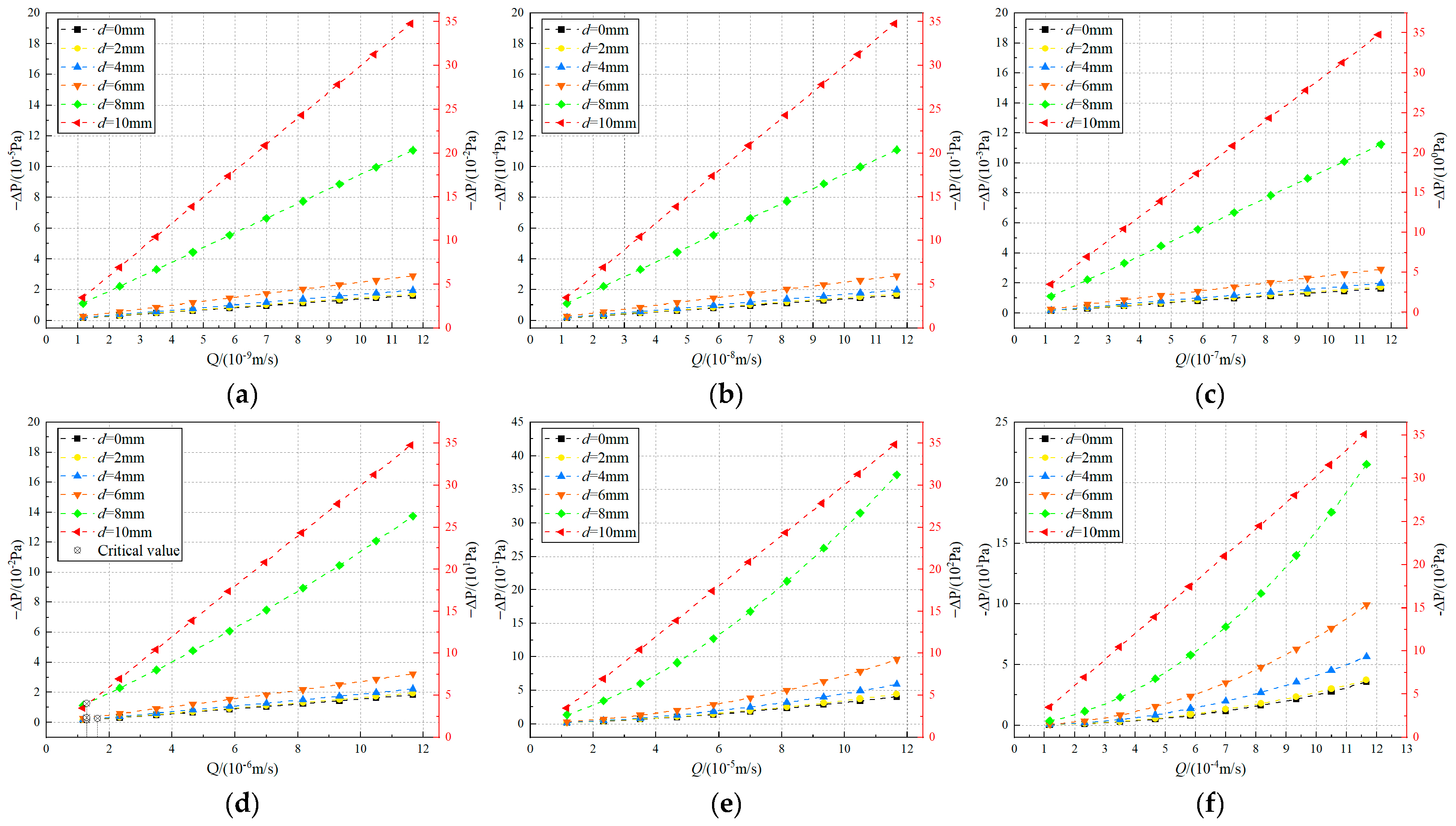
3.2. Pressure Drop and Volumetric Flow Rate in Horizontal Fractures
4. Analysis of Seepage Characteristics in Tortuous Fractures
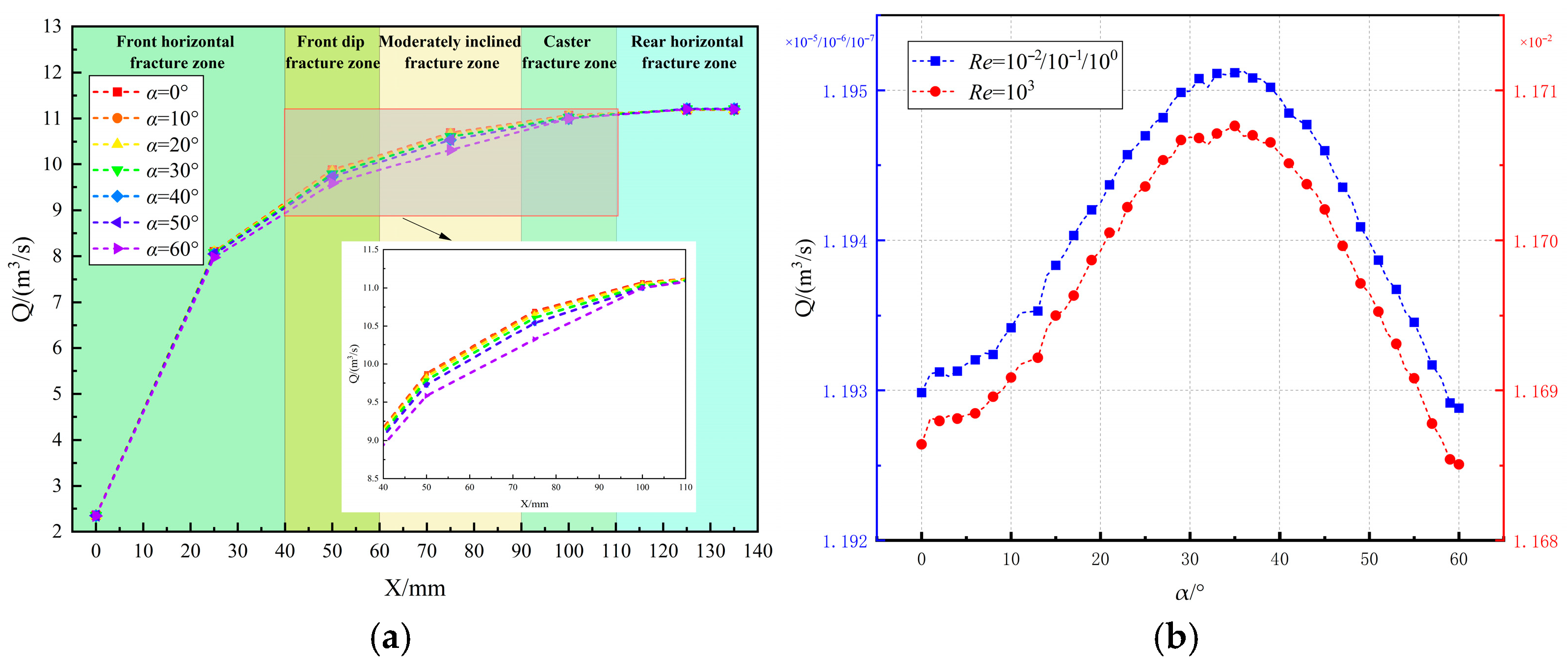
4.1. Flow Field Architectures of Tortuous Fractures Simulation
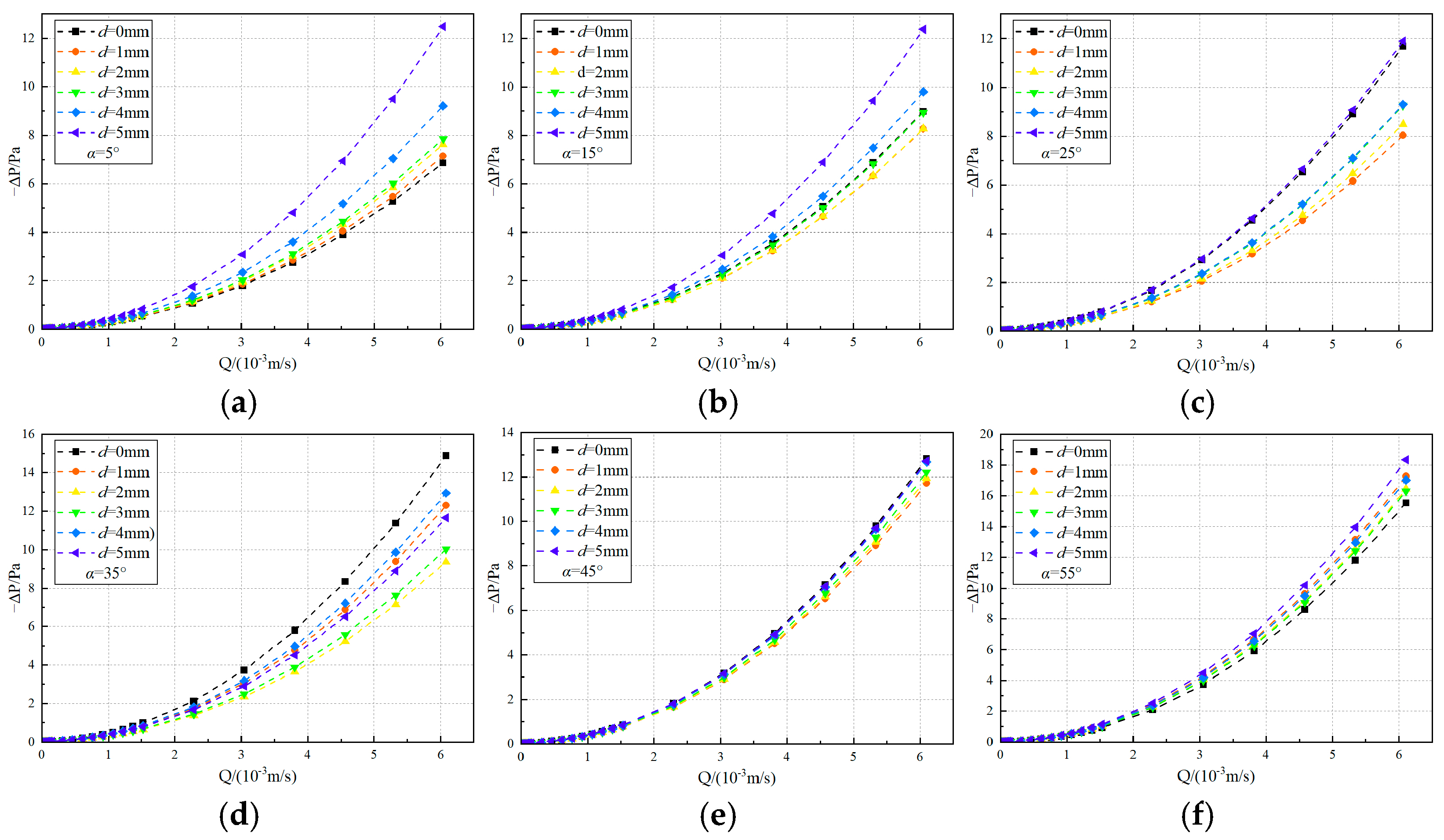
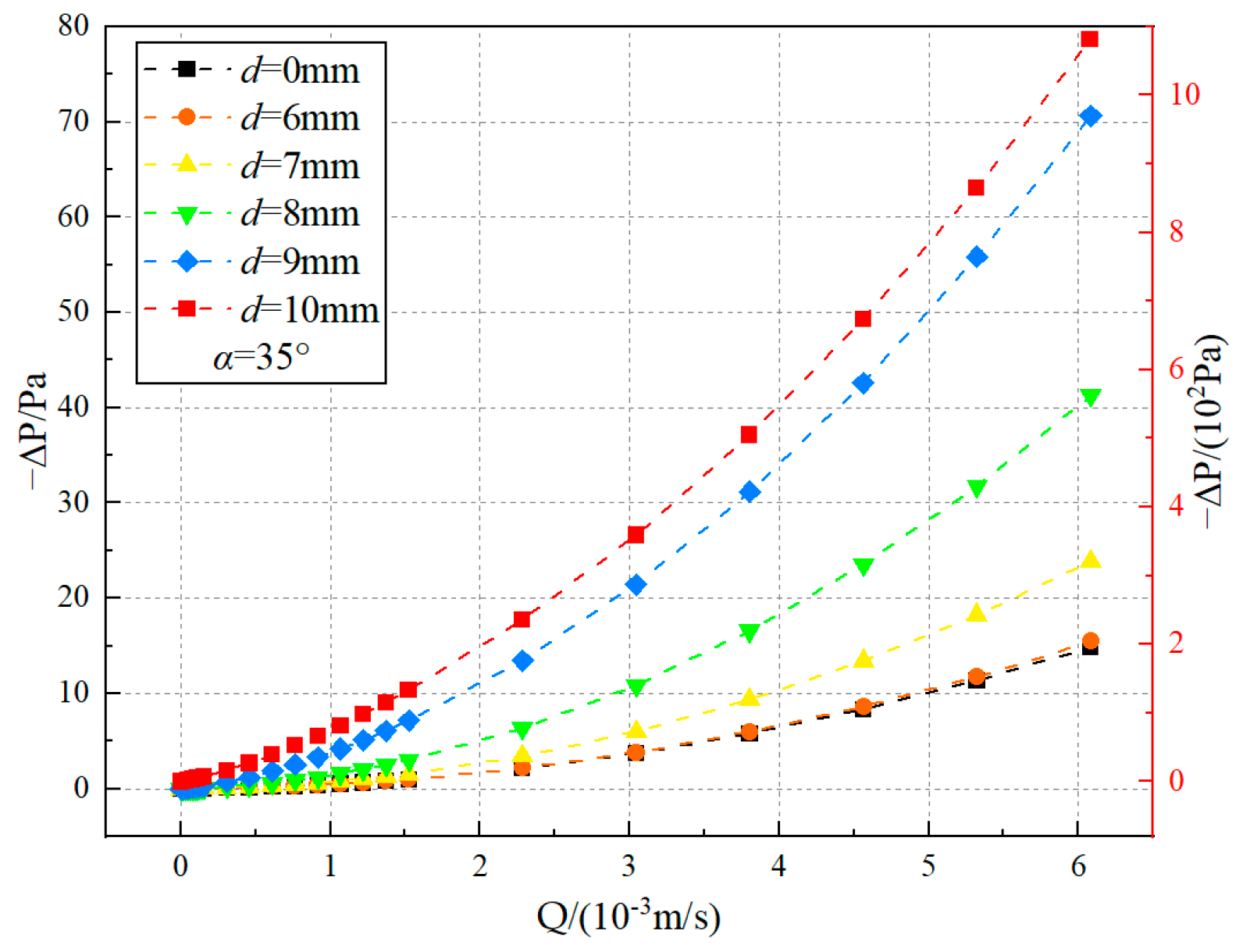
4.2. Pressure Drop and Volumetric Flow Rate in Tortuous Fractures
5. Conclusions
- (1)
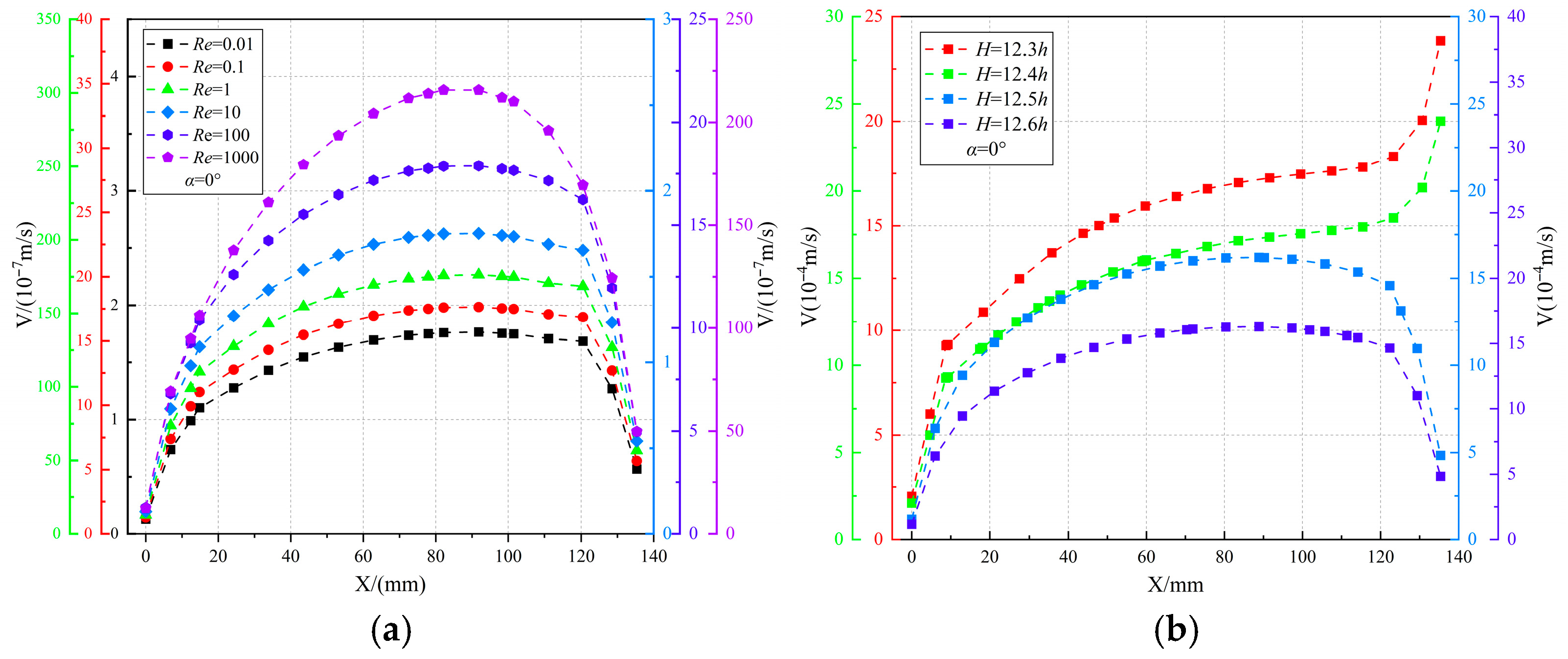
- Horizontal fractures continuously receive fluid influx from the surrounding porous matrix, where the flow field maintains remarkable symmetry. A critical matrix height-to-fracture aperture ratio (Hcrit ≈ 12.5 h) regulates the divergence and convergence of streamlines at the fracture outlet, governing the transition between different flow regimes.
- (2)
- The flow field within horizontal fractures undergoes substantial transformation when the Reynolds number exceeds a critical threshold (Recrit = 11–14), while the flow patterns and -ΔP-Q relationships remain essentially unchanged below this value. This demonstrates the existence of a distinct flow regime transition controlled by inertial effects.
- (3)
- Tortuous fracture geometries induce localized vortex formation and significant velocity fluctuations, particularly in the front and rear dip-angle zones. Compared to horizontal fractures, the tortuous configuration enhances fluid exchange efficiency between the porous matrix and fracture channels, while generating geometrically asymmetric flow fields in the adjacent porous media.
- (4)
- The volumetric flow rate in tortuous fractures exhibits a non-monotonic dependence on inclination angle, initially increasing then decreasing with rising dip angle to reach a maximum at approximately 36°. A distinct synergistic effect between fracture inclination angle and infill particle diameter jointly regulates local flow resistance and kinetic energy dissipation. This interaction produces systematic shifts in the relative positions of pressure-drop-flow-rate curves when d/h ≤ 0.5, while this phenomenon vanishes when the infill particle diameter becomes substantial (d/h > 0.5).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, J.; Yao, B.; Liu, Y.; Wang, D.; Cui, P.; Yao, S. Grout Diffusion Law and Variable Mass Seepage Model in Fractured Coal Mass. J. China Coal Soc. 2020, 45, 204–212. [Google Scholar] [CrossRef]
- Zheng, C.; Han, F.; Jiang, B.; Sheng, X.; Guofu, L.; Shuaili, L. Multi-Scale Pore-Fracture Evolution and Permeability Jump Law of Coal Under In Situ Hydraulic Fracturing. J. China Univ. Min. Technol. 2024, 53, 710–725. [Google Scholar] [CrossRef]
- Li, X.L.; Chen, S.J.; Li, Z.H.; Wang, E.Y.; Li, Z.H. Rock burst mechanism in coal rock with structural surface and the microseismic (MS) and electromagnetic radiation (EMR) response. Eng. Fail. Anal. 2021, 124, 105396. [Google Scholar] [CrossRef]
- Li, X.L.; Wang, E.Y.; Li, Z.H.; Liu, Z.; Song, D.; Qiu, L. Rock burst monitoring by integrated microseismic and electromagnetic radiation methods. Rock Mech. Rock Eng. 2016, 49, 4393–4406. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, S.; Li, L.; Shi, S.; Zhang, Q.; Chen, D.; Song, S. 3D Fluid-Solid Coupling Model Test on Mechanism of Water Inrush Caused by Permeability Instability in Karst Conduits of Tunnels. Chin. J. Rock Mech. Eng. 2015, 34, 1739–1749. [Google Scholar] [CrossRef]
- Li, S.; Lin, P.; Xu, Z.; Li, L.; Guo, M.; Sun, C.; Wang, J.; Song, S. Minimum Safe Thickness of Water and Mud Inrush in Filled Karst Water-Bearing Structures Based on Slice Method. Rock Soil Mech. 2015, 36, 1989–1994+2002. [Google Scholar] [CrossRef]
- Knabner, P.; Roberts, J.E. Mathematical analysis of a discrete fracture model coupling Darcy flow in the matrix with Darcy-Forchheimer flow in the fracture. ESAIM Math. Model. Numer. Anal. 2014, 48, 1451–1472. [Google Scholar] [CrossRef]
- Chen, Y.F.; Zhou, J.Q.; Hu, S.H.; Hu, R.; Zhou, C.-B. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures. J. Hydrol. 2015, 529, 993–1006. [Google Scholar] [CrossRef]
- Nordbotten, J.M.; Boon, W.M.; Fumagalli, A.; Keilegavlen, E. Unified approach to discretization of flow in fractured porous media. Comput. Geosci. 2019, 23, 225–237. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Qu, Z.G.; Yin, Y.; Kang, Q.; Yu, B.; Tao, W.-Q. Modeling of multi-scale transport phenomena in shale gas production—A critical review. Appl. Energy 2020, 262, 114575. [Google Scholar] [CrossRef]
- Gao, M.; Zhao, S.; Xi, G.; Iao, B.; Shi, X.; He, S. Fracture Evolution and Failure Characteristics of Surrounding Rock in Ultra-Thick Coal Seam Roadway Under Repeated Impact. J. China Univ. Min. Technol. 2024, 53, 634–646. [Google Scholar] [CrossRef]
- Guo, H.; Wang, K.; Cui, H.; Xu, C.; Yang, T.; Zhang, Y.; Teng, T. Experimental Study on Pore-Fracture Structure and Fractal Characteristics of Briquette Coal. J. China Univ. Min. Technol. 2019, 48, 1206–1214. [Google Scholar] [CrossRef]
- Pan, R.; He, X. Seepage Law of Rough Single Fracture Under Influence of Rock Fracture Surface Tortuosity. J. Liaoning Tech. Univ. (Nat. Sci. Ed.) 2020, 39, 293–298. [Google Scholar] [CrossRef]
- Yang, M.; Chen, M.; He, Y. Influence of Single Fracture Tortuosity on Fluid Seepage Process. Rock Soil Mech. 2001, 78–82. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, H.; Weng, L.; Liu, Q.; Shen, J. Seepage Characteristics of Fractured Sandstone Based on Real-Time Nuclear Magnetic Resonance Imaging Technology. Chin. J. Rock Mech. Eng. 2021, 40, 263–275. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Ni, X. Characteristics Analysis of Forchheimer-Type Non-Darcy Seepage Parameters. Water Resour. Power 2014, 32, 52–54+164. [Google Scholar] [CrossRef]
- Wang, D.; Wei, Q.; Wei, J.; Bai, X.; Yu, C.; Zhang, P. Fractal Characteristics of Coal Fractures and Fractal Seepage Model. J. China Univ. Min. Technol. 2020, 49, 103–109+122. [Google Scholar] [CrossRef]
- Zhao, Q.; Xu, G. Hybrid Method for Rotor Flow Field Simulation Based on Navier-Stokes Equations/Free Wake/Full Potential Equations. Acta Aerodyn. Sin. 2006, 1, 15–21. [Google Scholar] [CrossRef]
- Liu, M.; Hu, S.; Chen, Y.; Zhou, C. Analytical Model of Nonlinear Seepage Parameters for Fractured Rock Mass Based on High-Pressure Water Injection Test. J. Hydraul. Eng. 2016, 47, 752–762. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, S.; Zhang, Y.; Zhang, S.; Han, L. Mechanism of Pore and Fracture Structure Changes in Coals with Different Moisture Contents Under SCCO2. J. China Coal Soc. 2024, 49, 3143–3153. [Google Scholar] [CrossRef]
- Gong, H.; Liu, Y.; Zhao, H.; LI, Y.; Jing, S. Zoning Characteristics and Critical Stress Conditions of Floor Fracture Propagation in Stopes. J. China Univ. Min. Technol. 2024, 53, 1132–1143. [Google Scholar] [CrossRef]
- Zhong, C.; Leung Juliana, Y. Coupling Upscaled Discrete Fracture Matrix and Apparent Permeability Modelling in DFNWORKS for Shale Reservoir Simulation. Adv. Water Resour. 2024, 192, 104776. [Google Scholar] [CrossRef]
- Meng, R.; Hu, S.; Chen, Y.; Zhou, C. Permeability Characteristics of Fractured Rock Mass Based on Non-Darcy Flow Under High Seepage Pressure. Chin. J. Rock Mech. Eng. 2014, 33, 1756–1764. [Google Scholar] [CrossRef]
- Zhu, Y. Analysis of Influence of Fracture tortuosity Angle on Grouting Diffusion Radius. China Mine Eng. 2014, 43, 55–58+62. [Google Scholar] [CrossRef]
- Nian, G.; Chen, Z.; Zhou, Z.; Zhang, L.; Bao, M. Seepage and Stability Analysis of Fractured Rock Slope Based on Dual Media Model. J. China Coal Soc. 2020, 45 (Suppl. S2), 736–746. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, P.; Liu, W.; Hao, Y.; Yang, Y.; He, C. Dual-Permeability Model and Numerical Solution for Gas Seepage in Boreholes of Dual-Porosity Coal. J. China Univ. Min. Technol. 2016, 45, 1111–1117. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, X.; Wang, E. Quantitative evaluation of the onset and evolution for the non-Darcy behavior of the partially filled rough fracture. Water Resour. Res. 2024, 60, e2023WR036521. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory, 9th ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Brinkman, H.C. A Calculation of the Viscous Force Exerted by a Flowing Fluid on a Dense Swarm of Particles. Appl. Sci. Res. 1947, 1, 27–34. [Google Scholar] [CrossRef]
- Idelchik, I.E. Handbook of Hydraulic Resistance, 3rd ed.; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, G.; Lu, S. Analysis of Unsteady Seepage in Saturated-Unsaturated 3D Porous Media. Eng. J. Wuhan Univ. 2001, 5–8+26. [Google Scholar]
- Wei, M.; Huangpu, H.; Lu, C.; Gao, K.; Wei, L.; Guo, F. Experimental Measurement Method for Matrix and Fracture Permeability of Coal Rock. J. China Univ. Min. Technol. 2024, 54, 413–422. [Google Scholar] [CrossRef]
- Wang, G.; Chen, H.; Chen, X.; Yang, B. Seepage Characteristics of Variable Aperture Fractures in Coal Based on CT 3D Reconstruction. J. China Univ. Min. Technol. 2024, 53, 59–67. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, Q.; Kong, X.; Feng, J.; Yin, Z.; Wang, C. Experimental Study on Pore and Fracture Structure Evolution of Bituminous Coal Under Multiple Shock Loads. J. China Coal Soc. 2024, 49, 1882–1893. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
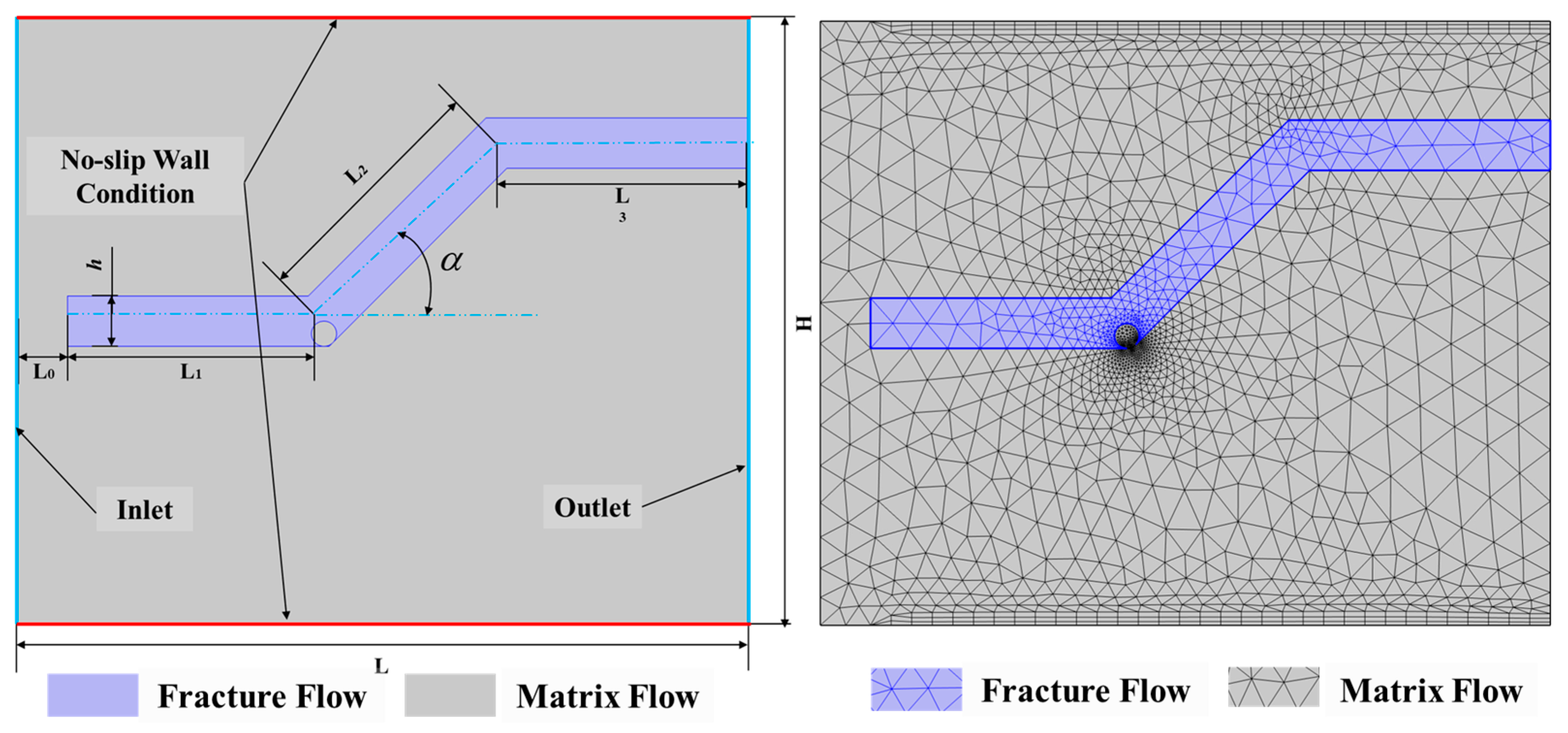






| Symbol | Value/Range |
|---|---|
| H | 125 mm |
| S | 135 mm |
| h | 10 mm |
| L0 | 10 mm |
| L1 | 50 mm |
| L2 | 50 mm |
| L3 | S–L1–L2 sin α |
| α | 0–60° |
| Re | 10−2–104 |
| d | 0–10 mm/dmax |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Kong, D.; Zhao, J.; Shi, L.; Mao, Z. Seepage Modeling in Filled Tortuous Fractures Coupled with Porous Media Matrix: Influence of Filling Material Properties. Water 2025, 17, 3386. https://doi.org/10.3390/w17233386
Liu W, Kong D, Zhao J, Shi L, Mao Z. Seepage Modeling in Filled Tortuous Fractures Coupled with Porous Media Matrix: Influence of Filling Material Properties. Water. 2025; 17(23):3386. https://doi.org/10.3390/w17233386
Chicago/Turabian StyleLiu, Weitao, Debin Kong, Jiyuan Zhao, Lihong Shi, and Zhenguo Mao. 2025. "Seepage Modeling in Filled Tortuous Fractures Coupled with Porous Media Matrix: Influence of Filling Material Properties" Water 17, no. 23: 3386. https://doi.org/10.3390/w17233386
APA StyleLiu, W., Kong, D., Zhao, J., Shi, L., & Mao, Z. (2025). Seepage Modeling in Filled Tortuous Fractures Coupled with Porous Media Matrix: Influence of Filling Material Properties. Water, 17(23), 3386. https://doi.org/10.3390/w17233386






