Rainfall Impact Experiments on a Clay Soil Covered by Rock Fragments
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup and Runs
2.2. Microplot Survey and 3D Model Analysis
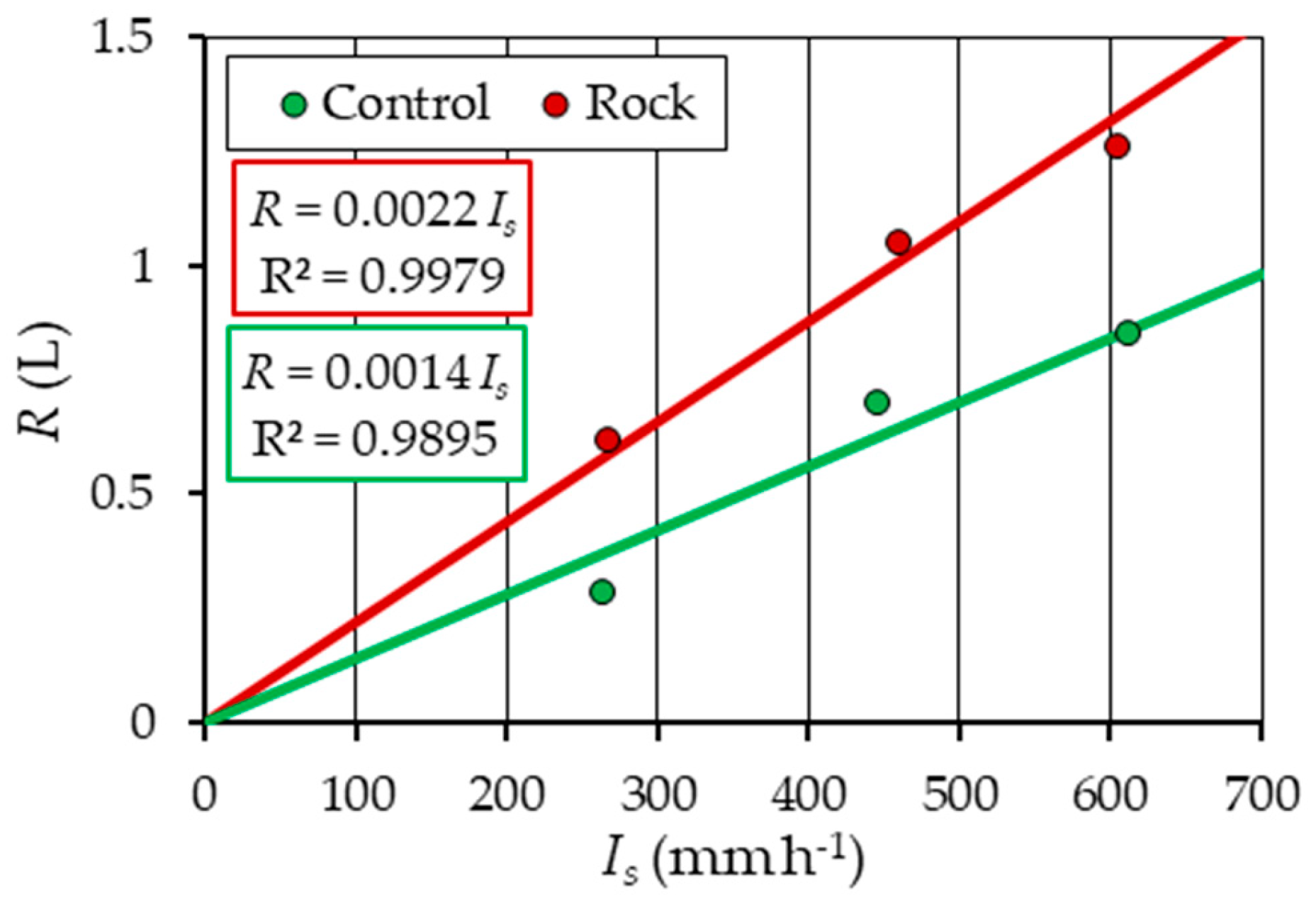
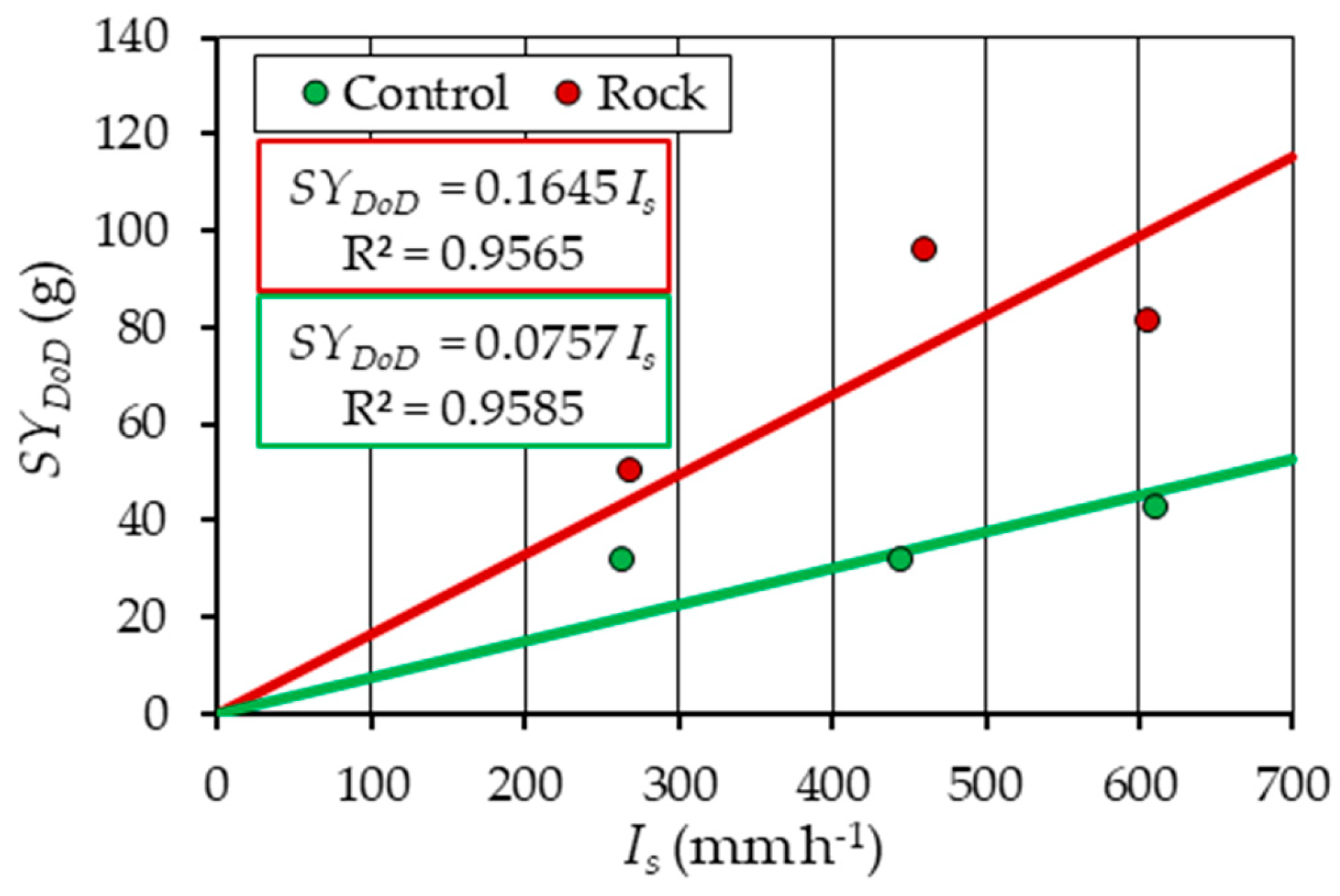
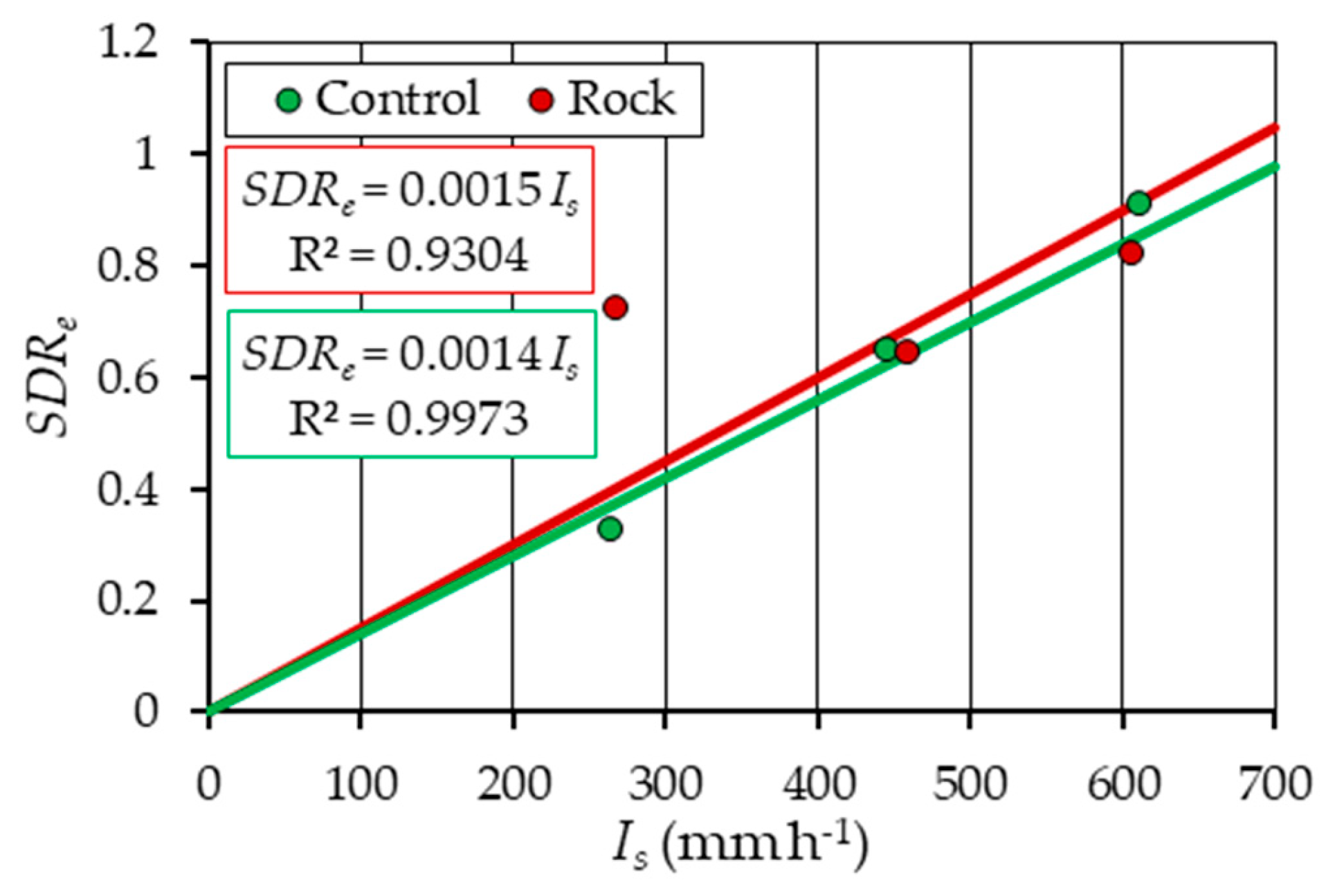
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Panagos, P.; Ballabio, C.; Poesen, J.; Lugato, E.; Scarpa, S.; Montanarella, L.; Borrelli, P. A soil erosion indicator for supporting agricultural, environmental and climate policies in the European Union. Remote Sens. 2020, 12, 1365. [Google Scholar] [CrossRef]
- Kuhn, N.J.; Greenwood, P.; Fister, W. Use of field experiments in soil erosion research. In Developments in Earth Surface Processes; Elsevier: Amsterdam, The Netherlands, 2014; Volume 18, pp. 175–200. [Google Scholar]
- Carollo, F.G.; Di Stefano, C.; Nicosia, A.; Palmeri, V.; Pampalone, V.; Ferro, V. A new strategy to assure compliance with soil loss tolerance at a regional scale. CATENA 2023, 223, 106945. [Google Scholar] [CrossRef]
- Di Stefano, C.; Nicosia, A.; Palmeri, V.; Pampalone, V.; Ferro, V. Rill flow resistance law under sediment transport. J. Soils Sediments 2022, 22, 334–347. [Google Scholar] [CrossRef]
- Poesen, J.; Ingelmo-Sanchez, F.; Mucher, H. The hydrological response of soil surfaces to rainfall as affected by cover and position of rock fragments in the top layer. Earth Surf. Process. Landf. 1990, 15, 653–671. [Google Scholar] [CrossRef]
- Poesen, J. Surface sealing as influenced by slope angle and position of simulated stones in the top layer of loose sediments. Earth Surf. Process. Landf. 1986, 11, 1–10. [Google Scholar] [CrossRef]
- Bunte, K.; Poesen, J. Effects of rock fragment covers on erosion and transport of noncohesive sediment by shallow overland flow. Water Resour. Res. 1993, 29, 1415–1424. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.; Niu, J.; Li, H.; Xiao, R.; Zheng, H.; Bech, J. Rock fragments and soil hydrological processes: Significance and progress. CATENA 2016, 147, 153–166. [Google Scholar] [CrossRef]
- Guo, T.; Wang, Q.; Li, D.; Zhuang, J. Effect of surface stone cover on sediment and solute transport on the slope of fallow land in the semi-arid loess region of northwestern China. J. Soils Sediments 2010, 10, 1200–1208. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Cai, C.; Shi, Z.; Xu, Q.; Fu, Z.; Guo, Z. Effects of rock fragment cover on hydrological response and soil loss from Regosols in a semi-humid environment in South-West China. Geomorphology 2012, 151, 234–242. [Google Scholar] [CrossRef]
- Simanton, J.R.; Renard, K.G. Seasonal change in infiltration and erosion from USLE plots in southeastern Arizona. Water Resour. Ariz. Southwest 1982, 12, 37–46. [Google Scholar]
- Poesen, J.W.; Torri, D.; Bunte, K. Effects of rock fragments on soil erosion by water at different spatial scales: A review. CATENA 1994, 23, 141–166. [Google Scholar] [CrossRef]
- Bunte, K.; Poesen, J. Effects of rock fragment size and cover on overland flow hydraulics, local turbulence and sediment yield on an erodible soil surface. Earth Surf. Process. Landf. 1994, 19, 115–135. [Google Scholar] [CrossRef]
- Li, L.; Nearing, M.A.; Polyakov, V.O.; Nichols, M.H.; Pierson, F.B.; Cavanaugh, M.L. Evolution of rock cover, surface roughness, and its effect on soil erosion under simulated rainfall. Geoderma 2020, 379, 114622. [Google Scholar] [CrossRef]
- Sun, J.; Yu, X.; Fan, D.; Huang, C. Hydrological and erosive response of soil surfaces to rainfall intensity as affected by gravel fragment coverage. J. Soil Water Conserv. 2018, 73, 353–362. [Google Scholar] [CrossRef]
- Ding, W.; Huang, C. Effects of soil surface roughness on interrill erosion processes and sediment particle size distribution. Geomorphology 2017, 295, 801–810. [Google Scholar] [CrossRef]
- Govers, G.; Takken, I.; Helming, K. Soil roughness and overland flow. Agronomie 2000, 20, 131–146. [Google Scholar] [CrossRef]
- Smith, M.W.; Cox, N.J.; Bracken, L.J. Applying flow resistance equations to overland flows. Prog. Phys. Geogr. 2007, 31, 363–387. [Google Scholar] [CrossRef]
- Alewell, C.; Borrelli, P.; Meusburger, K.; Panagos, P. Using the USLE: Chances, challenges and limitations of soil erosion modelling. Int. Soil Water Conserv. Res. 2019, 7, 203–225. [Google Scholar] [CrossRef]
- Pampalone, V.; Nicosia, A.; Palmeri, V.; Serio, M.A.; Ferro, V. Rill and interrill soil loss estimations using the USLE-MB equation at the Sparacia Experimental Site (South Italy). Water 2023, 15, 2396. [Google Scholar] [CrossRef]
- Flanagan, D.C.; Ascough, J.C.; Nearing, M.A.; Laflen, J.M. The water erosion prediction project (WEPP) model. In Landscape Erosion and Evolution Modeling; Springer: Boston, MA, USA, 2001; pp. 145–199. [Google Scholar]
- Flanagan, D.C.; Nearing, M.A. Sediment particle sorting on hillslope profiles in the WEPP model. Trans. ASAE 2000, 43, 573–583. [Google Scholar] [CrossRef]
- Gong, T.; Zhu, Y.; Shao, M. Effect of embedded-rock fragments on slope soil erosion during rainfall events under simulated laboratory conditions. J. Hydrol. 2018, 563, 811–817. [Google Scholar] [CrossRef]
- Li, X.; Fu, S.; Liu, B. Response of flow hydraulic parameters to different rock fragment coverages and sizes under simulated rainfall. Soil Till. Res. 2023, 230, 105707. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, K.; Peng, Y.; Rubinato, M.; Zhang, H.; Li, P. Effect of gravel coverage on the hydrodynamic characteristics of overland flow on the Loess Plateau in China. J. Hydrol. 2023, 627, 130322. [Google Scholar] [CrossRef]
- Laburda, T.; Krása, J.; Zumr, D.; Devátý, J.; Vrána, M.; Zambon, N.; Johannsen, L.L.; Klik, A.; Strauss, P.; Dostál, T. SfM-MVS Photogrammetry for splash erosion monitoring under natural rainfall. Earth Surf. Process. Landf. 2021, 46, 1067–1082. [Google Scholar] [CrossRef]
- Sochan, A.; Beczek, M.; Mazur, R.; Polakowski, C.; Ryżak, M.; Bieganowski, A. Splash erosion and surface deformation following a drop impact on the soil with different hydrophobicity levels and moisture content. PLoS ONE 2023, 18, e0285611. [Google Scholar] [CrossRef] [PubMed]
- Balaguer-Puig, M.; Marqués-Mateu, Á.; Lerma, J.L.; Ibáñez-Asensio, S. Estimation of small-scale soil erosion in laboratory experiments with Structure from Motion photogrammetry. Geomorphology 2017, 295, 285–296. [Google Scholar] [CrossRef]
- Kaiser, A.; Erhardt, A.; Eltner, A. Addressing uncertainties in interpreting soil surface changes by multitemporal high-resolution topography data across scales. Land Degrad. Dev. 2018, 29, 2264–2277. [Google Scholar] [CrossRef]
- Pampalone, V.; Carollo, F.G.; Nicosia, A.; Palmeri, V.; Di Stefano, C.; Bagarello, V.; Ferro, V. Measurement of water soil erosion at Sparacia experimental area (Southern Italy): A summary of more than twenty years of scientific activity. Water 2022, 14, 1881. [Google Scholar] [CrossRef]
- Kamphorst, A. A small rainfall simulator for the determination of soil erodibility. Neth. J. Agricul. Sci. 1987, 35, 407–415. [Google Scholar] [CrossRef]
- Carollo, F.G.; Caruso, R.; Ferro, V.; Serio, M.A. Characterizing the Kamphorst rainfall simulator for soil erosion investigations. J. Hydrol. 2024, 643, 132025. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning (No. 537); Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1978.
- Di Stefano, C.; Nicosia, A.; Pampalone, V.; Palmeri, V.; Ferro, V. New technique for measuring water depth in rill channels. CATENA 2019, 181, 104090. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Koci, J.; Jarihani, B.; Leon, J.X.; Sidle, R.; Wilkinson, S.; Bartley, R. Assessment of UAV and ground-based structure from motion with multi-view stereo photogrammetry in a gullied savanna catchment. ISPRS Int. J. Geo-Inf. 2017, 6, 328. [Google Scholar] [CrossRef]
- Wheaton, J.M.; Brasington, J.; Darby, S.E.; Sear, D.A. Accounting for uncertainty in DEMs from repeat topographic surveys: Improved sediment budgets. Earth Surf. Process. Landf. 2010, 35, 136–156. [Google Scholar] [CrossRef]
- Prosdocimi, M.; Calligaro, S.; Sofia, G.; Dalla Fontana, G.; Tarolli, P. Bank erosion in agricultural drainage networks: New challenges from structure-from-motion photogrammetry for post-event analysis. Earth Surf. Process. Landf. 2015, 40, 1891–1906. [Google Scholar] [CrossRef]
- Smith, M.W.; Vericat, D. From experimental plots to experimental landscapes: Topography, erosion and deposition in sub-humid badlands from structure-from-motion photogrammetry. Earth Surf. Process. Landf. 2015, 40, 1656–1671. [Google Scholar] [CrossRef]
- Vinci, A.; Todisco, F.; Brigante, R.; Mannocchi, F.; Radicioni, F. A smartphone camera for the structure from motion reconstruction for measuring soil surface variations and soil loss due to erosion. Hydrol. Res. 2017, 48, 673–685. [Google Scholar] [CrossRef]
- Rozenstein, O.; Karnieli, A. Comparison of methods for land-use classification incorporating remote sensing and GIS inputs. Appl. Geogr. 2011, 31, 533–544. [Google Scholar] [CrossRef]





| Authors | Rock Fragment Arrangement | Main Results |
|---|---|---|
| Poesen [6] | Embedded and resting | Arrangement effects on soil susceptibility to surface sealing |
| Poesen et al. [5] | Embedded and resting | Rock cover reduces runoff for resting elements and enhances runoff for embedded elements. For embedded fragments, the increase in rock cover percentage increases the impermeabilized area. |
| Bunte and Poesen [7] | Resting | When rock cover increases from 0% to 20%, an increment in sediment yield (scouring phenomena localized around each rock fragment) occurs. |
| Zhang et al. [8] | Embedded and resting | Relevance of rock element architecture (coverage, size, position, and morphology). |
| Guo et al. [9]; Wang et al. [10] | Resting | Runoff and soil erosion decrease with increasing rock coverage, from 0 to 40%. |
| Poesen et al. [12] | Resting | (1) Rock elements protect soil from raindrop impact and flow detachment, (2) rock coverage reduces degradation of the underlying soil, and (3) flow resistance of resting elements produces a retardation of flow velocity. |
| Bunte and Poesen [13] | Resting | Rock element size affects the relationship between hydrological processes and rock coverage. |
| Li et al. [14] | Embedded to resting | Surface rock cover increases as rainfall progresses, leading to reductions in flow velocity and soil loss rate. |
| Sun et al. [15] | Resting | Runoff and sediment yield decreased with an increase in coverage percentage and were negatively correlated with rainfall intensity. |
| Gong et al. [23] | Embedded to resting | Embedding pattern represents a transition status from the conditions below the soil surface to resting on the soil surface. Embedded elements can accelerate soil erosion. |
| Li et al. [24] | Resting | Rock fragments reduce flow velocity and increase flow resistance |
| Liu et al. [25] | Resting | Increase in gravel coverage decreases flow velocity and increases the Darcy–Weisbach friction factor. |
| Class of Rainfall Intensity | Pressure Head H (cm) | Simulated Rainfall Intensity Is (mm h−1) | Kinetic Power Pn (J m−2 s−1) | Natural Rainfall Intensity In (mm h−1) |
|---|---|---|---|---|
| Low | 1.9 | 260.2 | 0.25 | 35.9 |
| Intermediate | 3.9 | 444.0 | 0.43 | 57.3 |
| High | 5.9 | 605.2 | 0.59 | 75.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palmeri, V.; Guida, G.; Lucchese, A.; Nicosia, A.; Ferro, V. Rainfall Impact Experiments on a Clay Soil Covered by Rock Fragments. Water 2025, 17, 3387. https://doi.org/10.3390/w17233387
Palmeri V, Guida G, Lucchese A, Nicosia A, Ferro V. Rainfall Impact Experiments on a Clay Soil Covered by Rock Fragments. Water. 2025; 17(23):3387. https://doi.org/10.3390/w17233387
Chicago/Turabian StylePalmeri, Vincenzo, Gaetano Guida, Antonino Lucchese, Alessio Nicosia, and Vito Ferro. 2025. "Rainfall Impact Experiments on a Clay Soil Covered by Rock Fragments" Water 17, no. 23: 3387. https://doi.org/10.3390/w17233387
APA StylePalmeri, V., Guida, G., Lucchese, A., Nicosia, A., & Ferro, V. (2025). Rainfall Impact Experiments on a Clay Soil Covered by Rock Fragments. Water, 17(23), 3387. https://doi.org/10.3390/w17233387







