Abstract
Sandy beach resilience faces growing threats from extreme events and intensified human activity. Deep Learning (DL) has emerged as a powerful tool in coastal research, offering strengths in spatial feature extraction, nonlinear sequence modeling, acceleration of physical processes, and integration of multi-source data. This review frames resilience in three technical dimensions—resistance, recovery, and adaptation—and examines DL applications across three domains: first, monitoring and forecasting external forcing, including typhoon tracks and storm surge peak values; second, modeling and simulating beach processes, from rapid hydrodynamic forecasting to medium- and long-term shoreline evolution, and high-resolution sediment transport forecasting; and third, management and decision support, where DL methods and multi-scenario generation expand governance options, and interpretable features with uncertainty quantification enhance risk communication and policy adoption. DL complements traditional models by shortening the “observation–model–decision” cycle, expanding scenario analysis, and improving governance transparency. Challenges remain in cross-domain generalization, robustness in extreme scenarios, and data governance. This review confirms DL’s potential as a technology stack for enhancing sandy beach resilience and provides a methodological foundation for future research.
1. Introduction
Sandy beaches represent one of the most widespread zones of human–ocean interaction worldwide. They fulfill multiple ecological, tourism, and economic functions [1]. The dense population in coastal zones also necessitates that these areas maintain a certain degree of resilience to hazards such as extreme events and storms [2,3]. The nearshore geomorphology and sediment transport of sandy beaches are highly complex and extremely sensitive to variations in external forcing conditions [4]. In recent years, under global warming, the impacts of sea-level rise on coastal zones have become a major concern [5]. Moreover, researchers have found that rising sea levels have increased the frequency of extreme sea-level events [6] and coastal flooding [7]. Extensive observational data indicate that global wind speeds and wave heights have been rising over recent decades, with particularly pronounced increases in extreme values [8]. The effects of human activities on sandy beaches (e.g., hard engineering structures, beach nourishment, and land reclamation) should also not be underestimated [9,10]. Collectively, these factors have intensified beach erosion caused by extreme events (natural) and heightened ecological risks associated with long-term environmental changes (human-induced). Therefore, research on the resilience of sandy beaches has become increasingly urgent [11]. Such research requires an integrated assessment framework that accounts for both process mechanisms and risk management [12].
In recent years, numerous high-frequency and high-resolution data acquisition methods have developed rapidly, including coastal High-Frequency Radars (HFRs) [13,14], Argus video monitoring systems [15], and Unmanned Aerial Vehicles (UAVs) [16]. The establishment of multi-source data systems has greatly enhanced the spatiotemporal characterization of nearshore hydrodynamic and topographic processes. It can provide a solid foundation for research on the resilience of sandy beaches, including the identification of shoreline and cross-shore evolution, the impacts of storm events, and subsequent recovery processes. However, process-based numerical models such as Delft3D (v6.02.10) [17] and XBeach (v1.22.4867) [18] face several challenges in high-resolution, long-term, and multi-scenario simulations, including high computational costs, sensitivity to boundary conditions, and difficulties in simulating turbulence [4]. In studies of wave-dominated beaches, researchers have further considered the dynamic variability of wave time series and morphological instability to gain deeper insights into beach morphodynamics [19]. Nevertheless, even within the wave-dominated background, the effects of extreme events and the general applicability of these models remain unresolved. These limitations are particularly evident in tasks involving multi-scale coupling among wind, waves, currents, sediments, and topography. Consequently, it remains difficult to accurately quantify how sandy beaches respond to extreme forcing, thereby constraining the assessment of their resilience.
Artificial intelligence (AI), particularly deep learning (DL), has emerged as a new paradigm owing to its strengths in modeling large-sample, nonlinear, and multi-source data [20]. To address the issue of interpretability in DL, researchers have begun embedding physical priors and conservation laws into the learning process. The concept of theory-guided data science seeks to leverage established scientific knowledge to enhance the capability of data-driven models in advancing scientific discovery [21]. Similarly, physics-informed deep learning integrates physical principles derived from first-order laws into data-driven frameworks, thereby combining the advantages of both physics-based and data-driven approaches [22]. Moreover, the development of hybrid modeling strategies and the introduction of physics-consistent loss functions have further improved the ability of models to unify physical mechanisms with data representations [23]. Currently, research on sandy beach resilience primarily focuses on two aspects: the dynamic evolution of sandy beach topography and geomorphology under external forcing and the associated resilience-related mechanisms [18,19]; and the adaptability of sandy beach environments to engineering measures, together with the governing patterns of their feedback responses [9,12]. These studies provide an important foundation for understanding sandy beach resilience and for the subsequent application of DL as a research method. This paradigm is particularly well suited for studying the resilience of sandy beaches. On the one hand, it enables effective forecasting of environmental changes under extreme events. On the other hand, it accelerates the simulation of high-frequency coastline and profile dynamics across multiple scenarios. Consequently, it provides a novel quantitative tool for assessing the resilience of sandy beaches in terms of disturbance, response, and recovery processes.
Taking the resilience of sandy beaches as the core theme, this review divides resilience into three technical dimensions: resistance, recovery, and adaptation (Figure 1). The resistance dimension (e.g., short-term forecasting, setting early warning thresholds) addresses system responses to extreme events. Following such events, the recovery dimension (e.g., assessing profile recovery time) evaluates the system’s capacity to restore its pre-disturbance state. Over longer timescales, the adaptation dimension (e.g., scheme optimization, digital twins) aims to enhance the system’s robustness and sustainability.
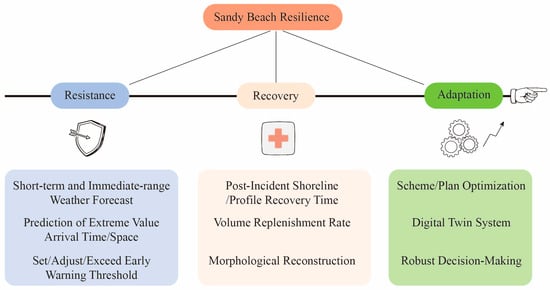
Figure 1.
Conceptual framework and technical process of sandy beach resilience.
Accordingly, rather than directly providing quantitative resilience values, this review establishes a comprehensive framework and analytical process based on three dimensions: resistance, recovery, and adaptation. Different from other reviews that broadly explore the application of AI in coastal sciences, this review focuses exclusively and specifically on DL, which currently exhibits the greatest potential for further development. By positioning DL as a supporting technology for resilience governance and systematically reviewing the progress, advantages, and limitations of DL, this review will explore its potential as an enabling technology for enhancing resilience across the three dimensions of resistance, recovery, and adaptation. Section 2 introduces DL methods across various capabilities. Section 3 reviews their application in meteorological disasters and external forcing forecasting. Section 4 reviews applications in coastal morphology and sediment dynamics. Section 5 reviews DL-based approaches for sandy beach management and decision-making.
2. Methods: Deep Learning
DL is a major subfield of machine learning (ML), centered on constructing multi-layer neural networks that emulate the way the human brain processes and learns from data. DL has achieved remarkable success across various fields, enabling machines to match or even surpass human performance in many tasks. In terms of sandy beach resilience research, DL applications primarily focus on capturing spatial features and modeling nonlinear relationships within time series data.
2.1. Literature Search and Data Sources
This review conducted a literature search and statistical analysis to explore the potential of integrating DL into research on sandy beach resilience. Peer-reviewed articles, review papers, and relevant reports published between 2010 and 2024 were collected from the Web of Science Core Collection database. Two main categories of keywords were used: sandy beaches and DL. Figure 2 presents the publication trends of these two categories over the past 15 years. As shown in Figure 2a, sustained attention has been given to the coastline evolution of sandy beaches, while studies and topics related to beach resilience have gradually increased year by year. Meanwhile, researchers have maintained strong interest in the practical implementation of sandy beach management and decision-making. Figure 2b indicates that over the past five years, scholars have shown growing enthusiasm for applying DL across various fields. The use of DL in spatial characterization and time-series analysis has become increasingly extensive. At the same time, researchers have recognized the non-interpretability of DL as a “black box”. In the past three years, researchers have increasingly focused on integrating physical knowledge into DL frameworks. Table 1 summarizes the widely used DL methods, outlining their respective advantages, disadvantages, and application scenarios. These methods all show considerable potential for application in sandy beach resilience research.
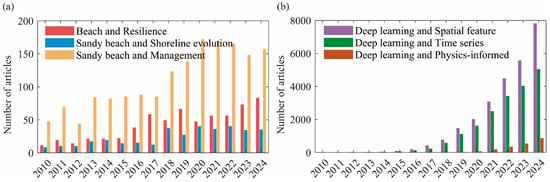
Figure 2.
The comparison of the literature sources in terms of (a) ‘Sandy beach’ and (b) ‘Deep learning’.
2.2. Spatial Characterization
The emergence of convolutional neural networks (CNN) has enabled DL to achieve remarkable progress in capturing spatial characterization, leading to their widespread application in computer vision [24]. By introducing a max-fusion strategy, methods based on fully convolutional networks (FCN, [25]) have achieved state-of-the-art performance in the semantic segmentation of very high-resolution remote sensing images [26]. SegNet employs nonlinear upsampling operations to avoid the need for learnable upsampling layers, thereby effectively extracting features from lower-resolution input feature maps [27]. To systematically aggregate multi-scale information without reducing spatial resolution, researchers have adopted dilated convolutions, which significantly improve the accuracy of dense prediction tasks [28]. The residual architecture of ResNet further facilitates model optimization, allowing networks to learn deeper hierarchical features and achieve higher accuracy [29]. Although these networks demonstrate translation invariance, they still face limitations such as insufficient boundary feature extraction, limited generalization ability, and reduced performance in complex scenes.
The Vision Transformer (ViT) introduces self-attention mechanisms into visual representation learning, directly modeling long-range dependencies and global relationships. Through pre-training and transfer learning, pure Transformer architectures applied to sequences of image patches have achieved outstanding performance in image classification tasks, while requiring fewer computational resources during training [30]. The Swin Transformer constructs a hierarchical Transformer architecture that derives feature representations through shifted-window computations. This hierarchical design and shifted-window mechanism enable flexible multi-scale information modeling, with computational complexity that scales linearly with image size [31]. SegFormer integrates a Transformer backbone with a lightweight multilayer perceptron (MLP) decoder, allowing it to output multi-scale features and aggregate information across different levels by combining local and global attention, thereby achieving strong representational capability [32].
Overall, Transformers excel in large-sample, cross-scale tasks, whereas CNNs demonstrate more stable performance in small-sample, single-task scenarios. Integrating the two enables their complementary strengths to be fully utilized: attention mechanisms or Transformer architectures capture global dependencies, while CNNs effectively represent local features. When supplemented with transfer learning, strong regularization, and other techniques, this hybrid approach provides robust feature representation in two-dimensional space.
2.3. Time Series and Cross-Scale Dependencies
Recurrent neural networks (RNN) have been widely applied in time-series modeling, with their core strength lying in extracting temporal information and handling cross-scale dependencies [33,34]. N-BEATS is a deep neural network architecture based on backward and forward residual connections. It offers several notable advantages, including interpretability, direct applicability across diverse target domains, and fast training speed [35]. DeepAR produces high-precision probabilistic forecasts by training an autoregressive RNN on large collections of related time series [36]. Informer employs self-attention distillation to highlight the most relevant attention features. It can handle extremely long input sequences, and significantly improve inference speed [37]. Temporal fusion Transformers (TFT) combine recurrent layers for local processing with interpretable self-attention layers for modeling long-term dependencies, achieving high performance across diverse scenarios [38]. It is noteworthy that in time-series modeling, the objective is to capture temporal relationships within ordered continuous data points. In some cases, simple single-layer linear models outperform existing complex models [39].
Overall, RNNs have traditionally been the primary choice for time-series modeling. However, emerging Transformer-based DL methods have increasingly demonstrated advantages in extracting temporal information. Nonetheless, these methods generally demand larger data volumes and stronger regularization compared to traditional models such as long short-term memory (LSTM) and gated recurrent unit (GRU). For different task scenarios, factors such as sample size, spatial and temporal scale, and computational cost must be fully considered when selecting an appropriate model architecture. At the same time, combining multiple models can be continuously explored to leverage the strengths of different approaches.
2.4. Physics-Informed/Physics-Guided DL
In natural systems, physical consistency and extrapolation stability often take precedence over in-training accuracy. Physics-guided (or physics-informed) DL mitigates the “black box” nature and data dependency issues by embedding governing equations, conservation laws, and boundary conditions into the learning process [40]. Cuomo et al. argued that most studies focus on customizing physics-informed neural networks (PINN) through variations in activation functions, gradient optimization techniques, network architectures, and loss function designs [41]. Brunton et al. combined sparsity-promoting techniques, ML, and nonlinear dynamical systems to derive governing equations from noisy measurement data [42]. Rudy et al. noted that this approach is computationally efficient and robust, and has been validated in canonical problems across multiple scientific domains, including the Navier–Stokes equations, diffusion equations, and so on [43]. Bar-Sinai et al. introduced data-driven discretization, which employs neural networks to estimate spatial derivatives and uses end-to-end optimization to ensure adherence to governing equations on low-resolution grids [44]. Graph network-based simulators (GNS) learn to simulate a variety of challenging physical domains, including fluids, deformable materials, and so on [45]. Kochkov et al. applied an end-to-end DL framework to enhance approximation processes in computational fluid dynamics for simulating two-dimensional turbulent flows [46].
In summary, DL integrated with physical knowledge can not only constrain model training by incorporating equation residuals, structured network layers, and similar physical constraints into the loss function, but also autonomously learn the physical representations embedded within the data. Building on this capability, end-to-end DL methods have been applied to enhance computational efficiency and simulate complex operating conditions.

Table 1.
Common types of DL and their application scenarios.
Table 1.
Common types of DL and their application scenarios.
| Type | Feature | Typical Advantage | Limitation/Risk | Application Scenario | Ref. |
|---|---|---|---|---|---|
| CNN | Local translation invariance; hierarchical texture; controllable multi-scale | Strong spatial feature recognition capability; computationally friendly | Weak temporal dependence; poor multi-scale processing capability; dependence on the quality of training samples | Raster image classification | [26] |
| ViT | Global self-attention; non-local interaction; hierarchical window | Global long-range dependence; cross-scale fusion | High demand for data and computing power; easy overfitting with small samples | Large-sample data; multi-scale scenario correlation | [30] |
| RNN | Control information extraction using a gating mechanism | Strong univariate feature extraction capability; good at capturing nonlinear dynamics | Poor interpretability; gradient vanishing in long sequences | Univariate sequences; short-to-medium-term sequences | [33] |
| Transformer-based long-time series | Sparse/selective attention mechanism; covariate embedding and interpretation | Global dependence; cross-variable; high parallel computing efficiency | Large scale of training samples; relatively complex model structure | Long sequences; multi-scenario and multi-source variables | [34,37] |
| Physics-guided/Physics-informed DL | Physical information embedding; physical boundary constraints | Physical consistency; interpretability; robust extrapolation; strong generalization | Difficulty in loss convergence; complexity in boundary handling; high computational cost | Sparse observation; tasks requiring conservation constraints for extrapolation | [46] |
3. Application of DL in Sandy Beach Hazards and Hydrodynamic Processes
3.1. Typhoon Track/Intensity and Storm Surge Peak Value Forecasting
External hydrodynamic conditions play a critical role in the study of sandy beach resilience. Sandy beaches are particularly sensitive to extreme events, especially storm surges induced by typhoons. For effective beach management, the timely provision of information such as the arrival time and potential intensity of storm surges is essential. Figure 3 compares the morphological responses and observation layouts of sandy beaches under storm and normal conditions. During storm events, the superposition of strong winds and storm surges generates intense waves that drive alongshore and offshore sediment transport, causing large-scale erosion and significant shoreline retreat. In contrast, during normal periods, wave energy diminishes, local sedimentation accretion occurs, and the beach enters a recovery state. In terms of monitoring, a multi-scale observation network typically comprises satellites, UAVs, real-time kinematic (RTK) systems, time-lapse cameras (TL cameras), wave buoys, tide gauges, and other instruments. This network synchronously collects data on shoreline morphology, topography, water levels, and wave dynamics, which are essential for event assessment, model calibration, and uncertainty quantification.
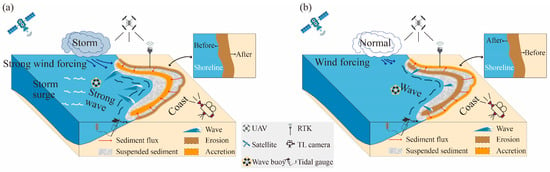
Figure 3.
Schematic of sandy beach morphology and observation system before and after storms. (a) Storm period: The generated intense waves cause shoreline retreat and extensive erosion (brown), accompanied by suspended sediment (gray) and alongshore/offshore sediment transport (red arrows). (b) Normal period: Weakened waves lead to local siltation and morphological recovery (orange). The inset at the top right compares shoreline positions before and after the storm.
Typical hydrodynamic models (e.g., ADCIRC (v56.0.2) [47], Delft3D (v6.02.10) [48], COAWST (v3.8) [49], FVCOM (v5.0) [50]) provide relatively accurate representations of environmental changes induced by extreme events by partitioning the computational domain into unstructured grids and appropriately characterizing physical processes, boundary conditions, and other factors. However, these models often simplify physical processes and incur high computational costs in high-resolution simulations. DL offers substantial advantages in forecasting extreme events due to its strong capability to capture nonlinear characteristics from large datasets. The application of DL in this field can be divided into meteorological and oceanographic domains. Rüttgers et al. utilized a large volume of satellite images as input to a generative adversarial network (GAN), achieving a six-hour typhoon track forecasting capability [51]. Giffard-Roisin et al. fused historical track data with reanalysis atmospheric images (three-dimensional fields of wind and pressure) to construct a neural network model capable of 24 h tropical cyclone track forecasting [52]. Stengel et al. enhanced the network’s physical fidelity and perceptual capabilities through adversarial training, achieving up to a 50-fold improvement in the resolution of wind data [53]. Recently, DL-based global data-driven weather forecasting models have achieved significant progress, including FourCastNet [54], GraphCast [55], Pangu-Weather [56], and Fuxi [57]. These models can rapidly generate global weather variables at a spatial resolution of 0.25° for the next 10 days at least. In particular, the high-precision forecasted wind and pressure fields provide more accurate boundary conditions for storm surge forecasting.
In terms of oceanic storm surge forecasting, most studies have employed models that establish relationships between time series data (e.g., wind speed, air pressure, station water levels) and extreme water level time series. Adeli et al. applied a ConvLSTM model, capable of capturing both temporal and spatial correlations, together with a residual connection network to enhance performance [58]. Their results demonstrated that, within an examined synthetic storm database, DL approach outperformed the previously Gaussian process model for storm surge forecasting. Ramos-Valle et al. utilized cyclone datasets generated by the Hybrid Weather Research and Forecasting (HWRF) model and found that RNN improved the accuracy of storm surge peak predictions to a notable extent [59]. Xie et al. developed a DL-based single-station water level prediction model for multi-station storm surge forecasting [60]. Their approach employed CNN to extract two-dimensional wind field information, which was fused with local water level features to improve temporal prediction efficiency. Jiang et al. proposed the Surge-NF model, incorporating a positional encoding module and a multi-task learning module [61]. Evaluation using the North Atlantic Coast Comprehensive Study (NACCS) database demonstrated that Surge-NF uniquely captured high-frequency spatial variation features and effectively leveraged task correlations. Tedesco et al. applied residual learning to enhance the residual component in the forecasting results of the Nordic4-SS model [62]. This method can be implemented operationally without replacing existing physical models. Cerrone et al. employed Transformers to improve the water level prediction capability of the National Oceanic and Atmospheric Administration’s (NOAA) Storm and Tidal Operational Forecast System (STOFS-2D-Global) over a seven-day forecasting cycle, with the most significant improvements observed at tide-dominated stations [63].
3.2. Large-Scale and Nearshore Wave Generation and Acceleration
In addition to the extreme water levels induced by typhoons, the dynamic environments that directly influence sandy beaches also include waves. For subsequent simulations of beach morphology and management, continuous, stable, and high-resolution wave data are indispensable. Traditionally, wave simulations have primarily relied on the Simulating Waves Nearshore model (SWAN 41.51) [64]. Data-driven DL methods, by contrast, mainly focus on sequence-to-sequence and image-to-image forecasting.
Wang et al. proposed a hybrid model combining Improved Empirical Wavelet Transform (IEWT) decomposition with a LSTM network for wave prediction [65]. Their results demonstrated that, compared to using LSTM alone, this hybrid model more accurately tracked variations in wave crests and troughs. Hao et al. integrated the strengths of LSTM and Empirical Mode Decomposition (EMD) to develop the EMD-LSTM method [66]. Based on significant wave height data from three offshore stations in China, their study indicated that the EMD-LSTM model exhibited superior performance in predicting nonlinear and non-stationary waves. Zhang et al. introduced the Numerical LSTM network to correct numerical wave height predictions [67]. Results showed that it significantly improved the accuracy of SWAN-derived wave height predictions in the Bohai Sea and around Xiaomai Island. Choi et al. employed a CNN to process raw wave images from buoys for short-term wave height forecasting [68]. Bai et al. developed a CNN-based two-dimensional deep learning model for regional wave field prediction in the South China Sea [69]. Their results indicated that the model not only accurately predicted temporal variations in wave height but also effectively estimated spatial distributions of the two-dimensional wave field and demonstrated potential for long-term forecasting. Bento et al. applied CNNs to wave data from three locations and conducted year-round testing, confirming the model’s ability to extract relevant temporal dependencies [70]. Mlakar et al. proposed deep learning wave emulating model (DELWAVE 1.0), comprising a convolution-based atmospheric encoder module, a temporal compression module, and a regression module [71]. DELWAVE successfully simulated nearshore wave dynamics as represented by SWAN at sparse locations, and effectively detected storm events. Kuhn explored the application of DL-based super-resolution techniques in coastal sea state prediction, including spectral wave modeling, neural network-based prediction on unstructured grids, and super-resolution reconstruction of wave spectra. This study demonstrated the potential of such approaches to accelerate wave prediction [72].
Figure 4 illustrates the workflow from observation to results. Multi-source data (including satellite cloud images, reanalysis variables, water levels, and wave spectra) undergo key feature extraction via DL methods such as LSTM, Transformer, and GNN. These methods rapidly generate core indicators and spatial distributions of typhoons, storm surges, and waves. The resulting outputs can be directly applied to beach risk assessment, serve as constraints for data assimilation and calibration of numerical models, and support uncertainty quantification and rolling updates. Table 2 summarizes the applications of DL in simulating and forecasting external dynamic processes based on typical tasks. In summary, the data-driven DL approach provides a faster and more accurate toolchain for external forcing forecasting and post-processing in oceanic applications. It offers significant advantages in low latency and high-frequency updates, with direct relevance to the management and application of sandy beaches.
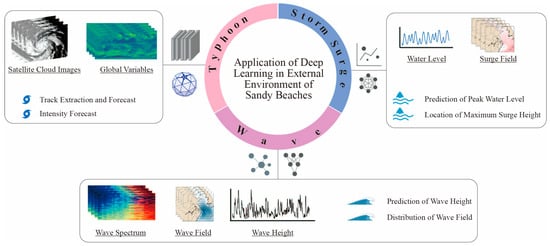
Figure 4.
Schematic framework for DL-based forecasting of external forcing on sandy beaches. The central loop organizes tasks around the “Typhoon–Storm Surge–Wave” sequence. On the left, satellite cloud images and reanalysis variables serve as inputs for typhoon track extraction and intensity prediction. On the right, water level sequences and storm surge fields are used to infer peak water levels and identify locations of maximum storm surges. At the bottom, wave spectra, wave fields, and wave height sequences are employed to predict significant wave heights and nearshore wave field distributions.

Table 2.
Application of DL in simulating and forecasting external dynamic processes.
4. Application of DL in Coastal Morphological Evolution and Sediment Simulation
4.1. Reconstruction and Evolution of Sandy Beach Profiles and Shorelines
The forecasting and monitoring of sandy beach morphological evolution are critical for enhancing their resilience. Traditional shoreline identification techniques based on remote sensing and satellite imagery are already well-developed [73]. However, these methods have limitations in addressing complex terrain, fine-scale geomorphology, and long-term trend prediction [74]. In recent years, DL has been increasingly applied to classification, identification, and forecasting tasks in this field. For example, CoastSat employs MLP to integrate satellite imagery and extract time-series shoreline positions for sandy coastlines worldwide with an accuracy of approximately 10 m, enabling efficient shoreline change monitoring [75]. U-Net combines skip connections and multi-scale feature fusion, making it suitable for land cover classification, extraction, and change detection from satellite imagery [76]. DeepLabv3 integrates an encoder–decoder structure with atrous separable convolution to flexibly control encoder feature resolution, achieving a balance between accuracy and computational efficiency [77]. Such functions hold potential for identifying fine geomorphic textures in sandy beaches, such as beach ridges and tidal creeks. Park and Song employed a U-Net semantic segmentation model based on attention mechanisms and a water index to automatically extract the land–sea boundary. They also applied transfer learning to address data scarcity in certain coastal areas, improving shoreline change monitoring efficiency and accuracy [78]. Scala et al. enhanced CNN by introducing a Sobel edge loss function and multi-class segmentation, enabling effective detection of land cover features that may be overlooked (e.g., cliff vegetation, coastal roads). Thereby, they significantly reduce uncertainties in shoreline delineation [79]. Feng et al. incorporated an Edge Depth Supervision (EDS) module, a Cooperative Semantic Depth Supervision (CSDS) module, and an Attention Fusion Module (AFM) to improve detailed shoreline edge feature extraction [80]. Dang et al. demonstrated the applicability of U-Net models for predicting coastal changes in Vietnam and globally [81]. Their findings suggest that waterline identification is suitable for monitoring seasonal tidal changes or immediate wave movement, whereas shoreline delineation is more appropriate for assessing coastal erosion caused by sea-level rise during storms.
The management of sandy beach resilience requires the ability to predict beach responses to storms and long-term changes in regional wave climates over seasonal to interannual time scales. Currently, most researchers in the field of profile and shoreline evolution forecasting employ one-dimensional shoreline equilibrium models. These models typically consider only wave-driven longshore sediment transport and describe shoreline displacement based on the concept that wave energy tends toward a dynamic equilibrium position [82,83]. DL has demonstrated advantages in capturing nonlinear relationships in time-series models across scales and offers significant improvements in computational efficiency [84]. As beach environments become increasingly complex, the application of DL to profile and shoreline forecasting has grown. Manamperi et al. modeled shoreline changes as a supervised learning task, employing LSTM to capture long-term dependencies and leveraging its memory mechanism to simulate shoreline evolution under continuous wave forcing [85]. Lee et al. developed an LSTM-based encoder–decoder network for effective spatiotemporal representation learning, enabling estimation of beach profile responses over weeks to months under varying hydrodynamic conditions [86]. Gomez-de la Peña et al. examined CNN and CNN-LSTM for predicting interannual shoreline positions, finding that DL methods outperform traditional equilibrium models in simulating observed variability and spatial distribution [87]. Adusumilli et al. successfully predicted beach width and seasonal average beach slope using tides and waves as inputs to a trained Deep Neural Network (DNN) [88]. Montaño et al. compared traditional shoreline models and DL methods for long-term shoreline evolution prediction, concluding that both approaches can reproduce shoreline changes under normal conditions, while model ensembles outperform single models in capturing extreme and rapid fluctuations [89].
In summary, traditional techniques, such as sub-pixel shoreline extraction and geometric correction, can be integrated into preprocessing, feature extraction, auxiliary evaluation, and post-processing workflows for DL methods, thereby enhancing the accuracy of shoreline detection [90,91,92]. Building on this foundation, long-term shoreline trend forecasting should fully leverage the advantages of DL to establish a comprehensive workflow encompassing identification, analysis, and forecasting. The robustness of such models also enables effective detection and prediction of erosion and accretion patterns on sandy beaches. They provide essential data and a priori insights to support regional research, coastal management, and the enhancement of sandy beach resilience [93,94].
4.2. Sediment Transport: Surrogate Modeling, High-Resolution Flow Field Driving with Physical Constraints
Sediment serves as the fundamental link between hydrodynamic changes and morphological evolution, whether in sandy beach profiles or shorelines. However, the highly stochastic and uncertain nature of sediment transport renders sediment-related numerical simulations computationally intensive, limiting their applicability for long-term simulations and forecasts. The profile and shoreline prediction models discussed in Section 4.1 generally simplify or omit complex sediment dynamics. The emergence of DL has prompted researchers to explore its potential for simulating and forecasting sediment transport. Weber de Melo et al. employed CNN that utilized two-dimensional hydrodynamic variables (vertically averaged flow velocity squared, bed shear stress) as inputs [95]. By extracting multi-scale features through a multi-branch structure, this model successfully captured the spatial distribution characteristics of sediment transport. This CNN-based approach avoids the computational complexity of solving differential equations inherent in traditional numerical models while maintaining acceptable simulation accuracy. Fajardo-Urbina et al. applied DL to predict the advection and diffusion of particle swarms over a tidal cycle, coupling it with a simplified Lagrangian model to achieve longer-term prediction results [96]. Xie et al. adopted a CNN-based approach to quantitatively model suspended sediment concentration (SSC), demonstrating its capability to predict hourly SSC variations while reducing computational costs and improving processing efficiency [97].
The primary driving force behind sediment transport originates from the flow field. To a large extent, the complexity and high computational cost of sediment transport arise from the computation of the flow field. Consequently, many researchers are exploring the use of DL to optimize or replace complex flow field calculations. Among the current approaches, Physics-Informed Neural Networks (PINNs) have emerged as a mainstream method. Once trained, PINNs can satisfy differential equations as well as prescribed initial and boundary conditions, making them a promising alternative to traditional numerical models (e.g., finite difference, finite volume, spectral methods) [98]. Dazzi tested the application of PINNs to solve the Shallow Water Equations (SWE) enhancement system, incorporating topography as a spatially variable feature during training and calculating the bed slope source term via automatic differentiation [99]. Qi et al. compared the performance of Physics-Informed Fully Connected Networks (PIFCNs) and Physics-Informed Convolutional Networks (PICNs) with a finite volume solver in a real flood event [100]. Their results demonstrated that, for predicting the temporal distribution of water depth, both PINN variants outperformed the finite volume model in balancing speed and accuracy, whereas the finite volume model yielded superior discharge predictions. Bihlo and Popovych applied PINNs to solve the SWE on a spherical surface, successfully avoiding boundary value loss functions by encoding boundary conditions within a custom neural network layer [101]. Huang et al. advanced PINN methodology by integrating both boundary and initial conditions directly into the governing equations, thereby eliminating the need to include their residuals in the loss function. This approach achieved better convergence, reduced memory consumption, and faster training, outperforming traditional PINNs in several aspects of hydrodynamic simulation [102].
Figure 5 illustrates two complementary pathways for integrating observational data and physical modeling. The first pathway relies on remote sensing and ground-based monitoring to perform target recognition and fine-grained land cover characterization, followed by time-series modeling to predict shoreline and profile evolution. The second pathway integrates physical mechanisms into the learning framework to generate high-resolution flow fields and free-surface evolution, upon which the spatiotemporal distribution of SSC is reconstructed. The first pathway emphasizes rapid “data-to-morphology” assessment, while the second highlights interpretable “mechanism-to-process” simulation. Table 3 summarizes the applications of DL in morphological evolution and sediment simulation based on typical tasks.
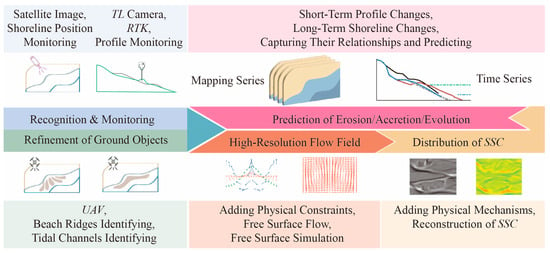
Figure 5.
Two application pathways of DL in sandy beach morphology, flow fields, and sediment dynamics. (Top) Observation-driven pathway: Construct shoreline/profile sequences using satellite imagery, TL cameras, and RTK technology; perform feature identification and monitoring; map time series; and predict erosion, accretion, and morphological evolution. (Bottom) Physics-guided pathway: Generate high-resolution flow fields under physical constraints and simulate free-surface processes (image adapted from [102]); subsequently reconstruct and infer the spatiotemporal distribution and dynamics of SSC (image adapted from [95]).

Table 3.
Application of DL in morphological evolution and sediment simulation.
5. Application of DL in Sandy Beach Management and Decision-Making
Sandy beaches represent a complex environmental system, and their management and decision-making are of critical importance. Effective management must address uncertain factors closely related to sandy beaches (e.g., topographic and demographic data, socio-economic development, ecological protection) [103]. Fundamentally, sandy beach management involves providing long-term, stable, and implementable solutions under multi-objective conditions and considerable uncertainty. DL offers promising approaches to address the nonlinear interactions among multiple objectives. For example, Kirezci et al. identified the spatial patterns and temporal evolution of “hotspot areas” using a simple linear superposition model based on global extreme sea level projections [104]. DL can further capture complex nonlinear relationships between variables and facilitate the application of transfer learning strategies in hotspot area analysis. Dal Barco et al. examined the relationships among various hazards across different spatiotemporal scales and analyzed multiple factors influencing coastline dynamics [105]. Their results showed that MLP achieved satisfactory performance in estimating daily impact risk when supplied with information on hazards, exposure, and vulnerability. Garzon et al. developed an early warning system for coastal erosion based on Bayesian networks, producing promising initial results [106]. The integration of DL could enhance such systems by improving prediction accuracy and generalization. Lundberg and Lee proposed an interpretable framework for DL prediction results, offering significant potential for answering management questions such as “Why is this coastal segment deemed high risk?” and “How will the risk change if sand dunes are restored or development is restricted?” [107]. The application of rigorous evaluation criteria can further provide comprehensive quantitative tools for diagnosing and interpreting DL results [108,109].
In recent years, in terms of operationalization and platformization, digital twin technologies have demonstrated the advantages of DL in two key aspects: the closed-loop capability of “from prediction to action” and the platform support for the “data–model–scenario–decision-making” process. Chen et al. proposed the architecture of a generative marine digital twin designed to integrate near-real-time observations, data assimilation, and DL surrogates into a unified data and computing infrastructure [110,111]. The core components of this system include a data pool, a DL-based marine model, and three-dimensional visual interaction functions. This architecture can integrate local-scale sandy beach management into a broader system, thereby lowering the collaboration threshold across departments and bridging spatiotemporal resolution gaps.
Overall, for the management and decision-making of sandy beaches, conventional collaborative analyses of multiple variables and traditional ML approaches remain the mainstream [106,112,113,114,115,116,117]. Nevertheless, DL holds considerable potential in this field. Various DL techniques can be deeply integrated into existing management and decision-making systems to enhance their performance. Figure 6 illustrates, from bottom to top, the closed-loop of beach management with digital twins as the central hub: multi-source data undergoes management and quality control to form data streams that drive traditional models and DL modules (physical/prediction, integrated decision support, and large language model (LLM) interaction).
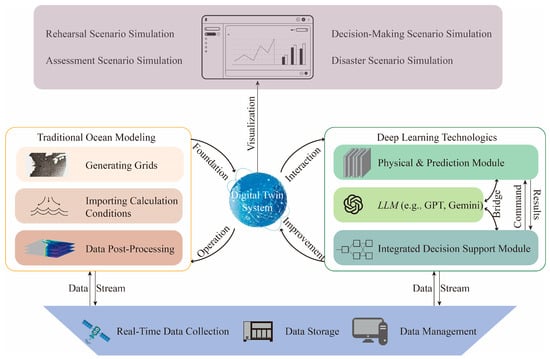
Figure 6.
Digital twin-driven framework for beach management and decision-making (bottom-top). The bottom layer comprises real-time data collection, storage, and management. Data streams are directed along two parallel paths: the traditional marine modeling module on the left, and the DL technology module on the right. At the core, the digital twin system performs data fusion, model execution, and updates, and outputs visualized scenario simulations upward. The Earth-style design illustrated here is adapted from [110].
First, within the physical/prediction module, DL can rapidly generate numerical predictions of various physical variables over a future time horizon through its high-precision forecasting capabilities. These forecasted data can serve two primary purposes: (1) they can be incorporated into the central digital twin system for visualization and for use as boundary conditions, and (2) they can provide a scientific reference for the subsequent integrated decision support module. Within the integrated decision support module, DL can leverage its strengths in addressing multi-scale and multi-modal tasks, enabling comprehensive consideration of future multi-factor and multi-category data. Moreover, based on the decisions proposed by decision-makers, this module can inversely drive the physical/prediction module to rapidly simulate and generate the physical data associated with these decisions. The resulting data can then be visualized within the central digital twin system, thereby supporting further evaluation by decision-makers. Throughout this workflow, LLMs can utilize their natural language processing capabilities to serve as an interface between decision-makers and the digital twin system. Their functions include, but are not limited to, enabling natural-language querying of the system, generating automated reports for stakeholders, and translating model outputs into accessible, plain-language risk assessment reports.
Digital twins enable unified coupling and visualization, rapidly generate results for drills, evaluations, decision-making, and disaster response, and facilitate continuous optimization through feedback loops. The management process can follow a pattern of “first using DL methods and multi-scenario generation to expand a variety of feasible solutions, then converging to a limited set of alternatives based on robust indicators”, while preserving interpretability and calibrated results for auditing purposes [118,119]. In conclusion, the role of DL in sandy beach management is not to replace physical–economic–ecological models but to integrate observation, scenario, impact, and action into an operable evidence chain. At the front end, DL enhances communication through risk maps and interpretability. At the middle end, DL screens combinations via surrogates and robust decision-making. At the back end, DL ensures implementation and traceability through platforms and verification.
6. Conclusions
Against the backdrop of increasingly frequent extreme events and intensified human activities, enhancing the resilience of sandy beaches has become an urgent priority for coastal areas. The resilience of sandy beaches represents a comprehensive capability that requires coordinated consideration of multiple processes and variables. In recent years, methods driven by DL have achieved continuous technological breakthroughs and cross-disciplinary integration. With its exceptional ability to extract spatial features, robust capacity to fit nonlinear sequences, acceleration of traditional physical processes, and capability to integrate multi-source data, DL offers promising opportunities for advancing the enhancement and management of sandy beach resilience.
Centering on the theme of sandy beach resilience, this review categorizes resilience capabilities into three technical levels: resistance, recovery, and adaptation. Corresponding to the natural impact sequence on sandy beaches, from atmosphere to water to land, this review addresses three key research aspects: monitoring and forecasting of the external forcing, modeling and acceleration of sandy beach evolution processes, and human-led decision-making and management. Based on this framework, this paper systematically reviews current applications of DL in each aspect and explores its potential future contributions.
First, this paper reviews and summarizes two major advantages of DL: its strong capability for spatial feature representation and its ability to capture nonlinear relationships in sequences, alongside an overview of cutting-edge physics-informed/guided DL. Second, building on these advantages, this review analyzes DL application scenarios and achievements in two areas: forecasting typhoon tracks and intensities, and predicting storm surge peak values. Third, regarding waves that directly influence sandy beaches, this review examines successful DL applications in accelerating the simulation and forecasting of wave fields, from both pure data-driven and physics-informed perspectives.
Fourth, focusing on the critical topographic evolution of sandy beaches, including sediment transport involved, this review identifies two main directions in current DL applications. The first direction simplifies or bypasses complex sediment and current processes, instead applying DL to predict one-dimensional profile changes or two-dimensional coastline movements, thereby enabling rapid depiction of medium- to long-term beach changes or short-term erosion and recovery processes under extreme events. The second direction addresses complex and uncertain sediment transport processes and the high-resolution flow fields that drive them. Here, DL combined with physics-informed constraints not only greatly improves computational efficiency but also enhances the physical credibility of the simulations and forecasts.
Finally, this review explores current methods and strategies for sandy beach management and decision-making, proposing a pathway for DL to integrate deeply into existing systems. This pathway involves first employing DL methods and multi-scenario generation to broaden feasible solutions, then narrowing these to a limited set of robust alternatives, while preserving interpretability and calibrated results to ensure auditability.
Overall, this review centers on sandy beaches, aligning DL methods with coastal process knowledge relevant to beach resilience. It emphasizes that DL is not a substitute for existing frameworks, but rather a complementary tool that enhances them. The value of DL lies in shortening the path from observation to action, broadening the scope of multi-scenario assessments, and improving data transparency for communication and decision-making. However, limitations mainly arise from challenges in cross-domain generalization, robustness under extreme conditions, and adherence to data governance requirements. On one hand, standardized datasets and corresponding benchmark tests need to be established to evaluate the forecasting performance of DL-based models. On the other hand, continued exploration is required to better integrate DL with physical laws, which will substantially enhance the credibility of DL in coastal applications. Furthermore, it is essential to investigate the potential of DL as a bridge of human–AI collaboration. Such efforts would enable the effective communication of DL-based predictions and associated uncertainties to decision-makers, thereby supporting more informed and efficient decision-making. Building on this foundation, future research should further explore and harness DL’s auxiliary and integrative capabilities to improve resilience metrics, and establish a complete, practical pathway for enhancing the resilience of sandy beaches.
Author Contributions
Conceptualization, Y.J. and Y.Z.; formal analysis, Y.J.; investigation, Y.J.; resources, J.Z.; writing—original draft preparation, Y.J.; writing—review and editing, Y.J. and Y.Z.; visualization, Y.J.; supervision, Y.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This review was funded by Hainan Provincial Natural Science Foundation of China (No. 423QN322).
Data Availability Statement
This review does not involve the generation or analysis of new empirical data. All findings are based on previously published, peer-reviewed literature, which is appropriately cited throughout the manuscript. No new data were created or analyzed in this study. Readers seeking additional details should consult the sources listed in the References section.
Acknowledgments
The authors are very much grateful to all anonymous reviewers for their constructive comments that significantly improved the quality of this review.
Conflicts of Interest
Author Y.Z. is employed by Shanghai Urban Construction Design & Research Institute (Group) Co., Ltd. The remaining authors Y.J. and J.Z. declare that this research is conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HFRs | High-Frequency Radars |
| UAVs | Unmanned Aerial Vehicles |
| AI | Artificial intelligence |
| DL | Deep learning |
| ML | Machine learning |
| CNN | Convolutional neural network |
| FCN | Fully convolutional network |
| ViT | Vision Transformer |
| MLP | Multilayer perceptron |
| RNN | Recurrent neural network |
| TFT | Temporal fusion transformers |
| LSTM | Long short-term memory |
| GRU | Gated recurrent unit |
| PINN | Physics-informed neural network |
| GNS | Graph network-based simulator |
| RTK | Real-time kinematic |
| TL cameras | Time-lapse cameras |
| GAN | Generative adversarial network |
| HWRF | Hybrid weather research and forecasting |
| NACCS | North Atlantic coast com-prehensive study |
| NOAA | National Oceanic and Atmospheric Administration |
| STOFS | Storm and tidal operational forecast system |
| SWAN | Simulating Waves Nearshore model |
| IEWT | Improved empirical wavelet transform |
| EMD | Empirical mode decomposition |
| DELWAVE | Deep learning wave emulating model |
| EDS | Edge depth supervision |
| CSDS | Cooperative semantic depth supervision |
| AFM | Attention fusion module |
| DNN | Deep Neural Network |
| SSC | Suspended sediment concentration |
| SWE | Shallow water equations |
| PIFCN | Physics-informed fully connected networks |
| PICN | Physics-informed convolutional networks |
| LLM | Large language model |
References
- Martínez, M.L.; Intralawan, A.; Vázquez, G.; Pérez-Maqueo, O.; Sutton, P.; Landgrave, R. The coasts of our world: Ecological, economic and social importance. Ecol. Econ. 2007, 63, 254–272. [Google Scholar] [CrossRef]
- Neumann, B.; Vafeidis, A.T.; Zimmermann, J.; Nicholls, R.J. Future coastal population growth and exposure to sea-level rise and coastal flooding-a global assessment. PLoS ONE 2015, 10, e0118571. [Google Scholar] [CrossRef]
- Small, C.; Nicholls, R.J. A Global Analysis of Human Settlement in Coastal Zones. J. Coast. Res. 2003, 19, 584–599. Available online: http://www.jstor.org/stable/4299200 (accessed on 27 August 2025).
- Amoudry, L.O.; Souza, A.J. Deterministic coastal morphological and sediment transport modeling: A review and discussion. Rev. Geophys. 2011, 49, RG2002. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Cazenave, A. Sea-level rise and its impact on coastal zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
- Wahl, T.; Haigh, I.D.; Nicholls, R.J.; Arns, A.; Dangendorf, S.; Hinkel, J.; Slangen, A.B.A. Understanding extreme sea levels for broad-scale coastal impact and adaptation analysis. Nat. Commun. 2017, 8, 16075. [Google Scholar] [CrossRef] [PubMed]
- Vitousek, S.; Barnard, P.L.; Fletcher, C.H.; Frazer, N.; Erikson, L.; Storlazzi, C.D. Doubling of coastal flooding frequency within decades due to sea-level rise. Sci. Rep. 2017, 7, 1399. [Google Scholar] [CrossRef]
- Young, I.R.; Ribal, A. Multiplatform evaluation of global trends in wind speed and wave height. Science 2019, 364, 548–552. [Google Scholar] [CrossRef] [PubMed]
- Defeo, O.; McLachlan, A.; Schoeman, D.S.; Schlacher, T.A.; Dugan, J.; Jones, A.; Lastra, M.; Scapini, F. Threats to sandy beach ecosystems: A review. Estuar. Coast. Shelf Sci. 2009, 81, 1–12. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Coastal erosion and control. Ocean Coast Manag. 2011, 54, 867–887. [Google Scholar] [CrossRef]
- Masselink, G.; Lazarus, E.D. Defining Coastal Resilience. Water 2019, 11, 2587. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiang, C.; Jiang, Y.; Zhu, Y.; Jin, Y.; Wang, X.; Feng, X.; Feng, W. A whole process resilience management practice in coastal engineering. Front. Mar. Sci. 2025, 11, 1518249. [Google Scholar] [CrossRef]
- Wang, Y.; Imai, K.; Horikawa, H. Tsunami Early Warning Using High--Frequency Ocean Radar System in the Kii Channel, Japan. Seismol. Res. Lett. 2025, 96, 990–1000. [Google Scholar] [CrossRef]
- Wang, Y.; Imai, K.; Miyashita, T.; Ariyoshi, K.; Takahashi, N.; Satake, K. Coastal tsunami prediction in Tohoku region, Japan, based on S-net observations using artificial neural network. Earth Planets Space 2023, 75, 154. [Google Scholar] [CrossRef]
- Holman, R.A.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Turner, I.L.; Harley, M.D.; Drummond, C.D. UAVs for coastal surveying. Coast. Eng. 2016, 114, 19–24. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.V.; van Kester, J.T.M.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Cueto, J.; Otero, L. Morphodynamic response to extreme wave events of microtidal dissipative and reflective beaches. Appl. Ocean Res. 2022, 101, 102283. [Google Scholar] [CrossRef]
- Castelle, B.; Masselink, G. Morphodynamics of wave-dominated beaches. Camb. Prism. Coast. Futures 2023, 1, e1. [Google Scholar] [CrossRef]
- Shen, C. A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Yu, R.; Wang, R. Learning dynamical systems from data: An introduction to physics-guided deep learning. Proc. Natl. Acad. Sci. USA 2024, 121, e2311808121. [Google Scholar] [CrossRef] [PubMed]
- Swischuk, R.; Mainini, L.; Peherstorfer, B.; Willcox, K. Projection-based model reduction: Formulations for physics-based machine learning. Comput. Fluids. 2019, 179, 704–717. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef]
- Sun, W.; Wang, R. Fully convolutional networks for semantic segmentation of very high resolution remotely sensed images combined with DSM. IEEE Geosci. Remote Sens. Lett. 2018, 15, 474–478. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, G.; Chen, C.; Pan, Z. Multi-scale dilated convolution of convolutional neural network for image denoising. Multimed. Tools Appl. 2019, 78, 19945–19960. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 30 June 2016. [Google Scholar]
- Wang, Y.; Huang, R.; Song, S.; Huang, Z.; Huang, G. Not all images are worth 16 × 16 words: Dynamic transformers for efficient image recognition. NeurIPS 2021, 34, 11960–11973. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Xie, E.; Wang, W.H.; Yu, Z.D.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. NeurIPS 2021, 34, 12077–12090. [Google Scholar]
- Yu, Y.; Si, X.S.; Hu, C.H.; Zhang, J.X. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Bai, S.; Kolter, J.Z.; Koltun, V. Convolutional sequence modeling revisited. In Proceedings of the ICLR 2018 Conference Paper 501 Official Comment, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar] [CrossRef]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are Transformers Effective for Time Series Forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef]
- Bar-Sinai, Y.; Hoyer, S.; Hickey, J.; Brenner, M.P. Learning data-driven discretizations for partial differential equations. Proc. Natl. Acad. Sci. USA 2019, 116, 15344–15349. [Google Scholar] [CrossRef]
- Sanchez-Gonzalez, A.; Godwin, J.; Pfaff, T.; Ying, R.; Leskovec, J.; Battaglia, P. Learning to simulate complex physics with graph networks. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 8459–8468. Available online: https://arxiv.org/abs/2002.09405 (accessed on 28 August 2025).
- Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine learning–accelerated computational fluid dynamics. Proc. Natl. Acad. Sci. USA 2021, 118, e2101784118. [Google Scholar] [CrossRef]
- Westerink, J.J.; Luettich, R.A.; Feyen, J.C.; Atkinson, J.H.; Dawson, C.; Roberts, H.J.; Powell, M.D.; Dunion, J.P.; Kubatko, E.J.; Pourtaheri, H. A Basin- to Channel-Scale Unstructured Grid Hurricane Storm Surge Model Applied to Southern Louisiana. Mon. Weather Rev. 2008, 136, 833–864. [Google Scholar] [CrossRef]
- Rueda-Bayona, J.G.; Osorio, A.F.; Guzmán, A. Set-up and input dataset files of the Delft3d model for hydrodynamic modelling considering wind, waves, tides and currents through multidomain grids. Data Br. 2019, 28, 104921. [Google Scholar] [CrossRef] [PubMed]
- Calvino, C.; Dabrowski, T.; Dias, F. A study of the sea level and current effects on the sea state in Galway Bay, using the numerical model COAWST. Ocean Dyn. 2022, 72, 761–774. [Google Scholar] [CrossRef]
- Gu, B.H.; Woo, S.B.; Kim, S. Improved estuaries salinity stratification at Gyeonggi Bay using data assimilation with Finite Volume Coastal Ocean Model (FVCOM). J. Coast. Res. 2019, 91, 416–420. [Google Scholar] [CrossRef]
- Rüttgers, M.; Lee, S.; Jeon, S.; You, D. Prediction of a typhoon track using a generative adversarial network and satellite images. Sci. Rep. 2019, 9, 6057. [Google Scholar] [CrossRef] [PubMed]
- Giffard-Roisin, S.; Yang, M.; Charpiat, G.; Kumler Bonfanti, C.; Kégl, B.; Monteleoni, C. Tropical Cyclone Track Forecasting Using Fused Deep Learning From Aligned Reanalysis Data. Front. Big Data 2020, 3, 1. [Google Scholar] [CrossRef] [PubMed]
- Stengel, K.; Glaws, A.; Hettinger, D.; King, R.N. Adversarial super-resolution of climatological wind and solar data. Proc. Natl. Acad. Sci. USA 2020, 117, 16805–16815. [Google Scholar] [CrossRef]
- Kurth, T.; Subramanian, S.; Harrington, P.; Pathak, J.; Mardani, M.; Hall, D.; Miele, A.; Kashinath, K.; Anandkumar, A. Fourcastnet: Accelerating global high-resolution weather forecasting using adaptive fourier neural operators. In Proceedings of the Platform for Advanced Scientific Computing Conference, Davos, Switzerland, 26–28 June 2023; pp. 1–11. [Google Scholar] [CrossRef]
- Lam, R.; Sanchez-Gonzalez, A.; Matthew Willson, M.; Wirnsberger, P.; Fortunato, M.; Alet, F.; Ravuri, S.; Ewalds, T.; Eaton-Rosen, Z.; Hu, W.H.; et al. Learning skillful medium-range global weather forecasting. Science 2023, 382, 1416–1421. [Google Scholar] [CrossRef]
- Bi, K.; Xie, L.X.; Zhang, H.H.; Chen, X.; Gu, X.T.; Tian, Q. Accurate medium-range global weather forecasting with 3D neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef]
- Sun, X.Y.; Zhong, X.H.; Xu, X.Z.; Huang, Y.Q.; Li, H.; Neelin, J.D.; Chen, D.L.; Feng, J.; Han, W.; Wu, L.B.; et al. A data-to-forecast machine learning system for global weather. Nat. Commun. 2025, 16, 6658. [Google Scholar] [CrossRef]
- Adeli, E.; Sun, L.N.; Wang, J.X.; Taflanidis, A.A. An advanced spatio-temporal convolutional recurrent neural network for storm surge predictions. Neural Comput. Appl. 2023, 35, 18971–18987. [Google Scholar] [CrossRef]
- Ramos-Valle, A.N.; Curchitser, E.N.; Bruyère, C.L.; McOwen, S. Implementation of an artificial neural network for storm surge forecasting. J. Geophys. Res. Atmos. 2021, 126, e2020JD033266. [Google Scholar] [CrossRef]
- Xie, W.; Xu, G.; Zhang, H.; Dong, C. Developing a deep learning-based storm surge forecasting model. Ocean Model. 2023, 182, 102179. [Google Scholar] [CrossRef]
- Jiang, W.; Zhong, X.; Zhang, J. Surge-NF: Neural Fields inspired peak storm surge surrogate modeling with multi-task learning and positional encoding. Coast. Eng. 2024, 193, 104573. [Google Scholar] [CrossRef]
- Tedesco, P.; Rabault, J.; Sætra, M.L.; Kristensen, N.M.; Aarnes, O.J.; Breivik, Ø.; Mauritzen, C.; Sætra, Ø. Bias correction of operational storm surge forecasts using Neural Networks. Ocean Model. 2024, 188, 102334. [Google Scholar] [CrossRef]
- Cerrone, A.R.; Westerink, L.G.; Ling, G.; Blakely, C.P.; Wirasaet, D.; Dawson, C.; Westerink, J.J. Correcting physics-based global tide and storm water level forecasts with the temporal fusion transformer. Ocean Model. 2025, 195, 102509. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Wang, J.; Bethel, B.J.; Xie, W.; Dong, C. A hybrid model for significant wave height prediction based on an improved empirical wavelet transform decomposition and long-short term memory network. Ocean Model. 2024, 189, 102367. [Google Scholar] [CrossRef]
- Hao, W.; Sun, X.; Wang, C.; Chen, H.; Huang, L. A hybrid EMD-LSTM model for non-stationary wave prediction in offshore China. Ocean Eng. 2022, 246, 110566. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Gao, S.; Ren, P. Ocean Wave Height Series Prediction with Numerical Long Short-Term Memory. J. Mar. Sci. Eng. 2021, 9, 514. [Google Scholar] [CrossRef]
- Choi, H.; Park, M.; Son, G.; Jeong, J.; Park, J.; Mo, K.; Kang, P. Real-time significant wave height estimation from raw ocean images based on 2D and 3D deep neural networks. Ocean Eng. 2020, 201, 107129. [Google Scholar] [CrossRef]
- Bai, G.; Wang, Z.; Zhu, X.; Feng, Y. Development of a 2-D deep learning regional wave field forecast model based on convolutional neural network and the application in South China Sea. Appl. Ocean Res. 2022, 118, 103012. [Google Scholar] [CrossRef]
- Bento, P.; Pombo, J.; Calado, M.D.R.; Mariano, S. Ocean wave power forecasting using convolutional neural networks. IET Renew. Power Gener. 2021, 15, 3341–3353. [Google Scholar] [CrossRef]
- Mlakar, P.; Ricchi, A.; Carniel, S.; Bonaldo, D.; Ličer, M. DELWAVE 1.0: Deep learning surrogate model of surface wave climate in the Adriatic Basin. Geosci. Model Dev. 2024, 17, 4705–4725. [Google Scholar] [CrossRef]
- Kuhn, J. Machine Learning Methods for the Analysis of Coastal Sea States. Ph.D. Thesis, Université de Pau et des Pays de l’Adour, Pau, France, 2024. [Google Scholar]
- Hu, R.; Fan, Y.; Zhang, X. Satellite-Derived Shoreline Changes of an Urban Beach and Their Relationship to Coastal Engineering. Remote Sens. 2024, 16, 2469. [Google Scholar] [CrossRef]
- Dey, M.; Priyaa, S.; Jena, B.K. A shoreline change detection (2012–2021) and forecasting using digital shoreline analysis system (DSAS) tool: A case study of Dahej Coast, Gulf of Khambhat, Gujarat, India. Indones. J. Geogr. 2021, 53, 295–309. [Google Scholar] [CrossRef]
- Vos, K.; Splinter, K.D.; Harley, M.D.; Simmons, J.A.; Turner, I.L. CoastSat: A Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model. Softw. 2019, 122, 104528. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 833–851. [Google Scholar]
- Park, S.; Song, A. Shoreline change analysis with Deep Learning Semantic Segmentation using remote sensing and GIS data. KSCE J. Civ. Eng. 2024, 28, 928–938. [Google Scholar] [CrossRef]
- Scala, P.; Manno, G.; Ciraolo, G. Semantic segmentation of coastal aerial/satellite images using deep learning techniques: An application to coastline detection. Comput. Geosci. 2024, 192, 105704. [Google Scholar] [CrossRef]
- Feng, J.; Wang, S.; Gu, Z. A novel sea-land segmentation network for enhanced coastline extraction using satellite remote sensing images. Adv. Space Res. 2024, 74, 2200–2213. [Google Scholar] [CrossRef]
- Dang, K.B.; Dang, V.B.; Ngo, V.L.; Vu, K.C.; Nguyen, H.; Nguyen, D.A.; Nguyen, T.D.L.; Pham, T.P.N.; Giant, T.L.; Nguyen, H.D.; et al. Application of deep learning models to detect coastlines and shorelines. J. Environ. Manag. 2022, 320, 115732. [Google Scholar] [CrossRef]
- Splinter, K.D.; Turner, I.L.; Davidson, M.A.; Barnard, P.; Castelle, B.; Oltman-Shay, J. A generalized equilibrium model for predicting daily to interannual shoreline response. J. Geophys. Res. Earth Surf. 2014, 119, 1936–1958. [Google Scholar] [CrossRef]
- Davidson, M.A.; Splinter, K.D.; Turner, I.L. A simple equilibrium model for predicting shoreline change. Coast. Eng. 2013, 73, 191–202. [Google Scholar] [CrossRef]
- Calkoen, F.; Luijendijk, A.; Rivero, C.R.; Kras, E.; Baart, F. Traditional vs. Machine-Learning Methods for Forecasting Sandy Shoreline Evolution Using Historic Satellite-Derived Shorelines. Remote Sens. 2021, 13, 934. [Google Scholar] [CrossRef]
- Manamperi, T.U.S.; Karunarathna, H.; Rahat, A.; Banno, M.; Pender, D.; Cristaudo, D. Machine Learning Techniques for Cross Shore Beach Change Forecasting. Coast. Eng. Proc. 2024, 38, 60. [Google Scholar] [CrossRef]
- Lee, Y.; Chang, S.; Kim, J.; Kim, I. Estimation of Beach Profile Response on Coastal Hydrodynamics Using LSTM-Based Encoder–Decoder Network. J. Mar. Sci. Eng. 2024, 12, 2212. [Google Scholar] [CrossRef]
- Gomez-de la Peña, E.; Coco, G.; Whittaker, C.; Montaño, J. On the use of convolutional deep learning to predict shoreline change. Earth Surf. Dyn. 2023, 11, 1145–1160. [Google Scholar] [CrossRef]
- Adusumilli, S.; Cirrito, N.; Engeman, L.; Fiedler, J.W.; Guza, R.T.; Lange, A.M.Z.; Merrifield, M.A.; O’Reilly, W.; Young, A.P. Predicting shoreline changes along the California coast using deep learning applied to satellite observations. JGR Mach. Learn. Comput. 2024, 1, e2024JH000172. [Google Scholar] [CrossRef]
- Montaño, J.; Coco, G.; Antolínez, J.A.A.; Beuzen, T.; Bryan, K.R.; Cagigal, L.; Castelle, B.; Davidson, M.A.; Goldstein, E.B.; Ibaceta, R.; et al. Blind testing of shoreline evolution models. Sci. Rep. 2020, 10, 2137. [Google Scholar] [CrossRef] [PubMed]
- Pardo-Pascual, J.E.; Almonacid-Caballer, J.; Ruiz, L.A.; Palomar-Vázquez, J. Automatic extraction of shorelines from Landsat TM and ETM+ multi-temporal images with subpixel precision. Remote Sens. Environ. 2012, 123, 1–11. [Google Scholar] [CrossRef]
- Pardo-Pascual, J.E.; Sánchez-García, E.; Almonacid-Caballer, J.; Palomar-Vázquez, J.M.; Priego de los Santos, E.; Fernández-Sarría, A.; Balaguer-Beser, Á. Assessing the Accuracy of Automatically Extracted Shorelines on Microtidal Beaches from Landsat 7, Landsat 8 and Sentinel-2 Imagery. Remote Sens. 2018, 10, 326. [Google Scholar] [CrossRef]
- Kim, T.; Lee, W.D. Review on applications of machine learning in coastal and ocean engineering. J. Ocean Eng. Technol. 2022, 36, 194–210. [Google Scholar] [CrossRef]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef]
- Mentaschi, L.; Vousdoukas, M.I.; Pekel, J.F.; Voukouvalas, E.; Feyen, L. Global long-term observations of coastal erosion and accretion. Sci. Rep. 2018, 8, 12876. [Google Scholar] [CrossRef]
- Weber de Melo, W.; Pinho, J.L.; Iglesias, I. Emulating the estuarine morphology evolution using a deep convolutional neural network emulator based on hydrodynamic results of a numerical model. J. Hydroinform. 2022, 24, 1254–1268. [Google Scholar] [CrossRef]
- Fajardo-Urbina, J.M.; Liu, Y.; Georgievska, S.; Gräwe, U.; Clercx, H.J.; Gerkema, T.; Duran-Matute, M. Efficient deep learning surrogate method for predicting the transport of particle patches in coastal environments. Mar. Pollut. Bull. 2024, 209, 117251. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.B.; Feng, X.R.; Gao, T.H.; Wang, Z.F.; Wan, K.; Yin, B.S. Application of deep learning in predicting suspended sediment concentration: A case study in Jiaozhou Bay, China. Mar. Pollut. Bull. 2024, 201, 116255. [Google Scholar] [CrossRef] [PubMed]
- Leiteritz, R.; Hurler, M.; Pfluger, D. Learning Free-Surface Flow with Physics-Informed Neural Networks. In Proceedings of the 2021 20th IEEE International Conference on Machine Learning and Applications (ICMLA), Virtual, 13–16 December 2021; IEEE: Pasadena, CA, USA, 2021; pp. 1668–1673. [Google Scholar] [CrossRef]
- Dazzi, S. Physics-informed neural networks for the augmented system of shallow water equations with topography. Water Resour. Res. 2024, 60, e2023WR036589. [Google Scholar] [CrossRef]
- Qi, X.; de Almeida, G.A.M.; Maldonado, S. Physics-informed neural networks for solving flow problems modeled by the 2D Shallow Water Equations without labeled data. J. Hydrol. 2024, 636, 131263. [Google Scholar] [CrossRef]
- Bihlo, A.; Popovych, R.O. Physics-informed neural networks for the shallow-water equations on the sphere. J. Comput. Phys. 2022, 456, 111024. [Google Scholar] [CrossRef]
- Huang, Y.H.; Xu, Z.; Qian, C.; Liu, L. Solving free-surface problems for non-shallow water using boundary and initial conditions-free physics-informed neural network (bif-PINN). J. Comput. Phys. 2023, 479, 112003. [Google Scholar] [CrossRef]
- Hinkel, J.; Lincke, D.; Vafeidis, A.T.; Perrette, M.; Nicholls, R.J.; Tol, R.S.J.; Marzeion, B.; Fettweis, X.; Ionescu, C.; Levermann, A. Coastal flood damage and adaptation costs under 21st century sea-level rise. Proc. Natl. Acad. Sci. USA 2014, 111, 3292–3297. [Google Scholar] [CrossRef]
- Kirezci, E.; Young, I.R.; Ranasinghe, R.; Muis, S.; Nicholls, R.J.; Lincke, D.; Hinkel, J. Projections of global-scale extreme sea levels and resulting episodic coastal flooding over the 21st Century. Sci. Rep. 2020, 10, 11629. [Google Scholar] [CrossRef] [PubMed]
- Dal Barco, M.K.; Maraschini, M.; Ferrario, D.M.; Nguyen, N.D.; Torresan, S.; Vascon, S.; Critto, A. A machine learning approach to evaluate coastal risks related to extreme weather events in the Veneto region (Italy). Int. J. Disaster Risk Reduct. 2024, 108, 104526. [Google Scholar] [CrossRef]
- Garzon, J.L.; Ferreira, O.; Plomaritis, T.A.; Zózimo, A.C.; Fortes, C.J.E.M.; Pinheiro, L.V. Development of a Bayesian network-based early warning system for storm-driven coastal erosion. Coast. Eng. 2024, 189, 104460. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Dimitriadis, T.; Gneiting, T.; Jordan, A.I. Stable reliability diagrams for probabilistic classifiers. Proc. Natl. Acad. Sci. USA 2021, 118, e2016191118. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly Proper Scoring Rules, Prediction, and Estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Chen, G.; Yang, J.; Huang, B.X.; Ma, C.Y.; Tian, F.L.; Ge, L.Y.; Xia, L.H.; Li, J.H. Toward digital twin of the ocean: From digitalization to cloning. Intell. Mar. Technol. Syst. 2023, 1, 3. [Google Scholar] [CrossRef]
- Papachristopoulou, K.; Ipektsidis, C.; Bye, B.L.; Berre, A.J.; Sylaios, G.; van Dam, S.; Chatziapostolidis, M. Digital Twins of the Ocean: From Idea to Practical Execution—The Paradigm of Iliad. In Proceedings of the OCEANS 2025 Brest, Brest, France, 16–19 June 2025; pp. 1–9. [Google Scholar] [CrossRef]
- Reguero, B.G.; Beck, M.W.; Bresch, D.N.; Calil, J.; Meliane, I. Comparing the cost effectiveness of nature-based and coastal adaptation: A case study from the Gulf Coast of the United States. PLoS ONE 2018, 13, e0192132. [Google Scholar] [CrossRef]
- Beck, M.W.; Losada, I.J.; Menéndez, P.; Reguero, B.G.; Díaz-Simal, P.; Fernández, F. The global flood protection savings provided by coral reefs. Nat. Commun. 2018, 9, 2186. [Google Scholar] [CrossRef]
- Menéndez, P.; Losada, I.J.; Torres-Ortega, S.; Narayan, S.; Beck, M.W. The Global Flood Protection Benefits of Mangroves. Sci. Rep. 2020, 10, 4404. [Google Scholar] [CrossRef] [PubMed]
- Narayan, S.; Beck, M.W.; Reguero, B.G.; Losada, I.J.; van Wesenbeeck, B.; Pontee, N.; Sanchirico, J.N.; Ingram, J.C.; Lange, G.-M.; Burks-Copes, K.A. The Effectiveness, Costs and Coastal Protection Benefits of Natural and Nature-Based Defences. PLoS ONE 2016, 11, e0154735. [Google Scholar] [CrossRef] [PubMed]
- Temmerman, S.; Horstman, E.M.; Krauss, K.W.; Mullarney, J.C.; Pelckmans, I.; Schoutens, K. Marshes and mangroves as nature-based coastal storm buffers. Annu. Rev. Mar. Sci. 2023, 15, 95–118. [Google Scholar] [CrossRef] [PubMed]
- Barzehkar, M.; Parnell, K.; Soomere, T. Incorporating a Machine Learning Approach into an Established Decision Support System for Coastal Vulnerability in the Eastern Baltic Sea. J. Coast. Res. 2025, 113, 58–62. [Google Scholar] [CrossRef]
- Marchau, V.A.W.J.; Walker, W.E.; Bloemen, P.J.T.M.; Popper, S.W. Decision Making Under Deep Uncertainty: From Theory to Practice; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Hu, W. Thoughts on the utilization and management of shorelines in typical sections of the middle and lower reaches of the Yangtze River. Water Resour. Dev. Res. 2025, 25, 32–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).