Variable Selection and Model Comparison for Optimizing Machine Learning-Based TOC Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Water Quality Data
2.1.1. Study Area
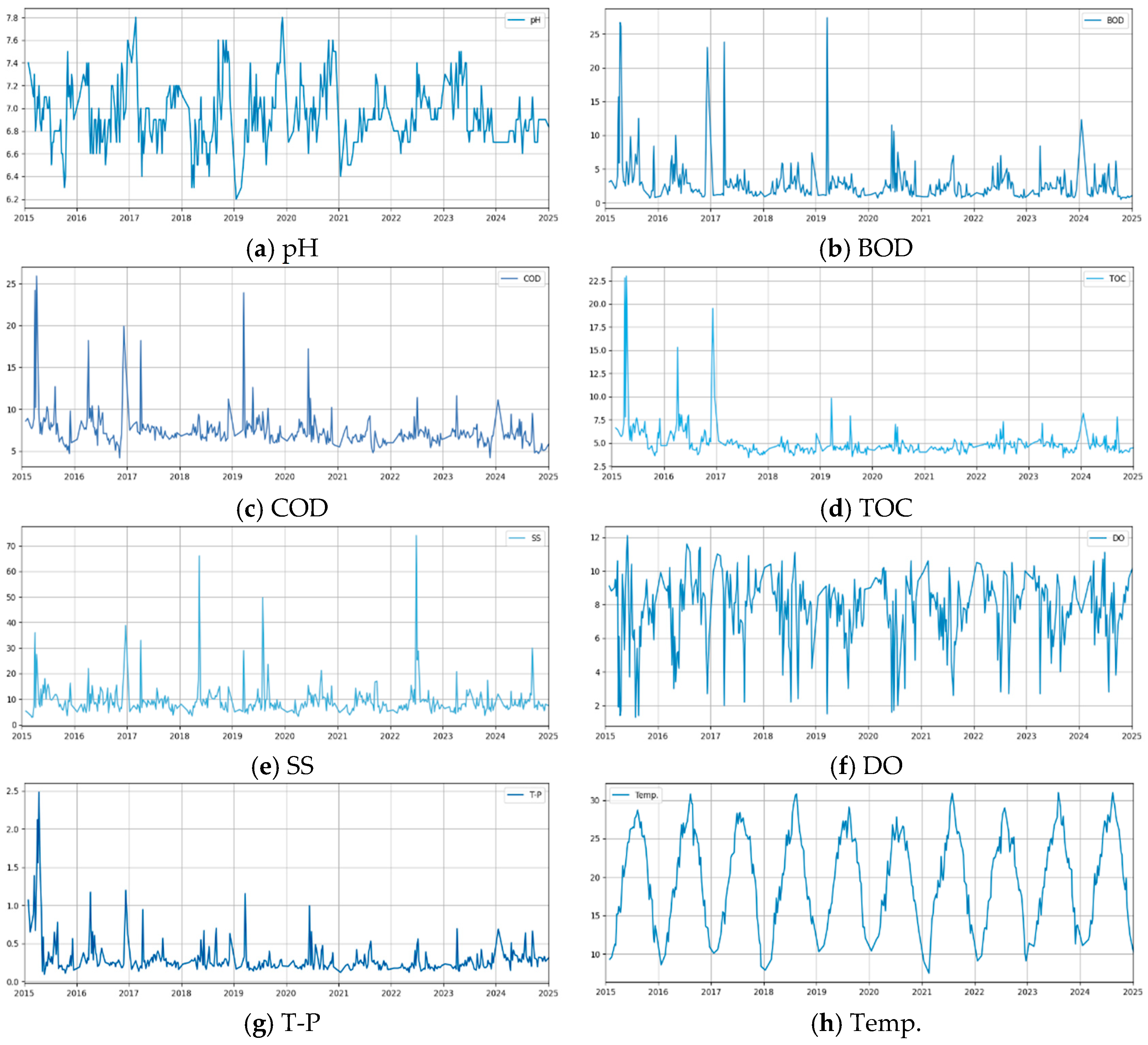
2.1.2. Data Description
2.2. Correlation Analysis
2.2.1. Pearson Correlation Coefficient Method
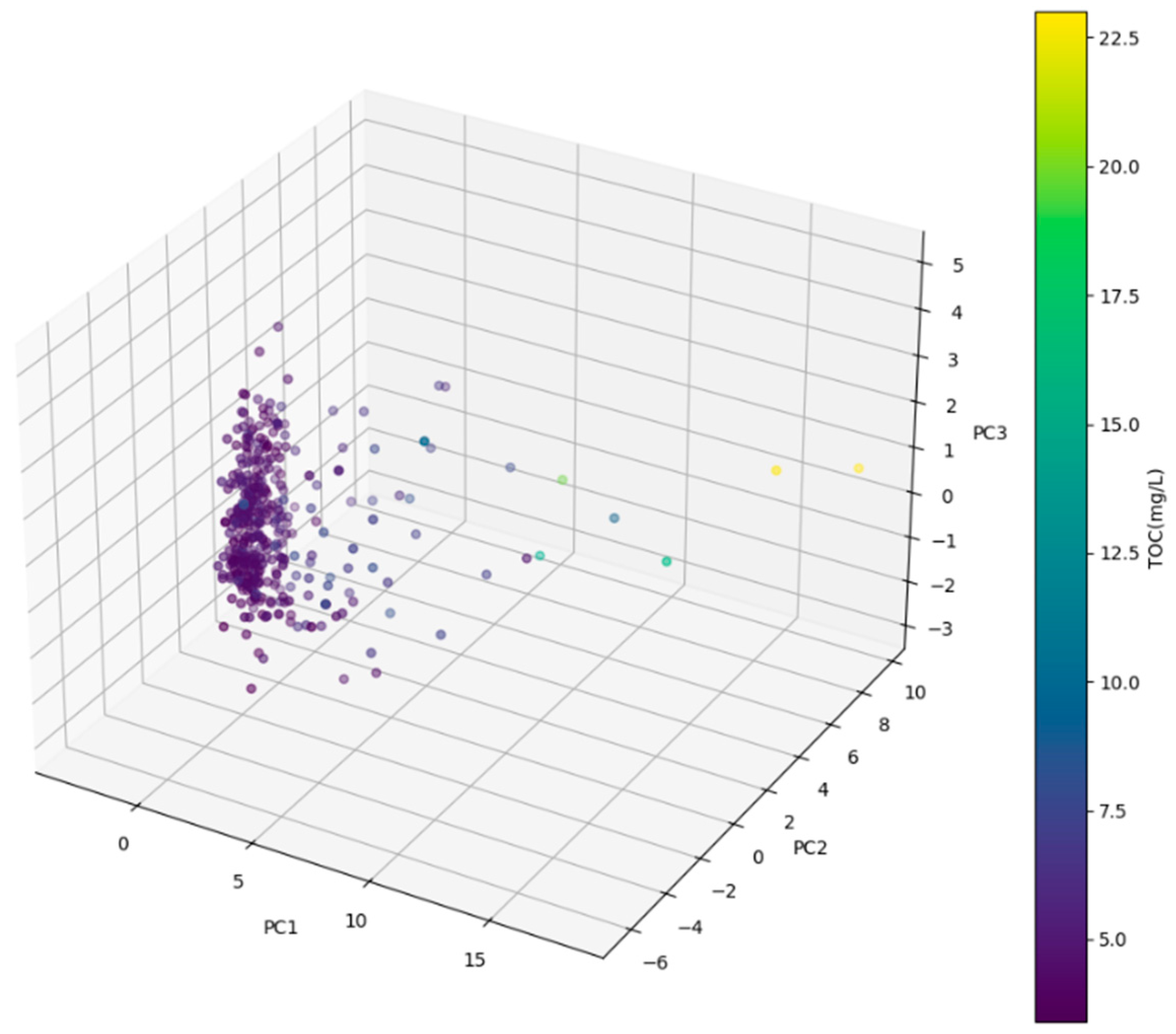
2.2.2. Principal Component Analysis
2.3. Machine Learning Algorithms
2.3.1. Multilayer Perceptron (MLP)
2.3.2. Random Forest (RF)
2.4. Exhaustive Search
2.5. Grid Search
3. Results and Discussion
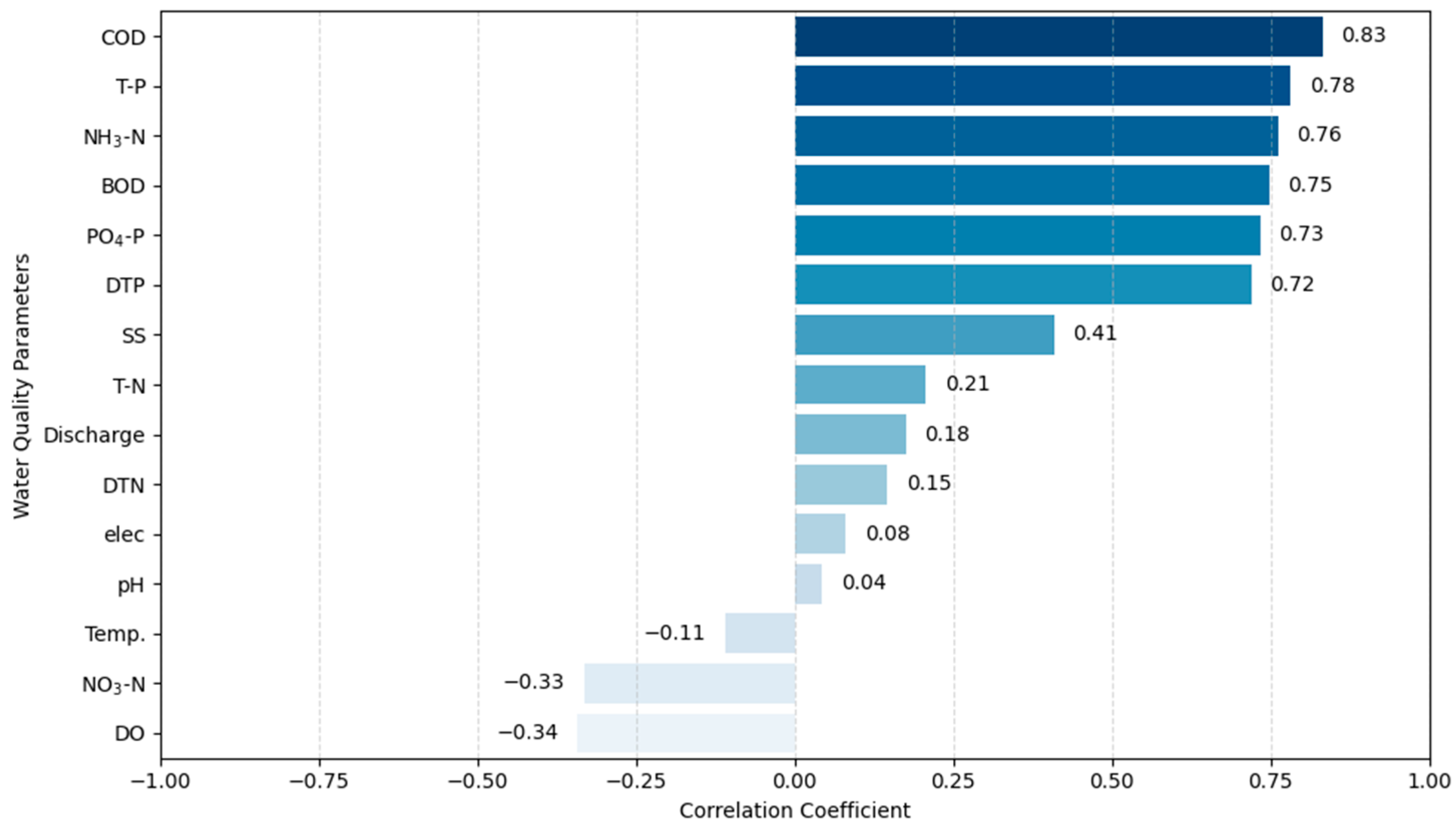
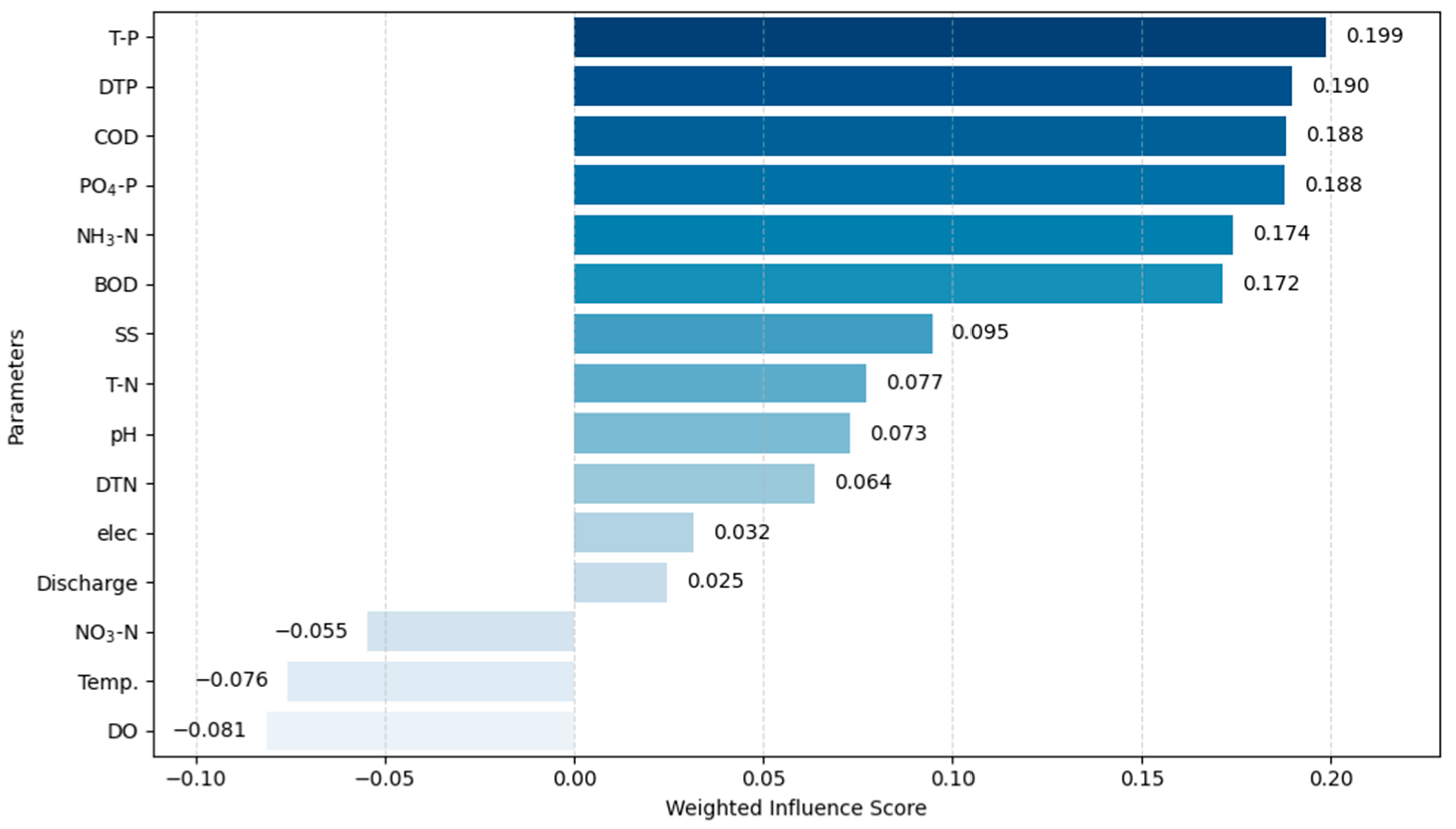
3.1. Correlation and Factor Analysis
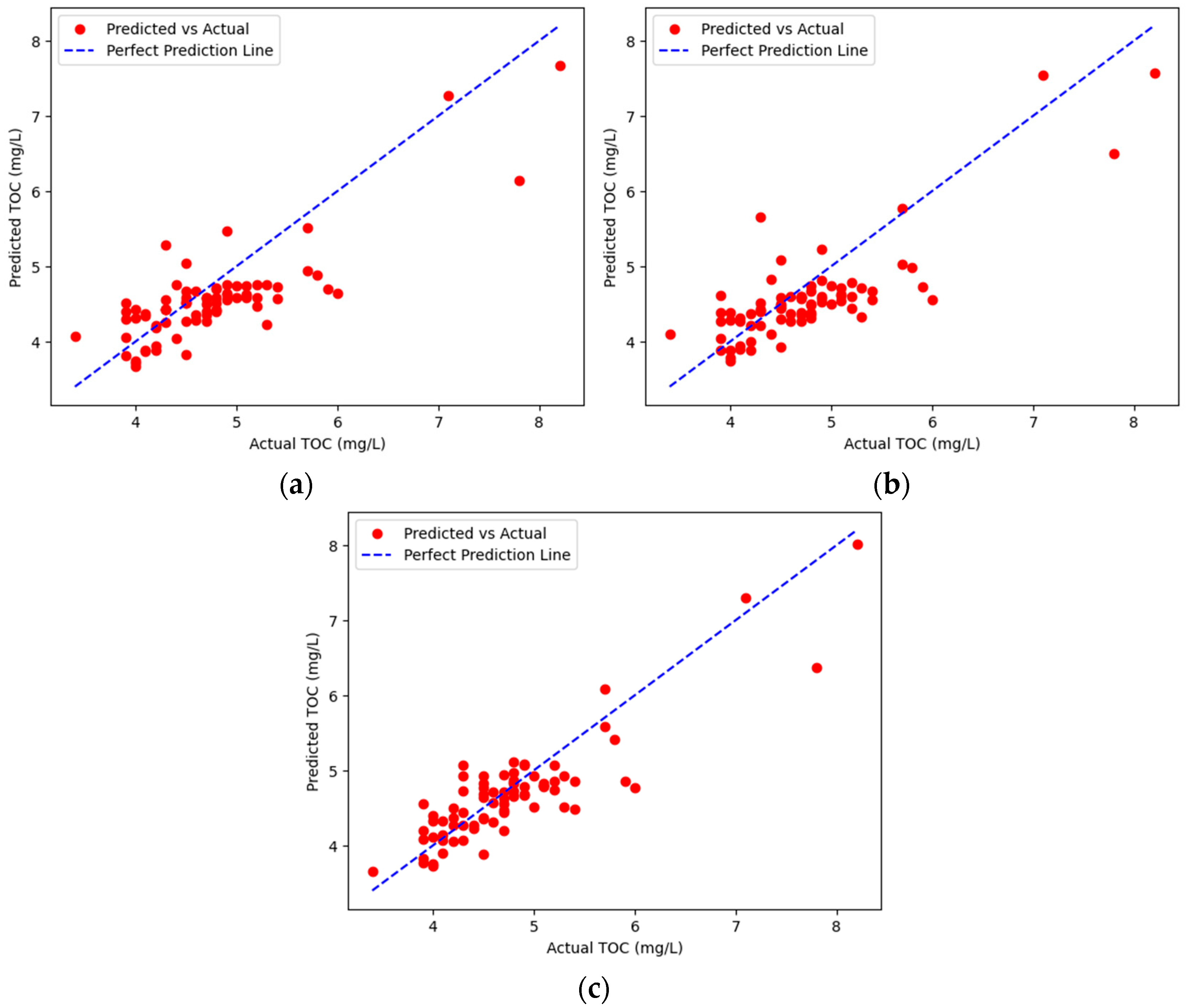
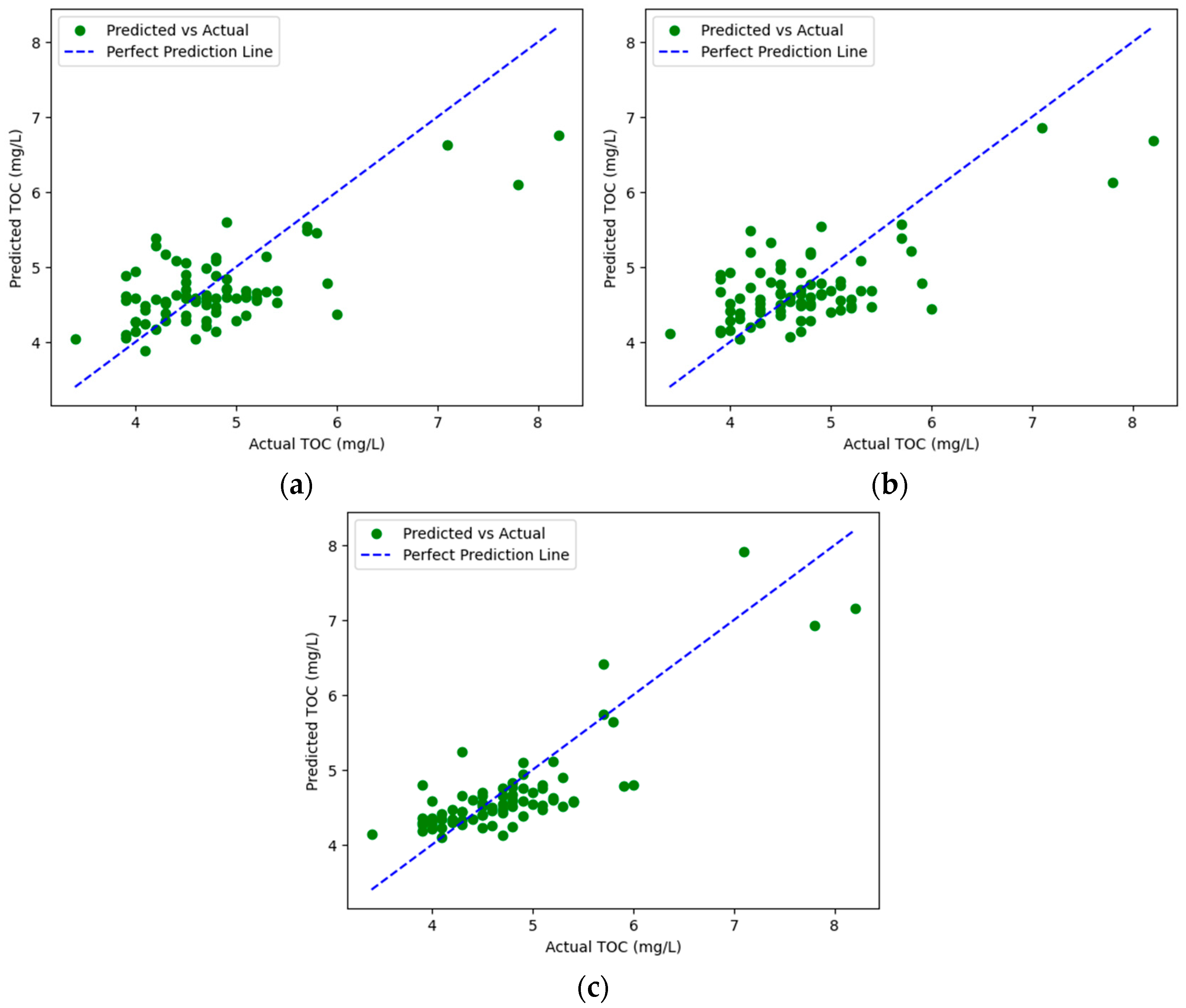
3.2. Development of TOC Prediction Models
3.3. Hyperparameter Tuning of TOC Prediction Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amarasinghe, H.A.U.; Gunawardena, H.D.; Jayatunga, Y.A. Correlation between biochemical oxygen demand (BOD) and chemical oxygen demand (COD) for different industrial waste waters. J. Natl. Sci. Found. Sri Lanka 1993, 21, 259–266. [Google Scholar] [CrossRef]
- Rudaru, D.G.; Lucaciu, I.E.; Fulgheci, A.M. Correlation between BOD5 and COD—Biodegradability indicator of wastewater. Rom. J. Ecol. Environ. Chem. 2022, 4, 80–86. [Google Scholar] [CrossRef]
- Alewi, H.K.; Abood, E.A.; Ali, G. An inquiry into the relationships between BOD5, COD, and TOC in Tigris River, Maysan Province, Iraq. Casp. J. Environ. Sci. 2022, 20, 37–43. [Google Scholar] [CrossRef]
- Choi, I.W.; Kim, J.H.; Im, J.K.; Park, T.J.; Kim, S.Y.; Son, D.H.; Huh, I.A.; Rhew, D.H.; Yu, S.J. Application of TOC standards for managing refractory organic compounds in industrial wastewater. J. Korean Soc. Water Environ. 2015, 31, 29–34. [Google Scholar] [CrossRef][Green Version]
- ES 04316.1a; Dissolved Organic Carbon—High Temperature Combustion Method. National Institute of Environmental Research (NIER): Incheon, Republic of Korea, 2024.
- ES 04316.2a; Dissolved Organic Carbon—Persulfate-Ultraviolet or Heated-Persulfate Oxidation Method. National Institute of Environmental Research (NIER): Incheon, Republic of Korea, 2024.
- Yoon, S.B.; Lee, C.H.; Kim, Y.D. Development of a real-time TOC estimation model using spectroscopic data and machine learning techniques. J. Water Environ. Technol. 2023, 56, 815–822. [Google Scholar] [CrossRef]
- Kokya, T.A.; Mehrdadi, N.; Ardestani, M.; Baghvand, A.; Kazemi, A.; Kalhori, A.A.M. Intelligent multivariate model for the optical detection of total organic carbon. J. Chil. Chem. Soc. 2016, 61, 3055–3060. [Google Scholar] [CrossRef]
- Kim, C.; Eom, J.B.; Jung, S.; Ji, T. Detection of Organic Compounds in Water by an Optical Absorbance Method. Sensors. 2016, 16, 61. [Google Scholar] [CrossRef]
- Guo, H.; Song, Y.; Tang, H.; Zhao, J. An ensemble deep neural network approach for predicting TOC concentration in lakes along the middle-lower reaches of Yangtze River. J. Intell. Fuzzy Syst. 2022, 42, 1455–1482. [Google Scholar] [CrossRef]
- Oh, H.; Park, H.Y.; Kim, J.I.; Lee, B.J.; Choi, J.H.; Hur, J. Enhancing machine learning models for total organic carbon prediction by integrating geospatial parameters in river watersheds. Sci. Total Environ. 2024, 943, 173743. [Google Scholar] [CrossRef]
- Kemei, E.K.; Van Laerhoven, K.; Karuri, N.W.; Kimutai, R. Multivariate prediction of total organic carbon in river water using random forest and deep learning regression algorithms. Appl. Comput. Intell. 2025, 5, 264–285. [Google Scholar] [CrossRef]
- Tomperi, J.; Isokangas, A.; Ruusunen, M. Practical data-based modelling approach for estimating river water turbidity and total organic carbon. Environ. Technol. 2025, 46, 4624–4640. [Google Scholar] [CrossRef]
- Goz, E.; Yuceer, M.; Karadurmus, E. Total organic carbon prediction with artificial intelligence techniques. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2019; Volume 46, pp. 889–894. [Google Scholar] [CrossRef]
- Nafsin, N.; Li, J. Prediction of total organic carbon and E. coli in rivers within the Milwaukee River basin using machine learning methods. Environ. Sci. Adv. 2023, 2, 278–293. [Google Scholar] [CrossRef]
- Jang, D. Analysis of the water quality improvement in urban Stream using MIKE 21 FM. Appl. Sci. 2021, 11, 8890. [Google Scholar] [CrossRef]
- Ministry of the Environment. Ecological River Restoration Guidebook; Ministry of the Environment: Sejong City, Republic of Korea, 2011.
- Ministry of Environment. Enforcement Decree of the Framework Act on Environmental Policy. Available online: https://elaw.klri.re.kr/kor_service/lawView.do?hseq=63038&lang=eng (accessed on 3 November 2025).
- Jung, J.-M.; Park, S.-H.; Lee, Y.-S.; Gim, J.-H. The development of infrared thermal imaging safety diagnosis system using Pearson’s correlation coefficient. J. Korean Sol. Energy Soc. 2019, 39, 55–65. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Helm, B.; Hettiarachchi, H.; Caucci, S.; Krebs, P. Quantifying the Information Content of a Water Quality Monitoring Network Using Principal Component Analysis: A Case Study of the Freiberger Mulde River Basin, Germany. Water 2020, 12, 420. [Google Scholar] [CrossRef]
- Huda, N.; Ahmed, T.; Masum, M.H.; Faruque, N.; Islam, M.S. Assessment of surface water quality using advanced statistical techniques around an urban landfill: A multi-parameter analysis. City Environ. Interact. 2025, 28, 100237. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hashi, E.K.; Zaman, M.S.U. Developing a hyperparameter tuning based machine learning approach of heart disease prediction. J. Appl. Sci. Process Eng. 2020, 7, 631–647. [Google Scholar] [CrossRef]
- Anil, N.; Ram, A.; Krishnan, M.S. Water quality analysis of canals using machine learning algorithms and hyperparameter turning. In Proceedings of the 4th International Conference on Computing Communication and Networking Technologies (ICCCNT), New Delhi, India, 6–8 July 2023; IEEE: New York, NY, USA, 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Elvin, E.; Wibowo, A. Forecasting water quality through machine learning and hyperparameter optimization. Indones. J. Electr. Eng. Comput. Sci. 2024, 33, 496–506. [Google Scholar] [CrossRef]
- Le, T.T.H.; Zeunert, S.; Lorenz, M.; Meon, G. Multivariate statistical assessment of a polluted river under nitrification inhibition in the tropics. Environ. Sci. Pollut. Res. Int. 2017, 24, 13845–13862. [Google Scholar] [CrossRef] [PubMed]
- Doan, V.T.; Le, C.C.; Le, H.V.T.; Trieu, N.A.; Vo, P.L.; Tran, D.A.; Nguyen, H.V.; Tabata, T.; Vu, T.T.H. Comprehensive Statistical Analysis for Characterizing Water Quality Assessment in the Mekong Delta: Trends, Variability, and Key Influencing Factors. Sustainability 2025, 17, 5375. [Google Scholar] [CrossRef]
- Scikit-Learn Developers. 11.2 Data Leakage—Common Pitfalls and Recommended Practices. Available online: https://scikit-learn.org/stable/common_pitfalls.html (accessed on 3 November 2025).
- Ju, K.B.; Jung, H.N.; Jang, D.W. Selection of optimal water quality parameters and model for TOC concentration estimation. Crisisonomy 2025, 21, 143–159. [Google Scholar] [CrossRef]
| Author | Site | Features | Prediction Methods |
|---|---|---|---|
| Guo et al., 2022 [10] | Yangtze River | Temp., pH, DO, EC, Chl-a, NH4 | DNN |
| Oh et al., 2024 [11] | Geumho River | pH, DO, EC, T-N, T-P, Turbidity, Temp., Discharge, Land Use, Slope, Flow Rate | XGBoost, DNN, MLR |
| Kemei et al., 2025 [12] | Duwamish River | Depth, Density, DOC, Light Transmissivity, PO4-P, Silica, TSS, Salinity, Date | RF, CNN, MLP |
| Tomperi et al., 2025 [13] | Southern Finland | Water Temperature, Water level | MLR, PLSR, NN |
| Goz et al., 2019 [14] | Yeşilırmak River | pH, Conductivity, Dissolved Oxygen, Temp. | ELM, KELM, ANN, PLSR |
| Nafsin & Li 2023 [15] | Milwaukee River | BOD, EC, Cl, NO3, VSS, DO, Turbidity, pH, TSS | ANN, SVM, RF, GBM |
| Category | pH | BOD (mg/L) | COD (mg/L) | TOC (mg/L) | SS (mg/L) | DO (mg/L) | T-P (mg/L) | |
|---|---|---|---|---|---|---|---|---|
| 10 years | Average | 6.94 | 2.6 | 7.25 | 4.81 | 9.30 | 7.84 | 0.27 |
| Grade | Ia | II | IV | III | Ia | Ia | IV | |
| 5 years | Average | 6.90 | 2.18 | 6.70 | 4.72 | 9.05 | 7.85 | 0.26 |
| Grade | Ia | II | IV | III | Ia | Ia | IV | |
| 1 year | Average | 6.8 | 1.2 | 6.2 | 4.5 | 7.1 | 10.4 | 0.34 |
| Grade | Ia | Ib | IV | III | Ia | Ia | IV | |
| Study | Application Area | Models Used | Key Tuned Hyperparameters | Performance Improvement |
|---|---|---|---|---|
| Hashi & Zaman, 2020 [24] | Heart disease prediction | LR, KNN, SVM, DT, RF | C, gamma, solver, max_depth, etc. | LR: 88.52% → 90.16% KNN: 90.16% → 91.80% SVM: 88.52% → 90.16% DT: 81.97% → 86.89% |
| Anil et al., 2023 [25] | Canal water quality prediction | RF | n_estimators, max_depth, min_samples_split, min_samples_leaf, max_features | CV score: 0.92 → 0.94 |
| Elvin & Wibowo, 2024 [26] | Water quality forecasting (multiple ML models) | XGBoost, RF, DT, Adaptive Boosting, SVM, Naive Bayes, Extra Tree | Model-specific tuned parameters | SVM: 78% → 90.06% XGBoost: 96.93% → 97.06% DT: 95% → 95.69% |
| Variable | PC1 | PC2 | PC3 |
|---|---|---|---|
| Variance ratio | 0.4134 | 0.2653 | 0.0784 |
| Temp. | 0.0797 | −0.3201 | −0.3017 |
| DO | −0.3017 | 0.1026 | 0.2049 |
| BOD | 0.3411 | 0.1610 | −0.0037 |
| COD | 0.3266 | 0.1857 | 0.0503 |
| SS | 0.2534 | −0.1278 | 0.3059 |
| T-N | −0.0852 | 0.4931 | −0.1198 |
| T-P | 0.3399 | 0.2169 | 0.0135 |
| pH | 0.0078 | 0.0151 | 0.8363 |
| EC | −0.1648 | 0.3783 | −0.0082 |
| DTN | −0.1127 | 0.4525 | −0.1235 |
| NH3-N | 0.3463 | 0.1389 | −0.0788 |
| NO3-N | −0.3015 | 0.2780 | 0.0472 |
| DTP | 0.3162 | 0.2224 | 0.0001 |
| PO4-P | 0.3129 | 0.2076 | 0.0152 |
| Discharge | 0.2012 | −0.1661 | −0.1836 |
| Study | PC (Explained Variance, %) | Major Loading Variables | Axis |
|---|---|---|---|
| This study | PC1 (41.3%) | BOD, COD, T-P, NH3-N, DTP, PO4-P, DO, NO3-N | Nutrient pollution and organic pollution axis |
| Le et al., 2017 [27] | PC1 (27.1%) | Conductivity, NH4-N, PO4-P, T-P | Nutrient pollution |
| PC2 (22.2%) | BOD5, COD, Norg | Organic pollution | |
| Doan et al., 2025 [28] | PC1 (23.1%) | BOD5, COD, TOC, Cd | Organic pollution |
| MLP | activation | alpha | learning_rate_init | hidden layer |
| relu | 0.0001 | 0.001 | (100) | |
| RF | n_estimators | max_depth | min_samples_split | min_samples_leaf |
| 100 | none | 2 | 1 |
| Rank | Features | R2 | RMSE | MAE |
|---|---|---|---|---|
| 1 | DO, COD, T-P, DTP, PO4-P | 0.7496 | 0.3946 | 0.2921 |
| 2 | DO, COD, T-P, NO3-N, PO4-P | 0.7353 | 0.4057 | 0.2933 |
| 3 | DO, COD, T-P, pH, PO4-P | 0.7289 | 0.4106 | 0.3065 |
| 4 | COD, SS, DTN | 0.7228 | 0.4152 | 0.3054 |
| 5 | DO, COD, T-P | 0.7219 | 0.4159 | 0.3132 |
| 6 | DO, COD, T-P, NO3-N, DTP | 0.7191 | 0.4179 | 0.3062 |
| 7 | DO, COD, SS, T-P, PO4-P | 0.7184 | 0.4185 | 0.3021 |
| 8 | COD, SS, T-N | 0.7168 | 0.4197 | 0.3129 |
| 9 | DO, BOD, COD, T-P, PO4-P | 0.7161 | 0.4202 | 0.3022 |
| 10 | DO, COD, SS, T-N, T-P | 0.7140 | 0.4218 | 0.3134 |
| Rank | Features | R2 | RMSE | MAE |
|---|---|---|---|---|
| 1 | Temp., BOD, COD, SS, Discharge | 0.6788 | 0.4470 | 0.3376 |
| 2 | Temp., BOD, COD, SS, DTP | 0.6528 | 0.4647 | 0.3511 |
| 3 | Temp., BOD, COD, SS, NH3-N | 0.6510 | 0.4659 | 0.3578 |
| 4 | Temp., BOD, COD | 0.6483 | 0.4677 | 0.3367 |
| 5 | Temp., DO, BOD, COD | 0.6414 | 0.4723 | 0.3752 |
| 6 | DO, BOD, COD, SS, Discharge | 0.6378 | 0.4746 | 0.3424 |
| 7 | BOD, COD, SS, pH, Discharge | 0.6352 | 0.4763 | 0.3693 |
| 8 | Temp., BOD, COD, T-P, DTP | 0.6296 | 0.4800 | 0.3606 |
| 9 | Temp., DO, BOD, COD, Discharge | 0.6279 | 0.4811 | 0.3723 |
| 10 | Temp., COD, SS, NH3-N | 0.6273 | 0.4814 | 0.3651 |
| Method | Feature | R2 | RMSE | MAE |
|---|---|---|---|---|
| Pearson correlation | BOD, COD, T-P, NH3-N, PO4-P | 0.6150 | 0.4893 | 0.3752 |
| PCA | COD, T-P, NH3-N, DTP, PO4-P | 0.6118 | 0.4913 | 0.3804 |
| Exhaustive search | DO, COD, T-P, DTP, PO4-P | 0.7496 | 0.3946 | 0.2921 |
| Method | Feature | R2 | RMSE | MAE |
|---|---|---|---|---|
| Pearson correlation | BOD, COD, T-P, NH3-N, PO4-P | 0.4774 | 0.5701 | 0.4421 |
| PCA | COD, T-P, NH3-N, DTP, PO4-P | 0.4574 | 0.5809 | 0.4484 |
| Exhaustive search | Temp., BOD, COD, SS, Discharge | 0.6788 | 0.4470 | 0.3376 |
| Parameter | Search Values List |
|---|---|
| hidden_layer_sizes | (100), (100, 50), (100, 100), (100, 50, 50), (100, 100, 50) |
| activation | ‘relu’, ‘tanh’ |
| alpha | 0.0001, 0.001, 0.00001, 0.0005 |
| learning_rate_init | 0.001, 0.003, 0.0005, 0.0001 |
| Parameter | Search Values List |
|---|---|
| n_estimators | 100, 200, 300, 400, 500 |
| max_depth | none, 6, 8, 10, 12 |
| min_samples_split | 2, 5, 10 |
| min_samples_leaf | 1, 2, 4 |
| Model | Default Hyperparameters | R2 RMSE MAE | Optimized Hyperparameters | R2 RMSE MAE | ||
|---|---|---|---|---|---|---|
| MLP | alpha | 0.0001 | 0.7496 0.3946 0.2921 | alpha | 0.001 | 0.7562 0.3894 0.2822 |
| activation | relu | activation | relu | |||
| learning_rate_init | 0.001 | learning_rate_init | 0.003 | |||
| hidden layer | (100) | hidden layer | (100) | |||
| RF | n_estimators | 100 | 0.6788 0.4470 0.3376 | n_estimators | 100 | 0.7058 0.4278 0.3212 |
| max_depth | none | max_depth | none | |||
| min_samples_split | 2 | min_samples_split | 10 | |||
| min_samples_leaf | 1 | min_samples_leaf | 1 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, K.B.; Jang, D.W. Variable Selection and Model Comparison for Optimizing Machine Learning-Based TOC Prediction. Water 2025, 17, 3367. https://doi.org/10.3390/w17233367
Ju KB, Jang DW. Variable Selection and Model Comparison for Optimizing Machine Learning-Based TOC Prediction. Water. 2025; 17(23):3367. https://doi.org/10.3390/w17233367
Chicago/Turabian StyleJu, Kang Bin, and Dong Woo Jang. 2025. "Variable Selection and Model Comparison for Optimizing Machine Learning-Based TOC Prediction" Water 17, no. 23: 3367. https://doi.org/10.3390/w17233367
APA StyleJu, K. B., & Jang, D. W. (2025). Variable Selection and Model Comparison for Optimizing Machine Learning-Based TOC Prediction. Water, 17(23), 3367. https://doi.org/10.3390/w17233367







