Simulation of the Telluric Electrical Field Frequency Selection Method and Its Application in Mineral Water Exploration
Abstract
1. Introduction
2. Basic Theory
2.1. Three-Dimensional Forward Modeling Theory of TEFSM
2.2. Finite Element Method with Unstructured Tetrahedral Mesh
2.3. Physical Significance of Galvanic Distortion
3. Simulation Analysis
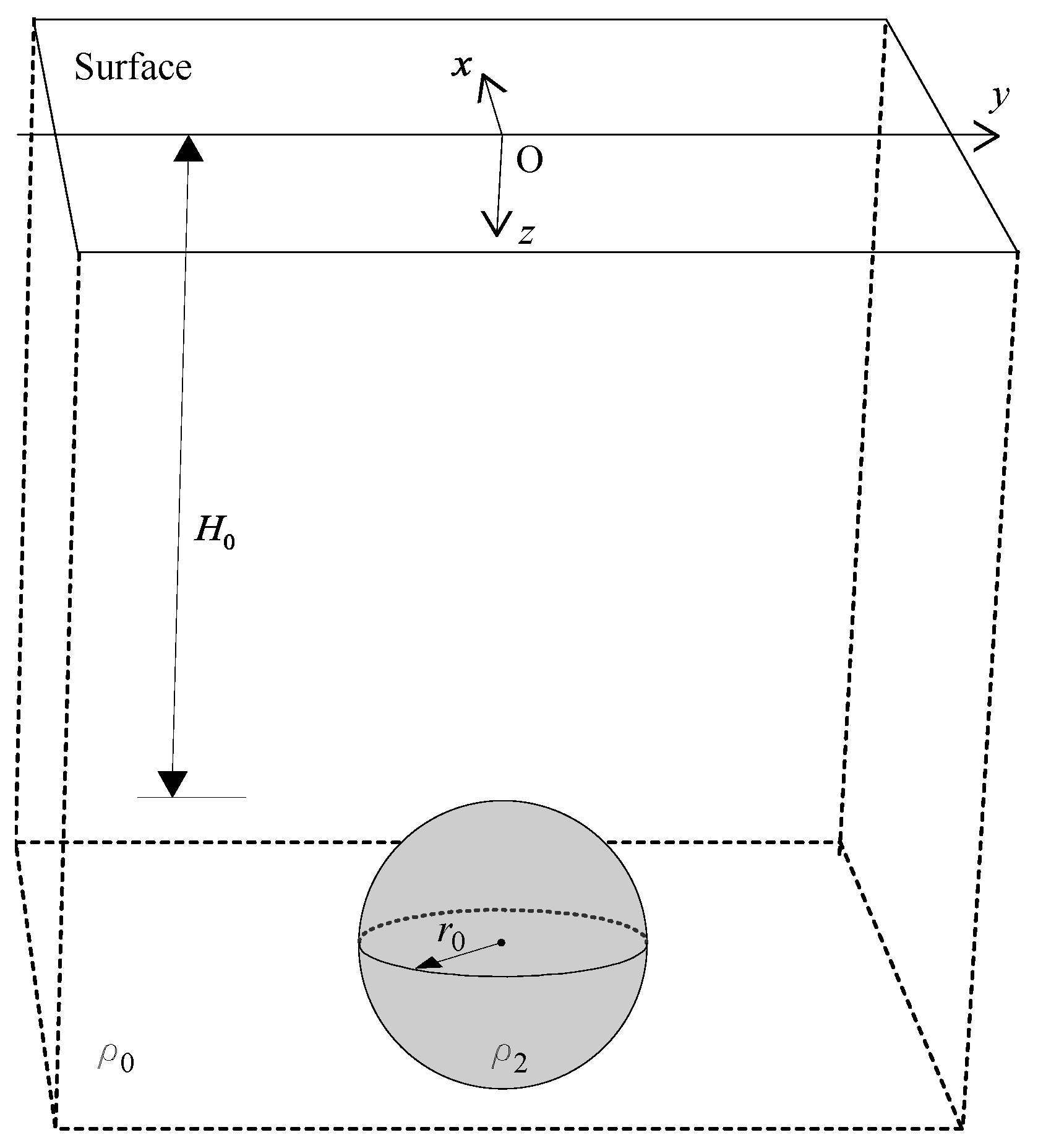
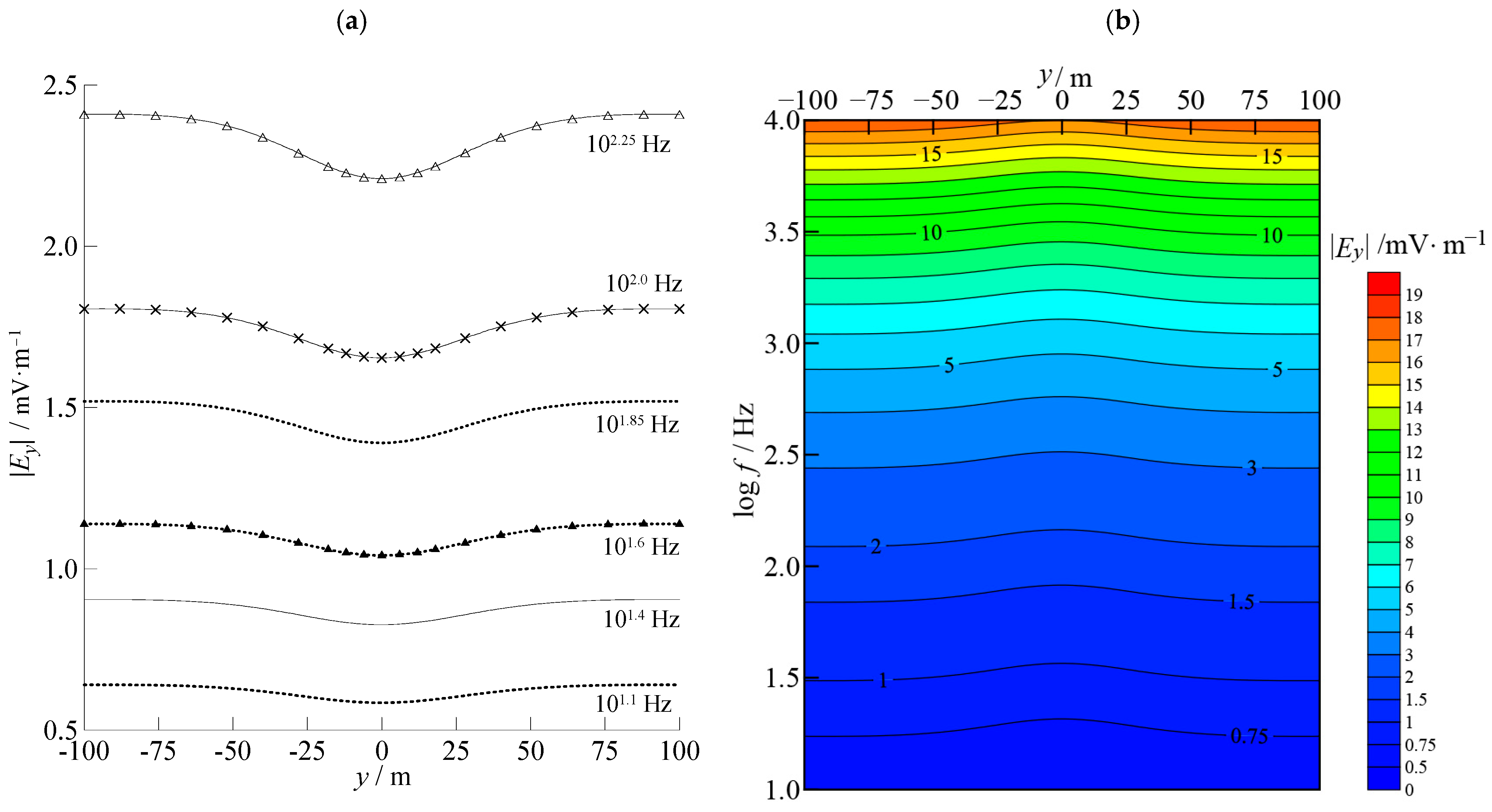
3.1. Galvanic Distortion Model
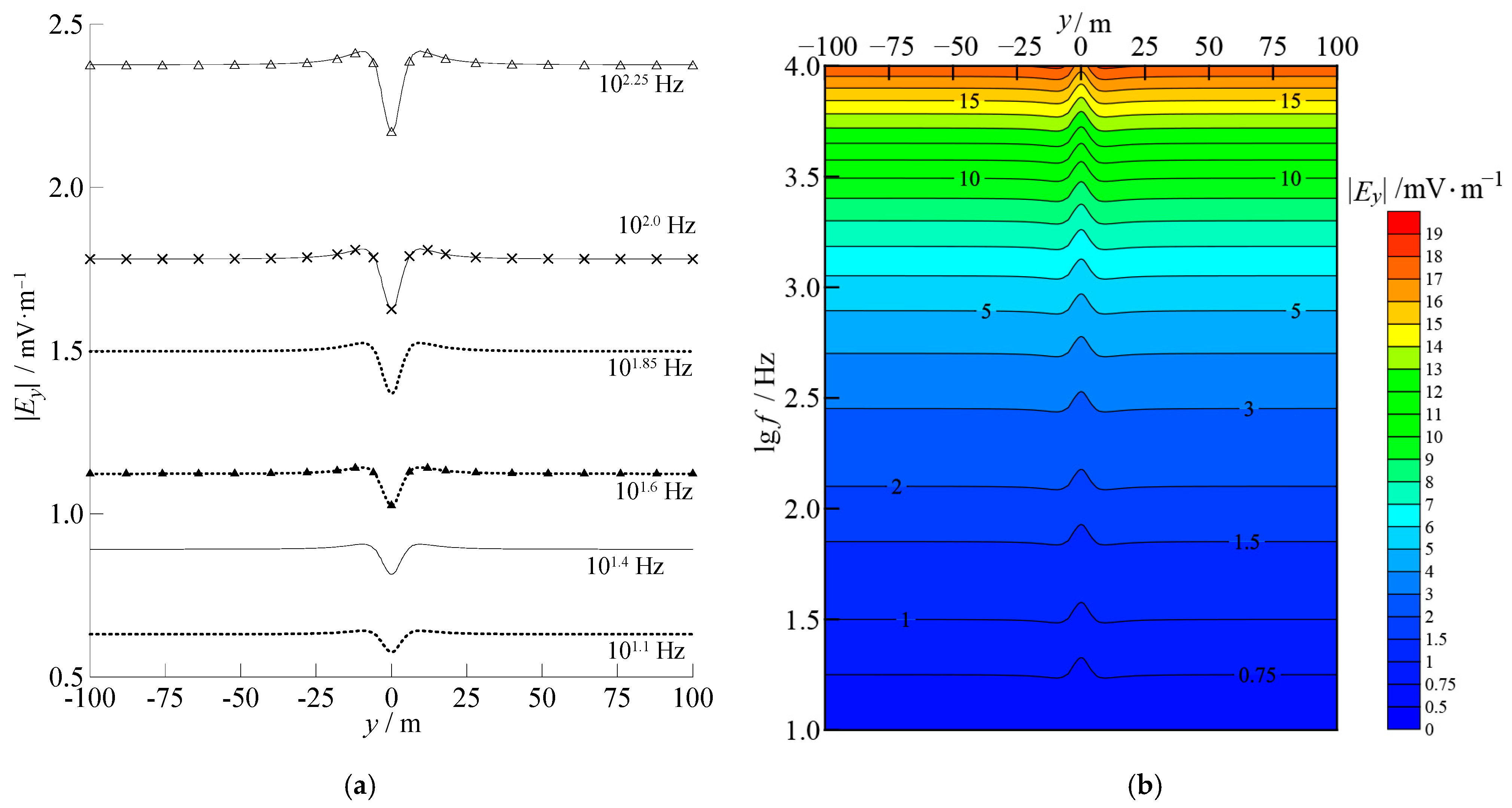
3.2. Sphere Model
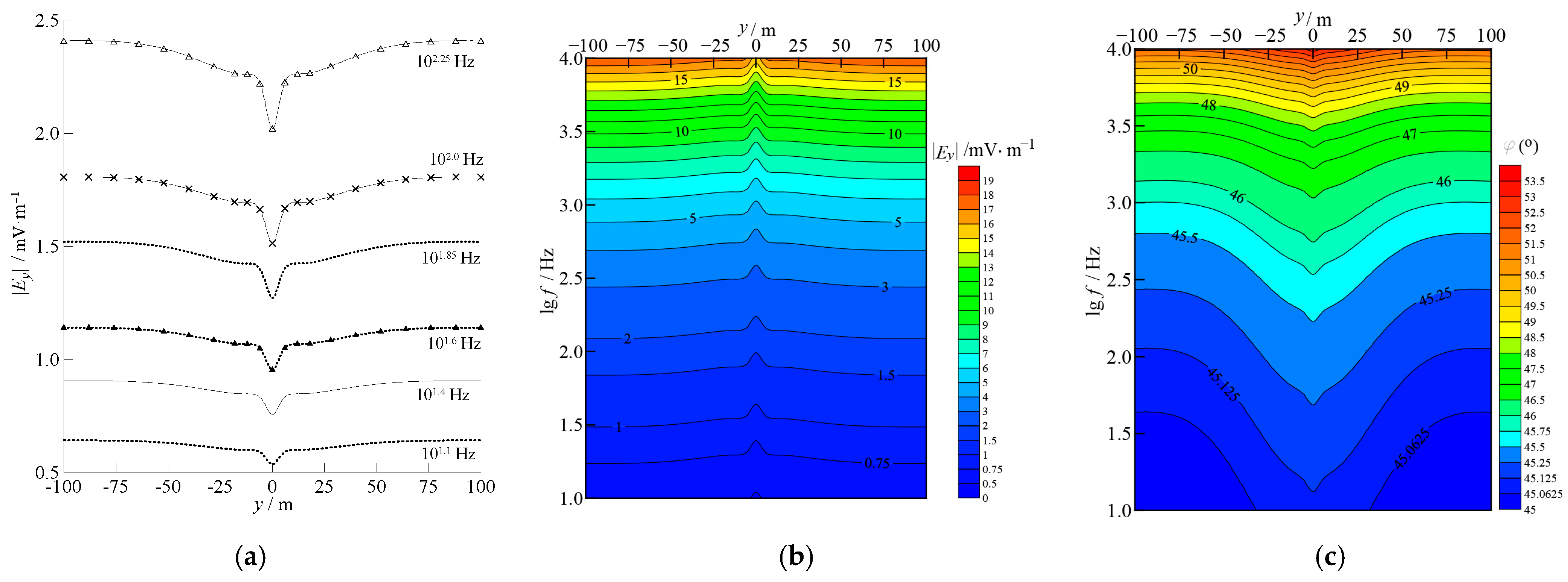
3.3. Sphere Model with Galvanic Distortion
4. A Case Study in Mineral Water Exploration
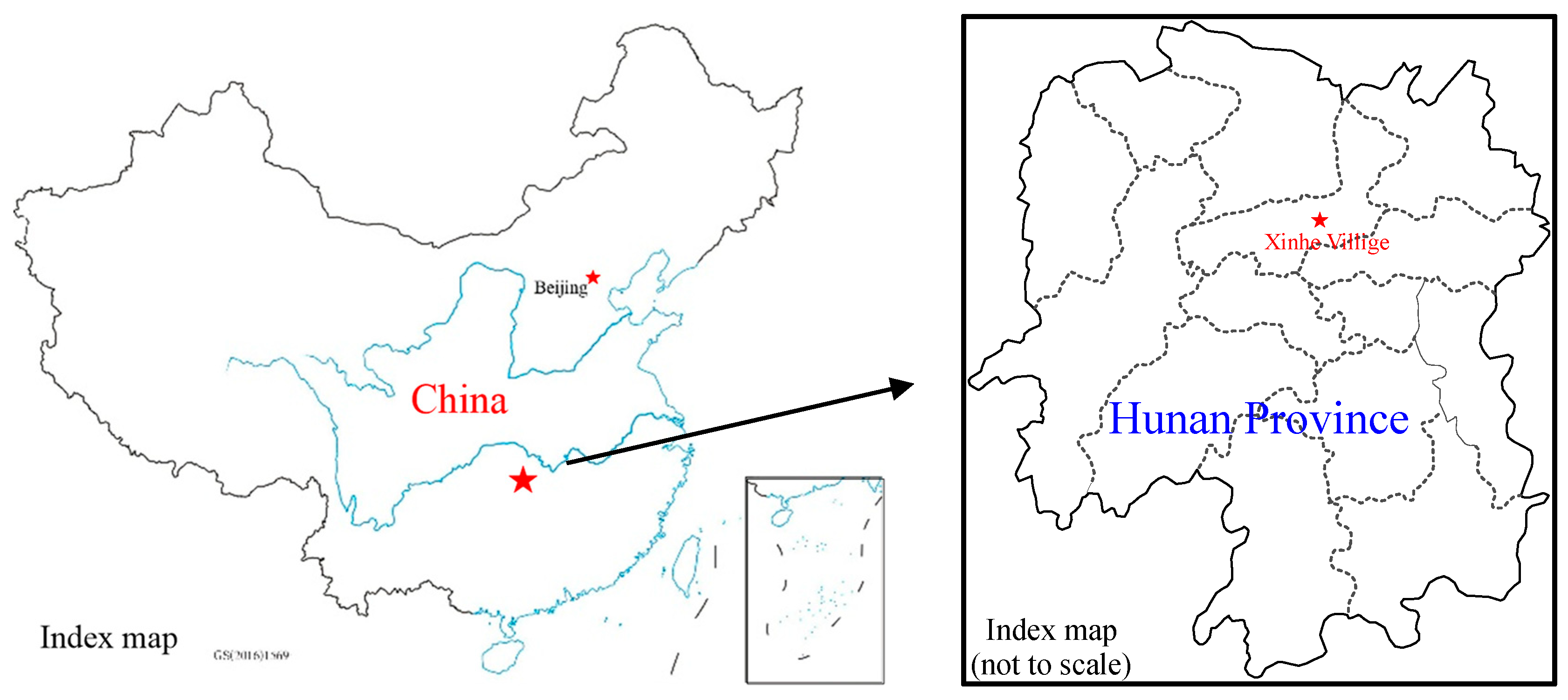
4.1. Study Area
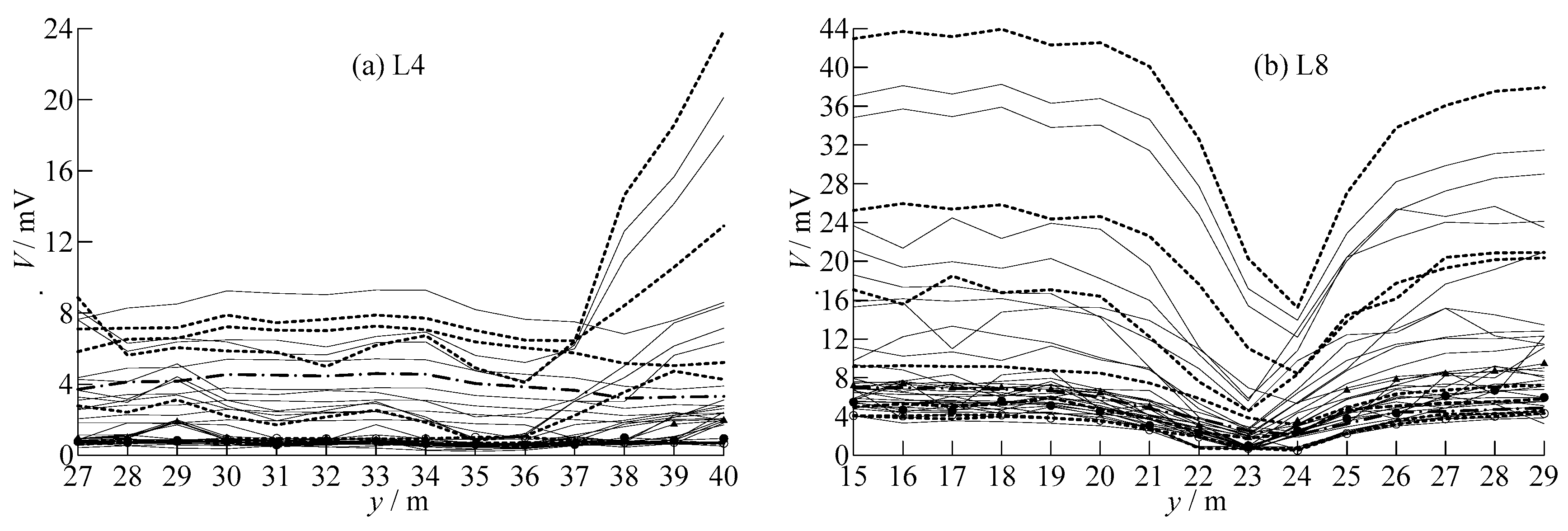
4.2. Field Data Collection and Analysis
4.3. Drilling Outcome
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gomo, M.; Ngobe, T. Groundwater exploration in a granite aquifer using the telluric electric frequency selection method (TEFSM) in Eswatini, Southern Africa. Sustain. Water Resour. Manag. 2024, 10, 22. [Google Scholar] [CrossRef]
- Yang, T.C.; Zhu, D.B.; Yawar, H.; Huang, R.; Yu, Q.; Ding, Q. Feasibility study of telluric magnetic field frequency selection method in groundwater exploration. J. Appl. Geophys. 2025, 233, 105608. [Google Scholar] [CrossRef]
- Cai, H.Z.; Xiong, B.; Zhdanov, M. Three-dimensional marine controlled-source electromagnetic modelling in anisotropic medium using finite element method. Chin. J. Geopohysics 2015, 58, 2839–2850. (In Chinese) [Google Scholar] [CrossRef]
- Gomo, M. Use of electric potential difference in audio magnetotelluric (AMT) geophysics for groundwater exploration. Groundw. Sustain. Dev. 2023, 20, 100864. [Google Scholar] [CrossRef]
- Liu, J.X.; Liu, R.; Guo, R.W.; Tong, X.; Xie, W. Research progress of electromagnetic method in nonferrous metal mineral exploration. Chin. J. Nonferrous Met. 2023, 33, 261–284. (In Chinese) [Google Scholar]
- Yao, H.B.; Ren, Z.Y.; Tang, J.T.; Lin, Y.; Yin, C.; Hu, X.; Huang, Q.; Zhang, K. 3D finite-element modeling of Earth induced electromagnetic field and its potential applications for geomagnetic satellites. Sci. China Earth Sci. 2021, 51, 1796–1812. (In Chinese) [Google Scholar] [CrossRef]
- Cagniard, L. Basic theory of the magneto-telluric method of geophysical prospecting. Geophysics 1953, 18, 605–635. [Google Scholar] [CrossRef]
- Liang, B.H. Introduction of electric pulse natural electric field method for water exploration. Karst Geol. Guangxi 1976, 2, 10–11. [Google Scholar]
- Yang, J. Experimental results and theoretical study of the stray current method in karst area. Geophys. Geochem. Explor. 1982, 6, 41–54. (In Chinese) [Google Scholar]
- Zhou, H.; Huang, C.L.; Zhou, Y. Underground magneto fluid detector and its application in mine flood detection. Miner. Eng. Res. 2009, 24, 42–45. (In Chinese) [Google Scholar]
- Yang, T.C.; Xia, D.L.; Wang, Q.R.; Fu, G.H. Theoretical Research and Application of Frequency Selection Method for Telluric Electricity Field; Central South University Press: Changsha, China, 2017. (In Chinese) [Google Scholar]
- Han, R.B.; Han, D. Theory and Practice of Frequency Selection Method for Telluric Current; Metallurgical Industry Press: Beijing, China, 2020. (In Chinese) [Google Scholar]
- Yang, T.C.; Gao, Q.S.; Li, H.; Fu, G. New Insights into the Anomaly Genesis of the Frequency Selection Method: Supported by Numerical Modeling and Case Studies. Pure Appl. Geophys. 2023, 180, 969–982. [Google Scholar] [CrossRef]
- Lu, Y.L.; Ding, H.Y.; Yang, T.C.; Liu, Y. Geothermal Water Exploration of the Maoyanhe Hot Spring Scienic Spot in Zhangjiajie Using the Natural Electric Field Frequency Selection Method. Water 2023, 15, 3418. [Google Scholar] [CrossRef]
- Yang, T.C.; Wang, D.Q.; Zhang, Y.P.; Fu, G.; Chen, B.; Yang, Z.; Cheng, H. Application research of comprehensive geophysical method to karst investigation in a productive mine. Prog. Geophys. 2020, 36, 1145–1153. (In Chinese) [Google Scholar]
- Adagunodo, T.A.; Ojoawo, A.I.; Anie, N.O.; Edukugho, P.O. Application of frequency selection and geoelectrical sounding methods for mapping of leachate’s pathways in an active dumpsite. SN Appl. Sci. 2023, 5, 352. [Google Scholar] [CrossRef]
- Yang, T.C.; Liang, J.; Cheng, H.; Cao, S.-J.; Dong, S.-Y.; Gong, Y.-F. The effect and the anomaly analysis of shallow groundwater exploration based on the frequency selection method of natural electric field. Geophys. Geochem. Explor. 2018, 42, 1194–1200. (In Chinese) [Google Scholar]
- Isah, A.; Akinbiyi, O.A.; Ugwoke, J.L.; Ayajuru, N.C.; Oyelola, R.O. Detection of groundwater level and heavy metal contamination: A case study of Olubunku dumpsite and environs, Ede North, Southwestern Nigeria. J. Afr. Earth Sci. 2022, 197, 104740. [Google Scholar] [CrossRef]
- Yulong, L.; Tianchun, Y.; Tizro, A.T.; Yang, L. Fast recognition on shallow groundwater and anomaly analysis using frequency selection sounding method. Water 2023, 15, 96. [Google Scholar] [CrossRef]
- Hu, F.; Yang, T.; Adagunodo, T.A.; Zhu, D.; Huang, R. Practice and theoretical analysis of ground penetrating radar in voids detection of urban underground pipe-jacking. J. Appl. Geophys. 2025, 233, 105639. [Google Scholar] [CrossRef]
- Bahr, K. Interpretation of the magnetotelluric impedance tensor: Regional induction and local telluric distortion. J. Geophys. 1988, 62, 119–127. [Google Scholar]
- Zhamaletdinov, A.A. A Method for Quantifying Static Shift Distortions Using a Magnetic Field of Controlled Source (CSAMT). Seism. Instrum. 2020, 56, 555–563. [Google Scholar] [CrossRef]
- Ward, S.H.; Hohmann, G.W. Electromagnetic theory for geophysical applications in Nabighian. In Electromagnetic Methods, Theory and Practice; Nabighian, M.N., Ed.; Society of Exploration Geophysicist: Houston, TX, USA, 1987; Volume 1, pp. 131–311. [Google Scholar]
- Hedlin, C. Removal of static shift in two dimensions by regularization inversion. Geophysics 1991, 56, 2102–2106. [Google Scholar] [CrossRef]
- Ogawa, Y.; Uchida, T. A two-dimension MT inversion assuming Gaussion static shift. Geophys. J. Int. 1996, 126, 69–76. [Google Scholar] [CrossRef]
- Jiang, E.; Chen, R.; Zhu, D.B.; Liu, W.; Pitiya, R. Static-shift suppression and anti-interference signal processing for CSAMT based on Guided Image Filtering. Earthq. Res. Adv. 2022, 2, 100117. [Google Scholar] [CrossRef]
- Melchinov, V.P.; Pavlov, A.A. Experience with a Water Detector in the Study of the Permafrost Structure. Geomagn. Aeron. 2022, 62, 271–277. [Google Scholar] [CrossRef]
- Guo, W.; Tang, X.G.; Sheng, G.Q. MT static correction of two-dimensional model based on the highest frequency phase method and spatial filtering method. Acta Seismol. Sin. 2022, 44, 1–15. (In Chinese) [Google Scholar]
- Tang, J.T.; He, J.S. Controlled Source Audio-Frequency Magnetotelluric and Its Applications; Central South University Press: Changsha, China, 2005. (In Chinese) [Google Scholar]
- Li, W.J. The Application of Geophysical Method in Karst Exploration; Chengdu University of Technology: Chengdu, China, 2020. (In Chinese) [Google Scholar]
- Berdichevsky, M.N.; Dmitriev, V.I. Distortion of magnetic and electrical fields by near-surface lateral inhomogeneities. Acta Geod. Geophys. Montan. 1976, 11, 447–483. [Google Scholar]
- Li, X.; Bai, D.H.; Yan, Y.L. Three-dimensional inversion of magnetotelluric resistivity model with galvanic distortion. Chin. J. Geophys. 2016, 59, 2302–2315. [Google Scholar] [CrossRef]
- Chave, A.D.; Smith, J.T. On electric and magnetic galvanic distortion tensor decompositions. J. Geophys. Res. Solid Earth 1994, 99, 4669–4682. [Google Scholar] [CrossRef]
- Bahr, K. Geological noise in magnetotelluric data: A classification of distortion types. Phys. Earth Planet. Inter. 1991, 66, 24–38. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, Y.X.; Liu, Y.; Zhang, S.; Zhang, L.; Li, D. Research on simulation and correction methods for static effect of electrical anisotropy in MT. Jt. Acad. Annu. Meet. China Earth Sci. 2016, 931–932. (In Chinese) [Google Scholar]







| Lithology | Apparent Resistivity (Ω·m) | Determination Method | |
|---|---|---|---|
| Range of Variation | Common Values | ||
| Silty clay | 20–200 | 40 | Outcrop small quadrupole configuration |
| Silty clay (less watery) | 20–200 | 127 | |
| Granite | 130–14,000 | 965 | |
| Fractured zone | 80–400 | 220 | Electrical sounding |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Yang, Z.; Qin, Q.; Adagunodo, T.A.; Zhu, M. Simulation of the Telluric Electrical Field Frequency Selection Method and Its Application in Mineral Water Exploration. Water 2025, 17, 3314. https://doi.org/10.3390/w17223314
Yang T, Yang Z, Qin Q, Adagunodo TA, Zhu M. Simulation of the Telluric Electrical Field Frequency Selection Method and Its Application in Mineral Water Exploration. Water. 2025; 17(22):3314. https://doi.org/10.3390/w17223314
Chicago/Turabian StyleYang, Tianchun, Zhu Yang, Qin Qin, Theophilus Aanuoluwa Adagunodo, and Maoyue Zhu. 2025. "Simulation of the Telluric Electrical Field Frequency Selection Method and Its Application in Mineral Water Exploration" Water 17, no. 22: 3314. https://doi.org/10.3390/w17223314
APA StyleYang, T., Yang, Z., Qin, Q., Adagunodo, T. A., & Zhu, M. (2025). Simulation of the Telluric Electrical Field Frequency Selection Method and Its Application in Mineral Water Exploration. Water, 17(22), 3314. https://doi.org/10.3390/w17223314






