AI-Based Time-Series Ensemble Approach Coupled with a Hydrological Model for Reservoir Storage Prediction in Korea
Abstract
1. Introduction
2. Materials and Methods
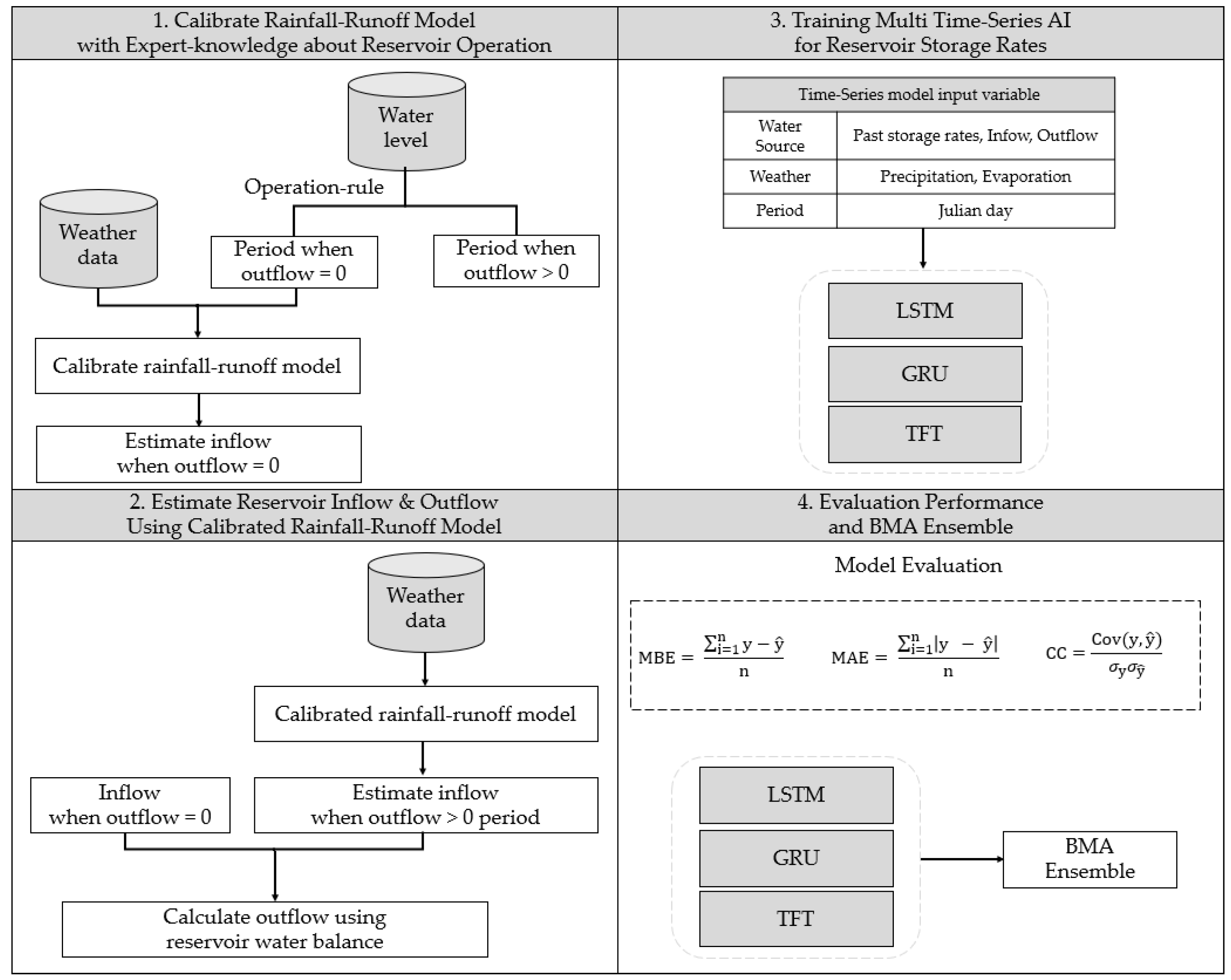
2.1. Overview
2.2. Study Area
2.3. Dataset
2.3.1. Reservoir Data
2.3.2. Meteorological Data
2.4. Rule-Based Rainfall–Runoff Process
2.4.1. Reservoir Water Balance
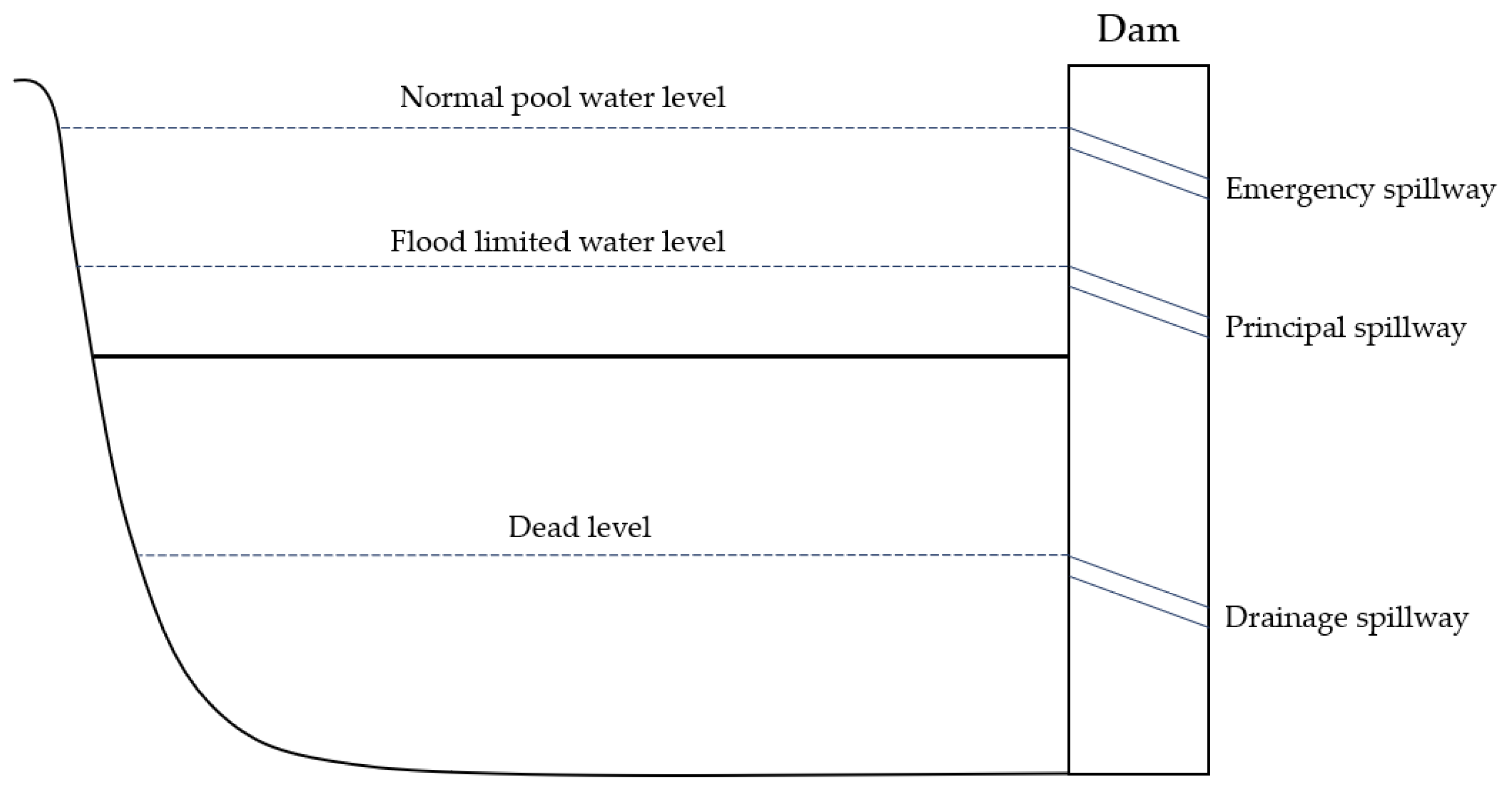
2.4.2. Reservoir Operation Rule
2.4.3. Inflow Reconstruction
2.4.4. Outflow Reconstruction
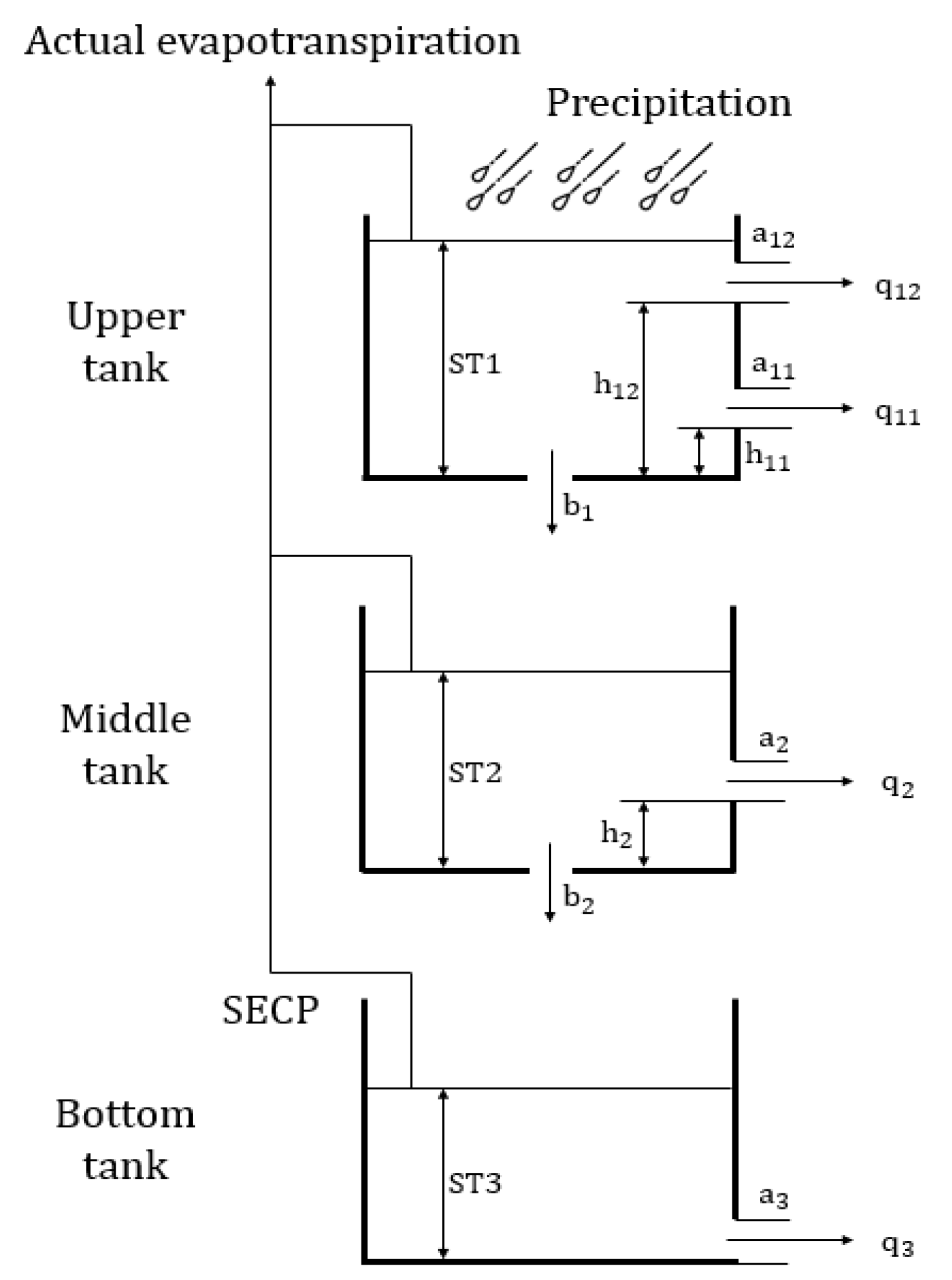
2.4.5. Three-Tank Model Simulation
2.4.6. Optimization and Performance Evaluation
2.5. Time-Series AI Models
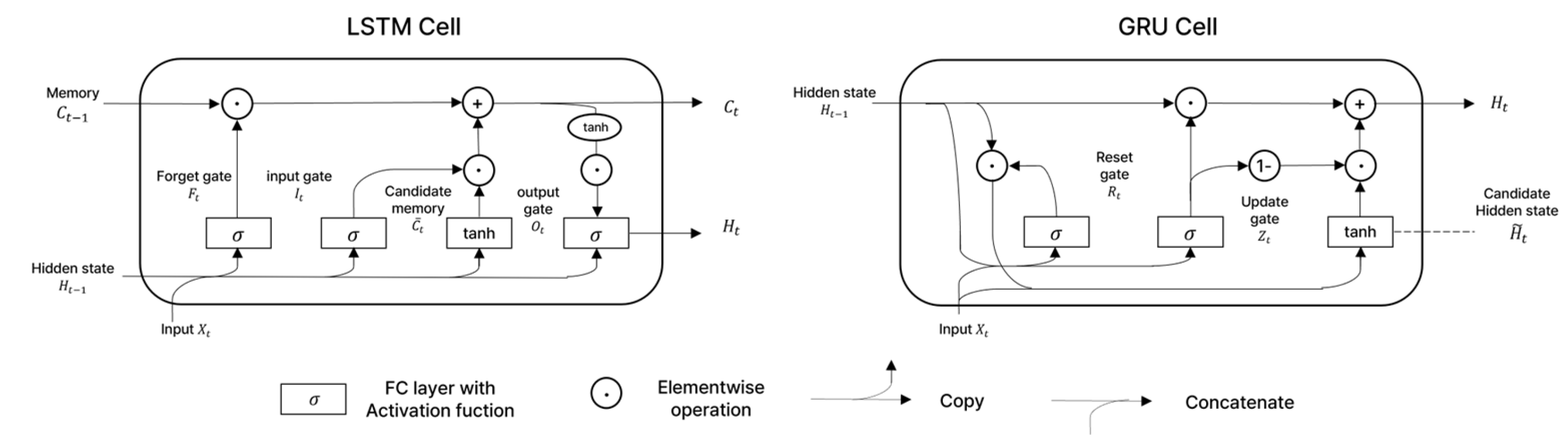
2.5.1. Recurrent Neural Network Model
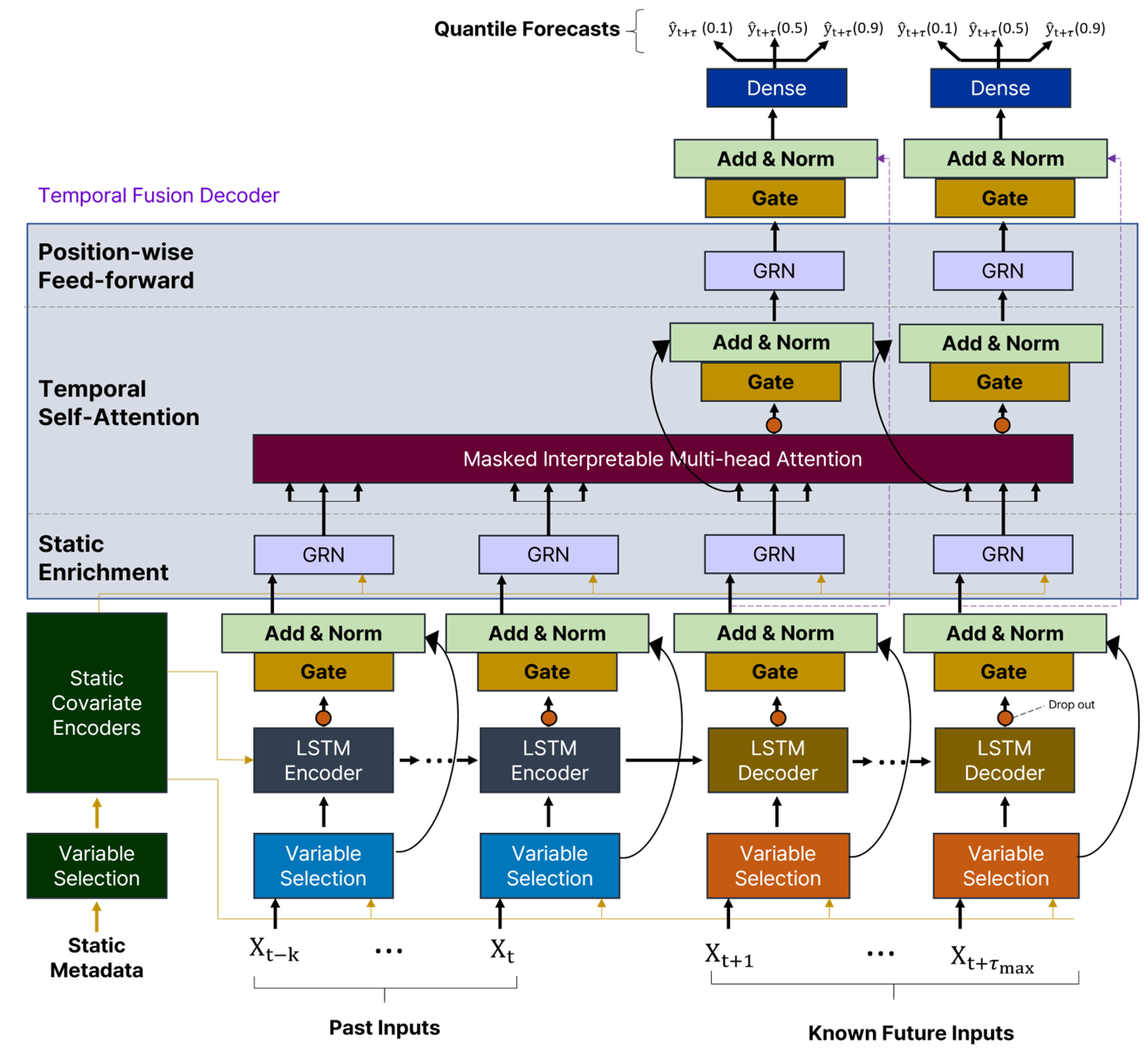
2.5.2. Transformer Model
2.6. Baysian Model Averaging Ensemble
3. Results
3.1. Data Analysis
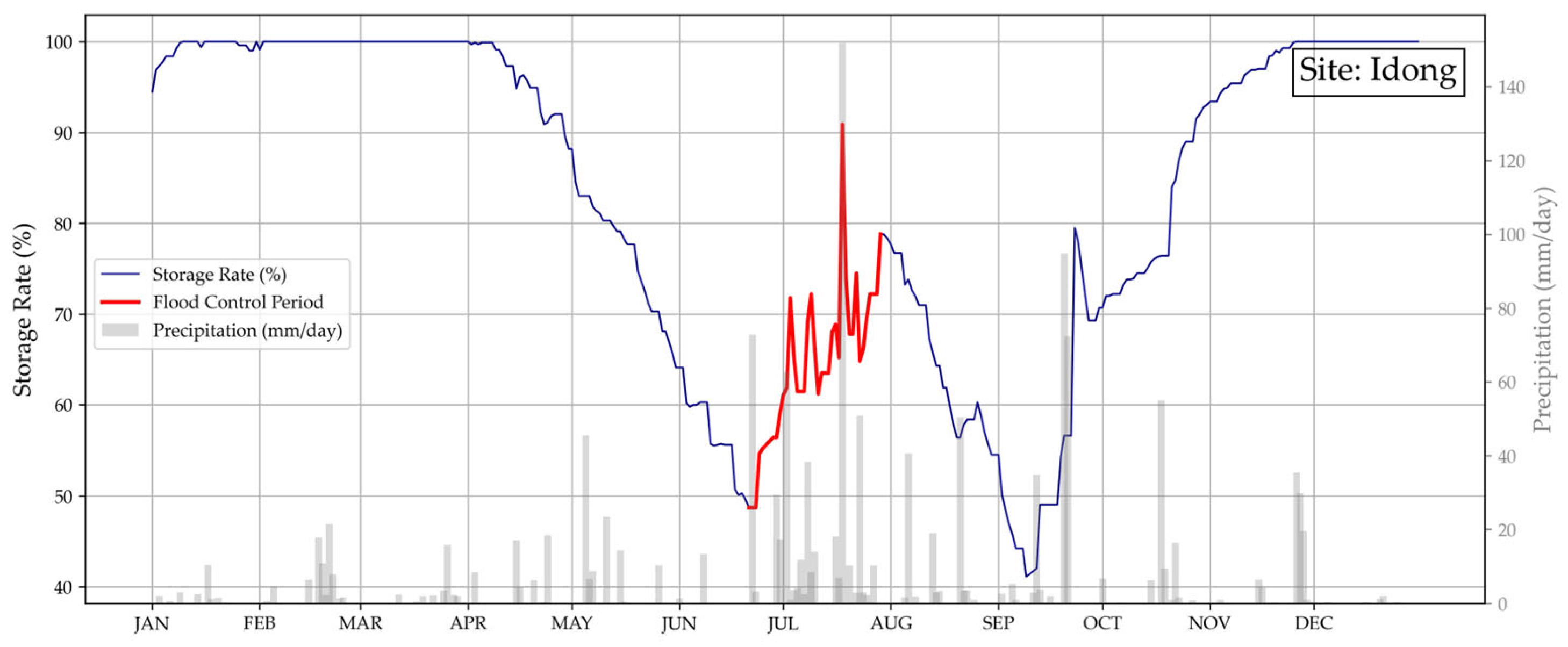
3.1.1. Water Storage Rates
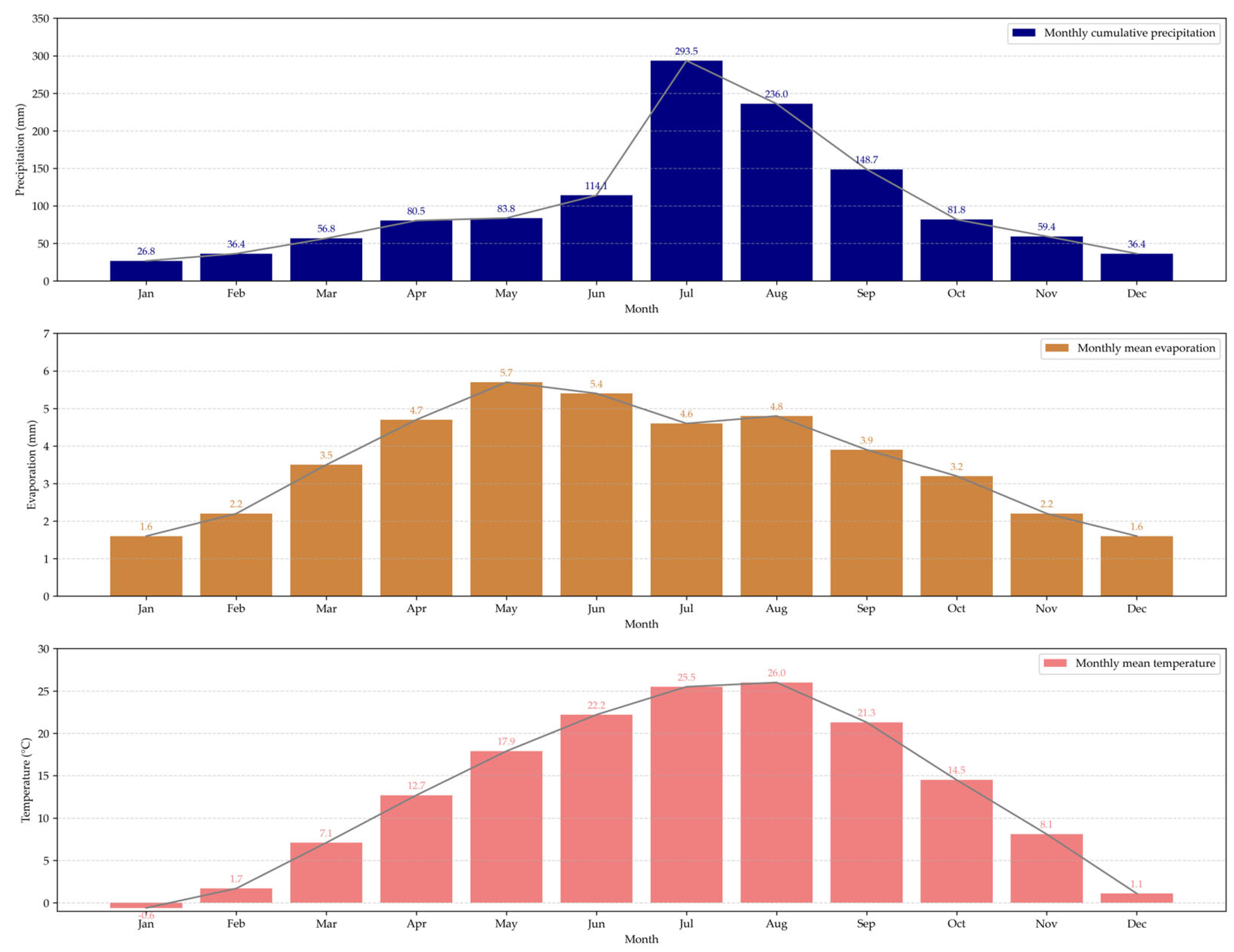
3.1.2. Meteorological Data
3.1.3. Inflow and Outflow
3.2. Water Storage Rates Prediction
3.2.1. Comparison of AI Models for Reservoir Storage Rates
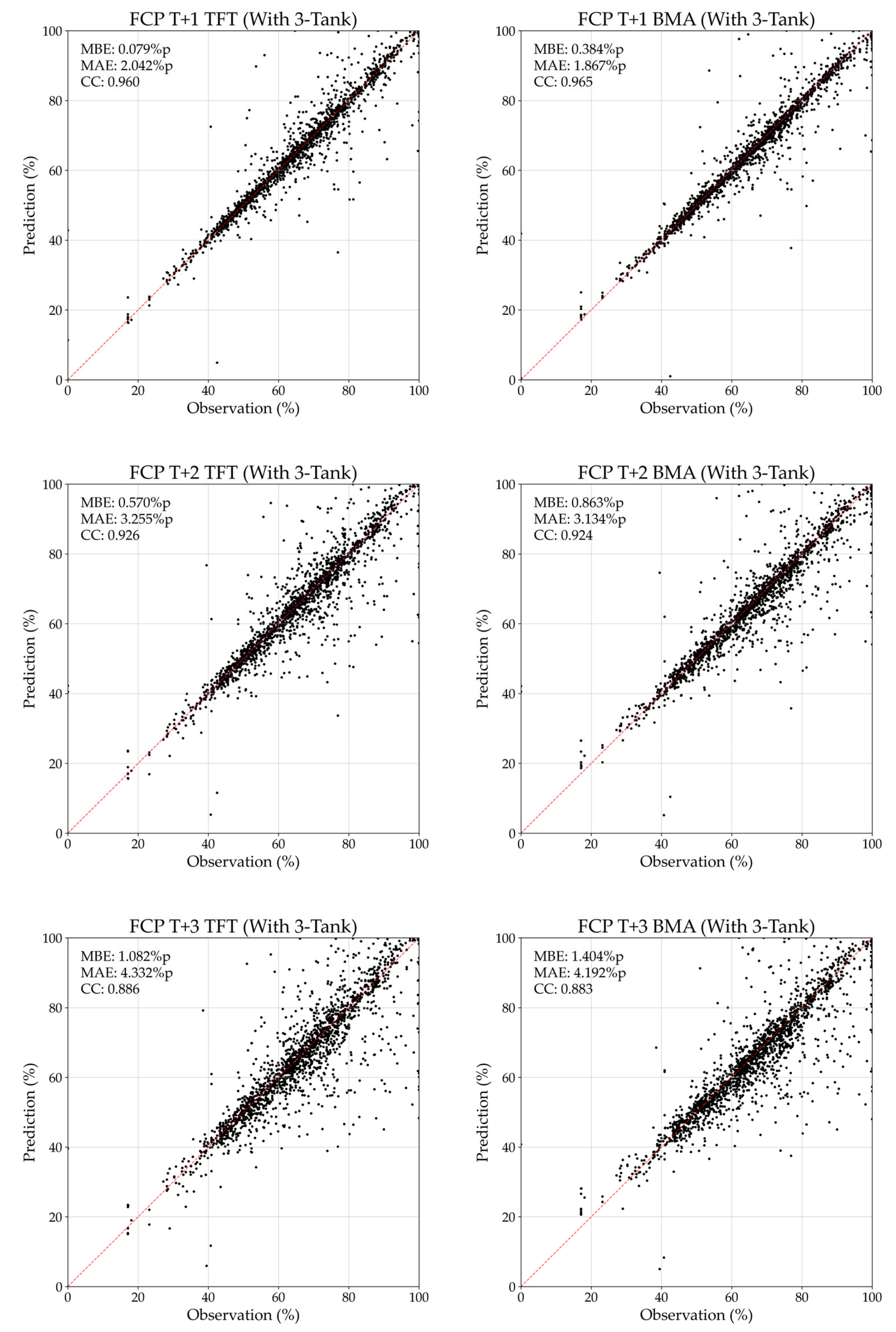
3.2.2. Comparison of AI Models for Flood Control Period
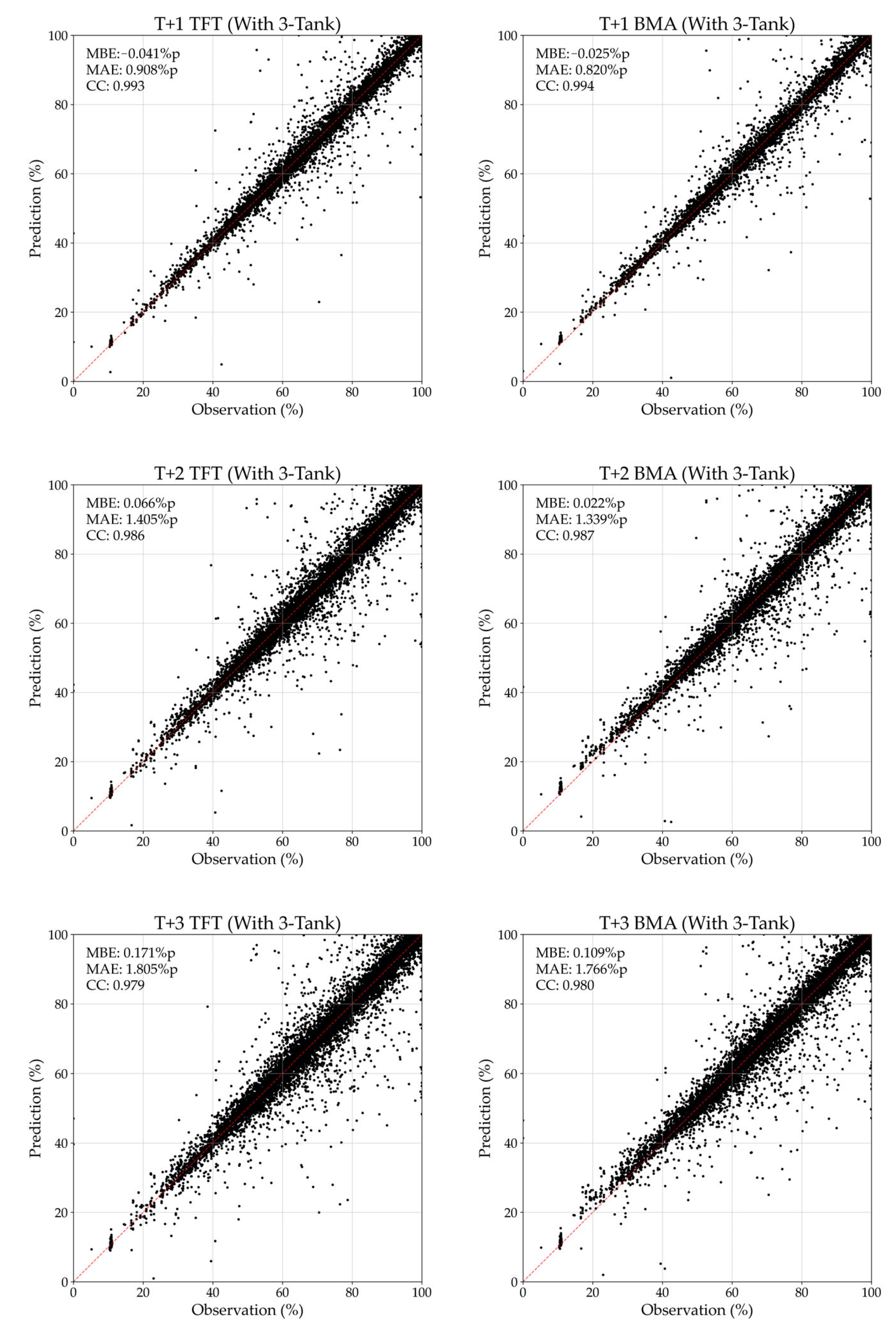
3.3. BMA Ensemble
3.4. Feature Importance
4. Discussion
4.1. Effect of BMA Ensemble
4.2. Roles of Inflow and Outflow Variables
4.3. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Reservoir Operation Rule
- In crop-growing periods, reservoir water is released only to provide the irrigation water supply. The crop-growing period consists of the interruption and drawdown periods.
- In the interruption period, irrigation water supply stops even when it is the middle of the crop-growing period (zero-outflow period).
- In the drawdown periods, reservoir water is released through the drainage spillway to supply irrigation water for the downstream areas.
- When the reservoir level decreases below the dead level, irrigation water supply stops (zero-outflow period).
- In the flood control period, the principal spillway release is made to accommodate space for excess water inflow to precent the reservoir water level from exceeding the flood-limited water level.
- When the irrigation periods overlap with the flood control periods, priority is given to flood control in reservoir operations; thus, irrigation water supply is released only when the reservoir water level drops below the flood-limited water level to protect downstream areas from flooding.
- In the non-flood control and non-crop-growing periods, the reservoir collects inflow from its upstream drainage areas until its water level reaches the normal pool water level for water supply during the next growing period.
- In the non-flood control period, when reservoir water level exceeds the normal pool water level, the surcharge water is discharged through the normal pool spillway.
References
- Kim, W.; Choi, S.; Kang, S.; Woo, S. Assessment of Future Water Security under Climate Change: Practical Water Allocation Scenarios in a Drought-Prone Watershed in South Korea. Water 2024, 16, 2933. [Google Scholar] [CrossRef]
- Ciampittiello, M.; Marchetto, A.; Boggero, A. Water Resources Management under Climate Change: A Review. Sustainability 2024, 16, 3590. [Google Scholar] [CrossRef]
- Bae, H.; Ji, H.; Lim, Y.; Ryu, Y.; Kim, M.; Kim, B. Characteristics of drought propagation in South Korea: Relationship between meteorological, agricultural, and hydrological droughts. Nat. Hazards 2019, 99, 1–16. [Google Scholar] [CrossRef]
- Noh, S.; Lee, G.; Kim, B.; Jo, J.; Woo, D. Climate change impact analysis on water supply reliability and flood risk using combined rainfall-runoff and reservoir operation modeling: Hapcheon-Dam catchment case. J. Korea Water Resour. Assoc. 2023, 56, 765–774. [Google Scholar] [CrossRef]
- Yi, S.; Yi, J. Reservoir-based flood forecasting and warning: Deep learning versus machine learning. Appl. Water Sci. 2024, 14, 237. [Google Scholar] [CrossRef]
- Cho, G.; Ahmad, M.J.; Choi, K. Water Supply Reliability of Agricultural Reservoirs under Varying Climate and Rice Farming Practices. Water 2021, 13, 2988. [Google Scholar] [CrossRef]
- Song, J.; Kang, M.; Song, I.; Jun, S. Water Balance in Irrigation Reservoirs Considering Flood Control and Irrigation Efficiency Variation. J. Irrig. Drain. Eng. 2016, 142, 04016003. [Google Scholar] [CrossRef]
- Wurbs, R.A. Reservoir-system simulation and optimization models. J. Water Resour. Plan. Manag. 1993, 119, 455–472. [Google Scholar] [CrossRef]
- Bengtsson, L.; Malm, J. Using rainfall-runoff modeling to interpret lake level data. J. Paleolimnol. 1997, 18, 235–248. [Google Scholar] [CrossRef]
- Wagener, T.; Wheater, H.; Gupta, H.V. Rainfall-Runoff Modelling in Gauged and Ungauged Catchments; Imperial College Press: London, UK, 2004; pp. 119–183. ISBN 1-86094-466-3. [Google Scholar]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell Press: Oxford, UK, 2012; ISBN 978-0-470-71459-1. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef]
- Singh, V.P.; Woolhiser, D.A. Mathematical modeling of watershed hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef]
- Gupta, H.V.; Wagener, T.; Liu, Y. Reconciling theory with observations: Elements of a diagnostic approach to model evaluation. Hydrol. Process. 2008, 22, 3802–3813. [Google Scholar] [CrossRef]
- Irvine, K.N.; Eberhardt, A.J. Multiplicative, Seasonal Arima Models for Lake Erie and Lake Ontario Water Levels1. J. Am. Water Resour. Assoc. 2007, 28, 385–396. [Google Scholar] [CrossRef]
- Das, M.; Ghosh, S.K.; Chowdary, V.M.; Saikrishnaveni, A.; Sharma, R.K. A Probabilistic Nonlinear Model for Forecasting Daily Water Level in Reservoir. Water Resour. Manag. 2016, 30, 3107–3122. [Google Scholar] [CrossRef]
- Ahn, T.; Lee, J.; Lee, J.; Yi, J.; Yoon, Y. A reservoir operation plan coupled with storage forecasting models in existing agricultural reservoir. J. Korea Water Resour. Assoc. 2004, 37, 77–86. [Google Scholar] [CrossRef]
- Kovvuri, A.R.; Uppalapati, P.J.; Bonthu, S.; Kandula, N.R. Water level forecasting in reservoirs using time series analysis–auto ARIMA model. In Proceedings of the International Conference on Cognitive Computing and Cyber Physical Systems (IC4S 2022), Ghaziabad, Indea, 24–26 November 2022; pp. 192–200. [Google Scholar]
- Khan, M.S.; Coulibaly, P. Application of support vector machine in lake water level prediction. J. Hydrol. Eng. 2006, 11, 199–205. [Google Scholar] [CrossRef]
- Khai, W.J.; Alraih, M.; Ahmed, A.N.; Fai, C.M.; El-Shafie, A.; El-Shafie, A. Daily forecasting of dam water levels using machine learning. Int. J. Civ. Eng. Technol. 2019, 10, 314–323. [Google Scholar] [CrossRef]
- Hipni, A.; El-shafie, A.; Najah, A.; Karim, O.A.; Hussain, A.; Mukhlisin, M. Daily Forecasting of Dam Water Levels: Comparing a Support Vector Machine (SVM) Model With Adaptive Neuro Fuzzy Inference System (ANFIS). Water Resour. Manag. 2013, 27, 3803–3823. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chang, Y.-T. Adaptive neuro-fuzzy inference system for prediction of water level in reservoir. Adv. Water Resour. 2006, 29, 1–10. [Google Scholar] [CrossRef]
- Valizadeh, N. Daily water level forecasting using adaptive neuro-fuzzy interface system with different scenarios: Klang Gate, Malaysia. Int. J. Phys. Sci. 2011, 6, 7379–7389. [Google Scholar] [CrossRef]
- Shrestha, B.P.; Duckstein, L.; Stakhiv, E.Z. Fuzzy rule-based modeling of reservoir operation. J. Water Resour. Plan. Manag. 1996, 122, 262–269. [Google Scholar] [CrossRef]
- Unes, F. Prediction of dam reservoir volume fluctuations using adaptive neuro fuzzy approach. Eur. J. Eng. Nat. Sci. 2017, 2, 144–148. [Google Scholar]
- Zhang, Y.; Dai, X.; Wan, R.; Yang, G.; Li, B. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47, 69–83. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Moalafhi, D.B.; Anderson, G.; Nkwae, B.; Odirile, P.; Parida, B.P.; Qi, J. Dam Water Level Prediction Using Vector AutoRegression, Random Forest Regression and MLP-ANN Models Based on Land-Use and Climate Factors. Sustainability 2022, 14, 14934. [Google Scholar] [CrossRef]
- Anindita, A.P.; Laksono, P.; Nugraha, I.G.B.B. Dam water level prediction system utilizing Artificial Neural Network Back Propagation: Case study: Ciliwung watershed, Katulampa Dam. In Proceedings of the 2016 International Conference on ICT For Smart Society (ICISS 2016), Surabaya, Indonesia, 20–21 July 2016; pp. 16–21. [Google Scholar]
- Nwobi-Okoye, C.C.; Igboanugo, A.C. Predicting water levels at Kainji Dam using artificial neural networks. Niger. J. Technol. 2013, 32, 129–136. [Google Scholar]
- Seo, Y.; Choi, E.; Yeo, W. Reservoir Water Level Forecasting Using Machine Learning Models. J. Korean Soc. Agric. Eng. 2017, 59, 97–110. [Google Scholar] [CrossRef]
- Li, K.; Wan, D.; Zhu, Y.; Yao, C.; Yu, Y.; Si, C.; Ruan, X. The applicability of ASCS_LSTM_ATT model for water level prediction in small- and medium-sized basins in China. J. Hydroinform. 2020, 22, 1693–1717. [Google Scholar] [CrossRef]
- Nie, Q.; Wan, D.; Wang, R. CNN-BiLSTM water level prediction method with attention mechanism. J. Phys. Conf. Ser. 2021, 2078, 12–32. [Google Scholar] [CrossRef]
- Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Baba, D. Convolutional Neural Network Coupled with a Transfer-Learning Approach for Time-Series Flood Predictions. Water 2019, 12, 96. [Google Scholar] [CrossRef]
- Kusudo, T.; Yamamoto, A.; Kimura, M.; Matsuno, Y. Development and Assessment of Water-Level Prediction Models for Small Reservoirs Using a Deep Learning Algorithm. Water 2021, 14, 55. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Z.; Van Thé, J.G.; Yang, S.X.; Gharabaghi, B. Flood Forecasting Using Hybrid LSTM and GRU Models with Lag Time Preprocessing. Water 2023, 15, 3982. [Google Scholar] [CrossRef]
- Joh, S.; Lee, Y. Prediction of water storage rate for agricultural reservoirs using univariate and multivariate LSTM models. Korean J. Remote Sens. 2023, 39, 1125–1134. [Google Scholar] [CrossRef]
- Xie, M.; Shan, K.; Zeng, S.; Wang, L.; Gong, Z.; Wu, X.; Yang, B.; Shang, M. Combined Physical Process and Deep Learning for Daily Water Level Simulations Across Multiple Sites in the Three Gorges Reservoir, China. Water 2023, 15, 3191. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L.; Zhang, Y.; Yao, Y.; Wang, R.; Dai, Y. Water-Level Prediction Analysis for the Three Gorges Reservoir Area Based on a Hybrid Model of LSTM and Its Variants. Water 2024, 16, 1227. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- Song, J.; Her, Y.; Kang, M. Estimating Reservoir Inflow and Outflow from Water Level Observations Using Expert Knowledge: Dealing with an Ill-Posed Water Balance Equation in Reservoir Management. Water Resour. Res. 2022, 58, e2020WR028183. [Google Scholar] [CrossRef]
- Available online: https://www.data.go.kr/data/15099919/openapi.do (accessed on 16 October 2025).
- Available online: https://www.data.go.kr/data/15099051/openapi.do (accessed on 16 October 2025).
- Bengio, S.; Vinyals, O.; Jaitly, N.; Shazeer, N. Scheduled sampling for sequence prediction with recurrent neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28. [Google Scholar]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2021, 379, 20200209. [Google Scholar] [CrossRef]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Kim, M.; Lee, W.K.; Son, Y.; Yoo, S.; Choi, G.M.; Chung, D.J. Assessing the impacts of topographic and climatic factors on radial growth of major forest forming tree species of South Korea. For. Ecol. Manag. 2017, 404, 269–279. [Google Scholar] [CrossRef]
- Wook, P.; Jong, J. Reservoir water monitoring system with automatic level meter. Korean Natl. Comm. Irrig. Drain. 2005, 12, 60–68. [Google Scholar]
- Available online: https://www.data.go.kr/data/15059093/openapi.do (accessed on 16 October 2025).
- Fu, G.; Liu, C.; Chen, S.; Hong, J. Investigating the conversion coefficients for free water surface evaporation of different evaporation pans. Hydrol. Process. 2004, 18, 2247–2262. [Google Scholar] [CrossRef]
- Habets, F.; Molenat, J.; Carluer, N.; Douez, O.; Leenhardt, D. The cumulative impacts of small reservoirs on hydrology: A review. Sci. Total Environ. 2018, 643, 850–867. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Her, Y.; Park, J.; Kang, M. Exploring parsimonious daily rainfall-runoff model structure using the hyperbolic tangent function and Tank model. J. Hydrol. 2019, 574, 574–587. [Google Scholar] [CrossRef]
- Vedula, S.; Kumar, D.N. An Integrated Model for Optimal Reservoir Operation for Irrigation of Multiple Crops. Water Resour. Res. 1996, 32, 1101–1108. [Google Scholar] [CrossRef]
- Dang, T.D.; Chowdhury, A.F.M.K.; Galelli, S. On the representation of water reservoir storage and operations in large-scale hydrological models: Implications on model parameterization and climate change impact assessments. Hydrol. Earth Syst. Sci. 2020, 24, 397–416. [Google Scholar] [CrossRef]
- Dessie, M.; Verhoest, N.E.C.; Pauwels, V.R.N.; Adgo, E.; Deckers, J.; Poesen, J.; Nyssen, J. Water balance of a lake with floodplain buffering: Lake Tana, Blue Nile Basin, Ethiopia. J. Hydrol. 2015, 522, 174–186. [Google Scholar] [CrossRef]
- Chen, S.-K.; Chen, R.-S.; Yang, T.-Y. Application of a tank model to assess the flood-control function of a terraced paddy field. Hydrol. Sci. J. 2014, 59, 1020–1031. [Google Scholar] [CrossRef]
- Fumikazu, N.; Toshisuke, M.; Yoshio, H.; Hiroshi, T.; Kimihito, N. Evaluation of water resources by snow storage using water balance and tank model method in the Tedori River basin of Japan. Paddy Water Environ. 2011, 11, 113–121. [Google Scholar] [CrossRef]
- Yokoo, Y.; Kazama, S.; Sawamoto, M.; Nishimura, H. Regionalization of lumped water balance model parameters based on multiple regression. J. Hydrol. 2001, 264, 209–222. [Google Scholar] [CrossRef]
- Atkinson, S.E.; Woods, R.A.; Sivapalan, M. Climate and landscape controls on water balance model complexity over changing timescales. Water Resour. Res. 2002, 38, 50-1–50-17. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Shin, M.J.; Kim, C.S. Assessment of the suitability of rainfall–runoff models by coupling performance statistics and sensitivity analysis. Hydrol. Res. 2017, 48, 1192–1213. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hochreiter, S.; Bengio, Y.; Frasconi, P.; Schmidhuber, J. Gradient flow in recurrent nets: The difficulty of learning long-term dependencies. In A Field Guide to Dynamical Recurrent Neural Networks; IEEE Press: Piscataway, NJ, USA, 2001; pp. 237–243. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014. [Google Scholar] [CrossRef]
- Yin, W.; Kann, K.; Yu, M.; Schütze, H. Comparative study of CNN and RNN for natural language processing. arXiv 2017. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian model averaging. Water Resour. Res. 2007, 43, W01411. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Kumar Biswas, N.; Hossain, F. A Multidecadal Analysis of reservoir storage change in developing regions. J. Hydrometeorol. 2022, 23, 71–85. [Google Scholar] [CrossRef]
- Bonnema, M.; David, C.H.; Frasson, R.P.D.M.; Oaida, C.; Yun, S.H. The global surface area variations of lakes and reservoirs as seen from satellite remote sensing. Geophys. Res. Lett. 2022, 49, e2022GL098987. [Google Scholar] [CrossRef]
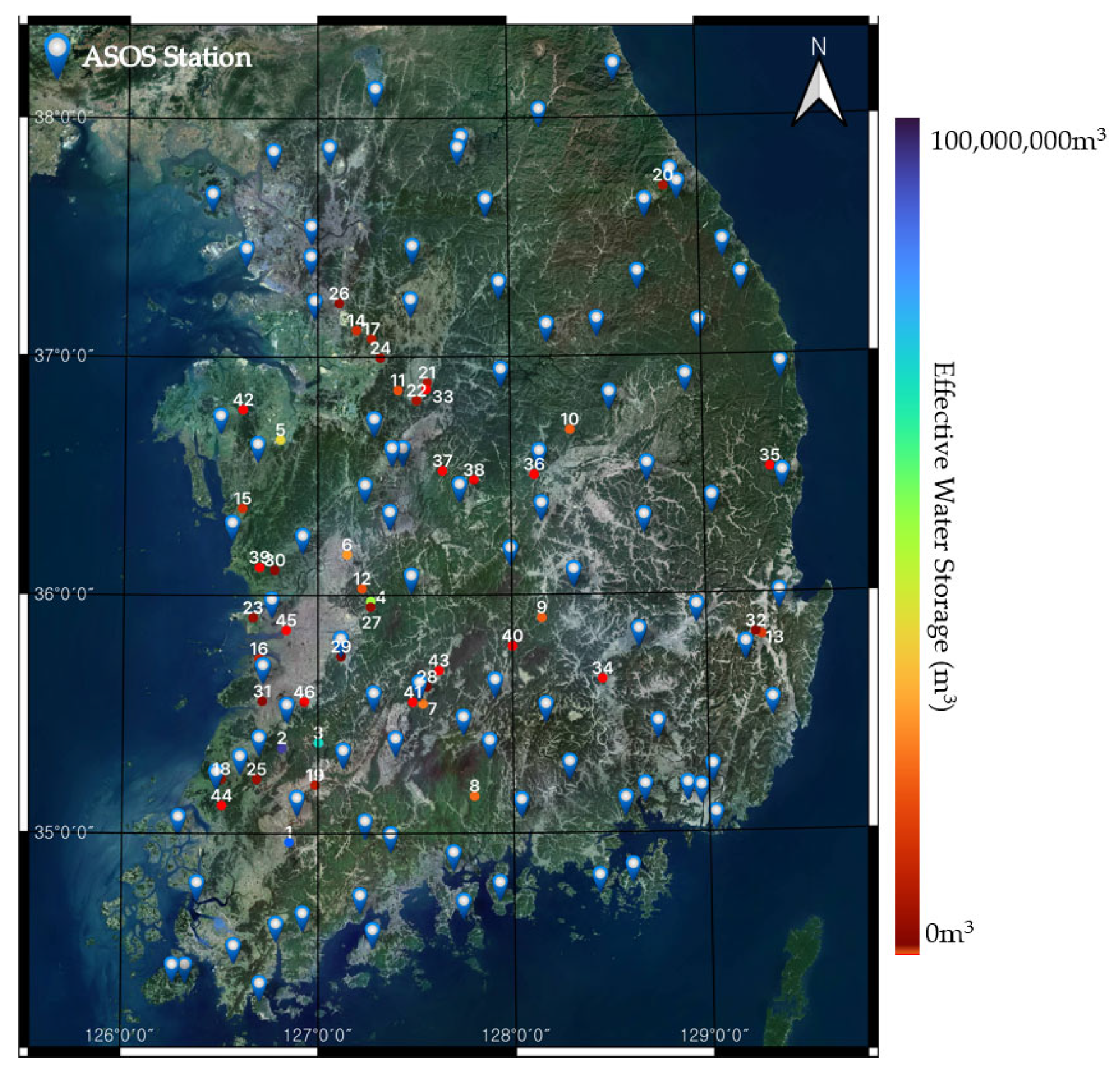

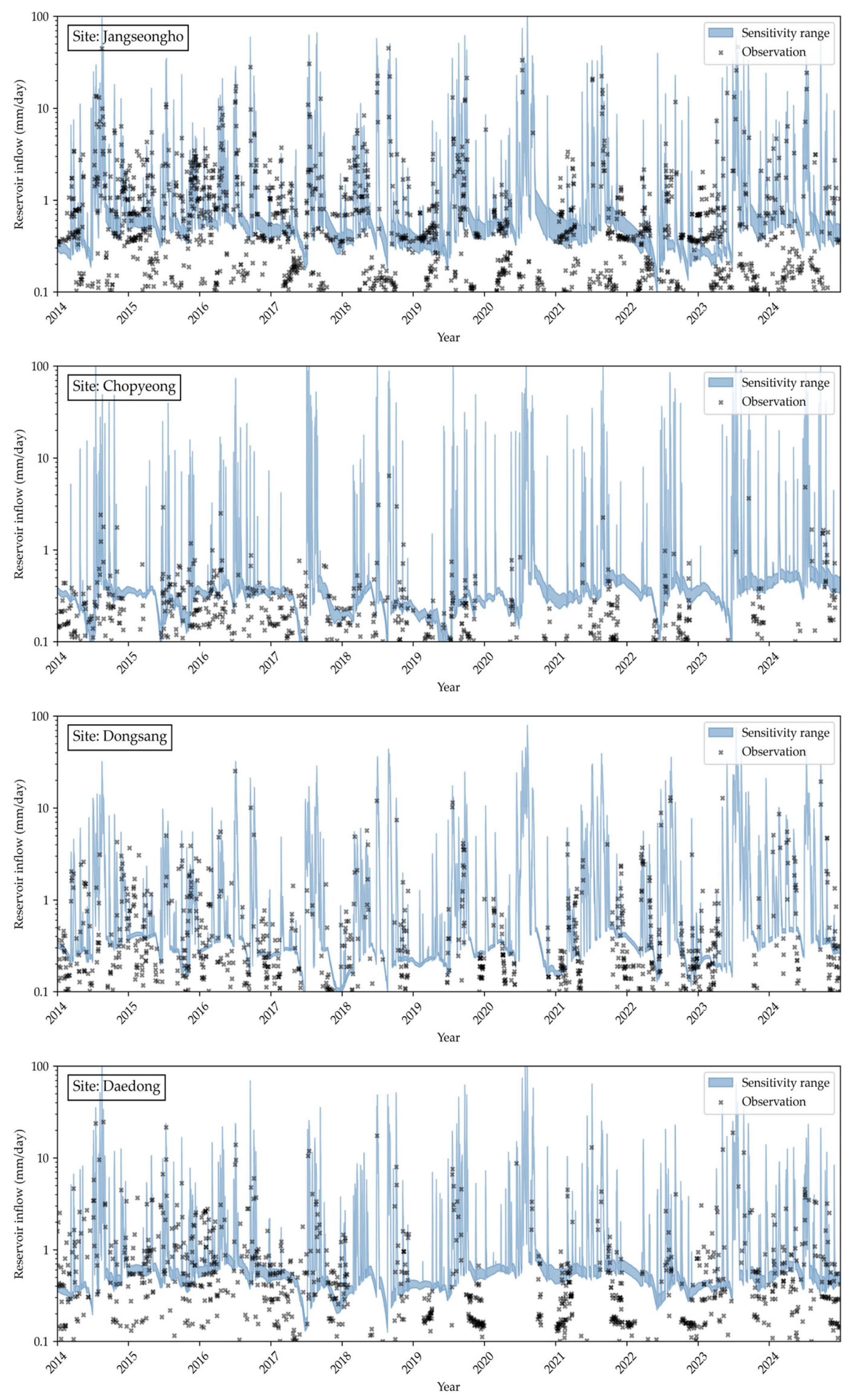

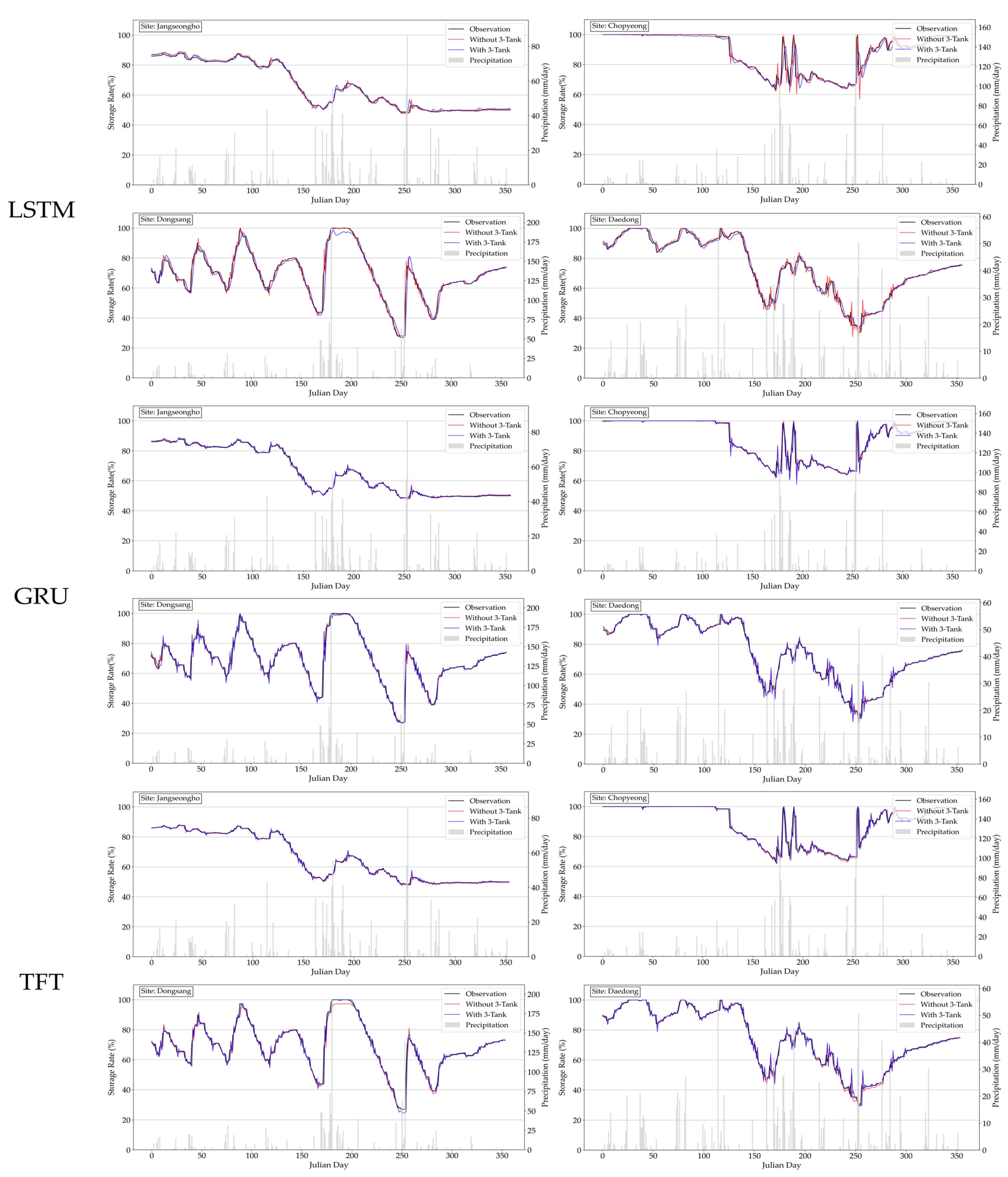

| No. | Reservoir | Latitude | Longitude | Effective Water Storage (m3) |
|---|---|---|---|---|
| 1 | Najuho | 34.964 | 126.852 | 107,000,000 |
| 2 | Jangseongho | 35.359 | 126.814 | 99,707,200 |
| 3 | Damyangho | 35.382 | 127.001 | 76,669,600 |
| 4 | Daea | 35.982 | 127.301 | 57,688,000 |
| 5 | Yedang | 36.653 | 126.805 | 46,070,200 |
| 6 | Tapjeong | 36.170 | 127.151 | 34,940,000 |
| 7 | Donghwa | 35.544 | 127.539 | 31,348,000 |
| 8 | Hadong | 35.156 | 127.800 | 30,336,900 |
| 9 | Seongju | 35.903 | 128.154 | 28,150,000 |
| 10 | Gyeongcheon (Gyeongsangbuk-do) | 36.691 | 128.311 | 27,200,000 |
| 11 | Baekgok | 36.860 | 127.417 | 26,372,000 |
| 12 | Gyeongcheon (Jeonrabuk-do) | 36.028 | 127.227 | 25,346,000 |
| 13 | Deokdong | 35.823 | 129.285 | 22,537,100 |
| 14 | Idong | 37.111 | 127.201 | 20,906,000 |
| 15 | Cheongcheon | 36.365 | 126.610 | 20,753,100 |
| 16 | Cheongho | 35.734 | 126.697 | 18,045,000 |
| 17 | Gosam | 37.076 | 127.281 | 15,217,000 |
| 18 | Bulgap | 35.229 | 126.506 | 15,200,000 |
| 19 | Gwangjuho | 35.204 | 126.985 | 15,198,000 |
| 20 | Obong | 37.710 | 128.819 | 14,329,100 |
| 21 | Maengdong | 36.892 | 127.57 | 13,910,000 |
| 22 | Chopyeong | 36.817 | 127.514 | 13,853,200 |
| 23 | Okgu | 35.906 | 126.666 | 12,826,100 |
| 24 | Geumgwang | 36.996 | 127.326 | 12,047,000 |
| 25 | Suyang | 35.228 | 126.686 | 11,834,100 |
| 26 | Giheung | 37.225 | 127.111 | 11,630,000 |
| 27 | Dongsang | 35.982 | 127.301 | 11,241,000 |
| 28 | Yongrim | 35.616 | 127.559 | 11,188,000 |
| 29 | Gui | 35.744 | 127.119 | 10,878,000 |
| 30 | Dongbu | 36.106 | 126.777 | 10,733,800 |
| 31 | Heungdeok | 35.556 | 126.714 | 9,946,000 |
| 32 | Bomun | 35.834 | 129.253 | 9,834,000 |
| 33 | Wonnam | 36.864 | 127.564 | 8,690,200 |
| 34 | Dalchang | 35.645 | 128.462 | 8,649,000 |
| 35 | Myogok | 36.526 | 129.346 | 8,441,000 |
| 36 | Otae | 36.504 | 128.123 | 8,291,000 |
| 37 | Gung | 36.521 | 127.647 | 8,222,000 |
| 38 | Biryong | 36.482 | 127.809 | 8,163,000 |
| 39 | Seobu | 36.117 | 126.699 | 7,989,000 |
| 40 | Gabuk | 35.785 | 128.001 | 7,979,000 |
| 41 | Jangnam | 35.552 | 127.486 | 7,920,800 |
| 42 | Gopung | 36.780 | 126.610 | 7,821,800 |
| 43 | Daegok | 35.684 | 127.622 | 7,712,000 |
| 44 | Daedong | 35.118 | 126.507 | 7,502,100 |
| 45 | Neung | 35.854 | 126.836 | 7,315,600 |
| 46 | Sucheong | 35.553 | 126.930 | 7,001,000 |
| Parameter | Physical Meaning | Range |
|---|---|---|
| Side-outlet coefficient for the 1st side outlet in the 1st tank | [0.08, 0.5] | |
| Side-outlet coefficient for the 2nd side outlet in the 1st tank | [0.08, 0.5] | |
| Height of side outlet for the 1st side outlet in the 1st tank (mm) | [5, 60] | |
| Height of side outlet for the 2nd side outlet in the 1st tank (mm) | [20, 110] | |
| Bottom-outlet coefficient for the 1st tank | [0.1, 0.5] | |
| Side-outlet coefficient in the 2nd tank | [0.03, 0.5] | |
| Height of side outlet in the 2nd tank | [0, 20] | |
| Bottom-outlet coefficient for the 2nd tank | [0.01, 0.35] | |
| Side-outlet coefficient in the 3rd tank | [0.003, 0.03] | |
| SECP | Soil evaporation compensation parameter | [0.001, 0.1] |
| Criteria | Equation | Range |
|---|---|---|
| , 1) | ||
| , 1) |
| Month | Average (%) | SD (%p) | MADD (%p) |
|---|---|---|---|
| 1 | 76.9 | 15.3 | 0.17 |
| 2 | 78.5 | 14.9 | 0.19 |
| 3 | 81.1 | 13.2 | 0.25 |
| 4 | 84.4 | 11.1 | 0.29 |
| 5 | 76.2 | 13.2 | 0.80 |
| 6 | 55.0 | 14.0 | 0.79 |
| 7 | 62.4 | 17.9 | 1.25 |
| 8 | 62.5 | 17.7 | 0.97 |
| 9 | 64.7 | 19.0 | 0.74 |
| 10 | 68.9 | 18.1 | 0.36 |
| 11 | 71.0 | 17.1 | 0.23 |
| 12 | 74.4 | 16.0 | 0.20 |
| Reservoir | Inflow (mm/Day) | Outflow (mm/Day) | |
|---|---|---|---|
| Zero Outflow Period | Nonzero Outflow Period | Nonzero Outflow Period | |
| Najuho | 0.658 | 1.192 | 0.595 |
| Jangseongho | 0.499 | 0.905 | 0.447 |
| Damyangho | 0.641 | 1.185 | 0.583 |
| Daea | 0.636 | 0.650 | 0.332 |
| Yedang | 0.301 | 0.927 | 0.517 |
| Tapjeong | 0.322 | 1.037 | 0.557 |
| Donghwa | 0.986 | 1.134 | 0.628 |
| Hadong | 0.478 | 0.644 | 0.316 |
| Seongju | 0.343 | 0.959 | 0.599 |
| Gyeongcheon (Gyeongsangbuk-do) | 0.520 | 1.490 | 0.853 |
| Baekgok | 0.410 | 0.946 | 0.492 |
| Gyeongcheon (Jeonrabuk-do) | 0.400 | 1.039 | 0.563 |
| Deokdong | 0.134 | 0.441 | 0.181 |
| Idong | 0.330 | 0.843 | 0.480 |
| Cheongcheon | 0.421 | 0.787 | 0.371 |
| Cheongho | 0.194 | 0.395 | 0.148 |
| Gosam | 0.405 | 0.563 | 0.296 |
| Bulgap | 0.230 | 0.648 | 0.329 |
| Gwangjuho | 0.285 | 0.611 | 0.285 |
| Obong | 0.436 | 0.765 | 0.531 |
| Maengdong | 0.431 | 0.743 | 0.219 |
| Chopyeong | 0.153 | 0.590 | 0.419 |
| Okgu | 0.398 | 0.614 | 0.201 |
| Geumgwang | 0.365 | 1.206 | 0.621 |
| Suyang | 0.457 | 0.773 | 0.381 |
| Giheung | 0.422 | 1.039 | 0.586 |
| Dongsang | 0.166 | 0.428 | 0.291 |
| Yongrim | 0.568 | 1.285 | 0.648 |
| Gui | 0.173 | 0.756 | 0.445 |
| Dongbu | 0.235 | 0.744 | 0.364 |
| Heungdeok | 0.519 | 1.024 | 0.436 |
| Bomun | 0.113 | 0.232 | 0.111 |
| Wonnam | 0.458 | 0.944 | 0.527 |
| Dalchang | 0.300 | 0.842 | 0.552 |
| Myogok | 0.306 | 0.492 | 0.309 |
| Otae | 0.190 | 0.490 | 0.327 |
| Gung | 0.711 | 0.936 | 0.527 |
| Biryong | 0.648 | 0.867 | 0.461 |
| Seobu | 0.363 | 0.898 | 0.486 |
| Gabuk | 0.292 | 0.761 | 0.430 |
| Jangnam | 0.532 | 1.042 | 0.670 |
| Gopung | 0.494 | 0.782 | 0.445 |
| Daegok | 1.036 | 1.507 | 0.756 |
| Daedong | 0.299 | 0.528 | 0.305 |
| Neung | 0.310 | 0.847 | 0.345 |
| Sucheong | 0.147 | 0.533 | 0.310 |
| Mean | 0.407 | 0.827 | 0.441 |
| Min | 0.113 | 0.232 | 0.111 |
| Max | 1.036 | 1.507 | 0.853 |
| SD | 0.200 | 0.279 | 0.161 |
| Reservoir | Reservoir | |||||
|---|---|---|---|---|---|---|
| Najuho | 0.795 | 0.743 | Geumgwang | 0.764 | 0.698 | |
| Jangseongho | 0.819 | 0.740 | Suyang | 0.815 | 0.615 | |
| Damyangho | 0.787 | 0.792 | Giheung | 0.721 | 0.648 | |
| Daea | 0.864 | 0.735 | Dongsang | 0.794 | 0.701 | |
| Yedang | 0.779 | 0.612 | Yongrim | 0.825 | 0.793 | |
| Tapjeong | 0.745 | 0.651 | Gui | 0.774 | 0.612 | |
| Donghwa | 0.868 | 0.803 | Dongbu | 0.726 | 0.624 | |
| Hadong | 0.846 | 0.899 | Heungdeok | 0.775 | 0.650 | |
| Seongju | 0.930 | 0.703 | Bomun | 0.858 | 0.611 | |
| Gyeongcheon (Gyeongsangbuk-do) | 0.793 | 0.689 | Wonnam | 0.857 | 0.601 | |
| Baekgok | 0.837 | 0.718 | Dalchang | 0.730 | 0.684 | |
| Gyeongcheon (Jeonrabuk-do) | 0.767 | 0.692 | Myogok | 0.760 | 0.792 | |
| Deokdong | 0.711 | 0.648 | Otae | 0.723 | 0.647 | |
| Idong | 0.725 | 0.664 | Gung | 0.831 | 0.806 | |
| Cheongcheon | 0.807 | 0.712 | Biryong | 0.805 | 0.698 | |
| Cheongho | 0.789 | 0.750 | Seobu | 0.707 | 0.630 | |
| Gosam | 0.729 | 0.634 | Gabuk | 0.848 | 0.698 | |
| Bulgap | 0.817 | 0.632 | Jangnam | 0.791 | 0.693 | |
| Gwangjuho | 0.851 | 0.822 | Gopung | 0.838 | 0.824 | |
| Obong | 0.797 | 0.633 | Daegok | 0.866 | 0.781 | |
| Maengdong | 0.871 | 0.721 | Daedong | 0.750 | 0.601 | |
| Chopyeong | 0.708 | 0.601 | Neung | 0.698 | 0.661 | |
| Okgu | 0.848 | 0.771 | Sucheong | 0.624 | 0.601 | |
| Mean | 0.791 | 0.696 | ||||
| Min | 0.624 | 0.601 | ||||
| Max | 0.930 | 0.899 | ||||
| SD | 0.060 | 0.074 | ||||
| Hyperparameters | LSTM | GRU | TFT |
|---|---|---|---|
| Batch size | 64 | 64 | 64 |
| Hidden size | 224 | 224 | 224 |
| Window size | 10 | 10 | 10 |
| Optimizer | Adam | Adam | Adam |
| Learning rate | 0.0001 | 0.0001 | 0.0015 |
| Epoch | 30 | 30 | 20 |
| Dropout | 0.7 | 0.4 | 0.3 |
| Loss Function | MSE Loss | MSE Loss | Quantile Loss |
| Hidden continuous size | NA | NA | 256 |
| Output quantile size | NA | NA | 7 |
| Num Attention head | NA | NA | 4 |
| 3TM Application | Lead Time | AI Model | MBE (%p) | MAE (%p) | CC |
|---|---|---|---|---|---|
| Without 3TM inflow and outflow | t + 1 | LSTM | 0.228 | 1.116 | 0.989 |
| GRU | 0.101 | 1.025 | 0.988 | ||
| TFT | 0.225 | 1.047 | 0.995 | ||
| t + 2 | LSTM | 0.474 | 1.994 | 0.979 | |
| GRU | 0.132 | 1.683 | 0.979 | ||
| TFT | 0.383 | 1.571 | 0.990 | ||
| t + 3 | LSTM | 0.619 | 2.711 | 0.968 | |
| GRU | 0.155 | 2.212 | 0.968 | ||
| TFT | 0.491 | 1.955 | 0.985 | ||
| With 3TM inflow and outflow | t + 1 | LSTM | −0.002 | 0.930 | 0.991 |
| GRU | 0.081 | 0.977 | 0.991 | ||
| TFT | −0.041 | 0.908 | 0.993 | ||
| t + 2 | LSTM | −0.063 | 1.506 | 0.982 | |
| GRU | 0.125 | 1.639 | 0.980 | ||
| TFT | 0.066 | 1.405 | 0.986 | ||
| t + 3 | LSTM | −0.133 | 2.025 | 0.971 | |
| GRU | 0.173 | 2.201 | 0.968 | ||
| TFT | 0.171 | 1.805 | 0.979 |
| 3TM Application | Lead Time | AI Model | MBE (%p) | MAE (%p) | CC |
|---|---|---|---|---|---|
| Without 3TM inflow and outflow | t + 1 | LSTM | −0.328 | 2.314 | 0.925 |
| GRU | −0.278 | 2.394 | 0.923 | ||
| TFT | 0.577 | 2.346 | 0.965 | ||
| t + 2 | LSTM | −1.293 | 3.800 | 0.851 | |
| GRU | −1.137 | 3.747 | 0.849 | ||
| TFT | 1.190 | 3.713 | 0.927 | ||
| t + 3 | LSTM | −2.295 | 5.190 | 0.778 | |
| GRU | −2.037 | 4.904 | 0.778 | ||
| TFT | 1.829 | 4.766 | 0.863 | ||
| With 3TM inflow and outflow | t + 1 | LSTM | −0.389 | 2.055 | 0.934 |
| GRU | −0.831 | 2.134 | 0.933 | ||
| TFT | 0.079 | 2.042 | 0.960 | ||
| t + 2 | LSTM | −1.204 | 3.373 | 0.864 | |
| GRU | −1.848 | 3.718 | 0.850 | ||
| TFT | 0.570 | 3.255 | 0.923 | ||
| t + 3 | LSTM | −1.965 | 4.494 | 0.792 | |
| GRU | −2.823 | 4.518 | 0.775 | ||
| TFT | 1.082 | 4.332 | 0.886 |
| Lead Time | Model with 3TM | MBE (%p) | MAE (%p) | CC |
|---|---|---|---|---|
| t + 1 | TFT | −0.041 | 0.908 | 0.993 |
| BMA | −0.025 | 0.820 | 0.994 | |
| t + 2 | TFT | 0.066 | 1.405 | 0.986 |
| BMA | 0.022 | 1.339 | 0.987 | |
| t + 3 | TFT | 0.171 | 1.805 | 0.979 |
| BMA | 0.109 | 1.766 | 0.980 |
| Lead Time | Model with 3TM | MBE (%p) | MAE (%p) | CC |
|---|---|---|---|---|
| t + 1 | TFT | 0.079 | 2.042 | 0.960 |
| BMA | 0.384 | 1.867 | 0.965 | |
| t + 2 | TFT | 0.570 | 3.255 | 0.926 |
| BMA | 0.863 | 3.134 | 0.924 | |
| t + 3 | TFT | 1.082 | 4.332 | 0.886 |
| BMA | 1.404 | 4.192 | 0.883 |
| Rank | Variable | Feature Importance (%) | Category |
|---|---|---|---|
| 1 | Past Reservoir Storage Rate | 43.42% | Water source |
| 2 | Inflow | 11.24% | Water source |
| 3 | Outflow | 10.78% | Water source |
| 4 | Precipitation | 9.50% | Meteorology |
| 5 | Relative Time Index | 9.15% | Temporal trend |
| 6 | Julian Day | 8.07% | Temporal trend |
| 7 | Evaporation | 7.84% | Meteorology |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Joh, J.S.-u.; Choi, M.; Kim, T.; Cho, J.; Lee, Y. AI-Based Time-Series Ensemble Approach Coupled with a Hydrological Model for Reservoir Storage Prediction in Korea. Water 2025, 17, 3296. https://doi.org/10.3390/w17223296
Park J, Joh JS-u, Choi M, Kim T, Cho J, Lee Y. AI-Based Time-Series Ensemble Approach Coupled with a Hydrological Model for Reservoir Storage Prediction in Korea. Water. 2025; 17(22):3296. https://doi.org/10.3390/w17223296
Chicago/Turabian StylePark, Jaeseong, Jason Sung-uk Joh, Minha Choi, Taejung Kim, Jaeil Cho, and Yangwon Lee. 2025. "AI-Based Time-Series Ensemble Approach Coupled with a Hydrological Model for Reservoir Storage Prediction in Korea" Water 17, no. 22: 3296. https://doi.org/10.3390/w17223296
APA StylePark, J., Joh, J. S.-u., Choi, M., Kim, T., Cho, J., & Lee, Y. (2025). AI-Based Time-Series Ensemble Approach Coupled with a Hydrological Model for Reservoir Storage Prediction in Korea. Water, 17(22), 3296. https://doi.org/10.3390/w17223296







