Intelligent Scheduling Method for Cascade Reservoirs Driven by Dual Optimization of Harris Hawks and Marine Predators
Abstract
1. Introduction
- (1)
- SPM chaotic mapping is introduced for population initialization to enhance population diversity, expand the search range, and significantly improve the quality of initial solutions.
- (2)
- A dual-period fluctuation decay strategy is introduced to control parameters for balancing the algorithm’s exploration and exploitation capabilities, ultimately achieving effective balance between global search and local fine search.
- (3)
- This study proposes HHONMPA, a hybrid algorithm whose core combines the predatory behavior of Harris hawks and the search mechanism of marine predators, integrating HHO’s powerful local search capability with MPA’s global search ability.
- (4)
- Comparative experiments on 12 CEC2017 test functions demonstrate that HHONMPA outperforms five comparative algorithms in optimization performance.
- (5)
- In the optimization problem of four cascaded reservoirs in the Jinsha River basin, compared with HHO and MPA, HHONMPA achieves faster convergence speed and higher accuracy, highlighting its tremendous potential in practical engineering applications.
2. Materials and Methods
2.1. Harris Hawk Optimization Algorithm
2.1.1. Exploration Phase
2.1.2. Exploitation Phase
2.2. Marine Predators Algorithm
2.2.1. Exploration Phase
2.2.2. Exploitation Phase
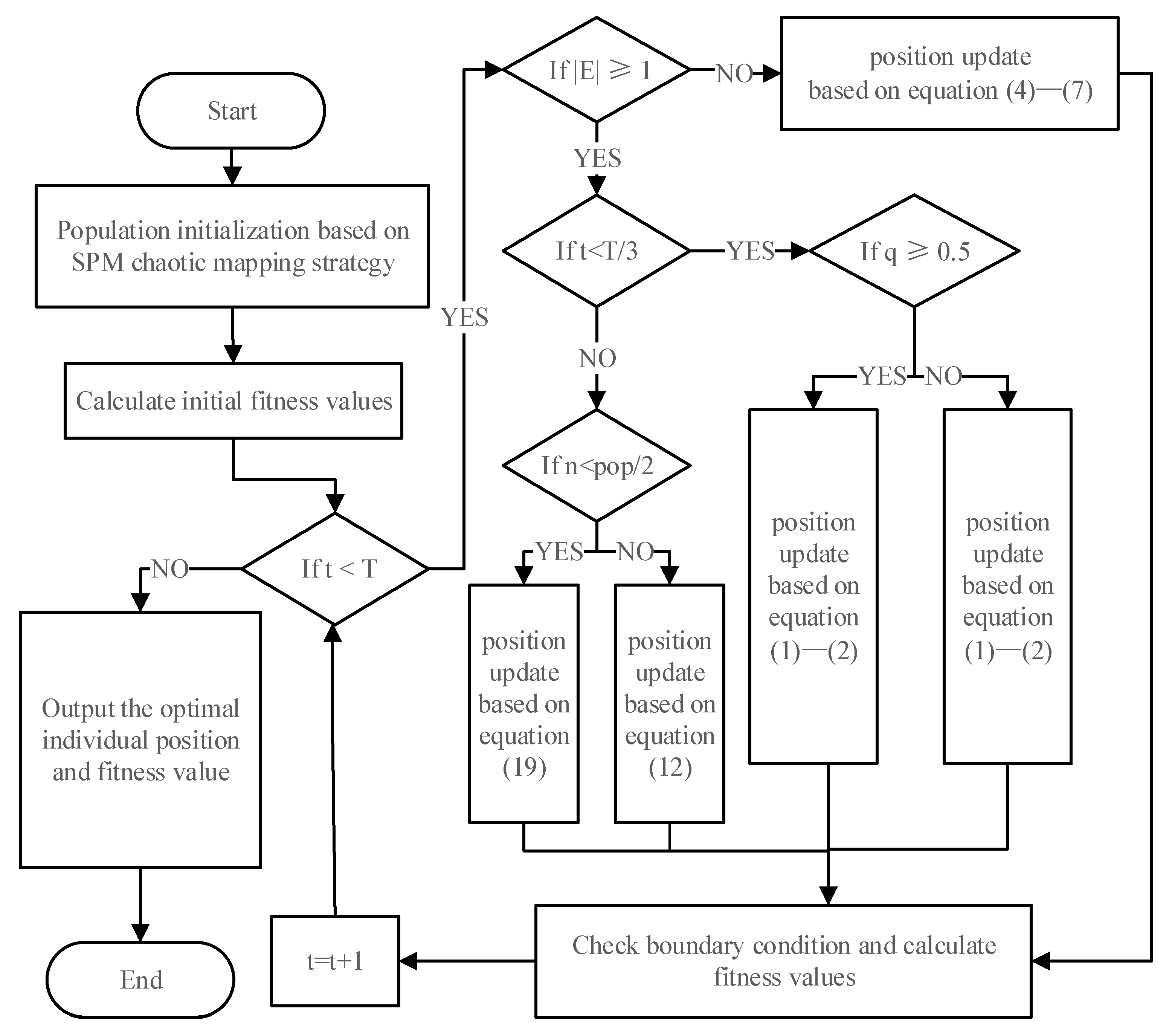
2.3. Proposed HHONMPA Algorithm
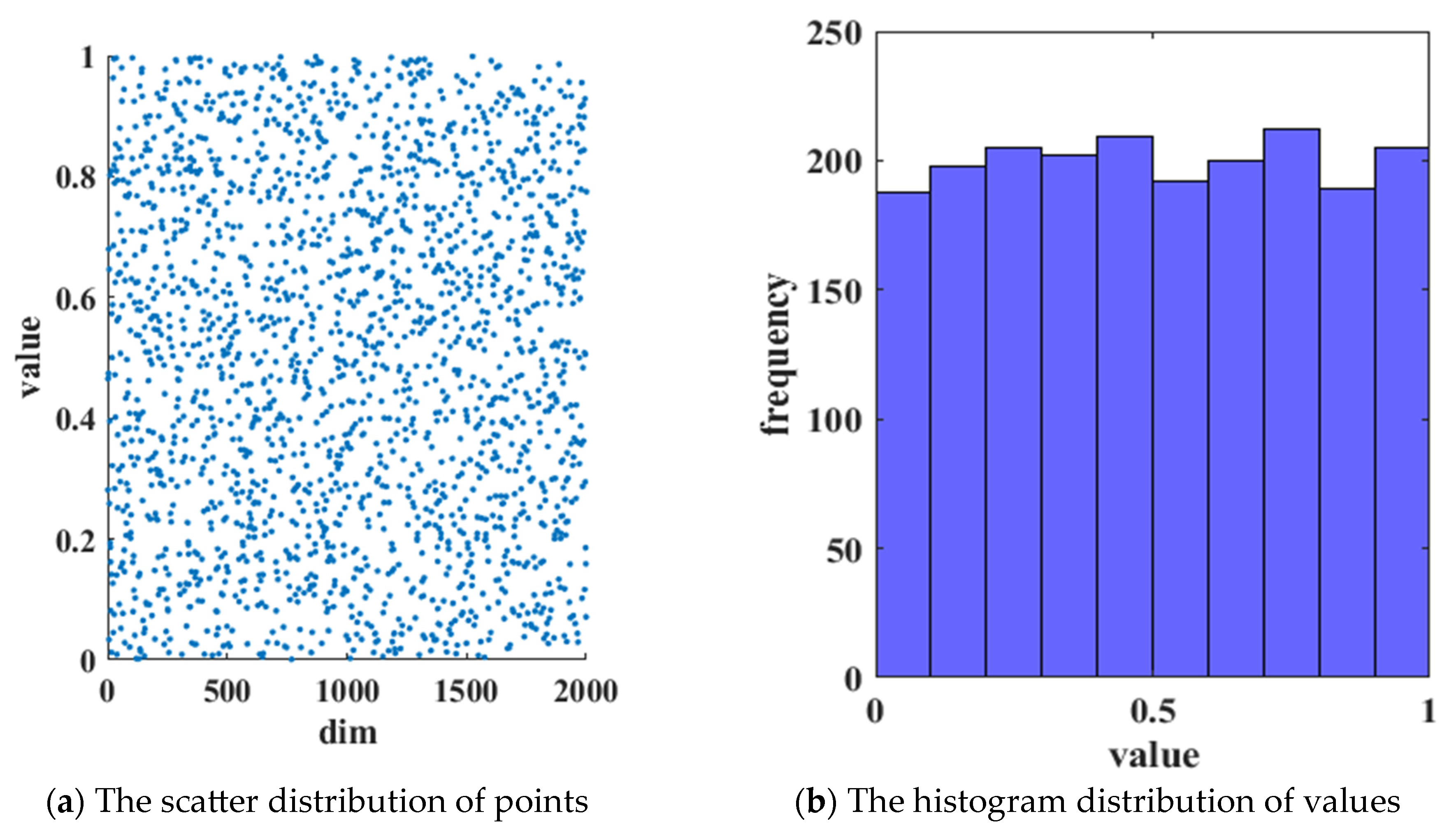
2.3.1. SPM Chaotic Mapping Strategy
2.3.2. Dual-Period Oscillation Attenuation Strategy
2.3.3. Update Rule Combining Levy and Differential Mutation Strategies
2.3.4. HHONMPA
3. Results and Discussion
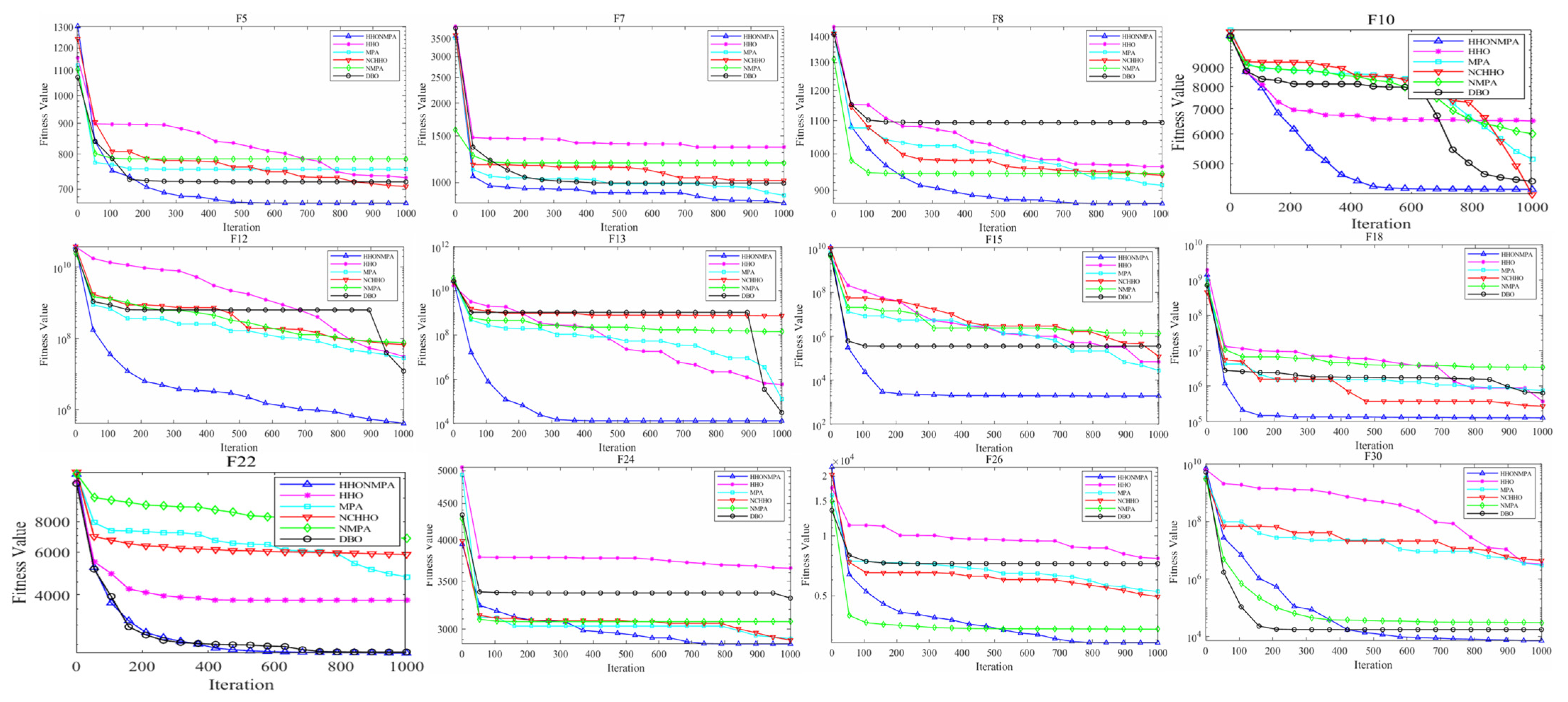
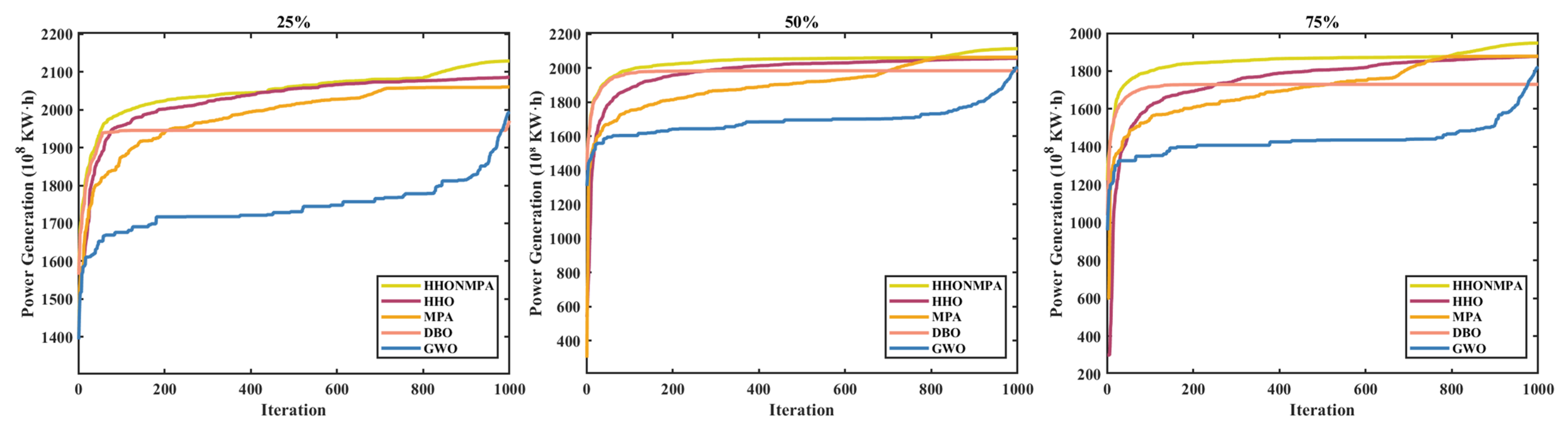
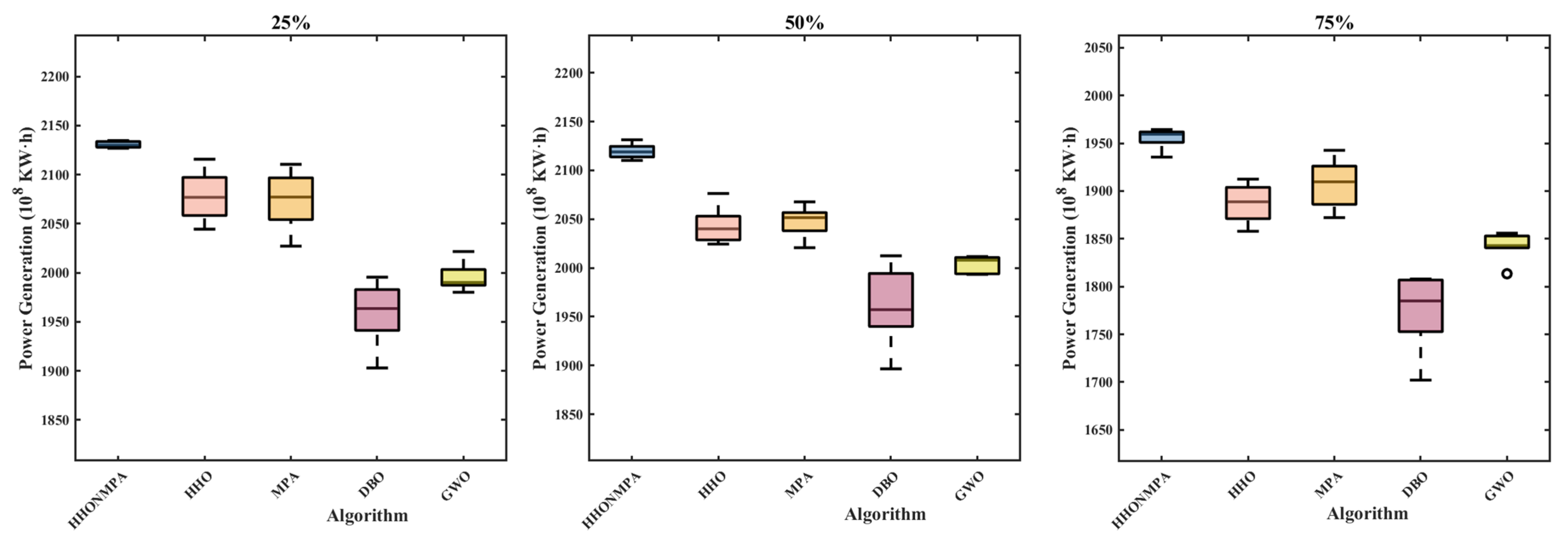
3.1. Algorithm Convergence Validation
3.2. Case Study Analysis of Cascade Reservoir Optimal Operation
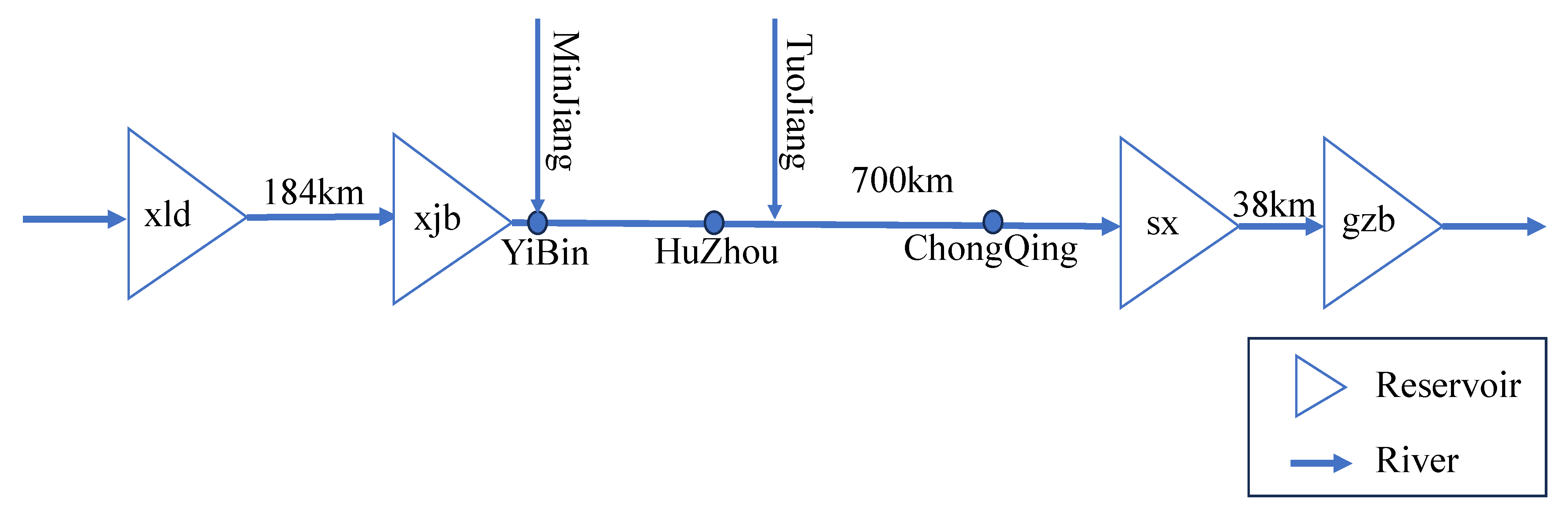
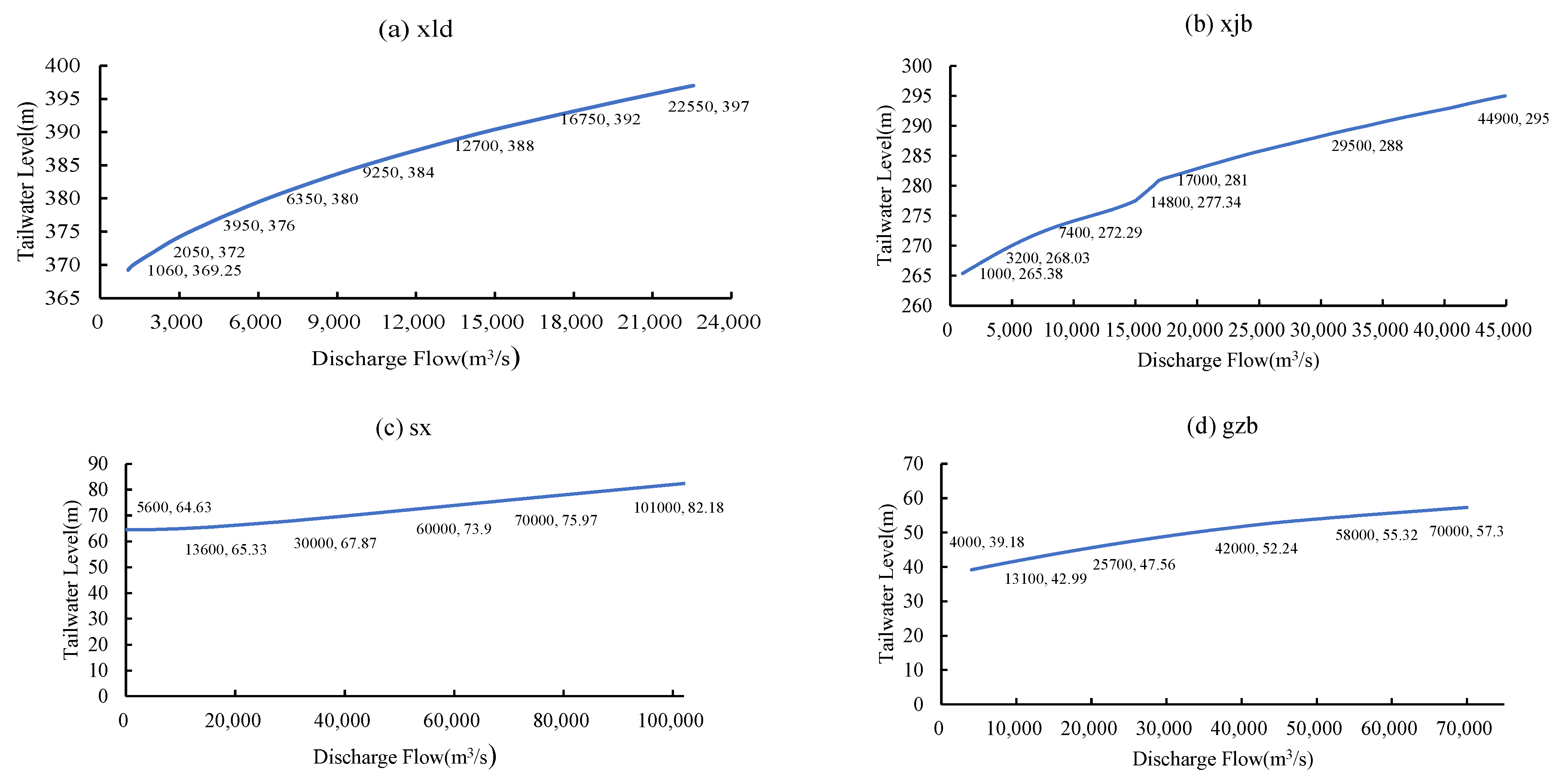
- Study area and cascade reservoir system
- 2.
- Hydrological characteristics and flow propagation
- 3.
- Reservoir technical specifications
- 4.
- Optimization problem formulation
- (1)
- Water Balance Constraints:
- (2)
- Head calculation formula:
- (3)
- Water level constraints:
- (4)
- Reservoir discharge constraints:
- (5)
- Water level fluctuation constraints:
- (6)
- Power output constraints:
- (7)
- initial and final water level constraints:
- (1)
- Inequality constraint handling strategy: Converting constrained optimization problems into unconstrained optimization problems. Inequality constraints mainly include water level constraints, flow rate constraints, and power output constraints.
- (2)
- Equality constraint handling strategy: Converting equality constraints into inequality constraints, then transforming inequality constraints into unconstrained problems. Equality constraints mainly include initial and final water level storage capacity constraints, water balance constraints, etc.
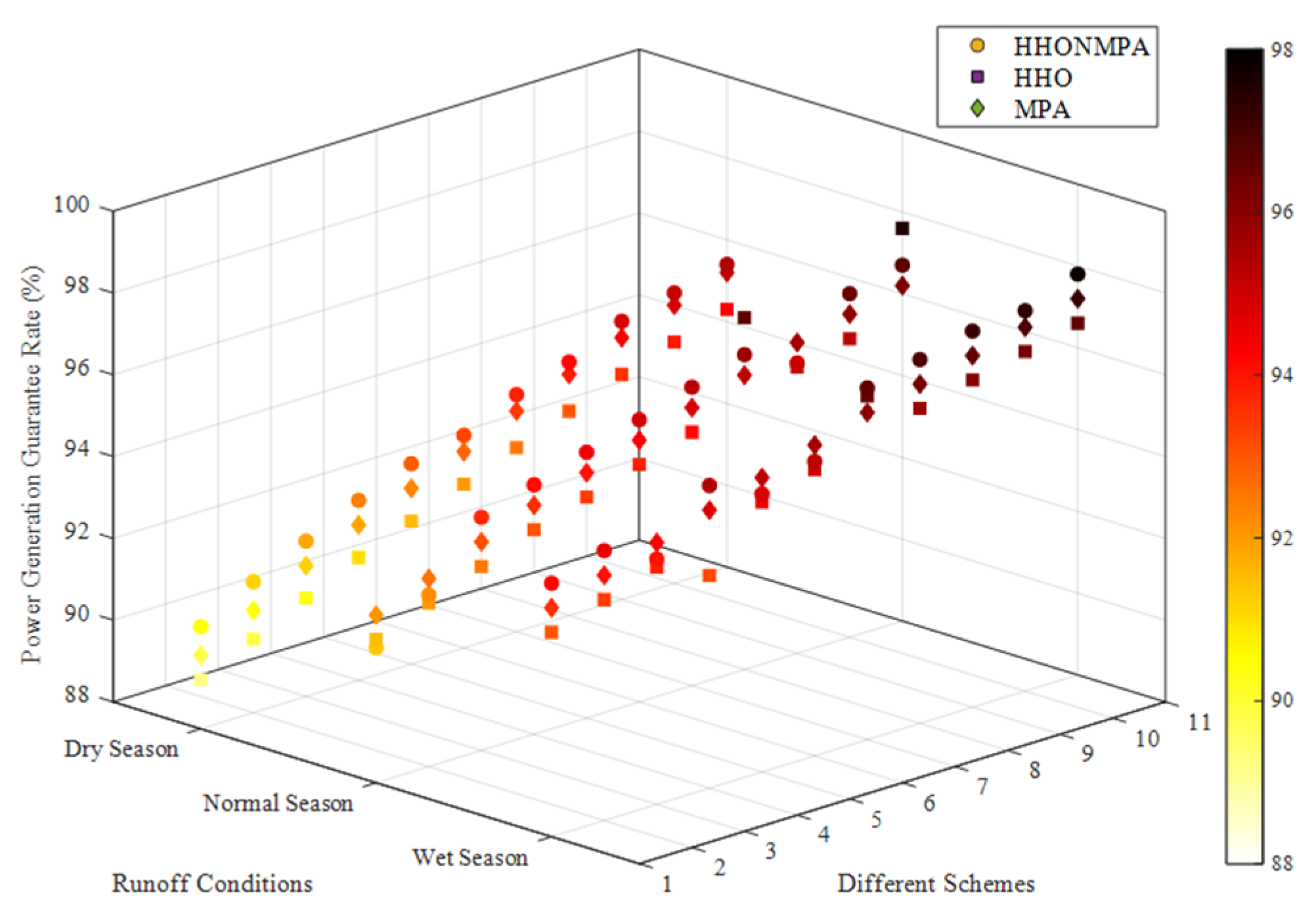
3.2.1. Analysis in Different Typical Year
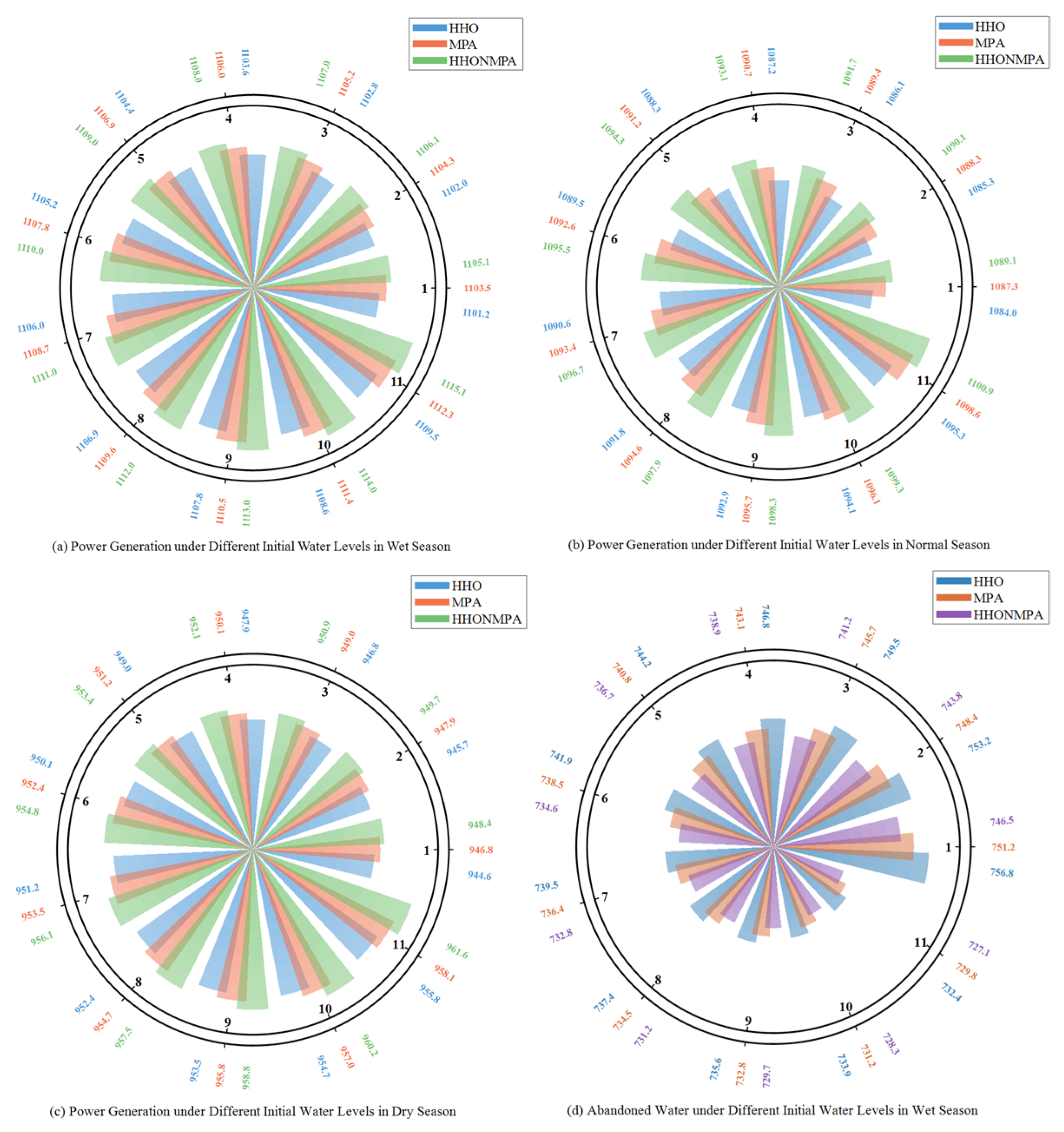
3.2.2. Analysis in Setting Different Initial Water Levels During Flood Season
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Y.; Guo, S.; Chang, F.-J.; Xu, C.-Y. Boosting hydropower output of mega cascade reservoirs using an evolutionary algorithm with successive approximation. Appl. Energy 2018, 228, 1726–1739. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Yao, L.; Liu, Y.; Jiang, Z.; Feng, Z.; Ouyang, S. Improved Multi-objective Moth-flame Optimization Algorithm based on R-domination for cascade reservoirs operation. J. Hydrol. 2020, 581, 124431. [Google Scholar] [CrossRef]
- Chen, H.-T.; Wang, W.-C.; Chen, X.-N.; Qiu, L. Multi-objective reservoir operation using particle swarm optimization with adaptive random inertia weights. Water Sci. Eng. 2020, 13, 136–144. [Google Scholar] [CrossRef]
- Xia, Y.; Feng, Z.-K.; Niu, W.-J.; Qin, H.; Jiang, Z.-Q.; Zhou, J.-Z. Simplex quantum-behaved particle swarm optimization algorithm with application to ecological operation of cascade hydropower reservoirs. Appl. Soft Comput. 2019, 84, 105715. [Google Scholar] [CrossRef]
- Boudjerda, M.; Touaibia, B.; Mihoubi, M.K.; Kisi, O.; Ehteram, M.; El-Shafie, A. Optimization of reservoir operation by sine cosine algorithm: A case of study in Algeria. Sustain. Comput. Inform. Syst. 2024, 44, 101035. [Google Scholar] [CrossRef]
- Jiang, Z.; Ji, C.; Qin, H.; Feng, Z. Multi-stage progressive optimality algorithm and its application in energy storage operation chart optimization of cascade reservoirs. Energy 2018, 148, 309–323. [Google Scholar] [CrossRef]
- Niu, W.-J.; Feng, Z.-K.; Cheng, C.-T.; Wu, X.-Y. A parallel multi-objective particle swarm optimization for cascade hydropower reservoir operation in southwest China. Appl. Soft Comput. 2018, 70, 562–575. [Google Scholar] [CrossRef]
- Emami, M.; Nazif, S.; Mousavi, S.-F.; Karami, H.; Daccache, A. A hybrid constrained coral reefs optimization algorithm with machine learning for optimizing multi-reservoir systems operation. J. Environ. Manag. 2021, 286, 112250. [Google Scholar] [CrossRef]
- Shen, X.; Wu, Y.; Li, L.; He, P.; Zhang, T. A Novel Hybrid Algorithm Based on Beluga Whale Optimization and Harris Hawks Optimization for Optimizing Multi-Reservoir Operation. Water Resour. Manag. 2024, 38, 4883–4909. [Google Scholar] [CrossRef]
- Turgut, M.S.; Turgut, O.E.; Afan, H.A.; El-Shafie, A. A novel Master–Slave optimization algorithm for generating an optimal release policy in case of reservoir operation. J. Hydrol. 2019, 577, 123959. [Google Scholar] [CrossRef]
- Ji, C.; Liu, Y.; Wang, Y.; Zhang, Y.; Xie, Y. Considering water propagation impact in short-term optimal operation of cascade reservoirs using Nested Progressive Optimality Algorithm. J. Hydrol. 2021, 602, 126764. [Google Scholar] [CrossRef]
- Gogula, S.; Vakula, V.S. Multi-objective Harris Hawks optimization algorithm for selecting best location and size of distributed generation in radial distribution system. Int. J. Cogn. Comput. Eng. 2024, 5, 436–452. [Google Scholar] [CrossRef]
- Manoj Kumar, V.; Bharatiraja, C.; Elrashidi, A.; AboRas, K.M. Chaotic Harris Hawks Optimization Algorithm for Electric Vehicles Charge Scheduling. Energy Rep. 2024, 11, 4379–4396. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, J.; Wu, Z.; He, S. A fusion algorithm based on whale and grey wolf optimization algorithm for solving real-world optimization problems. Appl. Soft Comput. 2023, 146, 110701. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Khan, Z.A.; Khan, T.A.; Waqar, M.; Chaudhary, N.I.; Raja, M.A.Z.; Shu, C.-M. Nonlinear marine predator algorithm for robust identification of fractional hammerstein nonlinear model under impulsive noise with application to heat exchanger system. Commun. Nonlinear Sci. Numer. Simul. 2025, 146, 108809. [Google Scholar] [CrossRef]
- Makhadmeh, S.N.; Fraihat, S.; Awad, M.; Sanjalawe, Y.; Al-Betar, M.A.; Awadallah, M.A. A crossover-integrated Marine Predator Algorithm for feature selection in intrusion detection systems within IoT environments. Internet Things 2025, 31, 101536. [Google Scholar] [CrossRef]
- Fahmy, H.; El-Gendy, E.M.; Mohamed, M.A.; Saafan, M.M. ECH3OA: An Enhanced Chimp-Harris Hawks Optimization Algorithm for copyright protection in Color Images using watermarking techniques. Knowl. Based Syst. 2023, 269, 110494. [Google Scholar] [CrossRef]
- Qiao, L.; Liu, K.; Xue, Y.; Tang, W.; Salehnia, T. A multi-level thresholding image segmentation method using hybrid Arithmetic Optimization and Harris Hawks Optimizer algorithms. Expert Syst. Appl. 2024, 241, 122316. [Google Scholar] [CrossRef]
- Liu, Z.; Fang, Y.; Liu, L.; Ma, S. A multi-leader Harris hawks optimizer with adaptive mutation and its application for modeling of silicon content in liquid iron of blast furnace. Math. Comput. Simul. 2023, 213, 466–514. [Google Scholar] [CrossRef]
- Lyu, L.; Yang, F. MMPA: A modified marine predator algorithm for 3D UAV path planning in complex environments with multiple threats. Expert Syst. Appl. 2024, 257, 124955. [Google Scholar] [CrossRef]
- Li, L.-L.; Ji, B.-X.; Liu, G.-C.; Yuan, J.-P.; Tseng, S.-W.; Lim, M.K.; Tseng, M.-L. Grid-connected multi-microgrid system operational scheduling optimization: A hierarchical improved marine predators algorithm. Energy 2024, 294, 130905. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Gezici, H.; Livatyali, H. An improved Harris Hawks Optimization algorithm for continuous and discrete optimization problems. Eng. Appl. Artif. Intell. 2022, 113, 104952. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, W.; Xu, H.; Wu, X.; Kim, J. Image encryption based on Logistic-Sine self-embedding chaotic sequence. Optik 2022, 271, 170075. [Google Scholar] [CrossRef]
- Yu, H.; Zhao, Z.; Heidari, A.A.; Ma, L.; Hamdi, M.; Mansour, R.F.; Chen, H. An accelerated sine mapping whale optimizer for feature selection. iScience 2023, 26, 107896. [Google Scholar] [CrossRef]
- Hasheminejad, A.; Rostami, M.J. A novel bit level multiphase algorithm for image encryption based on PWLCM chaotic map. Optik 2019, 184, 205–213. [Google Scholar] [CrossRef]
- Dehkordi, A.A.; Sadiq, A.S.; Mirjalili, S.; Ghafoor, K.Z. Nonlinear-based Chaotic Harris Hawks Optimizer: Algorithm and Internet of Vehicles application. Appl. Soft Comput. 2021, 109, 107574. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]


| Algorithm | Parameters |
|---|---|
| HHONMPA | Control coefficient CF ∈ [2, 0]; Initial state of the prey’s energy E0 ∈ [−1, 1]; Prey attack probability FADs = 0.2; Prey movement probability p = 0.5; Control coefficient ω ∈ [2, 0]. |
| HHO | Constant β = 1.5; Random jump strength J ∈ [0, 2]; Chance of a prey in successfully escaping q = 0.5; Initial state of the prey’s energy E0 ∈ [−1, 1]. |
| MPA | Prey attack probability FADs = 0.2; Prey movement probability p = 0.5; |
| NCHHO | Control coefficient CF ∈ [2, 0]; Constant β = 1.5; Random jump strength J ∈ [0, 2]; Chance of a prey in successfully escaping r = 0.5; Initial state of the prey’s energy E0 ∈ [−1, 1]. |
| NMPA | Control coefficient CF ∈ [2, 0]; Prey attack probability FADs = 0.2; Prey movement probability p = 0.5. |
| Type | No. | Description | Fi* (Optimal Value) |
|---|---|---|---|
| Simple Multimodal function | F5 | Shifted and Rotated Rastrigin’s Function | 500 |
| F7 | Shifted and Rotated Lunacek Bi-Rastrigin’s Function | 700 | |
| F8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| F10 | Shifted and Rotated Schwefel’s Function | 1000 | |
| Hybrid function | F12 | Hybrid Function 7 (N = 3) | 1200 |
| F13 | Hybrid Function 10 (N = 3) | 1300 | |
| F15 | Hybrid Function 10 (N = 4) | 1500 | |
| F18 | Hybrid Function 10 (N = 5) | 1800 | |
| Composition function | F22 | Composition Function 2 (N = 3) | 2200 |
| F24 | Composition Function 4 (N = 4) | 2400 | |
| F26 | Composition Function 6 (N = 5) | 2600 | |
| F30 | Composition Function 8 (N = 6) | 3000 |
| Fun | Metris | HHONMPA | HHO | MPA | NCHHO | NMPA | DBO |
|---|---|---|---|---|---|---|---|
| F5 | min | 5.65 × 102 | 7.06 × 102 | 5.67 × 102 | 6.40 × 102 | 6.74 × 102 | 6.70 × 102 |
| std | 3.72 × 101 | 3.76 × 101 | 6.11 × 101 | 4.42 × 101 | 4.60 × 101 | 4.05 × 101 | |
| avg | 6.20 × 102 | 7.59 × 102 | 6.29 × 102 | 7.11 × 102 | 7.48 × 102 | 7.30 × 102 | |
| median | 6.32 × 102 | 7.51 × 102 | 6.03 × 102 | 7.17 × 102 | 7.56 × 102 | 7.20 × 102 | |
| F7 | min | 8.00 × 102 | 1.25 × 103 | 8.73 × 102 | 9.97 × 102 | 1.12 × 103 | 9.07 × 102 |
| std | 1.77 × 101 | 4.73 × 101 | 7.17 × 101 | 6.66 × 101 | 8.15 × 101 | 9.64 × 101 | |
| avg | 8.30 × 102 | 1.31 × 103 | 9.48 × 102 | 1.06 × 103 | 1.22 × 103 | 1.03 × 103 | |
| median | 8.26 × 102 | 1.30 × 103 | 9.30 × 102 | 1.03 × 103 | 1.21 × 103 | 1.02 × 103 | |
| F8 | min | 8.64 × 102 | 9.48 × 102 | 8.72 × 102 | 8.91 × 102 | 9.11 × 102 | 9.52 × 102 |
| std | 3.61 × 101 | 1.62 × 101 | 1.70 × 101 | 2.55 × 101 | 3.19 × 101 | 5.75 × 101 | |
| avg | 9.11 × 102 | 9.73 × 102 | 9.06 × 102 | 9.45 × 102 | 9.65 × 102 | 1.05 × 103 | |
| median | 9.13 × 102 | 9.71 × 102 | 9.06 × 102 | 9.43 × 102 | 9.71 × 102 | 1.05 × 103 | |
| F10 | min | 3.51 × 103 | 4.49 × 103 | 4.16 × 103 | 3.79 × 103 | 4.53 × 103 | 4.69 × 103 |
| std | 6.40 × 102 | 7.83 × 102 | 4.87 × 102 | 1.91 × 103 | 7.12 × 102 | 8.49 × 102 | |
| avg | 4.64 × 103 | 6.02 × 103 | 4.72 × 103 | 5.96 × 103 | 5.57 × 103 | 6.12 × 103 | |
| median | 4.51 × 103 | 6.23 × 103 | 4.56 × 103 | 5.34 × 103 | 5.44 × 103 | 6.34 × 103 | |
| F12 | min | 4.06 × 105 | 1.15 × 107 | 6.32 × 106 | 4.18 × 107 | 3.73 × 106 | 2.39 × 106 |
| std | 1.66 × 108 | 2.54 × 107 | 1.05 × 108 | 1.32 × 108 | 1.15 × 108 | 8.24 × 107 | |
| avg | 5.72 × 107 | 2.92 × 107 | 8.88 × 107 | 1.78 × 108 | 1.13 × 108 | 4.01 × 107 | |
| median | 3.08 × 106 | 2.08 × 107 | 3.05 × 107 | 1.59 × 108 | 7.64 × 107 | 1.31 × 107 | |
| F13 | min | 5.94 × 103 | 3.39 × 105 | 3.61 × 104 | 7.39 × 104 | 7.33 × 104 | 3.09 × 104 |
| std | 3.33 × 108 | 2.65 × 105 | 9.26 × 107 | 2.33 × 108 | 5.52 × 107 | 6.95 × 105 | |
| avg | 1.14 × 108 | 7.14 × 105 | 2.98 × 107 | 7.39 × 107 | 3.28 × 107 | 4.31 × 105 | |
| median | 7.28 × 104 | 7.07 × 105 | 2.16 × 105 | 1.07 × 105 | 2.08 × 105 | 1.75 × 105 | |
| F15 | min | 1.93 × 103 | 3.22 × 104 | 2.28 × 104 | 2.65 × 104 | 2.90 × 104 | 1.89 × 104 |
| std | 1.07 × 104 | 4.54 × 104 | 1.22 × 107 | 8.14 × 105 | 2.10 × 106 | 1.07 × 105 | |
| avg | 9.22 × 103 | 8.32 × 104 | 4.37 × 106 | 5.18 × 105 | 1.26 × 106 | 1.03 × 105 | |
| median | 5.64 × 103 | 6.76 × 104 | 9.65 × 104 | 1.11 × 105 | 2.13 × 105 | 5.55 × 104 | |
| F18 | min | 8.38 × 104 | 3.39 × 105 | 2.35 × 105 | 2.65 × 105 | 1.88 × 105 | 1.14 × 105 |
| std | 1.04 × 106 | 4.86 × 106 | 1.02 × 106 | 3.32 × 106 | 1.74 × 106 | 3.42 × 106 | |
| avg | 6.18 × 105 | 3.38 × 106 | 1.60 × 106 | 2.48 × 106 | 2.13 × 106 | 3.11 × 106 | |
| median | 1.57 × 105 | 6.98 × 105 | 1.49 × 106 | 9.96 × 105 | 1.56 × 106 | 2.12 × 106 | |
| F22 | min | 2.30 × 103 | 2.41 × 103 | 2.47 × 103 | 2.50 × 103 | 2.51 × 103 | 2.33 × 103 |
| std | 3.45 × 100 | 1.84 × 103 | 1.91 × 103 | 1.35 × 103 | 1.82 × 103 | 2.03 × 103 | |
| avg | 2.30 × 103 | 7.19 × 103 | 4.49 × 103 | 3.31 × 103 | 5.22 × 103 | 4.20 × 103 | |
| median | 2.30 × 103 | 7.48 × 103 | 4.48 × 103 | 2.88 × 103 | 6.12 × 103 | 3.76 × 103 | |
| F24 | min | 2.86 × 103 | 3.27 × 103 | 2.90 × 103 | 2.90 × 103 | 2.94 × 103 | 2.96 × 103 |
| std | 1.20 × 101 | 1.19 × 102 | 5.33 × 101 | 6.74 × 101 | 1.22 × 102 | 1.03 × 102 | |
| avg | 2.88 × 103 | 3.48 × 103 | 2.94 × 103 | 2.96 × 103 | 3.12 × 103 | 3.17 × 103 | |
| median | 2.88 × 103 | 3.46 × 103 | 2.93 × 103 | 2.94 × 103 | 3.08 × 103 | 3.18 × 103 | |
| F26 | min | 2.90 × 103 | 6.69 × 103 | 4.35 × 103 | 3.83 × 103 | 3.28 × 103 | 3.79 × 103 |
| std | 6.18 × 10−1 | 8.56 × 102 | 4.71 × 102 | 5.34 × 102 | 1.09 × 103 | 1.08 × 103 | |
| avg | 2.90 × 103 | 8.00 × 103 | 4.82 × 103 | 5.04 × 103 | 4.50 × 103 | 6.15 × 103 | |
| median | 2.90 × 103 | 7.92 × 103 | 4.72 × 103 | 5.05 × 103 | 4.33 × 103 | 6.57 × 103 | |
| F30 | min | 5.52 × 103 | 1.58 × 106 | 1.78 × 106 | 6.09 × 105 | 1.30 × 104 | 1.72 × 104 |
| std | 1.23 × 103 | 3.77 × 106 | 6.70 × 106 | 1.12 × 107 | 1.36 × 106 | 1.54 × 106 | |
| avg | 7.61 × 103 | 5.36 × 106 | 9.06 × 106 | 8.99 × 106 | 4.63 × 105 | 1.06 × 106 | |
| median | 7.53 × 103 | 3.48 × 106 | 7.78 × 106 | 4.55 × 106 | 2.35 × 104 | 3.50 × 105 |
| Function | Type | HHO | MPA | NCHHO | NMPA | DBO |
|---|---|---|---|---|---|---|
| F5 | Simple Multimodal | + | + | + | + | + |
| F7 | Simple Multimodal | + | + | + | + | + |
| F8 | Simple Multimodal | + | + | + | − | + |
| F10 | Simple Multimodal | + | + | − | + | + |
| F12 | Hybrid | + | + | + | + | + |
| F13 | Hybrid | + | + | + | + | + |
| F15 | Hybrid | + | + | + | + | |
| F18 | Hybrid | + | + | + | + | + |
| F22 | Composition | + | + | + | + | + |
| F24 | Composition | + | + | − | − | + |
| F26 | Composition | + | = | + | + | + |
| F30 | Composition | + | + | + | + | + |
| +/=/− | 12/0/0 | 11/1/0 | 10/2/0 | 10/2/0 | 12/0/0 |
| River Reach | Distance (km) Traveled | Time (Days) | Lag Treatment |
|---|---|---|---|
| Xld-xjb | 157 | 1.2–1.5 | Within-period |
| Xjb-sx | 700 | 2.5–3 | Within-period |
| Sx-gzb | 38 | 0.3–0.5 | Within-period |
| Parameter | xld | xjb | sx | gzb |
|---|---|---|---|---|
| Regulation Capacity | Annual | Seasonal | Seasonal | Daily |
| Total Storage (108 m3) | 115.7 | 49.7 | 393.0 | 16.5 |
| Regulating Storage (108 m3) | 64.6 | 9.0 | 165.0 | 0.63 |
| Discharge Flow Range (m3/s) | [43,700, 1200] | [49,800, 1200] | [98,800, 4500] | [10,000, 4500] |
| Water Level Range (m) | [600, 540] | [380, 370] | [175, 145] | [66.0, 63.0] |
| Installed Capacity (MW) | 13,860 | 6400 | 22,500 | 2715 |
| Normal water level (m) | 600 | 380 | 175 | 66 |
| Maximum Water Level Variation (m/d) | 2 | 2 | 2 | 2 |
| Guaranteed Output (MW) | 3795 | 2009 | 4990 | 1040 |
| Ki | 8.5 | 8.5 | 8.5 | 8.5 |
| xld-H (m) | xld-V (108 m3) | xjb-H (m) | xjb-V (108 m3) | sx-H (m) | sx-V (108 m3) | gzb-H (m) | gzb-V (108 m3) |
|---|---|---|---|---|---|---|---|
| 540 | 51.122 | 365 | 36.628 | 365 | 36.628 | 62 | 5.981 |
| 541 | 51.942 | 366 | 37.429 | 366 | 37.429 | 62.1 | 6.008 |
| 542 | 52.771 | 367 | 38.239 | 367 | 38.239 | 62.2 | 6.035 |
| 543 | 53.61 | 368 | 39.061 | 368 | 39.061 | 62.3 | 6.061 |
| 544 | 54.458 | 369 | 39.893 | 369 | 39.893 | 62.4 | 6.088 |
| 545 | 55.316 | 370 | 40.736 | 370 | 40.736 | 62.5 | 6.115 |
| 546 | 56.182 | 371 | 41.59 | 371 | 41.59 | 62.6 | 6.142 |
| 547 | 57.058 | 372 | 42.456 | 372 | 42.456 | 62.7 | 6.169 |
| 548 | 57.943 | 373 | 43.332 | 373 | 43.332 | 62.8 | 6.196 |
| 549 | 58.836 | 374 | 44.22 | 374 | 44.22 | 62.9 | 6.223 |
| 550 | 59.739 | 375 | 45.117 | 375 | 45.117 | 63 | 6.251 |
| 551 | 60.651 | 376 | 46.025 | 376 | 46.025 | 63.1 | 6.278 |
| 552 | 61.571 | 377 | 46.943 | 377 | 46.943 | 63.2 | 6.305 |
| 553 | 62.5 | 378 | 47.872 | 378 | 47.872 | 63.3 | 6.333 |
| 554 | 63.437 | 379 | 48.814 | 379 | 48.814 | 63.4 | 6.36 |
| 555 | 64.382 | 380 | 49.767 | 380 | 49.767 | 63.5 | 6.388 |
| 556 | 65.336 | 381 | 50.733 | 381 | 50.733 | 63.6 | 6.416 |
| 557 | 66.298 | 382 | 51.709 | 382 | 51.709 | 63.7 | 6.443 |
| 558 | 67.268 | 383 | 52.692 | 383 | 52.692 | 63.8 | 6.471 |
| 559 | 68.245 | 384 | 53.681 | 384 | 53.681 | 63.9 | 6.499 |
| 560 | 69.23 | 385 | 54.672 | 385 | 54.672 | 64 | 6.527 |
| 561 | 70.223 | 154.5 | 224.716 | 64.1 | 6.555 | ||
| 562 | 71.223 | 155 | 228 | 64.2 | 6.583 | ||
| 563 | 72.231 | 155.5 | 231.287 | 64.3 | 6.611 | ||
| 564 | 73.248 | 156 | 234.597 | 64.4 | 6.639 | ||
| 565 | 74.273 | 156.5 | 237.929 | 64.5 | 6.668 | ||
| 566 | 75.306 | 157 | 241.285 | 64.6 | 6.696 | ||
| 567 | 76.349 | 157.5 | 244.667 | 64.7 | 6.724 | ||
| 568 | 77.401 | 158 | 248.076 | 64.8 | 6.753 | ||
| 569 | 78.462 | 158.5 | 251.512 | 64.9 | 6.781 | ||
| 570 | 79.533 | 159 | 254.977 | 65 | 6.81 | ||
| 571 | 80.614 | 159.5 | 258.473 | 65.1 | 6.839 | ||
| 572 | 81.704 | 160 | 262 | 65.2 | 6.867 | ||
| 573 | 82.804 | 160.5 | 265.573 | 65.3 | 6.896 | ||
| 574 | 83.914 | 161 | 269.206 | 65.4 | 6.925 | ||
| 575 | 85.032 | 161.5 | 272.896 | 65.5 | 6.954 | ||
| 576 | 86.159 | 162 | 276.641 | 65.6 | 6.983 | ||
| 577 | 87.295 | 162.5 | 280.441 | 65.7 | 7.012 | ||
| 578 | 88.44 | 163 | 284.294 | 65.8 | 7.041 | ||
| 579 | 89.593 | 163.5 | 288.198 | 65.9 | 7.07 | ||
| 580 | 90.754 | 164 | 292.151 | 66 | 7.099 | ||
| 581 | 91.923 | 164.5 | 296.152 | 66.1 | 7.128 | ||
| 582 | 93.1 | 165 | 300.2 | 66.2 | 7.158 | ||
| 583 | 94.285 | 165.5 | 304.301 | 66.3 | 7.187 | ||
| 584 | 95.478 | 166 | 308.463 | 66.4 | 7.216 | ||
| 585 | 96.68 | 166.5 | 312.687 | 66.5 | 7.246 | ||
| 586 | 97.89 | 167 | 316.973 | 66.6 | 7.275 | ||
| 587 | 99.108 | 167.5 | 321.321 | 66.7 | 7.304 | ||
| 588 | 100.335 | 168 | 325.732 | 66.8 | 7.334 | ||
| 589 | 101.57 | 168.5 | 330.205 | 66.9 | 7.364 | ||
| 590 | 102.814 | 169 | 334.74 | 67 | 7.393 | ||
| 591 | 104.067 | 169.5 | 339.338 | ||||
| 592 | 105.328 | 170 | 344 | ||||
| 593 | 106.598 | 170.5 | 348.718 | ||||
| 594 | 107.877 | 171 | 353.483 | ||||
| 595 | 109.165 | 171.5 | 358.293 | ||||
| 596 | 110.462 | 172 | 363.146 | ||||
| 597 | 111.768 | 172.5 | 368.038 | ||||
| 598 | 113.082 | 173 | 372.967 | ||||
| 599 | 114.406 | 173.5 | 377.93 | ||||
| 600 | 115.738 | 174 | 382.925 | ||||
| 174.5 | 387.949 | ||||||
| 175 | 393 |
| Time | Inflow-xld (m3/s) | Inflow-xjb (m3/s) | Inflow-sx (m3/s) | Inflow-gzb (m3/s) |
|---|---|---|---|---|
| 1 | 2150 | −54.6 | 4620 | 0 |
| 2 | 3170 | −45.8 | 5450 | 0 |
| 3 | 3070 | −29.2 | 4550 | 0 |
| 4 | 2240 | −42.2 | 3690 | 0 |
| 5 | 1360 | −10.1 | 2840 | 0 |
| 6 | 1500 | −10.7 | 3570 | 0 |
| 7 | 1680 | −2.22 | 4020 | 0 |
| 8 | 1830 | −13.1 | 5010 | 0 |
| 9 | 1550 | −10.7 | 5520 | 0 |
| 10 | 828 | −29.2 | 6260 | 0 |
| 11 | 369 | 36.5 | 6870 | 0 |
| 12 | 1050 | 76.8 | 8540 | 0 |
| 13 | 996 | 108 | 9030 | 0 |
| 14 | 1120 | −21.7 | 10,800 | 0 |
| 15 | 1920 | −27.8 | 8930 | 0 |
| 16 | 2000 | −11.7 | 8060 | 0 |
| 17 | 2520 | −15 | 10,800 | 0 |
| 18 | 4110 | −81.9 | 12,100 | 0 |
| 19 | 7110 | −157 | 18,800 | 0 |
| 20 | 6440 | −84.5 | 26,900 | 0 |
| 21 | 5710 | 4.33 | 16,900 | 0 |
| 22 | 5000 | −130 | 12,800 | 0 |
| 23 | 6150 | 13.4 | 17,100 | 0 |
| 24 | 6110 | 1.47 | 31,600 | 0 |
| 25 | 8630 | 202 | 28,800 | 0 |
| 26 | 8550 | 154 | 22,300 | 0 |
| 27 | 6650 | −76.2 | 21,200 | 0 |
| 28 | 5830 | −117 | 19,200 | 0 |
| 29 | 5380 | −114 | 12,200 | 0 |
| 30 | 4810 | −78.9 | 9060 | 0 |
| 31 | 5260 | −50 | 8370 | 0 |
| 32 | 4320 | −76.6 | 9910 | 0 |
| 33 | 2830 | −31.4 | 9690 | 0 |
| 34 | 2610 | −41.4 | 8850 | 0 |
| 35 | 2620 | −30.8 | 9370 | 0 |
| 36 | 2610 | −45.9 | 9810 | 0 |
| Station Name | Initial Water Level (m) | Final Water Level (m) |
|---|---|---|
| xld | 580.00 | 580.00 |
| xjb | 380.00 | 380.00 |
| sx | 175.00 | 168.00 |
| gzb | 64.50 | 64.50 |
| Frequency | Indicator | HHONMPA | HHO | MPA | DBO | GWO |
|---|---|---|---|---|---|---|
| 25% | Best | 2134.71 | 2115.69 | 2110.52 | 1995.55 | 2021.64 |
| Std | 3.23 | 28.09 | 31.31 | 33.21 | 14.87 | |
| Mean | 2130.53 | 2078.25 | 2073.81 | 1958.34 | 1995.45 | |
| Median | 2130 | 2076.86 | 2077.14 | 1963.6 | 1990.18 | |
| Worst | 2126.87 | 2044.47 | 2027.13 | 1903.02 | 1980.13 | |
| 50% | Best | 2121.32 | 2076.27 | 2067.69 | 2012.4 | 2011.59 |
| Std | 7.54 | 19.46 | 16.62 | 42.03 | 8.31 | |
| Mean | 2119.6 | 2043.76 | 2047.7 | 1959.61 | 2004.24 | |
| Median | 2118.88 | 2040.06 | 2051.52 | 1957.22 | 2007.93 | |
| Worst | 2110.21 | 2024.41 | 2020.71 | 1896.56 | 1993.37 | |
| 75% | Best | 1964.36 | 1912.5 | 1942.67 | 1807.91 | 1855.93 |
| Std | 10.72 | 21.27 | 27.61 | 42.1 | 15.06 | |
| Mean | 1955.34 | 1887.15 | 1907.73 | 1773.29 | 1841.47 | |
| Median | 1959.57 | 1888.75 | 1909.67 | 1784.99 | 1842.91 | |
| Worst | 1935.56 | 1857.92 | 1872.17 | 1702.11 | 1813.47 |
| Station | Initial Level (m) | Final Level (m) | Inflow (m3/s) | Generation Discharge (m3/s) | Power Output (WKW) | Power Generation (GKW h) |
|---|---|---|---|---|---|---|
| xld | 580.00 | 582.00 | 2150.00 | 1878.47 | 331.79 | 7.96 |
| xld | 582.00 | 584.00 | 3170.00 | 2894.77 | 515.16 | 12.36 |
| xld | 584.00 | 586.00 | 3070.00 | 2816.21 | 506.55 | 13.37 |
| xld | 586.00 | 588.00 | 2240.00 | 1957.01 | 355.90 | 8.54 |
| xld | 588.00 | 586.00 | 1360.00 | 1642.99 | 299.09 | 7.18 |
| xld | 586.00 | 584.00 | 1500.00 | 1848.96 | 333.17 | 6.40 |
| xld | 584.00 | 582.00 | 1680.00 | 1955.23 | 348.70 | 8.37 |
| xld | 582.00 | 580.00 | 1830.00 | 2101.53 | 371.23 | 8.91 |
| xld | 580.00 | 578.00 | 1550.00 | 1793.48 | 313.72 | 8.28 |
| xld | 578.00 | 576.00 | 828.00 | 1092.00 | 189.05 | 4.54 |
| xld | 576.00 | 574.00 | 369.00 | 628.84 | 107.76 | 2.59 |
| xld | 574.00 | 572.00 | 1050.00 | 1305.79 | 221.39 | 5.31 |
| xld | 572.00 | 570.00 | 996.00 | 1247.27 | 209.21 | 5.02 |
| xld | 570.00 | 568.00 | 1120.00 | 1366.76 | 228.23 | 5.48 |
| xld | 568.00 | 566.00 | 1920.00 | 2140.43 | 356.51 | 9.41 |
| xld | 566.00 | 564.00 | 2000.00 | 2238.19 | 372.09 | 8.93 |
| xld | 564.00 | 562.00 | 2520.00 | 2754.38 | 455.35 | 10.93 |
| xld | 562.00 | 560.00 | 4110.00 | 4340.67 | 705.40 | 16.93 |
| xld | 560.00 | 560.00 | 7110.00 | 7110.00 | 1127.08 | 27.05 |
| xld | 560.00 | 560.00 | 6440.00 | 6440.00 | 1027.07 | 24.65 |
| xld | 560.00 | 560.00 | 5710.00 | 5710.00 | 916.35 | 24.19 |
| xld | 560.00 | 560.00 | 5000.00 | 5000.00 | 805.71 | 19.34 |
| xld | 560.00 | 560.00 | 6150.00 | 6150.00 | 984.24 | 23.62 |
| xld | 560.00 | 562.00 | 6110.00 | 5900.30 | 951.62 | 25.12 |
| xld | 562.00 | 564.00 | 8630.00 | 8395.63 | 1226.05 | 29.43 |
| xld | 564.00 | 566.00 | 8550.00 | 8311.81 | 1242.45 | 29.82 |
| xld | 566.00 | 568.00 | 6650.00 | 6407.52 | 1056.83 | 25.36 |
| xld | 568.00 | 570.00 | 5830.00 | 5583.24 | 931.06 | 22.35 |
| xld | 570.00 | 572.00 | 5380.00 | 5128.73 | 861.68 | 20.68 |
| xld | 572.00 | 574.00 | 4810.00 | 4577.47 | 773.41 | 20.42 |
| xld | 574.00 | 576.00 | 5260.00 | 5000.16 | 849.20 | 20.38 |
| xld | 576.00 | 578.00 | 4320.00 | 4056.00 | 698.40 | 16.76 |
| xld | 578.00 | 580.00 | 2830.00 | 2562.18 | 447.32 | 10.74 |
| xld | 580.00 | 582.00 | 2610.00 | 2338.47 | 412.55 | 9.90 |
| xld | 582.00 | 582.00 | 2620.00 | 2620.00 | 464.21 | 11.14 |
| xld | 582.00 | 580.00 | 2610.00 | 2856.84 | 503.36 | 13.29 |
| xjb | 380.00 | 379.90 | 1823.87 | 1834.90 | 183.36 | 4.40 |
| xjb | 379.90 | 379.90 | 2848.97 | 2848.97 | 281.50 | 6.76 |
| xjb | 379.90 | 379.90 | 2787.01 | 2787.01 | 275.56 | 7.27 |
| xjb | 379.90 | 379.90 | 1914.81 | 1914.81 | 191.10 | 4.59 |
| xjb | 379.90 | 379.90 | 1632.89 | 1632.89 | 163.45 | 3.92 |
| xjb | 379.90 | 379.90 | 1838.26 | 1838.26 | 183.61 | 3.53 |
| xjb | 379.90 | 379.90 | 1953.01 | 1953.01 | 194.84 | 4.68 |
| xjb | 379.90 | 379.90 | 2088.43 | 2088.43 | 208.05 | 4.99 |
| xjb | 379.90 | 379.90 | 1782.78 | 1782.78 | 178.17 | 4.70 |
| xjb | 379.90 | 379.90 | 1062.80 | 1062.80 | 107.04 | 2.57 |
| xjb | 379.90 | 379.90 | 665.34 | 665.34 | 67.13 | 1.61 |
| xjb | 379.90 | 380.00 | 1382.59 | 1371.56 | 137.74 | 3.31 |
| xjb | 380.00 | 380.00 | 1355.27 | 1355.27 | 136.19 | 3.27 |
| xjb | 380.00 | 378.00 | 1345.06 | 1564.39 | 155.47 | 3.73 |
| xjb | 378.00 | 376.00 | 2112.63 | 2306.97 | 223.38 | 5.90 |
| xjb | 376.00 | 374.00 | 2226.49 | 2435.41 | 231.20 | 5.55 |
| xjb | 374.00 | 372.00 | 2739.38 | 2943.54 | 272.69 | 6.54 |
| xjb | 372.00 | 370.00 | 4258.77 | 4457.85 | 398.32 | 9.56 |
| xjb | 370.00 | 370.00 | 6953.00 | 6953.00 | 600.00 | 14.40 |
| xjb | 370.00 | 370.00 | 6355.50 | 6355.50 | 551.57 | 13.24 |
| xjb | 370.00 | 370.00 | 5714.33 | 5714.33 | 499.02 | 13.17 |
| xjb | 370.00 | 370.00 | 4870.00 | 4870.00 | 428.96 | 10.30 |
| xjb | 370.00 | 370.00 | 6163.40 | 6163.40 | 535.89 | 12.86 |
| xjb | 370.00 | 370.00 | 5901.77 | 5901.77 | 514.41 | 13.58 |
| xjb | 370.00 | 370.00 | 8597.63 | 8597.63 | 599.91 | 14.40 |
| xjb | 370.00 | 372.00 | 8465.81 | 8266.73 | 600.00 | 14.40 |
| xjb | 372.00 | 374.00 | 6331.32 | 6127.16 | 549.09 | 13.18 |
| xjb | 374.00 | 376.00 | 5466.24 | 5257.33 | 484.36 | 11.62 |
| xjb | 376.00 | 378.00 | 5014.73 | 4800.95 | 452.77 | 10.87 |
| xjb | 378.00 | 380.00 | 4498.57 | 4299.18 | 415.07 | 10.96 |
| xjb | 380.00 | 380.00 | 4950.16 | 4950.16 | 479.22 | 11.50 |
| xjb | 380.00 | 380.00 | 3979.40 | 3979.40 | 388.96 | 9.34 |
| xjb | 380.00 | 380.00 | 2530.78 | 2530.78 | 251.13 | 6.03 |
| xjb | 380.00 | 380.00 | 2297.07 | 2297.07 | 228.51 | 5.48 |
| xjb | 380.00 | 380.00 | 2589.20 | 2589.20 | 256.77 | 6.16 |
| xjb | 380.00 | 380.00 | 2810.94 | 2810.94 | 278.10 | 7.34 |
| sx | 175.00 | 175.00 | 6454.90 | 6454.90 | 622.51 | 14.94 |
| sx | 175.00 | 175.00 | 7284.90 | 7284.90 | 697.42 | 16.74 |
| sx | 175.00 | 174.60 | 6384.90 | 6811.37 | 651.06 | 17.19 |
| sx | 174.60 | 172.60 | 6538.97 | 8846.38 | 835.20 | 20.04 |
| sx | 172.60 | 170.60 | 5627.01 | 7867.06 | 729.36 | 17.50 |
| sx | 170.60 | 168.60 | 5484.81 | 8170.00 | 742.92 | 14.26 |
| sx | 168.60 | 166.60 | 5652.89 | 7686.10 | 685.59 | 16.45 |
| sx | 166.60 | 164.60 | 6848.26 | 8767.47 | 766.08 | 18.39 |
| sx | 164.60 | 162.60 | 7473.01 | 9130.21 | 781.50 | 20.63 |
| sx | 162.60 | 160.60 | 8348.43 | 10,074.47 | 844.00 | 20.26 |
| sx | 160.60 | 158.60 | 8652.78 | 10,283.79 | 852.32 | 20.46 |
| sx | 158.60 | 150.60 | 9602.80 | 15,620.86 | 1233.29 | 29.60 |
| sx | 150.60 | 150.60 | 9695.34 | 9695.34 | 735.71 | 17.66 |
| sx | 150.60 | 150.60 | 12,171.56 | 12,171.56 | 921.50 | 22.12 |
| sx | 150.60 | 145.00 | 10,285.27 | 13,305.79 | 973.49 | 25.70 |
| sx | 145.00 | 145.00 | 9624.39 | 9624.39 | 682.89 | 16.39 |
| sx | 145.00 | 145.00 | 13,106.97 | 13,106.97 | 926.77 | 22.24 |
| sx | 145.00 | 145.00 | 14,535.41 | 14,535.41 | 1026.19 | 24.63 |
| sx | 145.00 | 145.00 | 21,743.54 | 21,743.54 | 1519.95 | 36.48 |
| sx | 145.00 | 145.00 | 31,357.85 | 31,357.85 | 2105.74 | 50.54 |
| sx | 145.00 | 145.00 | 23,853.00 | 23,853.00 | 1661.61 | 43.87 |
| sx | 145.00 | 145.00 | 19,155.50 | 19,155.50 | 1344.24 | 32.26 |
| sx | 145.00 | 145.00 | 22,814.33 | 22,814.33 | 1592.05 | 38.21 |
| sx | 145.00 | 145.00 | 36,470.00 | 36,470.00 | 2067.09 | 54.57 |
| sx | 145.00 | 145.00 | 34,963.40 | 34,963.40 | 2078.96 | 49.90 |
| sx | 145.00 | 145.00 | 28,201.77 | 28,201.77 | 1948.92 | 46.77 |
| sx | 145.00 | 145.00 | 29,797.63 | 29,797.63 | 2052.66 | 49.26 |
| sx | 145.00 | 145.00 | 27,466.73 | 27,466.73 | 1900.87 | 45.62 |
| sx | 145.00 | 145.00 | 18,327.16 | 18,327.16 | 1287.61 | 30.90 |
| sx | 145.00 | 145.00 | 14,317.33 | 14,317.33 | 1011.07 | 26.69 |
| sx | 145.00 | 145.00 | 13,170.95 | 13,170.95 | 931.29 | 22.35 |
| sx | 145.00 | 145.00 | 14,209.18 | 14,209.18 | 1003.57 | 24.09 |
| sx | 145.00 | 152.00 | 14,640.16 | 10,351.62 | 765.87 | 18.38 |
| sx | 152.00 | 152.00 | 12,829.40 | 12,829.40 | 986.48 | 23.68 |
| sx | 152.00 | 152.00 | 11,900.78 | 11,900.78 | 915.94 | 21.98 |
| sx | 152.00 | 168.00 | 12,107.07 | −222.37 | −18.74 | −0.49 |
| gzb | 64.50 | 66.00 | 6508.03 | 6458.14 | 137.22 | 3.29 |
| gzb | 66.00 | 66.00 | 7391.31 | 7391.31 | 159.29 | 3.82 |
| gzb | 66.00 | 66.00 | 6887.38 | 6887.38 | 149.66 | 3.95 |
| gzb | 66.00 | 66.00 | 9053.03 | 9053.03 | 189.67 | 4.55 |
| gzb | 66.00 | 66.00 | 8010.84 | 8010.84 | 170.81 | 4.10 |
| gzb | 66.00 | 66.00 | 8333.23 | 8333.23 | 176.70 | 3.39 |
| gzb | 66.00 | 66.00 | 7818.27 | 7818.27 | 167.27 | 4.01 |
| gzb | 66.00 | 66.00 | 8969.06 | 8969.06 | 188.17 | 4.52 |
| gzb | 66.00 | 66.00 | 9355.09 | 9355.09 | 195.04 | 5.15 |
| gzb | 66.00 | 66.00 | 10,359.97 | 10,359.97 | 212.28 | 5.09 |
| gzb | 66.00 | 64.00 | 10,582.73 | 10,648.94 | 208.10 | 4.99 |
| gzb | 64.00 | 64.00 | 16,262.44 | 16,262.44 | 273.49 | 6.56 |
| gzb | 64.00 | 64.00 | 9956.50 | 9956.50 | 188.53 | 4.52 |
| gzb | 64.00 | 64.00 | 12,591.69 | 12,591.69 | 227.04 | 5.45 |
| gzb | 64.00 | 64.00 | 13,798.74 | 13,798.74 | 243.15 | 6.42 |
| gzb | 64.00 | 64.00 | 9880.99 | 9880.99 | 187.36 | 4.50 |
| gzb | 64.00 | 64.00 | 13,587.16 | 13,587.16 | 240.40 | 5.77 |
| gzb | 64.00 | 64.00 | 15,107.30 | 15,107.30 | 259.74 | 6.23 |
| gzb | 64.00 | 64.00 | 22,778.20 | 22,778.20 | 288.15 | 6.92 |
| gzb | 64.00 | 64.00 | 33,009.74 | 33,009.74 | 216.61 | 5.20 |
| gzb | 64.00 | 64.00 | 25,023.08 | 25,023.08 | 274.72 | 7.25 |
| gzb | 64.00 | 64.00 | 20,024.00 | 20,024.00 | 297.72 | 7.15 |
| gzb | 64.00 | 64.00 | 23,917.73 | 23,917.73 | 283.05 | 6.79 |
| gzb | 64.00 | 64.00 | 38,450.09 | 38,450.09 | 183.02 | 4.83 |
| gzb | 64.00 | 64.00 | 36,846.77 | 36,846.77 | 192.37 | 4.62 |
| gzb | 64.00 | 64.00 | 29,651.04 | 29,651.04 | 239.14 | 5.74 |
| gzb | 64.00 | 64.00 | 31,349.35 | 31,349.35 | 227.37 | 5.46 |
| gzb | 64.00 | 64.00 | 28,868.82 | 28,868.82 | 244.99 | 5.88 |
| gzb | 64.00 | 64.00 | 19,142.48 | 19,142.48 | 299.45 | 7.19 |
| gzb | 64.00 | 64.00 | 14,875.22 | 14,875.22 | 256.80 | 6.78 |
| gzb | 64.00 | 64.00 | 13,655.25 | 13,655.25 | 241.28 | 5.79 |
| gzb | 64.00 | 64.00 | 14,760.13 | 14,760.13 | 255.39 | 6.13 |
| gzb | 64.00 | 64.00 | 10,654.91 | 10,654.91 | 199.14 | 4.78 |
| gzb | 64.00 | 64.00 | 13,291.76 | 13,291.76 | 236.50 | 5.68 |
| gzb | 64.00 | 64.00 | 12,303.53 | 12,303.53 | 223.05 | 5.35 |
| gzb | 64.00 | 64.50 | −597.92 | −612.76 | −13.06 | −0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Qin, H.; Liu, S.; Chen, J.; Li, Y.; Zhu, X. Intelligent Scheduling Method for Cascade Reservoirs Driven by Dual Optimization of Harris Hawks and Marine Predators. Water 2025, 17, 3291. https://doi.org/10.3390/w17223291
Chen X, Qin H, Liu S, Chen J, Li Y, Zhu X. Intelligent Scheduling Method for Cascade Reservoirs Driven by Dual Optimization of Harris Hawks and Marine Predators. Water. 2025; 17(22):3291. https://doi.org/10.3390/w17223291
Chicago/Turabian StyleChen, Xiaolin, Hui Qin, Shuai Liu, Jiawen Chen, Yongxiang Li, and Xin Zhu. 2025. "Intelligent Scheduling Method for Cascade Reservoirs Driven by Dual Optimization of Harris Hawks and Marine Predators" Water 17, no. 22: 3291. https://doi.org/10.3390/w17223291
APA StyleChen, X., Qin, H., Liu, S., Chen, J., Li, Y., & Zhu, X. (2025). Intelligent Scheduling Method for Cascade Reservoirs Driven by Dual Optimization of Harris Hawks and Marine Predators. Water, 17(22), 3291. https://doi.org/10.3390/w17223291






