Data Assimilation for a Simple Hydrological Partitioning Model Using Machine Learning

Abstract

Predicting streamflow is a core element of efficient water resource management. Traditional hydrological models are constructed based on historical observational data, leading to cumulative prediction errors over time. To address this issue, this study proposes an Artificial Intelligence Filter (AIF) that integrates machine learning (ML) techniques into a data assimilation framework. The AIF learns the relationship between simulated streamflow and state variables (soil moisture, aquifer water level) and updates the state based on observed streamflow. This study applied the Simple Hydrologic Partitioning Model (SHPM) to four dam basins in southeastern Korea (Andong, Hapcheon, Miryang, Namgang). Model parameters were estimated using the Markov Chain Monte Carlo (MCMC) method, and results were compared with Open Loop (OL) simulations. After applying AIF, R² and NSE increased by an average of approximately 0.02–0.04, representing a 2–5% improvement, achieving enhanced performance in most basins. KGE decreased slightly in some basins but improved by an average of about 2%. These results demonstrate that AIF not only enhances the accuracy of hydrological models but also contributes to securing the reliability of water resource forecasts through data assimilation and supports efficient management decision-making.

1. Introduction

Water resource management is one of the critical factors for sustaining human society and ecosystems. River basin runoff prediction provides essential information for dam operation, flood and drought control, water supply allocation, and is indispensable for efficient water resource management.

Generally, predicting runoff in river basins begins with calibration and validation of parameters using observational data. However, uncertainties in input data, including precipitation, as well as estimated parameters, cause errors in hydrological models [1,2]. These errors accumulate over time [3].

In the field of hydrology, data assimilation techniques utilizing the Ensemble Kalman Filter (EnKF) [4] and the Particle Filter [5] have been primarily employed to minimize such errors [6,7,8,9,10,11]. Specifically, a study applying EnKF to the Simple Hydrologic Partitioning Model (SHPM), which explicitly implements the hydrological partitioning process, has been reported for analyzing four dam basins within the Nakdong River basin in Korea [12].

Meanwhile, various studies have applied machine learning (ML) to the field of hydrology [13,14,15,16,17]; most public organizations rarely directly apply ML results to streamflow prediction. This is because they require accountability for prediction outcomes and the provision of sound, hydrologically grounded justifications [18,19]. Against this backdrop, research has actively pursued improving prediction performance by combining ML with data assimilation rather than relying solely on ML for streamflow prediction. Boucher et al. [19] compared the performance of data assimilation using neural networks for soil moisture in the Génie Rural à 4 paramètres Journalier (GR4J) model with traditional data assimilation techniques, arguing that neural network-based data assimilation is a promising method. Kalu et al. [20] applied ML-based data assimilation to the Terrestrial Water Storage (TWS) model for African regions, demonstrating improved ability to predict. He et al. [21] enhanced prediction performance by combining data assimilation using EnKF with data assimilation using ML in the Weather Research and Forecasting (WRF) model. Jeung et al. [22] performed data assimilation using Reinforcement Learning on the Stormwater Management Model (SWMM), improving prediction performance for both quantity and quality. Jeong et al. [23] applied data assimilation based on Long Short-Term Memory (LSTM) to estimate rainfall loss, reasonably predicting high flows. Zhang et al. [24] reported that Deep Learning (DL)-based data assimilation outperformed EnKF-based data assimilation but noted a limitation: testing dozens of DL model structures during training revealed only a few yielded satisfactory performance. Yao et al. [25] applied DL-based data assimilation to a rainfall–runoff model and showed that it could serve as an alternative to EnKF when compared to EnKF assimilation results.

This study also aimed to support the model’s streamflow prediction by using a basic form of data assimilation called direct insertion [26,27,28], which updates the simulated state variables of the hydrological model using Random Forest (RF), a type of ML, rather than directly predicting streamflow using ML to support the model’s streamflow prediction. To this end, an Artificial Intelligence Filter (AIF) was built by training RF on the relationships between streamflow and meteorological data (precipitation and potential evapotranspiration (PET)) with state variables (soil moisture and aquifer water levels). This AIF was then used to update the state variables of the SHPM in four dam basins in the southeastern Korean Peninsula. The performance of the data assimilation results using the AIF was compared and analyzed with Open Loop (OL) results (without data assimilation) and results from data assimilation using EnKF.

This study established and tested the following three hypotheses:

• The predictive performance of the AIF is improved compared to that of the OL;
• The AIF will immediately respond to observed streamflow values and update itself with corresponding state variables;
• AIF will better predict streamflow than OL during periods of sustained non-precipitation.

To verify the first hypothesis, we compared the streamflow simulation results from OL with those from AIF data assimilation using four performance evaluation indices (R², NSE, KGE, pBias) for four Nakdong River dam basins. To verify the second hypothesis, changes in state variables before and after data assimilation were examined using state variable time series graphs and streamflow simulation result time series graphs. This allowed us to assess whether AIF appropriately updated state variables in response to observed streamflow values. To verify the final hypothesis, we compared OL’s streamflow simulation results and AIF-applied streamflow simulation results with observed streamflow data. This comparison was graphically plotted for intervals where the non-precipitation period lasted 10 days or longer.

Section 2 details the methodology, including comprehensive information on the study area encompassing the basins, used in the research, the applied hydrological model, and the core concepts of AIF. Section 3 presents the results, describing the parameter estimation outcomes of the hydrological model and the learning results of the AIF. Furthermore, Section 3 analyzed the performance of AIF data assimilation by comparing its results with those of OL and EnKF, using the hydrological model performance metrics R², NSE, KGE, and pBias. Section 4’s Discussion explains how state variables are updated during data assimilation and how this affects streamflow prediction.

2. Materials and Methods

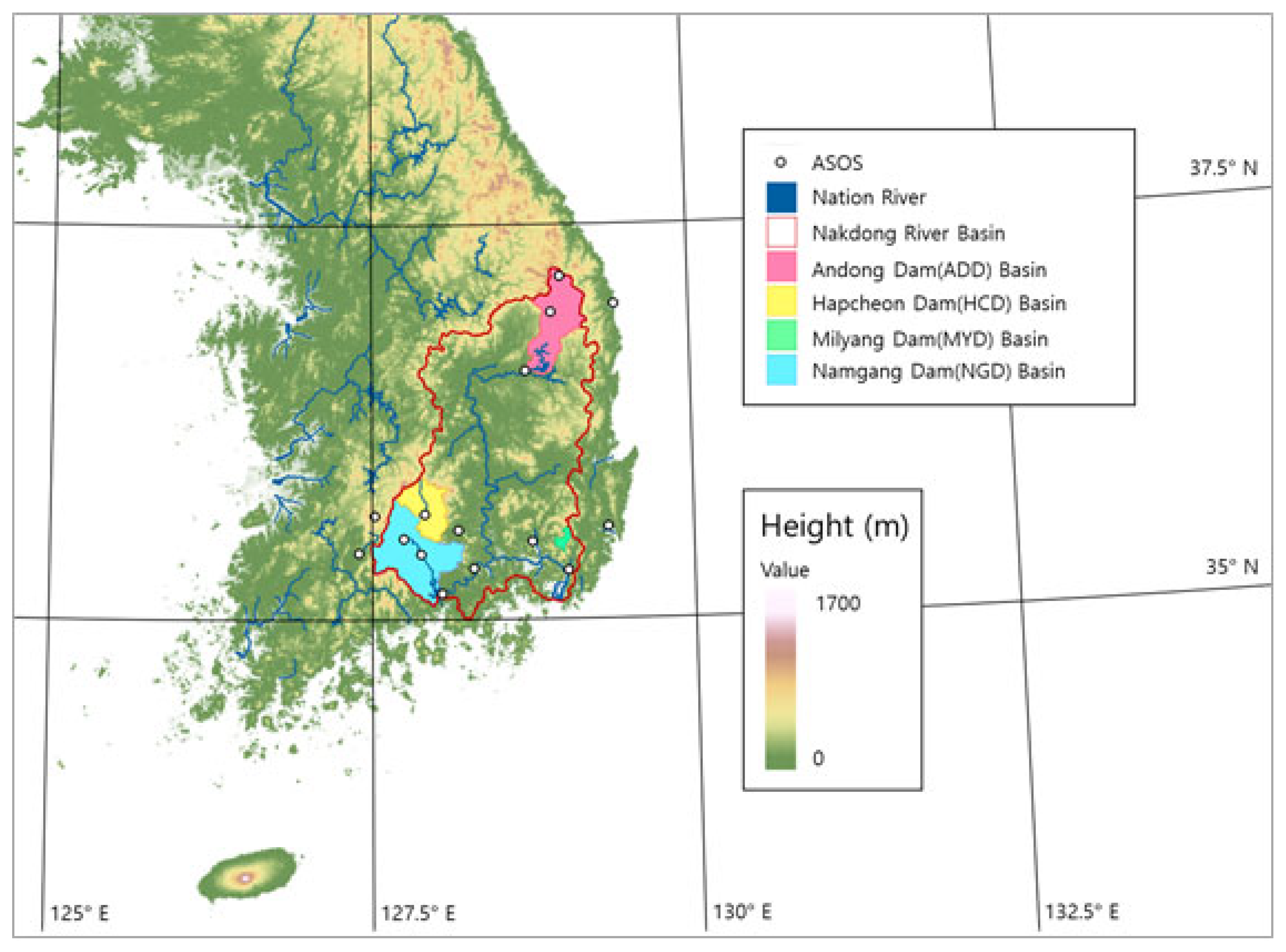
2.1. Data and Research Areas

This study was conducted on the four dams in the southeastern part of the Korean Peninsula: Andong Dam (ADD), Hapcheon Dam (HCD), Milyang Dam (MYD), and Namgang Dam (NGD). Although all are located within the same regional area, each basin exhibits distinct climatic and topographical conditions. The basin areas for each dam are the following: ADD 1584 km², HCD 925 km², MYD 95.40 km², and NGD 2285 km². Although the annual average precipitation and annual average PET differed among the four dam basins, they exhibited the characteristics of a monsoon climate, with heavy rainfall concentrated in summer and a clear distinction between dry and wet seasons. The SHPM streamflow simulation period is from 2004 to 2024. Model parameter calibration and AI training were conducted using data from 2004 to 2014, while parameter validation and data assimilation were conducted using data from 2014 to 2024. The initial year of each period, 2004 and 2014, was applied as a warm-up period.

The input variables for SHPM are daily precipitation and daily PET, which were converted to basin area averages using the Thiessen polygon method. PET was calculated using the Penman–Monteith (PM) method, which estimates daily PET from daily maximum temperature, daily minimum temperature, daily relative humidity, and daily wind speed data [29,30,31,32]. The meteorological data required for calculating daily precipitation and PET were collected from the Automated Synoptic Observing System (ASOS) operated by the Korea Meteorological Administration at stations near each dam basin. Additionally, observed streamflow data and dam basin area information required for SHPM construction were obtained from the Water Resources Management Information System (WAMIS) operated by the Ministry of Environment of the Republic of Korea. All simulations were performed continuously at daily intervals.

The area of the basins used in this study, along with the annual average precipitation, annual average PET, and annual average streamflow by period, are presented in

Table 1. Area and annual average information of the study basins.

Basin	Area (km2)	Period (Year)	Precipitaion (mm/Year)	PET (mm/Year)	Streamflow (mm/Year)
ADD	1584.00	2004–2014	1179.00	986.42	600.59
		2014–2024	1110.23	1002.15	543.83
HCD	925.00	2004–2014	1306.85	1078.25	673.66
		2014–2024	1201.27	1056.17	616.78
MYD	95.40	2004–2014	1330.80	1087.13	710.83
		2014–2024	1405.29	1139.08	929.29
NGD	2285.00	2004–2014	1416.09	1064.46	1006.75
		2014–2024	1426.81	1061.68	852.92

. The location of the basins and the meteorological observation stations is shown in Figure 1.

2.2. Simple Hydrologic Partitioning Model

This study employed the Simple Hydrologic Partitioning Model (SHPM) proposed by Choi et al. [12] as the hydrological model. SHPM defines a basin by vertically partitioning it into a surface layer, a soil layer, and an aquifer. Precipitation falling on the basin is divided into direct runoff flowing over the surface layer and soil moisture infiltrating into the soil layer. The moisture infiltrating into the soil layer either evaporates into the atmosphere or percolates deeper into the aquifer. Groundwater runoff occurs in proportion to the accumulated water level in the aquifer. Therefore, streamflow is calculated as the sum of the direct runoff originating from the surface layer and the groundwater runoff originating from the aquifer.

The precipitation $P$ falling on the surface layer is stored up to the maximum surface storage depth $d_s$, and the excess rainfall $B$ beyond this depth flows into the soil layer. The amount of water stored on the ground $d$ and the potential evapotranspiration $E$ influence the actual evapotranspiration $Ev$ as follows.

$${Ev}_t=\mathit{min}\left[E_t, d_t\right]$$

(1)

The sum of surface runoff $d$ and precipitation $P$ minus evapotranspiration $Ev$ is the maximum surface runoff. If this sum does not exceed $d_s$, excess rainfall $B$ does not occur.

$$B_t=max\left[\right(P_t+\left(d_t-Ev\right)-d_s),0]$$

(2)

If the sum of precipitation $P$ and surface storage $d$ does not exceed the maximum surface storage depth $d_s$, excess rainfall $B$ does not occur. Excess rainfall $B$ flowing along the surface is infiltrated into the soil layer according to the effective soil depth $n{Z}_r$. The infiltration volume $W$ and direct runoff $F$ are calculated using the following equation [12], inspired by the NRCS-CN method developed by the U.S. Natural Resources Conservation Service (NRCS) [33]. This method has been widely used as one approach to calculate surface runoff depth for a specific rainfall event [34].

$$W_t={\displaystyle \frac{B_{t}n{Z}_r\left(1-S_t\right)}{B_t+n{Z}_r\left(1-S_t\right)}}$$

(3)

$$F_t=B_t-W_t$$

(4)

Soil moisture is a normalized value between 0 and 1, and the evapotranspiration $V$ of water stored in the soil layer is calculated based on the critical soil moisture $S^{*}$ and the current soil moisture $S$.

$$V_t=\left(E_t-E{v}_t\right){\displaystyle \frac{S_t}{S^{*}}}, for 0\le {\mathrm{S}}_{\mathrm{t}}\le {\mathrm{S}}^{\mathrm{*}}$$

(5)

$$V_t=\left(E_t-E{v}_t\right), for S^{*}\le S_t\le 1$$

(6)

Subsequently, percolation occurs from the soil layer into the aquifer. The percolation rate $K$ is calculated based on the saturated hydraulic conductivity $K_s$ and the percolation coefficient $\beta$.

$$K_t=K_s{S}_t^{\beta }$$

(7)

The amount of water percolating into the aquifer $K$ recharges the aquifer water level $R$. Groundwater runoff $G$, originating from the aquifer, is calculated as proportional to the aquifer water level $R$ with the groundwater runoff coefficient $\alpha$. Finally, the streamflow $Q$ is calculated as the sum of direct runoff $F$ and groundwater runoff $G$.

$$R_t=R_{t-1}+K_t$$

(8)

$$G_t=\alpha R_t$$

(9)

$$Q_t=F_t+G_t$$

(10)

Therefore, the SHPM is defined by six parameters ($d_s$, $n{Z}_r$, $S^{*}$, $K_s$, $\beta$, $\alpha$). Daily precipitation and daily PET are input into the SHPM, and daily streamflow is output.

The Metropolis–Hastings (MH) algorithm was used for parameter estimation in SHPM. The MH algorithm is a type of Markov Chain Monte Carlo (MCMC) technique for generating samples from a posterior parameter distribution. It utilizes the principle that, when a sufficiently large number of samples are collected from a complex distribution, the samples converge to the posterior distribution regardless of the initial values [35,36,37,38] to estimate parameters.

2.3. Artificial Intelligence Filter

The Artificial Intelligence Filter (AIF) addressed in this study updates the state variables of the SHPM, a long-term continuous runoff model, on a daily scale through AI-based learning of state variables. It then performs data assimilation by directly inserting these updated state variables. All basins were assumed to be in steady state, and the six parameters of the SHPM were estimated. Therefore, to reduce model errors caused by observational errors, direct insertion data assimilation updating the state variables was used instead of modifying the parameters. The SHPM has two main state variables: soil moisture ($S$) and aquifer water level ($R$). However, these two state variables are not actual observed values but rather values conceptually representing the model’s physical processes; thus, they cannot be directly updated using observations. Consequently, this study used machine learning to estimate observed values for the state variables instead of replacing them with observed numerical values [19]. As demonstrated in the study by Boucher [19], when streamflow was observed, it was used to estimate and update the state variables, which were then utilized for predicting the next day’s streamflow.

Even though the SHPM is a hydrological model describing physical concepts, the process of back-estimating state variables from streamflow is difficult to clearly define using physical concepts alone. Therefore, this study learned the relationship between flow and state variables using machine learning techniques with statistical black-box characteristics and estimated state variables from observed flow. In other words, the core strategy of our paper is not to replace physical hydrological models with machine learning but to utilize machine learning to complement physical hydrological models. The state variable update procedure using AIF is as follows:

• Open Loop:
  First, observed precipitation and PET data are input into the SHPM, which was developed to collect training data for AI. This generates Open Loop (OL) data, namely simulated streamflow $Q$ and simulated state variables (soil moisture $S$, aquifer water levels $R$).

  $$\left[Q_t^s,S_t, R_t\right]=SHPM\left(P_t,E_t,S_{t-1},R_{t-1}\right)$$

  (11)
• Train AI:
  AIF begins with the assumption that the relationship between the simulated streamflow $Q^s$ and state variables $S$ and $R$, modeled as OL, is identical to the relationship between the observed streamflow $Q^o$ and the actual state variables $S^{+}$ and $R^{+}$.

  $$Q_t^s,P_t,E_t\leftrightarrow S_t≔Q_t^o,P_t,E_t,\leftrightarrow S_t^{+}$$

  (12)

  $$Q_t^s,P_t,E_t\leftrightarrow R_t≔Q_t^o,P_t,E_t,\leftrightarrow R_t^{+}$$

  (13)

  where $Q^s$ is the streamflow simulated by the SHPM, $Q^o$ is the observed streamflow, $P$ is the observed precipitation, $E$ is the PET calculated by the PM method, $S$ is the soil moisture simulated by the SHPM, $R$ is the aquifer water level simulated by the SHPM, $S^{+}$ is the soil moisture corresponding to the observed streamflow, and $R^{+}$ is aquifer water level corresponding to the observed streamflow.
  Based on these assumptions, the AI model is trained to estimate soil moisture $S$ and aquifer water level $R$ by inputting streamflow $Q^o$, precipitation $P$, and potential evapotranspiration $E$. In this case, soil moisture $S$ and aquifer water level $R$ were trained as separate models to enable their independent updates.
• Data Assimilation:
  Direct insertion is the most basic data assimilation technique, replacing one or more simulated state variables with observations [19]. At this stage, since the AIF has already learned the relationship between the streamflow $Q$ and the state variables $S$ and $R$, providing the observed streamflow, observed precipitation $P$, and potential evapotranspiration $E$ to the AIF allows it to calculate the estimates $S^{+}$ and $R^{+}$ for the state variables, even in the absence of observations for those variables.

  $$S_t^{+}=AI{F}_S\left(Q_t^o,P_t,E_t\right)$$

  (14)

  $$R_t^{+}={AIF}_R\left(Q_t^o,P_t,E_t\right)$$

  (15)
  The new state variables $S^{+}$ and $R^{+}$, estimated as AIF, are then passed back to the SHPM to update the state. The updated state variables are used to calculate the streamflow for the next time step.

  $$\left[Q_{t+1}^s\right]=SHPM\left(P_{t+1},E_{t+1},S_t^{+},R_t^{+}\right)$$

  (16)

A strategy was established to learn and update two state variables under various hydrological conditions. In SHPM, direct runoff occurs only during precipitation events, whereas baseflow persists regardless of precipitation. Baseflow is determined by the relationship between aquifer water level and the baseflow coefficient; thus, when precipitation is absent, changes in aquifer water level exert a relatively large influence on baseflow. Meanwhile, when precipitation occurs, the amount of moisture the soil can absorb varies depending on the current soil moisture condition. Due to this interrelationship between direct runoff, moisture absorption capacity, and soil moisture, it can be confirmed that direct runoff is significantly influenced by soil moisture conditions. However, it is impossible to completely exclude the influence of soil moisture on aquifer water levels during dry periods or the impact of aquifer water levels on baseflow during wet periods. Therefore, the AIF was developed using various data assimilation strategies.

• Strategy where only $S$ is updated when precipitation occurs and only $R$ is updated when non-precipitation occurs;
• Strategy where only $S$ is updated when precipitation occurs and both $S$ and $R$ are updated together when non-precipitation occurs;
• Strategy where both $S$ and $R$ are updated together when precipitation occurs and only $R$ is updated when non-precipitation occurs;
• Strategy where both $S$ and $R$ are updated regardless of precipitation occurrence.

Furthermore, just as the CN value affecting basin flow and storage capacity varies with preceding rainfall in the NRCS-CN method, state variables also change due to preceding rainfall in SHPM. State variables are categorized into soil moisture and aquifer water level. Both soil moisture, which directly affects soil infiltration, and aquifer water level, determined by groundwater recharge induced by soil moisture, are influenced by prior rainfall. That is, prior rainfall causes infiltration rates to decrease as soil moisture saturation increases and to increase as soil dries out, consequently altering the relationship with runoff. Considering this, during the machine learning training process, even identical state variables were trained differently depending on the hydrological situation. The AI models were separated and trained so that $S$ and $R$ were updated individually. To ensure both $S$ and $R$ were updated distinctively based on the hydrological situation, four AI models were ultimately designed.

• AIF estimating $S^{+}$ during precipitation;
• AIF estimating $R^{+}$ during precipitation;
• AIF estimating $S^{+}$ during non-precipitation;
• AIF estimating $R^{+}$ during non-precipitation.

This study employed the Random Forest algorithm, a decision tree-based approach, as the AI model for training. The Random Forest algorithm is one of the widely used learning methods in machine learning, performing predictions by constructing multiple decision trees. Random Forest was selected because it is robust against overfitting, less sensitive to outliers in the data, and offers the advantage of identifying which variables significantly influence predictions through feature importance calculations. The core hyperparameters for the Random Forest algorithm were determined as shown in the

Table 2. Key Random Forest Hyperparameters.

Hyperparameter	Value	Description
n_estimators	100	Number of decision trees to generate
criterion	MSE	Tree splitting criteria
max_depth	None	Maximum depth of tree
min_samples_split	2	Maximum number of samples for node splitting
max_leaf_nodes	None	Maximum number of leaf nodes

.

The overall process of this study was conducted by continuously simulating the three steps described earlier on a daily basis, and the entire flow is diagrammed in Figure 2.

2.4. Model Performance Evaluation

The accuracy of simulated streamflow was assessed using four performance metrics (R², NSE, KGE, pBias). To prevent calculations from being biased toward high flows, the square root was taken from the streamflow data when calculating all performance metrics. Generally, in daily simulations, R² ≥ 0.6, NSE ≥ 0.5, and KGE ≥ 0.6 are considered to reasonably reproduce the observed data [39,40,41]. R² is the coefficient of determination from linear regression analysis between observed and simulated data, while the Nash–Sutcliffe efficiency coefficient (NSE) is defined as follows [39]:

$$NSE={\displaystyle \frac{\sum _{i=1}^n{\left(\sqrt{Q_t^s}-\sqrt{Q_t^o}\right)}^2}{\sum _{i=1}^n{\left(\sqrt{Q_t^o}-\overline{\sqrt{Q^o}}\right)}^2}}$$

(17)

where $Q^o$ is observed streamflow and $Q^s$ is simulated streamflow. The Kling–Gupta efficiency coefficient (KGE) is defined as follows [42]:

$$KGE=\sqrt{{\left(r^{\prime }-1\right)}^2+{\left({\alpha }^{\prime }-1\right)}^2+{\left({\beta }^{\prime }-1\right)}^2}$$

(18)

where $r^{\prime }$ is the linear correlation coefficient between the observed data and the simulated data, ${\alpha }^{\prime }$ is the ratio of the standard deviation of the simulated data to the standard deviation of the observed data, and ${\beta }^{\prime }$ is the ratio of the mean of the simulated data to the mean of the observed data.

pBias is an indicator that expresses, as a percentage, how much the simulated data overestimates or underestimates the observed data. The closer it is to zero, the better the simulated data is interpreted as reproducing the observed data. A positive value indicates overestimation, while a negative value indicates underestimation. It is calculated as follows [16]:

$$pBias={\displaystyle \frac{\sum _{i=1}^n\left(\sqrt{Q_t^s}-\sqrt{Q_t^o}\right)}{\sum _{i=1}^n\left(\sqrt{Q_t^o}\right)}}\times 100\left(\%\right)$$

(19)

Additionally, the reliability of parameters estimated using the MH algorithm can be examined via the p-factor and r-factor [43]. The p-factor denotes the proportion of observed streamflow falling within the 95% PPU interval, while the r-factor represents the average width of the 95% PPU relative to the standard deviation of observed streamflow. Here, PPU is a value frequently used in uncertainty analysis, expressing the uncertainty of model prediction results as a percentage (%). The 95 PPU represents the range of the 95% prediction interval, calculated by excluding the top 2.5% and bottom 2.5% of multiple model simulations using estimated parameters. This interval encompasses 95% of the calculated streamflow values [12,44,45].

3. Results

3.1. Parameter Estimation

The results of parameter calibration for the SHPM using the MH algorithm are presented in

Table 3. Parameter estimation results of SHPM by MH algorithm.

Parameter	Basin
	ADD	HCD	MYD	NGD
$d_s$	6.001	4.586	4.782	4.950
$n{Z}_r$	262.950	407.365	211.183	307.956
$S^{*}$	0.554	0.723	0.648	0.689
$K_s$	169.536	134.132	143.295	145.789
$\beta$	3.149	4.555	3.051	3.561
$\alpha$	0.852	0.804	0.744	0.738
R2	0.811	0.840	0.731	0.826
NSE	0.789	0.813	0.727	0.821
KGE	0.878	0.883	0.833	0.854
pBias (%)	+6.37	−3.06	−0.81	−6.85
p-factor (%)	53.82	61.24	69.53	78.62
r-factor	0.28	0.30	0.29	0.29

. When examining the calibration period for streamflow using R², NSE, and KGE, all values exceeded 0.7, surpassing the metrics for reasonably reproducing observed data: R² ≥ 0.6, NSE ≥ 0.5, and KGE ≥ 0.6. The HCD and MYD basins simulated approximately 3% and 1% less than observed data, respectively, while the ADD and NGD basins simulated approximately 6% and 7% more than observed data. Based on the p-factor values, the reliability of parameters for the MYD and NGD basins was sufficient. Conversely, the reliability of the ADD and HCD basins was assessed as insufficient. However, the r-factor was similarly below 0.3 for all basins. Since a smaller r-factor value indicates higher reliability of the estimated parameters [46], the r-factor metric suggests high reliability of the estimated parameters. Synthesizing the performance metrics and uncertainty indicators, the R², NSE, KGE, and r-factor performance were sufficient, indicating that the SHPM parameters were estimated appropriately. Furthermore, the time series comparison in Figure 3 confirms that the simulated streamflow effectively reproduces the time series pattern of the observed streamflow.

Additionally, the simulated streamflow time series predicted by SHPM was compared with the observed streamflow time series during the calibration period. The time series comparison also confirmed that the simulated streamflow effectively reproduced the time series pattern of the observed streamflow (Figure 3).

3.2. Data Assimilation

OL was executed using parameters estimated for each dam basin, and simulation results for streamflow and state variables from 2005 to 2014 were collected. The collected simulation results were utilized as training data for AI learning. As described in Section 2.3, the two state variables (soil moisture and aquifer water level) were trained individually for each of the two hydrological conditions (wet or dry), resulting in the construction of four types of AIFs. All AIFs were trained using Random Forest, learning the relationship to output the target state variable given inputs of streamflow, precipitation, and PET. The Random Forest-based AIF can calculate the importance of each feature (streamflow, precipitation, PET). In most cases, the streamflow on the current day (day $t$) had the highest feature importance, exceeding 0.8. However, the AIF trained on the relationship between streamflow and aquifer water level under wet conditions where precipitation occurred showed the previous day’s (day $t-1$) streamflow as the feature with the highest importance.

After performing data assimilation using AIF, the results were compared with those from OL and from data assimilation using EnKF. Here, EnKF also applied the four strategies described in the methodology to derive results before comparison. Results were compared for each dam, and results by strategy were also compared. The accuracy of the simulation results was assessed using four performance metrics (R², NSE, KGE, pBias). When calculating the performance metrics, the streamflow data was squared to prevent bias toward high flow intervals, as these intervals constitute a small proportion of the total flow interval.

For ADD, performance improvements were observed across all metrics in the EnKF and AIF-based data assimilation methods compared to OL, in

Table 4. Performance comparison with data assimilation in ADD.

Simulation	R2	NSE	KGE	pBias (%)
OL	0.781	0.747	0.863	+3.14
EnKF 1	0.782	0.769	0.844	−0.96
EnKF 2	0.792	0.781	0.890	−0.57
EnKF 3	0.781	0.767	0.883	−0.96
EnKF 4	0.791	0.780	0.889	−0.57
AIF 1	0.790	0.779	0.885	+2.78
AIF 2	0.800	0.793	0.892	+0.91
AIF 3	0.784	0.770	0.885	+0.64
AIF 4	0.795	0.785	0.891	−0.38

. When applying AIF data assimilation, R² increased to a range of 0.784–0.800 (average 0.792) compared to OL’s 0.781, with Strategy 2 showing the highest value at 0.800. This corresponds to an improvement of 0.019 (approximately 2.4%). NSE improved from OL’s 0.747 to 0.770–0.793 (average 0.782). Strategy 2 showed the best result at 0.793, representing an improvement of 0.046 (approximately 6.2%), indicating that data assimilation significantly enhanced flow simulation accuracy. KGE improved from 0.863 for OL to a range of 0.885–0.892 (average 0.888). KGE also showed the highest value of 0.892 for Strategy 2, representing an improvement of 0.029 (approximately 3.4%). For EnKF, R² improved to a range of 0.767–0.781 (average 0.786), NSE improved to 0.770–0.793 (average 0.774), and KGE improved to 0.883–0.890 (average 0.887). pBias improved from OL’s 3.14% to AIF’s 0.38–2.78% in absolute terms, and EnKF showed a significant improvement to 0.57–0.96%. Overall, all indicators demonstrated improved performance compared to OL, with AIF showing a higher average improvement than EnKF.

For HCD,

Table 5. Performance comparison with data assimilation in HCD.

Simulation	R2	NSE	KGE	pBias (%)
OL	0.797	0.790	0.890	+0.62
EnKF 1	0.823	0.817	0.904	+1.52
EnKF 2	0.832	0.828	0.908	+0.35
EnKF 3	0.823	0.818	0.904	+1.53
EnKF 4	0.832	0.829	0.908	+0.36
AIF 1	0.823	0.822	0.886	+2.58
AIF 2	0.839	0.839	0.885	−1.00
AIF 3	0.819	0.817	0.888	+1.83
AIF 4	0.835	0.835	0.887	−1.31

confirms that overall performance has improved. When applying AIF data assimilation, R² increased to a range of 0.819–0.839 (average 0.829) compared to OL’s 0.797, with Strategy 2 showing the highest value at 0.839. This represents an improvement of 0.042 (approximately 5.3%). NSE improved from OL’s 0.790 to 0.817–0.839 (average 0.828). Strategy 2 showed the best result at 0.839, an improvement of 0.049 (approximately 6.2%). KGE remained stable within the range of 0.885–0.888 (average 0.886), showing little fluctuation from OL’s 0.890. Conversely, pBias increased from OL’s 0.62% to AIF’s 1.00% to 1.31% in absolute terms. For EnKF, R² improved to a range of 0.823–0.832 (average 0.827), NSE improved to 0.817–0.829 (average 0.823), and KGE improved to 0.904–0.908 (average 0.906). pBias fluctuated between 0.35% and 1.53% in absolute terms, compared to OL’s 0.62%, but showed improvement in some strategies. Therefore, both strategies demonstrated valid improvement effects in HCD. However, AIF showed significant performance improvements in R² and NSE, while EnKF showed performance improvements in KGE and pBias.

For MYD, performance improvements were observed across all metrics in the EnKF and AIF-based data assimilation methods compared to OL, in

Table 6. Performance comparison with data assimilation in MYD.

Simulation	R2	NSE	KGE	pBias (%)
OL	0.730	0.721	0.778	+7.81
EnKF 1	0.736	0.733	0.831	+0.07
EnKF 2	0.738	0.736	0.832	+0.75
EnKF 3	0.735	0.732	0.830	+0.06
EnKF 4	0.737	0.734	0.832	+0.73
AIF 1	0.754	0.753	0.815	+3.25
AIF 2	0.761	0.761	0.818	+0.05
AIF 3	0.748	0.747	0.827	+0.37
AIF 4	0.757	0.757	0.824	−1.60

. When applying AIF data assimilation, R² increased to a range of 0.748–0.761 (average 0.755) compared to OL’s 0.730, showing an improvement of approximately 0.031 (4.3%) to 0.761 in Strategy 2. NSE improved from OL’s 0.721 to 0.747–0.761 (average 0.755). Strategy 2 showed the highest value of 0.761, representing an improvement of 0.040 (approximately 5.5%). KGE improved from OL’s 0.778 to a range of 0.815–0.827 (average 0.821), with Strategy 3 showing the best performance at 0.827. pBias improved significantly in absolute terms, from 7.81% for OL to 0.05–3.25%. For EnKF, R² ranged from 0.735 to 0.738 (average 0.736), NSE improved to 0.732–0.736 (average 0.734), KGE to 0.830–0.832 (average 0.831), and pBias significantly improved to 0.06–0.75%. Thus, at MYD, both AIF and EnKF showed substantial performance improvements over OL across all metrics.

For NGD,

Table 7. Performance comparison with data assimilation in NGD.

Simulation	R2	NSE	KGE	pBias (%)
OL	0.796	0.781	0.891	−0.24
EnKF 1	0.793	0.777	0.887	−2.68
EnKF 2	0.798	0.786	0.892	−1.71
EnKF 3	0.791	0.774	0.885	−2.66
EnKF 4	0.796	0.783	0.891	−1.70
AIF 1	0.806	0.801	0.888	+2.31
AIF 2	0.816	0.814	0.890	+0.53
AIF 3	0.805	0.800	0.888	+1.89
AIF 4	0.815	0.813	0.890	+0.31

confirms that overall performance has improved. When applying AIF data assimilation, R² increased to a range of 0.805–0.816 (average 0.810) compared to OL’s 0.796, showing an improvement of approximately 0.020 (2.5%) to 0.816 in Strategy 2. NSE improved from OL’s 0.781 to 0.800–0.814 (average 0.807). Strategy 2 showed the best result of 0.814, representing an improvement of 0.033 (approximately 4.2%). KGE maintained a similar level, ranging from 0.888 to 0.890 (average 0.889) compared to OL’s 0.891. pBias increased somewhat in absolute terms, from OL’s 0.24% to AIF’s 0.31% to 2.31%. For EnKF, R² ranged from 0.791 to 0.798 (average 0.794), NSE ranged from 0.774 to 0.786 (average 0.780), KGE ranged from 0.885 to 0.892 (average 0.889), and pBias significantly improved to 0.06–0.75%.

Overall, performance metrics improved when applying AIF data assimilation across all four dams. While KGE performance decreased in HCD and NGD, it remained at a similar level, and R² and NSE showed significant overall improvement. For ADD and MYD, R², NSE, and KGE all improved compared to OL. R² and NSE showed overall improvement even compared to EnKF, suggesting that AIF not only enhances OL but also has the potential to replace EnKF. The increase and decrease values of the performance criteria are presented in

Table 8. Comparison of average performance improvement with data assimilation.

Simulation	R2	Δ R2	NSE	Δ NSE	KGE	Δ KGE
OL	0.776	-	0.760	-	0.856	-
EnKF 4	0.786	0.010	0.778	0.018	0.871	0.016
AIF 4	0.797	0.021	0.793	0.033	0.878	0.023

.

The comparison of performance metrics by strategy revealed that AIF demonstrated the best data assimilation performance based on R² and NSE in the second strategy, where S is always updated regardless of precipitation occurrence while R is updated only during non-precipitation events. Particularly in the ADD basin, the second strategy also outperformed both OL and EnKF in terms of KGE. Therefore, this study determined the second data assimilation strategy to be the optimal approach. The simulated streamflow results for each basin under this strategy are presented in a time series graph for comparison, as shown in Figure 4. Overall, predictions in extreme high-flow and low-flow intervals showed some differences, but in the intermediate flow interval, observed streamflow were reproduced relatively stably. Notably, AIF demonstrated the closest reproduction of the observed streamflow variation pattern in the intermediate flow interval.

4. Discussion

In this study, the MH algorithm was used to calibrate the parameters of the hydrological model SHPM, and data assimilation was performed by applying the AIF trained using ML techniques. The AIF learned the relationship between streamflow and state variables through past simulated data. Therefore, by simply inputting observational data, it can update the corresponding state variables. This offers the advantage of avoiding various constraints required by conventional data assimilation techniques.

Multiple AIFs, individually trained based on precipitation occurrence and state variable types, were applied using various strategies. Results from OL- and EnKF-based data assimilation were compared using four performance metrics: R², NSE, KGE, and pBias. Analysis results showed that AIF achieved an average R² of 0.797 (0.795–0.800), an average increase of 0.021 (approximately 2.7%) compared to OL’s average of 0.776. NSE improved from an average of 0.760 to an average of 0.793 (0.785–0.800), an average increase of 0.033 (approximately 4.4%). KGE improved from an average of 0.856 to 0.871 (0.865–0.892). This corresponds to relative improvements of approximately 2.7%, 4.4%, and 1.8%, respectively, demonstrating that AIF improves prediction performance more stably than OL. Compared to EnKF, it also showed generally similar or superior performance. EnKF’s R² increased by approximately 1.3% to an average of 0.786 (0.782–0.792), NSE improved by about 2.4% to an average of 0.778 (0.767–0.786), while KGE improved by approximately 2.6% to an average of 0.878 (0.883–0.890). Notably, the increase in NSE for AIF was approximately 4.4%, larger than the 2.4% increase for EnKF, suggesting AIF’s potential to replace EnKF. The average improvement observed in R², NSE, and KGE in this study was around 3%, which is relatively small numerically. However, since the hydrological model’s metrics were already considered quite high [2], even small numerical changes in performance metrics are considered meaningful in terms of error reduction. This suggests that data assimilation contributed to improving the model’s performance and reducing errors [47].

In this study, Strategy 2, which updates the state variable S regardless of precipitation occurrence and updates R only during non-precipitation periods, was evaluated as the optimal strategy. This strategy showed the greatest improvement in R² and NSE across all four dam basins, demonstrating enhanced AIF performance not only compared to OL but also surpassing EnKF. In some basins, it even outperformed EnKF based on KGE criteria. Therefore, Strategy 2 was evaluated as the optimal AIF strategy, and the results from the HCD basin, where R² and NSE showed the greatest improvement, were analyzed in detail.

We compared the daily changes in how AIF and EnKF updated S over the 20-day period from 17 January 2021 to 5 February 2021 (Figure 5). This period featured alternating cycles of precipitation and dry spells, making it suitable for detailed analysis of the update characteristics and differences between the strategies.

During the data assimilation process, the state variable soil moisture is updated from the simulated value ($S$) to the estimated value ($S^{+}$) based on observed streamflow. When observed streamflow is greater than simulated streamflow, soil moisture is updated in an increasing direction. Conversely, when observed streamflow is less than simulated streamflow, soil moisture is updated in a decreasing direction. Analysis of the updated soil moisture ($S^{+}$) considering this characteristic revealed that AIF more faithfully reproduces the magnitude of increases and decreases in observed streamflow compared to EnKF.

In the AIF, the state variable $R$ (aquifer water level) was updated only during dry conditions without precipitation, unlike $S$ (soil moisture). This period alternated between precipitation events and dry spells. During data assimilation, the state variable aquifer water level is updated from simulated values ($R^{-}$) to estimated values ($R^{+}$) based on observed streamflow. When observed streamflow is greater than simulated streamflow, the aquifer water level is updated in an increasing direction. Conversely, when observed streamflow is less than simulated streamflow, the aquifer water level is updated in a decreasing direction. Considering this characteristic, analysis of the updated aquifer water level ($R^{+}$) revealed that while AIF reproduces changes in observed streamflow, it does not perform data assimilation on days with precipitation. Consequently, $R^{+}$ was identical to $R^{-}$ during precipitation events, as shown in the graph (Figure 6). In contrast, the EnKF shows the aquifer water level changing minutely, similar to soil moisture, and generally following the observed streamflow, though it does not exhibit large numerical changes. Here, too, the AIF is judged to have more faithfully reproduced the range of increases and decreases in streamflow than the EnKF.

The simulated streamflow results from OL, EnKF, and AIF were compared with observed streamflow for the period from 18 September 2022 to 1 October 2022 (Figure 7). This period followed two days of concentrated heavy rainfall on September 5 (54.76 mm) and 6 (64.01 mm). This period saw no precipitation or only small amounts observed thereafter, causing streamflow to gradually decrease. It was a period lasting over 10 days with no precipitation.

During this period, as the dry spell persisted for over 10 days, no precipitation was input into the model, resulting in a gradual decrease in streamflow. For OL, the accumulated state variables, without correction, were directly reflected in the streamflow (groundwater runoff), showing significant deviation from the observed streamflow. EnKF partially reflected changes in observed streamflow through Kalman gain calculations but failed to sufficiently reproduce the initial sharp decrease in observed streamflow. In contrast, AIF utilized the learned relationship between streamflow and state variables to immediately reflect changes in observed streamflow by updating state variables, thereby reproducing the decreasing pattern of observed streamflow more rapidly and faithfully.

In Figure 5, Figure 6 and Figure 7, it was concluded that while EnKF has limitations in immediately updating state variables, AIF effectively reduces the simulation error of streamflow in SHPM by promptly responding to changes in streamflow and immediately updating state variables.

However, this study was conducted on four dams in southeastern Korea, and each dam exhibited differences in meteorological and topographical conditions. Nevertheless, improved model performance was observed at all dams, indicating that the model is not only reliable under specific conditions but also suggesting its potential effectiveness under diverse conditions. However, the four dams alone cannot be considered representative of all conditions. Since they were all nearby dams within Korea exhibiting monsoon climate characteristics, additional validation is required for application to regions outside the Korean Peninsula.

In this study, to analyze the error characteristics of streamflow simulation results, the pBias for each flow interval of Strategy 2’s AIF was compared and analyzed against EnKF and OL. Streamflow observation data from 2015 to 2024 were sorted in ascending order from the lowest value, then divided into five intervals. The lowest flow interval was designated as Seg. L (Low flow Segment), followed by Seg. D (Dry Segment), Seg. M (Middle flow Segment), Seg. W (Wet Segment), and Seg. H (High flow Segment). A smaller absolute value of pBias indicates higher agreement with observations. Negative values indicate that simulated results are smaller than observations, while positive values indicate larger results. In most dam basins, pBias was simulated as relatively large in the Seg. L interval, while it tended to be smaller in the Seg. H interval. AIF demonstrated its characteristic of assimilating data by learning the relationship between streamflow and state variables, generally showing lower absolute pBias values in Seg. D to Seg. W compared to high-flow and low-flow intervals. This is judged to be due to the nature of streamflow data, where data for normal flow conditions is relatively more abundant than data for extreme flows. Consequently, the AIF showed a smaller range of variation in bias across discharge segments compared to the existing OL and EnKF and demonstrated relatively stable simulation performance in the intermediate discharge segments (Seg. D~Seg. W). The pBias values for each flow rate range are presented in

Table 9. pBias (%) by flow rate section.

Dam	DA	Seg. L	Seg. D	Seg. M	Seg. W	Seg. H	Whole
ADD	OL	+47.00	−2.62	+4.17	+4.68	−0.04	+3.14
	EnKF 2	+46.31	−4.31	−2.44	+1.92	−4.72	−0.57
	AIF 2	+70.04	+1.47	−5.38	+2.14	−3.63	+0.91
HCD	OL	+18.25	−3.90	−1.87	+5.12	−5.18	+0.62
	EnKF 2	+21.99	−2.88	−2.59	+4.48	−3.64	+0.35
	AIF 2	+27.44	−0.33	−2.54	+1.04	−6.32	−1.00
MYD	OL	+92.04	+23.69	+15.22	+11.20	−10.46	+7.81
	EnKF 2	+52.36	+1.51	+1.94	+1.94	+7.62	−10.03
	AIF 2	+60.12	+1.62	+0.25	+6.53	−10.75	+0.05
NGD	OL	−15.43	−11.32	−2.32	+11.50	−3.95	−0.24
	EnKF 2	−8.01	−9.03	−3.43	+6.08	−4.55	−1.71
	AIF 2	+6.57	+0.35	+0.47	+5.63	−6.17	+0.53

.

Due to the characteristics of the southeastern Korean Peninsula, very heavy rain events occur only a few times per year, and on most days, only light precipitation occurs or none at all. Consequently, observed streamflow data also predominantly consists of low-flow periods, inherently limiting AIF to focus its learning on these low-flow events. Therefore, moving forward, it appears feasible to overcome this limitation by training AIF individually, considering the characteristics of streamflow across different scales rather than merely the presence or absence of precipitation.

However, when constructing AIFs by streamflow scale, a problem arises where high-flow data becomes relatively scarce. To address this, it is necessary to supplement the training data by acquiring additional observational data and applying data expansion techniques such as K-Nearest Neighbors (KNN)-based sampling or Generative Adversarial Networks (GANs).

While there are some variations depending on the dam basin and data assimilation strategy, the computational time for a 10-year long-term simulation using EnKF-based data assimilation implemented in Python version 3.11.5 on an Intel i7-6700 CPU from Intel Co. took approximately 70-80 min. In contrast, for AIF-based data assimilation, the majority of the total computational time occurred during the AIF training process, and data assimilation using the trained AIF was completed in a very short time. However, since AIF requires machine learning-based training, it has the limitation that the model size increases as the amount of training data grows. Compared to EnKF, which does not require separate storage space, this can impose a burden in terms of storage resources. Therefore, rather than simply increasing the amount of training data, it is necessary to mitigate the model size issue and prevent model overfitting by training the AIF using high-quality data.

In this study, only the current day (day $t$) and previous day (day $t-1$) observations were input into the AI for state variable update. As suggested by Boucher et al. [19], it is necessary to explore updating state variables using observations from various periods, ranging from day $t$ to day $t-d$, in the future. Furthermore, it is expected that the model’s ability to predict can be further enhanced by setting different sets of preceding $d$-days according to the hydrological characteristics of each basin and by exploring the optimal combination of preceding $d$-days for each of streamflow, precipitation, and PET.

5. Conclusions

This study estimated the parameters of the SHPM using the MH algorithm and examined the applicability of ML-based data assimilation techniques to improve the accuracy of the constructed SHPM. Specifically, an AIF was developed by learning the relationship between streamflow and state variables using RF. The built AIF improved the prediction performance of the SHPM by immediately reflecting observed streamflow to update state variables.

The AIF was applied to the basins of four dams in the southeastern part of the Korean Peninsula (ADD, HCD, MYD, NGD). For comparison, OL with estimated parameters and EnKF were selected. The comparison results showed that the data assimilation performance using AIF demonstrated improved performance compared to both OL and EnKF based on R² and NSE metrics. Particularly in the ADD basin, it also outperformed both OL and EnKF based on the KGE metric.

AIF has the advantage of directly updating state variables without complex calculations once trained AI models are fed observational data. While it accurately predicts streamflow during normal or intermediate flow periods, its limitation lies in training data being concentrated on low-flow events, as most of the year experiences no or minimal precipitation. Consequently, it showed limitations in reproducing high-flow streamflow. To improve this, it was proposed that AI should be trained separately for different scales of streamflow, and that AIF should be applied differently to update state variables depending on the scale of the observed streamflow. Furthermore, it appears necessary to supplement the insufficient training data for high-flow intervals using data augmentation techniques such as KNN-based sampling and GANs.

Nevertheless, all three hypotheses stated in the introduction were proven. Particularly, in sections where the dry period was prolonged and streamflow decreased sharply, the AIF faithfully reproduced the observed changes in streamflow, thereby demonstrating its potential for application as a data assimilation technique. Specifically, given its characteristic of appropriately reflecting state variables in reproducing normal-run streamflow, it is expected that AIF can be effectively utilized even during high-flow conditions if its limitations are addressed through future studies applying the proposed improvement measures.