Deep Learning-Based Rolling Forecasting of Dissolved Oxygen in Shandong Peninsula Coastal Waters
Abstract
1. Introduction
2. Dataset Description and Preprocessing
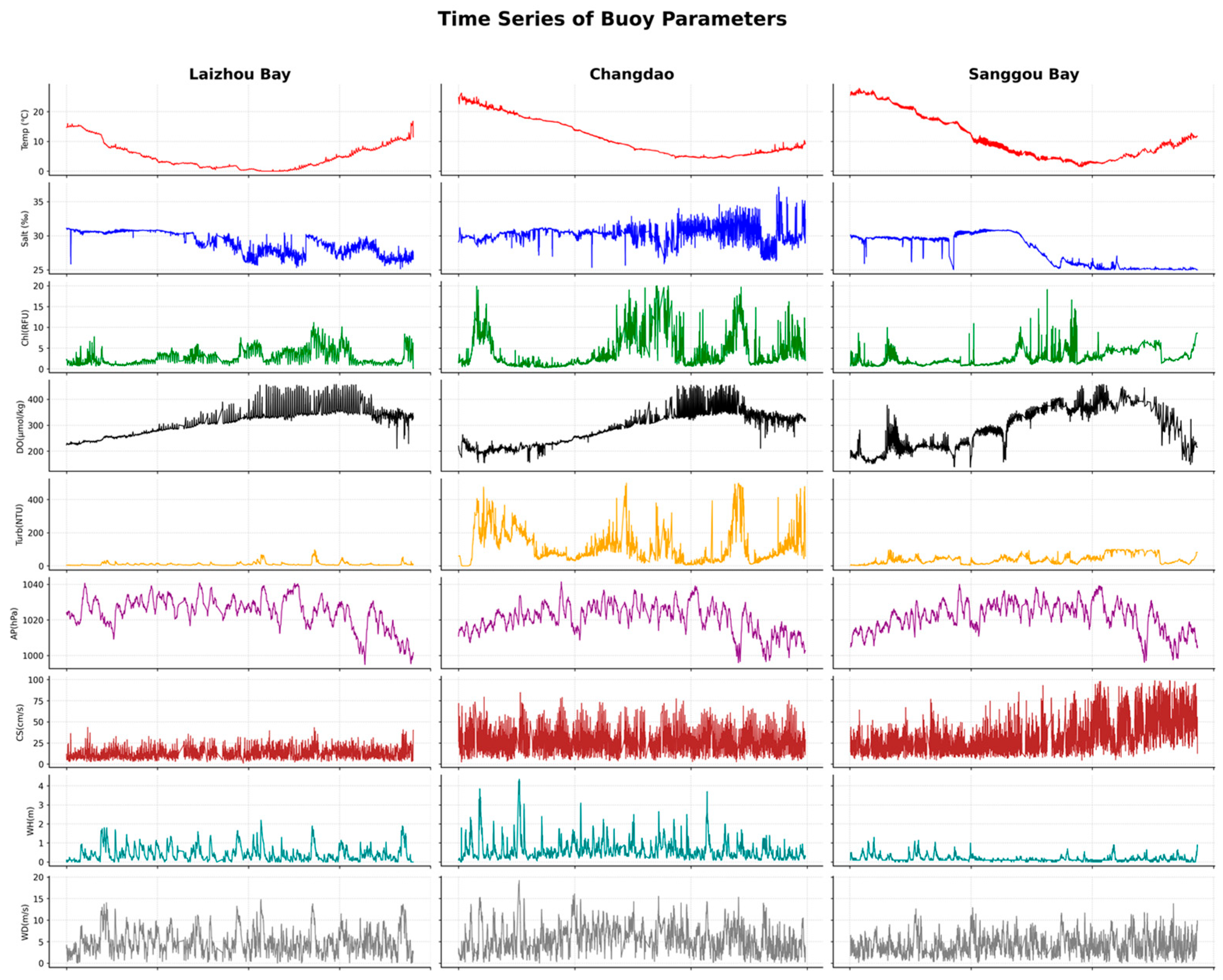
2.1. Data Source
2.2. Data Quality Control and Preprocessing
2.2.1. Quality Control of Buoy Data
2.2.2. Data Preprocessing of Buoy Data
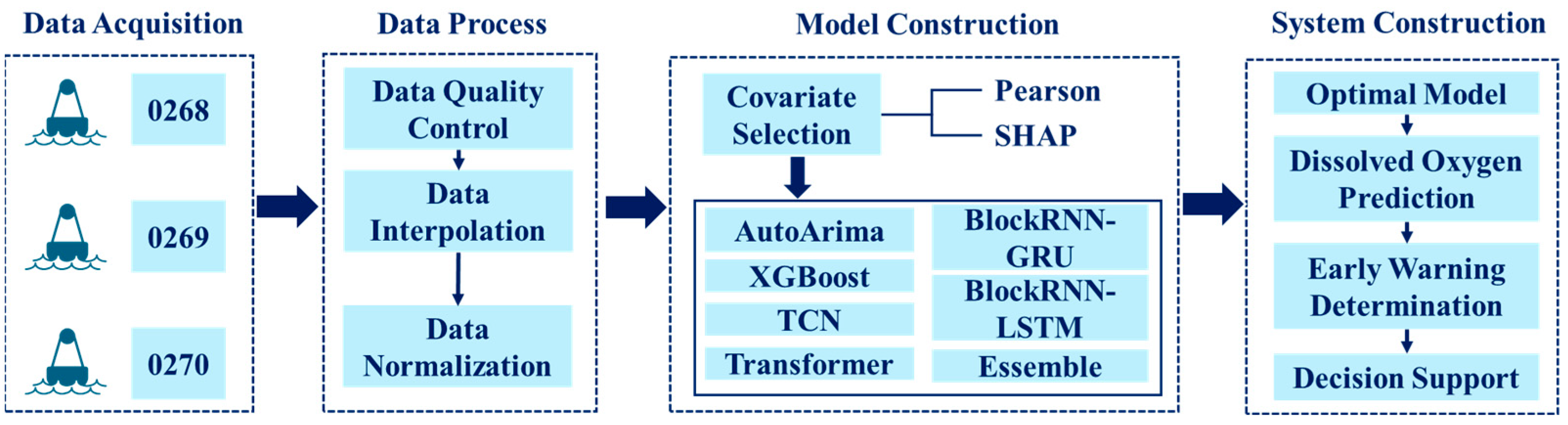
3. Model Construction
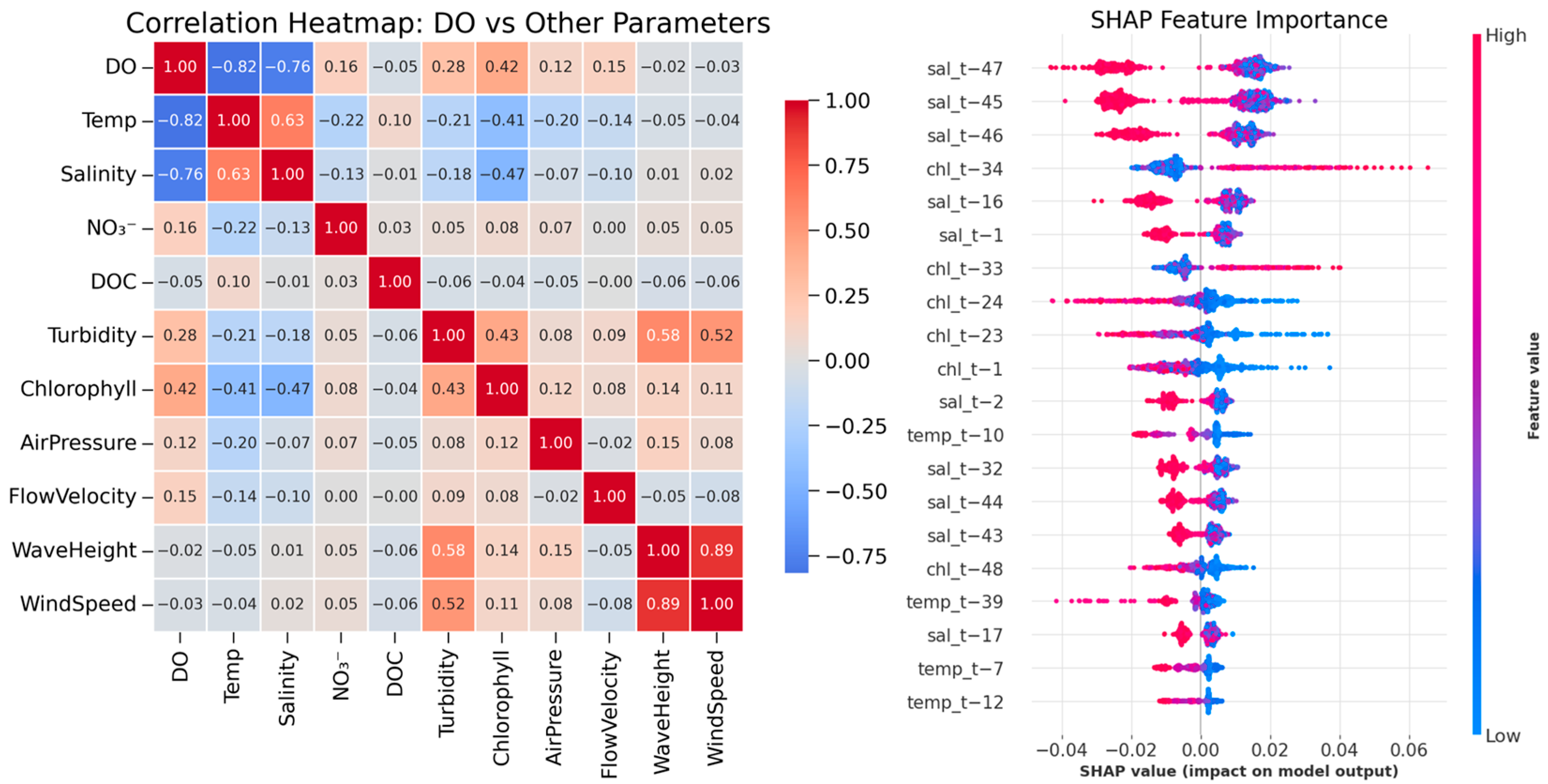
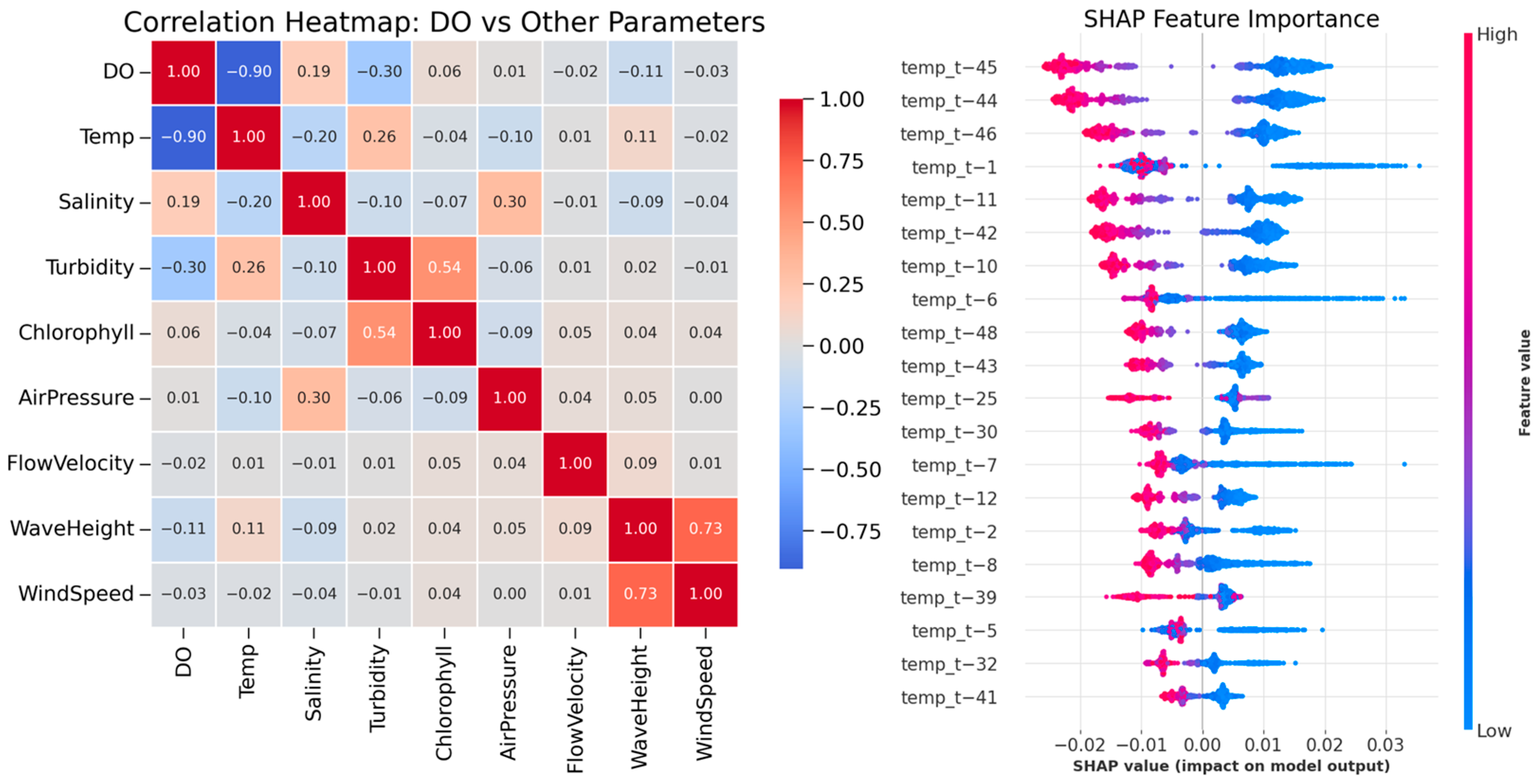
3.1. Covariate Selection for DO Forecasting
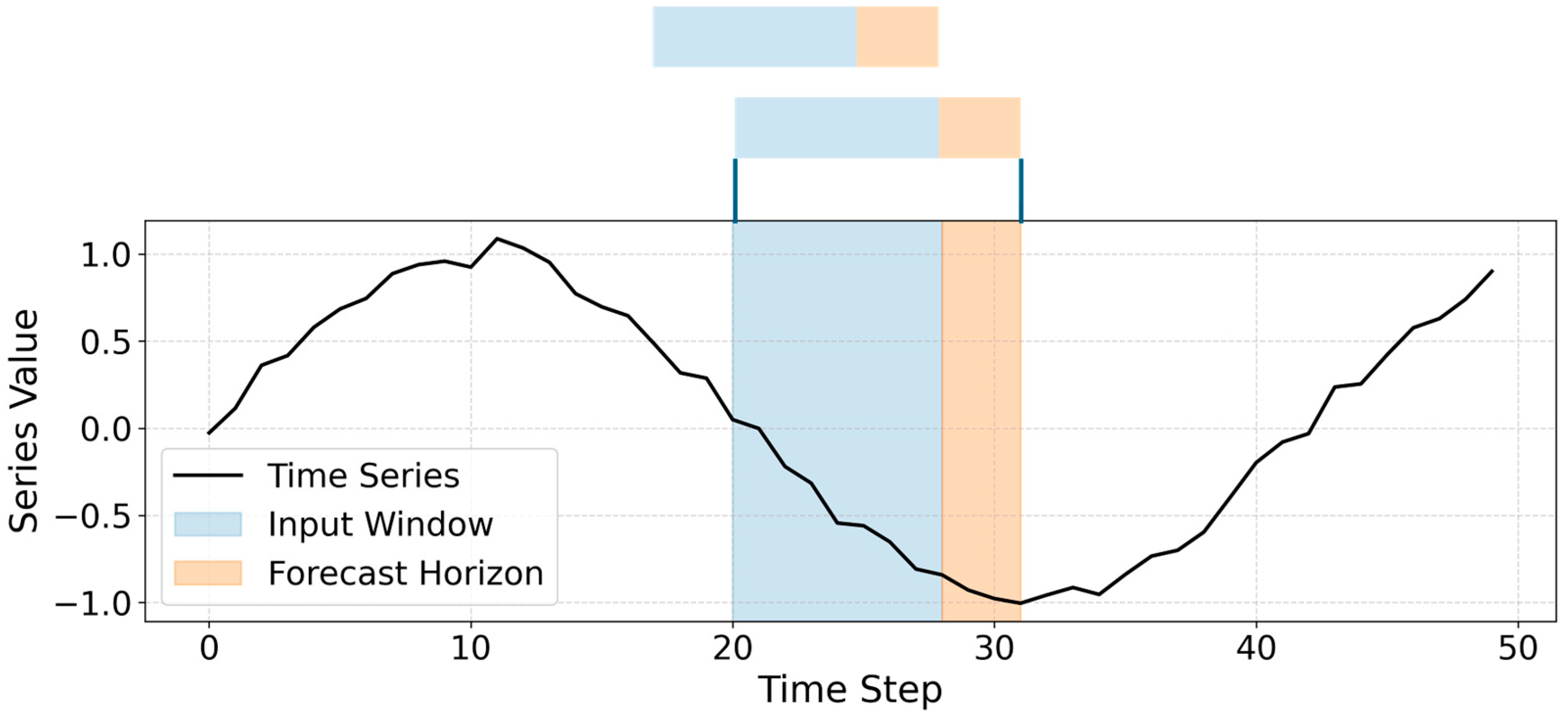
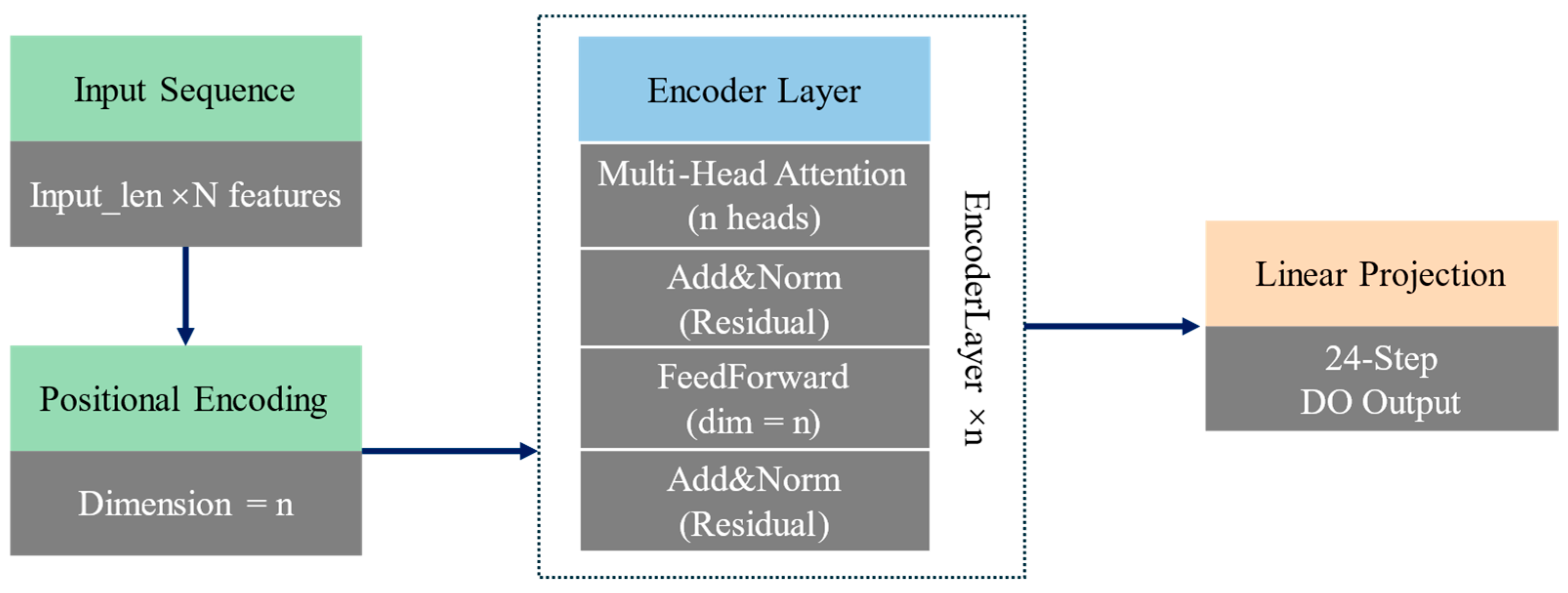
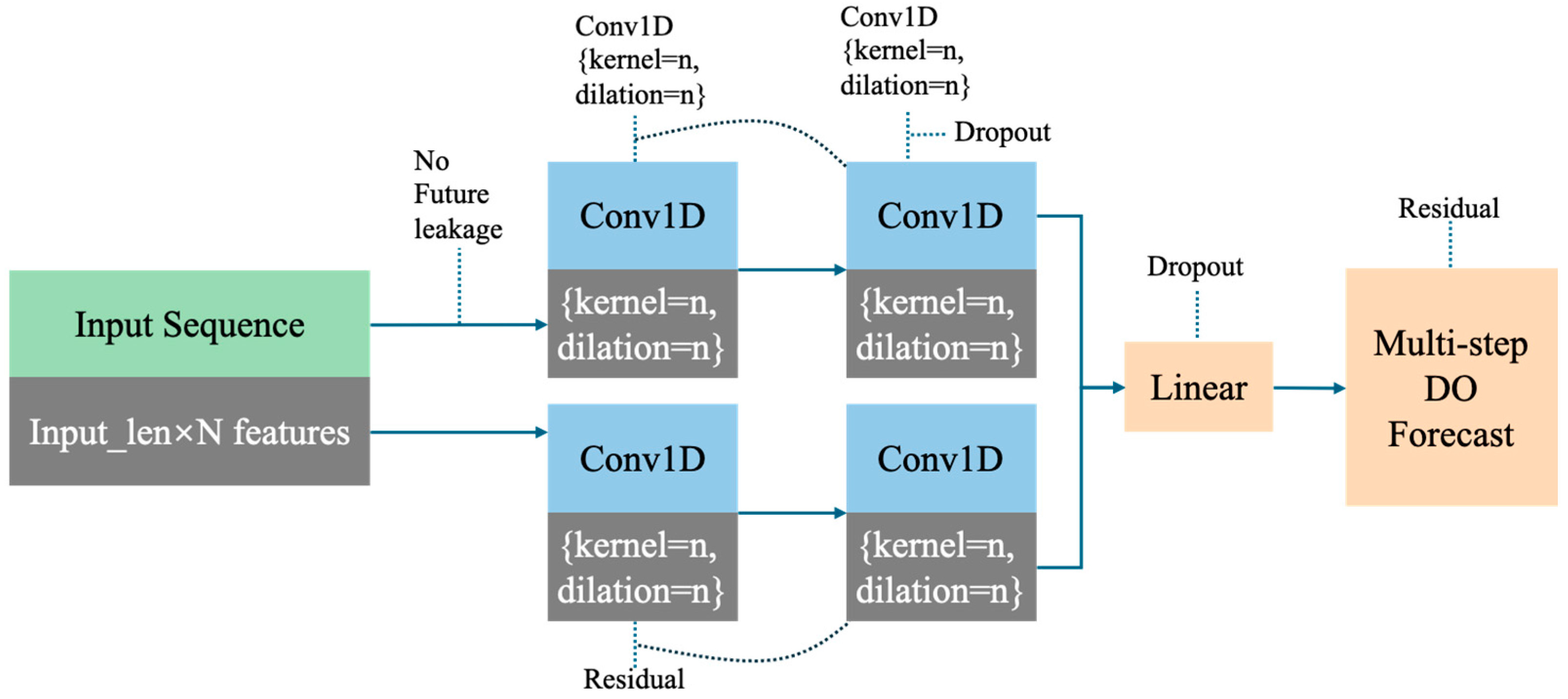
3.2. Forecasting Model Architectures
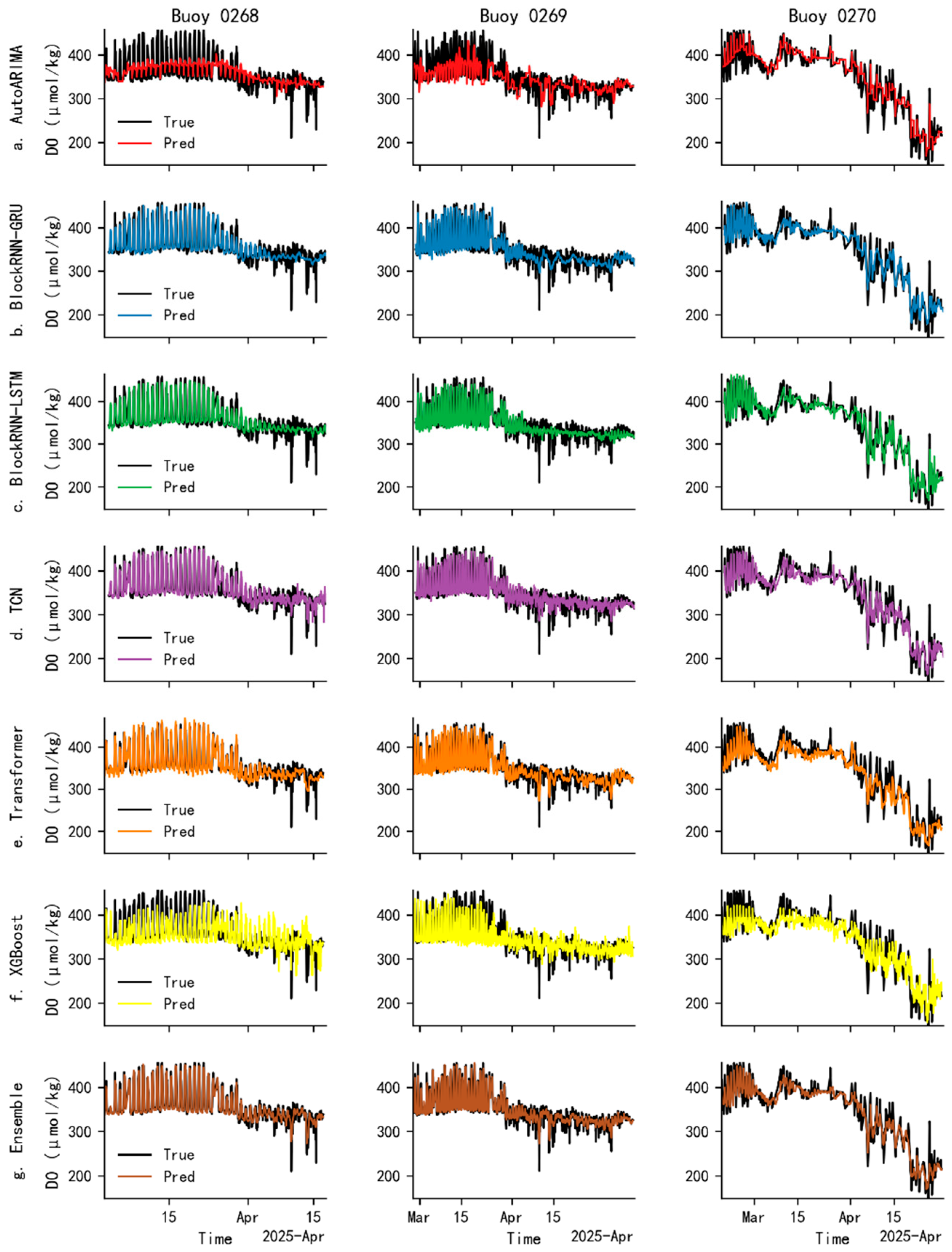
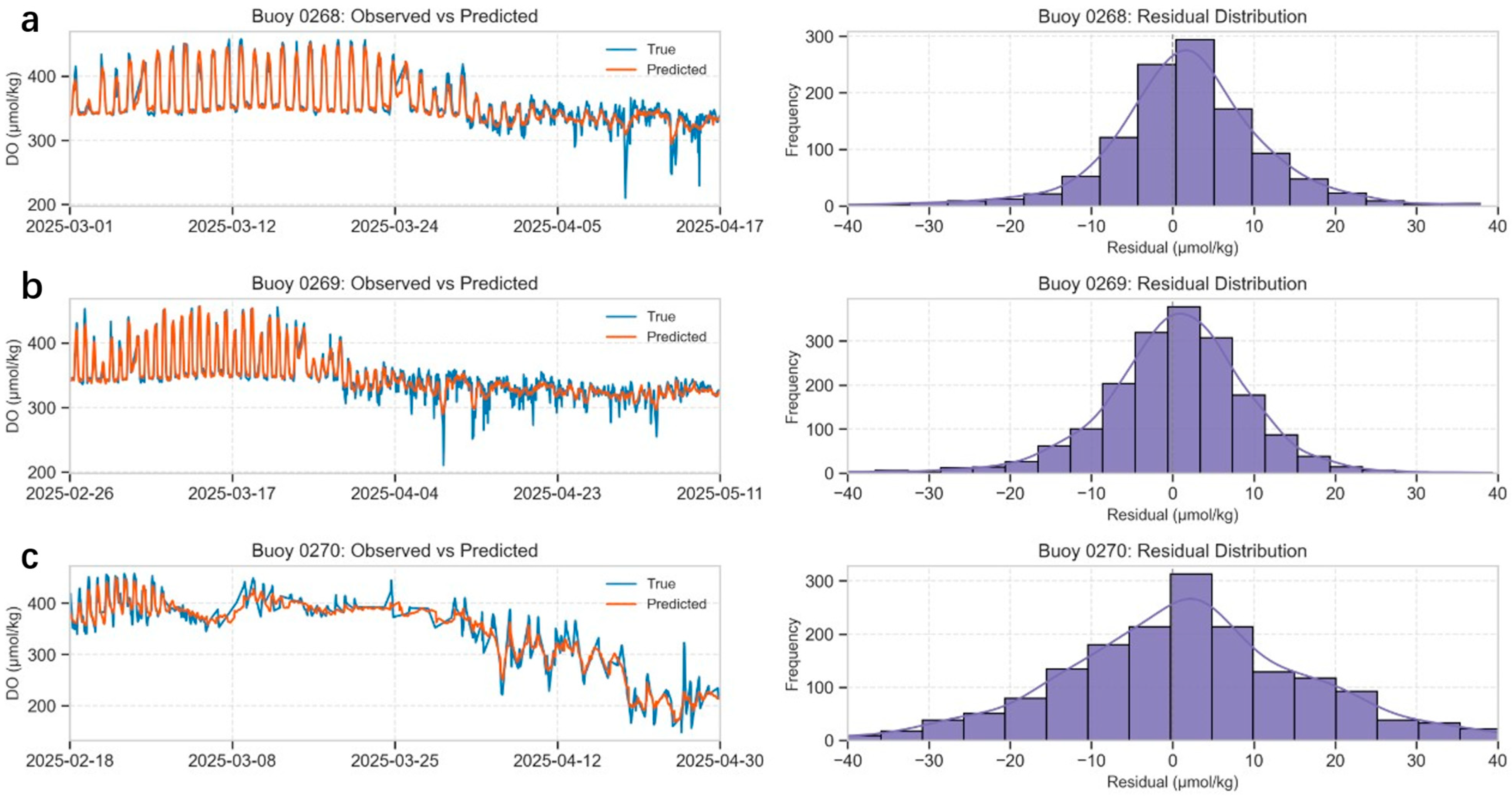
4. Results
5. Discussion
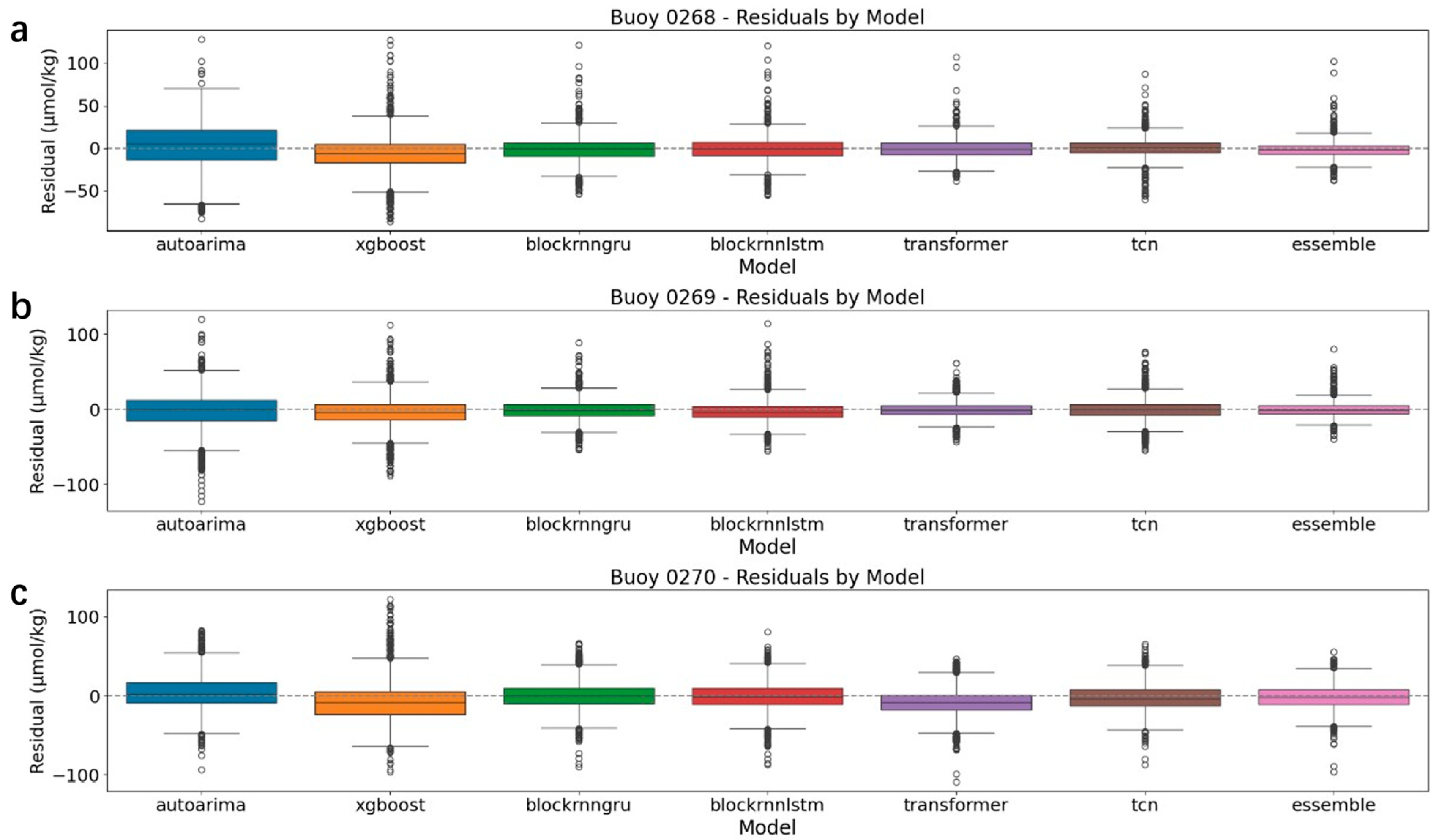
5.1. Model Residual Analysis
5.2. Evaluation of Ensemble Forecasting Models
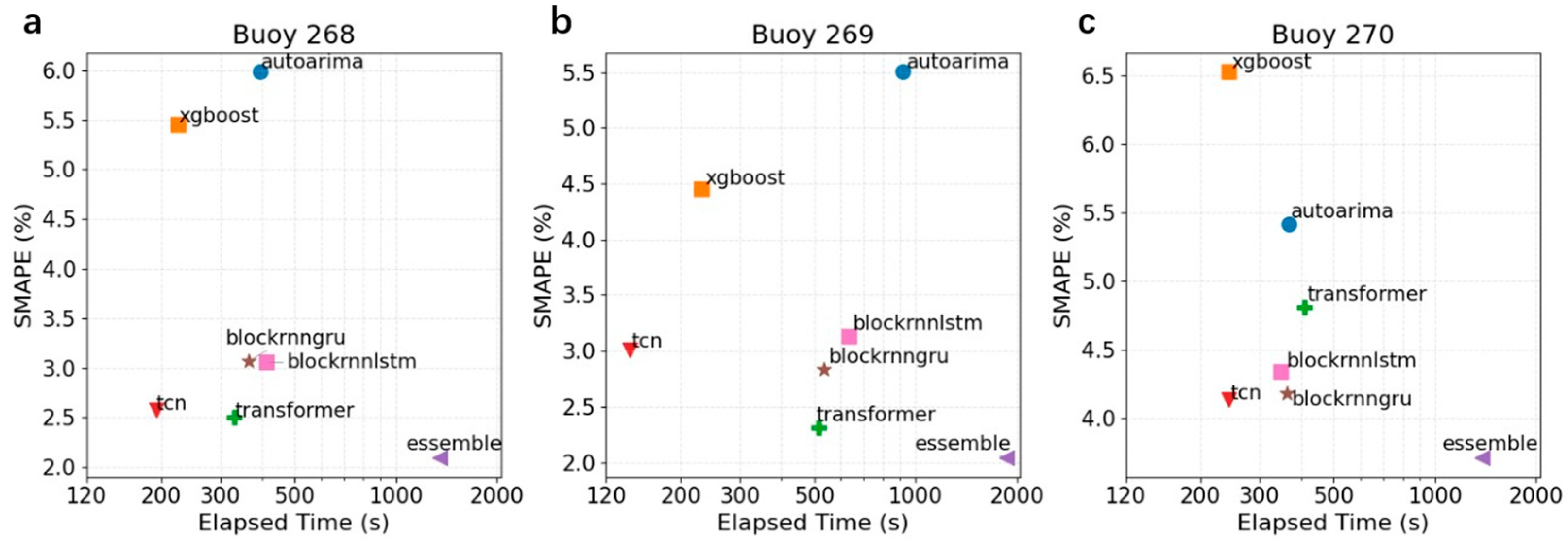
5.3. Comparison of Model Accuracy and Computational Efficiency for Each Buoy
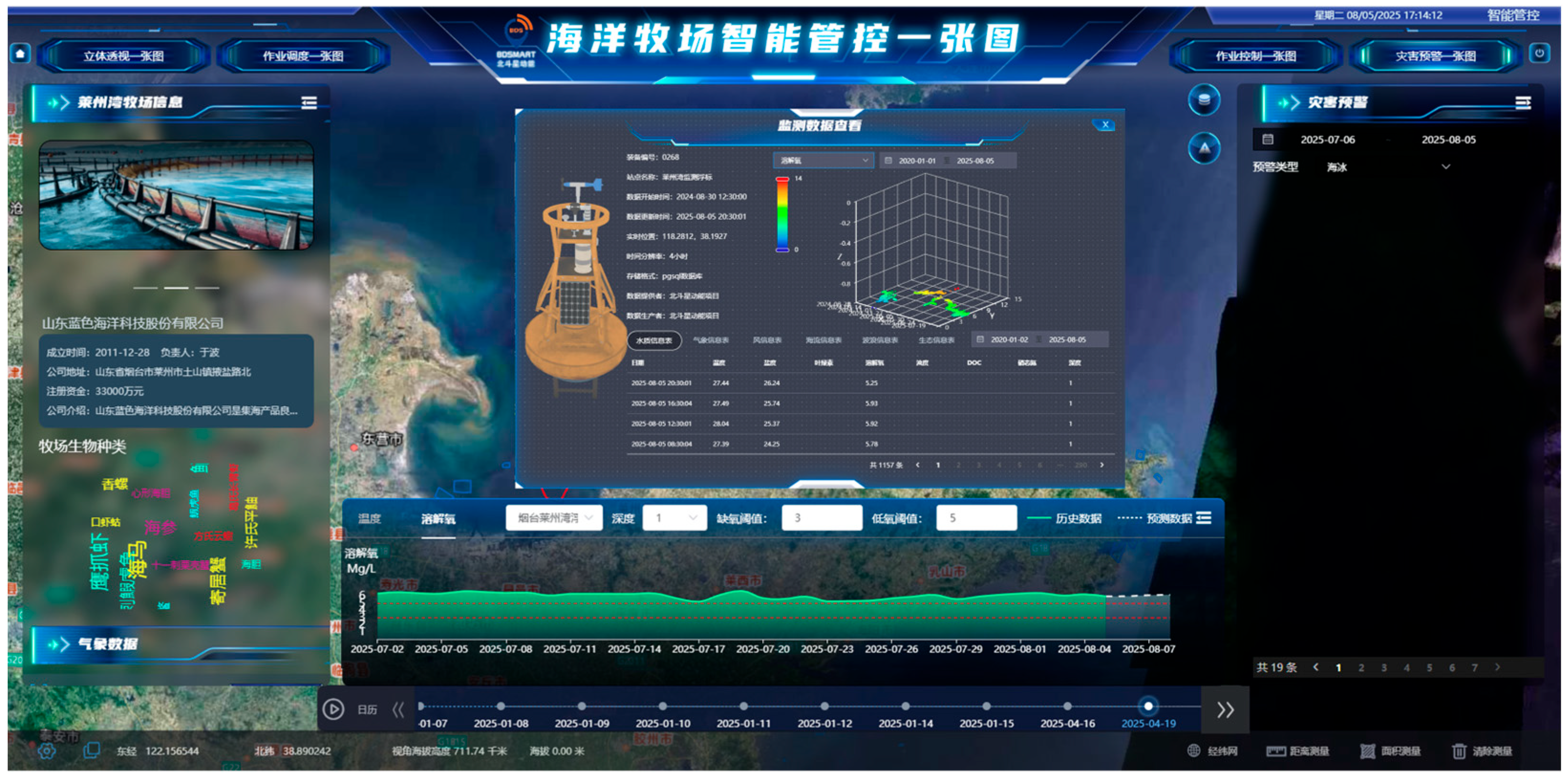
5.4. Low-Oxygen Early-Warning System for Marine Ranching
- (1)
- Ecological warning line (5 mg/L or 152 μmol/kg): Indicates the onset of mild hypoxia, where sensitive organisms may exhibit stress responses such as reduced feeding and metabolic activity. Enhanced monitoring and moderate adjustments in farming operations are recommended.
- (2)
- Hypoxia alert line (3 mg/L or 93 μmol/kg): Represents severe hypoxia levels, posing significant survival risks to cultured organisms. Immediate emergency interventions, such as oxygenation or water exchange, are advised.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Laffoley, D.; Baxter, J.M. Ocean Deoxygenation: Everyone’s Problem; IUCN: Gland, Switzerland, 2019; ISBN 978-2-8317-2014-2. [Google Scholar]
- Gachloo, M.; Liu, Q.; Song, Y.; Wang, G.; Zhang, S.; Hall, N. Using Machine Learning Models for Short-Term Prediction of Dissolved Oxygen in a Microtidal Estuary. Water 2024, 16, 1998. [Google Scholar] [CrossRef]
- Ahmed, A.A.M.; Jui, S.J.J.; Chowdhury, M.A.I.; Ahmed, O.; Sutradha, A. The Development of Dissolved Oxygen Forecast Model Using Hybrid Machine Learning Algorithm with Hydro-Meteorological Variables. Environ. Sci. Pollut. Res. 2023, 30, 7851–7873. [Google Scholar] [CrossRef]
- Liang, X.; Jian, Z.; Tan, Z.; Dai, R.; Wang, H.; Wang, J.; Qiu, G.; Chang, M.; Li, T. Dissolved Oxygen Concentration Prediction in the Pearl River Estuary with Deep Learning for Driving Factors Identification: Temperature, pH, Conductivity, and Ammonia Nitrogen. Water 2024, 16, 3090. [Google Scholar] [CrossRef]
- Moon, J.; Lee, J.; Lee, S.; Yun, H. Urban River Dissolved Oxygen Prediction Model Using Machine Learning. Water 2022, 14, 1899. [Google Scholar] [CrossRef]
- Chen, C.-C.; Gong, G.-C.; Chou, W.-C.; Shiah, F.-K. Hypoxia in Autumn of the East China Sea. Mar. Pollut. Bull. 2020, 152, 110875. [Google Scholar] [CrossRef]
- Garabaghi, F.H.; Benzer, S.; Benzer, R. Modeling Dissolved Oxygen Concentration Using Machine Learning Techniques with Dimensionality Reduction Approach. Environ. Monit. Assess. 2023, 195, 879. [Google Scholar] [CrossRef]
- Abba, S.I.; Linh, N.T.T.; Abdullahi, J.; Ali, S.I.A.; Pham, Q.B.; Abdulkadir, R.A.; Costache, R.; Nam, V.T.; Anh, D.T. Hybrid Machine Learning Ensemble Techniques for Modeling Dissolved Oxygen Concentration. IEEE Access 2020, 8, 157218–157237. [Google Scholar] [CrossRef]
- Granata, F.; Zhu, S.; Nunno, F.D. Dissolved Oxygen Forecasting in the Mississippi River: Advanced Ensemble Machine Learning Models. Environ. Sci. Adv. 2024, 3, 1537–1551. [Google Scholar] [CrossRef]
- Li, W.; Fang, H.; Qin, G.; Tan, X.; Huang, Z.; Zeng, F.; Du, H.; Li, S. Concentration Estimation of Dissolved Oxygen in Pearl River Basin Using Input Variable Selection and Machine Learning Techniques. Sci. Total Environ. 2020, 731, 139099. [Google Scholar] [CrossRef] [PubMed]
- Yang, J. Predicting Water Quality through Daily Concentration of Dissolved Oxygen Using Improved Artificial Intelligence. Sci. Rep. 2023, 13, 20370. [Google Scholar] [CrossRef]
- Olyaie, E.; Zare Abyaneh, H.; Danandeh Mehr, A. A Comparative Analysis among Computational Intelligence Techniques for Dissolved Oxygen Prediction in Delaware River. Geosci. Front. 2017, 8, 517–527. [Google Scholar] [CrossRef]
- Heddam, S. Intelligent Data Analytics Approaches for Predicting Dissolved Oxygen Concentration in River: Extremely Randomized Tree Versus Random Forest, MLPNN and MLR. In Intelligent Data Analytics for Decision-Support Systems in Hazard Mitigation: Theory and Practice of Hazard Mitigation; Deo, R.C., Samui, P., Kisi, O., Yaseen, Z.M., Eds.; Springer: Singapore, 2021; pp. 89–107. ISBN 978-981-15-5772-9. [Google Scholar]
- Hu, Y.; Liu, C.; Wollheim, W.M. Prediction of Riverine Daily Minimum Dissolved Oxygen Concentrations Using Hybrid Deep Learning and Routine Hydrometeorological Data. Sci. Total Environ. 2024, 918, 170383. [Google Scholar] [CrossRef]
- Wei, L.; Guan, L.; Qu, L. Prediction of Sea Surface Temperature in the South China Sea by Artificial Neural Networks. IEEE Geosci. Remote Sens. Lett. 2020, 17, 558–562. [Google Scholar] [CrossRef]
- Liang, W.; Liu, T.; Wang, Y.; Jiao, J.J.; Gan, J.; He, D. Spatiotemporal-Aware Machine Learning Approaches for Dissolved Oxygen Prediction in Coastal Waters. Sci. Total Environ. 2023, 905, 167138. [Google Scholar] [CrossRef]
- Chang, W.; Li, X.; Dong, H.; Wang, C.; Zhao, Z.; Wang, Y. Real-Time Prediction of Ocean Observation Data Based on Transformer Model. In Proceedings of the 2021 ACM International Conference on Intelligent Computing and Its Emerging Applications, Jinan, China, 28–29 December 2021; Association for Computing Machinery: New York, NY, USA, 2022; pp. 83–88. [Google Scholar]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-Term Water Quality Variable Prediction Using a Hybrid CNN–LSTM Deep Learning Model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Ayesha Jasmin, S.; Ramesh, P.; Tanveer, M. An Intelligent Framework for Prediction and Forecasting of Dissolved Oxygen Level and Biofloc Amount in a Shrimp Culture System Using Machine Learning Techniques. Expert Syst. Appl. 2022, 199, 117160. [Google Scholar] [CrossRef]
- Ziyad Sami, B.F.; Latif, S.D.; Ahmed, A.N.; Chow, M.F.; Murti, M.A.; Suhendi, A.; Ziyad Sami, B.H.; Wong, J.K.; Birima, A.H.; El-Shafie, A. Machine Learning Algorithm as a Sustainable Tool for Dissolved Oxygen Prediction: A Case Study of Feitsui Reservoir, Taiwan. Sci. Rep. 2022, 12, 3649. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, C.; Chen, J.; Jiang, H.; Li, D.; Zhang, J.; Han, B.; Chen, S.; Wang, C. Water Quality Parameters-Based Prediction of Dissolved Oxygen in Estuaries Using Advanced Explainable Ensemble Machine Learning. J. Environ. Manag. 2025, 380, 125146. [Google Scholar] [CrossRef]
- Xue, H.; Wang, L.; Li, D. Design and Development of Dissolved Oxygen Real-Time Prediction and Early Warning System for Brocaded Carp Aquaculture. In Proceedings of the Computer and Computing Technologies in Agriculture VI; Li, D., Chen, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 35–42. [Google Scholar]
- Fakhrudin, M.; Subehi, L.; Jasalesmana, T.; Dianto, A. Dissolved Oxygen and Temperature Stratification Analysis for Early Warning System Development in Preventing Mass Mortality of Fish in Lake Maninjau, West Sumatera-Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2019, 380, 012002. [Google Scholar] [CrossRef]
- Shaghaghi, N.; Fazlollahi, F.; Shrivastav, T.; Graham, A.; Mayer, J.; Liu, B.; Jiang, G.; Govindaraju, N.; Garg, S.; Dunigan, K.; et al. DOxy: A Dissolved Oxygen Monitoring System. Sensors 2024, 24, 3253. [Google Scholar] [CrossRef]
- Anupama, P.; Kumar, E.V.; Ajanth, S.; Anugna, K.; Venkatesh, J. ML-Based Predicting of Dissolved Oxygen Levels for Sustainable River Ecosystem Management. J. Sci. Eng. Technol. Manag. Sci. 2025, 2, 590–601. [Google Scholar] [CrossRef]
- Li, S.; Wang, B.; Deng, Z.; Wu, B.; Zhu, X.; Chen, Z. Data Quality Control Method of a New Drifting Observation Technology Named Drifting Air-Sea Interface Buoy. J. Ocean Univ. China 2024, 23, 11–22. [Google Scholar] [CrossRef]


| Buoy ID | Area | Parameter | Unit | Frequency (min) | Depth (m) |
|---|---|---|---|---|---|
| 0268 | Laizhou Bay | Sea Temperature | °C | 15 | −3, −6 |
| DO | μmol/kg | 30 | −1 | ||
| Salinity | ‰ | 15 | −3, −6 | ||
| NN | mg/L | 60 | −1 | ||
| DOC | μmol/kg | 60 | −1 | ||
| Turbidity | NTU | 30 | −1 | ||
| Chl-a | RFU | 30 | −1 | ||
| CV | m/s | 15 | −2, −4, −6 | ||
| AP | hPa | 15 | 2 | ||
| WS | m/s | 15 | 2 | ||
| WH | m | 15 | −1 |
| Model Category | Model Name | Core Structural Characteristics | Key Hyperparameters |
|---|---|---|---|
| Statistical | AutoARIMA | ARIMA with automatic order/seasonality selection | P = 5, q = 5, P = 2, Q = 2, m = 24, d = 1, D = 1 |
| Machine Learning | XGBoost | Gradient-boosted decision trees | n_estimators = 100, max_depth = 6, learning_rate = 0.3, subsample = 0.8, colsample_bytree = 0.8, min_child_weight = 5 |
| Deep Learning | BlockRNN-LSTM | Recurrent network with LSTM blocks (block-wise sequence modeling) | input_length = 144, output_length = 24, hidden_size = 32, n_layers = 3, dropout = 0.2, batch_size = 16 |
| Deep Learning | BlockRNN-GRU | Recurrent network with GRU blocks (block-wise sequence modeling) | input_length = 144, output_length = 24, hidden_size = 64, n_layers = 2, dropout = 0.2, batch_size = 16 |
| Deep Learning | TCN | Dilated causal 1D convolutions with residual/skip connections | input_length = 144, output_length = 24, kernel_size = 5, num_filters = 5, dilation = 2, dropout = 0.1 |
| Deep Learning | Transformer | Self-attention encoder–decoder with causal masking | input_length = 96, output_length = 24, d_model = 16, n_heads = 4, n_layers = 2, ff_dim = 64, dropout = 0.1, batch_size = 16 |
| Deep Learning | Ensemble (LSTM + GRU + TCN + Transformer) | Fusion of four deep nets (weighted averaging/stacking) | models = [GRUmodel, LSTMmodel, TCNmodel, Transmodel], fusion_strategy = NaiveEnsembleModel, weights = [0.25,0.25,0.25,0.25] |
| Model | Target Variable | Input Variables | Lag Range (hours) |
|---|---|---|---|
| AutoARIMA | DO | Time, DO | t-1~t-24 |
| XGBoost | DO | Time, DO, Temp, Sal, Chl | t-1~t-72 |
| BlockRNN-LSTM | DO | Time, DO, Temp, Sal, Chl | t-1~t-144 |
| BlockRNN-GRU | DO | Time, DO, Temp, Sal, Chl | t-1~t-144 |
| TCN | DO | Time, DO, Temp, Sal, Chl | t-1~t-144 |
| Transformer | DO | Time, DO, Temp, Sal, Chl | t-1~t-144 |
| EnsembleModel | DO | Time, DO, Temp, Sal, Chl | t-1~t-144 |
| Buoy ID | Model | Train | Test | ||||
|---|---|---|---|---|---|---|---|
| Mape | RMSE (μmol/kg) | R2 | Mape | RMSE (μmol/kg) | R2 | ||
| 0268 | AutoArima | 0.97% | 6.171 | 0.98 | 6.02% | 27.89 | 0.39 |
| XGBoost | 2.21% | 12.76 | 0.93 | 5.43% | 28.05 | 0.39 | |
| LSTM | 1.37% | 6.64 | 0.96 | 3.1% | 16.28 | 0.79 | |
| GRU | 1.47% | 5.97 | 0.97 | 3.09% | 15.97 | 0.8 | |
| Transformer | 2.40% | 10.66 | 0.95 | 2.53% | 12.33 | 0.88 | |
| TCN | 1.4% | 6.28 | 0.98 | 2.59% | 13.59 | 0.86 | |
| Essemble | 1.01% | 5.02 | 0.98 | 2.11% | 11.01 | 0.9 | |
| 0269 | AutoArima | 1.22% | 5.66 | 0.98 | 5.48% | 26.57 | 0.36 |
| XGBoost | 3.34% | 13.82 | 0.94 | 4.45% | 21.88 | 0.57 | |
| LSTM | 2.71% | 10.22 | 0.97 | 3.15% | 14.87 | 0.8 | |
| GRU | 2.57 | 9.55 | 0.97 | 2.85% | 13.44 | 0.83 | |
| Transformer | 2.86% | 11.06 | 0.96 | 2.32% | 10.83 | 0.89 | |
| TCN | 1.96% | 7.49 | 0.98 | 3.03% | 14.61 | 0.8 | |
| Essemble | 1.52% | 5.81 | 0.98 | 2.06% | 10.23 | 0.91 | |
| 0270 | AutoArima | 2.06% | 8.28 | 0.98 | 5.59% | 23.11 | 0.89 |
| XGBoost | 5.01% | 19.89 | 0.93 | 6.65% | 27.65 | 0.84 | |
| LSTM | 3.52% | 12.89 | 0.97 | 4.35% | 18.6 | 0.93 | |
| GRU | 3.64% | 13.19 | 0.97 | 4.22% | 17.9 | 0.93 | |
| Transformer | 4.74% | 17.13 | 0.94 | 4.7% | 19.9 | 0.92 | |
| TCN | 2.55% | 9.55 | 0.98 | 4.14% | 17.37 | 0.94 | |
| Essemble | 1.79% | 6.48 | 0.98 | 3.7% | 15.84 | 0.95 | |
| Buoy ID | Forecast Horizon | MAPE | RMSE (μmol/kg) | R2 |
|---|---|---|---|---|
| 0268 | 24 | 2.11% | 11.01 | 0.9 |
| 48 | 2.43% | 12.9 | 0.87 | |
| 72 | 2.83% | 13.96 | 0.84 | |
| 0269 | 24 | 2.06% | 10.23 | 0.91 |
| 48 | 2.47% | 11.91 | 0.87 | |
| 72 | 2.71% | 12.94 | 0.84 | |
| 0270 | 24 | 3.7% | 15.84 | 0.95 |
| 48 | 3.85% | 16.01 | 0.94 | |
| 72 | 4.17% | 17.2 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Song, J.; Li, X.; Zhong, G. Deep Learning-Based Rolling Forecasting of Dissolved Oxygen in Shandong Peninsula Coastal Waters. Water 2025, 17, 3102. https://doi.org/10.3390/w17213102
Wang Y, Song J, Li X, Zhong G. Deep Learning-Based Rolling Forecasting of Dissolved Oxygen in Shandong Peninsula Coastal Waters. Water. 2025; 17(21):3102. https://doi.org/10.3390/w17213102
Chicago/Turabian StyleWang, Yanjun, Jinming Song, Xuegang Li, and Guorong Zhong. 2025. "Deep Learning-Based Rolling Forecasting of Dissolved Oxygen in Shandong Peninsula Coastal Waters" Water 17, no. 21: 3102. https://doi.org/10.3390/w17213102
APA StyleWang, Y., Song, J., Li, X., & Zhong, G. (2025). Deep Learning-Based Rolling Forecasting of Dissolved Oxygen in Shandong Peninsula Coastal Waters. Water, 17(21), 3102. https://doi.org/10.3390/w17213102











