Estimation of Hydraulic Characteristics of Unsaturated Loess with SEM Images Based on Fractal Theory
Abstract
1. Introduction
2. Materials and Methods
2.1. Sampling and Preparation
2.2. Theoretical Background
2.2.1. Fractal Model of SWCC and Unsaturated Hydraulic Conductivity
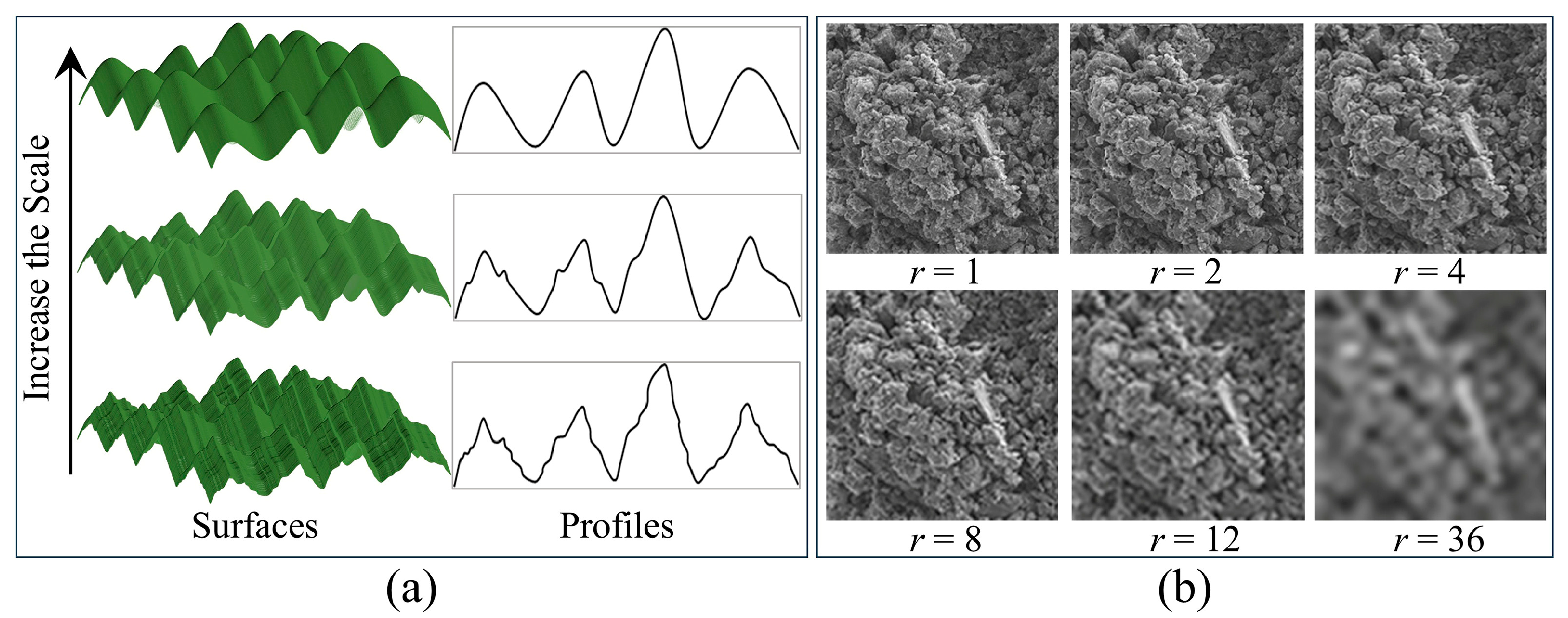
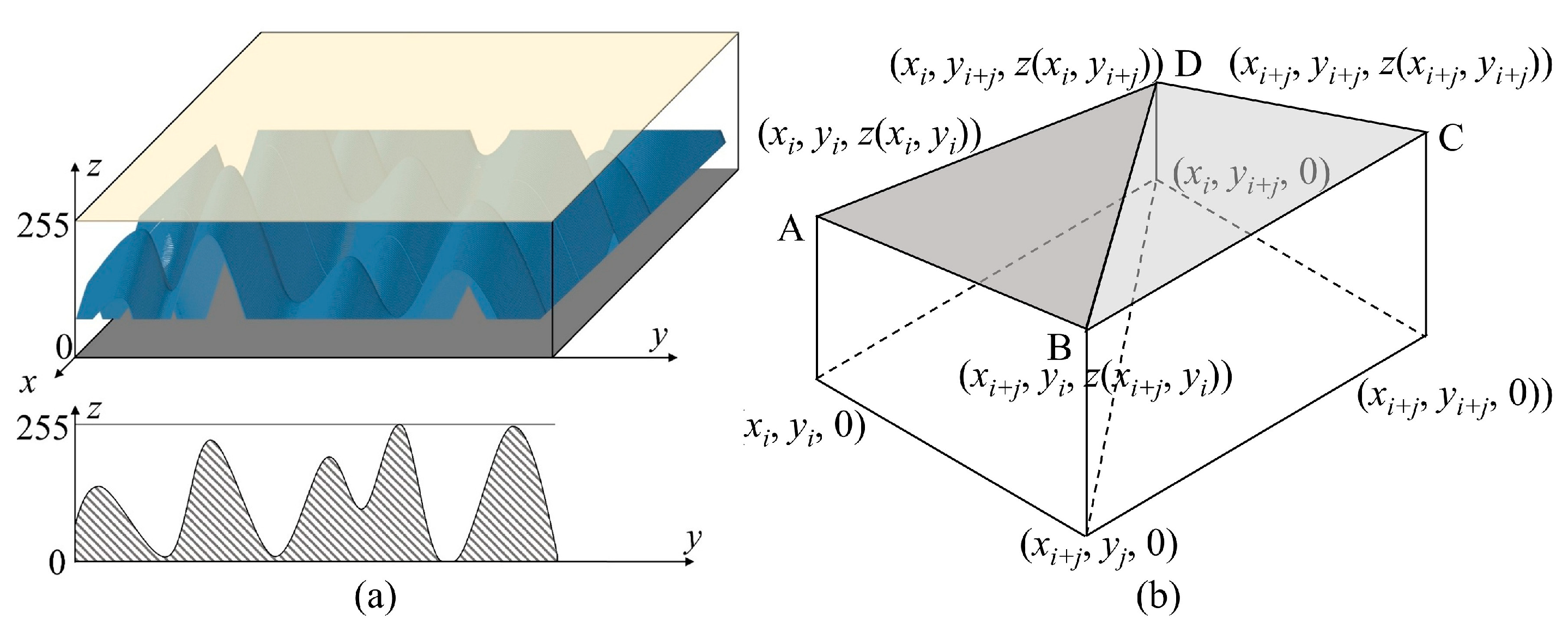
2.2.2. Theory of Three-Dimensional Fractal Dimension Calculation
2.2.3. Calculation of Key Parameters
2.2.4. Error Analysis
2.3. Laboratory Test
2.3.1. SEM Test
2.3.2. Measurement of SWCC and Unsaturated Hydraulic Conductivity
3. Results and Discussion
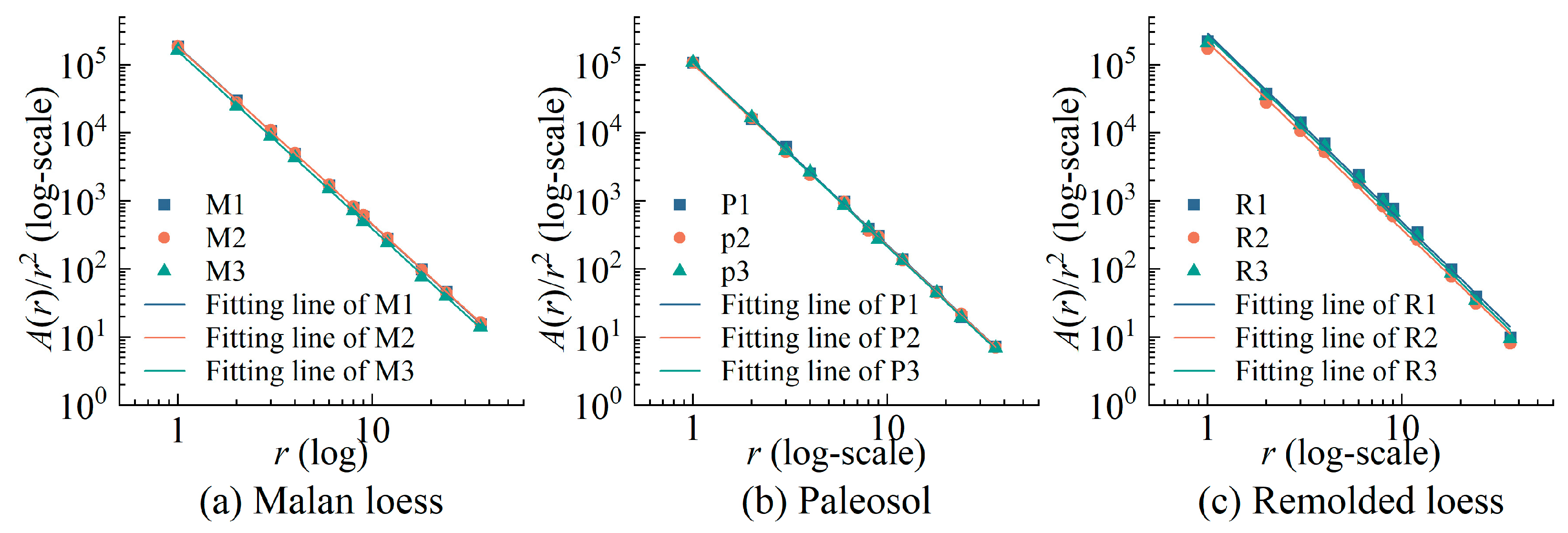
3.1. Three-Dimensional Fractal Dimension
3.2. Prediction Curve of Soil-Water Characteristics Based on Fractal Theory
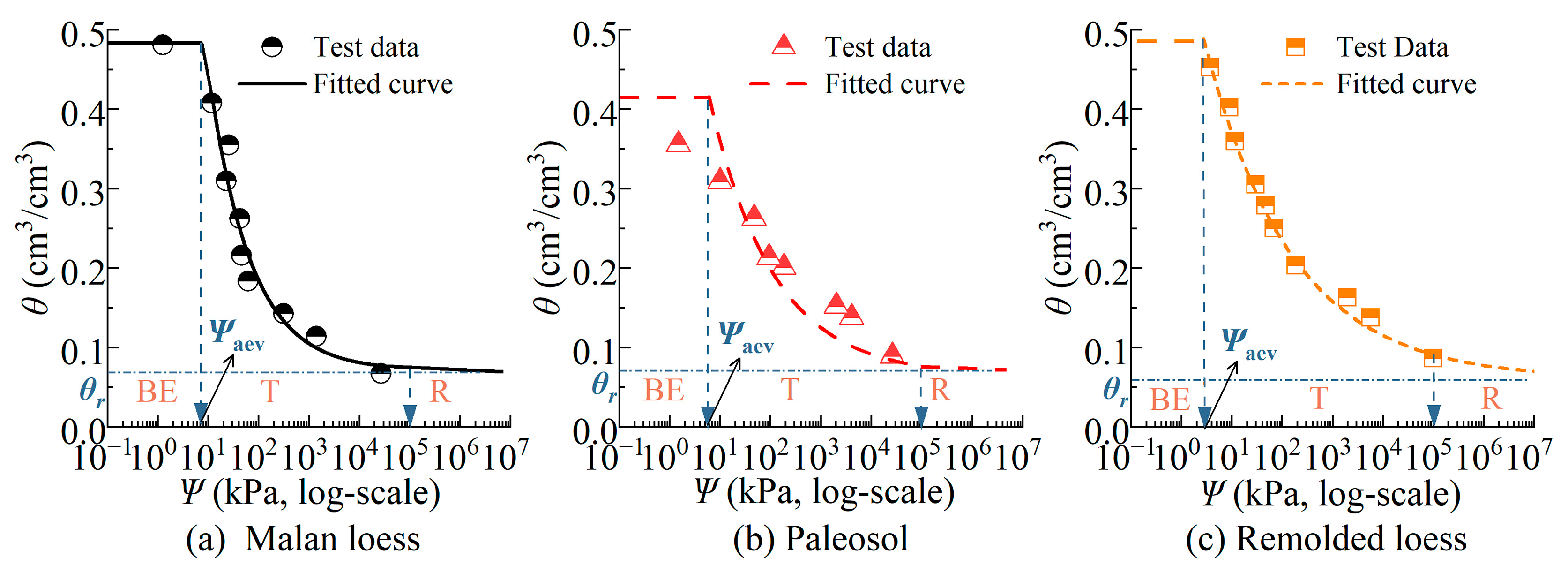
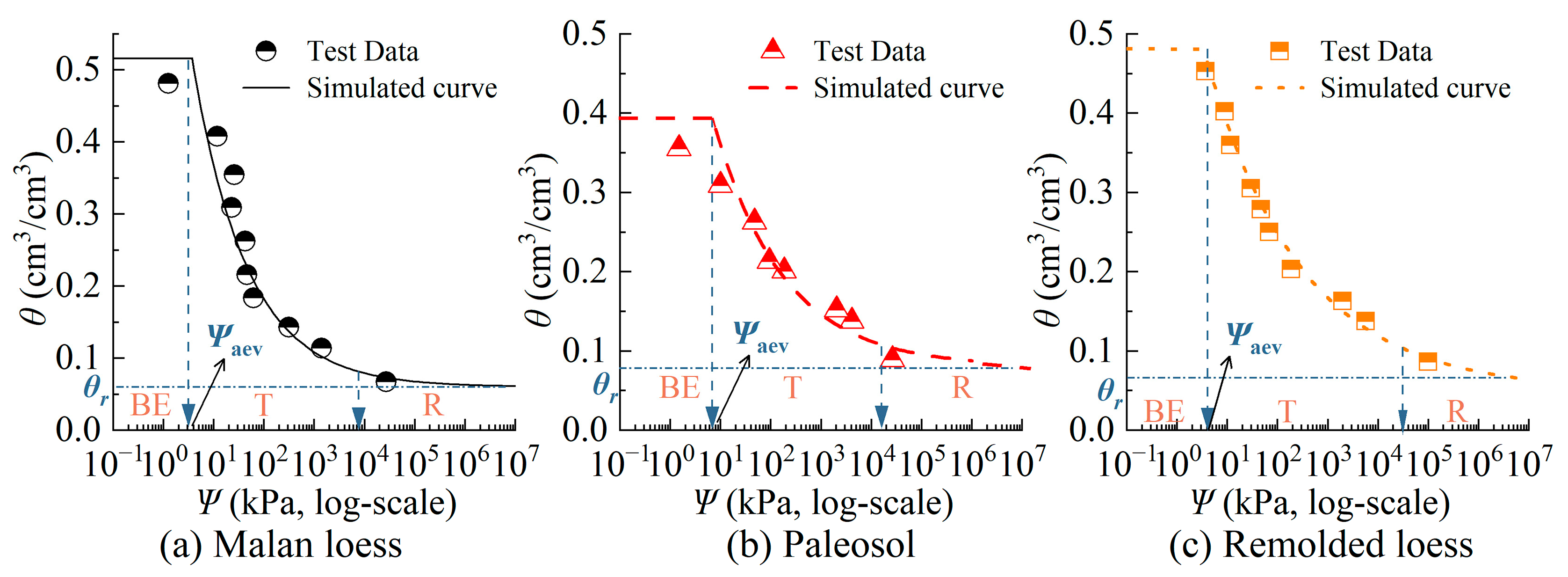
3.2.1. The Test Data of SWCC
3.2.2. The Predicted SWCC Based on Fractal Theory
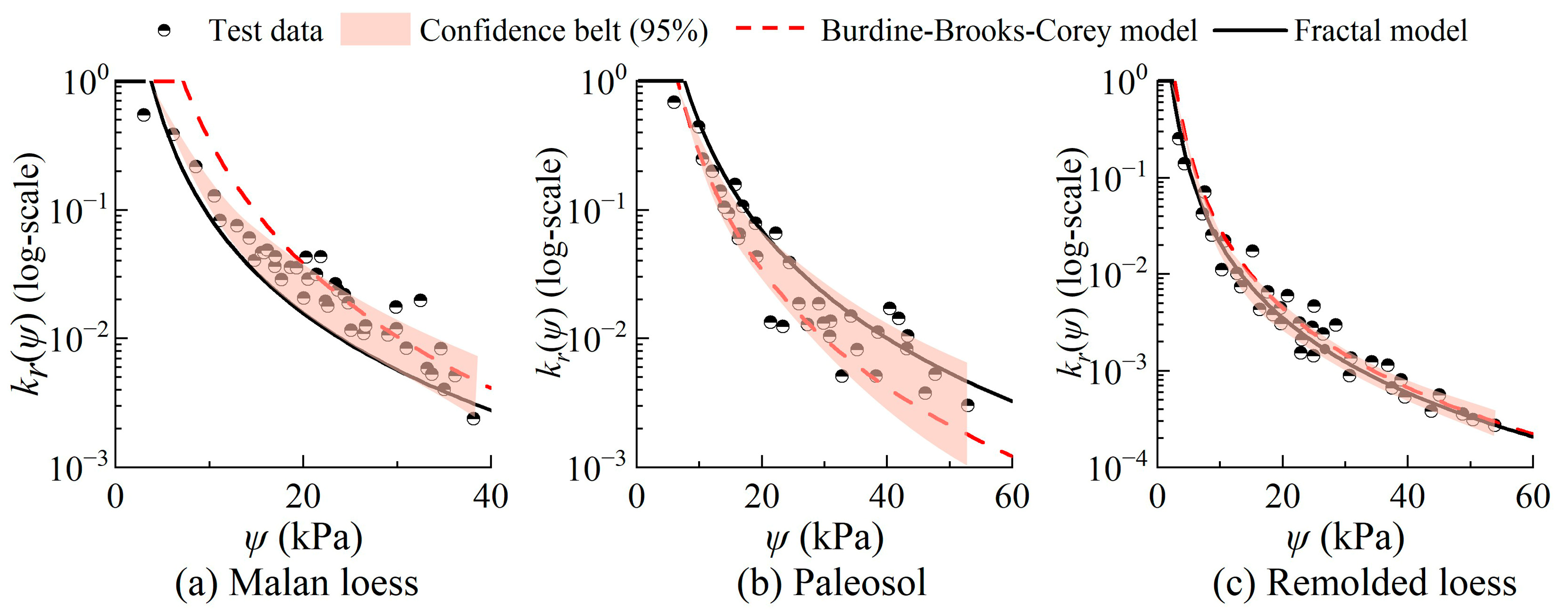
3.3. Prediction of Unsaturated Hydraulic Conductivity Based on Fractal Theory
4. Conclusions
- (1)
- Malan loess, paleosol, and remolded loess all exhibit fractal pore-surface characteristics, with three-dimensional fractal dimensions (Ds) being 2.611, 2.688, and 2.771, respectively. Pore structure complexity follows the order: remolded loess > paleosol > Malan loess.
- (2)
- For SWCC, the fractal model demonstrated relatively good predictive capabilities. The R2 and RMSE values of the fractal model for the three types of soil are: 0.891, 0.879, 0.973, and 0.0037, 0.0121, 0.0011. The water storage capacity of the three soils was in the order of paleosol > remolded loess > Malan loess.
- (3)
- Based on the analysis of three soil types, the fractal model demonstrates superior overall performance in predicting unsaturated hydraulic conductivity compared to the Burdine-Brooks-Corey model. While both models perform excellently for homogeneous remolded loess, the fractal model significantly outperforms the Burdine-Brooks-Corey model for the more heterogeneous natural soils (Malan loess and paleosol). This is quantitatively supported by higher R2 and substantially lower RMSE values for the fractal model’s predictions across these undisturbed soils.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Badakhsahan, E.; Vaunat, J.; Scarfone, R. A hysteretic water retention model incorporating the soil deformability and its application to rainfall-induced landslides. Comput. Geotech. 2025, 178, 106912. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H. Estimation of permeability function from the soil-water characteristic curve. Eng. Geol. 2015, 199, 148–156. [Google Scholar] [CrossRef]
- Lu, N.; Kaya, M.; Godt, J.W. Interrelations among the soil-water retention, hydraulic conductivity, and suction-stress characteristic curves. J. Geotech. Geoenviron. Eng. 2014, 140, 04014007. [Google Scholar] [CrossRef]
- Beyzaei, C.Z.; Bray, J.D.; Cubrinovski, M.; Bastin, S.; Stringer, M.; Jacka, M.; van Ballegooy, S.; Riemer, M.; Wentz, R. Characterization of silty soil thin layering and groundwater conditions for liquefaction assessment. Can. Geotech. J. 2020, 57, 253–276. [Google Scholar] [CrossRef]
- Liu, W.; Lin, G.C.; Su, X. Effects of pre-dynamic loading on hydraulic properties and microstructure of undisturbed loess. J. Hydrol. 2023, 622, 129690. [Google Scholar] [CrossRef]
- Peng, J.B.; Wang, Q.Y.; Zhuang, J.Q.; Leng, Y.Q.; Fan, Z.J.; Wang, S.K. Dynamic formation mechanism of landslide disaster on the Loess Plateau. J. Geomech. 2020, 26, 714–730. (In Chinese) [Google Scholar] [CrossRef]
- Xu, P.P.; Zhang, Q.Y.; Qian, H.; Hou, K. Investigation into microscopic mechanisms of anisotropic saturated permeability of undisturbed Q2 loess. Environ. Earth Sci. 2020, 79, 412. [Google Scholar] [CrossRef]
- Chen, Y.F.; Li, P.Y.; Wang, Y.H.; Li, J.H. Unraveling the Mystery of Water-Induced Loess Disintegration: A Comprehensive Review of Experimental Research. Sustainability 2024, 16, 2463. [Google Scholar] [CrossRef]
- Peng, D.L.; Xu, Q.; Liu, F.Z.; He, Y.S.; Zhang, S.; Qi, X.; Zhao, K.Y.; Zhang, X.L. Distribution and failure modes of the landslides in Heitai terrace, China. Eng. Geol. 2018, 236, 97–110. [Google Scholar] [CrossRef]
- Leshchinsky, B.; Olsen, M.J.; Mohney, C.; O’Banion, M.; Bunn, M.; Allan, J.; McClung, R. Quantifying the sensitivity of progressive landslide movements to failure geometry, undercutting processes and hydrological changes. J. Geophys. Res.-Earth Surf. 2019, 124, 616–638. [Google Scholar] [CrossRef]
- Chai, J.C.; Khaimook, P. Prediction of soil-water characteristic curves using basic soil properties. Transp. Geotech. 2020, 22, 100295. [Google Scholar] [CrossRef]
- Gao, X.L.; Zhang, Y.C.; Huang, H.W.; Liu, D.F.; Liu, Z.F. Soil-water characteristics and hysteresis effects of loess considering deformation. Rock Soil Mech. 2023, 44, 2350–2359. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, C.; Lourenço, S.D.N.; Dong, S.; Jiang, Y. Factors affecting the soil-water retention curve of Chinese loess. Bull. Eng. Geol. Environ. 2021, 80, 717–729. [Google Scholar] [CrossRef]
- Gao, Z.Y.; Chai, J.C. Method for predicting unsaturated permeability using basic soil properties. Transp. Geotech. 2022, 34, 100754. [Google Scholar] [CrossRef]
- Bordoni, M.; Bittelli, M.; Valentino, R.; Chersich, S.; Meisina, C. Improving the estimation of complete field soil water characteristic curves through field monitoring data. J. Hydrol. 2017, 552, 283–305. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Salim, N.M.; Irshayyid, E.J. Determination of the soil-water characteristic curve of unsaturated bentonite-sand mixtures. Environ. Earth Sci. 2017, 76, 201. [Google Scholar] [CrossRef]
- Li, X.J.; Hu, C.Z.; Li, F.Y.; Gao, H.L. Determining soil water characteristic curve of lime treated loess using multiscale structure fractal characteristic. Sci. Rep. 2020, 22, 21569. [Google Scholar] [CrossRef]
- Lu, N. Generalized soil water retention equation for adsorption and capillarity. J. Geotech. Geoenviron. Eng. 2016, 142, 04016051. [Google Scholar] [CrossRef]
- Yang, H.Q.; Zhang, L.L. Bayesian back analysis of unsaturated hydraulic parameters for rainfall-induced slope failure: A review. Earth-Sci. Rev. 2024, 251, 104714. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media and their relation to drainage design. Trans. ASAE 1964, 7, 26–28. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Pan, P.; Shang, Y.Q.; Lyu, Q.; Yang, Y. Periodic recurrence and scale-expansion mechanism of loess landslides caused by groundwater seepage and erosion. Bull. Eng. Geol. Environ. 2019, 78, 1143–1155. [Google Scholar] [CrossRef]
- Dawit, K.; Samuel, F. Comparison and applicability of selected soil erosion estimation models. Hydrology 2021, 9, 79–87. [Google Scholar] [CrossRef]
- Bayat, H.; Rastgo, M.; Zadeh, M.M.; Vereecken, H. Particle size distribution models, their characteristics and fitting capability. J. Hydrol. 2015, 529, 872–889. [Google Scholar] [CrossRef]
- Zhao, J.Y.; Li, S.Y.; Wang, C.; You, T.T.; Liu, X.Y.; Zhao, Y.C. A universal soil-water characteristic curve model based on the particle size distribution and fractal theory. J. Hydrol. 2023, 622, 129691. [Google Scholar] [CrossRef]
- Yang, C.L.; Wu, J.H.; Li, P.Y.; Wang, Y.H.; Yang, N.N. Evaluation of Soil-Water Characteristic Curves for Different Textural Soils Using Fractal Analysis. Water 2023, 15, 772. [Google Scholar] [CrossRef]
- Chen, K.; Liang, F.Y.; Wang, C. A fractal hydraulic model for water retention and hydraulic conductivity considering adsorption and capillarity. J. Hydrol. 2021, 602, 126763. [Google Scholar] [CrossRef]
- Tao, G.L.; Chen, Y.Y.; Xiao, H.L.; Chen, Y.; Peng, W. Comparative analysis of soil–water characteristic curve in fractal and empirical models. Adv. Mater. Sci. Eng. 2020, 2020, 1970314. [Google Scholar] [CrossRef]
- Rieu, M.; Sposito, G. Fractal fragmentation soil porosity and soil water properties. Soil Sci. Soc. Am. J. 1991, 55, 1231–1238. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Fractal scaling of soil particle size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar] [CrossRef]
- Xu, Y.F. Calculation of unsaturated hydraulic conductivity using a fractal model for the pore-size distribution. Comput. Geotech. 2004, 31, 549–557. [Google Scholar] [CrossRef]
- Tao, G.; Chen, Y.; Xiao, H.; Chen, Q.; Wan, J. Determining soil–water characteristic curves from mercury intrusion porosimeter test data using fractal theory. Energies 2019, 12, 752. [Google Scholar] [CrossRef]
- Chen, W.; Liang, Y.J. New methodologies in fractional and fractal derivatives modeling. Chaos Solitons Fractals 2017, 102, 72–77. [Google Scholar] [CrossRef]
- Islam, T.; Gandhi, P. Fabrication of multscale fractal-like structures by controlling fluid interface instability. Sci. Rep. 2016, 6, 37187. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. How long is the coast of britain? statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Zhu, Q.; Ying, H. The effect of pore size distribution on the fractal evaporative interface in porous media. Appl. Therm. Eng. 2024, 246, 122960. [Google Scholar] [CrossRef]
- Cousins, T.A.; Ghanbarian, B.; Daigle, H. Three-dimensional lattice boltzmann simulations of single-phase permeability in random fractal porous media with rough pore-solid interface. Transp. Porous Media 2018, 122, 527–546. [Google Scholar] [CrossRef]
- Xia, Y.X.; Cai, J.C.; Wei, W.; Hu, X.Y.; Wang, X.; Ge, X.M. A new method for calculating fractal dimensions of porous media based on pore size distribution. Fractals—Complex Geom. Patterns Scaling Nat. Soc. 2018, 26, 1850006. [Google Scholar] [CrossRef]
- Bai, Y.F.; Qin, Y.; Lu, X.R.; Zhang, J.T.; Chen, G.S.; Li, X.J. Fractal dimension of particle-size distribution and their relationships with alkalinity properties of soils in the western Songnen Plain, China. Sci. Rep. 2020, 10, 20603. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Daigle, H. Fractal dimension of soil fragment mass-size distribution: A critical analysis. Geoderma 2015, 245, 98–103. [Google Scholar] [CrossRef]
- Alaoui, A.; Lipiec, J.; Gerke, H.H. A review of the changes in the soil pore system due to soil deformation: A hydrodynamic perspective. Soil Tillage Res. 2011, 115–116, 1–15. [Google Scholar] [CrossRef]
- Sun, K.; Wang, H.; Pei, Z.Y.; Wang, H.C.; Sun, X.T.; Li, Y.; Sun, G.R.; Alatengsuhe; Yang, J.J.; Su, X.M. Particle-size fractal dimensions and pore structure characteristics of soils of typical vegetation communities in the Kubuqi Desert. Front. Environ. Sci. 2023, 10, 1044224. [Google Scholar] [CrossRef]
- Xiong, Q.R.; Baychev, T.G.; Jivkov, A.P. Review of pore network modelling of porous media: Experimental characterisations, network constructions and applications to reactive transport. J. Contam. Hydrol. 2016, 192, 101–117. [Google Scholar] [CrossRef]
- Wang, J.M.; Qin, Q.; Guo, L.L.; Feng, Y. Multi-fractal characteristics of three-dimensional distribution of reconstructed soil pores at opencast coal-mine dump based on high-precision CT scanning. Soil Tillage Res. 2018, 182, 144–152. [Google Scholar] [CrossRef]
- Liu, H.Q.; Xie, H.P.; Wu, F.; Li, C.B. A novel box-counting method for quantitative fractal analysis of three-dimensional pore characteristics in sandstone. Int. J. Min. Sci. Technol. 2024, 34, 479–489. [Google Scholar] [CrossRef]
- Wen, T.D.; Chen, X.R.; Luo, Y.W.; Shao, L.T.; Niu, G. Three-dimensional pore structure characteristics of granite residual soil and their relationship with hydraulic properties under different particle gradation by X-ray computed tomography. J. Hydrol. 2023, 618, 129230. [Google Scholar] [CrossRef]
- GB/T50123-2019; Standard for Geotechnical Testing Method; Ministry of Water Resources of the People’s Republic of China; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. China Architecture & Building Press: Beijing, China, 2019.
- Sun, Y.B.; Lu, H.Y.; An, Z.S. Grain size of loess, paleosol and red clay deposits on the Chinese Loess Plateau: Significance for understanding pedogenic alteration and palaeomonsoon evolution. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2006, 241, 129–138. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Eyo, E.U.; Ng’ambi, S.; Abbey, S.J. An overview of soil–water characteristic curves of stabilised soils and their influential factors. J. King Saud Univ.-Eng. Sci. 2022, 34, 31–45. [Google Scholar] [CrossRef]
- Zhang, J.H.; Hu, H.R.; Peng, J.H.; Zhang, Y.Y.; Zhang, A.S. Enhanced understanding of subgrade soil hydraulic characteristics: Effects of wetting–drying cycles and stress states on subgrade water migration. J. Hydrol. 2024, 635, 131165. [Google Scholar] [CrossRef]
- Soltani, A.; Azimi, M.; Boroomandnia, A.; O’Kelly, B.C. An objective framework for determination of the air-entry value from the soil–water characteristic curve. Results Eng. 2021, 12, 100298. [Google Scholar] [CrossRef]
- Fu, Y.P.; Liao, H.J.; Chai, X.Q.; Li, Y.; Lv, L.L. A hysteretic model considering contact angle hysteresis for fitting soil-water characteristic curves. Water Resour. Res. 2021, 57, e2019WR026889. [Google Scholar] [CrossRef]
- Xu, P.P.; Zhang, Q.Y.; Qian, H.; Li, M.N.; Yang, F.X. An investigation into the relationship between saturated permeability and microstructure of remolded loess: A case study from Chinese Loess Plateau. Geoderma 2021, 382, 114744. [Google Scholar] [CrossRef]
- Wen, T.D.; Luo, Y.W.; Tang, M.Y.; Chen, X.S.; Shao, L.T. Effects of representative elementary volume size on three-dimensional pore characteristics for modified granite residual soil. J. Hydrol. 2024, 643, 132006. [Google Scholar] [CrossRef]
- Cakmakyapan, S.; Demirhan, H. A Monte Carlo-based pseudo-coefficient of determination for generalized linear models with binary outcome. J. Appl. Stat. 2017, 44, 2458–2482. [Google Scholar] [CrossRef]
- Li, P.Y.; Li, J.H.; Wu, J.H.; Wang, Y.H.; Chen, Y.F. Effects of loess-paleosol interbedding on soil moisture transport and soil microstructure. Hydrogeol. Eng. Geol. 2024, 51, 1–11. (In Chinese) [Google Scholar]
- Luo, Y.W.; Wen, T.D.; Lin, X.; Chen, X.S.; Shao, L.T. Quantitative analysis of pore-size influence on granite residual soil permeability using CT scanning. J. Hydrol. 2024, 645, 132133. [Google Scholar] [CrossRef]
- Shwan, B.J. Soil–water retention curve determination for sands using the filter paper method. J. Geotech. Geoenviron. Eng. 2024, 150, 04024020. [Google Scholar] [CrossRef]
- ASTM D5298; Standard Test Method for Measurement of Soil Potential (Suction) Using Filter Paper. American Society for Testing and Materials: West Conshohocken, PA, USA, 2016. [CrossRef]
- Li, H.; Li, T.L.; Jiang, R.J.; Wang, Y.; Zhang, Y.G. A New Method to Simultaneously Measure the Soil–Water Characteristic Curve and Hydraulic Conductivity Function Using Filter Paper. Geotech. Test. J. 2020, 43, 1541–1551. [Google Scholar] [CrossRef]
- Nguyen, B.T.; Ishikawa, T.; Zhu, Y.L.; Subramanian, S.S.; Ngyuen, T.T. New simplified transient method for determining the coefficient of permeability of unsaturated soil. Eng. Geol. 2022, 300, 106564. [Google Scholar] [CrossRef]
- Liu, H.N.; Xie, Z.; Yu, R.X.; Zhang, N. A New Three-dimensional Fractal Dimension Model to Describe the Complexity of Concrete Pores. J. Adv. Concr. Technol. 2022, 20, 127–138. [Google Scholar] [CrossRef]
- Huang, C.Q.; Zhao, W.; Liu, F.; Tan, W.F.; Koopal, L.K. Environmental significance of mineral weathering and pedogenesis of loess on the southernmost Loess Plateau, China. Geoderma 2011, 163, 219–226. [Google Scholar] [CrossRef]
- Chai, N.P.; Zhao, Z.P.; Li, X.K.; Xiao, J.; Jin, Z.D. Chemical weathering processes in the Chinese Loess Plateau. Geosci. Front. 2024, 15, 101842. [Google Scholar] [CrossRef]
- Jiang, M.M.; Zhang, F.G.; Hu, H.J.; Cui, Y.J.; Peng, J.B. Structural characterization of natural loess and remolded loess under triaxial tests. Eng. Geol. 2014, 181, 249–260. [Google Scholar] [CrossRef]
- Raghuram, A.S.S.; Mounika, N.; Basha, B.M.; Moghal, A.A.B. Soil Water Characteristic Curves of Soils Exhibiting Different Plasticity. Int. J. Geosynth. Ground Eng. 2023, 9, 25. [Google Scholar] [CrossRef]
- Mu, Q.Y.; Meng, L.L.; Lu, Z.; Zhang, L.M. Hydro-mechanical behavior of unsaturated intact paleosol and intact loess. Eng. Geol. 2023, 323, 107245. [Google Scholar] [CrossRef]
- Krisnanto, S.; Rahardjo, H.; Fredlund, D.G.; Leong, E.C. Water content of soil matrix during lateral water flow through cracked soil. Eng. Geol. 2016, 210, 168–179. [Google Scholar] [CrossRef]
- Gao, X.Y.; Xie, W.L.; Yuan, K.Z.; Liu, Q.Q. Mechanical properties and microstructural evolution of Malan loess with depth: Insights from multivariate statistical models. Soil Tillage Res. 2025, 251, 106548. [Google Scholar] [CrossRef]
- Huang, C.Q.; Tan, W.F.; Wang, M.K.; Koopal, L.K. Characteristics of the fifth paleosol complex (S5) in the southernmost part of the Chinese Loess Plateau and its paleo-environmental significance. Catena 2014, 122, 130–139. [Google Scholar] [CrossRef]
- Shao, X.X.; Zhang, H.Y.; Tan, Y. Collapse behavior and microstructural alteration of remolded loess under graded wetting tests. Eng. Geol. 2018, 233, 11–22. [Google Scholar] [CrossRef]
- Rajput, U.; Sharma, S.; Swami, D.; Joshi, N. Rapid assessment of soil–water retention using soil texture-based models. Environ. Earth Sci. 2024, 83, 454. [Google Scholar] [CrossRef]
- Chen, M.Y.; Chen, X.Y.; Wang, L.; Tian, F.C.; Yang, Y.M.; Zhang, X.J.; Yang, Y.P. Water adsorption characteristic and its impact on pore structure and methane adsorption of various rank coals. Environ. Sci. Pollut. Res. 2022, 29, 29870–29886. [Google Scholar] [CrossRef] [PubMed]
- McDowell, T.M.; Mason, J.A.; Vo, T.; Marin-Spiotta, E. Hydrology of a semiarid loess-paleosol sequence, and implications for buried soil connection to the modern climate, plant-available moisture, and loess tableland persistence. J. Geophys. Res. Earth Surf. 2022, 127, e2022JF006800. [Google Scholar] [CrossRef]
- Xia, Y.X.; Cai, J.C.; Wei, W. Fractal structural parameters from images: Fractal dimension, lacunarity, and succolarity. Model. Flow Transp. Fractal Porous Media 2021, 2021, 11–24. [Google Scholar] [CrossRef]
- Burdine, N. Relative permeability calculations from pore size distribution data. J. Pet. Technol. 1953, 5, 71–78. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Loannidis, M.A.; Hunt, A.G. Theoretical insight into the empirical tortuosity-connectivity factor in the Burdine-Brooks-Corey water relative permeability model. Water Resour. Res. 2017, 53, 10395–10410. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Hou, X.K.; Shen, W.; Zhang, M.M.; Chen, J.C.; Li, P.; Li, T.L.; Hu, X.Y. Permeability and microstructure evolution of loess-paleosol sequence: Analysis of prediction model based on deposition time. Catena 2025, 257, 109176. [Google Scholar] [CrossRef]


| Parameters | Malan Loess | Paleosol | Remolded Loess |
|---|---|---|---|
| Nature density ρ (g/cm3) | 1.50 | 1.78 | — |
| Nature mass moisture content ω (g/g) | 0.154 | 0.140 | 0.120 |
| Dry density ρd (g/cm3) | 1.30 | 1.56 | 1.4 |
| Specific gravity Gs | 2.70 | 2.72 | 2.71 |
| Saturated mass moisture content (g/g) | 0.400 | 0.272 | 0.349 |
| Saturated volume moisture content θs (cm3/cm3) | 0.520 | 0.424 | 0.489 |
| Void ratio e0 | 1.085 | 0.744 | 0.935 |
| USCS classification | Silt | Silt | Silt |
| Samples | Quartz | Plagioclase | Feldspar | Illite | Muscovite | Kalbite | Calcite | Hematite |
|---|---|---|---|---|---|---|---|---|
| Malan loess | 42.2 | 13.8 | 12.2 | 10.8 | 10.1 | 7.7 | 2.5 | 0.7 |
| Paleosol | 43.6 | 15.4 | 4.3 | 16.8 | 13.2 | 6.7 | 0.0 | 0.0 |
| Samples | Expression of Fitting Line | r2 | Ds | ||
|---|---|---|---|---|---|
| Malan loess | M1 | y = −2.615x + 5.268 | 0.997 | 2.615 | 2.611 |
| M2 | y = −2.606x + 5.262 | 0.998 | 2.606 | ||
| M3 | y = −2.612x + 5.195 | 0.993 | 2.612 | ||
| Paleosol | P1 | y = −2.698x + 5.033 | 0.996 | 2.698 | 2.688 |
| P2 | y = −2.686x + 5.012 | 0.997 | 2.686 | ||
| P3 | y = −2.680x + 5.041 | 0.996 | 2.680 | ||
| Remolded loess | R1 | y = −2.761x + 5.342 | 0.996 | 2.761 | 2.771 |
| R2 | y = −2.770x + 5.315 | 0.996 | 2.770 | ||
| R3 | y = −2.781x + 5.246 | 0.997 | 2.781 | ||
| Samples | θr (cm3/cm3) | ψaev (kPa) | n | r2 |
|---|---|---|---|---|
| Malan loess | 0.0708 | 7.203 | 3.203 | 0.889 |
| Paleosol | 0.0827 | 6.541 | 3.026 | 0.854 |
| Remolded loess | 0.0623 | 2.74 | 2.726 | 0.962 |
| Samples | Malan Loess | Paleosol | Remolded Loess | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | P1 | P2 | P3 | R1 | R2 | R3 | |
| R (μm) | 110.7 | 45.9 | 69.7 | 15.3 | 18.8 | 27.4 | 45.5 | 52.2 | 44.9 |
| ψaev (kPa) | 1.335 | 3.221 | 2.119 | 9.689 | 7.849 | 5.397 | 3.245 | 2.832 | 3.292 |
| θr (cm3/cm3) | 0.0542 | 0.0592 | 0.0633 | 0.0821 | 0.0794 | 0.0824 | 0.0742 | 0.0734 | 0.0732 |
| (kPa) | 2.225 | 7.645 | 4.123 | ||||||
| (cm3/cm3) | 0.0589 | 0.0813 | 0.0716 | ||||||
| R2 | 0.891 | 0.879 | 0.973 | ||||||
| RMSE | 0.0037 | 0.0121 | 0.0011 | ||||||
| Samples | ksat (cm/s) | Burdine-Brooks-Corey Model | Fractal Dimension Model | ||
|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | ||
| Malan loess | 7.203 × 10−6 | 0.864 | 6.37 | 0.915 | 1.23 |
| Paleosol | 4.87 × 10−6 | 0.825 | 2.81 | 0.918 | 1.07 |
| Remolded loess | 1.68 × 10−5 | 0.925 | 1.01 | 0.929 | 0.043 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, P.; Wu, J.; He, X. Estimation of Hydraulic Characteristics of Unsaturated Loess with SEM Images Based on Fractal Theory. Water 2025, 17, 3072. https://doi.org/10.3390/w17213072
Wang Y, Li P, Wu J, He X. Estimation of Hydraulic Characteristics of Unsaturated Loess with SEM Images Based on Fractal Theory. Water. 2025; 17(21):3072. https://doi.org/10.3390/w17213072
Chicago/Turabian StyleWang, Yuanhang, Peiyue Li, Jianhua Wu, and Xiaodong He. 2025. "Estimation of Hydraulic Characteristics of Unsaturated Loess with SEM Images Based on Fractal Theory" Water 17, no. 21: 3072. https://doi.org/10.3390/w17213072
APA StyleWang, Y., Li, P., Wu, J., & He, X. (2025). Estimation of Hydraulic Characteristics of Unsaturated Loess with SEM Images Based on Fractal Theory. Water, 17(21), 3072. https://doi.org/10.3390/w17213072








