Rainfall and Runoff Characteristics of Alluvial Gullies in the Upper Burdekin Catchment
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Description
General Characteristics
2.2. Gully-Specific Description
2.3. Hydrological Monitoring
2.4. Rainfall Analysis
2.5. Data Preparation and Event Definition
2.6. Estimating Discharge
2.7. Rainfall-Runoff Analysis
2.8. Statistical Analysis
2.9. Infiltration Test
3. Results
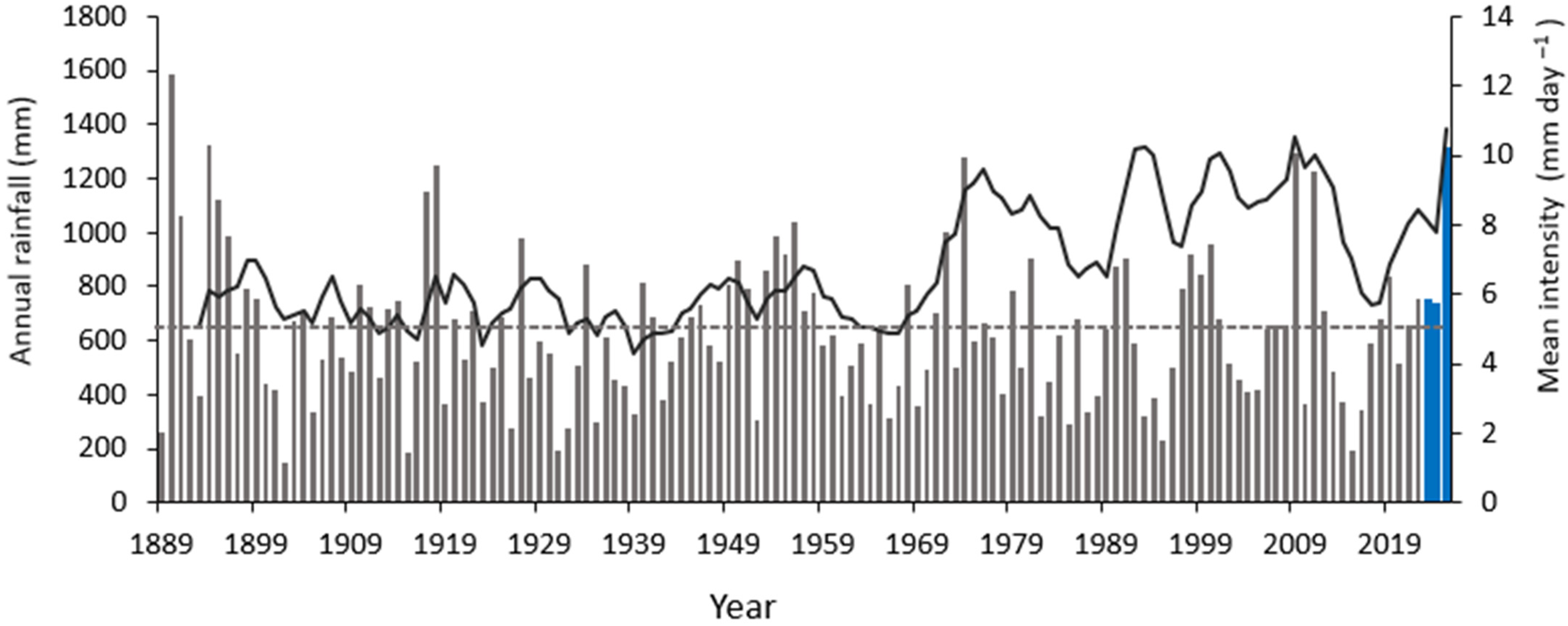
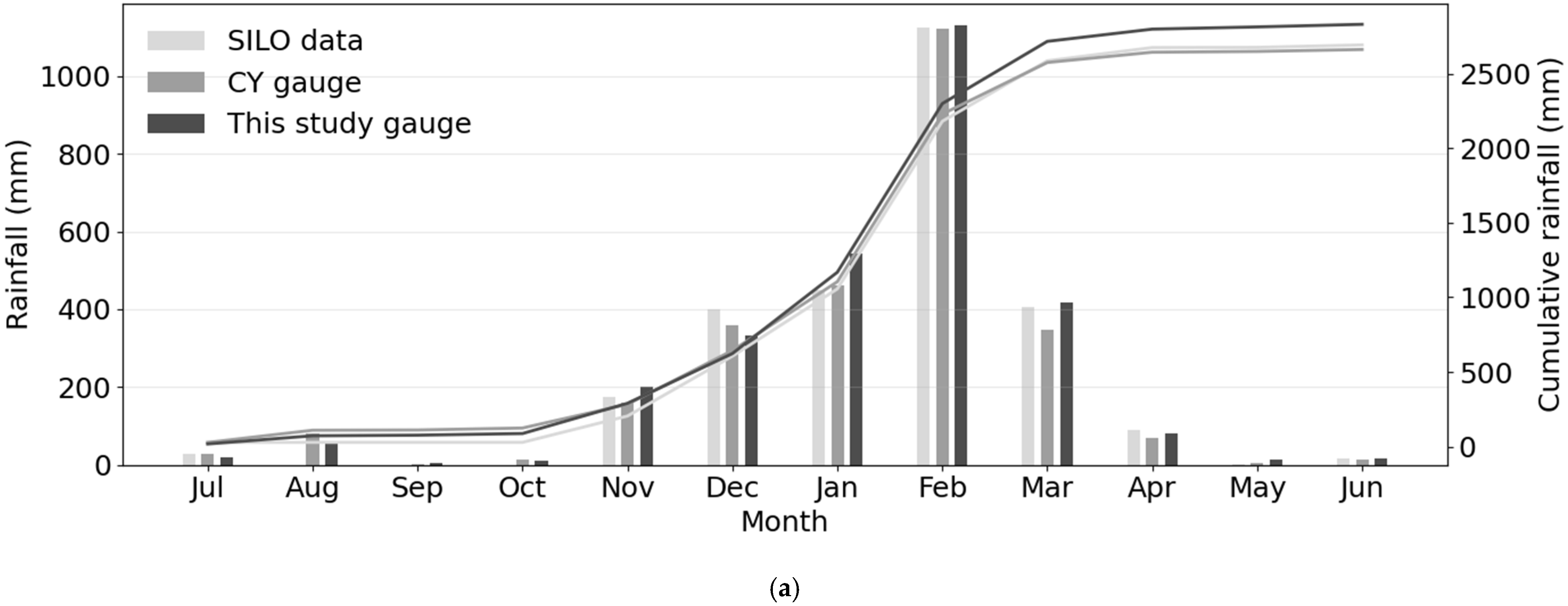
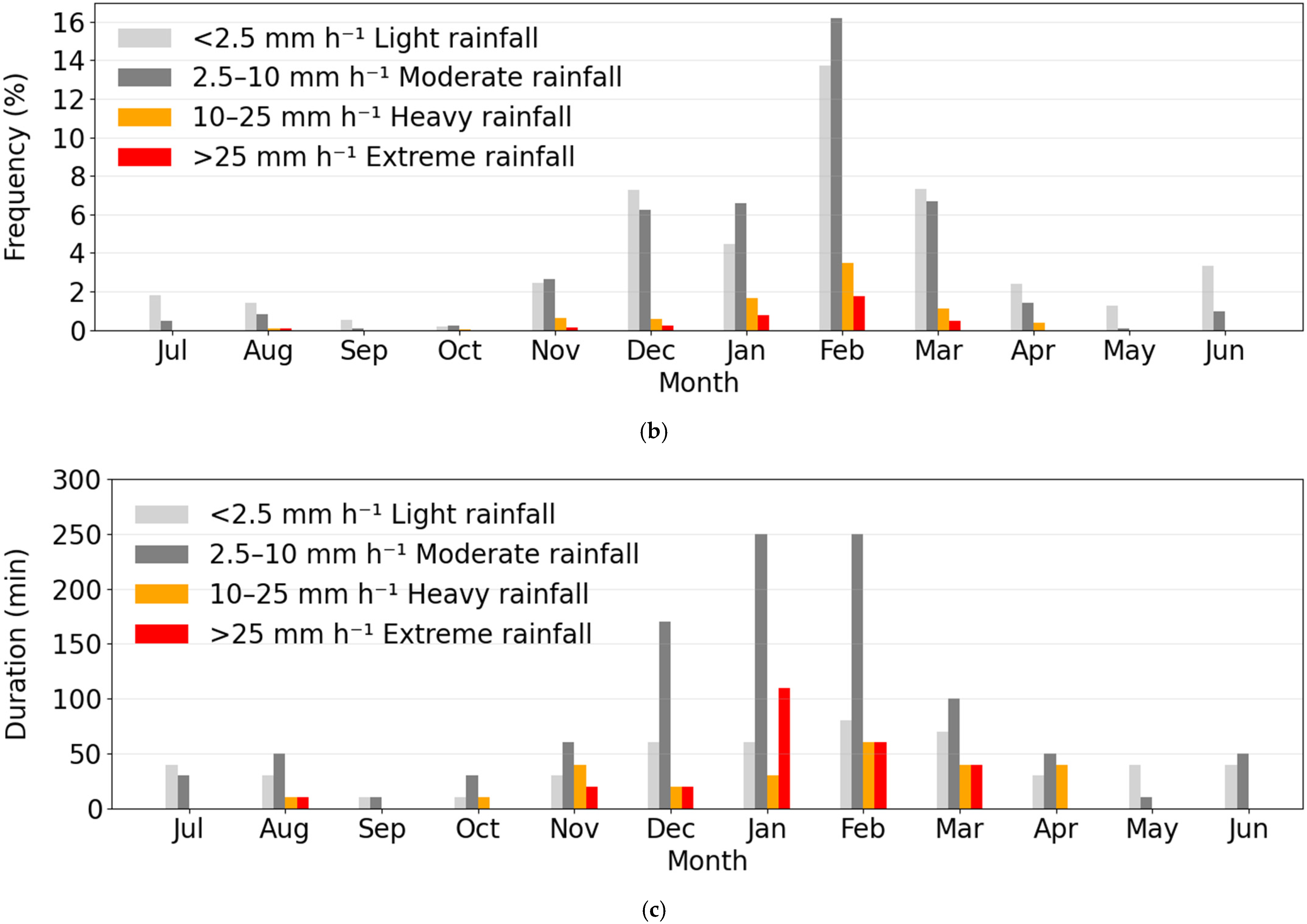
3.1. Rainfall Characteristics
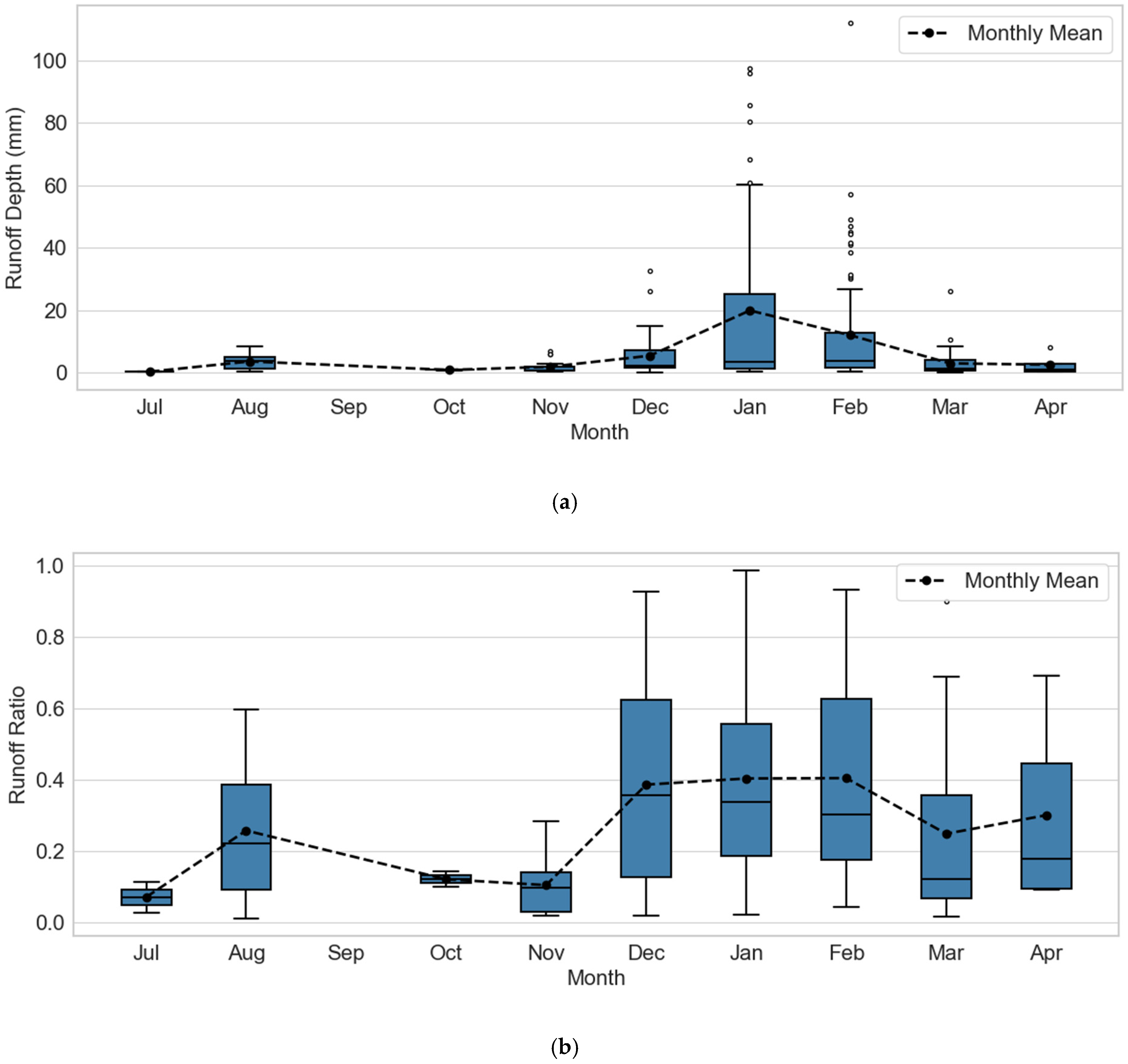
3.2. Runoff Variability
3.3. Relationship Between Rainfall Characteristics and Runoff
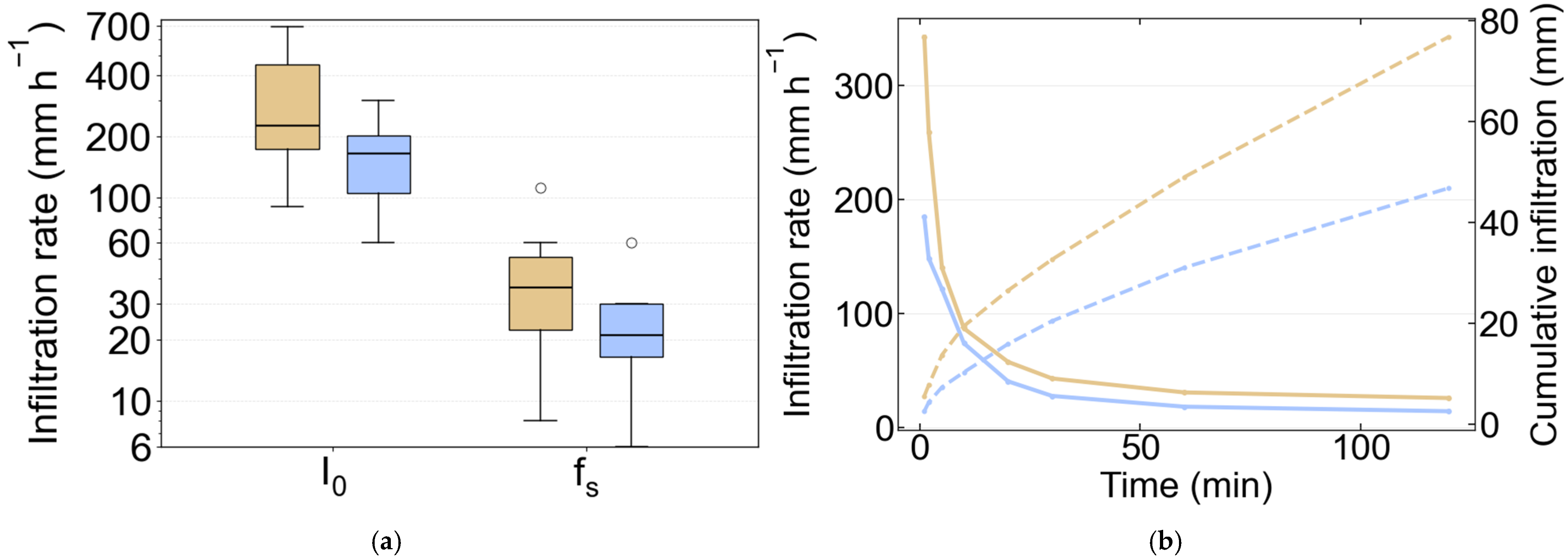
3.4. Near-Surface Soil Infiltration Characteristics
3.5. Divergent Rainfall-Runoff Responses in Low- vs. High-Aca Gullies
4. Discussion
4.1. Rainfall-Runoff Relationship
4.2. Divergence in Rainfall-Runoff Relationship
4.3. Conceptual Model of Rainfall-Runoff Process
4.4. Implications and Significance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | Full form |
| GBR | Great Barrier Reef |
| LiDAR | Light Detection and Ranging |
| DTM | Digital Terrain Model |
| DEM | Digital Elevation Model |
| SBLT | Submersible Level Transmitter |
| HEC-RAS | Hydrologic Engineering Center—River Analysis System |
| 2-D | Two Dimension |
| SILO | Scientific Information for Landowners |
| GIS | Geographic Information System |
| IQR | Interquartile Range |
| CV | Coefficient of Variation |
| F-test | Fisher’s test |
| 1dA | 1 Day |
| 2dA | 2 Day |
| RR | Runoff ratio |
References
- Horton, R.E. The Role of Infiltration in the Hydrologic Cycle. Trans. Am. Geophys. Union 1933, 14, 446–460. [Google Scholar] [CrossRef]
- Dunne, T.; Black, R.F. Partial Area Contributions to Storm Runoff in a Small New England Watershed. Water Resour. Res. 1970, 6, 1296–1311. [Google Scholar] [CrossRef]
- Buchanan, B.; Auerbach, D.A.; Knighton, J.; Evensen, D.; Fuka, D.R.; Easton, Z.; Wieczorek, M.; Archibald, J.A.; McWilliams, B.; Walter, T. Estimating Dominant Runoff Modes across the Conterminous United States. Hydrol. Process. 2018, 32, 3881–3890. [Google Scholar] [CrossRef]
- Agnew, L.J.; Lyon, S.; Gérard-Marchant, P.; Collins, V.B.; Lembo, A.J.; Steenhuis, T.S.; Walter, M.T. Identifying Hydrologically Sensitive Areas: Bridging the Gap between Science and Application. J. Environ. Manag. 2006, 78, 63–76. [Google Scholar]
- Walter, M.T.; Walter, M.F.; Brooks, E.S.; Steenhuis, T.S.; Boll, J.; Weiler, K. Hydrologically Sensitive Areas: Variable Source Area Hydrology Implications for Water Quality Risk Assessment. J. Soil Water Conserv. 2000, 55, 277–284. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, Z.; Zhang, G.; Jian, S.; Zhang, L.; Ran, G.; Zhao, D.; Lv, X.; Hu, C. Rainfall-Runoff Processes in the Loess Plateau, China: Temporal Dynamics of Event Rainfall-Runoff Characteristics and Diagnostic Analysis of Runoff Generation Patterns. Hydrol. Earth Syst. Sci. Discuss. 2020, 2020, 1–31. [Google Scholar]
- Yi, X.; Luo, J.; Wang, P.; Guo, X.; Deng, Y.; Du, T.; Wang, H.; Jiao, C.; Yuan, G.; Shao, M. Spatial and Temporal Variations in Soil Moisture for a Tamarisk Stand under Groundwater Control in a Hyper-Arid Region. Water 2023, 15, 3403. [Google Scholar] [CrossRef]
- Farley, K.A.; Jobbágy, E.G.; Jackson, R.B. Effects of Afforestation on Water Yield: A Global Synthesis with Implications for Policy. Glob. Chang. Biol. 2005, 11, 1565–1576. [Google Scholar] [CrossRef]
- Ilstedt, U.; Malmer, A.; Elke, V.; Murdiyarso, D. The Effect of Afforestation on Water Infiltration in the Tropics: A Systematic Review and Meta-Analysis. For. Ecol. Manage. 2007, 251, 45–51. [Google Scholar] [CrossRef]
- Arnold, J.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development 1. JAWRA J. Am. Assoc. Am. WATER Resour. Assoc. 1998, 34, 73–89. [Google Scholar]
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully Erosion and Environmental Change: Importance and Research Needs. Catena 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Valentin, C.; Poesen, J.; Li, Y. Gully Erosion: Impacts, Factors and Control. Catena 2005, 63, 132–153. [Google Scholar] [CrossRef]
- Nkonya, E.; Mirzabaev, A.; von Braun, J. Economics of Land Degradation and Improvement—A Global Assessment for Sustainable Development; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Marzen, M.; Iserloh, T.; Casper, M.C.; Ries, J.B. Quantification of Particle Detachment by Rain Splash and Wind-Driven Rain Splash. Catena 2015, 127, 135–141. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional Development of Streams and Their Drainage Basins: Hydrophysical Approach to Quantitative Morphology. Bull. Geol. Soc. Am. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Nearing, M.A.; Kimoto, A.; Nichols, M.H.; Ritchie, J.C. Spatial Patterns of Soil Erosion and Deposition in Two Small, Semiarid Watersheds. J. Geophys. Res. Earth Surf. 2005, 110, 1–11. [Google Scholar] [CrossRef]
- McCloskey, G.L.; Baheerathan, R.; Dougall, C.; Ellis, R.; Bennett, F.R.; Waters, D.; Darr, S.; Fentie, B.; Hateley, L.R.; Askildsen, M. Modelled Estimates of Fine Sediment and Particulate Nutrients Delivered from the Great Barrier Reef Catchments. Mar. Pollut. Bull. 2021, 165, 112163. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, S.N.; Olley, J.M.; Furuichi, T.; Burton, J.; Kinsey-Henderson, A.E. Sediment Source Tracing with Stratified Sampling and Weightings Based on Spatial Gradients in Soil Erosion. J. Soils Sediments 2015, 15, 2038–2051. [Google Scholar] [CrossRef]
- State of Queensland. Reef Water Quality Report Card 2020. Available online: https://reportcard.reefplan.qld.gov.au/ (accessed on 16 June 2025).
- Daley, J.S.; Stout, J.C.; Brooks, A.P. Prioritising Gully Remediation in a Great Barrier Reef Catchment: An Approach Using Two Independent Methods of Assessing Erosion Activity in 22,300 Gullies. J. Environ. Manage. 2024, 357, 120688. [Google Scholar] [CrossRef] [PubMed]
- Brooks, A.P.; Thwaites, R.; Spencer, J.; Pietsch, T.; Daley, J. A Gully Classification Scheme to Underpin Great Barrier Reef Water Quality Management: 1st Edition; Griffith Centre for Coastal Management, Griffith University: Brisbane, QLD, Australia, 2019. [Google Scholar]
- Jarihani, B.; Sidle, R.C.; Bartley, R.; Roth, C.H.; Wilkinson, S.N. Characterisation of Hydrological Response to Rainfall at Multi Spatio-Temporal Scales in Savannas of Semi-Arid Australia. Water 2017, 9, 540. [Google Scholar] [CrossRef]
- Post, D.A. Regionalizing Rainfall-Runoff Model Parameters to Predict the Daily Streamflow of Ungauged Catchments in the Dry Tropics. Hydrol. Res. 2009, 40, 433–444. [Google Scholar] [CrossRef]
- Jarvis, D.; Stoeckl, N.; Chaiechi, T. Applying Econometric Techniques to Hydrological Problems in a Large Basin: Quantifying the Rainfall-Discharge Relationship in the Burdekin, Queensland, Australia. J. Hydrol. 2013, 496, 107–121. [Google Scholar] [CrossRef]
- Prosser, I.P. Improving How Gully Erosion and River Sediment Transport Processes Are Represented in Queensland Catchment Models A Report to the Queensland Water Modelling Network; Department of Environment and Science: Brisbane, QLD, Australia, 2018.
- Bartley, R.; Hawdon, A.; Post, D.A.; Roth, C.H. A Sediment Budget for a Grazed Semi-Arid Catchment in the Burdekin Basin, Australia. Geomorphology 2007, 87, 302–321. [Google Scholar] [CrossRef]
- Koci, J.; Sidle, R.C.; Kinsey-Henderson, A.E.; Bartley, R.; Wilkinson, S.N.; Hawdon, A.A.; Jarihani, B.; Roth, C.H.; Hogarth, L. Effect of Reduced Grazing Pressure on Sediment and Nutrient Yields in Savanna Rangeland Streams Draining to the Great Barrier Reef. J. Hydrol. 2020, 582, 124520. [Google Scholar] [CrossRef]
- Hawdon, A.; Henderson, A.; Bartley, R.; Abbott, B.; Mitchell, K.; Marano, J.; Ahwang, K.; Behzadnia, S.; Maskell, T. Quantifying the Effectiveness of Gully Remediation on Water Quality: Results from Landholders Driving Change Monitoring and Demonstration Sites; Milestone Report to LDC; CSIRO Publishing: Melbourne, VIC, Australia, 2023. [Google Scholar]
- Brooks, A.P.; Spencer, J.; Doriean, N.J.C.; Thwaites, R.; Daley, J.; Pietsch, T.; Hacker, J.; Stout, J. The Effectiveness of Alluvial Gully Remediation in Great Barrier Reef Catchments. Int. Soil Water Conserv. Res. 2025, 13, 102–121. [Google Scholar] [CrossRef]
- State of Queensland. Reef 2050 Water Quality Improvement Plan 2017–2022; Department of the Environment, Tourism, Science and Innovation: Brisbane, QLD, Australia, 2018. [Google Scholar]
- Tindall, D.; Marchand, B.; Gilad, U.; Goodwin, N.; Denham, R.; Byer, S. Gully Mapping and Drivers in the Grazing Lands of the Burdekin Catchment Remote Sensing Centre On Behalf of Reef Water Quality Environmental Policy and Planning Department of Environment and Heritage Protection; Department of Science, Information Technology, Innovation: Brisbane, QLD, Australia, 2014.
- Geoscience Australia. Detailed Surface Geology–Upper Burdekin Basalt Provinces; Geoscience Australia: Canberra, ACT, Australia, 2020.
- Rogers, L.G.; Cannon, M.G.; Barry, E. V Land Resources of the Dalrymple Shire; Department of Natural Resources, Queensland: Brisbane, QLD, Australia, 1999.
- Isbell, R.F. The Australian Soil Classification, 2nd ed.; CSIRO Publishing: Melbourne, VIC, Australia, 2016. [Google Scholar]
- Sidle, R.C.; Jarihani, B.; Kaka, S.L.I.; Koci, J.; Al-Shaibani, A. Hydrogeomorphic Processes Affecting Dryland Gully Erosion: Implications for Modelling. Prog. Phys. Geogr. 2019, 43, 46–64. [Google Scholar] [CrossRef]
- Brooks, A.; Shellberg, J.; Knight, J.; Spencer, J. Alluvial Gully Erosion: An Example from the Mitchell Fluvial Megafan, Queensland, Australia Alluvial Gully Erosion: An Example from the Mitchell Fl Uvial Megafan, Queensland, Australia. Earth Surf. Process. Landf. 2009, 34, 613–628. [Google Scholar] [CrossRef]
- Nicholls, N. The El Niño/Southern Oscillation and Australian Vegetation. Vegetatio 1991, 91, 23–36. [Google Scholar] [CrossRef]
- Meehl, G.A.; Arblaster, J.M. Decadal Variability of Asian-Australian Monsoon-ENSO-TBO Relationships. J. Clim. 2011, 24, 4925–4940. [Google Scholar] [CrossRef]
- Lewis, S.E.; Bartley, R.; Wilkinson, S.N.; Bainbridge, Z.T.; Henderson, A.E.; James, C.S.; Irvine, S.A.; Brodie, J.E. Land Use Change in the River Basins of the Great Barrier Reef, 1860 to 2019: A Foundation for Understanding Environmental History across the Catchment to Reef Continuum. Mar. Pollut. Bull. 2021, 166, 112193. [Google Scholar] [CrossRef] [PubMed]
- Dunkerley, D. How Is the Intensity of Rainfall Events Best Characterised? A Brief Critical Review and Proposed New Rainfall Intensity Index for Application in the Study of Landsurface Processes. Water 2020, 12, 929. [Google Scholar] [CrossRef]
- Dunkerley, D.L. Rainfall Intensity Bursts and the Erosion of Soils: An Analysis Highlighting the Need for High Temporal Resolution Rainfall Data for Research under Current and Future Climates. Earth Surf. Dyn. 2019, 7, 345–360. [Google Scholar] [CrossRef]
- Dunkerley, D. Identifying Individual Rain Events from Pluviograph Records: A Review with Analysis of Data from an Australian Dryland Site. Hydrol. Process. 2008, 22, 5024–5036. [Google Scholar] [CrossRef]
- Visser, J.B.; Wasko, C.; Sharma, A.; Nathan, R. Changing Storm Temporal Patterns with Increasing Temperatures across Australia. J. Clim. 2023, 36, 6247–6259. [Google Scholar] [CrossRef]
- Wasko, C.; Sharma, A.; Johnson, F. Does Storm Duration Modulate the Extreme Precipitation-Temperature Scaling Relationship? Geophys. Res. Lett. 2015, 42, 8783–8790. [Google Scholar] [CrossRef]
- US Army Corps of Engineers. HEC-RAS River Analysis System, Version 6.0: User’s Manual; CPD-68; Hydrologic Engineering Center: Davis, CA, USA, 2021. [Google Scholar]
- Kinsey-henderson, A.; Hawdon, A.; Bartley, R.; Mitchell, K.; Marano, J.; Gibbs, M.; Morris, J.; Maskell, T. Estimating Velocity and Discharge in Gullies; CSIRO Publishing: Melbourne, VIC, Australia, 2024. [Google Scholar]
- Fujita, I.; Watanabe, H.; Tsubaki, R. Development of a Non-Intrusive and Efficient Flow Monitoring Technique: The Space-Time Image Velocimetry (STIV). Int. J. River Basin Manag. 2007, 5, 105–114. [Google Scholar] [CrossRef]
- Hou, X.; Cao, J.; Yang, H. Characteristics of Spatial and Temporal Distribution of Heavy Rainfall and Surface Runoff Generating Processes in the Mountainous Areas of Northern China. Water 2025, 17, 970. [Google Scholar] [CrossRef]
- Cook, F.J. The Twin-Ring Method for Measuring Saturated Hydraulic Conductivity and Sorptivity in the Field; CSIRO Publishing: Melboourne, VIC, Australia, 2002. [Google Scholar]
- Zhang, S.; Li, Z.; Lin, X.; Zhang, C. Assessment of Climate Change and Associated Vegetation Cover Change on Watershed-Scale Runoff and Sediment Yield. Water 2019, 11, 1373. [Google Scholar] [CrossRef]
- Mor-Mussery, A.; Laronne, J.B. The Effects of Gully Erosion on the Ecology of Arid Loessial Agro-Ecosystems, the Northern Negev, Israel. Catena 2020, 194, 104712. [Google Scholar] [CrossRef]
- Vandekerckhove, L.; Poesen, J.; Wijdenes, D.O.; Nachtergaele, J.; Kosmas, C.; Roxo, M.J.; De Figueiredo, T. Thresholds for Gully Initiation and Sedimentation in Mediterranean Europe. Earth Surf. Process. Landf. 2000, 25, 1201–1220. [Google Scholar] [CrossRef]
- Turner, R.D.R.; Vardy, S.; Warne, M. Sediment, Nutrient and Pesticide Loads: Great Barrier Reef Great Barrier Reef Catchment Loads Monitoring Program View Project Water Quality Guidelines View Project; Department of Science, Information Technology, Innovation and the Arts: Brisbane, QLD, Australia, 2014.
- Bartley, R.; Roth, C.H.; Ludwig, J.; McJannet, D.; Liedloff, A.; Corfield, J.; Hawdon, A.; Abbott, B.; Thurow, T.L.; Wilcox, B.P. Runoff and Erosion from Australia’s Tropical Semi-Arid Rangelands: Influence of Ground Cover for Differing Space and Time Scales. Hydrol. Process. 2006, 20, 3317–3333. [Google Scholar] [CrossRef]
- Douglas-Mankin, K.R.; Roy, S.K.; Sheshukov, A.Y.; Biswas, A.; Gharabaghi, B.; Binns, A.; Rudra, R.; Shrestha, N.K.; Daggupati, P. A Comprehensive Review of Ephemeral Gully Erosion Models. Catena 2020, 195, 104901. [Google Scholar] [CrossRef]
- Vanmaercke, M.; Poesen, J.; Van Mele, B.; Demuzere, M.; Bruynseels, A.; Golosov, V.; Bezerra, J.F.R.; Bolysov, S.; Dvinskih, A.; Frankl, A.; et al. How Fast Do Gully Headcuts Retreat? Earth-Science Rev. 2016, 154, 336–355. [Google Scholar] [CrossRef]
- Reef and Rainforest Research Centre (Ed.) Lessons for Gully Management: A Synthesis of Key Findings from the NESP Tropical Water Quality Hub Research; Report to the National Environmental Science Program; Reef and Rainforest Research Centre Limited: Cairns City, QLD, Australia, 2021. [Google Scholar]
- Koci, J.; Wilkinson, S.N.; Hawdon, A.A.; Kinsey-Henderson, A.E.; Bartley, R.; Goodwin, N.R. Rehabilitation Effects on Gully Sediment Yields and Vegetation in a Savanna Rangeland. Earth Surf. Process. Landf. 2021, 46, 1007–1025. [Google Scholar] [CrossRef]







| Gully | Catchment Area (m2) | Gullied Area (m2) | Aca | DtD (m) | Average Depth (m) |
|---|---|---|---|---|---|
| JJ2 | 76,140 | 12,932 | 5.9 | 497 | 7.7 |
| JJ5 | 94,190 | 6800 | 13.9 | 748 | 7.0 |
| Gil1 | 18,000 | 16,012 | 1.1 | 35 | 4.1 |
| Gil2 | 10,214 | 7467 | 1.4 | 7 | 4.6 |
| Lei1 | 11,206 | 9849 | 1.1 | 63 | 6.8 |
| Gully | Descriptive Statistics | P | Peak I10 | Mean Intensity | R | RR |
|---|---|---|---|---|---|---|
| (mm) | (mm h−1) | (mm h−1) | (mm) | |||
| JJ2 | Max | 99 | 113 | 45 | 96 | 0.96 |
| Min | 2 | 5 | <1 | <1 | 0.02 | |
| Mean | 15 | 29 | 6 | 6 | 0.45 | |
| Standard Deviation | 19 | 25 | 8 | 15 | 0.21 | |
| Coefficient of variation (%) | 121 | 84 | 127 | 264 | 84 | |
| JJ5 | Max | 195 | 98 | 32 | 112 | 0.69 |
| Min | 2 | 4 | <1 | <1 | 0.01 | |
| Mean | 22 | 30 | 7 | 8 | 0.34 | |
| Standard Deviation | 32 | 22 | 8 | 20 | 0.19 | |
| Coefficient of variation (%) | 142 | 73 | 117 | 259 | 110 | |
| Gil1 | Max | 99 | 101 | 63 | 98 | 0.99 |
| Min | 2 | 2 | <1 | <1 | 0.03 | |
| Mean | 15 | 31 | 12 | 10 | 0.61 | |
| Standard Deviation | 19 | 23 | 15 | 18 | 0.30 | |
| Coefficient of variation (%) | 125 | 76 | 126 | 180 | 65 | |
| Gil2 | Max | 88 | 106 | 72 | 80 | 0.91 |
| Min | 3 | 8 | <1 | 1 | 0.05 | |
| Mean | 20 | 39 | 15 | 13 | 0.52 | |
| Standard Deviation | 20 | 26 | 17 | 18 | 0.28 | |
| Coefficient of variation (%) | 102 | 66 | 120 | 141 | 61 | |
| Lei1 | Max | 90 | 109 | 38 | 86 | 0.95 |
| Min | 5 | 12 | 1 | <1 | 0.03 | |
| Mean | 31 | 41 | 10 | 13 | 0.68 | |
| Standard Deviation | 41 | 24 | 10 | 19 | 0.26 | |
| Coefficient of variation (%) | 134 | 58 | 107 | 145 | 65 |
| Wet Season (Nov–March) n = 204 | ||||||
|---|---|---|---|---|---|---|
| Parameter | Coefficient (ß) | Multiple R | Adjusted R2 | Standard Error | Intercept | p-Values |
| P | 0.66 | 0.90 | 0.81 | 8.17 | −3.84 | 0.00 |
| Duration | 0.04 | 0.51 | 0.26 | 16.01 | 3.63 | 0.00 |
| I10 | 0.34 | 0.45 | 0.20 | 16.60 | −2.44 | 0.00 |
| Mean Intensity | 0.12 | 0.08 | 0.00 | 18.55 | 8.53 | 0.23 |
| P & 1dA | P: 0.66; 1dA: 0.00 | 0.90 | 0.81 | 8.19 | −3.83 | P: 0.00; 1dA: 0.96 |
| P & 2dA | P: 0.66; 2dA: 0.01 | 0.90 | 0.81 | 8.18 | −3.91 | P: 0.00; 2dA: 0.71 |
| Metric | Gully Zone (n = 8) | Upslope Catchment Zone (n = 12) |
|---|---|---|
| Initial Infiltration Rate (mm h−1) | 165 (105–202) | 225 (172–450) |
| Steady-State Infiltration Rate, fs (mm h−1) | 21 (16–30) | 36 (22–51) |
| Time to Steady State, Ts (min) | 20 (18–26) | 25 (20–42) |
| Cumulative Infiltration at Ts (mm) | 14 (3–37) | 32 (10–157) |
| Cumulative Infiltration at 120 min (mm) | 53 (29–64) | 75 (45–126) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelgay, P.; Koci, J.; Jarihani, B.; Smithers, S.; Buono, L.F. Rainfall and Runoff Characteristics of Alluvial Gullies in the Upper Burdekin Catchment. Water 2025, 17, 3071. https://doi.org/10.3390/w17213071
Pelgay P, Koci J, Jarihani B, Smithers S, Buono LF. Rainfall and Runoff Characteristics of Alluvial Gullies in the Upper Burdekin Catchment. Water. 2025; 17(21):3071. https://doi.org/10.3390/w17213071
Chicago/Turabian StylePelgay, Phuntsho, Jack Koci, Ben Jarihani, Scott Smithers, and Luke Francis Buono. 2025. "Rainfall and Runoff Characteristics of Alluvial Gullies in the Upper Burdekin Catchment" Water 17, no. 21: 3071. https://doi.org/10.3390/w17213071
APA StylePelgay, P., Koci, J., Jarihani, B., Smithers, S., & Buono, L. F. (2025). Rainfall and Runoff Characteristics of Alluvial Gullies in the Upper Burdekin Catchment. Water, 17(21), 3071. https://doi.org/10.3390/w17213071







