Hyperspectral Remote Sensing and Artificial Intelligence for High-Resolution Soil Moisture Prediction

Abstract

Reliable field estimation of soil moisture supports hydrology and water resources management. This study develops a drone-based hyperspectral approach in which visible and near-infrared reflectance is paired one-to-one with gravimetric water content measured by oven drying, yielding 1000 matched samples. After standardization, outlier control, ranked wavelength selection, and light feature engineering, several predictors were evaluated. Conventional machine learning methods, including simple and multiple regression and tree-based ensembles, were limited by band collinearity and piecewise approximations and therefore failed to meet the accuracy target. Gradient boosting reached the target but used different trade-offs in variable sensitivity. An artificial neural network with three hidden layers, rectified linear unit activations, and dropout was trained using a feature count sweep and early stopping. With ten predictors, the model achieved a coefficient of determination of 0.9557, demonstrating accurate mapping from hyperspectral reflectance to gravimetric water content and providing a reproducible framework suitable for larger, multi date acquisitions and operational decision support.

1. Introduction

Soil moisture is a key factor in various fields such as agriculture, water resource management, environmental monitoring, and climate change research. In terms of the hydrological cycle, soil moisture contributes not only to runoff, vegetation production, and transpiration, but also to hydrothermal energy exchange, climate change, and land carbon uptake [1,2,3]. Therefore, monitoring the spatial and temporal changes in soil moisture content is essential, and reliable measurement and prediction methods are prerequisites for climate change mitigation and adaptation, precision agriculture, and food development [4,5,6].

However, soil moisture generally refers to the water content 5–15 cm below the top of the soil layer, and since it is vulnerable to evapotranspiration, its variability is highly dependent on measurement time and method [7,8,9]. Traditional measurement techniques, such as oven drying, in situ sensors, and the soil and water balance approach, have been mainly conducted through point-based sampling. While useful, these methods are limited in their ability to capture large scale variability, making extensive measurements virtually impossible [10,11,12]. Remote sensing using satellites has emerged as an alternative to overcome these constraints. In a relatively recent study, the normalized difference moisture index (NDMI) was calculated relatively accurately using satellite data [13]. However, it has faced challenges of limited spatial and temporal resolution, often resulting in insufficient accuracy for local to regional scale hydrological applications [14,15,16,17]. This limitation has created an urgent need for more precise and efficient soil moisture prediction techniques that can support practical water management.

Recently, spectral imaging technology has drawn increasing attention as a promising approach to large scale and near real time soil moisture monitoring [18,19]. Spectral data provide detailed information on land cover and vegetation characteristics by capturing hundreds of spectral bands from visible to near-infrared regions. Importantly, these data can reflect the optical, physical, and chemical properties of soil, making them a powerful tool for estimating soil moisture content. Compared to conventional optical imagery, hyperspectral data provide richer information and can be flexibly integrated into various hydrological and environmental monitoring methods.

Traditionally, converting hyperspectral information into soil moisture relied on empirical regression-based models, which are relatively simple and intuitive but often inadequate in addressing the high dimensionality and nonlinear characteristics of hyperspectral data. This limitation reduces predictive power and hinders generalization across diverse conditions. With the recent development of AI (Artificial Intelligence) technologies, machine learning and deep learning approaches have emerged as powerful alternatives capable of capturing nonlinear interactions and improving predictive accuracy [20,21,22,23,24,25,26,27].

Despite significant progress, several challenges remain. First, the high dimensionality of hyperspectral data increases computational cost and the risk of model overfitting. Second, most studies have been conducted with data collected from limited sites or under controlled laboratory conditions, which reduces applicability to real world environments. Third, natural variability in light, humidity, and temperature is often insufficiently reproduced, limiting the operational use of existing approaches. Therefore, the development of methodologies that can directly utilize hyperspectral data collected in the field is essential to enhance practical applicability and scalability.

The purpose of this study is to develop an efficient and robust algorithm for soil moisture prediction using hyperspectral data acquired in real environments. To achieve this, we collected 1000 field based hyperspectral datasets using a drone platform under diverse temporal and environmental conditions, combined with ground-truth soil moisture measurements. Based on these datasets, we designed and optimized AI-driven machine learning and deep learning models targeting a predictive accuracy of R² > 0.95 while minimizing computational complexity. This study is significant in that it demonstrates the feasibility of real world hyperspectral and AI integration for soil moisture prediction, thereby contributing to advanced hydrological applications and sustainable water resource management under climate variability.

2. Materials and Methods

2.1. Review of the Literature Measuring the Soil Moisture Using Spectral Information

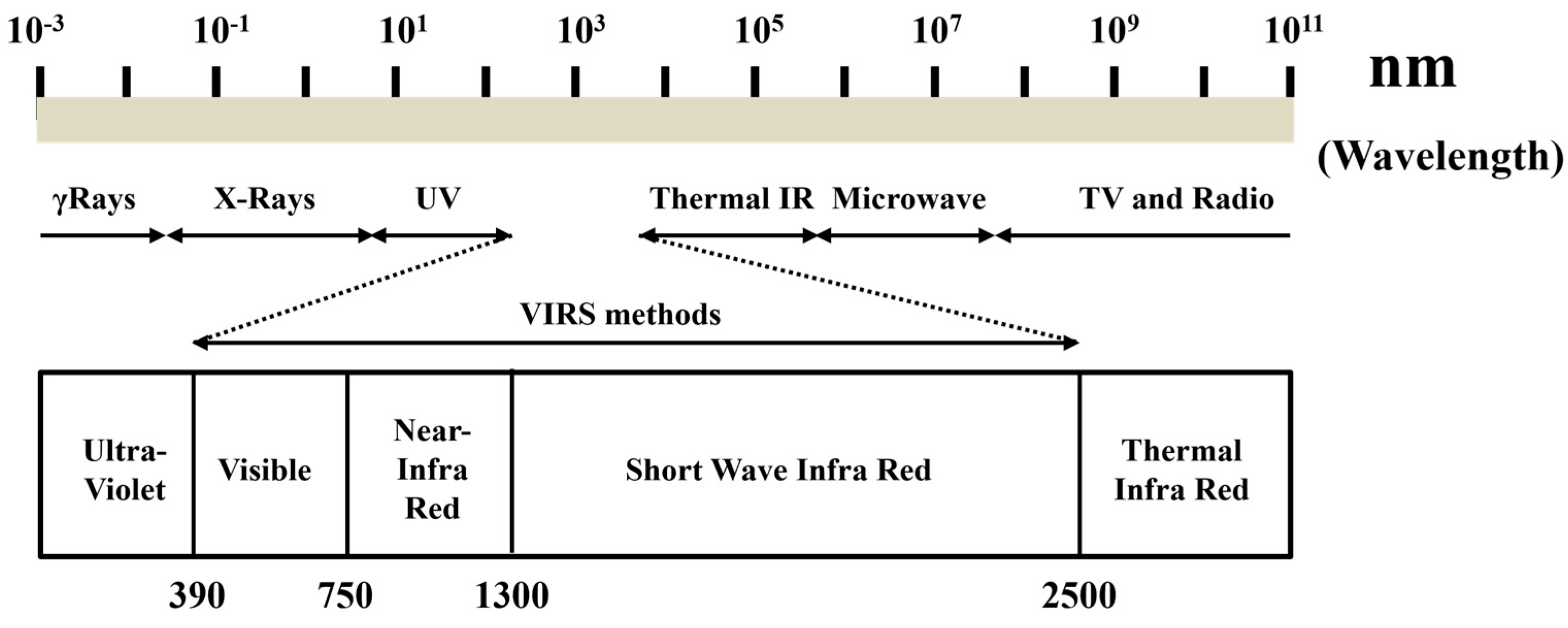
For soil studies, the visible/infrared reflectance spectroscopy (VIRS) wavelength range of 390–2500 nm is used [28]. Reflectance variability across this range arises from wavelength dependent interactions between electromagnetic radiation and matter; diagnostic absorptions are associated with specific bonds and cations (e.g., OH, N, CO₃, Cl, F, SO₄, Al, Fe, and Mg) that modulate spectral features. VIRS is divided into VIS (390–750 nm), NIR (750–1300 nm), and SWIR (1300–2500 nm), as shown in Figure 1, and VIS and NIR are often combined as VNIR.

Spectral sensing is suitable for determining soil moisture because it is fast, economical, and nondestructive, and because spectral signatures capture soil texture, mineralogy, organic matter, and the distribution of pore water and air, enabling inference of multiple soil properties [29,30]. The approach also imposes low environmental burden, as it does not require hazardous chemicals or destructive sample processing [31]. Spectral datasets are commonly classified as multispectral or hyperspectral. Multispectral imagery typically provides 5 to 12 bands (up to 36), with bandwidths of 50 to 200 nm, whereas hyperspectral sensors acquire at least 37 narrow bands of 1 to 15 nm that sample reflectance in a quasi-continuous manner [32,33,34,35]. In practice, the sparse and broad bands of multispectral data can miss narrow moisture-related absorptions and increase spectral mixing, limiting material separability and cross site transferability. By contrast, the dense narrow-band sampling of hyperspectral sensors supports continuum-removed metrics, derivative-based descriptors, and data-driven models that exploit fine spectral structure, improving the accuracy and robustness of soil moisture retrieval at the cost of larger data volumes and higher computational demand.

As noted in the ‘Introduction’, numerous studies have employed spectral information for the remote estimation of soil moisture, and a summary of recent research is provided in

Table 1. Summary of the literature measuring the soil moisture using spectral information.

Years [Ref.]	Spectral Information	Data Number	Preprocessing (Algorithm)	Used Wavelength (nm)	R2
2020 [20]	Measurement in laboratory	*D = 61 *T = 52	Competitive adaptive reweighted sampling (multiple linear regression)	695, 711, 736, 747, 767, 778, 796	0.83
2022 [21]	Utilization of dataset	*LD = 10,000 T = 133	Kernel ridge regression (variational heteroscedastic gaussian processes regression)	VIS–NIR	0.84
2022 [22]	Measurement in laboratory	*D = 54 *T = 30	Remove noise and first-order differential (principal component regression)	VIS–SWIR	0.932
2023 [23]	Utilization of dataset	*LD = 659 *T = Unknown	Data scaling and empirical mode decomposition (random forest)	RGB data (450, 550, 650)	0.951
2024 [24]	Measurement in laboratory	*D = 130 *T = 32	Above-mentioned boosting and Bagging et al. (stacking ensemble learning)	VIS-SWIR	0.952
2024 [25]	Utilization of past data	*D = 70 *T = 30	Estimation model for biocrusts (random forest model and backpropagation neural network mode)	RGB data (450, 550, 650)	RMSE (0.099)
2025 [26]	Utilization of past data	*D = 548 *T = 232	Principal component analysis (ANN model)	453, 557, 677, 814, 997	0.72
2025 [27]	Utilization of past data	Unknown	Savitzky–Golay filter and ID-CNN network (Lin’s Concordance Correlation)	VIS-NearInfraRed	0.90

Notes: *D is the number of data directly measured for training. *T is the number of data directly measured for test. *LD is the number of data taken from a large dataset or literature.

. Across this literature, several commonalities are evident. First, hyperspectral measurements are typically acquired in the laboratory after soil sampling, and the test phase used to demonstrate reliability often relies on very small sample sizes. Second, rather than using wavelength-resolved reflectance directly, most workflows apply preprocessing, such as data scaling and feature extraction, to transform spectra into derived variables on which the predictive algorithms are built. In addition, the exact wavelengths employed are specified in only a subset of papers; more commonly, authors report only the initial measured spectral range. Some studies also mix local measurements with external large-scaled resources, such as the European LUCAS 2015 dataset.

These common practices entail several limitations: (i) laboratory acquisition following field sampling fails to capture in situ variability in illumination, viewing geometry, and surface roughness, and small test sets can also inflate performance estimates, thereby reducing field transferability [36,37]; (ii) heavy transformation of the raw spectra may discard informative spectral structure and weaken physical interpretability and reproducibility, while feature selection performed on the full dataset risks information leakage that can overstate R-squared [38]. Beyond these, the frequent non-specification of selected wavelengths that report only broad coverage ranges hampers reproducibility, cross sensor standardization, and spectral interpretation of moisture-sensitive features (e.g., absorption/reflectance behaviors) [39]. Finally, combining external large datasets introduces a potential domain shift because of differences in sensors, spectral coverage, and acquisition protocols, which can bias fair comparison and cross site transfer unless explicitly harmonized [40].

2.2. Algorithm Design and Research Area

This study addresses limitations of prior approaches by excluding laboratory scanning and using hyperspectral reflectance acquired in the field by an unmanned aerial vehicle directly as training data. This design preserves field-dependent factors such as illumination, viewing geometry, surface roughness, and temporal moisture variability to mitigate the reduced transferability often observed with laboratory spectra. In addition, we avoid generating secondary indices through scaling or feature extraction and instead feed wavelength-resolved raw reflectance to retain spectral structure without loss. Finally, we avoid mixing external large datasets and construct our own corpus of 1000 paired observations (spectrum information and soil moisture) collected with the same sensor and protocol, thereby reducing both domain shift and the risk of optimistic bias associated with small test samples.

The detailed algorithmic workflow is illustrated in Figure 2. Ten ground points in the target area were marked with color spray. A UAV-mounted hyperspectral sensor acquired spectral data in the field, and soil moisture was measured immediately at the marked points after each flight. This procedure was repeated ten times per day over ten days to capture natural variability in illumination and humidity, yielding a total of n = 1000 one-to-one paired observations (spectrum and soil moisture).

In the training stage, each spectrum was paired with its soil moisture reference, and a minimal subset of wavelengths was selected to enable derivation of a relation with R² more than 0.95 while avoiding use of the full spectral range. In the validation stage, tenfold cross-validation was applied without a separate holdout split to improve mean performance and to minimize variance; this approach is widely used to obtain stable performance without an explicit data partition [41,42]. Finally, only algorithms that achieved R² ≥ 0.95 under cross-validation were advanced to the final test. To avoid high dimensional inputs and unnecessary computation, the method performs feature selection to retain a compact set of informative wavelengths. The design goals are as follows: (i) minimize the number of predictor variables so the model remains efficient for future processing, and (ii) ensure predictive reliability with a target R² of at least 0.95 under cross-validation.

The study area is located in Songdo, Incheon, Republic of Korea (WGS 84: 37.375294° N, 126.633010° E). The climate is marked by humid summers and cold winters. The specific site is a vegetation-free dirt athletic field on the Incheon National University campus, rectangular in shape (100 m × 60 m), with sandy soil. Although the use of a single site is a limitation, this location was selected because (i) soil moisture can be measured immediately at the same points after hyperspectral acquisition, minimizing label error and delay-related bias; (ii) the absence of vegetation, shadows, and strong surface heterogeneity reduces interference and prioritizes internal validity of the spectral moisture relation; (iii) the flat rectangular layout facilitates repeat flights, consistent viewing geometry, and application of panel based radiometric calibration; and (iv) on-campus access and flight permissions enable repeated observations over ten days, including a post-rain session.

2.3. Data Acquisition of Hyperspectral Information

Hyperspectral information was acquired using a UAV with RTK-GNSS and autonomous navigation (e.g., Matrice 300 Pro, DJI, Shenzhen, China), as shown in Figure 3. The payload consisted of a compact high sensitivity GNSS antenna (e.g., TW4721, Tallysman Wireless, Ottawa, ON, Canada) cabled to the camera for precise geo tagging, a VNIR hyperspectral camera (e.g., MicroHSI 410, Corning Incorporated, Corning, NY, USA), and a lightweight dedicated power module. The camera covers 398–982 nm; spectra were sampled every 4 nm to balance information content and processing time, yielding 147 bands per spectrum. This configuration offers mobility suitable for low-altitude surveys while maintaining positional accuracy and spectral fidelity.

Ground points without vegetation were marked with color spray to match the soil sampling locations. Flight polygons were planned to cover the marked area in one sortie under stable daylight. For each numbered point, a region of interest (ROI) was drawn on the hyperspectral information, and the mean reflectance within the ROI was used as the spectral descriptor. Example frames and ROIs are shown in Figure 4.

All UAV hyperspectral cubes were radiometrically calibrated and standardized before analysis. Raw digital data was corrected for dark current and sensor response using the manufacturer calibration data. For each flight, an in-scene reference reflectance panel (calibration tarp) with known spectral reflectance factors provided by the manufacturer was measured, and an empirical line procedure was used to convert the image to surface reflectance. Calibration coefficients were estimated per flight and applied to the full cube to ensure day to day consistency.

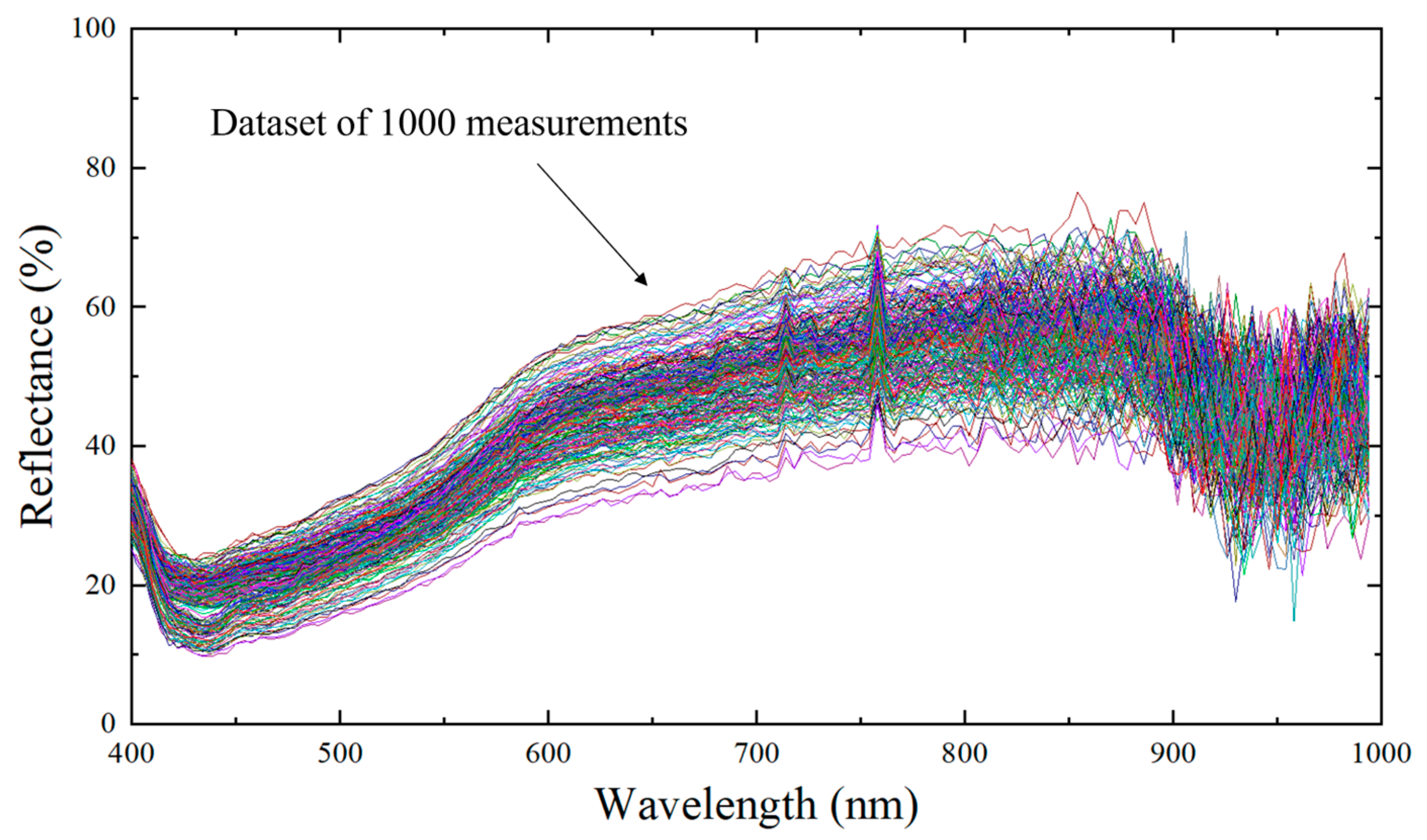
After calibration, spectra were resampled at 4 nm to balance information content and processing time, yielding 147 bands from 398 to 982 nm. The ensemble of calibrated spectra is shown in Figure 5. As is typical for visible to near-infrared soil spectra, reflectance declines toward about 430 nm, then increases toward about 880 nm, followed by band-dependent undulations. Identification of moisture-sensitive wavelengths is performed by the learning algorithm described later.

2.4. Measured Value of Soil Moisture

Soil moisture can also be called volumetric water content (VWC), which is the ratio of the volume of water to the unit volume of soil [43]. It can be expressed as the ratio of water per soil depth, percentage, or depth (assuming unit surface area) and is as Equation (1) [44], where θ_v is the volumetric water content, V_water is the volume of water, and V_soil is the volume of soil.

θ_v = V_water/V_soil

(1)

Indirect field sensors widely used to estimate soil moisture include time domain reflectometry, frequency domain reflectometry, amplitude domain reflectometry, time domain transmission, and phase transmission. Their accuracy depends on calibration, sensor type and material, and dry bulk density. Accordingly, soil water contents, which can obtain relatively accurate values, are used similarly. Soil water content is also called gravimetric water content (GWC). This has the advantage of being able to measure soil moisture by collecting an accurate amount of soil in the field and not requiring it in situ. This method is the most accurate measurement method available to date and is conducted according to the ASTM standard [45] as a metric for comparing and calibrating all other measurement techniques [46].

Soil water contents are expressed as Equation (2), where ω is gravimetric water content, m_water is the mass of water, and m_{dry soil} is the mass of dry soil.

ω = m_water/m_{dry soil} = (m_{wet soil} − m_{dry soil})/m_{dry soil}

(2)

The relation between VWC and GWC is given by Equation (3), where ω is gravimetric water content, ρ_d is the dry unit weight of soil, and ρ_w is the dry unit weight of water (9.81 kN/m³). If the soil’s dry unit weight is known, the gravimetric water content (GWC) can be readily converted to volumetric water content (VWC).

θ_v = ω × (ρ_d/ρ_w)

(3)

In this study, soil moisture must be, and was, measured in relatively high detail. Therefore, rather than VWC, which may have various variables, GWC, which can obtain reliable values, was selected as the data value. After hyperspectral imaging, the soil was collected directly above each numbered ground mark. The m_{wet soil} was recorded on site. Samples were transported to the laboratory and oven dried to constant mass to obtain m_{dry soil} following the applicable oven drying procedure.

Daily GWC distributions are shown in Figure 6. Measurements were not carried out on consecutive calendar days. Rainfall occurred between Day 2 and Day 3; the Day 3 measurement was executed after precipitation ceased. GWC increased and showed a wider spread on the post-rain day, whereas other days during summer exhibited generally low values and a low coefficient of variation.

Data were acquired from 20 to 29 April 2025, and the corresponding meteorological records are summarized in

Table 2. Weather in the research area on the measurement date.

Date	20 April	21 April	22 April	23 April	24 April	25 April	26 April	27 April	28 April	29 April
Temperature (Low/High)	10°/24°	12°/26°	15°/19°	10°/23°	9°/19°	5°/17°	6°/20°	8°/21°	8°/19°	5°/20°
Humidity (%)	79	75	92	71	65	45	64	56	60	48
Cloud Cover (1/10)	3.2	4.1	7.8	2.5	1.4	0.0	0.6	6.6	1.0	0.0
Rainfall (mm)	-	-	42.3	-	-	-	-	-	-	-
Sunshine Duration (h)	10.1	8.7	0.0	11.9	11.9	12.0	12.1	4.4	12.4	12.3

. During the period, temperature and humidity varied, and rainfall occurred between Day 2 and Day 3. Accordingly, the measurements align with the patterns in Figure 6 and capture substantial natural variability. This means that the training set covers both pre- and post-rain conditions and a broad range of meteorological covariates, enabling a rigorous assessment of the algorithm’s temporal stability and field applicability.

3. Results

3.1. Computational Learning Based on Artificial Intelligence

It is virtually impossible for humans to select appropriate variables (reflectance at specific wavelength) from 1000 graphs and make the R-square of 1000 results (GWC) more than 0.95. Accordingly, this study aims to develop an algorithm using computational learning through Artificial Intelligence (AI) technology.

Artificial Intelligence is used here as a term that includes machine learning (ML), artificial neural networks (ANNs), and deep learning (DL) [47]. The prediction of gravimetric water content from reflectance is a supervised regression task in which paired inputs and targets are available [48,49]. In this taxonomy, ML covers linear- and tree-based regressors and also includes dimensionality reduction for handling collinearity and noise [50]. ANN denotes neural network models with one or a few hidden layers that learn nonlinear relations from data [51]. DL extends ANN by employing many hidden layers and larger parameter counts; this can capture highly complex patterns but generally requires larger datasets and higher computational cost [52]. Figure 7 summarizes the relation among ML, ANN, and DL.

3.2. Algorithm Using Machine Learning

The prediction models based on machine learning included regression, random forest, and gradient boosting. In this study, regression was implemented as simple regression and multiple regression. Simple regression used a single reflectance value from each hyperspectral spectrum, and the following functional forms were fitted so that closed-form equations could be inspected: linear, polynomial of orders two through six, logarithmic, and exponential. Multiple regression allowed several reflectance values to be used at once and combined the same functional forms in an ensemble style. To control computation and reduce overfitting, the number of reflectance variables in multiple regression was limited to ten or fewer for the simple setting and to at most fifty for the extended combinations. The random forest model was first applied with a basic configuration and, when the target R² of 0.95 was not reached, feature engineering and hyper-parameter tuning were used. If the model also has difficulty satisfying the conditions, the gradient boosting model was considered.

3.2.1. Simple Regression

The results of simple regression are as follows. With a single variable, no functional form achieved R² of at least 0.95. For the linear model, the maximum R² was 0.416 at 434 nm. For the polynomial models, the maximum R² values were 0.440 at 434 nm for order two, 0.440 at 434 nm for order three, 0.448 at 434 nm for order four, 0.457 at 434 nm for order five, and 0.457 at 434 nm for order six. The maximum R² values of the logarithmic and exponential models were 0.439 at 434 nm and 0.387 at 430 nm, respectively.

To explore whether removal of outlying samples could rescue simple models, data points that deviated from the main trend were iteratively removed until R² reached 0.95 for each functional form.

Table 3. The number of data deletion and the equation to make R² at 0.95 when applying a simple regression model.

Model	Rank	The Number of Data Deletion	Variable	Equations
Linear	1	537	R(430)	ω = 0.187 − 0.008R
	2	548	R(426)	ω = 0.189 − 0.008R
	3	555	R(442)	ω = 0.186 − 0.008R
Polynomial (2nd order)	1	507	R(434)	ω = 8 × 10−4R2 − 0.016R + 0.191
	2	509	R(438)	ω = 6 × 10−4R2 − 0.014R + 0.194
	3	514	R(426)	ω = 6 × 10−4R2 − 0.013R + 0.196
Polynomial (3rd order)	1	498	R(434)	ω = 2 × 10−4R3 − 0.002R2 − 0.005R + 0.189
	1	498	R(442)	ω = 3 × 10−4R3 − 0.003R2 − 0.001R + 0.182
	3	505	R(438)	ω = 2 × 10−4R3 − 0.003R2 − 0.002R + 0.186
Polynomial (4th order)	1	476	R(434)	ω = −1 × 10−4R4 − 0.002R3 − 0.013R2 + 0.014R + 0.189
	2	477	R(426)	ω = −1 × 10−4R4 − 0.002R3 − 0.014R2 + 0.014R + 0.183
	3	480	R(438)	ω = −1 × 10−4R4 − 0.002R3 − 0.015R2 + 0.016R + 0.180
Polynomial (5th order)	1	446	R(434)	ω = 1 × 10−5R5 − 0.001R4 + 0.012R3 − 0.046R2 + 0.051R + 0.170
	2	451	R(430)	ω = 1 × 10−5R5 − 0.001R4 + 0.013R3 − 0.049R2 + 0.052R + 0.170
	3	452	R(438)	ω = 1 × 10−5R5 − 0.001R4 + 0.011R3 − 0.043R2 + 0.048R + 0.171
Polynomial (6th order)	1	421	R(430)	ω = −1 × 10−5R6 + 3 × 10−4R5 − 0.005R4 + 0.031R3 − 0.096R2 + 0.098R + 0.163
	2	436	R(434)	ω = −1 × 10−5R6 + 2 × 10−4R5 − 0.003R4 + 0.021R3 − 0.069R2 + 0.071R + 0.166
	3	440	R(438)	ω = −1 × 10−5R6 + 2 × 10−4R5 − 0.004R4 + 0.025R3 − 0.081R2 + 0.091R + 0.159
Log	1	498	R(430)	ω = 0.176 − 0.027log(R)
	2	504	R(422)	ω = 0.186 − 0.027log(R)
	3	512	R(434)	ω = 0.176 − 0.028log(R)
Exponential	1	520	R(430)	ω = exp(−1.672 − 0.054R)
	2	524	R(434)	ω = exp(−1.679 − 0.056R)
	3	528	R(426)	ω = exp(−1.661 − 0.050R)

lists the number of removed samples and the resulting equations for the top three wavelengths per model. At least 421 samples had to be eliminated to reach R² of 0.95, indicating that single variable equations are not viable for this dataset.

3.2.2. Multi-Regression

Because simple regression produced low R² and required extensive sample removal to approach 0.95, multiple regression was evaluated by combining two to four of the following forms: linear, second order polynomial, third order polynomial, logarithmic, and exponential. Combinations beyond third order polynomials were not considered because they induced numerical instability and excessive computation. The number of variables per model was limited to fifty.

Table 4. Results of multi-regression.

Case	Model		Maximum R2	Number of Variables
	Number	Combination
1	2	Linear + 2nd Polynomial	0.5731	6
2		Linear + 3rd Polynomial	0.5733	20
3		Linear + Log	0.5224	25
4		Linear +Exponential	0.5666	21
5		2nd Polynomial + Log	0.5226	34
6		2nd Polynomial + Exponential	0.5639	22
7		3rd Polynomial + Log	0.5261	21
8		3rd Polynomial + Exponential	0.5433	30
9		Log + Exponential	0.5581	10
10	3	Linear + 2nd Polynomial + Log	0.5784	7
11		Linear + 2nd Polynomial + Exponential	0.5467	26
12		Linear + 3rd Polynomial + Log	0.5524	21
13		Linear + 3rd Polynomial + Exponential	0.5452	32
14		Linear + Log + Exponential	0.5580	13
15		2nd Polynomial + Log + Exponential	0.5297	20
16		3rd Polynomial + Log + Exponential	0.5224	17
17	4	Linear + 2nd Polynomial + Log + Exponential	0.5401	12
18		Linear + 3rd Polynomial + Log + Exponential	0.5204	28

summarizes the maximum R² and the variable counts for each combination. The best case was Case 10, which combined linear, second order polynomial, and logarithmic models and reached R² of 0.5784 using seven variables. The worst was Case 4 with linear, third order polynomial, logarithmic, and exponential models. Although multiple regression improved upon the best simple regression value, which did not exceed about 0.48, it remained well below the target of 0.95, indicating the need for a different learning approach.

3.2.3. Random Forest

Given the limitations of regression, a random forest model was applied. Random forest is an ensemble of decision trees in which each tree provides a prediction and the ensemble aggregates the outputs [53]. The approach can mitigate overfitting through averaging and often improves accuracy with more trees, although bias reduction is limited and very large ensembles can increase memory use and computation without further gains [54].

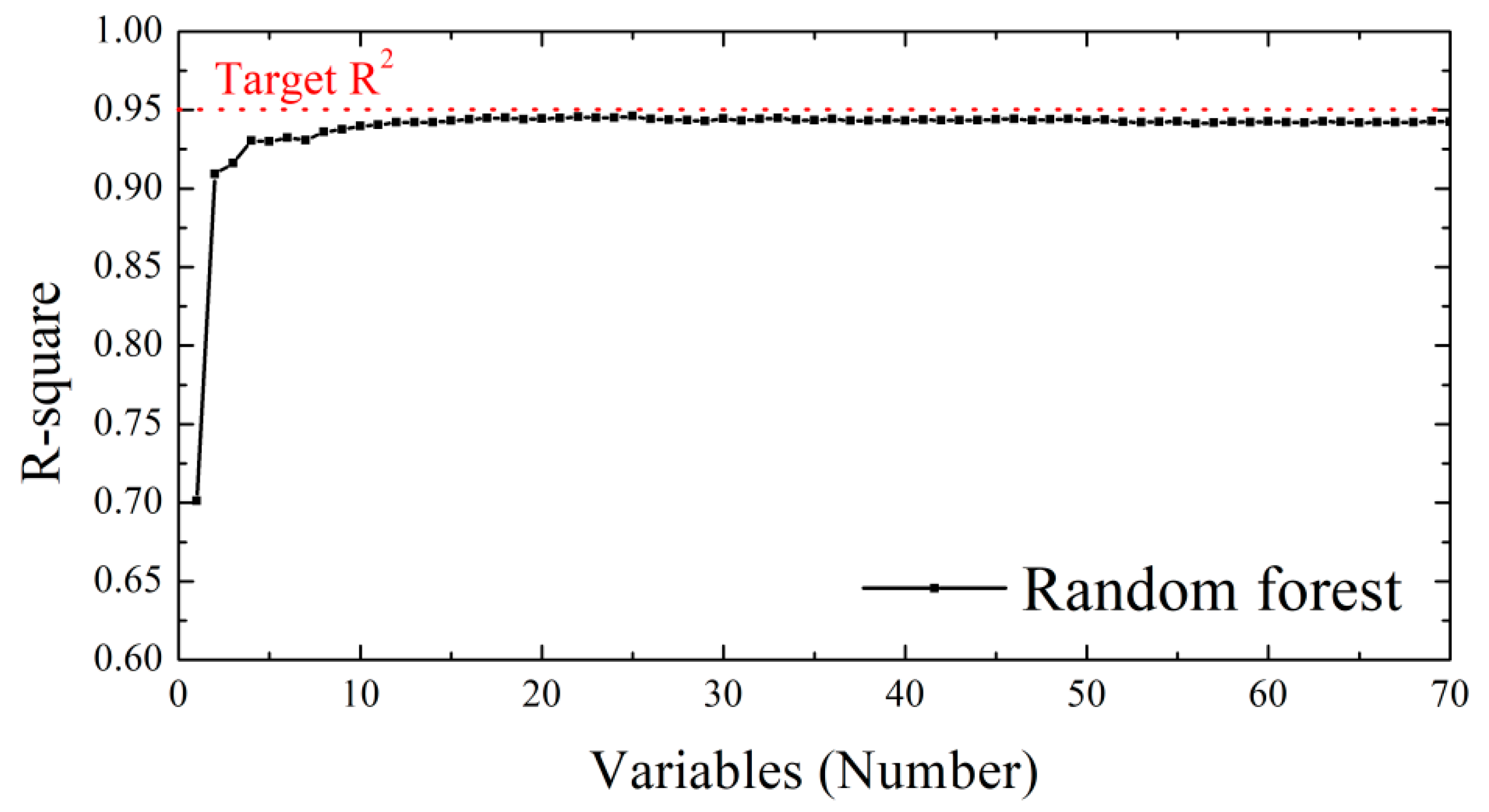
In this study, the number of trees was set to 200. A target-based optimization scheme was used in which the R² target was scanned from 0.30 to 0.95 in steps of 0.01. For each target, features were added in order of importance derived from the current forest, including nonlinear transformations such as interactions, logarithms, and square roots. When a target was reached, the feature set and performance were recorded, and the process continued to find the highest achievable target with the fewest features. Figure 8 shows the results. With a single variable, the R² was 0.7011. Even with one hundred variables, the maximum R² was 0.9406, which did not meet the 0.95 target. This indicates that a random forest was insufficient for the required accuracy in this dataset.

Here, in Figure 8, the variables denote the number of wavelengths used at each step. At a given subset size n, the wavelengths are the best-performing combination for that size, and the identities can change with n. For example, at n = 1, the selected band was 412 nm, and at n = 2, the optimal pair was 412 nm and 720 nm. For n ≥ 3, 412 nm may not remain in the optimal subset due to collinearity and interaction effects. Candidate ordering was obtained from random forest feature importance, and for each n the subset with the highest cross-validated R² was retained.

In detail, for subset size n = 1, all 147 bands were evaluated with ten-fold cross-validation and the band with the highest R² was selected. For n ≥ 2, an exhaustive combination search was avoided by a ranking and forward selection scheme. Bands were first ranked by random forest feature importance on standardized reflectance. A candidate pool consisting of the top M bands was formed, and greedy forward selection with ten-fold cross-validation added one band at a time to maximize R². Pruning and early stopping were applied when marginal gains became negligible or a target R² was reached. A small set of engineered terms derived from the top ranked bands was evaluated in the same loop. This reduces the combinatorial search for a procedure whose computational cost grows roughly in proportion to the size of the candidate pool (M) and the number of selected wavelengths (n), rather than exploding with the number of all possible combinations. The search therefore scales approximately linearly with M and with n, while still allowing interactions to enter through forward selection and a small set of engineered terms. Here, M was determined from random forest feature-importance ranking by retaining the top-ranked candidates; in this study, the top 50 wavelengths were used to define the candidate pool.

The same procedure applies to gradient boosting and artificial neural networks.

3.2.4. Gradient Boosting

In the random forest model, R² did not satisfy 0.95, so the gradient boosting model was applied. Gradient boosting builds a sequence of weak learners to improve the estimate of the response variable and is widely used in statistical learning [55]. The implementations considered were LightGBM and XGBoost [56,57]. LightGBM is optimized for efficiency on large and high dimensional data and often performs well in both speed and accuracy. XGBoost is a flexible distributed framework that integrates multiple weak learners into a strong learner and balances prediction error and model complexity to prevent overfitting.

Both models were trained with the same target based optimization used for random forest. The analysis results are shown in Figure 9. LightGBM reached the R² target when eighteen variables were used. XGBoost reached the target with only two variables and then maintained the same R² without additional variables. This indicates that XGBoost can achieve very high accuracy with a small number of predictors but may be sensitive to errors in those variables. LightGBM used more variables and thus a higher computation cost, but its gradual improvement and use of multiple predictors were considered more stable for operational use.

3.3. Algorithm Using Artificial Neural Network

3.3.1. Process

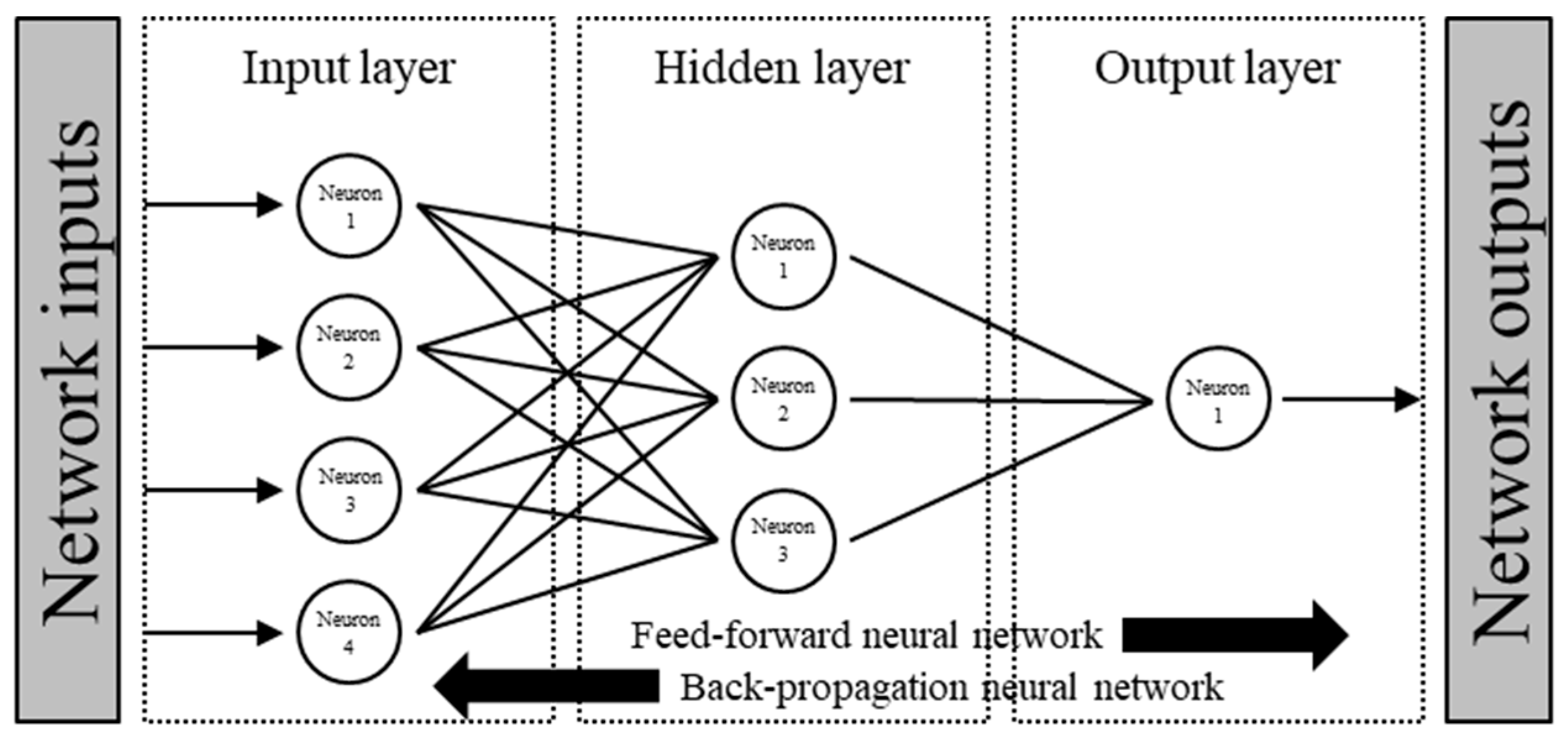
The assembled dataset was not well suited to standard machine learning algorithms. Therefore, an artificial neural network was employed. The architecture and learning principle are illustrated in Figure 10. In this study, the input layer consists of the selected n wavelengths of standardized reflectance (optionally including engineered features). The hidden part comprises three fully connected layers with 128, 64, and 32 neurons, each using a ReLU activation and dropout of 0.20 to learn nonlinearity while limiting overfitting. The output layer contains a single neuron that predicts the GWC.

A feed-forward neural network is a structure in which information moves in one direction from the input layer through the hidden layers to the output layer; it has no recurrence and offers simple computation for fast inference. A back-propagation neural network refers to the learning procedure that updates weights in the reverse direction by computing gradients of the loss function via the chain rule, repeatedly adjusting the weights to minimize the loss. The model used in this work is a feed-forward multilayer perceptron, and training is carried out with back propagation. Optimization uses Adam and the loss function is mean squared error.

The training process proceeds as follows:

• Feature ranking and engineering: Feature importance was estimated with a random forest regression to order candidates. Engineered features were added from top-ranked variables, namely an interaction term (product of the top two), a squared term of the top variable, the logarithm of the third variable for positive values, and the square root of the fourth variable for positive values.
• Architecture: A fully connected multilayer perceptron was used with three hidden layers of 128, 64, and 32 neurons. ReLU activation and dropout of 0.20 were applied. The output layer has one neuron to predict gravimetric water content. The loss function is mean squared error, and optimization uses Adam with a learning rate of 0.001. Computation uses float32 precision and random seeds were set to 42.
• Feature count sweep and early stopping: The number of features (n) was swept from 5 to 40. For each n, the top n features were used to train the network for 500 epochs with batch size of 32. After fitting, the coefficient of determination R² was computed and logged. When R² > 0.95 was achieved, the search stopped and that configuration was retained as the best.
• Artifacts: The best model was saved in ‘H5’ format and the scaler with joblib. A JSON file recorded original column names, variables used to create engineered features, and the final feature list. A workbook stores a summary, the performance by n, and predictions with residuals.

The validation process proceeds as follows:

• Cross-validation protocol: The selected configuration was evaluated using ten-fold cross-validation. For each fold, the model was trained and then evaluated by computing the coefficient of determination R² only.
• Metric aggregation: The R² values from the ten folds were averaged and reported as a single summary statistic. Additional stability diagnostics, such as standard deviation, confidence intervals, or residual analysis, were not included in the present study.

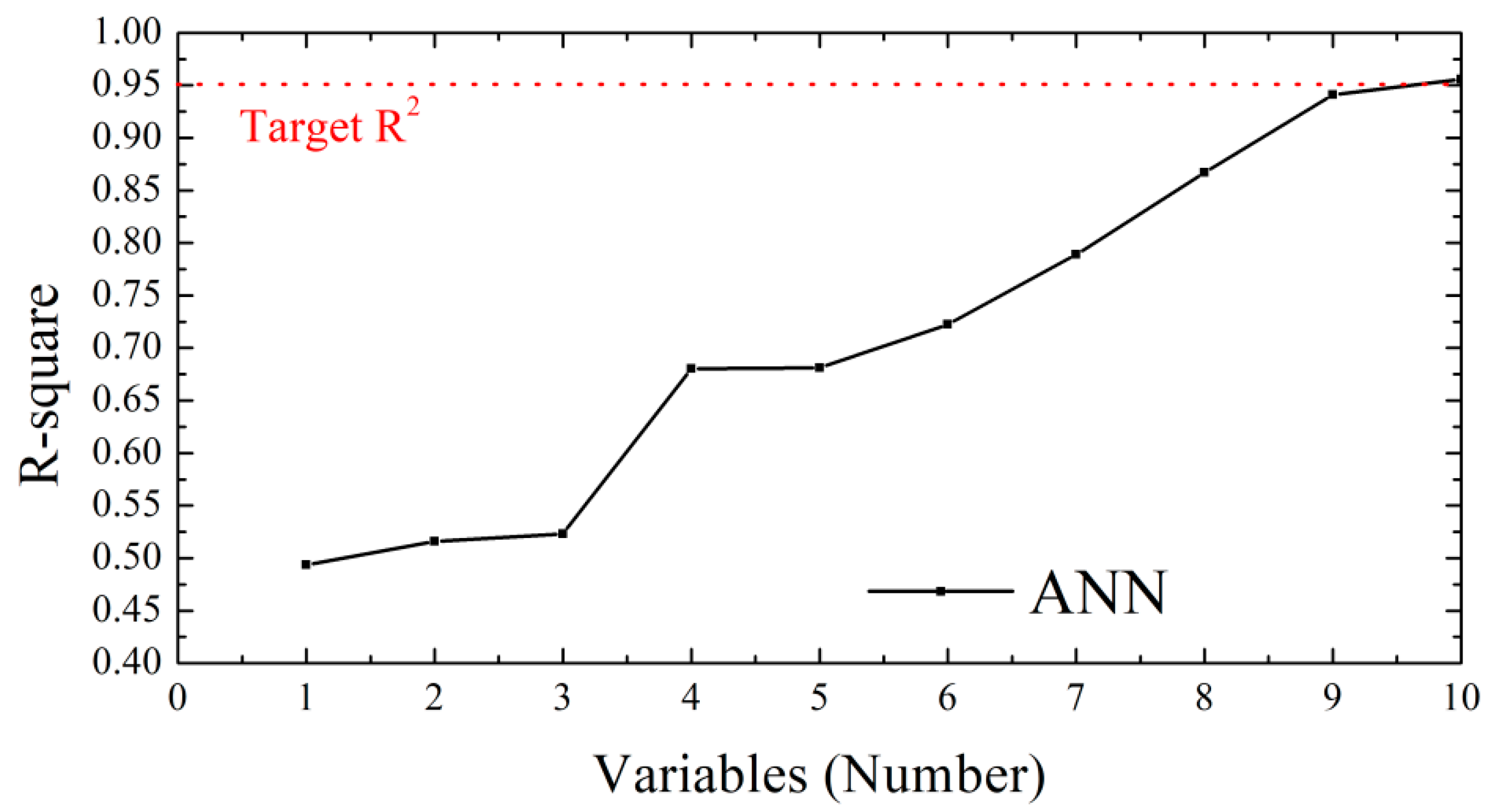
3.3.2. Cross-Validated Performance of the ANN

The artificial neural network showed a clear accuracy trend as the number of predictors increased, as shown in Figure 11. With one to three variables, the cross-validated coefficient of determination was about 0.50 to 0.60, indicating that a very small set of bands could not represent the nonlinear structure of the spectra. With four features, the value rose to about 0.70, suggesting that the inclusion of the most informative wavelengths began to recover the dominant moisture related patterns. From five to eight variables, accuracy improved steadily to about 0.85 to 0.90, reflecting the growing ability of the model to combine complementary bands and the engineered transforms. With ten variables, the network reached an R² of 0.9557, exceeding the study target of 0.95.

Here, the selected wavelengths were 400, 408, 412, 448, 560, 688, 696, 720, 728, and 776 nm. The ten selected wavelengths align with known moisture sensitive regions, which explains the ANN gain in accuracy. The 400–448 nm wavelengths capture ferric iron charge transfers, and there is a darkening blue region that strengthens with thin water films and organic matter, reinforcing the global-continuum damping caused by higher moisture. The 560 nm represents the green reflectance peak, sensitive to iron oxides and particle size, accounting for baseline albedo linked to mineralogy and dryness. The 688–728 nm span the red to near-infrared transition where slope and the shoulder near 680 to 700 nm respond strongly to moisture. The 776 nm sits on the long wavelength shoulder toward the 970 nm water overtone, summarizing curvature and overall albedo reduction as moisture increases.

Taken together, this set captures continuum attenuation, local features, and band interactions that moisture induces. The ANN can learn these nonlinear combinations, so a compact input still approximates the smooth mapping from spectra to gravimetric water content, yielding the observed R² near 0.956. Thus, the performance is supported by physically meaningful bands, improving both accuracy and interpretability, consistent with the established soil spectroscopy literature [58,59,60,61].

Training was numerically stable under the stated settings. Rectified linear unit activations and dropout regularization prevented divergence and reduced overfitting, and the use of fixed random seeds produced repeatable runs. The feature count sweep recorded in the Scores worksheet shows diminishing returns beyond the selected configuration: accuracy gains between nine and ten variables were material, whereas further additions produced only minor changes around the achieved level. This pattern supports the choice of a ten-variable input for operational use because it balances accuracy and computational load.

A qualitative inspection of fitted values indicated no obvious systematic bias across the range of gravimetric water content considered in this study. Residuals were centered near zero and did not display a monotonic trend with respect to the predicted values. This is consistent with the interpretation that the model captured the main nonlinear relations in the spectra. Nevertheless, the trained mapping remains data dependent.

From an implementation perspective the trained model is lightweight. The final architecture contains three hidden layers with 128, 64, and 32 units, which allows for a short inference time once the ten-dimensional predictor vector has been prepared. All artifacts required for reproduction have been saved: the model in H5 format, the scaler, the list of selected predictors including the engineered terms, and the history of accuracy as a function of variable count. These materials enable exact regeneration of the reported results and allow independent evaluation under alternative data splits if required by the review process.

3.3.3. Test Using ANN Algorithm

After model development, about 100 new paired observations were collected at the same site using the same field protocol as in training. Hyperspectral scenes were acquired by UAV, and gravimetric water content was measured immediately after imaging at the marked points. The trained ANN and the previously selected set of wavelengths were kept fixed with no refitting or hyper-parameter changes. The stored network weights were applied directly to the new data to generate predictions. Performance was assessed solely by the coefficient of determination R² between observed and predicted gravimetric water content on this external test set.

The final result is shown in Figure 12. The ANN achieved R² = 0.9513, indicating that most of the variance in the measurements is explained by the model. The errors were compact, with RMSE = 0.2398 and MAE = 0.1926, which show small average deviations and only a modest portion of larger errors. The mean bias error was −0.2130, indicating a systematic tendency to underestimate. In practice, an offset correction equal to the bias would remove this shift, after which RMSE and MAE would represent primarily random dispersion. Finally, the result indicates that the ANN maintained high explanatory power on unseen data and effectively met the research’s target performance. This supports field applicability and temporal stability within the same site and acquisition protocol.

Because the independent test area is a well-drained sandy field, moisture decayed rapidly after rainfall and the new acquisitions concentrated in a dry range of about 3–7 percent gravimetric water content. Reported claims of transferability are therefore restricted to within-site and within-sensor conditions and to the observed GWC range. Forthcoming data collection will target higher moisture states through immediate post-rainfall and early-morning acquisitions and, where permissible, controlled wetting of small plots under the same protocol.

4. Discussion

This study compared regression and artificial learning approaches for estimating soil moisture from hyperspectral reflectance and examined the role of nonlinearity and variable interactions in prediction accuracy. While multiple regression has often been favored for simplicity and interpretability, the present results confirm that linear formulations are limited for high dimensional spectroscopic data, where band correlations and overlapping absorptions induce nonlinear structure.

The artificial neural network provided the strongest overall performance. As the number of predictors increased, accuracy rose steadily and reached the target with a compact ten variable input, indicating that the network effectively represented smooth nonlinear mappings from spectra to gravimetric water content. This behavior is consistent with the view that hyperspectral-to-property relationships benefit from flexible function approximates that accommodate both local spectral features and their interactions. The result also shows that a compact neural network can rival or exceed state-of-the-art ensembles while keeping inference efficient.

This study did not precede model training with controlled laboratory spectroscopy. Instead, hyperspectral reflectance and GWC were acquired in the field nearly at the same time and used for learning. This field-first approach preserves real operating conditions such as illumination, viewing geometry, and surface roughness, thereby strengthening practical applicability. Panel-based empirical line calibration was applied to every flight to ensure radiometric consistency, and day-grouped cross-validation was used to check performance stability under temporal variability. To assess intra site temporal transferability, a date-grouped cross-validation was performed: all samples from one acquisition day were held out while the remaining days were used for training, cycling across days, including the post-rain session. In addition, an independent same-site test (~100 new spectrum–moisture pairs acquired after the model selection with the same sensor and protocol) was used to evaluate generalization under the operational acquisition pipeline. Reported claims of transferability are restricted to within-site and within-sensor conditions.

The present results demonstrate within-site temporal transferability under consistent sensor and protocol conditions, as supported by date-grouped cross-validation and an independent same-site test (R² = 0.9513; RMSE = 0.2398; MAE = 0.1926; and bias = −0.2130). However, the independent same-site test sampled a dry, narrow range due to rapid drainage and daytime evaporation on sandy soil. As a result, the present evidence supports within-site temporal transferability within the 3–7 percent GWC range. Planned actions include stratified evaluation by GWC bins once broader coverage is collected, immediate post-rainfall and early morning acquisitions to capture wetter states, controlled wetting of small plots where allowed, seasonal extension into the monsoon period, and subsequent multi-site validation.

In addition, several specific limitations are noted. First, the study area is a single vegetation-free sandy site on a university campus, and the observation period is ten days in April, with one rainfall event. Limited diversity in soil and season may bias results toward local radiometric and textural conditions. Second, the spectral range was restricted to 398 to 982 nm in visible and near-infrared light, so water-sensitive shortwave infrared bands were not included. Third, validation mainly relied on cross-validated R² and one external test from the same site, so error magnitude, bias, and transfer to other sites were not fully assessed. Fourth, feature ranking and selection were performed before cross-validation; without nesting, this can introduce a small optimistic bias.

To address these points, the plan is to (1) add at least two additional sites with different soil textures and repeat the same protocol across dry-down and post-rain periods, (2) add a shortwave infrared sensor, covering 1.0 to 2.5 μm, to account for the water absorption features near 1.4 and 1.9 μm, (3) establish fixed hold-out sets separated by date and site, with nested cross-validation for feature selection and hyper-parameter tuning, and (4) report R² together with RMSE, MAE, bias, and uncertainty intervals, including a small laboratory dry and rewet spectroscopy subset to cross-check key wavelengths where appropriate.