Impact of Climate Change on Reference Evapotranspiration: Bias Assessment and Climate Models in a Semi-Arid Agricultural Zone
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
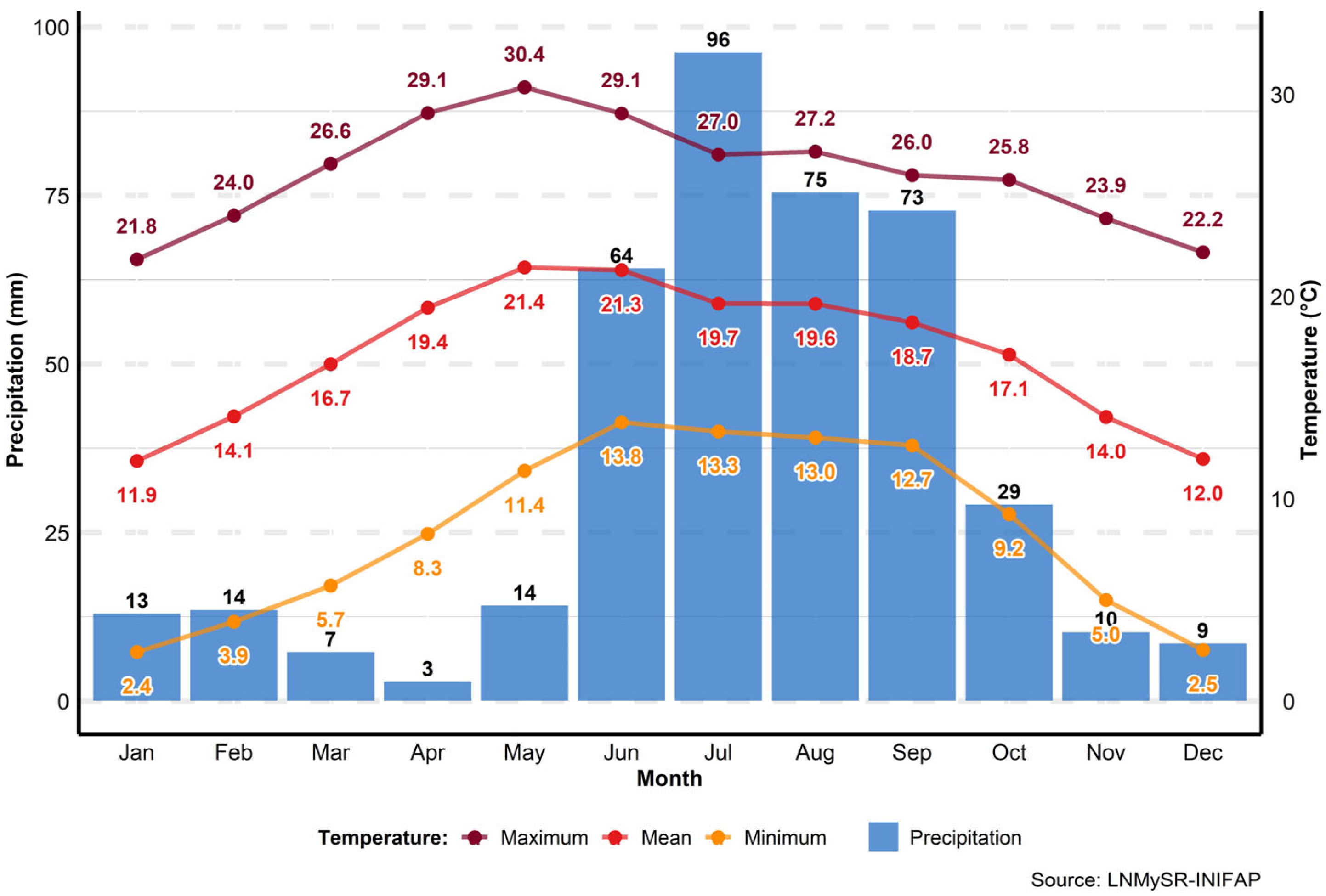
2.2. Automated Stations
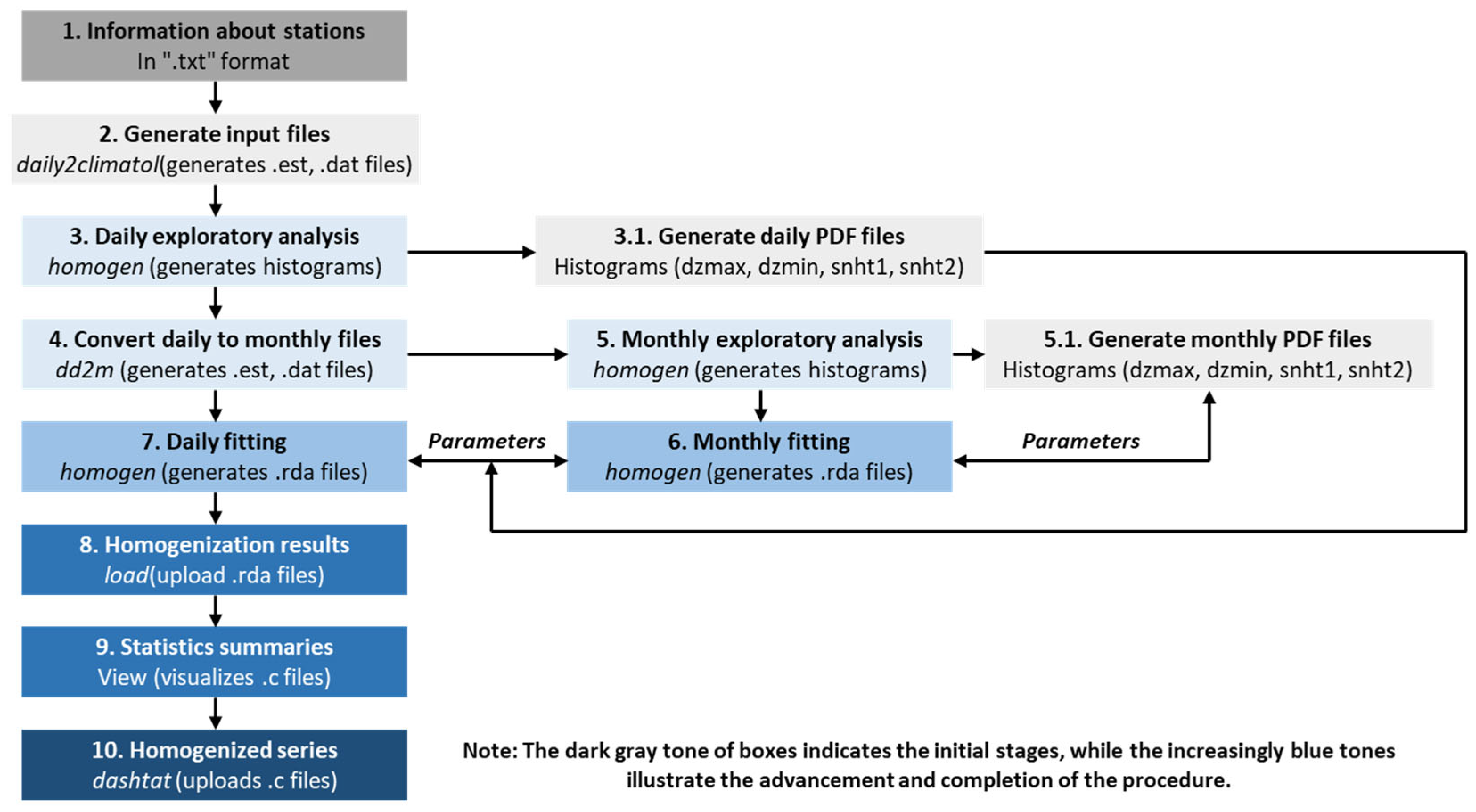
2.3. Climatol
2.4. Global Climate Models
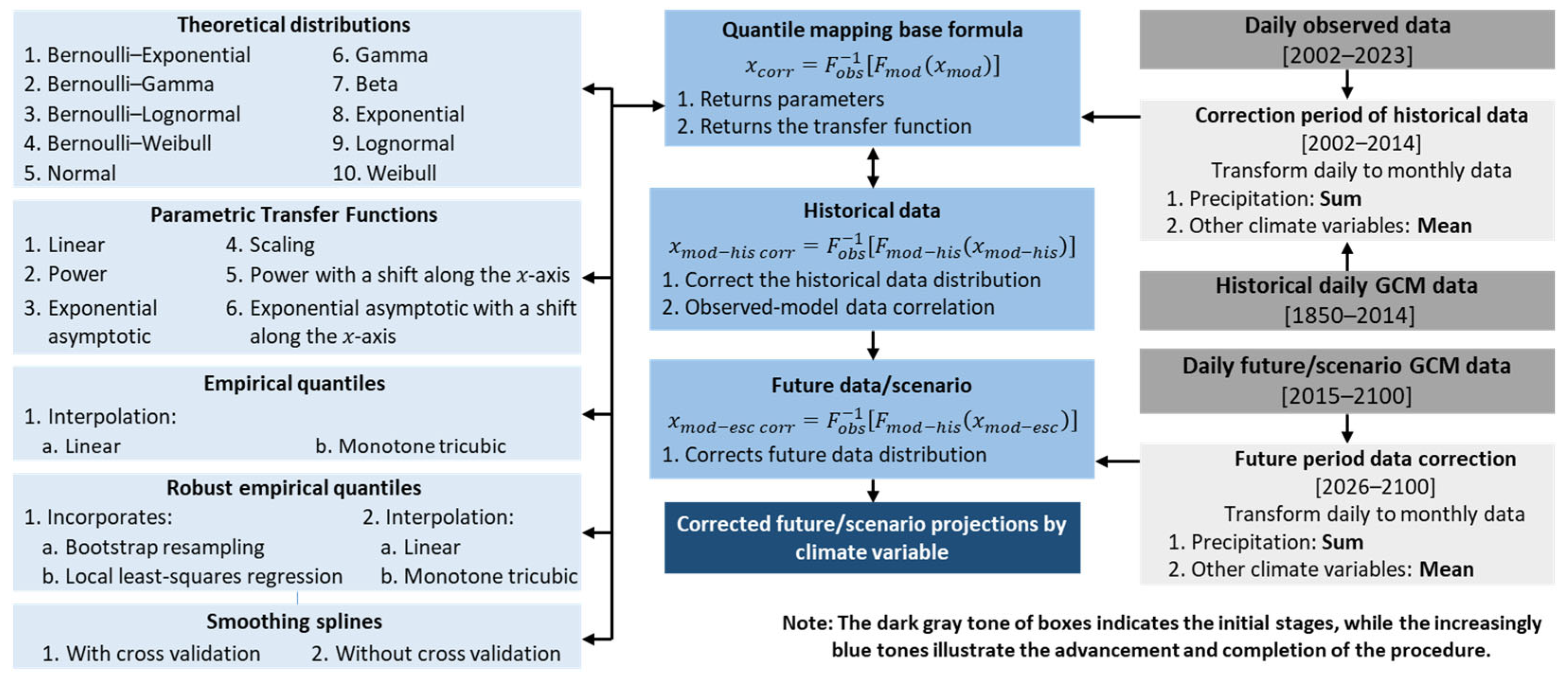
2.5. Bias Correction
2.5.1. Distribution-Derived Transformations (DIST)
2.5.2. Parametric Transfer Functions (PTF)
2.5.3. Empirical Quantiles (QUANT) and Robust Empirical Quantiles (RQUANT)
2.5.4. Smoothing Spline (SSPLIN)
2.6. Reference Evapotranspiration
2.7. Monte Carlo Method
2.7.1. Uncertainty/Variability in Simulated ET0
2.7.2. Analysis of Simulation and Estimate Bias
2.8. Sensitivity Analysis
3. Results and Discussion
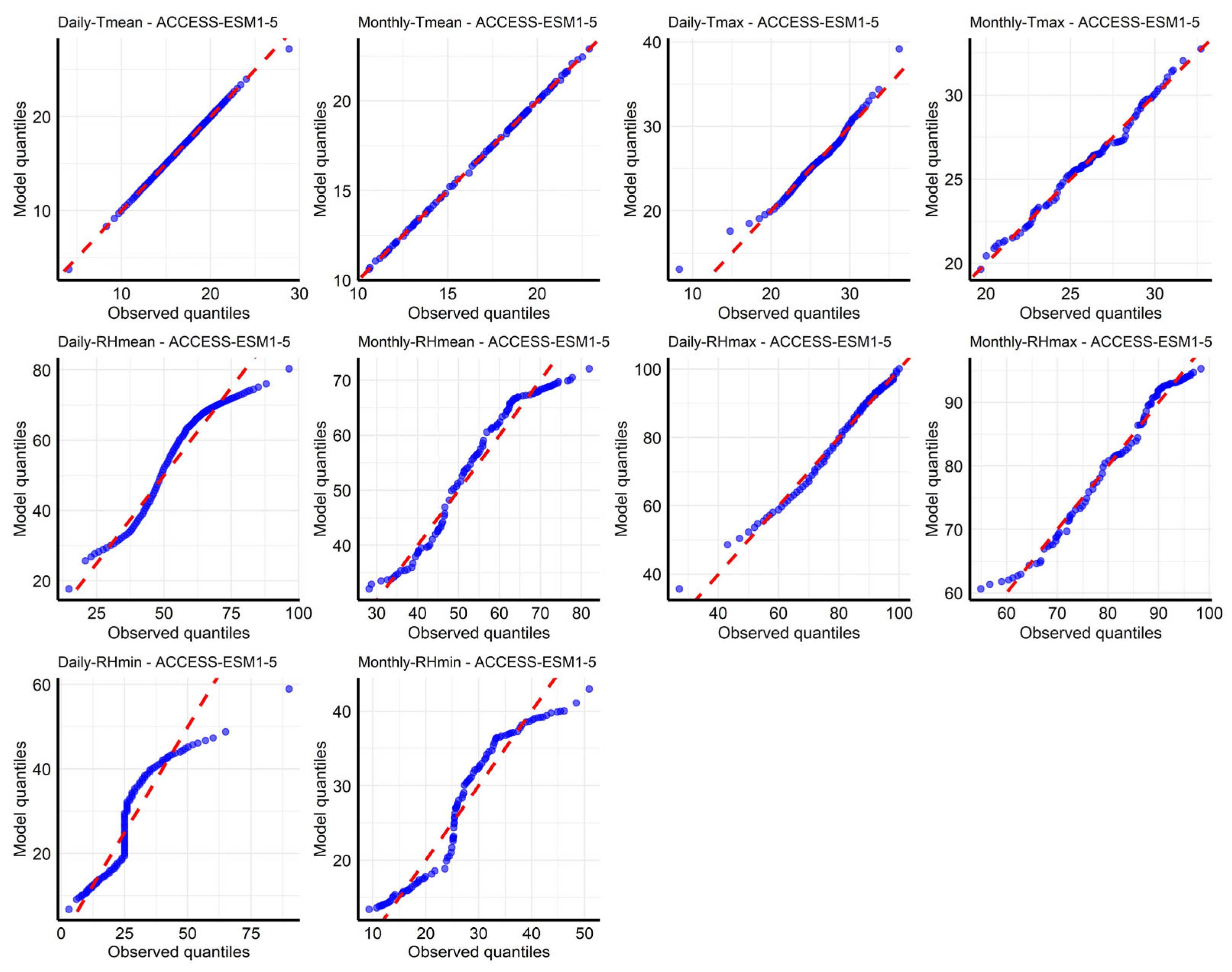
3.1. Evaluation of GCM Performance on Daily and Monthly Scales
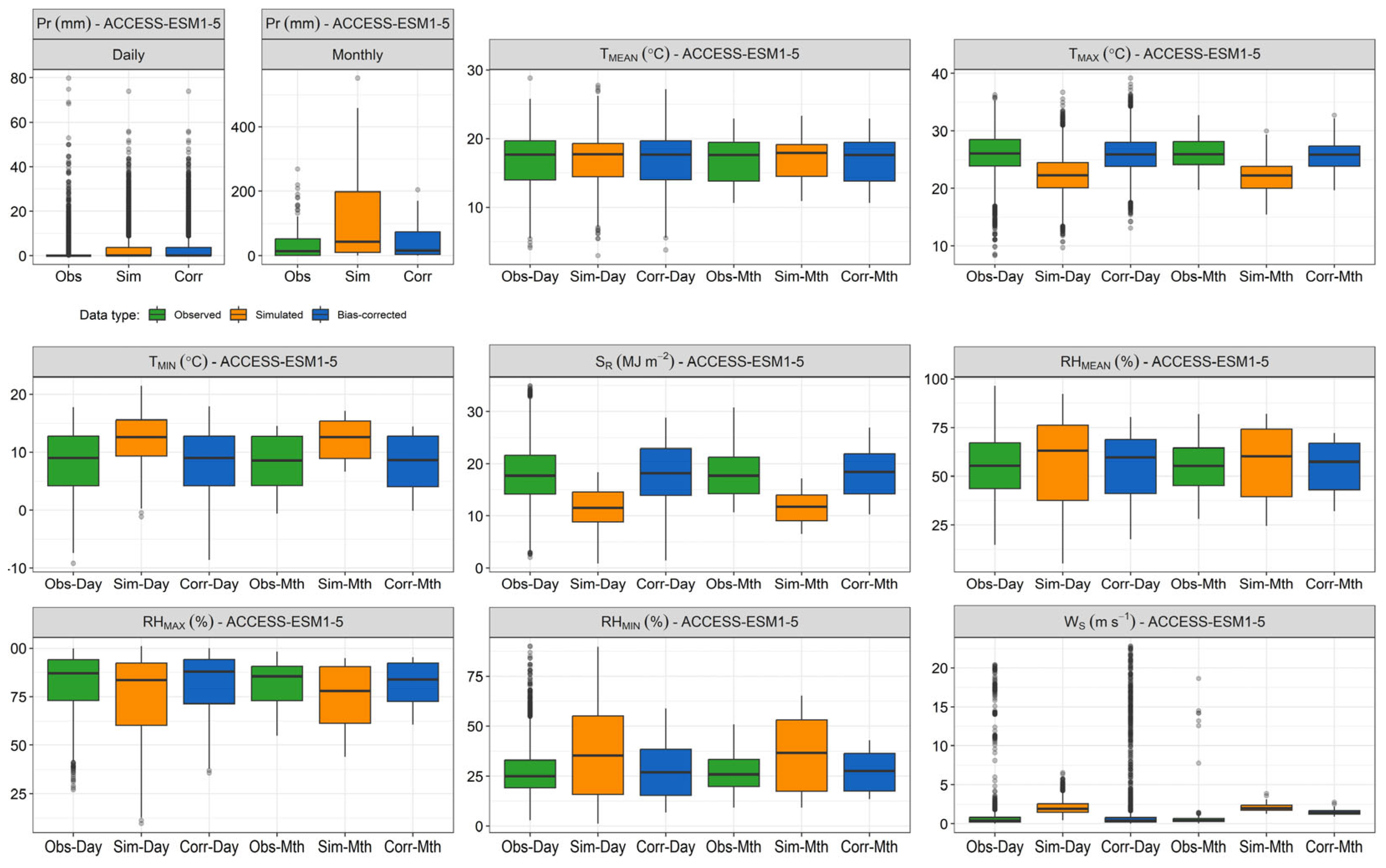
3.2. Evaluation of GCM Performance Before and After Bias Correction at Daily and Monthly Scales
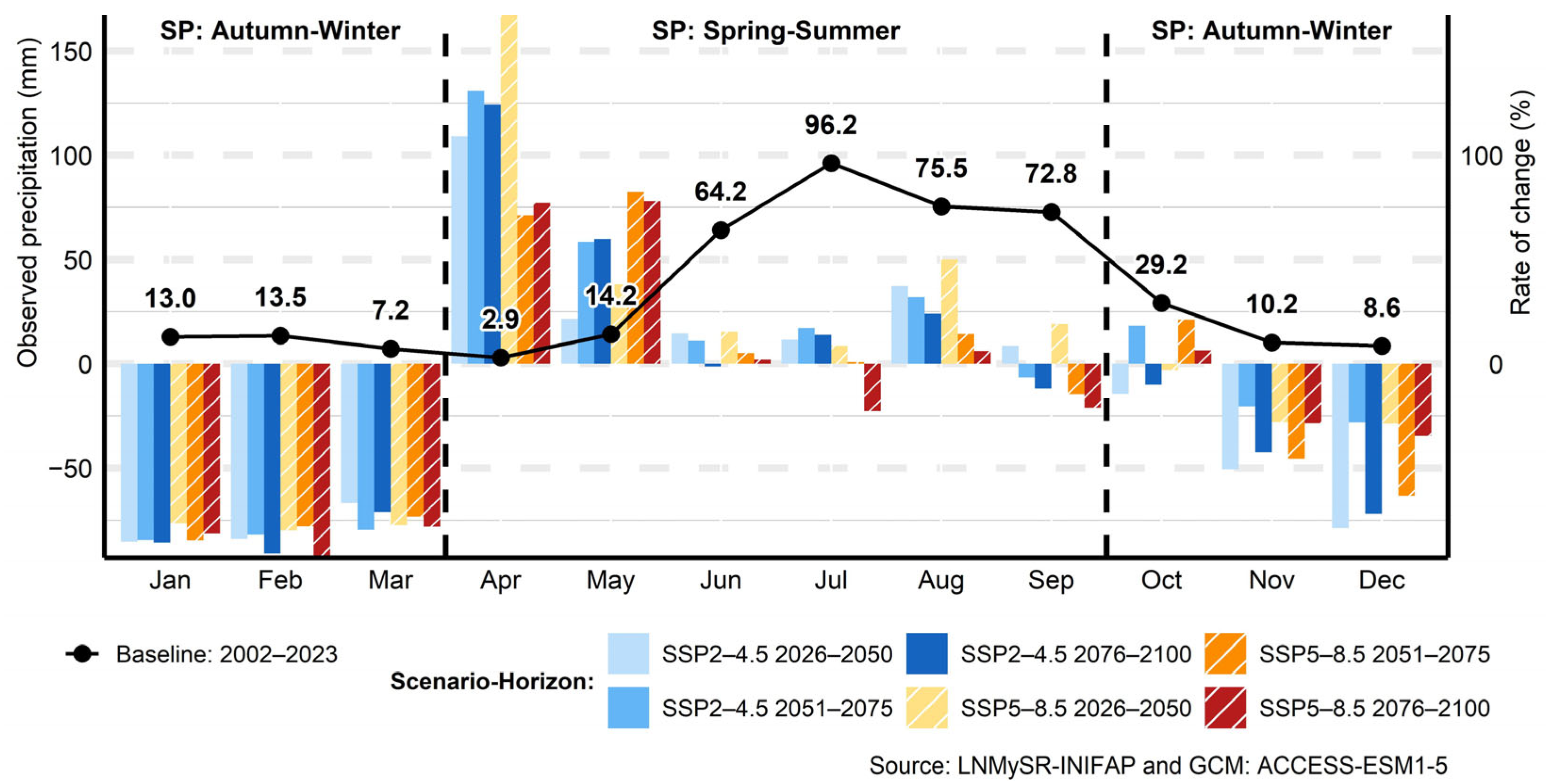
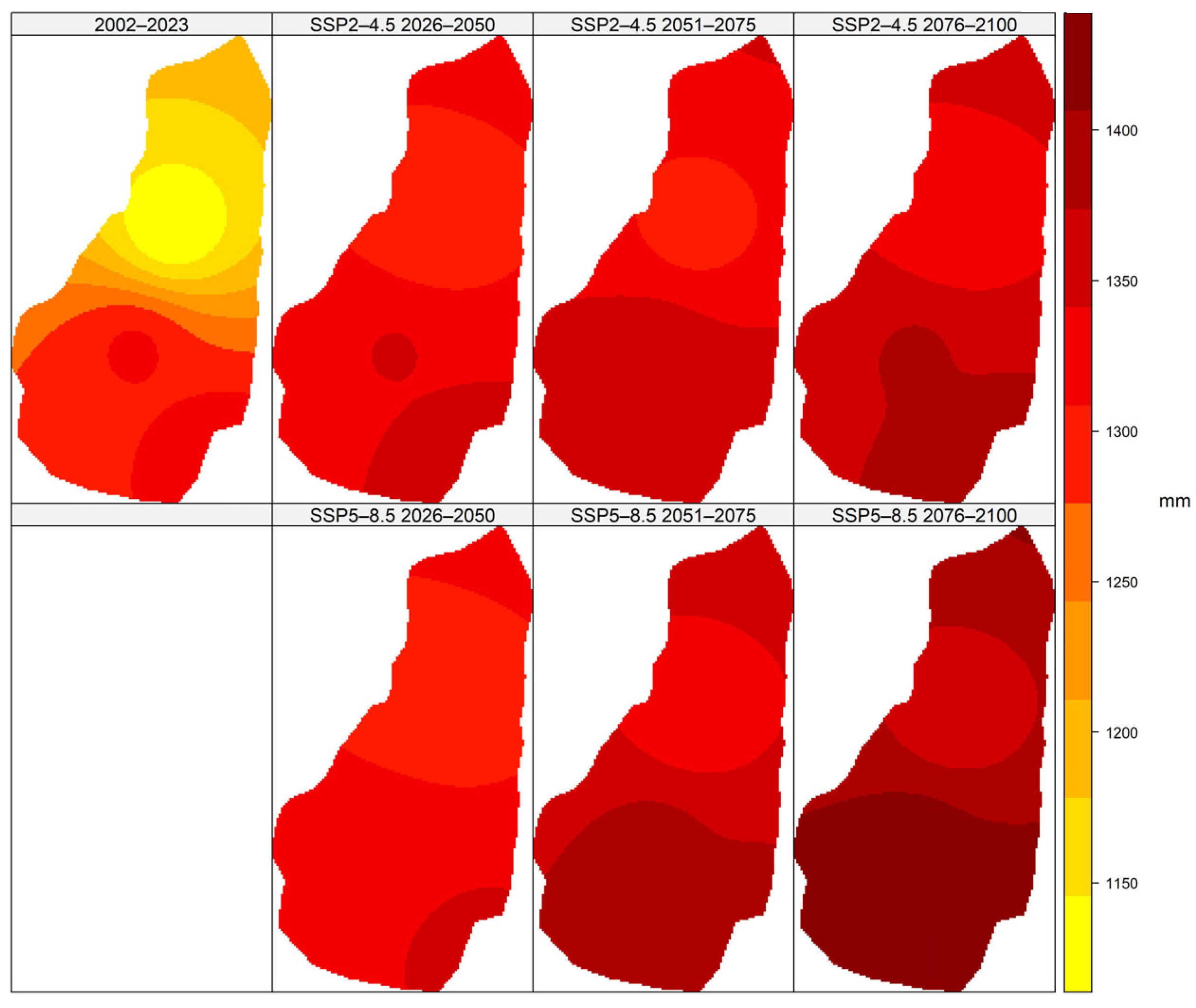
3.3. Precipitation
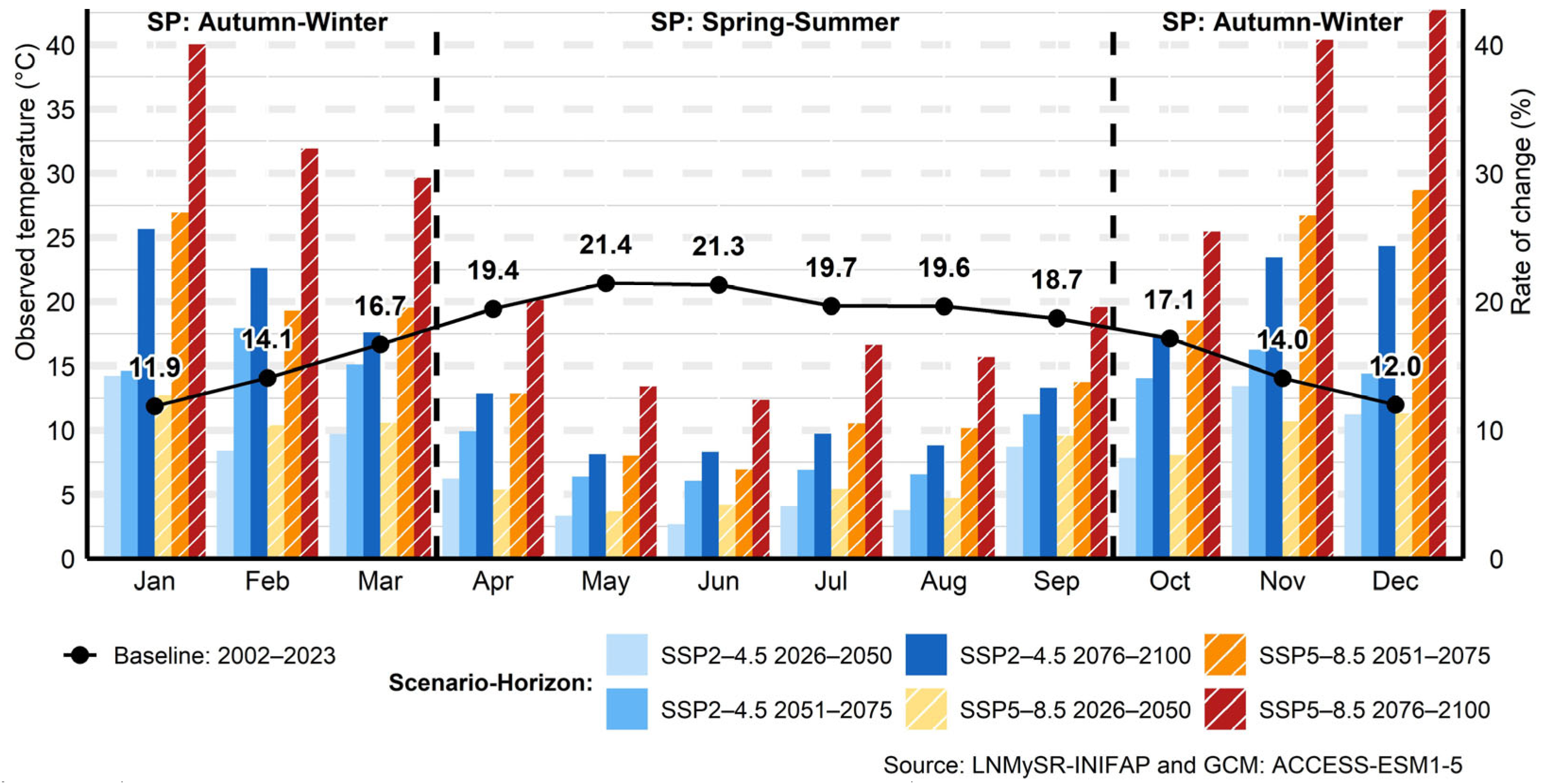
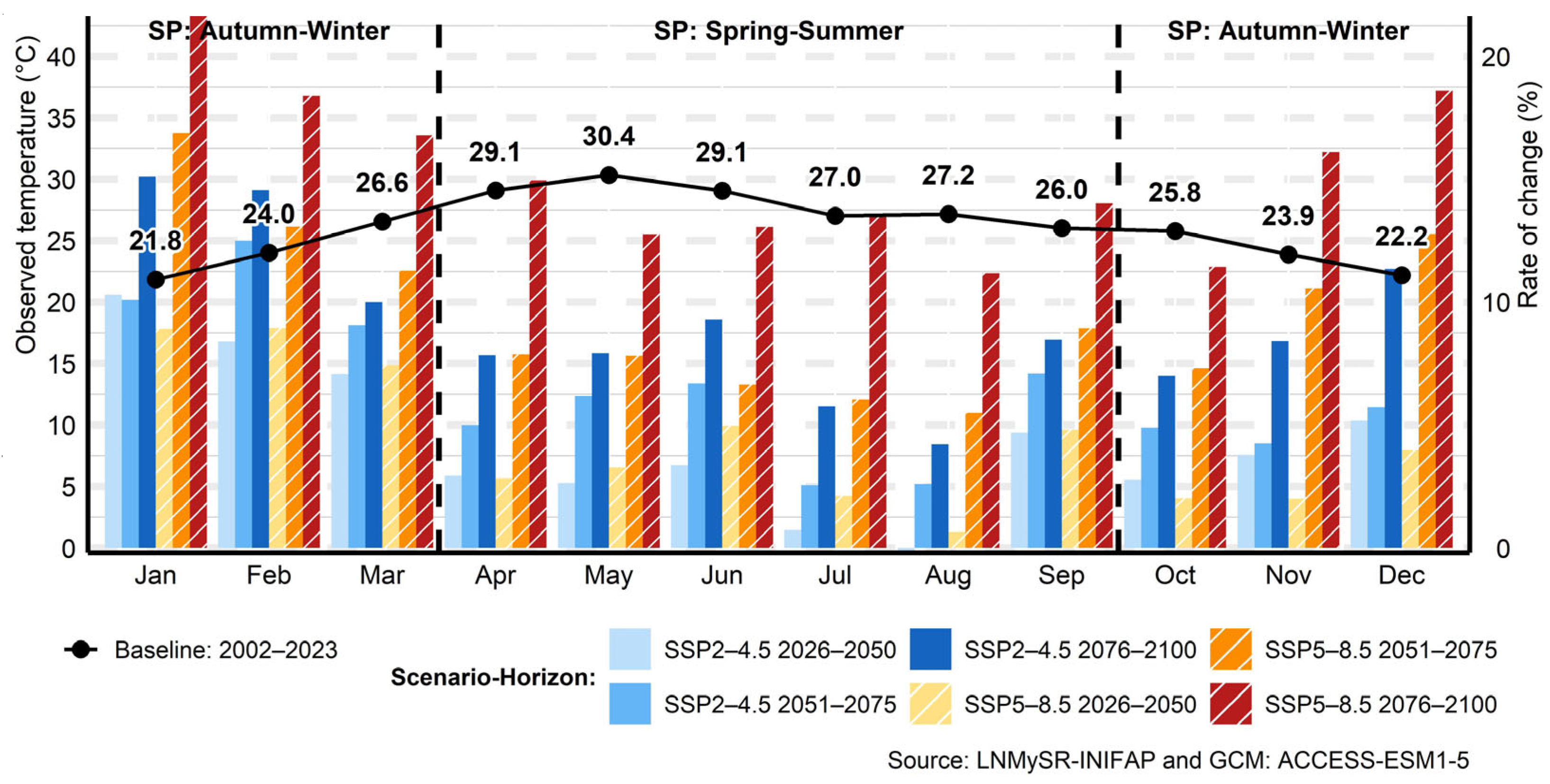
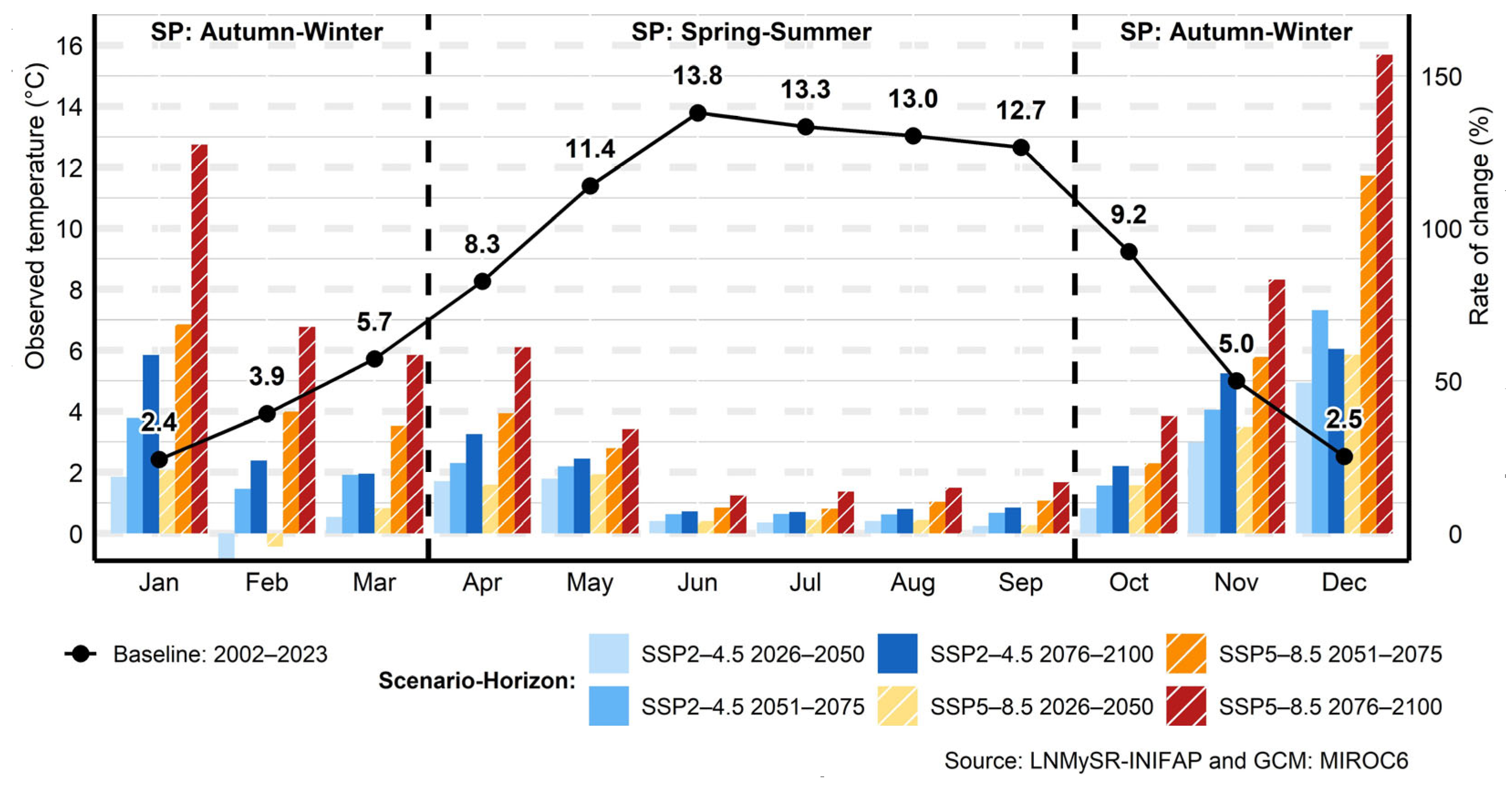
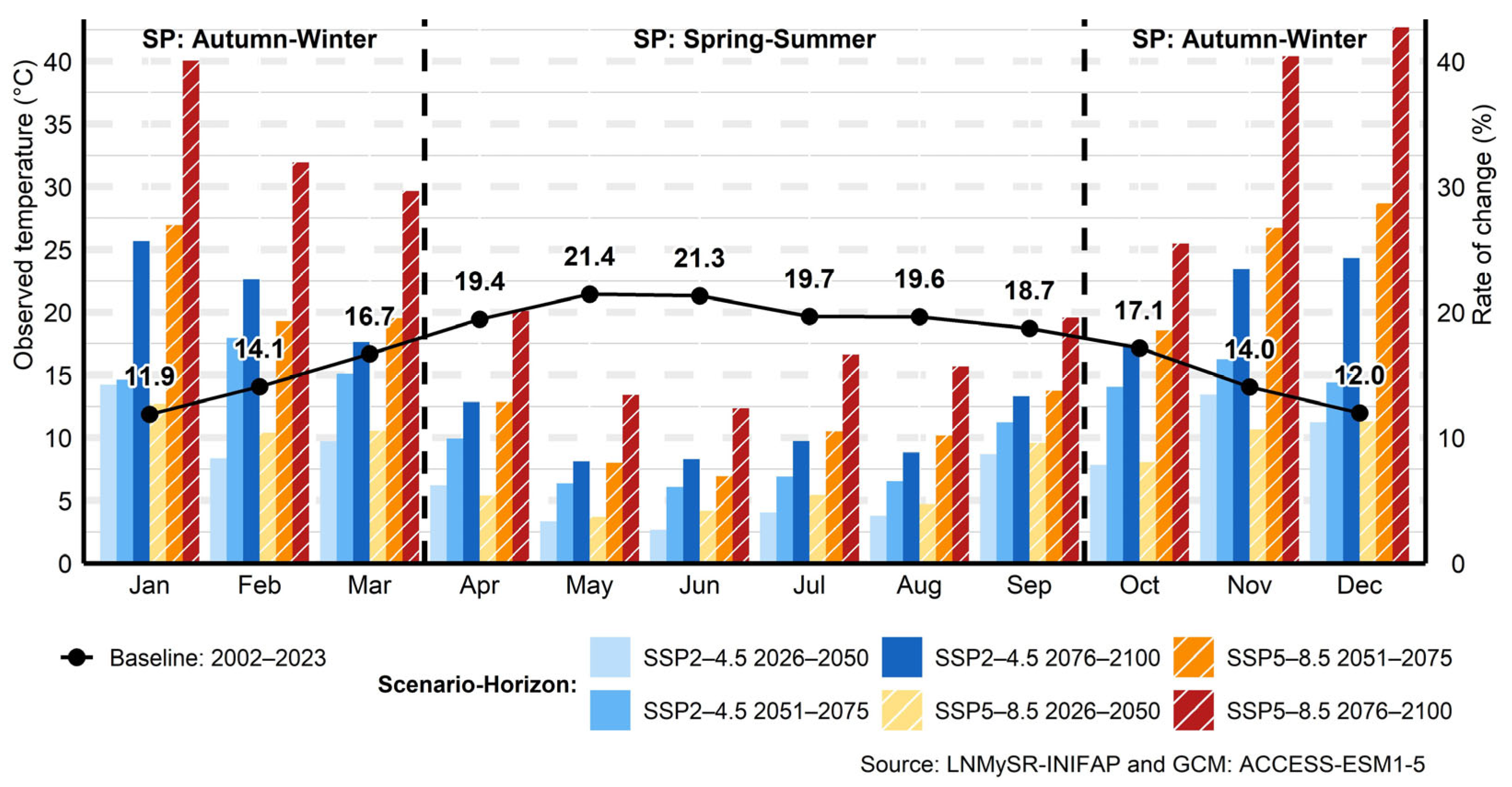
3.4. Temperature
3.4.1. Mean Temperature
3.4.2. Maximum Temperature
3.4.3. Minimum Temperature
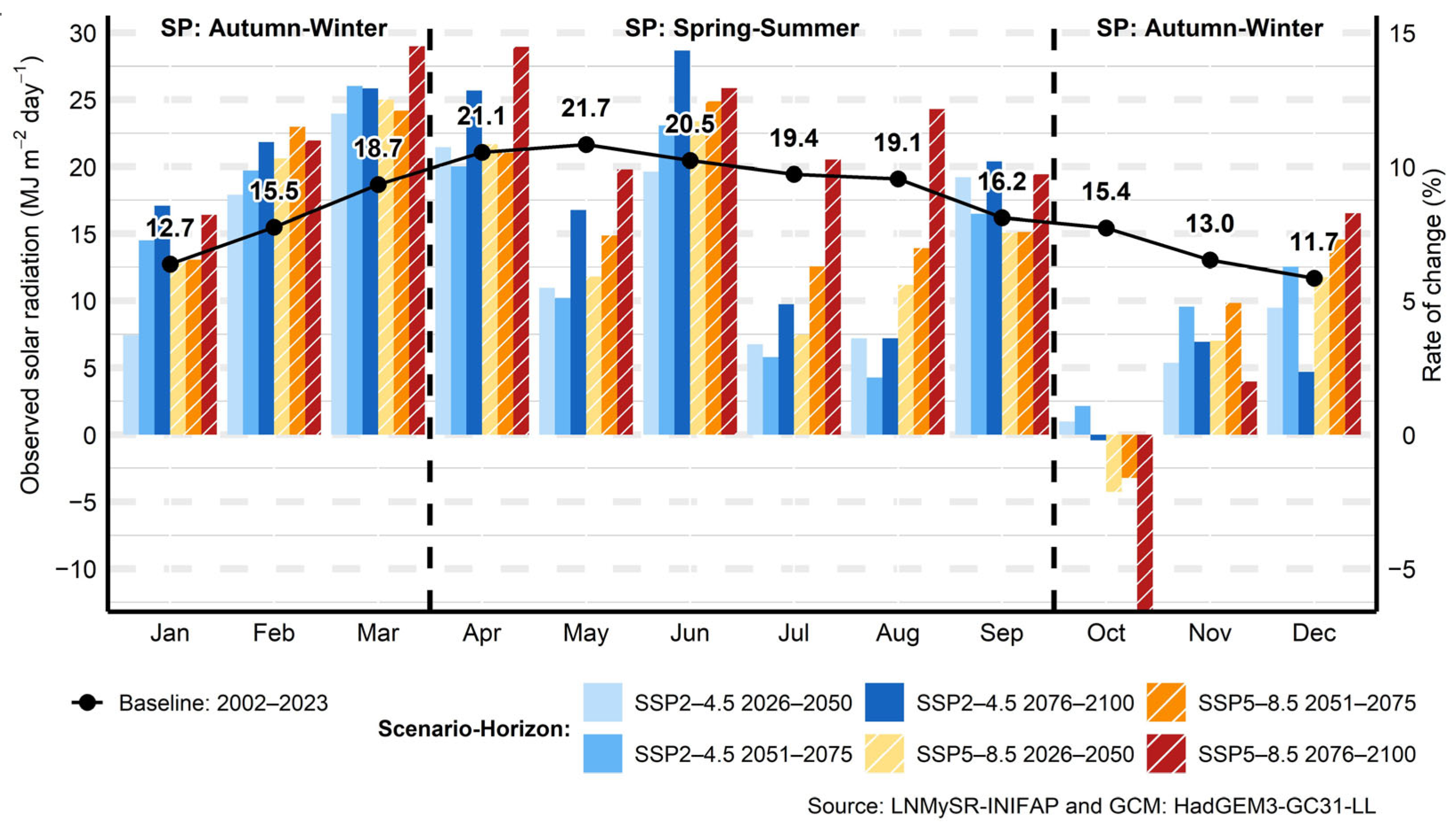
3.5. Solar Radiation
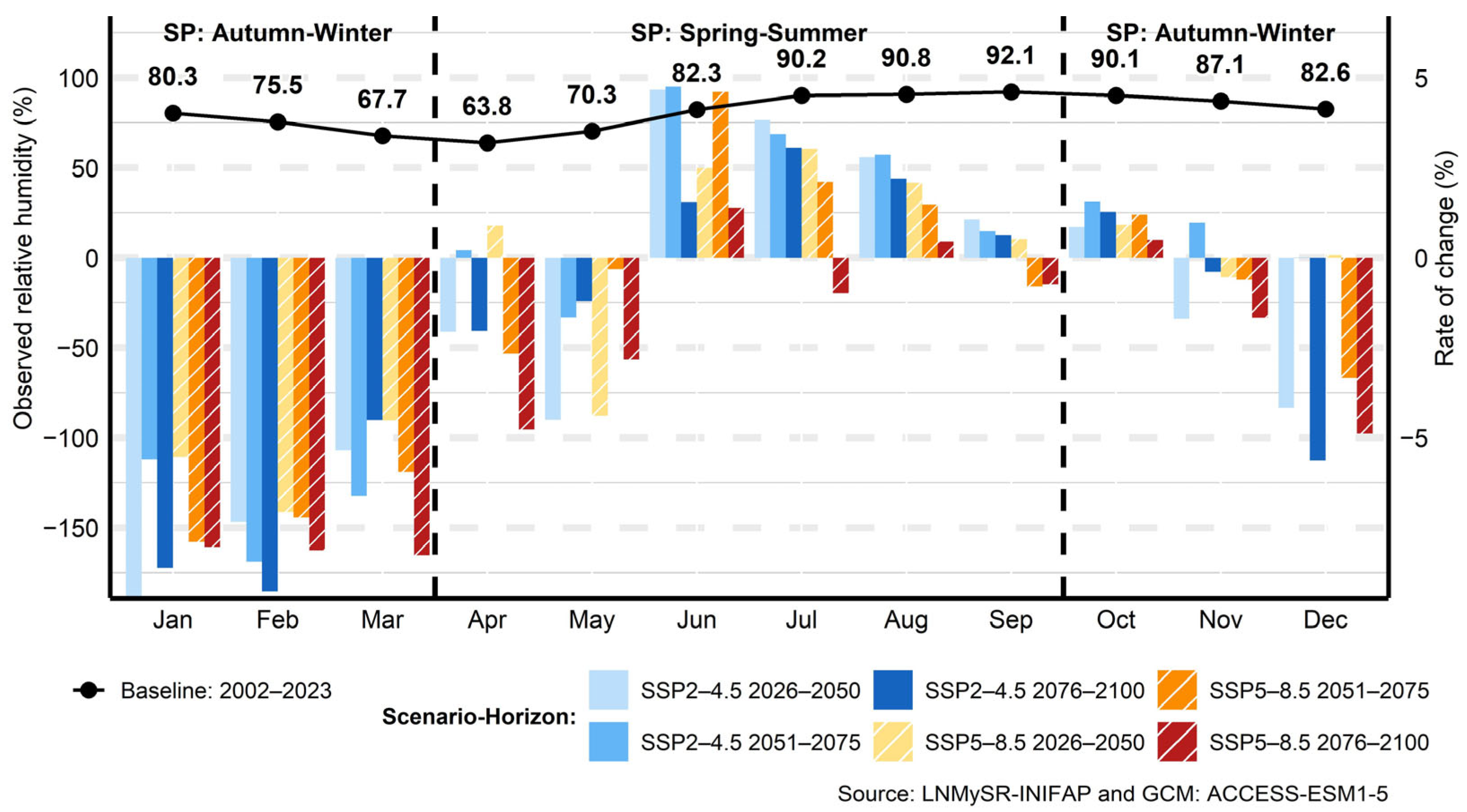
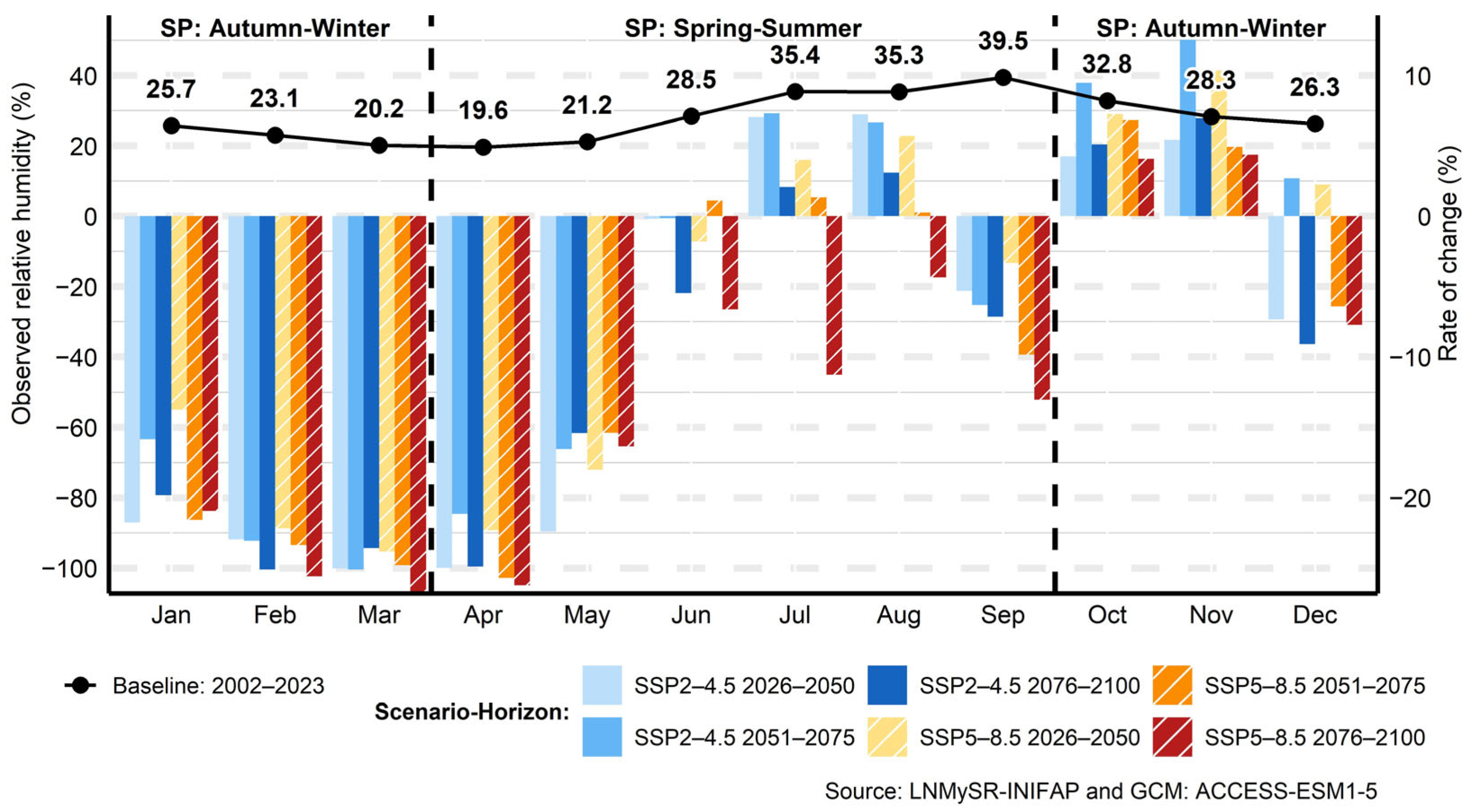
3.6. Relative Humidity
3.6.1. Mean Relative Humidity
3.6.2. Maximum Relative Humidity
3.6.3. Minimum Relative Humidity
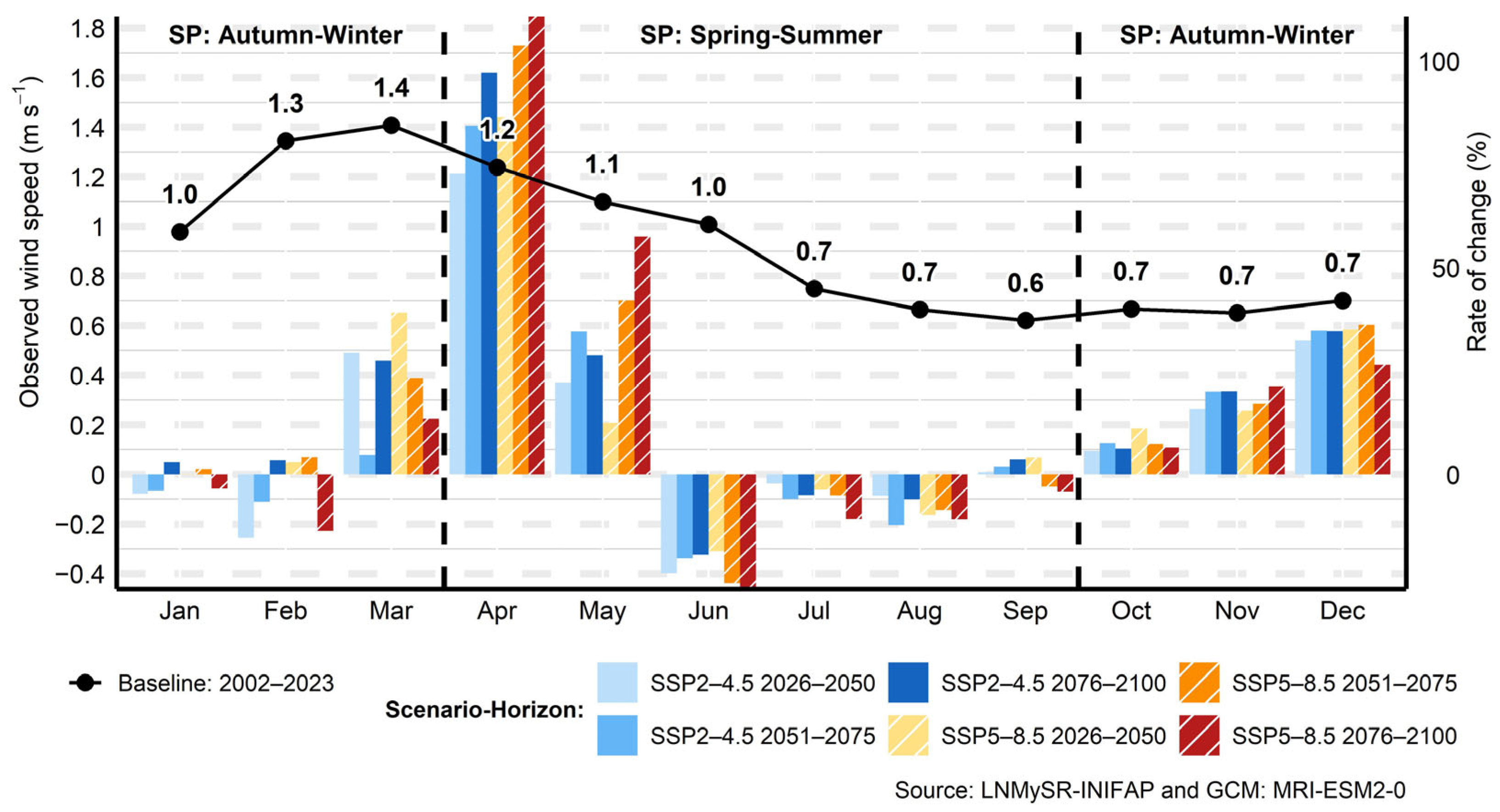
3.7. Wind Speed
3.8. Validation of the ACCESS-ESM1-5 Model Against the Multi-Model Ensemble
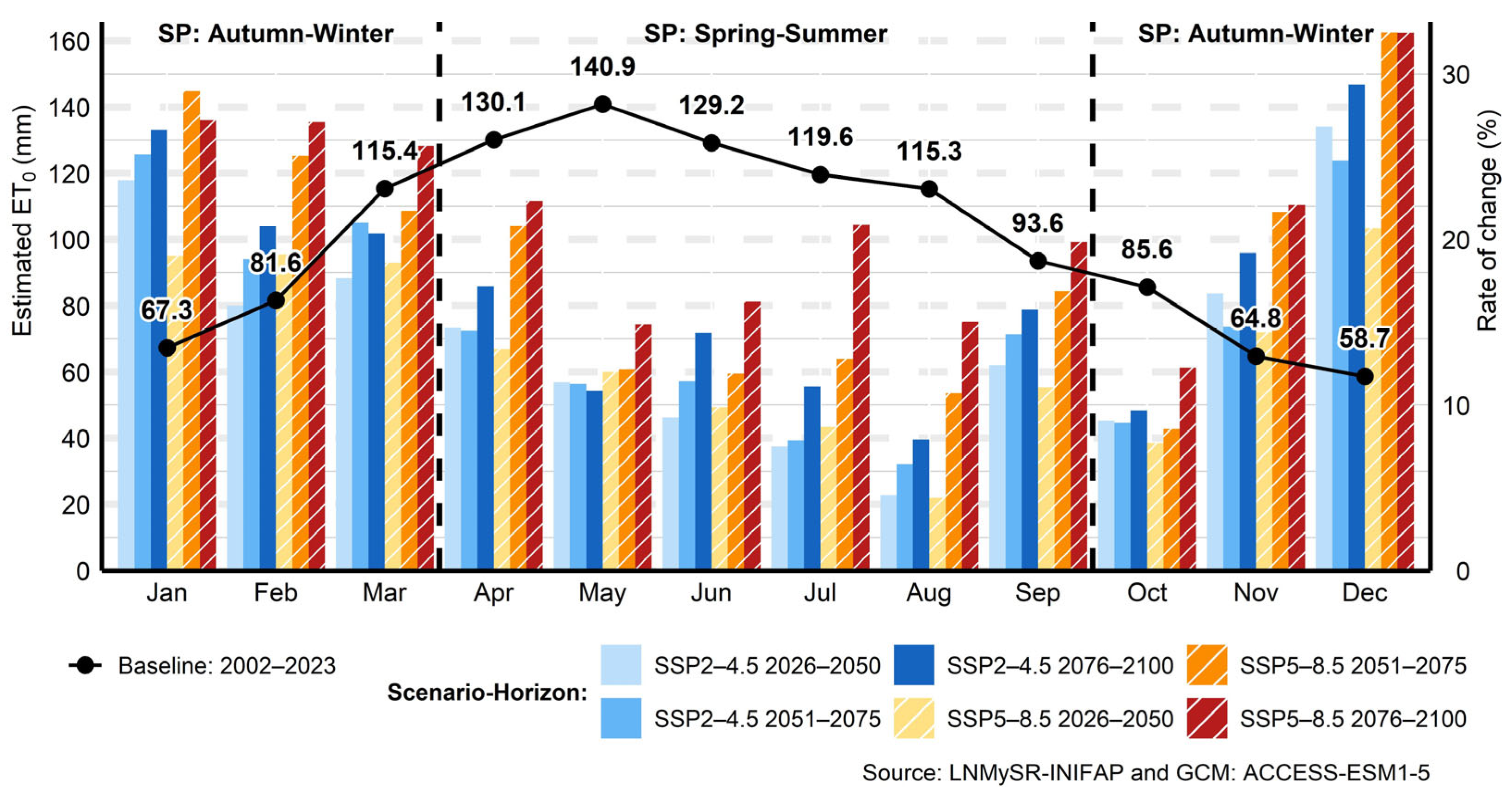
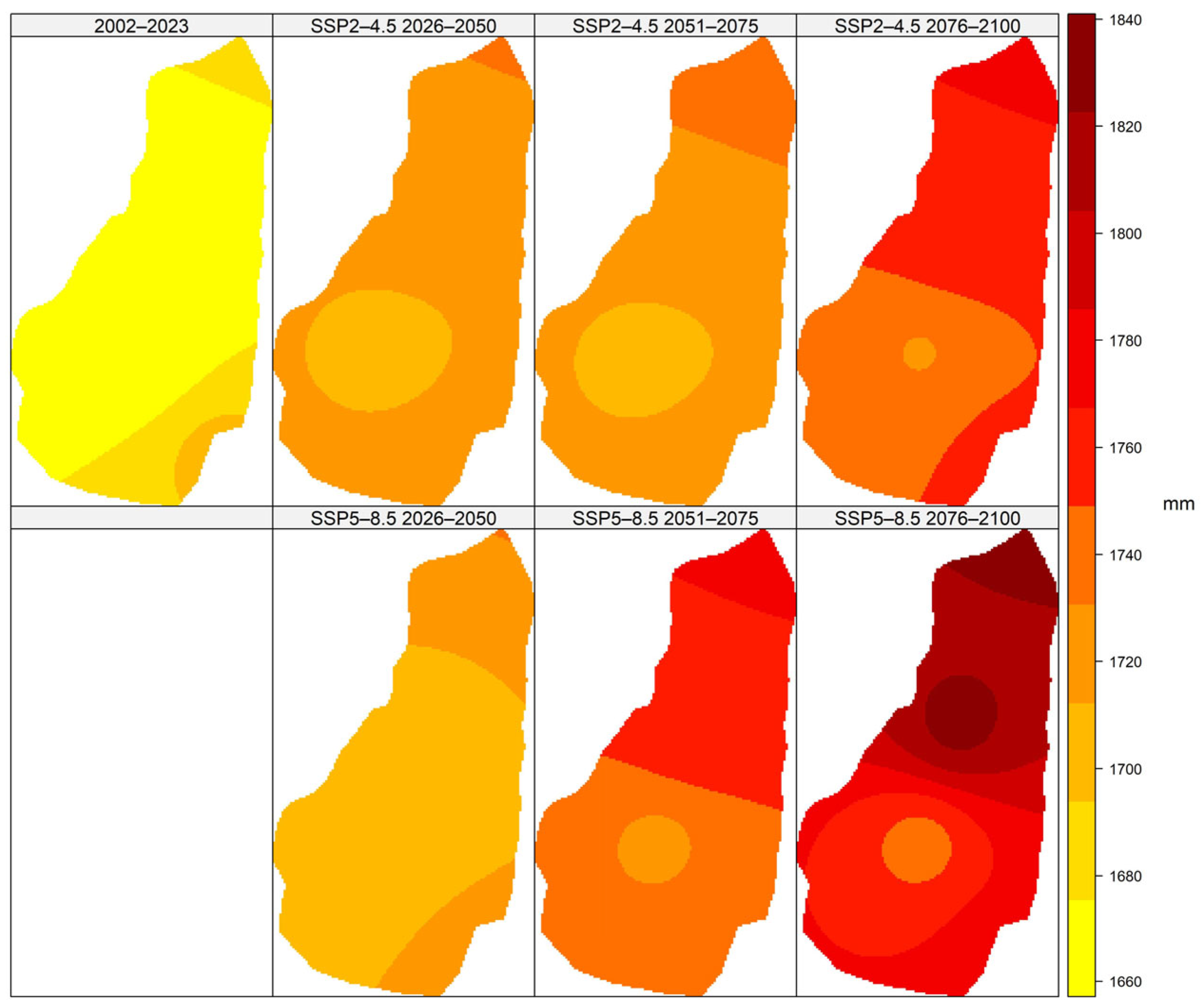
3.9. ET0 Estimates in Time Horizons
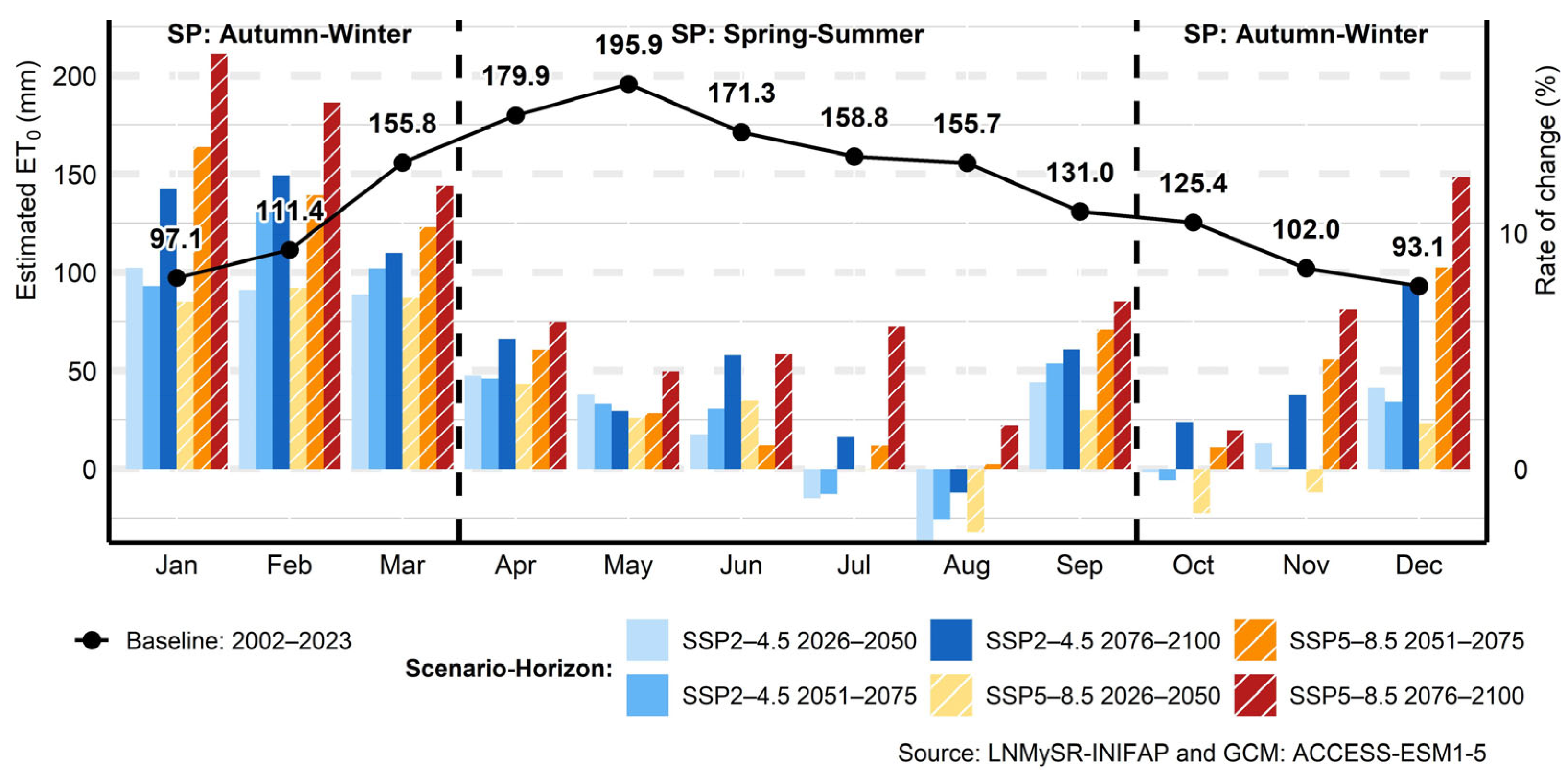
3.10. Analysis of Uncertainty and Bias in ET0
3.11. Sobol Analysis for ET0
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DR 001 | Irrigation District 001 Pabellón de Arteaga, Aguascalientes |
| Pr | Precipitation |
| TMAX | Temperature maximum |
| TMIN | Temperature minimum |
| TMEAN | Temperature mean |
| SR | Solar radiation |
| RHMAX | Maximum relative humidity |
| RHMIN | Minimum relative humidity |
| RHMEAN | Mean relative humidity |
| WS | Wind speed |
| GCM | Global Climate Models |
| SD | Standard Deviation |
| RMSE | Root Mean Square Error |
| SSP2-4.5 | Shared Socioeconomic Pathway 2–Representative Concentration Pathway 4.5 |
| SSP5-8.5 | Shared Socioeconomic Pathway 5–Representative Concentration Pathway 8.5 |
| DIST | Distribution-derived transformations |
| PTF | Parametric Transfer Functions |
| QUANT | Empirical quantiles |
| RQUANT | Robust empirical quantiles |
| SSPLIN | Smoothing Spline |
| ET0 | Reference evapotranspiration |
| FAO-56 | FAO Penman-Monteith |
| P-T | Priestley-Taylor |
| H-S | Hargreaves-Samani |
Appendix A









References
- Arnell, N.W.; Brown, S.; Gosling, S.N.; Gottschalk, P.; Hinkel, J.; Huntingford, C.; Lloyd-Hughes, B.; Lowe, J.A.; Nicholls, R.J.; Osborn, T.J.; et al. The Impacts of Climate Change across the Globe: A Multi-Sectoral Assessment. Clim. Change 2016, 134, 457–474. [Google Scholar] [CrossRef]
- Hicke, J.A.; Lucatello, S.; Mortsch, L.D.; Dawson, J.; Domínguez Aguilar, M.; Enquist, C.A.F.; Gilmore, E.A.; Gutzler, D.S.; Harper, S.; Holsman, K.; et al. North America. In Climate Change 2022: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Pörtner, H.-O., Roberts, D.C., Tignor, M.M.B., Poloczanska, E.S., Mintenbeck, K., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., Eds.; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Tao, S.; Xu, Y.; Liu, K.; Pan, J.; Gou, S. Research Progress in Agricultural Vulnerability to Climate Change. Adv. Clim. Change Res. 2011, 2, 203–210. [Google Scholar] [CrossRef]
- FAO; IFAD; UNICEF; WFP; WHO. The State of Food Security and Nutrition in the World 2022; FAO; IFAD; UNICEF; WFP; WHO: Rome, Italy, 2022; ISBN 978-92-5-136499-4.
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper; FAO: Rome, Italy, 1998; ISBN 92-5-104219-5.
- Yang, L.; Feng, Q.; Adamowski, J.F.; Yin, Z.; Wen, X.; Wu, M.; Jia, B.; Hao, Q. Spatio-Temporal Variation of Reference Evapotranspiration in Northwest China Based on CORDEX-EA. Atmos. Res. 2020, 238, 104868. [Google Scholar] [CrossRef]
- Yvoz, S.; Lechenet, M.; Amiotte-Suchet, P.; Castel, T.; Betting, E.; Ubertosi, M. Assessing Crop Water Deficiency for Regional Adaptation to Climate Change. Agric. Water Manag. 2025, 314, 109525. [Google Scholar] [CrossRef]
- Rahman, M.; Hasan, M.M.; Hossain, M.A.; Das, U.K.; Islam, M.M.; Karim, M.R.; Faiz, H.; Hammad, Z.; Sadiq, S.; Alam, M. Integrating Deep Learning Algorithms for Forecasting Evapotranspiration and Assessing Crop Water Stress in Agricultural Water Management. J. Environ. Manag. 2025, 375, 124363. [Google Scholar] [CrossRef]
- Gurara, M.A.; Jilo, N.B.; Tolche, A.D. Impact of Climate Change on Potential Evapotranspiration and Crop Water Requirement in Upper Wabe Bridge Watershed, Wabe Shebele River Basin, Ethiopia. J. Afr. Earth Sci. 2021, 180, 104223. [Google Scholar] [CrossRef]
- Escalante-Sandoval, C. Expected Impacts on Agriculture Due to Climate Change in Northern Mexico. In Water Resources of Mexico; Raynal-Villasenor, J.A., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 197–217. ISBN 978-3-030-40686-8. [Google Scholar]
- Ruiz-Alvarez, O.; Singh, V.P.; Enciso-Medina, J.; Munster, C.; Kaiser, R.; Ontiveros-Capurata, R.E.; Diaz-Garcia, L.A.; Costa dos Santos, C.A. Spatio-Temporal Trends in Monthly Pan Evaporation in Aguascalientes, Mexico. Theor. Appl. Clim. 2019, 136, 775–789. [Google Scholar] [CrossRef]
- Ruiz-Alvarez, O.; Singh, V.P.; Enciso-Medina, J.; Ontiveros-Capurata, R.E.; dos Santos, C.A.C. Observed Trends in Daily Temperature Extreme Indices in Aguascalientes, Mexico. Theor. Appl. Clim. 2020, 142, 1425–1445. [Google Scholar] [CrossRef]
- Sosa-Rodríguez, F.S. Política del cambio climático en México: Avances, obstáculos y retos. Real. Datos Espac. Rev. Int. Estad. Geogr. 2015, 6. [Google Scholar]
- Monterroso-Rivas, A.I.; Gómez-Díaz, J.D. Impacto del cambio climático en la evapotranspiración potencial y periodo de crecimiento en México: Cambio climático y ETP en México. Rev. Terra Latinoam. 2021, 39. [Google Scholar] [CrossRef]
- Ramirez Sanchez, H.U.; Fajardo Montiel, A.L.; Ortiz Bañuelos, A.D.; De la Torre Villaseñor, O. Impacts of Climate Change on the Water Sector in Mexico. Asian J. Environ. Ecol. 2022, 17, 37–57. [Google Scholar] [CrossRef]
- Sainz-Santamaria, J.; Martinez-Cruz, A.L. How Far Can Investment in Efficient Irrigation Technologies Reduce Aquifer Overdraft? Insights from an Expert Elicitation in Aguascalientes, Mexico. Water Resour. Econ. 2019, 25, 42–55. [Google Scholar] [CrossRef]
- Montiel-González, I.; Martínez-Santiago, S.; Santos, A.L.; Herrera, G.G. Impacto del cambio climático en la agricultura de secano de Aguascalientes, México para un futuro cercano (2015–2039). Rev. Chapingo Ser. Zonas Áridas 2017, XVI, 1–13. [Google Scholar] [CrossRef]
- Wamahiu, K.; Kala, J.; Andrys, J. Influence of Bias-Correcting Global Climate Models for Regional Climate Simulations over the CORDEX-Australasia Domain Using WRF. Theor. Appl. Clim. 2020, 142, 1493–1513. [Google Scholar] [CrossRef]
- Rocheta, E.; Evans, J.P.; Sharma, A. Correcting Lateral Boundary Biases in Regional Climate Modelling: The Effect of the Relaxation Zone. Clim. Dyn. 2020, 55, 2511–2521. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias Correction of Regional Climate Model Simulations for Hydrological Climate-Change Impact Studies: Review and Evaluation of Different Methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM Precipitation to the Station Scale Using Statistical Transformations – a Comparison of Methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Li, Y.; Qin, Y.; Rong, P. Evolution of Potential Evapotranspiration and Its Sensitivity to Climate Change Based on the Thornthwaite, Hargreaves, and Penman–Monteith Equation in Environmental Sensitive Areas of China. Atmos. Res. 2022, 273, 106178. [Google Scholar] [CrossRef]
- Hu, M.; Yu, Q.; Tang, H.; Wu, W. A New Factorial Sensitivity Model for Analyzing the Impacts of Climatic Factors on Crop Water Footprint. J. Clean. Prod. 2024, 434, 140194. [Google Scholar] [CrossRef]
- INIFAP Laboratorio Nacional de Modelaje y Sensores Remotos (LNMySR). Available online: https://clima.inifap.gob.mx/lnmysr/ (accessed on 19 September 2024).
- Guijarro, J.A. Climatol: Climate Tools Package for R; R Package Version 2025; CRAN. Available online: https://cran.r-project.org/web/packages/climatol/index.html (accessed on 10 May 2025).
- Kuya, E.K.; Gjelten, H.M.; Tveito, O.E. Homogenization of Norwegian Monthly Precipitation Series for the Period 1961–2018. Adv. Sci. Res. 2022, 19, 73–80. [Google Scholar] [CrossRef]
- Curci, G.; Guijarro, J.A.; Di Antonio, L.; Di Bacco, M.; Di Lena, B.; Scorzini, A.R. Building a Local Climate Reference Dataset: Application to the Abruzzo Region (Central Italy), 1930–2019. Int. J. Climatol. 2021, 41, 4414–4436. [Google Scholar] [CrossRef]
- Mundo-Molina, M. Climate Change Effects on Evapotranspiration in Mexico. Am. J. Clim. Change 2015, 4, 163–172. [Google Scholar] [CrossRef]
- National Research Council (NRC). A National Strategy for Advancing Climate Modeling; National Academies Press: Washington, DC, USA, 2012; ISBN 978-0-309-25977-4. [Google Scholar]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Lawrence Livermore National Laboratory (LLNL). Coupled Model Intercomparison Project Phase 6 (CMIP6); 2019. Available online: https://aims2.llnl.gov/search/cmip6 (accessed on 12 December 2024).
- Xu, C. Climate Change and Hydrologic Models: A Review of Existing Gaps and Recent Research Developments. Water Resour. Manag. 1999, 13, 369–382. [Google Scholar] [CrossRef]
- Bronstert, A.; Kolokotronis, V.; Schwandt, D.; Straub, H. Comparison and Evaluation of Regional Climate Scenarios for Hydrological Impact Analysis: General Scheme and Application Example. Int. J. Climatol. 2007, 27, 1579–1594. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation Downscaling under Climate Change: Recent Developments to Bridge the Gap between Dynamical Models and the End User. Rev. Geophys. 2010, 48, RG3003. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Enayati, M.; Bozorg-Haddad, O.; Bazrafshan, J.; Hejabi, S.; Chu, X. Bias Correction Capabilities of Quantile Mapping Methods for Rainfall and Temperature Variables. J. Water Clim. Change 2020, 12, 401–419. [Google Scholar] [CrossRef]
- Angus, J.E. The Probability Integral Transform and Related Results. SIAM Rev. 1994, 36, 652–654. [Google Scholar] [CrossRef]
- Ringard, J.; Seyler, F.; Linguet, L. A Quantile Mapping Bias Correction Method Based on Hydroclimatic Classification of the Guiana Shield. Sensors 2017, 17, 1413. [Google Scholar] [CrossRef]
- Hempel, S.; Frieler, K.; Warszawski, L.; Schewe, J.; Piontek, F. A Trend-Preserving Bias Correction – the ISI-MIP Approach. Earth Syst. Dyn. 2013, 4, 219–236. [Google Scholar] [CrossRef]
- Vannitsem, S.; Bremnes, J.B.; Demaeyer, J.; Evans, G.R.; Flowerdew, J.; Hemri, S.; Lerch, S.; Roberts, N.; Theis, S.; Atencia, A.; et al. Statistical Postprocessing for Weather Forecasts: Review, Challenges, and Avenues in a Big Data World. Bull. Am. Meteorol. Soc. 2021, 102, E681–E699. [Google Scholar] [CrossRef]
- Cantalejo, M.; Cobos, M.; Millares, A.; Baquerizo, A. A Non-Stationary Bias Adjustment Method for Improving the Inter-Annual Variability and Persistence of Projected Precipitation. Sci. Rep. 2024, 14, 25923. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Hansen, J.W. Bias Correction of Daily GCM Rainfall for Crop Simulation Studies. Agric. For. Meteorol. 2006, 138, 44–53. [Google Scholar] [CrossRef]
- Li, H.; Sheffield, J.; Wood, E.F. Bias Correction of Monthly Precipitation and Temperature Fields from Intergovernmental Panel on Climate Change AR4 Models Using Equidistant Quantile Matching. J. Geophys. Res. Atmos. 2010, 115, D10101. [Google Scholar] [CrossRef]
- Gudmundsson, L. Qmap: Statistical Transformations for Post-Processing Climate Model Output; R Package Version 2025; CRAN. Available online: https://cran.rproject.org/web/packages/qmap/index.html (accessed on 10 May 2025).
- Becker, R.A.; Chambers, J.M.; Wilks, A.R. The New S Language: A Programming Environment for Data Analysis and Graphics; Wadsworth & Brooks/Cole Advanced Books & Software: Pacific Grove, CA, USA, 1988; ISBN 978-0-534-09192-7. [Google Scholar]
- Wichura, M.J. Algorithm AS 241: The Percentage Points of the Normal Distribution. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1988, 37, 477–484. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 1, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1994; Volume 1, ISBN 978-0-471-58495-7. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards Applied Mathematics Series; Abramowitz, M., Stegun, I.A., Eds.; United States Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1972; Volume 55, ISBN 978-0-486-61272-0.
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 2, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1995; Volume 2, ISBN 978-0-471-58494-0. [Google Scholar]
- Shea, B.L. Algorithm AS 239: Chi-Squared and Incomplete Gamma Integral. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1988, 37, 466–473. [Google Scholar] [CrossRef]
- Thom, H.C.S. Approximate Convolution of the Gamma and Mixed Gamma Distributions. Mon. Weather Rev. 1968, 96, 883–886. [Google Scholar] [CrossRef]
- Mooley, D.A. Gamma Distribution Probability Model for Asian Summer Monsoon Monthly Rainfall. Mon. Weather Rev. 1973, 101, 160–176. [Google Scholar] [CrossRef]
- Cannon, A.J. Neural Networks for Probabilistic Environmental Prediction: Conditional Density Estimation Network Creation and Evaluation (CaDENCE) in R. Comput. Geosci. 2012, 41, 126–135. [Google Scholar] [CrossRef]
- Piani, C.; Weedon, G.P.; Best, M.; Gomes, S.M.; Viterbo, P.; Hagemann, S.; Haerter, J.O. Statistical Bias Correction of Global Simulated Daily Precipitation and Temperature for the Application of Hydrological Models. J. Hydrol. 2010, 395, 199–215. [Google Scholar] [CrossRef]
- Dosio, A.; Paruolo, P. Bias Correction of the ENSEMBLES High-Resolution Climate Change Projections for Use by Impact Models: Evaluation on the Present Climate. J. Geophys. Res. Atmos. 2011, 116, D16106. [Google Scholar] [CrossRef]
- Rojas, R.; Feyen, L.; Dosio, A.; Bavera, D. Improving Pan-European Hydrological Simulation of Extreme Events through Statistical Bias Correction of RCM-Driven Climate Simulations. Hydrol. Earth Syst. Sci. 2011, 15, 2599–2620. [Google Scholar] [CrossRef]
- Osuch, M.; Lawrence, D.; Meresa, H.K.; Napiorkowski, J.J.; Romanowicz, R.J. Projected Changes in Flood Indices in Selected Catchments in Poland in the 21st Century. Stoch. Environ. Res. Risk Assess. 2017, 31, 2435–2457. [Google Scholar] [CrossRef]
- Holthuijzen, M.; Beckage, B.; Clemins, P.J.; Higdon, D.; Winter, J.M. Robust Bias-Correction of Precipitation Extremes Using a Novel Hybrid Empirical Quantile-Mapping Method. Theor. Appl. Clim. 2022, 149, 863–882. [Google Scholar] [CrossRef]
- Boé, J.; Terray, L.; Habets, F.; Martin, E. Statistical and Dynamical Downscaling of the Seine Basin Climate for Hydro-Meteorological Studies. Int. J. Climatol. 2007, 27, 1643–1655. [Google Scholar] [CrossRef]
- Villani, V.; Rianna, G.; Mercogliano, P.; Zollo, A.L.; Schiano, P. Statistical Approaches versus Weather Generator to Downscale RCM Outputs to Point Scale: A Comparison of Performances. J. Urban Environ. Eng. 2015, 8, 142–154. [Google Scholar] [CrossRef]
- Koenker, R.; Ng, P.; Portnoy, S. Quantile Smoothing Splines. Biometrika 1994, 81, 673–680. [Google Scholar] [CrossRef]
- Kouhestani, S.; Eslamian, S.S.; Abedi-Koupai, J.; Besalatpour, A.A. Projection of Climate Change Impacts on Precipitation Using Soft-Computing Techniques: A Case Study in Zayandeh-Rud Basin, Iran. Glob. Planet. Change 2016, 144, 158–170. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Evapotranspiración del Cultivo—Guías para la Determinación de los Requerimientos de Agua de los Cultivos; Estudio FAO Riego y Drenaje; FAO: Rome, Italy, 2006; ISBN 92-5-304219-2.
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity Estimates for Nonlinear Mathematical Models. Math. Model. Comput. Exp. 1993, 4, 407–414. [Google Scholar]
- Flato, G.; Marotzke, J.; Abiodun, B.; Braconnot, P.; Chou, S.C.; Collins, W.; Cox, P.; Driouech, F.; Emori, S.; Eyring, V.; et al. Evaluation of Climate Models. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Maurer, E.P.; Das, T.; Cayan, D.R. Errors in Climate Model Daily Precipitation and Temperature Output: Time Invariance and Implications for Bias Correction. Hydrol. Earth Syst. Sci. 2013, 17, 2147–2159. [Google Scholar] [CrossRef]
- Maraun, D.; Shepherd, T.G.; Widmann, M.; Zappa, G.; Walton, D.; Gutiérrez, J.M.; Hagemann, S.; Richter, I.; Soares, P.M.M.; Hall, A.; et al. Towards Process-Informed Bias Correction of Climate Change Simulations. Nat. Clim Change 2017, 7, 764–773. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Calculation of Average, Uncertainty Range, and Reliability of Regional Climate Changes from AOGCM Simulations via the “Reliability Ensemble Averaging” (REA) Method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Athira, K.V.; Eswar, R.; Boulet, G.; Nigam, R.; Bhattacharya, B.K. Modeling Evapotranspiration at Larger Temporal Scales: Effects of Temporal Aggregation and Data Gaps. Remote Sens. 2022, 14, 4142. [Google Scholar] [CrossRef]
- Widmann, M.; Bretherton, C.S.; Salathé, E.P. Statistical Precipitation Downscaling over the Northwestern United States Using Numerically Simulated Precipitation as a Predictor. J. Clim. 2003, 16, 799–816. [Google Scholar] [CrossRef]
- Schmidli, J.; Frei, C.; Vidale, P.L. Downscaling from GCM Precipitation: A Benchmark for Dynamical and Statistical Downscaling Methods. Int. J. Climatol. 2006, 26, 679–689. [Google Scholar] [CrossRef]
- Vigna, I.; Bigi, V.; Pezzoli, A.; Besana, A. Comparison and Bias-Correction of Satellite-Derived Precipitation Datasets at Local Level in Northern Kenya. Sustainability 2020, 12, 2896. [Google Scholar] [CrossRef]
- Han, Z.-Y.; Tong, Y.; Gao, X.-J.; Xu, Y. Correction Based on Quantile Mapping for Temperature Simulated by the RegCM4. Adv. Clim. Change Res. 2018, 14, 331. [Google Scholar] [CrossRef]
- Robeson, S.M.; Maxwell, J.T.; Ficklin, D.L. Bias Correction of Paleoclimatic Reconstructions: A New Look at 1,200+ Years of Upper Colorado River Flow. Geophys. Res. Lett. 2020, 47, e2019GL086689. [Google Scholar] [CrossRef]
- Di Luca, A.; Pitman, A.J.; de Elía, R. Decomposing Temperature Extremes Errors in CMIP5 and CMIP6 Models. Geophys. Res. Lett. 2020, 47, e2020GL088031. [Google Scholar] [CrossRef]
- Babaousmail, H.; Ayugi, B.; Rajasekar, A.; Zhu, H.; Oduro, C.; Mumo, R.; Ongoma, V. Projection of Extreme Temperature Events over the Mediterranean and Sahara Using Bias-Corrected CMIP6 Models. Atmosphere 2022, 13, 741. [Google Scholar] [CrossRef]
- Di Virgilio, G.; Ji, F.; Tam, E.; Nishant, N.; Evans, J.P.; Thomas, C.; Riley, M.L.; Beyer, K.; Grose, M.R.; Narsey, S.; et al. Selecting CMIP6 GCMs for CORDEX Dynamical Downscaling: Model Performance, Independence, and Climate Change Signals. Earth’s Future 2022, 10, e2021EF002625. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Gao, Z.; Pan, Z.; Zhang, X. Historical and Projected Changes in Temperature Extremes Over China and the Inconsistency Between Multimodel Ensembles and Individual Models From CMIP5 and CMIP6. Earth Space Sci. 2023, 10, e2022EA002514. [Google Scholar] [CrossRef]
- Ossó, A.; Craig, P.; Allan, R.P. An Assessment of CMIP6 Climate Signals and Biases in Temperature, Precipitation and Soil Moisture over Europe. Int. J. Climatol. 2023, 43, 5698–5719. [Google Scholar] [CrossRef]
- Rahimi, S.; Huang, L.; Norris, J.; Hall, A.; Goldenson, N.; Risser, M.; Feldman, D.R.; Lebo, Z.J.; Dennis, E.; Thackeray, C. Understanding the Cascade: Removing GCM Biases Improves Dynamically Downscaled Climate Projections. Geophys. Res. Lett. 2024, 51, e2023GL106264. [Google Scholar] [CrossRef]
- Tong, Y.; Gao, X.; Han, Z.; Xu, Y.; Xu, Y.; Giorgi, F. Bias Correction of Temperature and Precipitation over China for RCM Simulations Using the QM and QDM Methods. Clim. Dyn. 2021, 57, 1425–1443. [Google Scholar] [CrossRef]
- Moya, H.; Althoff, I.; Celis-Diez, J.L.; Huenchuleo-Pedreros, C.; Reggiani, P. Impact of Future Climate Scenarios and Bias Correction Methods on the Achibueno River Basin. Water 2024, 16, 1138. [Google Scholar] [CrossRef]
- Mol, W.; Heusinkveld, B.; Mangan, M.R.; Hartogensis, O.; Veerman, M.; van Heerwaarden, C. Observed Patterns of Surface Solar Irradiance under Cloudy and Clear-Sky Conditions. Q. J. R. Meteorol. Soc. 2024, 150, 2338–2363. [Google Scholar] [CrossRef]
- Chen, G.; Wang, W.-C.; Bao, Q.; Li, J. Evaluation of Simulated Cloud Diurnal Variation in CMIP6 Climate Models. J. Geophys. Res. Atmos. 2022, 127, e2021JD036422. [Google Scholar] [CrossRef]
- Mol, W.B.; van Stratum, B.J.H.; Knap, W.H.; van Heerwaarden, C.C. Reconciling Observations of Solar Irradiance Variability With Cloud Size Distributions. J. Geophys. Res. Atmos. 2023, 128, e2022JD037894. [Google Scholar] [CrossRef]
- Dai, A. Recent Climatology, Variability, and Trends in Global Surface Humidity. J. Clim. 2006, 19, 3589–3606. [Google Scholar] [CrossRef]
- Casanueva, A.; Kotlarski, S.; Herrera, S.; Fischer, A.M.; Kjellstrom, T.; Schwierz, C. Climate Projections of a Multivariate Heat Stress Index: The Role of Downscaling and Bias Correction. Geosci. Model Dev. 2019, 12, 3419–3438. [Google Scholar] [CrossRef]
- Xu, Z.; Han, Y.; Tam, C.-Y.; Yang, Z.-L.; Fu, C. Bias-Corrected CMIP6 Global Dataset for Dynamical Downscaling of the Historical and Future Climate (1979–2100). Sci. Data 2021, 8, 293. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correction, Quantile Mapping, and Downscaling: Revisiting the Inflation Issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Berg, P.; Bosshard, T.; Bozhinova, D.; Bärring, L.; Löw, J.; Nilsson, C.; Strandberg, G.; Södling, J.; Thuresson, J.; Wilcke, R.; et al. Robust Handling of Extremes in Quantile Mapping—“Murder Your Darlings”. Geosci. Model Dev. 2024, 17, 8173–8179. [Google Scholar] [CrossRef]
- Liu, X.; Li, C.; Zhao, T.; Han, L. Future Changes of Global Potential Evapotranspiration Simulated from CMIP5 to CMIP6 Models. Atmos. Ocean. Sci. Lett. 2020, 13, 568–575. [Google Scholar] [CrossRef]
- Yahaya, I.; Li, Z.; Zhou, J.; Jiang, S.; Su, B.; Huang, J.; Xu, R.; Havea, P.H.; Jiang, T. Estimations of Potential Evapotranspiration from CMIP6 Multi-Model Ensemble over Africa. Atmos. Res. 2024, 300, 107255. [Google Scholar] [CrossRef]
- Muhammad, M.K.I.; Shahid, S.; Hamed, M.M.; Harun, S.; Ismail, T.; Wang, X. Development of a Temperature-Based Model Using Machine Learning Algorithms for the Projection of Evapotranspiration of Peninsular Malaysia. Water 2022, 14, 2858. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, Y.; Zhu, L.; Wan, Y.; Chai, M.; Ding, P. Estimating and Forecasting Daily Reference Crop Evapotranspiration in China with Temperature-Driven Deep Learning Models. Agric. Water Manag. 2025, 307, 109268. [Google Scholar] [CrossRef]
- Maqsood, J.; Farooque, A.A.; Abbas, F.; Esau, T.; Wang, X.; Acharya, B.; Afzaal, H. Application of Artificial Neural Networks to Project Reference Evapotranspiration Under Climate Change Scenarios. Water Resour. Manag. 2022, 36, 835–851. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Estévez, J.; García-Marín, A.P. Reference Evapotranspiration Projections in Southern Spain (until 2100) Using Temperature-Based Machine Learning Models. Comput. Electron. Agric. 2023, 214, 108327. [Google Scholar] [CrossRef]
- Kadkhodazadeh, M.; Valikhan Anaraki, M.; Morshed-Bozorgdel, A.; Farzin, S. A New Methodology for Reference Evapotranspiration Prediction and Uncertainty Analysis under Climate Change Conditions Based on Machine Learning, Multi Criteria Decision Making and Monte Carlo Methods. Sustainability 2022, 14, 2601. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y. Improving Probabilistic Hydroclimatic Projections through High-Resolution Convection-Permitting Climate Modeling and Markov Chain Monte Carlo Simulations. Clim. Dyn. 2019, 53, 1613–1636. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Rajulapati, C.R.; Andreadis, K.M.; Foufoula-Georgiou, E.; Clark, M.P.; Trenberth, K.E. Probabilistic Evaluation of Drought in CMIP6 Simulations. Earth’s Future 2021, 9, e2021EF002150. [Google Scholar] [CrossRef]
- Egli, M.; Humphrey, V.; Sippel, S.; Knutti, R. A Distinct Role for Aerosol and GHG Forcing in Historical CMIP6 Evapotranspiration Trends. Earth’s Future 2024, 12, e2024EF004973. [Google Scholar] [CrossRef]
- Dobrovolski, S.G.; Yushkov, V.P.; Solomonova, I.V. Stochastic Approach to the Evolution of the Global Water Cycle: Results of Historical Experiments on the CMIP-6 Models. Pure Appl. Geophys. 2024, 181, 2873–2893. [Google Scholar] [CrossRef]
- Sabino, M.; de Souza, A.P. Global Sensitivity of Penman–Monteith Reference Evapotranspiration to Climatic Variables in Mato Grosso, Brazil. Earth 2023, 4, 714–727. [Google Scholar] [CrossRef]
- Ha, P.T.; Hai, L.M.; Liem, N.D.; Dat, N.L.T.; Huyen, N.T.; Thuy, N.N.; Loi, N.K. Analyzing the Relationship between Meteorological Changes and Evapotranspiration Trends in Gia Lai Province, Central Highlands of Vietnam. J. Water Clim. Change 2024, 15, 554–568. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. Sensitivity of Potential Evapotranspiration to Changes in Climate Variables for Different Australian Climatic Zones. Hydrol. Earth Syst. Sci. 2017, 21, 2107–2126. [Google Scholar] [CrossRef]
- Cao, M.; Wang, W.; Xing, W.; Wei, J.; Chen, X.; Li, J.; Shao, Q. Multiple Sources of Uncertainties in Satellite Retrieval of Terrestrial Actual Evapotranspiration. J. Hydrol. 2021, 601, 126642. [Google Scholar] [CrossRef]
- Biazar, S.M.; Dinpashoh, Y.; Singh, V.P. Sensitivity Analysis of the Reference Crop Evapotranspiration in a Humid Region. Environ. Sci. Pollut. Res. 2019, 26, 32517–32544. [Google Scholar] [CrossRef] [PubMed]









| Distribution | PDF–f(x) | CDF–F(x) | F−1(p) | Reference |
|---|---|---|---|---|
| Bernoulli-Gamma (berngamma) | [44] | |||
| Normal (norm) | [45,46,47] | |||
| Beta (beta) | [45,48,49] | |||
| Gamma (gamma) | [45,48,50] | |||
| LogNormal (lnorm) | [45,47] | |||
| Exponential (exp) | [45,49] | |||
| Weibull (weibull) | [49] |
| Parametric Function | Equation | Reference |
|---|---|---|
| Scaling (scale) | [21] | |
| Power (power) | ||
| Linear (linear) | ||
| Exponential asymptotic (expasympt) | ||
| Power with a shift along the x-axis (power.x0) | ||
| Exponential asymptotic with a shift along the x-axis (expasympt.x0) |
| Method | p-Level Quantile | Fobs−1 [Fmod(xmod)] | Reference |
|---|---|---|---|
| QUANT (linear and tricub) | [21,36,57,58] | ||
| RQUANT (linear and tricub) | [36,44,59,60] |
| Method | Equation | Reference |
|---|---|---|
| FAO–56 | [64] | |
| P–T | [65] | |
| H–S | [66] |
| Variable | Station | Low Quantiles | Middle Quantiles | High Quantiles | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | % | 10 | % | 25 | % | 50 | % | 75 | % | 90 | % | 100 | % | ||
| Daily | MTh | Day | MTh | Day | MTh | Day | MTh | Day | MTh | Day | MTh | Day | MTh | ||
| Pr (mm) | Don Primo | 0.0 | 0.0 | 0.0 | 1.8 | 0.0 | 10.0 | 0.1 | 29.2 | 3.5 | 127.6 | 10.5 | 185.3 | 5.4 | 326.0 |
| CEPAB | 0.0 | 0.0 | 0.0 | 1.8 | 0.0 | 10.1 | 0.1 | 30.1 | 3.5 | 133.7 | 10.1 | 198.2 | 13.2 | 295.6 | |
| Makelisa | 0.0 | 0.0 | 0.0 | 1.8 | 0.0 | 9.8 | 0.1 | 28.6 | 3.5 | 145.8 | 10.3 | 190.7 | −0.1 | 281.6 | |
| Los Pinos | 0.0 | 0.0 | 0.0 | 1.8 | 0.0 | 10.0 | 0.1 | 33.9 | 3.5 | 152.2 | 10.9 | 189.2 | −7.6 | 372.6 | |
| TMAX (°C) | Don Primo | 1.2 | −3.8 | −3.8 | −3.9 | −3.5 | −3.9 | −3.7 | −3.4 | −3.9 | −4.0 | −2.7 | −2.9 | 0.9 | −2.1 |
| CEPAB | 2.0 | −4.1 | −3.8 | −4.1 | −3.7 | −3.7 | −3.9 | −3.8 | −4.0 | −4.2 | −2.8 | −3.1 | 0.1 | −2.9 | |
| Makelisa | 1.4 | −4.3 | −4.0 | −4.3 | −3.8 | −4.1 | −3.9 | −3.7 | −4.1 | −4.3 | −2.9 | −3.1 | 0.4 | −2.8 | |
| Los Pinos | 2.3 | −3.2 | −3.1 | −3.2 | −2.9 | −3.3 | −3.2 | −3.1 | −3.3 | −3.5 | −2.2 | −2.2 | 1.4 | −1.4 | |
| TMIN (°C) | Don Primo | 7.0 | 6.9 | 5.4 | 5.0 | 4.5 | 4.3 | 3.1 | 3.6 | 2.4 | 2.4 | 2.1 | 2.3 | 2.7 | 2.4 |
| CEPAB | 7.8 | 6.9 | 5.2 | 5.0 | 4.5 | 4.3 | 3.1 | 3.5 | 2.5 | 2.5 | 2.2 | 2.3 | 3.5 | 2.2 | |
| Makelisa | 8.1 | 7.2 | 5.9 | 5.3 | 5.1 | 4.7 | 3.6 | 4.1 | 2.8 | 2.6 | 2.3 | 2.5 | 3.7 | 2.6 | |
| Los Pinos | 9.1 | 8.9 | 7.4 | 6.8 | 6.5 | 6.0 | 4.7 | 5.2 | 3.6 | 3.4 | 2.9 | 3.2 | 4.3 | 3.3 | |
| TMEAN (°C) | Don Primo | −1.1 | 0.2 | 0.4 | 0.1 | 0.2 | 0.4 | −0.1 | 0.0 | −0.6 | −0.6 | −0.8 | −0.5 | 1.4 | 0.1 |
| CEPAB | −1.3 | 0.1 | 0.3 | 0.0 | 0.1 | 0.4 | −0.3 | 0.1 | −0.6 | −0.6 | −0.8 | −0.6 | 1.8 | 0.2 | |
| Makelisa | −1.2 | 0.3 | 0.6 | 0.2 | 0.4 | 0.6 | 0.0 | 0.3 | −0.4 | −0.3 | −0.5 | −0.3 | −1.0 | 0.4 | |
| Los Pinos | 2.0 | 1.6 | 1.6 | 1.3 | 1.4 | 1.6 | 0.6 | 0.7 | 0.2 | 0.1 | 0.2 | 0.4 | 2.7 | 1.7 | |
| SR (MJ m−2) | Don Primo | −1.4 | −4.4 | −4.5 | −5.2 | −5.6 | −5.6 | −5.9 | −5.6 | −7.0 | −7.2 | −9.7 | −9.3 | −16.1 | −13.2 |
| CEPAB | −0.9 | −2.0 | −4.1 | −5.0 | −5.4 | −5.5 | −6.6 | −6.3 | −7.8 | −7.4 | −9.6 | −9.0 | −14.7 | −11.4 | |
| Makelisa | −1.1 | −4.1 | −4.3 | −5.0 | −5.3 | −5.2 | −6.1 | −5.9 | −7.0 | −7.2 | −10.1 | −9.6 | −16.6 | −13.6 | |
| Los Pinos | −1.1 | −2.3 | −3.0 | −3.9 | −4.2 | −4.6 | −4.9 | −4.6 | −5.9 | −6.4 | −9.7 | −8.8 | −16.7 | −13.4 | |
| RHMAX (%) | Don Primo | −18.5 | −4.6 | −13.5 | −13.9 | −10.8 | −10.6 | −1.3 | −5.6 | −0.6 | −0.3 | −0.6 | −1.1 | 1.0 | −2.4 |
| CEPAB | −18.5 | −4.8 | −11.5 | −10.9 | −10.4 | −10.0 | −2.3 | −6.6 | −1.3 | 0.3 | −0.6 | −1.5 | 1.0 | −3.0 | |
| Makelisa | −17.5 | −10.9 | −17.5 | −16.3 | −12.8 | −11.6 | −3.3 | −7.5 | −1.6 | −0.2 | −1.6 | −2.4 | 1.0 | −3.6 | |
| Los Pinos | −21.5 | −13.7 | −23.5 | −20.7 | −17.8 | −16.7 | −5.3 | −9.4 | −2.6 | −2.0 | −1.6 | −2.4 | 1.0 | −2.4 | |
| RHMIN (%) | Don Primo | −1.8 | −0.2 | −1.5 | −1.7 | −2.2 | −2.8 | 10.3 | 10.3 | 22.0 | 20.1 | 19.0 | 17.1 | −1.3 | 15.8 |
| CEPAB | −2.5 | −0.1 | −1.5 | −0.9 | −2.2 | −1.9 | 10.3 | 10.2 | 21.9 | 20.1 | 19.0 | 17.6 | −1.3 | 16.4 | |
| Makelisa | −1.8 | 0.0 | −1.5 | −1.3 | −3.2 | −2.3 | 10.3 | 10.7 | 22.0 | 19.9 | 19.0 | 17.5 | −0.3 | 14.4 | |
| Los Pinos | −3.8 | −2.0 | −3.5 | −3.1 | −5.2 | −5.3 | 9.7 | 8.7 | 19.0 | 17.3 | 15.0 | 15.4 | −4.3 | 13.7 | |
| RHMEAN (%) | Don Primo | −8.6 | −1.8 | −7.3 | −7.7 | −4.1 | −4.5 | 9.4 | 6.2 | 10.4 | 10.8 | 5.0 | 6.5 | −4.6 | 3.3 |
| CEPAB | −8.1 | −0.6 | −6.7 | −5.9 | −4.0 | −4.0 | 9.2 | 6.0 | 10.4 | 11.0 | 6.1 | 6.0 | −1.6 | 4.2 | |
| Makelisa | −9.4 | −3.6 | −9.0 | −8.2 | −6.1 | −5.7 | 7.8 | 4.9 | 9.1 | 9.7 | 4.8 | 4.7 | −4.1 | 0.1 | |
| Los Pinos | −14.7 | −8.1 | −12.3 | −10.8 | −9.3 | −9.3 | 5.2 | 2.2 | 7.1 | 6.9 | 3.4 | 4.3 | −4.4 | 2.4 | |
| WS (m s−1) | Don Primo | 0.5 | 1.2 | 0.9 | 1.1 | 1.0 | 1.0 | 1.0 | 0.9 | 1.2 | 1.1 | 1.2 | 1.0 | 0.2 | 1.7 |
| CEPAB | 0.5 | 0.9 | 0.8 | 1.0 | 1.0 | 1.1 | 1.1 | 1.2 | 1.5 | 1.4 | 1.4 | 1.2 | −1.5 | −0.8 | |
| Makelisa | 0.5 | 1.2 | 1.0 | 1.3 | 1.3 | 1.4 | 1.5 | 1.6 | 1.8 | 1.7 | 1.9 | 1.5 | −13.9 | −14.8 | |
| Los Pinos | 0.5 | 1.0 | 0.9 | 1.1 | 1.0 | 1.0 | 1.0 | 1.1 | 1.2 | 1.1 | 1.3 | 1.1 | 1.2 | 1.7 | |
| Variable | Scale | Don Primo | r | CEPAB | r | Makelisa | r | Los Pinos | r |
|---|---|---|---|---|---|---|---|---|---|
| Pr | Daily | MPI-ESM1-2-LR (SSPLIN-CV-False) | 0.15 | MPI-ESM1-2-LR (SSPLIN-CV-False) | 0.18 | MPI-ESM1-2-LR (SSPLIN-CV-False) | 0.15 | MPI-ESM1-2-LR (SSPLIN-CV-False) | 0.14 |
| Monthly | ACCESS-ESM1-5 (QUANT-tricub) | 0.72 | ACCESS-ESM1-5 (PTF-scale) | 0.73 | ACCESS-ESM1-5 (PTF-scale) | 0.68 | ACCESS-ESM1-5 (PTF-scale) | 0.72 | |
| TMEAN | Daily | ACCESS-ESM1-5 (SSPLIN-CV-True) | 0.78 | ACCESS-ESM1-5 (QUANT-linear) | 0.78 | ACCESS-ESM1-5 (RQUANT-linear) | 0.78 | ACCESS-ESM1-5 (RQUANT-linear) | 0.79 |
| Monthly | ACCESS-ESM1-5 (SSPLIN-CV-False) | 0.94 | ACCESS-ESM1-5 (QUANT-linear) | 0.94 | ACCESS-ESM1-5 (QUANT-linear) | 0.94 | ACCESS-ESM1-5 (QUANT-linear) | 0.95 | |
| TMAX | Daily | ACCESS-ESM1-5 (PTF-power) | 0.60 | ACCESS-ESM1-5 (PTF-scale) | 0.61 | ACCESS-ESM1-5 (PTF-power) | 0.60 | ACCESS-ESM1-5 (PTF-power) | 0.60 |
| Monthly | ACCESS-ESM1-5 (PTF-power) | 0.85 | ACCESS-ESM1-5 (SSPLIN-CV-False) | 0.87 | ACCESS-ESM1-5 (PTF-power.x0) | 0.86 | ACCESS-ESM1-5 (QUANT-tricub) | 0.87 | |
| TMIN | Daily | MIROC6 (PTF-power.x0) | 0.76 | MIROC6 (PTF-power) | 0.76 | MIROC6 (PTF-power.x0) | 0.75 | MIROC6 (PTF-power.x0) | 0.74 |
| Monthly | MIROC6 (QUANT-tricub) | 0.94 | MIROC6 (RQUANT-linear) | 0.94 | MIROC6 (SSPLIN-CV-False) | 0.94 | MIROC6 (RQUANT-linear) | 0.94 | |
| SR | Daily | ACCESS-ESM1-5 (PTF-power.x0) | 0.48 | ACCESS-ESM1-5 (PTF-scale) | 0.56 | ACCESS-ESM1-5 (PTF-scale) | 0.53 | ACCESS-ESM1-5 (PTF-scale) | 0.47 |
| Monthly | HadGEM3-GC31-LL (PTF-scale) | 0.70 | HadGEM3-GC31-LL (PTF-scale) | 0.79 | HadGEM3-GC31-LL (PTF-scale) | 0.75 | HadGEM3-GC31-LL (PTF-scale) | 0.67 | |
| RHMEAN | Daily | ACCESS-ESM1-5 (PTF-linear) | 0.55 | ACCESS-ESM1-5 (PTF-expasympt) | 0.58 | ACCESS-ESM1-5 (PTF-power.x0) | 0.57 | ACCESS-ESM1-5 (PTF-power.x0) | 0.56 |
| Monthly | ACCESS-ESM1-5 (PTF-linear) | 0.80 | ACCESS-ESM1-5 (PTF-power.x0) | 0.82 | ACCESS-ESM1-5 (PTF-power.x0) | 0.81 | ACCESS-ESM1-5 (PTF-linear) | 0.81 | |
| RHMAX | Daily | ACCESS-ESM1-5 (PTF-linear) | 0.47 | ACCESS-ESM1-5 (PTF-scale) | 0.51 | ACCESS-ESM1-5 (PTF-linear) | 0.50 | ACCESS-ESM1-5 (PTF-linear) | 0.49 |
| Monthly | ACCESS-ESM1-5 (PTF-linear) | 0.78 | ACCESS-ESM1-5 (PTF-linear) | 0.83 | ACCESS-ESM1-5 (PTF-linear) | 0.81 | ACCESS-ESM1-5 (PTF-linear) | 0.81 | |
| RHMIN | Daily | ACCESS-ESM1-5 (PTF-expasympt) | 0.46 | ACCESS-ESM1-5 (PTF-linear) | 0.48 | ACCESS-ESM1-5 (PTF-linear) | 0.47 | ACCESS-ESM1-5 (PTF-expasympt) | 0.48 |
| Monthly | ACCESS-ESM1-5 (PTF-linear) | 0.72 | ACCESS-ESM1-5 (PTF-linear) | 0.73 | ACCESS-ESM1-5 (PTF-power.x0) | 0.72 | ACCESS-ESM1-5 (PTF-expasympt) | 0.75 | |
| WS | Daily | UKESM1-0-LL (PTF-scale) | 0.13 | ACCESS-ESM1-5 (SSPLIN-CV-TRUE) | 0.19 | ACCESS-ESM1-5 (SSPLIN-CV-TRUE) | 0.22 | CNRM-ESM2-1 (PTF-scale) | 0.15 |
| Monthly | MRI-ESM2-0 (PTF-scale) | 0.34 | IPSL-CM6A-LR (QUANT-tricub) | 0.47 | MRI-ESM2-0 (RQUANT-linear) | 0.36 | CNRM-ESM2-1 (SSPLIN-CV-True) | 0.44 |
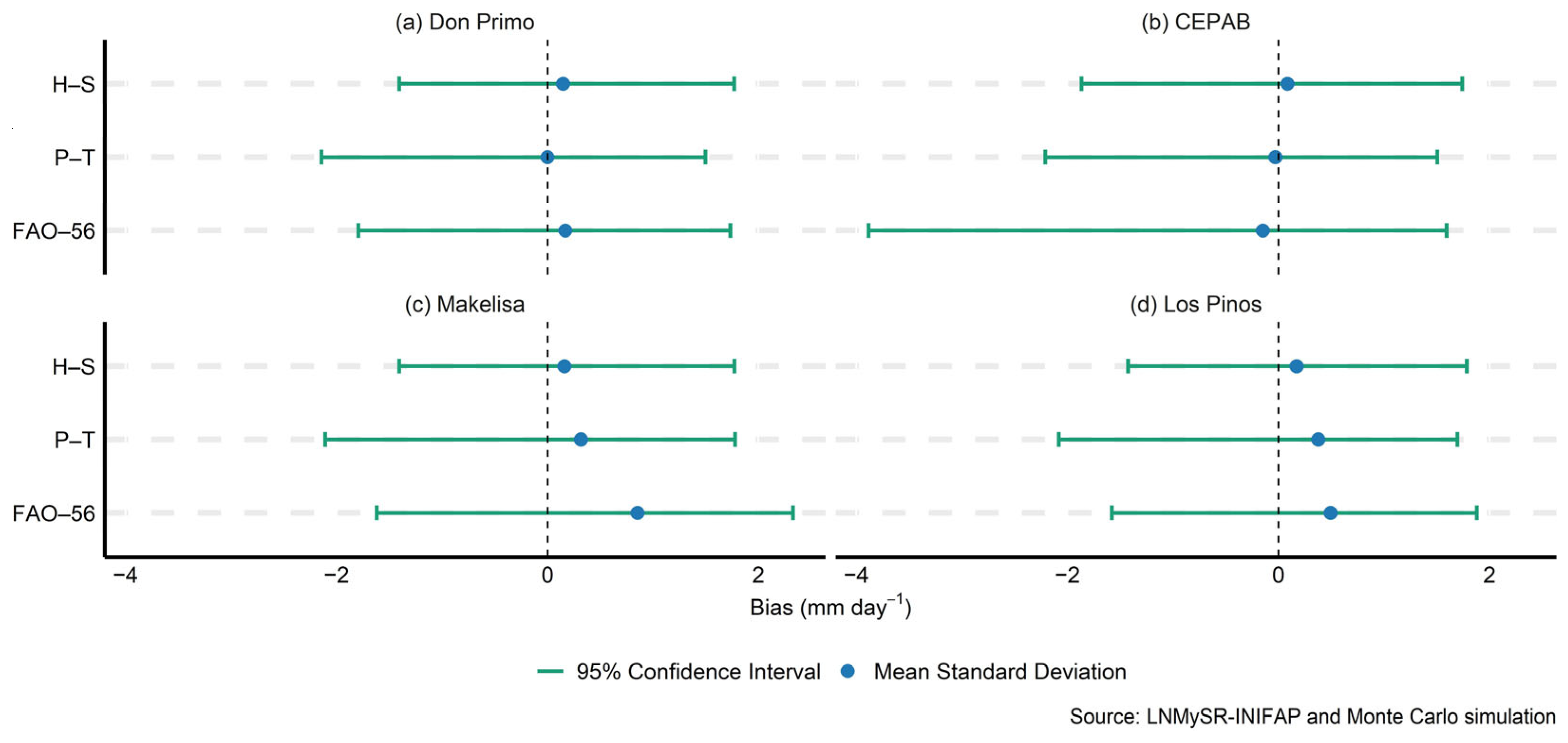
| Station | Method | μ | σ | CI2.5% mm day−1 | CI97.5% | CIRange | CV % |
|---|---|---|---|---|---|---|---|
| Don Primo | FAO–56 | 3.65 | 0.35 | 3.00 | 4.02 | 1.02 | 9.73 |
| P–T | 3.60 | 0.48 | 2.73 | 4.10 | 1.37 | 13.32 | |
| H–S | 4.69 | 0.79 | 3.42 | 5.60 | 2.18 | 16.80 | |
| CEPAB | FAO–56 | 3.57 | 0.37 | 2.90 | 3.95 | 1.05 | 10.32 |
| P–T | 3.63 | 0.49 | 2.74 | 4.13 | 1.39 | 13.43 | |
| H–S | 4.74 | 0.80 | 3.46 | 5.67 | 2.21 | 16.84 | |
| Makelisa | FAO–56 | 3.88 | 0.35 | 3.25 | 4.24 | 0.99 | 8.99 |
| P–T | 3.59 | 0.48 | 2.72 | 4.09 | 1.37 | 13.40 | |
| H–S | 4.78 | 0.81 | 3.48 | 5.72 | 2.24 | 16.89 | |
| Los Pinos | FAO–56 | 3.44 | 0.33 | 2.84 | 3.78 | 0.94 | 9.66 |
| P–T | 3.43 | 0.45 | 2.61 | 3.89 | 1.28 | 13.09 | |
| H–S | 4.72 | 0.80 | 3.43 | 5.65 | 2.22 | 16.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galván-Cano, O.; Bolaños-González, M.A.; Prado-Hernández, J.V.; Exebio-García, A.A.; López-Pérez, A.; Colín-García, G. Impact of Climate Change on Reference Evapotranspiration: Bias Assessment and Climate Models in a Semi-Arid Agricultural Zone. Water 2025, 17, 3040. https://doi.org/10.3390/w17213040
Galván-Cano O, Bolaños-González MA, Prado-Hernández JV, Exebio-García AA, López-Pérez A, Colín-García G. Impact of Climate Change on Reference Evapotranspiration: Bias Assessment and Climate Models in a Semi-Arid Agricultural Zone. Water. 2025; 17(21):3040. https://doi.org/10.3390/w17213040
Chicago/Turabian StyleGalván-Cano, Osvaldo, Martín Alejandro Bolaños-González, Jorge Víctor Prado-Hernández, Adolfo Antenor Exebio-García, Adolfo López-Pérez, and Gerardo Colín-García. 2025. "Impact of Climate Change on Reference Evapotranspiration: Bias Assessment and Climate Models in a Semi-Arid Agricultural Zone" Water 17, no. 21: 3040. https://doi.org/10.3390/w17213040
APA StyleGalván-Cano, O., Bolaños-González, M. A., Prado-Hernández, J. V., Exebio-García, A. A., López-Pérez, A., & Colín-García, G. (2025). Impact of Climate Change on Reference Evapotranspiration: Bias Assessment and Climate Models in a Semi-Arid Agricultural Zone. Water, 17(21), 3040. https://doi.org/10.3390/w17213040







