Bottle Test Free Chlorine Bulk Decay Coefficient Statistical Fitting for Water Supply Systems via State Estimation Techniques

Abstract

Free chlorine residual is the most widely adopted disinfectant residual in water supply systems. Chlorine is usually applied at treatment works, but it decays as water flows and spends time within the network. Chlorine decay is the result of a bulk and a wall decay component. Bulk decay may be considered invariable through the pipe network (it only depends on water composition) and is often characterized at the entrance to the system through bottle tests, which measure chlorine evolution over time in a laboratory environment to then adjust a model (dependent on one or more coefficients) that represents its behavior. Previous studies have acknowledged that the bulk decay coefficient varies widely and that free chlorine measurements are subject to measurement errors, but they have not quantified the impact of these errors on the bulk decay coefficient. The aim of this paper is to provide a methodology that statistically fits chlorine’s bulk decay coefficient based on bottle test results, with appropriate management of uncertainty effects. The proposal is to use state estimation techniques, which combine free chlorine measurements and system knowledge (in this case, a first-order bulk decay model) to provide the most likely chlorine behavior and its associated uncertainty. This approach goes one step beyond previous studies, which report only a single value of the bulk decay coefficient without accounting for randomness, and thus fail to assess true variability, leading to unrepresentative comparisons. Results for water samples from different sources demonstrate the importance of controlling the fitting process through state estimation to understand and compare the bulk decay coefficient.

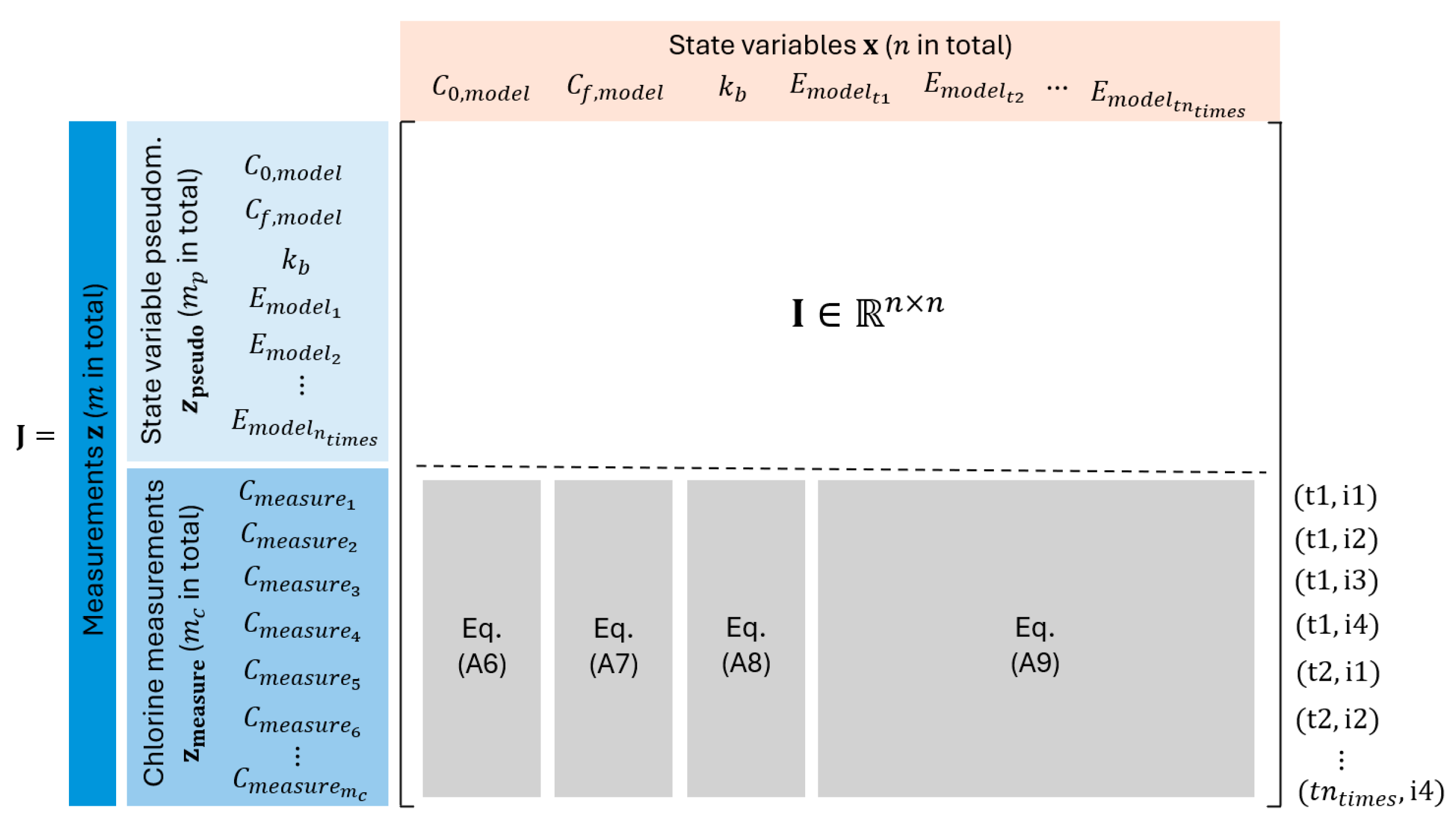
1. Introduction

Water supply systems often rely on disinfectant residuals to ensure water quality through the network. Free chlorine residual is the most widely adopted disinfectant residual in drinking water supply systems. According to the World Health Organization, the minimum residual concentration of free chlorine at the point of delivery should be 0.2 mg/L [1]. High chlorine levels are associated with issues such as odor/taste problems or disinfection by-product formation (e.g., [2]). Consequently, residual chlorine ranges between 0.2 and 5 mg/L [3] but is most often kept below 1–1.5 mg/L in practice [4].

To ensure adequate chlorine values, free chlorine is commonly measured at strategic points within the supply network and/or at the user tap. Online monitoring presents several advantages [5], but continuous chlorine analyzers are expensive and require systematic maintenance [6]. In practice, many chlorine monitoring plans still mainly rely on manual grab samples, especially in small urban or rural areas. Chlorine sampling at the water distribution system is basically conceived for quality assurance, and few utilities employ a systematic protocol to collect samples [7]. Previous authors have highlighted that sampling procedures could and should be improved beyond regulatory compliance to gain knowledge about network operation [8]. This would be especially interesting to better characterize (and model) the chlorine decay process, which is known to be complex [9].

Chlorine decay is usually divided into a bulk and a wall decay component (e.g., [10,11]). Bulk decay is determined by water quality characteristics only and is not influenced by the pipes within the water distribution system [12]. It is usually characterized at the entrance to the water distribution network through bottle tests [13,14]. Bottle tests involve measuring chlorine evolution over time in a laboratory environment to adjust the equation coefficients that describe the observed decay [15]. Different models can be adopted to simulate bulk decay [16,17], but first-order models (i.e., exponential decay) are most typically assumed (e.g., [9,18,19]). This implies that a single parameter, commonly known as the bulk decay coefficient or $k_b$, must be adjusted. This coefficient varies widely depending on the water source and temperature [18,20]. Wall decay refers to the chlorine reaction with the wall. This includes chlorine interaction with biofilms, corrosion products, and/or any other particles adhered to the wall [17], which may vary in space and time in the water distribution network. Different models have been presented to explain the wall component (e.g., [18,21,22]), but there is still no consensus on which is the best alternative to simulate this complex interaction. In practice, wall decay is often quantified as the difference between measurements of chlorine at a network position and the corresponding values obtained when assuming a bulk-decay (only) model [17,23]. This means that an accurate estimation of bulk decay is also key to characterizing the wall effect [16].

Despite the relevance of chlorine decay for the operation of water supply systems, to the best of the authors’ knowledge, no previous studies have assessed the impact of chlorine measurement errors on $k_b$ estimation. This can be problematic because several sources of error coexist when sampling free chlorine [24]. For example, measurement error is affected to some extent by the measurement principle. Either colorimetric methods (measurement of color intensity after applying a reaction product) or amperometric methods (measurement of ions based on electric current or changes in electric current) can be used to measure chlorine. DPD (N,N-diethyl-p-phenylenediamine) or colorimetric methods have typically been the most popular choice for free chlorine measurement (e.g., [5,25,26]) because they are less expensive; however, measurements may be subject to significant measurement errors and/or low repeatability among users [24]. Although less common, disposable sensor amperometry tests—such as those performed with Chlorosense or KEMIO devices [27]—are increasingly being adopted for grab sampling in the water supply (e.g., [28,29,30]) and food (e.g., [31,32]) industries. Previous studies have identified that LaMotte colorimeters (based on colorimetry) and Chlorosense devices (based on chronoamperometry) are associated with 5.1% [24] and 4.8% [26] measurement errors, respectively, under laboratory conditions. Water quality measurement errors (in general) have motivated the measurement of some parameters (such as coliforms) more than once (e.g., [19,33]). However, measurement replication is determined by the minimum accuracy required by regulators, and is not standard practice in the water sector, particularly with respect to chlorine measurements. Most chlorine studies in the water field are based on single measurements (e.g., [34]), and only a few microbiological studies mention replicate measurements in general (e.g., [19,35]) and triplicate measurements in particular (e.g., [36,37,38]). This context highlights that chlorine measurement strategies are varied and associated with different measurement errors. These errors propagate when computing the associated bulk decay coefficient.

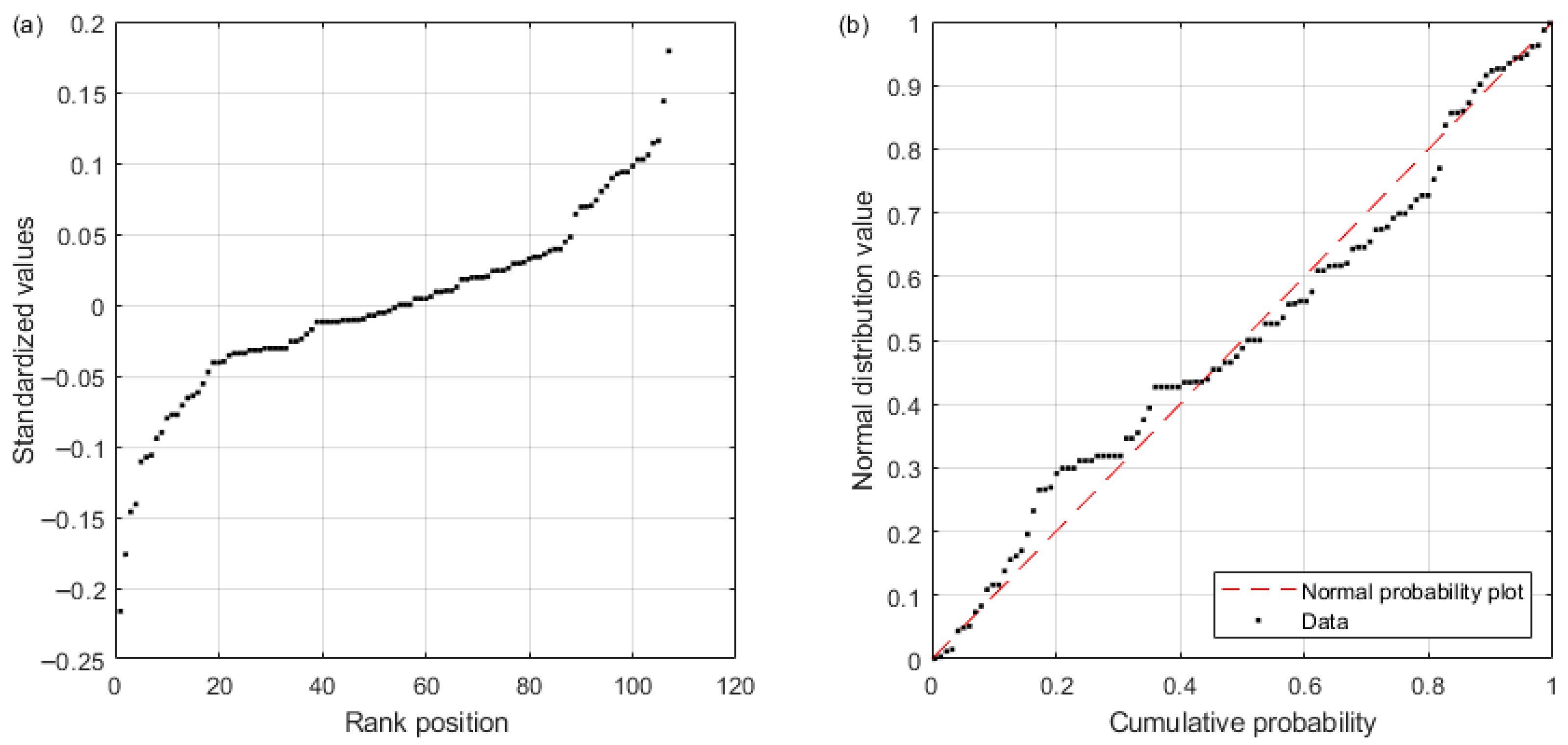
Figure 1 provides a conceptual representation of a chlorine bulk decay process, which is usually characterized through standard bottle tests (e.g., [15]). Standard bottle tests rely on individual measurements at each of the observed times, which are then used to adjust $k_b$ (best fit to data). This approach provides a single value of $k_b$ and does not enable us to account for the impact of chlorine measurements on the bulk decay coefficient. Figure 1a shows that if more than one measurement was taken at each time, there would be several possible curves (i.e., combinations of measurements) that could be fitted to chlorine measurements, i.e., there is a range of possible $k_b$ values. This means that, because chlorine measurements are not accurate enough, the bulk decay coefficient should be represented by a distribution function rather than a single value (Figure 1b). To overcome this issue, this work will develop a methodology to statistically characterize the bulk decay coefficient (mean and standard deviation) and will demonstrate with real values (see Results section and related appendices) that the variability of $k_b$ is not negligible and should be considered when comparing bulk decay coefficients. This approach could be key to assessing the impact of chlorine measurement and model errors on $k_b$ and so to understand chlorine dynamics in water supply systems.

Therefore, the aim of this paper is to develop a methodology that statistically fits chlorine’s bulk decay coefficient (mean value and standard deviation) at water supply systems, tracking uncertainty along the process. Following common practice in the field, the method relies on bottle test data, which in this case are fitted to a first-order bulk decay model; however, it could similarly be adapted to alternative models. The mean value of $k_b$ is here computed using state estimation techniques, which apply a non-linear mathematical algorithm to identify the most likely state of a variable (in this case, $k_b$) while considering (bottle test) measurement errors and system knowledge (in this case, the assumed bulk decay model). The associated standard deviation is computed by propagating measurement errors to the $k_b$ solution. This approach provides a solid framework to statistically characterize $k_b$. It goes one step further with respect to previous studies, which only provide one possible $k_b$ value (e.g., [18,20]). Systematic statistical fitting of $k_b$ (mean value and standard deviation) gives insight into the variability of the bulk decay coefficient, which could be crucial when analyzing changes over time and/or with temperature. Therefore, this work introduces a methodology to understand, monitor, and model chlorine decay processes under varying conditions, including those driven by climate change [39,40]. We want to highlight that this methodology constitutes a first scientific contribution intended to identify (and quantify) a problem that affects both industrial practice and research. The methodology has potential to evolve into a tool that can be operationally used by water utilities (knowledge transfer to industry) once chlorine decay processes are better understood on a scientific level (see Discussion section).

2. Methodology

This section provides a methodology to statistically fit the free chlorine bulk decay coefficient at water supply systems. The proposed method starts by carrying out a bottle test with replicate measurements (Section 2.1) for a bulk water sample taken at the water treatment plant immediately before chlorination. Measurement replication is not strictly necessary to apply the methodology presented in this work; however, it reduces the uncertainty of the bulk decay coefficient (see the Results section), and therefore it is strongly recommended here. Water is chlorinated, and decay is observed in a laboratory-controlled environment. Bottle test data are here adjusted to fit a first-order bulk decay process, which is formulated in Section 2.2. The state estimation mathematical apparatus to estimate the mean bulk decay coefficient is presented in Section 2.3. Section 2.4 presents the uncertainty assessment process to compute the standard deviation of the corresponding bulk decay coefficient. Section 2.5 establishes a framework for outlier detection based on uncertainty results. Figure 2 shows a schematic workflow of the proposed methodology, which will be explained in detail in the following subsections.

2.1. Bottle Tests (With Replicate Measurements)

Bottle tests are conceived to measure chlorine’s bulk decay in a laboratory-controlled environment. The general procedure described by [15] is followed in this work, although it is here adapted to include several measurements at each time. As explained in the Introduction, measurement replication is not common in the water supply field, but it will help to gain confidence in chlorine measurements, which, according to the literature, may be subjected to significant errors [24,26]. Palintest’s KEMIO is used in this work to measure free chlorine because, as explained in the Introduction, it is associated with lower errors and greater repeatability compared to colorimetric methods.

Bottle test key steps are now summarized as follows:

• Test preparation. Lab material is cleaned with 5% sodium hypochlorite (NaClO) solution and rinsed at least three times with MilliQ water. An isothermal bath is set to the goal temperature for the bottle test at least 2 h before taking the sample to ensure thermal equilibrium. If the isothermal bath can only heat (not refrigerate) the water sample, the goal temperature should be greater than the laboratory temperature (considering seasonal variability). The goal temperature should be kept below 30 °C to minimize sodium hypochlorite potential instabilities (e.g., [41,42]) and deviations in decay rate estimations ([13,43]). In this work, all bottle tests are carried out at 24 °C.
• Grab sample. A bulk water grab sample is taken at the water treatment plant immediately before chlorination. The water sample must be transported to the laboratory as soon as possible. Once at the laboratory, the temperature, pH, and Total Organic Carbon (TOC) of the sample are measured. Water is then transferred to a 3.8 L Winchester bottle, which is introduced in the isothermal bath for at least 2 h to ensure thermal equilibrium before chlorination.
• Chlorination. Temperature is measured before chlorination to confirm that the goal temperature has been reached. Sodium hypochlorite solution is added to the bottle for chlorination (80 $\mathsf{\mu }$L of 5% solution) with a high-resolution micropipette. This dose of solution leads to an Initial Chlorine Concentration (ICC) of approximately 1 mg/L for the grab samples considered in this work. Only one ICC is tested in this work, but different temperatures and ICC values could be explored if considered necessary as in [13].
• Distribution in subsamples. The bottle is agitated several times to ensure mixing. The total volume of the bottle is distributed in 125 mL amber glass bottles (30 subsamples in total). Each jar is leveled off, hermetically sealed, and submerged in the isothermal bath again. This whole process usually takes less than 15 min. ICC and pH are measured again for the remaining water in the Winchester bottle to validate previous measurements. ICC values measured in Steps 3 and 4 are averaged in this work for subsequent analysis.
• Chlorine measurements. Chlorine measurements are taken after approximately 1 h, 3 h, 10 h, 24 h, 48 h, and 96 h (or more depending on the observed decay from previous measurements). The concentration of free chlorine at 1 h is measured in this work for the sake of control, but is systematically excluded from the bulk decay coefficient analysis to avoid any potential particularities associated with the fast reactions that take place at treatment works after the first contact with the disinfectant [44]. At each time, 4 amber glass bottles are used to obtain 4 independent measurements (less than 10 min apart). Results are carefully noted down for later analysis (see Section 2.3). If available, extra subsamples can be used whenever a measurement is clearly off. These extra bottles are used when measurements at one time are more than 0.2 mg/L apart and/or when chlorine measurement values are below 0.1 mg/L (lower measurement range of the meter).

• A bottle test is considered finished when all measurements are made at the last time considered for the analysis (a maximum of 7 times) or when chlorine measurements reach 0 mg/L.

2.2. Bulk Decay Model

The methodology presented in this work (state estimation with uncertainty assessment) could be combined with any chlorine decay model. The first-order bulk decay model, which has been widely used in the literature (e.g., [9,18,19]), will be assumed in this work to facilitate notation and understanding. Appendix A.1 presents the formulation of the first-order bulk decay model, which assumes an exponential decay for free chlorine residual. The appendix derives that chlorine measurements, generally denoted as $C_{measure}$ [mg/L] can be expressed for each time $t$ and measurement replication $i$ as $C_{measure}\left(t,i\right);\forall t,i$:

$$C_{measure}\left(t,i\right)=C_{f,model}+\left(C_{0,model}-C_{f,model}\right)·e^{-k_b·t}+E_{model}\left(t\right)+E_{measure}(t,i)$$

(1)

where $C_{0,model}$ [mg/L] represents the initial chlorine concentration according to the adopted model, $t$ [hours] refers to the water age or time of residence (in this case, within the bottle test), and $k_b$ [1/h] is the chlorine decay bulk coefficient. It must be highlighted that the standard exponential equation [9] is here affected by a free chlorine concentration asymptote $C_{f,model}$ [mg/L] to represent that chlorine values may not reach 0 mg/L even after very long bottle tests. For example, chlorine concentrations do not reach 0 mg/L even after almost 400 h of testing in [17]. Since such a high-water age value (>16 days) is unlikely in most pipes within a water distribution system [45], $C_{f,model}$ is introduced here to generalize the traditional exponential model. Also, measured (rather than modeled) values are provided by Equation (1), so two additional errors must be included: the model error at each time $t$, $E_{model}\left(t\right)$ [mg/L], and the error in chlorine measurements at each time $t$ and for each replication $i$, $E_{measure}(t,i)$ [mg/L]. The model error $E_{model}\left(t\right)$ exists because the model does not reproduce real behavior exactly, and deviations may take place at each of the sampled times during the bottle test. Similarly, $E_{measure}(t,i)$ represents the error in chlorine measurements, which is different every time that chlorine is measured during the test. Both errors explain the difference between measured chlorine concentrations (as represented by Equation (1)) and modeled chlorine concentrations (as provided by the first two summation terms in Equation (1)).

Equation (1) is the fundamental decay equation assumed here to derive the state estimation (and uncertainty assessment) formulation that feeds from bottle test data (with replicate measurements) as described in Section 2.1. Equation (1) could be modified (and the state estimation formulation adapted) if more complex decay models, such as those proposed by [16,44] or [46], were adopted.

2.3. State Estimation

State estimation (SE) techniques provide the best estimate of the state of a process by combining measurements of the process state and a mathematical representation of the process [47]. State estimation techniques were developed in the 1970s in the field of power supply and control systems (e.g., [48,49]) but have been systematically applied to address other complex non-linear problems, such as those related to structural systems (e.g., [50]), traffic systems (e.g., [51]) and water supply systems (e.g., [52,53]) to name a few.

2.3.1. General Formulation

The SE problem can generally be formulated as an unconstrained weighted least squares optimization problem [54]:

$$\underset{\mathbf{x}}{\min }{f}_{obj}\left(\mathbf{x}\right)={\displaystyle \frac{1}{2}}{\mathsf{ϵ}\left(\mathbf{x}\right)}^T\mathbf{W}\mathsf{ϵ}\left(\mathbf{x}\right)={\displaystyle \frac{1}{2}}{\left[\mathbf{z}-g\left(\mathbf{x}\right)\right]}^T\mathbf{W}\left[\mathbf{z}-g\left(\mathbf{x}\right)\right]$$

(2)

where $f_{obj}$ is the objective function to minimize. The objective function depends on a vector of state variables $\mathbf{x}\in {\mathbb{R}}^n$, where $n$ is the number of state variables. State variables are the minimum subset of independent variables needed to compute the state of the system [55]. Vector $\mathsf{ϵ}\left(\mathbf{x}\right)\in {\mathbb{R}}^m$ represents the error or difference between measurements, which are represented by vector $\mathbf{z}\in {\mathbb{R}}^m$ ($m$ is the number of measurements), and modeled values through the non-linear relationship $g\left(\mathbf{x}\right):{\mathbb{R}}^n\to {\mathbb{R}}^m$. Matrix $\mathbf{W}\in {\mathbb{R}}^{m\times m}$ is a diagonal matrix for measurement weights, which is equal to the inverse of the measurement error variance-covariance matrix $\mathbf{W}={\mathbf{C}\mathbf{o}\mathbf{v}}_{\mathit{z}}^{-1}$. This matrix is typically diagonal (only variance values) because measurements are usually assumed independent (no covariance).

The state estimation problem described by Equation (2) is frequently solved algebraically. This means that the optimization problem is solved iteratively by relying on the normal equation method [52]:

$${\mathbf{x}}_{(v+1)}={\mathbf{x}}_{\left(v\right)}+{∆\mathbf{x}}_{(v+1)}$$

(3)

$${∆\mathbf{x}}_{(v+1)}={\left[{\mathbf{J}}_{\left(v\right)}^T{\mathbf{C}\mathbf{o}\mathbf{v}}_{\mathbf{z}}^{-1}{\mathbf{J}}_{\left(\mathit{v}\right)}\right]}^{-1}{\mathbf{J}}_{\left(v\right)}^T{\mathbf{C}\mathbf{o}\mathbf{v}}_{\mathbf{z}}^{-1}\mathsf{ϵ}\left({\mathbf{x}}_{\left(v\right)}\right)$$

(4)

where $\left(v\right)$ represents an iteration counter. Equation (3) implies that the state variable vector is updated at each iteration according to the vector of total variation for each state variable per iteration (as computed with Equation (4)). The iterative process finishes when the norm of the $∆\mathbf{x}$ vector is lower than a tolerance ($tol$ = 1 × 10⁻⁶ in this work) or when the iteration counter reaches a maximum number of iterations ($N_{max}$ = 100 in this work), leading to an optimal solution $\widehat{\mathbf{x}}$. Equation (4) involves the Jacobian matrix at each iteration ${\mathbf{J}}_{\left(\mathit{v}\right)}\in {\mathbb{R}}^{m\times n}$, which represents the derivative of measurements with respect to the state variables.

2.3.2. Adaptation for Bottle Test Free Chlorine Bulk Decay Coefficient Statistical Fitting

The general state estimation formulation (as defined in Section 2.3.1) should be adapted to fit the bulk decay coefficient $k_b$. Equation (1) represents chlorine measurements in terms of the assumed first-order decay model and model/chlorine measurement errors (full derivation in Appendix A.1). Equation (1) can easily be rearranged to express chlorine measurement errors (i.e., difference between chlorine measurements and model estimations) as:

$$E_{measure}\left(t,i\right)=C_{measure}\left(t,i\right)-\left[C_{f,model}+\left(C_{0,model}-C_{f,model}\right)·e^{-k_b·t}+E_{model}\left(t\right)\right]$$

(5)

It must be noted that measurement errors are embedded in the SE problem (Equation (2)) through the vector of measurements $\mathbf{z}\in {\mathbb{R}}^m$. This vector can intuitively be associated with chlorine measurements $C_{measure}\left(t,i\right)$. However, to be precise, the $\mathbf{z}$ vector may include chlorine measurements as represented by $C_{measure}\left(t,i\right)$ (vector ${\mathbf{z}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}}\in {\mathbb{R}}^{m_c}$, where $m_c$ is the number of chlorine measurements) and any other possible pseudomeasurements (vector ${\mathbf{z}}_{\mathbf{p}\mathbf{s}\mathbf{e}\mathbf{u}\mathbf{d}\mathbf{o}}\in {\mathbb{R}}^{m_p}$, where $m_p$ is the number of pseudomeasurements). Pseudomeasurements are estimations based on prior knowledge (e.g., [56]). It is reasonable to assume that we can have first (or a priori) estimations of some involved variables, such as the initial chlorine concentration $C_{0,model}$ or the final chlorine concentration $C_{f,model}$. This means that, in general, $\mathbf{z}=[{\mathbf{z}}_{\mathbf{p}\mathbf{s}\mathbf{e}\mathbf{u}\mathbf{d}\mathbf{o}};{\mathbf{z}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}}]$ and $m=m_p+m_c$.

Starting with chlorine measurements, it should be noted that chlorine values and measurement errors have been represented as dependent on time $t$ and replication $i$ in Equations (1) and (5) to facilitate the connection with the bottle test procedure described in Section 2.1. However, chlorine errors/values can also be expressed as vectors only dependent on the number of measurements $m_c$, without making explicit the time $t$ and replication $i$. Therefore, Equation (5) can be rewritten as:

$${\mathbf{E}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}}={\mathbf{C}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}}-\left[C_{f,model}+\left(C_{0,model}-C_{f,model}\right)·e^{-k_b·\mathbf{t}}+{\mathbf{E}}_{\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}}\right]$$

(6)

where ${\mathbf{E}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}}\in {\mathbb{R}}^{m_c}$ represents the vector of measurement errors, ${\mathbf{C}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}}\in {\mathbb{R}}^{m_c}$ is the vector of measured chlorine concentrations, and ${\mathbf{E}}_{\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}}\in {\mathbb{R}}^{n_{times}}$ is the vector of error models (one for each time), which is consistent with the time vector $\mathbf{t}\in {\mathbb{R}}^{n_{times}}$.

In this work, we assume that the rest of the variables involved in the first-order bulk chlorine decay model embedded in Equation (6) ($C_{0,model}$, $C_{f,model}$ and $k_b$) are pseudomeasured. The pseudomeasurement error vector can be generally written as:

$${\mathbf{E}}_{\mathbf{p}\mathbf{s}\mathbf{e}\mathbf{u}\mathbf{d}\mathbf{o}}={\mathbf{z}}_{\mathbf{p}\mathbf{s}\mathbf{e}\mathbf{u}\mathbf{d}\mathbf{o}}-g\left(\mathbf{x}\right)$$

(7)

The error vector $\mathsf{ϵ}\left(\mathbf{x}\right)$ in Equation (2) can therefore be particularized for this case as:

$$\mathsf{ϵ}\left(\mathbf{x}\right)=[{\mathbf{E}}_{\mathbf{p}\mathbf{s}\mathbf{e}\mathbf{u}\mathbf{d}\mathbf{o}},{\mathbf{E}}_{\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}}]$$

(8)

It is important to define the set of state variables represented by vector $\mathbf{x}$. Different sets of state variables are possible in any state estimation formulation [53]. In this work, the initial concentration of chlorine ($C_{0,model}$), the final concentration of chlorine ($C_{f,model}$), the chlorine decay bulk coefficient ($k_b$) and the vector of model errors (${\mathbf{E}}_{\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}}$) are considered state variables. The bulk decay coefficient is the main motivation for this formulation (it is the coefficient that we want to fit to the bottle test data), but additional variables are needed to estimate chlorine values/errors according to the assumed model. This assumption implies that there are $n=3+n_{times}$ state variables:

$$\mathbf{x}=[C_{0,model}; C_{f,model}; k_b; {\mathbf{E}}_{\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}} ]$$

(9)

Equations (8) and (9) (which also involve Equations (6) and (7)) adapt the SE problem described in Section 2.3.1 to adjust the bulk decay coefficient $k_b$ from the bottle test data.

It should be noted that the algebraic solution for the SE problem (Equations (3) and (4)) requires that the Jacobian matrix is of full rank. A necessary condition for this is that the number of measurements ($m$) is greater than the number of state variables ($n$). Several observations should be made regarding the number and characteristics of measurements/pseudomeasurements and state variables in this case:

• Measurements/pseudomeasurements. It has been assumed that a first (a priori) estimation of $C_{0,model},C_{f,model},k_b$ and ${\mathbf{E}}_{\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}}$ is available for SE purposes. This means that the number of pseudomeasurements equals the number of state variables ($m_p=n$) and ensures that the number of measurements $m=m_p+m_c=n+m_c$ is always greater than the number of state variables $n$. Pseudomeasurements are generally associated with high uncertainty (i.e., high standard deviation or variance) to allow measurements (with lower uncertainty) to condition state estimation results [54]. Assigning a high variance for pseudomeasurements implies a low weight, and so a low contribution to the state estimation process described by Equations (2)–(4). Because measurements have greater relative importance (i.e., they are associated with a lower error), the uncertainty of state variables as computed with state estimation (a posteriori) should be significantly lower than that assumed for pseudomeasurements (a priori). If this was not the case, measurements would not provide any additional information about the value of that variable. This will be highlighted when results are presented in Section 3. Pseudomeasurements are also measurements, but the term is used specifically to refer to those that are not well-known a priori and so should be associated with a higher variance to represent the lack of knowledge (e.g., [53,56]).

  Table 1. Default values for state variable pseudomeasurements and free chlorine measurements (KEMIO).

  Type	Variable	Notation	$\mathbf{Mean} \mathit{\mu }$ or Expected Value	$\mathbf{Standard} \mathbf{Deviation} \mathit{\sigma }$
  Pseudomeasurement	Initial chlorine concentration according to the model [mg/L]	$C_{0,model}$	ICC 1	0.50
  	Final chlorine concentration according to the model [mg/L]	$C_{f,model}$	0	0.01
  	First-order bulk decay coefficient [1/h]	$k_b$	0.01	0.50
  	Error model at each time [mg/L]	$E_{{model}_t};$ $t=1,2,\dots ,n_{times}$	0	0.01
  Measurement	Free chlorine concentration [mg/L]	$C_{measure}$	Variable 2	0.065 3

  ¹ As measured in the lab—average of ICC values from Steps 3 and 4 in Section 2.1. ² As measured in the lab—Step 5 in Section 2.1. ³ According to measurement error characterization tests using KEMIO equipment (Appendix A.2).

  summarizes the default values (mean and variance) that are adopted in this work for state variable pseudomeasurements. Mean values are used in this work as initial values for the corresponding state variables ${\mathbf{x}}_{\left(0\right)}$. Standard deviations are assumed to be low for variables that inspire relative confidence in the mean value. For example, we assume 0.01 mg/L for the standard deviation of $C_{f,model}$ (because chlorine concentration is expected to tend to zero), and $E_{{model}_t};t=1,2,\dots ,n_{times}$ (because the first-order bulk decay model is frequently adopted in the literature). On the contrary, standard deviations are considered high when there is low confidence in the assumed mean values. This is the case of $C_{0,model}$ (we assume 0.50 mg/L) because free chlorine measurements at the beginning of the bottle test (ICC measurements in Steps 3 and 4 in Section 2.1) have been found to vary noticeably. It is also the case of the bulk decay coefficient $k_b$, which is difficult to anticipate before the bottle test because it varies widely with the water source and temperature (e.g., [18,20]). A high standard deviation there (0.50 1/h) implies conceding low credibility to this first estimation. These default values may be changed depending on the SE results (see Figure 2) as discussed in the Results section.
• State variables. It has already been explained that $n=3+n_{times}$ (Equation (9)). This means that the number of state variables (and so the number of total measurements) depends on the number of times considered for the analysis. At each time (i.e., approximately 3 h, 10 h, 24 h, 48 h, and 96 h or more), measurements are replicated at least four times. Since the time window for all replications is smaller than 5 min, the average time of measurement is considered here. This implies that $n_{times}$ keeps relatively low in a bottle test (most likely between 5 and 7, depending on the chlorine decay evolution and the number of replications), and so there is more measurement redundancy, which is positive for state estimation applications [57].

• Table 1 gathers the mean and standard deviation assumed in this work for state variable pseudomeasurements. It also includes the assumed standard deviation for chlorine measurements. Free chlorine measurement error could either be assumed (according to previous works) or quantified. In this work, free chlorine measurement error (using the KEMIO device) characterization tests have been carried out as described in Appendix A.2 (which includes Figure A1).

These assumptions regarding measurements/pseudomeasurements and state variables are key to constructing the Jacobian matrix for this application. Jacobian matrix components are calculated by computing the derivatives of pseudomeasurements/measurements with respect to state variables. Appendix A.3 provides the formulation of matrix components for the assumed bulk decay model (see Figure A2). This formulation ensures that once the SE iterative process finishes (Equations (3) and (4)), the optimal solution $\widehat{\mathbf{x}}$ represents the most likely value of the state variables. This vector includes the bulk decay coefficient (Equation (9)), so the expected value of ${\widehat{k}}_b$ (and the rest of the state variables) is obtained (see Figure 2). The mean value of chlorine concentrations at each time (here denoted as $\widehat{\mathbf{C}}\in {\mathbb{R}}^{n_{times}}$) can be obtained by substituting $\widehat{\mathbf{x}}$ values in Equation (1).

2.4. Uncertainty Assessment

State variable uncertainty is typically computed according to the First-Order Second-Moment (FOSM) formulation [54]:

$${\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{x}}}={\left[{\mathbf{J}}^T{\mathbf{C}\mathbf{o}\mathbf{v}}_{\mathbf{z}}^{-1}\mathbf{J}\right]}^{-1}$$

(10)

where ${\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{x}}}\in {\mathbb{R}}^{n\times n}$ represents the state variable variance-covariance matrix. This matrix must be computed with the Jacobian matrix at the optimal solution $\widehat{\mathbf{x}}$. The diagonal of the matrix ${\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{x}}}$ contains the variance of the state variable vector, which includes the variance of the bulk decay coefficient ${\widehat{k}}_b$ (see Figure 2) in third position (Equation (9)).

The uncertainty of any other set of network variables can be computed by applying the FOSM again [58]. For example, the variance-covariance matrix of chlorine values at each time ${\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{C}}}\in {\mathbb{R}}^{n_{times}\times n_{times}}$ can be computed as:

$${\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{C}}}=\mathbf{K}{\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{x}}}{\mathbf{K}}^{\mathit{T}}$$

(11)

where $\mathbf{K}\in {\mathbb{R}}^{n_{times}\times n}$ is the Jacobian matrix of chlorine values at each time. It can be obtained by extracting the corresponding rows of the Jacobian matrix $\mathbf{J}$ at the optimal solution $\widehat{\mathbf{x}}$. The diagonal of matrix ${\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{C}}}$ gathers the variance of estimated chlorine values at each of the $n_{times}$.

2.5. Outlier Detection

The error or difference between measurements and estimated variables is crucial for outlier detection. In this work, standardized errors are computed for all measurements. This includes state variable pseudomeasurements and chlorine measurements, generally denoted as $\mathsf{ϵ}\left(\widehat{\mathbf{x}}\right)$ (see Equation (8)). Measurement errors are standardized $\overline{\mathsf{ϵ}}\left(\widehat{\mathbf{x}}\right)$ according to their initial variance, which is gathered in the measurement variance-covariance matrix ${\mathbf{C}\mathbf{o}\mathbf{v}}_{\mathbf{z}}$:

$$\overline{\mathsf{ϵ}}\left(\widehat{\mathbf{x}}\right)=\mathsf{ϵ}\left(\widehat{\mathbf{x}}\right)·\sqrt{{\mathbf{C}\mathbf{o}\mathbf{v}}_{\mathbf{z}}^{-1}}$$

(12)

Outliers can be identified by comparing standardized errors and confidence intervals. Different thresholds have been explored, but in this work, the tipping point is determined by the $\alpha =$ 99% Confidence Interval (CI), which is computed as:

$${CI}_{\mathbf{z}}=\pm {\mathsf{\Phi }}^{-1}\left(1-{\displaystyle \frac{\alpha }{2}}\right)$$

(13)

where ${\mathsf{\Phi }}^{-1}$ represents the inverse of the normal Cumulative Distribution Function (CDF). If the measurement standardized error (obtained from Equation (12)) is greater than the positive threshold or lower than the negative threshold of CI (Equation (13)), measurements can be identified as outliers. If any pseudomeasurement is identified as an outlier, the hypothesis behind this estimation should be revisited (see Figure 2). Chlorine measurement outliers represent measurement anomalies, which should be excluded from the state estimation process (i.e., SE should be re-run without conflictive chlorine measurements). We recommend removing outliers (i.e., deleting chlorine measurements) one by one to minimize data erasing (see Figure 2). The first outlier to be removed should be the one associated with the greatest standardized error in absolute value. State estimation results after removing each outlier should be assessed to decide if additional outliers should be removed. In case of doubt, all outliers identified when running state estimation for the first time should be removed.

Confidence intervals can also be derived for the most likely chlorine concentrations at each time. It has already been explained that the expected chlorine values $\widehat{\mathbf{C}}$ can be obtained by substituting the optimal SE solution $\widehat{\mathbf{x}}$ in Equation (1). The chlorine confidence interval here is computed as:

$${CI}_{\widehat{\mathbf{C}}}=\widehat{\mathbf{C}}\pm {\mathsf{\Phi }}^{-1}\left(1-{\displaystyle \frac{\alpha }{2}}\right)·\sqrt{diag\left({\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{C}}}\right)}$$

(14)

where $diag\left(\right)$ indicates the diagonal selection of a matrix, in this case, the chlorine variance-covariance matrix ${\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{C}}}$ (Equation (11)).

Finally, it must be highlighted that the chlorine confidence interval provided by Equation (14) considers the error associated with the real estimate of chlorine values through ${\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{C}}}$. This confidence interval does not consider measurement error, only the uncertainty of state variables. Since measurement error is inherent to chlorine measurements, ${CI}_{\widehat{\mathbf{C}}}$ could be expanded by considering the total variance of chlorine, which includes that associated with SE results (represented by ${\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{C}}}$) and measurement variance (${\sigma }_{C_{measure}}^2$):

$${TCI}_{\widehat{\mathbf{C}}}=\widehat{\mathbf{C}}\pm {\mathsf{\Phi }}^{-1}\left(1-{\displaystyle \frac{\alpha }{2}}\right)·\sqrt{diag\left({\mathbf{C}\mathbf{o}\mathbf{v}}_{\widehat{\mathbf{C}}}\right)+{\sigma }_{C_{measure}}^2}$$

(15)

where ${\sigma }_{C_{measure}}^2={0.065}^2$ (mg/L)² according to Table 1 (see details in Appendix A.2). Both ${CI}_{\widehat{\mathbf{C}}}$ and ${TCI}_{\widehat{\mathbf{C}}}$ will be computed in Section 3 to identify any potential bottle test measurement anomalies.

3. Results

The methodology described in Section 2 is applied in this work to characterize the bulk decay coefficient of three different water sources (A, B, and C). Water grab samples are taken immediately before chlorination at three treatment works in the region of Castilla-La Mancha (Spain). In order to assess the repeatability of the process and to highlight the physical meaning of state estimation/uncertainty assessment results, each bottle test is carried out three times (in parallel) in the exact same way for the water sample from each source. Replicated bottle tests will be denoted as “X-E01”, “X-E02”, and “X-E03”, with “X” being “A”, “B”, or “C” depending on the water source. This means that each grab sample presents a volume of approximately 12 L, and the laboratory process described in Section 2.1 is carried out in three parallel isothermal baths (i.e., chlorination happens at three different 3.8 L Winchester bottles) for each water source. Time blocks are slightly displaced among the 3 tests to ensure that the same person can carry out the triplicate lab test in parallel. Only one bottle test is needed to compute the uncertainty of the bulk decay coefficient with the methodology presented in this paper, but replication is carried out for these three samples to validate the method and to illustrate its relevance.

Table 2. Grab sample characteristics from sources A, B, and C.

Source/Treatment Works	Replication	TOC (mg/L)	Temperature (°C)	ICC (mg/L)	pH (-)
A (surface water)	E01	5.20	24.0	0.92	7.0
	E02		24.0	0.95	7.2
	E03		24.0	0.97	7.2
B (groundwater)	E01	0.83	24.0	1.00	6.0
	E02		24.0	1.06	6.3
	E03		24.0	1.03	6.2
C (groundwater)	E01	0.00	24.0	1.06	7.4
	E02		24.0	1.12	7.5
	E03		24.0	1.08	7.4

summarizes the main characteristics of the grab samples from each of the three sources/treatment works when processed at the laboratory before starting the bottle test. TOC is measured only once for the total volume of water (12 L), but temperature, pH and ICC are measured for each parallel bottle test (3.8 L) following the procedure described in Section 2.1. Table 2 shows that TOC is higher for treatment works A compared to B and C. Treatment works A receives the water from a reservoir (surface water), whereas treatment works B and C run on groundwater. Grab samples are taken in all three cases after water has gone through all treatment stages (except chlorination), so it can be assumed that source A is richer in organic matter than sources B and C (there was virtually no organic matter at source C when the sample was taken). The higher TOC for source A justifies the lower ICC values compared to sources B and C (chlorine reacts faster due to the greater presence of organic matter, lowering the ICC). pH values are slightly higher for treatment works A (7.0–7.2) and C (7.4–7.5) compared to B (6.0–6.3), but remain below 8, which is the maximum recommended pH for drinking water [59].

Table 3. Free chlorine measurements (with replications) during parallel bottle tests for: (a) treatment works A, (b) treatment works B and (c) treatment works C. Measurements from the first average time are in gray font. Outlier measurements are shaded in gray.

(a) Treatment works A
		A-E01			A-E02			A-E03
Meas. No.		Avg. Time [h]	Free Chlorine [mg/L]		Avg. Time [h]	Free Chlorine [mg/L]		Avg. Time [h]	Free Chlorine [mg/L]
0		1.25	0.74		1.21	0.87		1.03	0.67
0		1.25	0.79		1.21	0.79		1.03	0.79
0		1.25	0.75		1.21	0.88		1.03	0.77
0		1.25	0.78		1.21	0.75		1.03	0.79
1		3.17	0.57		2.94	0.72		2.77	0.50
2		3.17	0.61		2.94	0.67		2.77	0.43
3		3.17	0.59		2.94	0.62		2.77	0.46
4		3.17	0.60		2.94	0.83		2.77	0.49
5		8.49	0.53		2.94	0.64		8.07	0.31
6		8.49	0.36		8.27	0.40		8.07	0.35
7		8.49	0.36		8.27	0.45		8.07	0.35
8		8.49	0.40		8.27	0.39		8.07	0.37
9		8.49	0.54		8.27	0.49		26.06	0.09
10		26.47	0.06		26.25	0.06		26.06	0.08
11		26.47	0.15		26.25	0.15		26.06	0.06
12		26.47	0.07		26.25	0.07		26.06	0.07
13		26.47	0.15		26.25	0.11		45.56	0.02
14		26.47	0.25		26.25	0.09		45.56	0.02
15		46.09	0.02		26.25	0.08		45.56	0.07
16		46.09	0.02		45.84	0.05		45.56	0.02
17		46.09	0.02		45.84	0.05
18		46.09	0.02		45.84	0.07
19					45.84	0.02
(b) Treatment works B
		B-E01			B-E02			B-E03
Meas. No.		Avg. Time [h]	Free Chlorine [mg/L]		Avg. Time [h]	Free Chlorine [mg/L]		Avg. Time [h]	Free Chlorine [mg/L]
0		1.15	1.00		1.05	0.98		1.03	0.99
0		1.15	0.96		1.05	0.98		1.03	1.12
0		1.15	1.00		1.05	0.99		1.03	1.04
0		1.15	0.98		1.05	1.03		1.03	1.02
1		2.88	0.97		2.65	0.96		2.50	1.03
2		2.88	0.91		2.65	0.98		2.50	0.98
3		2.88	0.92		2.65	0.99		2.50	0.97
4		2.88	0.92		2.65	1.04		2.50	1.01
5		8.02	0.91		2.65	0.99		7.41	0.93
6		8.02	0.86		7.73	0.95		7.41	0.99
7		8.02	0.86		7.73	0.99		7.41	0.89
8		8.02	0.84		7.73	0.98		7.41	0.94
9		25.22	0.43		7.73	0.89		7.41	0.93
10		25.22	0.85		24.98	0.75		24.80	0.82
11		25.22	0.77		24.98	0.79		24.80	0.86
12		25.22	0.61		24.98	0.86		24.80	0.77
13		25.22	0.77		24.98	0.89		24.80	0.86
14		45.87	0.76		24.98	0.85		45.46	0.75
15		45.87	0.67		45.63	0.80		45.46	0.78
16		45.87	0.64		45.63	0.76		45.46	0.77
17		45.87	0.64		45.63	0.80		45.46	0.75
18		95.84	0.52		45.63	0.77		95.44	0.67
19		95.84	0.43		95.60	0.64		95.44	0.49
20		95.84	0.47		95.60	0.59		95.44	0.69
21		95.84	0.53		95.60	0.50		95.44	0.58
22		248.05	0.37		95.60	0.54		95.44	0.39
23		248.05	0.40		247.78	0.56		247.60	0.50
24		248.05	0.27		247.78	0.48		247.60	0.34
25		248.05	0.44		247.78	0.49		247.60	0.30
26		248.05	0.25		247.78	0.62		247.60	0.55
(c) Treatment works C
		C-E01			C-E02			C-E03
Meas. No.		Avg. Time [h]	Free Chlorine [mg/L]		Avg. Time [h]	Free Chlorine [mg/L]		Avg. Time [h]	Free Chlorine [mg/L]
0		1.20	0.98		1.15	1.02		1.10	0.99
0		1.20	1.15		1.15	0.99		1.10	1.00
0		1.20	1.00		1.15	0.97		1.10	0.94
0		1.20	1.08		1.15	0.99		1.10	1.04
1		2.97	1.03		2.90	0.95		2.67	0.91
2		2.97	1.01		2.90	0.95		2.67	0.96
3		2.97	0.97		2.90	0.98		2.67	0.97
4		2.97	1.00		2.90	0.87		2.67	1.01
5		8.83	0.94		8.52	1.12		8.10	0.95
6		8.83	0.98		8.52	0.86		8.10	0.93
7		8.83	1.04		8.52	0.86		8.10	0.97
8		8.83	0.96		8.52	1.00		8.10	0.97
9		23.95	0.98		23.87	0.97		23.80	0.88
10		23.95	0.94		23.87	0.92		23.80	0.84
11		23.95	0.99		23.87	0.95		23.80	0.98
12		23.95	1.04		23.87	1.00		23.80	0.98
13		48.77	0.88		48.52	0.88		48.52	0.53
14		48.77	0.84		48.52	0.88		48.52	0.85
15		48.77	0.95		48.52	0.89		48.52	0.90
16		48.77	0.99		48.52	0.90		48.52	0.84
17		120.10	0.70		119.88	0.80		48.52	0.69
18		120.10	0.84		119.88	0.77		119.58	0.86
19		120.10	0.68		119.88	0.91		119.58	0.65
20		120.10	0.73		119.88	0.80		119.58	0.56
21		293.47	0.61		119.88	0.78		119.58	0.78
22		293.47	0.55		293.05	0.73		293.41	0.54
23		293.47	0.70		293.05	0.55		293.41	0.67
24		293.47	0.57		293.05	0.65		293.41	0.67
25		293.47	0.60		293.05	0.57		293.41	0.63
26					293.05	0.62

gathers free chlorine measurements (with replications) over time for the three parallel bottle tests carried out with grab samples from sources A, B and C. Measurements for the first average time are represented in gray font and will be disregarded for the $k_b$ analysis as explained in Section 2.1. It should be noted that the number of average times ($n_{times}$) varies depending on the rate at which chlorine decays (4 effective times for A, 6 effective times for B and C). Chlorine decays faster for sample A due to its higher TOC. Measurements included in Table 3 are analyzed in the next subsections for samples A, B, and C (respectively) according to the procedure described in the methodology.

3.1. Treatment Works A

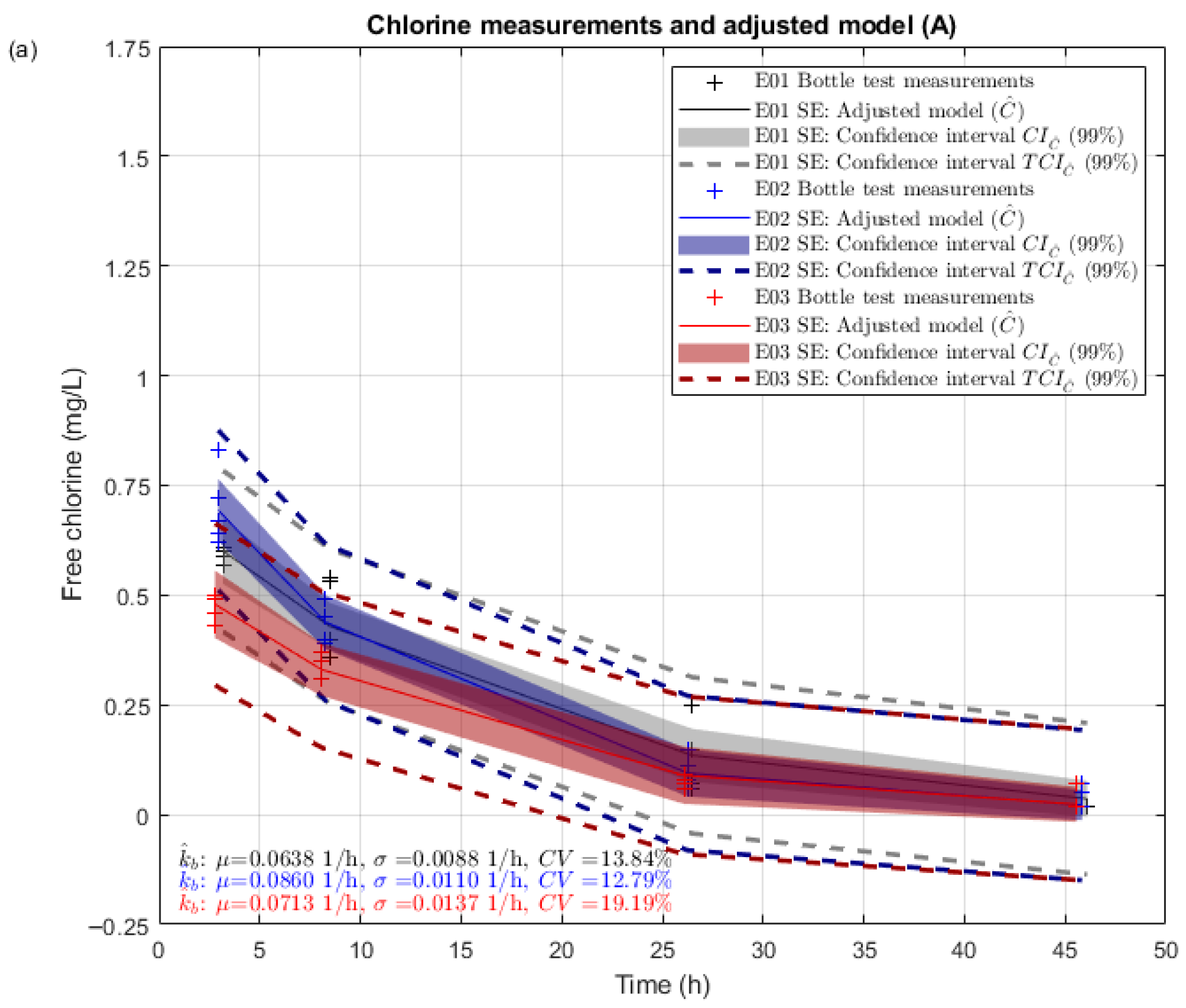
State estimation (Section 2.3), uncertainty quantification (Section 2.4), and outlier detection (Section 2.5) formulations are applied in this subsection to bottle test chlorine measurements for treatment works A (surface water). Figure 3 gathers the results for the first replication of the bottle test (A-E01). Figure 3a provides a representation of bottle test chlorine measurements and the adjusted first-order bulk decay model (with confidence intervals). This figure shows that there are four sets of chlorine measurements for each of the four average times included in Table 3 (disregarding the first hour values in gray). As expected, the confidence interval ${TCI}_{\widehat{\mathbf{C}}}$ (Equation (15)) is wider than ${CI}_{\widehat{\mathbf{C}}}$ (Equation (14)). For A-E01, all chlorine measurements lie within the expanded confidence interval ${TCI}_{\widehat{\mathbf{C}}}$. The estimated chlorine concentrations are approximately in the middle of the range of chlorine measurements at different times and reach 0 mg/L in less than 2 days. Figure 3a also includes the mean (0.0638 1/h), standard deviation (0.0088 1/h), and coefficient of variation (13.84%) of the bulk decay coefficient. The mean value lies within the range of bulk decay coefficients summarized by [20]. The coefficient of variation, 13.84% shows that there is a non-negligible uncertainty associated with the bulk decay coefficient.

Figure 3b shows the standardized errors of pseudomeasurements (i.e., state variables) as provided by Equation (12). The threshold value for outlier detection in this case (99% ${CI}_{\mathbf{z}}=\pm 2.58$) is clearly greater than error values, which are low for the first three state variables (${\widehat{C}}_{0,model}$, ${\widehat{C}}_{f,model}$ and ${\widehat{k}}_b$) and the remaining ${\widehat{\mathbf{E}}}_{\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}}$ state variables (4 because 4 average times are being considered). This is reasonable given that pseudomeasurements are a priori estimations of expected state variable values. Figure 3c presents the measurement (free chlorine) standardized errors as provided by Equation (12) as well. The threshold value for outlier detection is higher than the corresponding errors, so no outliers are detected.

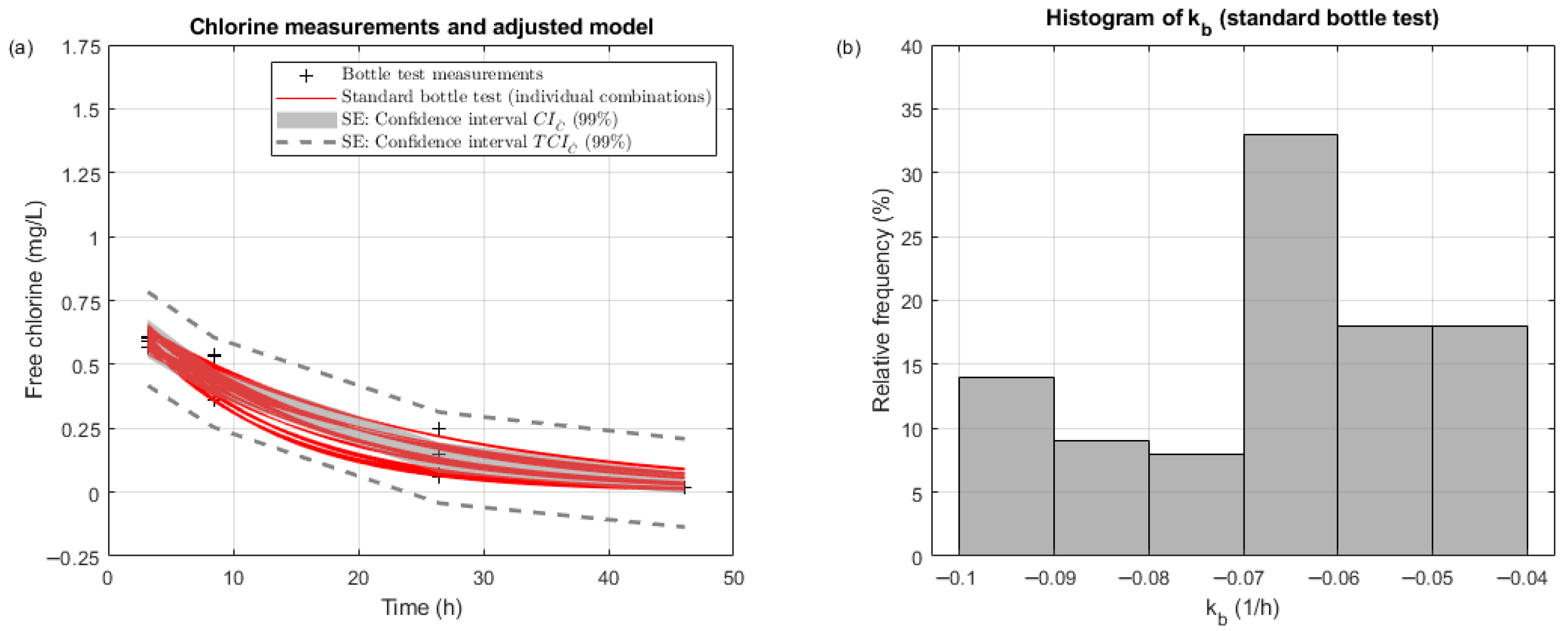
State estimation confidence intervals may be compared with standard bottle test results. As explained in the Introduction, standard bottle tests rely on taking one measurement at a time and conveniently adjusting the assumed model (in this case, an exponential fit for a first-order bulk decay model). Figure 4a shows that each combination of measurement replications leads to different fitted lines (in red) and $k_b$ values. There are 400 combinations for the 18 measurements taken in A-E01 (4 times with 4 or 5 replications). All fitted lines from these combinations (in red) fall within the ${TCI}_{\widehat{\mathbf{C}}}$ (Equation (15)). Figure 4b gathers the relative histogram of the bulk decay coefficients obtained from these combinations. This histogram is consistent with state estimation results (mean 0.0638 1/h, standard deviation 0.0088 1/h). Overall, Figure 4 (which is consistent with conceptual Figure 1) proves that chlorine measurement errors have an impact on the estimated bulk decay coefficient. State estimation presents added value with respect to the traditional approach because it consistently propagates uncertainty. The state estimation formulation characterizes the distribution of fitting curves affected by the uncertainty of the fitting data. Therefore, it is the most effective way to evaluate the fitting data uncertainty effect.

Table 4. SE Results—Basic statistical properties for all state variables in bottle tests A.

State Variable		Statistic	A-E01	A-E02	A-E03
$\mathrm{Initial} \mathrm{chlorine} \mathrm{concentration} {\widehat{C}}_{0,model}$		$\mathrm{Mean} \mu$ (mg/L)	0.74	0.89	0.59
		$\mathrm{Std} \sigma$ (mg/L)	0.05	0.06	0.05
		CV (%)	6.76	6.19	8.80
$\mathrm{Final} \mathrm{chlorine} \mathrm{concentration} {\widehat{C}}_{f,model}$		$\mathrm{Mean} \mu$ (mg/L)	−0.00	0.00	0.00
		$\mathrm{Std} \sigma$ (mg/L)	0.01	0.01	0.01
$\mathrm{Bulk} \mathrm{decay} \mathrm{coefficient} {\widehat{k}}_b$		$\mathrm{Mean} \mu$ (1/h)	0.0638	0.0860	0.0713
		$\mathrm{Std} \sigma$ (1/h)	0.0088	0.0110	0.0137
		CV (%)	13.84	12.79	19.19
$\mathrm{Model} \mathrm{error} {\widehat{\mathbf{E}}}_{\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}}$	Time 2	$\mathrm{Mean} \mu$ (mg/L)	−0.0008	0.0003	−0.0009
		$\mathrm{Std} \sigma$ (mg/L)	0.0099	0.0099	0.0099
	Time 3	$\mathrm{Mean} \mu$ (mg/L)	0.0011	−0.0006	0.0014
		$\mathrm{Std} \sigma$ (mg/L)	0.0097	0.0098	0.0098
	Time 4	$\mathrm{Mean} \mu$ (mg/L)	0.0001	−0.0002	−0.0014
		$\mathrm{Std} \sigma$ (mg/L)	0.0098	0.0097	0.0098
	Time 5	$\mathrm{Mean} \mu$ (mg/L)	−0.0015	0.0024	0.0008
		$\mathrm{Std} \sigma$ (mg/L)	0.0096	0.0096	0.0096

gathers basic statistical properties for all state variables and bottle tests from source A. The mean and standard deviation are included for all state variables, but the coefficient of variation (CV) is only included for those state variables whose mean value is expected to be different from zero (initial chlorine concentration and bulk decay coefficient according to Table 1). Table 4 shows that the mean initial chlorine concentration for the model varies between 0.59 and 0.89 mg/L depending on the bottle test. Its standard deviation varies between 0.05 and 0.06 mg/L, a range that is considerably lower than the standard deviation assumed for the corresponding pseudomeasurement (0.50 mg/L, see Table 1). This occurs because chlorine measurements (and the assumed model) help reduce the standard deviation of the pseudomeasured initial chlorine concentration (and the rest of the state variables) through the state estimation process. The mean of the final concentration (according to the model) and model errors tend to be zero, with a standard deviation consistent with the assumed 0.01 mg/L value (Table 1). The mean bulk decay coefficient adjusted for these replicate tests varies between 0.0638 and 0.0860 1/h. Its standard deviation is roughly 0.01 1/h, a value once again considerably lower than the standard deviation assumed a priori for the corresponding pseudomeasurement (0.50 1/h, see Table 1). Assuming a 99% level of confidence ($\pm 2.58$), the range of values for $k_b$ would be 0.0411–0.0865 1/h (A-E01), 0.0576–0.1144 1/h (A-E02), and 0.0360–0.1066 1/h (A-E03). The fact that there is some degree of overlap between the three replications (0.0576–0.0865 1/h) validates the state estimation approach presented here. The empirical coefficient of variation computed considering the three $k_b$ values adjusted with SE is 15.32%. This value is consistent with the CV values obtained for $k_b$ from SE (12.79–19.19%, average 15.27%). No outliers have been identified according to Equations (12)–(15) for these bottle tests.

3.2. Treatment Works B

SE results for bottle tests B are now presented. Figure 5a gathers state estimation results for the first bottle test (B-E01). Figure 5a is comparable to Figure 3a for test A-E01. In general, the adjusted model does not fit well to the range of chlorine measurements at each time, and this is especially visible at the third, fifth, and sixth effective times (there is one outlier at the third average time). Appendix B shows that pseudomeasurement errors (Figure A3a) keep within the CI range, but measurement 9 is an outlier (Figure A3b, Table 3). As already explained in Section 2.5, this chlorine measurement should be removed, and SE should be re-run. It is also interesting to highlight that chlorine measurements after almost 250 h are still clearly different from zero in Figure 5a. As mentioned in Section 2.2, tests longer than 250–300 h are out of practical interest because water age values over 10 days are unlikely in most pipes within a water distribution system, and this work intends to adjust a model useful to support network operation. Chlorine concentrations do not reach 0 mg/L for B-E01 (values between 0.25 and 0.44 mg/L at the last average time according to Table 3), B-E02 (0.48–0.62 mg/L), nor B-E03 (0.30–0.55 mg/L). These values pinpoint that it may be worth reconsidering the assumed statistical properties for the final chlorine concentration of the model. By default, we recommend assuming a mean value of 0 mg/L and a standard deviation of 0.01 mg/L for $C_{f,model}$ (Table 1), but it does not seem to be the best assumption for samples from source B.

Figure 5b shows the updated version of Figure 5a once chlorine measurement 9 (outlier) has been disregarded, and the standard deviation assumed for the final concentration of chlorine $C_{f,model}$ has been increased to 0.50 mg/L. This standard deviation shows a lack of confidence in the assumed final concentration (like for $C_{0,model}$ and $k_b$) and should allow the final chlorine concentration to differ from zero. Figure 5b (together with Figure A4a,b, see Appendix B) shows that there are no outliers after these changes are implemented, and there is a better fit for chlorine measurements overall. Removing the outlier does not have a significant effect on the estimated $k_b$, but increasing the standard deviation of $C_{f,model}$ significantly affects the mean bulk decay coefficient, which increases from 0.0046 1/h (Figure 5a) to 0.0133 1/h (Figure 5b). This change in assumption also implies a significant increase in the bulk decay coefficient standard deviation (from 0.0004 to 0.0026 1/h) and CV (from 9.30 to 19.80%). However, it is the most realistic approach given that chlorine concentrations during the bottle test do not reach 0 mg/L.

Table 5. SE Results—Basic statistical properties for all state variables in bottle tests B.

State Variable		Statistic	B-E01	B-E02	B-E03
$\mathrm{Initial} \mathrm{chlorine} \mathrm{concentration} {\widehat{C}}_{0,model}$		$\mathrm{Mean} \mu$ (mg/L)	0.94	1.01	0.99
		$\mathrm{Std} \sigma$ (mg/L)	0.03	0.03	0.03
		CV (%)	2.99	2.73	2.60
$\mathrm{Final} \mathrm{chlorine} \mathrm{concentration} {\widehat{C}}_{f,model}$		$\mathrm{Mean} \mu$ (mg/L)	0.32	0.52	0.38
		$\mathrm{Std} \sigma$ (mg/L)	0.04	0.04	0.06
		CV (%)	13.01	7.29	14.94
$\mathrm{Bulk} \mathrm{decay} \mathrm{coefficient} {\widehat{k}}_b$		$\mathrm{Mean} \mu$ (1/h)	0.0133	0.0168	0.0107
		$\mathrm{Std} \sigma$ (1/h)	0.0026	0.0038	0.0025
		CV (%)	19.80	22.85	23.70
$\mathrm{Model} \mathrm{error} {\widehat{\mathbf{E}}}_{\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}}$	Time 2	$\mathrm{Mean} \mu$ (mg/L)	0.0010	0.0001	0.0018
		$\mathrm{Std} \sigma$ (mg/L)	0.0098	0.0098	0.0098
	Time 3	$\mathrm{Mean} \mu$ (mg/L)	−0.0010	0.0000	−0.0010
		$\mathrm{Std} \sigma$ (mg/L)	0.0097	0.0097	0.0097
	Time 4	$\mathrm{Mean} \mu$ (mg/L)	−0.0013	−0.0017	−0.0019
		$\mathrm{Std} \sigma$ (mg/L)	0.0097	0.0096	0.0097
	Time 5	$\mathrm{Mean} \mu$ (mg/L)	0.0017	0.0029	0.0006
		$\mathrm{Std} \sigma$ (mg/L)	0.0097	0.0098	0.0097
	Time 6	$\mathrm{Mean} \mu$ (mg/L)	−0.0006	−0.0019	0.0007
		$\mathrm{Std} \sigma$ (mg/L)	0.0098	0.0098	0.0098
	Time 7	$\mathrm{Mean} \mu$ (mg/L)	0.0002	0.0008	−0.0000
		$\mathrm{Std} \sigma$ (mg/L)	0.0100	0.0100	0.0100

gathers the basic statistical properties for all state variables in bottle tests B. All results have been computed with the increased standard deviation for the final chlorine concentration pseudomeasurement ($C_{f,model}$). Apart from the outlier removed for B-E01 (previously explained), one outlier is removed for B-E02 (measurement 21) and B-E03 (measurement 22), as highlighted in Table 3. Table 5 shows that the initial chlorine concentration for the model varies between 0.94 and 1.01 mg/L depending on the bottle test replication. Its standard deviation has reduced with respect to the pseudomeasurement assumption (0.50 mg/L, see Table 1), as happened for sample A. The mean of the final concentration (according to the model) varies between 0.32 and 0.52 mg/L. Its standard deviation varies between 0.04 and 0.06 mg/L. This range is considerably lower than the standard deviation now assumed for $C_{f,model}$ (0.50 mg/L) but greater than the initially assumed 0.01 mg/L (see Table 1). The mean bulk decay coefficient adjusted for these replicate tests varies between 0.0107 and 0.0168 1/h. Its deviation ranges 0.0025–0.0038 1/h, narrowing down the uncertainty initially assumed for this pseudomeasurement (0.50 1/h). Like for source A, there is an overlap in the confidence intervals for $k_b$. The empirical coefficient of variation computed considering the three bulk decay coefficient values adjusted with SE is 22.51%. This value is greater than that obtained from A grab sample (15.32%), but it is still consistent with the CV values that are being obtained from SE for ${\widehat{k}}_b$ (19.80–23.70%, average 22.12%).

3.3. Treatment Works C

Figure 6a shows state estimation results for the first bottle test (C-E01). There are no outliers in this bottle test. However, the assumption of the final chlorine concentration reaching zero is dubious again (concentrations 0.55–0.70 mg/L after almost 300 h according to Table 3). Figure 6b shows the corresponding plot after increasing the assumed standard deviation for the final concentration of chlorine $C_{f,model}$ to 0.50 mg/L (as already performed for treatment works B). Releasing the asymptote condition leads to a more defined curvature and provides a better fit for the data. The $k_b$ coefficient increases (from 0.0019 1/h to 0.0054 1/h) but is still low in absolute terms. It is lower than the coefficients for treatment works A and B, and on the lower end of values in [20]. The increased standard deviation for the final chlorine concentration translates into a greater CV for $k_b$ (from 10.35% to 46.68%). This might suggest that different average times should be studied when analyzing bulk decay coefficients of water samples with low TOC to better capture the curvature and asymptote of the curve.

Table 6. SE Results—basic statistical properties for all state variables in bottle tests C.

State Variable		Statistic	C-E01	C-E02	C-E03
$\mathrm{Initial} \mathrm{chlorine} \mathrm{concentration} {\widehat{C}}_{0,model}$		$\mathrm{Mean} \mu$ (mg/L)	1.02	0.97	0.98
		$\mathrm{Std} \sigma$ (mg/L)	0.02	0.02	0.03
		CV (%)	2.40	1.97	2.69
$\mathrm{Final} \mathrm{chlorine} \mathrm{concentration} {\widehat{C}}_{f,model}$		$\mathrm{Mean} \mu$ (mg/L)	0.49	−0.03	0.60
		$\mathrm{Std} \sigma$ (mg/L)	0.12	0.48	0.05
		CV (%)	24.56	−1908.62	8.15
$\mathrm{Bulk} \mathrm{decay} \mathrm{coefficient} {\widehat{k}}_b$		$\mathrm{Mean} \mu$ (1/h)	0.0054	0.0014	0.0104
		$\mathrm{Std} \sigma$ (1/h)	0.0025	0.0009	0.0038
		CV (%)	46.68	60.84	36.40
$\mathrm{Model} \mathrm{error} {\widehat{\mathbf{E}}}_{\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{l}}$	Time 2	$\mathrm{Mean} \mu$ (mg/L)	−0.0010	−0.0021	−0.0009
		$\mathrm{Std} \sigma$ (mg/L)	0.0098	0.0097	0.0098
	Time 3	$\mathrm{Mean} \mu$ (mg/L)	−0.0015	0.0005	0.0002
		$\mathrm{Std} \sigma$ (mg/L)	0.0097	0.0097	0.0097
	Time 4	$\mathrm{Mean} \mu$ (mg/L)	0.0026	0.0024	0.0017
		$\mathrm{Std} \sigma$ (mg/L)	0.0097	0.0097	0.0097
	Time 5	$\mathrm{Mean} \mu$ (mg/L)	0.0015	−0.0010	−0.0011
		$\mathrm{Std} \sigma$ (mg/L)	0.0097	0.0096	0.0097
	Time 6	$\mathrm{Mean} \mu$ (mg/L)	−0.0025	0.0003	−0.0001
		$\mathrm{Std} \sigma$ (mg/L)	0.0098	0.0096	0.0098
	Time 7	$\mathrm{Mean} \mu$ (mg/L)	0.0010	−0.0002	0.0004
		$\mathrm{Std} \sigma$ (mg/L)	0.0100	0.0099	0.0100

provides a summary of SE results for bottle tests C, considering an increased standard deviation of 0.5 mg/L for the final chlorine concentration in all cases. Only one outlier has been removed for test C-E03 (measurement 13, see Table 3). Table 6 shows that the estimated mean final chlorine concentration is clearly above zero for C-E01 (0.49 mg/L) and C-E03 (0.60 mg/L) but remains close to zero for C-E02 (−0.03 mg/L). This happens because chlorine measurements present an almost linear behavior for the average times that have been analyzed in the bottle test. This means that the $k_b$ value is very low (the exponent of the exponential model tends to zero), and there is no clear asymptote for the final chlorine concentration. This is reinforced by the variation in estimated bulk decay coefficients across the three tests (from 0.0014 1/h to 0.0104 1/h). These results suggest that the low content of organic matter for treatment works C (i.e., negligible TOC) leads to more random results in terms of the bulk decay coefficient. This phenomenon can be attributed to the increased randomness of the inherently unstable chlorine reaction, which could be further exacerbated by the uneven distribution of organic matter across subsamples. Note that the CV obtained for estimated ${\widehat{k}}_b$ results (36.40–60.84%, average 47.97%) is lower than the coefficient of variation obtained when considering the three mean ${\widehat{k}}_b$ values adjusted with SE (78.65%). This means that three replications of the bottle test are not enough, i.e., there is some additional uncertainty due to the low representativeness of the samples.

4. Discussion

Results from Section 3 show that the bulk decay coefficient varies with the water source. The average bulk decay coefficient considering triplicate bottle tests is 0.0737 1/h (source A, surface water), 0.0136 1/h (source B, groundwater), and 0.0057 1/h (source C, groundwater) for the three-treatment works, respectively. These results reinforce the idea that $k_b$ increases with TOC (e.g., [15,18]). In this case, high TOC values correspond to surface water (A), but additional tests should be carried out at different locations to validate that this is always the case. For high $k_b$ values (A), the curvature of the exponential function is better defined, and chlorine values steadily approximate 0 mg/L without any outliers. This happens because chlorine measurements clearly decrease from time to time during the bottle test. However, for low $k_b$ values (B and C), the curvature is less defined, and chlorine values may not even reach 0 mg/L within a reasonable bottle test duration (<250–300 h). Since measurement values do not change clearly over time, the methodology depicted in Figure 2 (which includes measurement replication, state estimation, uncertainty quantification, outlier detection, and revision of pseudomeasurement assumptions) is essential for processing bottle test data from this type of water source. We must acknowledge that, based on the results, it seems that very low TOC values seem to be associated with very low bulk coefficients (as in treatment works C). This implies that chlorine will decay slowly through the network, and so the risk of falling below the recommended 0.2 mg/L free chlorine threshold will be low. The proposed methodology enables the identification of this type of water source by systematically computing the uncertainty of the bulk decay coefficient.

It should be noted that estimated bulk decay coefficients are associated with a non-negligible standard deviation (and CV). The average CV (according to ${\widehat{k}}_b$ SE results) considering triplicate bottle tests are 15.27%, 22.12% and 47.97% for sources A (surface water) and B/C (groundwater), respectively. The CV of grab sample B is higher than A mainly because of the need to increase the assumed standard deviation for the final concentration of the model, a decision that comes determined by chlorine measurements evolution over the bottle test, which do not tend to zero in the time window considered. The CV of grab sample C is even greater due to the low repeatability of bottle tests in water samples with low content of organic matter. Figure 7 summarizes bottle test chlorine measurements, adjusted first-order bulk decay models, and associated confidence intervals for grab samples A (Figure 7a), B (Figure 7b), and C (Figure 7c). Figure 7a presents a greater dispersion at the beginning of the bottle test due to the assumed high standard deviation for ICC (see Table 1). Figure 7b presents a greater dispersion at the end of the bottle test because of the increased standard deviation for $C_{f,model}$. Figure 7c presents a greater dispersion in between due to the additional sampling uncertainty. There is some degree of overlap in all of them.

High standard deviations for $k_b$ happen because, as proved by the triplicate bottle tests, the chemical reaction of chlorine does not always happen in the exact same way. This is especially noticeable when there is a low content of organic matter. Figure 7 highlights these differences by representing results for each replicate bottle test in different colors (black for E01, blue for E02, red for E03). Chlorine decays over time in different ways due to factors that are not included in the assumed model, which is not perfect. Also, sodium hypochlorite is known to experience instabilities (e.g., [41,42]), and this adds complexity to the chemical reaction. This work has proved that deviations are intrinsic to chlorine decay processes when they happen in bottles in a laboratory (controlled environment). Additional factors interact in service reservoirs or network tanks (e.g., irregular agitation, poorly preserved reactive agents, etc.). This does not mean that bottle tests should be systematically replicated in practice to estimate the associated dispersion, but it underscores that specific procedures (like state estimation and uncertainty assessment) should be implemented to process the results of a single bottle test. In this work, we have repeated each experiment three times to validate that the resulting $k_b$ distributions overlap, and so the methodology is consistent to identify the potential range of $k_b$. Our recommendation is to carry out only one bottle test with several replicate chlorine measurements at each time, and then quantify the uncertainty of $k_b$ with an appropriate statistical fitting process, as conceptually illustrated in Figure 1.

The most interesting aspect of the presented methodology is that the state estimation approach tracks the uncertainty of all involved variables regardless of the model adopted or the measurements available. This is crucial because results show that the uncertainty of the bulk decay coefficient is non-negligible, even with measurement replications, which reduce measurement error effects. The uncertainty of the bulk decay coefficient depends on the number of replications. The method presented in this work can be applied to compute the most likely value of $k_b$ with less data, without replications, or with fewer measurements over time, quantifying the impact of each of these scenarios in terms of uncertainty. Applying a standard statistical fit process to bottle test data without quantifying the associated uncertainty (traditional bottle test approach) may lead to bulk decay coefficients that are apparently inconsistent. The fact that a consistent procedure to compute the bulk decay coefficient has not been applied before could partly explain the wide range of bulk decay coefficient values registered for different water sources and/or temperatures in the past [18,20]. The CVs above 15% obtained here underscore that uncertainty is noticeable and should be considered when analyzing temporal shifts in $k_b$, for example, due to potential mixtures of water sources, seasonal variability, temperature changes, etc. Disregarding this uncertainty may lead to false conclusions. It should also be considered when evaluating chlorine decay at the wall, which is typically computed as the difference between the total decay and the modeled bulk decay [17,23]. This could, in turn, be useful to better understand biofilm formation and detachment processes [37,40]. The methodology presented here is developed to explain part of the observed behavior and is aligned with the general effort that is currently being made to systematically process and understand water quality data/dynamics in water distribution systems (e.g., [6,60,61,62,63,64]). At this stage, the proposed approach should be regarded as a methodology rather than a practical tool, requiring expert analysis and interpretation of results (research domain). More research is needed before establishing practical recommendations for implementation. For example, the methodology should be applied to a wider range of water compositions (beyond A, B, and C) and different chlorine measurement technologies/procedures (other than KEMIO and the proposed bottle test with replications). Moreover, all uncertainty sources should be mapped and their impacts assessed. In any case, this framework—combining state estimation and uncertainty assessment—has the potential to evolve into an operational tool for water utilities (knowledge transfer to industry) once the chlorine decay process is better understood.

5. Conclusions

This work highlights the importance of measurement uncertainty when computing the bulk chlorine decay coefficient $k_b$. Moreover, it provides a methodology to statistically fit the bulk chlorine decay coefficient $k_b$ (mean and standard deviation) from the bottle test results. The process starts by carrying out bottle tests (standard practice in the field) with replicate measurements. Then, state estimation is used to compute the mean value of the bulk decay coefficient by combining bottle test free chlorine measurements, a decay model (in this case, first-order bulk decay), and some a priori estimations or pseudomeasurements. The uncertainty (i.e., standard deviation) of all variables is then quantified by implementing the FOSM method, which enables computation of confidence intervals that can be used to identify measurement outliers and/or incorrect assumptions.

The method is applied to statistically fit the bulk decay coefficient at three treatment works (A, B, and C). Results (for triplicate bottle tests) validate the method and show that $k_b$ presents non-negligible uncertainty in some cases (>15%). The uncertainty of the bulk decay coefficient increases in this work for groundwater grab samples, which are associated with a lower content of organic matter. Computed $k_b$ standard deviations could further increase depending on the sampling strategy, measurement principle, etc. The state estimation approach presented in this work is designed to cope with a wide range of scenarios, assumptions, and/or models, so it provides a systematic methodology to effectively analyze and compare (considering uncertainty) bulk decay coefficients from different sources, at different moments, with different temperatures, etc. This approach may play a crucial role in explaining the variability of the bulk decay coefficient reported in previous works and could be essential to understand, monitor, and/or model chlorine decay at water supply systems.