Water and Salt Transport and Balance in Saline Soils Under Different Land Use Types in the Seasonally Frozen Zone of Songnen Plain
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area Overview
2.2. Data Collection
2.3. HYDRUS-3D Model Principles
2.3.1. Model Equations
Soil Water Transport Equation
Soil Heat Transport Equation
Soil Salinity Transport Equation
Root Water Uptake Equation
2.3.2. Model Initial and Boundary Conditions
Initial Conditions
Boundary Conditions
- (1)
- Upper Boundary Condition
- (2)
- Lower Boundary Condition
- (3)
- Other Boundary Surfaces
2.3.3. Model Evaluation Criteria
2.4. Soil Water–Salt Balance Equation
2.4.1. Soil Water Balance Equation
2.4.2. Soil Salt Balance Equation
3. Results and Discussion
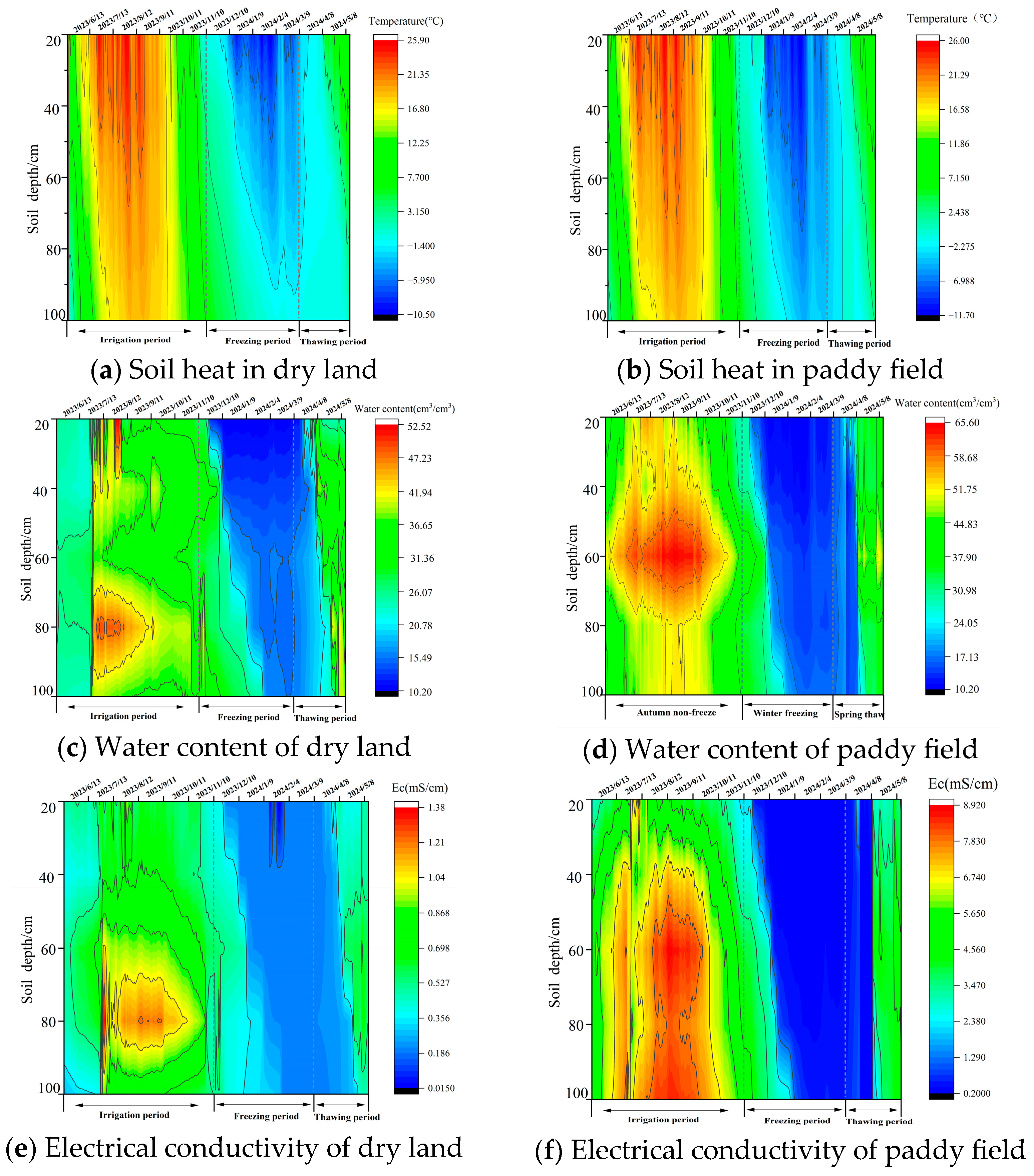
3.1. Dynamics of Soil Water, Heat, and Salinity Under Different Cropland Types
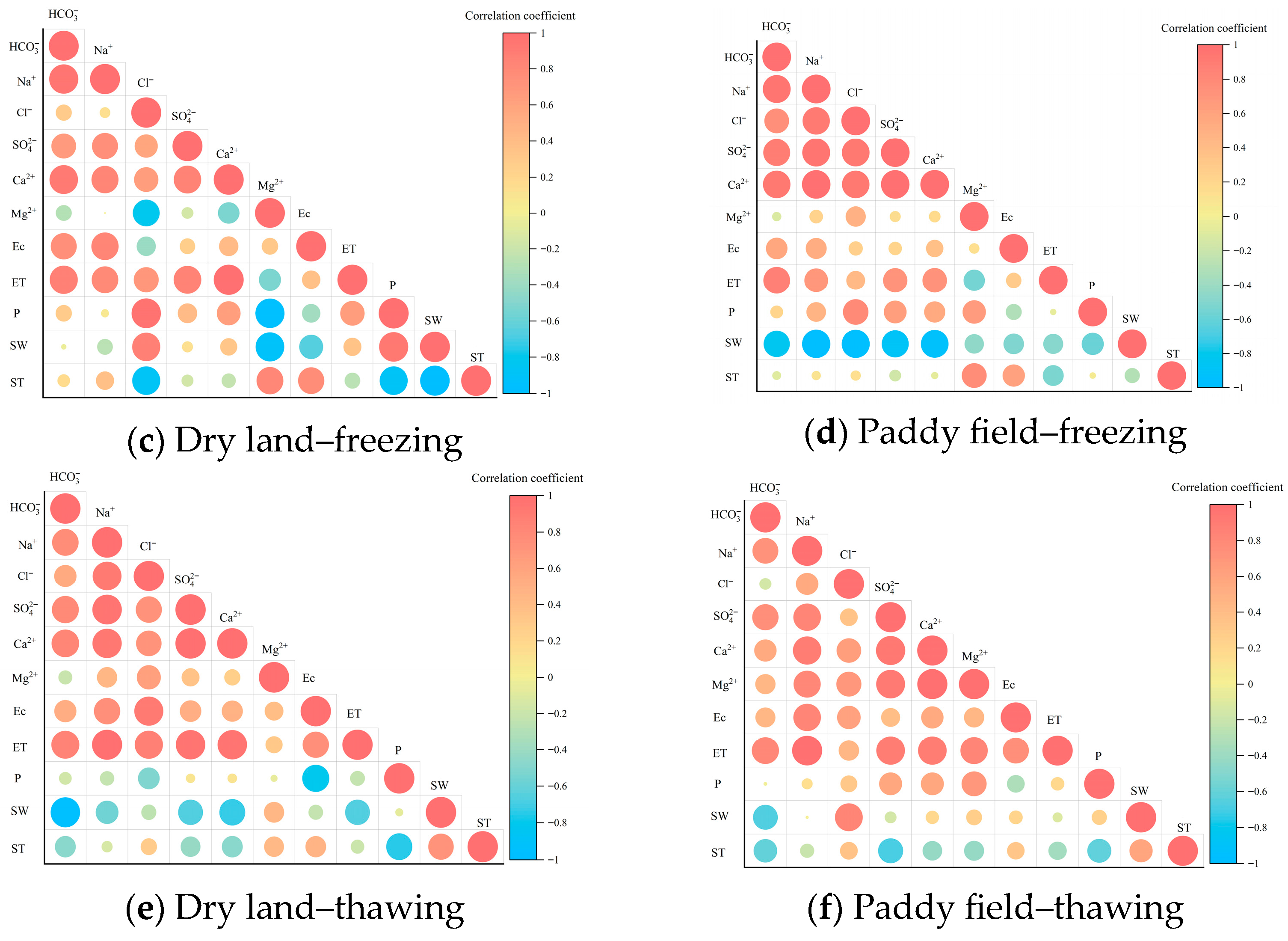
3.2. Correlation of Soil Water and Salinity by Cropland Type
3.3. Simulation of Soil Water and Salt Dynamics Across Cropland Types
3.3.1. Model Setup and Spatiotemporal Discretization
3.3.2. Model Parameter Calibration
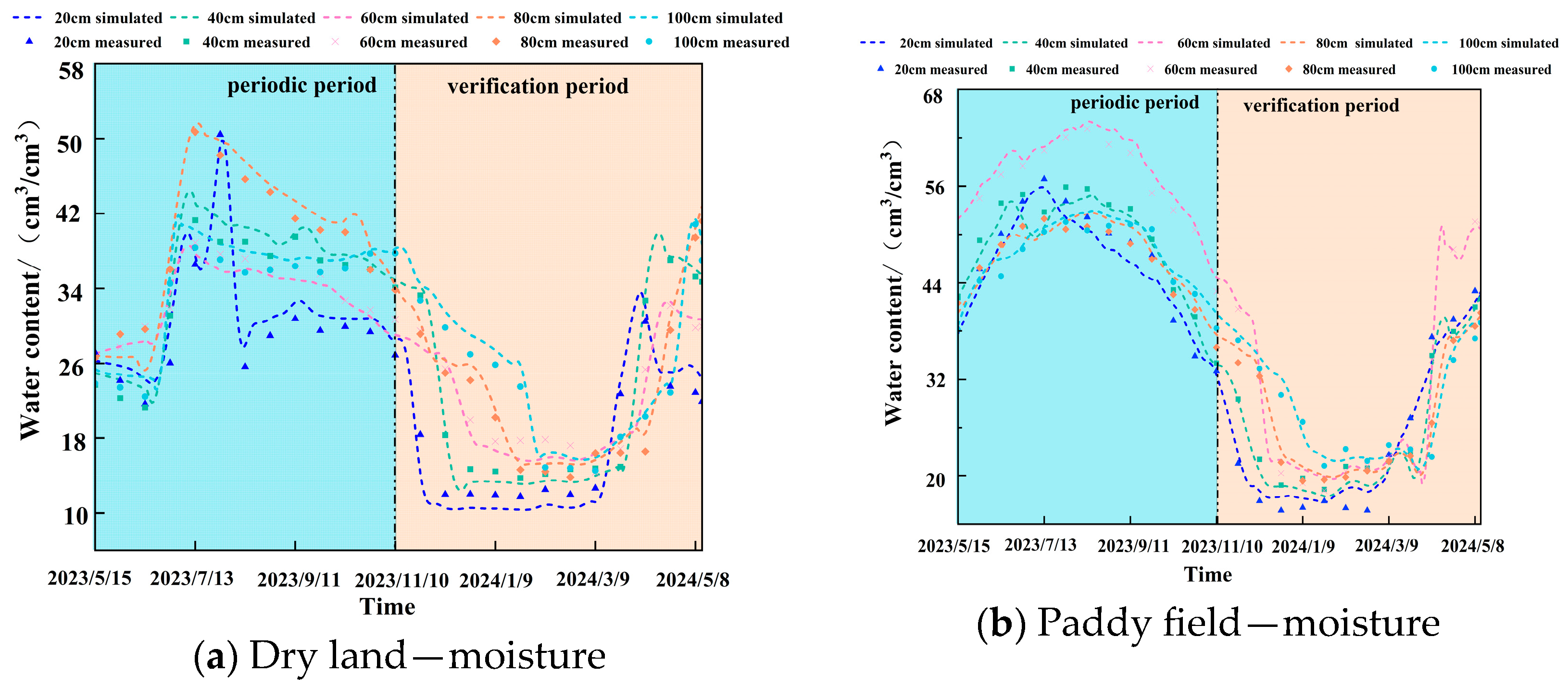
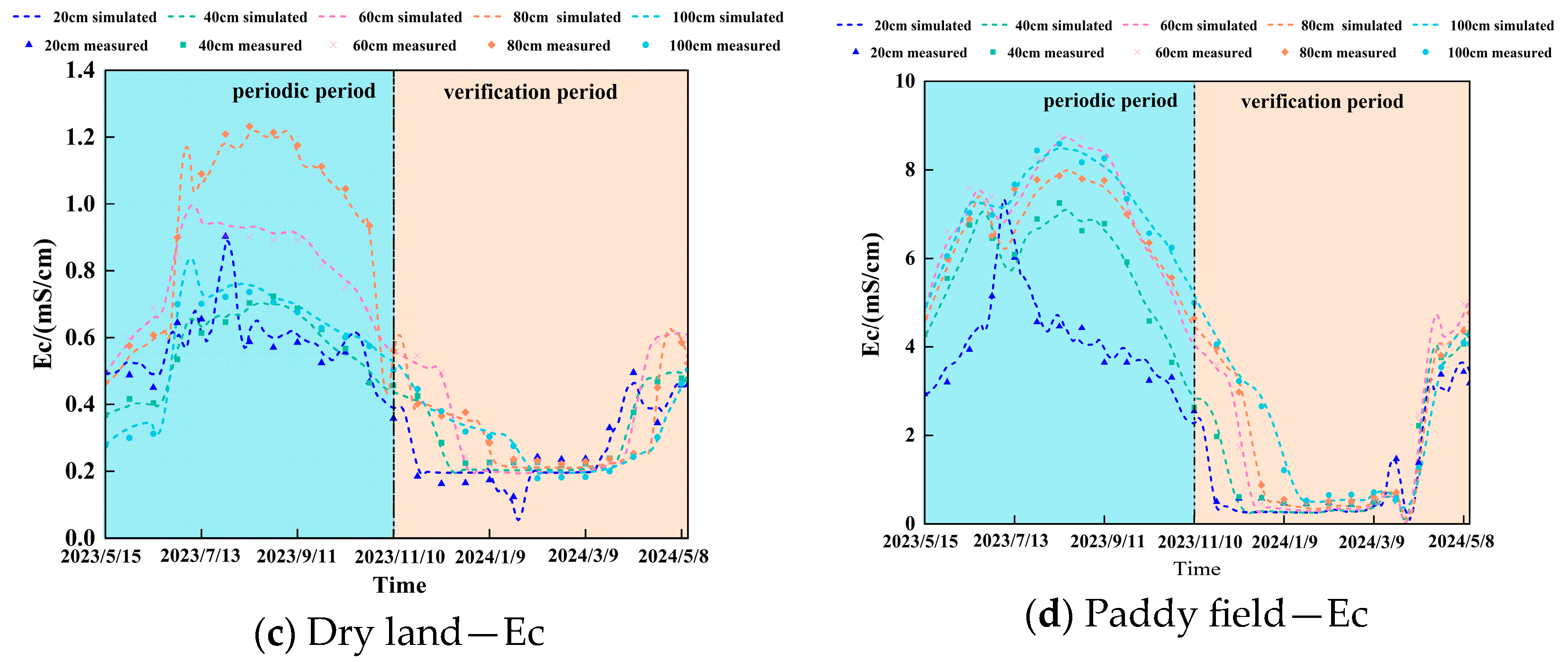
3.3.3. Model Calibration and Validation
3.3.4. Analysis of Simulation Results
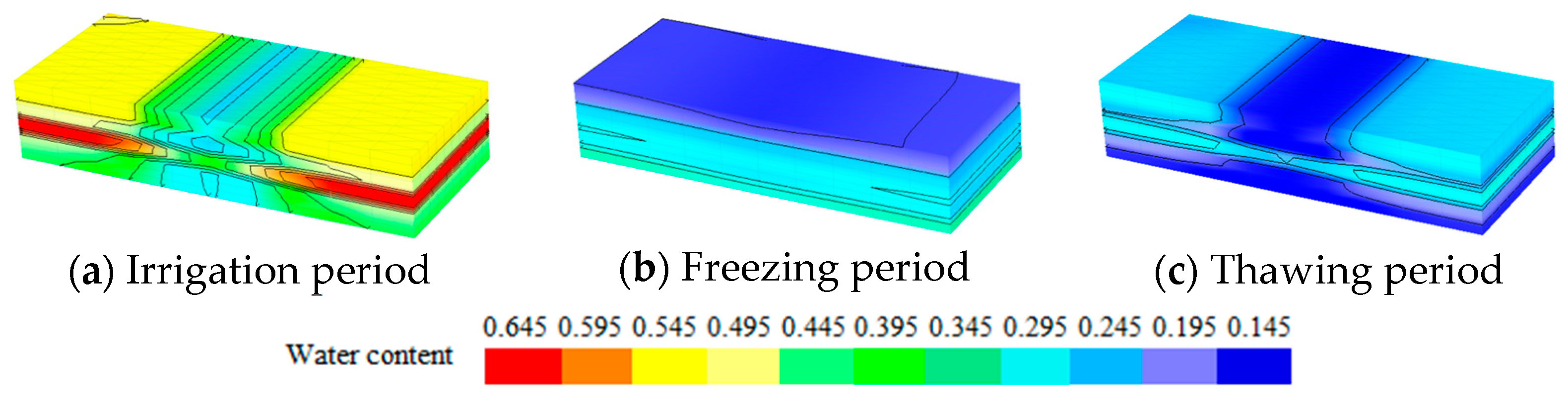
Simulation of Soil Water Dynamics
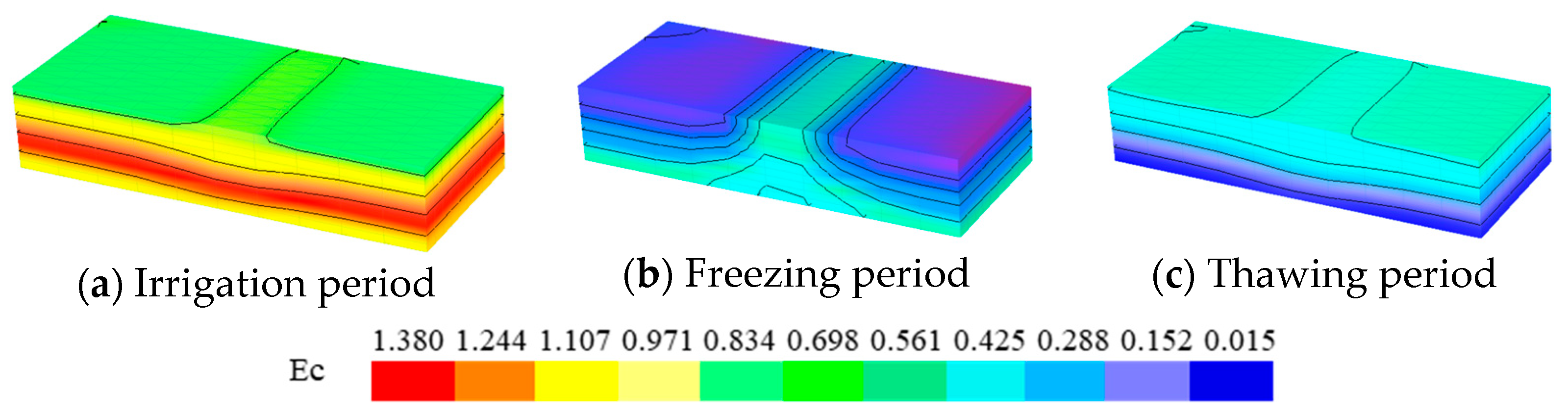
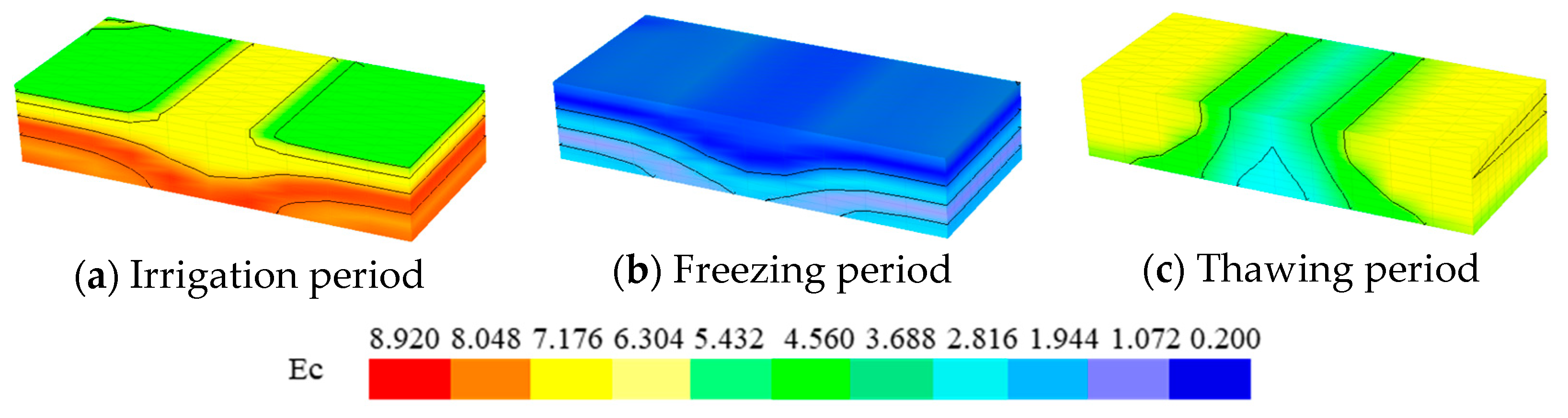
Simulation of Soil Salinity Dynamics
3.4. Water and Salt Dynamics in Saline Soils by Cropland Type
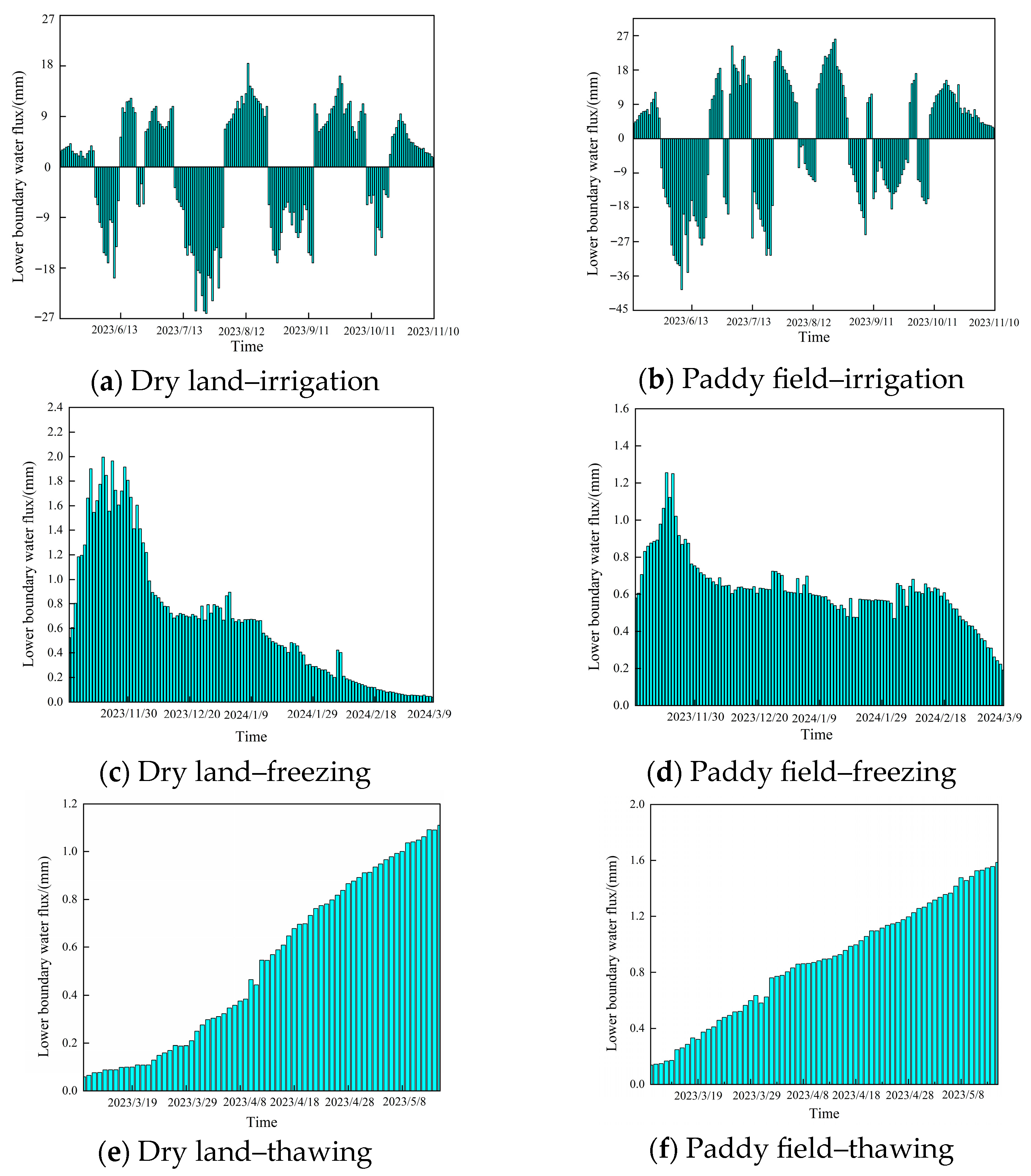
3.4.1. Water and Salt Fluxes at the Soil Profile Lower Boundary
3.4.2. Calculation of Soil Water and Salt Balance
4. Conclusions
- (1)
- During the irrigation period, peak soil water content and electrical conductivity (Ec) occurred at 80 cm in dryland fields and at 60 cm (water content) and 60–100 cm (Ec) in paddy fields. During the freezing period, soil water content and Ec decreased sharply across all depths with no significant stratification, and the Ec decline was more pronounced in paddy fields. In the thawing period, soil water content, Ec, and heat all showed increasing trends without apparent vertical heterogeneity. Over the full year, paddy fields exhibited higher Ec values than dryland fields, while both field types showed similar vertical distributions of soil heat.
- (2)
- Correlation analysis revealed that the main driving factors of soil salinization during the irrigation period were HCO3−, Na+, precipitation (P), and evapotranspiration (ET) in dryland fields, and HCO3−, Na+, and soil water content (SW) in paddy fields. During the freezing period, the dominant factors in both field types were HCO3−, Na+, SW, and soil temperature (ST). During the thawing period, the primary drivers were HCO3−, Na+, P, and ET in dryland fields, and HCO3−, Na+, and ET in paddy fields.
- (3)
- The HYDRUS-3D model simulated temporal patterns of water–salt transport and bottom boundary fluxes. In saline dryland fields, the bottom boundary water and salt fluxes were −54.68 mm and −565.4 kg/hm2 (irrigation), +79.26 mm and +326.85 kg/hm2 (freezing), and +35.51 mm and +376.55 kg/hm2 (thawing). In saline paddy fields, these values were −112.5 mm and −1217.0 kg/hm2 (irrigation), +74.54 mm and +280.07 kg/hm2 (freezing), and +58.9 mm and +299.35 kg/hm2 (thawing).
- (4)
- Based on bottom boundary water and salt fluxes simulated by the HYDRUS-3D model, the seasonal soil water–salt balance was quantitatively assessed for saline dry land and paddy fields. During the irrigation period, paddy fields achieved significant salt leaching, with a desalinization magnitude 3.36 times greater than that of dry lands. In the freezing period, the water storage in paddy soils was 1.94 times higher than in dry lands, while salt accumulation in dry lands exceeded that in paddy fields by 17%. During the thawing period, previously accumulated salts migrated upward as thawing progressed. Enhanced evaporation in dry lands led to secondary salinization, with water loss 1.61 times and salt accumulation 1.3 times that of paddy fields.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, Y.; Tashpolat, N. Current Status and Development Trend of Soil Salinity Monitoring Research in China. Sustainability 2023, 15, 5874. [Google Scholar] [CrossRef]
- Luo, P.; Zhao, L.; Chen, R.; Chen, P.; Dhital, Y.P.; Li, H.; Wang, D.; Yang, J.; Chen, Y.; Liu, Q.; et al. Leaching Salinity and Mulching Straws during Freeze-Thaw Period Enhance Post-Thawing Cotton Yield and Quality by Optimizing Soil Aggregates Stability. Soil Tillage Res. 2025, 250, 106506. [Google Scholar] [CrossRef]
- Yu, M.; Rui, X. Water and Salt Balance Model and Its Application in Yinbei Irrigation District, Ningxia. J. Hohai Univ. (Nat. Sci. Ed.) 2009, 37, 367–372. [Google Scholar] [CrossRef]
- Mao, J.; Wu, J.; Liu, Y.; Guo, C.; Xiao, C.; Lu, Y.; Zhao, L.; Zhang, R.; Zhang, H. A Model for Simulating Evaporation from Seasonally Frozen Saline Soil. J. Hydrol. 2025, 659, 133259. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, H.; Mo, Q.; Zhuo, C. Application of Hydrus-2D Model in Subsurface Drainage of Saline Soil in Coastal Forest Land-A Case Example of Fengxian, Shanghai. Sustainability 2024, 16, 4590. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, Y.; Huang, L.; Fang, R.; Liu, S.; Liu, T.; Huang, B. Effects of the Hydrolysis of Mudstone on Soil Infiltration: Experiments versus Numerical Modelling. J. Hydrol. 2025, 660, 133254. [Google Scholar] [CrossRef]
- Casillas-Trasvina, A.; Meles, M.B.; Cui, W.; Hatch, T.; Bradford, S.; Harter, T. Integrated Hydrologic Modeling of Groundwater Flow Dynamics and Recharge in the San Joaquin Valley. J. Hydrol. 2025, 660, 133377. [Google Scholar] [CrossRef]
- Jiang, J.; Feng, S.; Ma, J.; Huo, Z.; Zhang, C. Irrigation Management for Spring Maize Grown on Saline Soil Based on SWAP Model. Field Crops Res. 2016, 196, 85–97. [Google Scholar] [CrossRef]
- Xun, Y.; Xiao, X.; Sun, C.; Meng, H.; Gao, Y.; Huang, G.; Xu, X. Modeling Heat-Water-Salt Transport, Crop Growth and Water Use in Arid Seasonally Frozen Regions with an Improved Coupled SPAC Model. J. Hydrol. 2022, 615, 128703. [Google Scholar] [CrossRef]
- Yuan, C.; Feng, S.; Huo, Z.; Ji, Q. Simulation of Saline Water Irrigation for Seed Maize in Arid Northwest China Based on SWAP Model. Sustainability 2019, 11, 4264. [Google Scholar] [CrossRef]
- Yuan, C. Simulation of Water-Salt Transport and Balance in Cultivated-Wasteland System Based on SWAP Model in Hetao Irrigation District of China. Agric. Water Manag. 2024, 305, 109132. [Google Scholar] [CrossRef]
- Wang, Z.; Heng, T.; Li, W.; Zhang, J.; Yang, B.; Jiang, Y. Effects of Drainage Tile Spacing on Soil Salt Leaching under Drip Irrigation. Trans. Chin. Soc. Agric. Mach. 2017, 48, 253–261. [Google Scholar] [CrossRef]
- Li, J.; Huang, S.; Jiang, Z.; Xin, L.; Liu, X. Study on Soil Water and Salt Transport in Shallow-Buried Film Mulched Drip-Irrigated Maize Fields Based on HYDRUS-2D. Water-Saving Irrig. 2025, 6, 82–89. [Google Scholar] [CrossRef]
- He, X.; Liu, H.; Ye, J.; Yang, G.; Li, M.; Gong, P.; Aimaiti, A. Comparative Investigation on Soil Salinity Leaching under Subsurface Drainage and Ditch Drainage in Xinjiang Arid Region. Int. J. Agric. Biol. Eng. 2016, 9, 109–118. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, S.; Xu, D.; Qu, X. Experiment and Analysis on Flow Rate of Improved Subsurface Drainage with Ponded Water. Agric. Water Manag. 2016, 177, 1–9. [Google Scholar] [CrossRef]
- Hou, M.; Zhu, L.; Jin, Q. Surface Drainage and Mulching Drip-Irrigated Tomatoes Reduces Soil Salinity and Improves Fruit Yield. PLoS ONE 2016, 11, e0154799. [Google Scholar] [CrossRef]
- Jia, H.; Li, B.; Li, W. Simulation of water and salt transport under combined irrigation and drainage based on HYDRUS-1D model. Water Sav. Irrig. 2021, 1, 27–32. [Google Scholar]
- Hansson, K.; Simunek, J.; Mizoguchi, M.; Lundin, L.C.; van Genuchten, M.T. Water Flow and Heat Transport in Frozen Soil: Numerical Solution and Freeze-Thaw Applications. Vadose Zone J. 2004, 3, 693–704. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Z.; Cheng, H.; Zhu, X.; Huang, H.; Li, Z. Simulation of Field Water and Salt Transport under Ridge Irrigation Mode Based on HYDRUS-3D. Hydropower Water Resour. Technol. 2021, 52, 14–22. [Google Scholar] [CrossRef]
- Yan, Y.; Shi, H.; Miao, Q.; Wang, G.; Su, Y.; Yang, S. Analysis of Water and Salt Transport and Balance among Different Land Types in the Yellow River Irrigation District Based on a Dry Drainage Salt Control Model. Trans. Chin. Soc. Agric. Mach. 2024, 55, 346–359. [Google Scholar]
- Wang, G. Study on Water and Salt Transport and Salt Redistribution among Different Land Types in the Hetao Irrigation District. Ph.D. Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2022. [Google Scholar]
- Shao, J.; Li, S.; Yang, X.; Zhang, F.; Yang, H.; Peng, Z.; Zulfiqar, T. Evaluating Soil Salinity Dynamics under Drip Irrigation in the Manas River Basin, Xinjiang: A Long-Term Analysis (1996–2019). PeerJ 2025, 13, e19295. [Google Scholar] [CrossRef]
- Sun, W.; Shi, H.; Li, X.; Miao, Q.; Feng, Z.; Su, H. Simulation of Water Flux and Irrigation Schedule Optimization in Typical Sand-layered Farmland in Hetao Irrigation District. Trans. Chin. Soc. Agric. Mach. 2025, 56, 639–652. [Google Scholar] [CrossRef]
- Liu, J. Study on Water and Salt Transport and Plant Response Under Microtopography in the Soda Saline-Alkali Soil Region of the Songnen Plain. Master’s Thesis, University of Chinese Academy of Sciences (Northeast Institute of Geography and Agroecology, Chinese Academy of Sciences), Changchun, China, 2021. [Google Scholar] [CrossRef]
- Shi, Q. Experimental Study on Water and Salt Distribution Characteristics and Transport Simulation in the Da’an Irrigation District. Master’s Thesis, Changchun Institute of Technology, Changchun, China, 2024. [Google Scholar] [CrossRef]
- Li, S. Distribution Characteristics and Ecological Risk Assessment of Fluorine in the Da’an Irrigation District. Master’s Thesis, Liaoning Technical University, Fuxin, China, 2024. [Google Scholar] [CrossRef]
- Wang, X. Jilin Implements the “Ten Billion Jin Grain” Production Capacity Construction Project to Strive for the Vanguard of Agricultural Modernization. Rural Work Commun. 2023, 5, 55–56. [Google Scholar]
- Shi, Z. Effects of Freeze-Thaw Cycles on Dispersivity of Saline Soil in Western Jilin and Improvement Methods. Master’s Thesis, Jilin University, Changchun, China, 2021. [Google Scholar] [CrossRef]
- Li, J. Study on Water and Salt Transport Characteristics of Dispersive Saline Soil in Da’an Area, Jilin Province. Master’s Thesis, Jilin Jianzhu University, Changchun, China, 2024. [Google Scholar] [CrossRef]
- Chen, W.; Xu, S.; Sheng, T.; Ferre, T.P.A.; Zhu, Q.; He, Y.; Liu, Y. Numerical Simulations of Soil Water-Salt Movement Considering the Dynamics of Cotton Fine Root Growth under Film-Mulched Drip Irrigation. J. Hydrol. 2024, 638, 131543. [Google Scholar] [CrossRef]
- Guo, L.; Wang, Z.; Simunek, J.; He, Y.; Muhamma, R. Optimizing the Strategies of Mulched Brackish Drip Irrigation under a Shallow Water Table in Xinjiang, China, Using HYDRUS-3D. Agric. Water Manag. 2023, 283, 108303. [Google Scholar] [CrossRef]
- Zheng, C.; Šimůnek, J.; Zhao, Y.; Lu, Y.; Liu, X.; Shi, C.; Li, H.; Yu, L.; Zeng, Y.; Su, Z. Development of the Hydrus-1D Freezing Module and Its Application in Simulating the Coupled Movement of Water, Vapor, and Heat. J. Hydrol. 2021, 598, 126250. [Google Scholar] [CrossRef]
- Zhao, Y.; Si, B.; He, H.; Xu, J.; Peth, S.; Horn, R. Modeling of Coupled Water and Heat Transfer in Freezing and Thawing Soils, Inner Mongolia. Water 2016, 8, 424. [Google Scholar] [CrossRef]
- Bian, J.; Wu, J.; Nie, S.; Wang, Y.; Lin, X. The Parametric Uncertainty Estimation of Water and Nitrogen Transport Simulation in a Paddy Field Experiment Using HYDRUS-1D. Irrig. Drain. 2023, 72, 451–464. [Google Scholar] [CrossRef]
- Hou, C.; Shi, H.; Miao, Q.; Hu, Z.; Zhao, Y.; Yu, C.; Yan, Y.; Fan, L.; Zhang, T. Hydrochemical Characteristics of Groundwater and Water-Salt Transport in Different Land Types in Hetao Irrigation District. Arid Zone Res. 2024, 41, 1956–1968. [Google Scholar] [CrossRef]
- Ma, G.; Qu, Z.; Feng, X.; Wang, L.; Li, E.; Jin, C. Analysis of Water-Salt Balance Before and After Saline-Alkali Land Reclamation: A Case Study of Hetao Irrigation District. J. Irrig. Drain. 2021, 40, 95–103. [Google Scholar] [CrossRef]
- Gao, H.; Liu, X.; Gao, X.; Qu, Z. Transport law and balance analysis of salt and ions in salinized soil under different irrigation and drainage patterns. J. Soil Water Conserv. 2023, 37, 361–370. [Google Scholar] [CrossRef]





| Farmland Type | Soil Depth /(cm) | Grain Content/% | Bulk Density/(g/cm3) | Soil Type | ||
| Sand | Silt | Clay | ||||
| Dry land | 0–20 | 2.34 | 81.13 | 16.53 | 1.483 | Silt loam |
| 20–40 | 0.52 | 80.05 | 19.43 | 1.483 | Silty loam | |
| 40–60 | 2.2 | 76.34 | 21.46 | 1.517 | Silty loam | |
| 60–80 | 0.48 | 74.8 | 24.72 | 1.417 | Silty loam | |
| 80–100 | 0 | 70.86 | 29.14 | 1.617 | Silty clay loam | |
| Paddy field | 0–20 | 4.03 | 82.45 | 13.52 | 1.567 | Silty loam |
| 20–40 | 0.02 | 82.75 | 17.23 | 1.593 | Silty loam | |
| 40–60 | 0.02 | 71.26 | 28.72 | 1.450 | Silty clay loam | |
| 60–80 | 0.64 | 81.38 | 17.98 | 1.610 | Silty loam | |
| 80–100 | 0.02 | 79.95 | 20.03 | 1.682 | Silty loam | |
| Soil Depth/(cm) | 0–20 cm | 20–40 cm | 40–60 cm | 60–80 cm | 80–100 cm | |
| Dry land | SWC/(cm3·cm−3) | 0.267 | 0.250 | 0.275 | 0.274 | 0.254 |
| Ec/(mS/cm) | 0.513 | 0.382 | 0.512 | 0.468 | 0.279 | |
| SAR | 8.97 | 12.68 | 11.8 | 12.35 | 15.32 | |
| pH | 7.51 | 7.63 | 7.72 | 7.92 | 7.93 | |
| Organic matter/% | 2.190 | 1.038 | 1.306 | 1.076 | 0.620 | |
| Paddy field | SWC/(cm3·cm−3) | 0.351 | 0.391 | 0.486 | 0.362 | 0.342 |
| Ec/(mS/cm) | 3.070 | 4.441 | 4.930 | 4.714 | 5.010 | |
| SAR | 94.11 | 46.55 | 78.64 | 55.43 | 48.92 | |
| pH | 8.39 | 8.48 | 8.43 | 8.45 | 8.45 | |
| Organic matter/% | 0.562 | 0.398 | 0.413 | 0.563 | 0.624 | |
| Farmland Type | Soil Depth /(cm) | Content of the Eight Major Ions/(mg/kg) | |||||||
| CO32− | HCO3− | Cl− | SO42− | Na+ | Mg2+ | K+ | Ca2+ | ||
| Dry land | 0–20 | 0.0 | 698.8 | 88.8 | 105.3 | 165.5 | 20.1 | 17.2 | 95.4 |
| 20–40 | 0.0 | 685.4 | 88.8 | 90.2 | 221.7 | 14.2 | 12.9 | 92.2 | |
| 40–60 | 0.0 | 779.4 | 117.2 | 97.8 | 238.3 | 12.5 | 10.6 | 111.3 | |
| 60–80 | 66.1 | 1317.0 | 110.1 | 89.1 | 376.2 | 17.2 | 4.4 | 203.3 | |
| 80–100 | 33.1 | 1068.3 | 113.6 | 84.9 | 339.9 | 14.9 | 3.1 | 104.2 | |
| Paddy field | 0–20 | 3145.9 | 1343.8 | 3809.2 | 1364.2 | 3687.8 | 10.1 | 2.0 | 31.7 |
| 20–40 | 1639.0 | 1437.9 | 1047.3 | 557.8 | 1759.4 | 17.8 | 2.6 | 201.5 | |
| 40–60 | 1652.3 | 1343.8 | 1047.3 | 405.1 | 1543.2 | 7.7 | 1.3 | 75.4 | |
| 60–80 | 1321.8 | 2244.2 | 1054.4 | 700.2 | 2332.9 | 25.1 | 3.6 | 250.8 | |
| 80–100 | 1321.8 | 2163.6 | 1086.3 | 650.4 | 2156.7 | 23.1 | 2.9 | 271.0 | |
| Farmland Type | Ec/(mS/cm) | Na+/(mg/L) | HCO3−/(mg/L) | Cl−/(mg/L) |
| Dry land | 0.85 | 20.13 | 135.66 | 31.95 |
| Paddy field | 1.44 | 166.52 | 342.37 | 82.36 |
| Farmland Type | Soil Depth /(cm) | Content of the Eight Major Ions/(mg/kg) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| θr /(cm3/cm3) | θs /(cm3/cm3) | α /(cm−1) | n | l | Ks /(cm/day) | DL /(cm) | DT /(cm) | ||
| Dry land | 0–20 | 0.0698 | 0.4587 | 0.0061 | 1.62 | 0.5 | 12.6 | 7.69 | 1.13 |
| 20–40 | 0.0744 | 0.4408 | 0.0063 | 1.60 | 0.5 | 9.36 | 7.8 | 1.2 | |
| 40–60 | 0.0708 | 0.4279 | 0.0064 | 1.59 | 0.5 | 7.74 | 9.35 | 1.8 | |
| 60–80 | 0.0819 | 0.5250 | 0.0066 | 1.58 | 0.5 | 9.25 | 4.47 | 0.56 | |
| 80–100 | 0.0794 | 0.4126 | 0.0077 | 1.50 | 0.5 | 2.86 | 14.23 | 1.86 | |
| Paddy field | 0–20 | 0.0614 | 0.5672 | 0.0066 | 1.60 | 0.5 | 11.94 | 11.79 | 1.54 |
| 20–40 | 0.0677 | 0.5650 | 0.0068 | 1.57 | 0.5 | 6.53 | 13.06 | 2.45 | |
| 40–60 | 0.0812 | 0.6458 | 0.0075 | 1.52 | 0.5 | 3.74 | 6.08 | 0.85 | |
| 60–80 | 0.0672 | 0.5669 | 0.0069 | 1.56 | 0.5 | 5.76 | 13.89 | 2.66 | |
| 80–100 | 0.0672 | 0.5643 | 0.0073 | 1.52 | 0.5 | 3.72 | 17.40 | 3.94 | |
| Cropland Type | Cultivated Crop | h0 (cm) | hopt (cm) | h2H (cm) | h2l (cm) | H3 (cm) |
|---|---|---|---|---|---|---|
| Dry land | Maize | −15 | −30 | −325 | −600 | −8000 |
| Paddy field | Rice | −10 | −55 | −160 | −250 | −15,000 |
| Cropland Type | Soil Depth /(cm) | Soil Moisture Content | Soil Salinity | ||||
|---|---|---|---|---|---|---|---|
| RMSE | nRMSE | d | RMSE | nRMSE | d | ||
| Dry land | 0–20 | 0.025 | 7.16 | 0.92 | 0.032 | 5.79 | 0.87 |
| 20–40 | 0.020 | 4.98 | 0.95 | 0.020 | 3.65 | 0.95 | |
| 40–60 | 0.015 | 3.79 | 0.98 | 0.022 | 2.90 | 0.96 | |
| 60–80 | 0.024 | 5.33 | 0.94 | 0.021 | 2.24 | 0.97 | |
| 80–100 | 0.018 | 4.64 | 0.97 | 0.022 | 3.91 | 0.94 | |
| Paddy field | 0–20 | 0.030 | 8.72 | 0.88 | 0.038 | 7.071 | 0.91 |
| 20–40 | 0.025 | 3.61 | 0.93 | 0.025 | 3.486 | 0.95 | |
| 40–60 | 0.025 | 3.14 | 0.94 | 0.027 | 3.121 | 0.92 | |
| 0–20 | 0.025 | 7.16 | 0.92 | 0.032 | 5.79 | 0.87 | |
| 20–40 | 0.020 | 4.98 | 0.95 | 0.020 | 3.65 | 0.95 | |
| Cropland Type | Soil Depth /(cm) | Soil Moisture Content | Soil Salinity | ||||
|---|---|---|---|---|---|---|---|
| RMSE | nRMSE | d | RMSE | nRMSE | d | ||
| Dry land | 0–20 | 0.031 | 15.82 | 0.87 | 0.033 | 11.83 | 0.85 |
| 20–40 | 0.011 | 4.33 | 0.98 | 0.018 | 5.87 | 0.91 | |
| 40–60 | 0.018 | 7.07 | 0.95 | 0.018 | 5.10 | 0.92 | |
| 60–80 | 0.016 | 5.99 | 0.96 | 0.016 | 4.69 | 0.96 | |
| 80–100 | 0.018 | 6.42 | 0.96 | 0.012 | 3.89 | 0.98 | |
| Paddy field | 0–20 | 0.027 | 9.19 | 0.91 | 0.029 | 16.78 | 0.90 |
| 20–40 | 0.023 | 7.33 | 0.93 | 0.026 | 10.21 | 0.92 | |
| 40–60 | 0.015 | 3.99 | 0.98 | 0.017 | 8.62 | 0.93 | |
| 0–20 | 0.015 | 4.68 | 0.97 | 0.015 | 7.47 | 0.91 | |
| 20–40 | 0.023 | 6.54 | 0.94 | 0.016 | 5.80 | 0.96 | |
| Period | Cropland Type | Precipitation (mm) | Irrigation (mm) | Evapotranspiration (mm) | Drainage (mm) | Bottom Water Flux (mm) | Soil Water Change ΔW (mm) |
|---|---|---|---|---|---|---|---|
| Irrigation | Dry land | 445.2 | 71.3 | 480.4 | 0 | −54.68 | −18.58 |
| Paddy field | 445.2 | 397.2 | 523.18 | 145.8 | −112.5 | 60.92 | |
| Freezing | Dry land | 20.83 | 0 | 94.53 | 0 | 79.26 | 5.56 |
| Paddy field | 20.83 | 0 | 84.57 | 0 | 74.54 | 10.8 | |
| Thawing | Dry land | 38.22 | 0 | 118.25 | 0 | 35.51 | −44.52 |
| Paddy field | 38.22 | 0 | 112.39 | 0 | 58.9 | −15.27 |
| Period | Cropland Type | Irrigation Water Salt Load (kg/hm2) | Bottom Salt Flux (kg/hm2) | Return Flow Salt Load (kg/hm2) | Soil Salt Change ΔS (kg/hm2) |
|---|---|---|---|---|---|
| Irrigation | Dry land | 348.5 | −565.4 | 0 | −216.5 |
| Paddy field | 627.8 | −1217.0 | 138.26 | −727.46 | |
| Freezing | Dry land | 0 | 326.85 | 0 | 326.85 |
| Paddy field | 0 | 280.07 | 0 | 280.07 | |
| Thawing | Dry land | 0 | 376.55 | 0 | 376.55 |
| Paddy field | 0 | 299.35 | 0 | 299.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Wang, Y.; Bian, J.; Sun, X.; Wang, Y. Water and Salt Transport and Balance in Saline Soils Under Different Land Use Types in the Seasonally Frozen Zone of Songnen Plain. Water 2025, 17, 2974. https://doi.org/10.3390/w17202974
Chen C, Wang Y, Bian J, Sun X, Wang Y. Water and Salt Transport and Balance in Saline Soils Under Different Land Use Types in the Seasonally Frozen Zone of Songnen Plain. Water. 2025; 17(20):2974. https://doi.org/10.3390/w17202974
Chicago/Turabian StyleChen, Caidie, Yu Wang, Jianmin Bian, Xiaoqing Sun, and Yanchen Wang. 2025. "Water and Salt Transport and Balance in Saline Soils Under Different Land Use Types in the Seasonally Frozen Zone of Songnen Plain" Water 17, no. 20: 2974. https://doi.org/10.3390/w17202974
APA StyleChen, C., Wang, Y., Bian, J., Sun, X., & Wang, Y. (2025). Water and Salt Transport and Balance in Saline Soils Under Different Land Use Types in the Seasonally Frozen Zone of Songnen Plain. Water, 17(20), 2974. https://doi.org/10.3390/w17202974






