Research on the Influence Mechanism of Regulating Capacity and Flow Recession Process in the Karst Vadose Zone
Abstract
1. Introduction
2. Laboratory Experiments
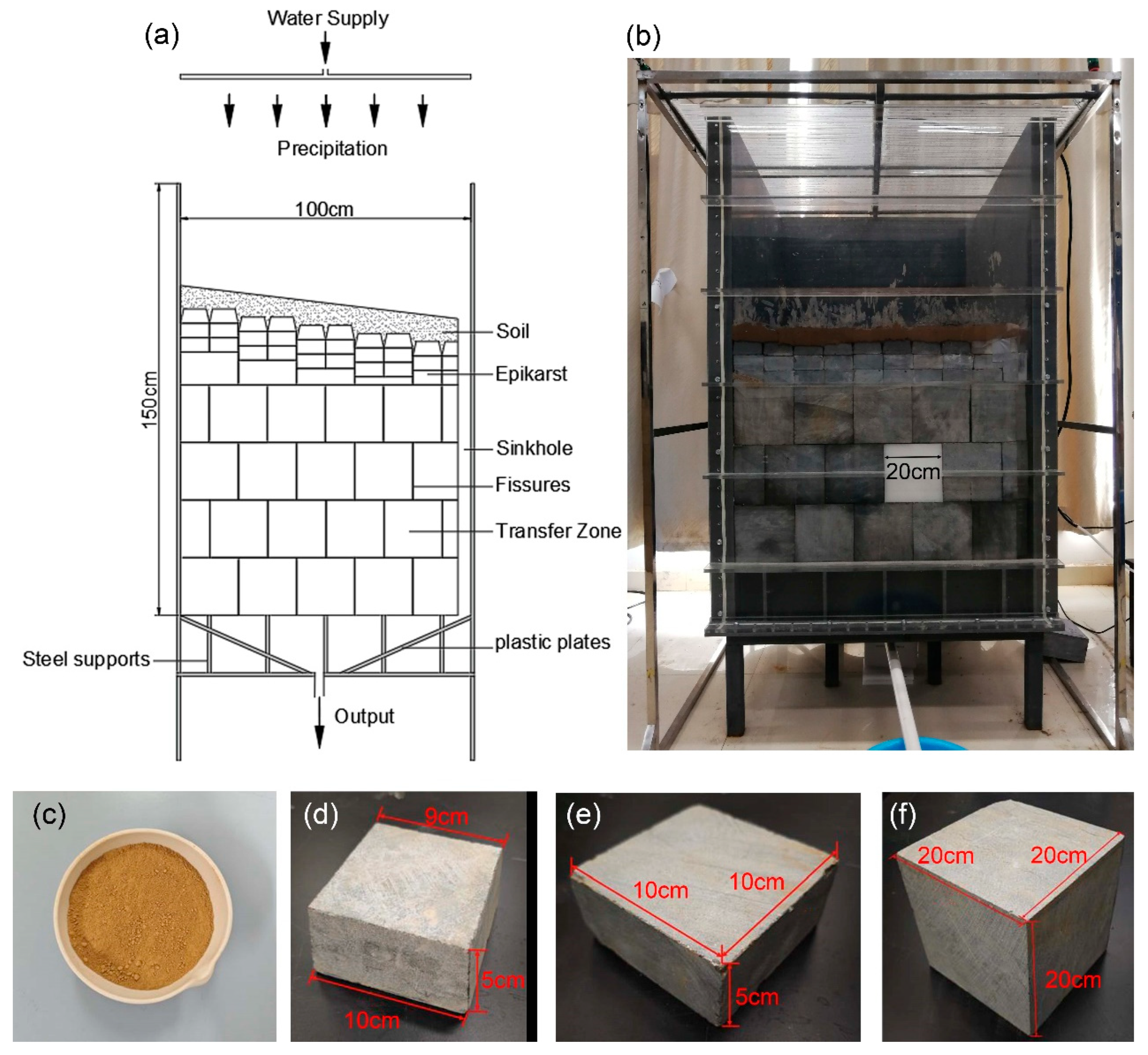
2.1. Experimental Model Setup
2.2. Experimental Design
- 1
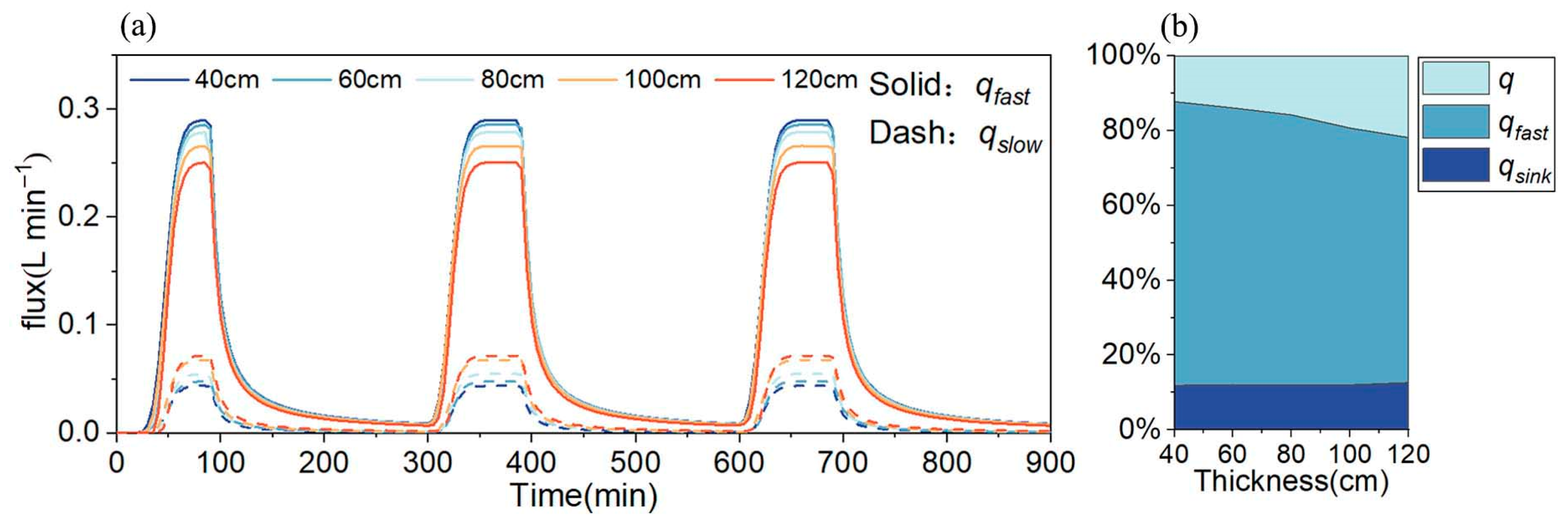
- Transfer zone thickness (Experiments: A1–A5). The vadose zone thickness results from the relative rates of movement of its upper boundary (surface) and lower boundary and it exhibits a wide range of variation, spanning orders of magnitude from meters to kilometers: up to 2000 m below the surface in the Caucasus Mountains [1]; 400–1000 m in the Xianglushan karst system of Yunnan Province, China [17]; around 400 m on the Javorniki–Snežnik Plateau in Slovenia [52]; and less than 10 m in the Chenqi karst system of Guizhou Province, China [53]. In this study, to investigate the influence of the thickness of the karst vadose zone, the thickness of the vadose zone was varied while the thicknesses of the soil layer and the epikarst zone were held constant. The experimental transfer zone thickness was categorized into 40, 60, 80, 100, and 120 cm. Other variables were held constant, with the surface slope set to 0°, the karstification degree set to two fractures, and the rainfall intensity set to 20 mm/h.
- 2
- Surface slope (Experiments: B1–B5). Slopes were set to 0°, 5°, 10°, 15°, and 20° in this experiment. The surface slope was adjusted by increasing the thickness of the transfer zone, thereby elevating the soil layer and epikarst around the sinkhole (Figure 1a). Under the influence of the surface slope, in addition to vertical infiltration, rainfall also generates horizontal runoff such as surface runoff, through flow and subcutaneous flow [54]. Relevant studies indicate that a critical rainfall intensity exists for generating surface runoff on karst slopes [55,56,57,58]. This value varies among experiments due to differences in experimental conditions. To ensure runoff generation during the investigation of surface slope effects, a pre-experiment was conducted, which determined a rainfall intensity of 60 mm/h. The transfer zone thickness was set to 80 cm and the karstification degree was set to one fracture.
- 3
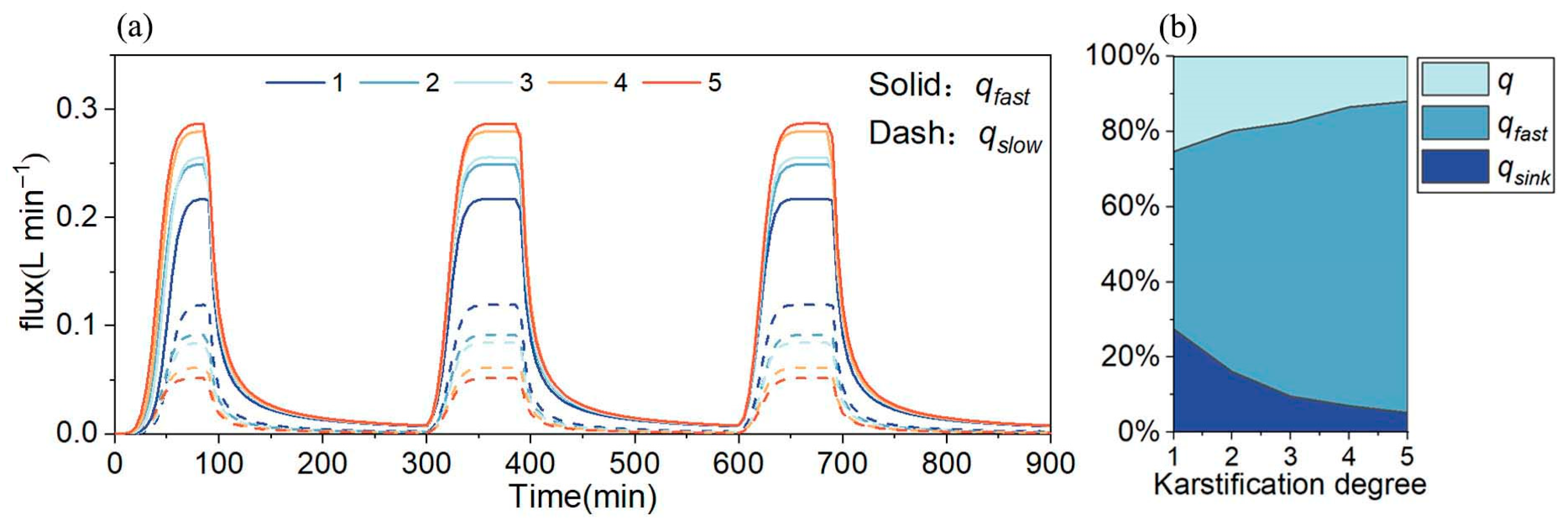
- Karstification degree (Experiments: C1–C5). The karstification degree reflects the intrinsic development of karst systems, influenced by factors such as rock solubility, permeability, and hydrochemical conditions [1]. A higher degree generally corresponds to a more fragmented medium, resulting in a greater permeability [59,60]. In this study, karstification was quantified based on fracture count. Five scenarios were established: one, two, three, and four fractures, along with fully fissured conditions (unsealed). The spatial distribution of fractures used to represent each degree is illustrated in Figure 2a–e. Other variables were held constant, with the transfer zone thickness set to 80 cm, the surface slope set to 0°, and the rainfall intensity set to 20 mm/h.
- 4
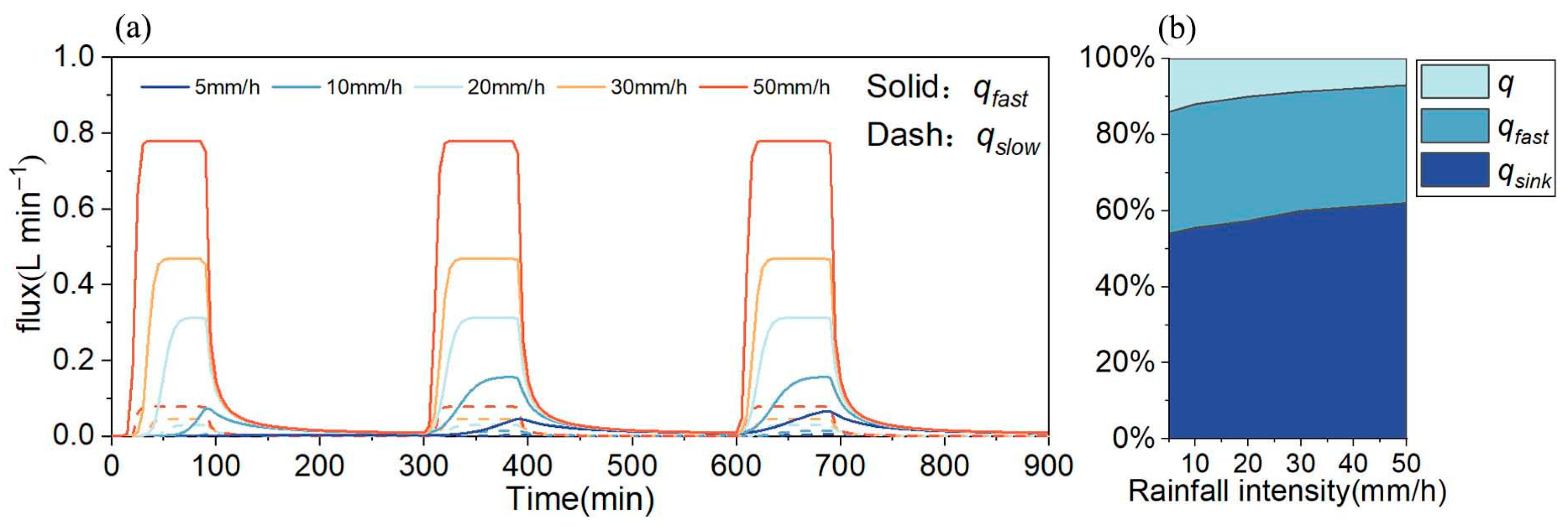
- Rainfall intensity (Experiments: D1–D5). The experimental rainfall intensities were set to 5, 10, 20, 30, and 50 mm h−1 (equivalent to 1.39 × 10−3, 2.78 × 10−3, 5.56 × 10−3, 8.33 × 10−3, and 1.39 × 10−2 expressed in mm s−1, respectively). During rainfall intensity experiments, other variables remained constant: a transfer zone thickness of 80 cm, a surface slope of 15°, and a karstification degree of two fractures.
2.3. Data Analysis Methods
3. Numerical Simulation
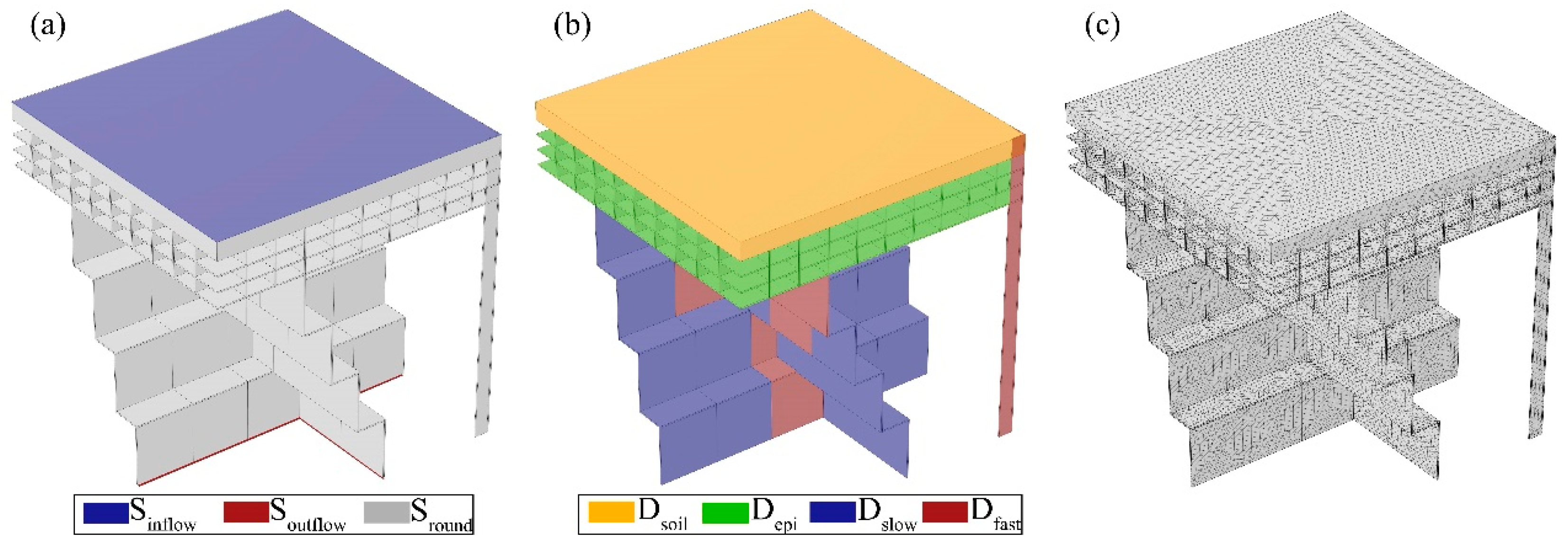
3.1. Numerical Model
3.2. Model Construction
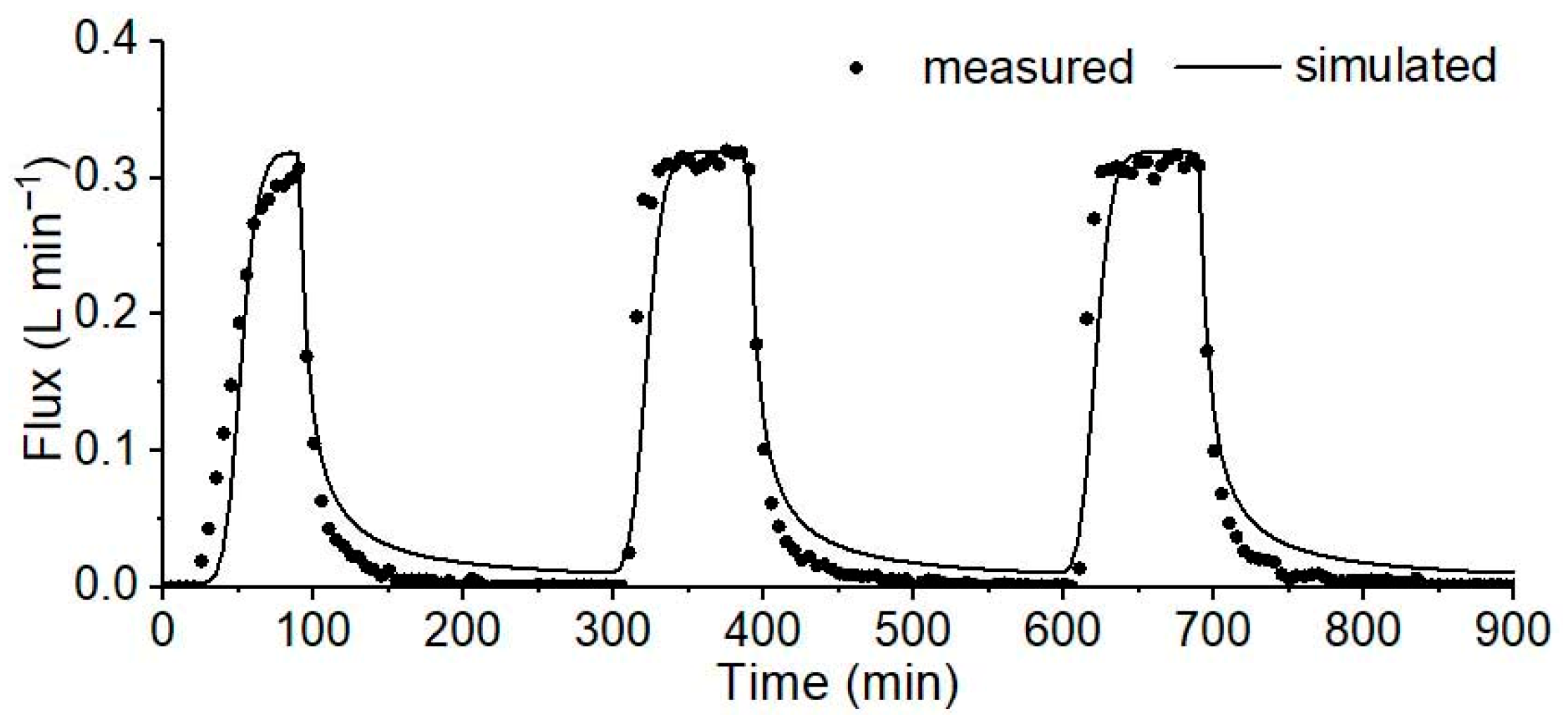
3.3. Model Evaluation Strategy
4. Results and Discussion
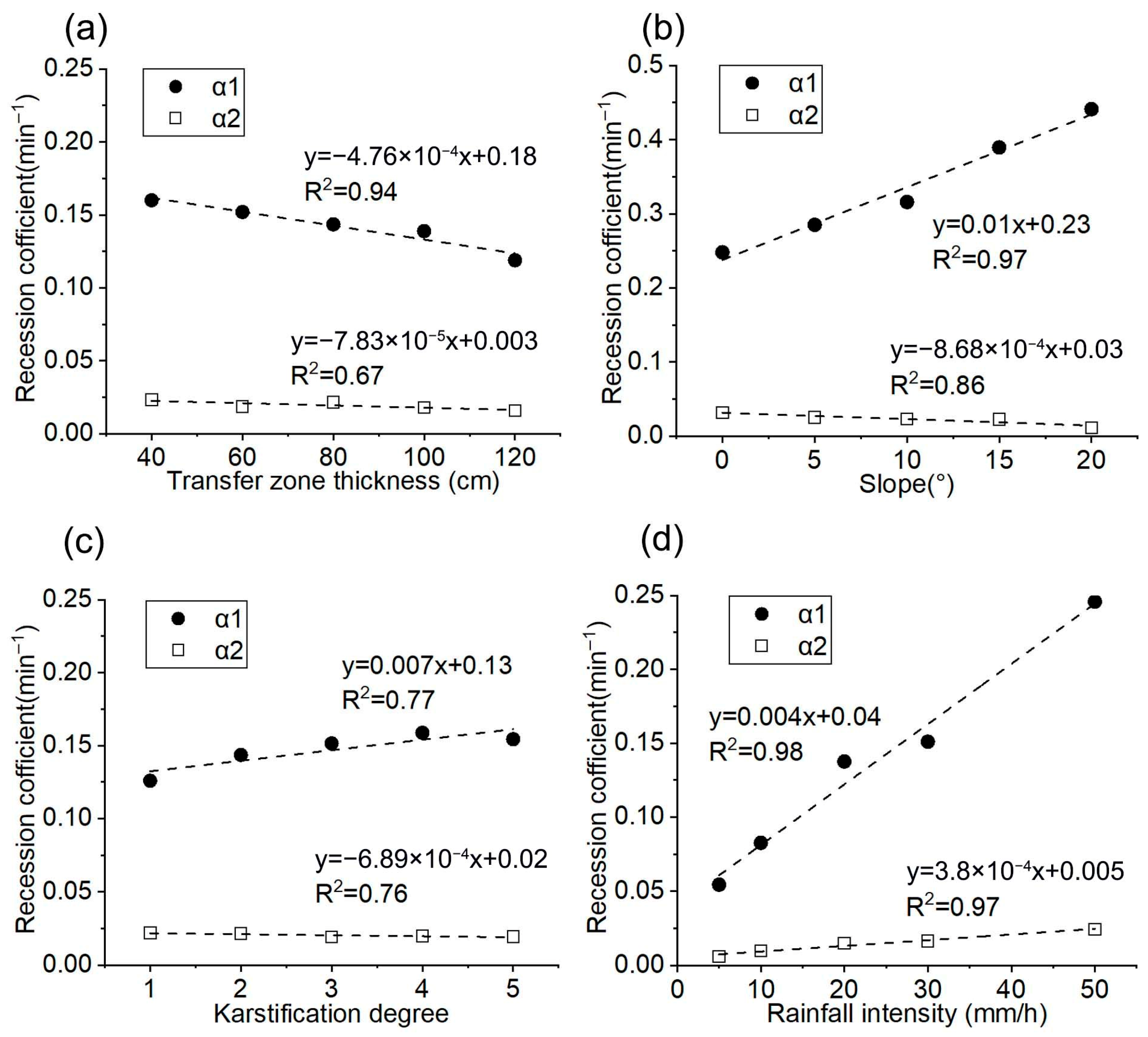
4.1. Factors Affecting Recession Process
4.2. Factors Affecting Regulating Capacity
4.3. Factors Affecting Division of Water Flow
4.4. Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ford, D.; Williams, P. Karst Hydrogeology and Geomorphology; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Wang, S.J.; Liu, Q.M.; Zhang, D.F. Karst Rocky Desertification in Southwestern China: Geomorphology, Landuse, Impact and Rehabilitation. Land Degrad. Dev. 2004, 15, 115–121. [Google Scholar] [CrossRef]
- Mudarra, M.; Andreo, B. Relative Importance of the Saturated and the Unsaturated Zones in the Hydrogeological Functioning of Karst Aquifers: The Case of Alta Cadena (Southern Spain). J. Hydrol. 2011, 397, 263–280. [Google Scholar] [CrossRef]
- Aquilina, L.; Ladouche, B.; Dörfliger, N. Recharge Processes in Karstic Systems Investigated through the Correlation of Chemical and Isotopic Composition of Rain and Spring-Waters. Appl. Geochem. 2005, 20, 2189–2206. [Google Scholar] [CrossRef]
- Bouwer, H. Artificial Recharge of Groundwater: Hydrogeology and Engineering. Hydrogeol. J. 2002, 10, 121–142. [Google Scholar] [CrossRef]
- El-hakim, M.; Bakalowicz, M. Significance and Origin of Very Large Regulating Power of Some Karst Aquifers in the Middle East. J. Hydrol. 2007, 333, 329–339. [Google Scholar] [CrossRef]
- Jiao, Y.; Liu, J.; Li, C.; Qiu, Q.; Yu, X.; Wang, W.; Zhang, G. Regulation Storage Calculation and Capacity Evaluation of the Underground Reservoir in the Groundwater Overdraft Area of Northern China. Environ. Earth Sci. 2020, 79, 18. [Google Scholar] [CrossRef]
- Baker, A.; Brunsdon, C. Non-Linearities in Drip Water Hydrology: An Example from Stump Cross Caverns, Yorkshire. J. Hydrol. 2003, 277, 151–163. [Google Scholar] [CrossRef]
- Aquilina, L.; Ladouche, B.; Dörfliger, N. Water Storage and Transfer in the Epikarst of Karstic Systems during High Flow Periods. J. Hydrol. 2006, 327, 472–485. [Google Scholar] [CrossRef]
- Berthelin, R.; Hartmann, A. The Shallow Subsurface of Karst Systems: Review and Directions. In Eurokarst 2018, Besançon. Advances in Karst Science; Bertrand, C., Denimal, S., Steinmann, M., Renard, P., Eds.; Springer: Cham, Switzerland, 2020; pp. 61–68. ISBN 9783030140151. [Google Scholar]
- Bonacci, O. Karst Hydrology; Spring: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Lee, E.S.; Krothe, N.C. Delineating the Karstic Flow System in the Upper Lost River Drainage Basin, South Central Indiana: Using Sulphate and Δ34SSO4 as Tracers. Appl. Geochem. 2003, 18, 145–153. [Google Scholar] [CrossRef]
- Yang, W.; Chen, L.; Huang, W.; Qian, Y.; Zhang, W. Enhancing Hourly Streamflow Simulation in Karst Basins: Development of the Modified DK-XAJ-EW Hydrological Model Integrating Epikarst Water Storage Function Dynamics. J. Hydrol. 2025, 658, 133170. [Google Scholar] [CrossRef]
- Sheffer, N.A.; Cohen, M.; Morin, E.; Grodek, T.; Gimburg, A.; Magal, E.; Gvirtzman, H.; Nied, M.; Isele, D.; Frumkin, A. Integrated Cave Drip Monitoring for Epikarst Recharge Estimation in a Dry Mediterranean Area, Sif Cave, Israel. Hydrol. Process. 2011, 25, 2837–2845. [Google Scholar] [CrossRef]
- Emblanch, C.; Zuppi, G.; Mudry, J.; Blavoux, B.; Batiot, C. Carbon 13 of TDIC to Quantify the Role of the Unsaturated Zone: The Example of the Vaucluse Karst Systems (Southeastern France). J. Hydrol. 2003, 279, 262–274. [Google Scholar] [CrossRef]
- Mazzilli, N.; Boucher, M.; Chalikakis, K.; Legchenko, A.; Jourde, H.; Champollion, C. Contribution of Magnetic Resonance Soundings for Characterizing Water Storage in the Unsaturated Zone of Karst Aquifers. Geophysics 2016, 81, 49–61. [Google Scholar] [CrossRef]
- Liu, R.; Wang, J.; Zhan, H.; Chen, Z.; Li, W.; Yang, D.; Zheng, S. Influence of Thick Karst Vadose Zone on Aquifer Recharge in Karst Formations. J. Hydrol. 2021, 592, 125791. [Google Scholar] [CrossRef]
- Xin, Y.; Zhou, Z.; Dou, Z.; Li, M.; Ma, J. Constant-Head and Variable-Head Injection Tests for Determining the Hydraulic Parameters of an Aquitard. Hydrogeol. J. 2020, 28, 2359–2372. [Google Scholar] [CrossRef]
- Xin, Y.; Zhou, Z.; Yu, F. Slug Tests for Determining the Hydraulic Parameters of an Unconfined Aquifer Considering Delayed Drainage Effect. J. Hydrol. 2025, 659, 133132. [Google Scholar] [CrossRef]
- Fiorillo, F. Tank-Reservoir Drainage as a Simulation of the Recession Limb of Karst Spring Hydrographs. Hydrogeol. J. 2011, 19, 1009–1019. [Google Scholar] [CrossRef]
- Fiorillo, F.; Pagnozzi, M.; Ventafridda, G. A Model to Simulate Recharge Processes of Karst Massifs. Hydrol. Process. 2014, 29, 2301–2314. [Google Scholar] [CrossRef]
- Olarinoye, T.; Gleeson, T.; Hartmann, A. Karst Spring Recession and Classification: Efficient, Automated Methods for Both Fast- and Slow-Flow Components. Hydrol. Earth Syst. Sci. 2022, 26, 5431–5447. [Google Scholar] [CrossRef]
- Bakshevskaia, V.A.; Pozdniakov, S.P.; Chiganov, I.A. Analysis of the Genetic Components of Groundwater (Spring) Discharge in a Fracture–Karst Massif. Water Resour. 2024, 51, S163–S172. [Google Scholar] [CrossRef]
- Tang, R.; Shu, L.; Lu, C.; Zhang, C.; Fan, J.; Appiah-Adjei, E.K. Laboratory Analog Analysis of Spring Recession Curve in a Karst Aquifer with Fracture and Conduit Domains. J. Hydrol. Eng. 2016, 21, 06015013. [Google Scholar] [CrossRef]
- Dewandel, B.; Lachassagne, P.; Bakalowicz, M.; Weng, P.; Al-malki, A. Evaluation of Aquifer Thickness by Analysing Recession Hydrographs. J. Hydrol. 2003, 274, 248–269. [Google Scholar] [CrossRef]
- Boussinesq, J. Essai Sur La Théorie Des Eaux Courantes Do Mouvement Non Permanent Des Eaux Souterraines. Acad. Sci. Inst. Fr. 1877, 23, 252–260. [Google Scholar]
- Bonacci, O. Karst Springs Hydrographs as Indicators of Karst Aquifers. Hydrol. Sci. J. 1993, 38, 51–62. [Google Scholar] [CrossRef]
- Griffiths, G.A.; Clausen, B. Streamflow Recession in Basins with Multiple Water Storages. J. Hydrol. 1997, 190, 60–74. [Google Scholar] [CrossRef]
- Vashisht, A.K.; Bam, B. Formulating the Spring Discharge-Function for the Recession Period by Analyzing Its Recession Curve: A Case Study of the Ranichauri Spring (India). J. Earth Syst. Sci. 2013, 122, 1313–1323. [Google Scholar] [CrossRef]
- Tallaksen, L. A Review of Baseflow Recession Analysis. J. Hydrol. 1995, 165, 349–370. [Google Scholar] [CrossRef]
- Chang, W.; Wan, J.; Tan, J.; Wang, Z.; Jiang, C.; Huang, K. Responses of Spring Discharge to Different Rainfall Events for Single-Conduit Karst Aquifers in Western Hunan Province, China. Int. J. Environ. Res. Public Health 2021, 18, 5775. [Google Scholar] [CrossRef]
- Kumar, V.; Sen, S. Evaluation of Spring Discharge Dynamics Using Recession Curve Analysis: A Case Study in Data-Scarce Region, Lesser Himalayas, India. Sustain. Water Resour. Manag. 2018, 4, 539–557. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Shoja, A. Effect of Annual Rainfall Amount on Characteristics of Karst Spring Hydrograph. Carbonates Evaporites 2014, 29, 279–289. [Google Scholar] [CrossRef]
- Maillet, E.T. Essais d’hydraulique Souterraine et Fluviale; Hermann: Paris, France, 1905. [Google Scholar]
- Luo, L.; Liang, X.; Luo, M.; Zhou, H. Applied Geochemistry Characterizing the Hierarchical Groundwater Flow Systems in Karstic. Appl. Geochem. 2022, 143, 105371. [Google Scholar] [CrossRef]
- Forkasiewicz, M.J.; Paloc, H. Régime de Tarissement de La Foux-de-La-Vis (Gard) Étude Préliminaire. Houille Blanche 1967, 53, 29–36. [Google Scholar] [CrossRef]
- Liu, R.; Wang, J.; Zhang, Y.; Reimann, T.; Hartmann, A. Laboratory and Numerical Simulations of Infiltration Process and Solute Transport in Karst Vadose Zone. J. Hydrol. 2024, 636, 131242. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Illman, W.A.; Field, M. Review of Laboratory Scale Models of Karst Aquifers: Approaches, Similitude, and Requirements. Groundwater 2020, 59, 163–174. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Z. Experimental Study on the Relation between the Fractal Characteristics and Solute Transport Parameters of Sandy Soil. J. Soils Sediments 2020, 20, 3181–3191. [Google Scholar] [CrossRef]
- Li, Y.; Shu, L.; Wu, P.; Zou, Z.; Lu, C.; Liu, B.; Niu, S.; Yin, X. Influence of the Karst Matrix Hydraulic Conductivity and Specific Yield on the Estimation Accuracy of Karstic Water Storage Variation. J. Hydrol. 2023, 626, 130186. [Google Scholar] [CrossRef]
- Luo, M.; Zhou, Z.; Chen, J.; Peng, X.; Zhao, Z.; Zhao, W. Identifying Solute Loss from Karst Conduit to Fissures under Concentrated Recharge Conditions. J. Hydrol. 2025, 647, 132370. [Google Scholar] [CrossRef]
- Gouy, A.; Collon, P.; Bailly-Comte, V.; Galin, E.; Antoine, C.; Thebault, B.; Landrein, P. KarstNSim: A Graph-Based Method for 3D Geologically-Driven Simulation of Karst Networks. J. Hydrol. 2024, 632, 130878. [Google Scholar] [CrossRef]
- Knöll, P.; Schiperski, F.; Roesrath, A.; Scheytt, T. Effects of Model Complexity on Karst Catchment Runoff Modeling for Flood Warning Systems. J. Hydrol. X 2025, 26, 100194. [Google Scholar] [CrossRef]
- Ohad, S.; Ovadia, L.; Yakov, L.; Haim, G. Groundwater Flow Modelling of a Large-Scale Thick Vadose Zone Including Two Perched Aquifers, the Jerusalem Mountains. Hydrol. Process. 2025, 39, e70216. [Google Scholar] [CrossRef]
- Poulain, A.; Watlet, A.; Kaufmann, O.; Van Camp, M.; Jourde, H.; Mazzilli, N.; Rochez, G.; Deleu, R.; Quinif, Y.; Hallet, V. Assessment of Groundwater Recharge Processes through Karst Vadose Zone by Cave Percolation Monitoring. Hydrol. Process. 2018, 32, 2069–2083. [Google Scholar] [CrossRef]
- Yan, Y.; Dai, Q.; Jin, L.; Wang, X. Geometric Morphology and Soil Properties of Shallow Karst Fissures in an Area of Karst Rocky Desertification in SW China. CATENA 2019, 174, 48–58. [Google Scholar] [CrossRef]
- Mangin, A. Contribution à l’étude Hydrodynamique des Aquifères Karstiques; Université de Dijon: Dijon, France, 1975. [Google Scholar]
- Williams, P.W. The Role of the Subcutaneous Zone in Karst Hydrology. J. Hydrol. 1983, 61, 45–67. [Google Scholar] [CrossRef]
- Bakalowicz, M. La Zone d’infiltration Des Aquifères Karstiques. Méthodes Dtétude. Structure et Fonctionnernent. Hydrogeol. J. 1995, 4, 3–21. Available online: https://digitalcommons.usf.edu/kip_articles/5677 (accessed on 13 October 2025).
- Hartmann, A.; Lange, J.; Vivó, À.; Mizyed, N.; Smiatek, G.; Kunstmann, H. A Multi-Model Approach for Improved Simulations of Future Water Availability at a Large Eastern Mediterranean Karst Spring. J. Hydrol. 2012, 468–469, 130–138. [Google Scholar] [CrossRef]
- Chang, Y.; Wu, J.; Jiang, G.; Liu, L.; Reimann, T.; Sauter, M. Modelling Spring Discharge and Solute Transport in Conduits by Coupling CFPv2 to an Epikarst Reservoir for a Karst Aquifer. J. Hydrol. 2019, 569, 587–599. [Google Scholar] [CrossRef]
- Petrič, M.; Kogovšek, J.; Ravbar, N. Effects of the Vadose Zone on Groundwater Flow and Solute Transport Characteristics in Mountainous Karst Aquifers–The Case of the Javorniki–Snežnik Massif (SW Slovenia). Acta Carsologica 2018, 47, 35–51. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Z.; Soulsby, C.; Cheng, Q.; Binley, A.; Jiang, R.; Tao, M. Characterizing the Heterogeneity of Karst Critical Zone and Its Hydrological Function: An Integrated Approach. Hydrol. Process. 2018, 32, 2932–2946. [Google Scholar] [CrossRef]
- Gunn, J. Point-Recharge of Limestone Aquifers—A Model from New Zealand Karst. J. Hydrol. 1983, 61, 19–29. [Google Scholar] [CrossRef]
- Gou, J.; Qu, S.; Shi, P.; Li, D.; Chen, X.; Wang, Y.; Shan, S.; Si, W. Application of Stable Isotope Tracer to Study Runoff Generation during Different Types of Rainfall Events. Water 2018, 10, 538. [Google Scholar] [CrossRef]
- Gou, J.; Qu, S.; Shi, P.; Wang, Y.; Shan, S.; Chen, X.; Li, D.; Si, W. Evaluating Runoff Generation in a Humid Bamboo Watershed Using Isotopic and Hydrochemical Tracer. J. Hydrol. Eng. 2019, 24, 05019003. [Google Scholar] [CrossRef]
- Wei, X.; Yan, Y.; Xie, D.; Ni, J.; Loáiciga, H.A. The Soil Leakage Ratio in the Mudu Watershed, China. Environ. Earth Sci. 2016, 75, 721. [Google Scholar] [CrossRef]
- Yan, Y.; Dai, Q.; Yuan, Y.; Peng, X.; Zhao, L.; Yang, J. Effects of Rainfall Intensity on Runoff and Sediment Yields on Bare Slopes in a Karst Area, SW China. Geoderma 2018, 330, 30–40. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, L.; Cao, Z.; Liu, J.; Xue, Y.; Wang, P.; Cao, X.; Liu, Y. Thermo-Mechanical Degradation and Fracture Evolution in Low-Permeability Coal Subjected to Cyclic Heating-Cryogenic Cooling. Phys. Fluids 2025, 37, 086617. [Google Scholar] [CrossRef]
- Teng, T.; Chen, Y.; Wang, Y.; Qiao, X. In Situ Nuclear Magnetic Resonance Observation of Pore Fractures and Permeability Evolution in Rock and Coal under Triaxial Compression. J. Energy Eng. 2025, 151, 04025036. [Google Scholar] [CrossRef]
- Bacdk, S.J.; Krothe, N.C. Derivation of Effective Hydraulic Parameters of a Karst Aquifer from Discharge Hydrograph Analysis. Water Resour. Res. 2001, 37, 13–19. [Google Scholar] [CrossRef]
- LA, R. Capillary Conduction of Liquids in Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar]
- van Genuchten, M. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, L.; Lingfan, Z.; Min, B.; Zihan, Z. Rock and Soil Mechanics Treatment of Two Boundary Conditions for Rainfall Infiltration in Slope and Its Application. Rock Soil Mech. 2021, 41, 4105–4115. [Google Scholar]
- Toss, D.K. Ground Water Hydrology; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Hou, X.P.; Fan, H.H. Study on Rainfall Infiltration Characteristics of Unsaturatedfractured Soil Based on COMSOL Multiphysics. Rock Soil Mech. 2022, 43, 563–572. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing Joint Probability Distributions of Soil Water Retention Characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Mualem, Y. A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Williams, P.W. The Role of the Epikarst in Karst and Cave Hydrogeology: A Review. Int. J. Speleol. 2008, 37, 1–10. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, Z.; Werner, A.D.; Chen, Y. Experimental Analysis of Intermittent Pumping Effects on Seawater Intrusion. Water Resour. Res. 2023, 59, e2022WR032269. [Google Scholar] [CrossRef]
- Hu, X.; Wang, X.; Gunzburger, M.; Hua, F.; Cao, Y. Experimental and Computational Validation and Verification of the Stokes-Darcy and Continuum Pipe Flow Models for Karst Aquifers with Dual Porosity Structure. Hydrol. Process. 2012, 26, 2031–2040. [Google Scholar] [CrossRef]





| Experimental Factors | NO. | Transfer Zone Thickness (cm) | Surface Slope (◦) | Karstification Degree | Rainfall Intensity (mm/h) |
|---|---|---|---|---|---|
| Transfer zone thickness | A1 | 40 | 0 | 2 | 20 |
| A2 | 60 | 0 | 2 | 20 | |
| A3 | 80 | 0 | 2 | 20 | |
| A4 | 100 | 0 | 2 | 20 | |
| A5 | 120 | 0 | 2 | 20 | |
| Surface slope | B1 | 80 | 0 | 1 | 60 |
| B2 | 80 | 5 | 1 | 60 | |
| B3 | 80 | 10 | 1 | 60 | |
| B4 | 80 | 15 | 1 | 60 | |
| B5 | 80 | 20 | 1 | 60 | |
| Karstification degree | C1 | 80 | 0 | 1 | 20 |
| C2 | 80 | 0 | 2 | 20 | |
| C3 | 80 | 0 | 3 | 20 | |
| C4 | 80 | 0 | 4 | 20 | |
| C5 | 80 | 0 | 5 | 20 | |
| Rainfall intensity | D1 | 80 | 15 | 2 | 5 |
| D2 | 80 | 15 | 2 | 10 | |
| D3 | 80 | 15 | 2 | 20 | |
| D4 | 80 | 15 | 2 | 30 | |
| D5 | 80 | 15 | 2 | 50 |
| Parameters | Description | Units | Value | Type * | |
|---|---|---|---|---|---|
| Soil layer | Ks_soil | Saturated hydraulic conductivity | m s−1 | 0.0054 | fixed |
| θs_soil | Volumetric saturated water content | - | 0.61 | fixed | |
| θr_soil | Volumetric residual water content | - | 0.1 | fitting | |
| α_soil | Parameter of VG model | m−1 | 7.5 | a | |
| n_soil | Parameter of VG model | - | 1.89 | a | |
| l_soil | Parameter of VG model | - | 0.5 | b | |
| Epikarst | K_epi | Saturated hydraulic conductivity | m s−1 | 0.08 | fixed |
| θs_epi | Volumetric saturated water content | - | 0.15 | fitting | |
| θr_epi | Volumetric residual water content | - | 0.015 | fitting | |
| Slow flow system | K_slow | Saturated hydraulic conductivity | m s−1 | 0.03 | fixed |
| θs_slow | Volumetric saturated water content | - | 0.2 | fitting | |
| θr_slow | Volumetric residual water content | - | 0.02 | fitting | |
| Fast flow system | K_fast | Saturated hydraulic conductivity | m s−1 | 0.83 | fixed |
| θs_fast | Volumetric saturated water content | - | 0.1 | fitting | |
| θr_fast | Volumetric residual water content | - | 0.01 | fitting | |
| Other parameters | α_fast | Parameter of VG model for epikarst, slow flow system, and fast flow system | m−1 | 9 | fitting |
| n_fast | Parameter of VG model for epikarst, slow flow system, and fast flow system | - | 2 | fitting | |
| l_fast | Parameter of VG model for epikarst, slow flow system, and fast flow system | - | 0.5 | b |
| NO. | NSE | NO. | NSE | NO. | NSE | NO. | NSE |
|---|---|---|---|---|---|---|---|
| A1 | 0.883 | B1 | 0.879 | C1 | 0.879 | D1 | 0.719 |
| A2 | 0.883 | B2 | 0.802 | C2 | 0.855 | D2 | 0.744 |
| A3 | 0.855 | B3 | 0.848 | C3 | 0.848 | D3 | 0.855 |
| A4 | 0.872 | B4 | 0.852 | C4 | 0.821 | D4 | 0.901 |
| A5 | 0.876 | B5 | 0.861 | C5 | 0.833 | D5 | 0.913 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Wang, J.; Zhu, S.; Zhang, Y.; Zheng, S.; Zhao, Y.; Qiao, F.; Yang, D. Research on the Influence Mechanism of Regulating Capacity and Flow Recession Process in the Karst Vadose Zone. Water 2025, 17, 2976. https://doi.org/10.3390/w17202976
Liu R, Wang J, Zhu S, Zhang Y, Zheng S, Zhao Y, Qiao F, Yang D. Research on the Influence Mechanism of Regulating Capacity and Flow Recession Process in the Karst Vadose Zone. Water. 2025; 17(20):2976. https://doi.org/10.3390/w17202976
Chicago/Turabian StyleLiu, Ruitong, Jinguo Wang, Shumei Zhu, Yuting Zhang, Shiyu Zheng, Yongsheng Zhao, Fei Qiao, and Dong Yang. 2025. "Research on the Influence Mechanism of Regulating Capacity and Flow Recession Process in the Karst Vadose Zone" Water 17, no. 20: 2976. https://doi.org/10.3390/w17202976
APA StyleLiu, R., Wang, J., Zhu, S., Zhang, Y., Zheng, S., Zhao, Y., Qiao, F., & Yang, D. (2025). Research on the Influence Mechanism of Regulating Capacity and Flow Recession Process in the Karst Vadose Zone. Water, 17(20), 2976. https://doi.org/10.3390/w17202976






