Study of the Motion Path of Water-Intercepting Aggregate in a Coal–Rock Mass Water Gush Roadway
Abstract
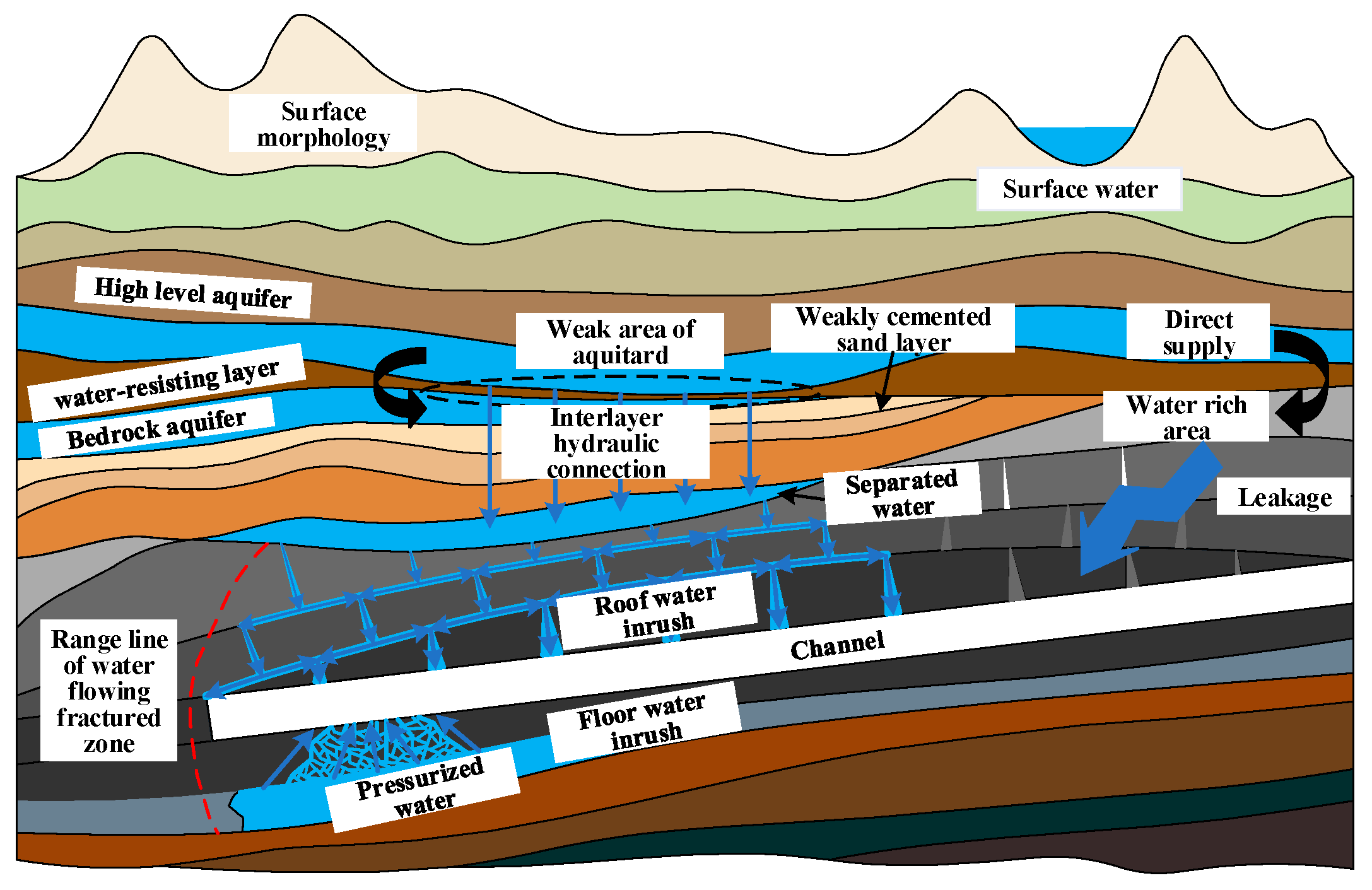
1. Introduction
2. Methods
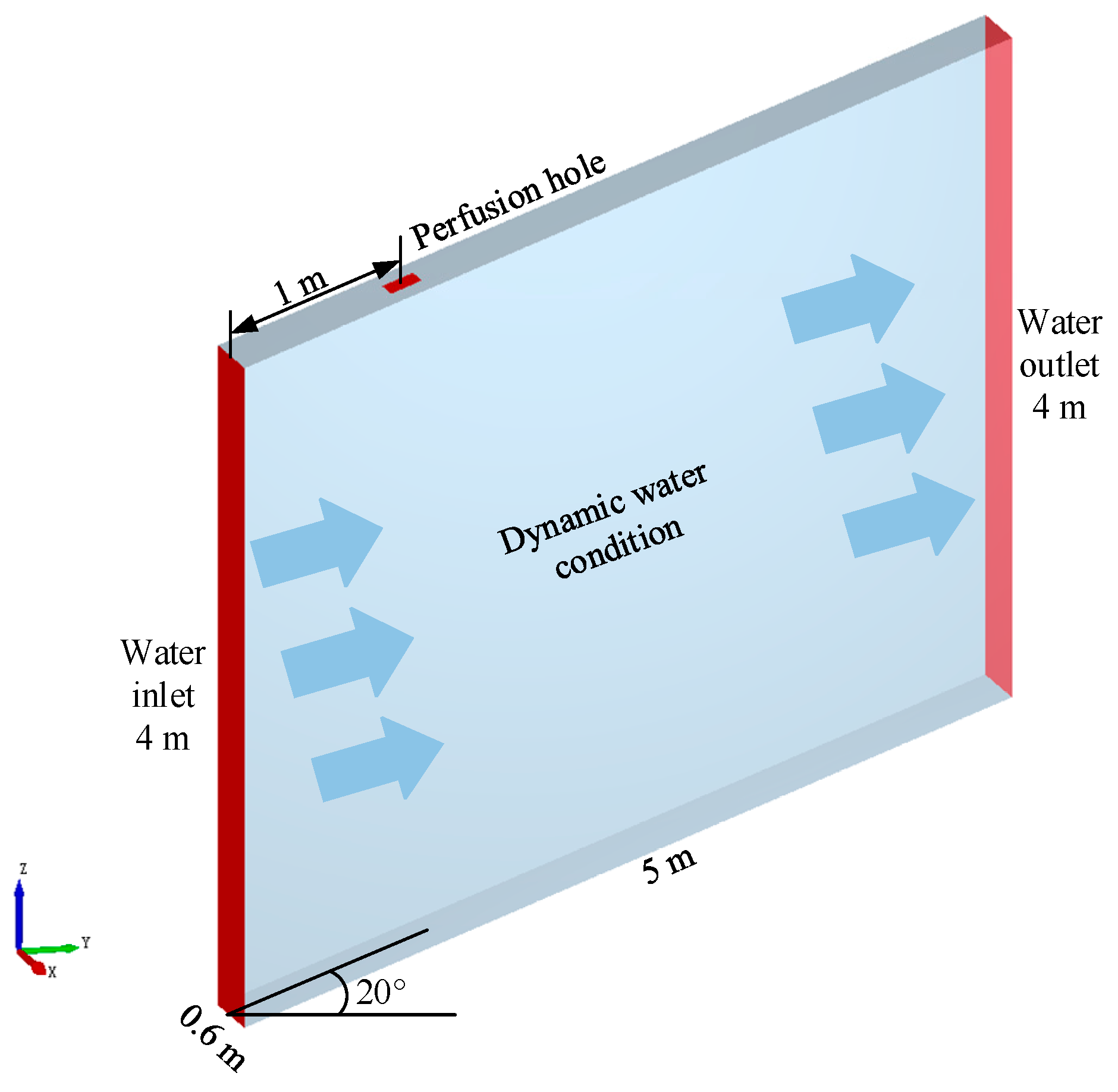
2.1. Numerical Model of Water-Intercepting Aggregate Motion Path
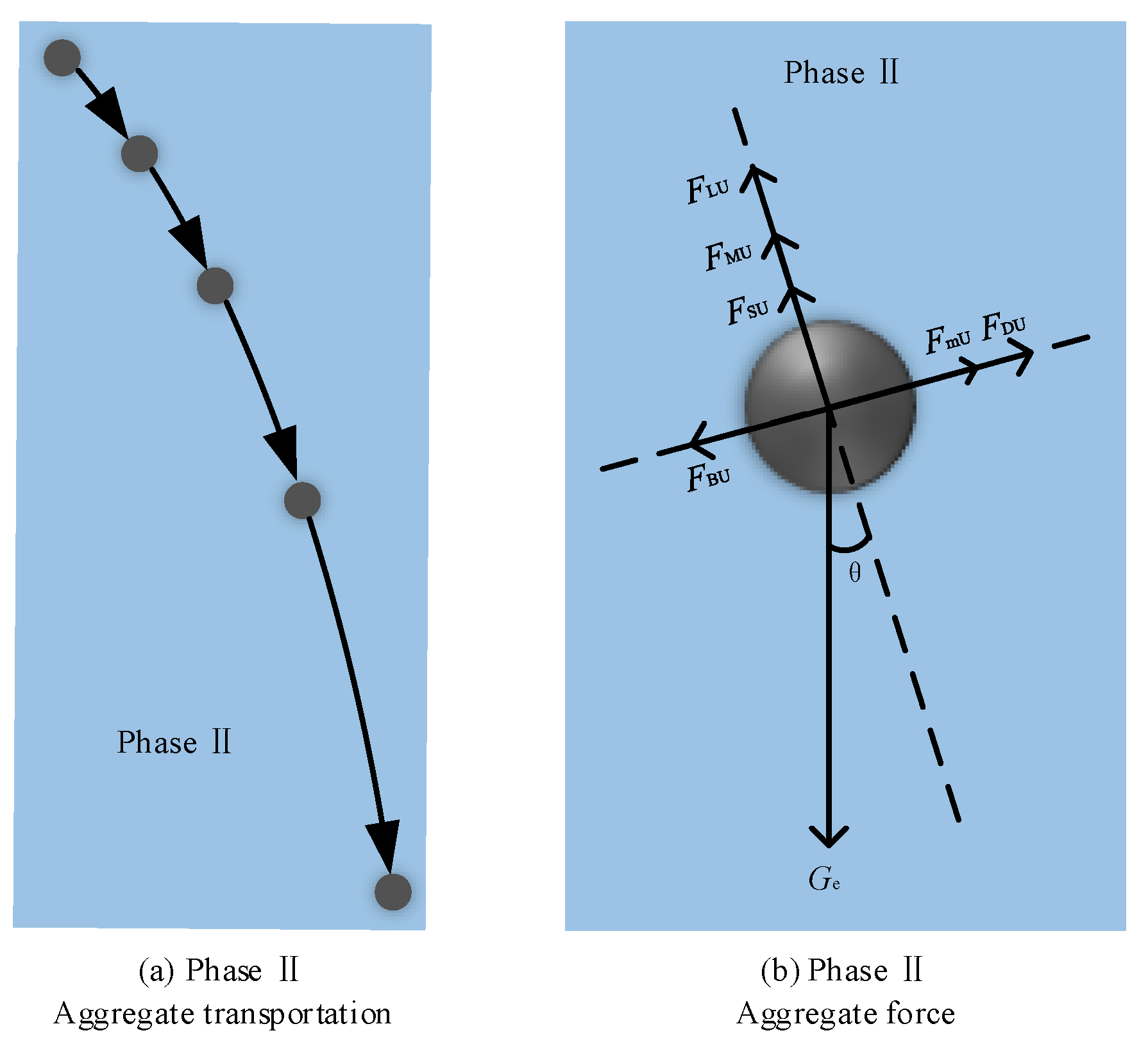
2.2. Theoretical Model of Water-Intercepting Aggregate Motion Path
3. Results and Discussion
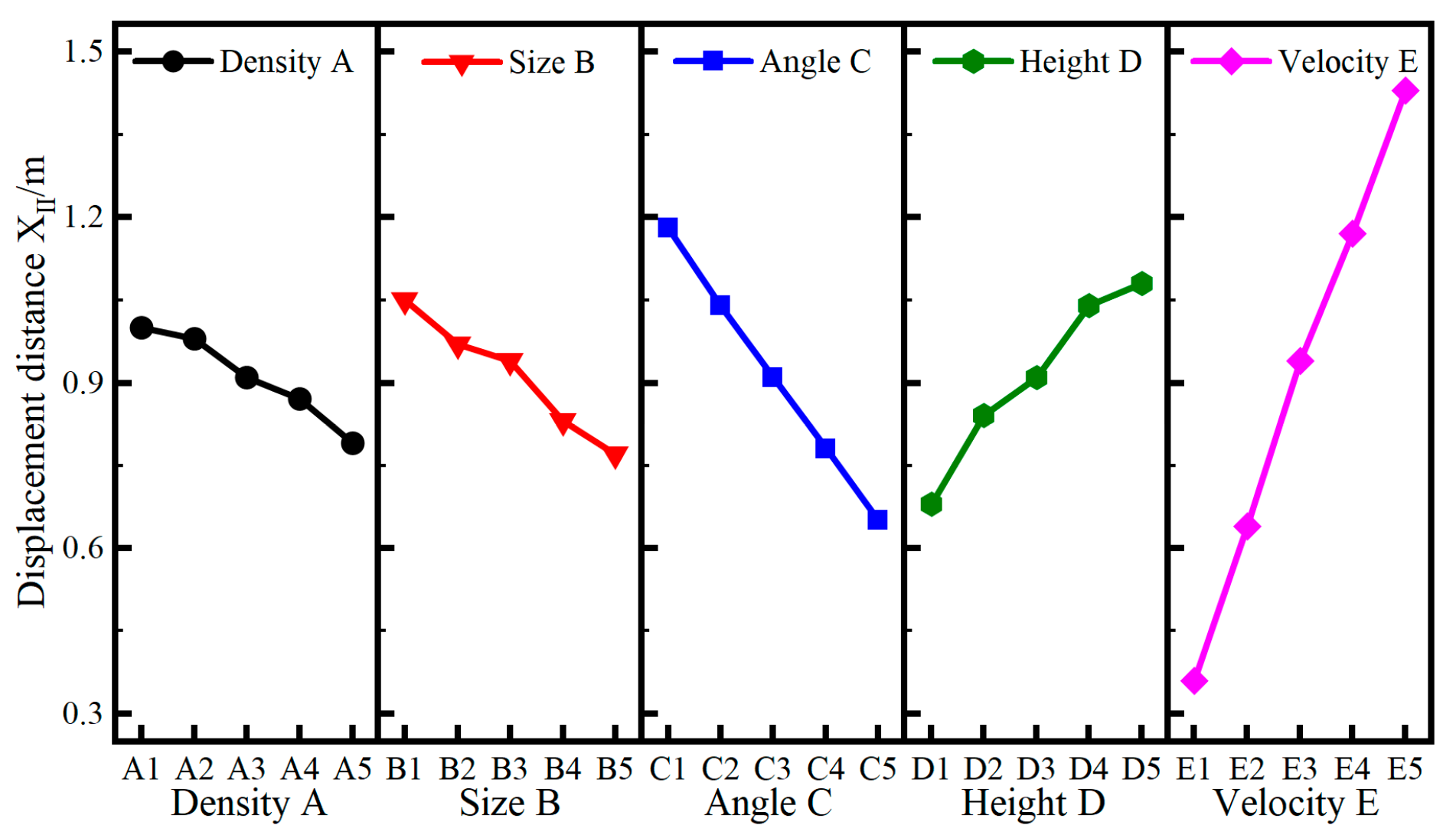
3.1. Analysis and Results of Factors Influencing the Motion Path of Aggregate
3.2. Discussion on Spacing Design of Perfusion Holes and Specific Construction Methods
4. Conclusions
- (1)
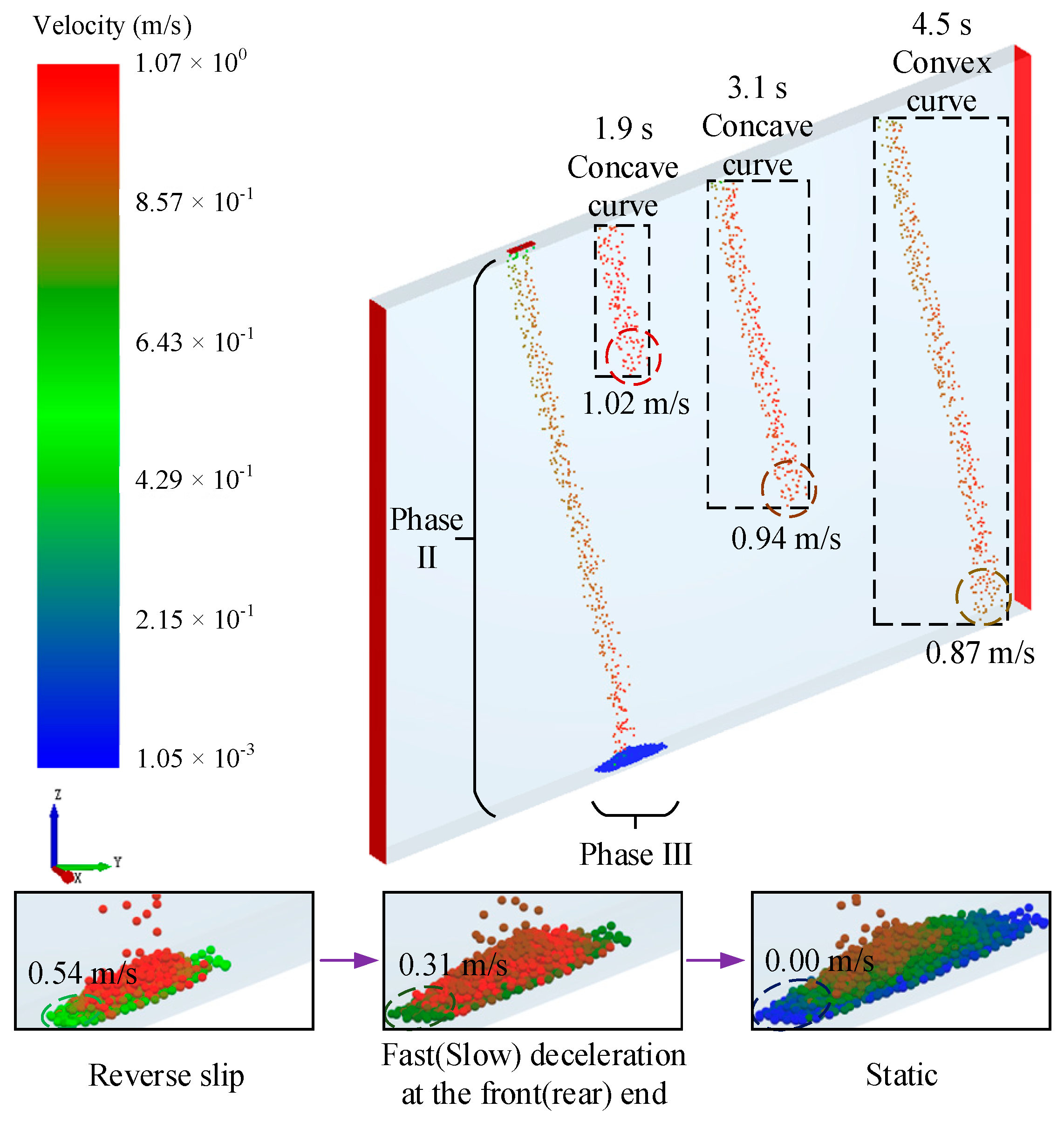
- A numerical model was constructed for large cross-sectional water gush roadway sections, and the CFD-DEM coupling method was used to simulate the water-intercepting aggregate motion process. Pursuant to the simulation results, the complete aggregate motion path was categorized into three characteristic phases: free fall, curvilinear projectile motion, and sliding.
- (2)
- The stage-by-stage force analysis of individual aggregate established a theoretical model for describing its motion path, with a derived formula for its displacement distance (along and vertically to the roadway). Then, the aggregate volume concentration Sv was introduced to modify this formula, so that it can also be applied to the aggregate particle group. The model’s error (compared with the numerical simulations) was within 10%. Parameter analysis showed that the aggregate density/size and the water gush roadway dip angle were negatively correlated with aggregate displacement distances in phase II and III, while the roadway height and current velocity were positively correlated—consistent with simulations.
- (3)
- When dealing with actual water gush conditions in coal mines, for water-intercepting aggregate that is locally available, based on the engineering data and combined with the existing aggregate density and size, the formulas in this paper can be used to calculate the aggregate displacement distance after entering the water gush roadway. On this basis, the subsequent spacing of the perfusion holes can be dynamically optimized. If there is no ready-made aggregate, the engineering data can be used to back-calculate the aggregate size and density that will ensure the vector sum of the aggregate motion in phase II and III approaches zero as closely as possible, thereby selecting the appropriate aggregate to significantly improve the water-intercepting efficiency after perfusing.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, D.; Duan, H.; Zhang, J.; Bai, H. A state-of-the-art review on rock seepage mechanism of water inrush disaster in coal mines. Int. J. Coal. Sci. Technol. 2022, 9, 50. [Google Scholar] [CrossRef]
- Sun, W.; Li, W.; Ren, L.; Li, K. Spatial and Temporal Characterization of Mine Water Inrush Accidents in China, 2014–2022. Water 2024, 16, 656. [Google Scholar] [CrossRef]
- Liang, D.; Jiang, Z.; Zhu, S.; Sun, Q.; Qian, Z. Experimental research on water inrush in tunnel construction. Nat. Hazard. 2016, 81, 467–480. [Google Scholar] [CrossRef]
- Li, L.; Tu, W.; Shi, S.; Chen, J.; Zhang, Y. Mechanism of water inrush in tunnel construction in karst area. Geomat. Nat. Hazards Risk. 2016, 7, 35–46. [Google Scholar] [CrossRef]
- Soni, A.K.; Wolkersdorfer, C. Mine water: Policy perspective for improving water management in the mining environment with respect to developing economies. Int. J. Min. Reclam. Environ. 2016, 30, 115–127. [Google Scholar] [CrossRef]
- Shi, Q.; Sakai, M. Recent progress on the discrete element method simulations for powder transport systems: A review. Adv. Powder Technol. 2022, 33, 103664. [Google Scholar] [CrossRef]
- Li, S.; Liu, R.; Zhang, Q.; Zhang, X. Protection against water or mud inrush in tunnels by grouting: A review. J. Rock Mech. Geotech. Eng. 2016, 8, 753–766. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, P.; Tian, S. Prevention and treatment technologies of railway tunnel water inrush and mud gushing in China. J. Rock Mech. Geotech. Eng. 2013, 5, 468–477. [Google Scholar] [CrossRef]
- Cao, Z.; Yi, X.; Yi, X.; Feng, D.; Li, Z.; Huang, C.; Wang, S.; Yu, Y.; Wang, W.; Zhai, M.; et al. Diffusion Evolution Rules of Grouting Slurry in Mining-induced Cracks in Overlying Strata. Rock Mech. Rock Eng. 2025, 58, 6493–6512. [Google Scholar] [CrossRef]
- Mou, L.; Dong, S.; Zhou, W.; Wang, W.; Li, A.; Shi, Z. Data Analysis and Key Parameters of Typical Water Hazard Control Engineering in Coal Mines of China. Mine Water Environ. 2020, 39, 331–344. [Google Scholar] [CrossRef]
- Zhai, M.; Bai, H. Precise application of grouting technology in underground coal mining: Water inrush risk of floor elimination. Environ. Sci. Pollut. Res. 2023, 30, 24361–24376. [Google Scholar] [CrossRef]
- Yilmaz, E. Innovative mine backfill materials and structures. Int. J. Min. Reclam. Environ. 2023, 37, 731–734. [Google Scholar] [CrossRef]
- Vlasak, P.; Kysela, B.; Chara, Z. Flow structure of coarse-grained slurry in a horizontal pipe. J. Hydrol. Hydromech. 2012, 60, 115–124. [Google Scholar] [CrossRef]
- Ravelet, F.; Bakir, F.; Khelladi, S.; Rey, R. Experimental study of hydraulic transport of large particles in horizontal pipes. Exp. Therm. Fluid Sci. 2013, 45, 187–197. [Google Scholar] [CrossRef]
- Arolla, S.K.; Desjardins, O. Transport modeling of sedimenting particles in a turbulent pipe flow using Euler–Lagrange large eddy simulation. Int. J. Multiph. Flow 2015, 75, 1–11. [Google Scholar] [CrossRef]
- Uzi, A.; Levy, A. Flow characteristics of coarse particles in horizontal hydraulic conveying. Powder Technol. 2018, 326, 302–321. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, S.; Kuang, S.; Luo, K.; Fan, J.; Yu, A. CFD-DEM modelling of hydraulic conveying of solid particles in a vertical pipe. Powder Technol. 2019, 354, 893–905. [Google Scholar] [CrossRef]
- Sui, W.; Liu, Z.; Zhang, G.; Mao, D.; Li, R.; Liang, J. Experimental investigation on grout propagation in poured aggregates for controlling water inrush in tunnels with flowing water. Geoenviron. Disasters 2023, 10, 15. [Google Scholar] [CrossRef]
- Su, P.; Wen, J.; Gu, S.; Liu, F.; Li, C. Study on the migration law of aggregate sediment in the water inrush channel of coal rock mass. Coal Sci. Technol. 2023, 51, 200–207. [Google Scholar]
- Luo, B.; Sun, Y.; Xu, Z.; Chen, G.; Zhang, L.; Lu, W.; Zhao, X.; Yuan, H. Damage Characteristics and Mechanism of the 2017 Groundwater Inrush Accident That Occurred at Dongyu Coalmine in Taiyuan, Shanxi, China. Water 2021, 13, 368. [Google Scholar] [CrossRef]
- Teng, T.; Chen, Y.; Wang, Y.; Qiao, X. In Situ Nuclear Magnetic Resonance Observation of Pore Fractures and Permeability Evolution in Rock and Coal under Triaxial Compression. J. Energy Eng. 2025, 151, 04025036. [Google Scholar] [CrossRef]
- Fei, Y.; Liu, S.; Xu, Y.; Zhao, L. Failure Analysis of Thin Bedrock and Clay Roof in Underground Coal Mining: Case Study in Longdong Coal Mine. Int. J. Geomech. 2020, 20, 04020187. [Google Scholar] [CrossRef]
- Gong, X.; Ma, D.; Wu, L.; Li, Q.; Li, Z.; Du, F.; Qiao, R.; Han, J. Water Inrush Mechanism During Mining Adjacent to Large Water-Conducting Faults. Water 2025, 17, 1508. [Google Scholar] [CrossRef]
- Cao, M.; Yin, S.; Lian, H.; Wang, X.; Wang, G.; Li, S.; Li, Q.; Xu, W. Failure Mechanism and Risk Evaluation of Water Inrush in Floor of Extra-Thick Coal Seam. Water 2025, 17, 743. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, L.; Cao, Z.; Liu, J.; Xue, Y.; Wang, P.; Cao, X.; Liu, Y. Thermo-mechanical degradation and fracture evolution in low-permeability coal subjected to cyclic heating–cryogenic cooling. Phys. Fluids 2025, 37, 086617. [Google Scholar] [CrossRef]
- Kong, D.; Pu, S.; Cheng, Z.; Wu, G.; Liu, Y. Coordinated Deformation Mechanism of the Top Coal and Filling Body of Gob-Side Entry Retaining in a Fully Mechanized Caving Face. Int. J. Geomech. 2021, 21, 04021030. [Google Scholar] [CrossRef]
- Zhao, J.; Shan, T. Coupled CFD-DEM simulation of fluid-particle interaction in geomechanics. Powder Technol. 2013, 239, 248–258. [Google Scholar] [CrossRef]
- Otieno, F.; Shukla, S.K. How does mine tailings slurry solids concentration affect stability of dam embankment slope? Int. J. Min. Reclam. Environ. 2024, 38, 281–292. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, G.; Song, S.; Zhang, L.; Sun, B. CFD investigation on dust dispersion pollution of down/upwind coal cutting and relevant countermeasures for spraying dustfall in fully mechanized mining face. Adv. Powder Technol. 2020, 31, 3177–3190. [Google Scholar] [CrossRef]
- Reddy, N.V.K.; Pothal, J.K.; Barik, R.; Senapati, P.K. Pipeline Slurry Transportation System: An Overview. J. Pipeline Syst. Eng. Pract. 2023, 14, 03123001. [Google Scholar] [CrossRef]
- Shen, B. Coal Mine Roadway Stability in Soft Rock: A Case Study. Rock Mech. Rock Eng. 2014, 47, 2225–2238. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Zhang, W. Reliability assessment of stability of underground rock caverns. Int. J. Rock Mech. Min. Sci. 2012, 55, 157–163. [Google Scholar] [CrossRef]
- He, Y.; Bayly, A.E.; Hassanpour, A. Coupling CFD-DEM with dynamic meshing: A new approach for fluid-structure interaction in particle-fluid flows. Powder Technol. 2018, 325, 620–631. [Google Scholar] [CrossRef]
- Stewart, C.; Balachandar, S.; Mcgrath, T.P. Soft-sphere simulations of a planar shock interaction with a granular bed. Phys. Rev. Fluids. 2018, 3, 034308. [Google Scholar] [CrossRef]
- Sobieski, W. Switch Function and Sphericity Coefficient in the Gidaspow Drag Model for Modeling Solid-Fluid Systems. Dry. Technol. 2009, 27, 267–280. [Google Scholar] [CrossRef]
- Wen, J.; Gu, S.; Su, P.; Li, J. Study on the two-phase coupling migration mechanism of deceleration aggregate and water in coal mine water inrush channel. Sci. Rep. 2025, 15, 11702. [Google Scholar] [CrossRef]
- Ekanayake, N.I.K.; Berry, J.D.; Harvie, D.J.E. Lift and drag forces acting on a particle moving in the presence of slip and shear near a wall. J. Fluid Mech. 2021, 915, A103. [Google Scholar] [CrossRef]
- Van Der Wijk, V.; Herder, J.L.; Demeulenaere, B. Comparison of Various Dynamic Balancing Principles Regarding Additional Mass and Additional Inertia. J. Mech. Rob. 2009, 1, 041006. [Google Scholar] [CrossRef]
- Bombardelli Fabián, A.; González Andrea, E.; Niño Yarko, I. Computation of the Particle Basset Force with a Fractional-Derivative Approach. J. Hydraul. Eng. 2008, 134, 1513–1520. [Google Scholar] [CrossRef]
- Hessenkemper, H.; Ziegenhein, T.; Rzehak, R.; Lucas, D.; Tomiyama, A. Lift force coefficient of ellipsoidal single bubbles in water. Int. J. Multiph. Flow 2021, 138, 103587. [Google Scholar] [CrossRef]
- Shorbagy, M.; Taha, H. Magnus Force Estimation Using Gauss’s Principle of Least Constraint. AIAA J. 2024, 62, 1962–1969. [Google Scholar] [CrossRef]
- Cui, Y.; Ravnik, J.; Hriberšek, M.; Steinmann, P. A novel model for the lift force acting on a prolate spheroidal particle in an arbitrary non-uniform flow. Part I. Lift force due to the streamwise flow shear. Int. J. Multiph. Flow 2018, 104, 103–112. [Google Scholar] [CrossRef]
- Gu, J.; Ma, D.Q.; Chen, W.; Qin, X.; Wang, X.L.; Yang, J.Z. Study on Settling Velocity of Sediment Particle Cloud in the Water. Adv. Mater. Res. 2013, 610–613, 2451–2454. [Google Scholar] [CrossRef]
- Kuang, C.; Zheng, H.; Gu, J.; Ma, D. Settling velocity of sediment particle clusters. J. Tongji Univ. (Nat. Sci.) 2016, 44, 1845–1850+1866. [Google Scholar]





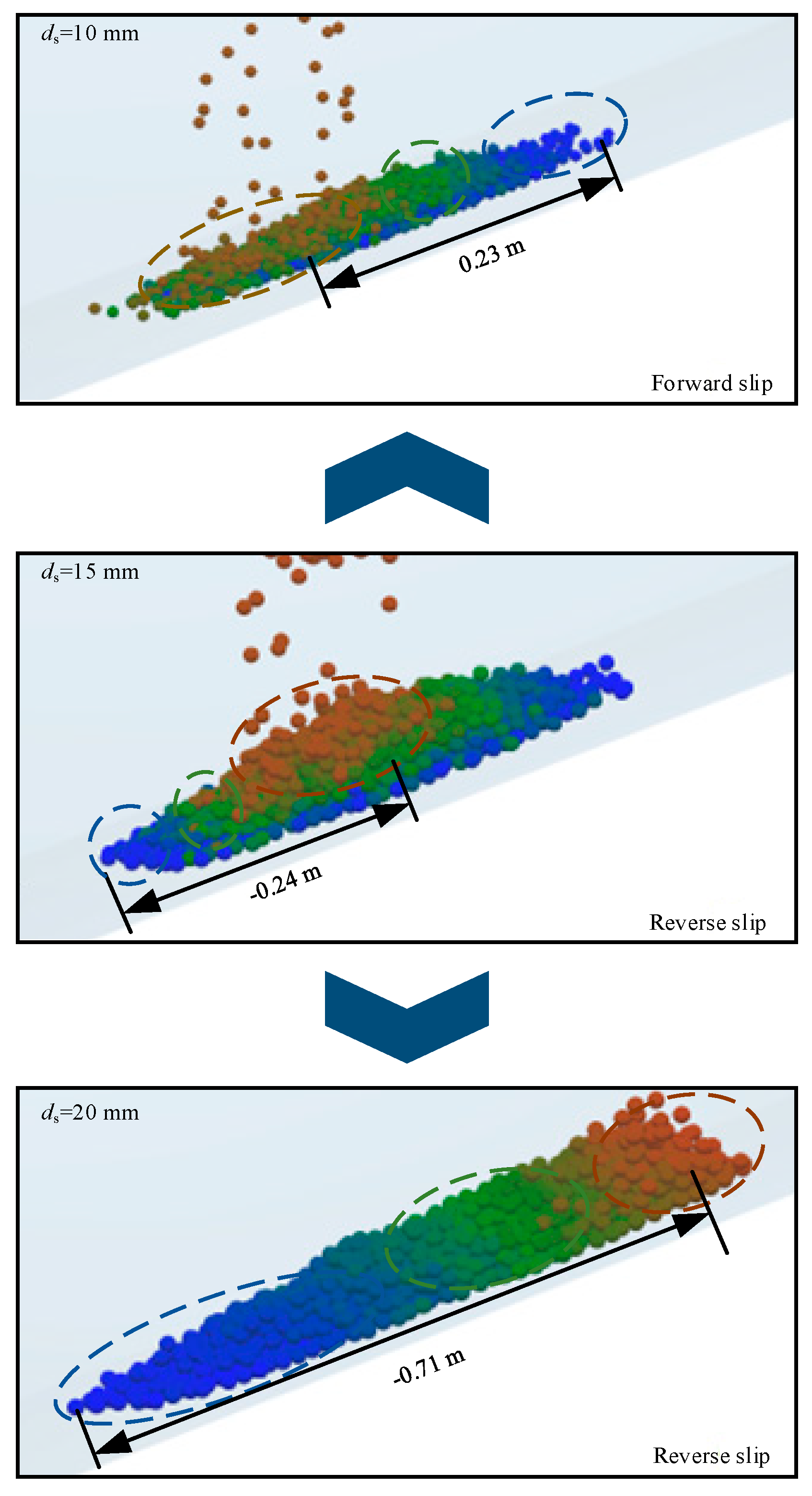
| Density ρs kg/m3 | Size ds mm | Coefficient of Restitution e | Coefficient of Friction f | Poisson’s Ratio ν | Elastic Modulus G Mpa |
|---|---|---|---|---|---|
| 2600 | 15 | 0.5 | 1 | 0.25 | 10 |
| Test Levels | Test Factors | ||||
|---|---|---|---|---|---|
| Density A, kg/m3 | Size B, mm | Dip Angle C, ° | Height D, m | Velocity E, m/s | |
| 1 | 1800 | 5 | 10 | 3.0 | 0.1 |
| 2 | 2200 | 10 | 15 | 3.5 | 0.3 |
| 3 | 2600 | 15 | 20 | 4.0 | 0.5 |
| 4 | 3000 | 20 | 25 | 4.5 | 0.7 |
| 5 | 3400 | 25 | 30 | 5.0 | 0.9 |
| Test Number | Allocation of Factor Levels | Test Factors | Phase II XII, m | Phase III XIII, m | ||||
|---|---|---|---|---|---|---|---|---|
| Density A, kg/m3 | Size B, mm | Angle C, ° | Height D, m | Velocity E, m/s | ||||
| 1 | A1B1C1D1E1 | 1800 | 5 | 10 | 3.0 | 0.1 | 0.57 | 0.28 |
| 2 | A1B2C3D4E5 | 1800 | 10 | 20 | 4.5 | 0.9 | 1.72 | 1.49 |
| 3 | A1B3C5D2E4 | 1800 | 15 | 30 | 3.5 | 0.7 | 0.97 | −0.09 |
| 4 | A1B4C2D5E3 | 1800 | 20 | 15 | 5.0 | 0.5 | 1.27 | 0.02 |
| 5 | A1B5C4D3E2 | 1800 | 25 | 25 | 4.0 | 0.3 | 0.47 | −1.54 |
| 6 | A2B1C5D4E3 | 2200 | 5 | 30 | 4.5 | 0.5 | 1.03 | 0.58 |
| 7 | A2B2C2D2E2 | 2200 | 10 | 15 | 3.5 | 0.3 | 0.77 | 0.06 |
| 8 | A2B3C4D5E1 | 2200 | 15 | 25 | 5.0 | 0.1 | 0.51 | −0.83 |
| 9 | A2B4C1D3E5 | 2200 | 20 | 10 | 4.0 | 0.9 | 1.7 | 0.61 |
| 10 | A2B5C3D1E4 | 2200 | 25 | 20 | 3.0 | 0.7 | 0.89 | −1.00 |
| 11 | A3B1C4D2E5 | 2600 | 5 | 25 | 3.5 | 0.9 | 1.38 | 1.14 |
| 12 | A3B2C1D5E4 | 2600 | 10 | 10 | 5.0 | 0.7 | 1.68 | 1.44 |
| 13 | A3B3C3D3E3 | 2600 | 15 | 20 | 4.0 | 0.5 | 0.91 | −0.25 |
| 14 | A3B4C5D1E2 | 2600 | 20 | 30 | 3.0 | 0.3 | 0.08 | −2.00 |
| 15 | A3B5C2D4E1 | 2600 | 25 | 15 | 4.5 | 0.1 | 0.51 | −1.65 |
| 16 | A4B1C3D5E2 | 3000 | 5 | 20 | 5.0 | 0.3 | 0.92 | 0.51 |
| 17 | A4B2C5D3E1 | 3000 | 10 | 30 | 4.0 | 0.1 | 0.13 | −1.33 |
| 18 | A4B3C2D1E5 | 3000 | 15 | 15 | 3.0 | 0.9 | 1.33 | 0.40 |
| 19 | A4B4C4D4E4 | 3000 | 20 | 25 | 4.5 | 0.7 | 0.99 | −0.65 |
| 20 | A4B5C1D2E3 | 3000 | 25 | 10 | 3.5 | 0.5 | 0.98 | −0.97 |
| 21 | A5B1C2D3E4 | 3400 | 5 | 15 | 4.0 | 0.7 | 1.33 | 1.19 |
| 22 | A5B2C4D1E3 | 3400 | 10 | 25 | 3.0 | 0.5 | 0.53 | −0.69 |
| 23 | A5B3C1D4E2 | 3400 | 15 | 10 | 4.5 | 0.3 | 0.96 | −0.15 |
| 24 | A5B4C3D2E1 | 3400 | 20 | 20 | 3.5 | 0.1 | 0.1 | −1.99 |
| 25 | A5B5C5D5E5 | 3400 | 25 | 30 | 5.0 | 0.9 | 1.02 | −1.16 |
| Test Number | Test Factors | ||||
|---|---|---|---|---|---|
| Density A | Size B | Angle C | Height D | Velocity E | |
| KII1 | 5.00 | 5.23 | 5.89 | 3.40 | 1.82 |
| KII2 | 4.90 | 4.83 | 5.21 | 4.20 | 3.2 |
| KII3 | 4.56 | 4.68 | 4.54 | 4.54 | 4.72 |
| KII4 | 4.35 | 4.14 | 3.88 | 5.21 | 5.86 |
| KII5 | 3.94 | 3.87 | 3.23 | 5.40 | 7.15 |
| II1 | 1.00 | 1.05 | 1.18 | 0.68 | 0.36 |
| II2 | 0.98 | 0.97 | 1.04 | 0.84 | 0.64 |
| II3 | 0.91 | 0.94 | 0.91 | 0.91 | 0.94 |
| II4 | 0.87 | 0.83 | 0.78 | 1.04 | 1.17 |
| II5 | 0.79 | 0.77 | 0.65 | 1.08 | 1.43 |
| RII | 0.21 | 0.27 | 0.53 | 0.40 | 1.07 |
| Test Number | Test Factors | ||||
|---|---|---|---|---|---|
| Density A | Size B | Dip angle C | Height D | Velocity E | |
| KIII1 | 0.16 | 3.70 | 1.21 | −3.01 | −5.52 |
| KIII2 | −0.58 | 0.97 | 0.02 | −1.85 | −3.12 |
| KIII3 | −1.32 | −0.92 | −1.24 | −1.32 | −1.31 |
| KIII4 | −2.04 | −4.01 | −2.57 | −0.38 | 0.89 |
| KIII5 | −2.80 | −6.32 | −4.00 | −0.02 | 2.48 |
| III1 | 0.03 | 0.74 | 0.24 | −0.60 | −1.10 |
| III2 | −0.12 | 0.19 | 0.00 | −0.37 | −0.62 |
| III3 | −0.26 | −0.18 | −0.25 | −0.26 | −0.26 |
| III4 | −0.41 | −0.80 | −0.51 | −0.08 | 0.18 |
| III5 | −0.56 | −1.26 | −0.80 | 0.00 | 0.50 |
| RIII | 0.59 | 2.00 | 1.04 | 0.60 | 1.60 |
| Density ρs kg/m3 | Size ds mm | Coefficient of Restitution e | Coefficient of Friction f | Poisson’s Ratio ν | Elastic Modulus G Mpa |
|---|---|---|---|---|---|
| 2600 | 10 | 0.5 | 0.1 | 0.25 | 10 |
| 15 | |||||
| 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, J.; Li, J.; Gu, S.; Liu, S.; Su, P.; Huang, R. Study of the Motion Path of Water-Intercepting Aggregate in a Coal–Rock Mass Water Gush Roadway. Water 2025, 17, 2956. https://doi.org/10.3390/w17202956
Wen J, Li J, Gu S, Liu S, Su P, Huang R. Study of the Motion Path of Water-Intercepting Aggregate in a Coal–Rock Mass Water Gush Roadway. Water. 2025; 17(20):2956. https://doi.org/10.3390/w17202956
Chicago/Turabian StyleWen, Jiahao, Jinhua Li, Shuancheng Gu, Suliu Liu, Peili Su, and Rongbin Huang. 2025. "Study of the Motion Path of Water-Intercepting Aggregate in a Coal–Rock Mass Water Gush Roadway" Water 17, no. 20: 2956. https://doi.org/10.3390/w17202956
APA StyleWen, J., Li, J., Gu, S., Liu, S., Su, P., & Huang, R. (2025). Study of the Motion Path of Water-Intercepting Aggregate in a Coal–Rock Mass Water Gush Roadway. Water, 17(20), 2956. https://doi.org/10.3390/w17202956






