Thermodynamic Experiments and Modelling of Cyclopentane Hydrates in the Presence of NaBr, KBr, K2SO4, NaBr–KBr, NaCl–NaBr, KCl–KBr, Na2SO4–K2SO4, and CaCl2–MgCl2
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Apparatus
2.3. Quick Dissociation Procedure
2.4. Slow Dissociation Procedure
3. Experimental Results
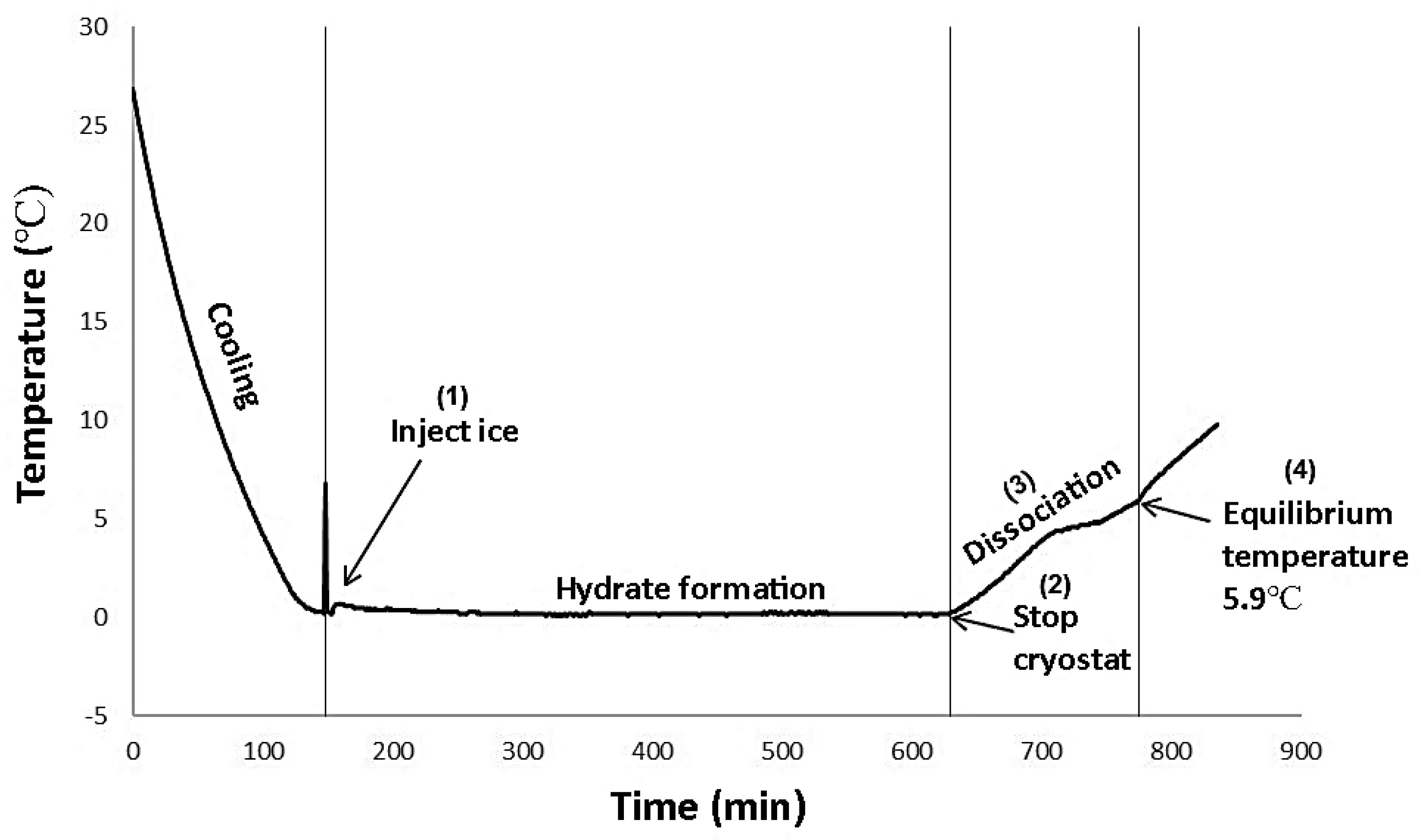
3.1. The Behavior of CPH Formation and Dissociation
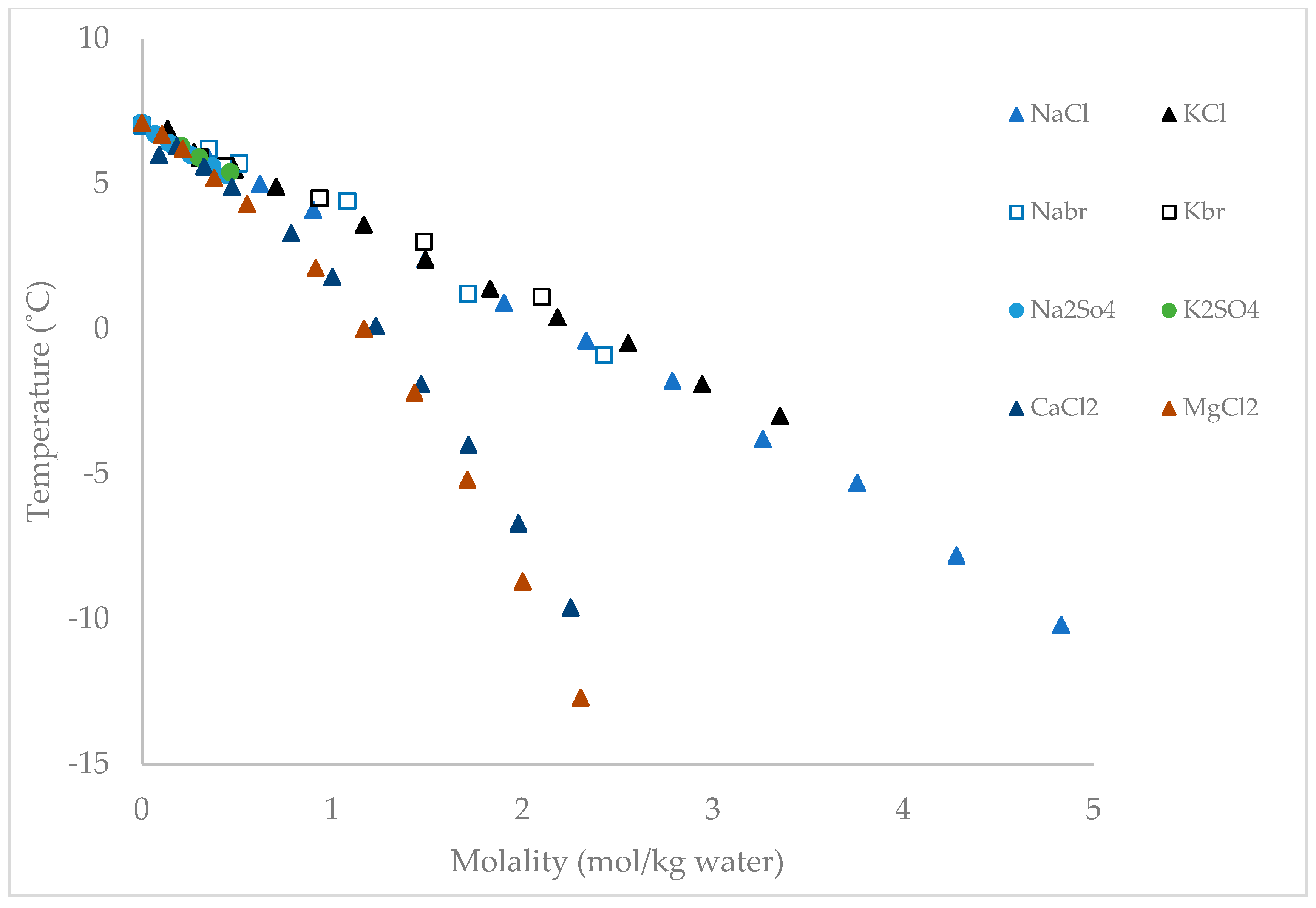
3.2. Experimental Dissociation Data of CPH in the Presence of Salts
4. Modeling CPH Thermodynamic Equilibrium
4.1. SFPD Approach
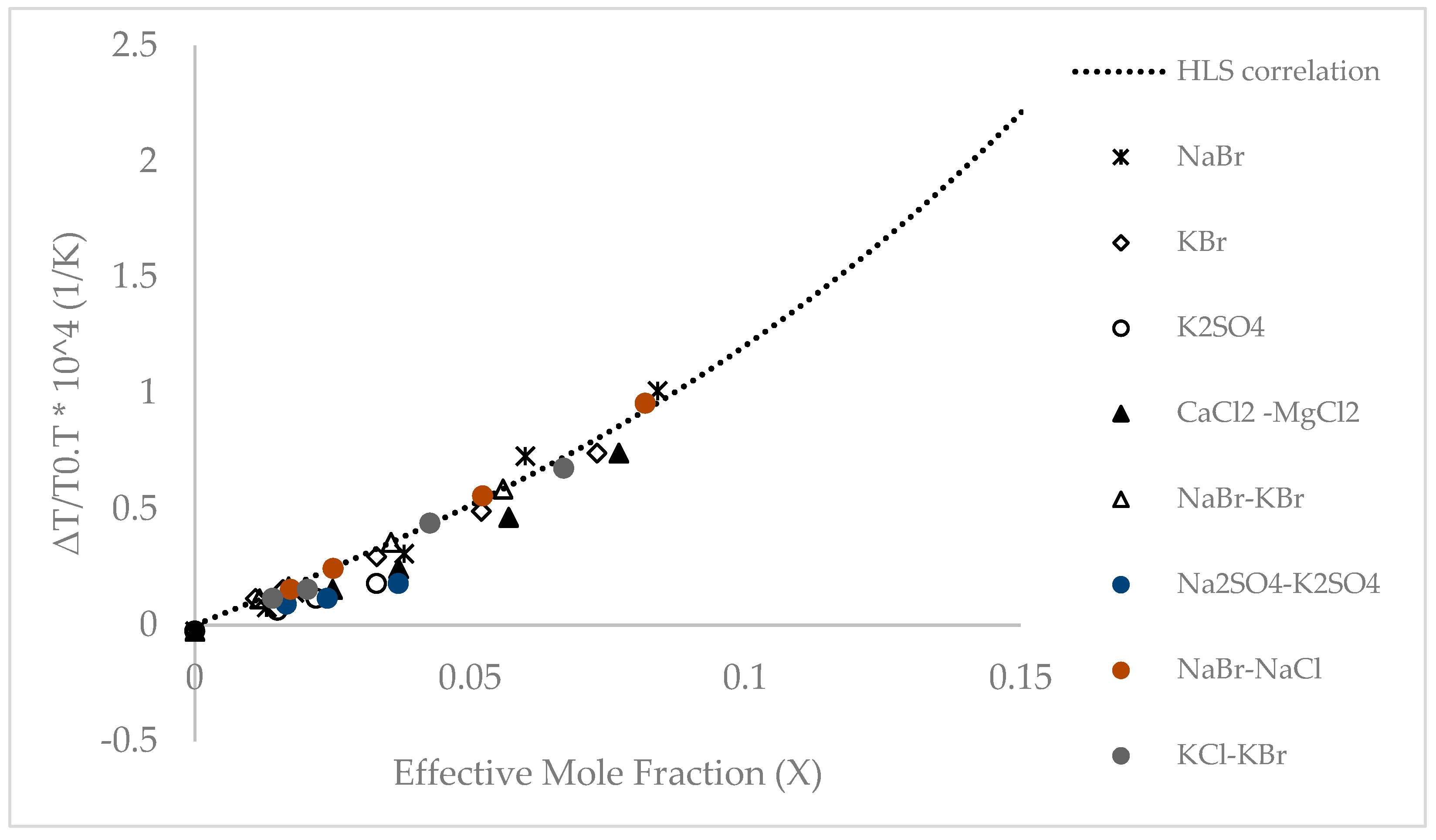
4.2. HLS Correlation
4.3. Kihara Approach
- (i)
- Each cavity encloses only one guest molecule
- (ii)
- The interaction between the guest molecule and the cavity can be described by a pair of the potential functions of the pair guest molecule
- (iii)
- The cavities are perfectly spherical
- (iv)
- Guest molecules do not deform cavities
- (v)
- There is no interaction between the guest molecules in different cavities.
4.4. ABOC Approach
5. Modeling Results
5.1. SFPD Approach
5.2. HLS Correlation
5.3. Kihara Approach
5.4. ABOC Approach
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Initial Conditions for Experiments
| No. | wt.% a,d,e | NaCl b (g) | NaBr b (g) | KBr b (g) | KCl b (g) | MgCl2 b (g) | CaCl2 b (g) | Na2SO4 b (g) | K2SO4 b (g) | msolution b (g) | msalt add b (g) | mice add b (g) | mCP c (mL) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 400 | 0 | 3 | 121.54 |
| 2 | 3.5 | 0 | 14.51 | 0 | 0 | 0 | 0 | 0 | 0 | 414.53 | 0.11 | 3 | 121.54 |
| 3 | 5.0 | 0 | 21.05 | 0 | 0 | 0 | 0 | 0 | 0 | 421.11 | 0.16 | 3 | 121.54 |
| 4 | 10.0 | 0 | 44.44 | 0 | 0 | 0 | 0 | 0 | 0 | 444.47 | 0.33 | 3 | 121.54 |
| 5 | 15.0 | 0 | 70.57 | 0 | 0 | 0 | 0 | 0 | 0 | 470.67 | 0.53 | 3 | 121.54 |
| 6 | 20.0 | 0 | 99.97 | 0 | 0 | 0 | 0 | 0 | 0 | 500.27 | 0.75 | 3 | 121.54 |
| 7 | 3.5 | 0 | 0 | 14.51 | 0 | 0 | 0 | 0 | 0 | 414.51 | 0.11 | 3 | 121.82 |
| 8 | 5.0 | 0 | 0 | 21.05 | 0 | 0 | 0 | 0 | 0 | 421.02 | 0.16 | 3 | 121.82 |
| 9 | 10.0 | 0 | 0 | 44.44 | 0 | 0 | 0 | 0 | 0 | 444.44 | 0.33 | 3 | 121.82 |
| 10 | 15.0 | 0 | 0 | 70.59 | 0 | 0 | 0 | 0 | 0 | 470.59 | 0.53 | 3 | 121.82 |
| 11 | 20.0 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 500 | 0.75 | 3 | 121.82 |
| 12 | 3.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14.51 | 414.51 | 0.11 | 3 | 121.82 |
| 13 | 5.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21.05 | 421.05 | 0.16 | 3 | 121.82 |
| 14 | 7.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 32.42 | 432.43 | 0.24 | 3 | 121.82 |
| 15 | 10.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 44.44 | 444.44 | 0.33 | 3 | 121.82 |
| 16 | 3.5 | 0 | 0 | 0 | 0 | 14.51 | 0 | 0 | 414.51 | 0.11 | 3 | 121.82 | |
| 17 | 5.0 | 0 | 0 | 0 | 0 | 21.05 | 0 | 0 | 421.05 | 0.16 | 3 | 121.82 | |
| 18 | 7.5 | 0 | 0 | 0 | 0 | 32.43 | 0 | 0 | 432.43 | 0.33 | 3 | 121.82 | |
| 19 | 10.0 | 0 | 0 | 0 | 0 | 44.44 | 0 | 0 | 444.44 | 0.53 | 3 | 121.82 | |
| 20 | 15.0 | 0 | 0 | 0 | 0 | 70.59 | 0 | 0 | 470.59 | 0.75 | 3 | 121.82 | |
| 21 | 3.5 | 0 | 14.51 | 0 | 0 | 0 | 0 | 0 | 414.51 | 0.11 | 3 | 121.82 | |
| 22 | 5.0 | 0 | 21.05 | 0 | 0 | 0 | 0 | 0 | 421.05 | 0.16 | 3 | 121.82 | |
| 23 | 10.0 | 0 | 44.44 | 0 | 0 | 0 | 0 | 0 | 444.44 | 0.33 | 3 | 121.82 | |
| 24 | 15.0 | 0 | 70.59 | 0 | 0 | 0 | 0 | 0 | 470.59 | 0.53 | 3 | 121.82 | |
| 25 | 20.0 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 500 | 0.75 | 3 | 121.82 | |
| 26 | 3.5 | 0 | 0 | 0 | 0 | 0 | 0 | 14.51 | 414.51 | 0.11 | 3 | 121.82 | |
| 27 | 5.0 | 0 | 0 | 0 | 0 | 0 | 0 | 21.05 | 421.05 | 0.16 | 3 | 121.82 | |
| 28 | 7.5 | 0 | 0 | 0 | 0 | 0 | 0 | 32.43 | 432.43 | 0.24 | 3 | 121.82 | |
| 29 | 3.5 | 7.25 | 7.25 | 0 | 0 | 0 | 0 | 0 | 0 | 414.5 | 0.11 | 3 | 121.82 |
| 30 | 5.0 | 10.53 | 10.53 | 0 | 0 | 0 | 0 | 0 | 0 | 421.06 | 0.16 | 3 | 121.82 |
| 31 | 10.0 | 22.22 | 22.22 | 0 | 0 | 0 | 0 | 0 | 0 | 444.44 | 0.33 | 3 | 121.82 |
| 32 | 15.0 | 35.29 | 35.29 | 0 | 0 | 0 | 0 | 0 | 0 | 470.58 | 0.53 | 3 | 121.82 |
| 33 | 20.0 | 50 | 50 | 0 | 0 | 0 | 0 | 0 | 0 | 500 | 0.75 | 3 | 121.82 |
| 34 | 3.5 | 0 | 0 | 7.25 | 7.25 | 0 | 0 | 0 | 0 | 414.5 | 0.11 | 3 | 121.82 |
| 35 | 5.0 | 0 | 0 | 10.53 | 10.53 | 0 | 0 | 0 | 0 | 421.06 | 0.16 | 3 | 121.82 |
| 36 | 10.0 | 0 | 0 | 22.22 | 22.22 | 0 | 0 | 0 | 0 | 444.44 | 0.33 | 3 | 121.82 |
| 37 | 15.0 | 0 | 0 | 35.29 | 35.29 | 0 | 0 | 0 | 0 | 470.58 | 0.53 | 3 | 121.82 |
| 38 | 20.0 | 0 | 0 | 50 | 50 | 0 | 0 | 0 | 0 | 500 | 0.75 | 3 | 121.82 |
| No. | wt.% a,c,d,e | NaCl b (g) | NaBr b (g) | KBr b (g) | KCl b (g) | MgCl2 b (g) | CaCl2 b (g) | Na2SO4 b (g) | K2SO4 b (g) | msolution b (g) | msalt add b (g) | mice add b (g) | mCP b (g) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 600 | - | 5 | |
| 2 | 3.5 | 0 | 16.9767 | 0 | 0 | 0 | 0 | 0 | 0 | 485.0767 | - | 3.8 | |
| 3 | 5.0 | 0 | 30.0879 | 0 | 0 | 0 | 0 | 0 | 0 | 600.2 | - | 1.6 | |
| 4 | 10.0 | 0 | 60.278 | 0 | 0 | 0 | 0 | 0 | 0 | 602.77 | - | 1 | |
| 5 | 15.0 | 0 | 90.04 | 0 | 0 | 0 | 0 | 0 | 0 | 600.95 | 0.87 | 4.9 | |
| 6 | 20.0 | 0 | 100.367 | 0 | 0 | 0 | 0 | 0 | 0 | 500.17 | - | 1.689 | |
| 7 | 3.5 | 0 | 0 | 17.656 | 0 | 0 | 0 | 0 | 0 | 503.22 | - | 1.134 | |
| 8 | 5.0 | 0 | 0 | 25.104 | 0 | 0 | 0 | 0 | 0 | 500.14 | - | 0.976 | |
| 9 | 10.0 | 0 | 0 | 50.121 | 0 | 0 | 0 | 0 | 0 | 500.28 | - | 0.43 | |
| 10 | 15.0 | 0 | 0 | 75.119 | 0 | 0 | 0 | 0 | 0 | 500.11 | - | 0.7 | |
| 11 | 20.0 | 0 | 0 | 100.22 | 0 | 0 | 0 | 0 | 0 | 499.97 | - | 0.544 | |
| 12 | 3.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21.03 | 600.41 | - | 0.5 | 52.67 |
| 13 | 5.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 600 | - | 1.2 | 52.67 |
| 14 | 7.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 45.01 | 600.49 | - | 0.2 | 49.45 |
| 15 | 3.5 | 0 | 0 | 0 | 0 | 10.5 | 10.53 | 0 | 0 | 601.76 | - | 1 | 48.11 |
| 16 | 5.0 | 0 | 0 | 0 | 0 | 15 | 15.03 | 0 | 0 | 603.35 | - | 1.16 | 44.28 |
| 17 | 7.5 | 0 | 0 | 0 | 0 | 22.5 | 22.52 | 0 | 0 | 600.12 | - | 2.4 | 44.15 |
| 18 | 10.0 | 0 | 0 | 0 | 0 | 30 | 30.01 | 0 | 0 | 600.52 | - | 1.6 | 48.39 |
| 19 | 3.5 | 0 | 17.50 | 17.50 | 0 | 0 | 0 | 0 | 0 | 1000.27 | 0 | 0.16 | |
| 20 | 5.0 | 0 | 15.00 | 15.02 | 0 | 0 | 0 | 0 | 0 | 600.11 | 0 | 0.26 | |
| 21 | 10 | 0 | 30.00 | 30.02 | 0 | 0 | 0 | 0 | 0 | 600.19 | 0 | 0.08 | |
| 22 | 15 | 0 | 45.01 | 44.99 | 0 | 0 | 0 | 0 | 0 | 600.04 | 0 | 0.10 | |
| 23 | 3.5 | 0 | 0 | 0 | 0 | 0 | 0 | 17.5 | 17.51 | 1000.01 | - | 1.18 | |
| 24 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 25.05 | 25 | 1005.82 | - | 1.13 | |
| 25 | 7.5 | 0 | 0 | 0 | 0 | 0 | 0 | 37.6 | 37.04 | 1000.29 | - | 1.06 | |
| 26 | 3.5 | 17.5 | 17.518 | 0 | 0 | 0 | 0 | 0 | 0 | 1000.05 | - | 0.77 | |
| 27 | 5 | 25 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 1000.08 | - | 0.57 | |
| 28 | 10 | 50.01 | 50.01 | 0 | 0 | 0 | 0 | 0 | 0 | 1000.53 | - | 0.71 | |
| 29 | 15 | 75.01 | 75.02 | 0 | 0 | 0 | 0 | 0 | 0 | 1002.73 | - | 1.8 | |
| 30 | 20 | 100 | 100.02 | 0 | 0 | 0 | 0 | 0 | 0 | 1000.02 | - | 3.32 | |
| 31 | 3.5 | 0 | 0 | 17.56 | 17.54 | 0 | 0 | 0 | 0 | 1000.05 | - | 1.54 | |
| 32 | 5 | 0 | 0 | 25.01 | 25 | 0 | 0 | 0 | 0 | 1000.26 | - | 1.06 | |
| 33 | 10 | 0 | 0 | 50 | 50.02 | 0 | 0 | 0 | 0 | 1001.37 | - | 1.38 | |
| 34 | 15 | 0 | 0 | 75.008 | 74.448 | 0 | 0 | 0 | 0 | 1025.25 | - | 1.37 | |
| 35 | 20 | 0 | 0 | 100.07 | 100.28 | 0 | 0 | 0 | 0 | 1000.35 | - | 1.38 |
Appendix B. Experimental Results
| Solution Concentration (wt.%) | Te-quick a (°C) (400 rpm) | Te-quick a (°C) (500 rpm) | Te-slow a (°C) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NaCl b,c,d | NaBr b,c,d | KBr b,c,d | KCl b,c,d | MgCl2 b,c,d | CaCl2 b,c,d | Na2SO4 b,c,d | K2SO4 b,c,d | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7.3 | - | 7 |
| 0 | 3.50 | 0 | 0 | 0 | 0 | 0 | 0 | 6.3 | - | 6.2 |
| 0 | 5.00 | 0 | 0 | 0 | 0 | 0 | 0 | 5.9 | - | 5.7 |
| 0 | 10.00 | 0 | 0 | 0 | 0 | 0 | 0 | 4.6 | - | 4.4 |
| 0 | 15.00 | 0 | 0 | 0 | 0 | 0 | 0 | 2.3 | - | 1.2 |
| 0 | 20.00 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | - | −0.9 |
| 0 | 0 | 3.50 | 0 | 0 | 0 | 0 | 0 | 6.6 | 6.4 | 5.9 |
| 0 | 0 | 5.00 | 0 | 0 | 0 | 0 | 0 | 6.2 | 6 | 5.6 |
| 0 | 0 | 10.00 | 0 | 0 | 0 | 0 | 0 | 5.2 | 4.7 | 4.5 |
| 0 | 0 | 15.00 | 0 | 0 | 0 | 0 | 0 | 3.5 | 3 | 3 |
| 0 | 0 | 20.00 | 0 | 0 | 0 | 0 | 0 | 2.3 | 1.4 | 1.1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3.50 | 6.6 | 6.6 | 6.3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5.00 | 6.4 | 6.2 | 5.9 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7.50 | - | 5.9 | 5.4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10.00 | - | 5.8 | - |
| 0 | 0 | 0 | 0 | 1.75 | 1.75 | 0 | 0 | - | 5.6 | 5.6 |
| 0 | 0 | 0 | 0 | 2.50 | 2.50 | 0 | 0 | - | 4.8 | 4.9 |
| 0 | 0 | 0 | 0 | 3.75 | 3.75 | 0 | 0 | - | 3.3 | 3.2 |
| 0 | 0 | 0 | 0 | 5.00 | 5.00 | 0 | 0 | - | 1 | 1.1 |
| 0 | 0 | 0 | 0 | 7.50 | 7.50 | 0 | 0 | - | 0.3 | - |
| 0 | 1.75 | 1.75 | 0 | 0 | 0 | 0 | 0 | - | 6.3 | 5.3 |
| 0 | 2.50 | 2.50 | 0 | 0 | 0 | 0 | 0 | - | 5.8 | 5.5 |
| 0 | 5.00 | 5.00 | 0 | 0 | 0 | 0 | 0 | - | 4.4 | 3.8 |
| 0 | 7.50 | 7.50 | 0 | 0 | 0 | 0 | 0 | - | 2.4 | 1.9 |
| 0 | 10.00 | 10.00 | 0 | 0 | 0 | 0 | 0 | - | 0.4 | - |
| 0 | 0 | 0 | 0 | 0 | 0 | 1.75 | 1.75 | - | 6.4 | 6.1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 2.50 | 2.50 | - | 6.1 | 5.9 |
| 0 | 0 | 0 | 0 | 0 | 0 | 3.75 | 3.75 | - | 5.5 | 5.4 |
| 1.75 | 1.75 | 0 | 0 | 0 | 0 | 0 | 0 | - | 6.1 | 5.6 |
| 2.50 | 2.50 | 0 | 0 | 0 | 0 | 0 | 0 | - | 5.3 | 4.9 |
| 5.00 | 5.00 | 0 | 0 | 0 | 0 | 0 | 0 | - | 2.7 | 2.5 |
| 7.50 | 7.50 | 0 | 0 | 0 | 0 | 0 | 0 | - | −0.2 | −0.5 |
| 10.00 | 10.00 | 0 | 0 | 0 | 0 | 0 | 0 | - | −3.1 | −4.0 |
| 0 | 0 | 1.75 | 1.75 | 0 | 0 | 0 | 0 | - | 6.1 | 5.9 |
| 0 | 0 | 2.50 | 2.50 | 0 | 0 | 0 | 0 | - | 5.5 | 5.6 |
| 0 | 0 | 5.00 | 5.00 | 0 | 0 | 0 | 0 | - | 3.7 | 3.4 |
| 0 | 0 | 7.50 | 7.50 | 0 | 0 | 0 | 0 | - | 1.2 | 1.6 |
| 0 | 0 | 10.00 | 10.00 | 0 | 0 | 0 | 0 | - | −0.8 | −0.9 |
Appendix C. Equilibrium Temperature of CPH in the Presence of Na2SO4, CaCl2, MgCl2, NaCl, and KCl [27,30]
| Concentration a,b,c (wt.%) | in Na2SO4 d (°C) | in CaCl2 d (°C) | in MgCl2 d (°C) | in NaCl d (°C) | in KCl d (°C) |
|---|---|---|---|---|---|
| 0 | 7.1 | 7.1 | 7.1 | 7.1 | 7.1 |
| 1 | 6.7 | 6 | 6.7 | 6.4 | 6.9 |
| 2 | 6.4 | 6.3 | 6.2 | 5.9 | 6.1 |
| 3.5 | 6 | 5.6 | 5.2 | 5 | 5.5 |
| 5 | 5.6 | 4.9 | 4.3 | 4.1 | 4.9 |
| 6 | 5.3 | - | - | - | - |
| 8 | - | 3.3 | 2.1 | 2.4 | 3.6 |
| 10 | - | 1.8 | 0 | 0.9 | 2.4 |
| 12 | - | 0.1 | −2.2 | −0.4 | 1.4 |
| 14 | - | −1.9 | −5.2 | −1.8 | 0.4 |
| 16 | - | −4 | −8.7 | −3.8 | −0.5 |
| 18 | - | −6.7 | −12.7 | −5.3 | −1.9 |
| 20 | - | −9.6 | −17.6 | −7.8 | −3 |
| 22 | - | −13.2 | - | −10.2 | - |
| 23 | - | −15.1 | - | −11.6 | - |
| 25 | - | −19.6 | - | - | - |
Appendix D. Molarity, Water Activity, and Effective Mole Fraction
| Concentration (wt.%) | K2SO4 | KBr | NaBr-KBr | NaBr | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Molarity | Water Activity | X | Molarity | Water Activity | X | Molarity | Water Activity | X | Molarity | Water Activity | X | |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 3.5 | 0.208 | 0.992 | 0.015 | 0.305 | 0.99 | 0.011 | 0.329 | 0.989 | 0.012 | 0.353 | 0.988 | 0.013 |
| 5 | 0.302 | 0.989 | 0.022 | 0.442 | 0.986 | 0.016 | 0.477 | 0.984 | 0.017 | 0.512 | 0.983 | 0.018 |
| 7.5 | 0.465 | 0.983 | 0.033 | - | - | - | - | - | - | - | - | - |
| 10 | 0.638 | 0.978 | 0.045 | 0.934 | 0.97 | 0.033 | 1.007 | 0.967 | 0.036 | 1.08 | 0.964 | 0.038 |
| 15 | - | - | - | 1.483 | 0.953 | 0.052 | 1.599 | 0.948 | 0.056 | 1.715 | 0.941 | 0.060 |
| 20 | - | - | - | 2.101 | 0.934 | 0.073 | 2.265 | 0.925 | 0.078 | 2.43 | 0.914 | 0.084 |
| Concentration (wt.%) | NaCl-NaBr | KCl-KBr | CaCl2-MgCl2 | Na2SO4-K2SO4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Molarity | Water Activity | X | Molarity | Water Activity | X | Molarity | Water Activity | X | Molarity | Water Activity | X | |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 3.5 | 0.487 | 0.984 | 0.017 | 0.396 | 0.987 | 0.014 | 0.354 | 0.983 | 0.025 | 0.232 | 0.991 | 0.017 |
| 5 | 0.706 | 0.977 | 0.025 | 0.574 | 0.982 | 0.020 | 0.514 | 0.974 | 0.037 | 0.336 | 0.988 | 0.024 |
| 7.5 | - | - | - | - | - | - | 0.791 | 0.957 | 0.057 | 0.518 | 0.982 | 0.037 |
| 10 | 1.491 | 0.95 | 0.052 | 1.212 | 0.962 | 0.043 | 1.084 | 0.936 | 0.077 | - | - | - |
| 15 | 2.367 | 0.919 | 0.082 | 1.925 | 0.94 | 0.067 | 1.722 | - | - | - | - | - |
| 20 | 3.354 | 0.881 | 0.114 | 2.727 | 0.915 | 0.094 | - | - | - | - | - | - |
| wt.% | Na2SO4 | CaCl2 | MgCl2 | NaCl | KCl | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Molarity | Water Activity | X | Molarity | Water Activity | X | Molarity | Water Activity | X | Molarity | Water Activity | X | Molarity | Water Activity | X | |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 0.071 | 0.997 | 0.005 | 0.091 | 0.996 | 0.007 | 0.106 | 0.995 | 0.008 | 0.173 | 0.994 | 0.0062 | 0.135 | 0.996 | 0.0049 |
| 2 | 0.144 | 0.994 | 0.01 | 0.184 | 0.991 | 0.013 | 0.214 | 0.99 | 0.015 | 0.349 | 0.989 | 0.0125 | 0.274 | 0.991 | 0.0098 |
| 3.5 | 0.255 | 0.99 | 0.018 | 0.327 | 0.984 | 0.023 | 0.381 | 0.981 | 0.027 | 0.621 | 0.98 | 0.0221 | 0.487 | 0.984 | 0.0174 |
| 5 | 0.371 | 0.986 | 0.027 | 0.474 | 0.977 | 0.034 | 0.553 | 0.971 | 0.039 | 0.901 | 0.971 | 0.0319 | 0.706 | 0.978 | 0.0251 |
| 6 | 0.449 | 0.984 | 0.032 | - | - | - | 0.67 | 0.048 | - | - | - | - | - | - | |
| 8 | - | - | - | 0.784 | 0.959 | 0.056 | 0.913 | 0.947 | 0.065 | 1.489 | 0.951 | 0.0522 | 1.166 | 0.963 | 0.0411 |
| 10 | - | - | - | 1.001 | 0.944 | 0.071 | 1.167 | 0.926 | 0.082 | 1.903 | 0.937 | 0.0662 | 1.49 | 0.954 | 0.0523 |
| 12 | - | - | - | 1.229 | 0.927 | 0.087 | 1.432 | 0.902 | 0.101 | 2.335 | 0.922 | 0.0807 | 1.829 | 0.943 | 0.0638 |
| 14 | - | - | - | 1.467 | 0.907 | 0.103 | 1.71 | 0.872 | 0.119 | 2.788 | 0.906 | 0.0956 | 2.184 | 0.932 | 0.0756 |
| 16 | - | - | - | 1.716 | 0.885 | 0.12 | 2.001 | 0.838 | 0.139 | 3.262 | 0.888 | 0.1109 | 2.555 | 0.921 | 0.0879 |
| 18 | - | - | - | 1.978 | 0.859 | 0.138 | 2.306 | 0.798 | 0.159 | 3.759 | 0.869 | 0.1267 | 2.944 | 0.909 | 0.1007 |
| 20 | - | - | - | 2.253 | 0.83 | 0.156 | 2.626 | 0.751 | 0.181 | 4.281 | 0.848 | 0.1431 | 3.353 | 0.896 | 0.1139 |
| 22 | - | - | - | - | - | - | - | - | - | 4.83 | 0.824 | 0.16 | - | - | - |
| 23 | - | - | - | - | - | - | - | - | - | 5.115 | 0.812 | 0.1686 | - | - | - |

Appendix E. Modeling Results of CPH in the Presence of Salts
| Solution Concentration (wt.%) | SFPD | HLS | Kihara | ABOC | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NaCl (wt.%) | NaBr (wt.%) | KBr (wt.%) | KCl (wt.%) | MgCl2 (wt.%) | CaCl2 (wt.%) | Na2SO4 (wt.%) | K2SO4 (wt.%) | Texp (°C) | Tpred (°C) | ΔT (°C) | Tpred (°C) | ΔT (°C) | Tpred (°C) | ΔT (°C) | Tpred (°C) | ΔT (°C) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 6.8 | 0.2 | 6.8 | 0.2 | 7.3 | 0.3 | 6.88 | 0.12 |
| 0 | 3.50 | 0 | 0 | 0 | 0 | 0 | 0 | 6.2 | 5.65 | 0.55 | 5.82 | 0.38 | 6.17 | 0.03 | 5.78 | 0.42 |
| 0 | 5.00 | 0 | 0 | 0 | 0 | 0 | 0 | 5.7 | 5.2 | 0.5 | 5.43 | 0.27 | 5.7 | 0.00 | 5.32 | 0.38 |
| 0 | 10.00 | 0 | 0 | 0 | 0 | 0 | 0 | 4.4 | 3.56 | 0.84 | 3.83 | 0.57 | 3.88 | 0.52 | 3.55 | 0.85 |
| 0 | 15.00 | 0 | 0 | 0 | 0 | 0 | 0 | 1.2 | 1.55 | 0.35 | 1.9 | 0.7 | 1.69 | 0.49 | 1.37 | 0.17 |
| 0 | 20.00 | 0 | 0 | 0 | 0 | 0 | 0 | −0.9 | −0.96 | 0.06 | −0.51 | 0.39 | −1.01 | 0.11 | −1.23 | 0.33 |
| AAD | 0.42 | AAD | 0.42 | AAD | 0.24 | AAD | 0.38 | |||||||||
| 0 | 0 | 3.50 | 0 | 0 | 0 | 0 | 0 | 5.9 | 5.83 | 0.07 | 5.97 | 0.07 | 6.37 | 0.47 | 5.96 | 0.06 |
| 0 | 0 | 5.00 | 0 | 0 | 0 | 0 | 0 | 5.6 | 5.47 | 0.13 | 5.59 | 0.01 | 6 | 0.4 | 5.59 | 0.01 |
| 0 | 0 | 10.00 | 0 | 0 | 0 | 0 | 0 | 4.5 | 4.07 | 0.43 | 4.24 | 0.26 | 4.47 | 0.03 | 4.11 | 0.39 |
| 0 | 0 | 15.00 | 0 | 0 | 0 | 0 | 0 | 3 | 2.61 | 0.39 | 2.63 | 0.37 | 2.83 | 0.17 | 2.51 | 0.49 |
| 0 | 0 | 20.00 | 0 | 0 | 0 | 0 | 0 | 1.1 | 0.92 | 0.18 | 0.64 | 0.46 | 0.98 | 0.12 | 0.70 | 0.40 |
| AAD | 0.23 | AAD | 0.23 | AAD | 0.25 | AAD | 0.25 | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3.50 | 6.3 | 6.02 | 0.28 | 5.66 | 0.64 | 6.55 | 0.25 | 6.15 | 0.15 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5.00 | 5.9 | 5.74 | 0.16 | 5.12 | 0.78 | 6.28 | 0.38 | 5.87 | 0.03 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7.50 | 5.4 | 5.2 | 0.2 | 4.24 | 1.16 | 5.71 | 0.31 | 5.32 | 0.08 |
| AAD | 0.21 | AAD | 0.69 | AAD | 0.31 | AAD | 0.10 | |||||||||
| 0 | 0 | 0 | 0 | 1.75 | 1.75 | 0 | 0 | 5.6 | 5.2 | 0.4 | 4.89 | 0.71 | 5.7 | 0.1 | 5.32 | 0.28 |
| 0 | 0 | 0 | 0 | 2.50 | 2.50 | 0 | 0 | 4.9 | 4.41 | 0.49 | 3.92 | 0.98 | 4.85 | 0.05 | 4.48 | 0.42 |
| 0 | 0 | 0 | 0 | 3.75 | 3.75 | 0 | 0 | 3.2 | 2.95 | 0.25 | 2.18 | 1.02 | 3.23 | 0.03 | 2.89 | 0.31 |
| 0 | 0 | 0 | 0 | 5.00 | 5.00 | 0 | 0 | 1.1 | 1.1 | 0.00 | 0.23 | 0.87 | 1.19 | 0.09 | 0.89 | 0.21 |
| AAD | 0.27 | AAD | 0.76 | AAD | 0.11 | AAD | 0.27 | |||||||||
| 0 | 1.75 | 1.75 | 0 | 0 | 0 | 0 | 0 | 5.3 | 5.74 | 0.44 | 5.91 | 0.61 | 6.30 | 1.00 | 5.87 | 0.57 |
| 0 | 2.50 | 2.50 | 0 | 0 | 0 | 0 | 0 | 5.5 | 5.29 | 0.21 | 5.51 | 0.01 | 5.80 | 0.30 | 5.41 | 0.09 |
| 0 | 5.00 | 5.00 | 0 | 0 | 0 | 0 | 0 | 3.8 | 3.81 | 0.01 | 4.03 | 0.23 | 4.20 | 0.40 | 3.83 | 0.03 |
| 0 | 7.50 | 7.50 | 0 | 0 | 0 | 0 | 0 | 1.9 | 2.17 | 0.27 | 2.27 | 0.37 | 2.37 | 0.47 | 2.04 | 0.14 |
| AAD | 0.23 | AAD | 0.28 | AAD | 0.49 | AAD | 0.19 | |||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1.75 | 1.75 | 6.1 | 5.92 | 0.18 | 5.54 | 0.56 | 6.45 | 0.35 | 6.05 | 0.05 |
| 0 | 0 | 0 | 0 | 0 | 0 | 2.50 | 2.50 | 5.9 | 5.65 | 0.25 | 4.96 | 0.94 | 6.17 | 0.27 | 5.78 | 0.12 |
| 0 | 0 | 0 | 0 | 0 | 0 | 3.75 | 3.75 | 5.4 | 5.11 | 0.29 | 3.92 | 1.48 | 5.60 | 0.20 | 5.22 | 0.18 |
| AAD | 0.23 | AAD | 0.79 | AAD | 0.28 | AAD | 0.12 | |||||||||
| 1.75 | 1.75 | 0 | 0 | 0 | 0 | 0 | 0 | 5.6 | 5.29 | 0.31 | 5.48 | 0.12 | 5.79 | 0.19 | 5.41 | 0.19 |
| 2.50 | 2.50 | 0 | 0 | 0 | 0 | 0 | 0 | 4.9 | 4.67 | 0.23 | 4.88 | 0.02 | 5.13 | 0.23 | 4.76 | 0.14 |
| 5.00 | 5.00 | 0 | 0 | 0 | 0 | 0 | 0 | 2.5 | 2.34 | 0.16 | 2.6 | 0.10 | 2.55 | 0.05 | 2.23 | 0.27 |
| 7.50 | 7.50 | 0 | 0 | 0 | 0 | 0 | 0 | −0.5 | −0.48 | 0.02 | −0.27 | 0.23 | −0.50 | 0.00 | −0.74 | 0.24 |
| 10.00 | 10.00 | 0 | 0 | 0 | 0 | 0 | 0 | −4.0 | −4.36 | 0.36 | −4.1 | 0.10 | −4.37 | 0.37 | −4.47 | 0.47 |
| AAD | 0.21 | AAD | 0.13 | AAD | 0.19 | AAD | 0.24 | |||||||||
| 0 | 0 | 1.75 | 1.75 | 0 | 0 | 0 | 0 | 5.9 | 5.56 | 0.34 | 5.73 | 0.17 | 6.07 | 0.17 | 5.69 | 0.21 |
| 0 | 0 | 2.50 | 2.50 | 0 | 0 | 0 | 0 | 5.6 | 5.11 | 0.49 | 5.24 | 0.36 | 5.60 | 0.00 | 5.22 | 0.38 |
| 0 | 0 | 5.00 | 5.00 | 0 | 0 | 0 | 0 | 3.4 | 3.38 | 0.02 | 3.44 | 0.04 | 3.70 | 0.30 | 3.36 | 0.04 |
| 0 | 0 | 7.50 | 7.50 | 0 | 0 | 0 | 0 | 1.6 | 1.46 | 0.14 | 1.23 | 0.37 | 1.57 | 0.03 | 1.28 | 0.32 |
| 0 | 0 | 10.00 | 10.00 | 0 | 0 | 0 | 0 | −0.9 | −0.87 | 0.03 | −1.59 | 0.69 | −0.90 | 0.00 | −1.13 | 0.23 |
| AAD | 0.20 | AAD | 0.30 | AAD | 0.13 | AAD | 0.22 | |||||||||
References
- Sloan, E.D.; Koh, C.A. Clathrate Hydrates of Natural Gases, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Sloan, E.D. Fundamental principles and applications of natural gas hydrates. Nature 2003, 426, 353–359. [Google Scholar] [CrossRef]
- Koh, C.A.; Sloan, E.D.; Sum, A.K.; Wu, D.T. Fundamentals and applications of gas hydrates. Annu. Rev. Chem. Biomol. Eng. 2011, 2, 237–257. [Google Scholar] [CrossRef]
- Sloan, E.D.; Koh, C.A.; Sum, A.; Ballard, A.L.; Creek, J.L.; Eaton, M.; Lachance, J.; McMullen, N.; Palermo, T.; Shoup, G.; et al. Natural Gas Hydrates in Flow Assurance; Gulf Professional Publishing (Elsevier): Oxford, UK, 2011. [Google Scholar]
- Mimachi, H.; Takeya, S.; Yoneyama, A.; Hyodo, K.; Takeda, T.; Gotoh, Y.; Murayama, T. Natural gas storage and transportation within gas hydrate of smaller particle: Size dependence of self-preservation phenomenon of natural gas hydrate. Chem. Eng. Sci. 2014, 118, 208–213. [Google Scholar] [CrossRef]
- Sun, Z.G.; Wang, R.; Ma, R.; Guo, K.; Fan, S. Natural gas storage in hydrates with the presence of promoters. Energy Convers. Manag. 2003, 44, 2733–2742. [Google Scholar] [CrossRef]
- Burnol, A.; Thinon, I.; Ruffine, L.; Herri, J.M. Influence of impurities (nitrogen and methane) on the CO2 storage capacity as sediment-hosted gas hydrates—Application in the area of the Celtic Sea and the Bay of Biscay. Int. J. Greenh. Gas Control 2015, 35, 96–109. [Google Scholar] [CrossRef]
- Babu, P.; Linga, P.; Kumar, R.; Englezos, P. A review of the hydrate based gas separation (HBGS) process for carbon dioxide pre-combustion capture. Energy 2015, 85, 261–279. [Google Scholar] [CrossRef]
- Herslund, P.J.; Thomsen, K.; Abildskov, J.; von Solms, N.; Galfré, A.; Brântuas, P.; Kwaterski, M.; Herri, J.-M. Thermodynamic promotion of carbon dioxide-clathrate hydrate formation by tetrahydrofuran, cyclopentane and their mixtures. Int. J. Greenh. Gas Control 2013, 17, 397–410. [Google Scholar] [CrossRef]
- Herri, J.-M.; Bouchemoua, A.; Kwaterski, M.; Brântuas, P.; Galfré, A.; Bouillot, B.; Douzet, J.; Ouabbas, Y.; Cameirao, A. Enhanced selectivity of the separation of CO2 from N2 during crystallization of semi-clathrates from quaternary ammonium solutions. Oil Gas Sci. Technol. 2014, 69, 947–968. [Google Scholar] [CrossRef]
- Poothia, T.; Mehra, D.; Singh, J.; Rawat, P.B.S.; Pandey, G. Role of CO2 Capture and Sequestration (CCS) Using Gas Hydrate Based Technology for Sustainable Energy. Energy Proc. 2021, 20, 548. [Google Scholar] [CrossRef]
- Duc, N.H.; Chauvy, F.; Herri, J.M. CO2 capture by hydrate crystallization—A potential solution for gas emission of steelmaking industry. Energy Convers. Manag. 2007, 48, 1313–1322. [Google Scholar] [CrossRef]
- Yin, Z.; Zheng, J.; Kim, H.; Seo, Y.; Linga, P. Hydrates for cold energy storage and transport: A review. Adv. Appl. Energy 2021, 2, 100022. [Google Scholar] [CrossRef]
- Hashemi, H.; Babaee, S.; Mohammadi, A.H.; Naidoo, P.; Ramjugernath, D. Experimental study and modeling of the kinetics of refrigerant hydrate formation. J. Chem. Thermodyn. 2015, 82, 47–52. [Google Scholar] [CrossRef]
- Wang, X.; Dennis, M.; Hou, L. Clathrate hydrate technology for cold storage in air conditioning systems. Renew. Sustain. Energy Rev. 2014, 36, 34–51. [Google Scholar] [CrossRef]
- Hong, S.; Moon, S.; Lee, Y.; Lee, S.; Park, Y. Investigation of thermodynamic and kinetic effects of cyclopentane derivatives on CO2 hydrates for potential application to seawater desalination. Chem. Eng. J. 2019, 363, 99–106. [Google Scholar] [CrossRef]
- Ho-Van, S.; Bouillot, B.; Douzet, J.; Babakhani, S.M.; Herri, J.M. Cyclopentane hydrates—A candidate for desalination? J. Environ. Chem. Eng. 2019, 7, 103359. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, S.; Mao, N.; He, T. Progress and prospect of hydrate-based desalination technology. Front. Energy 2022, 16, 445–459. [Google Scholar] [CrossRef]
- Sahu, P.; Krishnaswamy, S.; Ponnani, K.; Pande, N.K. A thermodynamic approach to selection of suitable hydrate formers for seawater desalination. Desalination 2018, 436, 144–151. [Google Scholar] [CrossRef]
- Lv, Y.N.; Wang, S.S.; Sun, C.Y.; Gong, J.; Chen, G.J. Desalination by forming hydrate from brine in cyclopentane dispersion system. Desalination 2017, 413, 217–222. [Google Scholar] [CrossRef]
- Serikkali, A.; Van, H.N.; Pham, T.-K.; Le, Q.D.; Douzet, J.; Herri, J.-M.; Bouillot, B. Phase equilibrium and dissociation enthalpies of CO2/cyclopentane hydrates in presence of salts for water treatment and CO2 capture: New experimental data and modeling. Fluid Phase Equilib. 2022, 556, 113410. [Google Scholar] [CrossRef]
- Xu, H.; Khan, M.N.; Peters, C.J.; Sloan, E.D.; Koh, C.A. Hydrate-Based Desalination Using Cyclopentane Hydrates at Atmospheric Pressure. J. Chem. Eng. Data 2018, 63, 1081–1087. [Google Scholar] [CrossRef]
- Lee, J.; Kim, K.S.; Seo, Y. Thermodynamic, structural, and kinetic studies of cyclopentane + CO2 hydrates: Applications for desalination and CO2 capture. Chem. Eng. J. 2019, 375, 121974. [Google Scholar] [CrossRef]
- Han, S.; Rhee, Y.W.; Kang, S.P. Investigation of salt removal using cyclopentane hydrate formation and washing treatment for seawater desalination. Desalination 2017, 404, 132–137. [Google Scholar] [CrossRef]
- Ahmadpanah, S.J.; Manteghian, M.; Ganji, H. Effect of cyclopentane on hydrate-based desalination efficiency at different operating condition. J. Taiwan Inst. Chem. Eng. 2023, 143, 104653. [Google Scholar] [CrossRef]
- Parker, A. Potable water from sea-water. Nature 1942, 149, 184–186. [Google Scholar] [CrossRef]
- Ho-Van, S.; Bouillot, B.; Douzet, J.; Babakhani, S.M.; Herri, J.M. Implementing Cyclopentane Hydrates Phase Equilibrium Data and Simulations in Brine Solutions. Ind. Eng. Chem. Res. 2018, 57, 14774–14783. [Google Scholar] [CrossRef]
- Hassanpouryouzband, A.; Joonaki, E.; Farahani, M.V.; Takeya, S.; Ruppel, C.; Yang, J.; English, N.J.; Schicks, J.M.; Edlmann, K.; Mehrabian, H.; et al. Gas hydrates in sustainable chemistry. Chem. Soc. Rev. 2020, 49, 5225–5309. [Google Scholar] [CrossRef]
- Mezher, T.; Fath, H.; Abbas, Z.; Khaled, A. Techno-economic assessment and environmental impacts of desalination technologies. Desalination 2011, 266, 263–273. [Google Scholar] [CrossRef]
- Ho-Van, S.; Bouillot, B.; Douzet, J.; Babakhani, S.M.; Herri, J.M. Experimental measurement and thermodynamic modeling of cyclopentane hydrates with NaCl, KCl, CaCl2, or NaCl-KCl present. AIChE J. 2018, 64, 2207–2218. [Google Scholar] [CrossRef]
- Kamochi, K.; Tripathi, A.; Taoka, M.; Ohmura, R.; Yasuda, K. Phase equilibrium conditions in cyclopentane hydrate forming systems coexisting with sodium chloride aqueous solution under atmospheric pressure and vacuum condition. J. Chem. Thermodyn. 2022, 175, 106886. [Google Scholar] [CrossRef]
- Zylyftari, G.; Lee, J.W.; Morris, J.F. Salt effects on thermodynamic and rheological properties of hydrate forming emulsions. Chem. Eng. Sci. 2013, 95, 148–160. [Google Scholar] [CrossRef]
- Baek, S.; Min, J.; Lee, J.W. Equilibria of cyclopentane hydrates with varying HLB numbers of sorbitan monoesters in water-in-oil emulsions. Fluid Phase Equilib. 2016, 413, 41–47. [Google Scholar] [CrossRef]
- Kishimoto, M.; Iijima, S.; Ohmura, R. Crystal growth of clathrate hydrate at the interface between seawater and hydrophobic-guest liquid: Effect of elevated salt concentration. Ind. Eng. Chem. Res. 2012, 51, 5224–5229. [Google Scholar] [CrossRef]
- Sakemoto, R.; Sakamoto, H.; Shiraiwa, K.; Ohmura, R.; Uchida, T. Clathrate Hydrate Crystal Growth at the Seawater/Hydrophobic−Guest−Liquid Interface. Cryst. Growth Des. 2010, 10, 1296–1300. [Google Scholar] [CrossRef]
- Delroisse, H.; Torré, J.P.; Dicharry, C. Effect of a hydrophilic cationic surfactant on cyclopentane hydrate crystal growth at the water/cyclopentane interface. Cryst. Growth Des. 2017, 17, 5098–5107. [Google Scholar] [CrossRef]
- McAuliffe, C. Solubility in water of paraffin, cycloparaffin, olefin, acetylene, cycloolefin, and aromatic hydrocarbons. J. Phys. Chem. 1966, 70, 1267–1275. [Google Scholar] [CrossRef]
- Dean, J.A. LANGE’S HANDBOOK OF CHEMISTRY. Mater. Manuf. Process. 1990, 5, 687–688. [Google Scholar] [CrossRef]
- Sabil, K.M.; Román, V.R.; Witkamp, G.J.; Peters, C.J. Experimental observations on the competing effect of tetrahydrofuran and an electrolyte and the strength of hydrate inhibition among metal halides in mixed CO2 hydrate equilibria. J. Chem. Thermodyn. 2010, 42, 400–408. [Google Scholar] [CrossRef]
- Cha, M.; Hu, Y.; Sum, A.K. Methane hydrate phase equilibria for systems containing NaCl, KCl, and NH4Cl. Fluid Phase Equilib. 2016, 413, 2–9. [Google Scholar] [CrossRef]
- Ling, Z.; Shi, C.; Li, F.; Fu, Y.; Zhao, J.; Dong, H.; Yang, Y.; Zhou, H.; Wang, S.; Song, Y. Desalination and Li+ enrichment via formation of cyclopentane hydrate. SePurif. Technol. 2020, 231, 115921. [Google Scholar] [CrossRef]
- Hildebrand, J.H.; Scott, R.L. Regular Solutions; Prentice-Hall International Series in Chemistry; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Hu, Y.; Lee, B.R.; Sum, A.K. Universal correlation for gas hydrates suppression temperature of inhibited systems: I. Single salts. AIChE J. 2017, 63, 5111–5124. [Google Scholar] [CrossRef]
- Hu, Y.; Lee, B.R.; Sum, A.K. Universal correlation for gas hydrates suppression temperature of inhibited systems: II. Mixed salts and structure type. AIChE J. 2018, 64, 2240–2250. [Google Scholar] [CrossRef]
- Hu, Y.; Sa, J.; Lee, B.R.; Sum, A.K. Universal correlation for gas hydrates suppression temperature of inhibited systems: III. salts and organic inhibitors. AIChE J. 2018, 64, 4097–4109. [Google Scholar] [CrossRef]
- Sa, J.H.; Sum, A.K. Universal correlation for gas hydrates suppression temperature of inhibited systems: IV. Water activity. AIChE J. 2021, 67, e17293. [Google Scholar] [CrossRef]
- van der Waals, J.H.; Platteeuw, J.C. Clathrate Solutions. Adv. Chem. Phys. 1958, 2, 1–57. [Google Scholar] [CrossRef]
- Miyawaki, O.; Saito, A.; Matsuo, T.; Nakamura, K. Activity and Activity Coefficient of Water in Aqueous Solutions and Their Relationships with Solution Structure Parameters. Biosci. Biotechnol. Biochem. 1997, 61, 466–469. [Google Scholar] [CrossRef]
- Nakajima, M.; Ohinura, R.; Mori, Y.H. Clathrate hydrate formation from cyclopentane-in-water emulsions. Ind. Eng. Chem. Res. 2008, 47, 8933–8939. [Google Scholar] [CrossRef]
- Herri, J.M.; Bouchemoua, A.; Kwaterski, M.; Fezoua, A.; Ouabbas, Y.; Cameirao, A. Gas hydrate equilibria for CO2-N2 and CO2-CH4 gas mixtures-Experimental studies and thermodynamic modelling. Fluid Phase Equilib. 2011, 301, 171–190. [Google Scholar] [CrossRef]
- Stackelberg, M.V.; Müller, H.R. On the Structure of Gas Hydrates. J. Chem. Phys. 1951, 19, 1319–1320. [Google Scholar] [CrossRef]
- Handa, Y.P.; Tse, J.S. Thermodynamic properties of empty lattices of structure I and structure II clathrate hydrates. J. Phys. Chem. 1986, 90, 5917–5921. [Google Scholar] [CrossRef]
- Parrish, W.R.; Prausnitz, J.M. Dissociation Pressures of Gas Hydrates Formed by Gas Mixtures. Ind. Eng. Chem. Process Des. Dev. 1972, 11, 26–35. [Google Scholar] [CrossRef]
- Takeuchi, F.; Ohmura, R.; Yasuoka, K. Statistical-thermodynamics modeling of clathrate-hydrate-forming systems suitable as working media of a hydrate-based refrigeration system. Int. J. Thermophys. 2009, 30, 1838–1852. [Google Scholar] [CrossRef]











| Material | Chemical Formula | Mol. Weight (g/mole) | Solubility in Water (g/L) | Purity |
|---|---|---|---|---|
| CP | C5H10 | 70.13 | 0.156 (25 °C) [37] | 96% |
| Sodium bromide | NaBr | 102.89 | 900 (20 °C) [38] | 98% |
| Potassium bromide | KBr | 119.00 | 678 (25 °C) [38] | 99.5% |
| Sodium sulfate | Na2SO4 | 142.04 | 280 (20 °C) [38] | 99.5% |
| Potassium sulfate | K2SO4 | 174.26 | 110 (20 °C) [38] | 99% |
| Calcium chloride | CaCl2.2H2O | 110.98 | 420 (20 °C) [38] | 99% |
| Magnesium chloride | MgCl2.6H2O | 95.21 | 546 (20 °C) [38] | 98% |
| Potassium chloride | KCl | 74.55 | 340 (20 °C) [38] | 99% |
| Sodium chloride | NaCl | 58.4 | 360 (20 °C) [38] | 99.5% |
| Parameter | Unit | Value | Citation |
|---|---|---|---|
| J/mol | [1] | ||
| J/mol.K | −38.12 | [1] | |
| J/mol/K2 | 0.141 | [1] | |
| 10−6 m3/mol | 4.99644 | [1] | |
| J/mol | 1068 | [52] | |
| J/mol | 764 | [52] |
| Kihara Parameter | Unit | Value | Citation |
|---|---|---|---|
| Å | 0.8968 | [54] | |
| Å | 2.72 | [30] | |
| K | 265.5 | [30] |
| SFPD Approach | HLS Correlation | Kihara Approach | ABOC Approach | |
|---|---|---|---|---|
| NaBr | 0.42 | 0.42 | 0.24 | 0.38 |
| KBr | 0.23 | 0.23 | 0.25 | 0.25 |
| K2SO4 | 0.21 | 0.69 | 0.31 | 0.10 |
| CaCl2-MgCl2 | 0.27 | 0.76 | 0.11 | 0.27 |
| NaBr-KBr | 0.23 | 0.28 | 0.49 | 0.19 |
| Na2SO4-K2SO4 | 0.23 | 0.79 | 0.28 | 0.12 |
| NaCl-NaBr | 0.21 | 0.13 | 0.19 | 0.24 |
| KCl-KBr | 0.20 | 0.30 | 0.13 | 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, T.-K.; Hoang, Q.-T.T.; Le, C.-A.T.; Tran, T.-H.; Bun, K.; Le, N.-T.T.; Ho, V.-S.; Ngo, V.-H.; Le, Q.-D.; Naukanova, M.; et al. Thermodynamic Experiments and Modelling of Cyclopentane Hydrates in the Presence of NaBr, KBr, K2SO4, NaBr–KBr, NaCl–NaBr, KCl–KBr, Na2SO4–K2SO4, and CaCl2–MgCl2. Water 2025, 17, 2916. https://doi.org/10.3390/w17192916
Pham T-K, Hoang Q-TT, Le C-AT, Tran T-H, Bun K, Le N-TT, Ho V-S, Ngo V-H, Le Q-D, Naukanova M, et al. Thermodynamic Experiments and Modelling of Cyclopentane Hydrates in the Presence of NaBr, KBr, K2SO4, NaBr–KBr, NaCl–NaBr, KCl–KBr, Na2SO4–K2SO4, and CaCl2–MgCl2. Water. 2025; 17(19):2916. https://doi.org/10.3390/w17192916
Chicago/Turabian StylePham, Trung-Kien, Quynh-Trang Thi Hoang, Cham-Anh Thi Le, Thi-Huyen Tran, Koemhong Bun, Ngoc-Tuyet Thi Le, Van-Son Ho, Van-Hieu Ngo, Quang-Duyen Le, Madina Naukanova, and et al. 2025. "Thermodynamic Experiments and Modelling of Cyclopentane Hydrates in the Presence of NaBr, KBr, K2SO4, NaBr–KBr, NaCl–NaBr, KCl–KBr, Na2SO4–K2SO4, and CaCl2–MgCl2" Water 17, no. 19: 2916. https://doi.org/10.3390/w17192916
APA StylePham, T.-K., Hoang, Q.-T. T., Le, C.-A. T., Tran, T.-H., Bun, K., Le, N.-T. T., Ho, V.-S., Ngo, V.-H., Le, Q.-D., Naukanova, M., Abuhuraira, M., Cameirao, A., Douzet, J., Herri, J.-M., & Bouillot, B. (2025). Thermodynamic Experiments and Modelling of Cyclopentane Hydrates in the Presence of NaBr, KBr, K2SO4, NaBr–KBr, NaCl–NaBr, KCl–KBr, Na2SO4–K2SO4, and CaCl2–MgCl2. Water, 17(19), 2916. https://doi.org/10.3390/w17192916







