Research on Anomaly Detection in Wastewater Treatment Systems Based on a VAE-LSTM Fusion Model
Abstract
1. Introduction
- (i)
- Fusion of spatial and temporal features for spatio-temporal anomaly detection.
- (ii)
- Adaptive learning of high-dimensional data without manual feature engineering.
- (iii)
- Robustness against low-frequency and stealthy attacks.
- (iv)
- Lightweight deployment with near real-time inference on edge devices.
2. Anomaly Detection Method for Water Treatment Systems
2.1. Water Treatment System Anomaly Detection Model
2.2. Data Preprocessing
2.3. Variational Autoencoder for Anomaly Detection
2.4. Anomaly Detection Method Based on Long Short-Term Memory Recurrent Neural Network
2.5. Combined Anomaly Detection Method for Water Treatment Data Based on VAE-LSTM
2.6. Algorithm Performance Evaluation Metrics
3. Experimental Platform
4. Experimental Environment and Optimal Hyperparameter Calculation
4.1. Experimental Environment
4.2. Hyperparameter Optimization Calculation
4.2.1. Principle of Bayesian Optimization
4.2.2. Bayesian Optimization Objectives and Hyperparameters
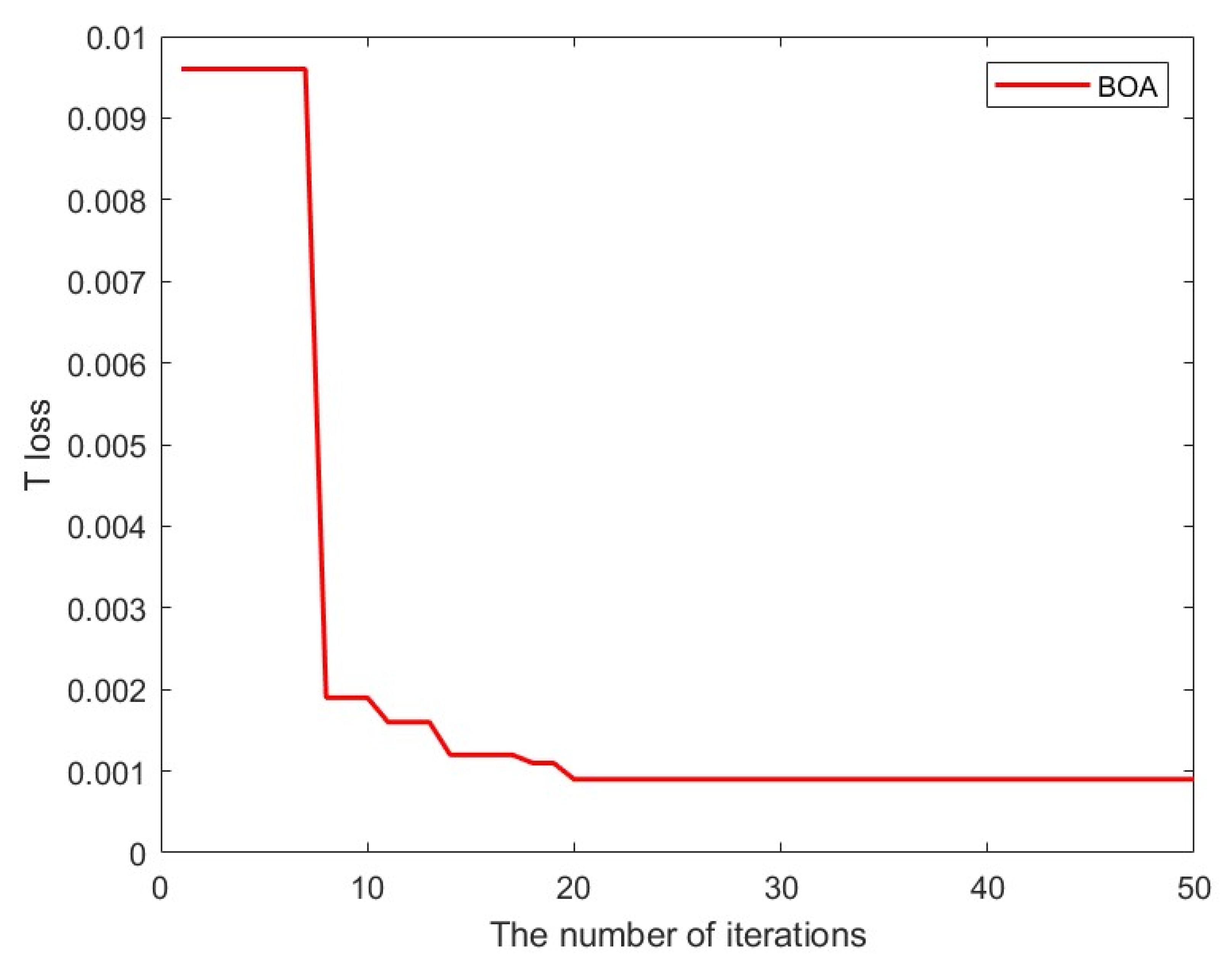
4.2.3. Optimal Hyperparameter Calculation
4.3. Model Training
5. Algorithm Experiments and Comparisons
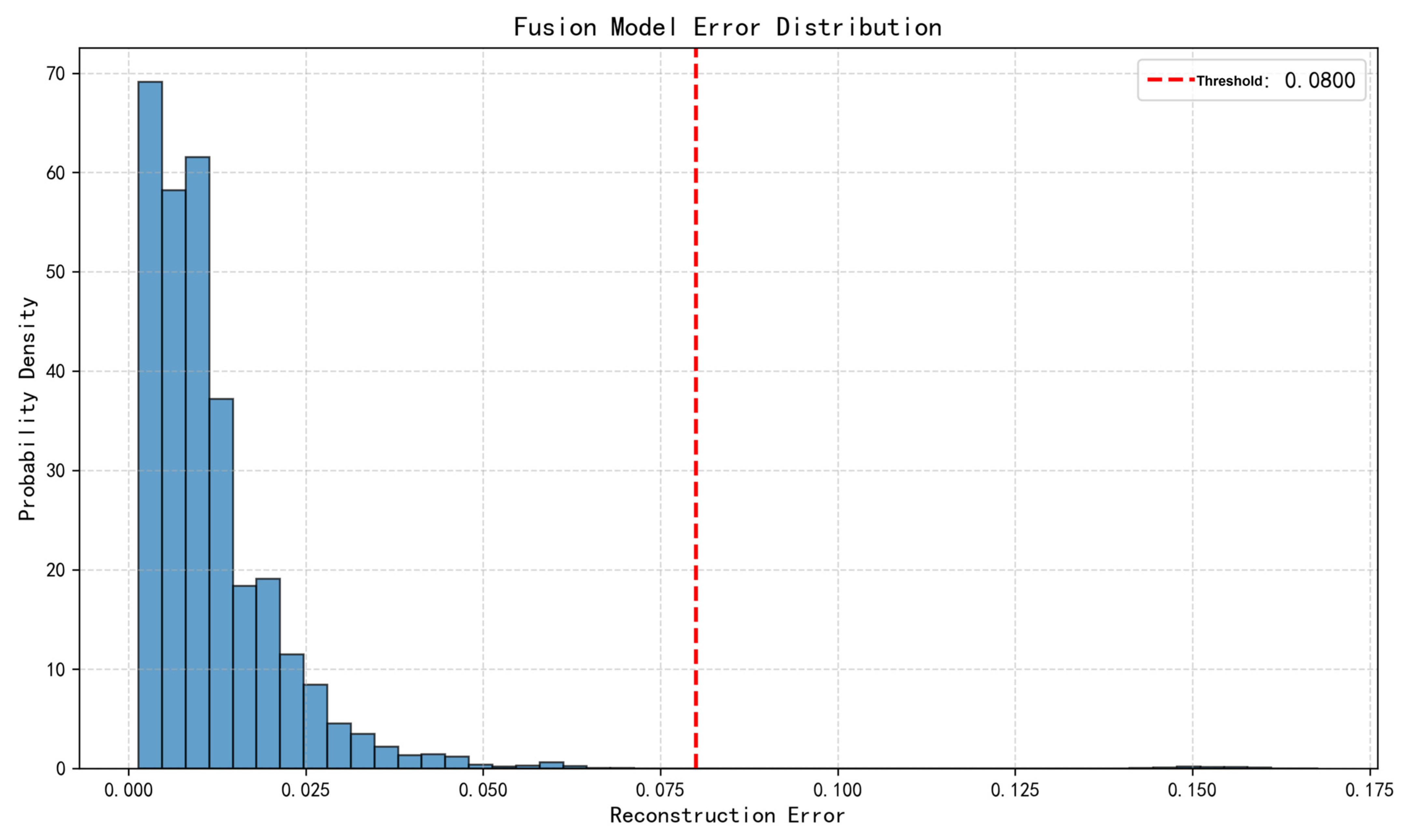
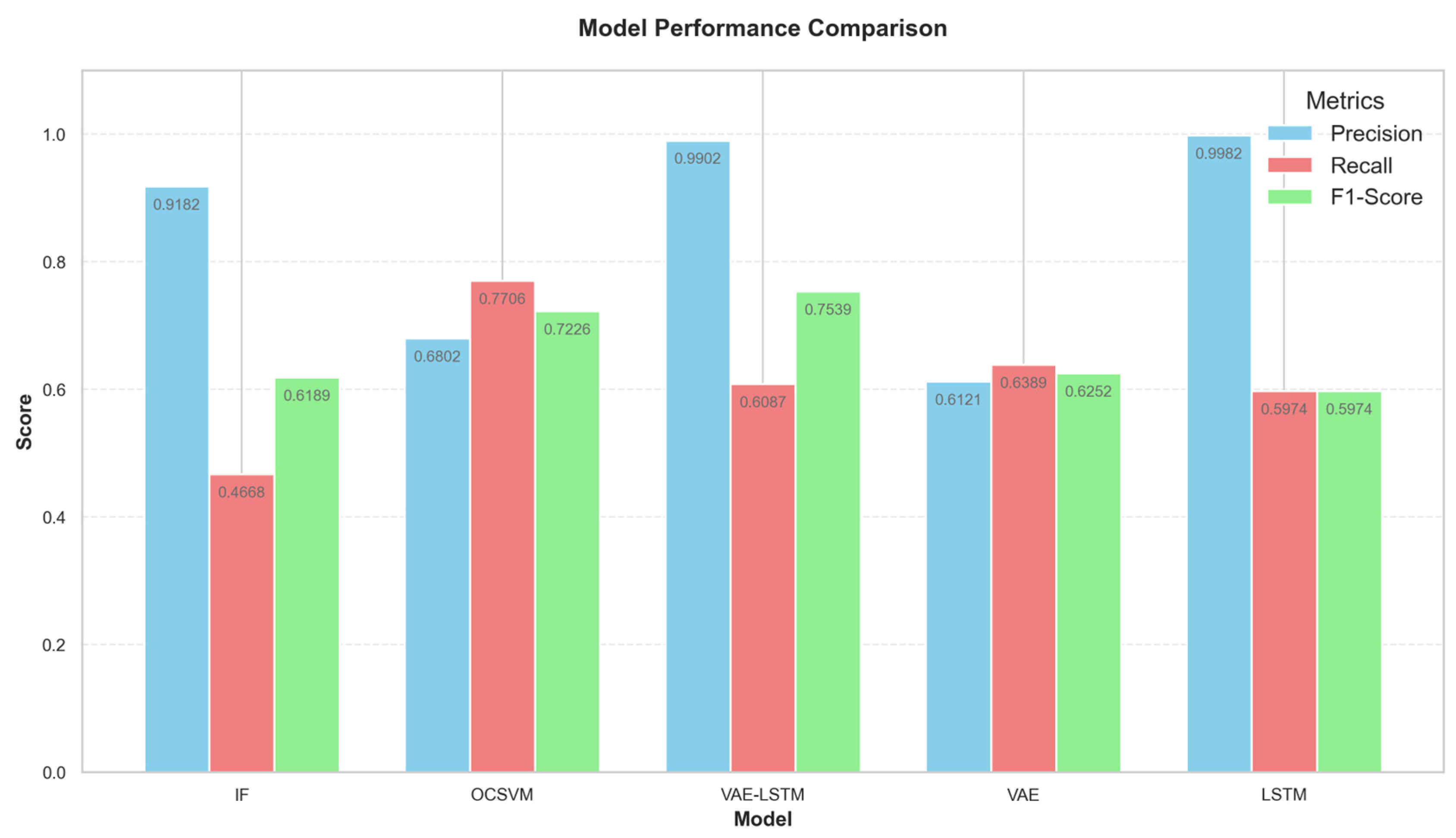
5.1. Comparison of Algorithms and Ablation Study
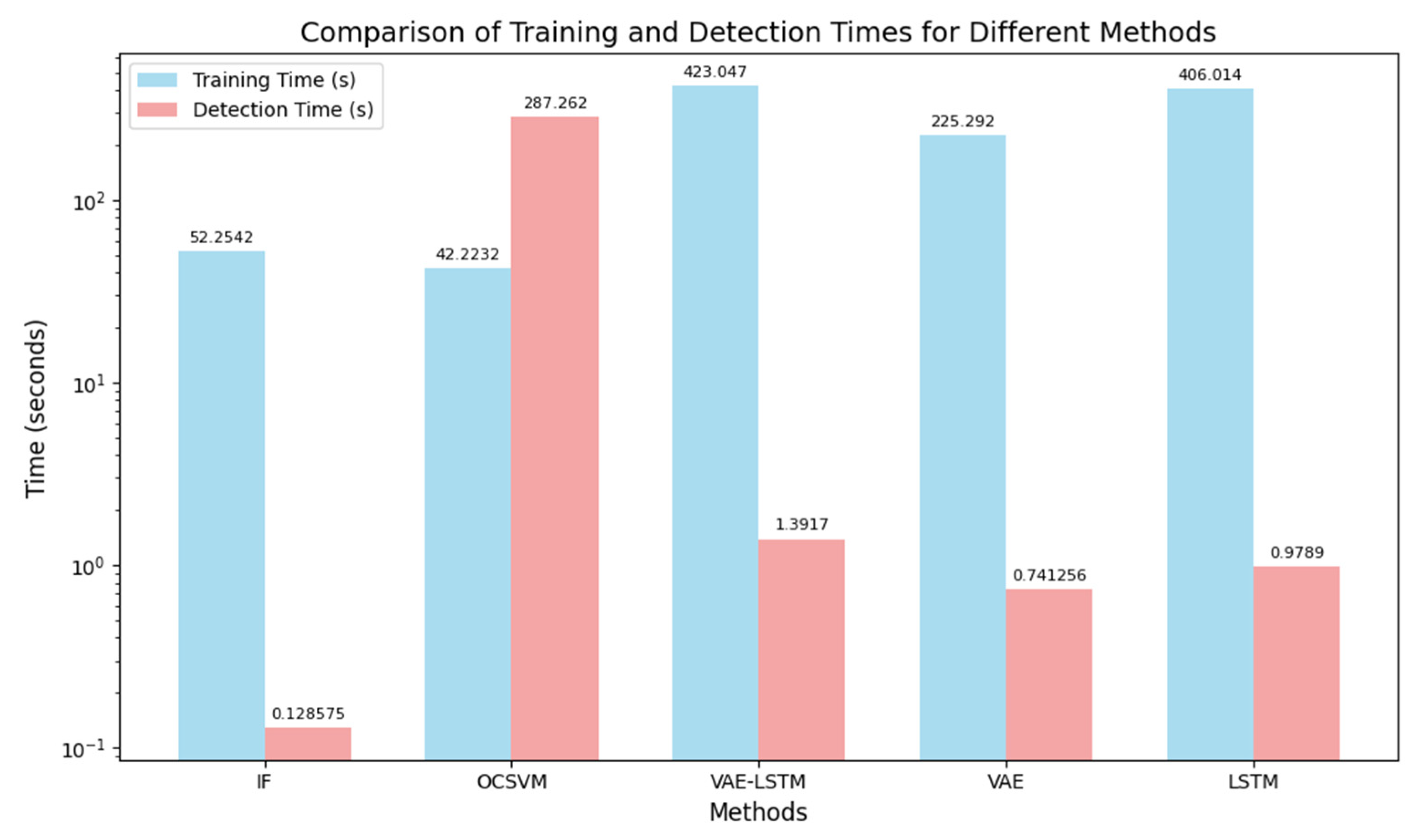
5.2. Comparison of Training and Testing Time
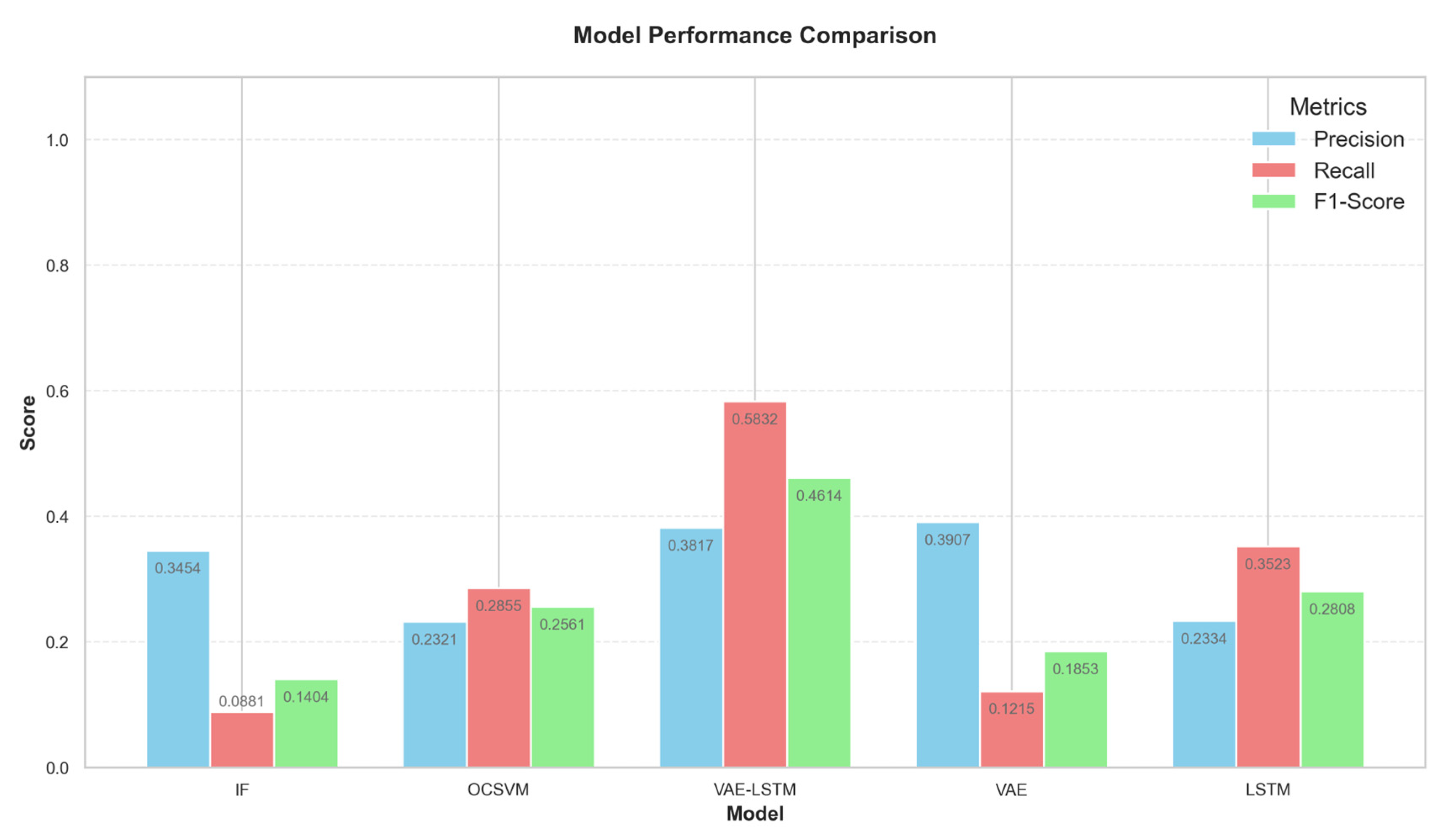
5.3. WADI Water Treatment System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cordeiro, S.; Ferrario, F.; Pereira, H.X.; Ferreira, F.; Matos, J.S. Water Reuse, a Sustainable Alternative in the Context of Water Scarcity and Climate Change in the Lisbon Metropolitan Area. Sustainability 2023, 15, 12578. [Google Scholar] [CrossRef]
- Solanki, S.D.; Bhalani, J.; Ahmad, N. Exploring a Novel Strategy for Detecting Cyber-Attack by Using Soft Computing Technique: A Review. In Soft Computing Techniques and Applications. Advances in Intelligent Systems and Computing; Borah, S., Pradhan, R., Dey, N., Gupta, P., Eds.; Springer: Singapore, 2021; Volume 1248. [Google Scholar] [CrossRef]
- El Kafhali, S.; El Mir, I.; Hanini, M. Security Threats, Defense Mechanisms, Challenges, and Future Directions in Cloud Computing. Arch. Comput. Methods Eng. 2022, 29, 223–246. [Google Scholar] [CrossRef]
- Kaittan, K.H.; Mohammed, S.J. PLC-SCADA automation of inlet wastewater treatment processes: Design, implementation, and evaluation. J. Eur. Systèmes Autom. 2024, 57, 787–796. [Google Scholar] [CrossRef]
- Ning, S.; Hong, S. Programmable logic controller-based automatic control for municipal wastewater treatment plant optimization. Water Pract. Technol. 2022, 17, 378–384. [Google Scholar] [CrossRef]
- Gönen, S.; Sayan, H.H.; Yılmaz, E.N.; Üstünsoy, F.; Karacayılmaz, G. False data injection attacks and the insider threat in smart systems. Comput. Secur. 2020, 97, 101955. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Z.; Ding, Y.; Ngai, E.C.; Yang, S.-H. Anomaly detection using isomorphic analysis for false data injection attacks in industrial control systems. J. Frankl. Inst. 2024, 361, 107000. [Google Scholar] [CrossRef]
- Zhang, J.; Tao, Y.; Li, M. Design of Industrial Gateway on Modbus TCP. Mach. Electron. 2014, 50–53. [Google Scholar] [CrossRef]
- Andrysiak, T.; Saganowski, Ł.; Maszewski, M.; Marchewka, A. Detection of Network Attacks Using Hybrid ARIMA-GARCH Model. In Advances in Dependability Engineering of Complex Systems. DepCoS-RELCOMEX 2017. Advances in Intelligent Systems and Computing; Zamojski, W., Mazurkiewicz, J., Sugier, J., Walkowiak, T., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2018; Volume 582. [Google Scholar] [CrossRef]
- Gan, Z.; Zhou, X. Abnormal Network Traffic Detection Based on Improved LOF Algorithm. In Proceedings of the 2018 10th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 25–26 August 2018; pp. 142–145. [Google Scholar] [CrossRef]
- Elnour, M.; Meskin, N.; Khan, K.; Jain, R. A Dual-Isolation-Forests-Based Attack Detection Framework for Industrial Control Systems. IEEE Access 2020, 8, 36639–36651. [Google Scholar] [CrossRef]
- Vos, K.; Peng, Z.; Jenkins, C.; Shahriar, R.; Borghesani, P.; Wang, W. Vibration-based anomaly detection using LSTM/SVM approaches. Mech. Syst. Signal Process. 2022, 169, 108752. [Google Scholar] [CrossRef]
- Nizan, O.; Tal, A. k-NNN: Nearest Neighbors of Neighbors for Anomaly Detection. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision Workshops (WACVW), Waikoloa, HI, USA, 1–6 January 2024; pp. 1005–1014. [Google Scholar] [CrossRef]
- Cicceri, G.; Maisano, R.; Morey, N.; Distefano, S. A novel architecture for the smart management of wastewater treatment plants. In Proceedings of the 2021 IEEE International Conference on Smart Computing (SMARTCOMP), Irvine, CA, USA, 23–27 August 2021; pp. 392–394. [Google Scholar]
- Cicceri, G.; Maisano, R.; Morey, N.; Distefano, S. Swims: The smart wastewater intelligent management system. In Proceedings of the 2021 IEEE International Conference on Smart Computing (SMARTCOMP), Irvine, CA, USA, 23–27 August 2021; IEEE: New York, NY, USA; pp. 228–233. [Google Scholar]
- Garcia-Alvarez, D.; Fuente, M.J.; Vega, P.; Sainz, G. Fault Detection and Diagnosis using Multivariate Statistical Techniques in a Wastewater Treatment Plant. IFAC Proc. Vol. 2009, 42, 952–957. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Lima, L.O.M.; Goncalves, L.C.; Menezes, G.C.; de Oliveira, L.S. IoT-based Wireless Sensor Networks for Monitoring Drinking Water Treatment Plants. In Proceedings of the 2024 Symposium on Internet of Things (SIoT), Rio de Janeiro, Brazil, 15–18 October 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Singh, M.; Ahmed, S. IoT based smart water management systems: A systematic review. Mater. Today Proc. 2021, 46 Pt 11, 5211–5218. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Qiao, Q.; Tavares, A.; Liang, Y. Water Quality Prediction Based on Machine Learning and Comprehensive Weighting Methods. Entropy 2023, 25, 1186. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.H.; Nguyen, C.N.; Dao, X.T.; Duong, Q.T.; Pham Thi Kim, D.; Pham, M.-T. Variational autoencoder for anomaly detection: A comparative study. arXiv 2024, arXiv:2408.13561. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutnik, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Padilla, R.; Netto, S.L.; da Silva, E.A.B. A Survey on Performance Metrics for Object-Detection Algorithms. In Proceedings of the 2020 International Conference on Systems, Signals and Image Processing (IWSSIP), Niteroi, Brazil, 1–3 July 2020; pp. 237–242. [Google Scholar] [CrossRef]
- Goh, J.; Adepu, S.; Junejo, K.N.; Mathur, A. A dataset to support research in the design of secure water treatment systems. In Conference on Research in Cyber Security; Springer: Singapore, 2016. [Google Scholar]
- Ahmed, C.M.; Palleti, V.R.; Mathur, A.P. WADI: A water distribution testbed for research in the design of secure cyber physical systems. In Proceedings of the 3rd International Workshop on Cyber-Physical Systems for Smart Water Networks (CySWATER 2017), Pittsburgh, PA, USA, 21 April 2017; pp. 25–28. [Google Scholar]
- Papenmeier, L.; Poloczek, M.; Nardi, L. Understanding High-Dimensional Bayesian Optimization. arXiv 2025, arXiv:2502.09198. [Google Scholar]
- Al Farizi, W.S.; Hidayah, I.; Rizal, M.N. Isolation Forest Based Anomaly Detection: A Systematic Literature Review. In Proceedings of the 2021 8th International Conference on Information Technology, Computer and Electrical Engineering (ICITACEE), Semarang, Indonesia, 23–24 September 2021; pp. 118–122. [Google Scholar] [CrossRef]
- Miao, X.; Liu, Y.; Zhao, H.; Li, C. Distributed Online One-Class Support Vector Machine for Anomaly Detection Over Networks. IEEE Trans. Cybern. 2019, 49, 1475–1488. [Google Scholar] [CrossRef] [PubMed]
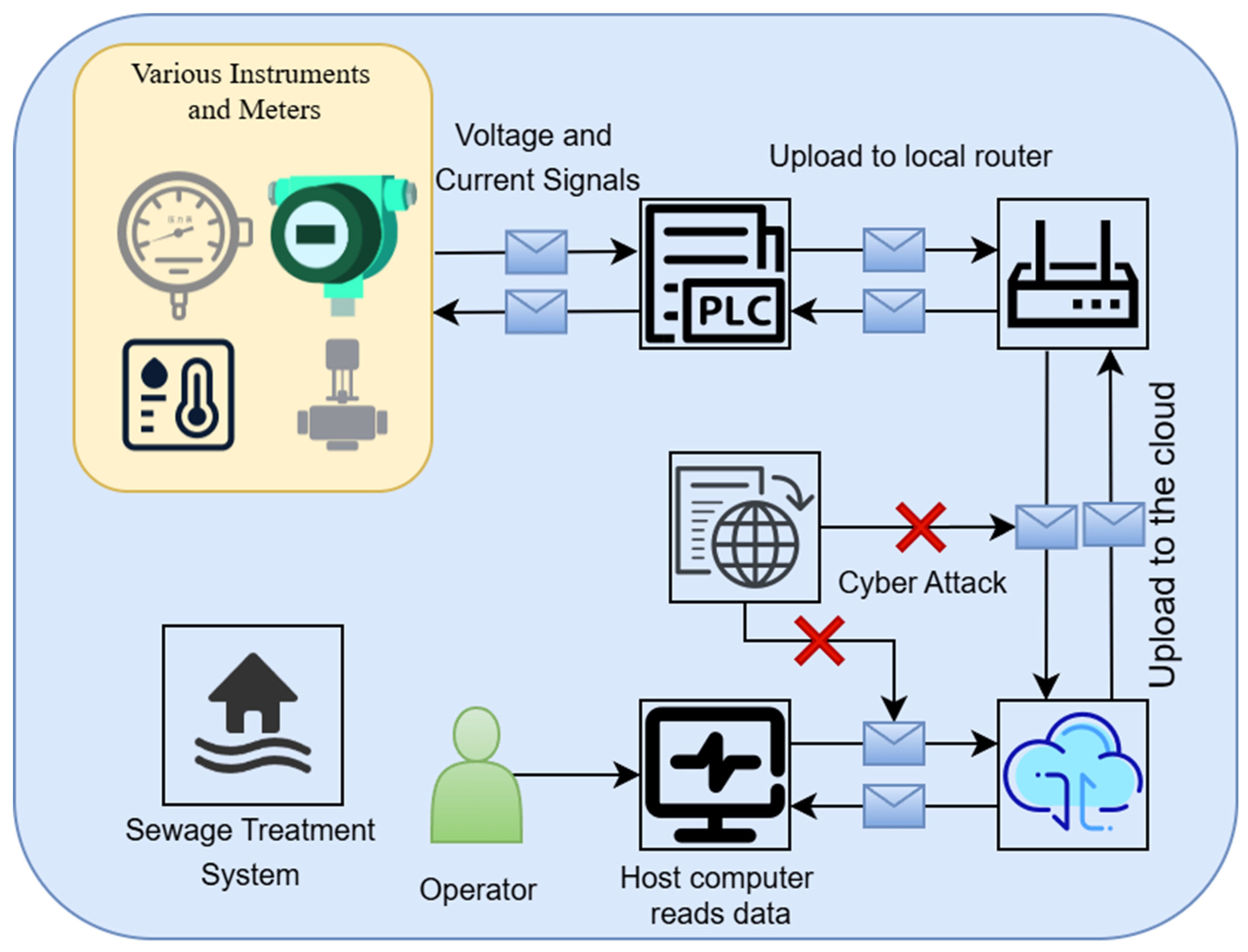
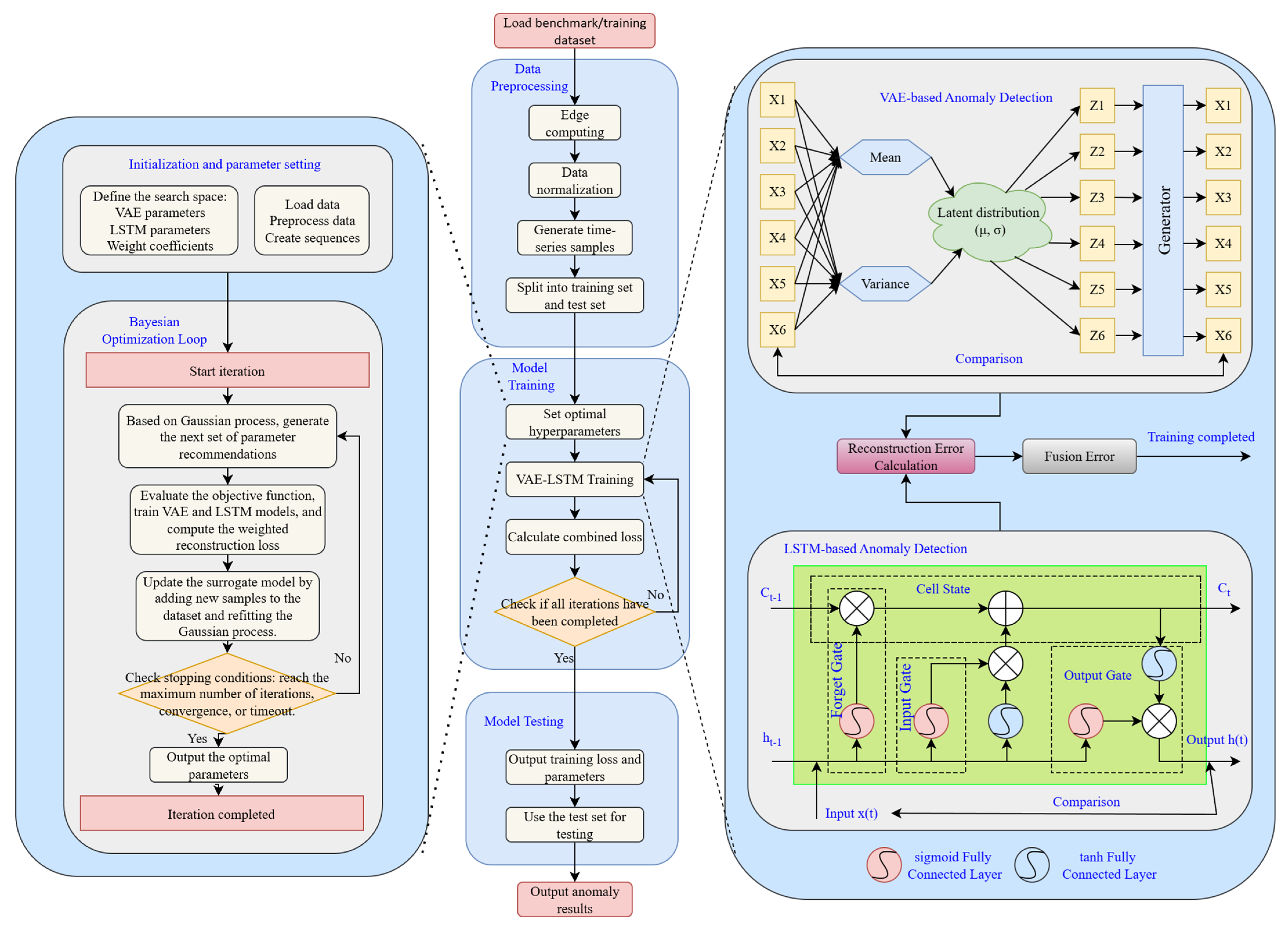


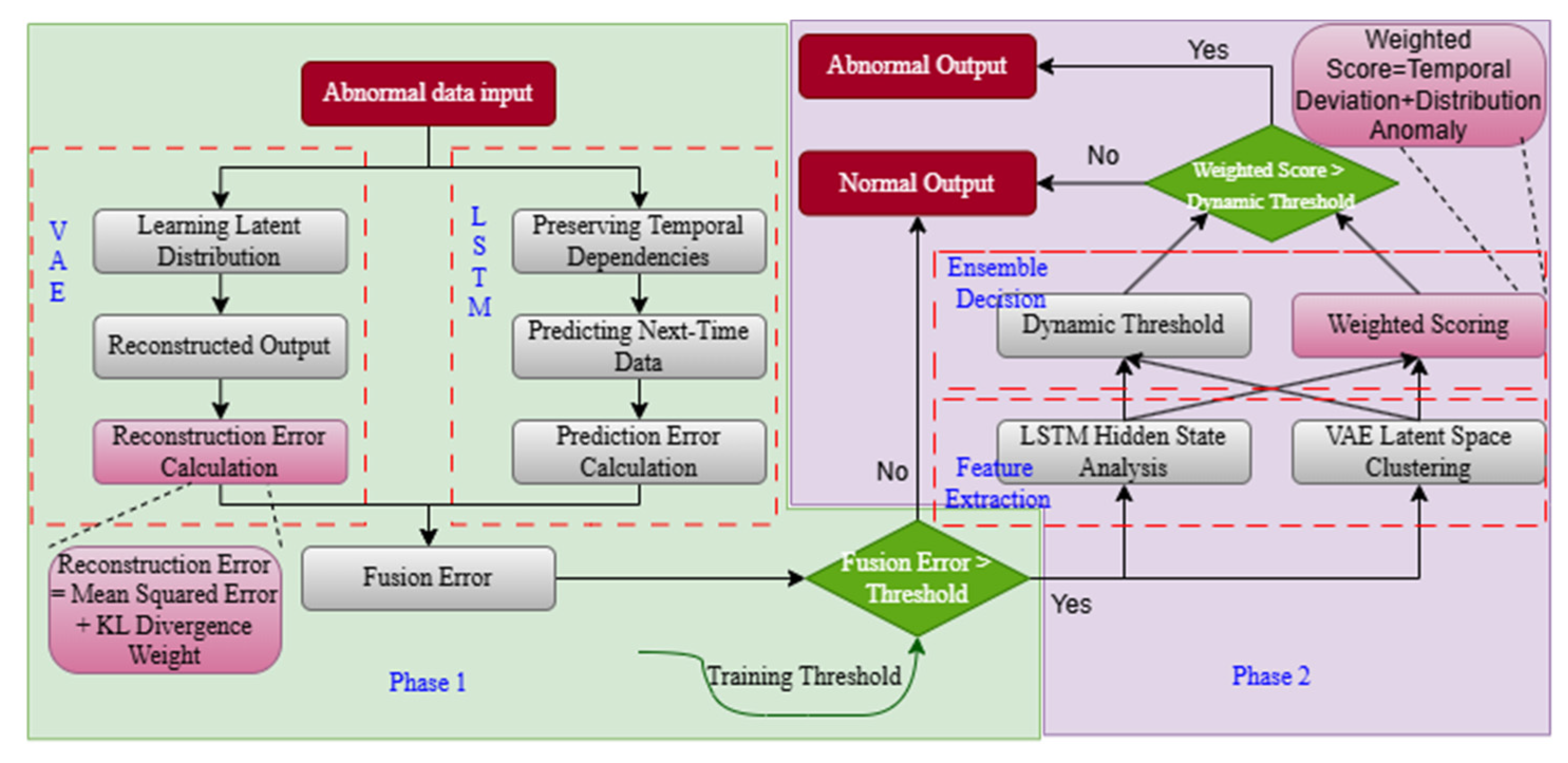
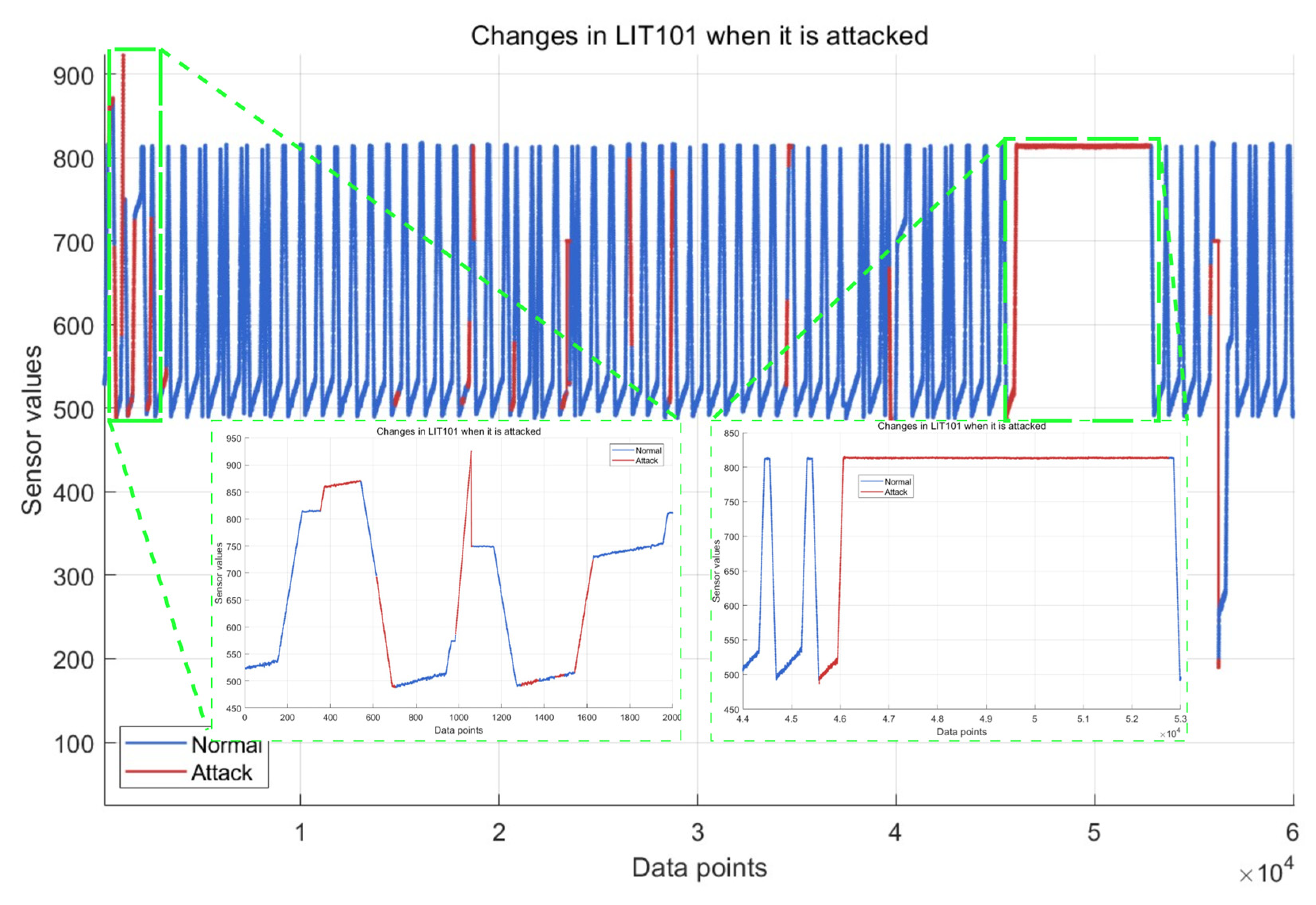
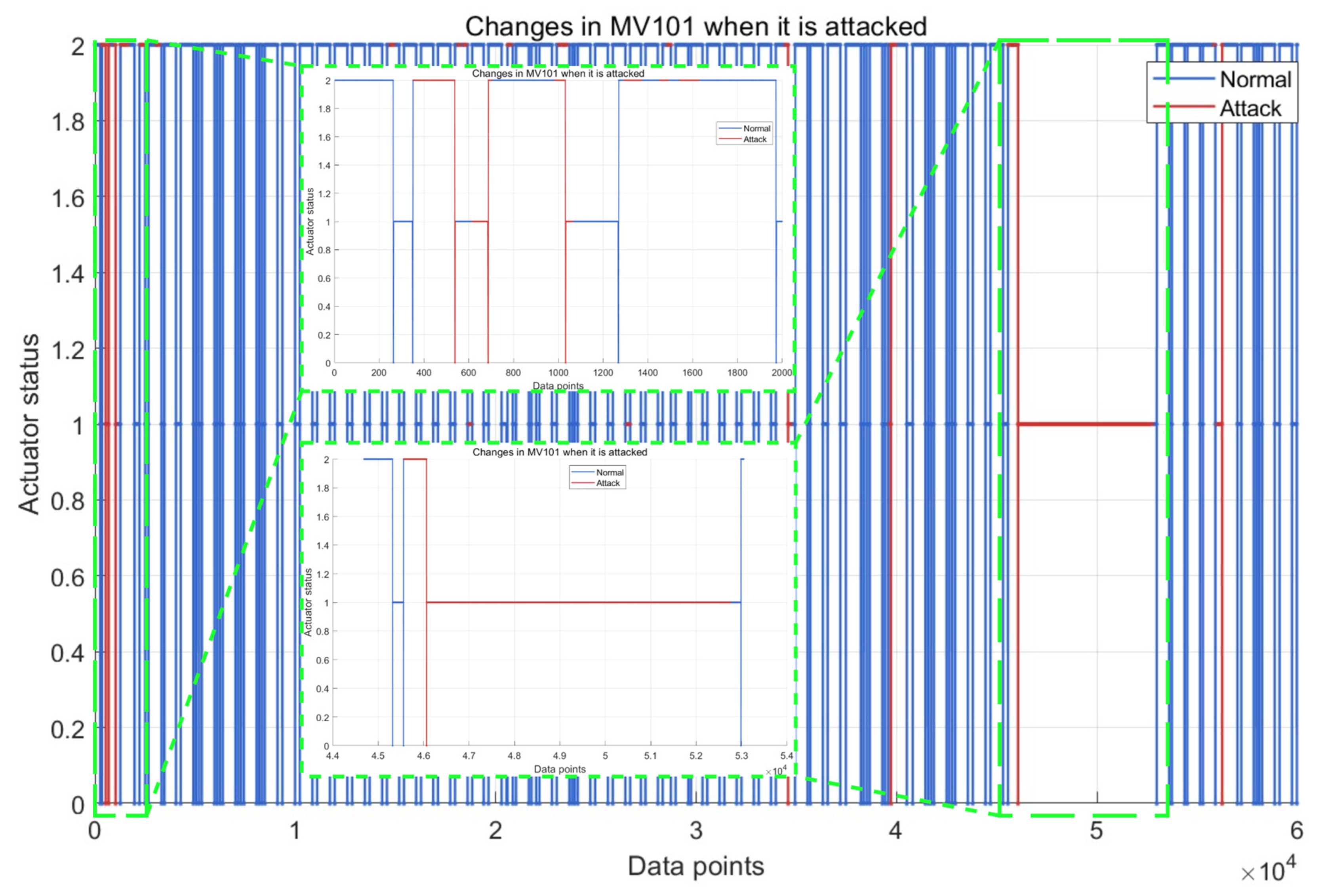
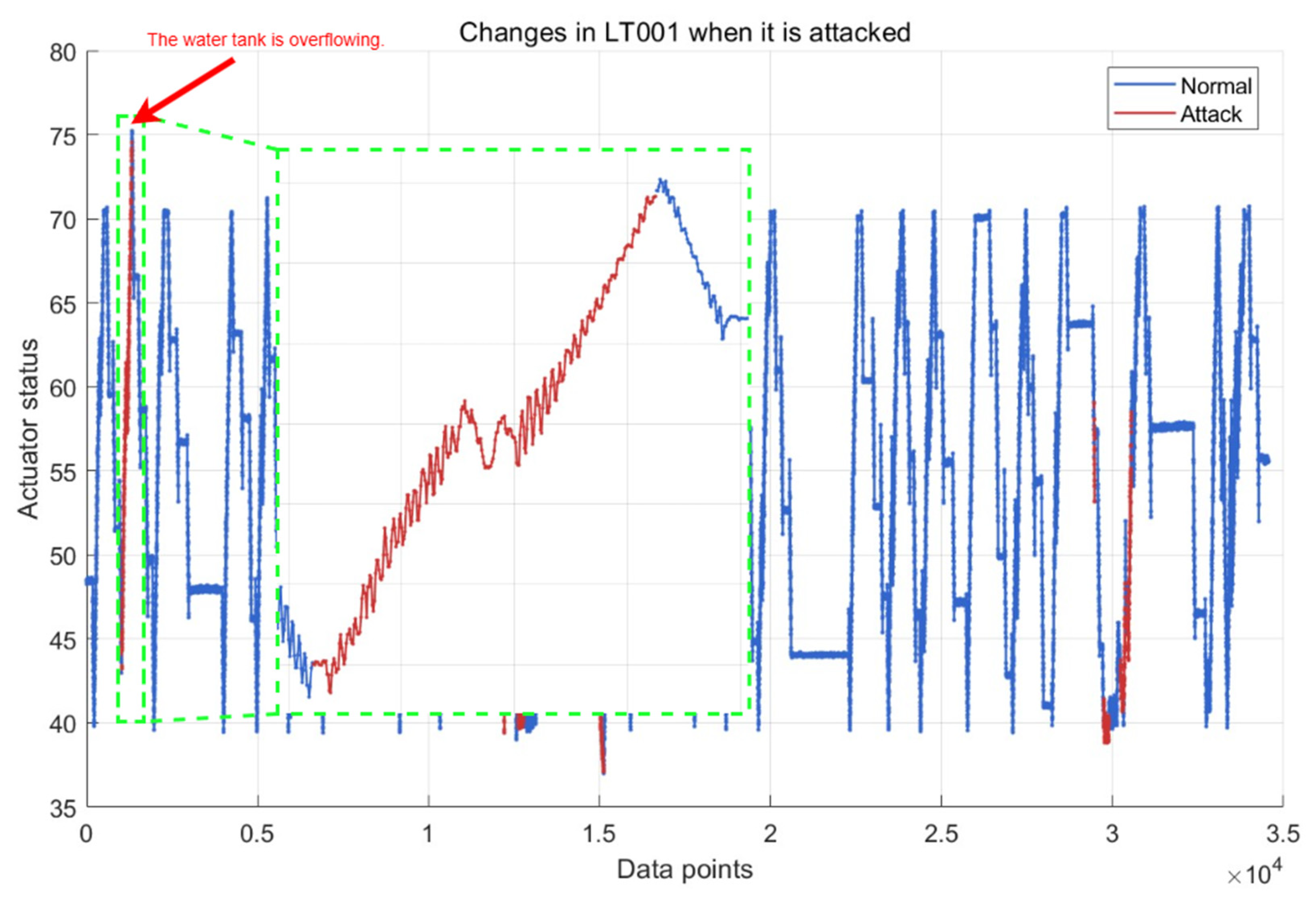
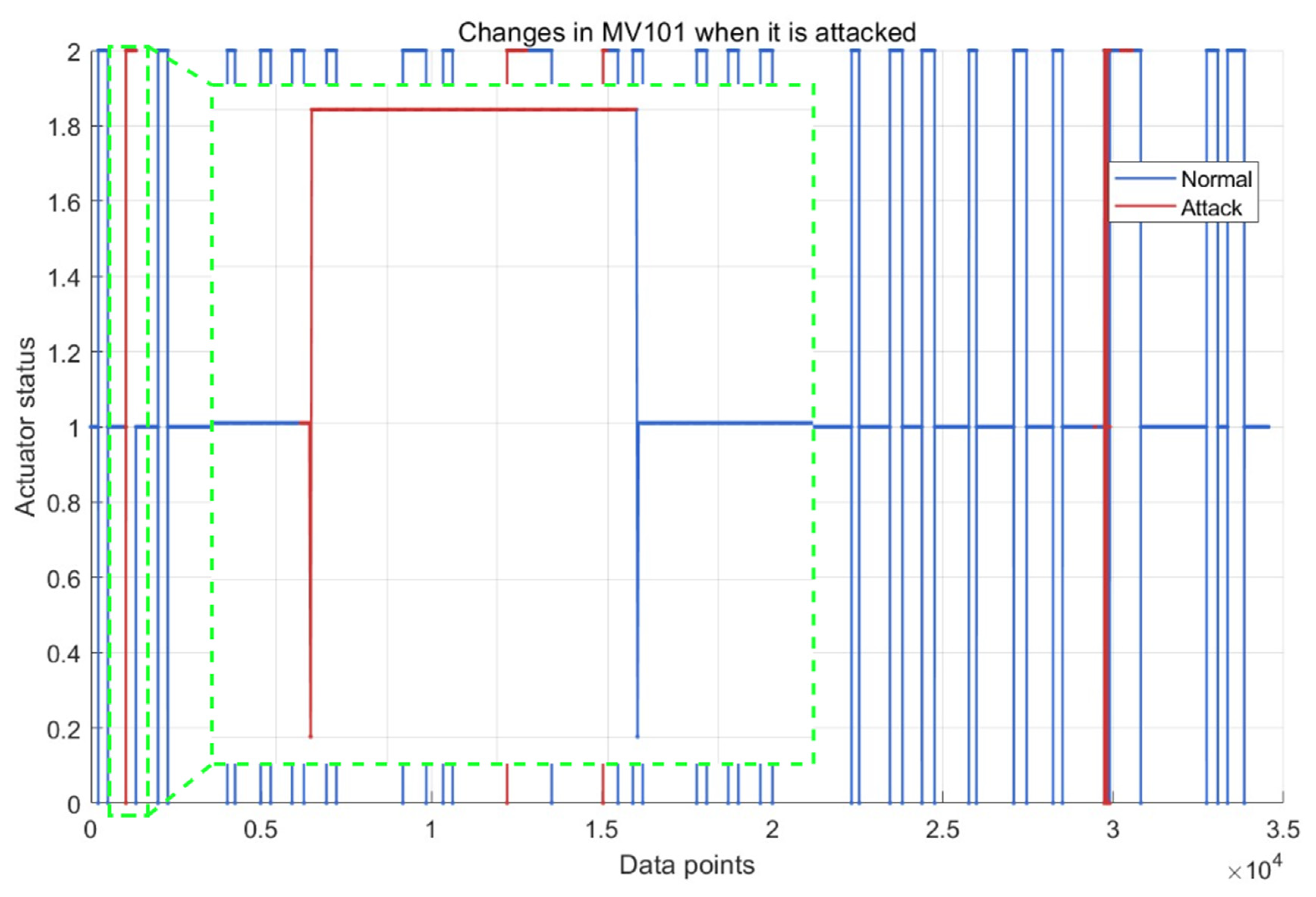
| Water Treatment Step | Step Description | Monitored Sensor ID | Monitored Actuator ID |
|---|---|---|---|
| Step 1 | Raw Water Intake | FIT101 LIT101 | MV101 P101 P102 |
| Step 2 | Chemical Dosing | AIT201 AIT202 AIT203 FIT201 | MV201 P201 P202 P203 P204 P205 P206 |
| Step 3 | Ultrafiltration (UF) System Filtration | DPIT301 FIT301 LIT301 | MV301 MV302 MV303 MV304 P301 P302 |
| Step 4 | UV Disinfection and Dechlorination | AIT401 AIT402 LIT401 | P401 P402 P403 P404 UV401 |
| Step 5 | Feed to Reverse Osmosis (RO) System | AIT501 AIT502 AIT503 AIT504 FIT501 FIT502 FIT503 FIT504 PIT501 PIT502 PIT503 | P501 P502 |
| Step 6 | Backwash Cleaning of UF | FIT601 | P601 P602 P603 |
| Water Treatment Step | Step Description | Monitored Sensor ID | Monitored Actuator ID |
|---|---|---|---|
| Step 1 | Wastewater enters the main network 1-T001 1-T002 | 1-LT-001 1-FS-001 | 1-MV-001 1-MV-005 1-P-005 |
| Step 2A | Storage in elevated tanks 2-T-001 2-T-002 | 2-LT-001 2-PIT-001 2-FS-001 2-FS-002 | 2-MV-001 2-MV-002 2-MV-003 2-MV-004 2-MV-005 2-MV-006 2-P-003 2-P-004 |
| Step 2B | Residential water storage 2-T101 2-T201 2-T301 2-T401 2-T501 2-T601 | 2-FQ-101 2-FQ-201 2-FQ-301 2-FQ-401 2-FQ-501 2-FQ-601 2-PIT-002 | 2-MV-101 2-MV-201 2-MV-301 2-MV-401 2-MV-501 2-MV-601 2-MCV-101 2-MCV-201 2-MCV-301 2-MCV-401 2-MCV-501 2-MCV-601 |
| Step 3 | Water recirculation to the main network 3-T-002 | 3-LT-001 3-FS-001 3-FS-002 | 3-MV-002 3-P-003 3-P-004 |
| Dataset | Number of Training Samples | Number of Testing Samples | Number of Available Signal Groups |
|---|---|---|---|
| SWaT December 2015 | 495,000 | 449,919 | 51 |
| WaDi October 2017 | 1,209,600 | 172,806 | 123 |
| Parameter Name | Description | Parameter Setting |
|---|---|---|
| vae_latent_dim | VAE latent dimension | Integer, range [2, 20] |
| vae_hidden_dim | VAE hidden layer dimension | Integer, range [10, 100] |
| kl_weight | KL divergence weight | Real, range [0.1, 1.0] |
| lstm_layers | LSTM number of layers | Integer, range [1, 3] |
| lstm_hidden | LSTM hidden units | Integer, range [32, 128] |
| lstm_bi | Bidirectional LSTM | Boolean, False or True |
| lstm_dropout | LSTM dropout rate | Real, range [0.0, 0.5] |
| a | VAE reconstruction loss weight | Real, range [0.0, 0.9] |
| c | LSTM reconstruction loss weight | Real, range [0.0, 0.9] |
| Hyperparameter | V_Latent_Dim | Vae_Hidden_Dim | Kl_Weight | Lstm_Layers |
|---|---|---|---|---|
| Optimal Value | 2 | 30 | 1.0 | 2 |
| lstm_hidden | lstm_bi | lstm_dropout | a | c |
| 64 | False | 0.355 | 0.0599 | 0.037 |
| Parameter Name | Description | Parameter Setting |
|---|---|---|
| n_estimators | Number of trees in the Isolation Forest | 100 |
| max_samples | Number of samples randomly drawn to build each tree | auto |
| contamination | Proportion of anomalies in the dataset | 0.1 |
| max_features | Proportion of features randomly selected to build each tree | 1.0 |
| bootstrap | Whether to use bootstrap sampling when building each tree | False |
| random_state | Random seed | 42 |
| Parameter Name | Description | Parameter Setting |
|---|---|---|
| kernel | Type of kernel function | rbf |
| degree | Degree for the polynomial kernel function | 3 |
| nu | Upper bound on the fraction of support vectors and lower bound on training error | 0.05 |
| tol | Error tolerance for stopping criterion | 0.001 |
| cache_size | Size of the kernel computation cache | 200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Gong, Z.; Zhang, X. Research on Anomaly Detection in Wastewater Treatment Systems Based on a VAE-LSTM Fusion Model. Water 2025, 17, 2842. https://doi.org/10.3390/w17192842
Liu X, Gong Z, Zhang X. Research on Anomaly Detection in Wastewater Treatment Systems Based on a VAE-LSTM Fusion Model. Water. 2025; 17(19):2842. https://doi.org/10.3390/w17192842
Chicago/Turabian StyleLiu, Xin, Zhengxuan Gong, and Xing Zhang. 2025. "Research on Anomaly Detection in Wastewater Treatment Systems Based on a VAE-LSTM Fusion Model" Water 17, no. 19: 2842. https://doi.org/10.3390/w17192842
APA StyleLiu, X., Gong, Z., & Zhang, X. (2025). Research on Anomaly Detection in Wastewater Treatment Systems Based on a VAE-LSTM Fusion Model. Water, 17(19), 2842. https://doi.org/10.3390/w17192842







