Multivariate Modeling of Drought Index in Northeastern Thailand Using Trivariate Copulas

Abstract

This study develops an integrated drought assessment framework based on trivariate copula modeling to simultaneously evaluate three key drought characteristics: duration, severity, and peak intensity. Meteorological data from stations across 23 meteorological stations in Northeastern Thailand, covering the period of 2007–2025, were analyzed. The Standardized Precipitation–Evapotranspiration Index (SPEI) was employed to characterize multidimensional drought conditions. The trivariate copula approach provides a flexible and robust statistical framework, enabling the separation of marginal distributions from dependence structures, capturing nonlinear and tail dependencies more effectively than traditional methods. Results demonstrate that this modeling framework significantly improves the accuracy of drought risk estimation and enables the calculation of joint return periods for extreme drought events. These findings offer valuable insights with respect to designing adaptive water resource management strategies, enhancing agricultural resilience, and strengthening early warning systems under future climate variability.

1. Introduction

Thailand is currently facing one of its most severe droughts in nearly four decades, with significant implications for water resources, agriculture, and economic stability [1]. Approximately half of the country’s major reservoirs are holding less than 50% of their capacity, while critically low river levels have allowed seawater intrusion to affect freshwater supplies [2,3]. This situation poses a considerable threat to agricultural productivity in a country where more than 12 million Thai laborers (30%) work in agriculture [4].

The primary drivers of this drought include a shortened monsoon season and below-average rainfall in 2019. Reports from the Mekong River Commission (MRC) indicate that monsoon rains in the Lower Mekong Basin, which encompasses Laos, Thailand, Cambodia, and Vietnam, arrived nearly two weeks late and ended three weeks early. Furthermore, the impacts of an El Niño event intensified the situation by raising temperatures and increasing evapotranspiration rates. As a result, Thailand entered the dry season with already depleted water resources, which further exacerbated the severity of the drought [1].

Drought is a significant environmental hazard that profoundly impacts food security, water availability, and economic resilience, particularly in agriculturally dependent countries such as Thailand [5]. Effective monitoring and management of drought require precise assessment tools that can comprehensively reflect the complex climatic factors driving drought conditions [6,7]. Various drought indices have been developed to quantify droughts from different perspectives. The Standardized Precipitation Index (SPI) [8] is widely used for meteorological drought monitoring because of its multi-scalar flexibility; however, it considers only precipitation and ignores the role of evapotranspiration, which is increasingly critical under global warming. The Palmer Drought Severity Index (PDSI) [9] integrates precipitation and temperature through a soil–water balance model. Still, it is sensitive to calibration parameters and less suitable for regions with diverse hydroclimatic conditions. The Streamflow Drought Index (SDI) [10] effectively characterizes hydrological drought but requires long and continuous discharge records, which are rarely available in rainfed agricultural areas of Northeastern Thailand. In contrast, the Standardized Precipitation–Evapotranspiration Index (SPEI) [11] combines precipitation with potential evapotranspiration, thereby incorporating both water supply and atmospheric demand. This makes it more robust for detecting droughts under climate variability and climate change. Accordingly, this study adopts the SPEI as the primary drought index. Nevertheless, we acknowledge that using only the SPEI is a limitation, and future studies should integrate multiple indices to capture meteorological, agricultural, and hydrological drought dimensions more comprehensively.

The Northeastern region of Thailand faces multidimensional drought risks, involving declines in precipitation, soil moisture, and surface runoff. These factors often exhibit nonlinear relationships and tend to co-occur during severe drought events. Consequently, it is essential to develop multivariate statistical models to analyze the joint behavior of drought indicators. The trivariate copula framework offers a suitable approach, as it allows for flexible modeling by separating the choice of marginal distributions for each variable from its dependence structure. Moreover, this method effectively captures tail dependence. It enables the calculation of joint return periods for extreme drought events, which is critical for water resource planning and early warning systems in the Mun-Chi river basin of Northeastern Thailand [11,12,13].

Traditional drought analyses have often relied on univariate or bivariate statistical approaches. While univariate indices provide valuable insights, they fail to capture interdependencies among drought characteristics such as duration, severity, and peak intensity. Bivariate copula models have been increasingly applied in drought studies to model dependencies between two variables (e.g., duration and severity). Still, they cannot adequately describe the simultaneous occurrence of three inter-related drought characteristics. The trivariate copula approach offers a more comprehensive framework by modeling joint probabilities across three dimensions, thereby improving the assessment of compound drought risks. Although multivariate copula methods have been applied in various hydrological contexts, their trivariate applications to drought remain limited. Recent advances, such as the three-dimensional copula modeling of climate extremes [14], demonstrate the potential of this method.

In such contexts, the application of trivariate copula models offers a more robust and flexible analytical framework. Unlike bivariate models, trivariate copulas can represent the joint behavior of three variables simultaneously, providing a more comprehensive understanding of drought dynamics. This is particularly advantageous when analyzing key characteristics of drought, such as duration, severity, and peak, together rather than in isolation or in pairs. Modeling these characteristics jointly enables a more accurate estimation of joint return periods and the probability of concurrent extreme events, which are crucial for practical drought risk assessment and resource planning. Moreover, trivariate copulas help capture complex tail dependencies and non-linear interactions that simpler models often miss. By accounting for higher dimensional dependence structures, they improve the reliability of drought characterization and enhance the predictive capabilities of early warning systems. This makes them a valuable tool in regions facing increasing climate variability, such as Thailand, where decision-makers require more precise and integrated information to support water management, agriculture, and disaster preparedness [15,16,17].

This study primarily aims to conduct a risk analysis of compound drought events in Northeastern Thailand by integrating the SPEI with other key drought characteristics—namely, duration, severity, and peak intensity—through a trivariate copula framework. By capturing the inter-relationships among multiple drought indicators, this approach aims to enhance the precision of drought assessment, provide deeper insights into drought risk, and inform adaptive strategies for water resource management and agricultural resilience in an increasingly variable climate. Section 2 presents the study area and meteorological data; Section 3 describes the methodological framework, including the calculation of the SPEI, marginal distributions of drought characteristics, and trivariate copula modeling; Section 4 provides the results, including the characterization of drought events and a joint probability analysis; and finally, Section 7 presents the conclusions drawn from this study.

2. Study Area and Data

2.1. Study Area

Northeastern Thailand, known as the Isan region, is the country’s most significant geographical area, spanning approximately 168,854 km² and encompassing 23 meteorological stations [18]. Situated on the Khorat Plateau, the region is bordered by the Mekong River to the north and east, forming the international boundaries with Laos and Cambodia [19] (see Figure 1).

The climate is classified as tropical savanna, with a distinct wet season from May to October and a dry season from November to April [20]. Annual rainfall ranges between 1000 and 1400 mm, with substantial spatial and temporal variability that frequently leads to drought episodes [21]. The topography is characterized by undulating plains and plateaus, with elevations of 100–300 m above sea level [22]. Soils are predominantly sandy loam to clay loam with low organic matter content and limited water-holding capacity [23]. These physical and climatic factors strongly influence agricultural productivity and water resource availability [24].

The hydrology is dominated by three major river systems: the Mekong, Chi, and Mun rivers [25]. The Mekong flows along the northern and eastern borders, while the Chi and Mun rivers are major tributaries feeding the Mekong. The Mun River traverses the southern provinces, including Surin and Si Sa Ket, which are the focal areas of this study. Agriculture—primarily rainfed rice cultivation—remains the dominant livelihood, making the region highly sensitive to rainfall variability [18,21,26].

2.2. Data

Meteorological data were obtained from the Thailand Meteorological Data Service Center for four stations located in Northeastern Thailand (

Table 1. Meteorological stations used in Northeastern Thailand.

Station Code	Station Name	Province	Latitude	Longitude
48353	Loei	Loei	17.4500	101.7333
48354	Udon Thani	Udon Thani	17.3833	102.8000
48355	Sakon Nakhon Agromet	Sakon Nakhon	17.1250	104.0610
48356	Sakon Nakhon	Sakon Nakhon	17.1500	104.1333
48357	Nakhon Phanom	Nakhon Phanom	17.4108	104.7825
48358	Nakhon Phanom Agromet	Nakhon Phanom	17.4431	104.7736
48381	Khon Kaen	Khon Kaen	16.4611	102.7897
48382	Maha Sarakham	Maha Sarakham	16.2472	103.0681
48383	Mukdahan	Mukdahan	16.5414	104.7289
48384	Tha Phra Agromet	Khon Kaen	16.3333	102.8167
48390	Kalasin	Kalasin	16.3320	103.5875
48404	Roi Et Agromet	Roi Et	16.0732	103.6084
48405	Roi Et	Roi Et	16.0200	103.7439
48407	Ubon Ratchathani	Ubon Ratchathani	15.2500	104.8667
48408	Ubon Ratchathani Agromet	Ubon Ratchathani	15.2391	105.0235
48409	Si Saket Agromet	Si Saket	15.0000	104.0500
48416	Thatum	Surin	15.3167	103.6833
48431	Nakhon Ratchasima	Nakhon Ratchasima	14.9683	102.0860
48432	Surin	Surin	14.8833	103.5000
48433	Surin Agromet	Surin	14.8833	103.4500
48434	Chok Chai	Nakhon Ratchasima	14.7189	102.1686
48435	Pakchong Agromet	Nakhon Ratchasima	14.6439	101.3319
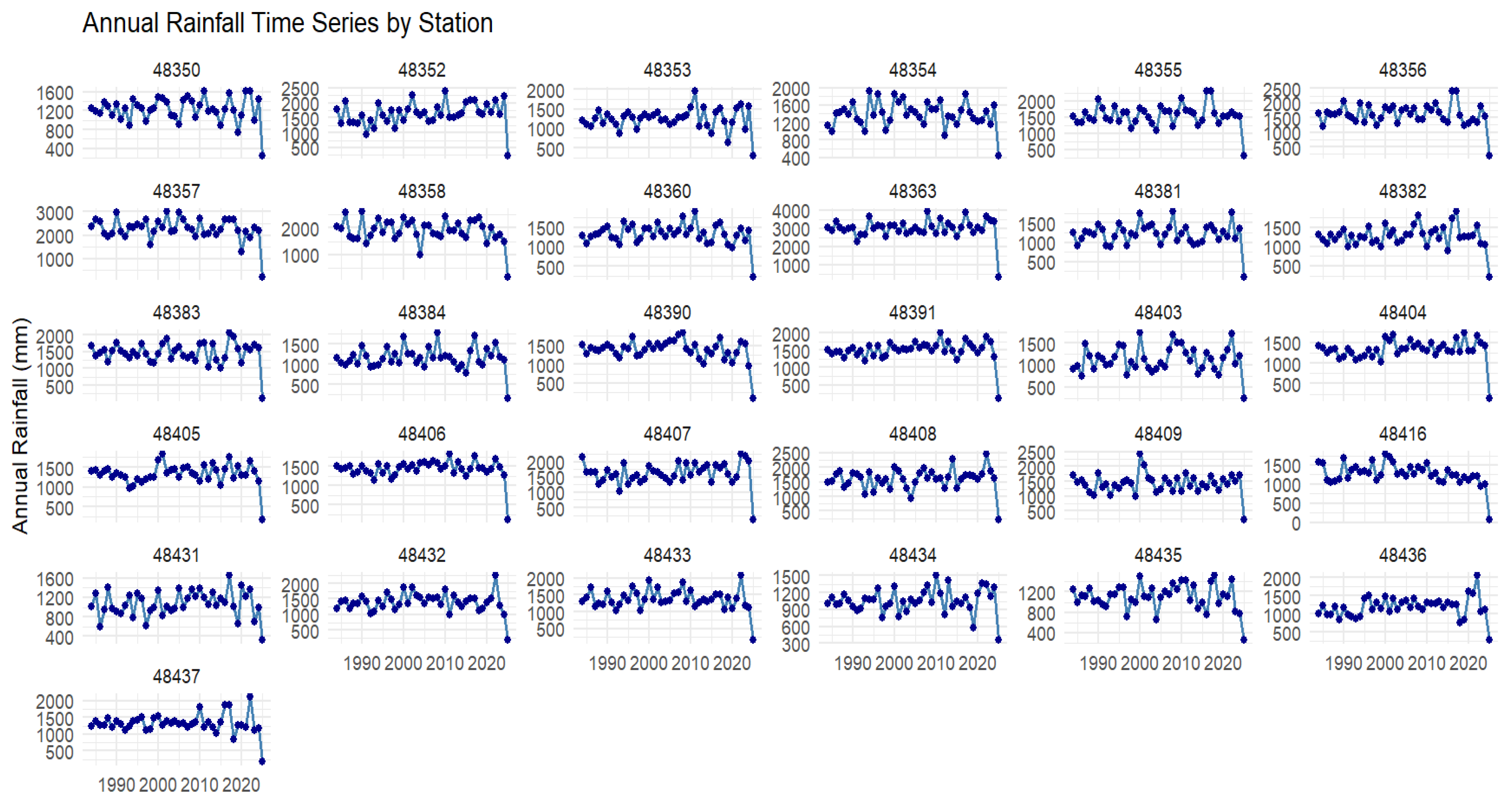
48437	Buriram	Buriram	15.2258	103.2481

) for the period of 2007–2025. The dataset comprised monthly precipitation and temperature records, which were aggregated to annual rainfall to visualize rainfall variability for the period of 1984–2025 (Figure 2). The Standardized Precipitation–Evapotranspiration Index (SPEI) was calculated from precipitation and temperature data to capture both water supply and atmospheric demand. A moving average was applied to account for seasonal variation, and the SPEI was computed at 1-, 3-, 6-, and 12-month timescales. The 3-month SPEI (SPEI3) was emphasized because it aligns with the typical length of the wet season and the regional crop-growing period, effectively reflecting short-term drought conditions relevant to agricultural decision-making. Previous studies have shown that the SPEI3 exhibits the strongest correlation with overall agricultural yields during critical growth months, highlighting its suitability for assessing impacts of drought on crop production. The studies reported in [27,28,29] showed that the SPEI3 is more sensitive to short-term droughts, capturing changes in duration and severity promptly, especially during the dry season, which is critical for cropping . Using longer timescales would increase model complexity and data requirements without clear benefits for assessing short-term drought risk (duration, severity, and peak intensity).

3. Materials and Methods

3.1. The Standardized Precipitation–Evapotranspiration Index (SPEI)

The Standardized Precipitation–Evapotranspiration Index (SPEI) [11] was employed to assess drought conditions at multiple temporal scales (1, 3, 6, and 12 months). The SPEI integrates precipitation (water supply) and temperature (atmospheric demand) to produce a robust measure of drought severity, overcoming the limitations of precipitation-only indices. The SPEI is calculated from the climatic water balance (precipitation minus potential evapotranspiration), then standardized to a mean of zero and a variance of one. This standardization allows for comparison of drought anomalies across locations and time periods. In this study, the standardization reference period covers the full observation record.

For the 3-month scale, cumulative precipitation and temperature were aggregated over consecutive 3-month windows to capture short-term drought variability. This approach effectively reflects localized and rapid changes in water availability. Drought classification followed the thresholds in

Table 2. SPEI classification and corresponding cumulative probabilities of occurrence.

SPEI	Category
≥2.0	Extremely wet
$1.5\le \mathrm{SPEI}<2.0$	Moderately wet
$1.0\le \mathrm{SPEI}<1.5$	Slightly wet
$-1.0<\mathrm{SPEI}<1.0$	Near normal
$-1.5<\mathrm{SPEI}\le -1.0$	Mild drought
$-2.0<\mathrm{SPEI}\le -1.5$	Moderate drought
≤−2.0	Extreme drought

.

3.2. Drought Event Extraction Using Run Theory

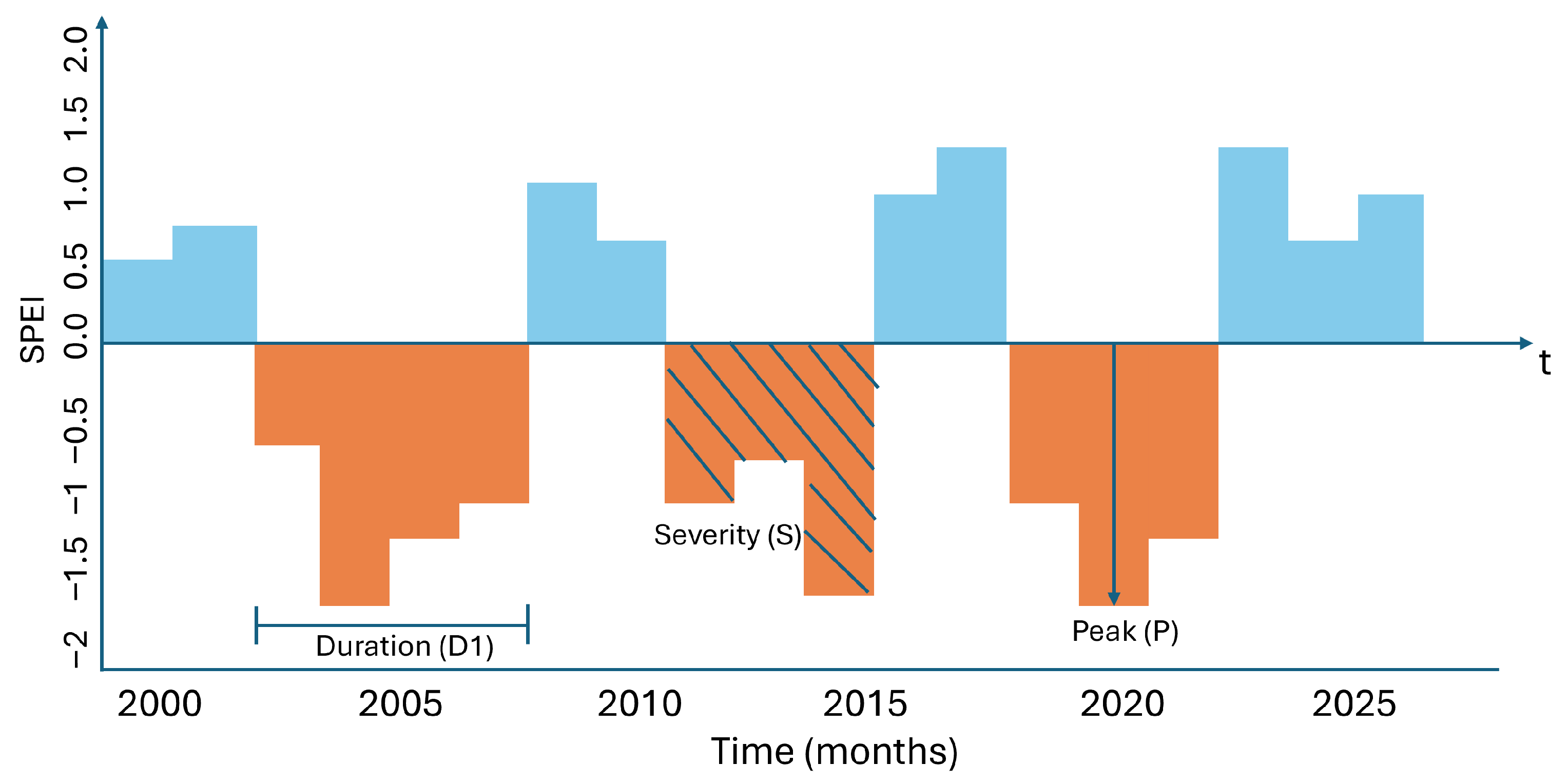
Drought events were identified using the run theory [30], applied to the SPEI time series. A drought event was defined as a continuous period of months with SPEI values below 0, representing water deficit conditions. The drought characteristics of interest—duration (D), severity (S), and peak intensity (P)—were extracted as follows:

• Duration (D): the number of consecutive months with SPEI $<0$;
• Severity (S): the cumulative SPEI deficit over the event, i.e., the sum of negative SPEI values;
• Peak intensity (P): the minimum SPEI value within the drought period.

To avoid artificial merging of distinct drought events, short gaps of one month with SPEI $>-0.9$ between drought periods were treated as separate events. Sensitivity tests confirmed that this approach did not significantly affect the estimated joint probabilities of drought characteristics. Figure 3 illustrates the run-theory approach applied to the SPEI series.

3.3. Marginal Distribution

The effectiveness of modeling drought characteristics using joint distributions largely depends on the selection of appropriate marginal distributions that accurately represent the S and D data. In this study, we evaluated the suitability of six candidate probability distributions: normal (norm), logistic (logis), Weibull (weibull), gamma (gamma), lognormal (lnorm), and exponential (exp). Parameter estimation for each distribution was conducted using Maximum Likelihood Estimation (MLE). The best fitting marginal distributions for each of the S, D, and P series were determined using the Kolmogorov–Smirnov (KS) goodness-of-fit test [31]. Among the six estimated distributions, the one yielding the lowest Akaike Information Criterion (AIC) value [32] was selected as the most suitable fit for the respective series at the given time scale.

3.4. Copula Analysis

Sklar’s theorem [33] provides the theoretical foundation for copula modeling, stating that any multivariate joint distribution can be decomposed into its marginal distributions linked by a copula function. Formally, for continuous random variables ($X_1,X_2,\dots ,X_n$) with marginal CDFs ($F_1,F_2,\dots ,F_n$), the joint distribution is expressed as follows:

$$F(x_1,x_2,\dots ,x_n)=C(F_1\left(x_1\right),F_2\left(x_2\right),\dots ,F_n\left(x_n\right)),$$

(1)

where $C:{[0,1]}^n\to [0,1]$ is a copula function capturing the dependence structure, independent of the marginals. When marginals are continuous, C is unique and differentiable, with the density function expressed as follows:

$$c(u_1,u_2,\dots ,u_n)={\displaystyle \frac{{\partial }^{n}C(u_1,u_2,\dots ,u_n)}{\partial u_1\partial u_2\cdots \partial u_n}},$$

(2)

where $u_i=F_i\left(x_i\right)$.

Copula Families and Determination

To model the complex dependence among drought characteristics (duration (D), severity (S), and peak (P)), five copula functions were evaluated: Clayton, Gumbel, and Frank from the Archimedean family and Gaussian and Student’s t from the Elliptical family [34,35]. Archimedean copulas are well-suited for asymmetric tail dependence commonly observed in hydrological extremes, while Elliptical copulas capture symmetric dependencies. Each copula was fitted individually to every station and drought characteristic series.

3.5. Copula Analysis

Sklar’s theorem, first introduced in [33], forms the theoretical foundation of copula theory. It states that any multivariate joint distribution (F) can be decomposed into its marginal distribution functions linked together by a copula function (C). Formally, for continuous random variables ($X_1,X_2,\dots ,X_n$) with marginal cumulative distribution functions (CDFs; $F_1,F_2,\dots ,F_n$), the joint distribution function can be expressed as follows:

$$F(x_1,x_2,\dots ,x_n)=C\left(F_1\left(x_1\right),F_2\left(x_2\right),\dots ,F_n\left(x_n\right)\right),$$

(3)

where $C:{[0,1]}^n\to [0,1]$ is a copula function capturing the dependence structure among the variables, independent of their marginals.

When the marginal distributions are continuous, the copula function is unique and differentiable, allowing for the definition of the copula density function as the n-th-order partial derivative:

$$c(u_1,u_2,\dots ,u_n)={\displaystyle \frac{{\partial }^{n}C(u_1,u_2,\dots ,u_n)}{\partial u_1\partial u_2\cdots \partial u_n}},$$

(4)

where $u_i=F_i\left(x_i\right)$ represents the probability integral transforms of the marginals and within $[0,1]$.

3.5.1. Copula Functions Used in This Study

To model the complex dependence among drought characteristics (duration (D), severity (S), and peak (P)), five copula functions were evaluated: Clayton, Gumbel, and Frank from the Archimedean family and Gaussian and Student’s t from the Elliptical family [34,35]. Archimedean copulas are well-suited for asymmetric tail dependence commonly observed in hydrological extremes, while Elliptical copulas capture symmetric dependencies. Each copula was fitted individually to every station and drought characteristic series.

Table 3. Summary of copula functions used in this study.

Family	Name	Copula Function	Parameter (s)
Archimedean	Clayton	${\left(max\left\{u_1^{-\theta }+u_2^{-\theta }+u_3^{-\theta }-2,0\right\}\right)}^{-1/\theta }$	$\theta >0$
	Gumbel	$exp\left(-{\left[{(-ln{u}_1)}^{\theta }+{(-ln{u}_2)}^{\theta }+{(-ln{u}_3)}^{\theta }\right]}^{1/\theta }\right)$	$\theta \ge 1$
	Frank	$-{\displaystyle \frac{1}{\theta }}ln\left[1+{\displaystyle \frac{{\prod }_{i=1}^3(e^{-\theta u_i}-1)}{{(e^{-\theta }-1)}^2}}\right]$	$\theta \ne 0$
Elliptical	Gaussian	${\Phi }_{\Sigma }\left({\Phi }^{-1}\left(u_1\right),{\Phi }^{-1}\left(u_2\right),{\Phi }^{-1}\left(u_3\right)\right)$	Correlation matrix ($\Sigma$)
	Student’s t	$t_{\Sigma ,\nu }\left(t_{\nu }^{-1}\left(u_1\right),t_{\nu }^{-1}\left(u_2\right),t_{\nu }^{-1}\left(u_3\right)\right)$	$\nu$ degrees of freedom ($\Sigma$)

summarizes these copula functions, along with their parameter ranges.

3.5.2. Dependence Measurement: Kendall’s Tau

Before fitting copulas, the dependence between pairs of variables is assessed using Kendall’s tau coefficient [36], which is defined as follows:

$$\tau ={\displaystyle \frac{2}{n(n-1)}}\sum _{i<j}\mathrm{sgn}(x_i-x_j)\mathrm{sgn}(y_i-y_j),$$

(5)

where $\mathrm{sgn}(·)$ is the sign function and n is the sample size. This nonparametric rank correlation helps identify strongly dependent pairs for copula modeling.

3.5.3. Parameter Estimation via Pseudo-Maximum Likelihood

Copula parameters are estimated by maximizing the pseudo-log-likelihood function, which uses the transformed data (pseudo-observations) derived from the empirical distribution functions of the marginals. Specifically, the estimator ($\widehat{\theta }$) is obtained as follows:

$$\widehat{\theta }=arg\underset{\theta }{max}\sum _{i=1}^{n}lnc\left(u_{1i},u_{2i},\dots ,u_{ni};\theta \right),$$

(6)

where $c(·)$ is the copula density from Equation (4) and $u_{ji}={\widehat{F}}_j\left(x_{ji}\right)$ represents the pseudo-observations obtained from the empirical CDFs [34,37].

3.5.4. Two-Dimensional Copula Functions

For two continuous random variables (X and Y) with marginal distribution functions (F and G) and a joint distribution (H), the copula (C) links marginals to the joint distribution as follows:

$$H(x,y)=C\left(F\left(x\right),G\left(y\right)\right).$$

(7)

In this study, Archimedean copulas were primarily employed to model dependence between pairs of drought characteristics.

3.5.5. Three-Dimensional Copula Functions

Extending to three dimensions, the copula function links the marginal distributions of three drought characteristics (e.g., duration (X), severity (Y), and peak (Z)) in a joint distribution:

$$F(x,y,z)=C\left(F_X\left(x\right),F_Y\left(y\right),F_Z\left(z\right)\right),$$

(8)

where C represents the selected copula family capturing the multivariate dependence structure. Due to the skewness often observed in drought data, Clayton and Gumbel–Hougaard copulas were selected for the modeling of asymmetric tail dependencies. The joint distribution was constructed by combining the fitted marginal distributions with the copula as per Sklar’s theorem.

3.6. Goodness-of-Fit Statistical Tests

The goodness-of-fit test is a statistical method used to assess the correlation between variables and determine if the collected data conform to a specific distribution. This test evaluates the performance of both marginal and joint probability functions. It plays a crucial role in hypothesis testing by checking the normality of residuals and comparing two samples (observed and from the marginal distribution) to verify whether they originate from identical distributions. In this study, the estimation of empirical non-exceedance probabilities for drought duration (D) and drought severity (S) utilized the Kolmogorov–Smirnov test and Cramer–von Mises test, which were employed to evaluate the performance of the joint probabilities in the bivariate case.

3.6.1. Kolmogorov–Smirnov (K-S) Test

The Kolmogorov-Smirnov (K-S) test is preferred, since it does not make any assumptions about the distribution of data. This method compares the maximum gap between the experimental cumulative distribution function and the theoretical cumulative distribution function. The K-S test ($D_{n,n^{\tau }}$) is used to determine whether the parameters are acceptable or not and is expressed [31] as follows:

$$D_{n,n^{\tau }}=\underset{x}{sup}|F_{1,n}\left(x\right)-F_{2,n^{\tau }}\left(x\right)|,$$

where $F_{1,n}$ = experimental distribution, $F_{2,n^{\tau }}$ = theoretical distribution, and sup = supremum function. To perform the goodness-of-fit test, the null hypothesis is applied; it is only accepted when the gap between the theoretical and the expected value is smaller than expected for the given sample.

3.6.2. Cramer–von Misés (CvM) Test

The fitness test for the extreme value copula function is performed by using the Cramer–von Misés test [38] with a parametric bootstrap, as represented by Equation (9),

$$S_n^{gof}={\mathit{\int }}_{{[0,1]}^d}n{(C_n\left(u\right)-C_{{\theta }_n}\left(u\right))}^{2}d{C}_n\left(u\right)=\sum _{i=1}^n{(C_n\left(u_i\right)-C_{{\theta }_n}\left({\widehat{u}}_i\right))}^2,$$

(9)

an approximate p-value for the test based on $S_n^{gof}$ can be obtained by means of a parametric bootstrap, whose asymptotic validity is investigated in [39].

3.7. Model Selection

Model selection is a fundamental step in statistical analysis, focused on identifying the model that best balances goodness of fit with model complexity. In the context of drought analysis using joint distributions, this process requires careful selection of both the marginal distributions, which describe the individual behavior of each variable, and the copula function, which captures the dependence structure among these variables.

3.7.1. Akaike Information Criterion (AIC)

The Akaike Information Criterion (AIC), introduced in [32], is a widely used statistical measure for model selection that balances model fit and complexity. It is defined as follows:

$$\mathrm{AIC}=2k-2ln\left(L\right),$$

where k is the number of estimated parameters in the model and L is the maximum value of the likelihood function for the model. The first term ($2k$) penalizes model complexity to avoid overfitting, while the second term ($-2ln\left(L\right)$) rewards a better fit to the observed data.

In this study, the AIC was computed after estimating parameters for the candidate probability distributions of the S, D, and P series. For each series, AIC values were calculated and compared across the six candidate distributions. The distribution with the lowest AIC value was selected as the most suitable model for the respective series, as a lower AIC indicates a better trade-off between goodness of fit and model parsimony [40].

3.7.2. Cross-Validation Copula Information Criterion (xv-CIC)

A recent advancement in copula model selection is the Copula Information Criterion (CIC), developed to address limitations of the traditional AIC when applied in semiparametric contexts based on the pseudo-maximum likelihood estimation (pseudo-MLE) framework [41]. Building on this, the Cross-Validation Copula Information Criterion (xv-CIC) was introduced as a first-order approximation to leave-one-out cross-validation, tailored for copula models and designed to enhance selection accuracy under weak regularity conditions [42].

The xv-CIC maintains a structure analogous to the AIC but incorporates bias-correction terms derived from cross-validation theory, offering a more justified alternative for copula model comparison based on predictive performance [41]. In practice, xv-CIC is calculated for each candidate copula model, and the model with the highest xv-CIC score (or lowest information loss) is selected as the most suitable representation of the multivariate dependence structure.

For example, in applications such as hydrological copula modeling, researchers often compute both AIC and xv-CIC values: the preferred copula model is one that simultaneously minimizes AIC and maximizes xv-CIC, ensuring a balance between goodness of fit and validation-based predictive reliability [43].

3.8. Joint Recurrence Period

The joint drought frequency was analyzed in terms of the joint return periods, which were the average elapsed time between the occurrences of two droughts with specific characteristic variables. According to the theory of return period [44], the return period of a univariate variable can be estimated as follows:

$$T={\displaystyle \frac{N}{m(1-F(x\left)\right)}},$$

where $F\left(x\right)$ is the distribution function of drought characteristic variables, N is the length of the data series, and m is the number of drought events. However, a drought is considered a multivariate event characterized by drought duration, severity, and peak intensity; the joint return period estimated by bivariate and trivariate drought characteristic variables provides more useful information for drought assessments. Therefore, in this study, the joint return periods were estimated using the proposed methodology. The joint return periods were calculated for two cases: return period of $T_{and}$$D\ge d$ and $S\ge s$ (AND case) and a return period of $T_{or}$ for $D\ge d$ or $S\ge s$ (OR case). The frequency distribution functions of drought duration (D), severity (S), and peak intensity (P) are assumed as u, v, and S, respectively; then, $T_{and}$ and $T_{or}$ between drought duration (D) and severity (S) are estimated:

$$T_{and}={\displaystyle \frac{N}{nP(D\le d\cup S\le s)}}={\displaystyle \frac{N}{n[1-C(u,v\left)\right]}},$$

(10)

$$T_{or}={\displaystyle \frac{N}{nP(D\le d\cap S\le s)}}={\displaystyle \frac{N}{n[1u-v+C(u,v\left)\right]}},$$

(11)

where d and s are the given drought duration and severity, respectively.

The $T_{and}$ and $T_{or}$ of drought duration (D), severity (S), and peak intensity (P), respectively, are expressed as follows:

$$T_{and}={\displaystyle \frac{N}{nP(D\le d\cup S\le s\cup W\le w)}}={\displaystyle \frac{N}{n[1-C(u,v,w\left)\right]}},$$

(12)

$$\begin{array}{ll}{T}_{or}& ={\displaystyle \frac{N}{nP(D\le d\cap S\le s\cap W\le w)}}\\ & ={\displaystyle \frac{N}{n\left[1-u-v-w+C(u,v)+C(u,w)+C(v,w)-C(u,v,w)\right]}}\end{array}$$

(13)

where $u,v,w$ are the marginal probabilities of duration, severity, and peak intensity, respectively, and $C(·)$ is the fitted trivariate copula function.

3.9. Risk Analysis

The concept of return period can be extended to the multivariate context, resulting in what is known as the joint return period. In particular, joint (or primary) return periods can be characterized using logical conjunctions, such as the “AND” case and “OR” case, which define the probability of co-occurrence of two or more extreme events. In hydrological applications, the return period typically refers to the expected time interval between events of a certain magnitude, such as heavy inundation. When assessing the reliability of hydrological infrastructure, it is essential to consider the service lifetime, denoted by N years. The risk of failure due to an extreme event, such as drought, can be quantified in terms of the return period (T). This risk is defined as the probability that at least one such event will occur during the service period and is given by the following expression [45]:

$$R=1-{\left(1-{\displaystyle \frac{1}{T}}\right)}^N,$$

where R represents the cumulative risk of failure, T is the return period associated with the drought event under the defined conditions, and N is the duration over which the risk is evaluated [46].

4. Results

4.1. Drought Evolution Characterization

In this study, researchers focused on assessing drought duration (D), drought severity (S), and drought peak (P) using the hydrological drought index. They utilized 24 years of precipitation data spanning from 2007 to 2025. Estimates for the 3-month Standardized Precipitation Evapotranspiration Index (SPEI3) were conducted at 23 stations. The SPEI-3 drought index, which represents 3-month rainfall anomalies, is used to describe the drought time series. The statistical results of drought characteristic variables are shown in the analysis in

Table 4. The duration of the drought, the severity, and the peak of the drought of the SPEI3 drought index classified by station.

Station Code	Drought Duration: D			Drought Severity: S			Drought Peak: P
	Mean	Max	Skewness	Mean	Max	Skewness	Mean	Max	Skewness
48353	10.7000	28.0000	1.1164	9.1589	0.4564	2.0032	1.0476	0.3235	0.3533
48354	11.0000	49.0000	1.8483	10.2422	0.0167	1.4644	0.7088	0.0167	0.6276
48355	7.0667	20.0000	1.1146	6.0421	0.0623	1.6747	0.9865	0.0623	0.4496
48356	4.9545	20.0000	1.8964	4.0354	0.0148	2.4834	0.7838	0.0148	0.6965
48357	4.9130	18.0000	1.8926	3.9394	0.0064	2.2273	0.9044	0.0064	0.1881
48358	5.3333	35.0000	3.0406	4.2103	0.0067	3.4054	0.7169	0.0067	0.6438
48381	7.9286	32.0000	1.7797	6.5557	0.0072	2.0392	0.6146	0.0072	0.8678
48382	7.0667	28.0000	2.1242	6.1298	0.3698	2.3083	0.8446	0.3607	0.9319
48383	5.9412	20.0000	1.3763	5.1502	0.0984	1.7937	0.8655	0.0984	0.5112
48384	5.1000	28.0000	2.8211	4.3465	0.0658	3.0880	0.6918	0.0658	0.9695
48390	4.7273	28.0000	2.6458	4.1143	0.0063	3.3761	0.6502	0.0063	1.3556
48404	4.1538	12.0000	1.1643	3.3639	0.0092	1.8580	0.9176	0.0092	0.0506
48405	6.3529	17.0000	0.7196	5.2291	0.0523	1.0392	0.8563	0.0523	0.5597
48407	13.2857	55.0000	1.7770	14.0265	0.1599	1.7163	0.8506	0.1599	1.0095
48408	4.5833	20.0000	2.2859	3.5410	0.0077	2.6405	0.8374	0.0077	0.3341
48409	8.0000	28.0000	1.6207	6.6022	0.0032	2.0297	0.9990	0.0032	0.1951
48431	16.8333	59.0000	1.8209	15.2846	0.0428	2.2018	0.6645	0.0341	1.4339
48432	5.5263	21.0000	1.6700	4.7772	0.1217	1.8512	1.0731	0.1217	0.1190
48433	9.0000	58.0000	3.1545	7.4221	0.0113	3.3476	0.7004	0.0113	0.9499
48434	10.7000	59.0000	2.4069	9.3062	0.0346	2.9751	0.4967	0.0346	1.9296
48435	7.6429	43.0000	2.4649	6.4542	0.0230	3.0921	0.7087	0.0230	0.9048
48437	6.4375	58.0000	3.8478	5.5157	0.0261	3.9719	0.5424	0.0261	2.0000

.

4.2. Marginal Probability Distribution

To identify the most suitable statistical representation for each drought characteristic, six candidate distributions (Normal, Logistic, Weibull, Gamma, Lognormal, and Exponential) were fitted using MLE. The K–S test was applied to evaluate the adequacy of each fit. The best-fit marginal distributions, presented in

Table 5. Marginal distribution of drought characteristics and goodness-of-fit test of each station.

Station Code	Duration	K-S Test (p-Value)	Severity	K-S Test (p-Value)	Peak	K-S Test (p-Value)
48353	exp	0.2445 (0.5883)	lnorm	0.2783 (0.3531)	logis	0.1582 (0.9313)
48354	lnorm	0.4008 (0.1110)	lnorm	0.5437 (0.5100)	logis	0.2884 (0.3702)
48355	lnorm	0.2362 (0.3728)	lnorm	0.3358 (0.5200)	logis	0.1675 (0.7340)
48356	lnorm	0.2448 (0.1432)	lnorm	0.2949 (0.3440)	logis	0.1292 (0.8111)
48357	norm	0.2318 (0.1689)	norm	0.2274 (0.1582)	logis	0.1177 (0.8711)
48358	gamma	0.3482 (0.1230)	exp	0.3961 (0.1800)	logis	0.2717 (0.0736)
48381	lnorm	0.3043 (0.1495)	lnorm	0.5372 (0.4300)	logis	0.3229 (0.0847)
48382	logis	0.3495 (0.5120)	exp	0.3614 (0.2920)	exp	0.3476 (0.0401)
48383	lnorm	0.2943 (0.1053)	lnorm	0.3427 (0.2760)	logis	0.1708 (0.6432)
48390	logis	0.3250 (0.1920)	exp	0.4104 (0.4454)	logis	0.2094 (0.2522)
48404	lnorm	0.2553 (0.6750)	lnorm	0.2325 (0.1019)	logis	0.1537 (0.5215)
48405	logis	0.2837 (0.1296)	lnorm	0.4151 (0.3600)	logis	0.2537 (0.1882)
48407	lnorm	0.5213 (0.4450)	lnorm	0.5818 (0.0890)	logis	0.3152 (0.4066)
48408	logis	0.2286 (0.1628)	logis	0.2989 (0.2130)	logis	0.1552 (0.5577)
48409	exp	0.3431 (0.2200)	logis	0.3251 (0.0031)	logis	0.1957 (0.1898)
48416	logis	0.3068 (0.0984)	logis	0.3559 (0.2550)	logis	0.1974 (0.5000)
48432	lnorm	0.2748 (0.0975)	norm	0.3343 (0.1700)	exp	0.2467 (0.1473)
48433	logis	0.3072 (0.0669)	logis	0.3925 (0.5200)	exp	0.2040 (0.3891)
48434	exp	0.4881 (0.1710)	exp	0.6887 (0.0566)	logis	0.2917 (0.3002)
48435	logis	0.3864 (0.3060)	exp	0.4261 (0.0800)	logis	0.1847 (0.6602)
48437	gamma	0.5085 (0.4553)	exp	0.4918 (0.4450)	norm	0.1668 (0.7049)

, were subsequently used as inputs for copula-based joint probability modeling.

Results show that Lognormal or Logistic distributions most frequently described drought duration and severity, whereas the Logistic distribution best captured the majority of stations’ peak drought intensity. Some stations (e.g., 48358, 48434, and 48437) showed a better fit with Gamma or Exponential distributions, reflecting localized hydrological variability.

Correlation Between Drought Variables

The dependence among drought characteristics was evaluated using Kendall’s tau to quantify monotonic associations between duration (D), severity (S), and peak intensity (P) (

Table 6. Kendall’s tau correlations among drought characteristics at each station.

Station Code	Kendall’s Tau
	D-S	D-P	S-P
48416	0.8107	0.5791	0.7833
48433	0.8051	0.5270	0.7124
48432	0.8280	0.5964	0.7789
48353	0.8540	−0.9556	−0.8090
48354	0.9129	−0.8333	−0.7303
48355	0.8281	−0.8476	−0.6703
48356	0.8200	−0.9048	−0.7463
48357	0.8411	−0.8261	−0.6745
48358	0.7002	−0.9238	−0.6276
48381	0.9021	−0.9560	−0.9258
48382	0.8197	0.8667	0.7994
48383	0.8850	−0.7941	−0.6832
48390	0.8452	−0.9048	−0.7502
48404	0.8685	−0.8892	−0.7691
48405	0.8428	−0.8382	−0.7191
48407	0.9258	0.9048	0.9258
48408	0.7162	−0.8913	−0.6166
48409	0.4720	0.3175	0.7882
48434	0.8485	−0.9556	−0.8485
48435	0.8546	−0.8901	−0.7359
48437	0.7851	−0.8667	−0.6390

). Across most stations, D and S exhibited strong positive correlations ($\tau >0.80$), consistent with the expectation that more extended droughts accumulate greater deficits. In contrast, the relationship between D and P varied markedly: some stations (e.g., 48353, 48354, and 48356) showed strong negative correlations ($\tau <-0.80$), whereas others (e.g., 48407, 48382, and 48409) exhibited positive dependence. Similarly, correlations between S and P ranged from strongly negative to strongly positive.

This spatial heterogeneity suggests that peak drought intensity does not necessarily coincide with prolonged or severe droughts, reflecting influences of local climate variability and watershed-specific characteristics. Such complex, non-uniform dependence structures underscore the need for higher dimensional copula modeling to represent joint drought behavior in the region accurately.

4.3. Bivariate Copula Analysis of Drought Characteristics

To examine the pairwise dependence among drought characteristics, bivariate copula models were fitted for each variable pair (D–S, D–P, and S–P) at all stations. The estimated parameters and the best-fitting copula types for each station are summarized in

Table 7. Summary of best bivariate copula for drought characteristic pairs (D–S, D–P, and S–P) at each station.

Station Code	D–S		D–P		S–P
	Copula	Sn (p-Value)	Copula	Sn (p-Value)	Copula	Sn (p-Value)
48353	Gumbel	0.0373 (0.0538)	Gumbel	0.0489 (0.0834)	Gumbel	0.0567 (0.0850)
48354	Gumbel	0.0336 (0.3461)	Frank	0.0372 (0.1926)	Clayton	0.0490 (0.1632)
48355	Frank	0.0451 (0.0475)	Frank	0.0522 (0.1354)	Frank	0.0601 (0.0145)
48356	Frank	0.0317 (0.0035)	Frank	0.0410 (0.1789)	Frank	0.1568 (0.0649)
48357	Gumbel	0.0613 (0.0804)	Frank	0.0531 (0.1230)	Frank	0.1187 (0.0524)
48358	Gumbel	0.1459 (0.0475)	Frank	0.0666 (0.0897)	Frank	0.1771 (0.5494)
48381	Frank	0.0433 (0.4081)	Frank	0.0510 (0.1575)	Gumbel	0.0472 (0.3092)
48382	Gumbel	0.0890 (0.0734)	Gumbel	0.0622 (0.0913)	Frank	0.0807 (0.0255)
48383	Frank	0.0403 (0.2992)	Frank	0.0488 (0.1872)	Frank	0.1832 (0.4995)
48390	Gumbel	0.0650 (0.2223)	Frank	0.0577 (0.1548)	Frank	0.2994 (0.5049)
48404	Frank	0.0300 (0.1863)	Frank	0.0399 (0.0984)	Frank	0.1036 (0.0304)
48405	Gumbel	0.0511 (0.0235)	Frank	0.0488 (0.0862)	Frank	0.0804 (0.1033)
48407	Gumbel	0.0201 (0.4461)	Frank	0.0330 (0.2042)	Frank	0.1102 (0.0105)
48408	Gumbel	0.0820 (0.0365)	Frank	0.0599 (0.1035)	Frank	0.0331 (0.0704)
48409	Gumbel	0.0373 (0.1943)	Gumbel	0.0388 (0.1273)	Gumbel	0.0326 (0.3741)
48416	Gumbel	0.0336 (0.3461)	Frank	0.0489 (0.0834)	Gumbel	0.0279 (0.8666)
48432	Gumbel	0.0288 (0.2093)	Gumbel	0.0422 (0.1645)	Gumbel	0.0391 (0.0874)
48433	Frank	0.0434 (0.6128)	Gumbel	0.0444 (0.1930)	Clayton	0.0548 (0.2013)
48434	Gumbel	0.0366 (0.0235)	Frank	0.0411 (0.1532)	Clayton	0.0724 (0.0654)
48435	Frank	0.0535 (0.3002)	Frank	0.0502 (0.1756)	Frank	0.0651 (0.1014)
48437	Gumbel	0.0840 (0.0964)	Frank	0.0601 (0.0899)	Frank	0.1586 (0.5005)

.

The results of the bivariate analysis reveal that drought duration and severity (D–S) generally show the strongest dependence, which is most frequently described by either Gumbel or Frank copulas. In contrast, the dependences between severity and peak intensity (S–P) and between duration and peak intensity (D–P) are weaker and tend to vary across stations. While these pairwise models help to clarify important aspects of the relationships between drought characteristics, they are limited in their ability to represent the full complexity of drought behavior.

In practice, extreme droughts in Northeastern Thailand rarely occur in isolation. Long-duration events are often accompanied by high severity and, in many cases, sharp intensity peaks. This compound nature of drought cannot be sufficiently represented by analyzing variable pairs separately, since such an approach overlooks higher order interactions that are central to understanding the overall drought process.

For this reason, extending the analysis from bivariate to trivariate copulas provides clear advantages. The trivariate framework integrates duration, severity, and peak intensity within a single model, allowing for a more realistic representation of drought dynamics. In particular, it enables the estimation of joint recurrence periods (JRPs) for compound droughts, an essential step in assessing risks that only emerge when multiple drought attributes co-occur. As a result, the trivariate copula approach offers a more robust foundation for identifying vulnerable areas and developing targeted drought risk management strategies in the region.

4.4. Drought Risk Analysis Based on a Three-Dimensional Copula Function

The results of the drought risk analysis based on the three-dimensional extreme value copula function are summarized in

Table 8. Best fitting copula function and goodness-of-fit test results for trivariate drought variables (D: duration; S: severity; P: peak) at each station.

Station Code	Copula Type	Estimated $\mathit{\theta }$ (s.e.)	Sn (p-Value)	xv-CIC
48353	Clayton	1.2500 (0.4000)	0.0457 (0.4568)	17.4321
48355	Clayton	0.9500 (0.3000)	0.0523 (0.3789)	15.9876
48356	Clayton	1.1000 (0.3500)	0.0489 (0.4124)	18.1234
48357	Clayton	1.5000 (0.4500)	0.0600 (0.3501)	16.7890
48358	Clayton	0.8500 (0.2800)	0.0399 (0.4902)	14.5678
48381	Clayton	1.3500 (0.3700)	0.0501 (0.4288)	17.2233
48382	Frank	16.5895 (7.3777)	0.0573 (0.4940)	28.0882
48383	Clayton	1.2000 (0.3300)	0.0426 (0.4659)	16.5432
48390	Clayton	0.9000 (0.2900)	0.0372 (0.5123)	15.9876
48404	Clayton	1.0500 (0.3100)	0.0444 (0.3988)	17.6543
48408	Clayton	1.3000 (0.3800)	0.0412 (0.4390)	18.4321
48409	Gumbel	2.0577 (0.3858)	0.0852 (0.0255)	22.3623
48416	Frank	10.0596 (3.5446)	0.0813 (0.2592)	20.7610
48432	Gumbel	3.4602 (0.9830)	0.0700 (0.1234)	28.4253
48433	Frank	9.4165 (2.4582)	0.0805 (0.4271)	19.3832
48434	Clayton	0.8800 (0.2700)	0.0389 (0.4802)	15.3456
48435	Clayton	1.4000 (0.4000)	0.0500 (0.4012)	17.8765
48437	Clayton	1.1000 (0.3400)	0.0432 (0.4610)	16.9999

. This study incorporates the joint probability distribution, marginal distributions, and recurrence periods for three key drought characteristics: duration, severity, and peak intensity.

4.4.1. Copula Function Preference

To assess drought risk, the copula function was selected to represent the dependency structure among the three key variables: duration, severity, and peak intensity. The selection process was based on goodness-of-fit (GOF) tests, including the Sn statistic and its p-Value, as well as the cross-validated copula information criterion (xv-CIC). The copula with the best statistical performance for each station was chosen as the final model.

Table 8 shows that Clayton, Frank, and Gumbel copulas were alternately preferred depending on the station, highlighting the spatial variability in the dependence structure of drought events. The Gumbel copula best represented stations 48409 and 48432, whereas many others fit the Clayton copula and a few (e.g., 48382, 48416, and 48433) aligned with the Frank copula.

4.4.2. Joint Probability Distribution

The joint probability distribution of drought characteristics was modeled using a trivariate copula function, which effectively captures the complex dependence structure among drought duration (D), severity (S), and peak intensity (P). Unlike traditional univariate approaches, this multivariate framework integrates the marginal distributions of each variable with a flexible dependence structure, allowing for a comprehensive representation of compound drought behaviors and interactions.

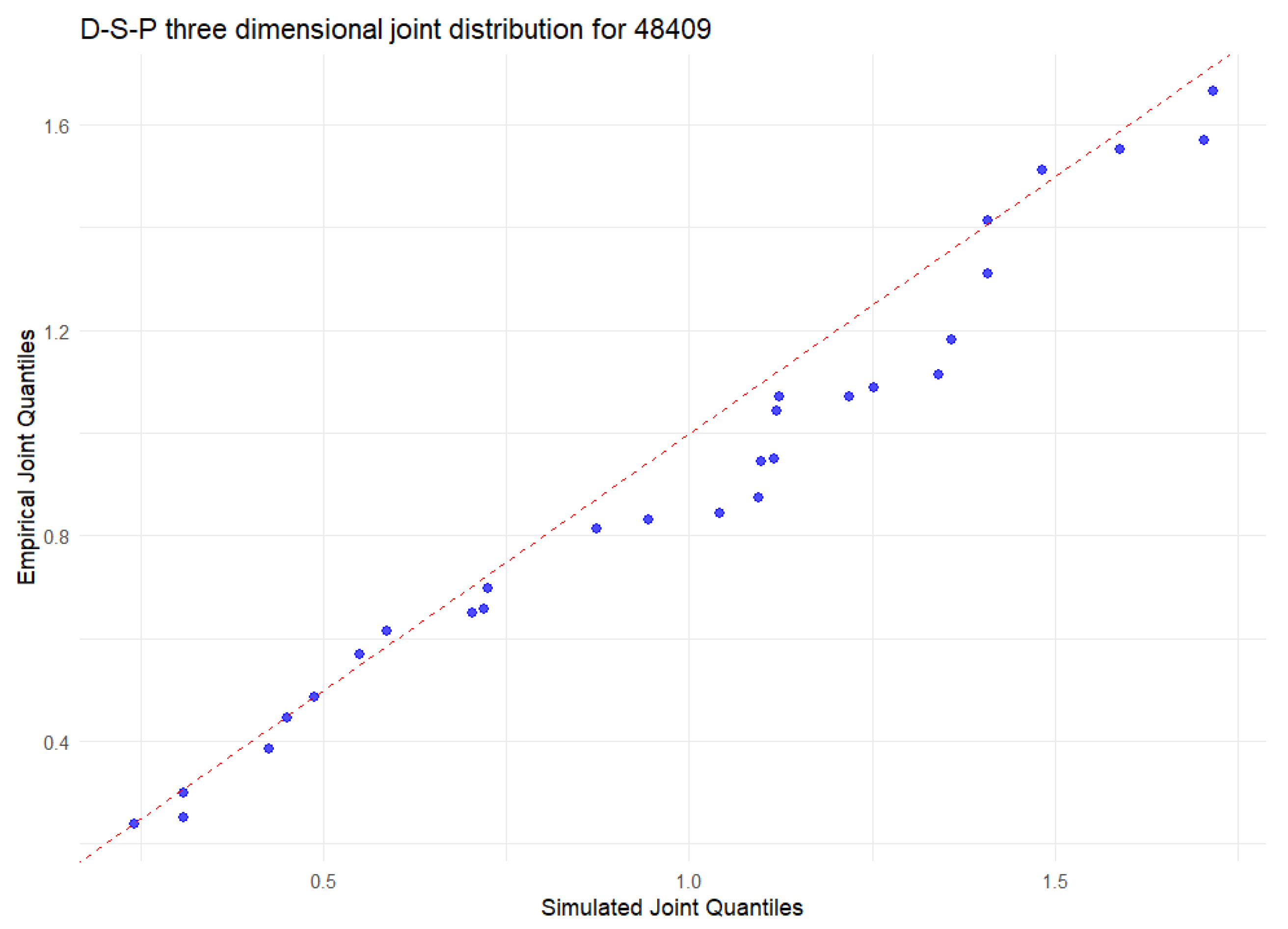
Figure 4 presents the Q-Q plot used to evaluate the goodness-of-fit of the copula model at Station 48409. The proximity of the data points to the 45-degree reference line confirms that the selected copula adequately captures the joint distribution of the three drought variables.

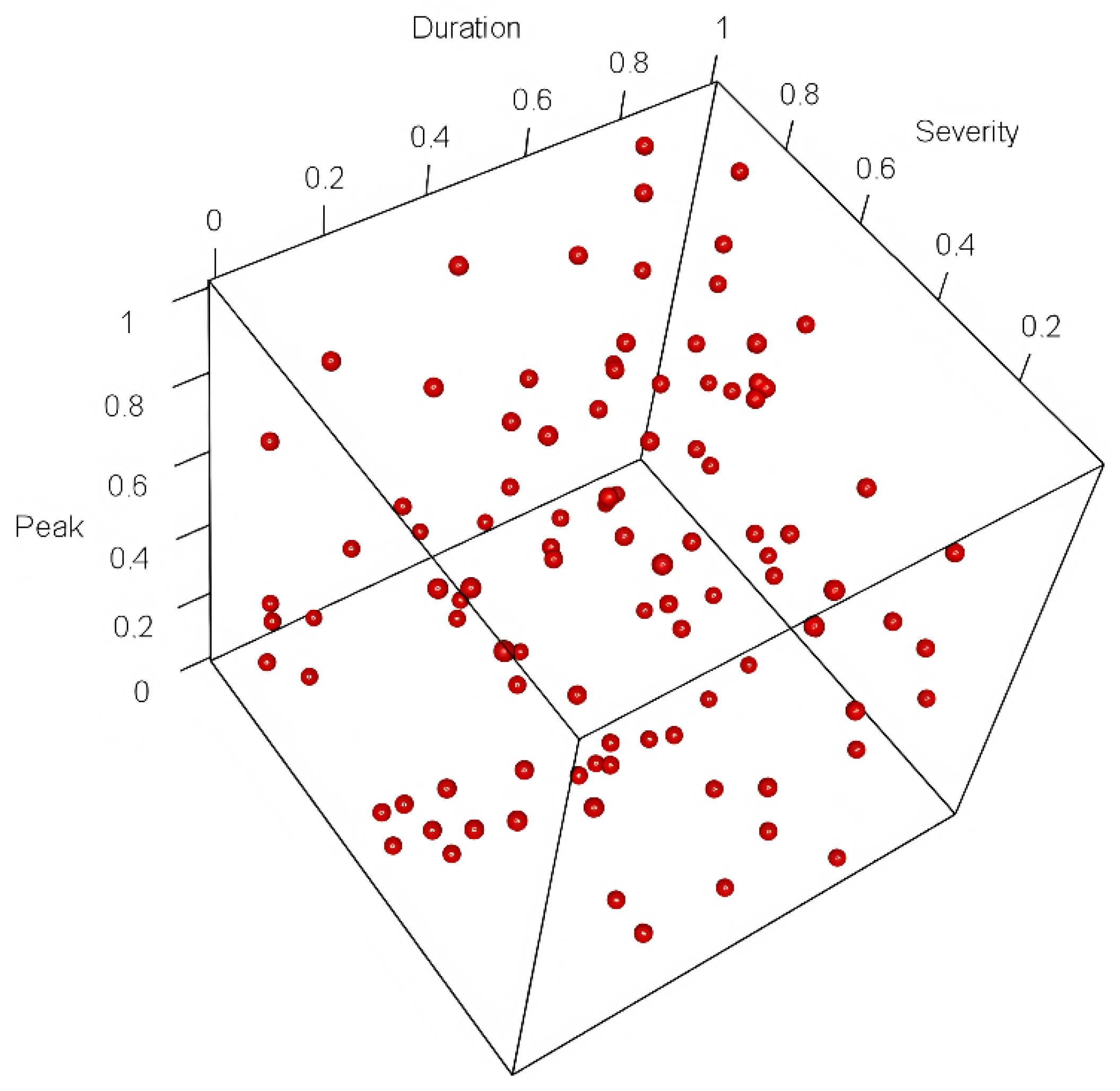
In Figure 5, the clustering of points around the mid-range duration and severity values highlights that moderate droughts occur most frequently, whereas events with simultaneous extremes across all three dimensions are comparatively rare. This visualization provides the empirical distribution of observed drought events in three-dimensional space.

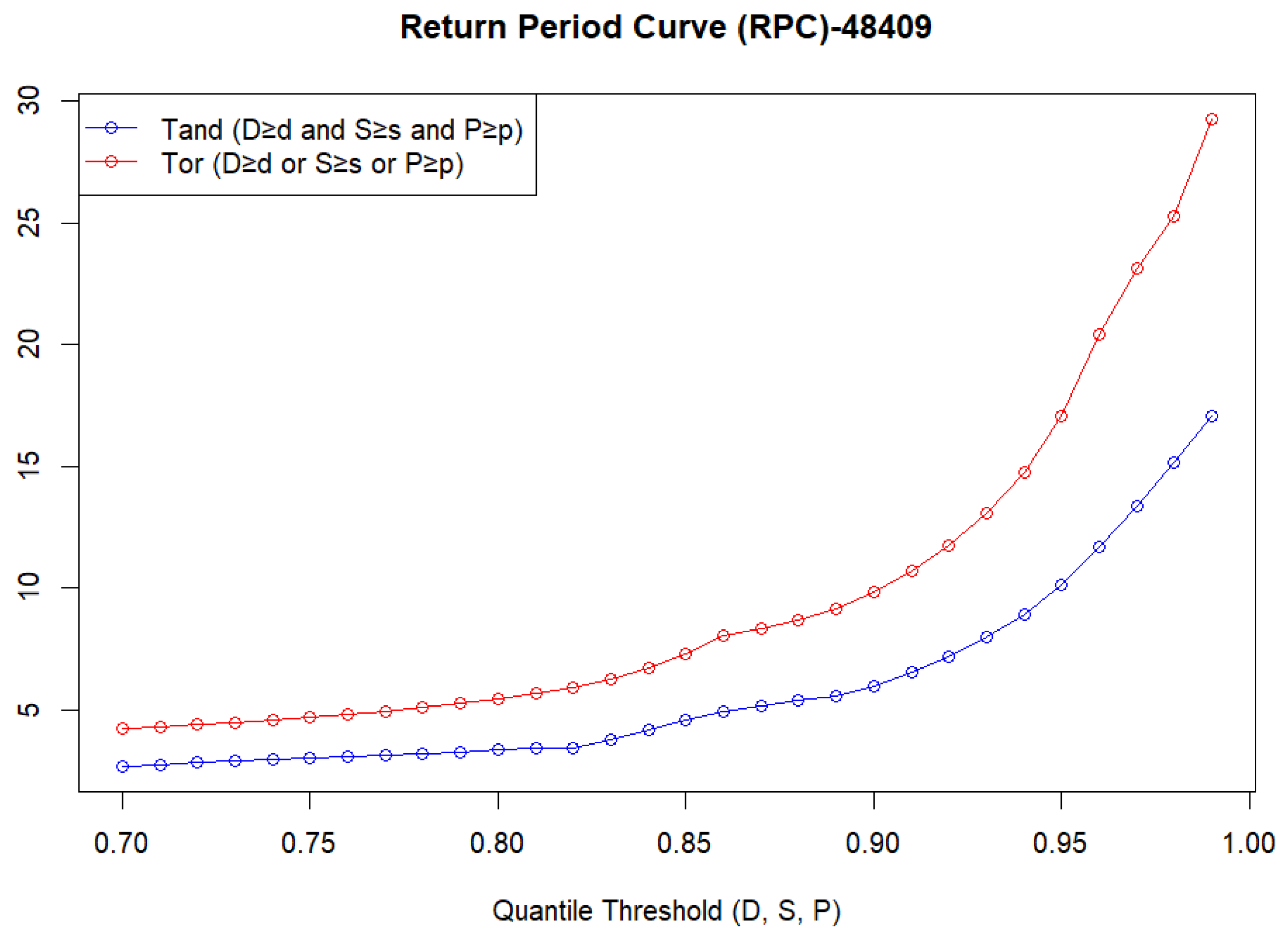
Figure 6 illustrates the joint return period curve at Station 48409, showing that the likelihood of drought events decreases as their severity and duration increase. The increasing trend in return periods for more extreme conditions underlines the rarity of such compound drought events.

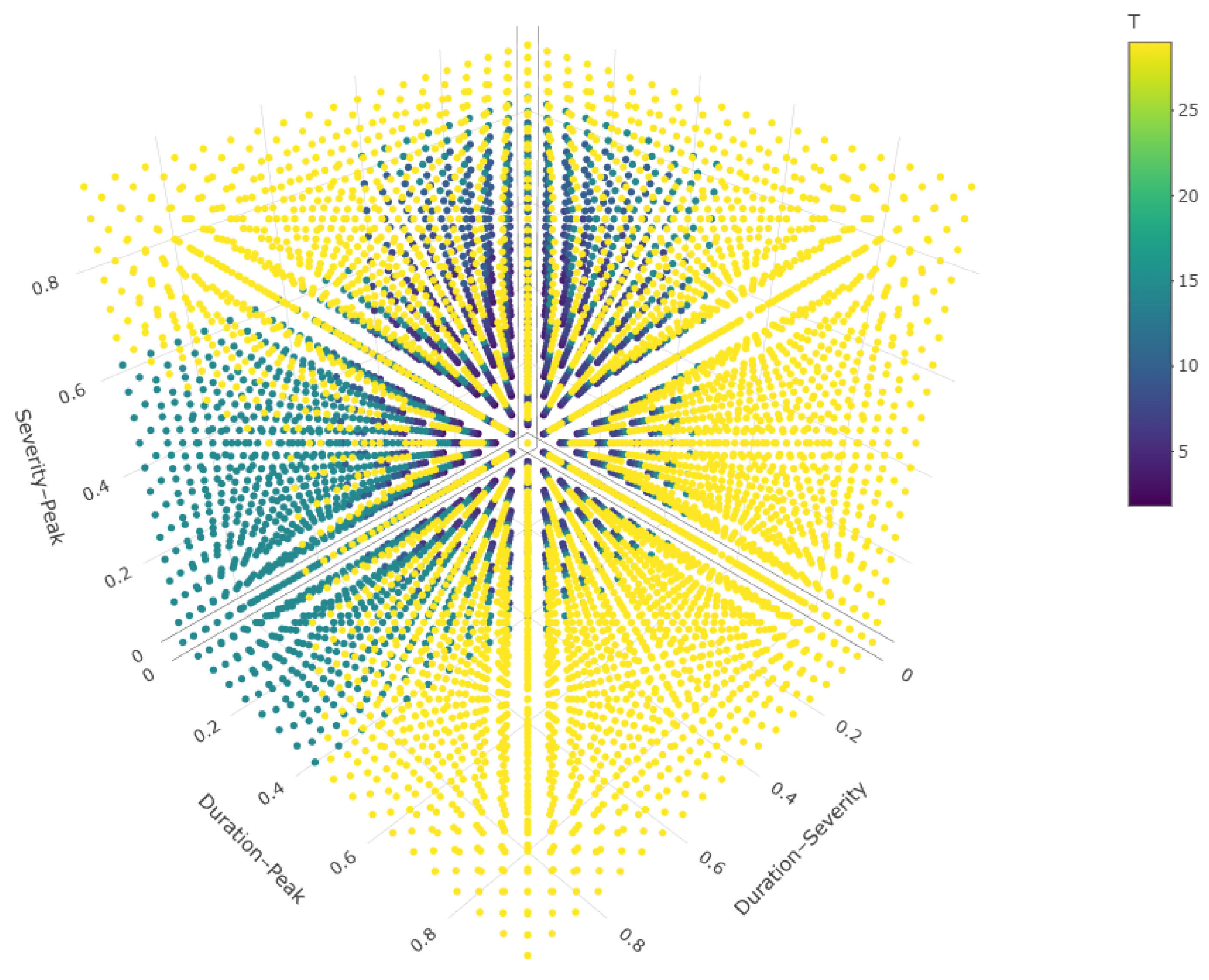
Figure 7 shows the three-dimensional joint return-period surface under the AND condition, where all drought variables exceed their respective thresholds simultaneously. Peaks in this surface correspond to rare, extreme drought events, emphasizing the compounded risk that may be underestimated by analyses considering variables independently.

Overall, these findings demonstrate the strength of the copula-based multivariate approach in providing a nuanced understanding of drought risk. This method captures the interplay among multiple drought characteristics, thereby offering more reliable information for water resource management and drought mitigation planning.

4.4.3. Joint Recurrence Period

The joint recurrence period (JRP) quantifies the expected time interval between occurrences of simultaneous extreme drought conditions defined by drought duration, severity, and peak intensity.

Table 9. Joint return periods (JRPs) and risk values for drought characteristics in the Upper Northeastern region.

Station Code	Quantile Level	Joint Return Periods (JRPs)		Risk Value (R)
		Tand [Years]	Tor [Years]	Tand	Tor
48353	0.80	2.8810	5.5658	0.3471	0.1797
	0.85	3.3960	6.7136	0.2945	0.1490
	0.90	4.1566	8.4040	0.2406	0.1190
	0.95	5.3916	11.1424	0.1855	0.0897
48354	0.80	3.1326	4.7515	0.3192	0.2105
	0.85	3.6780	5.6538	0.2719	0.1769
	0.90	4.4669	6.9563	0.2239	0.1438
	0.95	5.7079	9.0020	0.1752	0.1111
48355	0.80	3.0233	6.5721	0.3308	0.1522
	0.85	3.4229	7.6268	0.2921	0.1311
	0.90	4.6166	10.5554	0.2166	0.0947
	0.95	6.5866	15.6313	0.1518	0.0640
48356	0.80	2.9997	6.7091	0.3334	0.1491
	0.85	3.7528	8.6633	0.2665	0.1154
	0.90	4.9838	11.8672	0.2006	0.0843
	0.95	7.4366	18.2412	0.1345	0.0548
48357	0.80	3.1495	6.5055	0.3175	0.1537
	0.85	3.8841	8.2492	0.2575	0.1212
	0.90	5.2137	11.3790	0.1918	0.0879
	0.95	8.3506	19.4918	0.1198	0.0513
48358	0.80	2.5527	8.6192	0.3917	0.1160
	0.85	3.2179	11.5068	0.3108	0.0869
	0.90	4.2005	15.8153	0.2381	0.0632
	0.95	6.1720	24.4384	0.1620	0.0409

,

Table 10. Joint return periods (JRPs) and risk values for drought characteristics in the Middle Northeastern region.

Station Code	Quantile Level	Joint Return Periods (JRPs)		Risk Value (R)
		Tand [Years]	Tor [Years]	Tand	Tor
48381	0.80	3.3119	5.2993	0.3019	0.1887
	0.85	4.0103	6.5207	0.2494	0.1534
	0.90	5.1050	8.4312	0.1959	0.1186
	0.95	7.0643	11.8454	0.1416	0.0844
48382	0.80	3.5990	4.9192	0.2779	0.2033
	0.85	4.3892	6.0610	0.2278	0.1650
	0.90	5.6415	7.8677	0.1773	0.1271
	0.95	7.9265	11.1612	0.1262	0.0896
48383	0.80	3.2174	5.5602	0.3108	0.1798
	0.85	3.9549	6.9630	0.2529	0.1436
	0.90	5.2281	9.3649	0.1913	0.1068
	0.95	7.4865	13.6575	0.1336	0.0732
48390	0.80	3.1551	6.4082	0.3170	0.1560
	0.85	4.0502	8.5564	0.2469	0.1169
	0.90	4.9721	10.7305	0.2011	0.0932
	0.95	7.7361	16.9993	0.1293	0.0588
48404	0.80	3.4364	6.4373	0.2910	0.1553
	0.85	4.1173	7.8221	0.2429	0.1278
	0.90	5.6271	10.9233	0.1777	0.0915
	0.95	8.9620	17.9942	0.1116	0.0556
48405	0.80	3.1361	6.4544	0.3189	0.1549
	0.85	3.7110	7.7815	0.2695	0.1285
	0.90	4.6553	10.0757	0.2148	0.0992
	0.95	6.9119	15.2618	0.1447	0.0655

and

Table 11. Joint return periods (JRPs) and risk values for drought characteristics in the Lower Northeastern region.

Station Code	Quantile Level	Joint Return Periods (JRPs)		Risk Value (R)
		Tand [Years]	Tor [Years]	Tand	Tor
48407	0.80	3.3769	3.8976	0.2961	0.2566
	0.85	3.9020	4.5219	0.2563	0.2211
	0.90	4.6243	5.3799	0.2162	0.1859
	0.95	5.6803	6.6337	0.1760	0.1507
48408	0.80	2.7240	8.8138	0.3671	0.1135
	0.85	3.3503	11.3905	0.2985	0.0878
	0.90	4.3271	15.4216	0.2311	0.0648
	0.95	6.5627	24.5573	0.1524	0.0407
48409	0.80	2.9816	6.4260	0.3354	0.1556
	0.85	4.0176	8.7604	0.2489	0.1142
	0.90	5.2381	11.7973	0.1909	0.0848
	0.95	8.8180	20.6019	0.1134	0.0485
48416	0.80	3.2285	5.9042	0.3097	0.1694
	0.85	3.7849	7.8740	0.2642	0.1270
	0.90	4.6014	11.5959	0.2173	0.0862
	0.95	5.9646	20.5492	0.1677	0.0487
48432	0.80	3.2611	5.8425	0.3066	0.1712
	0.85	3.9542	8.1843	0.2529	0.1222
	0.90	4.9032	12.5486	0.2039	0.0797
	0.95	6.8597	27.9112	0.1458	0.0358
48433	0.80	3.2197	5.5727	0.3106	0.1794
	0.85	3.8996	6.8251	0.2564	0.1465
	0.90	4.0789	7.1663	0.2452	0.1395
	0.95	8.1029	15.3758	0.1234	0.0650
48434	0.80	2.5774	5.2742	0.3880	0.1896
	0.85	3.1992	6.5215	0.3126	0.1533
	0.90	4.1183	8.5174	0.2428	0.1174
	0.95	5.3400	11.2984	0.1873	0.0885
48435	0.80	2.9644	5.7690	0.3373	0.1733
	0.85	3.6767	7.3187	0.2720	0.1366
	0.90	4.6648	9.5055	0.2144	0.1052
	0.95	6.4340	13.4135	0.1554	0.0746
48437	0.80	2.6985	6.8138	0.3706	0.1468
	0.85	3.4806	9.1829	0.2873	0.1089
	0.90	4.3524	11.8084	0.2298	0.0847
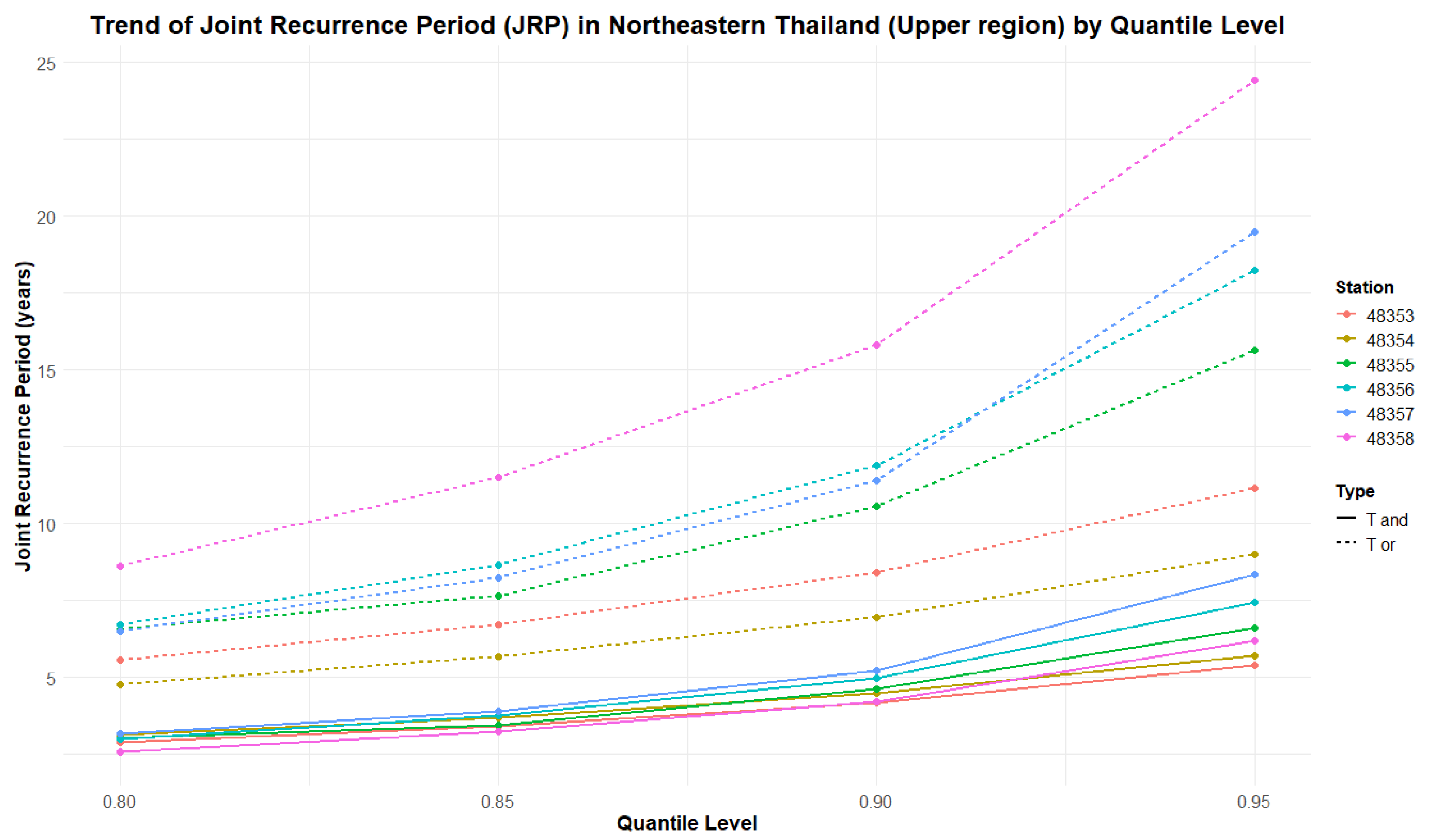
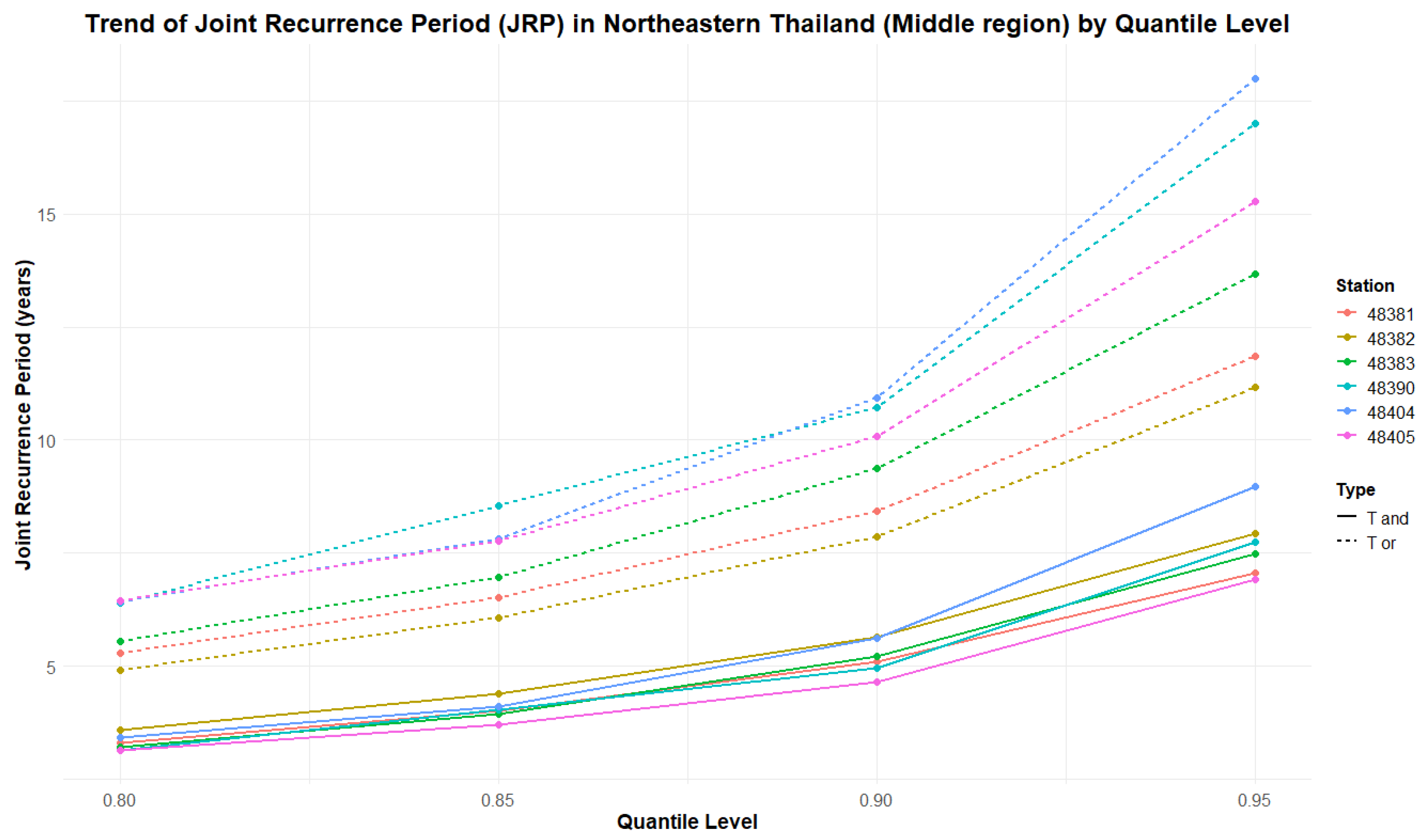
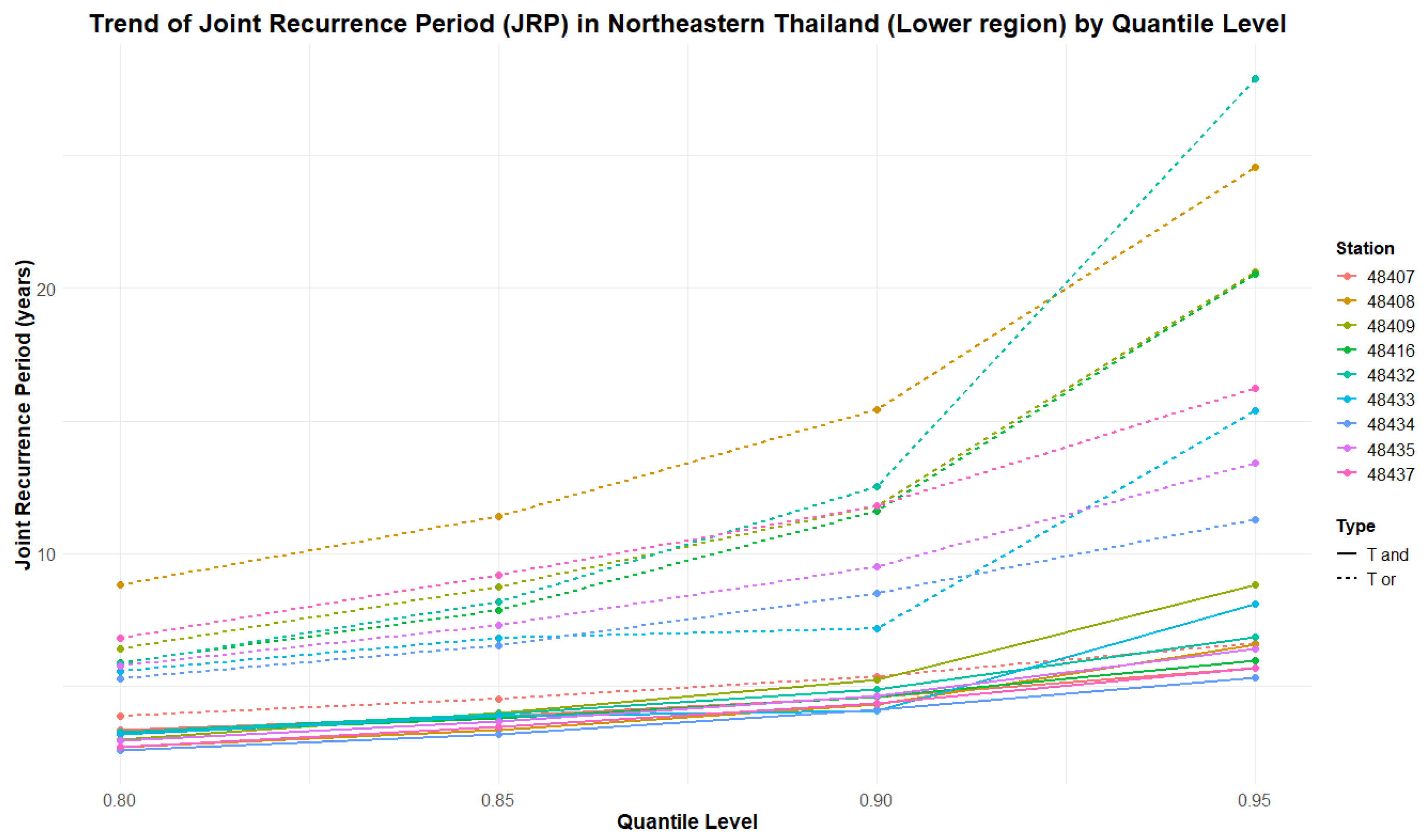
	0.95	5.6951	16.2345	0.1756	0.0616

summarize the estimated JRPs and associated risk values for selected meteorological stations across the Upper, Middle, and Lower regions of Northeastern Thailand. Thresholds were defined using quantiles of historical data, and JRPs were calculated using the fitted trivariate copula models.

5. Analysis of Compound Drought Recurrence

The analysis reveals that at all stations, the “AND” recurrence period ($T_{\mathbf{and}}$), which represents the simultaneous exceedance of thresholds for all drought variables, is consistently shorter than the “OR” recurrence period ($T_{\mathbf{or}}$), where the exceedance of any single variable’s threshold is sufficient. This result confirms that compound extreme droughts occur less frequently than droughts caused by individual variables, which aligns with our intuitive understanding. Joint recurrence periods (JRPs) were calculated to quantify the likelihood of simultaneous exceedance of drought thresholds in duration, severity, and peak intensity. Table 9, Table 10 and Table 11 present JRPs and corresponding risk values for stations grouped into Upper, Middle, and Lower Northeastern Thailand. Overall, JRPs increased substantially for higher quantile thresholds, confirming that extreme compound droughts are infrequent but pose significant risk. Spatial differences in JRPs highlight the importance of region-specific drought preparedness strategies (Figure 8, Figure 9 and Figure 10).

Key Observations from the Analysis

• Quantile Levels: Increasing quantile thresholds lead to longer recurrence periods, indicating that more severe and rarer drought events have longer recurrence intervals. For example, at Station 48409, $T_{\mathrm{and}}$ increases from approximately 2.81 years at the 0.80 quantile to 6.41 years at the 0.95 quantile.
• Spatial Variability: The varying recurrence periods across stations reflect the specific climatic and hydrological conditions of each area. Station 48409 shows higher $T_{\mathrm{or}}$ values, suggesting that single-variable droughts occur less frequently, while Station 48433 exhibits longer $T_{\mathrm{and}}$ values at high quantiles, highlighting the rarity of compound extremes in that specific area.
• Risk Values: The associated risk values (R) decrease as recurrence periods increase, which is consistent with the reduced probability of severe droughts. At Station 48409, $R_{\mathrm{and}}$ declines from 0.3562 at the 0.80 quantile to 0.1559 at the 0.95 quantile.

In summary, the analysis shows a consistent relationship across all stations and regions: The “AND” recurrence period ($T_{\mathrm{and}}$) is always shorter than the “OR” period ($T_{\mathrm{or}}$), confirming that compound drought events are less frequent than single-variable ones. Increasing quantile thresholds indicate greater drought severity but lower frequency. Finally, spatial variability emphasizes the need for localized risk assessments and tailored water management strategies.

6. Regional Comparison: Lower, Middle, and Upper Northeastern Thailand

A regional comparison of Joint Return Periods (JRPs) and risk values reveals clear spatial distinctions among the subregions of Northeastern Thailand:

• The Lower Northeastern region has the shortest $T_{\mathbf{and}}$ values. Stations in this region generally experience shorter compound recurrence periods, which means compound drought events occur more frequently. This pattern may be influenced by regional climate variability, lower elevations, and the hydrological features of the Mun and Chi river basins, which tend to reduce soil moisture availability during the dry season.
• The Middle Northeastern region has the longest $T_{\mathbf{or}}$ values. This region shows comparatively longer single-variable recurrence periods, possibly due to more stable rainfall patterns and its intermediate topography within the Khorat Plateau.
• The Upper Northeastern region has the highest $T_{\mathbf{and}}$ values at higher quantiles. The occurrence of compound droughts is the rarest in this region, as reflected by the longer $T_{\mathrm{and}}$ values at high quantiles. This could be attributed to the mitigating influences of the Mekong River and significant seasonal inflows from upstream catchments in Laos.
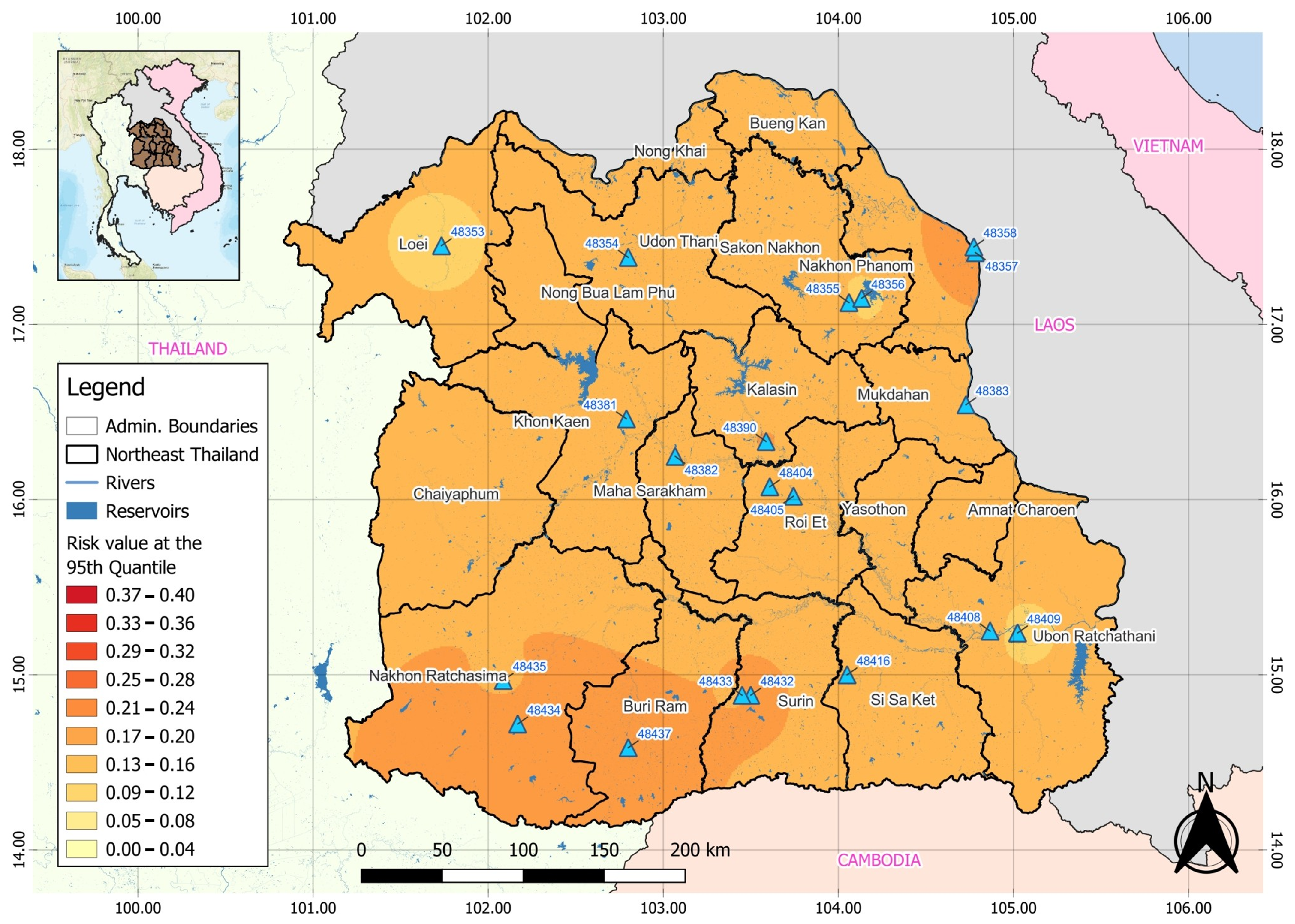
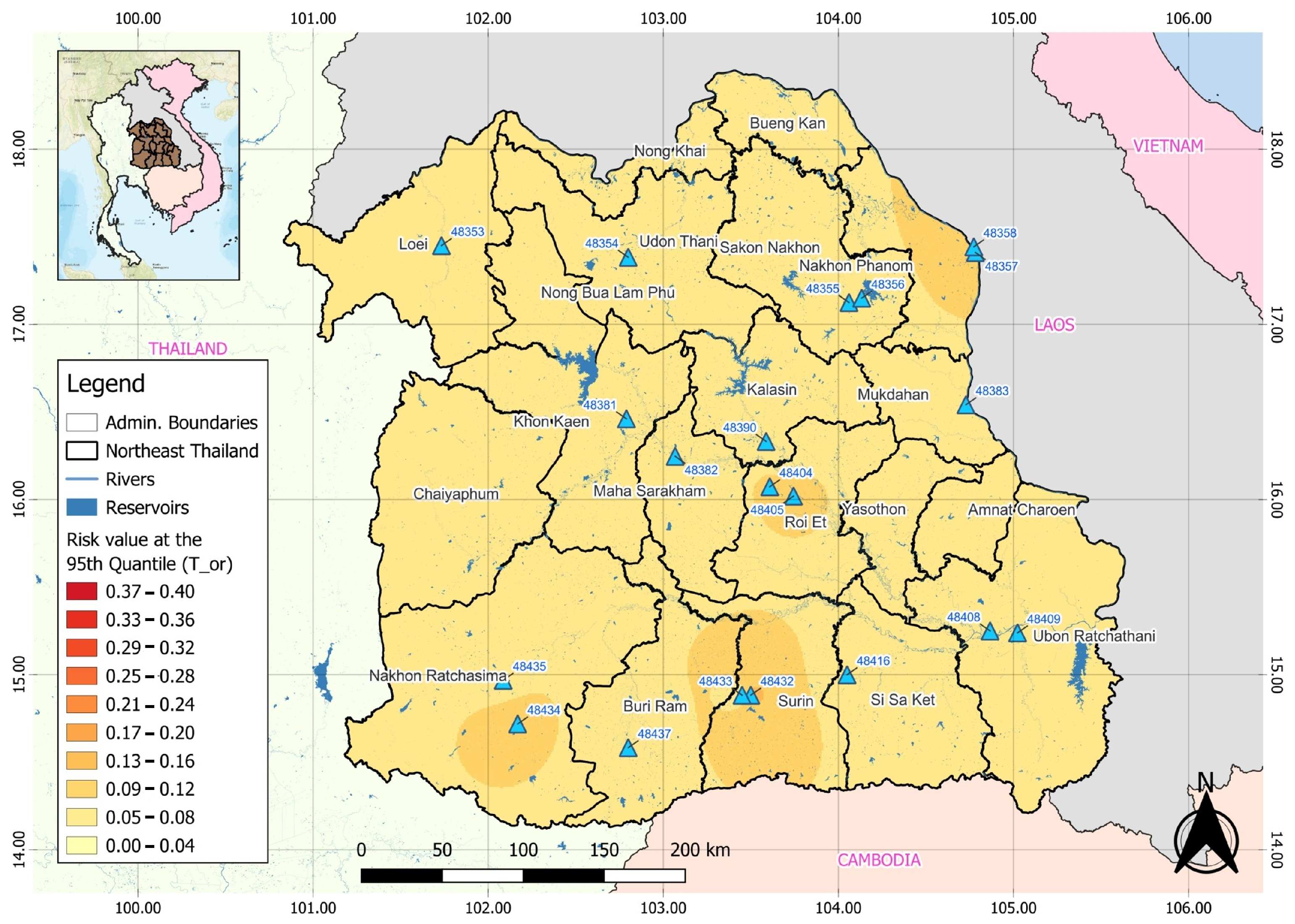
• Risk values follow a south-to-north gradient. The risk values ($R_{\mathrm{and}}$ and $R_{\mathrm{or}}$) progressively decline from the Lower to the Upper regions, which aligns with the observed spatial drought frequencies shown in Figure 11 and Figure 12.

Both compound and single-variable droughts occur more frequently in the Lower Northeastern region, which highlights the urgency of targeted water management and drought mitigation efforts in these southern provinces. Conversely, while droughts in the Upper Northeastern region occur less frequently, their potential severity when they do happen calls for continued vigilance and proactive planning.

These findings highlight the value of trivariate copula models in capturing the interdependencies among drought characteristics. The insights derived from these models offer a robust basis for regional drought risk management and strategic planning, ensuring a more comprehensive understanding of compound drought behavior.

The trivariate copula-based model demonstrates superior performance in capturing the dependence among drought duration, severity, and peak intensity compared to traditional univariate or bivariate methods. As shown in the RPC and return-period surfaces, the AND-type joint return periods grow exponentially with increasing thresholds, indicating the rarity of compound extreme events. The OR-type return periods remain relatively low, suggesting that at least one extreme attribute occurs frequently.

The use of the Clayton, Frank, and Gumbel copulas for the majority of stations reflects a pronounced upper tail dependence, consistent with the expected behavior of severe droughts in semi-arid regions of Thailand. This result supports the suitability of Archimedean copulas for the modeling of such extremes. Additionally, the Sn test and xv-CIC model selection criteria confirm the adequacy of copula fitting across all four stations.

Importantly, this modeling approach enables a more nuanced interpretation of drought risk, as it allows for the quantification of compound recurrence intervals and multivariate hazard interactions.

7. Discussion

This study presents an integrated multivariate approach using trivariate copula modeling to evaluate drought risk by jointly examining duration, severity, and peak intensity. The analysis reveals essential dependencies among these drought attributes, facilitating the estimation of joint recurrence periods (JRPs) for compound extreme drought events. These findings align with recent literature emphasizing the need for multivariate frameworks to capture the complexity of drought behavior beyond univariate assessments [47,48].

Our results show that compound drought events, reflected by AND-type joint return periods, occur less frequently than single-variable extremes described by OR-type return periods. This observation is consistent with previous studies, which note that simultaneous extremes are comparatively rare but often have greater impacts [49]. The identified spatial patterns reveal higher drought occurrence frequencies in the Lower Northeastern region, highlighting the importance of region-specific water management strategies. Conversely, droughts in the Upper Northeastern region are less frequent but potentially more severe, suggesting the necessity of continued vigilance and preparedness [50].

The dependence analysis using Kendall’s tau confirmed consistently strong positive correlations between drought duration and severity across most stations ($\tau >0.80$), whereas the correlations involving peak intensity (D–P and S–P) varied spatially, with some stations exhibiting negative or weak associations. This heterogeneity indicates that peak drought intensity does not always coincide with prolonged or severe events, emphasizing the need for a trivariate copula framework to adequately capture these complex interrelationships, as supported by multivariate hydrological studies [35,51,52].

The dominance of the Gumbel copula in fitting most stations indicates strong upper-tail dependence among drought characteristics, which is expected in semi-arid climates such as this study area [53]. This supports the applicability of Archimedean copulas in modeling compound drought risk and demonstrates their usefulness in early warning and drought preparedness systems [54].

Nevertheless, certain limitations should be acknowledged. The spatial coverage is limited due to the relatively small number of meteorological stations, which may restrict the generalizability of our findings. Additionally, focusing solely on the 3-month SPEI index constrains the scope to short- and medium-term droughts, potentially neglecting longer-duration hydrological or agricultural droughts [11]. The assumption of stationarity in the modeling framework does not incorporate potential changes driven by climate variability or change, which could influence the accuracy of long-term drought risk projections [55]. Furthermore, the choice of copula families affects the results; symmetric copulas like the Frank copula may underestimate tail dependence, thereby affecting extreme event characterization [56].

In our study area, multiple SPEI timescales (3, 6, and 12 months) were potentially valuable. However, we focused on the 3-month SPEI (SPEI3) for several reasons. First, previous Thai case studies [28] showed that SPEI3 captures short-term droughts affecting agriculture during the growing season and produces moderate drought durations comparable to or longer than those of the SPEI6 and SPEI12. Second, analyses in Northern Thailand’s Upper Nan River Basin [29] indicated that SPEI3 responds more promptly to changes in drought duration and severity, particularly in the dry season, which is critical for cropping. Third, including longer timescales would increase model complexity and data requirements (e.g., longer stationary periods and tail estimation) without significant benefits in assessing short-term drought risk (duration, severity, and peak intensity). Therefore, SPEI3 was adopted exclusively, while future research should consider SPEI6 and SPEI12 to evaluate long-term or hydrological droughts.

However, reliance on SPEI and meteorological indicators alone entails further limitations, as such indices may not adequately represent the tangible impacts of drought on agricultural production and hydrological processes. Previous research has demonstrated the value of linking drought indices with crop yield data to capture agricultural sensitivity [57,58] and with streamflow records to improve hydrological drought assessments [10,11,59]. To strengthen the robustness of the present framework, future studies should undertake validation using independent datasets such as crop yield records, soil moisture data, and streamflow observations. The integration of agricultural and hydrological data would not only provide empirical evidence of the socio-economic and water resource consequences of drought but also enhance the policy relevance and practical applicability of SPEI-based multivariate assessments.

Future research should expand both spatial and temporal data coverage by incorporating additional meteorological stations, remote sensing products, and reanalysis datasets to enhance representativeness and reliability. Incorporating multiple drought indicators, such as the Palmer Drought Severity Index or soil moisture, could yield a more comprehensive understanding of drought dynamics [50]. Methodological advancements that consider non-stationary and asymmetric copula models would also enhance the realism of drought risk estimates under changing climate conditions [60]. Finally, integrating hydrometeorological risk assessments with socio-economic and agricultural impact models can support the development of practical, context-specific drought management strategies [61].

8. Conclusions

In this study, we developed a comprehensive framework for assessing drought risk using trivariate copula modeling that integrates duration, severity, and peak intensity. The analysis utilized the 3-month Standardized Precipitation–Evapotranspiration Index (SPEI-3) values from four meteorological stations located in Surin and Si Sa Ket provinces. Marginal distributions of the individual drought variables were determined, and their dependence structures were modeled using various copula families, with the Frank copula providing the best fit based on goodness-of-fit tests and cross-validation metrics.

This research has direct practical implications for water resource management, agricultural planning, and drought risk reduction. The integrated drought index can support the design of adaptive irrigation strategies, guide agricultural insurance schemes, and enhance regional drought early warning systems. Moreover, the findings provide policy-relevant insights for the development of climate resilience strategies in Northeastern Thailand, where agriculture is highly vulnerable to climate variability.

The proposed approach allowed us to estimate joint return periods of extreme droughts, providing a more nuanced perspective on compound drought risks. For example, drought events exceeding the 90th percentile in all three attributes correspond to a joint recurrence interval exceeding 59 years, highlighting the importance of multivariate consideration in drought risk assessments.

Overall, the findings highlight the benefits of employing trivariate copula models for more precise drought risk quantification. This methodology provides valuable information for policymakers and stakeholders, particularly in agricultural regions vulnerable to climate variability, and can be adapted for use in other settings as a robust tool for integrated drought risk management.

Finally, it is essential to note that the current analysis has not been directly validated against hydrological records or agricultural yield data. While indirect comparisons with regional drought reports provide supportive evidence, comprehensive validation remains an essential step for strengthening the operational utility of this modeling framework. Future studies integrating observed crop yields, reservoir inflows, and soil moisture datasets will be crucial for enhancing the reliability and policy relevance of drought risk assessments. In addition, this study relied exclusively on the SPEI, which, although it integrates precipitation and evapotranspiration, does not fully represent the processes of hydrological or agricultural drought. Future research should incorporate complementary indices such as the SPI, SDI, or PDSI to broaden the multidimensional perspective. Moreover, although SPEI3 was emphasized here due to its direct relevance to seasonal cropping cycles, extending the analysis to longer accumulation periods (SPEI-6 and SPEI-12) would provide further insights into long-term hydrological drought dynamics.