Evaporation of a Sessile Water Drop Subjected to Vertical Vibration: The Drying Kinetics near the Resonance Frequency
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Preparation of the Experiments
2.3. Measurement Protocol
2.4. Data Analysis
3. Results and Discussion
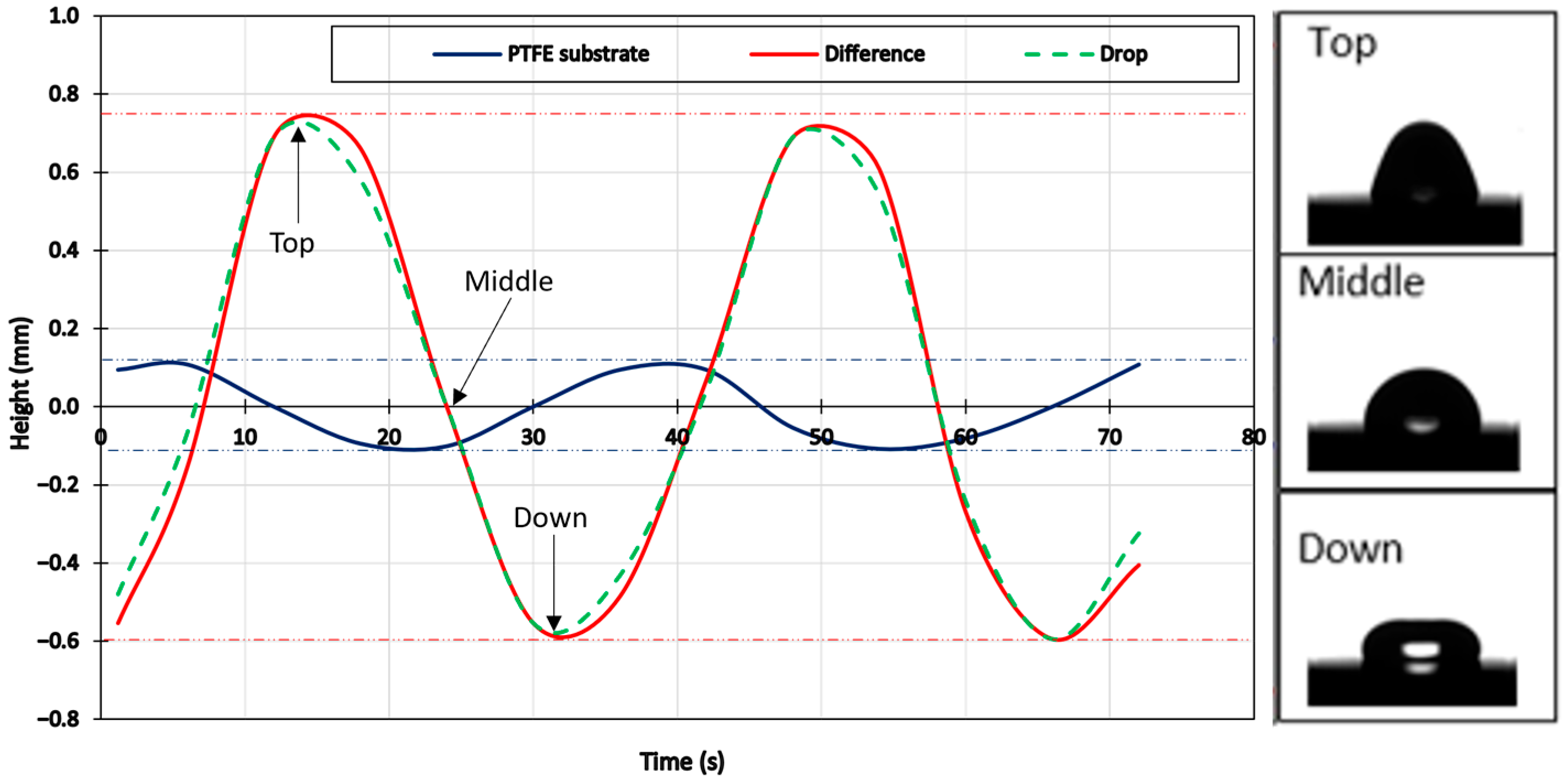
3.1. Study of Vibration
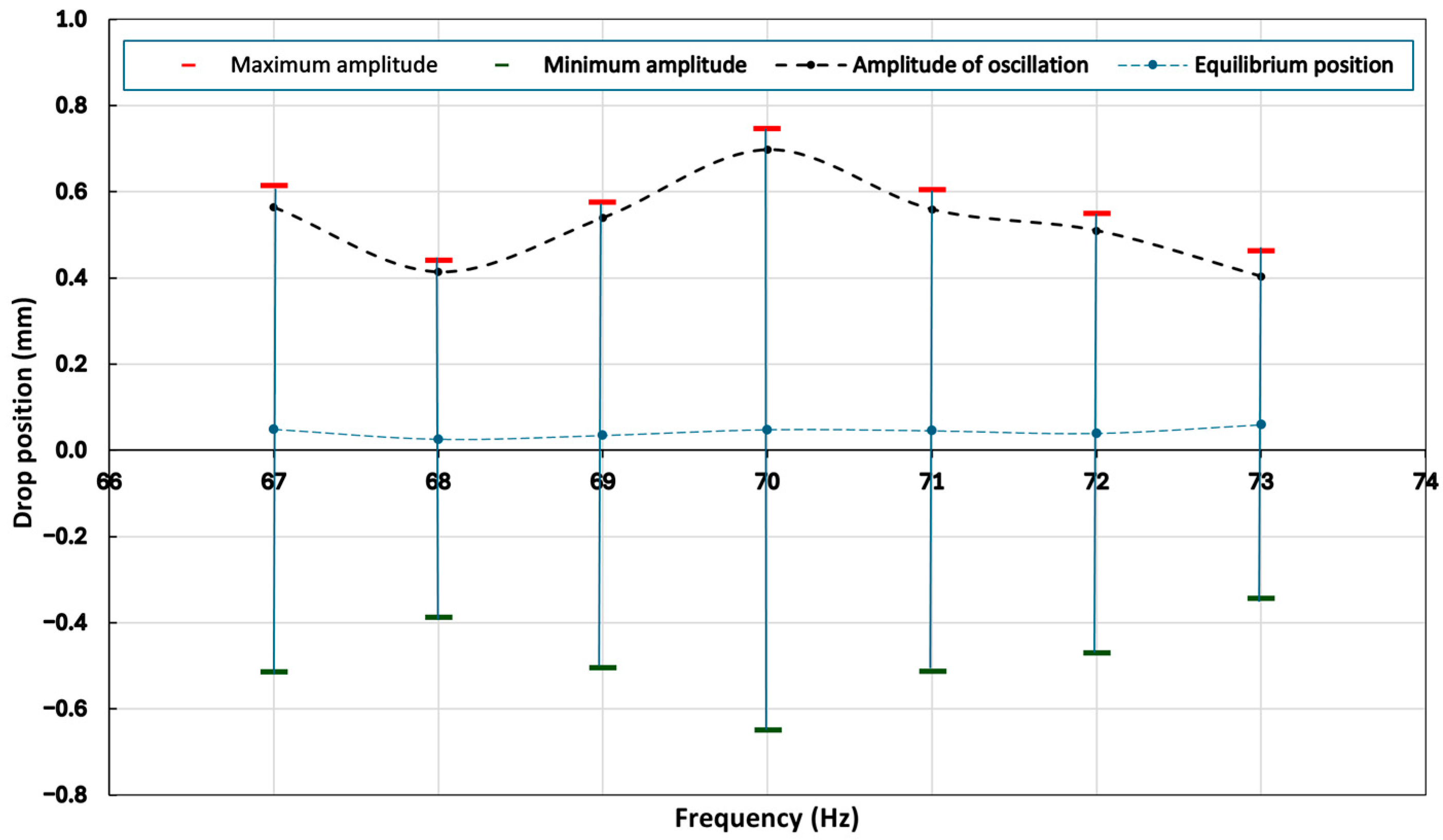
3.2. Determination of the Resonance Frequency
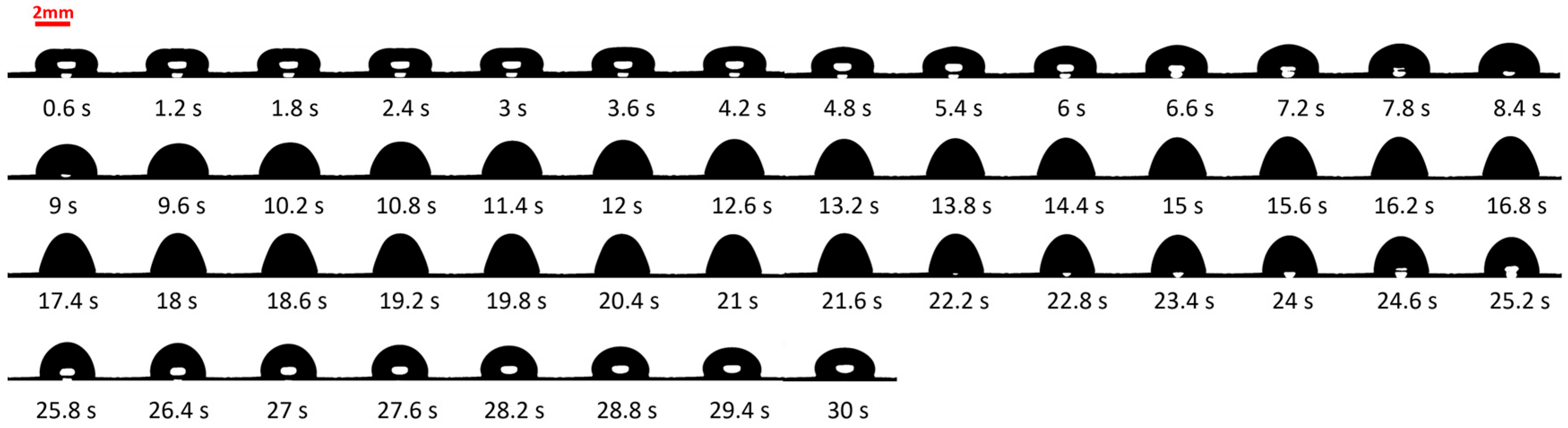
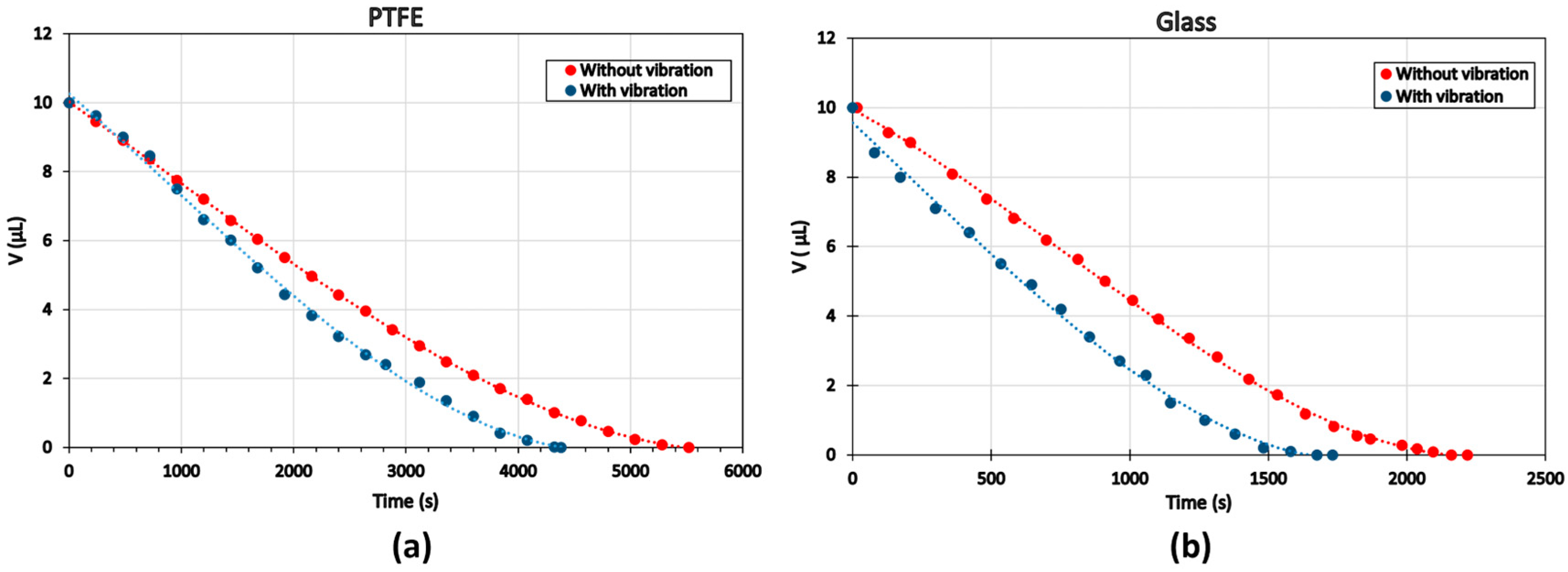
3.3. Effect of Vibration
- The frequency was chosen to obtain resonance with the initial 10 μL drop;
- The potential vibration amplitude necessarily decreases with drop size.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | Abbreviation |
| A | Amplitude (mm) |
| D | Diameter (mm) |
| E | Thickness (mm) |
| F | Frequency (Hz) |
| Fr | Resonance frequency (Hz) |
| HR | Relative humidity (%) |
| K | Thermal conductivity [W/(m.K)] |
| M | Mass (mg) |
| mev | Evaporation rate (mg/s) |
| T | Temperature (°C) |
| T | Time (s) |
| V | Drop volume (µL) |
| Θ | Contact angle (°) |
| σ | Water conductivity (ms/cm) |
| Ρ | Water resistivity (MΩ.cm) |
| Subscripts | |
| TOC | Total Organic Carbon (PPB) |
References
- Popov, Y.O. Evaporative Deposition Patterns: Spatial Dimensions of the Deposit. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 71, 036313. [Google Scholar] [CrossRef]
- Calvert, P. Inkjet Printing for Materials and Devices. Chem. Mater. 2001, 13, 3299–3305. [Google Scholar] [CrossRef]
- Jeanne, B. Study of Very High Injection Pressure Effect on the Performances of a Gasoline Direct Injection Engine Using Optical Diagnoses. (236P). Ph.D. Dissertation, University of Rouen, Rouen, France, 2004. [Google Scholar]
- Maatar, A.; Chikh, S.; Ait Saada, M.; Tadrist, L. Transient Effects on Sessile Droplet Evaporation of Volatile Liquids. Int. J. Heat Mass Transf. 2015, 86, 212–220. [Google Scholar] [CrossRef]
- Wakata, Y.; Chao, X.; Sun, C.; Diddens, C. Evaporation of acoustically levitated bicomponent droplets: Mass and heat transfer characteristics. J. Fluid Mech. 2024, 984, A17. [Google Scholar] [CrossRef]
- Picknett, R.G.; Bexon, R. The Evaporation of Sessile or Pendant Drops in Still Air. J. Colloid Interface Sci. 1977, 61, 336–350. [Google Scholar] [CrossRef]
- Yu, Y.-S.; Wang, Z.; Zhao, Y.-P. Experimental and Theoretical Investigations of Evaporation of Sessile Water Droplet on Hydrophobic Surfaces. J. Colloid Interface Sci. 2012, 365, 254–259. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.A.H.; Nguyen, A.V.; Hampton, M.A.; Xu, Z.P.; Huang, L.; Rudolph, V. Theoretical and Experimental Analysis of Droplet Evaporation on Solid Surfaces. Chem. Eng. Sci. 2012, 69, 522–529. [Google Scholar] [CrossRef]
- Mollaret, R.; Sefiane, K.; Christy, J.R.E.; Veyret, D. Experimental and Numerical Investigation of the Evaporation into Air of a Drop on a Heated Surface. Chem. Eng. Res. Des. 2004, 82, 471–480. [Google Scholar] [CrossRef]
- Xu, W.; Leeladhar, R.; Kang, Y.T.; Choi, C.-H. Evaporation Kinetics of Sessile Water Droplet on Micro Pillared Super Hydrophobic Surfaces. Langmuir 2013, 29, 6032–6041. [Google Scholar] [CrossRef]
- Shanahan, M.E.R. Simple Theory of Stick-Slip Wetting Hysteresis. Langmuir 1995, 11, 1041–1043. [Google Scholar] [CrossRef]
- Ge, W.-K.; Lu, G.; Xu, X.; Wang, X.-D. Droplet spreading and permeating on the hybrid-wettability porous substrates: A lattice Boltzmann method study. Open Phys. 2016, 14, 483–491. [Google Scholar] [CrossRef]
- Frank, X.; Perré, P.; Li, H.Z. Lattice Boltzmann investigation of droplet inertial spreading on various porous surfaces. Phys. Rev. E 2015, 91, 052405. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Guo, B.; Yang, Z. An experimental investigation on the evaporation and condensation heat transfer of air-cooled multi-port flat heat pipes. Int. J. Heat Mass Transf. 2022, 187, 122554. [Google Scholar] [CrossRef]
- Khilifi, D.; Foudhil, W.; Fahem, K.; Harmand, S.; Ben Jabrallah, S. Study of the Phenomenon of the Interaction between Sessile Drops during Evaporation. Therm. Sci. 2019, 23, 1105–1114. [Google Scholar] [CrossRef]
- Foudhil, W.; Khilifi, D.; Dutil, Y.; Harmand, S.; Jabrallah, S.B. Experimental and Three-Dimensional Numerical Study of the Single/Multiple Sessile Droplets Evaporation. Heat Transf. Eng. 2023, 44, 1926–1945. [Google Scholar] [CrossRef]
- Dou, S.; Hao, L. Numerical study of droplet evaporation on heated flat and micro-pillared hydrophobic surfaces by using the lattice Boltzmann method. Chem. Eng. Sci. 2021, 229, 116032. [Google Scholar] [CrossRef]
- Colin, J.; Chen, W.; Casalinho, J.; Amara, M.E.A.B.; Stambouli, M.; Perré, P. Drying Intensification by Vibration: Fundamental Study of Liquid Water inside a Pore. In Proceedings of the 21th International Drying Symposium, Valencia, Spain, 11–14 September 2018. [Google Scholar]
- Vorobev, A.; Prokopev, S.; Lyubimova, T. Liquid/liquid displacement in a vibrating capillary. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2023, 381, 20220090. [Google Scholar] [CrossRef]
- Kim, H.-Y. Drop Fall-off from the Vibrating Ceiling. Phys. Fluids 2004, 16, 474–477. [Google Scholar] [CrossRef]
- Ercolin, E.M.; Fricke, J.; Lehmann, D.; Schaldach, G.; Nestorović, T.; Thommes, M. Elucidation of Droplet Formation Mechanisms by Vibrating Mesh Atomizers. Chem. Eng. Technol. 2025, 48, e70063. [Google Scholar] [CrossRef]
- DePaoli, D.W.; Feng, J.Q.; Basaran, O.A.; Scott, T.C. Hysteresis in Forced Oscillations of Pendant Drops. Phys. Fluids 1995, 7, 1181–1183. [Google Scholar] [CrossRef]
- Wilkes, E.D.; Basaran, O.A. Hysteretic Response of Supported Drops during Forced Oscillations. J. Fluid Mech. 1999, 393, 333–356. [Google Scholar] [CrossRef]
- Adachi, K.; Takaki, R. Vibration of a Flattened Drop. I. Observation. J. Phys. Soc. Jpn. 1984, 53, 4184–4191. [Google Scholar] [CrossRef]
- Okada, M.; Okada, M. Observation of the Shape of a Water Drop on an Oscillating Teflon Plate. Exp. Fluids 2006, 41, 789–802. [Google Scholar] [CrossRef]
- Ilyukhina, M.A.; Makov, Y.N. Analysis of Shape Perturbations of a Drop on a Vibrating Substrate for Different Wetting Angles. Acoust. Phys. 2009, 55, 722–728. [Google Scholar] [CrossRef]
- Dong, L.; Chaudhury, A.; Chaudhury, M.K. Lateral Vibration of a Water Drop and Its Motion on a Vibrating Surface. Eur. Phys. J. E 2006, 21, 231–242. [Google Scholar] [CrossRef]
- Sanyal, A.; Basu, S. Evolution of Internal Flows in Mechanically Oscillating Sessile Droplets Undergoing Evaporation. Chem. Eng. Sci. 2017, 163, 179–188. [Google Scholar] [CrossRef]
- Rahimzadeh, A.; Eslamian, M. Experimental Study on the Evaporation of Sessile Droplets Excited by Vertical and Horizontal Ultrasonic Vibration. Int. J. Heat Mass Transf. 2017, 114, 786–795. [Google Scholar] [CrossRef]
- Daniel, S.; Chaudhury, M.K.; De Gennes, P.-G. Vibration-Actuated Drop Motion on Surfaces for Batch Microfluidic Processes. Langmuir 2005, 21, 4240–4248. [Google Scholar] [CrossRef] [PubMed]
- Barwari, B.; Rohde, M.; Wladarz, O.; Burgmann, S.; Janoske, U. Motion of adhering droplets induced by overlapping of gravitational and periodical acceleration. Int. J. Multiph. Flow 2021, 135, 103537. [Google Scholar] [CrossRef]
- Hu, H.; Larson, R.G. Evaporation of a sessile droplet on a substrate. J. Phys. Chem. B 2002, 106, 1334–1344. [Google Scholar] [CrossRef]
- Barash, L.Y.; Bigioni, T.P.; Vinokur, V.M.; Shchur, L.N. Evaporation and fluid dynamics of a sessile drop of capillary size. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2009, 79, 046301. [Google Scholar] [CrossRef]
- Rahimzadeh, A.; Eslamian, M. Evaporation of dimethylformamide sessile drops on stationary and vibrating substrates. In Proceedings of the 13th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics (HEFAT 2017), HEFAT, Portorož, Slovenia, 17–19 July 2017; pp. 387–390. [Google Scholar]
- Hu, H.; Larson, R.G. Analysis of the microfluid flow in an evaporating sessile droplet. Langmuir 2005, 21, 3963–3971. [Google Scholar] [CrossRef]
- Yamada, T.; Sugimoto, T.; Higashiyama, Y.; Takeishi, M.; Aoki, T. Resonance phenomena of a single water droplet located on a hydrophobic sheet under AC electric field. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference, 36th IAS Annual Meeting (Cat. No.01CH37248), Chicago, IL, USA, 30 September–4 October 2001; Volume 3, pp. 1530–1535. [Google Scholar] [CrossRef]
- Chang, C.-T.; Bostwick, J.; Steen, P.H.; Daniel, S. Substrate constraint modifies the Rayleigh spectrum of vibrating sessile drops. Phys. Rev. E 2013, 88, 023015. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.S.; Rabbi, R.Z.; Kiyama, A.; Truscott, T. Acoustics of Drop Impact on Hydrophobic Surfaces and Liquid Pools. Berkeley Program Law Econ. 2022, 151 (Suppl. S4), A62. [Google Scholar] [CrossRef]
- Šikalo, Š.; Wilhelm, H.-D.; Roisman, I.V.; Jakirlić, S.; Tropea, C. Dynamic contact angle of spreading droplets: Experiments and simulation. Phys. Fluids 2005, 17, 062103. [Google Scholar] [CrossRef]
- Pittoni, P.G.; Lin, C.-H.; Yu, T.-S.; Lin, S.-Y. On the Uniqueness of the Receding Contact Angle: Effects of Substrate Roughness and Humidity on Evaporation of Water Drops. Langmuir 2014, 30, 9346–9354. [Google Scholar] [CrossRef]
- Zhao, L.; Cheng, J. Analyzing the Molecular Kinetics of Water Spreading on Hydrophobic Surfaces via Molecular Dynamics Simulation. Sci. Rep. 2017, 7, 10880. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J.; Zhang, D.; Jian, M.; Liu, H.; Zhang, X. Droplet Sliding: The Numerical Observation of Multiple Contact Angle Hysteresis. Langmuir 2019, 35, 9970–9978. [Google Scholar] [CrossRef]
- Dorrer, C.; Rühe, J. Advancing and receding motion of droplets on ultra-hydrophobic post surfaces. Langmuir 2006, 22, 7652–7657. [Google Scholar] [CrossRef]
- Sterlyagov, A.N.; Hизoвцев, М.И. The experimental study of the evaporation of water and nanofluid droplets on the surfaces of materials with different thermal conductivities. Koллoидный Жypнaл 2023, 85, 85–92. [Google Scholar] [CrossRef]
- Borodulin, V.; Letushko, V.; Nizovtsev, M.; Sterlyagov, A. Experimental study of water evaporation of sessile droplets on a solid substrate with different thermal conductivities. MATEC Web Conf. 2017, 115, 08005. [Google Scholar] [CrossRef]
- Schofield, F.G.H.; Pritchard, D.E.; Wilson, S.; Sefiane, K. The Lifetimes of Evaporating Sessile Droplets of Water Can Be Strongly Influenced by Thermal Effects. Fluids 2021, 6, 141. [Google Scholar] [CrossRef]
- Ait Saada, M.; Chikh, S.; Tadrist, L. Effect of substrate thickness and thermal conductivity on an evaporating sessile drop. J. Phys. Conf. Ser. 2012, 395, 012140. [Google Scholar] [CrossRef]





| Substrate | ||
|---|---|---|
| Glass |  |  |
| PTFE |  |  |
| Substrate | Advancing Angle () | Receding Angle () | Hysteresis (CAH) |
|---|---|---|---|
| Glass | 51 | 25 | 26 |
| PTFE | 112 | 91 | 21 |
| Substrate | With Vibration | Without Vibration | Difference |
|---|---|---|---|
| PTFE | 4380 s | 5520 s | +20.6% |
| Glass | 1676 s | 2191 s | +23.5% |
| Time Interval (s) | Slope (Without Vibration) (µL/s) | Slope (With Vibration) (µL/s) |
|---|---|---|
| 0–500 | −0.0059 | −0.0071 |
| 500–1000 | −0.0003101 | −0.0004427 |
| Time Interval (s) | Slope (Without Vibration) (µL/s) | Slope (With Vibration) (µL/s) |
|---|---|---|
| 0–500 | −0.00551 | −0.00814 |
| 500–1000 | −0.00563 | −0.00736 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakoubi, W.; Foudhil, W.; Casalinho, J.; Jabrallah, S.B.; Perré, P. Evaporation of a Sessile Water Drop Subjected to Vertical Vibration: The Drying Kinetics near the Resonance Frequency. Water 2025, 17, 2808. https://doi.org/10.3390/w17192808
Yakoubi W, Foudhil W, Casalinho J, Jabrallah SB, Perré P. Evaporation of a Sessile Water Drop Subjected to Vertical Vibration: The Drying Kinetics near the Resonance Frequency. Water. 2025; 17(19):2808. https://doi.org/10.3390/w17192808
Chicago/Turabian StyleYakoubi, Wejden, Walid Foudhil, Joel Casalinho, Sadok Ben Jabrallah, and Patrick Perré. 2025. "Evaporation of a Sessile Water Drop Subjected to Vertical Vibration: The Drying Kinetics near the Resonance Frequency" Water 17, no. 19: 2808. https://doi.org/10.3390/w17192808
APA StyleYakoubi, W., Foudhil, W., Casalinho, J., Jabrallah, S. B., & Perré, P. (2025). Evaporation of a Sessile Water Drop Subjected to Vertical Vibration: The Drying Kinetics near the Resonance Frequency. Water, 17(19), 2808. https://doi.org/10.3390/w17192808








